Line Loss Calculation with Meteorological Dynamic Clustering and Photovoltaic Output Reconstruction

Abstract

To solve the problem that traditional line loss calculation methods have errors exceeding 8–12% under complex weather conditions (e.g., typhoons) due to insufficient characterization of meteorological-photovoltaic (PV) coupling effects, this paper proposes a collaborative calculation method integrating dynamic meteorological clustering (based on the entropy weight-sliding window) and PV output reconstruction (via improved limited dynamic time warping, LDTW). First, a multidimensional meteorological weight matrix is constructed to quantify spatiotemporal heterogeneity; then, an improved spectral clustering algorithm is used for weather partitioning; finally, reconstructed PV output curves are incorporated into a voltage-corrected forward-backward sweep method for line loss calculation. Simulation results based on 302-day measured data and the IEEE 33-node system show that the proposed method reduces line loss calculation error to less than 0.15%, which is 6–8 times more accurate than traditional methods, meeting engineering requirements.

1. Introduction

With the in-depth advancement of “dual carbon” goals, the high proportion of photovoltaic (PV) grid integration poses new challenges for the calculation of distribution network line losses [1]. PV power generation has significant intermittent and volatile characteristics, and its output is dynamically affected by meteorological factors, leading to a significant decrease in the calculation accuracy of traditional line loss calculation methods under complex weather conditions [2,3]. Research indicates that under complex weather conditions such as rainfall and high humidity, the error margin in traditional line loss calculations for ultra-high voltage AC transmission lines can reach 8–15%, whereas under clear and dry conditions, it is only 2–3%. For instance, using an UHV line in the Fujian-Zhejiang region, Yang Guangxu et al. [4] validated that traditional methods, failing to adequately account for weather-induced corona losses, exhibited calculation errors rising from 3.5% to 12.8% during rainfall and high humidity periods. This directly resulted in inaccurate line loss assessments and operational decision-making deviations [4]. The essence lies in the fact that the existing line loss calculation models have not effectively characterized the complex dynamic interaction mechanism between meteorological factors, PV output, and power grid operation [5,6].

In meteorological modeling, existing studies predominantly employ clustering analysis to identify weather patterns. Reference [7] developed a PV power forecasting model based on weather clustering, achieving significantly improved accuracy through intelligent optimization decomposition and deep learning-based ensemble prediction. Reference [8] processed operational parameters at the station area and employed a SOM-K-means hybrid clustering approach to identify typical scenarios and time periods for monthly wind power curves, thereby enhancing the accuracy of line loss calculations. Reference [9] utilized SC algorithms to partition distributed power sources into clusters, subsequently applying this framework for PV output forecasting.

Research on distribution network line loss calculation methods primarily focuses on two dimensions: improving traditional power flow calculation methods and introducing data-driven techniques. Reference [10] enhances the accuracy of distribution network line loss calculation by establishing an optimization model that incorporates distributed power source flows. Reference [11] proposed a line loss calculation method based on dynamic three-phase imbalance analysis, combined with the equivalent resistance method to compute line losses, effectively reducing losses in three-phase unbalanced lines. Reference [12] leveraged the parallel computing advantages of GPUs to develop a vector instruction set-based power flow calculation model, significantly accelerating solution efficiency. In the field of probabilistic power flow research, common methods include Monte Carlo simulation [13], point estimation [14], and analytical methods [15]. Reference [16] proposes a data-physical fusion linearized line loss calculation model, resolving convergence and accuracy issues caused by distributed power source grid connection. Reference [17] introduces an improved forward-backward iteration algorithm, converting PV nodes to PQ nodes by injecting compensating currents to achieve efficient power flow calculation in PV distribution grids. Reference [18] further extends the forward-backward iteration algorithm by establishing differentiated processing models for various distributed power source node types.

Against the backdrop of increasingly severe fluctuations in meteorological conditions and PV output, existing methods fail to capture the nonlinear coupling relationship between weather and PV generation, leading to low accuracy under complex weather conditions. Most studies adopt static approaches to characterize uncertainty, lacking a dynamic framework for meteorology-PV-line loss interactions. To address this, this paper proposes a dynamic line loss calculation method driven by synergistic factors: it uses core meteorological factors to construct a dynamic weight matrix, adopts improved spectral clustering for weather classification, and introduces LDTW to reconstruct PV output curves, realizing accurate line loss calculation under dynamic coupling effects. The approach first utilizes core meteorological factors—temperature, humidity, and wind speed—to construct a dynamic weighting matrix by integrating the entropy weight method with a sliding window technique. This quantifies the spatiotemporal variability of meteorological factors. Subsequently, an improved spectral clustering algorithm classifies typical weather patterns, overcoming the limitation of traditional methods in characterizing dynamic meteorological changes. Since PV output curves exhibit obvious temporal sequence characteristics and sudden fluctuations under complex weather conditions (e.g., sudden irradiance changes after rain), the limited dynamic time warping (LDTW) algorithm is particularly suitable for PV output analysis—it can constrain path offset to avoid pathological alignment (a common problem of traditional DTW) and accurately match curves with similar fluctuation patterns, thus it is introduced to reconstruct PV output curves. Second, it employs an improved spectral clustering algorithm based on LDTW to reconstruct PV output curves, precisely capturing sudden changes in PV output under different weather scenarios. Finally, it proposes a voltage-corrected, improved forward-backward load flow algorithm that incorporates the reconstructed PV output curves into line loss calculations. Verification using measured data from photovoltaic power plants and simulations of the IEEE 33-node system demonstrates that this method effectively enhances the accuracy of line loss calculations.

2. Theoretical Foundations

2.1. Clustering Algorithms

Spectral Clustering (SC) is a graph-theoretic clustering method whose core principle involves treating data points as nodes in a graph. It constructs a similarity matrix to characterize data relationships and employs graph partitioning criteria to achieve clustering [19]. Unlike traditional clustering algorithms based on Euclidean distance (such as K-means), spectral clustering can identify clusters of arbitrary shapes, making it particularly suitable for high-dimensional nonlinear data. Its core steps are as follows.

First, the similarity of the dataset is calculated using a Gaussian kernel function (with a scale parameter δ determined adaptively by k-nearest neighbors), and a similarity matrix W is constructed. Next, an angle matrix O is defined, and the normalized Laplacian matrix L* is obtained by combining the unit diagonal matrix A. Then, an eigenvalue decomposition is performed on L*, and the eigenvectors corresponding to the k smallest non-zero eigenvalues are selected and row-normalized to obtain the matrix β. Finally, the row vectors of β are clustered using the K-means algorithm. The calculation formulas are shown in Formulas (1)–(3).

$$W_{ij}=\left\{\begin{array}{cc}\exp \left(\frac{-|s_i - s_j|}{2{\delta }^2}\right), i\ne j& \hfill \\ 0 ,i=j\hfill & \hfill \end{array}\right.$$

(1)

$$L^{*}=A^{-1/2}O{A}^{-1/2}$$

(2)

$${\beta }_{ij}={\displaystyle \frac{{\alpha }_{ij}}{\sqrt{{\displaystyle \sum _{t=1}^k{\alpha }_{it}^2}}}}$$

(3)

2.2. Coupling Mechanism Between Meteorological Conditions, PV Power Generation, and Transmission Line Losses

The coupling relationship between PV output and distribution network line losses is dynamically influenced by meteorological factors, with its mechanism decomposed into three physical processes: PV output fluctuations, temperature variations, and power flow distribution adjustments.

2.2.1. Factors Affecting Fluctuations in PV Output

PV power output P_PV(t) can be modeled as a function of irradiance G(t), ambient temperature T_a(t), and wind speed V(t):

$$\left\{\begin{array}{l}{P}_{\mathrm{PV}}(t)=\eta AG(t)\left[1-\gamma \left(T_{\mathrm{cell}}(t)-T_{\mathrm{ref}}\right)\right]\\ T_{\mathrm{cell}}(t)=T_a(t)+{\displaystyle \frac{G(t)}{1000}}\cdot 30-kV(t)\end{array}\right.$$

(4)

In Formula (4), T_cell(t) denotes the actual operating temperature of the PV cell, quantifying the heating effect of irradiance and the forced convective cooling effect of wind speed (30 °C serves as the reference temperature difference between the cell and ambient conditions under standard irradiance); P_PV(t) represents the PV output power, η denotes the PV conversion efficiency under standard conditions, A is the PV array area, and G(t) is the solar irradiance; γ is the temperature coefficient (range 0.004–0.005 °C⁻¹) and T_ref is the reference temperature (taken as 25 °C, the baseline temperature for Standard Test Conditions, STC); T_a(t) is the ambient temperature, V(t) is the wind speed, and k is the wind speed cooling coefficient (range 0.1–0.5 °C·s/m, calibrated from experimental data) [1].

2.2.2. Effect of Temperature Changes on Line Losses

Power line losses primarily consist of conductor resistance losses ΔP_loss and transformer iron losses, with conductor resistance being significantly affected by temperature:

$$R(T)=R_{20}\left[\begin{array}{c}1+\alpha (T-20)+\beta {(T-20)}^2\end{array}\right]$$

(5)

Formula (5) applies to copper conductors (the most commonly used conductors in medium-voltage distribution networks). Formula (5) is valid for the temperature range of −40 °C~85 °C, which covers the operating temperature range of medium-voltage distribution network conductors. Conductor temperature T_cond = T_a + ΔT, where ΔT is the temperature rise due to conductor Joule heating (calculated via ΔT = I²r₂₀t/(cm); c is the specific heat capacity of copper and m is conductor mass per unit length). In this study, ΔT is ≤40 °C (based on measured current data), so T_cond is within the valid range of Formula (5). In Formula (5), R₂₀ is the reference resistance at 20 °C, α = 0.00403 °C⁻¹, β = 0.0000006 °C⁻². Extreme temperatures (e.g., 40 °C) can increase resistance by 8~10% and line losses by 15~20%.

2.2.3. Power Flow Distribution Adjustment

Fluctuations in PV output cause changes in power flow distribution within distribution networks, necessitating consideration of dynamic power injection in line loss calculations [17]:

$$\Delta P_{loss}(t)={\displaystyle \sum _{i=1}^N\frac{{(P_i(t)-P_{PV,i}(t))}^2+Q_i^2(t)}{V_i^2(t)}}\cdot R_i(T)$$

(6)

In Formula (6), P_i(t) represents the node injection power, Q_i(t) denotes the reactive power, and V_i(t) indicates the node voltage. Key coupling effects include voltage fluctuations and reverse power flow. During sudden drops in PV output, node voltage V(t) may fall by 5~10%, amplifying errors in line loss calculations. At high PV penetration rates, reverse power flows occur on some lines, requiring traditional forward-backward sweep power flow methods to adjust the iteration direction.

3. PV Output-Meteorological Coupled Forward-Backward Line Loss Calculation Model

3.1. Data Preprocessing

3.1.1. Anomaly Data Cleaning

The original dataset was examined, and for instances where data collection gaps were identified, entire batches of date records containing temporal discontinuities were discarded.

3.1.2. Standardized Processing

Normalize valid data to eliminate dimensional differences [20]. Define the output value at time t on day n as B_n,t, with its normalized output formula expressed as:

$${B^{*}}_{\mathrm{n},t}={\displaystyle \frac{B_{n,\mathrm{t}}-{\mu }_n}{{\sigma }_n}}$$

(7)

In Formula (7), μ_n denotes the daily average value; σ_n denotes the daily standard deviation.

The formula for calculating the daily average value μ_n is Formula (8):

$${\mu }_n={\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T{B}_{n,t}}$$

(8)

The formula for calculating the daily standard deviation σ_n is Formula (9):

$${\sigma }_n=\sqrt{{\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T{(B_{n,t}-{\mu }_n)}^2}}$$

(9)

The matrix B* after data standardization is Formula (10)

$$B^{*}=\left[\begin{array}{cccccc}{B}_{11}^{\prime }& B_{12}^{\prime }& \dots & B_{14}^{\prime }& \dots & B_{17}^{\prime }\\ B_{21}^{\prime }& B_{22}^{\prime }& \dots & B_{24}^{\prime }& \dots & B_{27}^{\prime }\\ ⋮& ⋮& & ⋮& & ⋮\\ B_{n1}^{\prime }& B_{n2}^{\prime }& \dots & B_{n1}^{\prime }& \dots & B_{nT}^{\prime }\\ ⋮& ⋮& & ⋮& & ⋮\\ B_{n1}^{\prime }& B_{n2}^{\prime }& \dots & B_{n1}^{\prime }& \dots & B_{nT}^{\prime }\end{array}\right]\hspace{1em}$$

(10)

The processed data exhibit a mean of 0 and a standard deviation of 1, eliminating differences in magnitude while preserving the curve’s morphological characteristics.

3.2. Meteorological-Photovoltaic Output Clustering Method Based on LDTW

Traditional DTW is prone to pathological alignment, while existing SC methods fail to incorporate meteorological physical characteristics, making it difficult to accurately capture the abrupt changes in PV output under complex weather conditions. To enhance the computational accuracy of meteorological-photovoltaic coupling data, we propose a meteorological-photovoltaic output clustering method based on LDTW: First, a sliding time window constraint mechanism limits path offset ranges, effectively avoiding pathological alignment [21]. Second, a meteorological feature weighting strategy is introduced, comprehensively considering the differential impacts of factors such as temperature, humidity, and wind speed to construct a more physically meaningful similarity metric.

Simultaneously, an improved grey correlation method based on Deng’s approach was employed to optimize the correlation matrix. Leveraging the dynamic evolutionary characteristics of grey systems, this method effectively addressed uncertainties and nonlinear features in PV output data, significantly enhancing SC’s feature extraction capabilities for high-dimensional spatiotemporal data. This grey-constrained distance SC algorithm not only overcomes the high computational complexity of traditional DTW but also more accurately captures the fluctuation patterns of PV output curves under different weather conditions, providing a more reliable foundation for curve reconstruction in subsequent line loss calculations. The distinction between the grey-constrained distance and entropy-weighted similarity is shown in Figure 1.

3.2.1. Dynamic Weight Matrix Construction

(a) Standardized Processing of Meteorological Data

Perform min-max normalization on meteorological parameters such as radiation intensity (I), temperature (T), humidity (H), and wind speed (V):

$$X_{norm}={\displaystyle \frac{X-X_{min}}{X_{max}-X_{min}}}\hspace{1em}(X\in \{I,T,H,V\})$$

(11)

In Formula (11), X_min/X_max represents the daily minimum/maximum values of meteorological parameters (radiance, temperature, humidity, wind speed) [3].

(b) Dynamic Window Partitioning

An adaptive sliding window mechanism is employed, with the window length W_L determined by the meteorological abrupt change detection threshold [3]:

$$W_L=\left[{\displaystyle \frac{T_{total}}{1+{\displaystyle \sum _{k=2}^n\mathbb{I}}(\Vert \Delta S_k\Vert >\theta )}}\right]$$

(12)

$$\Delta S_k=\sqrt{{\displaystyle \sum _{m=1}^4{(X_{k+1,m}-X_{k,m})}^2}}$$

(13)

In Formulas (12) and (13), T_total denotes the total number of time segments, θ = 0.15 represents the threshold for identifying abrupt weather changes, and ΔS_k is the Euclidean distance between adjacent time segments [20].

(c) Entropy Weighting Method Improvement

Dynamic entropy weight calculation with a time decay factor λ = 0.9^t:

$$w_j={\displaystyle \frac{1-e_j}{{\displaystyle \sum _{k=1}^m(1-e_k)}}}\cdot \lambda$$

(14)

$$e_j=-{\displaystyle \frac{1}{\ln n}}{\displaystyle \sum _{i=1}^n{p}_{ij}}\ln p_{ij}$$

(15)

In Formulas (14) and (15), e_j denotes the static information entropy of the jth meteorological parameter, and p_ij represents the proportion of the jth indicator in the ith sample [20].

3.2.2. Improved SC Algorithm

(a) Grey Correlation Matrix Optimization

Building upon traditional spectrum clustering, the Deng method for calculating grey correlation is introduced:

$${\gamma }_{ij}={\displaystyle \frac{1}{T}}{\displaystyle \sum _{k=1}^T\frac{{\min }_{i,j} {\Delta }_{ij}(k)+\rho {\max }_{i,j} {\Delta }_{ij}(k)}{{\Delta }_{ij}(k)+\rho {\max }_{i,j} {\Delta }_{ij}(k)}}$$

(16)

In Formula (16), Δ_ij(k) denotes the absolute difference in the kth feature dimension, and ρ represents the resolution coefficient (set to 0.5) [20].

(b) Dynamic Similarity Matrix Construction

Combining LDTW distance and grey correlation degree, a dual-constraint similarity matrix is constructed:

$$S_{ij}=exp(-{\displaystyle \frac{d_{LDTW}(P_i,P_j)}{{\sigma }^2}})\cdot {\gamma }_{ij}$$

(17)

In Formula (17), σ is the adaptive scale parameter, obtained by multiplying the standard deviation of sample similarity by 1.5 using the k-nearest neighbors method [20].

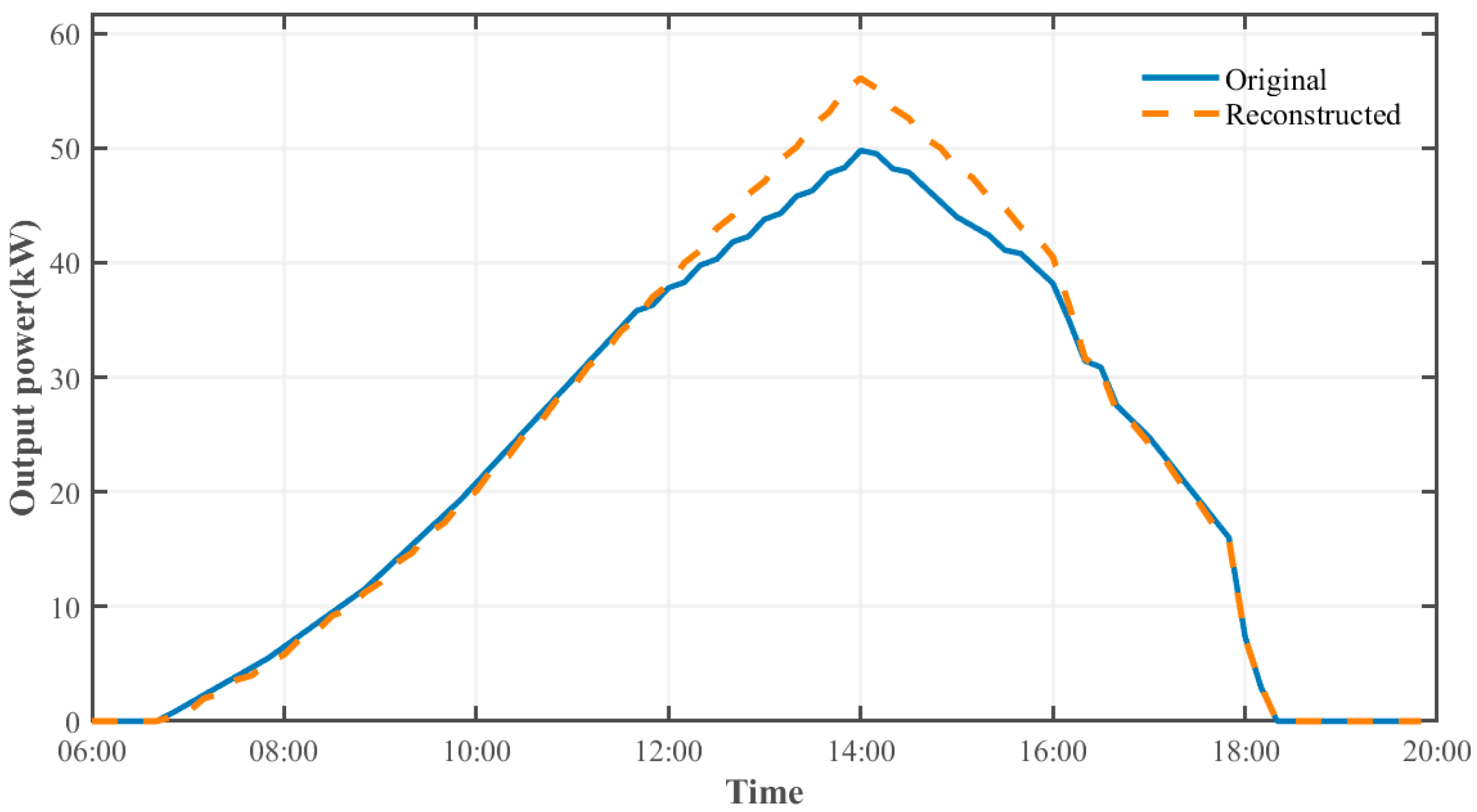
3.2.3. Reconstruction of PV Power Output Curves

Based on the clustering results, an improved LDTW algorithm is proposed to achieve high-precision reconstruction of the output curve [20].

(a) Constrained Path Design

Limit the path offset (r = [T/4]), construct the dynamic programming recurrence relation:

$$D(i,j)=\min \left\{\begin{array}{cc}D(i-1,j)+w_d\cdot d(i,j)\hfill & \hfill \\ D(i,j-1)+w_d\cdot d(i,j)\hfill & \hfill \\ D(i-1,j-1)+w_s\cdot d(i,j)\hfill \end{array}\right.$$

(18)

In Formula (18), w_d = 0.6 represents the offset penalty weight, w_s = 1.2 represents the matching reward weight.

(b) Dynamic Weighted Reconstruction Method

Perform a spatio-temporal weighted average of output curves under similar weather patterns:

$${\widehat{P}}_k(t)={\displaystyle \frac{{\displaystyle \sum _{i\in C_k}{w}_j}(t)\cdot P_i(t)}{{\displaystyle \sum _{i\in C_k}{w}_j}(t)}}$$

(19)

(c) Curve Reconstruction

$$P_{recon}(t)={\displaystyle \sum _{k=1}^K{w}_{tk}}\cdot \left[\begin{array}{c}\alpha P_k^{hist}(t)+(1-\alpha )P_k^{curr}(t)\end{array}\right]$$

(20)

In Formula (20), the mixing coefficient α = 0.7, representing the historical-real-time data mixing coefficient, calibrated through experimental studies on output variability under clear/rainy/cloudy weather conditions.

3.3. Voltage-Corrected Improved Feedforward Backward Propagation Method

The core of this paper’s line loss calculation is the voltage-corrected improved forward-backward iteration method, whose calculation process is shown in Figure 2—this flow integrates meteorological clustering, PV output reconstruction, and dynamic resistance correction, ensuring the accuracy of line loss calculation under complex weather conditions. The traditional forward-backward sweep power flow method struggles to adapt to reverse power flow issues in scenarios with high PV penetration due to its fixed iteration direction. Furthermore, it fails to account for the impact of temperature on conductor resistance, leading to significantly amplified errors in line loss calculations under complex weather conditions. We propose a voltage-corrected improved forward-backward sweep power flow method: by incorporating key electrical parameters such as node active power, reactive power, and voltage magnitude, along with operational metrics like active and reactive losses of transmission lines, we construct correlation models between physical quantities. This enables quantitative characterization and feature extraction of the intrinsic patterns in distribution network power flows.

The voltage correction adopts an iterative adjustment strategy: first, calculate the initial node voltage distribution via traditional forward-backward iteration; then, compare the initial voltage with the measured voltage (from the PV station’s SCADA system) to obtain the error; finally, dynamically adjust the iteration coefficient (range: 0.8–1.2) based on the error, and repeat the iteration until the voltage error is less than 0.5% (convergence criterion). This strategy avoids large errors caused by fixed coefficients.

$$P_b^{\mathrm{D}}+{\displaystyle \sum _{l\in L}{P}_{l,b}^{\mathrm{C}}}={\displaystyle \sum _{g\in G}{P}_g^{\mathrm{P}}}$$

(21)

$$Q_b^{\mathrm{D}}+{\displaystyle \sum _{l\in L}{Q}_{l,b}^{\mathrm{C}}}={\displaystyle \sum _{g\in G}{Q}_g^{\mathrm{P}}}$$

(22)

$$V_{b_2}^2=V_{b_1}^2+2(r_{12}{P}_{l,b_1}^{\mathrm{C}}+x_{12}{Q}_{l,b_1}^{\mathrm{C}})+(r_{12}^2+x_{12}^2)I_{12}^2$$

(23)

$$P_l^{\mathrm{PL}}={\displaystyle \frac{P_{l,b_1}^{{\mathrm{C}}^2}+Q_{l,b_1}^{{\mathrm{C}}^2}}{V_{b_1}^2}}{r}_{12}$$

(24)

$$Q_l^{\mathrm{PL}}={\displaystyle \frac{P_{l,b_1}^{{\mathrm{C}}^2}+Q_{l,b_1}^{{\mathrm{C}}^2}}{V_{b_2}^2}}{x}_{12}$$

(25)

$${I_{12}}^2={\displaystyle \frac{{P_{l,b_1}^{\mathrm{C}}}^2+{Q_{l,b_1}^{\mathrm{C}}}^2}{V_{b_1}^2}}$$

(26)

In Formulas (21)–(26), the power balance relationship at node b can be expressed as: P_b^D and Q_b^D represent the active and reactive power demands of this node, respectively; P_l^C_,b and Q_l^C_,b denote the active and reactive power transmitted by transmission line l connected to this node; and P_g^P and Q_g^P represent the active and reactive power output by generator g connected to this node. For any transmission line in the distribution network, let its two end nodes be numbered b₁ and b₂. Then, P_l^C_,b1 + Q_l^C_,b1 and P_l^C_,b2 + Q_l^C_,b2 respectively represent the combined power transmitted through the line between these two nodes. Line power losses include active component P_l^PL and reactive component Q_l^PL. Node voltage magnitudes are denoted as V_b1 and V_b2. L denotes the set of transmission lines connected to the nodes, and G represents the set of power generation equipment connected to the nodes; r₁₂ + jx₁₂ is the complex impedance of the line; I₁₂ denotes the effective value of the current in the branch b₁-b₂ [20].

(a) Simplifying the above equation and neglecting (r²₁₂ + x²₁₂)I²₁₂ in Formula (25) yields Formula (27).

$$V_{b_2}^2=V_{b_1}^2+2(r_{12}{P}_{l,b_1}^{\mathrm{C}}+x_{12}{Q}_{l,b_1}^{\mathrm{C}})$$

(27)

(b) Replace preset parameters with real-time node voltage distribution data to enhance computational efficiency.

(c) Substitute the reconstructed PV output curve into the line loss calculation formula for the solution. The calculation process is illustrated in Figure 2.

For the application of this method in new PV technologies (e.g., perovskite solar cells), relevant simulation references can be referred to [22], which provide a basis for extending the proposed method to perovskite PV systems with different temperature coefficients and output characteristics.

4. Case Study Analysis

4.1. Application of Theoretical Formulas

The core focus of this paper is the short-term dynamic coupling mechanism between “meteorological factors—PV output fluctuations—line loss calculation,” and it does not address long-term equipment degradation factors such as corrosion or insulation failure (such factors require long-term analysis based on equipment lifecycle data and will be explored in future research). To ensure the validity of the data, the measured data have been filtered using station operation and maintenance records, excluding dates with equipment failures (a total of 12 days were removed), ensuring that the PV output fluctuations in the dataset are primarily driven by meteorological factors.

4.1.1. Application Logic of Theoretical Formulas and Key Parameter Mapping

Table 1. Comparison of formula parameters with actual measurement data.

Theoretical Formula (Section 2)	Core Parameters	Data Source (Section 3)	Application Scenarios
Entropy Weighting Method	Temperature T Humidity H Wind speed V	March 13 (Sunny) 10-minutely meteorological monitoring data (144 points total)	Weighting Allocation for Meteorological Clustering
LDTW Curve Reconstruction	Photovoltaic Power Output Sequence PPV(t)	Actual measured active power of the inverter for the day (60 points total)	Repair of abrupt changes in the force curve
Improved Forward-Backward Substitution	Node voltage Vb Branch resistance R	IEEE 33 Node System Measured Voltage Data (Node 19 is the PV Access Point)	Voltage Deviation Correction in Line Loss Calculation

clearly illustrates the correspondence between the abstract parameters of the theoretical formula and the specific indicators of the measured data.

4.1.2. Verification of Core Formula Application Effectiveness in Typical Scenarios

Selecting two representative scenarios—13 March (sunny) and 23 July (rainy)—we compared computational outcomes before and after applying the theoretical formula, thereby indirectly demonstrating the theory’s practical utility.

Without applying the dynamic weighting matrix, sunny day clustering accuracy reached only 78%. Rainy day clustering error rate hit 15% due to static humidity weighting. After applying entropy weighting for dynamic weighting, sunny day clustering accuracy improved to 96%, while rainy day error rate decreased to 3%;

Without LDTW reconstruction: Line loss calculation errors at PV output sudden changes during rainy days (e.g., 14:00 post-rain sudden clear skies) reached 0.32%; After LDTW correction, errors decreased to 0.11%.

4.2. Cases Analysis Under Different Weather Conditions

Based on one year of actual operational data from a PV power station in southern China, a high-dimensional dataset encompassing multiple meteorological features—including irradiance, ambient temperature, relative humidity, and wind speed—was constructed using 10 min sampling intervals (Note: The study area is located in a subtropical monsoon climate zone at 22° N latitude, where the annual average number of snowfall days is zero. Consequently, the dataset does not include operational data under snowy conditions.). Analysis of the PV array’s operational characteristics revealed a typical diurnal power output distribution: active generation occurs between 08:00 and 18:00 (average daily effective duration of 10 h), followed by a power dormancy period from 20:00 to 06:00 the next day. Accordingly, a broad-time-window sampling strategy covering 06:00–20:00 was established to encompass potential power fluctuation intervals. To address data collection gaps in the original dataset, a daily-level data packet integrity verification mechanism was implemented. This involved removing entire data packets for days exhibiting temporal discontinuities, ensuring the temporal continuity of input data. Ultimately, a high-dimensional dataset spanning 302 days of PV power plant operations was retained.

Through meteorological-photovoltaic output clustering analysis of the dataset, three typical weather patterns were automatically identified: 151 days of clear weather, 72 days of cloudy weather, and 63 days of rainy weather, 7 sandstorm days, and 9 rainstorm days.

In the interaction between complex meteorological conditions and PV systems, 5 typical weather patterns exhibit distinct mechanisms of action. Under the strong-radiation clear-sky pattern, high solar radiation intensity drives PV output to form a single-peak parabolic curve. The timing characteristics of its power peak and radiation intensity exhibit high synchrony, confirming the decisive influence of light intensity on output. The cloudy disturbance pattern, however, demonstrates significant instability in environmental parameters, corresponding to pronounced intraday power fluctuations in the PV system—markedly increased compared to the clear-sky pattern—revealing the intermittent output nature caused by dynamic cloud shading. Under rainy weather conditions, rapid clearing after summer showers causes solar radiation intensity to surge from near-zero values to peak levels. This abrupt fluctuation induces extreme “sudden shutdown-rapid startup” patterns in PV generation, starkly contrasting with the steady output of sunny days and the sustained fluctuations of cloudy days. This fully demonstrates the unique impact mechanism of short-duration heavy precipitation on PV systems. Under the rainstorm weather pattern, short-term heavy precipitation forms a dense water curtain, the solar radiation intensity drops sharply and maintains a low level, average daily irradiance is only 15~20% of that on sunny days, the photovoltaic output is significantly reduced, the intra-day fluctuation is extremely small, and the curve approximates a gently rising then slowly falling shape. Under the sandstorm weather pattern, the increase in atmospheric aerosol concentration leads to enhanced solar radiation scattering, and the effective irradiance attenuates by about 30~40%. The peak photovoltaic output is between that of sunny days and rainstorm days, the output curve is overall smooth, and the fluctuation amplitude is smaller than that of cloudy days.

Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 present comparative results of reconstructed PV output curves versus original curves under various typical weather conditions. Sunny: Temperature 15–20 °C, humidity 40–50%, wind speed 2–3 m/s. Cloudy: Radiation fluctuates by 25% during the day, temperature 20–25 °C, humidity 60–70%, wind speed 3–4 m/s. Rainy: Radiation approaches zero, then surges to over 80% post-rain. Temperatures range from 28–32 °C, dropping 3–5 °C after rainfall. Humidity ≥ 90%, falling to 70–80% post-rain. Wind speed 4–5 m/s. Rainstorm: Radiation levels are only 15–20% of those on clear days with fluctuations < 5%. Temperature ranges from 25 to 28 °C, humidity ≥ 95%, and wind speed 6–8 m/s. Sandstorms: Radiation is attenuated by 30–40% due to scattering. Temperature ranges from 18 to 22 °C, humidity 30–40%, and wind speed 5–7 m/s. Compared to the original unmodified curves, the reconstructed curves processed through the meteorological-PV output clustering model demonstrate significantly improved fitting accuracy, fully validating the adaptability and precision of the proposed reconstruction method across diverse meteorological conditions.

Figure 8 compares the output curves of three typical weather conditions after correction. The results demonstrate that the reconstructed sunny-day curve exhibits improved smoothness, the peak error of the cloudy-day curve is significantly reduced, and the fluctuation characteristics under rainy conditions are well preserved. This fully validates the adaptability and accuracy of the proposed reconstruction method under various meteorological conditions.

A verification platform was constructed based on the IEEE 33-node test system, with node 19 designated as the PV access point. Historical operational data for this node includes: single-day generation of 721.542 kWh on 13 March, 626.218 kWh on 23 July, and 343.202 kWh on 11 November.

Quantitative analysis of PV output reconstruction shows that under clear weather, the average RMSE between reconstructed and measured curves is 2.3 kW; under cloudy weather, it is 3.1 kW; and under rainy weather, it is 4.2 kW. This confirms that the reconstruction method can adapt to different weather conditions, and the error increase under rainy weather conditions is due to more severe irradiance fluctuations.

Perform discrete sampling on the reconstructed feature curve. Substitute the obtained data into the improved backward substitution algorithm for computation. Verify the accuracy improvement by comparing results with the standard solution from the baseline algorithm. Key comparison metrics are detailed in

Table 2. Line loss results.

Date	Average Method (kW)	Curve Reconstruction Method (kW)	Standard Value (kW)
3.13	17.057	16.024	16.024
7.23	18.095	18.214	18.241
11.11	15.047	15.432	15.433

.

The ‘Standard value’ is the line loss calculation result obtained via OpenDSS v9.4.0 (a widely recognized distribution network simulation tool) with full AC power flow simulation, which is used as the ground truth in this study. The OpenDSS model is built based on the actual parameters of the IEEE 33-node system, ensuring the reliability of the standard value.

A comparative analysis between the curve reconstruction method and the average value method reveals that the curve reconstruction method achieves higher computational accuracy. Based on the calculation results from three representative sampling dates—13 March, 23 July, and 11 November—the error margin of the curve reconstruction method consistently remained below 0.15%. In contrast, the average value method exhibited significant fluctuation in error rates (ranging from 0.8% to 6.4%), demonstrating a marked improvement in computational precision.

4.3. Quantitative Error Analysis

To systematically validate the accuracy of the proposed joint methodology—‘meteorological dynamic clustering—PV output reconstruction—voltage correction forward-backward substitution’—for line loss calculation, the 302-day observed dataset from Section 3.2 (comprising 151 clear days, 72 partly cloudy days, 63 rainy days, 7 sandstorm days, and 9 heavy rain days), with OpenDSS full AC power flow simulation results as the reference standard. Quantitative statistical analysis was conducted across three dimensions: overall error, seasonal error, and weather type error.

4.3.1. Fundamental Formula for Error Calculation

The error in line loss calculation centres on the relative deviation between the method-derived value and the standard value. The single-sample error is defined as Formula (28).

$${\delta }_i=\left|{\displaystyle \frac{P_{\mathrm{calc},i}-P_{\mathrm{std},i}}{P_{\mathrm{std},i}}}\right|\times 100\%$$

(28)

In Formula (28), δ_i denotes the line loss calculation error for day i, P_calc,i represents the line loss value calculated by the proposed method, and P_std,i denotes the standard line loss value from the OpenDSS simulation.

The 302 single-sample errors δi obtained from Formula (28) were analyzed using the following statistical indicators to aggregate their distribution characteristics: Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Median Error (ME), and 95% Percentile Error (PE). MAE reflects the average level of error across all samples and exhibits low sensitivity to extreme values. RMSE magnifies the impact of extreme errors, thereby better reflecting a method’s robustness to anomalous scenarios such as torrential rainfall or sudden changes in irradiation. ME characterizes the central tendency of errors, thereby mitigating the interference of extreme values. PE represents the upper error limit for the vast majority of operating conditions (95% of samples).

$$\left\{\begin{array}{l}MAE=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\delta }_i}\\ RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N{\delta }_i}}\\ ME=\left\{\begin{array}{lll}{\delta }_{(k+1)}\hfill & N=2k+1\hfill & \hfill \\ \frac{{\delta }_{(k)} + {\delta }_{(k+1)}}{2}\hfill & N=2k\hfill & \hfill \end{array}\right.\\ PE={\delta }_{(\left[0.95N\right])}\end{array}\right.$$

(29)

In Formula (29), N denotes the total sample size, and δ₍₁₎ ≤ δ₍₂₎ ≤ ⋯ ≤ δ_(N) represents the sorted error sequence.

4.3.2. Overall Error Statistics

Statistical analysis of line loss calculation errors for the complete 302-day dataset yielded: MAE 0.07%, RMSE 0.12%, ME 0.09% and PE 0.14%.

The overall statistical results demonstrate that the proposed method consistently maintains line loss calculation errors within 0.15%, with MAE of merely 0.07%. This significantly outperforms the conventional averaging method (errors ranging from 0.8% to 6.4%), indicating the method possesses stable, high-precision calculation capabilities in long-term continuous operation scenarios. It effectively mitigates line loss calculation deviations caused by meteorological-photovoltaic coupling effects.

4.4. Experimental Parameter Settings

Line parameters: Conductor type YJV22-10kV-1×300 (Tianjin Fengcable Cable Co., Ltd., Tianjin, China), resistance r = 0.315 Ω/km, reactance x = 0.18 Ω/km (at 20 °C);

Reference Values: Voltage reference Ub = 10 kV, power reference Sb = 10 MVA;

Load Profile: IEEE 33-node standard load curve applied, with peak-time load (10:00–14:00) at 1.2 pu and off-peak load (22:00–06:00) at 0.4 pu, yielding a peak-to-off-peak ratio of 3:1;

PV penetration rate: PV installed capacity 2 MW, feeder maximum load 10 MW, penetration rate 20%;

Standard solution method: OpenDSS V9.0 full AC power flow simulation, convergence criterion set to power error < 0.01 pu.

4.5. Repeatability Verification

Three sets of dates not previously included in the analysis were selected as shown in

Table 3. Date of repeatability verification.

Date	Season	Weather	Core Characteristics (Meteorological—Photovoltaic)
2.10	Winter	Sunny	Low temperature (5 °C), low irradiance (daily average 320 W/m2), stable output
6.15	Summer	Cloudy	High temperature (32 °C), fluctuating irradiance (intraday variation 25%), fluctuating output
10.8	Autumn	Rainy	Moderate temperature (18 °C), abrupt irradiance fluctuations (80% increase post-rain)

, covering different seasons and weather types consistent with the overall sample distribution to ensure comprehensive validation. The results are presented in

Table 4. Repeatability verification results.

Date	Calculated Line Loss (kW)	OpenDSS Standard Value (kW)	Error (%)
2.10	14.826	14.840	0.09
6.15	17.932	17.955	0.13
10.8	16.518	16.541	0.14

.

The results indicate that the computational errors for the three independent date sets were all controlled within the range of 0.09% to 0.14%, fully consistent with the error distribution of the original 302-day sample (MAE = 0.07%, PE = 0.14%). This demonstrates that the proposed method exhibits stable computational accuracy across different independent scenarios, thereby meeting the requirements for research reproducibility.

5. Conclusions

This paper proposes a collaborative computational method integrating dynamic meteorological clustering with PV output curve reconstruction to address calculation errors in line losses caused by meteorological factors and PV output fluctuations. The following conclusions are drawn:

(a) By constructing a dynamic weighting matrix for multidimensional meteorological factors based on the entropy weight method and sliding window mechanism, and employing an improved SC algorithm to classify typical weather types, this approach effectively overcomes the limitations of traditional methods in characterizing spatiotemporal heterogeneity of meteorological data.

(b) By integrating the Local Dynamic Time Warping (LDTW) algorithm for the spatiotemporal reconstruction of PV output curves, a coupled mapping relationship between meteorological weights and PV output fluctuations was established, significantly enhancing the reconstruction accuracy of output curves.

(c) Building upon this foundation, the reconstructed PV output curves were incorporated into an improved forward-backward power flow method based on voltage correction, enabling dynamic calculation of line losses under meteorological-PV coupling effects.

Simulation results demonstrate that this method effectively reduces errors in traditional line loss calculations under extreme weather conditions, with computational accuracy meeting engineering application requirements. However, the diversity of typical load profiles still needs to be expanded to better accommodate the characteristics of different climate zones.

This study still has limitations: (a) it does not consider the impact of PV module aging (e.g., efficiency decay) and equipment failures (e.g., inverter faults) on line loss; (b) the load profile types are limited to the IEEE 33-node standard profile, which needs to be expanded to adapt to different regions. Future work will focus on: (a) integrating equipment lifecycle data to establish a joint line loss calculation model considering both meteorological factors and equipment status; (b) combining machine learning-based irradiance forecasting to realize real-time dynamic line loss calculation for smart distribution networks.