Thermo-Economic Assessment of the Organic Rankine Cycle Combined with an Ejector Cooling Cycle Driven by Low-Grade Waste Heat

Abstract

This paper proposes an energy, exergy, economic, and exergoeconomic (4E) analysis of an Organic Rankine Cycle (ORC) enhanced by an ejector refrigeration system. The two systems are combined via an intercooler, where the unwanted heat is transferred to the ejector cooling loop. The major objective is to reduce the discharge pressure of the expander so that higher power is achieved. However, the combined system requires more equipment and energy input, and, hence, 4E analysis is an efficient tool for assessing the feasibility of it in practical use based on a comprehensive analysis. This study aims to provide a systematic 4E-based evaluation of an ORC integrated with an ejector cooling cycle under realistic tropical conditions. The innovation of this work lies in combining unified thermodynamic, economic, and exergoeconomic assessments to quantify both performance enhancement and cost interactions attributable to condenser-side cooling. The findings offer significant insights into the dominant thermal–economic trade-offs, identify key cost drivers within the ORC + ECC configuration, and highlight operating conditions that maximize the power output and minimize the electricity generation cost. These results contribute practical guidelines for improving the feasibility and deployment of ORC–ejector systems for low-grade heat recovery applications. A theoretical model is formulated to examine both energy and exergy performance indicators together with key economic metrics. Parametric investigations are conducted to investigate the effects of the intercooler temperature (16–22 °C) and generator temperature (70–85 °C) on overall system performance. It is found that the integration of an ejector cooling cycle (ORC + ECC) can significantly enhance the thermo-economic potential of waste heat power generation systems compared to a standard ORC, from both exergoeconomic and LCOE perspectives. The exergoeconomic analysis identified that, while the expander dominates the cost of the standard ORC, the condenser and cooling tower become critical components of the ORC + ECC due to their high exergy-destruction costs. At the system level, the LCOE results confirm that the ORC + ECC can achieve 37–38% lower electricity generation costs compared to the standard ORC.

1. Introduction

The global demand for electricity has been increasing because of rapid economic, industrialization, and population growth. The increasing need for electricity not only has a negative impact on the primary energy source but also contributes to environmental degradation and greenhouse gas emissions. Consequently, many researchers have focused on the development of energy conversion technologies that are more efficient, cost-effective, and sustainable [1]. A promising solution is the development of thermal machines driven by low-grade heat to produce electrical energy. This allows industrial waste heat sources or renewable heat sources to be recovered to produce useful mechanical work.

The Organic Rankine Cycle (ORC) is a widely adopted technology for waste heat recovery [2]. ORCs use low-boiling organic fluids to efficiently convert low-grade heat into electricity. However, conventional ORCs have notable performance limitations with low-temperature heat sources. The condenser is the primary weakness, as condensation at higher temperatures and pressures causes significant exergy destruction. This reduces the expansion ratio in the expander and lowers both thermodynamic and exergy efficiency. These challenges are especially pronounced in the tropical climates common in Southeast Asia [3,4]. In an Organic Rankine Cycle (ORC), the condensation pressure fundamentally governs thermal efficiency because it is associated with the expander pressure ratio. A higher condensation pressure decreases the pressure ratio across the expander, reducing the available work done and lowering the cycle’s thermodynamic performance. On the other hand, lowering the condensation pressure improves the expansion ratio and enhances both energy and exergy efficiencies, which demonstrates the strong influence of condenser-side cooling strategies on overall ORC viability.

To address these limitations, advanced condenser-side cooling strategies have been developed. One promising approach is integrating the ejector cooling cycle (ECC/EERC) into the ORC. The ejector cooling cycle can be used to cool down the ORC’s condenser, which can reduce the condensation temperature and pressure. This means that the expander’s backpressure is reduced, which can yield more net power output and better system efficiency [5,6]. Various hybrid configurations have been studied, including ORC + ECC for combined power and cooling [7], ejector–ORC (EORC) for enhanced power output [8], ORC–ejector expansion (EERC) to reduce condenser load, and poly-generation systems that produce electricity, heat, and cooling [9]. Empirical results confirm these benefits. For example, an ORC + ECC using an R134a/R123 blend achieved 27.5% energy efficiency and 14.9% exergy efficiency at heat source temperatures of 140–190 °C. Another system generated 500 kW of electricity with 21.5% energy efficiency and 28.2% exergy efficiency. However, Yang et al. [4] found that over 40% of exergy losses still occur in the ejector, indicating that while the ECC improves performance, the ejector remains a key area for further optimization.

Recently, the ORC analysis framework has been developed to include 4E (energy, exergy, economic, and exergoeconomic) analysis, providing a more integrated assessment of system performance. The 4E approach connects thermodynamic behavior with cost indicators such as the LCOE and SUCP. Permana et al. [10] highlighted the techno-economic linkage in ORC assessment using 4E analysis. Fergani et al. [11] found that the condenser has the highest avoided cost, about 77%, emphasizing its importance in cost and exergy interactions. Additionally, several studies have applied the 4E framework to combined ORC systems, such as ORC–absorption and ORC–ejector refrigeration, often using multi-objective optimization to balance exergy efficiency and overall cost [12].

While the ECC/EERC and the 4E framework continue to advance ORC assessments, alternative strategies are still being explored. The Absorption Cooling Cycle can significantly reduce the condenser temperature when excess heat is available, but it requires high capital investment and adds system complexity [13,14]. In contrast, vapor-compression refrigeration (VCRC) offers flexibility and ease of control but increases electricity demand, which can negatively impact the SUCP and LCOE, especially with high electricity prices. Absorption systems are often preferred for large-scale plants with stable heat sources [15], while VCRC is more suitable for small- to medium-scale applications where controllability is a priority despite higher electricity use.

Integrating an ejector into an ORC system can lower the cost per unit of generated energy. Tashtoush et al. [5] identified the ejector and condenser as the main cost drivers, a finding supported by Tao et al. [6], who reported a specific unit cost of product (SUCP) of 45.1 USD/MWh for an ORC–ejector system, compared to 53.4 USD/MWh for a standard configuration. Ben Hamida et al. [16] further showed that, in ship waste heat recovery, the ORC–ejector system could produce 72 kW of electricity at 60.4% exergy efficiency, with an SUCP of 1259 USD/GJ, which could be reduced to 902 USD/GJ under optimized conditions.

A comparative assessment of condenser-side cooling strategies under hot and humid conditions demonstrates that the ECC/EERC approach offers superior techno-economic performance compared to conventional absorption and vapor-compression systems. As shown in

Table 1. Condenser-side cooling strategies (hot–humid conditions).

Criteria	Ejector Cooling Cycle (ECC/EERC)	Absorption Chiller	Vapor-Compression Refrigeration (VCRC)
Thermal effect	Reduces Tcond by ~5–10 K; lowers expander backpressure; increases Wnet	Deep Tcond reduction (>10 K) if stable surplus heat	Deep and controllable Tcond reduction across a wide load range
Electricity demand	Not required (heat-driven)	Not required (heat-driven)	High (extra compressor power) → may worsen SUCP/LCOE when electricity price is high
Complexity (O&M)	Moderate; no moving parts in ejector	High; absorber/generator + large HX	Moderate; compressor + advanced controls
CAPEX	Low–moderate	High (large HX + absorber/generator)	Moderate
Exergy destruction	Concentrated at ejector (design-sensitive)	Condenser destruction suppressed; added HX introduces losses	Condenser exergy destruction reduced; compressor exergy losses increase
4E indicators	SUCP/LCOE improvement (5–15% typical in studies), especially with high electricity tariff	Can improve if surplus heat is abundant/inexpensive; otherwise, CAPEX dominates	Typically worsens under high electricity price
Scale suitability	Small–medium plants in hot–humid regions with high electricity prices	Large plants with steady surplus heat (cogeneration/industrial)	Small–medium where controllability is paramount and electricity is relatively cheap
Main advantage	Simple, near-zero electricity, favorable OPEX	Deep cooling, strong thermodynamic benefit	Highest flexibility and control
Main limitation	Ejector geometry optimization: notable exergy losses remain	High CAPEX/O&M; depends on reliable surplus heat	High electricity demand → SUCP/LCOE penalties

, integrating an ejector into the ORC cycle reduces the condensing temperature by 5 to 10 K, which lowers expander backpressure and increases both net power output and exergy efficiency, with minimal additional electricity use [2,7,8]. This benefit is especially relevant in tropical regions, where high ambient and cooling water temperatures increase condenser irreversibility [3,4]. Absorption systems can achieve deeper condenser cooling and better thermodynamic performance when excessive heat is available, but their high capital costs and operational complexity restrict their use to large-scale plants with stable heat sources [8,13]. Vapor-compression refrigeration (VCRC) provides the greatest operational flexibility and control, but its high electricity demand raises the SUCP and LCOE, reducing economic viability in regions with high electricity prices. From an exergoeconomic perspective, the ejector–condenser interaction is the research challenge, consistent with previous studies highlighting the impact of condenser-side irreversibility on system-wide cost and exergy relationships [11,12]. Overall, these findings indicate that the ECC/EERC achieves optimization between performance and economic viability for ORC deployment in hot and humid climates, while absorption and VCRC systems may only be suitable under specific conditions.

1.1. Research Gaps

The Organic Rankine Cycle (ORC) is a promising technology for converting low-grade heat into electricity. In tropical regions, high cooling water temperatures and humidity make the condenser a significant bottleneck. Higher condensing temperatures and pressures increase exergy destruction and reduce expander output, lowering overall system efficiency [12,15]. The ejector cooling cycle (ECC/EERC) has been proposed to address this issue (seen from

Table 2. Options to lower ORC condensing temperature/pressure (ΔTcond) with 4E-relevant notes.

Option	Mechanism/Driving Source	Typical ΔTcond (K)	Effect on Wnet/ORC Efficiency	Electric Load/OPEX	Complexity and Risks	Suitable Context	Example References (Author—Year)
Ejector cooling (ECC/EERC)	High-pressure motive vapor entrains low-pressure suction vapor to reduce backpressure; EERC recovers throttling losses via momentum transfer	≈5–15 (depends on ER/NXP/AR and condenser UA)	Wnet ↑; expander pressure ratio ↑; exergy destruction of condenser ↓; EERC mitigates valve throttling loss	Very low (no electric compressor)	Requires careful geometry tuning (ER, NXP, AR); off-design choking/instability possible; needs appropriate control	Hot ambient sink; need power + cooling; low-maintenance preference	[3,4,6,7,8,15,17,18]
Absorption-assisted (AORC)	Waste heat drives an absorption chiller (LiBr–H2O/NH3–H2O) to supply cooling and depress Tcond	≈8–20 (single effect at ~80–120 °C; deeper with double effect)	Wnet ↑ without extra electric load; strong reduction in condenser exergy destruction	Low (mainly pump work)	Higher system complexity; LiBr crystallization risk; vacuum and corrosion control required	Sufficient waste heat available; high cooling COP desired; deeper Tcond depression	[9]
Vapor-compression chiller (VCRC)	Electric compressor provides cooling to assist the condenser	≈10–30 (scalable with chiller size and ambient conditions)	ORC Wnet ↑ markedly, but net gain depends on compressor power; SUCP/LCOE may worsen under high electricity prices	High (direct electric consumption)	Simple hardware/control; cost-effectiveness sensitive to power price and chiller COP	Needs large ΔTcond; limited footprint; low/cheap electricity	[19]

Remark: ↑ means the parameters of interest is increased. ↓ means the parameters of interest is decreased.

) by reducing the condensing temperature, pressure, and expander backpressure with minimal additional electrical consumption [2,7]. Despite these advances, several key research gaps still remain.

First, most studies focus on temperate or generalized tropical conditions, with limited analysis of actual tropical operating environments. This gap creates uncertainty in the reliability of economic indicators such as the levelized cost of electricity (LCOE) and specific unit cost of product (SUCP) when heat sources and energy prices fluctuate [1,6]. Second, many studies focus solely on energy and exergy indicators, with limited use of exergoeconomic indices such as the exergoeconomic factor f_k and the relative cost difference r_k. These indices are essential for identifying key cost drivers and prioritizing component-level investments [10,11]. Third, most ejector design studies rely on single-objective optimization, such as maximizing the entrainment ratio, and often overlook multi-objective approaches. Multi-objective optimization should consider trade-offs among the net power output, exergy efficiency, flow stability, and capital and operating expenditures (CAPEX/OPEX) [5,9].

Fourth, there is a lack of systematic comparative studies between the conventional ORC and ORC + ECC within the 4E analytical framework. While some research has examined absorption-based systems [13,14] and vapor-compression refrigeration cycles, no studies have directly compared the standard ORC with the ORC + ECC under consistent boundary conditions such as hot and cold source profiles, energy pricing, and tropical environments. Such analyses are essential to validate the thermo-economic feasibility of the ORC + ECC and to determine when investments in these combined systems offer better returns than conventional ORC systems.

These research gaps highlight the need for research on ORC + ECC architectures within the 4E framework, focusing on systematic comparisons between the conventional ORC and ORC + ECC under consistent conditions. Such analyses are crucial for identifying cost-effective design strategies and supporting the practical implementation of ORC + ECC technologies in tropical climates.

This study extends previous ORC + ECC analyses by establishing a systematic 4E (energy, exergy, economic, and exergoeconomic) framework that simultaneously evaluates thermodynamic behavior and economic feasibility under relatively high ambient temperatures. The proposed methodology explicitly links the second-law indicators (η_ex, Ėx_D) with key cost metrics (NPV, LCOE, and SUCP) to identify the dominant components contributing to exergy destruction and cost. Moreover, the current research fills the gap of limited quantitative comparison between standard ORC and ORC–ejector configurations by providing a unified boundary condition and consistent techno-economic assumptions, allowing direct evaluation of system-level improvement potential. Such refinement strengthens the rationale for the following objectives.

1.2. Research Objectives

As explained above, this research aims to develop and evaluate the performance of an ORC–ejector cooling cycle system based on the 4E framework, encompassing energy, exergy, economic, and exergoeconomic analyses. A theoretical model is formulated to quantify both energy and exergy performance indicators together with key economic metrics. Parametric and scenario-based analyses are conducted to investigate the effects of the intercooler temperature (16–22 °C) and generator temperature (70–85 °C) on overall system performance. Furthermore, the cost structure of each component is analyzed using the exergoeconomic factor (f_k) and relative cost difference (r_k) indices, thereby identifying major cost drivers and guiding investment prioritization. Finally, an integrated engineering and economic improvement approach is proposed to minimize exergy degradation and maximize the net present value (NPV) of the ORC–ejector cooling cycle system.

Accordingly, the objectives of this research are not only to evaluate the energy and exergy performance but also to quantify the cost-related impacts using exergoeconomic indicators. This dual-perspective approach contributes to a deeper understanding of how thermal parameters and investment decisions influence overall cycle sustainability and profitability.

2. Thermodynamics Model and Methods

2.1. System Description

2.1.1. Conventional Organic Rankine Cycle

The conventional Organic Rankine Cycle (ORC) operates based on a simple Rankine Cycle that converts low-grade thermal energy into mechanical shaft power. In this study, an organic refrigerant, R245fa, is considered as the working fluid due to its favorable thermophysical properties for medium-temperature heat sources. Figure 1 depicts the cycle’s components and the thermodynamic states of the cycle. High-pressure vapor is produced when heat is added into the generator, in which low-temperature liquid is heated from state 4 to 1. Later, the high-pressure vapor undergoes an expansion process to produce the shaft power (1 to 2) flowing through the expander. The low-pressure vapor (expander’s exhaust) is condensed within the condenser as the unwanted heat is released into the surroundings (2 to 3). The liquified refrigerant is fed back into the generator via the liquid pump (3 to 4) to complete the cycle’s operation.

2.1.2. Combined Organic Rankine Cycle with Ejector Cooling Cycle (ORC + ECC)

In the combined system (ORC + ECC), the major objective is to reduce the expander’s discharge pressure so that the expansion pressure ratio is higher. Hence, the combined system has high potential to yield higher mechanical shaft power. The key is to add an intercooler (heat exchanger) into the system so that the two cycles (ORC and ejector cooling cycle) can be operated simultaneously. A schematic diagram of the combined ORC + ECC is shown in Figure 2 and the flow process on T-s diagram is shown in Figure 3. It is seen that the high-pressure vapor produced by the generator is divided into two streams. Part of high-pressure stream flows through the ORC loop, while the rest flows through the ejector cooling loop. For the ECC loop, the high-pressure vapor (known as the primary fluid) is accelerated through the primary nozzle, which later draws a secondary fluid from the intercooler, causing a cooling effect to be produced at the intercooler. Hence, the exhaust vapor from the ORC loop is cooled at a lower temperature, which results in a lower condensation pressure (lower expander’s backpressure). The primary and secondary fluids are mixed within the mixing chamber and undergo the pressure recovery effect via the impact of the shock wave before discharging to the condenser. As a result, the EEC loop can release unwanted heat at a relatively high ambient temperature. It is noticeable that the combined system still functions at a relatively high ambient temperature, which is similar to the conventional ORC system (proposed in Section 2.1.1); however, the combined system (ORC + ECC) can operate with a higher expansion pressure ratio across the expander, which has high potential to yield more mechanical shaft power. However, the ORC + ECC requires more heat input and more equipment, for which the value of installation is questionable. Therefore, this research is focused on answering this question with the use of 4E analysis, aiming to provide clarification on the advantages of the ORC + ECC based on this analysis.

2.2. Thermodynamic Model

This section introduces and explains the modeling approach used to assess both the standard ORC and the ORC + ECC, which is considered as a tool to assess the performance of both systems. This section begins by introducing the ejector model to verify and predict the cooling performance so that the shaft power and thermal efficiency produced by the combined system can be predicted accurately.

2.2.1. Ejector Model

The ejector model in this study assumes steady-state and adiabatic flow conditions. For simplicity, the expansion process of the motive (primary) flow inside the nozzle and the mixing process with the suction (secondary) flow are considered quasi-isentropic. This assumption allows an analytical estimation of velocity and pressure distributions while maintaining acceptable accuracy. Similar assumptions have been adopted in Li et al. [8] and Sun et al. [20]. Figure 4 shows the ejector components and the significant location where the mathematical model must be developed for predicting them. The governing equations of mass, momentum, and energy conservation for the ejector are formulated based on the steady-flow control volume approach described in previous studies [3,4,7,8,17,20].

The classical thermodynamic model with isentropic correction has been widely used for the performance evaluation of single- and two-stage ejector refrigeration systems. In this work, the same theoretical foundation is adopted, and the real-gas properties of R245fa are calculated using REFPROP v10 to ensure realistic simulation results. The entrainment ratio (μ) and the relationships between the motive, suction, and mixed flows are expressed as follows:

$$\mu ={\displaystyle \frac{{\dot{m}}_e}{{\dot{m}}_g}}$$

(1)

where μ is the entrainment ratio; ṁ_e is the mass flow rate of the secondary fluid [kg/s]; and ṁ_g is the mass flow rate of the primary fluid [kg/s].

The primary fluid in section 2 is described by the following Mach number (M_g2):

$$M_{g2}=\sqrt{{\displaystyle \frac{2{\eta }_n}{k-1}}[{({\displaystyle \frac{p_g}{p_2}})}^{({\displaystyle \frac{k-1}{k}})}-1]}$$

(2)

where M_g2 is the Mach number of the primary flow at the nozzle exit; p_g and p₂ are the total and outlet static pressures [Pa]; η_n is the nozzle efficiency; and k is the specific heat ratio of the working fluid.

This equation is used to determine the Mach number at the nozzle exit (M_g2) under the assumption of isentropic expansion with a given nozzle efficiency (η_n). The relationship accounts for the pressure ratio between the inlet gas pressure (p_g) and the downstream pressure (p₂), as well as the specific heat ratio of the working fluid (k). These parameters directly influence the dimensionless flow velocity and hence the Mach number obtained at the nozzle outlet.

The secondary fluid in section 2 is described by the following Mach number (M_e2):

$$M_{e2}=\sqrt{{\displaystyle \frac{2}{k-1}}[{({\displaystyle \frac{p_g}{p_2}})}^{({\displaystyle \frac{k-1}{k}})}-1]}$$

(3)

where M_e2 is the Mach number of the secondary flow in section 2; p_g and p₂ are the total and outlet static pressures; and k is the specific heat ratio of the working fluid.

The Mach number of the secondary fluid in section 2 (M_e2) is expressed by the following relation. It is derived from the isentropic flow assumption, considering the pressure ratio between the inlet gas pressure (p_g) and the downstream pressure (p₂), together with the specific heat ratio of the working fluid (k).

The mixture in section 4 is described by the following critical Mach number (M₄*):

$$M_4^{*}={\displaystyle \frac{{\eta }_m{M}_{g2}^{*}+\mu M_{e2}^{*}\sqrt{T_e/T_g}}{\sqrt{(1+\mu )(1+\mu \frac{T_e}{T_g})}}}$$

(4)

where M₄* is the critical Mach number of the mixed flow in section 4; M_g2* and M_e2* are the (choked) Mach numbers of the motive and entrained streams in section 2; η_m is the mixing efficiency; μ is the entrainment ratio; and T_e and T_g are the static temperatures of the entrained and motive streams in section 2 (the ratio T_e/T_g is dimensionless). Kinetic and potential energy changes are neglected.

The relationship between the actual Mach number and the critical Mach number is derived from the isentropic flow equations:

$$M^{*}=\sqrt{{\displaystyle \frac{M^2(k+1)}{M^2(k-1)+2}}}$$

(5)

where M* is the critical Mach number; M is the actual Mach number; and k is the specific heat ratio of the working fluid.

The hybrid fluid in section 5 is described by the following critical Mach number ($M^5$):

$$M^5=\sqrt{{\displaystyle \frac{M_4^2+\left(\frac{2}{k-1}\right)}{M_4^2\left(\frac{2k}{k-1}\right)+1}}}$$

(6)

where M⁵ is the critical Mach number of the hybrid (mixed) flow in section 5; M₄ is the Mach number of the mixed flow in section 4; and k is the specific heat ratio of the working fluid.

After the shock wave, the pressure rise of the hybrid fluid is determined as follows:

$${\displaystyle \frac{P_5}{P_4}}={\displaystyle \frac{1+{kM}_4^2}{1+{kM}_5^2}}$$

(7)

where p₅ and p₄ are the static pressures after and before the shock wave [Pa]; M₄ and M₅ are the Mach numbers of the hybrid flow in sections 4 and 5; and k is the specific heat ratio of the working fluid.

Sections 2, 3, and 4 are assumed to have the same pressure.

$$p_2=p_3=p_4$$

(8)

The backpressure of the ejector is as follows:

$${\displaystyle \frac{p_c}{p_5}}={[{\displaystyle \frac{{\eta }_d(k-1)}{2}}{M}_5+1]}^{{\displaystyle \frac{k}{k-1}}}$$

(9)

where p_c is the condenser pressure of the ejector; p₅ is the static pressure in section 5; η_d is the diffuser efficiency; M₅ is the Mach number of the hybrid flow in section 5; and k is the specific heat ratio of the working fluid.

2.2.2. Conservation Equation of Mass and Energy

The mass flow rate and energy balance of the system are commonly considered as the assumptions for the assessment of thermal systems. Hence, the mass flow rate and energy transfer of each cycle’s components are considered as the significant parameters for the 1st law of thermodynamics analysis.

Table 3. Input parameters for 4E analysis.

Parameters	Value	Unit
Reference pressure	101.325	kPa
Reference temperature	298.15	K
Enthalpy of water in dead state (h)	104.9	kJ/kg
Entropy of water in dead state (s)	0.3672	kJ/kg.K
Enthalpy of R245fa in dead state (h)	424.7	kJ/kg
Entropy of R245fa in dead state (s)	1.781	kJ/kg.K
Mass flow rate of ORC system (both systems)	3.091	kg/s
Ambient relative humidity	70	%

summarizes the main input variables, including the reference pressure and temperature, enthalpy and entropy values for water and R245fa at 298.15 K, and the system’s mass flow rate. The ambient relative humidity was set to 70%, representing the typical hot–humid tropical conditions in Thailand.

Table 4. Operating and efficiency parameters of the ORC–ejector cooling system.

Subsystem	Parameter	Symbol	Value	Unit
Heat source temperature	Vapor generator temperature	Th,in	95	°C
	Vapor generator pressure	Pgen	1001	kPa
	Thermal efficiency	ηgen	0.90	–
Expander	Pressure ratio (varied with Tint)	PRexp	7.5–9.9	–
	Isentropic efficiency	ηexp	0.80	–
Pumps	ORC working fluid pump efficiency	ηpump,wf	0.85	–
	Cooling water pump efficiency	ηpump,cw	0.85	–
	Hot water pump efficiency	ηpump,hw	0.85	–
Mass flow rates	Mass flow rate of cooling water	ṁcw	75.76	kg/s
	Mass flow rate of hot water	ṁhw	81.8	kg/s

Note: All pump efficiencies were assumed to be identical, 85% (0.85), for simplicity.

presents the operating and performance parameters adopted in the simulation of the ORC–ejector cooling system. The hot water generator conditions represent the waste heat source, while component efficiencies and mass flow rates were assumed according to ORC practice [1,2].

These baseline parameters were used for all simulation cases. The selected efficiencies are based on commercially available ORC components, ensuring that the numerical results are realistic and comparable with published data.

The integrated ORC system with an ejector refrigeration cycle requires additional mass flow rates compared to the standard ORC. The primary mass flow (additional mass flow rate) follows the same path as the working fluid, passing through the pump, generator, and ejector nozzle, then moving through the condenser and vapor–liquid separator before returning to the pump. The secondary mass flow circulates only within the ejector refrigeration cycle, passing through the intercooler, ejector, condenser, and vapor–liquid separator. Mass and energy conservation principles form the basis for thermodynamic modeling of this system. The mass balance equations for each component are as follows:

$$\sum {\dot{m}}_i=\sum {\dot{m}}_o$$

(10)

The energy conservation equation can be written as follows:

$$\dot{Q}-\dot{W}=\sum {\dot{m}}_o{h}_o-{\sum {\dot{m}}_{i}h}_i$$

(11)

where $\dot{Q}$ is the heat transfer rate [kW]; $\dot{W}$ is the work output rate [kW]; $\dot{m}$ is the mass flow rate [kg/s]; and $h$ is the specific enthalpy [kJ/kg].

The heat input in the generator:

$$\dot{Q}=\dot{m}(h-h_o)$$

(12)

The work at the expander:

$$\dot{W}=\dot{m}(h-h_o)$$

(13)

2.2.3. Exergy Input and Exergy Destruction

Exergy represents the maximum useful work obtainable as a system moves toward equilibrium with its environment, which reflects energy quality rather than just quantity. Unlike standard energy analysis, exergy analysis accounts for the second law of thermodynamics and the irreversibility of all processes. In the present work, exergy analysis provides a more detailed evaluation of the ORC + ECC compared to the conventional ORC, which makes it possible to identify and minimize high-quality energy losses for system optimization. The primary parameter is the exergy rate of each working state through the cycle, which can be calculated as follows:

$$\dot{E}x=\dot{m}e$$

(14)

$$e=h-h_0-T_0(s-s_0)$$

(15)

In the ORC, exergy input is the exergy that the working fluid R245fa receives from the heat source. Total exergy destruction is the sum of losses in all system components. The overall exergy loss includes both the destruction and the exergy released to the cooling water at the condenser. Total exergy loss can also be seen as the difference between the exergy recovered from the cooling water and the net shaft power produced by the cycle.

$$\dot{E}{x}_{loss}=\dot{E}{x}_{in}-{\dot{W}}_{net}$$

(16)

Exergy destruction for each system component is calculated differently, as summarized in Table 5. Determination of these values is essential for comprehensive exergy analysis and subsequent performance evaluations of the system.

All governing equations for energy and exergy balance (Equations (10)–(16)) were formulated based on standard thermodynamic and exergetic relations [21,22].

Table 5. Exergy destruction and efficiency in each component [22,23].

Component	Exergy Destruction		Exergy Efficiency
	$\dot{E}{x}_D^i=\dot{E}{x}_F-\dot{E}{x}_P-\dot{E}{x}_L$	(17a)	${\eta }_{ex}={\displaystyle \frac{\dot{E}{x}_P}{\dot{E}{x}_F}}$	(17b)
ORC pump	$\dot{W}+\dot{E}{x}_7-\dot{E}{x}_1$	(18a)	${\displaystyle \frac{(\dot{E}{x}_1-\dot{E}{x}_7){\eta }_{pump}}{{\dot{W}}_{pump}}}$	(18b)
ORC generator	$\dot{E}{x}_Q^{gen}+\dot{E}{x}_1-\dot{E}{x}_2$	(19a)	${\displaystyle \frac{\dot{E}{x}_2-\dot{E}{x}_1}{\dot{E}{x}_Q^{gen}}}$	(19b)
Expander	$\dot{E}{x}_{2a}-\dot{E}{x}_3-\dot{W}$	(20a)	${\displaystyle \frac{\dot{W}}{\dot{E}{x}_{2a}-\dot{E}{x}_3}}$	(20b)
ORC intercooler	$\dot{E}{x}_3+\dot{E}{x}_f-\dot{E}{x}_4-\dot{E}{x}_g$	(21a)	${\displaystyle \frac{\dot{E}{x}_g-\dot{E}{x}_f}{\dot{E}{x}_3-\dot{E}{x}_4}}$	(21b)
Low-pressure pump	$\dot{W}+\dot{E}{x}_5-\dot{E}{x}_6$	(22a)	${\displaystyle \frac{(\dot{E}{x}_6-\dot{E}{x}_5){\eta }_{Pump}}{\dot{W}}}$	(22b)
Ejector	${\dot{m}}_p{e}_{2b}+{\dot{m}}_s{e}_a-({\dot{m}}_p+{\dot{m}}_s)e_b$	(23a)	${\displaystyle \frac{{\dot{m}}_m{e}_b-{\dot{m}}_s{e}_a}{{\dot{m}}_p{e}_{2b}}}$	(23b)
Condenser	$\dot{E}{x}_b-\dot{E}{x}_c$	(24a)	${\displaystyle \frac{\dot{E}{x}_h-\dot{E}{x}_j}{\dot{E}{x}_b-\dot{E}{x}_c}}$	(24b)
Cooling tower	$\dot{E}{x}_h-\dot{E}{x}_i$	(25a)	0	(25b)
Cooling water pump	$\dot{W}+\dot{E}{x}_i-\dot{E}{x}_j$	(26a)	${\displaystyle \frac{(\dot{E}{x}_j-\dot{E}{x}_i){\eta }_{Pump}}{\dot{W}}}$	(26b)
Working fluid pump	$\dot{W}+\dot{E}{x}_e-\dot{E}{x}_f$	(27a)	${\displaystyle \frac{(\dot{E}{x}_f-\dot{E}{x}_e){\eta }_{Pump}}{\dot{W}}}$	(27b)

where T_hw,in is the inlet temperature of the hot water [°C]; P_gen is the generator pressure [kPa]; η_gen, η_exp, and η_pump are the thermal, isentropic, and pump efficiencies of the generator, expander, and pumps, respectively; ${\dot{m}}_{wf}$ and ${\dot{m}}_{cw}$ are the mass flow rates of the working and cooling fluids [kg/s]; and ${\dot{E}x}_F$ denotes the exergy fuel or total exergy input [kW_ex].

Table 5. Exergy destruction and efficiency in each component [22,23].

Component	Exergy Destruction		Exergy Efficiency
	$\dot{E}{x}_D^i=\dot{E}{x}_F-\dot{E}{x}_P-\dot{E}{x}_L$	(17a)	${\eta }_{ex}={\displaystyle \frac{\dot{E}{x}_P}{\dot{E}{x}_F}}$	(17b)
ORC pump	$\dot{W}+\dot{E}{x}_7-\dot{E}{x}_1$	(18a)	${\displaystyle \frac{(\dot{E}{x}_1-\dot{E}{x}_7){\eta }_{pump}}{{\dot{W}}_{pump}}}$	(18b)
ORC generator	$\dot{E}{x}_Q^{gen}+\dot{E}{x}_1-\dot{E}{x}_2$	(19a)	${\displaystyle \frac{\dot{E}{x}_2-\dot{E}{x}_1}{\dot{E}{x}_Q^{gen}}}$	(19b)
Expander	$\dot{E}{x}_{2a}-\dot{E}{x}_3-\dot{W}$	(20a)	${\displaystyle \frac{\dot{W}}{\dot{E}{x}_{2a}-\dot{E}{x}_3}}$	(20b)
ORC intercooler	$\dot{E}{x}_3+\dot{E}{x}_f-\dot{E}{x}_4-\dot{E}{x}_g$	(21a)	${\displaystyle \frac{\dot{E}{x}_g-\dot{E}{x}_f}{\dot{E}{x}_3-\dot{E}{x}_4}}$	(21b)
Low-pressure pump	$\dot{W}+\dot{E}{x}_5-\dot{E}{x}_6$	(22a)	${\displaystyle \frac{(\dot{E}{x}_6-\dot{E}{x}_5){\eta }_{Pump}}{\dot{W}}}$	(22b)
Ejector	${\dot{m}}_p{e}_{2b}+{\dot{m}}_s{e}_a-({\dot{m}}_p+{\dot{m}}_s)e_b$	(23a)	${\displaystyle \frac{{\dot{m}}_m{e}_b-{\dot{m}}_s{e}_a}{{\dot{m}}_p{e}_{2b}}}$	(23b)
Condenser	$\dot{E}{x}_b-\dot{E}{x}_c$	(24a)	${\displaystyle \frac{\dot{E}{x}_h-\dot{E}{x}_j}{\dot{E}{x}_b-\dot{E}{x}_c}}$	(24b)
Cooling tower	$\dot{E}{x}_h-\dot{E}{x}_i$	(25a)	0	(25b)
Cooling water pump	$\dot{W}+\dot{E}{x}_i-\dot{E}{x}_j$	(26a)	${\displaystyle \frac{(\dot{E}{x}_j-\dot{E}{x}_i){\eta }_{Pump}}{\dot{W}}}$	(26b)
Working fluid pump	$\dot{W}+\dot{E}{x}_e-\dot{E}{x}_f$	(27a)	${\displaystyle \frac{(\dot{E}{x}_f-\dot{E}{x}_e){\eta }_{Pump}}{\dot{W}}}$	(27b)

where T_hw,in is the inlet temperature of the hot water [°C]; P_gen is the generator pressure [kPa]; η_gen, η_exp, and η_pump are the thermal, isentropic, and pump efficiencies of the generator, expander, and pumps, respectively; ${\dot{m}}_{wf}$ and ${\dot{m}}_{cw}$ are the mass flow rates of the working and cooling fluids [kg/s]; and ${\dot{E}x}_F$ denotes the exergy fuel or total exergy input [kW_ex].

3. Economic Model

In this context, engineering economics employs both quantitative and qualitative methods to evaluate the effectiveness of a proposed project by comparing it to an alternative improvement technique. It also determines whether the design constitutes a sound investment. Economic analysis considers the initial investment as well as the cash flows generated by the project during its operational phase.

Cost estimation divides the project’s cash flows into two categories: total cost (representing the initial investment) and operating costs (including annual maintenance and operational expenses). Regardless of the chosen methodology, both cost types and the anticipated project lifetime must be incorporated. Economic analysis evaluates these factors collectively to determine the project’s financial feasibility and profitability.

Fixed capital cost comprises the initial investment in system equipment and installation costs incurred at the project’s outset, including connection equipment and working fluid. Variable or operating costs primarily encompass operation and maintenance expenses as well as energy costs such as fuel consumption.

The benefits of energy investments are typically assessed using the Energy Return on Investment (EROI), which is defined as the ratio of energy produced to energy consumed. This metric indicates the energy input required to generate a specific amount of usable energy. However, evaluating the benefits of waste heat recovery-to-power generation projects is often more complex than evaluating those of conventional electricity generation systems that rely on well-defined fuel sources. A comprehensive economic assessment is therefore essential to demonstrate the effectiveness of a proposed system. In this context, the total project investment consists of several cost components, as outlined in Equation (28) [22].

$$FC=C_{invs}+C_{inst}$$

(28)

Equation (28) defines the total fixed capital investment (FC) as the sum of all component purchase costs, installation costs, and system installation with interconnecting piping [22]. Equation (29) specifies the cost of installed equipment.

$$C_{invs}=\sum _{i=0}^n{Z}_i$$

(29)

where FC is the total fixed capital investment cost [THB]; C_invs is the total purchase cost of installed equipment [THB]; C_inst represents the installation and interconnection costs [THB]; and Z_i is the purchase cost of the ith component in the system [THB].

The cost of part i is the cost reported in 2024 using the CEPCI, as per Equation (30).

$$Z_{2024}=Z_{referenceyear}\times \left({\displaystyle \frac{Costindexfor2024}{Costindexfororigindyear}}\right)$$

(30)

The cost of system installation and piping is assumed to be 10% of the total equipment cost. ($C_{inst}$) is defined as follows:

$$C_{inst}=0.1\times C_{invs}$$

(31)

The plant operation cost (OC) consists of the cost of plant operation and maintenance (C_O&M) and the total cost of energy. The system uses electrical energy (C_TE) to operate, as shown in Equation (32).

$$OC=C_{O\&M}+C_{TE}$$

(32)

The operation and maintenance cost is 6% of the cost of the equipment installed in the system, as shown in Equation (33).

$$C_{O\&M}=0.06\left(C_{invs}\right)$$

(33)

The total cost of energy consists of electricity cost and fuel cost, and the heat pump system does not include fuel cost in the total cost, as shown in Equation (34).

$$C_{ TE }=C_{ Elec }+C_f$$

(34)

where C_O&M is the operating and maintenance cost, C_TE is the total cost of energy, C_Elec is the total cost of electricity, and C_f is the cost of fuel.

The components included in the system can be valued using the equations for calculating the price of equipment in a heat pump system, as shown in

Table 6. The cost formulation for the Cascade Organic Rankine Cycle combined with an ejector cooling cycle.

Component	Cost Function	Reference
Heat Exchangers	$Z_{ \mathit{HE} }=130{(A_{ \mathit{HE} }/0.93)}^{0.78}$	[13]
Low-Pressure Pump	$Z_{Pump}=705.48\times {\dot{W}}_{Pump}^{0.71}(1+{\displaystyle \frac{0.2}{1-{\eta }_{Pump}}})$	[13]
ORC Pump	$Z_{Pump}=705.48\times {\dot{W}}_{Pump}^{0.71}(1+{\displaystyle \frac{0.2}{1-{\eta }_{Pump}}})$	[13]
Ejector	$Z_{Ejec}=1000\times 16.14\times 0.989\times (\dot{m}(T_i/{(0.001P_i)}^{0.05})P_e^{-0.75})$	[13]
Cooling Water Pump	$Z_{Pump}=705.48\times {\dot{W}}_{Pump}^{0.71}(1+{\displaystyle \frac{0.2}{1-{\eta }_{Pump}}})$	[13]
Receiver Tank	$Z_{Rec}=3647.5\times 0.32\times {({\displaystyle \frac{Vol}{0.32}})}^{0.3}\times 0.985$	[14]
Liquid Accumulator	$Z_{Liq}=3647.5\times 0.32\times {({\displaystyle \frac{Vol}{0.32}})}^{0.3}\times 0.985$	[14]
Water Storage	$Z_{ws}=3647.5\times 0.32\times {({\displaystyle \frac{Vol}{0.32}})}^{0.3}\times 0.985$	[14]
Cooling Tower	$Z_{CT}=\left[746.749{(F_{in})}^{0.79}{(R)}^{0.57}{(A)}^{-0.9924}{(0.022T_{WB}+0.39)}^{2.447}\right]$	[15]
Expander	$Z_{Exp}=3880\times W_{exp}^{0.7}(1+{({\displaystyle \frac{0.05}{1-{\eta }_{exp}}})}^3)$	[22]
ORC Vapor Generator	$Z_{ORC,Gen}=\mathrm{1,7500}{({\displaystyle \frac{A_{evap}}{100}})}^{0.6}$	[24]
ORC Intercooler	$Z_{ORC,Int}=8000{({\displaystyle \frac{A_{Int}}{100}})}^{0.6}$	[25]
Condenser	$Z_{Cond}=8000{({\displaystyle \frac{A_{Cond}}{100}})}^{0.6}$	[25]

.

Investment analysis based on the discount rate method adjusts the value of cash flows to their present value. The equation for the net present value (NPV) is provided in Equation (35), while the payback period (PP) is defined separately in Equation (37).

$$NP{V}_n=-FC+\sum _{n=0}^{20}Y{(1+i)}^{-n}$$

(35)

In this analysis, i represents the appropriate interest rate and business opportunity cost, assumed to be 15%. The variable n denotes the lifetime of the proposed system, taken as 20 years, while Y represents the net cash flow at the end of year n, as expressed in Equation (36) [22].

$$Y=AI-\left(\begin{array}{c}{C}_{O\&M}+C_{TE}\end{array}\right)$$

(36)

where AI is the annual revenue C_O&M, and n is the operating and maintenance cost. The payback period of the system is considered to be year n when the NPV is greater than zero.

$$PP=min\{n:NPV(n)>0)$$

(37)

where FC is the total fixed capital investment cost [THB]; n is the project lifetime, taken as 20 years; Y is the annual net cash flow [THB/yr]; AI is the annual income or revenue from electricity generation [THB/yr]; C_O&M is the annual operation and maintenance cost [THB/yr]; C_TE is the annual total energy cost [THB/yr]; and PP is the payback period, expressed in years.

4. Exergoeconomic Model

The exergoeconomic model integrates thermodynamic performance with economic evaluation by assigning monetary values to exergy. This quantifies both investment and exergy-destruction costs within system components, helping identify key cost sources and informing strategies to improve efficiency and reduce overall energy conversion costs [26,27,28].

By combining the exergy balance equation with the exergoeconomic equation, Equation (38) is obtained.

$$E{x}_F^k=E{x}_P^k+E{x}_D^k$$

(38)

where ${\dot{E}x}_F^{\hspace{0.17em}k}$ is the exergy rate of the fuel supplied to component k [kW_ex], ${\dot{E}x}_P^{\hspace{0.17em}k}$ is the exergy rate of the product generated by component k [kW_ex], and ${\dot{E}x}_D^{\hspace{0.17em}k}$ is the exergy-destruction rate of component k [kW_ex].

The cost rate associated with exergy destruction in component k is evaluated by multiplying the unit cost of fuel with the exergy-destruction rate, as expressed in Equation (39).

$${\dot{C}}_D^k=c_F^k\dot{E}{x}_D^k$$

(39)

In the cost balance equation, the total cost rate of the product streams of component k equals the sum of the fuel cost rate entering the component and the cost rate related to the capital investment and O&M of component k, as expressed in Equation (40).

$$\sum {\dot{C}}_F^k+{\dot{Z}}_k=\sum {\dot{C}}_P^k$$

(40)

Solving the cycle cost balance equations enables the identification of the individual exergy-based costs of each component and provides an accurate thermo-economic assessment that accounts for capital investment, maintenance, energy costs, and energy quality within the cycle. The capital investment cost rate of component k, along with the mechanical and thermal cost rates, can be expressed as follows:

$${\dot{Z}}_k={\dot{Z}}_k^{CI}+{\dot{Z}}_k^{OM}$$

(41)

The cost rate of an inlet thermomechanical stream i is evaluated by multiplying the unit exergy cost with the exergy rate of the stream:

$${\dot{C}}_i=c_i\dot{E}{x}_i=c_i{\dot{m}}_{i}e{x}_i$$

(42)

Similarly, the cost rate of a product (outlet) stream e is expressed as follows:

$${\dot{C}}_e=c_e\dot{E}{x}_e=c_e{\dot{m}}_{e}e{x}_e$$

(43)

The cost rate associated with mechanical power is obtained by multiplying the unit cost of work by the shaft power:

$${\dot{C}}_w=c_w\dot{W}$$

(44)

The cost rate related to thermal exergy transfer is as follows:

$${\dot{C}}_Q=c_Q\dot{E}{x}_Q$$

(45)

In this study, ${\dot{Z}}_k^{OM}$ denotes the operation and maintenance cost rate of component $k$ [THB/hr], while $c$ and $\dot{C}$ represent the unit exergy cost and the cost rate [THB/hr], respectively. In addition, ${\dot{Z}}_k^{CI}$ corresponds to the annualized capital investment cost of each component [THB/hr].

The cost associated with exergy destruction in component k is obtained by multiplying the unit cost of fuel with the exergy-destruction rate, as defined by the exergy balance relations. Based on these definitions, the cost balance for component k can be written as follows:

$${\dot{C}}_Q^k+\sum _i{\dot{C}}_i^k+{\dot{Z}}_k=\sum _e{\dot{C}}_e^k+{\dot{C}}_W^k$$

(46)

For a steady-state control volume, the cost balance may be expressed in expanded form, as shown in Equation (47):

$$c_Q^k\dot{E}{x}_Q^k+\sum _i{\left(c_i\dot{E}{x}_i\right)}_k+{\dot{Z}}_k=\sum _e{\left(c_e\dot{E}{x}_e\right)}_k+c_W^k{\dot{W}}_k$$

(47)

In Equation (47), the total cost of all outgoing exergy streams from any component must equal the total cost required to generate those streams, which includes the cost of incoming exergy flows, fixed costs, and other associated expenses [29]. In general, a component may have several outgoing exergy streams (n_e), each representing an unknown cost variable in the exergoeconomic formulation shown in

Table 7. Cost balance and auxiliary equations of the components.

Components	Cost Equations	Auxiliary Equations
ORC Pump	${\dot{C}}_W^{pump}+{\dot{C}}_7+{\dot{Z}}_{pump}={\dot{C}}_1$	cF = 2.87 THB/kWh
LP Pump	${\dot{C}}_W^{pump}+{\dot{C}}_5+{\dot{Z}}_{pump}={\dot{C}}_6$	cF = 2.87 THB/kWh
ORC Generator	${\dot{C}}_Q+{\dot{C}}_1+{\dot{Z}}_{evap}={\dot{C}}_2$	cQ = 0.46584 kWh
Expander	${\dot{C}}_{2a}+{\dot{Z}}_{exp}={\dot{C}}_W^{exp}+{\dot{C}}_3$	c2 = c2a, cW = 3.3 THB/kWh, c3 = c2a
Intercooler	${\dot{C}}_3+{\dot{C}}_f+{\dot{Z}}_{int}={\dot{C}}_g+{\dot{C}}_4$	cS = cg
Ejector	${\dot{C}}_P+{\dot{C}}_S+{\dot{Z}}_{ejec}={\dot{C}}_b$	c2a = cP
Condenser	${\dot{C}}_b+{\dot{C}}_j+{\dot{Z}}_{cond}={\dot{C}}_h+{\dot{C}}_c$	ch = cc
Cooling Tower	${\dot{C}}_h+{\dot{Z}}_{CT}={\dot{C}}_j$

Note: (i) The electricity cost c_F = 2.87 THB/kWh_ex is based on the 2023 industrial tariff in Thailand (MEA/PEA) and is used as the fuel exergy cost following the SPECO methodology. (ii) The thermal exergy cost c_Q = 0.46584 THB/kWh_ex is derived from the boiler fuel cost and corresponding heat production rate, consistent with standard SPECO cost–exergy allocation rules [16]. (iii) The cooling water pumping electricity cost c_W = 3.3 THB/kWh_ex corresponds to the industrial tariff for auxiliary systems (MEA/PEA, 2023).

. However, only one cost balance equation is available for each component. Therefore, n_e−1 auxiliary equations are required, which are obtained from the Fuel Rule (F) and Product Rule (P), ensuring that the unit exergy cost of each stream can be uniquely determined.

The Fuel Rule defines the relationship between the exergy of the inlet and outlet streams that constitute the fuel of component k. According to this rule, the unit exergy cost of the fuel stream must be equal to the weighted average unit cost of the exergy supplied by the upstream components. This rule is used to establish auxiliary equations for all exergy-removal cases. The number of auxiliary equations generated equals the number of product streams defined as fuel for the next component in the system, consistent with the principles of exergoeconomic cost analysis, as expressed in Equation (48):

$$c_F^k={\displaystyle \frac{C_F^k}{\dot{E}{x}_F^k}}={\displaystyle \frac{1}{\dot{E}{x}_F^k}}\sum _{j=1}^{n_{j,F,k}}{c}_j\times \dot{E}{x}_i$$

(48)

Here, $c_F^{\hspace{0.17em}k}$ represents the unit exergy cost of fuel for component $k$ [THB/kW_ex], ${Ċ}_F^k$ denotes the total fuel cost rate [THB/hr], and ${\dot{E}x}_F^{\hspace{0.17em}k}$ is the exergy rate of the fuel stream [kW_ex].

Equation (41) defines the capital investment cost rate of component k, which is evaluated using the component purchase cost and the associated maintenance factor. Accordingly, this cost rate can be reformulated as follows:

$${\dot{Z}}_k={\displaystyle \frac{Z_k\times CRF\times \phi }{N}}$$

(49)

Here, N denotes the number of operating hours per year, and $\phi$ is the annual maintenance factor, assumed to be 6% of the component value [22]. The parameter i represents the interest rate, which strongly influences the payback period, while n indicates the equipment lifetime in years. The capital recovery factor (CRF) is calculated as a function of i and n, as expressed in Equation (50):

$$CRF={\displaystyle \frac{i\times (1+i{)}^n}{(1+i{)}^n-1}}$$

(50)

where CRF is the capital recovery factor.

The cost balance for each component in the cycle is solved to estimate the exergy-destruction cost rate associated with that component. In cases where the cost balance equation involves multiple inflows or outflows, the number of unknown cost parameters exceeds the number of available cost balance equations. To address this, auxiliary exergy equations based on the Fuel and Product Rules are applied, ensuring that the number of unknowns matches the number of governing equations [30]. By applying Equation (41) to each component, together with the auxiliary equations, a system of linear equations is obtained to determine the specific exergy costs.

$$\left[\dot{E}{x}_k\right]\times \left[c_k\right]=\left[{\dot{Z}}_k\right]$$

(51)

where the equation consists of the exergy rate matrix (from the exergy analysis), the exergy cost vector (to be estimated), and the factor vector (from the economic analysis), respectively [31]. The matrix form of the organic power cycle from Equation (51) is shown below.

$$\left[\begin{array}{cccc}\dot{E}{x}_2& 0& 0& 0\\ -\dot{E}{x}_2& \dot{E}{x}_3& 0& 0\\ 0& -\dot{E}{x}_4& \dot{E}{x}_4& 0\\ 0& 0& -\dot{E}{x}_4& \dot{E}{x}_1\end{array}\right]\times \left[\begin{array}{c}{c}_2\\ c_3\\ c_4\\ c_1\end{array}\right]=\left[\begin{array}{c}{\dot{E}}_Q·c_Q+{\dot{Z}}_{Evop}\\ {\dot{W}}_{Exp}·c_W+{\dot{Z}}_{Exp}\\ {\dot{Z}}_{Cond}\\ {\dot{W}}_{Pump}·c_W+{\dot{Z}}_{Pump}\end{array}\right]$$

where $c_w=c_{elec}$ is the cost of electricity, taken as THB 3.3 per unit. By solving these equations with the auxiliary equations shown in Table 7, the cost rates of each flow stream can be determined, which are then used to evaluate the cost rates of exergy destruction for each component of the cycle.

5. Results and Discussion

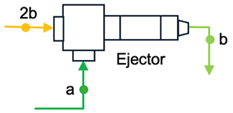
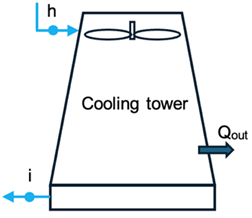
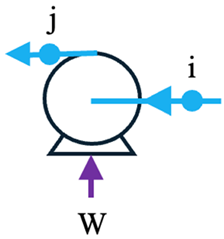
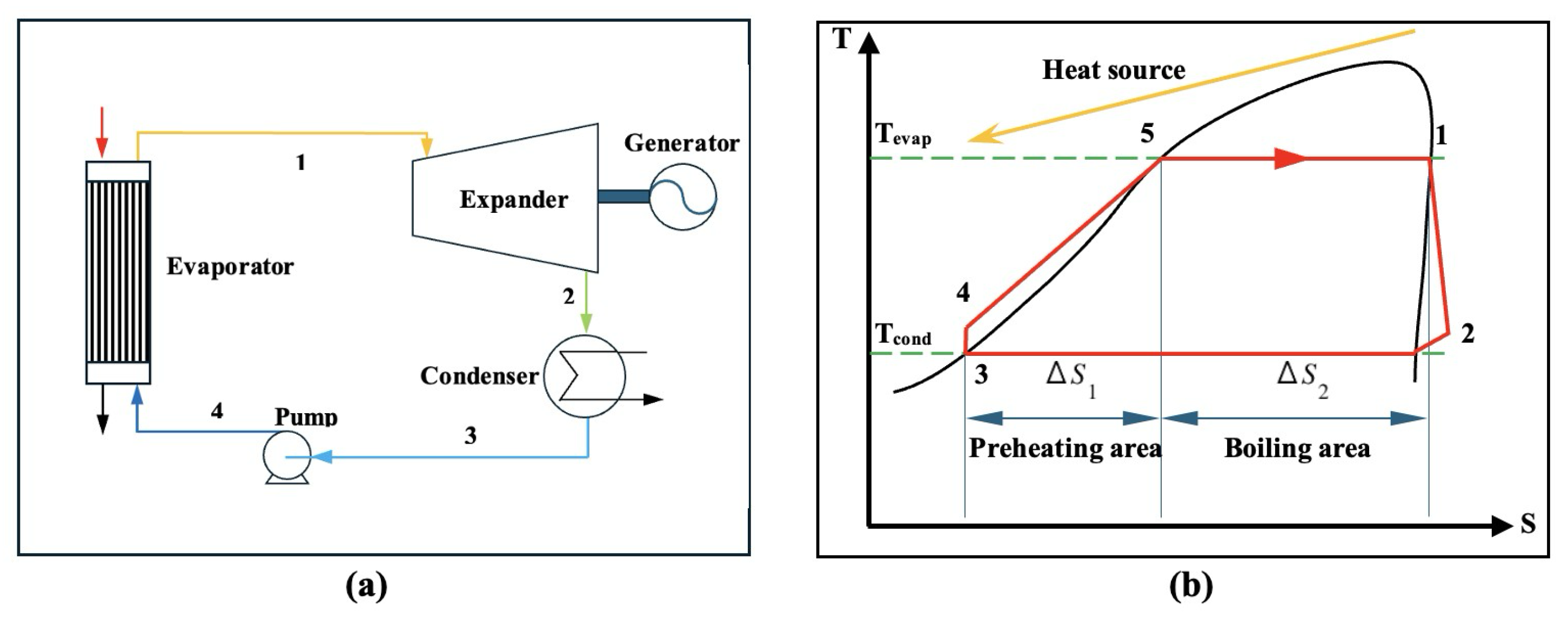
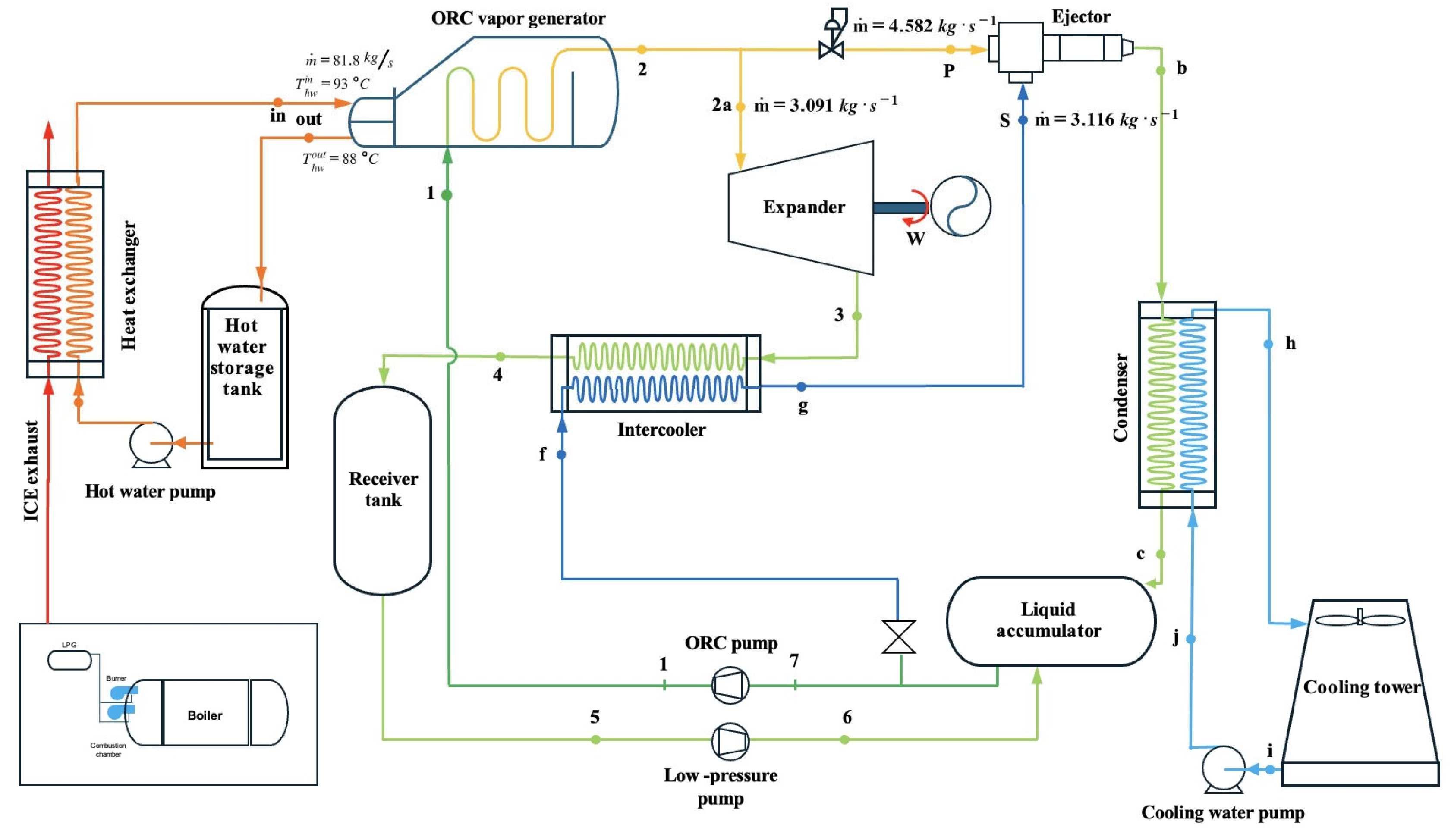
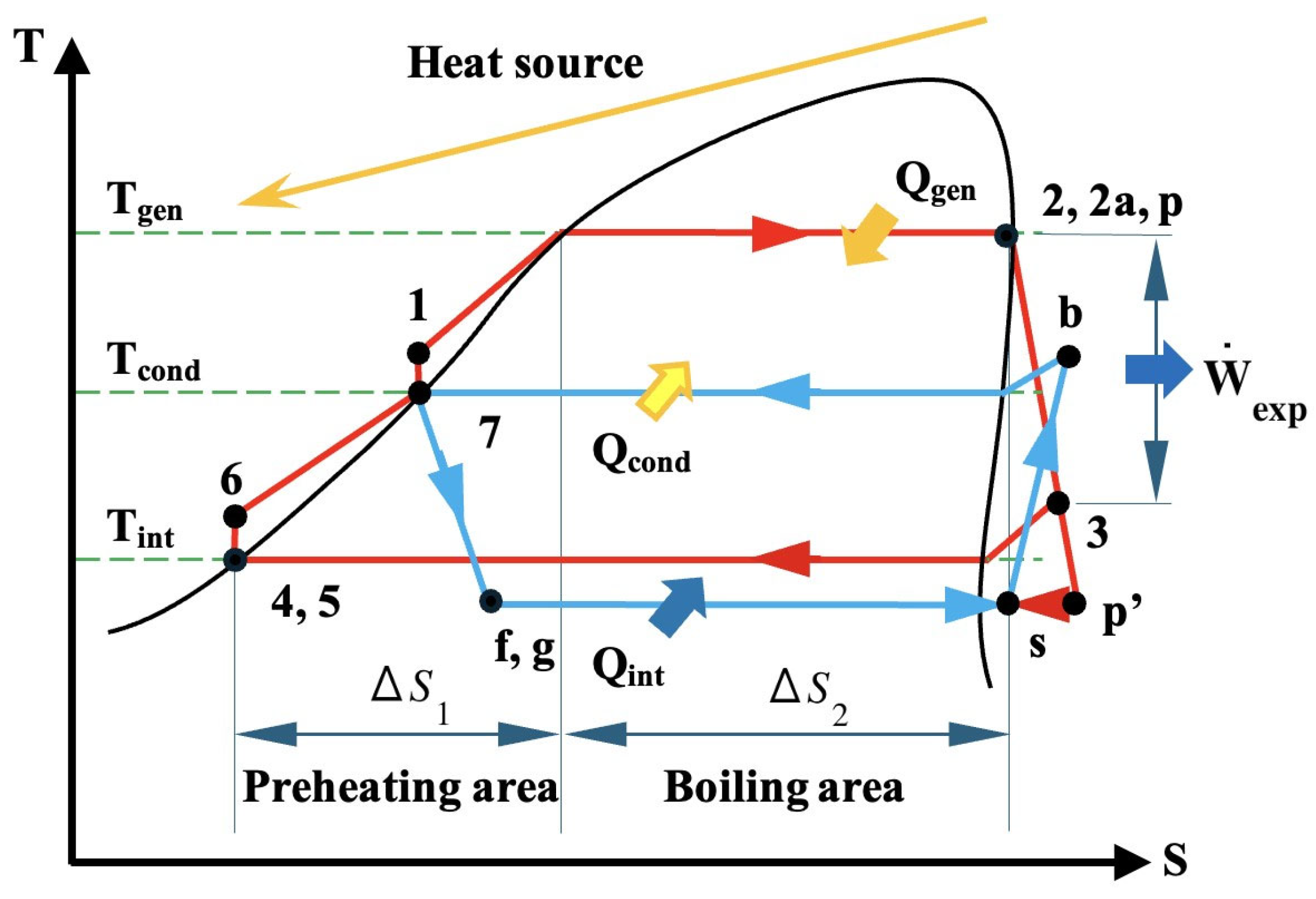
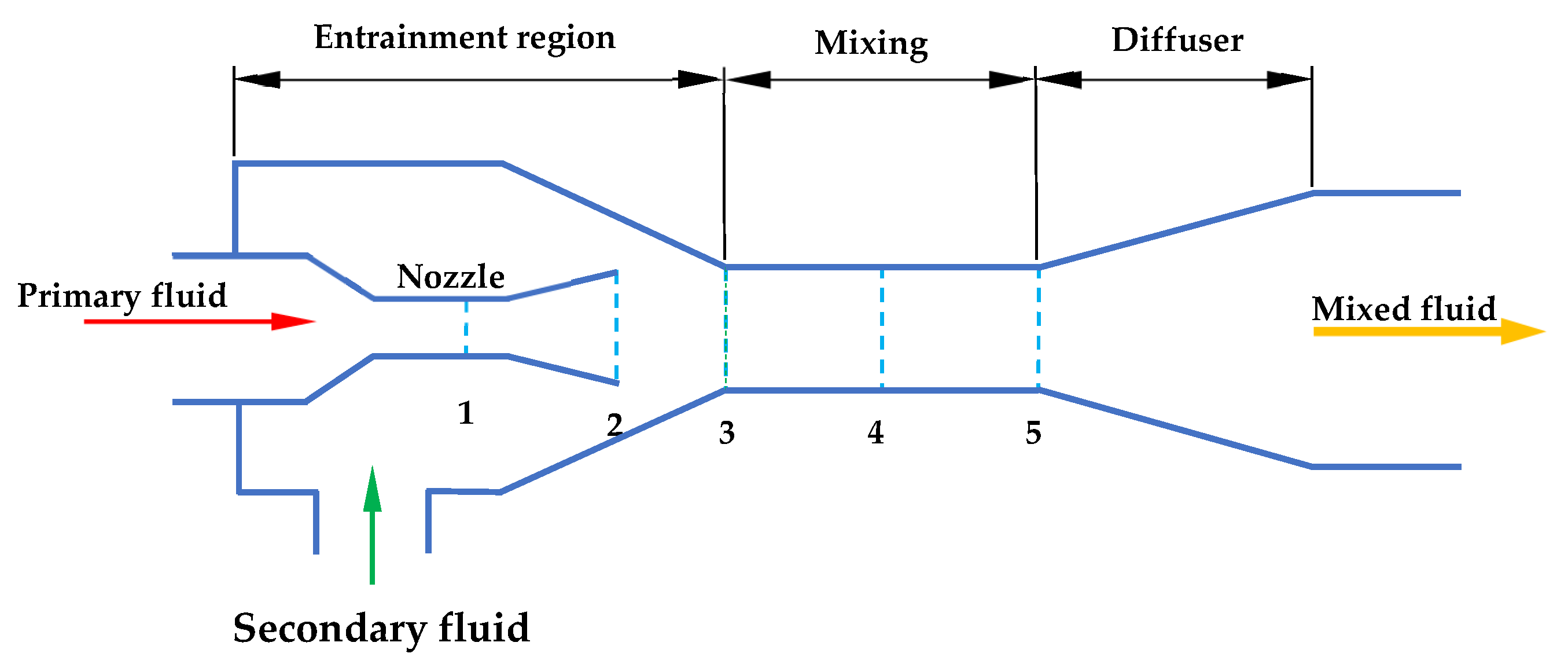
This section presents the economic modeling results and analyzes how key design choices affect the performance of a standard ORC compared to an integrated ORC–ejector refrigeration system. The conventional ORC, used as the baseline, operates with a vapor generator at 90 °C and releases unwanted heat at 30 °C, with an exergy input of 148.781 kW and a shaft work output of 79.717 kW.

5.1. Discussion Based on Energy and Exergy

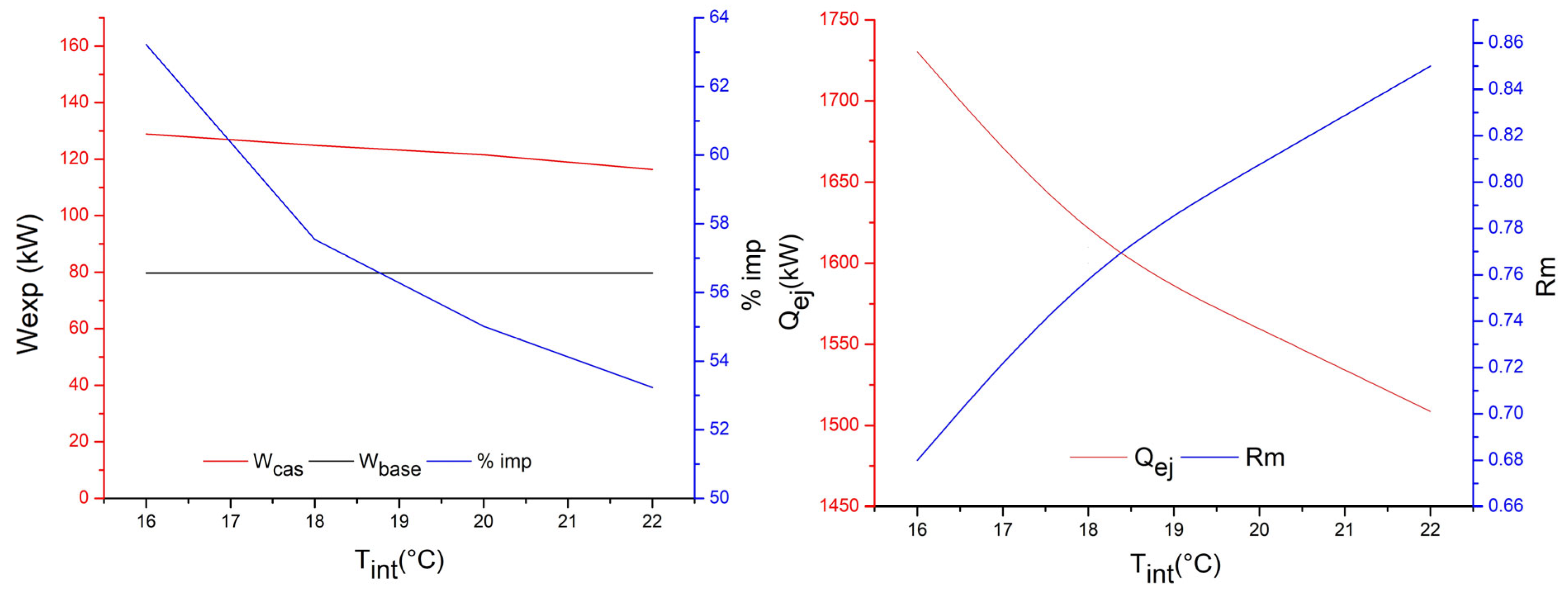
In the ORC–ejector system, the intercooler temperature has a significant impact on the temperature lift across the expander and the exergy supplied to the cycle. Increasing the intercooler temperature from 16 °C to 22 °C decreases the exergy input from 366.852 kW to 312.551 kW (

Table 8. The exergy input and expander work output vary with different intercooler temperatures.

Intercooler Temperature (°C)	Exergy Input (kW)	Work at Expander (kW)
Baseline (16)	148.7	79.7
16	366.8	128.9
18	335.7	124.9
20	333.6	121.6
22	312.5	116.3

Note: Baseline refers to the conventional ORC.

). This is the result of a decrease in the temperature difference between the hot and cold streams, which mitigates the heat transfer driving force and increases system irreversibilities. This behavior is consistent with the exergy-destruction patterns reported by Chen et al. [32] for ORCs under variable heat sink conditions. Higher intercooler temperatures also increase entropy generation during pre-expansion heating, consistent with the second law of thermodynamics characteristics described by Tsatsaronis & Winhold [26] and supported by recent ORC + ECC studies [2,32].

The effect of the intercooler temperature on the mechanical output is consistent with previous findings. As shown in Table 8, increasing the intercooler temperature reduces the shaft power output from 128.926 kW at 16 °C to 116.345 kW at 22 °C. This result is consistent with the exergy changes predicted by Equation (15), where useful work (W_exp) is associated with the exergy difference between pre- and post-expansion states. Lower intercooler temperatures increase the pre-expansion specific exergy, thereby improving the conversion of thermal energy into mechanical shaft power. These findings agree with the thermodynamic behavior observed in multi-level waste heat ORC plants, where the expander work output is highly sensitive to the pre-expansion exergy defined by the thermal boundary conditions [33].

These findings confirm that lowering the intercooler temperature reduces thermal irreversibilities, which results in increased exergy being delivered to the expander. This can enhance overall cycle performance. This mechanism accounts for the significant improvement in the ORC + ECC compared to the conventional ORC, especially at relatively low intercooler temperatures. This trend is in good agreement with previous work on ejector-assisted ORC configurations in which a lower condensation pressure can really enhance both thermodynamic and exergoeconomic performance [12,21,34,35].

The present work also investigates the impact of the vapor generator temperature on the thermodynamic performance of the ORC + ECC. The exergy input and mechanical output are examined, and the results are shown in

Table 9. The exergy input and expander work output vary with different generator temperatures.

Generator Temperature (°C)	Exergy Input (kW)	Work at Expander (kW)
Baseline (90)	148.7	79.7
85	329.5	121.2
90	366.8	128.9
95	404.8	134.9
100	439.8	142.0

Note: Baseline refers to the standard ORC (Std. ORC) configuration without ejector integration.

. It can be seen that increasing the generator temperature from 85 °C to 100 °C increases the exergy supplied to the cycle from 329.5 kW to 439.8 kW. This is the result of a larger temperature difference between the heat source and working fluid during the heating process. Higher generator temperatures also reduce entropy generation in the vapor generator and, hence, can improve the exergy quality of the working fluid.

An increase in the exergy input has high potential to yield a higher shaft power output. As shown in Table 9, the expander shaft work rises from 121.2 kW at 85 °C to 142.0 kW at 100 °C. According to Equation (15), the useful work output is proportional to the exergy difference across the expander (due to a larger expansion pressure ratio). Therefore, a higher generator temperature has high potential for thermal-to-mechanical power conversion, decreasing the irreversibilities associated with the expansion process.

The overall trend indicates that the working temperature of the vapor generator is a key parameter in the performance of both the conventional ORC and the ORC + ECC. Higher generator temperatures increase the available exergy and move the system closer to its optimal thermodynamic path in which the expander efficiency and overall cycle efficiency are improved. This interpretation agrees with classical exergetic analyses of thermal systems [21,26] and is supported by ORC + ECC investigations that show a reduction in the exergy destruction and higher shaft work at higher heat source temperatures. The improvement mechanism is also consistent with the experimentally validated ejector-assisted ORC behavior proposed by Chen et al. [2].

A comparison of the effects of varying the intercooler temperature and generator temperature shows that the exergy input and shaft power output respond differently. Increasing the intercooler temperature from 16 °C to 22 °C reduces the exergy input from 366.8 kW to 312.5 kW and decreases the shaft work output from 128.9 kW to 116.3 kW. This behavior agrees with heat transfer and second-law principles: a higher cold-side temperature lowers the thermal potential difference and reduces the available exergy.

Increasing the generator temperature from 85 °C to 100 °C raises the exergy input from 329.5 kW to 439.8 kW and increases the shaft work output to 142.0 kW. This improvement results from a vapor-greater hot-side thermal potential difference, which boosts the evaporating pressure, heat exchange effectiveness, and conversion of thermal energy into mechanical work. These findings are in good agreement with thermodynamic analyses of ORC systems operating under high source temperatures by Dai et al. (2009) [7] and Zhang et al. (2019) [36].

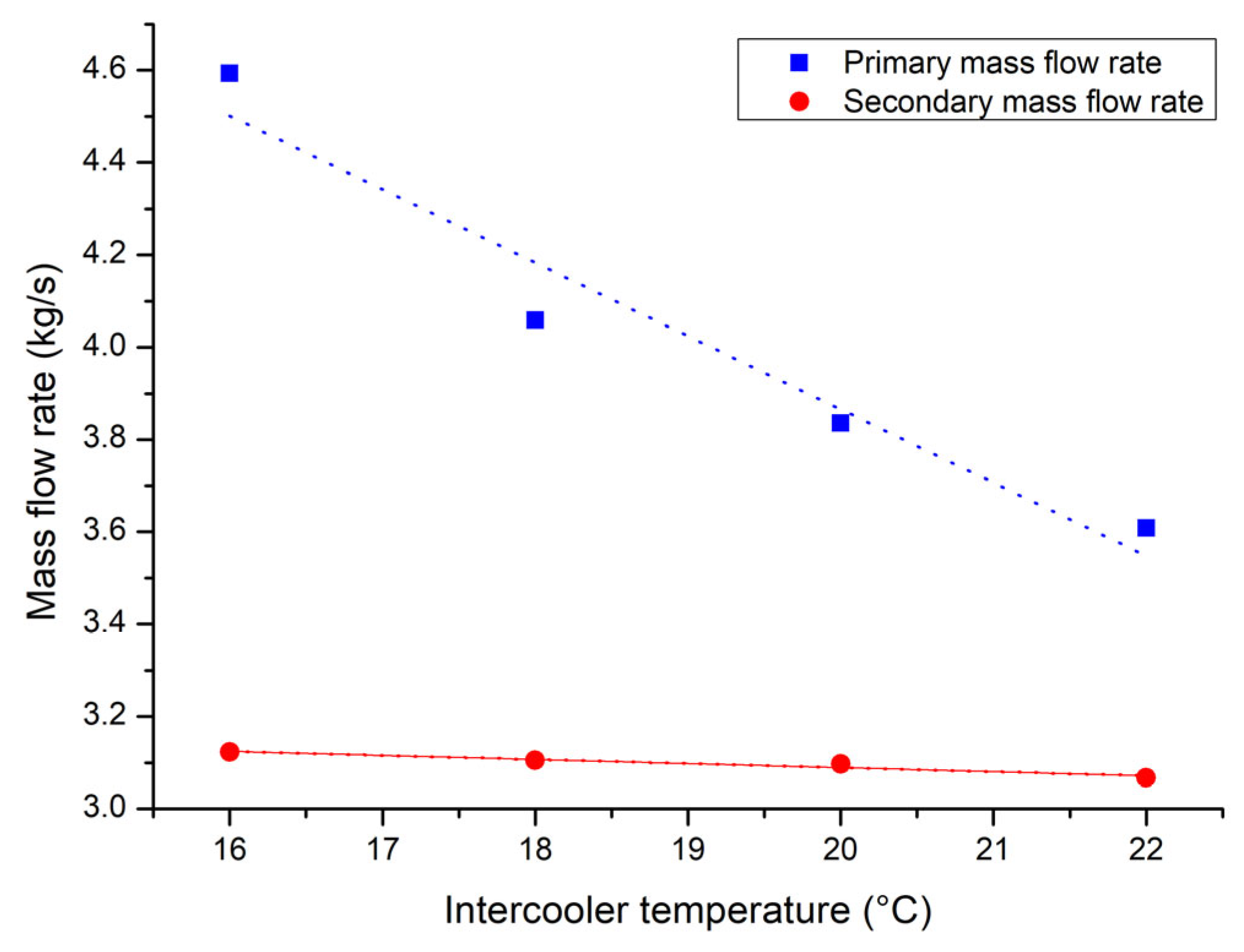
Figure 5 shows the primary and secondary mass flow rates against the intercooler temperature and indicates that increasing the intercooler temperature from 16 °C to 22 °C reduces the primary mass flow from 4.6 kg/s to 3.6 kg/s, while the secondary mass flow decreases slightly. The primary flow rate decreases because higher intercooler temperatures lower the working fluid density and suction pressure, which results in a lower mass entrainment capability. The slight decrease in the secondary mass flow rate is due to less sensitivity to the cold-side temperature in this operating range, consistent with characteristics reported in ejector-based ORC studies by Chen et al. [2] and recent preheated-ejector ORC studies by Hu et al. [37].

In an ejector cooling cycle, the intercooler temperature directly relates to the thermodynamic state of the primary (motive) and secondary (suction) streams. As the intercooler temperature increases, a higher secondary flow rate can be produced at a fixed primary mass flow rate (or a higher ability to produce cooling capacity). In other words, a lower primary mass flow rate is required for achieving an identical cooling capacity. This results in a higher entrainment performance when operating at higher intercooler temperatures. A lower primary mass flow rate means that the heat input to the system is decreased accordingly, which may provide better thermal performance of the whole system. However, the power generation results shown in Figure 6 do not hold true. This behavior is consistent with modern ejector flow dynamics reported in recent ORC + ECC studies [5,13,38]. Figure 6 shows that as the intercooler inlet temperature increases, the expander work output produced by the ORC + ECC decreases from 128.93 kW at 16 °C to 118.50 kW at 22 °C, even though the mass flow rate of the ECC is reduced (decreasing heat input). The reason for this is that at a lower intercooler temperature, the expansion pressure ratio across the expander is larger, which can yield higher shaft power. Under the same operating conditions (same heat source/heat sink), the baseline ORC remains nearly constant at around 80 kW due to the condenser operating at an ambient temperature, unlike in the case of the ORC + ECC. As a result, the improvement potential of the ORC + ECC over the baseline drops from approximately 62% to just above 50%. This confirms that lower intercooler temperatures significantly enhance the energy conversion efficiency of the integrated system.

As the intercooler temperature increases, the ECC requires a lower heat load from approximately 1720 kW to 1510 kW because of a reduction in the thermal driving potential between the hot and cold streams. Conversely, the entrainment ratio increases from 0.67 to 0.85 with higher intercooler temperatures, which indicates better mixing and momentum transfer processes inside the ejector when the intercooler temperature is increased. These trends are consistent with the experimentally validated ejector performance characteristics reported in Chen et al. [2].

These findings highlight a clear thermodynamic trade-off:

• Lower intercooler temperatures: higher expander work and greater exergy efficiency but require a higher heat load at the ejector.
• Higher intercooler temperatures: lower heat demand and a higher entrainment ratio but reduced mechanical output.

Similar temperature-dependent thermodynamic behavior has been documented in ejector-assisted ORC systems, where the interaction between the ejector suction temperature and primary/secondary flow dynamics governs exergy performance [2,32].

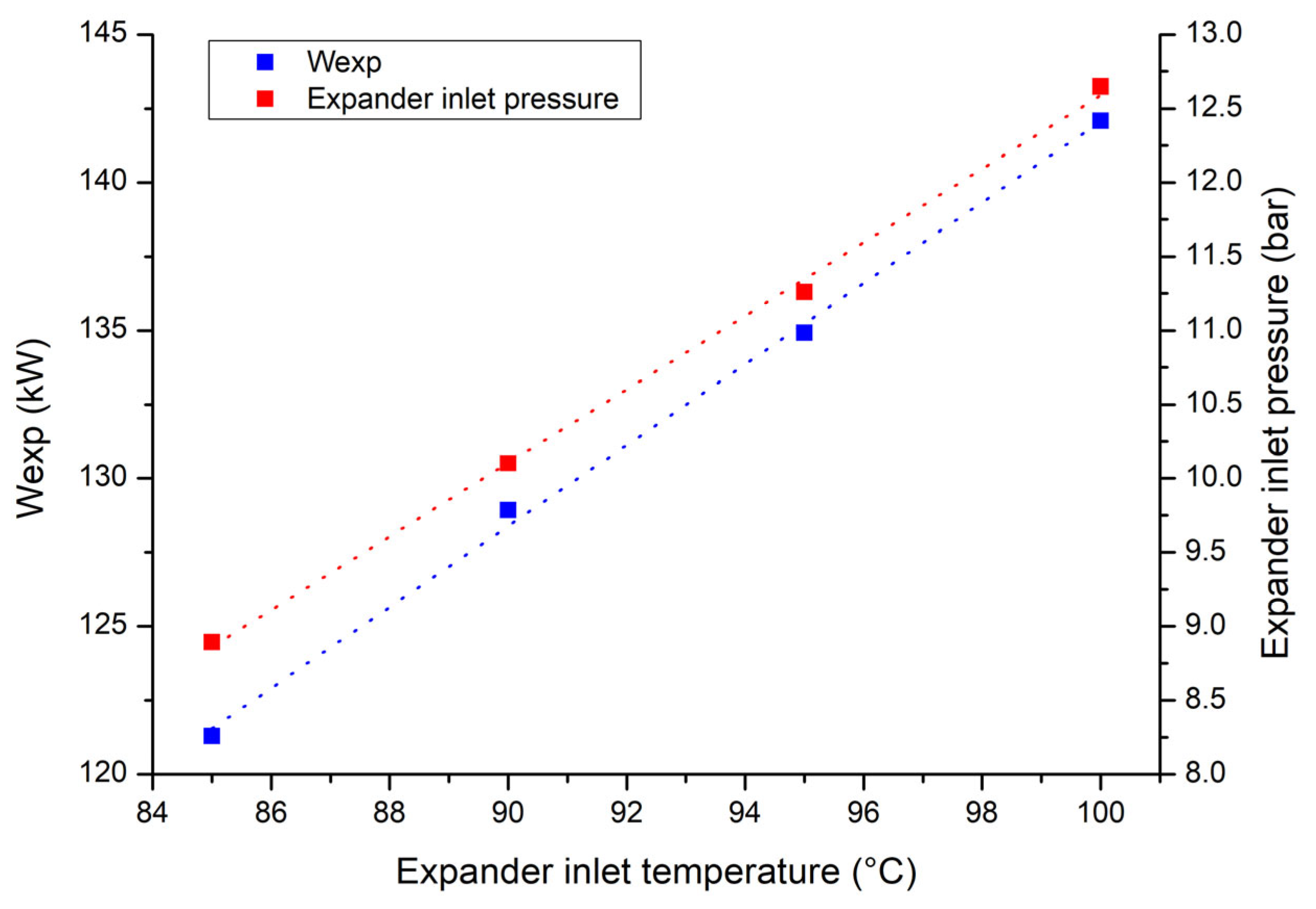
Figure 7 also shows that increasing the expander inlet temperature from 85 °C to 100 °C raises the mechanical power output from approximately 121 kW to 142 kW, while the inlet pressure rises from about 8.25 bar to 12.4 bar. This combined increase in pressure and temperature improves the specific exergy of the working fluid entering the expander, resulting in greater expansion work. This outcome is consistent with the published work in [7,39], in which higher upstream temperatures enhance the thermodynamic driving potential and reduce internal irreversibilities.

Furthermore, higher inlet temperatures increase inlet specific exergy, which can improve the energy conversion of thermal energy into mechanical power output. This in good agreement with previous work [2,21].

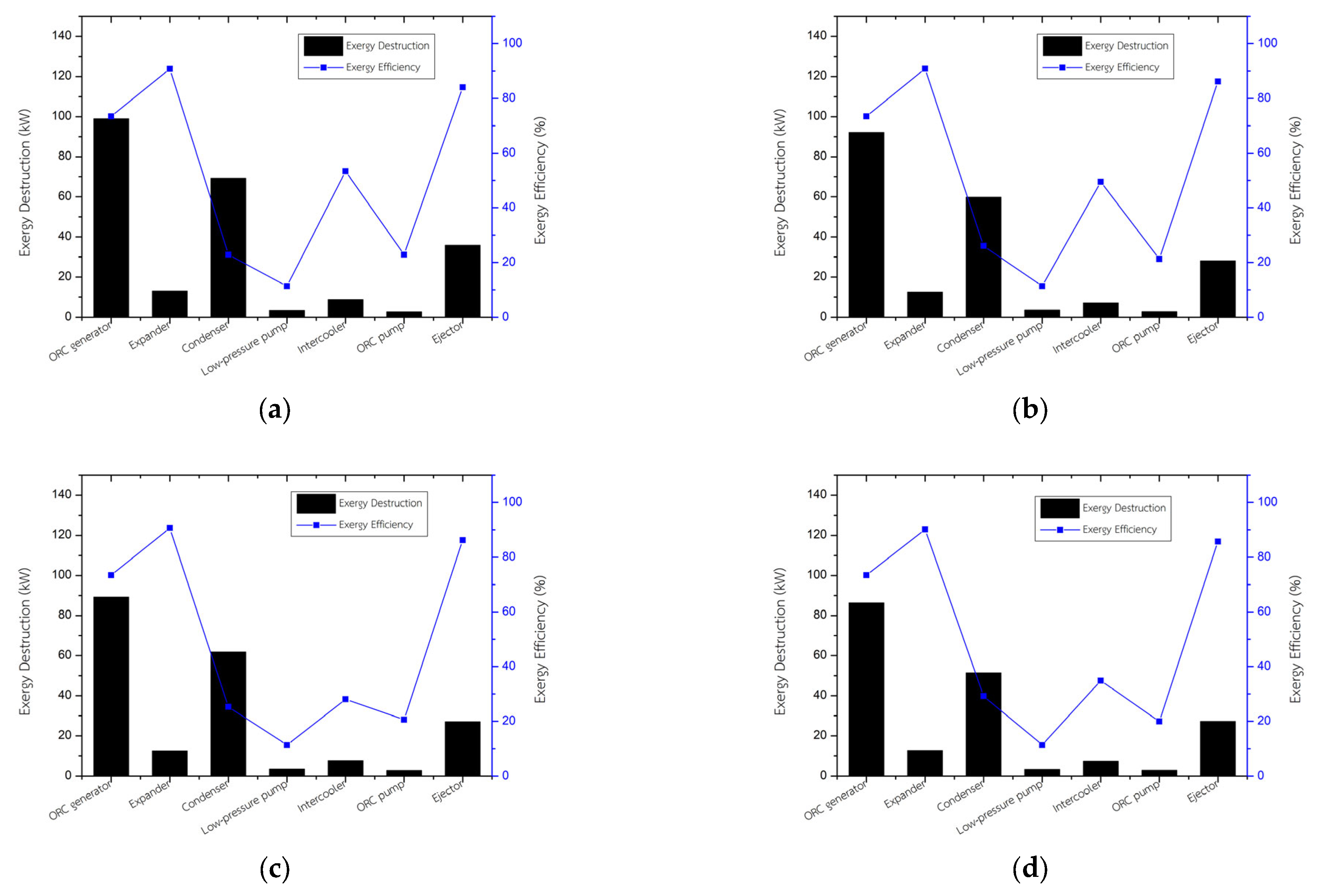
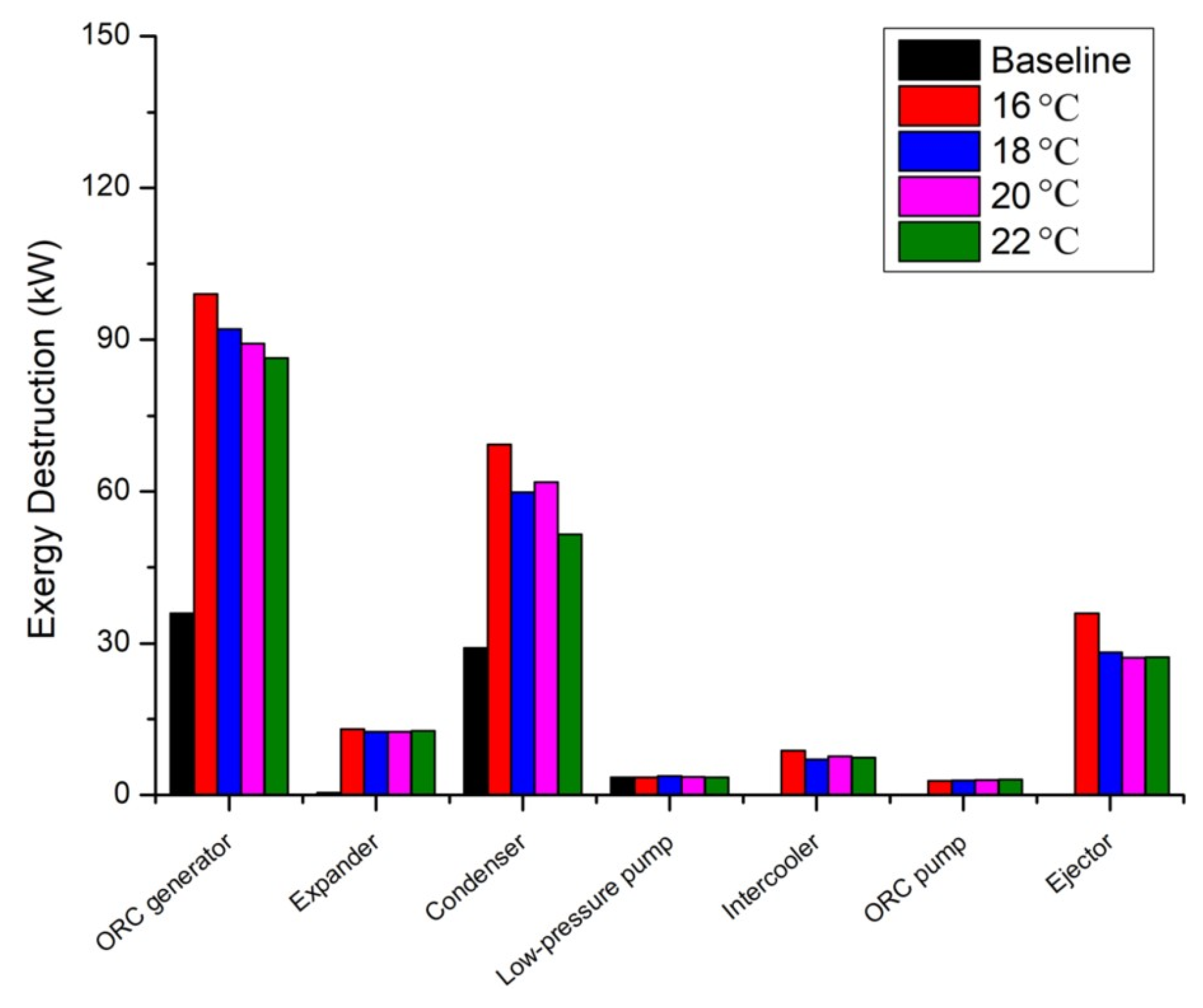
This study proposes a comparison of the exergy destruction of two ORC configurations: a conventional ORC and the ORC + ECC. Four intercooler outlet temperatures (16 °C, 18 °C, 20 °C, and 22 °C) are examined to assess how the change in the intercooler temperature affects the exergy destruction in key system components. Figure 8 presents the variation in exergy destruction across key ORC–ejector system components at intercooler inlet temperatures ranging from 16 °C to 22 °C. In the comparison, the vapor generator of both systems is the major source of thermodynamic irreversibility (highest exergy destruction). The exergy destruction rises from 35.97 kW to 96.2 kW at 16 °C, then decreases to 88.1 kW at 22 °C. This pattern highlights the generator’s sensitivity to the temperature difference during heat addition, as higher thermal driving forces increase entropy generation [8,39]. The condenser follows a similar trend, increasing from 29.12 kW to 67.4 kW at 16 °C, then decreasing to 54.1 kW at 22 °C. The pump, intercooler, and ORC pump each contribute less than 9 kW under all conditions. Ejector-side irreversibilities peak at 32.8 kW at 16 °C and stabilize near 27.5 kW at higher temperatures, consistent with ejector behavior under varying primary and secondary flow conditions [2,36]. Expander exergy destruction shows the greatest improvement over the baseline system. At 16 °C, expanders in the ejector-assisted ORC deliver 128.5 kW of useful work, decreasing to 120.2 kW at 22 °C. This result supports the principle that lower intercooler temperatures increase the pre-expansion specific exergy and reduce expansion losses [7].

Overall, although the ejector cooling side introduces some additional irreversibilities, its integration consistently reduces exergy destruction in major components compared to the baseline ORC. Its capacity to limit irreversibility at higher intercooler temperatures demonstrates improved adaptability and cycle stability, which are important advantages for low-grade waste heat applications.

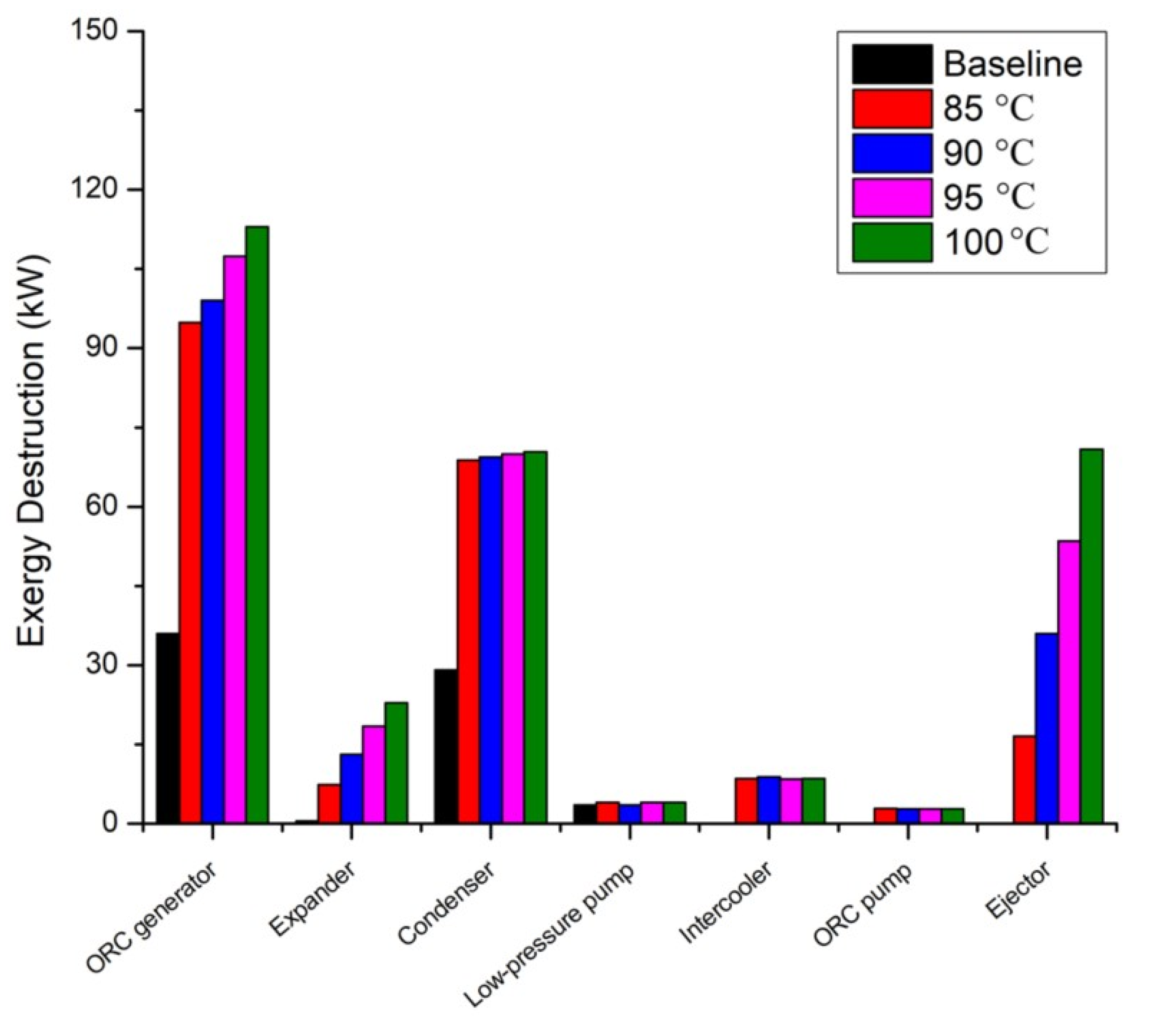
Figure 9 shows the distribution of exergy destruction among the main components of the ORC–ejector system at generator temperatures of between 85 °C and 100 °C. As the heat source temperature rises, the ORC generator experiences the largest increase in irreversibility, from 94.2 kW at 85 °C to 112.4 kW at 100 °C, which is much higher than the baseline of 35.9 kW. This trend aligns with second-law principles: a greater temperature difference between the external heat source and the working fluid increases entropy generation during vaporization, resulting in higher exergy destruction in the boiler [21,30]. Expander exergy destruction also increases significantly, from 9.7 kW to 25.1 kW, as the generator temperature rises. This higher expander irreversibility results from the greater exergy supplied to the expander at elevated heat source temperatures. Although more exergy is available, some is inevitably lost due to internal irreversibility resulting from higher flow velocities, an increased specific volume, and greater deviation from isentropic expansion [8]. Condenser exergy destruction remains relatively stable at 67–69 kW, nearly double the baseline value of 29.1 kW. These higher condensation losses result from the increased condenser load at elevated generator temperatures, which cause larger temperature differences during heat release. The pump, intercooler, and ORC pump together contribute less than 10 kW, showing that mechanical work losses are minor compared to thermal components. Ejector-side exergy destruction increases moderately, from 19.8 kW at 85 °C to 34.7 kW at 100 °C. This is due to greater momentum exchange and mixing losses caused by higher primary flow pressure and velocity at elevated generator temperatures [2].

Despite higher exergy destruction in several components, the system offers a clear benefit: the expander work output rises significantly, from 120.3 kW to 145.6 kW, compared to 83.2 kW in the baseline ORC. This shows that higher generator temperatures improve thermomechanical power recovery, even as the exergy destruction increases. Overall, the results confirm that higher heat source temperatures enhance useful exergy and second-law efficiency, despite increased component-level losses.

To provide a clear comparison, Figure 8 and Figure 9 are simultaneously interpreted based on the dominant sources of exergy destruction. In all cases, the ORC generator and condenser remain the major source of exergy destruction because of a large temperature difference during heat addition and release. When the ECC is integrated into the ORC, there is a decrease in the condensation temperature, which shifts part of the exergy destruction away from the expander toward the condenser and cooling tower. This is the result of operating with a lower expander backpressure and the working characteristics of the ejector cooling loop. Lowering the expander’s backpressure via an intercooler is key to reducing the exergy destruction at the expander. Hence, the ORC + ECC can achieve better expander performance and greater useful exergy output. In contrast, the baseline ORC maintains a higher expander irreversibility fraction due to the higher condensation pressure. These trends are consistent with the second law of thermodynamic behavior reported in recent ORC studies [11,38,40]. Therefore, Figure 8 and Figure 9 together clarify how condenser-side cooling and the intercooler temperature shape system-wide irreversibilities (indicating exergy destruction). This allows us to demonstrate the better thermodynamic quality in the ORC–ejector even when the system is operated under tropical conditions (similar ambient temperature to the conventional ORC).

Figure 10 presents the exergy destruction and exergy efficiency of each component of the ORC + ECC under intercooler temperatures of 16–22 °C. A decrease in the intercooler temperature can significantly mitigate exergy destruction, especially in the heat exchanger components (vapor generator and condenser), which agrees with second law of thermodynamics principles [21,30].

At 16 °C, the highest exergy destruction (about 110 kW) is found at the vapor generator. The exergy destruction decreases when the intercooler temperature increases. The reason for this is a smaller temperature difference between the working fluid and the heat source. The condenser is the second-largest source of exergy destruction, decreasing from approximately 70 kW at 16 °C to 50 kW at 22 °C. This is due to the phase transition during the condensation process. At the ejector, the exergy destruction remains moderate (25–35 kW), with an exergy efficiency of around 80%. This indicates that the ejector maintains strong entrainment performance regardless of the intercooler temperature, consistent with previous findings [2,9]. The expander achieves the highest exergy efficiency among all components, typically above 90%, with destruction of 8–12 kW. Such results indicate that the mechanical expansion process generates less destruction than thermal processes. Lower intercooler temperatures can increase the specific exergy at the expander inlet, thereby improving the conversion to shaft power. All liquid pumps exhibit relatively low exergy destruction (less than 10 kW), with exergy efficiencies ranging from 40% to 70%. Slight variations in the intercooler temperature have a slight impact on the changes in the working fluid density and pumping power, as noted in previous ORC optimization studies [8,36]. This has a slight impact on exergy destruction when varying the intercooler temperature.

Overall, Figure 10 confirms that lower intercooler temperatures can improve component exergy efficiencies and reduce system irreversibilities (lower total exergy destruction), especially in the generator and condenser. This is consistent with the earlier conclusion that the intercooler temperature is a key design variable affecting both thermal performance and second-law efficiency in the ORC + ECC.

Figure 11 illustrates the exergy destruction and component efficiencies of the ORC + ECC as the generator temperature increases from 85 °C to 100 °C. It can clearly be seen that higher generator temperatures reduce the exergy destruction in components associated with heat addition and expansion, thereby strengthening thermodynamic performance. This behavior is consistent with fundamental exergy theory and previous analyses of high-temperature ORC configurations [2,36].

The vapor generator has the highest exergy destruction among all components, increasing from 105 kW at 85 °C to about 115 kW at 100 °C. This rise is due to a larger temperature difference between the heat source and the working fluid during the heating process. Although the entropy generation in the generator is increased, the higher inlet temperature significantly increases the specific exergy of the vapor entering the expander. This effect enables a greater yield of useful mechanical work. The condenser has the second-highest exergy destruction (around 65–70 kW under the investigated temperatures, with exergy efficiencies of between 20% and 30%). A slight change in the exergy destruction of the condenser indicates that the changes in the generator temperature have a slight effect on the condensation irreversibilities. This means the exergy destruction in the condenser primarily depends on the temperature difference during heat release rather than upstream heat addition. The expander performs the highest thermodynamic performance, as it shows the lowest exergy destruction, with efficiencies of up to 90% at all generator temperatures. Exergy destruction increases from about 10 kW at 85 °C to nearly 23 kW at 100 °C due to higher specific exergy at the expander inlet. This can increase the useful mechanical work; however, entropy generation during the expansion process through the expander is also increased. Despite this, high efficiency shows the potential of converting exergy input into useful mechanical work. The ejector shows a moderate increase in exergy destruction, from about 20 kW at 85 °C to over 60 kW at 100 °C, while maintaining efficiency near 80%. This is due to increased entrainment and higher motive flow velocity at higher generator temperatures, as also reported in recent ORC–ejector studies [9,36]. Although higher generator temperatures are the cause of more mixing irreversibilities being produced in the ejector, the performance is acceptable because the increased motive flow exergy supports efficient momentum transfer between streams.

Overall, the component-level analysis in Figure 11 shows that increasing the generator temperature enhances the available exergy, improves expander performance, and increases cycle efficiency, despite higher destruction in thermal components. This confirms that the generator temperature is a key thermodynamic factor controlling power recovery and second-law efficiency in the ORC + ECC.

The ORC + ECC can perform lower total exergy destruction than the conventional ORC, as presented in Figure 8, Figure 9, Figure 10 and Figure 11. The key to this is thermodynamic improvement by means of the ejector cooling cycle. The ejector can produce lower suction, which results in a cooling effect produced at the intercooler. Furthermore, pressure recovery via the presence of a shock wave (known as the pressure lift effect) is a significant process in which the system can release unwanted heat at a relatively high condenser pressure. This results in decreased entropy generation during phase change and reduces exergy destruction in both the condenser and the expander. A lower expander discharge pressure via the intercooler can lead to a higher expansion pressure ratio across the expander, which results in higher useful exergy (mechanical shaft power) and less exergy destruction within the expander.

5.2. Discussion Based on Economics and Exergoeconomics

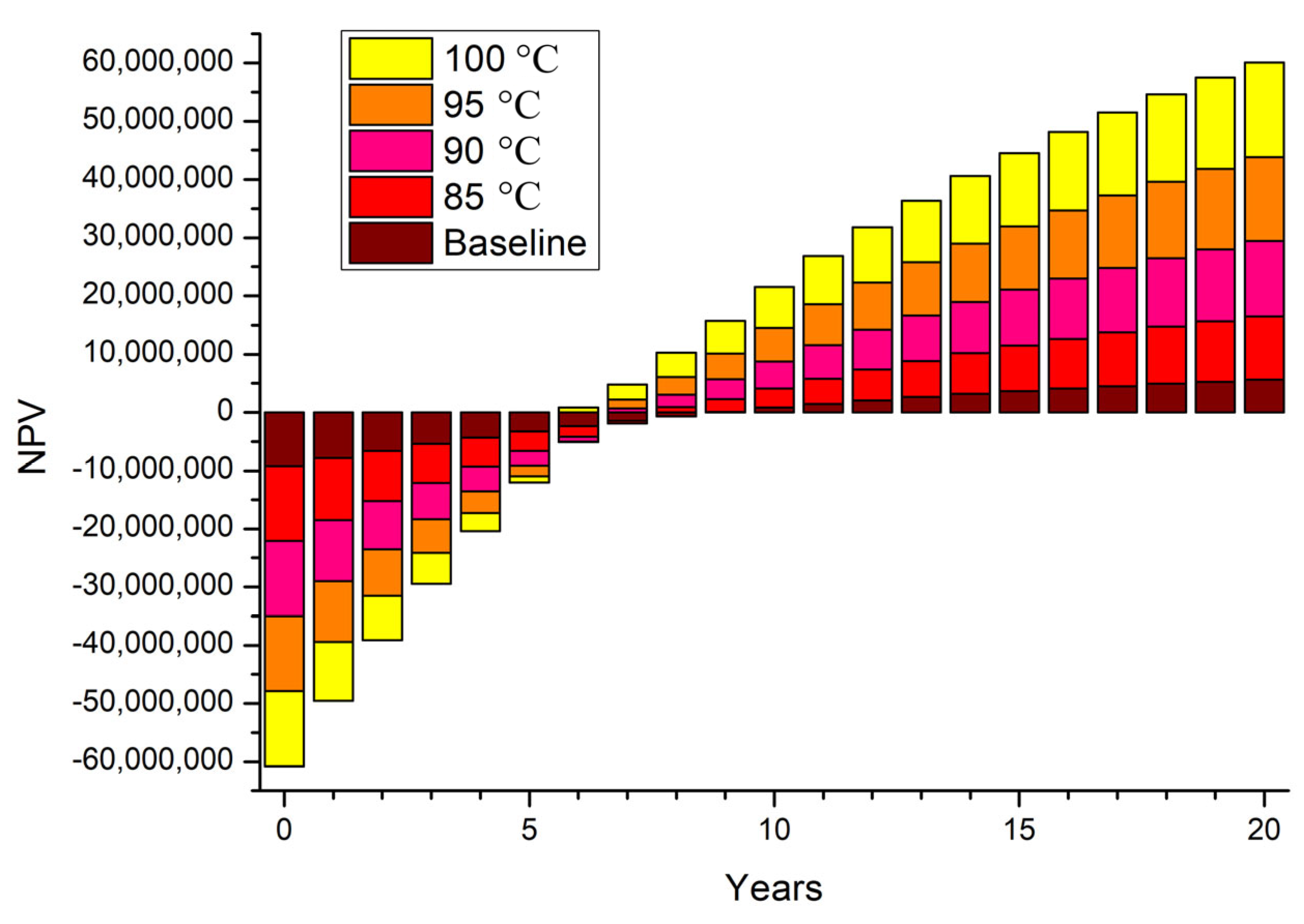
Figure 12 illustrates the long-term techno-economic performance of the ORC–ejector system by means of evaluating the net present value (NPV) over a 20-year period for intercooler temperatures of 16 °C, 18 °C, 20 °C, and 22 °C. All scenarios start with a negative NPV at year zero due to high initial capital costs, consistent with typical ORC investment behavior reported in the literature [1,34]. As the operation continues, annual revenues from power generation accumulate, and the NPV becomes positive, marking the start of economic recovery. Lower intercooler temperatures significantly improve profitability. The 16 °C case achieves the shortest payback period (about 6 years), followed by 18 °C (about 7 years) and 20–22 °C (about 8 years). Superior economic performance at lower intercooler temperatures aligns with thermodynamic trends: a reduced intercooler temperature increases the temperature gradient at the condenser, strengthens heat transfer, and improves the expander shaft power [8,17]. This increase in the mechanical output directly leads to higher annual electricity sales and faster capital recovery.

By year 20, the 16 °C configuration achieves the highest NPV, followed by 18 °C, 20 °C, and 22 °C. All ORC–ejector configurations outperform the baseline ORC without ejector integration, which has a delayed payback period of about 10 years. Similar improvements in economic feasibility have been reported in hybrid ORC + ECC and waste heat recovery systems [6,7,28].

These results confirm that the intercooler temperature is a key factor affecting both thermodynamic and economic performance. Lowering the inlet temperature improves cycle exergy efficiency, reduces irreversibility at the condenser–ejector interface, and significantly increases long-term profitability, consistent with exergy–economic coupling principles in ORC systems [21]. Optimal intercooler temperature selection is therefore critical for commercial viability in low-grade heat recovery ORC projects.

Figure 13 shows the economic performance of the ORC and ORC–ejector systems at generator temperatures of 85 °C, 90 °C, 95 °C, and 100 °C over a 20-year project. As with typical ORC investments, all scenarios start with negative NPVs due to initial capital costs [1,34]. As electricity sales increase, annual cash flows become positive, which in turn raises the NPV.

Higher generator temperatures significantly improve long-term profitability. The shortest payback period occurs at 100 °C (approximately 6 years), followed by 95 °C (approximately 7 years) and 90 °C (approximately 7–8 years). The slowest recovery is at 85 °C and in the baseline ORC, both reaching the break-even point at around year 8. This trend reflects the thermodynamic behavior discussed earlier: higher generator temperatures increase the pre-expansion specific exergy, enhance the expander work output, and improve the thermal-to-mechanical conversion efficiency [7,17]. The resulting increase in electricity production leads to stronger annual revenues and faster capital recovery. By year 20, the highest NPV is achieved at 100 °C, followed by 95 °C, 90 °C, 85 °C, and the non-ejector baseline. The growing gap between the 100 °C and baseline systems over time demonstrates the compounding financial benefits of higher generator temperatures. Similar improvements from high-temperature heat addition in ORC and ORC + ECC systems have been reported in recent thermo-economic studies on high-temperature preheating or geothermal-driven ejector cycles [6,28,36].

Overall, the results confirm that the generator temperature is a key factor in the economic feasibility of ORC–ejector systems. Higher generator temperatures provide greater exergy input, increased mechanical output, and improved annual profit margins, which align with exergoeconomic principles linking component irreversibilities to system-wide cost performance [21,39]. Therefore, adopting higher generator temperatures significantly enhances both the economic sustainability and long-term investment viability of ORC-based power generation systems.

To clarify the economic and technical benefits of the ejector-assisted ORC, we conducted a detailed analysis linking cost trends to system thermodynamics. The observed improvements in the NPV and reduced payback periods in Figure 12 and Figure 13 result from the ejector subsystem’s thermodynamic advantages. By lowering the condenser pressure and increasing the expander pressure ratio, the ejector enhances the shaft work output, which boosts annual electricity revenue and accelerates capital recovery. These results align with previous studies identifying the condenser backpressure as a key factor in ORC profitability [1,17]. Moreover, at lower intercooler temperatures, the ejector subsystem extracts more secondary flow, reduces heat release losses, and improves heat source utilization in the generator and pre-expansion stages. This increases thermal efficiency and net electricity generation. Similar economic gains from ejector-based cooling have been reported in hybrid ORC + ECC systems [6,9]. Consequently, the ORC + ECC consistently achieves higher annual cash inflow and a shorter payback period than the standalone ORC. From an investment perspective, the NPV analysis demonstrates that ORC systems are economically sensitive to thermodynamic improvements. The lowest intercooler temperature (16 °C) yields the highest cumulative NPV by maximizing power output and minimizing internal irreversibilities. This pattern matches findings in the literature, where greater exergy availability leads to improved cost-effectiveness [34,39]. Conversely, higher intercooler temperatures reduce the temperature lift and exergy input, weakening revenue and extending payback periods.

Overall, the economic advantage of the integrated ORC + ECC system stems from a combination of the following: (i) a higher net power output from reduced condenser pressure, (ii) improved heat source utilization and less destruction at low intercooler temperatures, and (iii) increased annual revenue from electricity generation. Together, these factors confirm that ejector-assisted operation is both more profitable and technically superior to the conventional ORC.

The long-term economic performance of the ORC + ECC shows a clear dependence on the generator temperature, which directly governs the second-law behavior of the cycle. As the generator temperature increases from 85 °C to 100 °C, the exergy supplied to the expander increases, while the internal irreversibilities decrease, yielding a higher useful work output. This thermodynamic enhancement translates into higher annual electricity revenue and a faster capital recovery.

At 100 °C, the system achieves the highest NPV with a payback period of approximately six years, followed by 95 °C (year 7), 90 °C (years 7–8), and 85 °C, which approaches the baseline system in both return magnitude and recovery time. These results indicate that an insufficient heat source temperature of 85 °C limits the exergy available to the expander, reducing economic benefits despite the presence of the ejector subsystem.

From a second-law perspective, higher generator temperatures enhance the exergy efficiency of heat addition, reduce the relative exergy destruction in both the boiler and the expander, and increase the specific shaft work delivered to the expander. These results are consistent with observations from recent ORC + ECC studies, where improved exergy quality at the heat source boundary was shown to be a key determinant of cost-effective electricity generation. Likewise, the beneficial trend aligns with Yang et al. [40], who demonstrated that higher expander pressure ratios driven by higher inlet temperatures directly strengthen the thermodynamic driving force and improve overall cost-effectiveness.

The exergoeconomic interpretation further clarifies this relationship: higher generator temperatures reduce the unit exergy cost of power c_w by lowering avoidable exergy destruction in the expander, while the ejector subsystem suppresses condenser-side irreversibilities, thereby reducing cost contributions from the cooling tower and condenser. As the generator temperature increases, the exergoeconomic factor f_k for high-impact components shifts in a favorable direction, indicating that a greater share of useful work is obtained per unit of capital-related cost. These combined second-law and exergoeconomic mechanisms provide strong evidence that the generator temperature is a dominant driver of long-term profitability for ORC + ECC under tropical operating conditions.

Consequently, higher generator temperatures strengthen both thermodynamic and cost-based performance, resulting in a significantly higher NPV over 20 years compared to the baseline ORC.

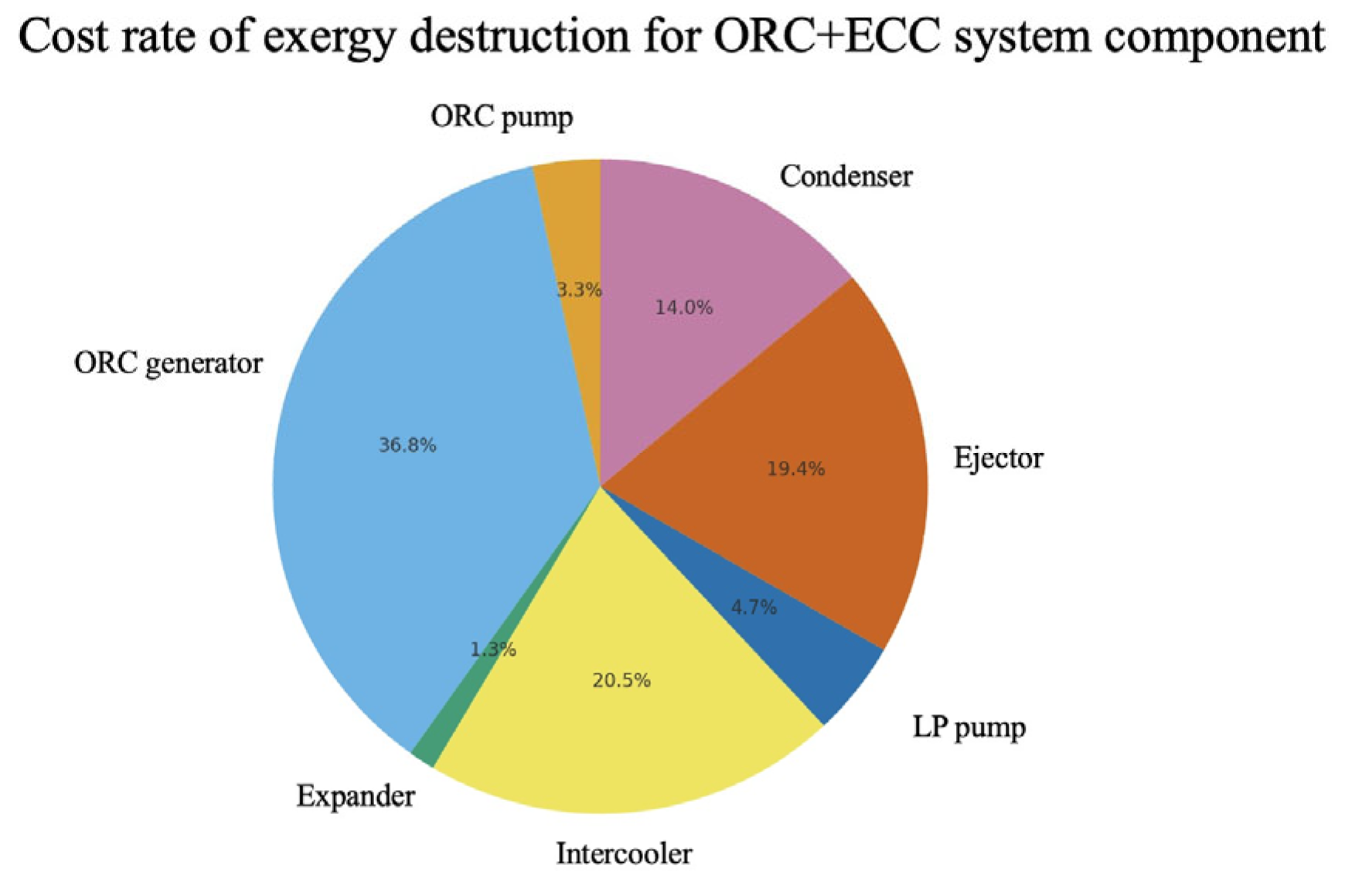
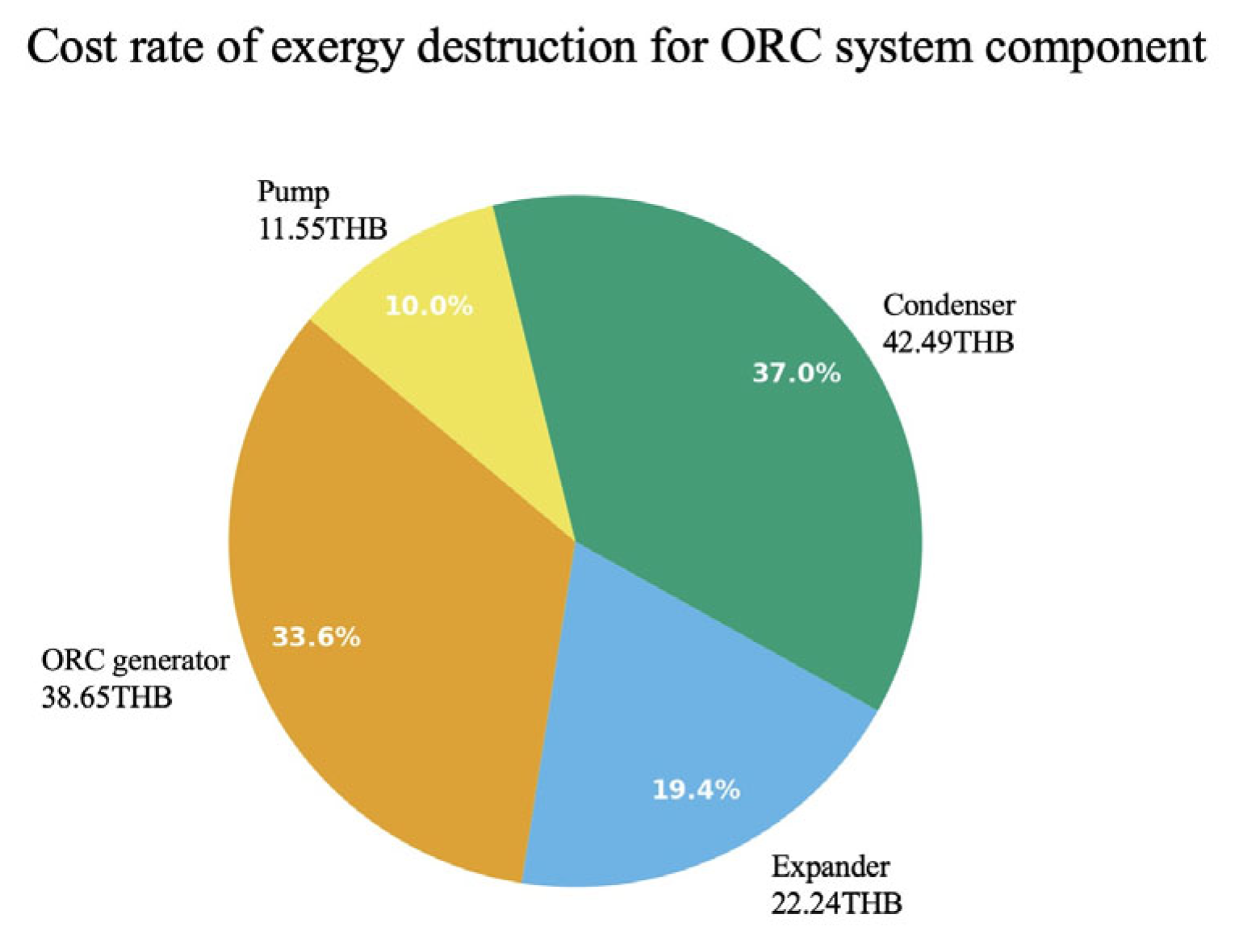
From the calculated costs, the exergy-destruction cost of each component can also be determined under the chosen reference parameter values. Figure 14 and

Table 10. Exergy flow rates, cost flow rates, and unit exergy cost associated with each state of ORC.

State	$\dot{\mathit{E}}$x (kW)	c (THB/kWh)	$\dot{\mathit{C}}$ (THB/hr)
1	23.87672	4.09124	97.69
2	112.91900	0.90863	102.60
3	51.63390	1.45935	75.35
4	22.51670	3.53479	79.59

show that the generator has the highest exergy-destruction cost, followed by the condenser [41].

The high exergy-destruction costs of the generator and condenser are mainly due to their significant exergy-destruction rates. In contrast, the pump’s cost is primarily driven by high fuel expenses rather than exergy destruction.

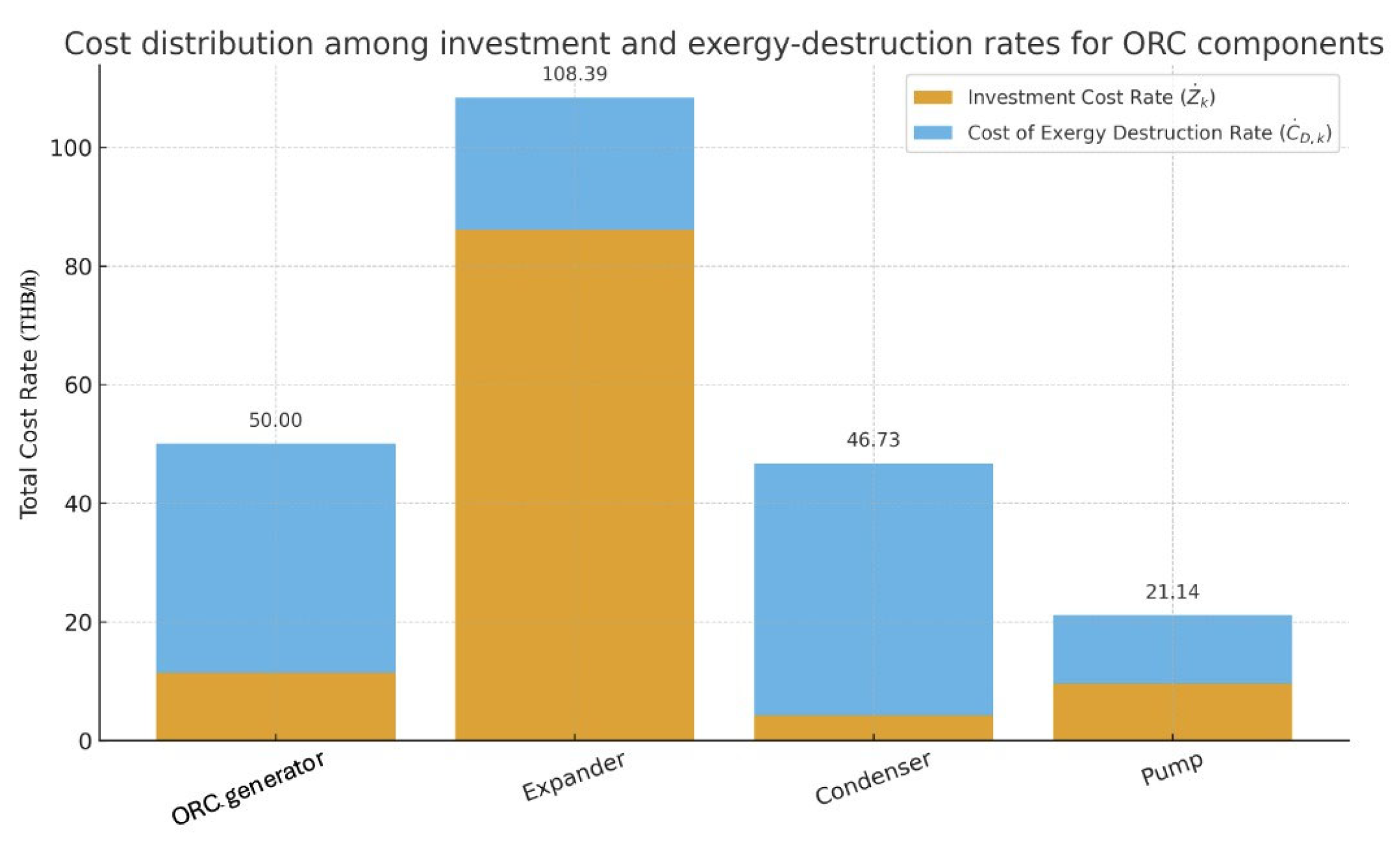
Before implementing any design or investment changes, we analyze the components with consideration given to the cost distribution, exergoeconomic significance, and how efficiency improvements affect the total investment cost. Figure 15 illustrates the distribution between investment costs and exergy destruction.

From an exergoeconomic perspective, the expander should be prioritized because it has the highest combined investment and exergy-destruction costs. The exergoeconomic factor assesses the relationship between the exergy efficiency and investment cost for these components.

Table 11. Investment cost rate, cost rate of exergy destruction, total cost rate, exergoeconomic factor, and relative cost difference associated with ORC components.

Component	${\dot{\mathit{Z}}}_{\mathit{k}}$ (THB/hr)	${\dot{\mathit{C}}}_{\mathit{D}}^{\mathit{k}}$ (THB/hr)	${\dot{\mathit{Z}}}_{\mathit{k}}+{\dot{\mathit{C}}}_{\mathit{D}}^{\mathit{k}}$ (THB/hr)	fk (%)	rk (%)
Generator	11.35	38.65	50.00	22.7	95.05
Expander	86.15	22.24	108.39	79.5	263.1
Condenser	4,24	42.49	46.73	9.1	142.2
Pump	9.59	11.55	21.14	45.4	23.98

presents the values for each component.

When analyzing the system components by considering both the investment cost rate and the exergy-destruction cost rate, the expander was found to have the highest total cost compared to the other components of the system. This outcome is primarily attributed to its significantly higher investment cost, as shown in

Table 12. Exergy flow rates, cost flow rates, and unit exergy cost associated with each state of the Cascade Organic Rankine Cycle combined with an ejector cooling cycle.

Stream	Component/State Description	c (THB/kWh)	$\dot{{\mathit{E}}_{\mathit{x}}}$ (kW)	$\dot{\mathit{C}}$ (THB/hr)
1	ORC Pump outlet to generator return	0.447	53.346	23.860
2	Generator outlet to ejector/expander inlet	0.810	338.431	274.195
2a	Split line to expander inlet	1.659	140.135	232.482
3	Expander outlet to intercooler inlet	0.000	2.333	0.000
4	Intercooler outlet to receiver tank inlet	0.119	21.246	2.528
5	Receiver tank outlet to low-pressure pump	0.003	21.246	0.063
6	Low-pressure pump outlet	0.944	21.458	20.252
7	Accumulator outlet to ORC pump/intercooler	0.071	51.973	3.686
g	Intercooler outlet to ejector	0.983	21.108	20.748
b	Ejector outlet to condenser inlet	1.310	189.639	248.407
h	Condenser outlet	2.034	111.348	226.530
j	Cooling tower outlet to condenser	1.000	48.118	48.118

.

Following the expander, the generator and condenser exhibited the next highest combined investment and exergy-destruction costs, with total costs of 50.00 and 46.73 THB/hr, respectively. In contrast to the expander, both components exhibit a high exergy-destruction cost rate (${\dot{C}}_D$), with the generator at 77.3% and the condenser at 90.9%, representing a higher proportion than the investment cost rate (${\dot{Z}}_k$).

For the pump, non-exergy-related costs and the total costs of components are divided rather equally, indicating that the current investment costs of these components are reasonable. In contrast, generators and condensers are estimated to have low exergoeconomic factors (f_k), indicating that cost savings from the exergy-destruction cost rate (${\dot{C}}_D$) in these components should be considered to reduce exergy losses and improve overall system efficiency.

Meanwhile, for pumps, improving component efficiency is more economically feasible, even if it results in an increased equipment investment cost.

The exergy costs for each stream in the ORC + ECC system is depicted in Figure 16 which shows how the unit cost and cost flow are distributed by the exergy rate. Streams 2, b, and h have the highest costs, identifying the condenser and cooling tower as key points in the cost distribution due to their large heat transfer requirements. Streams with a high unit cost but low exergy, such as Streams 6 and g, illustrate the secondary role of sub-flows from the intercooler and ejector in the overall cost structure. Streams 3 (c = 0) and 5 (c = 0.003) have very low unit costs, as exergy transfer here does not add significant cost. However, these streams are still necessary to maintain the balance equations in the SPECO method.

Unit costs (c) across streams vary significantly, from 0.0 to 2.03 THB/kWh. This aligns with Tsatsaronis and Winhold (1985) [26], who found that systems with multiple heat transfer circuits, such as the ORC + ECC, naturally produce cost imbalances in streams related to heat dissipation. Recent exergoeconomic studies [31] also confirm that heat exchangers are central to economic optimization due to their capital costs and influence on system performance.

Therefore, the condenser and cooling tower emerge as the highest-cost sources in ORC + ECC systems. They should be prioritized for design improvements, such as enhancing heat exchange efficiency, reducing exergy destruction, and developing advanced cooling water management strategies, to reduce the overall system cost [12,42,43].

The ORC + ECC demonstrates significant exergoeconomic potential in both the investment cost rate (${\dot{Z}}_k$) and the exergy-destruction cost rate (${\dot{C}}_D^k$).

For a standard ORC (shown in Table 11), the expander has the highest total cost at 108.4 THB/hr, primarily due to investment rather than exergy destruction. This aligns with Rosen and Dincer (2003) [41], who noted that the expander often dominates ORC system costs because of its high price and ongoing maintenance. The condenser (46.7 THB/hr) and generator (50 THB/hr) also contribute significantly, but their costs are mainly driven by exergy destruction [1,12,27].

For the ORC + ECC system (shown in

Table 13. The investment cost rate, cost rate of exergy destruction, total cost rate, exergoeconomic factor, and relative cost difference associated with the components of the Cascade Organic Rankine Cycle combined with an ejector cooling cycle.

Component	${\dot{\mathit{Z}}}_{\mathit{k}}$ (THB/hr)	${\dot{\mathit{C}}}_{\mathit{D}}^{\mathit{k}}$ (THB/hr)	${\dot{\mathit{Z}}}_{\mathit{k}}+{\dot{\mathit{C}}}_{\mathit{D}}^{\mathit{k}}$ (THB/hr)	fk (%)	rk (%)
ORC Pump	8.17	0.79	8.96	91.2	59.9
LP Pump	8.17	1.89	10.06	81.2	98.6
Generator	14.74	102.5	117.24	12.6	74.6
Expander	207.24	7.55	214.79	96.5	98.9
Intercooler	21.03	2.91	23.94	87.8	67.7
Ejector	4.95	47.9	52.85	9.4	18.6
Condenser	46.07	86.4	132.47	34.7	63.1
Cooling Tower	11.01	128.6	139.61	7.9	50.8

and Figure 17), the cost structure shifts, with the cooling tower (approximately 139.6 THB/hr) and condenser (approximately 132.5 THB/hr) incurring the highest total costs, mainly from exergy destruction. This is especially notable in circuits requiring significant heat exchange with cooling water. The generator (approximately 117.5 THB/hr) also shows substantial economic losses due to exergy destruction, supporting Tsatsaronis and Winhold (1985) [26], who identified heat exchangers as a common source of exergy cost in energy systems [12,42,44].

Incorporating an ejector cooling cycle (ECC) can enhance waste energy utilization and operational flexibility. However, it also increases exergy-destruction costs in heat transfer equipment, especially condensers and cooling towers. Future ORC + ECC system designs should focus on improving the thermal and exergy efficiency of heat exchangers and implementing advanced cooling water management to reduce overall system costs [10,18,26,41].

5.3. Comparative Evaluation of Conventional ORC and ORC + ECC

Exergoeconomic analysis depicted in

Table 14. Comparison of component-level cost structure, cost sources, and improvement strategies between the conventional ORC and the ORC + ECC with corresponding scholarly conclusions.

Aspect	Standard ORC	ORC + ECC	Scholarly Conclusion
Component with highest total cost	Expander (≈108.4 THB/h) [12,41]	Cooling tower (≈139.6 THB/h) and condenser (≈132.5 THB/h) [18,26,44]	In the standard ORC, the expander is the main bottleneck, while in the ORC + ECC, the cost bottleneck shifts to heat exchangers [18,44]
Main source of cost	High investment cost rate (${\dot{Z}}_k$) of the expander [12,41]	High exergy-destruction cost rate (${\dot{C}}_D^k$) in cooling tower and condenser [26,44]	The ORC + ECC is more sensitive to exergy destruction than investment costs [18,44]
Generator	≈50 THB/h, mainly due to exergy destruction [12,26]	≈117.5 THB/h, dominated by exergy destruction [44]	The generator remains a critical component in both systems [44]
Pumps	≈21.1 THB/h, the lowest in the system [10,39]	≈14–20 THB/h, also relatively low [10]	Pumps are not cost bottlenecks [10,39]
Improvement strategies	Reduce expander investment cost [12,41]	Improve heat transfer efficiency and cooling water management [18,26,42]	The ORC + ECC requires focus on heat exchanger optimization [18,44]

shows that in a standard ORC, the expander incurs the highest total cost (≈108.4 THB/hr), mainly due to capital investment rather than exergy destruction. This aligns with previous findings that the expander is typically the most expensive component and a key factor in ORC cost-effectiveness. The generator (≈50 THB/hr) and condenser (≈46.7 THB/hr) also contribute significantly, primarily through exergy-destruction costs from heat exchange losses. The pump has the lowest total cost (≈21.1 THB/hr) because of its lower electrical consumption [12,26,42,44].

When the ejector cooling (ECC) circuit is added to the system, the cost structure changes significantly, with the cooling tower (≈139.6 THB/hr) and condenser (≈132.5 THB/hr) becoming the highest-total-cost components, unlike in the conventional ORC, where the expander is the main bottleneck. This shift is driven by higher exergy-destruction costs in the heat transfer equipment, owing to the substantial heat released into the cooling water to maintain temperature and pressure balance in the circuit. In addition, the generator (≈117.5 THB/hr) still plays a significant role, exhibiting considerable economic losses from exergy destruction. These findings are consistent with the observation of Tsatsaronis and Winhold (1985) that heat exchangers often dominate the exergy cost burden in systems with multiple coupled circuits and with later studies on ORC–ejector/combined power–cooling configurations [12,44].

Overall, the results indicate that the standard ORC is dominated by the expander as the main cost determinant, whereas in the ORC + ECC, the cost bottleneck shifts to the cooling tower and condenser. This implies that future ORC + ECC improvements should prioritize optimizing heat transfer performance and cooling water management to reduce exergy losses and, consequently, total system costs [12,26,42,44].

The LCOE analysis depicted in

Table 15. Levelized cost of electricity (LCOE) results for the standard ORC and the Cascade Organic Rankine Cycle combined with an ejector cooling cycle systems under different scenarios.

Case	Discount Rate (%)	Lifetime (yr)	Hours/yr	LCOE Std. ORC (THB/kWh)	LCOE ORC + ECC (THB/kWh)
Best	8	25	8760	3.103	1.931
Base	10	20	8760	3.518	2.201
Worst	12	15	7000	5.044	3.171

indicates that the ORC + ECC provides a clear economic advantage over the standard ORC, with an approximately 37–38% lower LCOE in all scenarios. This reduction highlights the benefits of using an ejector cooling cycle to harness waste heat for power generation, especially in tropical regions where heat transfer is limited. These results confirm that the ORC + ECC can reduce electricity generation costs, enhance commercial viability, and support more sustainable power systems [12,26,41,42,44].

5.4. LCOE Sensitivity Analysis

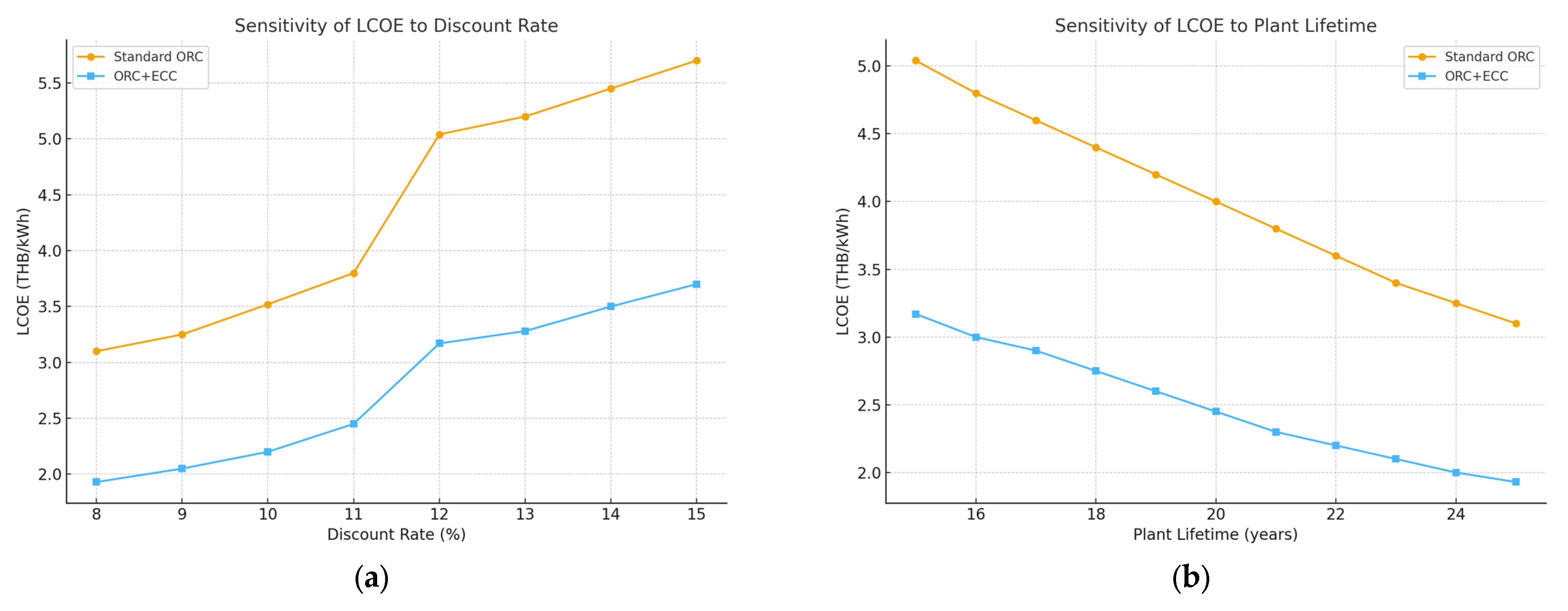
The sensitivity analysis of the LCOE in relation to discount rates and plant lifetimes are shown in Figure 18. They revealed similar trends for both the standard ORC and ORC + ECC systems. As discount rates increased from 8 to 15 percent, the LCOE rose for both systems, highlighting the impact of financial costs. The ORC + ECC system consistently maintained a 35 to 40 percent lower LCOE than the standard ORC, with this advantage growing at higher discount rates. This demonstrates that the ORC + ECC provides greater economic flexibility in challenging financial environments.

For plant lifetimes of between 15 and 25 years, the LCOE for both systems declined as the investment costs were spread over longer periods. The ORC + ECC system showed a greater reduction, reaching an LCOE of below 2.0 THB/kWh under favorable conditions, compared to approximately 3.1 THB/kWh for the standard ORC. This demonstrates that the ORC + ECC offers both improved thermodynamic integration and long-term economic sustainability.

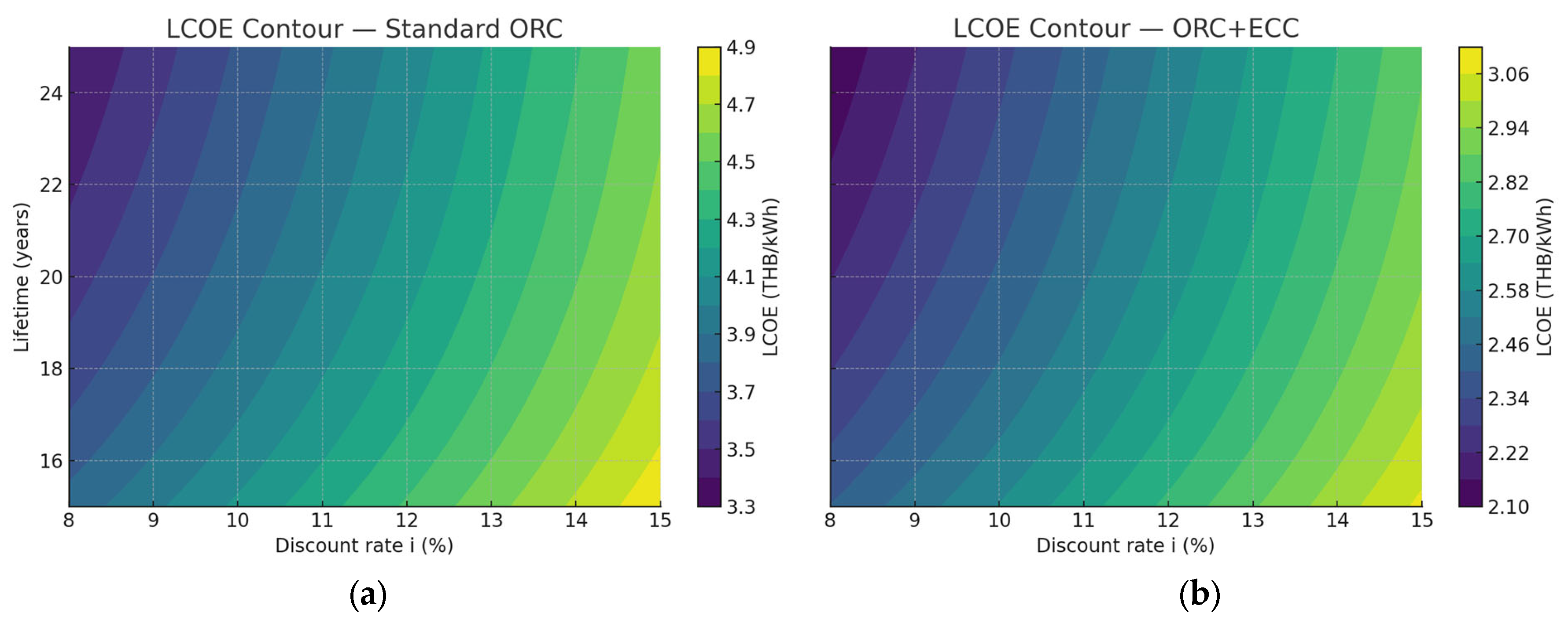
These sensitivity analyses are also presented by the contour plot as shown in Figure 19. The contour plots confirm that the ORC + ECC consistently outperforms the standard ORC across all financial scenarios, especially at higher discount rates and for longer lifetimes. This underscores the strong potential of the ORC + ECC for waste heat power generation, particularly in hot and humid climates where cooling is a significant challenge [12,18,26,41,42,44].

The levelized cost of electricity (LCOE) shown in Figure 20 is a key metric for assessing the economic feasibility of the proposed ORC + ECC. With a total investment of THB 12.90 million, a 20-year lifespan, and a 15% discount rate, the system’s annualized cost is approximately 2.84 million THB/year, excluding fuel costs. This increases to 3.06 million THB/year when accounting for the opportunity cost of waste heat.

Given the system’s net power generation capacity of 133.253 kW and operation at 8000 h per year, the total electricity generation amounts to 1,066,024 kWh annually. The calculated LCOE is 2.66 THB/kWh (excluding waste heat costs) and 2.87 THB/kWh (including waste heat costs), which is competitive compared to standard ORC systems reported in the literature, typically ranging from 0.08 to 0.12 USD/kWh (≈2.9 to 4.3 THB/kWh) under similar scales and operating conditions [23].

Sensitivity analysis over 10- to 15-year project lifetimes at a 15% discount rate shows that both the standard ORC and ORC + ECC systems have a lower LCOE as the project life increases due to capital costs being spread over more years. The ORC + ECC system consistently achieves a lower LCOE than the standard ORC, regardless of whether the opportunity cost of waste heat is included. This highlights the economic advantage of the ORC + ECC in financially constrained scenarios and emphasizes the need for designs that optimize heat transfer and minimize exergy losses [12,26,41,42,44].

The results indicate that, when waste heat is treated as a free energy source, the ORC + ECC can produce electricity at a cost lower than the average industrial electricity tariff in Thailand (≈3.3 THB/kWh). Even when the opportunity cost of waste heat is considered, the system remains competitive with the grid price, reflecting the strong economic potential of waste heat recovery technologies, particularly in tropical climates [12,41].

Furthermore, sensitivity to net power was observed: when the net power decreases from 160 kW to 133 kW, the LCOE increases from approximately 2.2 THB/kWh to 2.7 THB/kWh. This underscores the importance of optimizing exergy efficiency and minimizing irreversibilities in key components such as the generator and expander. Exergoeconomic studies have shown that these components are primary sources of exergy-destruction costs; thus, enhancing their thermodynamic performance directly increases the economic viability of the system [27,42,44].

6. Conclusions

This research compared the performance of the conventional ORC with the ORC + ECC. The study examined how varying intercooler temperatures (16–22 °C) and generator temperatures (85–100 °C) affect energy, exergy, power, and economic outcomes. The results show that both parameters significantly impact system performance, and the integrated configuration offers notable improvements in power generation, thermodynamic efficiency, and financial feasibility over the baseline ORC:

• Thermodynamic analysis showed that lowering the intercooler temperature increases the exergy input and expander shaft power, reaching 128.93 kW at 16 °C. Higher intercooler temperatures reduce the thermal potential difference and work output. Increasing the generator temperature from 85 °C to 100 °C raised the exergy input from 329.52 kW to 439.87 kW and expander work from 121.29 kW to 142.09 kW.
• Exergy-destruction analysis showed that the ORC generator is the dominant source of exergy destruction contributions [29,31], followed by the condenser, ejector side, and expander, while the pumps and auxiliary components contributed negligibly. Importantly, the integration of the ejector cycle redistributed exergy destruction among components and across lower generator temperatures.
• Comparative analysis indicated that the intercooler temperature primarily affects heat exchange components. Lower intercooler temperatures enhance generator and condenser efficiency by reducing irreversibilities. The generator temperature more strongly influences power-related components, with higher values increasing the expander output but also exergy destruction in the generator and ejector. The expander consistently achieves the highest efficiency, while the condenser remains the least efficient across all conditions.
• The economic assessment, based on NPV and payback period analysis, further demonstrated the superiority of the integrated system. At a generator temperature of 100 °C, the payback period was reduced to about 6 years, compared to nearly 10 years for the standard ORC, while the NPV over a 20-year lifetime was considerably higher. Additionally, lower intercooler temperatures produced better financial outcomes due to improved energy conversion efficiency and increased electricity generation. These findings emphasize an inverse relationship between the intercooler temperature and financial performance, highlighting the importance of optimizing thermal parameters not only for efficiency but also for economic viability.
• This research demonstrates that the integration of an ejector cooling cycle (ORC + ECC) can significantly enhance the thermo-economic potential of waste heat power generation systems compared to a standard ORC, from both exergoeconomic and LCOE perspectives. The exergoeconomic analysis identified that, while the expander dominates the cost structure in the standard ORC, the condenser and cooling tower become the critical cost bottlenecks in the ORC + ECC due to their high exergy-destruction costs. At the system level, the LCOE results confirm that the ORC + ECC can achieve 37–38% lower electricity generation costs compared to the standard ORC across best, base, and worst cases and remains competitive with industrial electricity prices in Thailand. Sensitivity analysis further revealed that the ORC + ECC maintains a distinct advantage under higher discount rates, longer lifetimes, and higher net power, highlighting its robustness under varying financial and operational conditions. Therefore, future ORC + ECC system designs should focus on optimizing heat exchanger efficiency, cooling water management, and exergy recovery strategies to reduce irreversibilities and further enhance economic sustainability.

In summary, combining ejector cooling with the ORC effectively maximizes waste heat recovery, improves efficiency, and delivers strong investment returns. This configuration also adapts well to practical conditions, especially in hot and humid environments where conventional ORCs face challenges. Future research should focus on the multi-objective optimization of working fluids and system parameters, experimental validation at larger scales, and incorporating environmental indicators into the exergoeconomic framework for a more comprehensive assessment of sustainability.