A Hierarchical Control Framework for HVAC Systems: Day-Ahead Scheduling and Real-Time Model Predictive Control Co-Optimization

Abstract

Heating, ventilation, and air conditioning (HVAC) systems are the primary energy consumers in modern office buildings, with chillers consuming the most energy. As critical components of building air conditioning, the effective functioning of HVAC systems holds substantial importance for energy preservation and emission mitigation. To enhance the operational performance of HVAC systems and accomplish energy conservation objectives, precise cooling load forecasting is essential. This research employs an office facility in Binzhou City, Shandong Province, as a case investigation and presents a day-ahead scheduling-based model predictive control (MPC) approach for HVAC systems, which targets minimizing the overall system power utilization. An attention mechanism-based long short-term memory (LSTM) neural network forecasting model is developed to predict the building’s cooling demand for the subsequent 24 h. Based on the forecasting outcomes, the MPC controller adopts the supply–demand equilibrium between cooling capacity and cooling demand as the central constraint and utilizes the particle swarm optimization (PSO) algorithm for rolling optimization to establish the optimal configuration approach for the chiller flow rate and temperature, thereby realizing the dynamic control of the HVAC system. To verify the efficacy of this approach, simulation analysis was performed using the TRNSYS simulation platform founded on the actual operational data and meteorological parameters of the building. The findings indicate that compared with the conventional proportional–integral–derivative (PID) control approach, the proposed day-ahead scheduling-based MPC strategy can attain an average energy conservation rate of 9.23% over a one-week operational period and achieve an energy-saving rate of 8.25% over a one-month period, demonstrating its notable advantages in diminishing building energy consumption.

1. Introduction

1.1. Background

As living conditions progressively improve, energy usage in buildings has experienced consistent growth, now representing approximately 30% of worldwide energy demand [1]. HVAC systems constitute over half of the overall building energy requirements, indicating substantial opportunities for efficiency improvements. Given the escalating concerns about climate change, nations globally are placing greater emphasis on energy conservation and carbon reduction. Optimizing HVAC system efficiency has emerged as a critical research focus [2].

Within HVAC installations, chillers function as primary cooling components and generally account for over 40% of complete system energy usage [3]. Chiller energy optimization can substantially enhance air conditioning system efficiency, thereby supporting building energy conservation goals. Chiller control strategies are essential for maintaining system stability and achieving optimal energy efficiency [4]. In actual engineering and testing processes, inappropriate chiller control strategies are often the most common problem. This mainly stems from the uncertainty of building cooling load variations, making it difficult for chillers to respond and adjust in a timely manner, thus affecting the operational efficiency and stability of the system [5]. In terms of system refrigeration, traditional fixed temperature control strategies maintain constant chilled water supply temperature, ignoring the correlation between unit cooling capacity and building cooling load. In multi-chiller systems, fixed start–stop scheduling strategies often result in energy waste. Furthermore, traditional feedback control methods such as proportional–integral–derivative (PID) control struggle to handle nonlinear variations in building systems with large inertia and long time delays. This results in control overshoot or temperature fluctuations, affecting energy efficiency.

To overcome the shortcomings of the aforementioned traditional strategies, developing advanced control strategies capable of dynamic adjustment has become imperative. To solve complex problems such as load optimization distribution and the dynamic optimization of chilled water temperature in multi-chiller systems, the control system must possess the capability to predict building cooling loads and plan optimal control in advance. Therefore, this study presents a day-ahead scheduling-based model predictive control (MPC) method. This method achieves real-time optimization and dynamic system control through future cooling load prediction, thereby significantly minimizing total energy expenditure across operational cycles.

1.2. Literature Review

1.2.1. Building Cooling Load Prediction Models

Accurate cooling load prediction is essential for building energy conservation, not only serving as the basis for optimizing building energy supply strategies but also providing crucial data support for the MPC of HVAC systems [6]. Numerous researchers have conducted extensive research on building cooling load prediction models. Based on modeling approaches, cooling load prediction models can be categorized into three types: white-box, black-box, and gray-box models [7]. White-box models use forward modeling methods based on physical mechanisms that mathematically describe cooling load formation processes. Due to their involvement of detailed physical laws, they are typically computationally complex [8]. Black-box models, on the other hand, employ data-driven reverse modeling methods that utilize historical operational data of buildings for training, enabling the models to gradually adapt to actual operating conditions [9]. Currently, artificial neural networks (ANNs) and support vector machines (SVMs) are the most widely applied models for constructing cooling load prediction models [10]. However, these traditional models can be improved in capturing deep temporal dependencies in data.

In recent years, deep learning models, particularly long short-term memory (LSTM) neural networks, have provided new approaches to addressing these problems. Extensive research has demonstrated the superiority of LSTM and its variants in time series prediction. Panagiotou and Dounis [11] examined eight machine learning predictors for short-term load forecasting in a hospital building, comparing LSTM networks with artificial neural networks (ANNs) using backpropagation and metaheuristic optimization algorithms, as well as adaptive neuro-fuzzy inference systems (ANFISs). The results demonstrated that LSTM networks exhibited superior performance in capturing the temporal dependencies of building energy consumption. Song et al. [12] proposed a model combining the whale optimization algorithm (WOA) with bidirectional long short-term memory (BiLSTM) for chiller energy consumption prediction. The results demonstrated that WOA-BiLSTM outperformed both the WOA-LSTM and BiLSTM models in hourly prediction accuracy and validated the method’s applicability across data sets with different time steps. Zheng et al. [13] constructed a cooling load prediction model that integrates dynamic multi-zone modeling with intelligent terminal control, combining Convolutional Neural Networks (CNNs), BiLSTM, and the Sparrow Search Algorithm (SSA), significantly improving prediction accuracy. The experimental results show that the SSA-CNN-BiLSTM model outperforms the CNN-BiLSTM and BiLSTM models in cooling load prediction accuracy.

The aforementioned studies demonstrate that LSTM and its improved models exhibit high accuracy and reliability in cooling load prediction. However, while existing research has primarily focused on improving prediction accuracy through algorithmic innovations, limited attention has been given to the integration of these prediction models with real-time control optimization frameworks.

1.2.2. HVAC System Optimization and Control Strategies

On the basis of meeting building cooling load requirements, improving energy efficiency through optimizing operational control strategies is another key approach for the energy-saving management of HVAC systems. The academic community has conducted extensive research on the optimization of HVAC system operational parameters. Qiu et al. [14] developed a stochastic multi-objective optimization strategy for chiller operation and validated through TRNSYS simulation that it outperformed traditional strategies in both reducing energy consumption and improving indoor comfort. Ding et al. [15] proposed an energy system operation strategy combining scenario analysis with multi-objective particle swarm optimization, which achieved a 38.98% reduction in heating system operating costs and a 2.24-fold improvement in the system coefficient of performance while ensuring indoor thermal comfort. Wang et al. [16] employed a machine learning-based control strategy to resolve the conflict between electricity consumption and cooling demand when HVAC systems participate in grid frequency regulation. The strategy dynamically adjusts chilled water outlet temperature and indoor temperature setpoints, thereby reducing HVAC energy consumption. Empirical studies have demonstrated the effectiveness of PSO in HVAC applications. Turley et al. [17] developed an occupancy-aware HVAC control system using MPC with PSO to determine optimal control actions. The PSO-based MPC approach minimized a cost function that combined energy consumption and occupant discomfort, achieving significant energy savings while maintaining thermal comfort in residential buildings. Within the MPC framework for air conditioning systems, Chen et al. [18] compared various optimization algorithms and found that PSO exhibited the highest prediction accuracy, achieving an energy-saving rate of 7.1% for air conditioning systems. Existing research indicates that optimization algorithms, particularly PSO, can effectively determine the optimal operating parameters of air conditioning systems under specific conditions.

However, controlling these optimized parameters in practice requires further exploration. Therefore, determining optimal operating parameters and implementing appropriate control techniques are crucial for building energy conservation. Currently, although PID control is still widely applied in HVAC systems due to its simple structure [19], it has many shortcomings when dealing with the nonlinear, multivariable coupling, and time-varying characteristics of modern building HVAC systems [20], making it unable to achieve the efficient management of HVAC systems and thus limiting the system’s energy-saving potential.

1.2.3. MPC in Building Energy Systems

MPC is an emerging control technology that effectively handles nonlinearity, time delays, and multiple constraints. In recent years, MPC has been extensively researched and applied in building energy conservation [21]. Existing research indicates that compared with traditional control methods, MPC has significant advantages in reducing energy consumption and improving indoor comfort. Yang et al. [22] proposed an adaptive machine learning-based model predictive control system. The experimental results showed that compared with traditional control methods, this system reduced office cooling energy consumption by 58.5% and lecture hall cooling energy consumption by 36.7% across multiple buildings while significantly improving indoor thermal comfort. Chinde and Woldekidan [23] proposed an MPC-based optimal scheduling method for chiller systems with thermal energy storage (TES) at the Dallas Fort Worth Airport central plant. The simulation results demonstrated that this method could achieve approximately 10% cost savings and a 7% improvement in unit efficiency. Zhao et al. [24] proposed an MPC strategy combined with an LSTM prediction model for the energy-saving optimization of data center chiller systems. TRNSYS simulation validation showed that this method outperformed PID and fuzzy control by reducing machine room temperature fluctuations by 27.77% and 18.08%, respectively; decreasing energy consumption by 11.81% and 7.58%, respectively; and effectively reducing the PUE index of data centers. Kim et al. [25] implemented MPC in a chiller system that integrated thermal energy storage and behind-the-meter photovoltaic systems for district cooling. The MPC approach outperformed conventional control strategies by achieving an approximately 25% reduction in excess photovoltaic power generation and a 10% reduction in greenhouse gas emissions. Blum et al. [26] implemented MPC using Modelica-based open-source tools in an actual office building, achieving approximately 40% energy savings in HVAC systems. Ascione et al. [27] combined MPC with different thermal comfort models to optimize cooling systems in near-zero-energy buildings. The results showed that compared with fixed setpoint control, MPC could reduce energy costs by approximately 28% while ensuring comfort. Wang et al. [28] proposed a nonlinear MPC strategy for chiller–AHU systems, focusing on the coordinated optimization of fans, water pumps, and chillers. The results showed that this strategy outperformed traditional PI control by reducing total energy consumption by 6.2% and electricity costs by 12.3%. Vallianos et al. [29] analyzed data from multiple buildings in Ontario and Quebec, Canada, demonstrating that MPC strategies are key technologies for achieving building energy flexibility and reducing loads during high-electricity-price periods.

Although MPC has achieved significant progress in multi-chiller systems, its practical implementation remains constrained by computational complexity. The direct application of MPC to systems with discrete equipment on–off decisions and continuous operating parameters necessitates solving mixed-integer nonlinear programming (MINLP) problems [30]. The fundamental challenge of MINLP problems lies in their combinatorial decision space, which grows exponentially with the expansion of prediction horizons and system scale, a phenomenon that has been confirmed in recent studies [31]. Li et al. [32] employed advanced dynamic programming and decomposition strategies specifically designed to mitigate the combinatorial explosion problem. Although the single-step computation time has been substantially reduced, when this computational burden is extended to the 24 h prediction horizon commonly used in day-ahead scheduling, the prohibitive computational cost remains a significant barrier to real-time control implementation. To address the high computational time and method scalability issues, Risbeck et al. [33] proposed a decomposition strategy that separates the continuous model from the mixed-integer model, yet computational efficiency remains a critical challenge. These computational difficulties have motivated researchers to explore alternative approaches. Li et al. [34] demonstrated that hierarchical decomposition strategies can reduce computational complexity by decomposing the original problem into multiple subproblems, thereby providing a more efficient and feasible solution pathway while maintaining control performance.

Overall, existing research and applications demonstrate that MPC can effectively improve HVAC energy efficiency through flexible and precise control while meeting building cooling demands. However, how to construct and implement MPC that aligns with HVAC operational characteristics and achieve accurate, flexible control in actual engineering practice remains a key challenge.

1.3. Research Objectives and Contributions

Based on operational data from the building energy management system, this study analyzes the operational characteristics of chillers and proposes an HVAC system operation strategy that combines day-ahead scheduling with MPC. To address the computational challenges posed by traditional MINLP formulations while maintaining control effectiveness, this study develops a hierarchical framework that strategically decouples discrete scheduling decisions from continuous parameter optimization. This research encompasses two major contributions:

(1)

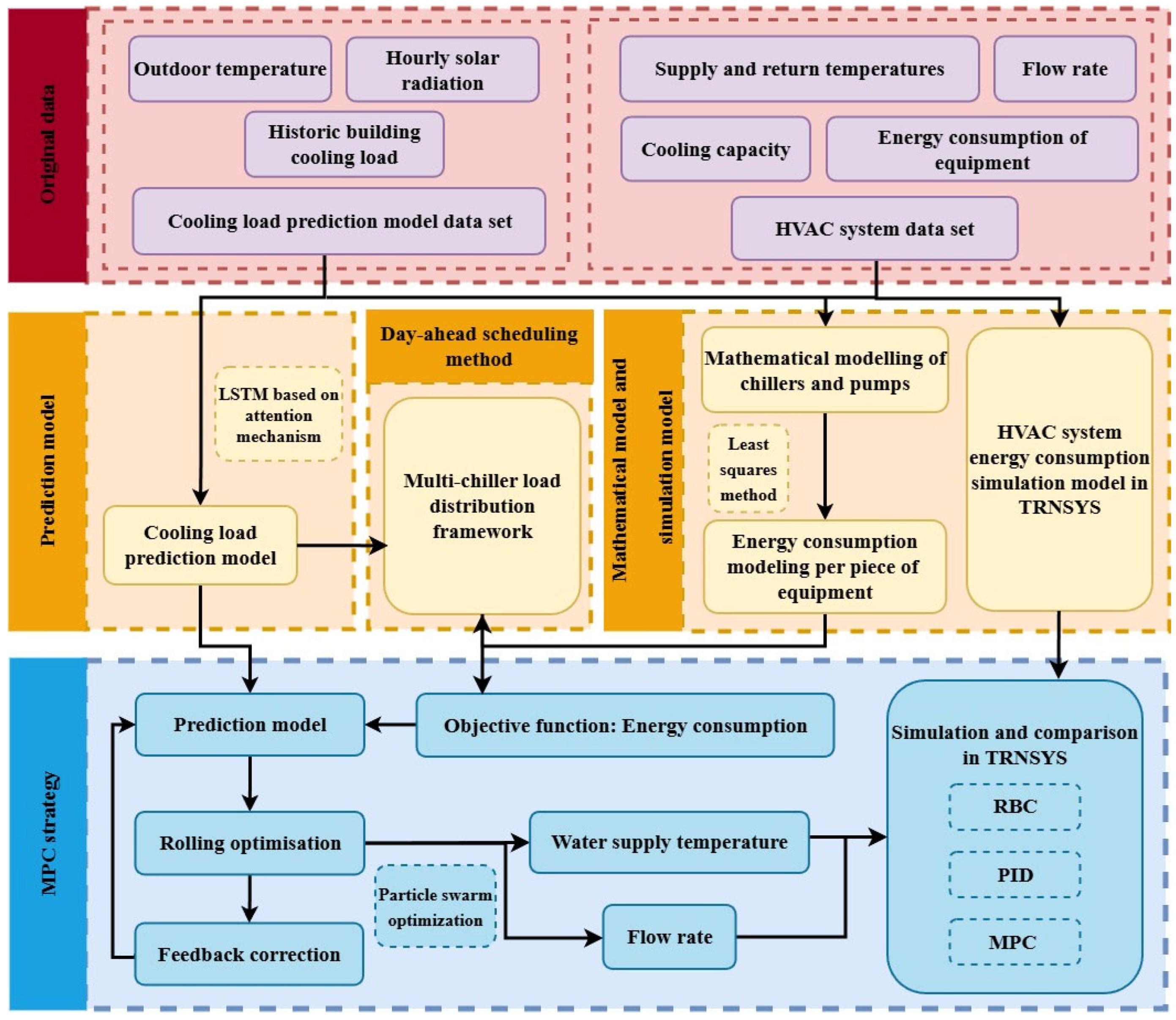
A hierarchical control framework for HVAC systems is constructed, avoiding the complexity of mixed-integer optimization. A two-layer control framework for HVAC systems is constructed. The day-ahead scheduling method combined with MPC forms a two-layer control framework. The upper layer adopts a day-ahead scheduling strategy, using an attention mechanism-based LSTM neural network to predict building cooling load demand for the next 24 h and optimize load distribution and start–stop strategies for each chiller in advance, thus eliminating the need to use an integer optimization solver. The lower layer employs MPC for the real-time adjustment of flow rates and temperatures, treating the discrete decisions of the upper layer as given boundary conditions. This hierarchical strategy fundamentally transforms the computationally intensive MINLP problem into load scheduling-based and continuous optimization problems, thereby enabling the implementation of the optimization strategy for control purposes.

(2)

The PSO algorithm is adopted to perform the rolling optimization of control parameters and generate optimal control signals. The control signals are fed into the TRNSYS simulation model and compared with conventional PID control. System power consumption serves as the objective function to quantify the energy-saving effectiveness of the proposed MPC approach in HVAC systems, thereby demonstrating its superiority over conventional control methods.

2. Materials and Methods

Figure 1 illustrates the technical roadmap for this investigation. This research employs an attention mechanism-based LSTM neural network to construct a cooling load prediction model and develops an MPC strategy that combines prediction algorithms with rolling optimization. During chiller system operation, three key factors must be considered: the power consumption of chillers, pumps, and cooling towers. The optimization objective minimizes total system power consumption to adapt to chiller system operational characteristics.

2.1. MPC Strategy for HVAC System

2.1.1. MPC Principle

MPC is an advanced control strategy that utilizes system models to optimize performance. Its fundamental principle involves obtaining optimal control sequences by solving constrained optimization problems over a finite time horizon at each sampling instant. MPC comprises three key components: a prediction model, rolling optimization, and feedback correction [35,36,37]. MPC predicts future system outputs using a model that characterizes the system’s dynamic behavior. By incorporating current system states and projected control inputs, the model predicts system behavior over a specified future time horizon. A rolling optimization strategy is adopted, where at the current moment, based on the system state and prediction model, an objective function containing tracking error and control energy consumption is minimized within the prediction horizon while satisfying system dynamic constraints as well as input–output constraint conditions. The core feature of MPC lies in its feedback correction mechanism, which executes only the first control action of the optimized control sequence, then performs state estimation and rolling optimization again at the next moment based on the actual system output, thereby achieving robust compensation for model uncertainties and external disturbances.

2.1.2. Day-Ahead Scheduling-Based MPC Algorithm Framework

The HVAC system adopts a two-layer optimal control framework to achieve intelligent scheduling and energy-efficient operation of chillers. The core optimization problem involves determining optimal chiller flow rates and temperatures while satisfying building cooling load requirements. Therefore, the MPC variables are defined as chilled water supply temperature T_chws(t + n), chilled water flow rate V_chw(t + n), and cooling water flow rate V_cw(t + n). Here, t represents the current time, n represents the step size within the prediction horizon, t + n represents the future time after predicting n time steps forward from the current time, and t − n represents the historical time before predicting n time steps backward from the current time. In this study, the prediction horizon is 24 h, and the control time step is 1 h. The analysis assumes that HVAC system cooling capacity equals building load demand, expressed as Q_load(t + n) = Q_ch(t + n).

To address potential forecast deviations and enhance system robustness, the hierarchical control framework employs a two-layer strategy: while the upper-layer day-ahead scheduling uses 24 h predictions for chiller operation planning, the lower-layer MPC controller performs rolling optimization with real-time updates at 1 h intervals, allowing the system to adapt to forecast errors by continuously adjusting operational parameters to maintain supply–demand balance.

Figure 2 presents the control algorithm structure, illustrating the MPC framework for HVAC systems with day-ahead scheduling.

The upper-layer day-ahead scheduling framework is responsible for formulating the start–stop strategy and operation mode selection of chillers. It determines whether centrifugal chillers or screw chillers should be started by predicting cooling load demand and judging whether it exceeds the 1500 kW threshold. The 1500 kW threshold, approximately equal to the screw chiller’s rated capacity, serves as the decision point for chiller selection. When the predicted cooling load is below 1500 kW, the screw chiller alone efficiently meets the demand. When the load exceeds 1500 kW, the centrifugal chiller is activated to ensure optimal system performance and prevent the screw chiller from operating beyond its rated capacity. The system sets strict operational constraints while considering equipment shutdown time constraints and minimum continuous operation time constraints, namely that centrifugal chiller shutdown time does not exceed 2 h and each unit operates continuously for at least 2 h daily. Through runtime monitoring and constraint checking, the system ensures reliable and stable operation while reducing unit start–stop energy consumption by minimizing frequent start–stop operations. During operation, the system continuously monitors equipment status, checks whether continuous operation time limits are met, and dynamically switches between different types of chillers based on actual load demand. Through reasonable start–stop sequence arrangement and operation time optimization, unnecessary start–stop operations are minimized to the greatest extent, thereby reducing additional energy consumption during the start–stop process. This ensures that the system achieves the minimization of start–stop energy consumption while meeting cooling demands, providing operating boundaries for lower-layer real-time optimization.

The lower-layer MPC optimization framework constructs an LSTM–attention-based cooling load prediction model using historical outdoor temperature T_out(t − n), historical solar irradiance I_sol(t − n), and historical cooling load Q_load(t − n) as input parameters. This model integrates energy consumption models for centrifugal chillers, screw chillers, chilled water pumps, and cooling water pumps. The PSO algorithm solves the optimization problem by minimizing total system power consumption while satisfying three constraint types: cooling load balance, temperature limits, and flow rate limits. This approach enables the real-time optimization and adjustment of equipment operating parameters.

This hierarchical control architecture effectively combines the global planning capability of day-ahead scheduling with the real-time optimization characteristics of MPC, achieving energy-saving optimal control under dynamic load conditions.

The objective function is expressed in Equation (1), incorporating Equations (2)–(4).

$$P_{total}=min(\sum _{i=0}^n{P}_{chiller}+\sum _{i=0}^n{P}_{chwp}+\sum _{i=0}^n{P}_{cwp}+\sum _{i=0}^n{P}_{ct})$$

(1)

$$P_{chiller}=P_{centrifugal}+P_{screw}$$

(2)

$$P_{chwp}=P_{chwp1}+P_{chwp2}$$

(3)

$$P_{cwp}=P_{cwp1}+P_{cwp2}$$

(4)

To ensure normal and efficient HVAC system operation, each operating parameter must vary within a reasonable range [38]. The maximum and minimum values from actual operational data serve as upper and lower limits for optimization constraints. Equation (5) illustrates these constraint conditions.

$$\left\{\begin{array}{l}5 °\mathrm{C}\le {\mathrm{T}}_{\mathrm{chws}}\le 12 °\mathrm{C}\hfill \\ 10 °\mathrm{C}\le {\mathrm{T}}_{\mathrm{chwr}}\le 15 °\mathrm{C}\hfill \\ 32 °\mathrm{C}\le {\mathrm{T}}_{\mathrm{cws}}\le 40 °\mathrm{C}\hfill \\ 21 °\mathrm{C}\le {\mathrm{T}}_{\mathrm{cwr}}\le 33 °\mathrm{C}\hfill \\ 2 °\mathrm{C}\le {\mathrm{T}}_{\mathrm{chwr}}-{\mathrm{T}}_{\mathrm{chws}}\le 6 °\mathrm{C}\hfill \\ 2 °\mathrm{C}\le {\mathrm{T}}_{\mathrm{cws}}-{\mathrm{T}}_{\mathrm{cwr}}\le 6 °\mathrm{C}\hfill \\ 10 {\mathrm{m}}^3/\mathrm{h}\le {\mathrm{V}}_{\mathrm{chw}}\le 480 {\mathrm{m}}^3/\mathrm{h}\hfill \\ 10 {\mathrm{m}}^3/\mathrm{h}\le {\mathrm{V}}_{\mathrm{cw}}\le 600 {\mathrm{m}}^3/\mathrm{h}\hfill \\ Q_{ch}=C\times \rho \times V_{chw}\times (T_{chwr}-T_{chws})\hfill \\ Q_{ch}+P_{chiller}=C\times \rho \times V_{cw}\times (T_{cws}-T_{cwr})\hfill \end{array}\right.$$

(5)

2.1.3. PSO Algorithm

Particle swarm optimization (PSO), also known as the particle swarm algorithm, is an evolutionary computational technique that was developed in 1995 [39]. Its design inspiration comes from biomimetic research on bird flocking foraging behavior. The algorithm’s core mechanism involves approximating the global optimal solution through collaborative search by a group of candidate solutions (particles) within the solution space. Each particle dynamically adjusts its movement trajectory based on its individual historical best position (p_best) and the swarm’s historical best position (g_best) [39]. The iterative process of the algorithm begins with the random initialization of all particle positions and velocities. Subsequently, in each iteration step, particles modify their state parameters according to velocity update equations and position update equations. The algorithm introduces an inertia weight coefficient ω to balance global exploration and local exploitation capabilities. This maintains strong global search characteristics during the early search phase, preventing premature convergence to local optimal solutions.

A key advantage of PSO lies in its gradient-free nature, enabling it to circumvent the dependence of classical optimization algorithms on the differentiability of objective functions. This characteristic makes PSO particularly suitable for HVAC system optimization, as analytical gradients of such complex nonlinear models are typically difficult to obtain or computationally prohibitive. Traditional gradient-based Lagrangian methods encounter convergence difficulties under the low-load operating conditions of chillers [40], a limitation that is particularly pronounced for HVAC systems operating under part-load conditions. PSO effectively circumvents this issue, maintaining stable optimization performance across the entire operating range. Compared to genetic algorithms (GAs), PSO significantly improves convergence speed and reduces computational overhead through direct particle updates and information-sharing mechanisms while ensuring comparable solution quality [41,42]. Studies have demonstrated that PSO not only overcomes the divergence problems of Lagrangian methods in multi-chiller optimization but also outperforms GAs in energy consumption minimization [43]. In this study, the PSO algorithm is executed using Python’s PySwarm library (version 3.12.3). As shown in

Table 1. Parameters of particle swarm optimization.

Parameter	Description	Value
K	Population size data	50
d	Number of iterations	100
ω	Parameters of particle swarm optimization	0.7
c1	Learning coefficient, controls the speed at which particles move toward their individual optimal positions	1.0
c2	Social coefficient, controls the speed at which particles move toward the global optimal position	0.5

, specific parameter values are selected in this study [44].

2.2. Prediction Model

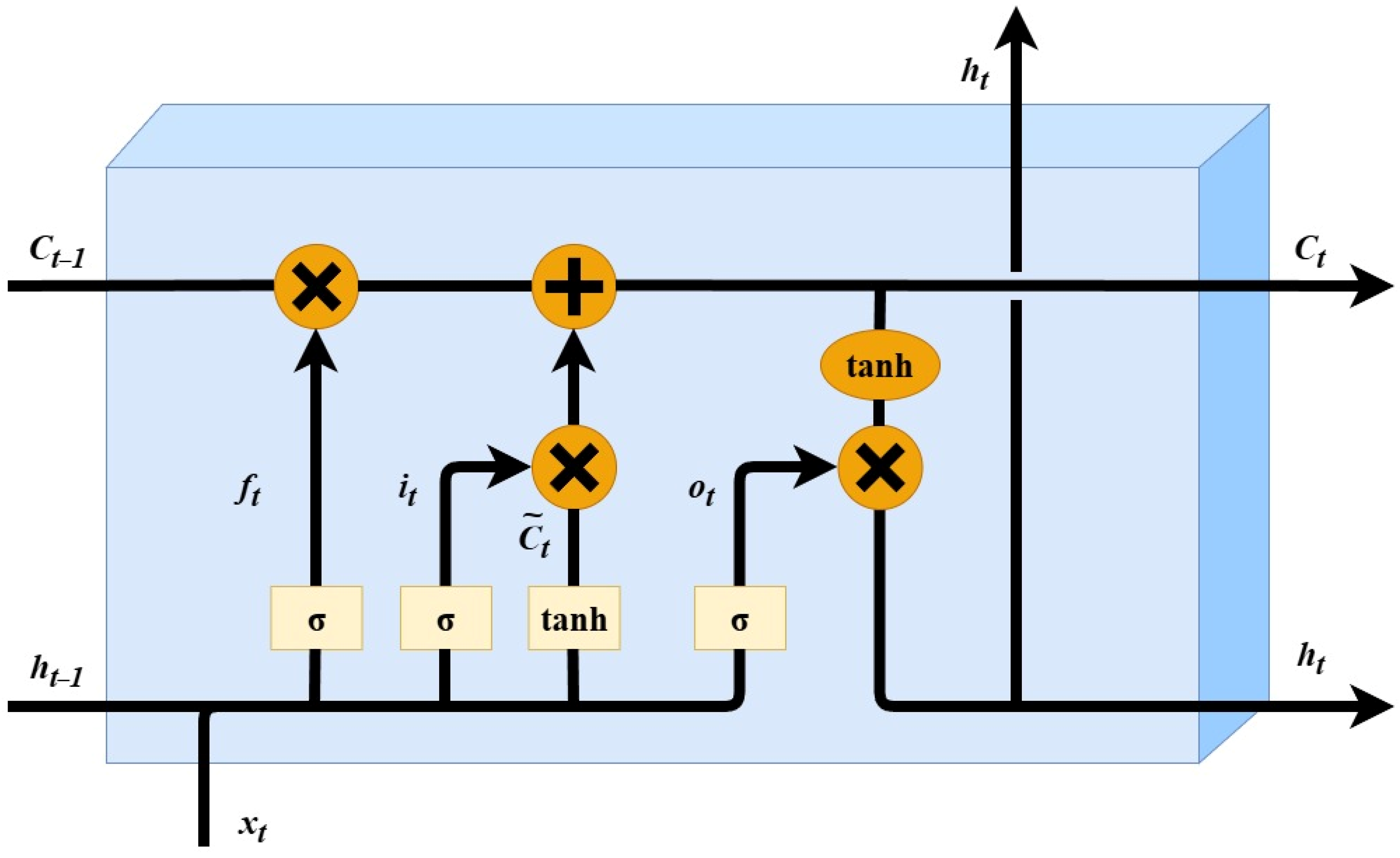
2.2.1. Long Short-Term Memory (LSTM)

Long short-term memory (LSTM) networks, as an improved architecture of Recurrent Neural Networks (RNNs), significantly mitigate the gradient vanishing and explosion problems encountered by traditional RNNs in long-sequence learning through the introduction of gating units and cell state mechanisms [45]. As illustrated in Figure 3, the core architecture of LSTM comprises three types of gating units: the forget gate (f) is responsible for filtering and retaining critical information from historical data while eliminating redundant information; the input gate (i) regulates the extent to which new information is integrated into the cell state; and the output gate (o) controls the amount of information output at the current time step.

The LSTM network takes x_t as input, with the hidden state denoted as h_t−1 and the cell state as C_t−1. The network is trained synchronously through backpropagation through time (t), with the computational equations presented in Equations (6)–(11) as follows [46]:

$$i_t=\sigma \left(w_{xi}{x}_t+w_{hi}{h}_{t-1}+b_i\right)$$

(6)

$$f_t=\sigma \left(w_{xf}{x}_t+w_{hf}{h}_{t-1}+b_f\right)$$

(7)

$$o_t=\sigma \left(w_{xo}{x}_t+w_{ho}{h}_{t-1}+b_o\right)$$

(8)

$${\tilde{C}}_t=tanh\left(w_{xc}{x}_t+w_{hc}{h}_{t-1}+b_c\right)$$

(9)

$$C_t=f_t\odot C_{t-1}+i_t\odot {\tilde{C}}_t$$

(10)

$$h_t=o_t\odot tanh\left(C_t\right)$$

(11)

where ω and b are the trainable weight and bias, respectively. σ(x) represents the Sigmoid activation function mapping to the range of [0, 1], and tanh(x) denotes the hyperbolic tangent activation function mapping to the range of [−1, 1]. x⊙y represents the Hadamard product of vectors x and y.

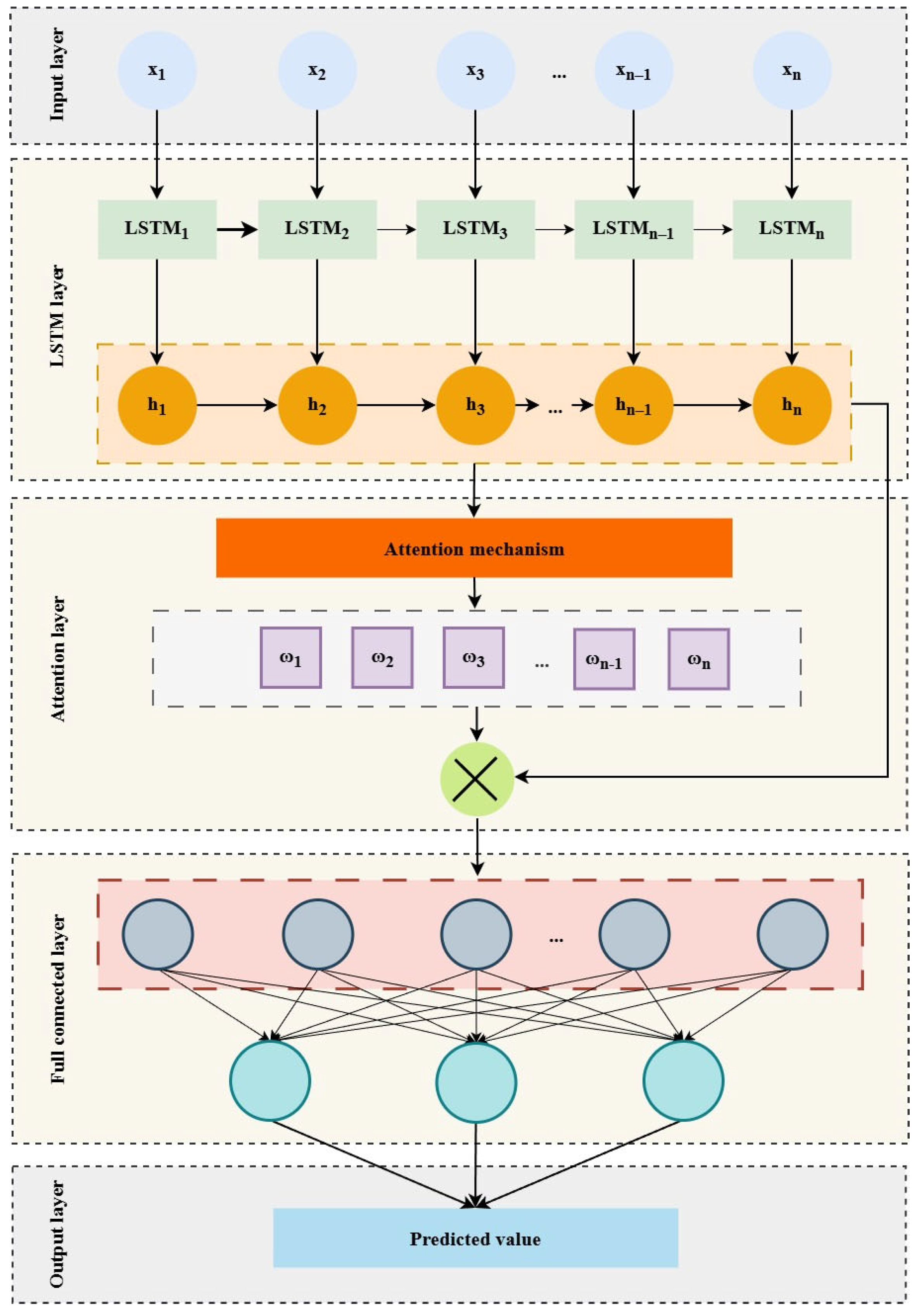
2.2.2. Attention Mechanism

The attention mechanism comprises several sequential steps including attention score computation, weight distribution, and context vector generation [47]. Specifically, the alignment model calculates the score e_t,i based on the encoder hidden state h_i and the previous decoder output s_t−1, which quantifies the relevance between each component of the input sequence and the current output at position t. As shown in Equation (12), the scoring function a(x) can be implemented through a feedforward neural network. Subsequently, the attention weights α_t,i are obtained by applying softmax normalization to the scores, as presented in Equation (13). The final context vector c_t is computed as the weighted sum of all encoder hidden states and fed into the decoder at each time step, with the calculation formulated in Equation (14).

$$e_{t,i}=a(s_{t-1},h_i)$$

(12)

$${\alpha }_{t,i}=softmax(e_{t,i})$$

(13)

$$c_t=\sum _{i=1}^T{\alpha }_{t,i}{h}_i$$

(14)

2.2.3. Attention Mechanism-Based LSTM Cooling Load Prediction Model

This study employs an attention mechanism-based LSTM model to predict building cooling load for the next 24 h. LSTM neural networks effectively capture long-term dependencies in time series data through their long- and short-term memory mechanisms and show significant advantages in handling complex temporal patterns. Additionally, LSTM exhibits higher accuracy in building cooling load applications. The introduction of attention mechanisms further enhances model performance. These mechanisms can dynamically allocate weights and adaptively focus on the importance of different time steps and different features, effectively handling input variables with different correlation coefficients. This model leverages LSTM’s ability to capture temporal dependencies while dynamically evaluating the importance of different time steps and features through attention mechanisms, thereby achieving more accurate predictions [40].

The model architecture comprises five components, i.e., the input layer, LSTM layer, attention layer, fully connected layer, and output layer [48]. The input layer feeds the raw data into the model as input. The LSTM layer extracts high-level temporal features from the input sequence through long short-term memory units. The attention mechanism layer calculates weight coefficients for each time step and performs a weighted fusion of hidden states to highlight critical information. The fully connected layer implements full connectivity mapping between adjacent layer neurons. The output layer completes the time series prediction based on the extracted feature vectors. Figure 4 illustrates the model architecture.

Table 2. Model parameter settings.

Structure	Parameter
Hidden size	64
Num layers	2
Batch size	32
Learning rate	0.001
Dropout	0.2
Epochs	50
Model optimizer	Adam
Patience	15
Iterations	200

lists the model configuration parameters. The model input features include historical building cooling load, outdoor temperature, and solar irradiance across different time steps.

The original data underwent preprocessing, where linear interpolation was employed to correct single-point outliers and supplement missing data, continuous multi-point anomalous data were removed, and all input variables were normalized to eliminate dimensional effects. The data were partitioned into training and validation sets with an 8:2 proportion, and LSTM network hyperparameters were optimized through grid search and cross-validation [49]. During the training process, batch size and training epochs were dynamically adjusted until the loss function converged to prevent overfitting. The MAPE, RMSE, and R² metrics were used to validate the model’s prediction accuracy, stability, and generalization capability on both the training and testing sets.

2.3. Evaluation Metrics

This study employs the coefficient of determination R-Square (R²), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE). The calculation formulas are given by Equations (6) and (7):

$$R^2=1-{\displaystyle \frac{\sum _{i=1}^n(y_i-y_i^{\prime })}{\sum _{i=1}^n(y_i-y_{\mathrm{mean}})}}\times 100\%$$

(15)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\cdot \sum _{i=1}^n{(y_i-y_i^{\prime })}^2}$$

(16)

$$MAPE={\displaystyle \frac{1}{n}}\cdot \sum _{i=1}^n{\displaystyle \frac{|y_i-y_i^{\prime }|}{y_i}}\times 100\%$$

(17)

where n represents the sample size, $y_i$ represents the measured value, $y_i^{\mathrm{\prime }}$ represents the predicted value, and $y_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ represents the mean of measured values.

3. System Simulation

3.1. System Description

The building considered in this research project is located in Binzhou City, constructed in May 2008, with a floor area of approximately 46,000 m². The building consists of one basement level and 27 floors above ground, with the chiller plant room located on the first basement level. The system configuration is shown in Figure 5.

The HVAC system of this office building employs water-cooled chillers with cooling towers for heat dissipation. The refrigeration equipment mainly includes one screw chiller, one centrifugal chiller, four circulating water pumps, and two cooling towers. The building underwent equipment upgrades in 2023, with variable frequency drives (VFDs) installed for the chillers and circulating water pumps. The detailed parameters are shown in

Table 3. HVAC system equipment parameter information.

Equipment Name	Parameter	Quantity	Remark
Screw chiller	Rated cooling capacity: 1508 kW Rated power: 258 kW Refrigeration coefficient of performance: 5.85	1	Fixed-frequency chiller
Centrifugal chiller	Rated cooling capacity: 3516 kW Rated power: 627 kW Refrigeration coefficient of performance: 5.6	1	Inverter chiller
Chilled water pump 2	Flow rate: 500 m3/h Power: 37 kW	2	Inverter pumps Two pumps, one backup
Chilled water pump 1	Flow rate: 600 m3/h Power: 75 kW	1
Cooling water pump 2	Flow rate: 340 m3/h Power: 30 kW	2	Inverter pumps Two pumps, one backup
Cooling water pump 1	Flow rate: 600 m3/h Power: 55 kW	1
Cooling tower	Flow: 500 m3/h Power: 22.5 kW	2	Fixed-frequency cooling tower

.

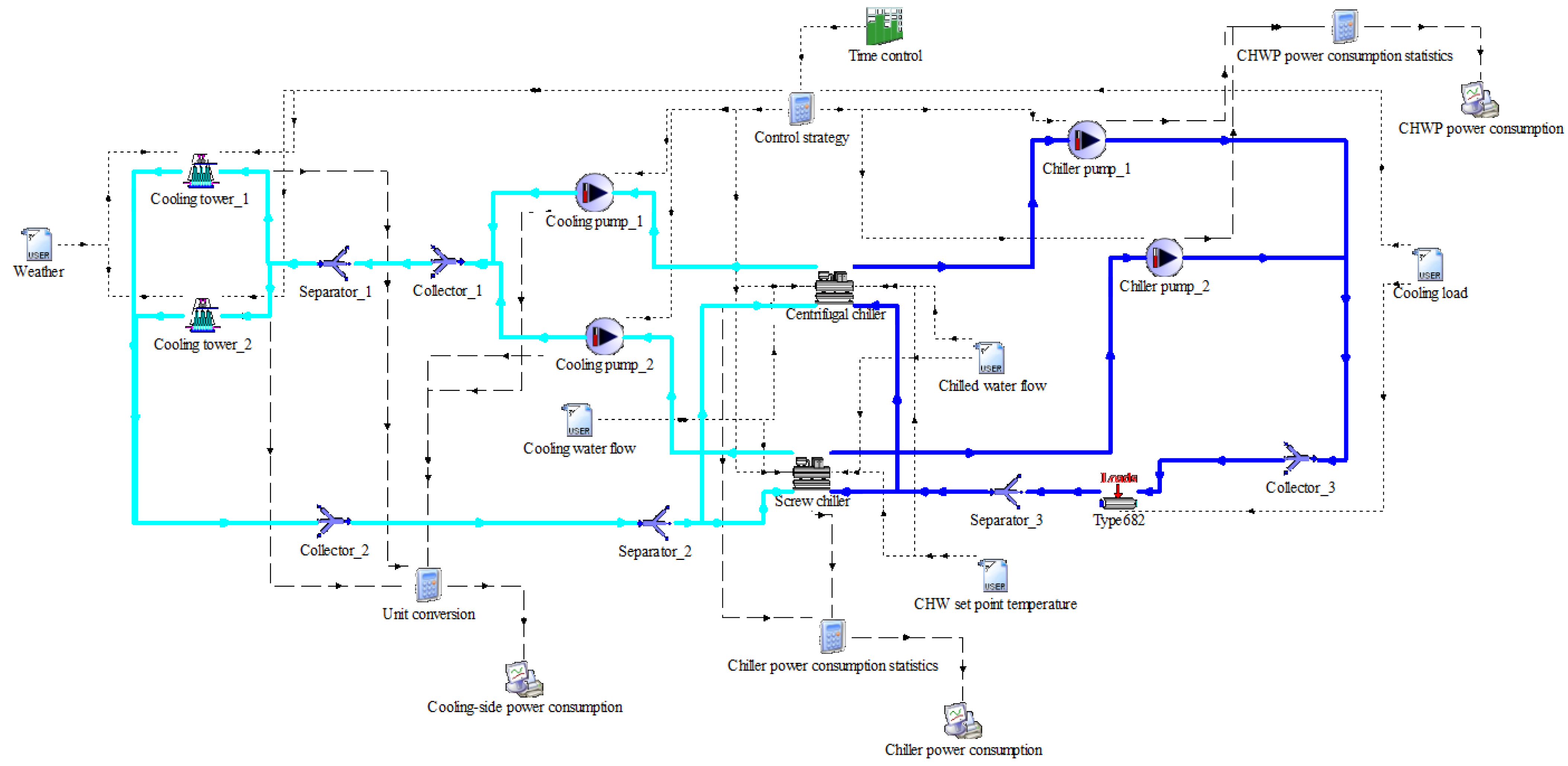
3.2. TRNSYS Simulation Model Development

3.2.1. Input Data

Input Data Building Cooling Load Analysis

Figure 6 shows the hourly cooling load variations in the building from 17 May to 27 September 2024, with the peak cooling load reaching 2390 kW.

The total rated cooling capacity of the configured chillers is 5024 kW, while the actual peak cooling load accounts for only 47.57% of this cooling capacity, indicating significant redundancy in the chiller configuration. The centrifugal chiller operated only during the high-load period from 21 July to 9 August, with the screw chiller operating alone during the remaining time. This operating strategy may result in a mismatch between cooling supply capacity and actual demand. Therefore, it is necessary to optimize the chiller start–stop control strategy to achieve dynamic balance between cooling capacity and cooling load.

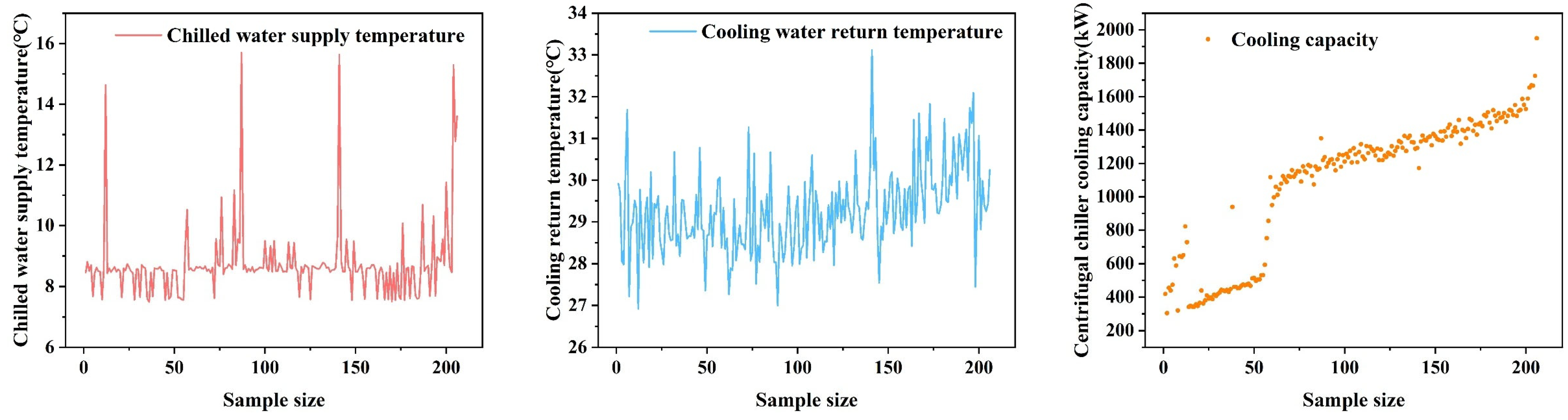
Chiller Raw Data

The centrifugal chiller operated from 21 July to 9 August, while the screw chiller operated during the remaining periods. Figure 7 and Figure 8 present the key parameters during the operation of each unit.

Operational data show that the centrifugal chiller had a mean chilled water supply temperature of 8.74 °C and a mean cooling water return temperature of 29.27 °C, while the screw chiller had a mean chilled water supply temperature of 8.62 °C and a mean cooling water return temperature of 27.02 °C. Both units demonstrated similar performance in chilled water supply temperature control, whereas the higher cooling water return temperature of the centrifugal chiller was mainly influenced by the ambient temperature during its operating period.

3.2.2. Equipment Mathematical Models

Chiller Mathematical Model

Chiller energy consumption is closely related to several factors: cooling capacity Q_ch, chilled water inlet and outlet temperatures T_chwr and T_chws, and cooling water inlet and outlet temperatures T_cwr and T_cws. For chiller energy consumption modeling, the model provided by the American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE) is widely recognized for its accuracy and broad application [50], as shown in Equation (8).

$$P_{chiller}=a_1+a_2(T_{cwr}-T_{chws})+a_3{(T_{cwr}-T_{chws})}^2+a_4{Q}_{ch}+a_5{Q}_{ch}^2+a_6(T_{cwr}-T_{chws})Q_{ch}$$

(18)

To ensure prediction accuracy, this study established separate mathematical models based on actual operational data from both chillers. This study collected 788 operational data points for the screw chiller and 206 data points for the centrifugal chiller. All data were partitioned into training and validation subsets using a 7:3 proportion. Multiple linear regression utilizing the least squares method was employed for parameter fitting.

Table 4. Chiller energy consumption regression parameters.

	a1	a2	a3	a4	a5	a6
Screw chiller	79.7500	−8.2072	0.2477	0.2010	0.000025	0.0008
Centrifugal chiller	−41.0327	22.2174	−0.5752	0.0435	0.000033	0.0009

presents the fitted parameters of the chiller energy consumption models obtained through regression analysis.

Chilled Water Pump Mathematical Model

To establish chilled water pump energy consumption models, this study collected actual operational data from two pumps with different specifications. For the 37 kW chilled water pump, 430 data sets were collected: 300 for training and 130 for validation. For the 75 kW chilled water pump, 208 data sets were collected: 146 for training and 62 for validation. This corresponds to a 70% training and 30% validation split.

Based on the collected operational data, linear regression analysis using the least squares method was employed to establish mathematical models for the two chilled water pumps [50]. The detailed formulations are presented in Equations (9) and (10).

$$P_{chwp1}=-2.9234-0.0377\times V_{chw}+0.0003\times V_{chw}^2$$

(19)

$$P_{chwp2}=12.8382-0.1253\times V_{chw}+0.0008\times V_{chw}^2$$

(20)

Cooling Water Pump Mathematical Model

For the cooling water pumps, 430 operational data sets were collected for the 30 kW unit and 208 sets for the 55 kW unit. All data were partitioned into training and validation subsets using a 7:3 proportion. Using the collected operational data, linear regression analysis was performed using the least squares method, successfully establishing energy consumption mathematical models for both cooling water pumps [50]. The specific expressions are shown in Equations (11) and (12).

$$P_{cwp1}=11.399-0.0811\times V_{cw}+0.0003\times V_{cw}^2$$

(21)

$$P_{cwp2}=20.009-0.1486\times V_{cw}+0.0005\times V_{cw}^2$$

(22)

To verify the accuracy of the established mathematical models, error analysis was conducted on the data set using Equations (18)–(22), with the results of detailed calculation presented in

Table 5. Error assessment of mathematical models of chillers and pumps.

	Training Set			Validation Set
	R2	RMSE	MAPE	R2	RMSE	MAPE
Centrifugal chiller	0.9090	13.9	5.14%	0.9061	10.5	3.90%
Screw chiller	0.9844	6.9	4.54%	0.9867	7.4	4.85%
Chilled water pump 1	0.9270	3.1	6.63%	0.9383	2.4	5.00%
Chilled water pump 2	0.9130	3.2	6.87%	0.9036	3.5	7.43%
Cooling water pump 1	0.9044	3.5	8.97%	0.9196	3.2	8.46%
Cooling water pump 2	0.9093	3.7	8.89%	0.9053	3.4	8.25%

. The model validation results indicate that all models achieved R² values exceeding 90% and MAPE values below 10%, demonstrating that the established energy consumption mathematical models for chillers and chilled water pumps possess high prediction accuracy and reliability.

It is noteworthy that there exists a significant difference in R² between the two chillers, which is primarily attributed to the varying amounts of measured data. Constrained by the unit operation strategy, the centrifugal chiller operates within the 0–55% partial load ratio range, resulting in relatively limited measured data samples in this interval. Due to the strong nonlinear characteristics exhibited by centrifugal compressors under low-load conditions, coupled with the lack of data in the partial load range, the model’s fitting accuracy is affected to some extent. In comparison, the cooling water pump exhibits larger fitting errors, mainly because the cooling water system is significantly influenced by outdoor environmental parameters (such as dry-bulb and wet-bulb temperatures) and cooling tower performance fluctuations, which increases the uncertainty of the mathematical model. Nevertheless, the R², RMSE, and MAPE of the aforementioned fitting results are within the acceptable range for engineering applications, meeting the accuracy requirements for system performance prediction.

The pump power regression models follow the conventional modeling approaches commonly used in the literature, where power consumption is expressed as a polynomial function of flow rate. While pressure and rotational speed are important parameters influencing pump operation, the flow rate serves as a comprehensive indicator that inherently reflects their combined effects under actual operating conditions. The available data from the building energy management system includes flow rate and power consumption measurements but does not provide direct recordings of pressure or rotational speed. Therefore, the regression models utilize the flow–power relationship derived from operational data, which achieved satisfactory accuracy for the operational range of this study and provided adequate prediction capability for MPC implementation.

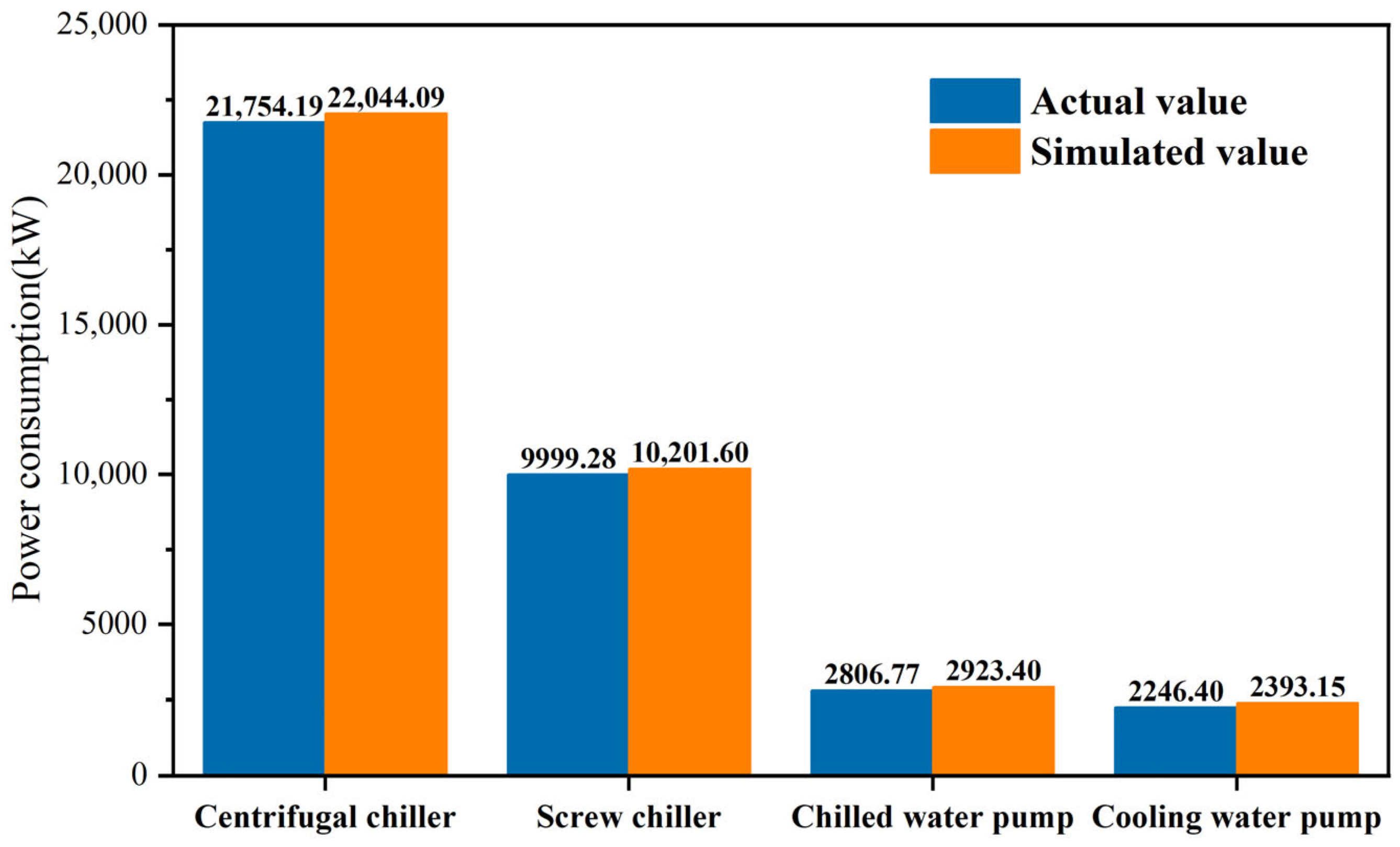
3.2.3. Simulation Model Validation

In this study, the HVAC system simulation model was constructed using the TRNSYS18 platform. The constructed simulation model is shown in Figure 9.

To ensure that the simulation model can accurately reflect the operational characteristics of the actual system, model accuracy verification is required. The selection of corresponding TRNSYS functional modules for each major equipment in the simulation model is shown in

Table 6. TRNSYS modules selected for each device.

Equipment Name	TRNSYS Modules	Diagram
Chiller	Type666
Pump	Type110
Cooling tower	Type126
Separator	Type647
Collector	Type649
Load reading	Type682
Input	Type9e
Output	Type65a
Schedule	Type14h

. The configuration of these modules is based on the technical parameters and operational characteristics of the actual equipment.

The office building design parameters specify a chilled water supply temperature of 7 °C and a supply–return water temperature difference of 5 °C. However, operational data reveal that the actual average chilled water supply temperature is 9.30 °C, with an average supply–return water temperature difference of only 1.89 °C. This indicates significant deviation from design conditions.

To verify the established model, this investigation selected chilled water supply temperature, chilled water flow rate, and cooling water flow rate as the primary input parameters. The model was validated by collecting hourly electricity consumption data from each equipment unit over seven consecutive days. A comparison between the total system electricity consumption and actual total electricity consumption over 168 h is shown in Figure 10.

Table 7. MAPE values for daily power consumption of each equipment unit.

Day	Centrifugal Chiller (%)	Screw Chiller (%)	Chilled Water Pumps (%)	Cooling Water Pumps (%)
1	3.64	2.45	3.74	5.75
2	4.22	2.87	3.65	5.55
3	6.88	3.65	5.46	5.34
4	7.23	4.02	5.64	6.73
5	7.29	4.62	4.35	6.50
6	4.87	3.23	6.36	6.32
7	4.02	2.63	6.67	6.92
Average	5.45	3.35	5.12	6.15

presents the MAPE values for the daily electricity consumption of each equipment unit. The table shows that MAPE values for all equipment units remain within 7%, demonstrating the reliability and effectiveness of the TRNSYS model. The RMSE values for the daily electricity consumption of each equipment unit are shown in

Table 8. RMSE values for daily power consumption of each equipment unit.

Day	Centrifugal Chiller (kWh)	Screw Chiller (kWh)	Chilled Water Pumps (kWh)	Cooling Water Pumps (kWh)
1	9.22	3.86	1.75	2.24
2	10.65	4.43	1.71	2.27
3	17.36	5.52	2.54	2.13
4	18.21	6.12	2.63	2.62
5	18.33	7.07	2.04	2.51
6	12.32	4.92	2.96	2.50
7	10.12	4.04	3.13	2.70
Average	13.74	5.15	2.47	2.42

.

3.2.4. Prediction Model Accuracy Analysis

The cooling load prediction model was constructed using 345 hourly data samples, covering operating conditions across 23 working days and 9 rest days. The data was partitioned into 242 samples for training and 103 samples for validation, representing a 7:3 proportion. Figure 11 shows the model verification results, while

Table 9. Evaluation indicators for predictive model.

Cooling Load Prediction Model	R2	RMSE	MAPE
Training set	96.77%	45.35	4.92%
Test set	95.04%	51.12	5.39%

presents the evaluation metric results. The findings indicate that the prediction model exhibits excellent fitting performance on both the training and testing sets, with R² values exceeding 95%, and the RMSE and MAPE of the testing set meet the requirements of the ASHRAE standard [51]. Therefore, the established prediction model demonstrates high accuracy.

The aforementioned model predictive control optimization and prediction models are implemented in the Python environment. The decision variables obtained from the optimization solution are stored in text file (.txt) format and imported into the simulation platform through the TRNSYS Type 9e data reader module.

4. Results and Discussion

4.1. Electricity Consumption Comparison

Using the TRNSYS platform, seven consecutive days are selected as representative operating periods with a 1 h simulation time step to evaluate system electricity consumption under three control strategies: RBC, PID, and MPC. The PID control strategy regulates the chilled water flow rate based on return water temperature. The RBC strategy is a fixed operating schedule strategy that assigns different predetermined setpoints to chillers.

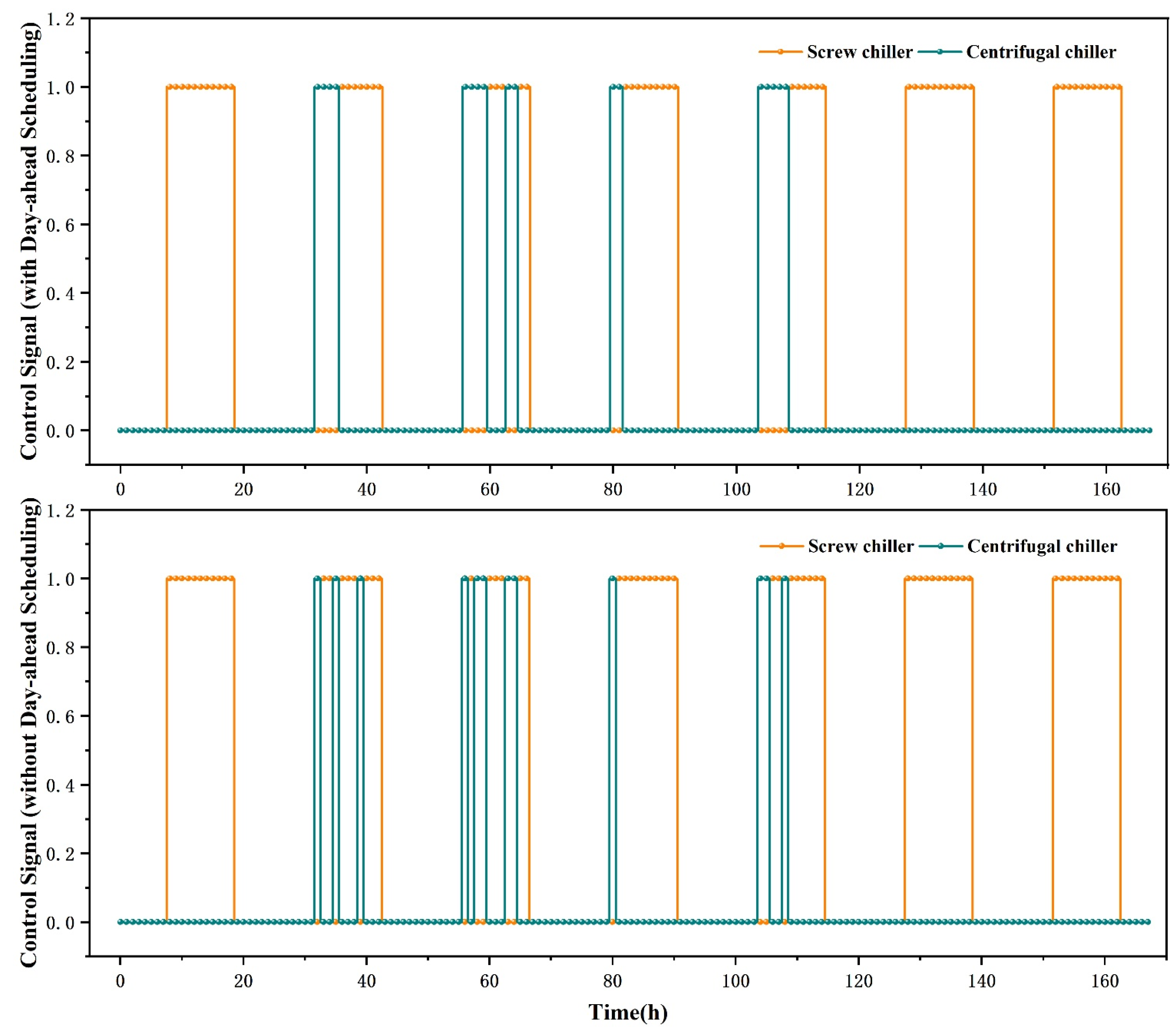
4.1.1. Equipment Start–Stop Operation

Based on the variation patterns of building cooling load, a day-ahead scheduling method is established. The original unit operation strategy involves the independent operation of either the screw chiller or centrifugal chiller. The day-ahead operation adjustment method configures the coordinated operation of the units, with each unit set to operate continuously for no less than 2 h and no more than two start–stop cycles per day. Both units adopt the intermittent operation mode, starting operation from 8:00 to 18:00 daily and shutting down during other hours. The chilled water pumps and cooling water pumps start and stop synchronously with the units.

Figure 12 shows the start–stop control signals for both chiller units during a 168 h operation cycle under the conventional single MPC strategy and the day-ahead scheduling-based MPC strategy. The results show that the conventional single MPC strategy leads to the frequent start–stop cycling of the chiller units, while the day-ahead scheduling-based MPC strategy significantly improves the unit operation mode by extending the continuous operation time of each unit and effectively reducing the number of start–stop cycles, thereby minimizing energy consumption losses caused by frequent cycling.

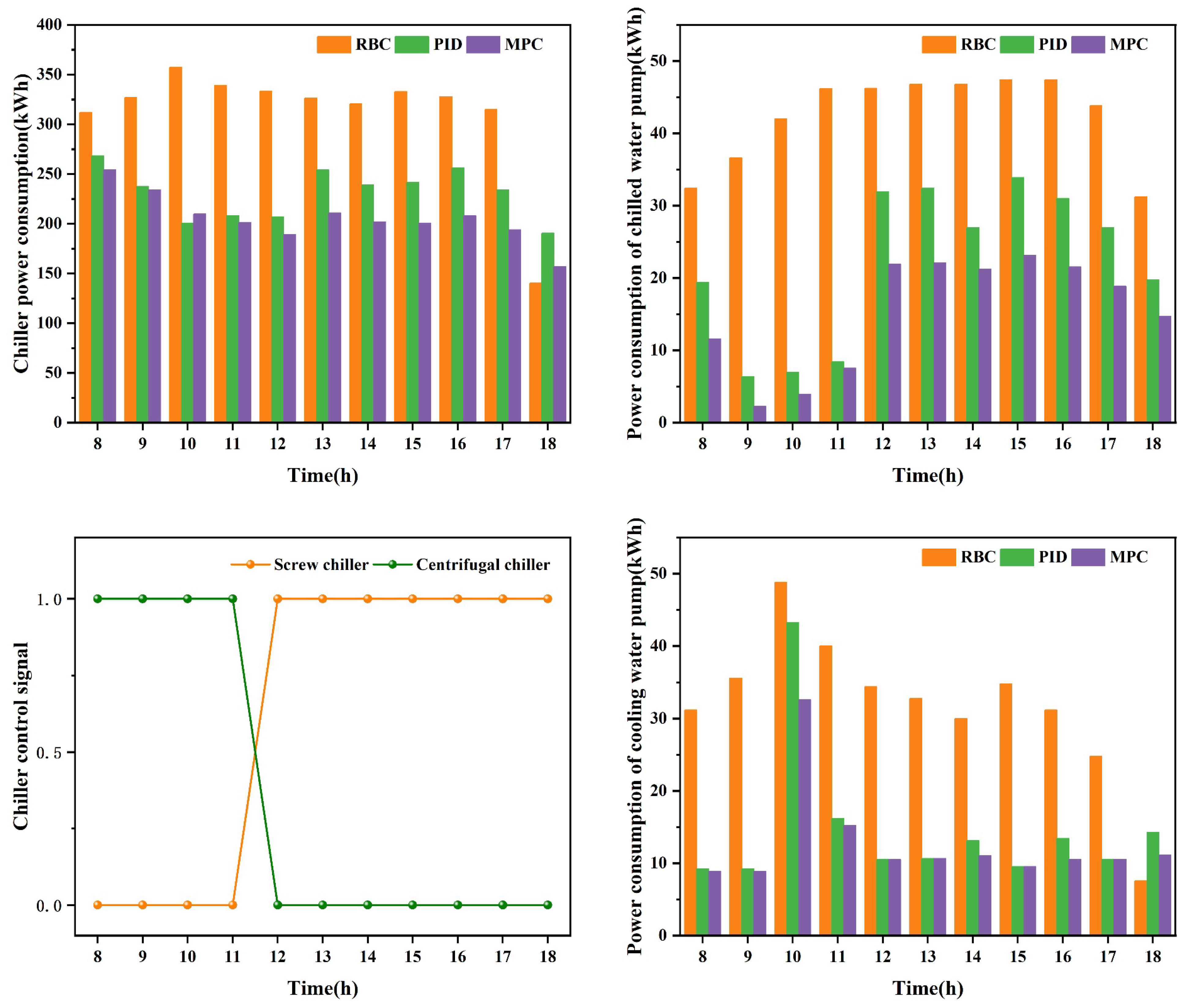
4.1.2. Daily Equipment Electricity Consumption Comparison

Comparative analysis based on single-day operational data reveals significant differences among the three control strategies in terms of equipment energy consumption and operational characteristics. The chiller unit start–stop control results show that unit switching occurred at 11:00, with the centrifugal chiller shutting down and the screw chiller starting up. The day-ahead scheduling MPC strategy performs unit start–stop control based on load variations.

Figure 13 presents the comparison results of chiller unit operational electricity consumption. The RBC strategy exhibits the highest electricity consumption during the 8:00 to 18:00 operation period, reaching 3430.19 kWh, while the PID control strategy consumes 2536.52 kWh. The MPC strategy demonstrates optimal performance with an electricity consumption of only 2260.27 kWh, achieving 10.89% energy savings compared to PID control and 34.11% energy savings compared to RBC. An analysis of chilled water pump and cooling water pump electricity consumption indicates that the three control strategies exhibit similar variation trends, but pump energy consumption is the lowest under MPC. The comprehensive analysis results demonstrate that the proposed day-ahead scheduling-based MPC strategy offers significant energy-saving advantages over conventional RBC and PID control strategies, substantially reducing total system electricity consumption.

4.1.3. Seven-Day Power Consumption Analysis

A comparative analysis of the RBC, PID, and MPC strategies is conducted using the TRNSYS simulation platform. Figure 14 presents the total electricity consumption for each equipment unit from 29 July to 4 August 2024, under the three control strategies, while Figure 15 shows the proportional distribution of electricity consumption by equipment unit. The results show that MPC achieves significantly superior energy savings compared to the PID control and RBC strategies, with lower hourly electricity consumption across all equipment units.

The electricity consumption analysis results based on one week of operational data reveal significant differences in equipment electricity consumption distribution among the three control strategies. The RBC strategy exhibits the highest total system electricity consumption at 26,807.36 kWh, with the centrifugal chiller consuming 21,754.19 kWh, accounting for 81.15% of total consumption, while chilled water pumps and cooling water pumps account for 10.47% and 8.38%, respectively. The PID control strategy significantly reduces system electricity consumption through optimized control, with a total consumption of 16,513.40 kWh, achieving 38.40% energy savings compared to the RBC strategy. The screw chiller becomes the primary energy-consuming equipment, accounting for 62.86%, while the centrifugal chiller’s proportion decreases to 22.57%. The MPC strategy demonstrates optimal energy-saving performance, further reducing total system electricity consumption to 15,289.88 kWh, achieving 42.96% and 7.41% energy savings compared to the RBC and PID strategies, respectively. The screw chiller accounts for 60.69% and the centrifugal chiller for 26.12%, resulting in a more rational distribution of equipment electricity consumption. The analysis results indicate that the day-ahead scheduling-based MPC strategy achieves a significant reduction in system electricity consumption and coordinated equipment operation through optimized load allocation and operational parameters.

The analysis results of system (chiller units + pumps + cooling tower) electricity consumption based on one week of operational data are shown in Figure 16, revealing significant differences among the three control strategies in terms of equipment electricity consumption distribution and energy-saving efficiency. The daily electricity consumption distribution shows that the RBC strategy exhibits the highest electricity consumption, with weekday (days of 1–5) daily consumption remaining within 4320.60 to 4696.40 kWh, while weekend consumption (days of 6–7) decreases to the range of 3003.69 to 3174.19 kWh due to the decreased building load demand. The PID control strategy achieves electricity consumption reduction through closed-loop feedback control mechanisms, with weekday consumption being reduced to the range of 3066.94 to 3281.13 kWh and weekend consumption further being decreased to the range of 1382.72 to 1453.73 kWh. The MPC strategy demonstrates optimal energy-saving effects, with weekday electricity consumption stably controlled within 2575.74 to 3124.97 kWh and weekend consumption being maintained at approximately 1300 kWh.

The energy-saving efficiency evaluation results indicate that MPC achieves energy savings of 33.46–40.38% compared to the RBC strategy on weekdays, with a significant improvement to 55.83–59.68% on weekends. PID control achieves approximately 30% energy savings compared to the RBC strategy on weekdays and reaches 55.83% on weekends. MPC achieves energy savings of 4.69–16.01% compared to the PID control strategy on weekdays and maintains energy-saving advantages during weekends, with an average weekly energy-saving rate of 9.23%. Comprehensive analysis demonstrates that the MPC strategy can achieve effective energy savings under different operating conditions, particularly showing significant advantages during weekends when system loads are lower, validating the effectiveness of this control strategy.

4.2. Overall Performance Evaluation of Proposed MPC Strategy

Figure 17 illustrates a comparison of total system power consumption among the three control strategies over a one-month operational period from 21 July to 21 August 2024. The results indicate that the MPC strategy achieves a total power consumption of 86,368.06 kWh, representing a reduction of 28.86% compared to the RBC strategy (121,401.34 kWh) and 8.25% compared to the PID control strategy (93,493.19 kWh). This validates the effectiveness of the bi-level MPC optimization strategy in achieving energy-efficient HVAC system operation.

The day-ahead scheduling-based HVAC system MPC strategy proposed in this study achieves significant energy-saving effects by integrating an LSTM neural network prediction model with an attention mechanism and particle swarm optimization algorithm. The attention mechanism effectively enhances cooling load prediction accuracy, providing a reliable data foundation for MPC, while the particle swarm optimization algorithm demonstrates excellent global search capability in solving multi-constraint optimization problems. Compared with the conventional PID control strategy, the proposed MPC strategy achieves an average energy-saving rate of 9.23% over a one-week operational cycle and 8.25% over a one-month operational cycle, validating the effectiveness of MPC in energy-efficient HVAC system operation. The day-ahead scheduling strategy combined with rolling optimization mechanism enables the system to plan chiller unit operation modes 24 h in advance and dynamically adjust according to load variations, effectively reducing additional electricity consumption caused by frequent unit start–stop cycling. This control approach transforms the traditional passive response mode of HVAC systems, achieving precise equipment control through predictive decision-making, significantly improving system operational performance, and opening novel pathways for the development of building energy management technologies.

5. Conclusions

This study addresses the energy-saving optimization problem of HVAC systems in an office building in Binzhou City, developing a day-ahead scheduling-based MPC strategy through theoretical modeling, algorithm optimization, and simulation validation, leading to the following main conclusions:

(1)

The LSTM neural network with an attention mechanism accurately predicts 24 h building cooling load demand. The attention mechanism automatically identifies critical time steps and input features affecting load variations, demonstrating stronger feature extraction capabilities compared to traditional LSTM models. Grid search and cross-validation optimization provide a high-precision prediction foundation for the MPC strategy.

(2)

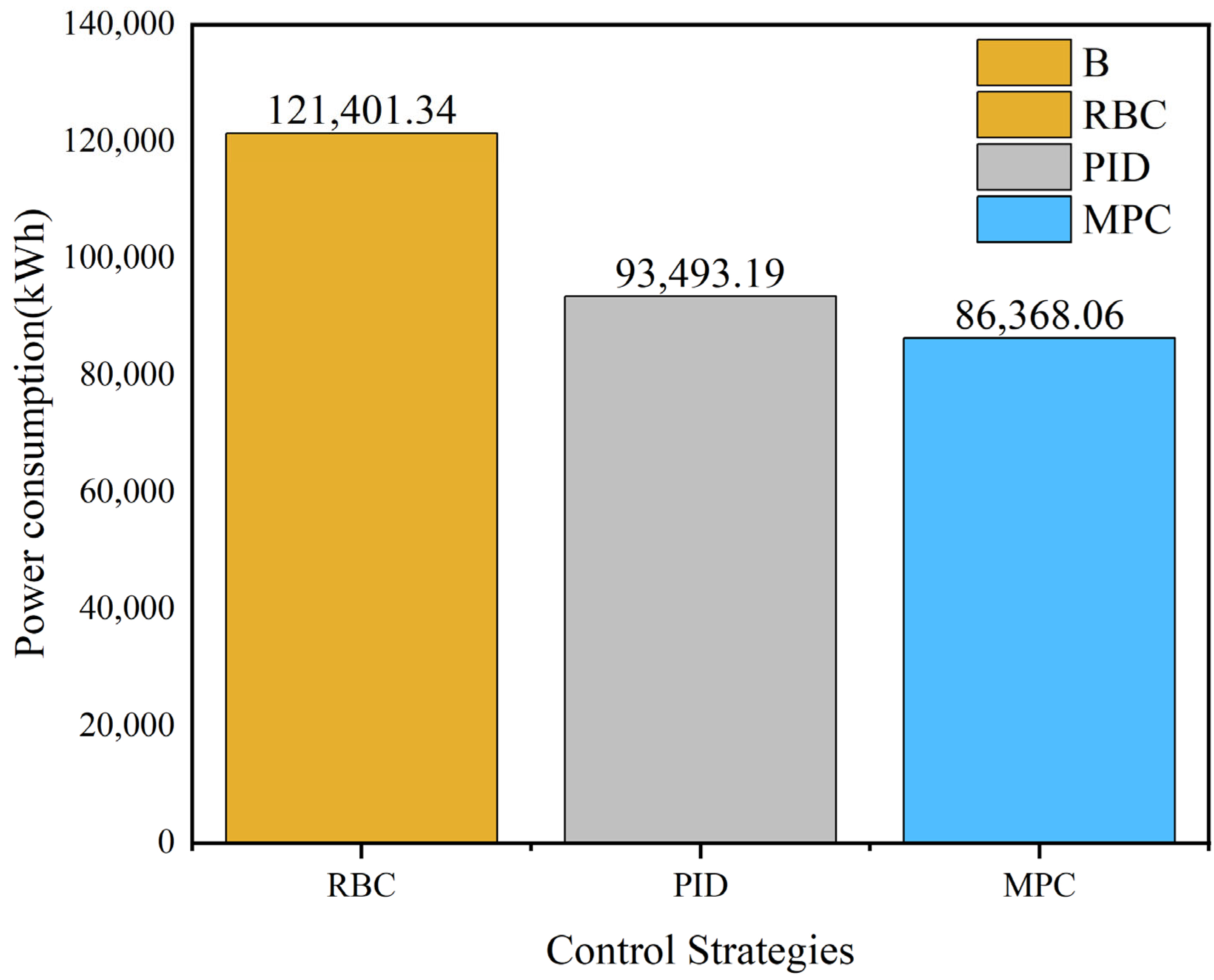
The day-ahead MPC strategy demonstrates excellent electricity-saving performance. Weekly operation achieves 41.07% electricity savings versus traditional RBC and 9.23% versus PID control. Daily chiller electricity consumption shows 34.11% savings compared to RBC and 10.89% compared to PID control. Over a month of operation, it achieves energy savings of 8.25% compared to PID control, thereby validating the strategy’s electricity-saving potential.

(3)

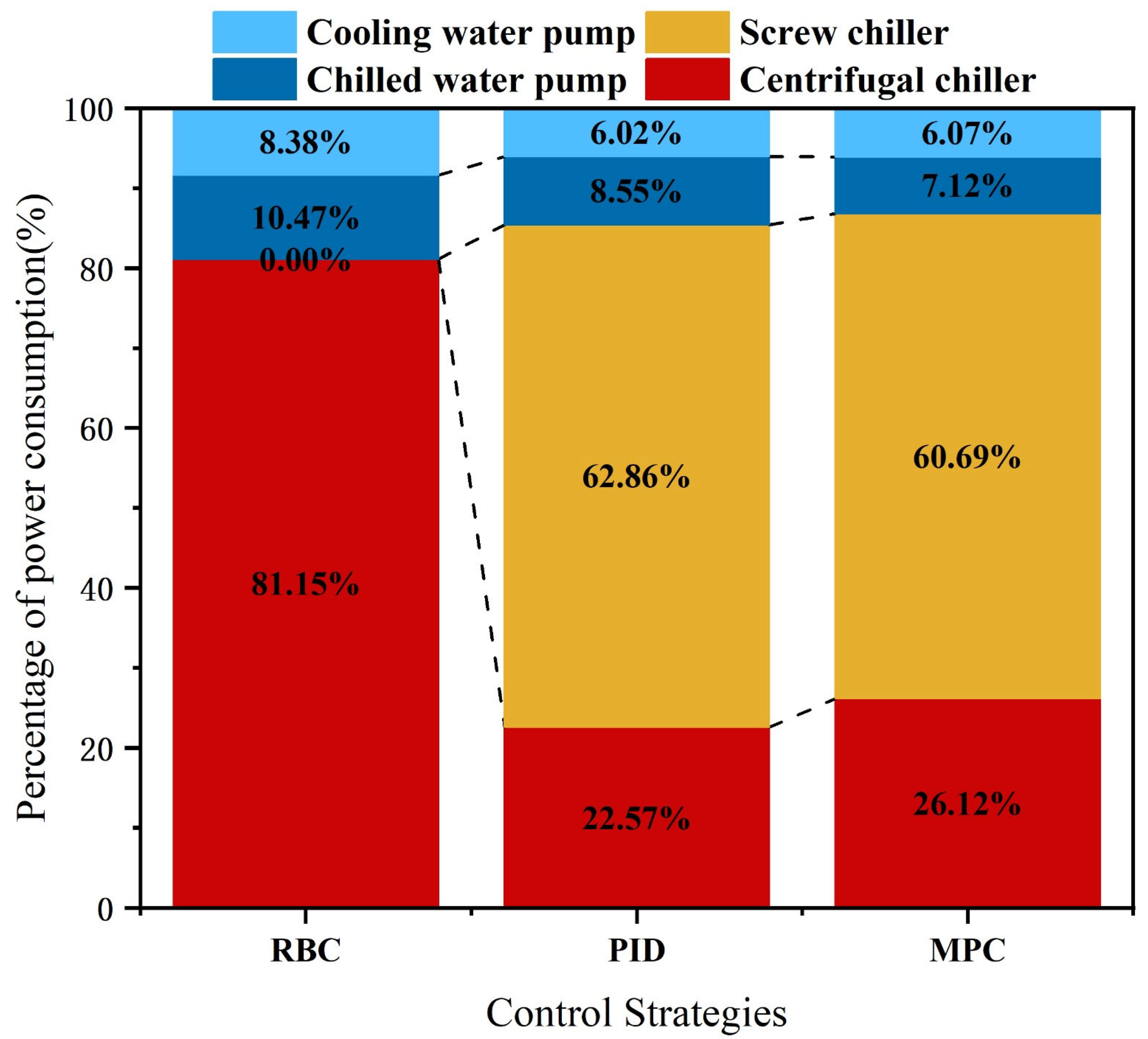
The day-ahead MPC strategy achieves rational coordinated operation and optimal load allocation among equipment. The system switches equipment based on load variations, with an electricity consumption of 60.69% for screw chillers and 26.12% for centrifugal chillers. Compared to RBC’s single dominant mode with 81.15% centrifugal chiller usage, the equipment configuration is more balanced and efficient.

(4)

The MPC strategy maintains excellent electricity-saving effects and system stability under different operating conditions. Electricity-saving rates reach 35–40% on weekdays and 60% on weekends. MPC adapts to load variations while maintaining stable performance, providing technical feasibility validation for practical engineering applications.

(5)

Future work can focus on integrating other deep learning algorithms to improve load prediction accuracy, particularly under abnormal operating conditions and extreme weather events; incorporating explicit temporal features (such as hour of day, day of week, and day type) into the LSTM model to enhance prediction accuracy for atypical days including holidays and special events; developing adaptive MPC algorithms to enhance robustness against model uncertainties and external disturbances; and extending research to energy storage systems, heat pump systems, and hybrid energy systems to evaluate MPC strategy applicability. Due to the lack of measured data on an indoor thermal comfort environment in this study, thermal comfort indicators could not be incorporated into the current MPC framework. Future research will consider installing indoor environmental monitoring equipment and integrating thermal comfort metrics into the optimization objective function to achieve the synergistic optimization of power consumption and thermal comfort.