Fault Diagnosis Method for High-Voltage Direct Current Transmission System Based on Multimodal Sensor Feature-LightGBM Algorithm: A Case Study in China
Abstract
1. Introduction
- (1)
- Given the issues of class imbalance and a small sample size in the original samples, this study introduces a data augmentation method with multiple types of noise to preprocess the data.
- (2)
- To comprehensively reflect the operating state of the HVDC system, this study conducts multi-modal feature fusion. By integrating the time-series features in the time domain, frequency domain, and wavelet domain, and incorporating the Pearson correlation features among sensors, a comprehensive feature vector is constructed.
- (3)
- In the feature selection stage, the recursive feature elimination (RFE) algorithm is used for automatic feature selection. This algorithm can screen out the key features that make the most significant contributions to fault diagnosis, avoiding interference from excessive irrelevant features to the model. Finally, the key features are input into LightGBM classifier to achieve accurate fault diagnosis.
2. Typical Faults of HVDC Systems and Data Processing
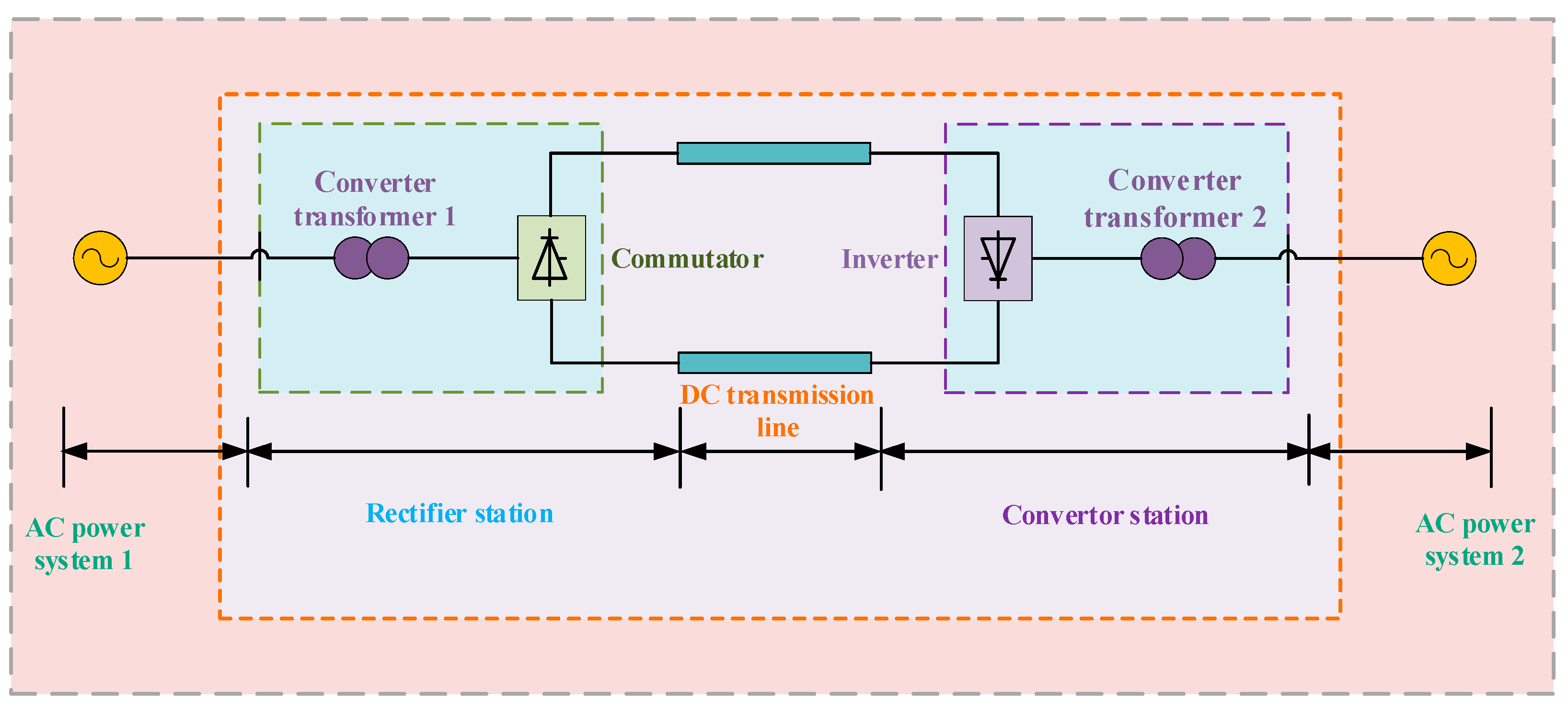
2.1. High Voltage Direct Current Transmission System
2.2. Typical Faults of HVDC Systems
2.2.1. AC Faults
2.2.2. DC Faults
2.2.3. Converter Valve Faults
2.2.4. Inverter Commutation Failures
2.3. Data Processing
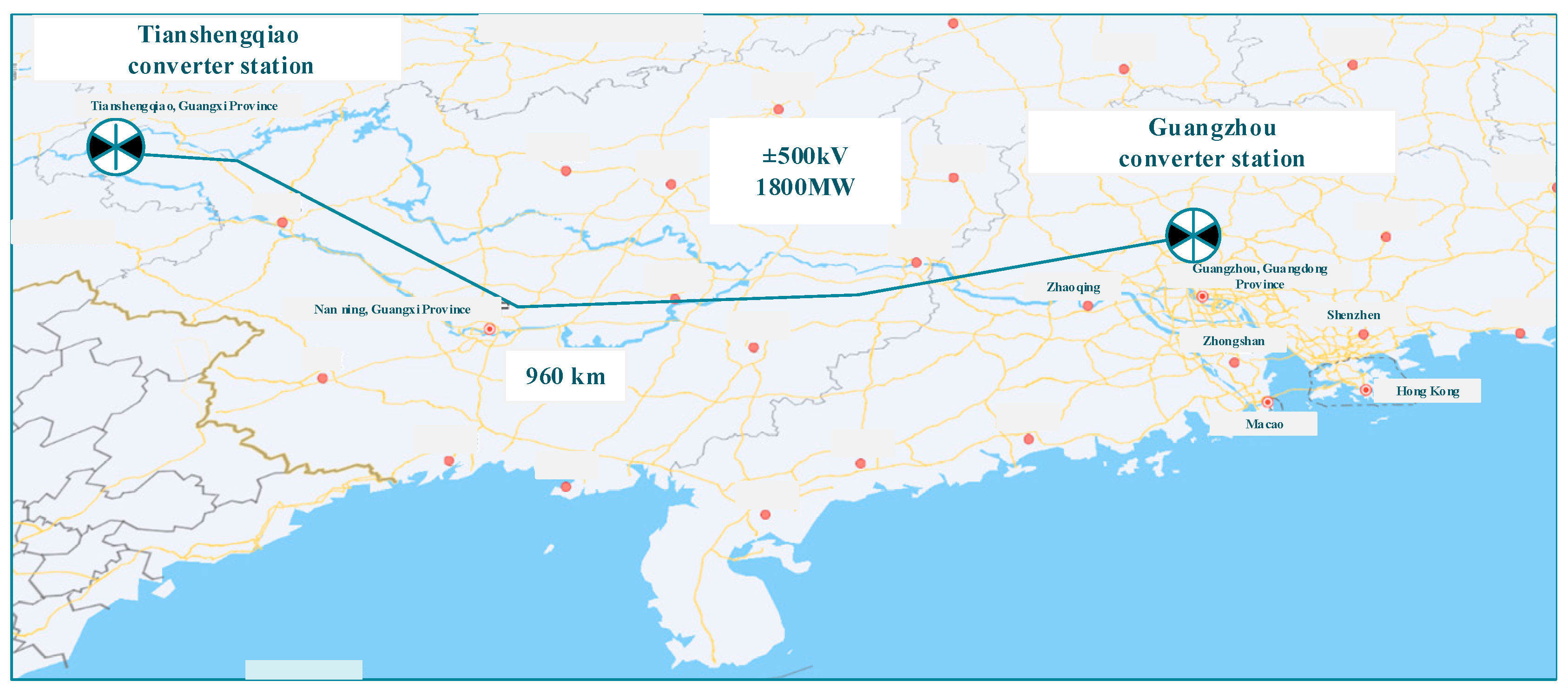
2.3.1. Data Sources
2.3.2. Data Augmentation
2.3.3. Data Normalization
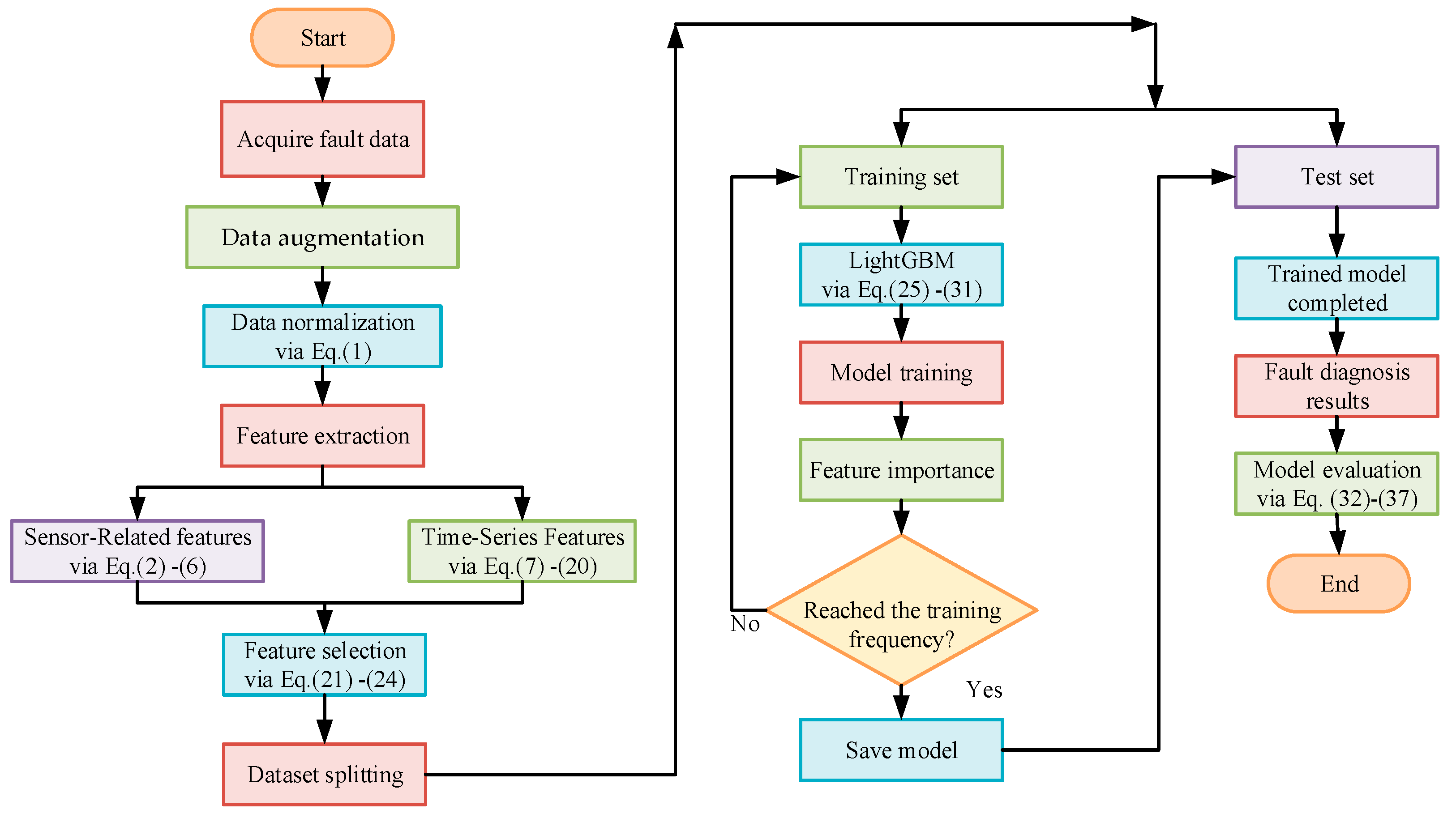
3. Fault Diagnosis Model Based on MSF-LightGBM
3.1. Feature Extraction
- (1)
- Sensor-related features
- (2)
- Time-series features
3.2. Feature Selection
- (1)
- Initial training
- (2)
- Elimination of weak features
- (3)
- Recursive iteration
3.3. LightGBM
3.4. MSF-LightGBM
4. Case Study
4.1. Experimental Environment Configuration
4.2. Experimental Settings
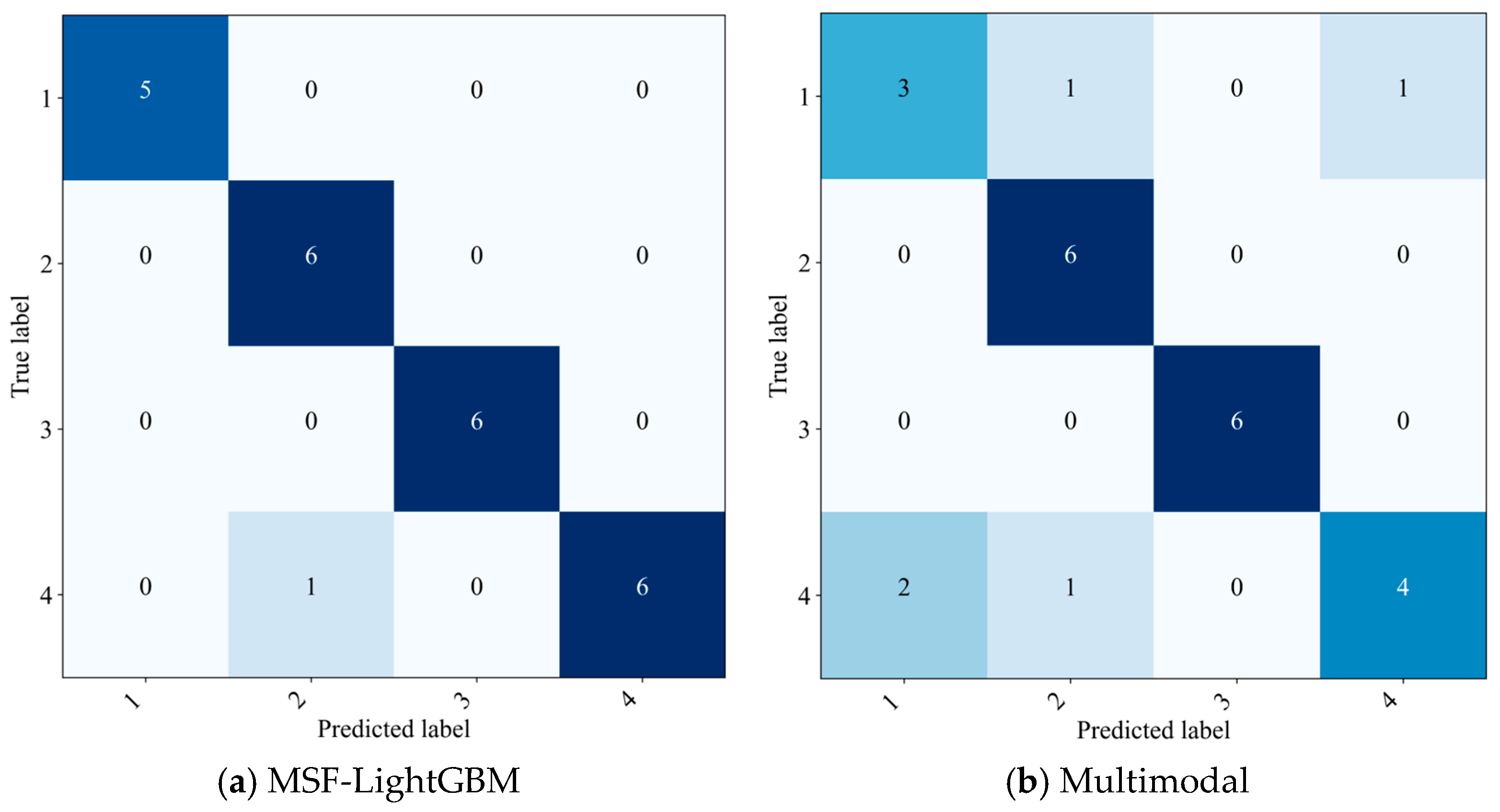
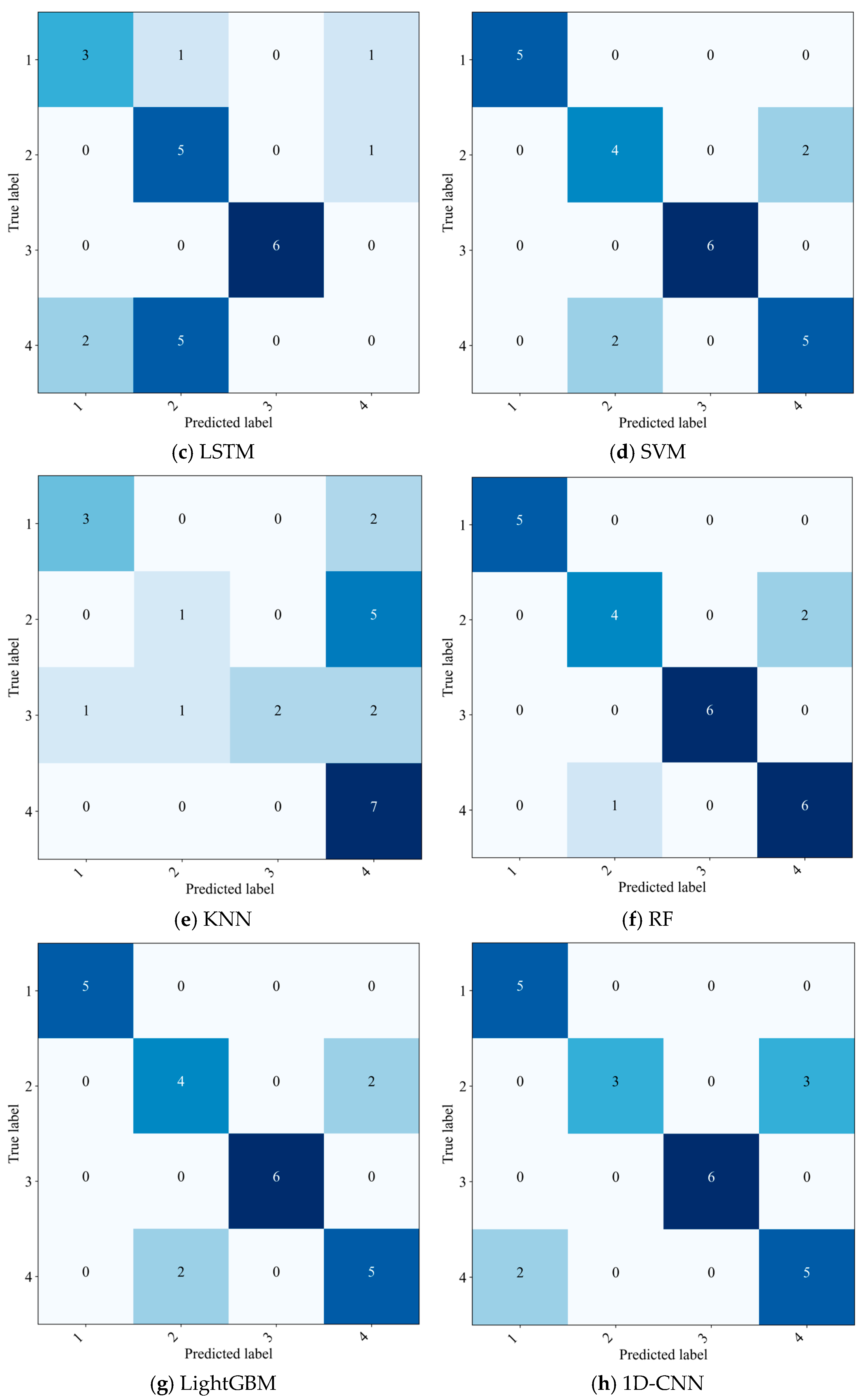
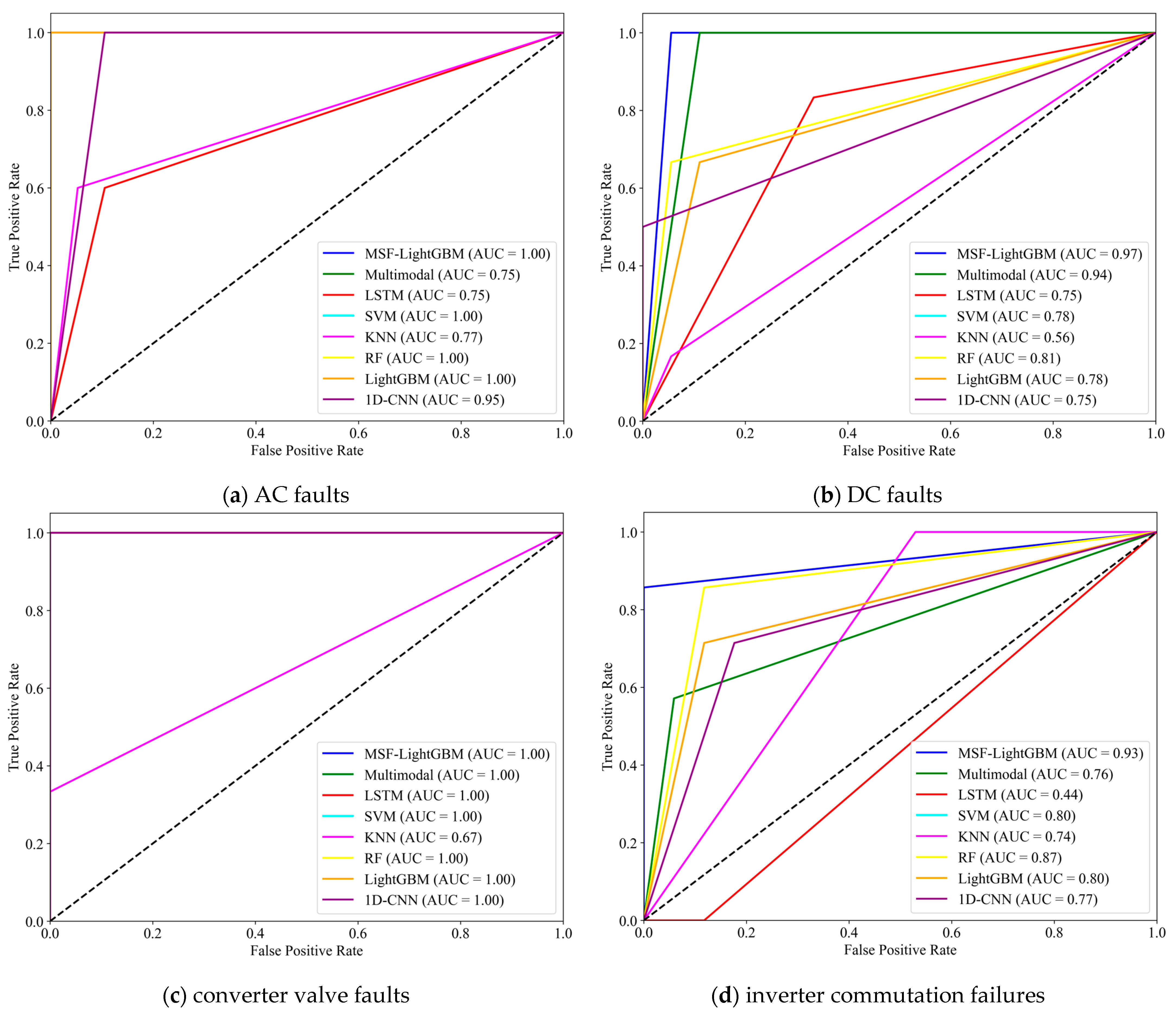
4.3. Comparative Experiment
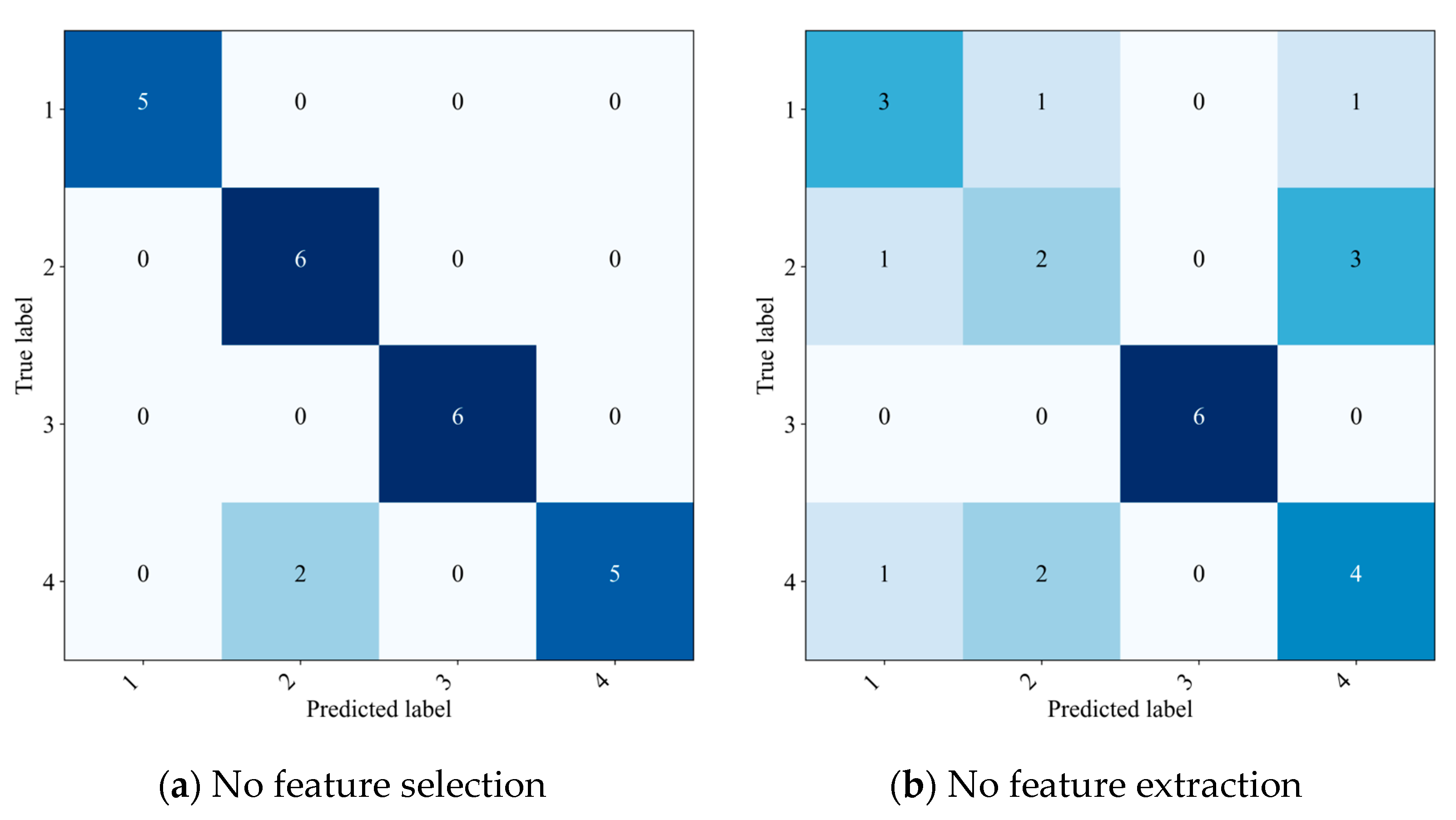
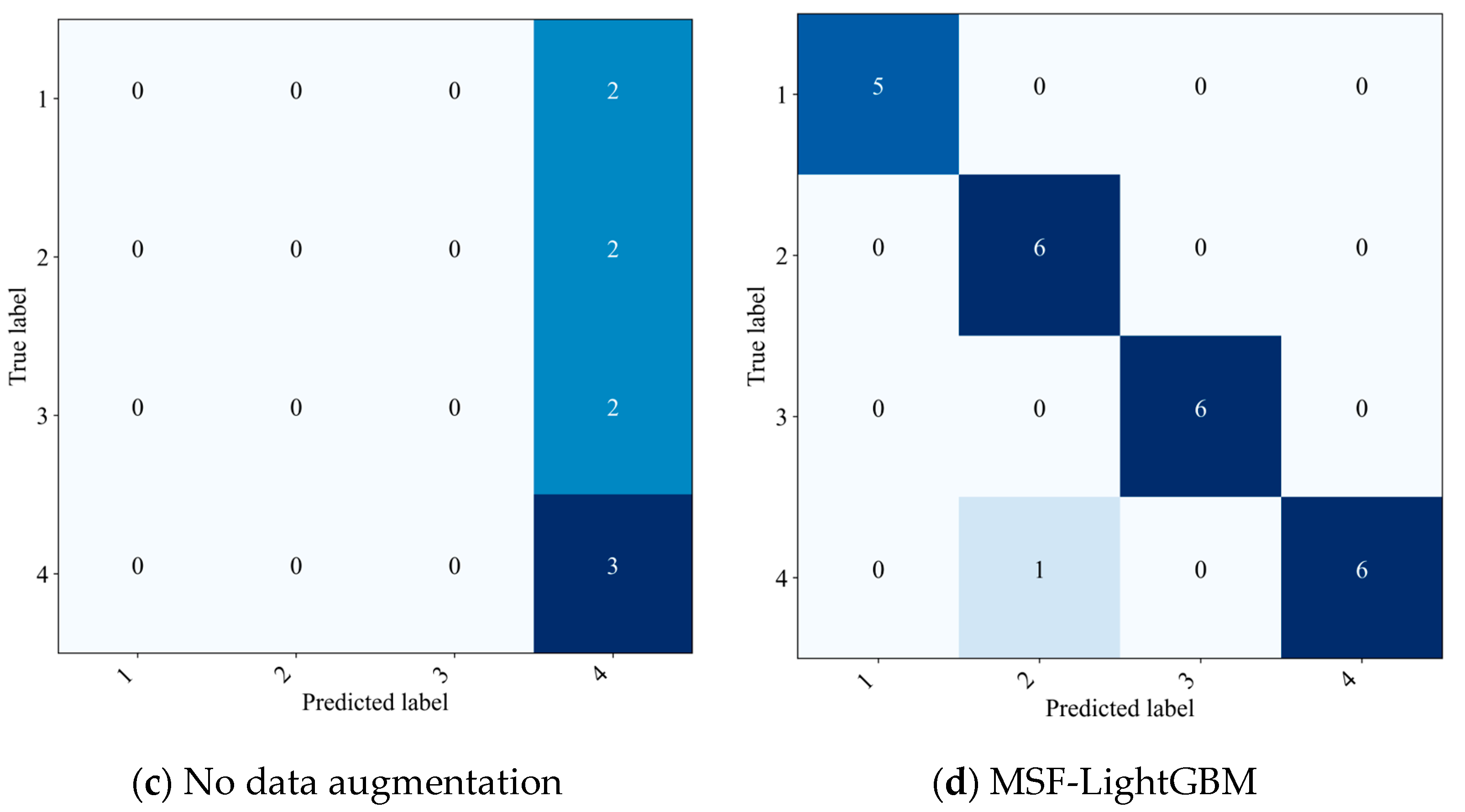
4.4. Ablation Experiment
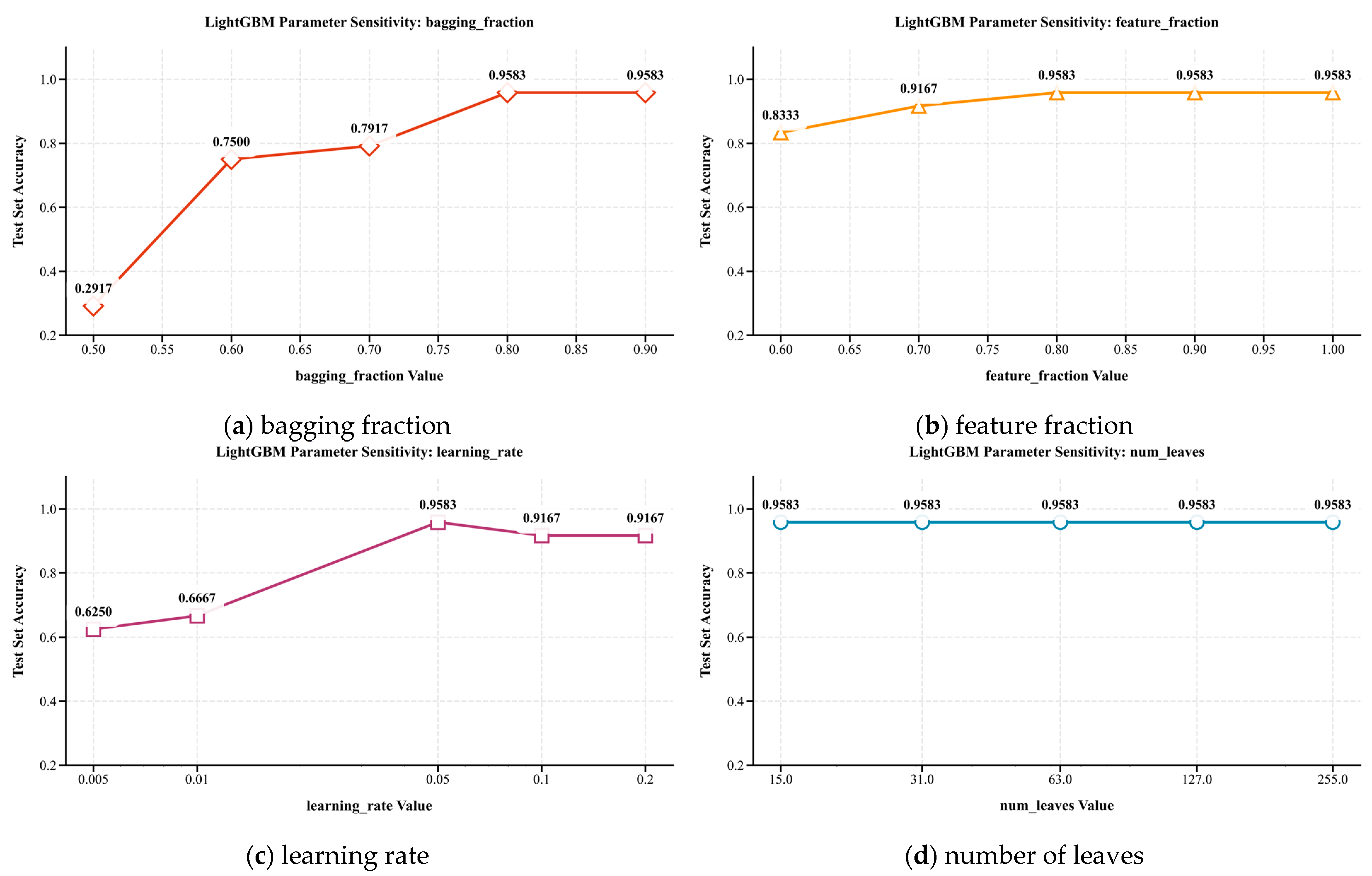
4.5. Sensitivity Analysis
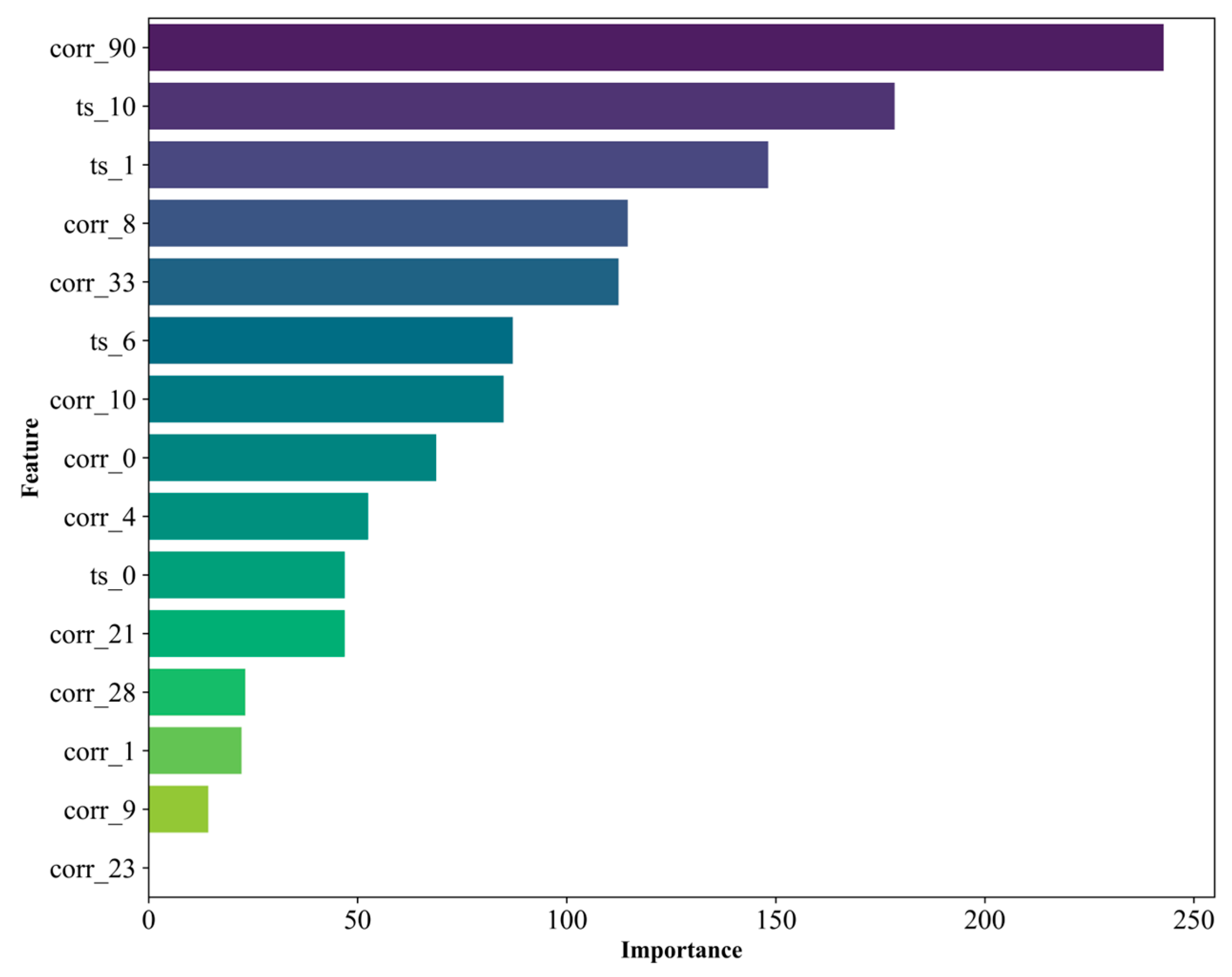
4.6. Analysis of Feature Importances
4.7. Leave-One-(Original)-Event Cross-Validation
5. Conclusions and Future Work
- (1)
- A data augmentation method with multi-type noise injection is adopted to adjust the sample size of each fault category to the target distribution. This resolves the model bias problem caused by minority-class faults in the original data, and the model’s Balanced Accuracy for minority-class faults increases from 0.5 to 0.9752.
- (2)
- By fusing time-series features and sensor correlation features, a comprehensive feature vector is constructed to capture the instantaneous mutation, frequency-domain distribution, and inter-sensor collaborative change information of fault signals. Compared with single-modal feature input for LightGBM, the F1-score has improved from 0.8452 to 0.9615. The multi-modal feature fusion enables the model to reveal the intrinsic physical characteristics of different HVDC faults, which helps field operators quickly locate fault sources. This shortens the fault recovery time, reduces economic losses caused by system downtime, and improves the availability of the HVDC transmission system.
- (3)
- Feature selection is carried out through RFE to screen out key features, reducing the interference of redundant features. Combined with the efficient classification capability of LightGBM, the model’s accuracy, recall, and F1-score on the test set all reach above 0.95, and the average AUC value of the four ROC curves is 0.975, which is significantly superior to traditional algorithms.
- (4)
- From the perspective of engineering application, the MSF-LightGBM model integrates data balance, multi-modal feature mining, and efficient classification into a modular framework, which is easy to implement and promote in actual HVDC control systems. Its high diagnostic accuracy helps reduce the dependence on manual experience in fault diagnosis, standardize the fault handling process, and lower the operation and maintenance costs of HVDC projects. This provides a reliable technical solution for the intelligent development of power grids and supports the stable operation of long-distance, large-capacity HVDC transmission systems.
- (1)
- Construct a mixed sample library containing both single faults and composite faults to address the problem of multi-fault superposition;
- (2)
- Validate the proposed model on completely independent HVDC systems from different projects or operators, with a focus on enhancing its cross-system generalization capability and robustness;
- (3)
- To address the issue of information leakage, data augmentation should be performed after splitting the training and test sets. Specifically, only the training set is augmented, while the original data are retained for the test set, thereby ensuring the authenticity of the experiment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| AUC | area under the curve |
| AC | alternating current |
| BP | back propagation |
| BiGRU | bidirectional gated recurrent unit |
| CatBoost | categorical boosting |
| CEEMDAN | complete ensemble empirical mode decomposition with adaptive noise |
| CNN | convolutional neural network |
| DC | direct current |
| DFT | discrete fourier transform |
| DWT | discrete wavelet transform |
| FN | false negative |
| FP | false positive |
| FPR | false positive rate |
| GAF | gramian angular field |
| HVDC | high-voltage direct current |
| KNN | K-nearest neighbors |
| LightGBM | light gradient boosting machine |
| MSF-LightGBM | multimodal sensor feature-light gradient boosting machine |
| PCA | principal component analysis |
| RF | random forest |
| RFE | recursive feature elimination |
| ROC | receiver operating characteristic |
| SVM | support vector machine |
| TN | true negative |
| TP | true positive |
| TPR | true positive rate |
| WPT | wavelet packet transform |
| 1D-CNN | one-dimensional convolutional neural network |
| Variables | |
| covariance between sensor j and sensor k in the i-th sample | |
| dimension of the time-series features | |
| DFT function | |
| the l-th component of the DFT result of the i-th sample | |
| number of samples that are actually negative but predicted as positive by the model | |
| number of samples that are actually positive but predicted as negative by the model | |
| classification value of the i-th base learner | |
| number of features | |
| number of samples | |
| number of training set samples in a specific fixed leaf node | |
| standard deviation of the data. | |
| constants to prevent division by zero errors | |
| set of all decision tree split nodes | |
| TP | number of samples that are actually positive and predicted as positive by the model |
| TN | number of samples that are actually negative and predicted as negative by the model |
| approximation coefficients | |
| detail coefficients | |
| standardized data | |
| original data | |
| the l-th feature value of the i-th sample | |
| input sample | |
| mean | |
| standard deviation | |
| standard deviations of sensor j in the i-th sample | |
| standard deviations of sensor k in the i-th sample | |
| decrease value of the loss function caused by this split | |
References
- Han, J.Y.; Wang, J.X.; He, Z.H.; An, Q.; Song, Y.Y.; Mujeeb, A.; Tan, C.W.; Gao, F. Hydrogen-powered smart grid resilience. Energy Convers. Econ. 2023, 4, 89–104. [Google Scholar] [CrossRef]
- Zhang, W.Z.; Xu, C.B. Capacity configuration optimization of photovoltaic-battery-electrolysis hybrid system for hydrogen generation considering dynamic efficiency and cost learning. Energy Convers. Econ. 2024, 5, 78–92. [Google Scholar] [CrossRef]
- Chen, X.P.; Wang, L.; Jiang, Y.N.; Wang, J.X. A peer-to-peer joint energy and reserve market considering renewable generation uncertainty: A generalized Nash equilibrium approach. Energy Convers. Econ. 2024, 5, 179–192. [Google Scholar] [CrossRef]
- Wang, J.B.; Wen, J.F.; Wang, J.R.; Yang, B.; Jiang, L. Water electrolyzer operation scheduling for green hydrogen production: A review. Renew. Sustain. Energy Rev. 2024, 203, 114779. [Google Scholar] [CrossRef]
- Hassan, S.J.U.; Mehdi, A.; Haider, Z.; Song, J.S.; Abraham, A.D.; Shin, G.S.; Kim, C.H. Towards medium voltage hybrid AC/DC distribution systems: Architectural Topologies, planning and operation. Int. J. Electr. Power Energy Syst. 2024, 159, 110003. [Google Scholar] [CrossRef]
- Guo, H.L.; Zhang, Z.R.; Xu, Z. Parallel converter-based hybrid HVDC System for integration and delivery of large-scale renewable energy. J. Mod. Power Syst. Clean Energy 2025, 13, 688–697. [Google Scholar] [CrossRef]
- Zhang, T.; Yao, J.; Lin, Y.C.; Jin, R.Y.; Zhao, L.S. Impact of control interaction of wind farm with MMC-HVDC transmission system on distance protection adaptability under symmetric fault. Prot. Control Mod. Power Syst. 2025, 10, 83–101. [Google Scholar] [CrossRef]
- Shafique, G.; Boukhenfouf, J.; Gruson, F.; Colas, F.; Guillaud, X. DC voltage control with grid-forming capability for enhancing stability of HVDC system. J. Mod. Power Syst. Clean Energy 2025, 13, 66–78. [Google Scholar] [CrossRef]
- Su, C.S.; Yin, C.Y.; Li, F.T.; Han, L. A Novel Recovery Strategy to Suppress Subsequent Commutation Failure in an LCC-Based HVDC. Prot. Control Mod. Power Syst. 2024, 9, 38–51. [Google Scholar] [CrossRef]
- Farkhani, J.S.; Çelik, Ö.; Ma, K.; Bak, C.L.; Chen, Z. Fault detection, classification, and location based on empirical wavelet transform-teager energy operator and ANN for hybrid transmission lines in VSC-HVDC systems. J. Mod. Power Syst. Clean Energy 2025, 13, 840–851. [Google Scholar] [CrossRef]
- Li, X.Y.; Wu, X.D.; Wang, T.Y.; Xie, Y.N.; Chu, F.L. Fault diagnosis method for imbalanced data based on adaptive diffusion models and generative adversarial networks. Eng. Appl. Artif. Intell. 2025, 147, 110410. [Google Scholar] [CrossRef]
- Li, T.; Li, Y.L.; Chen, X.L. Fault Diagnosis with wavelet packet transform and principal component analysis for multi-terminal hybrid HVDC network. J. Mod. Power Syst. Clean Energy 2021, 9, 1312–1326. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, J.W.; Shi, Z.; Zhao, H.B.; Wang, Y.; Xing, Y.H.; Zhang, X.W.; Wang, Y.J.; Zhu, H.X. A fault identification method of hybrid HVDC system based on wavelet packet energy spectrum and CNN. Electronics 2024, 13, 2788. [Google Scholar] [CrossRef]
- Wang, Y.T.; Zheng, D.K.; Jia, R. Fault diagnosis method for MMC-HVDC based on Bi-GRU neural network. Energies 2022, 15, 994. [Google Scholar] [CrossRef]
- Yousaf, M.Z.; Liu, H.; Mustafa, A. Deep learning-based robust DC fault protection scheme for meshed HVDC grids. CSEE J. Power Energy Syst. 2023, 9, 2423–2434. [Google Scholar] [CrossRef]
- Cao, R.R.; Yang, T.G.; Li, G.H.; Chen, S.L. Diagnosis of commutation failure in a high voltage direct current transmission system based on fuzzy entropy feature vectors and a PCNN-GRU. IEEE Access 2025, 13, 110709–110724. [Google Scholar] [CrossRef]
- Wu, J.Y.; Li, Q.; Chen, Q.; Zhang, N.; Mao, C.Z.; Yang, L.T.; Wang, J.Y. Fault diagnosis of the HVDC system based on the CatBoost algorithm using knowledge graphs. Front. Energy Res. 2023, 11, 1144785. [Google Scholar] [CrossRef]
- Zheng, R.N.; Hu, Z.S.; Wen, Z.X.; Wang, J.J. AC fault detection method for HVDC system. Guangdong Electr. Power 2020, 33, 97–104. (In Chinese) [Google Scholar]
- Lin, S.; Mu, D.L.; Liu, L.; Lei, Y.Q.; Dong, X.Z. A novel fault diagnosis method for DC filter in HVDC systems based on parameter identification. IEEE Trans. Instrum. Meas. 2020, 69, 5969–5971. [Google Scholar] [CrossRef]
- Liu, C.C.; Zhou, F.; Wang, F. Fault diagnosis of commutation failure using wavelet transform and wavelet neural network in HVDC transmission system. IEEE Trans. Instrum. Meas. 2021, 70, 3525408. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Q.; Wu, J.Y.; Qiu, T.Q.; Zhang, C.H.; Huang, Y.L.; Guo, J.B.; Yang, B. XGBoost-based intelligent decision making of HVDC system with knowledge graph. Energies 2023, 16, 2405. [Google Scholar] [CrossRef]
- Chen, Q.; Li, Q.; Wu, J.; He, J.; Mao, C.; Li, Z.; Yang, B. State Monitoring and Fault Diagnosis of HVDC System via KNN Algorithm with Knowledge Graph: A Practical China Power Grid Case. Sustainability 2023, 15, 3717. [Google Scholar] [CrossRef]
- Wu, Z.L.; Fan, X.Y.; Bian, G.B.; Liu, Y.H.; Zhang, X.K.; Chen, Y.Q. Short-term wind power forecast with turning weather based on DBSCAN-RFE-LightGBM. Renew. Energy 2025, 251, 123217. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Wang, L.S.; Wang, P.B. Microgrid fault detection method based on lightweight gradient boosting machine–neural network combined modeling. Energies 2024, 17, 2699. [Google Scholar] [CrossRef]
- Huang, Y.F.; Tao, J.; Zhao, J.Y.; Sun, G.; Yin, K.; Zhai, J.Y. Graph structure embedded with physical constraints-based information fusion network for interpretable fault diagnosis of aero-engine. Energy 2023, 283, 129120. [Google Scholar] [CrossRef]
- Lim, J.S.; Cho, H.; Kwon, D.; Hong, J. The development of Bi-LSTM based on fault diagnosis scheme in MVDC system. Energies 2024, 17, 4689. [Google Scholar] [CrossRef]
- Xu, B.B.; Wang, T.Z.; Luo, K.; Gao, D.J. A fault diagnosis method based on wavelet singular entropy and SVM for VSC-HVDC converter. Wuhan Univ. J. Nat. Sci. 2020, 25, 359–368. [Google Scholar]
- He, Z.X.; Chu, P.P.; Li, C.X.; Zhang, K.J.; Wei, H.K.; Hu, Y.H. Compound fault diagnosis for photovoltaic arrays based on multi-label learning considering multiple faults coupling. Energy Convers. Manag. 2023, 279, 116742. [Google Scholar] [CrossRef]
- Amiri, A.F.; Oudira, H.; Chouder, A.; Kichou, S. Faults detection and diagnosis of PV systems based on machine learning approach using random forest classifier. Energy Convers. Manag. 2024, 301, 118076. [Google Scholar] [CrossRef]
- Zhou, S.Q.; Zhang, D.Q.; Wang, M.; Liu, Z.Y.; Gan, W.; Zhao, Z.C.; Xue, S.S.; Müller, B.; Zhou, M.M.; Ni, X.Q.; et al. Risk-driven composition decoupling analysis for urban flooding prediction in high-density urban areas using Bayesian-Optimized LightGBM. J. Clean. Prod. 2024, 457, 142286. [Google Scholar] [CrossRef]
- Ucar, K. Improving electric vehicle state of charge estimation with wavelet transform-integrated 1D-CNN pooling layers. J. Energy Storage 2025, 117, 116202. [Google Scholar] [CrossRef]
- Jiang, Z.; Yang, B.; Zheng, R.Y.; Hou, Y.T.; Li, H.B.; Gao, D.K.; Guo, Z.X.; Jiang, L. Fault diagnosis of proton exchange membrane fuel cell using multiple convolutional neural networks with multi-scale attention mechanism. Inf. Sci. 2025, 720, 122524. [Google Scholar] [CrossRef]
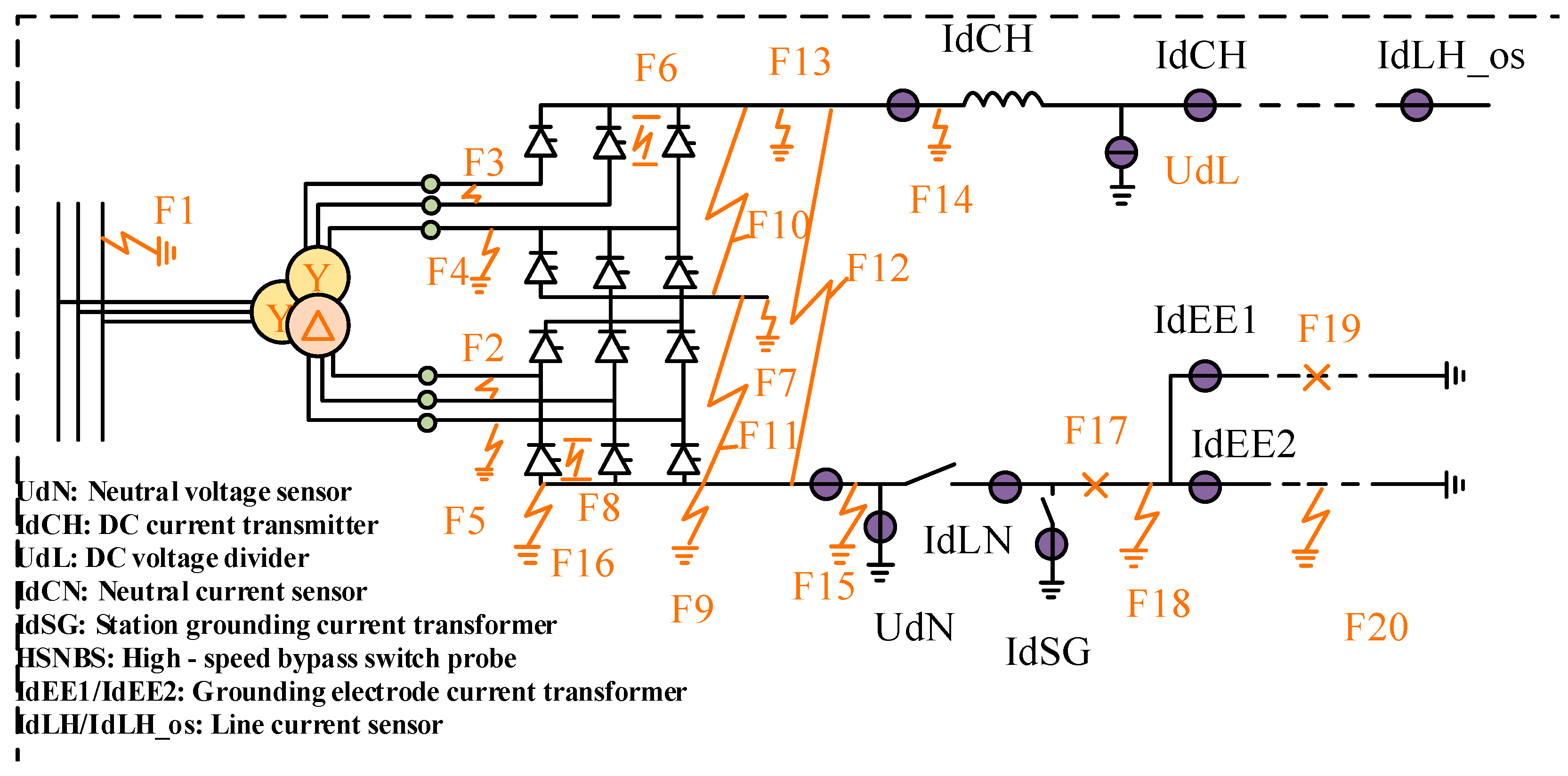
| Fault Point | Fault Type | Fault Point | Fault Type |
|---|---|---|---|
| F1 | A/B/C phase ground | F11 | D valve short circuit |
| F2 | Interphase short circuit | F12 | Valve short circuit |
| F3 | Interphase short circuit | F13 | Y valve high voltage side fault |
| F4 | A/B/C phase ground | F14 | High voltage bus fault |
| F5 | A/B/C phase ground | F15 | Neutral bus fault |
| F6 | Y bridge short circuit | F16 | Line ground |
| F7 | Y-D midpoint failure | F17 | Neutral bus disconnection |
| F8 | D bridge short circuit | F18 | Neutral bus ground |
| F9 | Y valve low Voltage side fault | F19 | Ground pole line disconnection |
| F10 | Y valve short circuit | F20 | Ground pole line ground |
| Signal | Description Meaning | Signal | Description Meaning |
|---|---|---|---|
| UACA(V) | A-phase AC voltage | IACD_L3(A) | C-phase AC current of D-bridge valve side |
| UACB(V) | B-phase AC voltage | UDL(V) | DC line voltage |
| UACC(V) | C-phase AC voltage | UDN(V) | Neutral bus voltage |
| IACY_L1(A) | A-phase AC current of Y-bridge valve side | IDN(A) | Neutral bus current |
| IACY_L2(A) | B-phase AC current of Y-bridge valve side | IDE(A) | Grounding pole bus current |
| IACY_L3(A) | C-phase AC current of Y-bridge valve side | IDH(A) | High-voltage bus current |
| IACD_L1(A) | A-phase AC current of D-bridge valve side | IDL(A) | DC line current |
| IACD_L2(A) | B-phase AC current of D-bridge valve side |  |  |
| Types | Parameters | Value |
|---|---|---|
| LightGBM | num_class | 4 |
| num_leaves | 31 | |
| learning_rate | 0.05 | |
| feature_fraction | 0.9 | |
| bagging_fraction | 0.8 | |
| bagging_freq | 5 | |
| Multimodal | image_size | 32 |
| batch_size | 32 | |
| epochs | 100 | |
| learning_rate | 0.001 | |
| LSTM | units | 128 |
| dropout_rate | 0.2 | |
| learning_rate | 0.001 | |
| epochs | 100 | |
| batch_size | 8 | |
| num_layers | 2 | |
| SVM | C | 2 |
| kernel | rbf | |
| gamma | scale | |
| KNN | n_neighbors | 15 |
| weights | uniform | |
| leaf_size | leaf_size | |
| p | 1 | |
| n_estimators | 30 | |
| RF | max_depth | 3 |
| min_samples_split | 20 | |
| min_samples_leaf | 10 | |
| max_features | 0.3 | |
| 1D-CNN | learning_rate | 0.001 |
| dropout_rate | 0.2 | |
| output dimension of fully connected layer | 4 | |
| batch_size | 8 | |
| epochs | 50 | |
| convolution kernel size | 3 |
| Types | Precision | Accuracy | Recall | F1-Score | Balanced Accuracy |
|---|---|---|---|---|---|
| MSF-LightGBM | 0.9643 | 0.9583 | 0.9643 | 0.9615 | 0.9752 |
| Multimodal | 0.7875 | 0.7917 | 0.7929 | 0.7810 | 0.8620 |
| LSTM | 0.5136 | 0.5833 | 0.6083 | 0.5471 | 0.7346 |
| SVM | 0.8452 | 0.8333 | 0.8452 | 0.8452 | 0.8940 |
| KNN | 0.6719 | 0.5417 | 0.5250 | 0.5063 | 0.6828 |
| RF | 0.8875 | 0.8750 | 0.8810 | 0.8818 | 0.9188 |
| LightGBM | 0.8452 | 0.8333 | 0.8452 | 0.8452 | 0.8940 |
| 1D-CNN | 0.8348 | 0.7917 | 0.8036 | 0.7917 | 0.8666 |
| Types | Precision | Accuracy | Recall | F1-Score | Balanced Accuracy |
|---|---|---|---|---|---|
| MSF-LightGBM | 0.9643 | 0.9583 | 0.9643 | 0.9615 | 0.9752 |
| No feature selection | 0.9375 | 0.9167 | 0.9286 | 0.9226 | 0.9504 |
| No feature extraction | 0.6250 | 0.6250 | 0.6262 | 0.6242 | 0.7497 |
| No data augmentation | 0.0833 | 0.3333 | 0.2500 | 0.1250 | 0.500 |
| Round | Test Event | Accuracy |
|---|---|---|
| 1 | AC faults_1 | 0.4 |
| 2 | AC faults_2 | 1.0 |
| 3 | AC faults_3 | 1.0 |
| 4 | AC faults_4 | 1.0 |
| 5 | AC faults_5 | 0 |
| 6 | DC faults_1 | 1.0 |
| 7 | DC faults_2 | 0.2 |
| 8 | DC faults_3 | 1.0 |
| 9 | DC faults_4 | 1.0 |
| 10 | DC faults_5 | 1.0 |
| 11 | DC faults_6 | 0.8 |
| 12 | DC faults_7 | 1.0 |
| 13 | converter valve faults_1 | 1.0 |
| 14 | converter valve faults_2 | 1.0 |
| 15 | converter valve faults_3 | 1.0 |
| 16 | converter valve faults_4 | 1.0 |
| 17 | converter valve faults_5 | 1.0 |
| 18 | converter valve faults_6 | 1.0 |
| 19 | converter valve faults_7 | 1.0 |
| 20 | inverter commutation failures_1 | 0 |
| 21 | inverter commutation failures_2 | 0 |
| 22 | inverter commutation failures_3 | 1.0 |
| 23 | inverter commutation failures_4 | 1.0 |
| 24 | inverter commutation failures_5 | 1.0 |
| 25 | inverter commutation failures_6 | 1.0 |
| 26 | inverter commutation failures_7 | 1.0 |
| 27 | inverter commutation failures_8 | 1.0 |
| 28 | inverter commutation failures_9 | 0.6 |
| Mean Value | / | 0.821 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Li, Y.; Zhang, S.; Ma, Y.; Qiu, Y.; Luo, X.; Yang, B. Fault Diagnosis Method for High-Voltage Direct Current Transmission System Based on Multimodal Sensor Feature-LightGBM Algorithm: A Case Study in China. Energies 2025, 18, 6253. https://doi.org/10.3390/en18236253
Li Q, Li Y, Zhang S, Ma Y, Qiu Y, Luo X, Yang B. Fault Diagnosis Method for High-Voltage Direct Current Transmission System Based on Multimodal Sensor Feature-LightGBM Algorithm: A Case Study in China. Energies. 2025; 18(23):6253. https://doi.org/10.3390/en18236253
Chicago/Turabian StyleLi, Qiang, Yingfei Li, Shihong Zhang, Yue Ma, Yinan Qiu, Xiaohang Luo, and Bo Yang. 2025. "Fault Diagnosis Method for High-Voltage Direct Current Transmission System Based on Multimodal Sensor Feature-LightGBM Algorithm: A Case Study in China" Energies 18, no. 23: 6253. https://doi.org/10.3390/en18236253
APA StyleLi, Q., Li, Y., Zhang, S., Ma, Y., Qiu, Y., Luo, X., & Yang, B. (2025). Fault Diagnosis Method for High-Voltage Direct Current Transmission System Based on Multimodal Sensor Feature-LightGBM Algorithm: A Case Study in China. Energies, 18(23), 6253. https://doi.org/10.3390/en18236253






