Numerical Analysis of Heavy Oil-Water-Air Flow in a Horizontal Pipe Using Core Annular Flow Adapting Large Eddy Simulations

Abstract

This study focuses on the suitability of Core Annular Flow (CAF) technologies for transporting heavily viscous oil lubricated with water in a horizontal conduit. Using Computational Fluid Dynamics (CFD) and Large Eddy Simulation (LES) techniques with ANSYS Fluent software (Ansys 2022 R2), the research aims to analyze the flow behaviour of heavy oil-water mixtures in horizontal pipes. Specifically, the study examines turbulent CAF to gain insights into how gravity influences the three-phase flow of heavy oil, water, and air. The simulations consider standard horizontal pipes and explore the impact of temperature variations and the presence of air on the annular flow’s behaviour and pressure gradients. The study’s findings, supported by both simulated and experimental results from literature, demonstrate consistent outcomes and contribute to understanding the effectiveness of LES in modelling such complex flows. Overall, this work is novel because it uses an integrated approach to apply advanced numerical techniques, such as LES, to heavy oil, water, and air flows in a horizontal pipe. This approach advances both fundamental understanding and real-world applications in industrial contexts.

1. Introduction

Heavyweight oils are oils identified by their high kinematic viscosity and greater specific gravity. As indicated by Bannwart et al. [1], for oil to be deemed heavy, it should have an API gravity of between 10° API and 20° API, a density of more than 900 kg/m³, a viscosity of approximately 0.1 Pa·s, and a viscosity greater than 100 cP. Due to the recent fall in light oil production, the importance of heavy oil is predicted to increase. However, the high viscosity of heavy oil is a major obstacle to its utilization; in particular, it is difficult to transport, and refinement costs are high due to its greater density. The principal challenge during transportation is the potential for a significant pressure drop and high friction, resulting from the viscous effects of heavy oil in flow. Therefore, the transportation of high-density oil from the manufacturing area to the refinement area and then into the place of consumption is an important obstacle currently affecting the scale of heavy oil production. Trevisan [2] mentioned these points, and possibilities for overcoming these obstacles by reducing the pressure drop during flow using various alternative types of technology mentioned in the literature review. Thus, it has been established by Trevisan [2] that it is possible to reduce viscosity. However, each of these techniques mentioned in the literature review was subject to limitations, either technical or financial. CAF is recognized as one of the most important technologies used to transport heavy oil, and it has great efficiency when compared to the remainder of the techniques used in this field. This technique involves injecting water, which is less viscous, near the pipe surface to prevent contact between the high-density oil and the inner side of the pipe wall. This technique provides a marked result in pressure drop reduction throughout the flow and thus reduces transportation costs. Bannwart [3] described the problems users of the CAF technique can encounter during practical application; for example, if contact arises between the inside surface of the pipe and the heavy oil, this leads to a substantial rise in the pressure drop within the transportation system, with observable impact. However, the most important feature of this technology is the lack of modification required; therefore, a change in the viscosity of an oil is not required, but the pressure drop during transportation significantly reduces the cost. In the literature review, many studies and research works connected to the development and improvement of CAF were mentioned, e.g., Anand et al. [4], Bensakhria et al. [5], Crivelaro et al. [6], Gosh et al. [7], Raghvendra et al. [8] and Rodriguez et al. [9]. Furthermore, it is crucial to explore and investigate the effect of the presence of air, considered the third level in CAF (along with water and oil) to measure the resulting decrease in pressure. Therefore, heavy oil, water, and air are considered the three phases of CAF. Some researchers mentioned in the literature review described three-phase CAF. These were all conducted experimentally and involved modeling techniques, e.g., Ferreira et al. [10], Bannwart et al. [1], Poesio et al. [11], Strazza et al. [12] and Trevisan, [2].

Flow patterns and the drop in pressure for a heavy oil-water-air flow are achieved in crystal tubing of a diameter of 2.84 cm, heavy oil at 3.4 Pa·s viscosity, and 970 kg/m³ at 20 °C temperature, water with air under various incorporations of distinct compositions, horizontal, vertical, and inclined pipes was conducted by Bannwart et al. [1]. Nine flow patterns were established and verified in this study. Their investigation obtained that, when related to the flow of two-phase heavy oil-water only, the presence of air increases the speed of the mixture and, accordingly, a greater drop in pressure. A further experimental investigation linked CAF and a novel database for liquid-liquid-gas three-phase flow to propose a modest model for locating and determining a pressure drop, as conducted and presented by Poesio et al. [11]. Their study observed the impact of injecting air into a controlled pressure drop with liquid-liquid in an annular flow. In addition to this, they detected an error rate of below ±15% in the measurement data linked to the proposed model. An additional experimental study of heavy water-oil-air three-phase flow was conducted by Strazza et al. [12]. They focused on the effect of gas present in a two-phase liquid-liquid core annular flow. The flow map they created based on their results revealed that the rise in air flow, and the reliability of the oil core, result in separation in a chaotic flow model. The drop in pressure values obtained was related to the suggested hypothetical model for the flow of highly viscous oil, water, and air core three-phase flow. Finally, they acquired a variation among the experimental and projected drop of 20%. Heavy oil-water-air three-phase flow in a horizontal pipe has been analyzed using the CAF technique. Identification of an optimal number of grids to achieve the highest precision is accomplished using a grid independent method. The primary goal of the investigation described in this study is to numerically estimate the flow of heavy water-oil-air under varied thermal and air volume fraction circumstances. This study examines the factors that encourage core flow to occur in pipes because it is a practical necessity for heavy oil production and transportation.

2. Methodology and Numerical Formulation

The LES model is used to perform small-scale simulations and to produce information and data on SGS models for high-concentration impacts. Consequently, the SGS model requires greater accuracy to be effective and to be suited to changing local conditions. Therefore, the LES model is used in a straight horizontal pipe in this study. The results obtained from the model were validated with the results stated by Ferreira et al. [10], who described how to obtain proper results and design a model, and how to manage accurate effects to produce accurate and useful information.

2.1. LES for CAF Simulation Using CFD in the Horizontal Pipe

Figure 1 shows the three-phase flow in a selected pipe created from a 3D-dimensional model. It should be underlined that incoming liquids included heavy crude oil, water, and air. After that, the straight pipe was modeled. It is important to create a mesh of the geometry using hexahedral structured components to quantitively examine the behavior of the CAF for an oil-water mixture in the presence of air.

Table 1. Fluid thermophysical properties at 25 °C.

Property	Water Phase	Oil Phase	Air Phase
Density (ρ), kg/m3	997.2	971	0.778
Viscosity (μ), Pa·s	0.001375	0.64	1.794e−0.5
Specific heat (J/kg·K)	4,181,700	1,800,000	1025,766
Interfacial Tension N/m	0.019	0.019	0.019

shows the thermophysical properties of water, oil, and air at 25 °C.

The dimensions of the model selected for the analysis is shown in

Table 2. Dimensions of the horizontal pipe.

Length	Diameter
3 m	0.0284 m

.

Using the formulae listed in

Table 3. Equations used in the present study to find the viscosities of three fluids.

Phases	Equations	Units
Heavy oil	${\mu }_o=0.6402+18.9612\times e^{(-0.07444\times T)}$	Pa·s
Water	${\mu }_w=({\displaystyle \frac{997.2}{2.443299\times {10}^{-2}\times T^{-6.153676}}}$)	Pa·s
Air	${\mu }_g=2.8\times {11}^{-7}\times T^{0.735476}$	Pa·s

, which were derived from various bases, the viscosity of the three phases for the CAF model flow was computed. Kreith and Bohn [13], Santana et al. [14], and Trevisan [2] provided the formulae needed to calculate the viscosity of water, air, and heavy oil. The following equations were applied to determine the viscosities of water-heavy oil-air three-phase fluid:

The equation used to calculate the fluid properties relies on statistics given by Kreith and Bohn [13]. The choice of temperature is in the range of 0 °C ≤ T ≤ 100 °C.

2.2. VOF Model

The VOF model is based on three multiphase flow models that use the Euler-Euler technique. The phases in the VOF model are made for two or more unmixable fluids, in which the location of the fluid interface is of concern. In the selected VOF model, the volume fraction continuity equation in one or more phases is solved with a single set of momentum equations, and is calculated as follows:

$${\displaystyle \frac{𝜕\left({\rho }_k{\alpha }_k\right)}{𝜕t}}+\nabla ·\left({\rho }_k{\alpha }_{k}u\right)=0$$

(1)

where ${\alpha }_k$ is the volume fraction for an auxiliary status. The volume fraction for the status contains a value of 1 when a control volume is filling up with the $k^{th}$ liquid, a value of 0 when the control volume is unfilled with the $k^{th}$ liquid, and a value between 0 and 1 if an interaction is used for the cell. The status of the volume fraction does not recognize interaction. Subsequently, various interact arrangements could be matched to a similar value for the status of volume fraction, and numerous systems were proposed to follow the interaction precisely,

When the boundary length scales get close to the computing grid scale, the VOF model’s accuracy decreases. The VOF model can therefore be thought of as general modeling for usage in situations where the interface length scale is considerable. The VOF model is regarded as an adequate and suitable model for simulating CAF in a pipe because the interface relating to heavy oil and water is, in terms of approach magnitude, larger than the pipe diameter.

2.3. Development of Model and LES Method

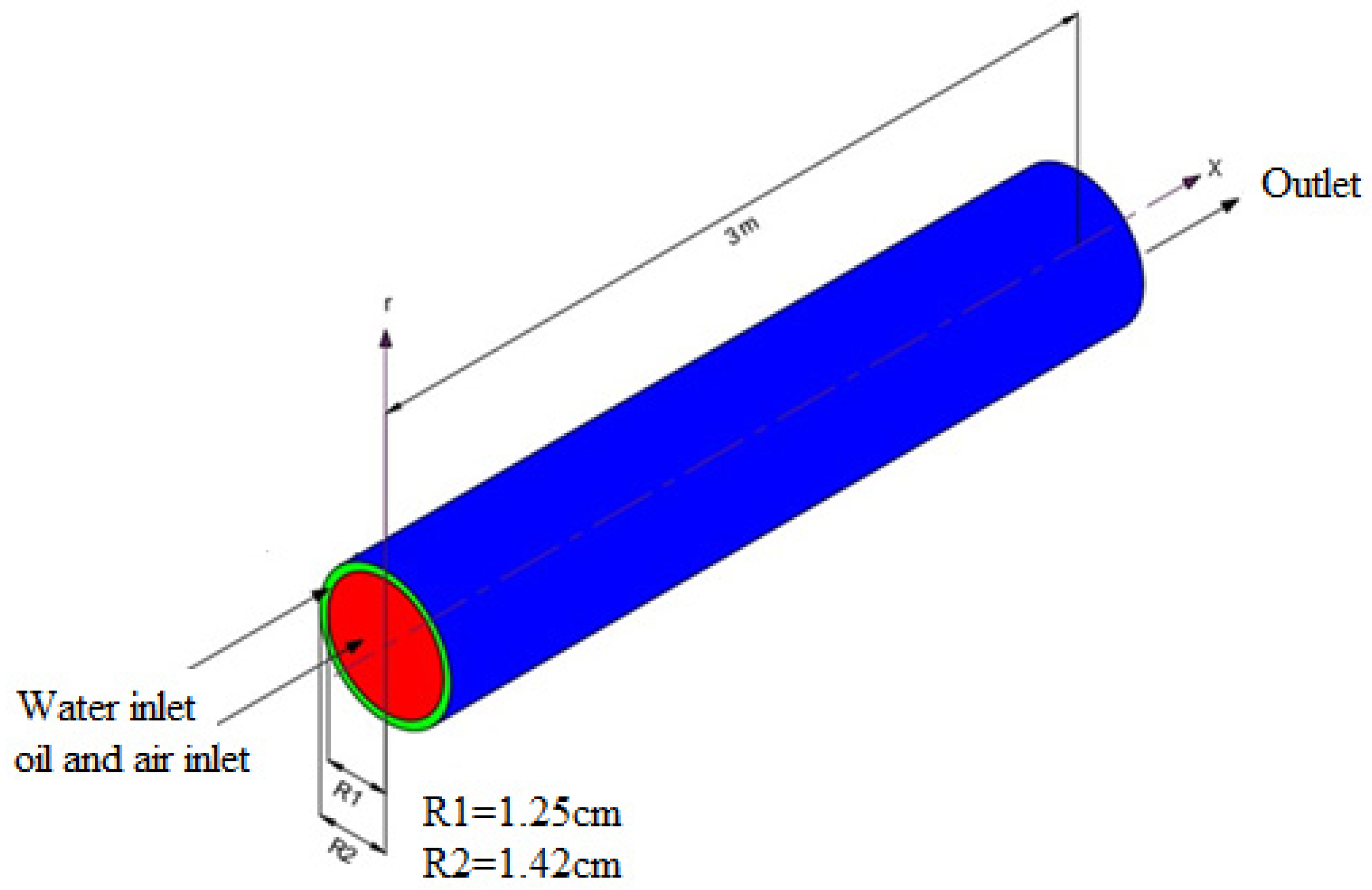
Physical Model

A model study was selected from the literature review (Ferreira et al. [10]) for reproduction, with some minor simplifications and modifications. The 3D model of the selected three phases for the CAF model for the selected pipe was built as indicated in Figure 2. Initially, the horizontal pipe contains two inlets, and water is injected near the pipe wall and oil with air into the core of the pipe. High-density crude oil and water are the inflow fluids. The horizontal straight pipe geometry, dimensions, and properties are shown in Table 1 and Table 2. Three-phase flow in the horizontal pipe depends on various parameters; e.g., diameter, pipe roughness, pipe material, friction pressure gradient, velocity, and physical properties. The ANSYS Fluent package was used to solve this model. In addition, the SGS model and the governing equations are discretized using FVM. The governing equations were then resolved using a segregated solver. The computation was then accomplished for turbulent unsteady flows to examine the underlying improvements before studying the initial development of CAF. Additionally, this study investigated unsteady streams, non-miscible liquid pairs, constant fluid characteristics, and the co-axial entry of liquids. The length of the computational flow field in horizontal pipes is 3 m long and 0.0284 m is the inside diameter of the pipe selected, while high-density oil forms the core (viscosity μ = 0.64 Pa·s and density ρ = 971 kg/m³) and water is taken as the annular fluid (viscosity μ = 0.001375 Pa·s and density ρ = 997.2 kg/m³).

2.4. Governing Equations

In the present study of the three-phase CAF approach in the straight pipe, for heavy oil, water, and airflow, the following conditions were considered during the simulation:

• The model should be incompressible and support transient flow.
• There should be no chemical reactions between the oil and water during the simulation.
• Gravitational and drag impacts should be presented.
• The viscosities of the heavy oil, air, and water should be presented as temperature functions.
• The interfacial transport of mass between the oil, water, and air phases is zero.

Regarding the points mentioned above, the conservation equations for energy, mass, and momentum were utilized for the multiphase flow of highly viscous oil, water, and air (H. K. Versteeg and W. Malalasekera [15].

A low conservation of mass is applied to derive the continuity equation. Therefore, the continuity equation can be defined thus:

$${\displaystyle \frac{𝜕u_i}{𝜕t}}=0$$

(2)

where $u_i$ is the velocity field and i is in the set {1, 2, 3, etc.}. Repeated indices are summarized according to Einstein’s summation convention.

Viscosity is assumed to be of constant viscosity, all types of bodily forces will be neglected, and the momentum equation or Navier-Stokes equation is considered in the form below:

$${\displaystyle \frac{𝜕u_i}{𝜕t}}+{\displaystyle \frac{𝜕}{x_j}}\left(u_i{u}_j\right)=-{\displaystyle \frac{1}{{\rho }_0}}{\displaystyle \frac{𝜕P}{𝜕x_i}}+{\displaystyle \frac{𝜕}{𝜕x_j}} [v ({\displaystyle \frac{𝜕u_i}{𝜕x_j}}+{\displaystyle \frac{𝜕u_j}{𝜕x_i}})]$$

(3)

where ρ, $P,$ and v are the density, pressure, and kinematic viscosity, respectively. This vector equation, together with the continuity equation, is called the Navier-Stokes equation (N-S equation).

Specific heat $c_p$ is presumed to be constant, and the energy and temperature relationship is e = $c_p$T. The energy equation can be calculated as:

$${\displaystyle \frac{𝜕T}{𝜕t}}+{\displaystyle \frac{𝜕u_{j}T}{𝜕x_j}}={\displaystyle \frac{v}{Pr}} {\displaystyle \frac{{𝜕}^{2}T}{{𝜕x}_j{𝜕x}_j}}$$

(4)

where the Prandtl number is calculated and introduced as Pr = ${\displaystyle \frac{c_{p}v}{\rho k}}$, and k is thermal conductivity. Therefore, if the Reynolds number is high, the computational cost will also be high. Therefore, this method is required to reduce the requirement for a full solution, by introducing a model that incorporates turbulent behavior on the smallest spatial scales. This model is an LES, with a spatial filtering process that softens and smooths turbulent behavior by removing the smallest spatial scales applied. After applying the filter, the resulting equations then contain an SGS stress tensor. Therefore, the continuity equation, the N-S equation, and energy after filtering are obtained in the form below:

$${\displaystyle \frac{𝜕{\overline{u}}_i}{𝜕x_i}}=0$$

(5)

$${\displaystyle \frac{𝜕{\overline{u}}_i}{𝜕t}}+{\displaystyle \frac{𝜕}{𝜕x_j}}\left({\overline{u}}_i{\overline{u}}_j\right)=-{\displaystyle \frac{1}{{\rho }_0}}{\displaystyle \frac{𝜕\overline{P}}{𝜕x_i}}+{\displaystyle \frac{𝜕}{𝜕x_j}} [v ({\displaystyle \frac{𝜕{\overline{u}}_i}{𝜕x_j}}+{\displaystyle \frac{𝜕{\overline{u}}_j}{𝜕x_i}})+{\tau }_{ij}]$$

(6)

where the SGS stress tensor ${\tau }_{ij}$ is given by:

$${\tau }_{ij} = {\overline{u}}_i{\overline{u}}_j - \overline{u_i{u}_j},$$

(7)

The LES model addresses unstable fields in space and time if Δx is small enough. The majority of SGS models make an eddy viscosity assumption (Boussinesq’s hypothesis) when modeling the SGS stress tensor:

$${\tau }_{ij}=2 v_t {\overline{S}}_{ij}+{\displaystyle \frac{1}{3}} {\tau }_{ll}{\delta }_{ij}$$

(8)

where,

$${\overline{S}}_{ij}={\displaystyle \frac{1}{2}} ({\displaystyle \frac{𝜕{\overline{u}}_i}{𝜕x_j}}+{\displaystyle \frac{𝜕{\overline{u}}_j}{{𝜕x}_i}})$$

(9)

Therefore, the LES Equation (3) becomes:

$${\displaystyle \frac{𝜕{\overline{u}}_i}{𝜕t}}+{\overline{u}}_j{\displaystyle \frac{𝜕{\overline{u}}_i}{𝜕x_j}}=-{\displaystyle \frac{1}{{\rho }_0}}{\displaystyle \frac{𝜕\overline{P}}{𝜕x_i}}+2 {\displaystyle \frac{𝜕}{𝜕x_j}} \left[\right(v+v_t) {\overline{S}}_{ij}]$$

(10)

The modified pressure $\overline{P}$ = $\overline{p}$ − (1–3)${\rho }_0{\tau }_{ij}$ was introduced, and will be decided with the help of a filtered continuity Equation (2), by examining the deviation of Equation (7). This implies variations of the eddy viscosity ($v_t$).

Under generally non-restrictive assumptions made by Leonard [16], filtering and differentiation are replaced as:

$$\overline{{\displaystyle \frac{𝜕u}{𝜕x}}}=𝜕\overline{u}/𝜕x$$

(11)

An equation for $\overline{u}$ is obtained by applying N-S equations with the same spatial filter function:

$${\displaystyle \frac{𝜕\overline{u}}{𝜕t}}+\nabla · \overline{uu}=-\nabla \overline{P}+v{\nabla }^2\overline{u}$$

(12)

Consequently, for constant density flow, P = p/ρ. Because filtered non-linear terms $\left(\overline{uu}\right)$ cannot be expressed in terms of known resolved components $\left(\overline{u}\right)$, nonlinear terms are not closed, much like in conventional turbulence modeling.

To prevent this problem, an SGS stress is initiated, such that:

$$\overline{uu} = \overline{u}\overline{u}+\tau .$$

(13)

Then the momentum equation becomes:

$${\displaystyle \frac{𝜕\overline{u}}{𝜕t}}+\nabla · \overline{uu}=-\nabla \overline{P}+v{\nabla }^2\overline{u}-\nabla ·\tau$$

(14)

The turbulence modeling goal seeks to measure the SGS stress $(\tau$) from the determined velocity field ($\overline{u})$.

Filtering incompressible N-S equations can be defined thus:

$${\displaystyle \frac{𝜕\overline{u_i}}{𝜕t}}+{\displaystyle \frac{𝜕\left(\overline{u_i}\overline{u_j}\right)}{{𝜕x}_j}}={\displaystyle \frac{𝜕\overline{P}}{{𝜕x}_i}}+v {\displaystyle \frac{{𝜕}^2\overline{u_i}}{{𝜕x}_j^2}}-{\displaystyle \frac{𝜕(\overline{u_i{u}_j}-\overline{u_i}\overline{u_j})}{{𝜕x}_j}}$$

(15)

The SGS stress tensor is defined thus:

$${\tau }_{ij}=\overline{u_i{u}_j}-\overline{u_i} \overline{u_j}$$

(16)

The equation above is similar to the original equation except for the last part, which is the SGS contribution of the unresolved/sub-grid filter field to the resolved/filtered field.

The energy equation is computed as:

$${\displaystyle \frac{𝜕\overline{T}}{𝜕t}}+{\displaystyle \frac{𝜕\overline{u_i}\overline{T}}{𝜕x_j}}={\displaystyle \frac{𝜕}{𝜕x_j}} \left[\left({\displaystyle \frac{v}{Pr}}+{\displaystyle \frac{v_t}{{Pr}_t}}\right){\displaystyle \frac{𝜕\overline{T}}{𝜕x_j}}\right]$$

(17)

where $\overline{a}$ represents an amount spatially filtered, and $v_t$ is an unknown quantity connected to the SGS scales, which must be modeled.

When the N-S equations are combined with the energy equation, the energy equation will be given as:

$${\displaystyle \frac{𝜕\overline{T}}{𝜕t}}+{\displaystyle \frac{\left(\overline{u_i}\overline{T}\right)}{𝜕x_i}}={\displaystyle \frac{1}{Re· Pr}} \times {\displaystyle \frac{{𝜕}^2\overline{T}}{𝜕x_i^2}}-{\displaystyle \frac{𝜕q_i}{𝜕x_i}}$$

(18)

where Re indicates the Reynolds number, and Pr is the Prandtl number. $q_i$ are the SGS heat flux, w is modeled by the SGS model, and the constant value of 0.85 is utilized for the turbulent Prandtl number. The SGS heat flux in the energy equation is calculated as follows:

$$q_i={\displaystyle \frac{c_{s}V}{{Pr}_T}}\left|\overline{S}\right|{\displaystyle \frac{𝜕\overline{T}}{𝜕x_i}}$$

(19)

where ${Pr}_T$ is the turbulent Prandtl number.

In this chapter, the Smagorinsky-Lilly model is also applied, as in the other chapters in this study.

2.5. Numerical Methodology

In the present work, the PISO technique for the LES model was used. For the LES model’s diffusion terms, a linear central differentiation scheme with an unlimited second order was adopted. The superficial Reynolds numbers (Reso) for heavy oil, water, and air were computed as follows:

$${Re}_{so}={\displaystyle \frac{D{U}_{so}{\rho }_o}{{\mu }_o}}, {Re}_{sw}={\displaystyle \frac{D{U}_{sw}{\rho }_w}{{\mu }_w}} \mathrm{and} {Re}_{sa}={\displaystyle \frac{D{U}_{sa}{\rho }_a}{{\mu }_a}}$$

(20)

where the letters o, w, and a stand for the phases of oil, water, and air, respectively, and the letter s stands for surface conditions. The inlet diameter of the pipe, density, viscosity, and velocity are denoted by the letters D, ρ, μ, and U respectively. As determined by the Reynolds Transport Theorem, the principles of the laws of conservation apply to fluid dynamics. The LES model uses the N-S equations to operate and typically lowers processing costs by narrowing the scale for the solution length.

2.6. Selected Boundary Conditions

• At pipe inlet
  In the present model, high-density oil and air velocities are indicated in the core space of the horizontal pipe. Simultaneously, the water velocity is indicated in the horizontal pipe’s annular space as shown in Figure 2.
  The inlet boundary conditions are:

  (a)

  In the annular space representing the water inlet, the mean velocity and volume fraction of water in the direction of x are presented as follows:

  $$R_i<\gamma <R_e,atx=0;\left\{\begin{array}{c}{u}_w\ne 0\\ v_w=w_w=0\\ u_o=v_o=w_o=0\\ u_a=v_a=w_a=0\\ r_o=r_a=0\\ r_w=1\\ T=T_w\end{array}\right.$$

  where u, v, e, v denote vector components of velocity in the x, y, and $z$ directions, w, o, and a denote water, oil, and air phases, respectively, and T is the temperature.

  (b)

  The core space representing the oil inlet, the mean velocity component, and the volume fraction of oil and air in the x-axis was taken as:

  $$0<y<R_i,atx=0;\left\{\begin{array}{c}{u}_0=u_a\ne 0\\ v_0=w_0=0\\ v_a=w_a=0\\ u_w=v_w=w_w=0\\ r_o=0.95\\ r_a=0.05\\ r_w=0\\ T=T_0=T_a\end{array}\right.$$

• At pipe outlet

A pressure outlet is used at the outlet, and the diffusion fluxes for variables in the exit position were set at zero.

3.

Pipe wall boundary conditions.

A no-slip stationary and no-penetration boundary was inserted on the wall pipe as shown in

Table 4. Pipe wall boundary condition.

Motion	Stationary
Shear condition	No slip

:

$$U_z=0 \left(\mathrm{No}\text{-}\mathrm{slip}\right) \mathrm{and} U_r=0 \left(\mathrm{No}\text{-}\mathrm{penetration}\right)$$

$$y=R_e,at 0\le x\le L; \left\{\begin{array}{c}{u}_w=v_w=w_w=0\\ u_o=v_o=w_o=0\\ u_a=v_a=w_q=0\\ T=T_p=288 \mathrm{K}\end{array}\right.$$

The gradient for the quantities near the wall was mostly high and essentially required additional fine grids close to the wall to capture the change in quantities, and subsequently to make the calculation appear more expansive, though time-consuming. In addition to the need for a large memory, the computer processing must be fast and require complex equations. In this study, the focus of a fine mesh on the wall will be increased as the study develops.

A boundary layer was applied in this study on the wall to advance the performance of the wall function and to meet the requirement of a dimensionless wall distance ($y^{+}$).

The $y^{+}$ is calculated as:

$$y^{+}={\displaystyle \frac{\rho u_{\tau }y}{\mu }}$$

(21)

where $u_{\tau }$ is the friction velocity at the nearest wall, y is the distance to the nearest wall, and $\mu$ is the local kinematic viscosity of the fluid:

$$\begin{gathered} u_{\tau }=\sqrt{{\displaystyle \frac{{\tau }_{\omega }}{\rho }}}, {\tau }_{\omega }=C_f. {\displaystyle \frac{1}{2}}\rho (U_{\mathrm{f}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{m} \mathrm{v}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}}), C_f=[2 {{\log }_{10}{(Re}_x)-0.65]}^{-2.3}, \\ \mathit{Re}={\displaystyle \frac{\rho ·U_{f\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{m} \mathrm{v}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}}·L_{b\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{d} \mathrm{l}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}}}{\mu }} \end{gathered}$$

(22)

Therefore, the selected boundary conditions and the ANSYS fluent boundary condition must match for the analytical calculations. Oil and water are permitted to flow from the inlet at a uniform speed of 1.5 and 2.2 m/s, respectively. At the outlet section (x = L), a constant mean pressure pest = 101,325 Pa, was specified, where L is the pipe length.

In this work, a root means square (RMS) residue equal to 10⁻⁷ kg/s was set as the convergence standard. The thermophysical properties of the liquids utilized in the simulation are given in Table 1, Table 2 and Table 3.

2.7. Discretization Result Systems and Computational Set-Up

The solution techniques utilized when the solver was running are illustrated in

Table 5. Solution control method used in ANSYS Fluent.

Momentum Explicit Relaxation Factor	0.3
Pressure Explicit Relaxation Factor	0.3

and

Table 6. Computational setup used for computation.

Turbulent Model	LES, Smagorinsky-Lilly model
Material	oil, water, and air
Numerical Details
Pressure-Velocity Coupling	PISO
Descretisation Momentum	Bounded Central differencing
Pressure	PRESTO
Gradient	Least square cells based
Time	Bounded second order implicit
Boundary conditions
Inlet	velocity
outlet	pressure
Simulation factor
Total simulation time	80–190 s
Start data sampling	40 s
Time step	0.001
courant number	Between 0.5–0.85 in all simulations
Residual Criteria	1 × 107

. Additionally, the relaxation factors began at very low numbers (0.1–0.3) and evaded divergence. As the LES flow produced initially at 100 steps, the relaxation factors were moderately expanded as they approached unity, with scaled residuals used in the order of ${1\mathrm{e}}^{-7}$ continuity for momentum. Screens were made available to track the velocity at focal points and secure places along the pipe once the simulations attained measurably stable and factually strong states. The implicit time-stepping plan was considered and approved for the time step, and the time step size was set to be identical to 0.001. Using a second-order central differencing strategy, the diffuse phrases were discretized. A convection boundedness basis was mostly used in the first-order upwind plan. With no specific wall treatment in the SGS model, a no-slip condition was applied to the solid walls. As per the study by Ferreira et al. [10], numerical values for the inflow velocities, density, and viscosity were calculated, as shown in Table 1 and Table 2. The characteristics of the simulation set-up are given in Table 6. Initial velocity and the pressure field for the LES simulation were acquired. In addition, the velocity inlet profile was obtained.

The default value of 1 is the under-relaxation factor retained for density and body force.

3. Results and Discussion

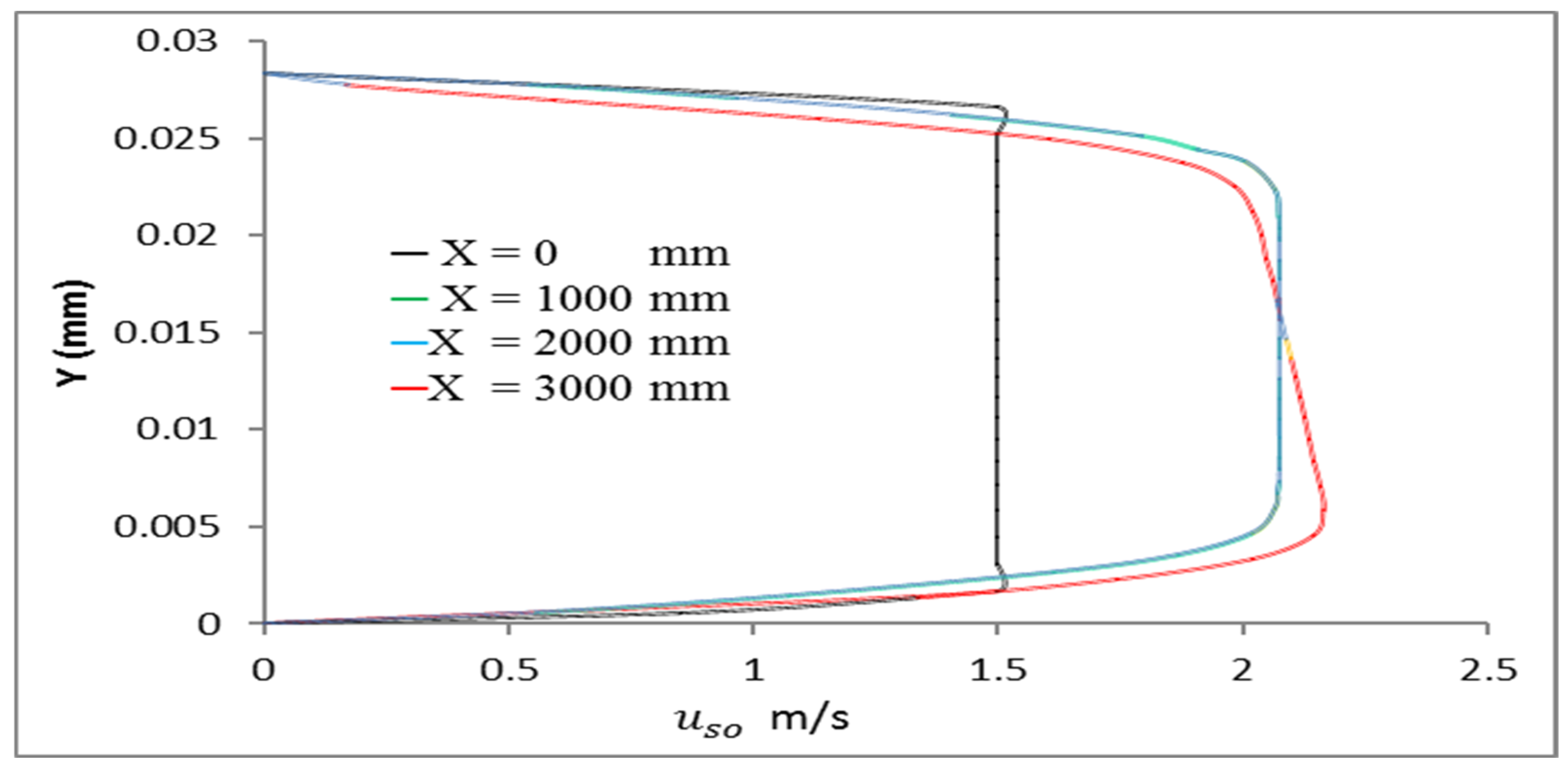
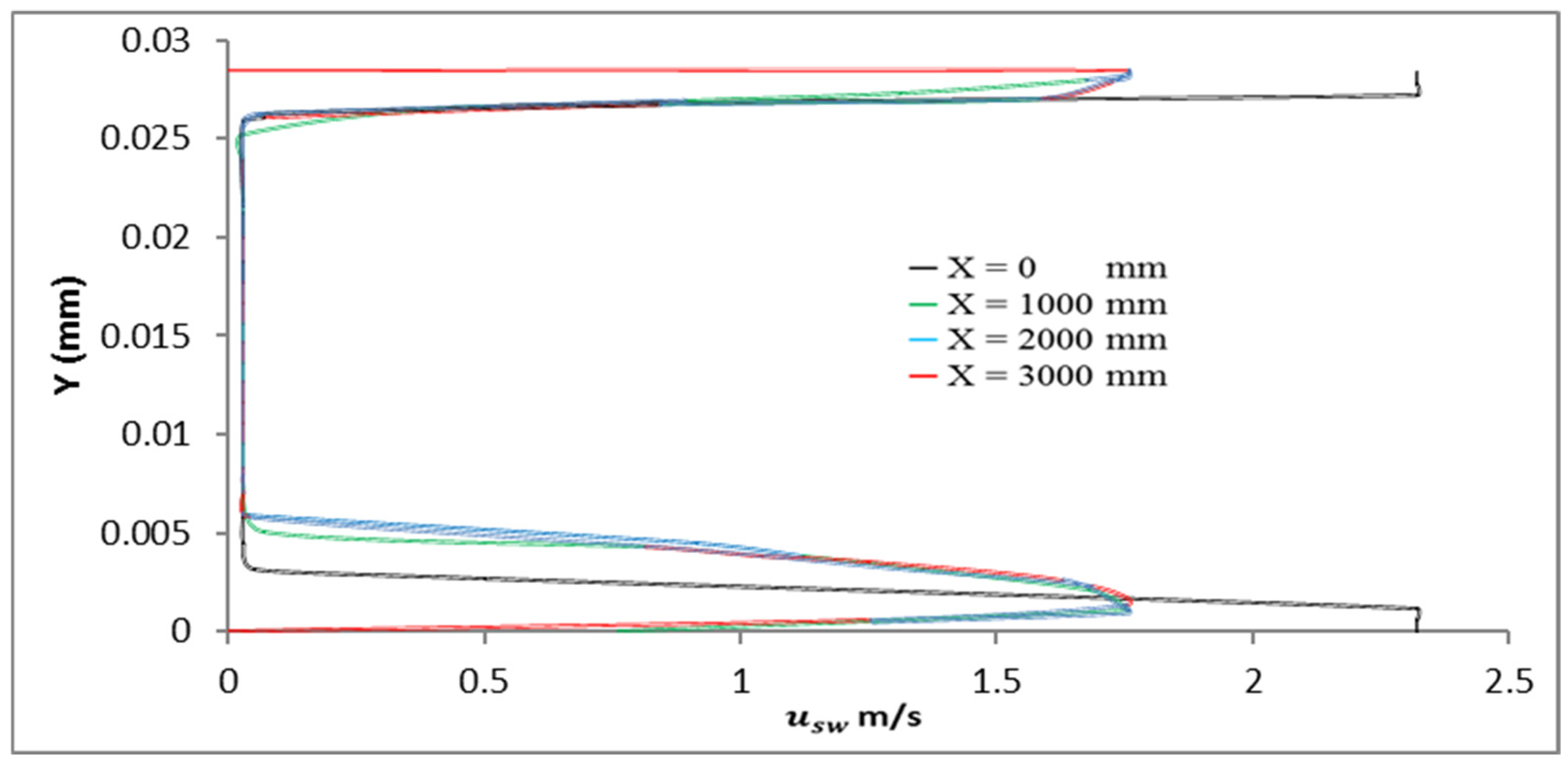
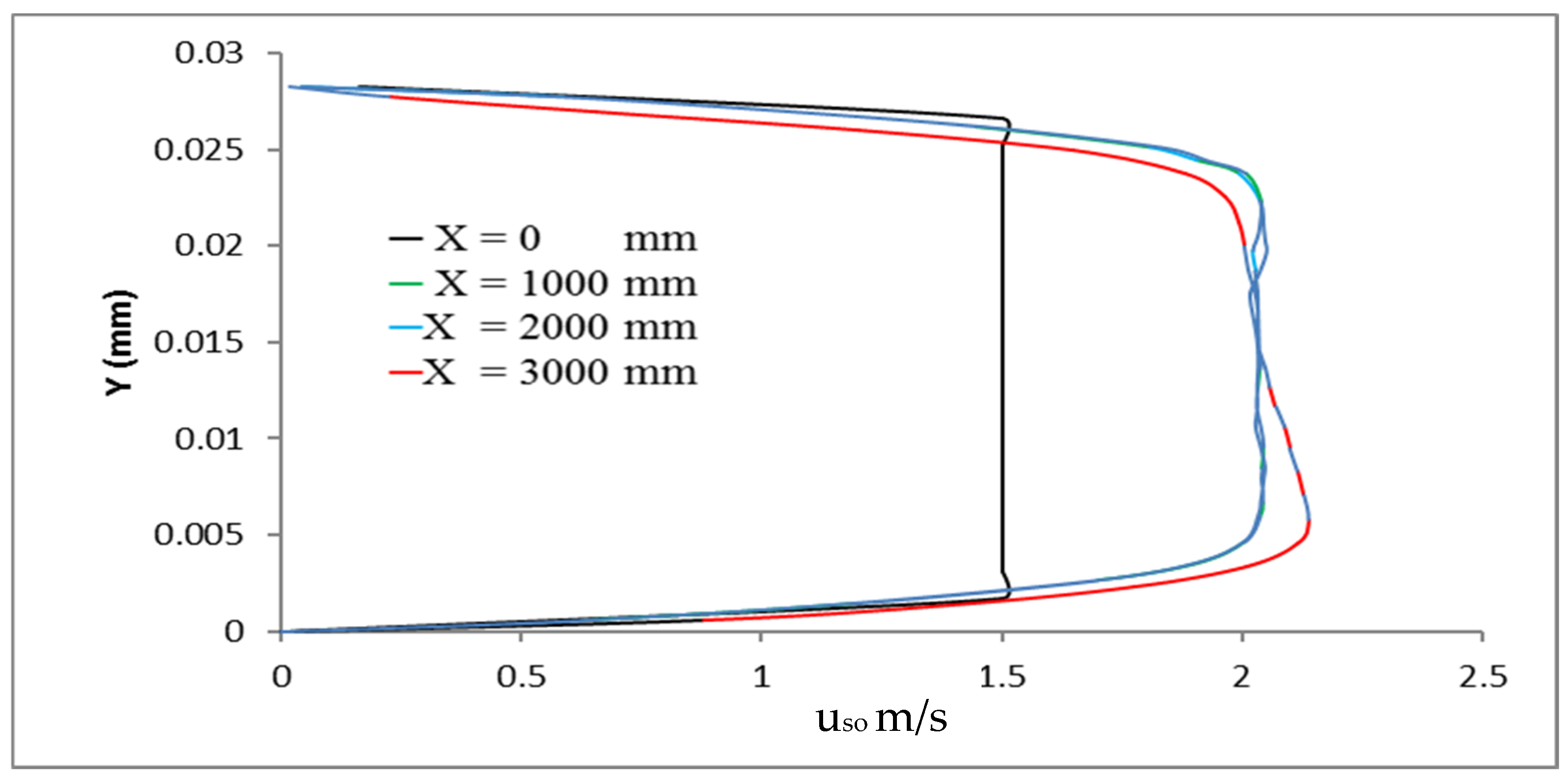
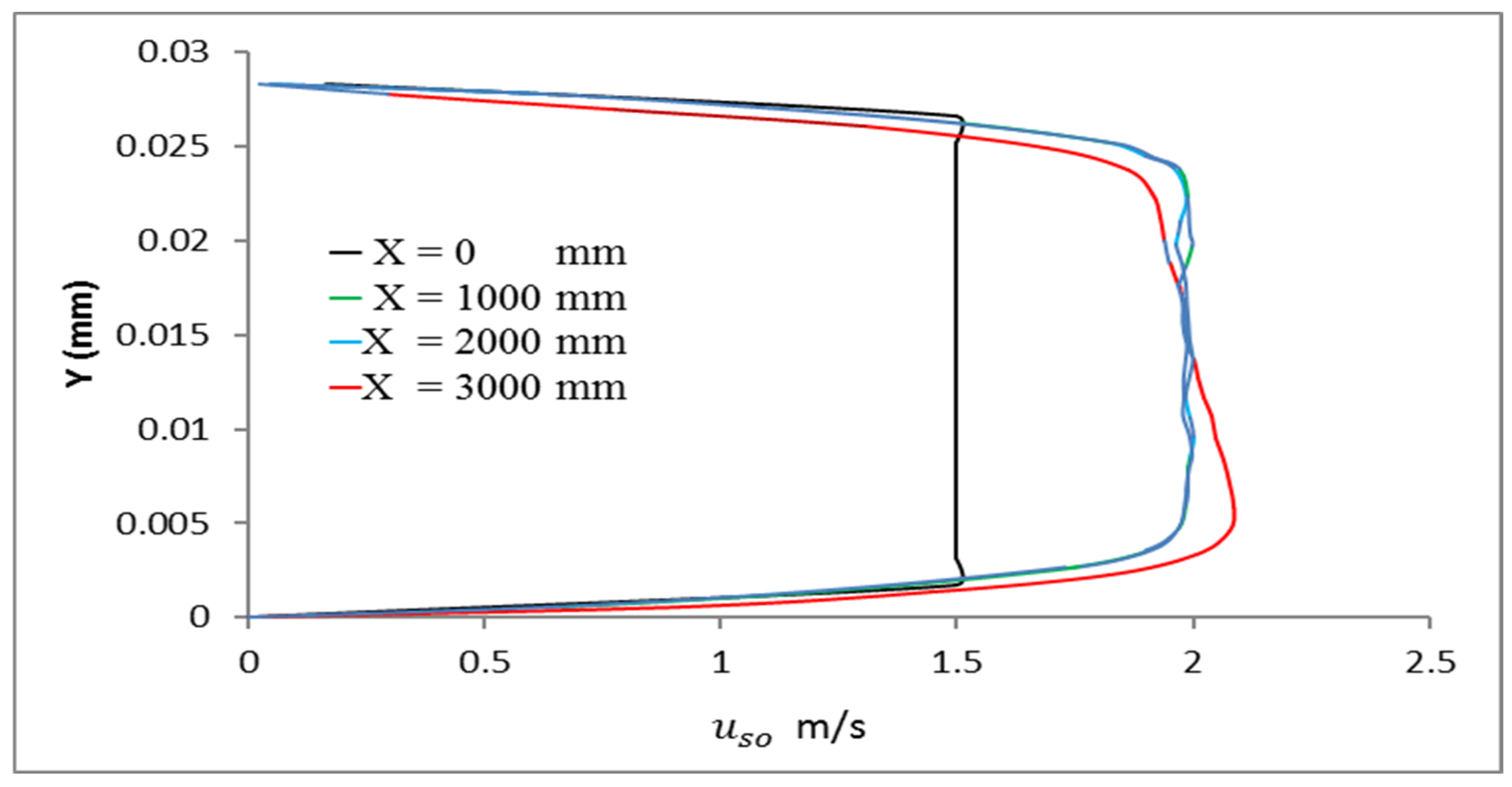
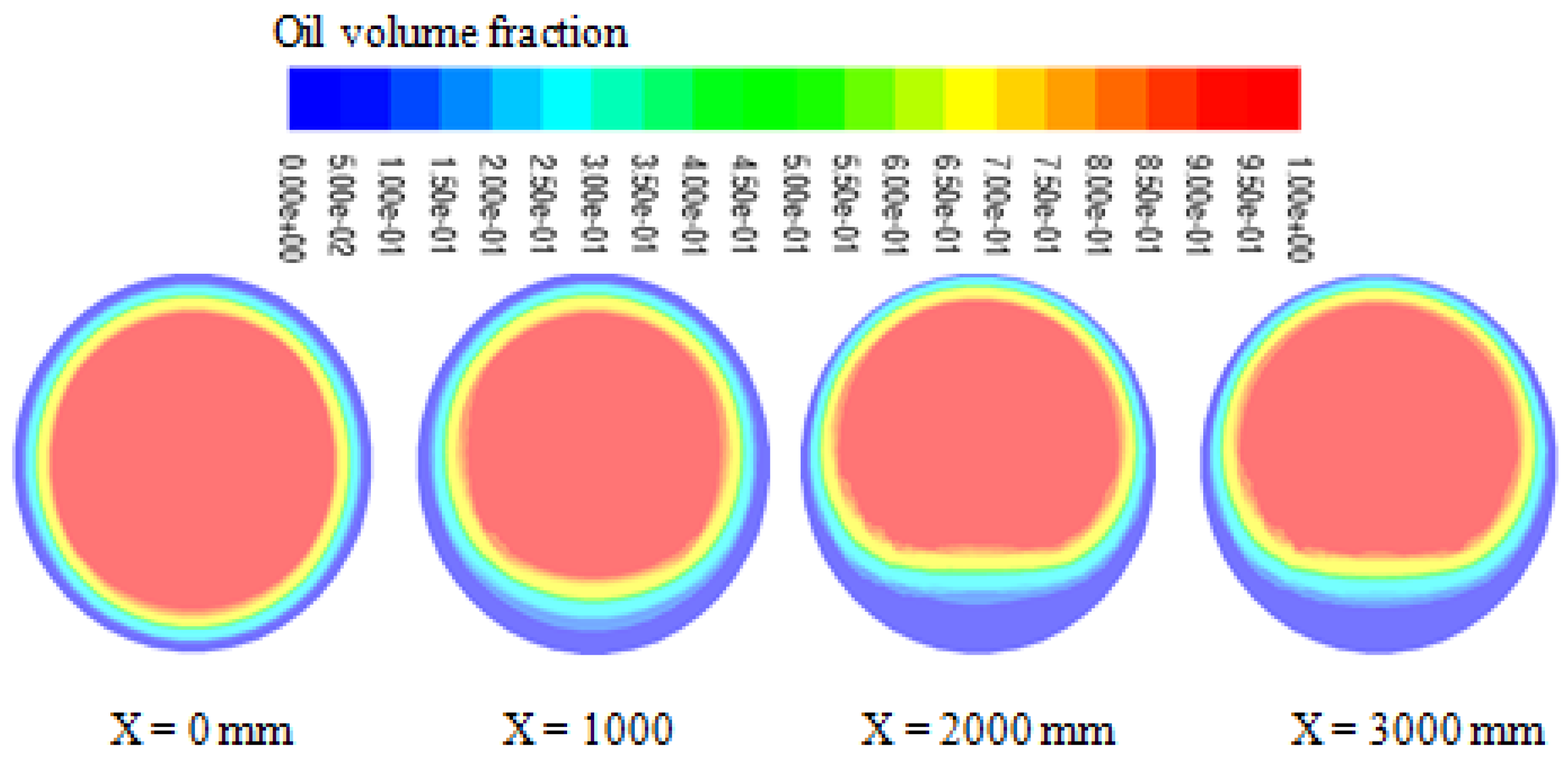
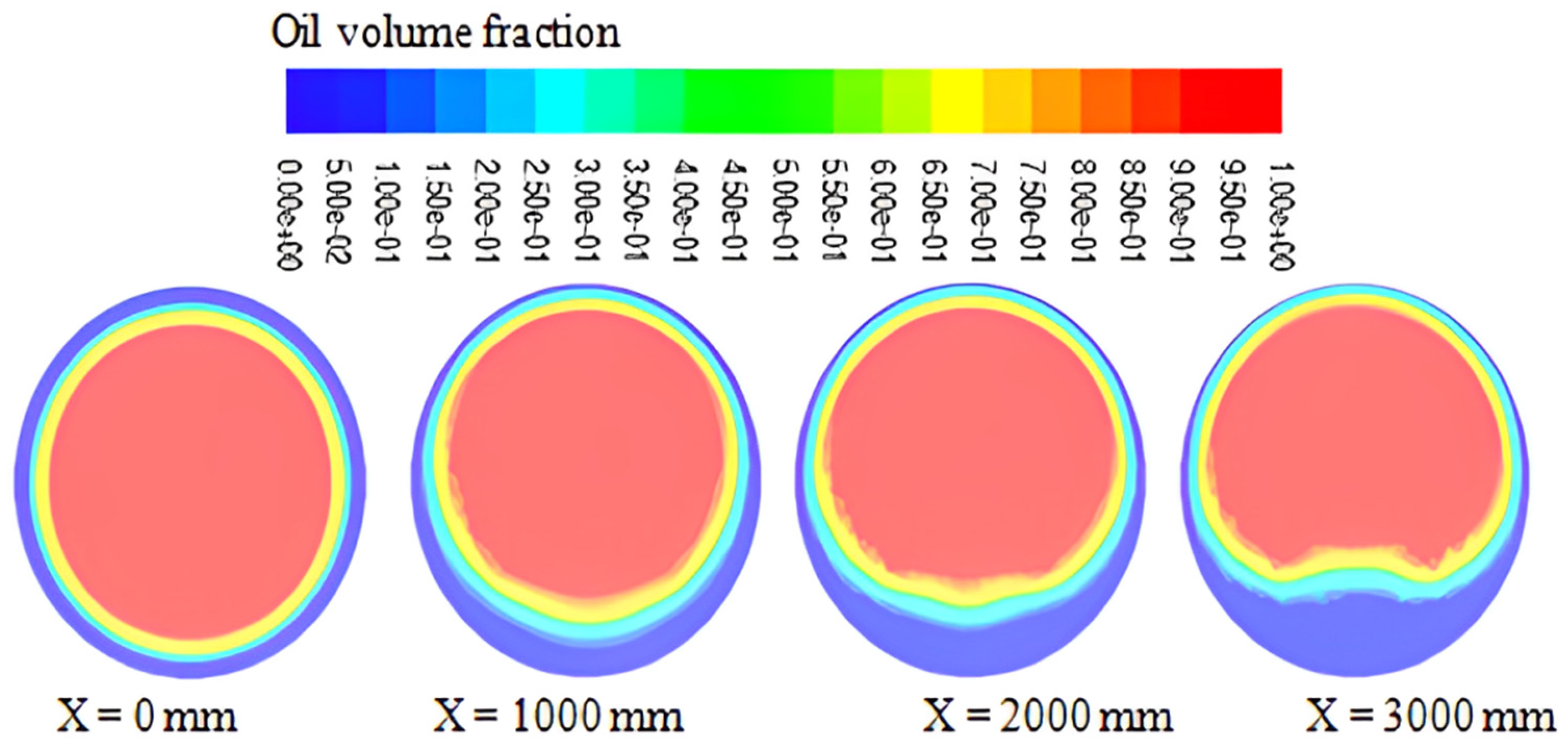
3.1. Air Phase Impact

The oil-water flow and the oil-water-air flow at four places in the axial axis, Z = 0 m, were both accomplished under the same conditions and are both described and shown as superficial velocity profiles in Figure 3, Figure 4, Figure 5 and Figure 6.

According to the velocity profiles that were obtained and shown in Figure 3, Figure 4, Figure 5 and Figure 6, the introduction of the air phase to heavy oil-water flow results in significant modifications to the fluid dynamics of the water and oil phases. Due to the increase in water flow in that area, it affects the velocity gradient in the lower portion of the pipe. Bannwart et al. [1], Poesio et al. [17,18], and Strazza et al. [12] all independently noted this behavior. Figure 5 and Figure 6, which depict the performance of the volumetric fraction field of oil in the pipe at various axial points, also clearly show an impact. In essence, the presence of air causes the heavy oil to be elevated more effectively, increasing the area filled by the annular section of water in the bottom portion of the pipe, which is closest to the wall. As a result, with three-phase flow as opposed to two-phase flow, the divergence between buoyancy and lubricating forces is more pronounced. In addition, the behavior and the impact of the air phase are evident in Figure 7, Figure 8 and Figure 9, which show results at different temperatures.

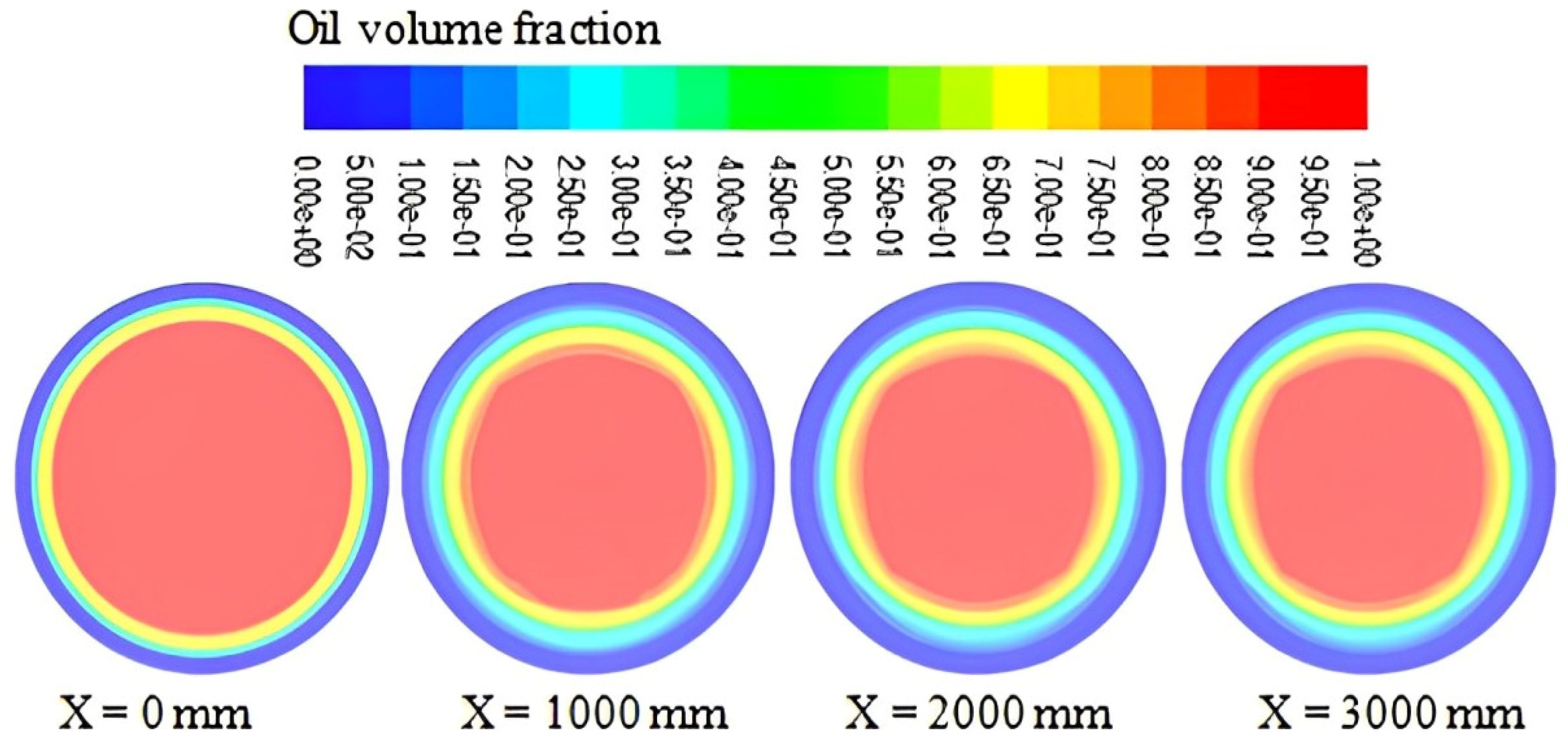
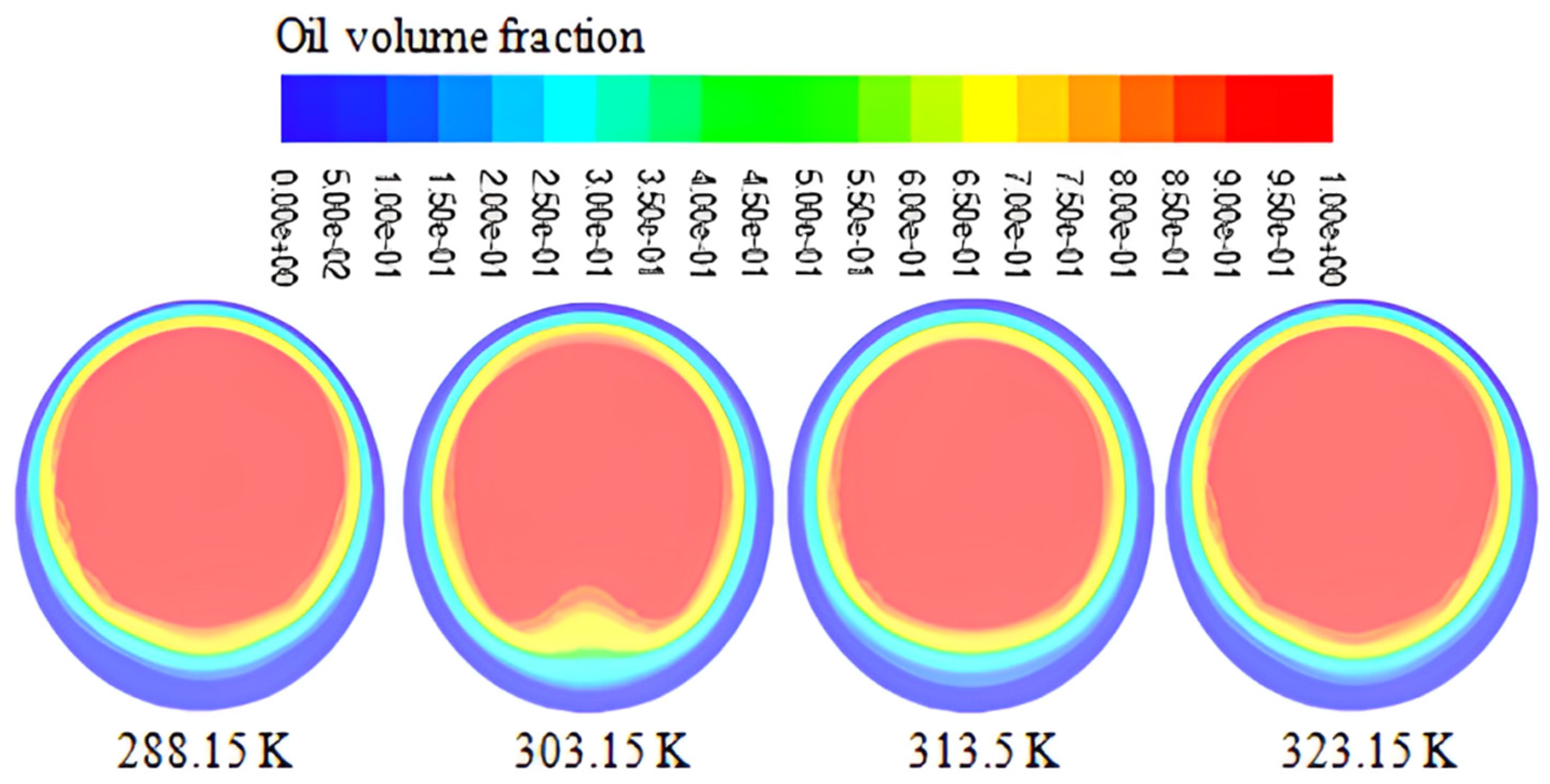
3.2. Temperature Change Impact

Figure 10 shows the surface velocity profiles for the three phases of high-viscosity heavy oil, water, and air at different temperatures (288.15 K, 303.15 K, and 323.15 K) when measured at axial points equal to X = 1000 mm and Z = 0 mm. It has been noted that a tiny difference in the oil phase’s surface velocity occurs when the temperature of the phases increases at the pipe’s entrance because of a change in viscosity.

Figure 11 shows the volume percentage of the oil phase at X = 1000 mm at different phase temperatures (288.15 K, 303.15 K, 313.15 K, and 323.15 K) at the pipe entry. The level of oil in the core is expected to rise as the temperature rises. Oil viscosity decreases as a result of temperature changes, but viscous forces that hinder the flow of this fluid are also minimized and reduced.

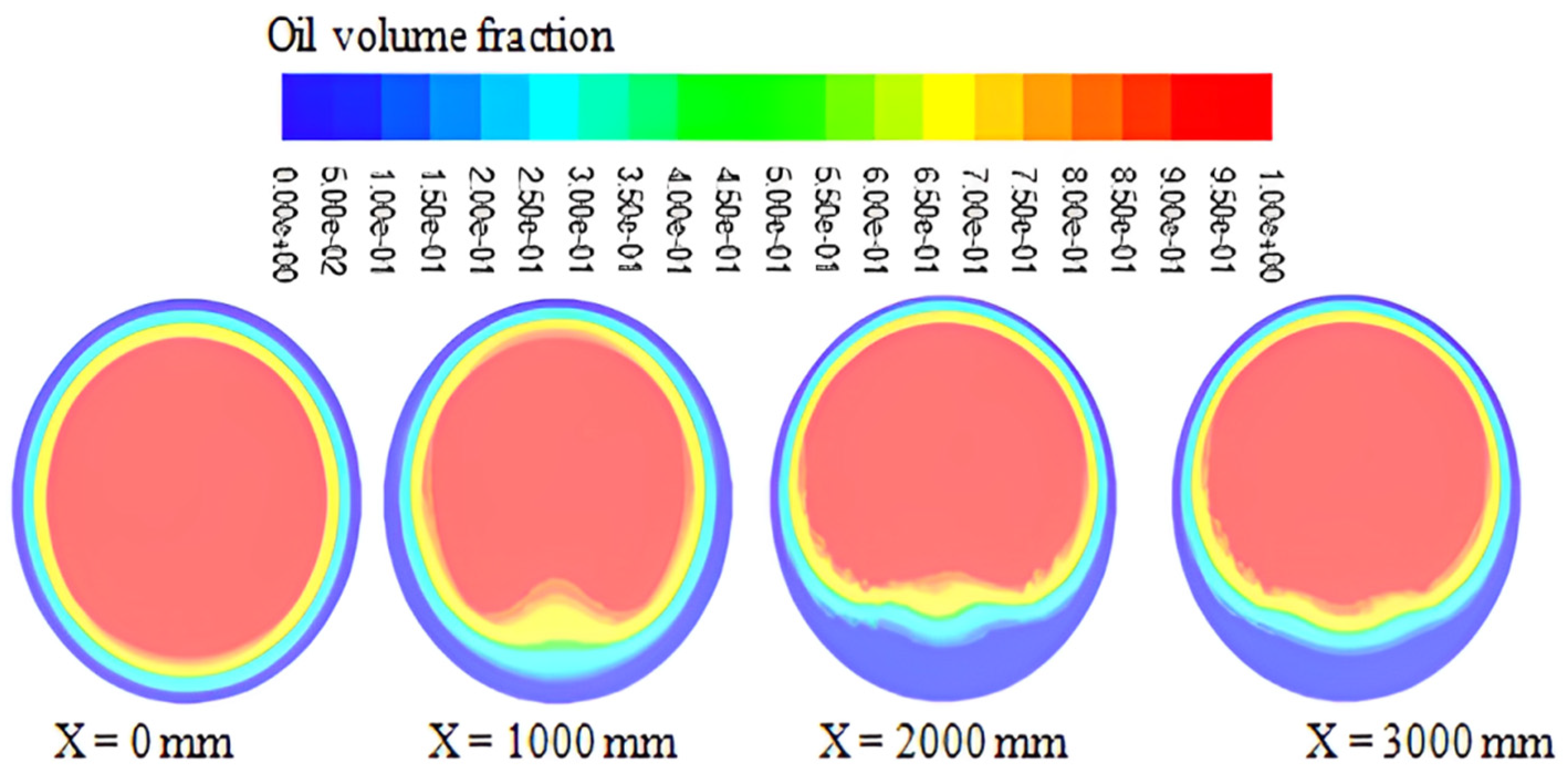
3.3. Effect of Temperature and the Presence of Air on Pressure Drop

For two-phase flow and heavy oil-water-air flow,

Table 7. Pressure drop at different temperatures.

Cases	To, Tw and Ta (K)	ΔP Pa/m
Two-phase	313.15 (To and Tw)	1191.15
Three-phase	288.15	1582.81
Three-phase	303.15	1469.338
Three-phase	313.15	1462.23
Three-phase	313.15	1434.72

provides values for the pressure drop as a function of temperature (288.15 K, 303.15 K, 313.15 K, and 323.15 K for T_o, T_w, and T_a) (313.15 K for T_w and T_o alone). In the temperature range between 288.15 K and 313.15 K, the pressure drop, P, for heavy oil-water-air appears to decrease as the temperature rises. As the temperature rises, the oil and water lose some of their viscosity, which lowers the pressure drop and minimizes flow resistance in the pipe. The viscosity of the air likewise increases with temperature, but at a lower volume fraction, therefore the effect is less significant than in the case of the heavy oil-water mixture. The presence of air increases the flow’s pressure drop when the heavy oil-water flow (313.15 K for T_w and T_o only) is contrasted with heavy oil-water-air (313.15 K for T_o, T_w, and T_a). The simultaneous flow of heavy oil, water, and gas is affected by a similar behavior, as illustrated and discussed by Bannwart et al. [1] and Trevisan [2]. These outcomes were attained, in a nutshell, because the fluid’s velocity is increased by the presence of air. Additionally, the velocity increase causes the friction factor to climb even more, which raises the pressure drop in the heavy oil-water flow.

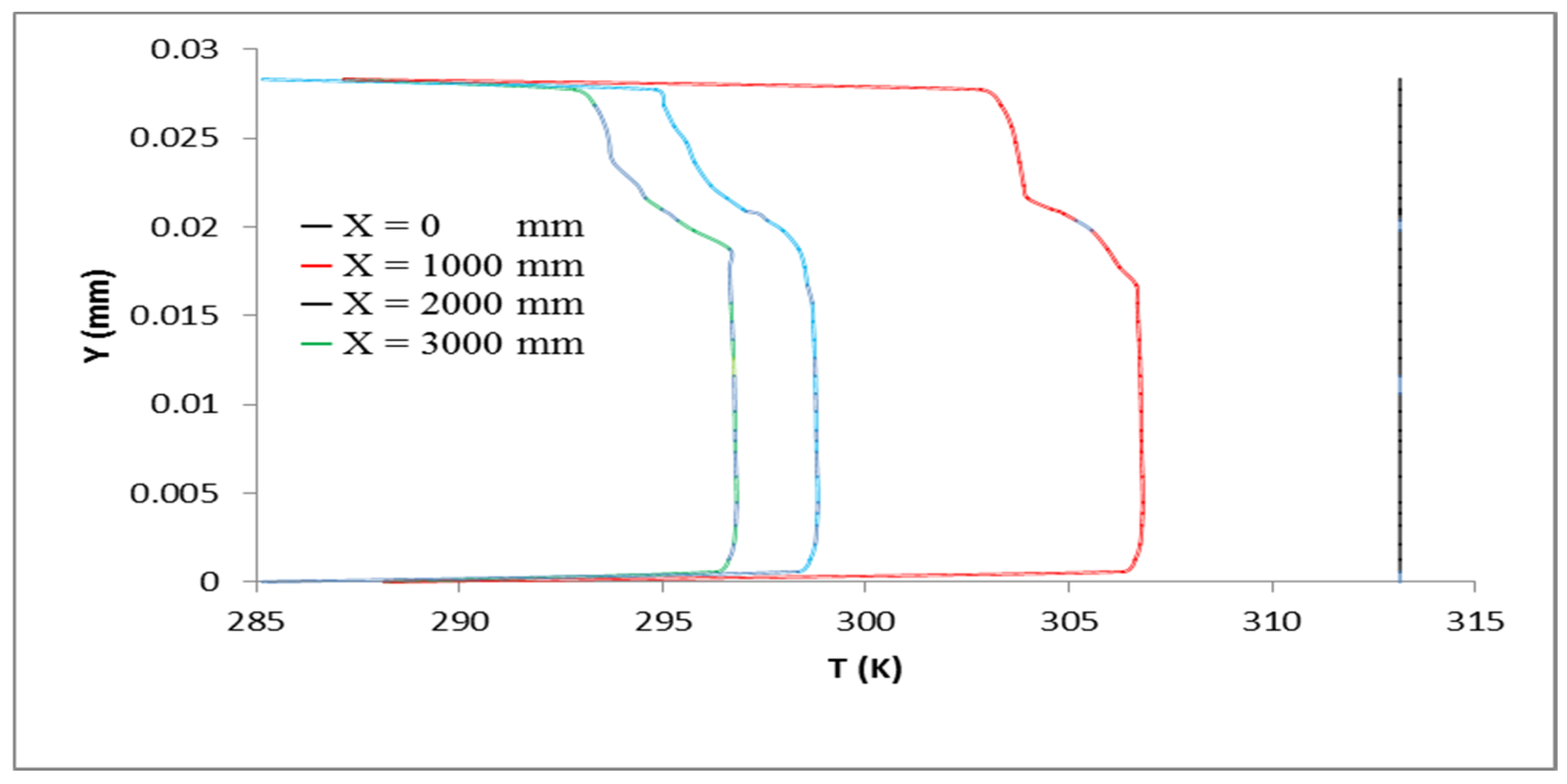
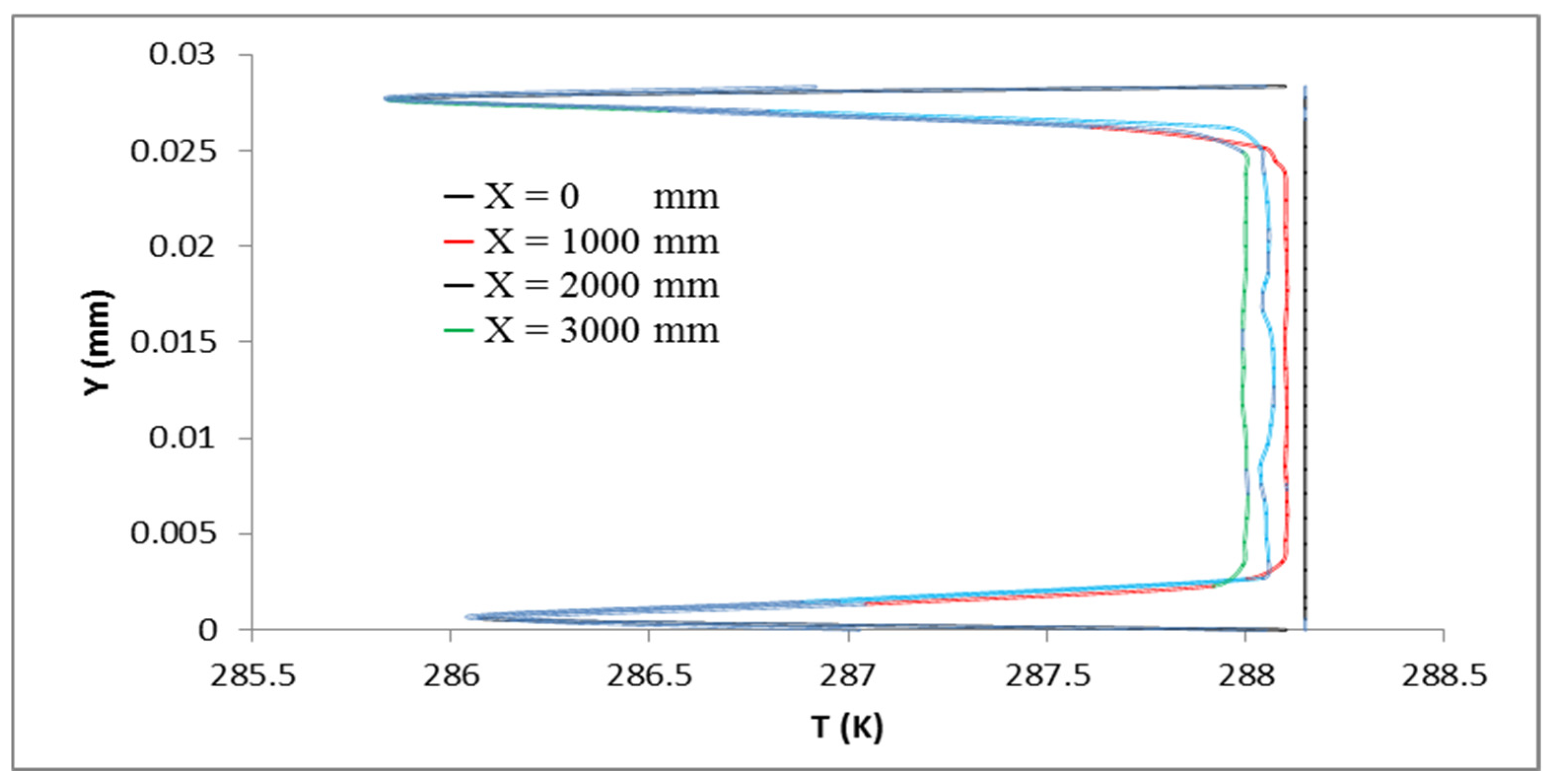
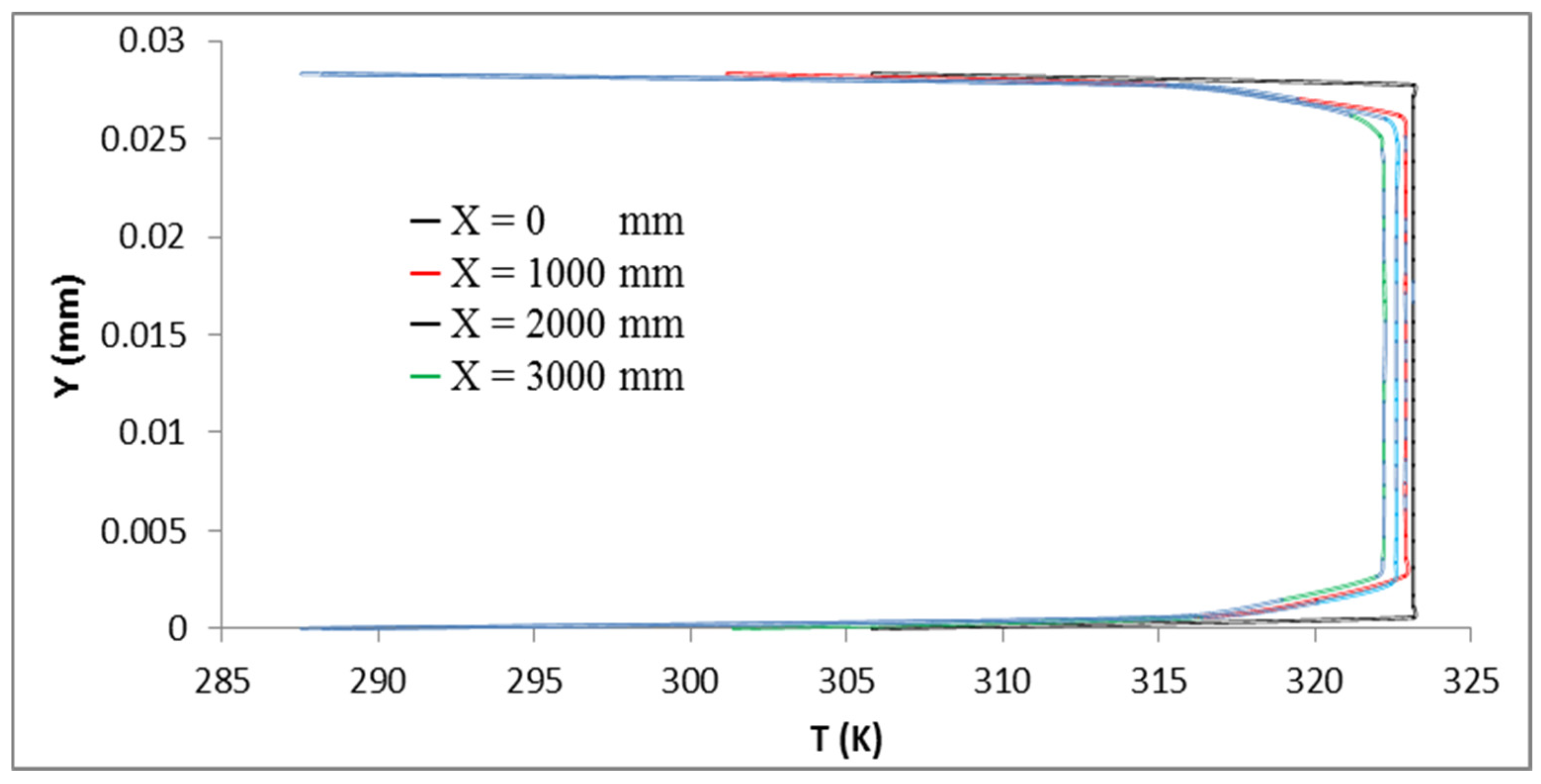
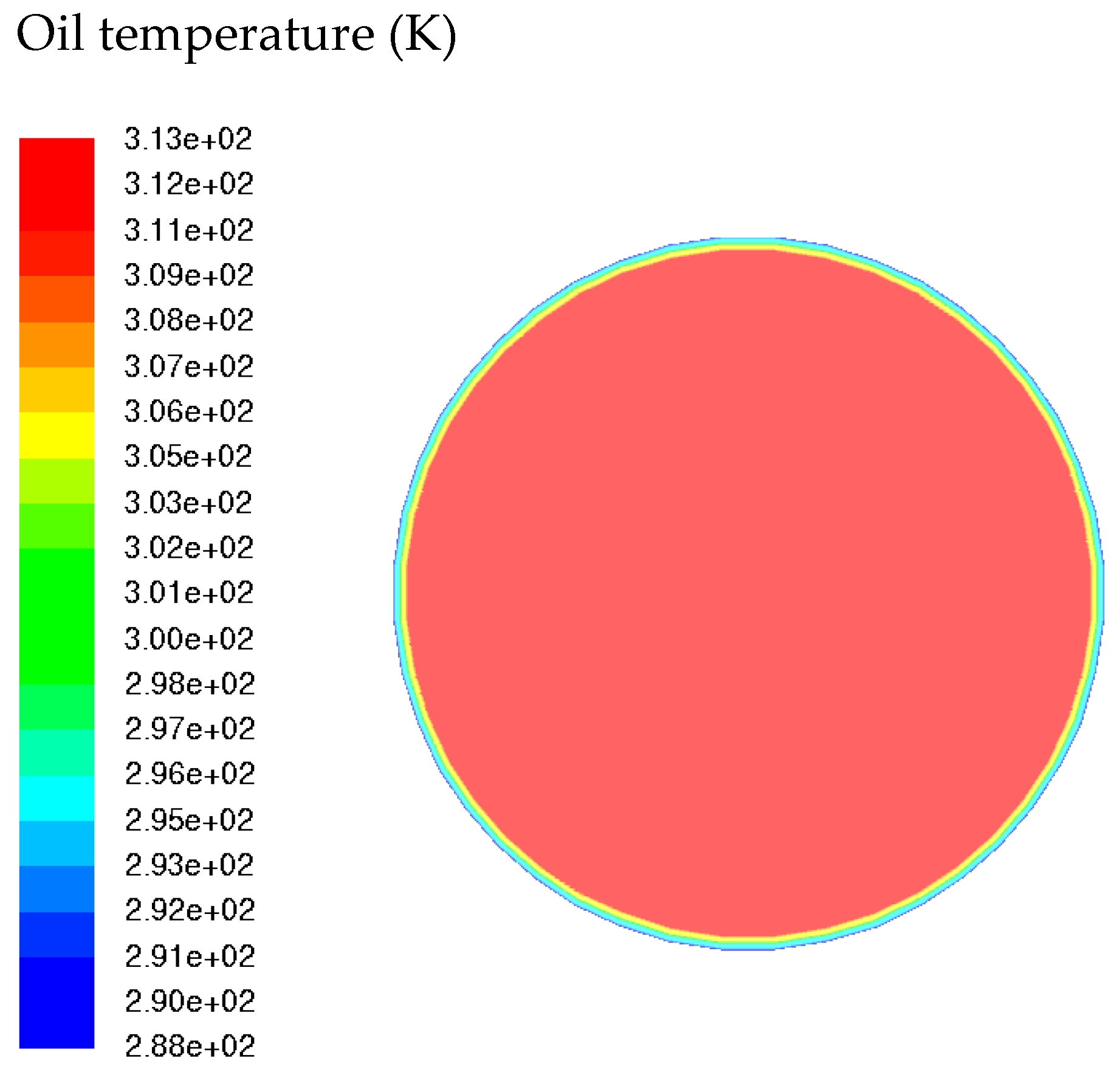
3.4. Temperature Profile Fields

Figure 12 and Figure 13 show the temperature profiles (313.15 K) for oil and water at axial points (0 mm, 1 mm, 2 mm, and 3 mm) along the pipe. The boundary conditions shown in the picture make it obvious that the water temperature at the pipe inlet (0 m) is generally uniform. The temperature begins to drop as fluids are moved out of the pipe input area. Due to the boundary circumstances, it is also possible to see an active, intense, and strong temperature gradient close to the pipe wall. Figure 12 explains the oil temperature profile along the pipe, which demonstrates uniform conduct in the pipe’s middle. However, a slight temperature drop can be seen when the oil begins to move farther from the pipe’s entry. The fact that the temperature of the pipe wall is lower than the temperature of the oil can be attributed to heat transfer. Figure 13 depicts the water temperature profile along the pipe and demonstrates that the upper part of the pipe is where the water encounters the biggest drop in temperature. This is due to the propensity of water to collect at the lower region, where the water film framed above the flow is slightly thinner. As a result, this film has a more noticeable effect at the low temperatures specified for the pipe wall. Figure 12 and Figure 13 can be compared, and it becomes clear that the oil is hotter than the water at the pipe’s exit. This is due to the proximity of the water to the pipe wall, which keeps the oil from coming into direct contact with the pipe wall. As a result, the water performs the role of a thermal insulator. The oil temperature profiles (288.15 K, 303.15 K, and 323.15 K) along the pipe are further clarified and explained in Figure 14, Figure 15 and Figure 16, demonstrating the presence of uniform conduits in the pipe’s center as well. However, a slight temperature drop can be seen when the oil begins to move farther from the pipe’s entry.

Figure 17 and Figure 18 provide a detailed illustration of the temperature fields for oil and water (313.15 K) along the pipe at X = 1000 mm. Figure 19, Figure 20 and Figure 21, on the other hand, show the oil temperature fields along the pipe at X = 1000 mm (323.15 K, 303.15 K, and 288.15 K, respectively). The section regions close to the pipe wall are where the majority of temperature variations take place. It is therefore likely that a thermal boundary layer has formed next to the pipe entrance as a result of the temperature difference between the pipe wall and the surrounding fluids. Figure 17 and Figure 18 support this conclusion by showing that the temperature distributions in the oil and water phases fluctuate along the pipe and that the water is susceptible to the largest variation and temperature drop. Regarding the temperature of the air phase, which is dispersed and abundant in the oil core, the profile of the air temperature is comparable to that of the heavy oil, showing a uniform position in the pipe’s center and focal point.

4. Summary

(1)

The developed numerical model predicts how a non-isothermal three-phase flow of water, oil, and air behaves in a straight pipe.

(2)

Despite temperature variations, the continuous aqueous film (CAF) is created and sustained. The unconventional core of the oil-air mixture tends towards stratification, avoiding the pipe wall and forming due to a fine water film.

(3)

This investigation demonstrated that the presence and proximity of air in a dense two-phase flow of water and oil significantly influence the distribution of oil inside the straight pipe and the velocity profiles of the phases. However, the CAF maintains its characteristic formation.

(4)

The viscosity of the water and oil decreases with increasing temperature during fluid flow through the pipe, resulting in a reduced pressure drop. Conversely, the presence of air causes an increase in pressure drop.

(5)

The profiles of the temperature of the water, heavy oil, and air phases alongside the pipe revealed an expected lesser temperature near the pipe surface, which lowers the temperature of the liquids by the time they depart the pipe. Due to its proximity to the pipe wall, annular water experiences this temperature drop more dramatically.

(6)

The research outcomes, backed by simulations and experimental evidence from existing literature, consistently show results that enhance our understanding of how well LES can model intricate flow dynamics like those studied in this investigation.

(7)

Comprehending the characteristics of heavy oil-water-air flows is essential for numerous industrial uses, including the transportation and processing of oil. Improved design and operational techniques for pipelines and processing facilities handling heavy oils under multi-phase flow circumstances may result from the study’s conclusions.

(8)

Overall, this work is novel because it uses an integrated approach to apply advanced numerical techniques, such as LES, to heavy oil, water, and air flows in a horizontal pipe. This approach advances both fundamental understanding and real-world applications in industrial contexts.