The Impact of Online Shopping on Retail Building Space and Energy Demand in the U.S.

Abstract

Online shopping is widely believed to reduce demand for retail stores and presumably decrease energy consumption in the retail sector, yet this relationship has not been studied empirically. We address this gap by first developing a regression model that empirically links historical retail building space needs to in-store shopping time. The historical online shopping time is taken from the 2003–2023 American Time Use Survey, which is then extrapolated to 2030 under two scenarios: a slower growth scenario based on 2003–2023 trends, and a faster growth scenario based on 2015–2023, reflecting a more recent acceleration of online shopping. Future energy use in retail buildings is estimated by combining predicted building space demand with extrapolated trends in energy intensity. Monte Carlo analysis is used to quantify uncertainty. Results show that by 2030, retail building energy demand will decline by 6–12% under the slower growth scenario and by 11–20% under the faster growth scenario, relative to 2018. These changes correspond to reductions in total U.S. commercial building energy demand of 0.7–1.3% and 1.3–2.2%, respectively. While potential increases in warehouse space, delivery services, and residential energy use are not analyzed here, the findings have significant implications regarding e-commerce for retail space and urban energy demand.

1. Introduction

Understanding and predicting energy demand is crucial for sustainable energy futures. Analysis of energy consumption patterns enable policymakers, researchers, and industries to better manage resource utilization, mitigate environmental impacts, and develop strategies for long-term sustainability. Energy demand patterns influence nearly every facet of modern economies, shaping infrastructure development, industrial productivity, household consumption, and environmental sustainability [1,2,3]. A robust understanding of these patterns facilitates identifying inefficiencies and reducing unnecessary consumption, which contributes to resource conservation and cost-effectiveness. Beyond these operational benefits, a deeper comprehension of energy demand dynamics is crucial for addressing the challenges posed by evolving societal behaviors and technological advancements.

Traditional energy demand models, which primarily focus on economic and technological determinants [4,5,6], often fail to capture the evolving complexities of modern consumption patterns, leading to gaps in policy design and implementation. For instance, understanding how digitalization, remote work, and e-commerce reshape energy use is essential for developing responsive and adaptive energy policies [7,8,9,10,11,12]. These behavioral shifts, driven by evolving consumer habits and technological advancements, can significantly alter energy consumption patterns [13,14]. For example, the COVID-19 pandemic accelerated the transition to e-commerce, leading to a marked increase in online shopping activities [13], and also drove widespread adoption of remote work, reduced commuting and driving. All of which have had profound implications for energy demand and consumption. Additionally, studies have examined factors driving consumer involvement in energy consumption and the effectiveness of behavioral interventions to reduce household energy demand [14,15]. Among these behavioral shifts, the growth of e-commerce stands out for its potential to reshape the retail sector by changing how much physical store space is needed. This in turn can have substantial implications for energy demand in retail buildings, which is a critical component of urban energy use.

Online shopping has grown rapidly in the 21st century [16]. The wide variety of options available online, including those not found locally, and the ease of price comparisons significantly enhance the shopping experience [17]. In addition, online shopping saves time by eliminating the need to walk around to search for products in physical stores, wait in checkout lines, and deal with crowds [18]. The implementation of easy-to-return and exchange policies further alleviate concerns about product satisfaction [19]. Online commerce is transforming the retail sector, e.g., e-commerce sales reached USD1.2 trillion, which accounts for 16% of total U.S. retail sales in 2024 [20]. The trend has shown a steady rise over the past two decades, with a Compound Annual Growth Rate (CAGR) of 11%. A survey conducted in the U.S. by [21] revealed that 43% of respondents searched for and purchased products solely online, 36% used a combination of in-store and online channels, and 21% searched for and purchased solely in physical stores. This data highlights the growing shift towards e-commerce and its increasing prominence in the retail landscape.

E-commerce has a complex relationship with energy demand, affecting vehicle use (personal and freight), building space and consumption (retail and warehouses), packaging, and internet energy use. Prior work has attempted to quantify these relationships. In personal transport, several studies have found that e-commerce can reduce the need for consumer travel to physical stores, potentially lowering energy use and carbon emissions [22,23,24]. For example, research on e-grocery and fast-moving consumer goods demonstrates that consolidated van deliveries can substantially decrease private vehicle trips and associated emissions [22,24]. However, other studies highlight that online shopping may not always substitute for store visits, as it can serve as an information channel, potentially increasing total store trips when consumers still desire in-person product inspection [25,26]. In terms of freight transport, the growth of home deliveries has shifted energy and emissions from consumers’ cars to commercial delivery vehicles [7,11,22,27]. Efficiently routed delivery can reduce last mile emissions compared to individual car trips to stores, but if deliveries are frequent, fragmented, or require express shipping, these gains may be diminished or reversed [22,24]. Additionally, the need for rapid fulfillment and narrow time windows, particularly in the grocery sector, can increase e-commerce last mile delivery mileage and emissions if not managed optimally [24]. The packaging sector has also seen an increase in material use with e-commerce, as goods shipped directly to consumers typically require more individualized and protective packaging compared to bulk shipments to stores [7,22,27,28,29]. Regarding warehouse operations, e-commerce often enables more centralized and automated warehousing, which can lower energy intensity per item compared to dispersed retail storage [22].

In this study, we focus on a poorly understood aspect of the relationship between e-commerce and energy use: The effect of online shopping on retail building space and energy consumption. In particular, we will connect consumer behavior, by which we mean time spent in retail stores and shopping online, with total retail space in the U.S. as well as energy consumption. The idea is that demand for retail versus online shopping tracks with the time that consumers spend in each type of shopping. The American Time Use Survey enables characterization of these times at the national level, and over time (2003–2023) [30]. The broader energy impacts across warehousing, logistics, packaging and IT infrastructure are acknowledged but not modeled here.

To justify the focus on retail building energy use, note that the sector accounts for a substantial share of commercial energy demand. Retail buildings accounted for 17% of on-site energy use in the U.S. commercial building sector as of 2018 [31]. Given this scale, even modest changes in retail space utilization can have notable effects on urban energy consumption. It is widely expected that online commerce should lead to reductions in brick-and-mortar stores. Early scenario work by [32] estimated that the rise of e-commerce could reduce total retail and wholesale trade activity by 25% based on assumptions, which, if realized, would translate to a 12.5% reduction in building use for these sectors. More recent studies imply that physical stores for clothing, electronics, food, drink, and cosmetics may decrease in the long run due to the substitution effect of e-shopping on shopping trips to physical stores [23]. The retail contraction is reflected in the closure of large department stores and mid-tier retailers, colorfully referred to as the “retail apocalypse” [33,34]. A study by [35] found that the convenience and accessibility of online shopping have led to a decline in foot traffic in traditional brick-and-mortar stores, prompting retailers to downsize or close physical locations. This trend is further corroborated by data indicating a reduction in retail space per capita in the U.S., declining from 56.5 square feet in 2009 to 54.3 square feet in 2023 [36,37]. Ref. [38] suggest a negative correlation between the growth of e-commerce and the commercial real estates market in China. However, their analysis did not quantify how online shopping affects the retail building sector.

Prior life cycle assessment studies are the only body of literature to quantify the connection between e-commerce and retail store energy consumption. In comparative analyses of the environmental impacts of online versus traditional shopping channels, these studies included retail store energy consumption as a component of the footprint of traditional shopping [7,24,39,40,41]. Such studies assumed a proportional relationship between retail building energy consumption and retail floor space or retail sales (i.e., energy/area or energy/USD), which is then multiplied by an assumed or literature-derived average retail space or retail sales per item (i.e., area/item or USD/item). This approach has two key limitations. First, there is no empirical evidence to confirm that the relationship between in-store shopping and retail footprint is proportional. Our study is the first to move beyond this untested assumption by directly measuring the relationship using observed empirical data. Second, prior studies using this assumption do not have a time dimension and thus do not address when, or by how much, retail space and energy use will decline in response to e-commerce growth. Our study addresses this limitation by explicitly incorporating time dynamics to estimate the magnitude and timing of building space and energy changes.

The analysis in this paper addresses the following research questions: First, what is the impact of online shopping on retail building space in the U.S. over the past two decades? Second, what is the expected future growth in e-commerce to 2030 and how will this affect retail building space? Third, how do changes in retail building space affect energy consumption? Specifically, we decompose the effect of e-commerce on energy as (1) its effects on retail space demand and (2) the concomitant effect on building energy use. Uncertainties in projected energy demand are estimated through Monte Carlo Analysis and scenario analysis.

Contributions of this paper include the following: This is the first empirical quantification of the link between shoppers’ use of retail stores (time use) and their physical extent (building space). Refs. [36,37] note a decline in retail space, and ref. [38] suggests that online shopping contributes to this decline, but the relationship has not been quantified. Also, this is the first empirical estimate of how e-commerce affects retail building energy use. Previous life cycle assessments [7,24,39,40,41] estimate reduced retail energy use by assuming a reduction proportional to e-commerce share of sales. In contrast, we build an empirical regression relationship. In addition, we clarify the expected time lags over which changes in consumer behavior (time spent online shopping) leads to changes retail building infrastructure, which has not been previously quantified.

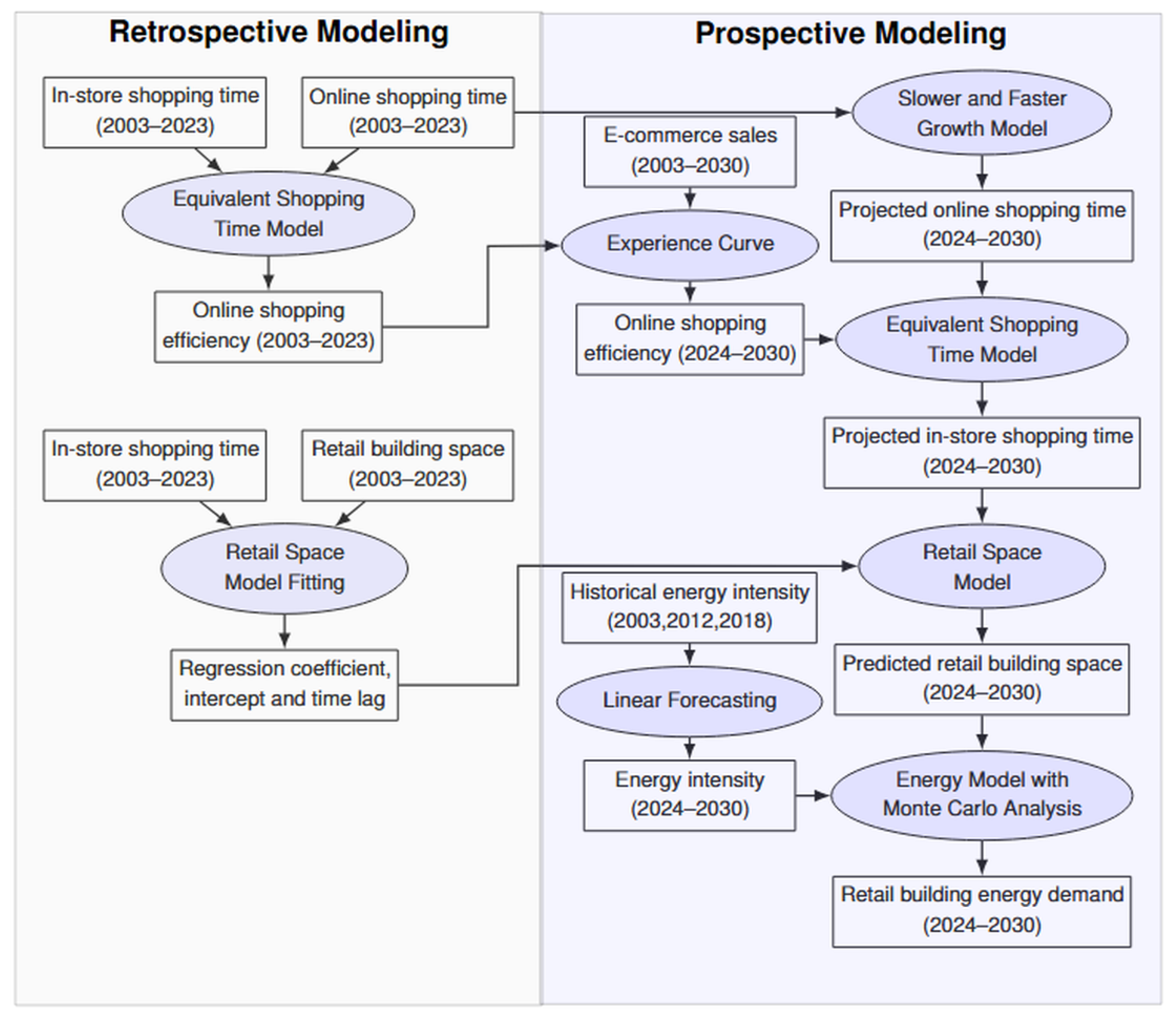
2. Methods

The goal of this work is to develop a model that predicts retail building space and energy demand as a function of online shopping time, and then develop scenarios for future online shopping time to predict space and energy use in retail building to 2030. The approach is summarized in Figure 1. The American Time Use Survey (ATUS) [30] is used to develop a time series of annual online and in-store shopping time by U.S. consumers from 2003–2023. The CoStar database [37] and Commercial Building Energy Consumption Survey (CBECS) [31] provide annual data on total retail space in the U.S. Following CBECS definitions, retail buildings are those used for the sale and display of goods, which includes grocery stores, food markets, convenience stores, retail stores, as well as enclosed and strip malls, but excludes warehouse and storage facilities. We use this historical data to develop an empirical regression model that predicts retail space from time spent in stores over the prior several years.

The next step is to connect online shopping time to in-store shopping time. This is achieved by observing that pre-e-commerce (1985–1998) total shopping time is roughly constant (12 h/month) [42,43], but more recently (2003–2023) declining with increasing use of e-commerce [30,42]. We then assume a constant time budget for “equivalent shopping time” [42], leading to an efficiency factor for e-commerce as it satisfies a given amount of shopping demand in less time than in-store shopping. Historical progress in the time efficiency of e-commerce can then be derived from data on in-store and online shopping time [42].

These models are calibrated with historical data and then used in prospective forecasting to 2030. The future online shopping time in the U.S. is forecast by extrapolating historical trends; these results are used in the above models to forecast in-store shopping time, and in turn, estimate future retail space. Extrapolation is complicated by an apparent discontinuity in historical trends in online shopping time, which increases from 2015 more rapidly compared to previous years. We handle this via scenario analysis, one extrapolating to 2030 from the 2003–2023 trend (slower growth scenario) and a second extrapolating from the 2015–2023 period (faster growth scenario). Lastly, we connect retail space to national energy use by extrapolating historical trends in energy consumed per area (energy intensity), which can be derived from data in the CBECS.

To assess uncertainty in these results, we conduct statistical analysis to develop distributions for input parameters, and perform Monte Carlo Analysis to find the distribution of final results, such as the predicted future retail energy demand. Each modeling step is described in more detail below.

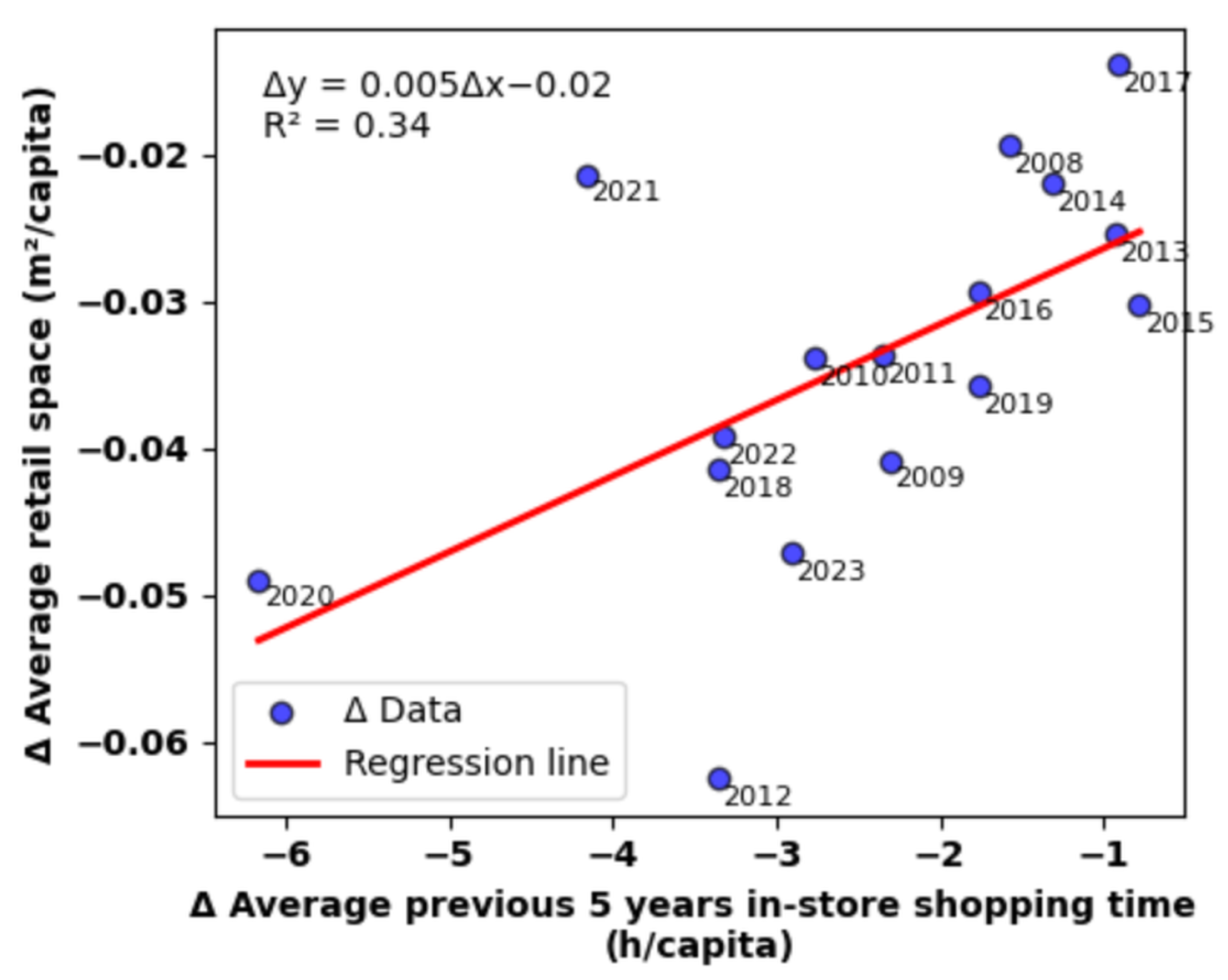
2.1. Retrospective Modeling: Regression Model of Retail Space and In-Store Shopping Time

In-store shopping time of consumers is treated as the driver for retail building space. There are other underlying drivers, such as population and economic growth, and we presume that these connect to in-store shopping time, which directly correlates with the need for physical retail infrastructure. A regression model is developed to quantify the relationship between in-store shopping time and the demand for retail space. This model links behavioral change, represented by time spent shopping in physical stores, to physical retail space demand, measured as retail floor space per capita. To remove long-term effects that arise from economic change and population growth, the model is specified in terms of year-to-year changes rather than absolute values.

The decision by business owners to open or close stores should depend on the state of sales in recent years and when the building lease renewal is coming up. To account for a combination of time lag and aggregation from these effects, we use the following metric to capture the “recent state of business” that drives retail space decisions: the average of the previous n years of in-store shopping time per capita. The selection of the lag variable (n) is performed empirically by searching for an average duration with the best fit. Thus, we model year-to-year changes in average retail floor area per capita as a linear function of year-to-year changes in the previous n-year moving average of in-store shopping time per capita at the national level.

The historical in-store shopping time in the U.S. is constructed using data from the ATUS. Conducted annually since 2003 by the U.S. Bureau of Labor Statistics, ATUS provides detailed records of participants’ daily activities, including their location and duration. For this study, we define “in-store shopping time” as time spent on “shopping activities” that occur in “grocery stores”, “other stores”, or “malls”, as defined in the ATUS survey. The only purchase categories available in ATUS for purchases are gasoline/groceries/other. Because there is no online purchasing of gasoline, online shopping would be limited to groceries versus other. Furthermore, ATUS does not query the type of product respondents research prior to purchase, meaning that certain shopping activities (researching, waiting, comparing) could not be disaggregated at all. Given these limitations in the source data, we aggregate all purchase-related activities into a single shopping activity in this paper.

The average in-store shopping time per capita is calculated by dividing the total in-store shopping time of all consumers by the total population in the U.S. for each calendar year from 2003 to 2023. The regression model is formulated as follows:

$$\begin{array}{cc}\hfill \mathrm{\Delta }\mathrm{Avg}.\mathrm{retail}{\mathrm{space}}_t\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right)& ={\beta }_1\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{h}}}\right)\mathrm{\Delta }\mathrm{Avg}.\text{in-store}\mathrm{shopping}{\mathrm{time}}_t^{\left(n\right)}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}}}\right)\hfill \\ \hfill & +{\beta }_0\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right),\hfill \end{array}$$

(1)

where

$$\begin{array}{c}\hfill \mathrm{\Delta }\mathrm{Avg}.\mathrm{retail}{\mathrm{space}}_t\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right)=\mathrm{Avg}.\mathrm{retail}{\mathrm{space}}_t\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right)-\mathrm{Avg}.\mathrm{retail}{\mathrm{space}}_{t-1}\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right),\end{array}$$

(2)

and

$$\begin{array}{c}\hfill \mathrm{\Delta }\mathrm{Avg}.\text{in-store}\mathrm{shopping}{\mathrm{time}}_t^{\left(n\right)}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}}}\right)=\mathrm{Avg}.\text{in-store}\mathrm{shopping}{\mathrm{time}}_t^{\left(n\right)}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}}}\right)\\ \hfill -\mathrm{Avg}.\text{in-store}\mathrm{shopping}{\mathrm{time}}_{t-1}^{\left(n\right)}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}}}\right),\end{array}$$

(3)

and

$$\begin{array}{c}\hfill \mathrm{Avg}.\text{in-store}\mathrm{shopping}{\mathrm{time}}_t^{\left(n\right)}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}}}\right)=\left({\displaystyle \frac{1}{n}}\right)\sum _{i=0}^{n-1}\mathrm{Avg}.\text{in-store}\mathrm{shopping}{\mathrm{time}}_{t-i}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}}}\right),\end{array}$$

(4)

and t refers to a year between 2003 and 2023, and n represents the number of years used in computing the moving average of average in-store shopping time. ${\beta }_1\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{h}}}\right)$ is the estimated coefficient that quantifies the sensitivity of changes in retail floor area to changes in in-store shopping time, while ${\beta }_0\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right)$ is the model intercept. $\mathrm{\Delta }\mathrm{Avg}.\mathrm{retail}{\mathrm{space}}_t\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right)$ is the year-to-year change in the average retail floor area per capita, and $\mathrm{\Delta }\mathrm{Avg}.\text{in-store}\mathrm{shopping}{\mathrm{time}}_t^{\left(n\right)}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}}}\right)$ represents the year-to-year change in the n-year moving average of in-store shopping time per capita. $\mathrm{Avg}.\text{in-store}\mathrm{shopping}{\mathrm{time}}_t^{\left(n\right)}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}}}\right)$ is defined as the arithmetic mean of average in-store shopping time per capita over the previous n years, which captures multi-year behavioral trends. $\mathrm{Avg}.\text{in-store}\mathrm{shopping}{\mathrm{time}}_t\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}}}\right)$ is the average in-store shopping time per capita in year t. This equation allows the regression to capture realistically include both short-term variations and delayed structural adjustments in retail building space in response to changes in consumer shopping behavior.

The typical retail lease duration is approximately 5.5 years [44]. We test different values of time lag from 1 to 10 years, respecting both the duration of retail leases and the idea that retail decisions likely depend on multi-year shopping trends. Within this range, we choose a preferred time lag by identifying the model that yields the lowest p-value of regression coefficient and highest $R^2$. Because a lag of up to 10 years is tested, the earliest in-store shopping data (2003) can only be used to predict retail space in 2013. As a result, retail building space data prior to 2013 cannot be consistently paired with lagged predictors across all time lags. To ensure that model comparisons are not influenced by differences in sample size, the analysis is therefore restricted to the period 2013–2023 of retail space. This alignment allows each lag structure to be evaluated on an equivalent dataset, ensuring that observed differences in performance reflect the effect of the lag rather than variations in the number of data points.

The historical retail space data is derived by integrating information from the CoStar database and the CBECS. One of the primary challenges in this process is the absence of annual retail building space data. The CoStar database provides annual statistics on commercial building space, which aggregates retail spaces alongside other commercial categories, such as restaurants and bank branches. Similarly, while CBECS offers detailed data on the U.S. commercial building space area, it is conducted only periodically (in 2003, 2012, and 2018) and does not provide annual data on retail space. As a result, neither CoStar nor CBECS alone can fully address the need for annual retail space data. CBECS does, however, include floor space information categorized by principal building activities, such as grocery stores/food markets, enclosed malls, restaurants, banks/financial institutions, and other uses. This detailed categorization enables the identification of retail-specific spaces within the broader classifications provided by the CoStar database. By integrating these datasets, annual retail space use is estimated. A retail index is developed using CBECS data to estimate the proportion of commercial floor space that is dedicated to retail activities. The retail index is defined as

$$\mathrm{Retail}{\mathrm{index}}_t={\displaystyle \frac{\mathrm{Retail}{\mathrm{space}}_t\left({\mathrm{m}}^2\right)}{\mathrm{Retail}{\mathrm{space}}_t\left({\mathrm{m}}^2\right)+\mathrm{Other}\mathrm{commercial}\mathrm{building}{\mathrm{space}}_t\left({\mathrm{m}}^2\right)}},$$

(5)

where t refers to the years in which CBECS surveys were conducted (2003, 2012, and 2018). The retail space encompasses stores, malls, and other retail-specific establishments. The other commercial building space, as aggregated in the CoStar commercial building data, includes categories such as restaurants and bank branches. The retail index for intermediate years is calculated using linear interpolation, enabling a continuous estimation of the proportion of retail space within the total commercial floor space.

Once the retail index is established, it is applied to the commercial building space data provided by the CoStar database to estimate annual retail space. The estimation is calculated using the following equation:

$$\mathrm{Retail}{\mathrm{space}}_t\left({\mathrm{m}}^2\right)=\mathrm{Retail}{\mathrm{index}}_t\times \mathrm{Commercial}\mathrm{building}{\mathrm{space}}_t\left({\mathrm{m}}^2\right),$$

(6)

In this equation, t represents the year. The retail index is derived from CBECS database, and commercial building space is from CoStar.

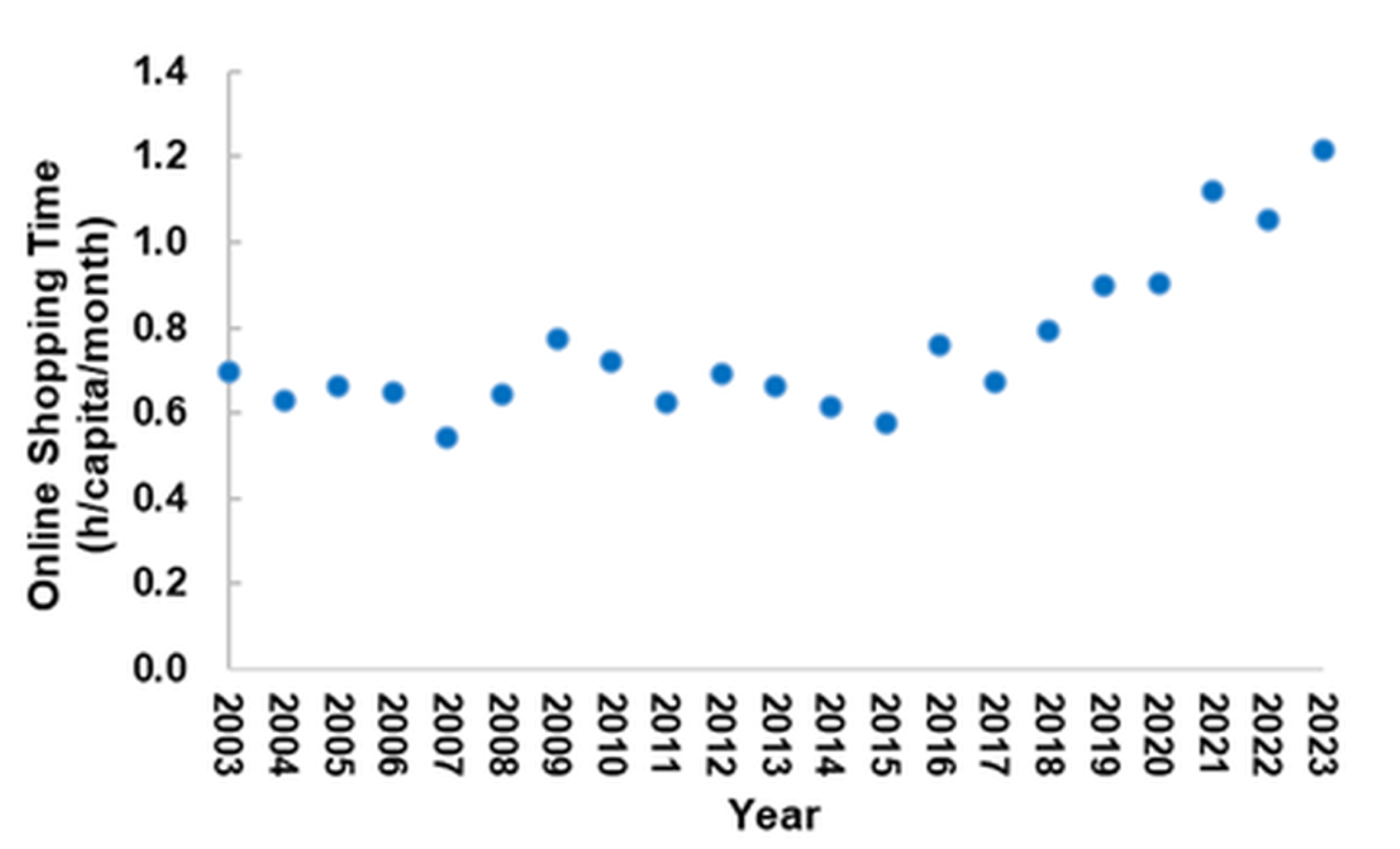
2.2. Retrospective Modeling: Model Connecting Online and In-Store Shopping Times

Online and in-store shopping times are presumably connected, i.e., if a consumer purchases a good online that they would have otherwise purchase in-store, online shopping time increases and in-store shopping time decreases. However, the magnitude of this relationship is not a priori obvious, e.g., if a consumer spends 5 min buying a desired good online, the reduction in in-store time is unknown and potentially larger than the 5 min increase in online shopping time. The first step in developing a relationship between in-store and online shopping time is to develop a time series dataset for both. We use the term “shopping time” throughout this article to refer to average per capita time spent shopping. In-store shopping time is directly available from ATUS by aggregating times spent shopping in store locations. ATUS does not specifically track online shopping time, but one can infer it by examining time spent shopping in non-store locations, e.g., home. This does not perfectly match online shopping because it includes “other” shopping types such as shopping at garage sales or purchasing from printed catalogs, which are neither online nor in-store shopping. From the American Heritage Time Use Study [43], one can see that pre-e-commerce, “other” shopping times were small compared to in-store shopping time, e.g., 0.23 h/capita/month vs. 12 h/capita/month in-store. To construct online shopping, we thus assume a constant at 0.23 h/capita/month of “other shopping”, thus defining online shopping time as total non-store shopping minus “other” shopping, see [42] for details.

An online shopping experience is not necessarily entirely online. A customer might order online, but they may pick their order up or make a post-purchase return by bringing the product to a store. ATUS classifies picking up or returning an order as an in-store activity. This portion of an online purchases, when they occur, are thus counted as in-store. This suits the models constructed, as picking up or returning an order call for retail space, which is driven by in-store shopping time.

To quantify how the growth of online shopping influences total shopping time, we introduced the concept of “online shopping time efficiency”, which quantifies the effect whereby buying goods online typically requires less consumer time compared to purchasing the same items in stores. Over the past two decades, improvements in technology, logistics, and user interface design have made online shopping increasingly efficient, reducing the amount of time consumers need to spend on purchases. This efficiency was further conceptualized through “equivalent shopping time,” defined as the total amount of time consumers historically allocate to all shopping activities. Before the dawn of e-commerce, time use data from the American Heritage Time Use Study [43] indicate a nearly constant shopping time of 12 h/capita/month from 1985–1998. As online shopping has become more prevalent and more efficient, the share of time spent in stores declines, but the total shopping itself—in terms of goods acquired and services consumed—remains comparable. This concept is expressed mathematically as follows:

$$\begin{array}{cc}\hfill \mathrm{Equivalent}\mathrm{shopping}\mathrm{time}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}·\mathrm{month}}}\right)& =\text{In-store}\mathrm{shopping}\mathrm{time}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}·\mathrm{month}}}\right)\hfill \\ \hfill & +K\times \mathrm{Online}\mathrm{shopping}\mathrm{time}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}·\mathrm{month}}}\right)\hfill \\ \hfill & +\mathrm{Other}\mathrm{shopping}\mathrm{time}\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}·\mathrm{month}}}\right),\hfill \end{array}$$

(7)

where K is the efficiency of online shopping (greater than 1). As online shopping becomes more efficient compared to traditional in-store shopping, the value of K increases. Data show a decrease in total shopping times from 2003 to 2023, defined as the summation of per capita monthly in-store, online shopping, and other shopping times. We assume the equivalent shopping time remains constant from 2003 to 2023, which necessarily means that e-commerce enables the same utility (12 h of equivalent shopping time) despite decreases in actual total shopping time. In short, e-commerce allows consumers to do the same amount of shopping in less total time.

The historical online shopping efficiency (from 2003 to 2023) can be computed using Equation (7). The future online shopping time efficiency, K, was projected using an experience curve model that relates historical efficiency to annual e-commerce sales [42], as detailed in Appendix A. The result is a base case learning rate of 15%, with a range of 12–19% based on uncertainties. Using uncertainties associated with learning rate and the growth trend of the e-commerce sector, a range of K values is predicted for the period from 2024 to 2030, which range from 4.9 to 6.6. This range provides insights into the evolution of online shopping efficiency under varying market conditions [42].

2.3. Prospective Modeling: Forecast Online and In-Store Shopping Times

The future in-store shopping time is predicted based on the historical online shopping time and the interactive relationship between in-store and online shopping times illustrated in Equation (7). Figure 2 illustrates the historical monthly online shopping time from 2003 to 2023. The data reveals two distinct phases. From 2003 to 2014, online shopping time exhibited relatively modest annual growth (average +0.022 h/capita/month), with minor fluctuations. However, starting in 2015, there was a rapid annual increase in online shopping time (average +0.074 h/capita/month). This shift reflects some combinations of advancements in e-commerce platforms, improved logistics systems, and growing consumer preferences for online shopping.

To account for these distinct phases of online shopping time, two scenarios are proposed. The first scenario forecasts future online shopping time based on the entire dataset spanning 2003 to 2023, assuming a consistent growth trend throughout the period, and we refer to it as the slower e-commerce growth scenario. However, as evident from the data (Figure 2), online shopping time experienced a marked acceleration starting around 2015. To better capture this rapid growth phase, the second scenario, the faster e-commerce growth scenario, focuses on predicting future online shopping time using a subset of the data from 2015 to 2023, which allows for a better representation of recent behavioral shifts in online shopping trends.

The choice between slower and faster growth scenarios remains uncertain due to the inherent complexities of consumer shopping behavior and the multitude of influencing factors. The rapid growth of online shopping since 2015 introduces complexities in forecasting, as it remains unclear whether this growth will plateau, accelerate further, or stabilize at a new baseline. If a more conservative outlook is adopted—anticipating that online shopping will continue to grow gradually— the slower e-commerce growth scenario provides a more appropriate forecast by reflecting the long-term trend. However, this model may underrepresent the recent rapid acceleration in online shopping observed in the last decade. Conversely, if one assumes that the rapid growth observed from 2015 to 2023 will persist, then the faster e-commerce growth scenario offers a more suitable projection, but risks overlooking the influence of long-term historical patterns that could impact future trends. By constructing separate scenarios, we capture uncertainty in future online shopping trends.

Once the future online shopping time is predicted in both scenarios, the corresponding in-store shopping time is derived from Equation (7), where in-store shopping time is treated as the only unknown variable, since equivalent shopping time and other shopping time are both assumed to be constant and K is predicted based on previous research [42].

When the in-store shopping time is predicted, the average in-store shopping time per capita within a calendar year can be calculated using the following equation:

$$\begin{array}{c}\hfill \mathrm{Avg}.\text{in-store}\mathrm{shopping}{\mathrm{time}}_t\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}}}\right)=\text{In-store}\mathrm{shopping}{\mathrm{time}}_t\left({\displaystyle \frac{\mathrm{h}}{\mathrm{capita}·\mathrm{month}}}\right)\\ \hfill \times 12\mathrm{months},\end{array}$$

(8)

where t refers to a year, and the left hand side of this equation coresponds to the right hand side of Equation (4). This equation accounts for the monthly in-store shopping time per capita, scales it to an annual basis by multiplying by 12 months. The resulting annual average in-store shopping time serves as the input variable for Equation (4) to predict future retail space demand.

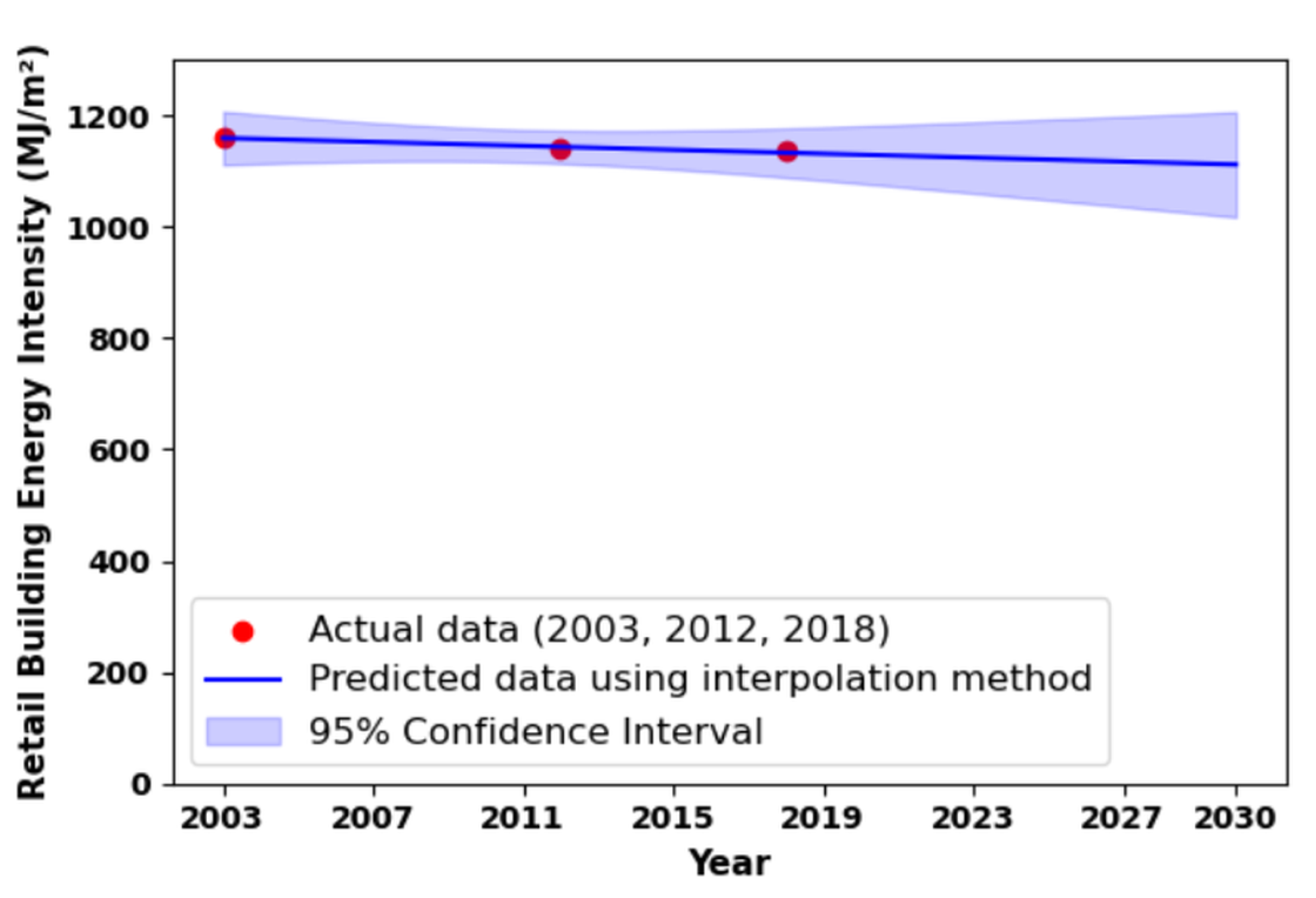
2.4. Prospective Modeling: Forecast Retail Space and Retail Building Energy Demand

Using coefficient ${\beta }_1$, intercept ${\beta }_0$, and time lag n from the regression model (Equation (1)), the future retail space can be predicted given a forecast of in-store shopping time. Our prediction of future in-store shopping time integrates consumer behavior (refers specifically to measurable shopping patterns, which is shopping time in retail stores and online) and accounts for the impact of online shopping on in-store shopping time.

Next, the future retail building energy demand can be predicted by multiplying the predicted retail building space by building energy intensity. Energy intensity, defined as energy consumption per unit of floor space, is a key metric for estimating retail building energy demand based on space [45]. The CBECS database provides energy-related building characteristics and energy consumption data, including retail building floor space and corresponding major fuel consumption, including site electricity, natural gas, and fuel oil, for a given calendar year. Using this data, retail energy intensity can be calculated with the following equation:

$$\mathrm{Retail}\mathrm{energy}{\mathrm{intensity}}_t\left({\displaystyle \frac{\mathrm{MJ}}{{\mathrm{m}}^2}}\right)={\displaystyle \frac{\mathrm{Retail}\mathrm{building}\mathrm{energy}{\mathrm{consumption}}_t\left(\mathrm{MJ}\right)}{\mathrm{Retail}{\mathrm{space}}_t\left({\mathrm{m}}^2\right)}},$$

(9)

where t refers to the years in which CBECS surveys were conducted (2003, 2012, and 2018).

To estimate annual retail energy intensity for intermediate years, a linear regression model is applied, assuming that energy intensity changes gradually over time. This approach leverages the available CBECS data to provide a continuous estimate of retail energy intensity, facilitating predictions of retail building energy consumption across years where direct survey data is unavailable. To account for model uncertainty, a 95% confidence interval (CI) is incorporated, providing a statistical range within which the true energy intensity is likely to fall.

The future retail building energy demand can be derived as follows:

$$\begin{array}{cc}\hfill \mathrm{Retail}\mathrm{building}\mathrm{energy}{\mathrm{demand}}_t\left(\mathrm{MJ}\right)& =\hfill \\ \hfill \left(\mathrm{Avg}.\mathrm{retail}{\mathrm{space}}_{t-1}\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right)+\mathrm{\Delta }\mathrm{Avg}.\mathrm{retail}{\mathrm{space}}_t\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right)\right)\\ \hfill \times {\mathrm{Population}}_t\times \mathrm{Retail}\mathrm{energy}{\mathrm{intensity}}_t\left({\displaystyle \frac{\mathrm{MJ}}{{\mathrm{m}}^2}}\right),\end{array}$$

(10)

where t refers to the target year for prediction (2024–2030), and Retail building energy demand_t (MJ) represents the total national energy demand from retail buildings in year t. $\mathrm{Avg}.\mathrm{retail}{\mathrm{space}}_{t-1}\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right)$ denotes the average retail floor area per capita in the previous year, and $\mathrm{\Delta }\mathrm{Avg}.\mathrm{retail}{\mathrm{space}}_t\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right)$ is the predicted year-to-year change in average retail space obtained from the regression model defined in Equation (1). The term $\left(\mathrm{Avg}.\mathrm{retail}{\mathrm{space}}_{t-1}\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right)+\mathrm{\Delta }\mathrm{Avg}.\mathrm{retail}{\mathrm{space}}_t\left({\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{capita}}}\right)\right)$ therefore represents the estimated average retail floor area per capita in year t. This value is multiplied by the total population in year t (${\mathrm{Population}}_t$) to obtain the total national retail floor area. Finally, the total floor area is multiplied by the corresponding $\mathrm{Retail}\mathrm{energy}{\mathrm{intensity}}_t\left({\displaystyle \frac{\mathrm{MJ}}{{\mathrm{m}}^2}}\right)$ to estimate total retail building energy demand. The ATUS provides historical annual population data from 2003 to 2023. Additionally, projections from the U.S. Census Bureau indicate that the U.S. population is expected to grow by approximately 2.3 million people annually by 2030 [46]. Using this projected growth rate, we estimated the future population of the U.S. through 2030. This formulation integrates shopping behavior, retail space demand, and energy efficiency to estimate future retail building energy demand.

2.5. Monte Carlo Analysis for Retail Building Energy Demand

Estimating retail energy demand involves multiple sources of uncertainty, both in historical estimations (2003–2023) and in future projections (2024–2030). These uncertainties stem from variability in key input parameters, making it essential to adopt a robust analytical approach capable of quantifying and managing these uncertainties. Monte Carlo analysis is particularly well-suited for this purpose, as it allows for the probabilistic simulation of energy demand by accounting for variations in input variables.

The use of Monte Carlo analysis is crucial for enhancing the reliability of energy demand predictions. Traditional point estimates may fail to capture the full range of possible outcomes, leading to overconfidence in a single prediction. Instead, Monte Carlo simulations provide a probabilistic framework that not only quantifies uncertainty but also helps decision-makers assess risk more effectively [47]. By incorporating uncertainty into the modeling process, this method enhances the robustness of the implications for policy planning, infrastructure investment, and energy management strategies in the retail sector.

For historical estimation, the energy demand is computed by multiplying retail space by retail energy intensity, where the retail space is derived by multiplying commercial building space by retail index. The formula is

$$\begin{array}{cc}\hfill \mathrm{Historical}\mathrm{retail}\mathrm{building}\mathrm{energy}{\mathrm{consumption}}_t\left(\mathrm{MJ}\right)=\mathrm{Commercial}\mathrm{building}{\mathrm{space}}_t\left({\mathrm{m}}^2\right)& \\ \hfill \times \mathrm{Retail}{\mathrm{index}}_t\times \mathrm{Retail}\mathrm{energy}{\mathrm{intensity}}_t\left({\displaystyle \frac{\mathrm{MJ}}{{\mathrm{m}}^2}}\right),\end{array}$$

(11)

where t refers to a year from 2003 to 2023, $\mathrm{Commercial}\mathrm{building}{\mathrm{space}}_t\left({\mathrm{m}}^2\right)$ is the commercial building space in year t which is directly obtained from the CoStar database [37]. $\mathrm{Retail}{\mathrm{index}}_t$ and $\mathrm{Retail}\mathrm{energy}{\mathrm{intensity}}_t\left({\displaystyle \frac{\mathrm{MJ}}{{\mathrm{m}}^2}}\right)$ are computed based on Equations (5) and (9), which introduce uncertainty into the model, as they are derived from linear regression interpolation based three years data from CBECS and inherently follow a normal distribution. The mean and standard deviation of these parameters can be estimated from the regression models, enabling the application of Monte Carlo simulations to generate a probabilistic distribution of historical energy demand. By simulating 10,000 iterations, this approach provides a more comprehensive understanding of how variations in model inputs influence overall energy consumption estimates. A total of 100,000 iterations were also implemented for a sample case, which changed the result for energy demand in 2030 by less than 0.1%. Thus, the analysis converges by 10,000 iterations, which is used for computational efficiency. The resulting distribution allows for the construction of a 95% confidence, offering a statistically sound representation of uncertainty in historical retail building energy demand.

For future projections, online shopping time is first predicted using a linear regression model based on historical online shopping trends. This predicted value, which follows a normal distribution, is then used as an input into Equation (7) to estimate in-store shopping time, which is subsequently used in Equation (8) to determine average in-store shopping time. Finally, the average in-store shopping time is applied in Equation (10) to compute future retail building energy demand. While equivalent shopping time and other shopping time are treated as constants and U.S. population growth is modeled as a fixed annual increase of approximately 2.3 million people until 2030, other variables introduce uncertainty. Specifically, online shopping efficiency K is characterized by a defined range and a preferred (most likely) value, as shown in

Table 1. Online shopping efficiency K for Monte Carlo analysis based on the research of [42]. K is defined in Equation (7), where it refers to the number of minutes a consumer would spend on equivalent in-store shopping for every 1 min of online shopping. K increases gradually over time as a result of improvements of online shopping platforms, indicating increased time gains when using e-commerce. The lower and upper bounds of K are the range derived from the uncertainties in both the learning rate of time-efficiency improvement and the projected growth of the e-commerce sales. These three points (lower, preferred, and upper) are used to create the triangular distributions used in the Monte Carlo analysis.

Year	Lower	Preferred	Upper
2024	4.9	4.9	5.4
2025	5.0	5.0	5.6
2026	5.0	5.1	5.8
2027	5.1	5.2	6.0
2028	5.2	5.4	6.1
2029	5.3	5.5	6.3
2030	5.4	5.6	6.6

. For instance, in 2030, K ranges from 5.4 to 6.6, with a preferred value of 5.6, resulting in an asymmetric distribution. Given this asymmetry, a triangular distribution is used to model K, as it effectively captures both the uncertainty and the skewed nature of the distribution. Additionally, the retail energy intensity, regression coefficient ${\beta }_1$, and intercept ${\beta }_0$ follow normal distributions. The inputs and corresponding parameters for historical and future Monte Carlo analysis are shown in

Table 2. Inputs for Monte Carlo analysis of historical and future retail building energy demand. (ATUS = American Time Use Survey [30]).

	Equation	Inputs	Distribution	Parameters and Corresponding Source
Historical Estimation	(11)	Commercial building space	None	Directly obtained from CoStar Database [37].
		Retail index	Normal	Mean and standard deviation from linear interpolation model for annual retail index.
		Retail energy intensity	Normal	Mean and standard deviation from regression model for energy intensity.
Future Prediction	(7)	Online shopping time	Normal	Mean and standard deviation from regression model to predict future online shopping time.
		Equivalent shopping time	None	Assumed to be 12 h/capita/month; see details in Section 2.2.
		Other shopping time	None	Assumed to be 0.23 h/capita/month; see details in Section 2.2.
		Online shopping efficiency K	Triangular	(lower, peak, upper) from [42].
	(10)	Population in the U.S.	None	ATUS provides population data for 2003–2023, then increases by 2.3 million annually until 2030 [46].
		Retail energy intensity	Normal	Mean and standard deviation from regression model for energy intensity.
		Coefficient ${\beta }_1$	Normal	Mean and standard deviation of coefficient from regression model defined in Equation (1).
		Coefficient ${\beta }_0$	Normal	Mean and standard deviation of intercept from regression model defined in Equation (1).

. The Monte Carlo simulations incorporating these uncertainties with 10,000 iterations allow for the derivation of a 95% CI, indicating an uncertainty range in possible future energy demand outcomes.

3. Results

3.1. Year-to-Year Change Retail Space Regression Model

As described in Section 2.1, we use U.S. national data from 2003 to 2023 on retail space to develop the regression model in Equation (1) for predicting year-to-year change in average retail space based on year-to-year change of previous n years of in-store shopping time. To determine the most appropriate time lag, we search for the value of n ranging from 1 to 10 years with lowest p-value and highest $R^2$. This occurs for a time lag of 5 years, for which the coefficient ${\beta }_1$ is 0.005 m²/h (standard deviation is 0.002 m²/h), intercept ${\beta }_0$ is −0.02 m²/capita (standard deviation is 0.006 m²/capita), with lowest p-value of 0.02 and highest $R^2$ of 0.34 among all the time lag windows. While this value of $R^2$ indicates limitations of time use as a predictor of retail space, uncertainty is accounted for by including confidence intervals for regression coefficients in the Monte Carlo simulation. The actual dataset for regression model and the regression line is shown in Figure 3. Each blue point represents year-to-year change data in one observation year, and the red line indicates the fitted regression line based on the best-fit model with a 5-year averaging window (n = 5). This result suggests that changes in consumer shopping behavior, as reflected in reduced in-store shopping time, translate into measurable adjustments in retail building space with an average delay of approximately 5 years. The model indicates that every hour reduction in previous 5 years of average in-store shopping time per capita is associated with a decrease of 0.005 m² in average retail floor area per capita in a calendar year.

3.2. Future In-Store Shopping Time Prediction

Table 3. Projected mean and 95% confidence interval (CI) values of online and in-store shopping time (h/capita/month) from 2024 to 2030. The slower e-commerce growth scenario extrapolates future online shopping time based on long-term trends (2003–2023), while the faster e-commerce growth scenario relies on more recent patterns (2015–2023). Both models project a continued increase in online shopping time and a corresponding decline in in-store shopping time. However, faster e-commerce growth indicates a sharper reduction in in-store shopping, suggesting that the recent acceleration in online shopping activity may further accelerate the transition away from traditional retail shopping.

Year	Online Shopping Time				In-Store Shopping Time
	(h/capita/month)				(h/capita/month)
	Slower E-Commerce Growth Scenario		Faster E-Commerce Growth Scenario		Slower E-Commerce Growth Scenario		Faster E-Commerce Growth Scenario
	Mean	95% CI	Mean	95% CI	Mean	95% CI	Mean	95% CI
2024	1.0	0.9∼1.1	1.3	1.2∼1.3	7.0	6.4∼7.6	5.7	5.1∼6.2
2025	1.0	0.9∼1.1	1.3	1.2∼1.4	6.7	6.0∼7.4	5.1	4.4∼5.7
2026	1.0	0.9∼1.2	1.4	1.3∼1.5	6.5	5.7∼7.2	4.6	3.7∼5.3
2027	1.1	0.9∼1.2	1.5	1.3∼1.6	6.2	5.4∼7.0	3.8	3.0∼4.9
2028	1.1	0.9∼1.2	1.5	1.4∼1.7	6.0	5.1∼6.9	3.4	2.5∼4.3
2029	1.1	1.0∼1.3	1.6	1.5∼1.8	5.7	4.7∼6.6	2.7	1.5∼3.8
2030	1.1	1.0∼1.3	1.7	1.5∼1.9	5.4	4.2∼6.5	2.0	0.6∼3.3

presents the mean and 95% confidence interval (CI) results of Monte Carlo simulations for forecasting future in-store shopping time based on two modeling scenarios. The slower e-commerce growth scenario reflects a conservative trajectory of online shopping growth, extrapolated from historical trends spanning 2003 to 2023, while the faster e-commerce growth scenario captures a more accelerated growth pattern observed in the more recent period from 2015 to 2023. The simulations incorporate uncertainty by accounting for the variability in predicted online shopping time and the online shopping efficiency parameter, K, which evolves over time and is modeled using a triangular distribution.

Under slower e-commerce growth, the mean value of online shopping time rises modestly from 1.0 to 1.1 h/capita/month between 2024 and 2030. But during the same period, in-store shopping time decreases from 7.0 to 5.4 h/capita/month. Although the increase in online shopping time is relatively small, the increasing time efficiency of online shopping means that consumers accomplish more effective shopping online in less time, leading to a notable decline in in-store shopping time. In contrast, the faster e-commerce growth scenario projects a more rapid increase in online shopping time, from 1.3 to 1.7 h, accompanied by a sharper drop in in-store shopping time, from 5.7 to 2.0 h/capita/month.

The projections between the two scenarios illustrate how variations in online shopping behavior can significantly affect time spent in physical stores. Faster e-commerce growth suggests a faster reduction in in-store activity, which may lead to substantial changes in retail space utilization and associated energy demands. Despite their differences, both models consistently predict a decline in in-store shopping time, reinforcing the long-term trend toward increased reliance on e-commerce platforms. These findings emphasize the importance of incorporating behavioral dynamics into forecasting models for energy use in the retail sector.

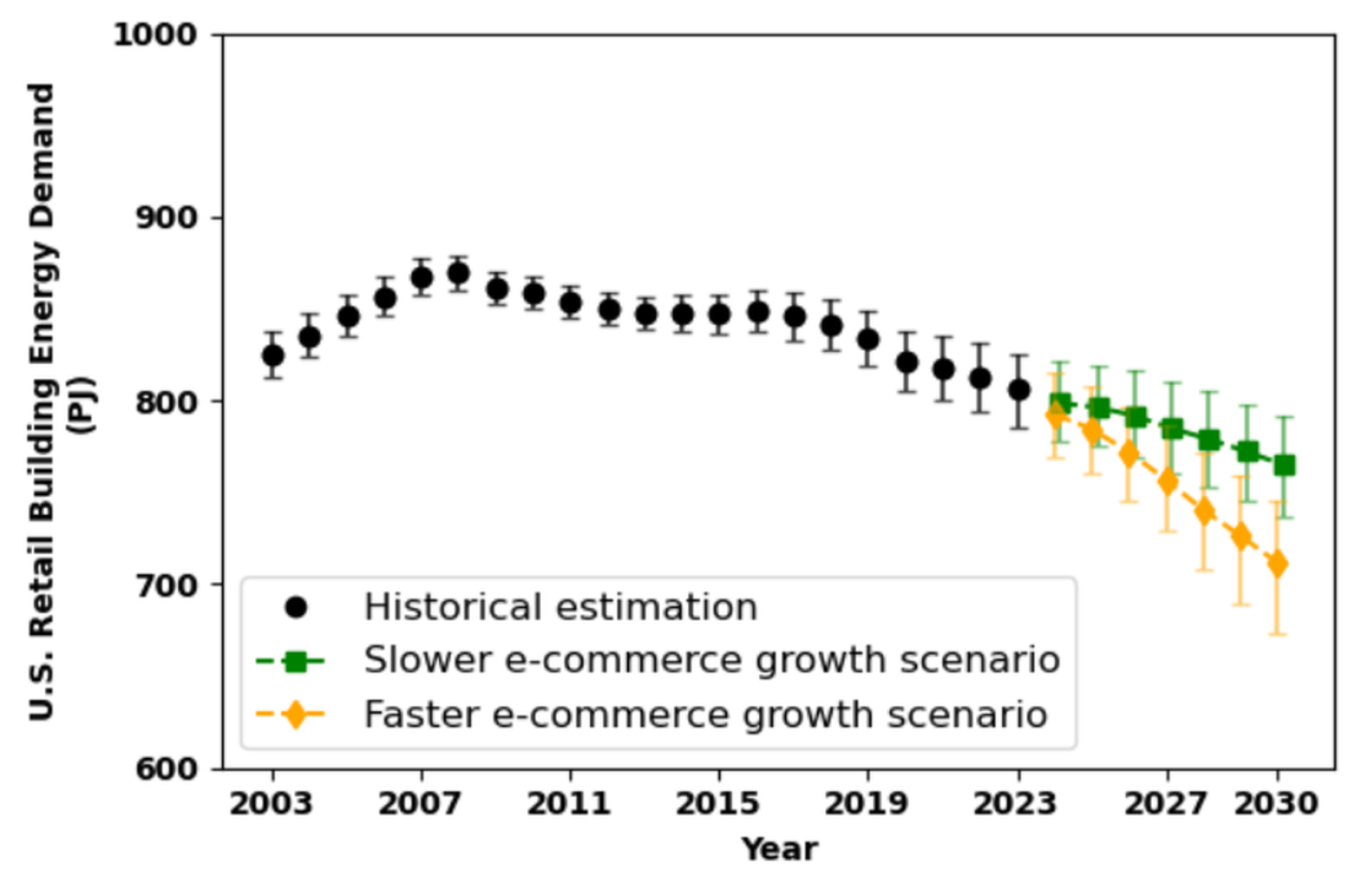
3.3. Future Retail Building Energy Demand in the U.S.

The retail building energy intensity values, based on data from the CBECS for the years 2003, 2012, and 2018, are calculated as 1160, 1140 and 1130 MJ/m², respectively. These values represent the energy consumption per unit area of retail buildings for each surveyed year. Using the linear regression model, annual energy intensity values were derived for the intervening years and extrapolated to future years through 2030.

As shown in Figure 4, the energy intensity is expected to decline over time, following the observed trend from 2003, 2012, and 2018. This trend reflects that newer buildings are designed to achieve higher energy efficiency through advancements in construction techniques, materials, and technologies. By 2030, the mean energy intensity is estimated to reach 1110 MJ/m², representing a 2% decrease compared to the 2018 level of 1130 MJ/m². The confidence interval shows that while the predicted mean energy intensity (blue line) is the most likely estimate, actual values may lie within the shaded region (light blue area).

Although CBECS data for retail buildings are available only for select years (2003, 2012, and 2018), the assumption of a gradual decline in energy intensity is supported by broader trends across commercial and residential sectors. Historical data from the Residential Energy Consumption Survey (RECS) indicate long-term reductions in energy intensity in residential buildings due to advancements in technology, such as more efficient lighting and appliances [48]. Similarly, the Building Performance Database (BPD) reports a general decline in energy use intensity across various commercial building types, driven by technological improvements and stricter building codes [49]. The primary drivers of these reductions—such as advancements in lighting, HVAC efficiency, and building codes—apply broadly to the retail sector as well. Furthermore, projections from the Energy Information Administration’s Annual Energy Outlook (AEO) anticipate continued improvements in building energy efficiency across the U.S. [50]. These trends reinforce the validity of the interpolation approach used in this study, suggesting that the projected decline in retail energy intensity is consistent with observed patterns in the broader building energy landscape.

The projected retail space and retail building energy demand with 95% confidence intervals in the U.S. from 2024 to 2030 is shown in

Table 4. Projected retail space and retail building energy demand based on Monte Carlo Simulations from 2024 to 2030. The slower e-commerce growth scenario extrapolates future online shopping time based on long-term trends (2003–2023), while the faster e-commerce growth scenario relies on more recent patterns (2015–2023) when e-commerce was growing faster. The faster e-commerce growth scenario shows a steeper decline in both retail space and energy demand. (CI = Confidence Interval; PJ = Petajoule).

Year	Slower E-Commerce Growth Scenario				Faster E-Commerce Growth Scenario
	Retail Space (Million m2)		Energy Demand (PJ)		Retail Space (Million m2)		Energy Demand (PJ)
	Mean	95% CI	Mean	95% CI	Mean	95% CI	Mean	95% CI
2024	710	690∼730	800	780∼820	710	690∼730	790	770∼820
2025	710	690∼730	800	770∼820	700	680∼720	780	760∼810
2026	710	690∼730	790	770∼810	690	670∼710	770	750∼800
2027	700	680∼720	780	760∼810	680	650∼700	760	730∼790
2028	700	680∼720	780	750∼800	660	640∼690	740	710∼770
2029	690	670∼720	770	740∼800	650	620∼680	730	690∼760
2030	690	660∼710	760	740∼790	640	610∼670	710	680∼750

. We can see that the faster e-commerce growth scenario shows a sharper decline in both retail space and retail building energy demand compared with the slower e-commerce growth scenario. The historical and projected retail building energy demand from 2003 to 2030 is shown in Figure 5. The black error bars represent historical energy demand estimates, while the green and yellow error bars illustrate the projected energy demand under slower and faster e-commerce growth, respectively. The historical estimation is computed based on Equation (11), and the uncertainty comes from the interpolation procedures of retail index and retail energy intensity based on three years of surveyed data from CBECS [31]. As shown, historical energy consumption in retail buildings has declined gradually from approximately 830 PJ in 2003 to about 810 PJ in 2023, suggesting a slow but steady contraction in energy use, reflecting the improvements in energy efficiency and the gradual decline of in-store shopping time.

For future projections, both scenarios predict a continued decline in energy demand, but with different magnitudes. The slower e-commerce growth scenario assumes a conservative scenario in which online shopping grows gradually, leading to a moderate reduction in in-store shopping time and, consequently, a steady decrease in retail space demand and associated energy consumption. Under this scenario, the mean value of energy demand drops from 800 PJ in 2024 to 760 PJ in 2030, as detailed in Table 4. In contrast, faster e-commerce growth incorporates a more aggressive online shopping growth, based on behavioral acceleration observed since 2015. This results in a steeper decline in energy demand, falling from 790 PJ in 2024 to 710 PJ by 2030.

According to the latest CBECS survey conducted in 2018 [31], U.S. commercial buildings consumed approximately 7200 PJ of energy. Based on our model, retail buildings accounted for an estimated 740 million m² of floor space and 840 PJ of energy demand in 2018. By 2030, the 95% CI for retail space is projected to be 660–710 million m² under the slower e-commerce growth scenario (a 4–10% reduction from 2018), and 610–670 million m² under the faster growth scenario (a 9–18% reduction). For retail building energy demand, Table 4 shows that the 2030 projection ranges from 740–790 PJ under the slower growth scenario (a 6–12% reduction) and from 680–750 PJ under the faster scenario (an 11–20% reduction). Notably, the predictive model incorporates only a 2% reduction in energy intensity by 2030—reflecting anticipated improvements in building technologies—yet projects substantially larger reductions in total energy demand. This contrast indicates the significant influence of shifting consumer behavior from in-store to online shopping.

The results have implications for national commercial building energy consumption too. By 2030, the retail building energy demand is projected to decrease by approximately 50–100 PJ under the slower e-commerce growth scenario and by 90–160 PJ under the faster e-commerce growth scenario, relative to the 2018 level. These reductions correspond to approximately 0.7–1.3% and 1.3–2.2%, respectively, of the total 2018 national commercial building energy consumption.

Table 5. Summary of the results of slower and faster e-commerce growth scenarios for the U.S. retail sector. The table compares the slower and faster growth trajectory in online shopping time and the corresponding predictions for in-store shopping time, retail floor space, and energy demand in 2030. The results show that the faster e-commerce growth scenario has a sharper decline in both retail space and energy demand.

	Slower E-Commerce Growth Scenario	Faster E-Commerce Growth Scenario
Annual growth of online shopping time	+0.022 h/capita/month each year	+0.074 h/capita/month each year
Time spent online shopping in 2030	1.1 h/capita/month	1.7 h/capita/month
Time spent in-store shopping in 2030	5.4 h/capita/month	2.0 h/capita/month
Retail space (2018 baseline)	740 million m2
Retail space change (compared to 2018)	−4% to −10%	−9% to −18%
Retail energy demand (2018 baseline)	840 Peta Joules
Retail energy demand change (compared to 2018)	−6% to −12%	−11% to −20%

summarizes results of the analysis. In the slower growth scenario, online shopping time increases by +0.022 h/capita/month each year, reaching 1.1 h/month by 2030 and leaving 5.4 h/month in-store; in the faster growth scenario, it rises by +0.074 h/capita/month each year to 1.7 h/month, with in-store time falling to 2.0 h/month. In the faster growth e-commerce scenario, per capita in-store shopping time falls from the historical level of 11 h/month down to 2 h/month, which would represent a significant challenge to brick and mortar retail. The only reason that this decline is not reflected in the 2030 space and energy results is because of our use of a lagging factor of 5 years averaging between in-store shopping and space needs. However, if retail stores do respond to the lagging 5 years of shopping activity, this merely delays the retail decline due to the 82% drop in in-store shopping. Starting from a 2018 baseline of 740 million m² of retail space and 840 PJ of retail energy use, the model projects retail space declines of 4–10% (slower) and 9–18% (faster), and retail energy declines of 6–12% (slower) and 11–20% (faster) by 2030. They indicate continued behavioral shifts towards use of e-commerce, with a more dramatic change in the faster growth scenario. Note that consumers are expected to spend less time overall shopping, leading to the question, not addressed here, of what activities they do with the saved time [51]. There are resulting large reductions in retail building space, and we can expect to even more abandoned retail stores and malls. The energy use of retail buildings is expected to drop, dramatically in the faster growth scenario.

4. Discussion

This study finds growth in e-commerce leads to declining time spent on in-store shopping, and in turn induces reductions in retail building space and energy demand. Historical analysis shows a gradual reduction in energy use from 2003 to 2023, and projections for 2024–2030 indicate continued declines under both slower and faster e-commerce growth scenarios. U.S. retail building space and energy demand in 2030 are expected to be 4–18% and 6–20% lower compared to 2018, respectively. The reduction in building space calls for additional efforts from urban planners and developers to repurpose abandoned retail space. The reduction in energy demand is positive from an environmental perspective, but the net energy effects of e-commerce is not yet well understood due to complex effects on multiple sectors: Personal and freight transport, packaging, warehousing, and IT infrastructure.

• Implications for the retail sector—The transition towards e-commerce has profound implications for urban planning, management, and the development of sustainable cities. The need to adapt physical retail spaces for alternative uses or improve their energy efficiency to mitigate wasteful consumption is growing. As brick-and-mortar retail spaces contract, city planners may need to repurpose vacant commercial properties, adapt zoning regulations, and reconsider infrastructure needs to support mixed-use developments, residential conversions, or logistics hubs for e-commerce fulfillment [52]. Our analysis does not break out how different bricks and mortar retail sectors will evolve—instead, we quantify the overall scale of continued decline in the U.S. Commentors have considered this question, debating, for example, how the declining demand for retail space could indicate a shift toward smaller, experience-driven stores rather than large-format retail outlets [53]. This trend suggests that future retail spaces may prioritize flexible layouts, omni-channel integration, and energy-efficient designs to align with evolving consumer behaviors and sustainability objectives. Planners should therefore view the transition not as a “retail apocalypse” but as a functional transformation. Some retail will remain, driven by demand to see some products in person, along with the need for convenient e-commerce returns. The excess space needs repurposing, calling for flexibility and creativity in planning and development. Future analyses should explore repurposing, assessing social, economic, and energy attributes.
• Implications for the energy sector—Energy demand forecasts are important in planning expansion and retirement of supply and for prioritization of energy efficiency programs. There is a tendency for analysts to overpredict energy demand, e.g., [54], and often do not include behavioral change as an explicit element of the forecast. This analysis suggests that behavioral change could lead to energy reductions in the retail sector that are more rapid than might otherwise be expected. We do not consider here the total effect of e-commerce on energy demand, which includes changes in transport, packaging, warehousing, and other behavioral changes. For example, increased online shopping affects urban transportation patterns, potentially reducing consumer travel for shopping but increasing freight traffic. Some of these effects have been estimated in prior literature [11], and it is important to refine these estimates and put them in a temporal context.
• Forecasting—The forecast cannot be “validated” today, one has to wait to compare the actual evolution in 2024–2030 with model predictions. We offer thoughts on the robustness of the forecast: We saw that the historical behavior for online shopping time did not show a single historical pattern; thus, two scenarios were developed—forecasting from 2003–2023 (slower growth) and 2015–2025 (faster growth). We rely on Monte Carlo simulation and the two online shopping growth scenarios to characterize uncertainty in the forecast. We believe this is a careful treatment of uncertainty associated with extrapolating historical trends. It is always possible that future disruptions change the trajectory, such uncertainty is inherent in forecasting. We argue that a retrospective forecast is useful in planning, when utilizing it is important to monitor trends to detect disruptive changes. Expert judgment is another approach used in forecasting, sometimes individuals assert their vision, while in expert elicitation, the collective opinion of a group of experts is developed. We do not comment on the relative accuracy of retrospective versus expert forecasting, but do want to report relevant expert assessments. While there are no formal expert elicitations forecasting e-commerce growth, there is a variety of prospective views from individual experts/teams. Ref. [55] predicts that U.S. e-commerce will continue its rapid expansion, reaching USD1.7 trillion in sales by 2028 at a modest and stable growth of around 8.5% annually, which lies within the growth rate range used in our model (3.6–10.1%, see details in [42]). McKinsey suggests that while U.S. online sales accelerated to 18% annual growth between 2019 and 2023, they “could now normalize at a more modest but still healthy growth rate” of around 6% a year, close to pre-pandemic rates [56].
• Assumptions, Caveats, and Uncertainties—Data limitations led to a number of assumptions with modeling and construction of time series to run the models. The lack of a direct measure of online shopping time in ATUS led to estimating it based on total non-store shopping time minus “other” shopping time (e.g., garage sales); the latter assumed constant because of historical data. There is no annual source of data in the U.S. on retail space and retail energy use, so we estimate annual figures via a combination of extrapolation of data from 2003, 2012, and 2018 from CBECS and annual data on total commercial building space from CoStar. The evident technological progress in e-commerce suggests it must be accounted for to explain consumer behavior, which we accomplish via definition of K (shopping efficiency), based on the idea that total equivalent shopping time should be constant. Pre-e-commerce shopping time data supports these assumptions and there are prior examples of constant time budgets for an activity type, particularly transport [57]. While we believe we have explained their logical basis and they do explain historical trends well, they are all assumptions. Improvements in data availability would improve estimations of the relationship between online shopping and retail buildings, as well as transport and other activities it influences. In particular, recall that ATUS data on shopping time aggregates all retail purchases in into a single measure. As the adoption rate of e-commerce varies by sector, forecasting using the aggregate is presumably less accurate further in the future. ATUS could call out online shopping as an activity, similar to time use surveys in some countries that already do this. Linking the U.S. Consumer Expenditure Survey [58] with ATUS, e.g., one as a sub-cohort of the other, would open potential for many analyses clarifying linkages between activities and purchase behavior. One-off surveys could clarify how consumers use online shopping for which products. While we hope to see more resolved analyses of relationships between e-commerce, consumer behavior and energy in the future, this work provides a first reference point for the connection between online shopping and the retail building sector.