A Review of Key Technologies for Active Midpoint Clamping (ANPC) Topology in Energy Storage Converters: Modulation Strategies, Redundant Control, and Multi-Physics Field Co-Optimization
Abstract
1. Introduction
- Modulation strategies: This paper synthesizes and compares improved MPC and adaptive SVM methods—covering realization mechanisms, complexity reduction (~60%), THD control (<3%), and a hybrid, condition-aware modulation scheme suited to wide-range operating points.
- Redundant/fault-tolerant control: This paper summarizes a three-layer protection architecture (prediction–tolerance–health) with demonstrated metrics (prediction accuracy > 95%, recovery time < 100 μs), highlighting implementation pathways on modern digital platforms and the trade-offs among response speed, device stress, and availability.
- Multi-physics field co-optimization: This paper reviews coupled electro-thermal–mechanical modeling and design, emphasizing SiC/IGBT hybrid integration and 3D interconnect/packaging that raise power density to 4.5 kW/kg, and we discuss comprehensive evaluation frameworks that consider lifecycle cost and reliability.
2. Modulation Strategy of ANPC Topology in Energy Storage Converter
2.1. Current Status of Modulation Strategy Development
| Point | Time | Core Methodology/Technology | Problems/Breakthroughs |
|---|---|---|---|
| Basic SVPWM phase | 2010–2015 | Direct porting of NPC topological modulation methods | There is the problem of a single choice of zero vector [7] |
| Loss equalization modulation stage [8] | 2015–2018 | Introduction of dynamic zero-vector assignment | Achieved a breakthrough in reducing the loss imbalance by 40% [11] |
| Intelligent modulation stage [25,26] | 2018–present | Integration of MPC with AI and its enhancements | Recent advances include neural network prediction of switching sequences [22] |
2.2. Improved MPC Modulation Strategy
2.3. AI-Enhanced Control Strategies for ANPC Converters
3. Redundant Control Techniques for ANPC Topology in Energy Storage Converters
3.1. History of Redundant Control Technology
3.2. Core Algorithm and Model Analysis
3.3. Key Measured Parameters and Performance Indicators in Fault Diagnosis
4. Multi-Physics Field Co-Optimization of ANPC Topology in Energy Storage Converters
4.1. Current Status of the Development of Multi-Physics Field Co-Optimization Technology
4.2. Modeling of ANPC Topology with Coupled Multi-Physics Fields
4.3. Efficiency Analysis and Comparison of ANPC Converters Under Multi-Physics Constraints
5. Synergy Analysis of Three Key Technologies
6. Technical Challenges and Future Trends of ANPC Topologies in Energy Storage Converters
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ANPC | Active neutral-point clamped |
| THD | Total harmonic distortion |
| SiC | Silicon carbide device |
| IRENA | International Renewable Energy Agency |
| PCS | Power conversion system |
| ANPC | Active midpoint clamping |
| NPC | Neutral-point clamped |
| MPC | Model predictive control |
| FCS-MPC | Finite control set–model predictive control |
| SOC | State of charge |
| DNN | Deep neural network |
| RL | Reinforcement learning |
| HIL | Hardware in loop |
| DT | Digital twin |
| AI | Artificial intelligence |
| PINN | Physics-informed NN |
| MTBF | Mean time between failure |
| GA | Genetic algorithm |
| EMI | Electromagnetic interference |
References
- Yuksel, A.; Sefa, I.; Altin, N. DC-Link Voltage Stabilization and Capacitor Size Reduction in Active Neutral-Point-Clamped Inverters Using an Advanced Control Method. Energies 2025, 18, 3143. [Google Scholar] [CrossRef]
- Zhou, J.; Li, J. Waveform Optimization Control of an Active Neutral Point Clamped Three-Level Power Converter System. Electronics 2024, 13, 1980. [Google Scholar] [CrossRef]
- Teston, S.A.; Vilerá, K.V.; Mezaroba, M.; Rech, C. Control System Development for the Three-Ports ANPC Converter. Energies 2020, 13, 3967. [Google Scholar] [CrossRef]
- Dargahi, V.; Corzine, K.A.; Enslin, J.H.; Rodriguez, J.; Blaabjerg, F. Improved Active-Neutral-Point-Clamped (I-ANPC) Multilevel Converter: Fundamental Circuit Topology, Innovative Modulation Technique, and Experimental Validation. In Proceedings of the 2018 IEEE Power and Energy Conference at Illinois (peci), Champaign, IL, USA, 22–23 February 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Teston, S.A.; Mezaroba, M.; Rech, C. ANPC Inverter with Integrated Secondary Bidirectional Dc Port for ESS Connection. IEEE Trans. Ind. Appl. 2019, 55, 7358–7367. [Google Scholar] [CrossRef]
- Wang, H.; Ma, X.; Sun, H. Active Neutral-Point-Clamped (ANPC) Three-Level Converter for High-Power Applications with Optimized PWM Strategy. In Proceedings of the PCIM Asia 2020; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Shanghai, China, 16–18 November 2020; pp. 1–8. [Google Scholar]
- Woldegiorgis, D.; Mantooth, H.A. Precise Electro-Thermal Power Loss Model of a Three-Level ANPC Inverter with Hybrid Si/SiC Switches. Chin. J. Electr. Eng. 2022, 8, 76–89. [Google Scholar] [CrossRef]
- Abarzadeh, M.; Khan, W.A.; Weise, N.; Al-Haddad, K.; EL-Refaie, A.M. A New Configuration of Paralleled Modular ANPC Multilevel Converter Controlled by an Improved Modulation Method for 1 MHz, 1 MW EV Charger. IEEE Trans. Ind. Appl. 2021, 57, 3164–3178. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Wang, Z.; Yang, Y.; Blaabjerg, F. Simplified Thermal Modeling for IGBT Modules with Periodic Power Loss Profiles in Modular Multilevel Converters. IEEE Trans. Ind. Electron. 2019, 66, 2323–2332. [Google Scholar] [CrossRef]
- Khoshkbar Sadigh, A.; Dargahi, V.; Naderi, R.; Corzine, K.A. Active Voltage Balancing and Thermal Performance Analysis of Dual Flying-Capacitor Active Neutral-Point-Clamped (DFC-ANPC) Inverters. IEEE Trans. Ind. Appl. 2021, 57, 637–649. [Google Scholar] [CrossRef]
- Dermouche, R.; Talaoubrid, A.; Barazane, L.; Sellami, Y.; Tadjine, M.; Zioui, N. Qualitative and Quantitative Analysis of the Reliability of NPC and ANPC Power Converters for Aeronautical Applications. Alex. Eng. J. 2022, 61, 4863–4873. [Google Scholar] [CrossRef]
- Cai, X.; Zhang, Z.; Zhang, J.; Li, Z.; Kennel, R.; Zhang, Z. Improved Predictive Control of Three-Level-NPC Power Converters. In Proceedings of the 6th IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (precede 2021), Jinan, China, 20–22 November 2021; IEEE: New York, NY, USA, 2021; pp. 393–402. [Google Scholar]
- Sharma, P.V.V.R.; K, N. A Review on Intelligence Algorithms for THD Minimization in Multi-Level Inverter. Int. J. Modell. Simul. 2024, 45, 1671–1687. [Google Scholar] [CrossRef]
- Ye, H.; Lin, M.; Basaran, C. Failure Modes and FEM Analysis of Power Electronic Packaging. Finite Elem. Anal. Des. 2002, 38, 601–612. [Google Scholar] [CrossRef]
- Plesca, A. Thermal Analysis of Power Semiconductor Device in Steady-State Conditions. Energies 2019, 13, 103. [Google Scholar] [CrossRef]
- Almpanis, I.; Evans, P.; Li, K.; Lophitis, N. IGBT Model for Circuit Simulations: Implementation of the Nonlinear Voltage-and Current-Dependent Capacitance Method to Silicon IGBTs. In Proceedings of the 2024 IEEE Design Methodologies Conference (DMC), Grenoble, France, 18–20 November 2024; pp. 1–3. [Google Scholar]
- Pedersen, K.B.; Pedersen, K. Dynamic Modeling Method of Electro-Thermo-Mechanical Degradation in IGBT Modules. IEEE Trans. Power Electron. 2016, 31, 975–986. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.W.; Tian, H.; Zargari, N.R.; Cheng, Z. A Modular Design Approach to Provide Exhaustive Carrier-Based PWM Patterns for Multilevel ANPC Converters. IEEE Trans. Ind. Appl. 2019, 55, 5032–5044. [Google Scholar] [CrossRef]
- Yang, C.; Gui, W.; Chen, Z.; Zhang, J.; Peng, T.; Yang, C.; Karimi, H.R.; Ding, S.X. Voltage Difference Residual-Based Open-Circuit Fault Diagnosis Approach for Three-Level Converters in Electric Traction Systems. IEEE Trans. Power Electron. 2020, 35, 3012–3028. [Google Scholar] [CrossRef]
- Li, G.; Xu, S.; Sun, Z.; Yao, C.; Ren, G.; Ma, G. Open-Circuit Fault Diagnosis for Three-Level ANPC Inverter Based on Predictive Current Vector Residual. IEEE Trans. Ind. Appl. 2023, 59, 6837–6851. [Google Scholar] [CrossRef]
- Surapu, P.R.; Sandeep, N.; Verma, A.K. Five-Level ANPC Inverter with Full DC-Bus Utilization. IEEE Trans. Power Electron. 2024, 39, 83–87. [Google Scholar] [CrossRef]
- Rzepka, F.; Hematty, P.; Schmitz, M.; Kowal, J. Neural Network Architecture for Determining the Aging of Stationary Storage Systems in Smart Grids. Energies 2023, 16, 6103. [Google Scholar] [CrossRef]
- Zjavka, L. Power Quality Daily Predictions in Smart Off-Grids Using Differential, Deep and Statistics Machine Learning Models Processing NWP-Data. Energy Strategy Rev. 2023, 47, 101076. [Google Scholar] [CrossRef]
- Zjavka, L. Power Quality 24-Hour Prediction Using Differential, Deep and Statistics Machine Learning Based on Weather Data in an off-Grid. J. Frankl. Inst. 2023, 360, 13712–13736. [Google Scholar] [CrossRef]
- Meraj, S.T.; Yahaya, N.Z.; Hossain Lipu, M.S.; Islam, J.; Haw, L.K.; Hasan, K.; Miah, M.d.S.; Ansari, S.; Hussain, A. A Hybrid Active Neutral Point Clamped Inverter Utilizing Si and Ga2O3 Semiconductors: Modelling and Performance Analysis. Micromachines 2021, 12, 1466. [Google Scholar] [CrossRef] [PubMed]
- Selvakumar, P.; Muthukumaran, G. An Intelligent Technique for Fault Detection and Localization of Three-Level ANPC Inverter with NP Connection for Electric Vehicles. Adv. Eng. Softw. 2023, 176, 103354. [Google Scholar] [CrossRef]
- Kouro, S.; Cortes, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model Predictive Control-a Simple and Powerful Method to Control Power Converters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Katkout, A.; Nasser, T.; Essadki, A. Robust Multiobjective Model Predictive Control with Computation Delay Compensation for Electric Vehicle Applications Using PMSM with Multilevel Inverter. Math. Probl. Eng. 2020, 2020, 7015865. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, S.; Feng, L.; Li, Z.; Feng, J. An Optimized Model Predictive Control Method for Hybrid ANPC with Fixed Switching Frequency. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 2246–2257. [Google Scholar] [CrossRef]
- Su, S.; Xie, Q.; Wang, M.; Wang, Y.; Chen, J.; Hu, Z. Simple Voltage Balancing Control of Four-Level Inverter. Electronics 2024, 13, 3878. [Google Scholar] [CrossRef]
- Van Der Broeck, C.H.; Conrad, M.; De Doncker, R.W. A Thermal Modeling Methodology for Power Semiconductor Modules. Microelectron. Reliab. 2015, 55, 1938–1944. [Google Scholar] [CrossRef]
- Zhao, S.; Feng, Z.; Sun, Z.; Zhang, X.; Zhao, Z.; Zhao, T.; Cao, Q. A Efficiency Optimization and Loss Balancing Method for Hybrid Three-Level Active Neutral Point Clamped Inverter. Electr. Eng. 2025, 107, 7575–7586. [Google Scholar] [CrossRef]
- Sun, Z.; Ma, G.; Xu, S.; Zhang, H.; Ren, G. Reduced Vector Model Predictive Control of ANPC Inverter for PMSM Drives with Optimized Commutation. IEEE Trans. Transport. Electrific. 2022, 8, 3177–3191. [Google Scholar] [CrossRef]
- Dargahi, V.; Corzine, K.A.; Enslin, J.H.; Sadigh, A.K.; Rodriguez, J.; Blaabjerg, F. Logic-Equations-Based Modulation Technique for Natural Balance Control of an Improved Active-Neutral-Point-Clamped (I-ANPC) Multilevel Converter. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ecce), Portland, OR, USA, 23–27 September 2018; IEEE: New York, NY, USA, 2018; pp. 3004–3011. [Google Scholar]
- Li, J.; Dan, Z.; Jiang, J. Fast Finite Control Set Model Predictive Control for Three-Phase Five-Level Nested Neutral Point Piloted Converter. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 1140–1145. [Google Scholar]
- Xu, S.; Yao, C.; Ren, G.; Sun, Z.; Wu, S.; Ma, G. Weighting Factors Autotuning of FCS-MPC for Hybrid ANPC Inverter in PMSM Drives Based on Deep Residual Networks. IEEE Trans. Power Electron. 2024, 39, 16540–16552. [Google Scholar] [CrossRef]
- Cao, H.; Lin, N.; Darvish, P.; Yang, Y.; Wang, Z.; Zhao, Y. Enhanced Triple Phase Shift Modulation Strategy for ANPC-DAB Converter to Extend Soft Switching Range. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024; pp. 445–452. [Google Scholar]
- Zhiwei, Z.; Sihui, Z.; Yuchao, Z.; Cunxin, Y.; Chenwei, M.; Wensheng, S. Digital Twin Approach for Parameters Monitoring of a Three-Phase Three-Level ANPC Inverter. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 3111–3116. [Google Scholar]
- Custodio, P.; McBride, B.; Le, T.; Jackson, J.; Haulmark, K.; Di, J.; Farnell, C.; Mantooth, H.A. Digital Twin of an ANPC Inverter with Integrated Design-for-Trust. In Proceedings of the 2022 IEEE Design Methodologies Conference (DMC), Bath, UK, 1–2 September 2022; pp. 1–7. [Google Scholar]
- Fazio, P.; Marchesoni, M.; Parodi, G. Fault Detection and Reconfiguration Strategy for ANPC Converters. In Proceedings of the 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. DS1b.17-1–DS1b.17-5. [Google Scholar]
- Kwon, B.-H.; Bae, K.-C.; Kim, S.-M.; Lee, K.-B. Detecting Method for an Open-Switch Fault of SiC MOSFET and Si IGBT in Hybrid ANPC Inverter System. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 2928–2932. [Google Scholar]
- Kuprat, J.; Debbadi, K.; Schaumburg, J.; Liserre, M.; Langwasser, M. Thermal Digital Twin of Power Electronics Modules for Online Thermal Parameter Identification. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 1020–1029. [Google Scholar] [CrossRef]
- Foshati, A.; Ejlali, A. Digital Twin-Based Cyber Redundancies to Achieve Cost-Effective Fault Tolerance. IEEE Internet Things J. 2025, 12, 31302–31309. [Google Scholar] [CrossRef]
- Wei, J.; Kundur, D.; Zourntos, T.; Butler-Purry, K.L. A Flocking-Based Paradigm for Hierarchical Cyber-Physical Smart Grid Modeling and Control. IEEE Trans. Smart Grid 2014, 5, 2687–2700. [Google Scholar] [CrossRef]
- Li, N.; Zhou, R.; Hu, Q.; Liu, X. Mechanical Fault Diagnosis Based on Redundant Second Generation Wavelet Packet Transform, Neighborhood Rough Set and Support Vector Machine. Mech. Syst. Signal Process. 2012, 28, 608–621. [Google Scholar] [CrossRef]
- Messaoudi, H.; Bennani Ben Abdelghani, A.; Bellaaj, N.M.; Orabi, M. Thermal Performance-Based Comparative Study of PWM Strategies for Three-Level ANPC Converter. In Proceedings of the 2016 7th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 22–24 March 2016; pp. 1–6. [Google Scholar]
- Aleenejad, M.; Mahmoudi, H.; Moamaei, P.; Ahmadi, R. A New Fault-Tolerant Strategy Based on a Modified Selective Harmonic Technique for Three-Phase Multilevel Converters with a Single Faulty Cell. IEEE Trans. Power Electron. 2016, 31, 3141–3150. [Google Scholar] [CrossRef]
- Tian, J.; Zhuo, C.; Wang, F.; Deng, H. An RMS Current Minimization Method for Three-Level ANPC-DAB-Based Distributed Energy Storage System with Full Operation ZVS. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 2388–2405. [Google Scholar] [CrossRef]
- Yang, W.; Xu, S.; Chen, X.; Chai, Y. Diagnosis of Current Sensors Incipient Faults in Three-Phase Three-Level NPC Rectifiers Based on Adaptive Sliding Mode Observer. IEEE Sens. J. 2024, 24, 34654–34663. [Google Scholar] [CrossRef]
- Dwivedi, D.; Chinmaya, K.A. A Novel Three-Level Dual-Output Active Neutral-Point Clamped (ANPC) Converter. IEEE Trans. Ind. Electron. 2025, 72, 4457–4469. [Google Scholar] [CrossRef]
- Fard, M.T.; Luckett, B.J.; He, J. Digital Twin Enabled Open-Circuit Fault Diagnosis for Five-Level ANPC Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 2766–2780. [Google Scholar] [CrossRef]
- Mirza, A.Y.; Bazzi, A.M.; Cao, Y. Reconfiguration of Multilevel Inverters and Their Impact on Insulation Breakdown Time. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; IEEE: New York, NY, USA, 2023; pp. 881–884. [Google Scholar]
- Pribadi, J.; Lee, D.-C. Reconfiguration of Four-Level Active Neutral-Point-Clamped Inverters for Fault-Tolerant Operation. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 1437–1442. [Google Scholar]
- Li, G.; Xu, S.; Yao, C.; Ren, G.; Ma, G. Adaptive Fault-Tolerant Operation of Three-Level ANPC Inverter in PMSM Drives Using Model Predictive Control. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 2045–2050. [Google Scholar]
- Zhang, B.; Zou, Z.-X.; Wang, Z. Analysis and Comparison of Three-Level ANPC with Different Commutation Modes. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; pp. 867–873. [Google Scholar]
- Niederhofer, S.; Rennhofer, M.; Hofmann, R. Risk Analysis of Coupled PV-Electrolyser Systems. Renew. Energy 2025, 254, 123539. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Gao, Z.; Sun, F.; Hu, W. A Case Study of Multiobjective Automatic Design for Active Neutral Point Clamped Inverter Based on Machine Learning. IEEE Trans. Ind. Electron. 2025, 72, 6583–6593. [Google Scholar] [CrossRef]
- Li, J.; Huang, A.Q.; Liang, Z.; Bhattacharya, S. Analysis and Design of Active NPC (ANPC) Inverters for Fault-Tolerant Operation of High-Power Electrical Drives. IEEE Trans. Power Electron. 2012, 27, 519–533. [Google Scholar] [CrossRef]
- Sathik, M.J. A Nine Level ANPC Boost Type Inverter Topology with Reduced Component Stress. IEEE Trans. Circuits Syst. II 2024, 71, 380–384. [Google Scholar] [CrossRef]
- Ciappa, M. Selected Failure Mechanisms of Modern Power Modules. Microelectron. Reliab. 2002, 42, 653–667. [Google Scholar] [CrossRef]
- Ni, P.; Ye, Z.; Cao, C.; Guo, Z.; Zhao, J.; He, X. Cooperative Game-Based Collaborative Optimal Regulation-Assisted Digital Twins for Wide-Area Distributed Energy. Energies 2023, 16, 2598. [Google Scholar] [CrossRef]
- Lazarevic, V.Z.; Vasic, M. High-Frequency GaN-Based ANPC Three-Level Converter as a Low-Noise Arbitrary PWL Voltage Generator. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 5997–6008. [Google Scholar] [CrossRef]
- Caballero, L.; Busquets-Monge, S.; Rates, S. Enhanced Power Device Configuration and Operation of a Grid-Connected Active-Neutral-Point-Clamped Inverter for Wind Energy Conversion Systems. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (epe’16 Ecce Europe), Karlsruhe, Germany, 5–9 September 2016; IEEE: New York, NY, USA, 2016. [Google Scholar]
- Cao, Y.; Lyu, H.; Mertens, A. Mission Profile-Based Operation Strategies to Improve the Reliability of an ANPC Inverter in Future Electrified Aircraft Propulsion Systems. In Proceedings of the 2024 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 19–21 June 2024; pp. 1–8. [Google Scholar]
- Saponara, S. Distributed Measuring System for Predictive Diagnosis of Uninterruptible Power Supplies in Safety-Critical Applications. Energies 2016, 9, 327. [Google Scholar] [CrossRef]
- Zhe, L.; Ling, F.; Zhaohui, W.; Jianghua, F. Model Predictive Control of SiC&Si Hybrid ANPC Inverter. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 2807–2811. [Google Scholar]
- Wang, K.; Xu, L.; Zheng, Z.; Li, Y. Capacitor Voltage Balancing of a Five-Level ANPC Converter Using Phase-Shifted PWM. IEEE Trans. Power Electron. 2015, 30, 1147–1156. [Google Scholar] [CrossRef]
- Woldegiorgis, D.; Mantooth, A. Accurate Power Loss Model of a Three-Level ANPC Inverter Utilizing Hybrid Si/SiC Switching Devices. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 2380–2385. [Google Scholar]
- Gao, N.; Zhang, B.; Wu, W.; Blaabjerg, F. Finite Control Set Model Predictive Control Integrated with Disturbance Observer for Battery Energy Storage Power Conversion System. J. Power Electron. 2021, 21, 342–353. [Google Scholar] [CrossRef]
- Tian, J.; Zhuo, C.; Wang, F.; Deng, H. Full-Power-Range Multiobjective Optimization Scheme for Three-Level ANPC-DAB-Based Distributed Generation System. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 1754–1768. [Google Scholar] [CrossRef]
- Gao, S.; Xu, Y.; Zhang, Z.; Wang, Z.; Zhou, X.; Wang, J. Multiagent Imitation Learning-Based Energy Management of a Microgrid with Hybrid Energy Storage and Real-Time Pricing. IEEE Internet Things J. 2025, 12, 19801–19817. [Google Scholar] [CrossRef]
- Kljajić, R.; Marić, P.; Mišljenović, N.; Dubravac, M. An Optimized Strategy for the Integration of Photovoltaic Systems and Electric Vehicles into the Real Distribution Grid. Energies 2024, 17, 5602. [Google Scholar] [CrossRef]
- Li, C.; Lu, R.; Li, C.; Li, W.; Gu, X.; Fang, Y.; Ma, H.; He, X. Space Vector Modulation for SiC and Si Hybrid ANPC Converter in Medium-Voltage High-Speed Drive System. IEEE Trans. Power Electron. 2020, 35, 3390–3401. [Google Scholar] [CrossRef]
- Mu, X.; Chen, H.; Wang, X.; Wu, W.; Wang, H.; Yuan, L.; Chung, H.S.-H.; Blaabjerg, F. A Review of Hybrid Three-Level ANPC Inverters: Topologies, Comparison, Challenges and Improvements in Applications. Energies 2025, 18, 2613. [Google Scholar] [CrossRef]
- Mariethoz, S. Optimal Common Mode Control for Neutral Point Potential Ripple Minimization on ANPC Converter. In Proceedings of the 2024 Energy Conversion Congress & Expo Europe (ECCE Europe), Darmstadt, Germany, 2–6 September 2024; pp. 1–7. [Google Scholar]
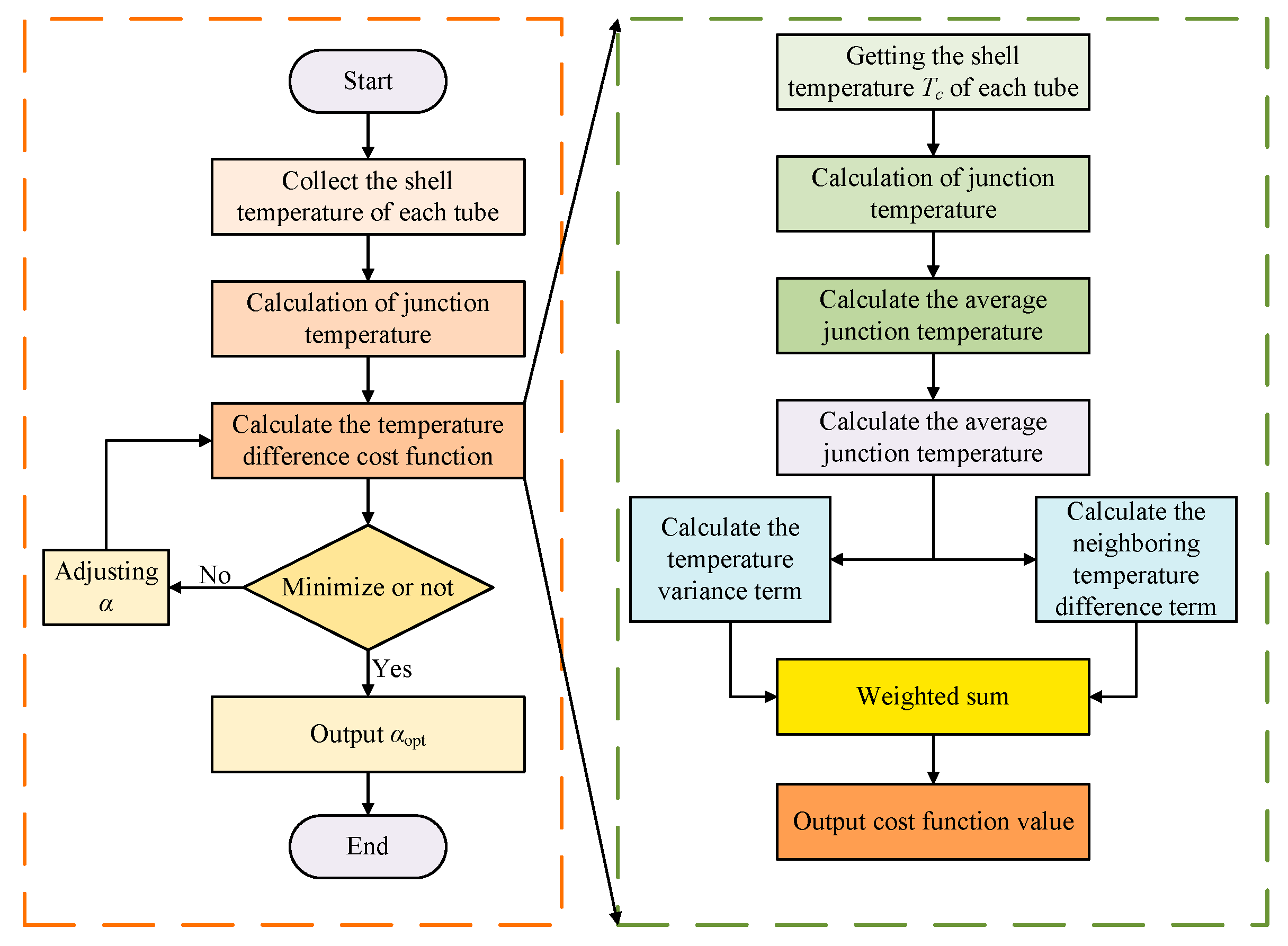
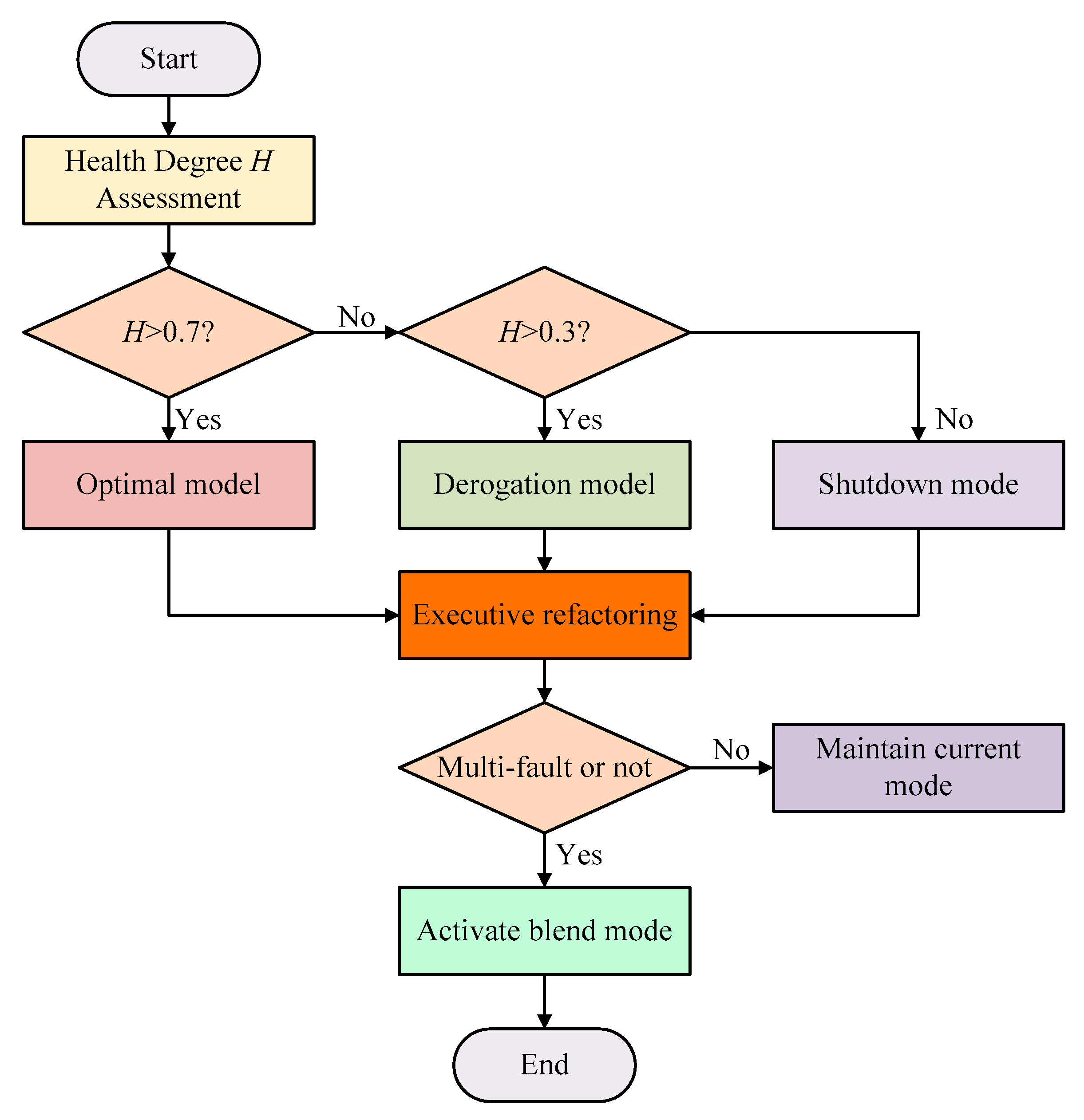
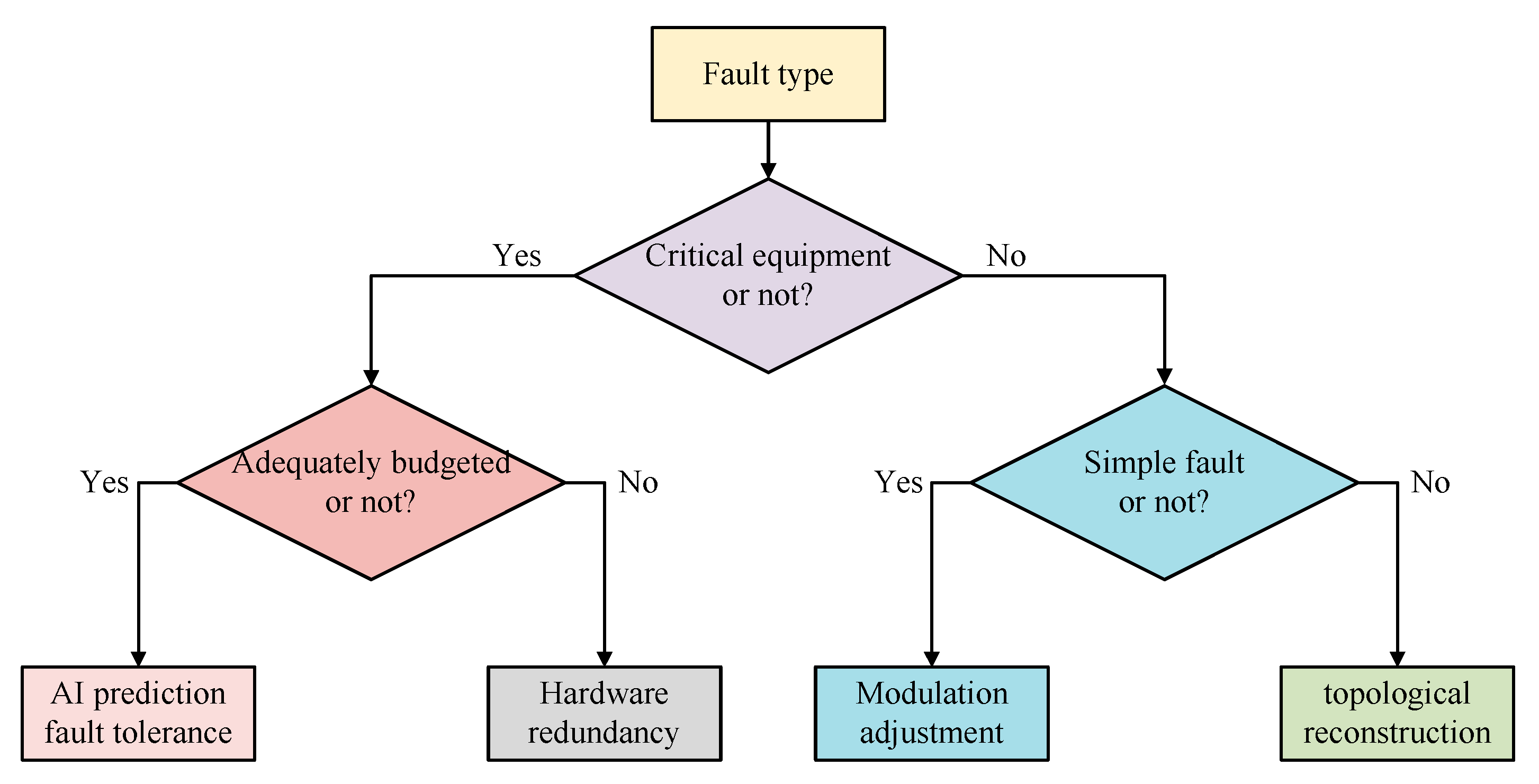
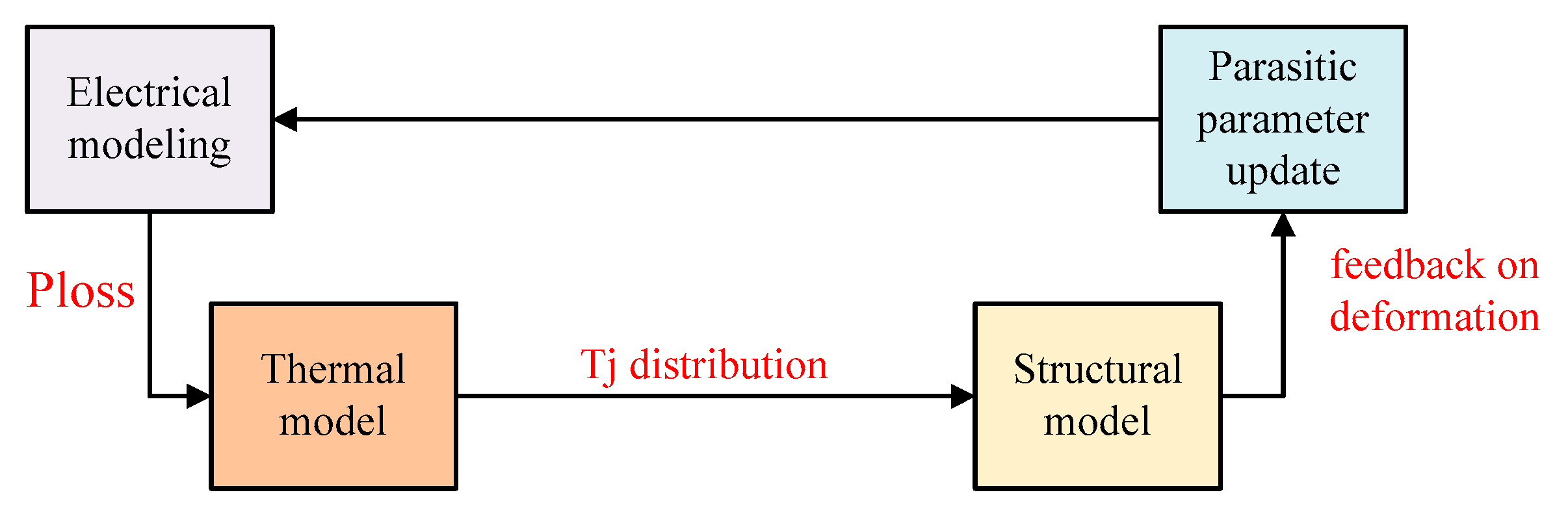
| Comparison Dimension | Traditional SVPWM [1] | MPC [6] | Improved FCS-MPC [18] | Mixing and Modulation [27] | Hysteresis Loop Control [33] |
|---|---|---|---|---|---|
| Rationale | Based on voltage vector synpaper | Rolling optimization + direct control | Finite state optimization + multi-objective constraints | SVPWM and MPC dynamic switching | Current error band control |
| Control variable | Vector action time | Direct output of switching status | Optimized switching sequence | Modulation mode flag bit | Hysteresis loop bandwidth |
| Dynamic response | Medium (0.5–1 ms) | Fast (<100 μs) | Ultra-fast (<50 μs) | Adaptive (50–200 μs) | Fastest (10–50 μs) |
| THD performance | 3–5% | 4–6% | 2.5–4% | 3–4% | 5–8% |
| Switching loss | Fixed (1.8–2.2 kW) | Variable (2.0–2.5 kW) | Optimized distribution (1.5–2.0 kW) | 1.7–2.1 kW | Randomized (2.5–3.5 kW) |
| Center-point balance | Additional control ring required | Built-in balance control | Multi-objective collaborative optimization | Model related | Uncontrolled |
| Computational complexity | Low (50 million cycles per second (MCPS)) | High (300 MCPS) | Medium–high (200 MCPS) | Medium (100 MCPS) | Very low (10 MCPS) |
| Parameter sensitivity | Low | Medium | High | Medium | Extremely high |
| Cost of realization | Low (DSP is sufficient) | High (requires FPGA) | Medium–high (FPGA + coprocessor) | Medium (DSP + FPGA) | Very low (analog circuitry possible) |
| Applicable scenarios | Steady-state operating conditions | High dynamic response requirements | High-reliability systems | Wide-range operation | Low-cost simple system |
| Typical switching frequency | Fixed (10–20 kHz) | Variable (8–25 kHz) | Optimization tuning (12–18 kHz) | Dual frequency switching | Random (5–30 kHz) |
| Temperature equalization | Wrong (ΔT > 25 °C) | Medium (ΔT ≈ 15 °C) | Excellent (ΔT < 10 °C) | Virtuous (ΔT ≈ 12 °C) | Extremely poor (ΔT > 30 °C) |
| Impact of communication delays | Insensitive | Sensitivities | More sensitive | Moderately sensitive | Highly sensitive |
| Latest improvement directions | Virtual vector synpaper | Multi-step prediction optimization | AI vector pre-screening | Intelligent mode switching | Adaptive hysteresis loop |
| Control Method | Core AI Algorithm | Key Performance Metrics | Computational Load | Advantages | Challenges |
|---|---|---|---|---|---|
| Traditional FCS-MPC [12,27] | Mathematical model (e.g., Equation (8)); cost function minimization (e.g., Equation (6)). | THD: 2.5–4% Switching loss: baseline Dynamic response: <50 μs | High (evaluates all vectors) | Intuitive; excellent dynamics | High computational burden; parameter sensitivity |
| DNN-assisted MPC [22,36] | DNN for vector pre-selection; offline-trained to map states to a reduced candidate set. | THD: <2.8% Switching loss: ↓ ~32% Dynamic response: <45 μs | ~40% reduction vs. MPC | Drastically reduces online computation; maintains performance | Offline training data coverage; model generalization |
| RL-guided modulation | RL for online weighting-factor tuning in cost function (e.g., adjusts in Equation (22)). | THD: <2.5% Switching loss: ↓ ~25% Dynamic response: <40 μs | Medium–high (online policy inference) | Adapts to aging and parameter drift; robust performance | Complex training; stability proof required |
| Physics-informed NN (PINN) | Neural network trained with physics-based loss terms (e.g., Kirchhoff’s laws); used for system-state prediction. | Model accuracy: >95% Enables more accurate MPC predictions | High (offline training) Medium (inference) | Improved generalization with limited data; physically plausible outputs | Complex loss function formulation |
| LSTM-based prediction | Long short-term memory (LSTM) network for forecasting load current or grid voltage disturbances. | Prediction horizon: 1–5 ms Enables proactive control | Medium (inference) | Improves disturbance rejection; enhances stability | Requires historical data; sensitive to noise |
| Point | Time | Core Technology | Strengths and Weaknesses/Achievements |
|---|---|---|---|
| First generation [37] | Before 2015 | Hardware redundancy (add spare bridge arm) | Disadvantage: 30% higher cost |
| Second generation | 2015–2020 | Software fault tolerance (modulation policy adjustment) | Typical scenarios result in <2% deterioration in THD after failure |
| Third generation | 2020–present | Predictive fault tolerance (blending digital twins with AI technology) [44] | Latest results: 500 h-earlier failure warning time |
| H Range | Health Level | Control Strategy | Maintenance Recommendations |
|---|---|---|---|
| 0.8–1.0 | - | Full-power operation | Routine inspection |
| 0.6–0.8 | Favorable | Moderate reductions | Enhanced monitoring |
| 0.4–0.6 | Warnings | Power limit 50% | Scheduled maintenance |
| <0.4 | Distress | Immediate shutdown | Emergency replacement |
| Comparison Dimension | Optimization Mode (Sopt) [38] | Derating Mode (Sderate) [46] | Shutdown Mode (Sshutdown) [49] |
|---|---|---|---|
| Trigger condition | H > 0.7 | 0.3 < H ≤ 0.7 | H ≤ 0.3 |
| Power output capacity | 100% rated power | 50–70% of rated power | 0% (switching standby unit) |
| Modulation strategy | Full state-space modulation | Limit switching frequency (20–30% frequency reduction) | Disable fault phase |
| THD change | <3% (baseline) | 1–2% increase | Faulty phase THD > 10% |
| Efficiency impact | No loss | 2–3% reduction in efficiency | Zero system efficiency |
| Cutoff time | Gradual transition (5–10 ms) | Fast switching (1–5 ms) | Emergency action (<100 μs) |
| Thermal management requirements | Normal cooling | Enhanced cooling (+20% airflow) | Forced cooling (100% fan) |
| Device stress | Even distribution | Redistribution to health devices | Complete uninstallation |
| Communications needs | Routine condition monitoring | Real-time health degree transmission | Fault alarm broadcast |
| Reliability indicators | Mean time between failure (MTBF) > 100,000 h | MTBF ≈ 50,000 h | Reliance on redundant systems |
| Typical application scenarios | Uptime | Mild aging | Catastrophic failure |
| Control complexity | Low (standardized algorithms) | Medium (downsizing strategy required) | High (fast protection) |
| Hardware cost impact | none | Reserve capacity | Redundant design required |
| Latest improvement directions | Artificial intelligence optimization | Predictive downscaling | Self-healing reconfiguration |
| Maintenance intervention requirements | Routine inspection | Planned maintenance | Immediate repairs |
| Sensor configuration [50] | Basic temperature/current | Enhanced temperature monitoring | High-speed fault detection |
| Control chip requirements | Conventional DSP | DSP + FPGA | Specialized protection chip |
| Typical fault coverage | Malfunction | Moderate aging failure | Severe short-circuit fault |
| Comparison Dimension | Hardware Redundancy Program | Modulation Adjustment Program | Topology Reconfiguration Scheme | AI Predictive Fault Tolerance Program |
|---|---|---|---|---|
| Rationale | Add spare bridge arm [35] | Adjustment of PWM modulation strategy [42] | Reconfiguration of current paths [54] | Machine learning predicts failures and intervenes early [48,50,55] |
| Response time | <100 μs | 1–10 ms | 100–500 μs | Pre-emptive (1–10 s in advance) |
| Cost increase | +25% | +5% | +15% | +30% |
| Power derating | 0% | 20% | 10% | <5% |
| Deterioration of THD | 0% | +1.5% | +0.8% | +0.3% |
| Reliability improvement | 40% increase in MTBF [35] | 15% increase in MTBF [42] | 25% increase in MTBF [54] | 60% increase in MTBF [56] |
| Applicable fault types | Arbitrary device failure | Single-tube open/driver failure [42] | Multi-tube failure | Compound potential failure |
| Maintenance complexity | High (requires periodic switching of standby units) | Low | Medium | Very high (requires data training) |
| Computing resource requirements | Low (DSP is sufficient) | Medium (DSP + FPGA) | Medium (FPGA) | High (GPU acceleration) |
| Temperature effect | Ageing of spare units | Uneven heat distribution | Localized hotspot risk | Optimal thermal management |
| Typical application scenarios | Military/aerospace power supplies | Commercial and industrial energy storage | Electric vehicle drives | Smart grid |
| Latest technological improvements | Intelligent rotation strategy | Adaptive derating algorithm [5] | 3D package redundancy design | Digital twins + deep learning [57] |
| Diagnosis Method | Core Measured Parameters | Key Parameters/Indicators | Detection Time | Accuracy | Implementation Complexity | Typical Scenario |
|---|---|---|---|---|---|---|
| Residual-based current analysis [46,47] | ) | ) | 1–5 ms | >95% | Medium (DSP) | General industrial drives, UPS |
| Observer-based voltage estimation [49,54] | Switching node voltage , DC-link voltage ) | Voltage residual , observer gain ), estimation error | 100–500 μs | >98% | High (FPGA) | High-speed traction, EV drives |
| Thermal network and Health Index [42,48] | ) | ) | Seconds to minutes | >90% (trending) | Medium–high (DSP + model) | Predictive maintenance, long-term reliability |
| AI-driven multi-sensor fusion [20,51,57] | ) | ), confidence score | <100 μs (inference) | >99% | Very high (GPU/accelerator) | Smart grids, Mission-critical systems |
| Time | Research Dimension | Key Results |
|---|---|---|
| 2010–2016 | Electro-thermal coupling | A junction temperature estimation error of <3 °C is realized, which lays the foundation for the subsequent study of more complex multi-physics fields, and the ability to control the temperature characteristics of the device is improved by establishing the correlation model between electricity and heat [17]. |
| 2016–2020 | Electro-thermal–force coupling | On the basis of electric–thermal coupling research, further incorporating the force factor constructed a more comprehensive coupling model, so that the mechanical stress was reduced by 25%, effectively improving the reliability of the device due to excessive stress [21]. |
| 2020–present | Holo-physical field digital twin | Integration of electric, thermal, force, and other multi-physical field elements; construction of a full physical field digital twin model; virtual prototype accuracy > 95%; able to more accurately simulate the actual system operating state, providing a strong support for system optimization and failure prediction [60,61,62]. |
| Optimization Methods | Core Idea | Applicable Scenarios | Computational Efficiency | Accuracy |
|---|---|---|---|---|
| Parameter scanning method [69] | Full factorial experimental design | Simple system/initial design | Low | Medium |
| Gradient optimization | Iterative search based on sensitivity analysis | Continuous variable problem | High | High |
| Genetic algorithm (GA) [67] | Global search for simulating biological evolution | Multi-peak/discrete optimization | Medium | Medium to high |
| Agent model optimization | Approximate modeling as an alternative to simulation | High-dimensional complex systems [73] | Extremely high | Dependency model |
| Deep learning optimization [68] | Neural networks build response surfaces | Ultra-multiparameter nonlinear systems | Very high (after training) | High |
| Co-simulation optimization [66] | Multi-software real-time data exchange | Strongly coupled-field problem | Low | Very high |
| Scenario | Load Level | fsw (kHz) | Temp (°C) | Conduction Loss (W) | Switching Loss (W) | Total Loss (W) | Efficiency (%) |
|---|---|---|---|---|---|---|---|
| 1 | 50% | 5 | 25 | 520 | 180 | 700 | 99.0 |
| 2 | 100% | 5 | 25 | 1050 | 350 | 1400 | 98.6 |
| 3 | 100% | 2.5 | 25 | 1050 | 210 | 1260 | 98.9 |
| 4 | 100% | 10 | 25 | 1050 | 580 | 1630 | 97.9 |
| 5 | 100% | 5 | 80 | 1180 | 380 | 1560 | 98.0 |
| 6 | 75% | 5 | 40 | 800 | 260 | 1060 | 99.1 |
| Aspect | Influencing Factors | Key Observations | Practical Implications |
|---|---|---|---|
| Stability | Load level, switching frequency, parasitic | Stable midpoint at partial load; high dv/dt and parasitic oscillations at high switching frequency | Requires optimized modulation and laminated busbar design |
| Reliability | Thermal stress, current imbalance, fault tolerance | Predictive redundancy and thermal balancing reduce device overstress; MTBF can be improved by >50% | Fault-tolerant control and AI-assisted balancing enhance reliability |
| Longevity | Junction temperature fluctuation (ΔT), ambient temperature | Keeping ΔT < 20 °C slows aging; lifetime extension of 20–30% demonstrated in prototypes | Electro-thermal co-optimization and digital twin predictive maintenance prolong service life |
| Relationship | Core Role | Key Logic |
|---|---|---|
| Modulation ↔ Redundant control [2] | Dynamic strategies (e.g., FCS-MPC, hysteresis) require strong redundancy (AI, hardware); steady-state SVPWM only needs basic schemes | Control complexity directly drives redundancy requirements |
| Modulation ↔ Multi-field optimization [3] | Modulation determines electrical loss, thermal distribution, and computational load [67] | Strategy choice sets optimization focus (low loss vs. thermal balancing) |
| Redundant control ↔ Modulation [9] | Redundancy requires seamless state switching and stable electro-thermal data from modulation | Fault-tolerant schemes constrain modulation design |
| Redundant control ↔ Multi-field optimization [16] | Hardware aging and reconfiguration create structural/thermal constraints; AI prediction adds computational–thermal demands | Redundancy adds extra optimization boundaries |
| Multi-field optimization ↔ Modulation [60] | High-T environments favor low-loss MPC; strongly coupled systems need hybrid/adaptive modulation | Boundary conditions narrow strategy selection |
| Multi-field optimization ↔ Redundant control [74] | Compute limits may exclude AI-based fault tolerance, leaving simpler redundancy; packaging constrains topology reconfiguration | Optimization feasibility defines redundancy options |
| Challenge | Expression | Impact | Bottleneck |
|---|---|---|---|
| Electromagnetic compatibility at high frequency | High dv/dt and di/dt, parasitism trigger oscillations, electromagnetic interference (EMI) increases [58] | Disturbs peripheral devices, lowers control accuracy, requires bulky EMI filters | Empirical filter design, no systematic EMI optimization models |
| Multi-physics coupling accuracy | Strong nonlinear interaction of electrical, thermal, and structural fields; models oversimplified | Prediction errors (>5 °C) distort reliability and efficiency evaluation [67] | Difficult to quantify dynamic parameters; multi-scale models too costly for real-time use |
| Wide-temperature range reliability [66] | Large temp. swings (−40 to 85 °C) accelerate aging, solder fatigue, and device stress [75] | Higher failure risk, shorter lifetime, frequent derating reduces efficiency | Thermal designs cannot handle wide ranges; lack of life-cycle temperature–reliability mapping |
| Direction | Core Objective | Technology Path | Expected Benefits |
|---|---|---|---|
| AI-driven intelligent modulation [59] | Overcome adaptability limits of traditional modulation under high-frequency/complex conditions | Deep learning-based EMI–loss mapping; RL-based PWM optimization; load prediction with neural nets | EMI decline > 30%; efficiency rise 1.5–2%; lightweight filter design |
| Digital twin-assisted predictive maintenance [60] | Improve accuracy of multi-physics modeling for health prediction and lifetime management | Build electro-thermal–structural digital twins; integrate vibration/temp. sensing; train aging prediction models | Modeling error < 2 °C; fault warning accuracy > 90%; device life rise 20–30%; MTBF rise 50% |
| Wide-bandwidth device integration [67] | Break Si-device limits in high-frequency and wide-temperature scenarios | Develop ANPC with SiC/GaN; optimize driver and packaging [75]; adaptive thermal solutions (−50 to 125 °C) | Switching freq. > 50 kHz; power density rise 40–60%; conduction loss decline 40%; reliability rise 50% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Cao, S.; Yi, B.; Zhu, L.; Luo, P.; Xu, W.; Chen, G.; Li, D. A Review of Key Technologies for Active Midpoint Clamping (ANPC) Topology in Energy Storage Converters: Modulation Strategies, Redundant Control, and Multi-Physics Field Co-Optimization. Energies 2025, 18, 6169. https://doi.org/10.3390/en18236169
Huang H, Cao S, Yi B, Zhu L, Luo P, Xu W, Chen G, Li D. A Review of Key Technologies for Active Midpoint Clamping (ANPC) Topology in Energy Storage Converters: Modulation Strategies, Redundant Control, and Multi-Physics Field Co-Optimization. Energies. 2025; 18(23):6169. https://doi.org/10.3390/en18236169
Chicago/Turabian StyleHuang, Hui, Shuai Cao, Bin Yi, Lianghe Zhu, Pandian Luo, Wei Xu, Gouyi Chen, and Dake Li. 2025. "A Review of Key Technologies for Active Midpoint Clamping (ANPC) Topology in Energy Storage Converters: Modulation Strategies, Redundant Control, and Multi-Physics Field Co-Optimization" Energies 18, no. 23: 6169. https://doi.org/10.3390/en18236169
APA StyleHuang, H., Cao, S., Yi, B., Zhu, L., Luo, P., Xu, W., Chen, G., & Li, D. (2025). A Review of Key Technologies for Active Midpoint Clamping (ANPC) Topology in Energy Storage Converters: Modulation Strategies, Redundant Control, and Multi-Physics Field Co-Optimization. Energies, 18(23), 6169. https://doi.org/10.3390/en18236169






