Prediction of Fluid Pressure Dynamics in Deflagration Fracturing for Unconventional Reservoir Stimulation Based on Physics-Guided Graph Neural Network
Abstract
1. Introduction
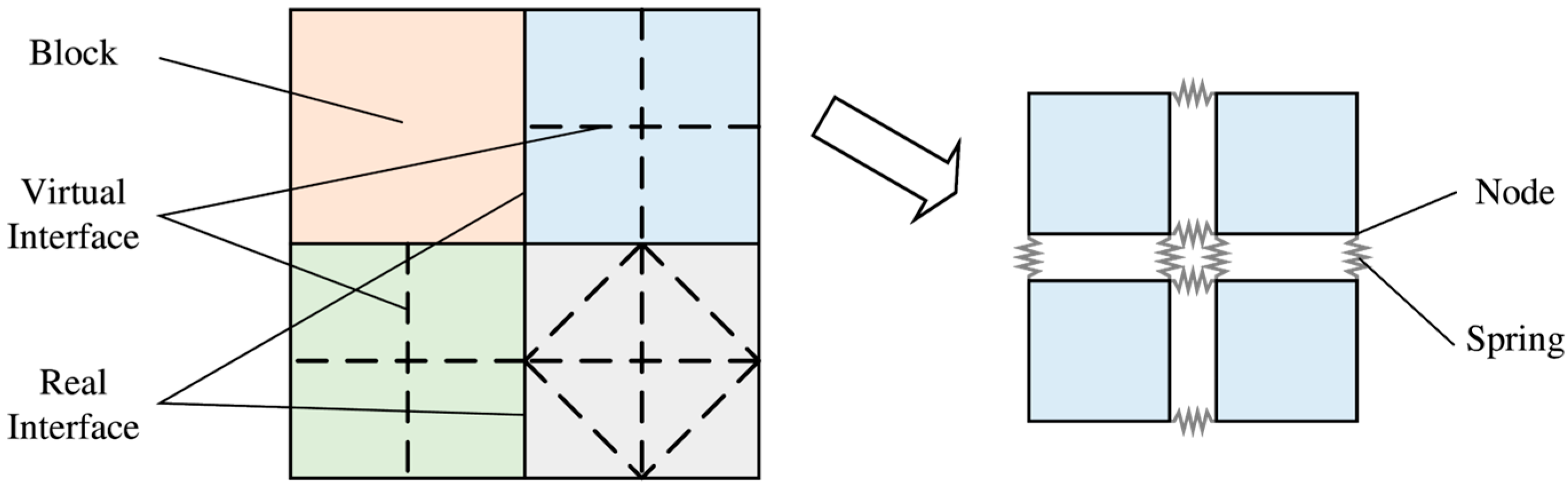
2. CDEM Based Numerical Model
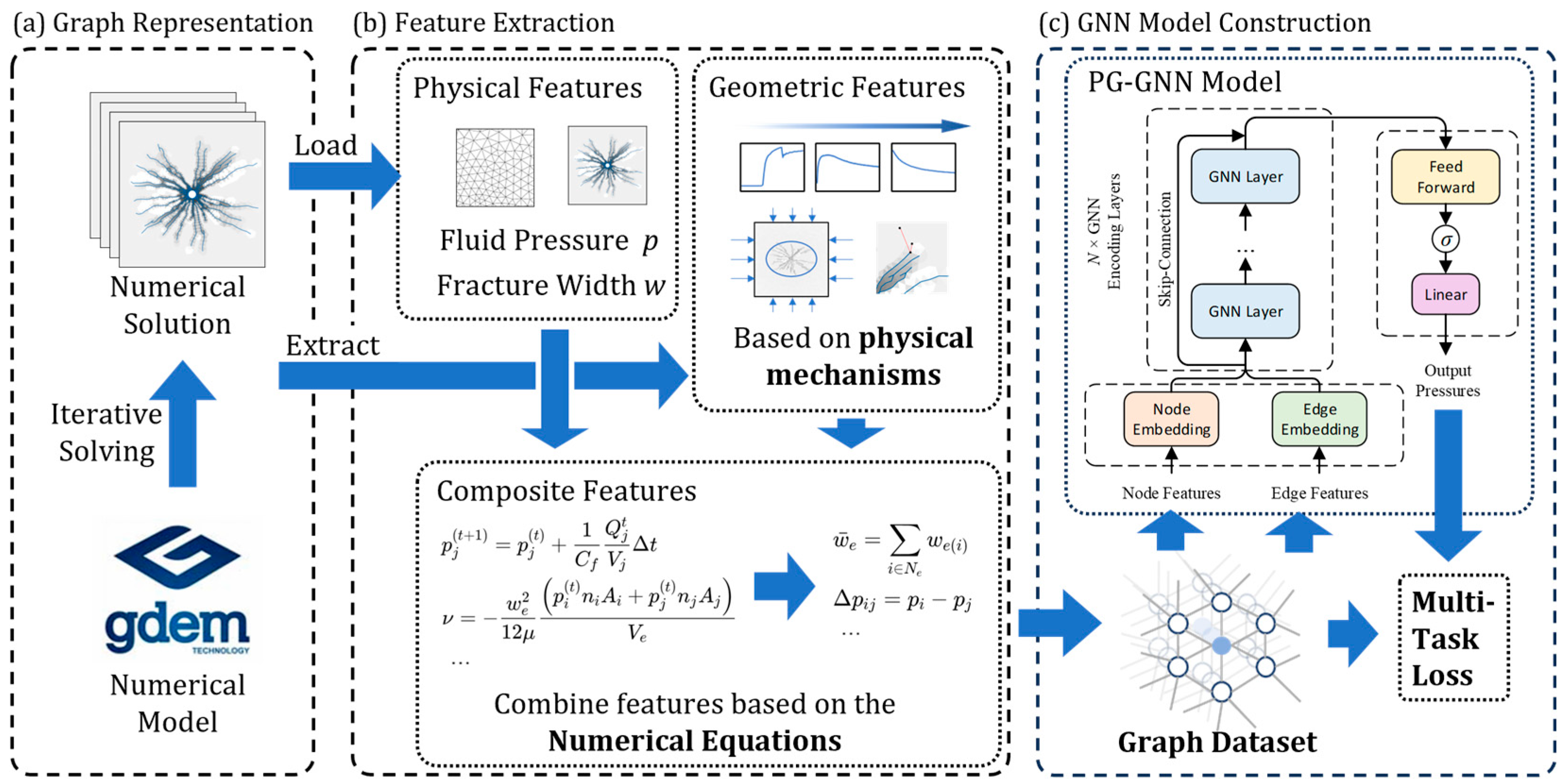
3. The Proposed Method
3.1. Graph-Based Representation
3.2. Physics-Guided Feature Construction
3.2.1. Physical Features
- (1)
- Fluid pressure at the previous time step,
- (2)
- Equivalent fracture width,
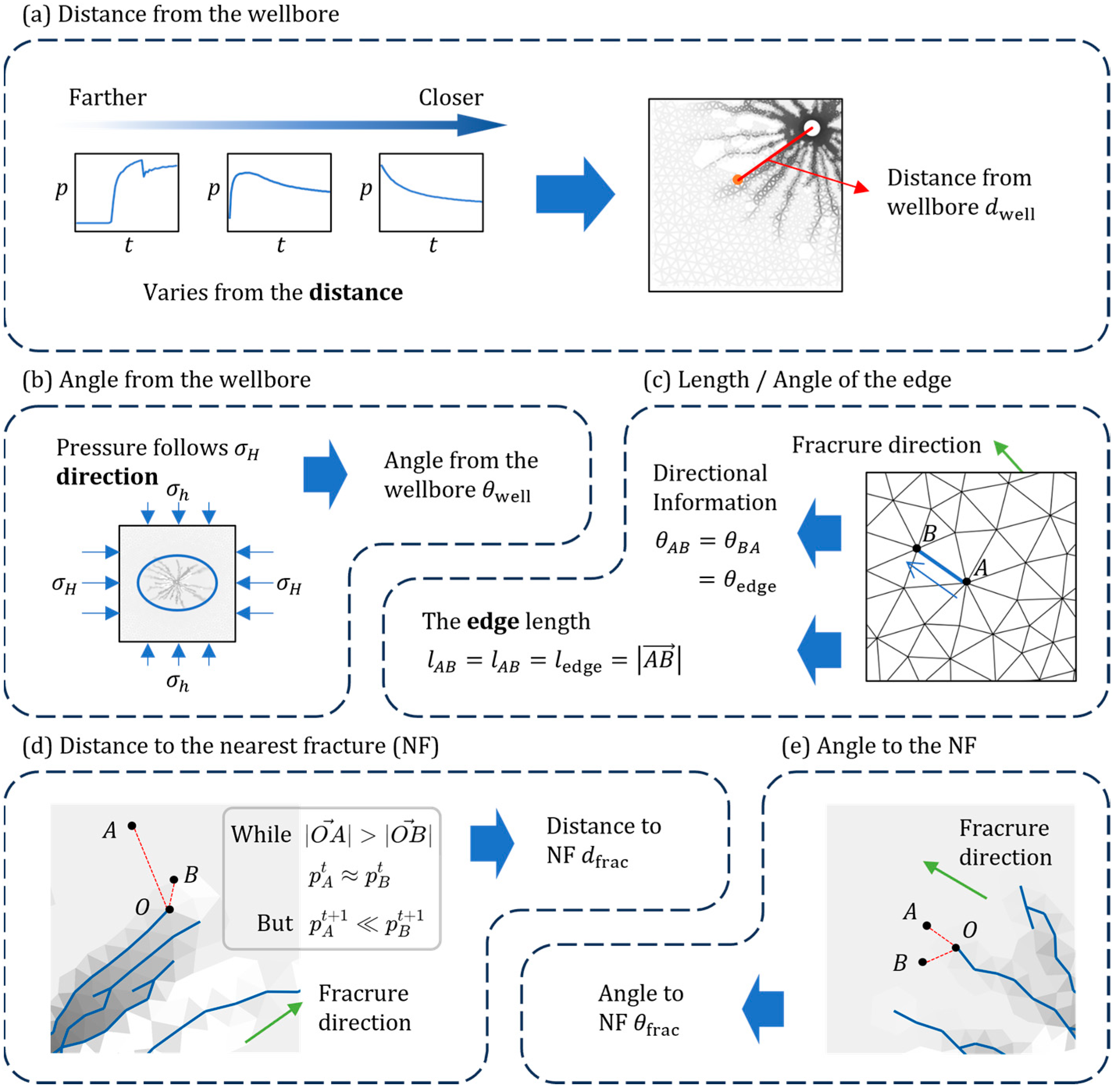
3.2.2. Geometric Features
- (1)
- Distance from the Wellbore,
- (2)
- Angle between the line connecting the node and the wellbore center and the direction of maximum horizontal stress , denoted
- (3)
- Edge length and orientation
- (4)
- Minimum distance between a node and the nearest fracture path,
- (5)
- Relative angle between a node and the adjacent fracture path,
3.2.3. Physics-Guided Composite Features
- (1)
- Fluid pressure difference on edge,
- (2)
- Coupled pressure-width term,
- (3)
- Projected pressure difference along fracture direction,
- (4)
- Average fracture width in node neighborhood,
3.3. PG-GNN Architecture
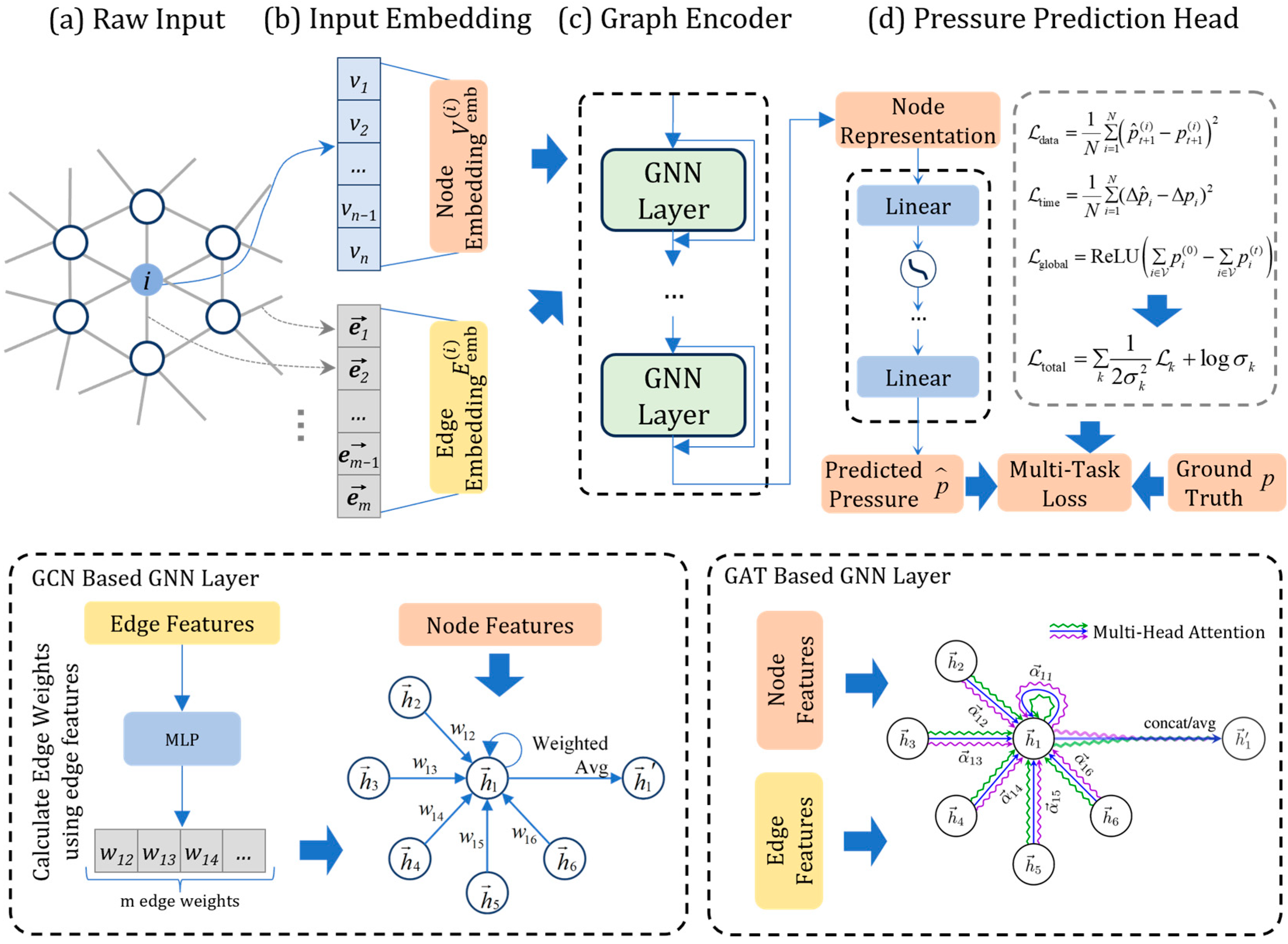
3.3.1. Input Embedding
3.3.2. Graph Encoder
- (1)
- Overall Structure
- (2)
- Multi-Layer GNN
- (3)
- GNN Layer Based on Modified GCN
- (4)
- GNN Layer Based on GAT
- (5)
- Skip Connections
3.3.3. Pressure Prediction Head
3.4. Optimization Objectives
- (1)
- Data Loss
- (2)
- Temporal Difference Constraint
- (3)
- Global Pressure Constraint
- (4)
- Uncertainty-Weighted Loss Integration
4. Experiments and Results
4.1. Dataset and Data Preparation
- (1)
- The node set consists of all nodes in the triangular mesh, where each node represents a spatial location in the reservoir domain.
- (2)
- The edge set is constructed based on the connectivity of the triangular mesh, where each edge connects two adjacent nodes in the mesh.
- (3)
- Both nodes and edges carry the physical field information specifies to the timestep , including the features described in Section 3.2, such as fluid pressure, equivalent fracture width, and geometric features.
4.2. Experiment Settings
4.2.1. Evaluation Metrics
4.2.2. Baselines
- (1)
- MLP: A fully connected multilayer perceptron model that only takes node features as input. Due to its lack of graph structure modeling and physical constraints, the MLP is trained solely using the data loss term.
- (2)
- Pure GCN: A Graph Convolutional Network model consisting only of graph encoding layers, which uses both node and edge features as input. The GCN is trained with the full loss function, including the data loss, temporal difference constraint, and global pressure constraint. This model serves as a baseline to assess the effectiveness of the physics-guided components.
4.3. Results
4.3.1. Overall Performance
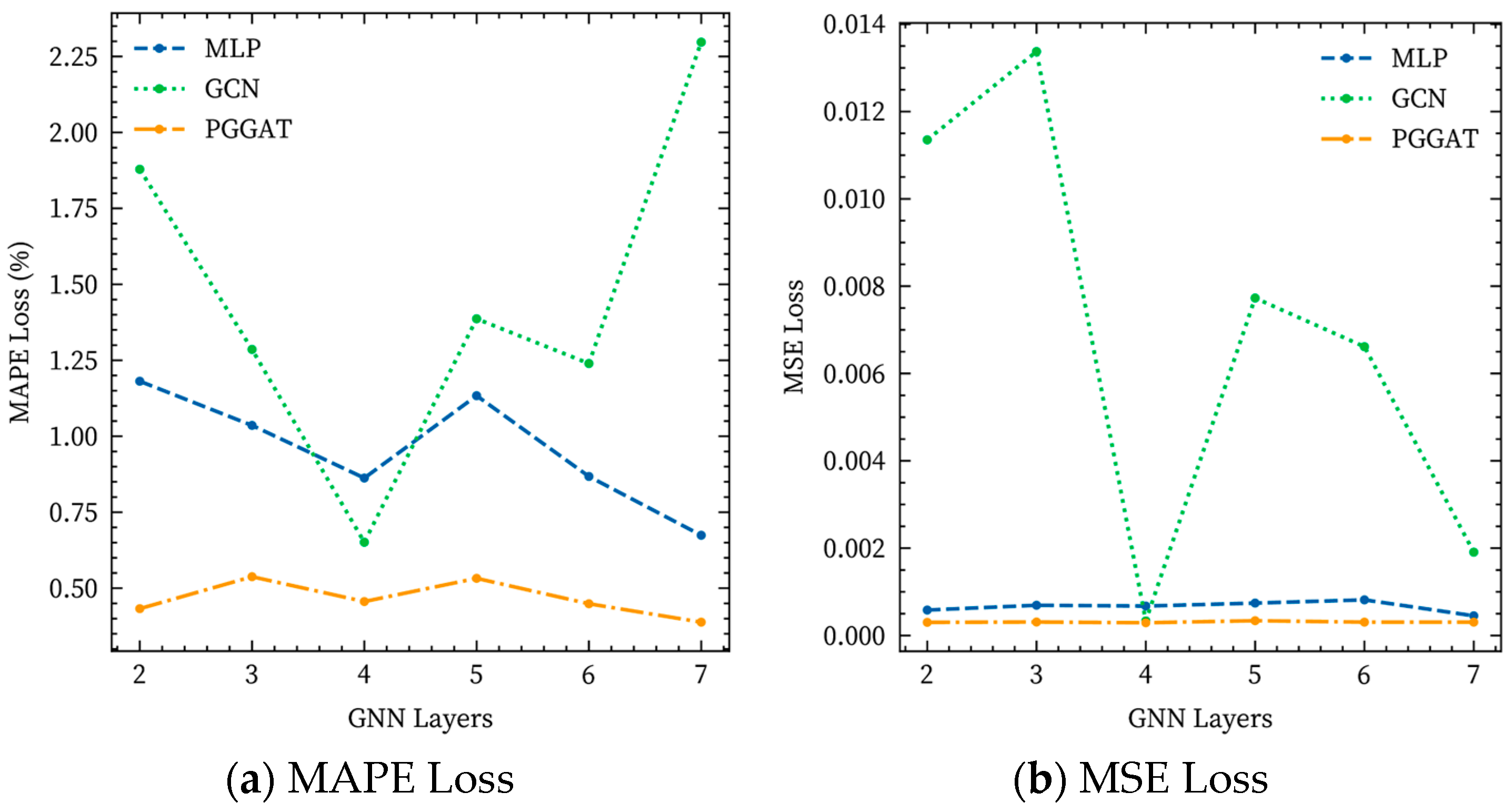
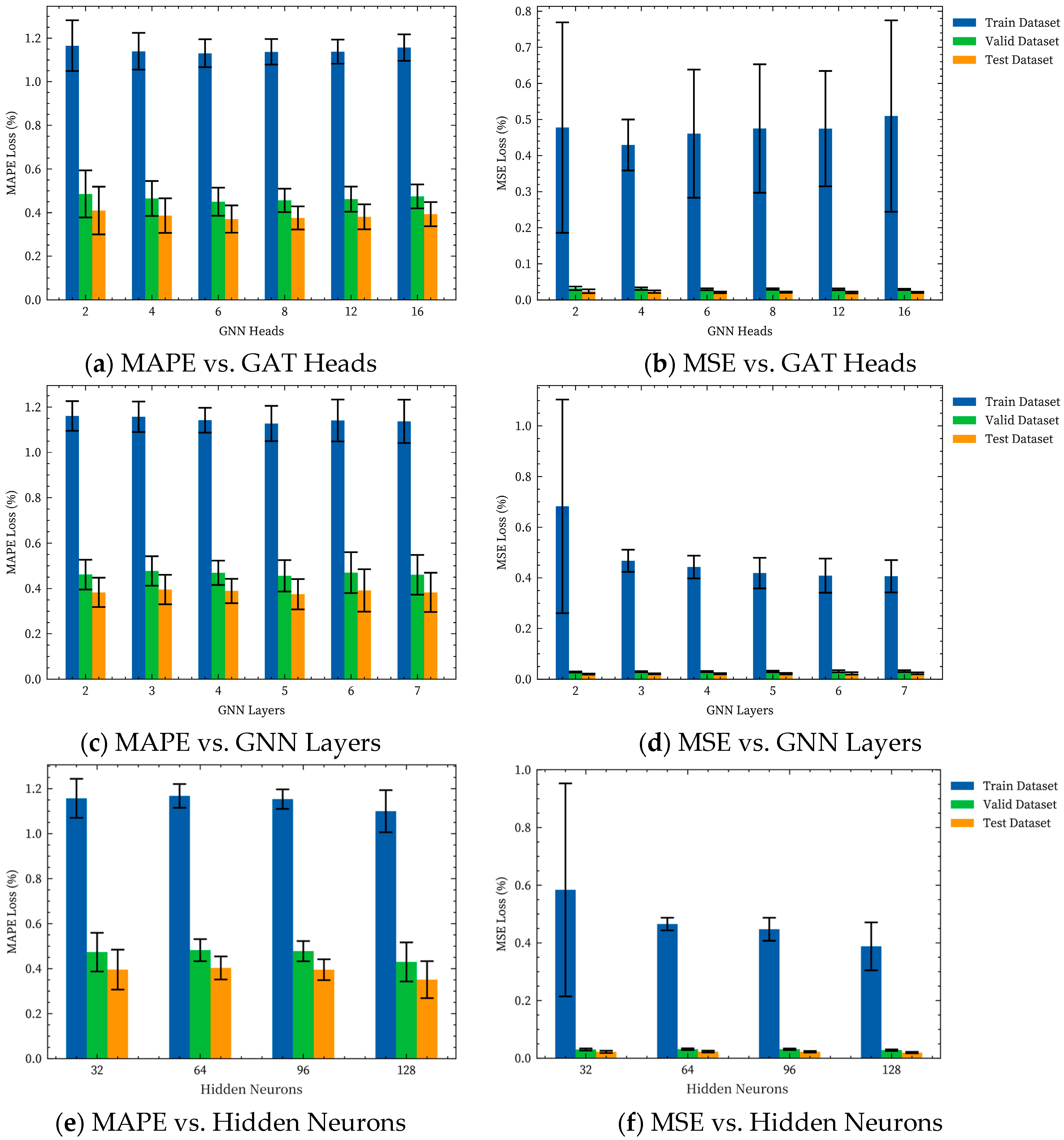
4.3.2. Hyperparameter Analysis
4.3.3. Efficiency Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CDEM | Continuum-Based Discrete Element Method |
| FEM | Finite Element Method |
| DEM | Discrete Element Method |
| PDE | Partial Differential Equation |
| CNN | Convolutional Neural Network |
| RBF | Radial Basis Function |
| Bi-LSTM | Bidirectional Long Short-Term Memory |
| FNO | Fourier Neural Operator |
| Adam | Adaptive Moment Estimation |
| MAPE | Mean Absolute Percentage Error |
| MSE | Mean Squared Error |
| ReLU | Rectified Linear Unit |
| CBM | Coalbed Methane |
Appendix A
Appendix A.1
| GNN Layer Size | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| Training Data Set | ||||||
| Mean (%) | 1.161 | 1.157 | 1.142 | 1.128 | 1.141 | 1.137 |
| Std | 0.066 | 0.067 | 0.055 | 0.077 | 0.092 | 0.095 |
| Validation Data Set | ||||||
| Mean (%) | 0.461 | 0.477 | 0.469 | 0.456 | 0.470 | 0.460 |
| Std | 0.066 | 0.065 | 0.054 | 0.069 | 0.090 | 0.088 |
| Test Data Set | ||||||
| Mean (%) | 0.383 | 0.396 | 0.389 | 0.375 | 0.392 | 0.383 |
| Std | 0.065 | 0.065 | 0.054 | 0.067 | 0.093 | 0.086 |
| GNN Layer Size | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| Training Data Set | ||||||
| ) | 68.253 | 46.742 | 44.291 | 41.881 | 40.864 | 40.641 |
| ) | 42.175 | 4.369 | 4.485 | 6.043 | 6.751 | 6.377 |
| Validation Data Set | ||||||
| ) | 2.831 | 2.955 | 2.997 | 3.054 | 3.123 | 3.173 |
| ) | 0.216 | 0.204 | 0.231 | 0.346 | 0.435 | 0.375 |
| Test Data Set | ||||||
| ) | 2.033 | 2.126 | 2.152 | 2.186 | 2.284 | 2.319 |
| ) | 0.233 | 0.217 | 0.241 | 0.331 | 0.480 | 0.381 |
| GNN Head Size | 2 | 4 | 6 | 8 | 12 | 16 |
|---|---|---|---|---|---|---|
| Training Data Set | ||||||
| Mean (%) | 1.165 | 1.140 | 1.131 | 1.137 | 1.138 | 1.157 |
| Std | 0.117 | 0.085 | 0.065 | 0.059 | 0.055 | 0.061 |
| Validation Data Set | ||||||
| Mean (%) | 0.486 | 0.465 | 0.450 | 0.456 | 0.462 | 0.474 |
| Std | 0.108 | 0.080 | 0.065 | 0.054 | 0.058 | 0.055 |
| Test Data Set | ||||||
| Mean (%) | 0.410 | 0.387 | 0.371 | 0.376 | 0.381 | 0.393 |
| Std | 0.109 | 0.079 | 0.062 | 0.053 | 0.057 | 0.055 |
| GNN Head Size | 2 | 4 | 6 | 8 | 12 | 16 |
|---|---|---|---|---|---|---|
| Training Data Set | ||||||
| ) | 47.758 | 42.931 | 46.073 | 47.492 | 47.761 | 50.936 |
| ) | 29.171 | 7.076 | 17.757 | 17.821 | 15.977 | 26.528 |
| Validation Data Set | ||||||
| ) | 3.205 | 3.125 | 2.933 | 3.024 | 2.933 | 2.915 |
| ) | 0.506 | 0.354 | 0.273 | 0.194 | 0.255 | 0.188 |
| Test Data Set | ||||||
| ) | 2.411 | 2.279 | 2.083 | 2.170 | 2.074 | 2.079 |
| ) | 0.541 | 0.349 | 0.239 | 0.188 | 0.250 | 0.189 |
| Hidden Neurons Size | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| Training Data Set | ||||
| Mean (%) | 1.157 | 1.168 | 1.154 | 1.100 |
| Std | 0.087 | 0.053 | 0.043 | 0.094 |
| Validation Data Set | ||||
| Mean (%) | 0.473 | 0.482 | 0.478 | 0.430 |
| Std | 0.086 | 0.049 | 0.045 | 0.087 |
| Test Data Set | ||||
| Mean (%) | 0.396 | 0.403 | 0.395 | 0.351 |
| Std | 0.089 | 0.051 | 0.046 | 0.082 |
| Hidden Neurons Size | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| Training Data Set | ||||
| ) | 58.382 | 46.534 | 44.732 | 38.796 |
| ) | 36.931 | 2.197 | 3.997 | 8.307 |
| Validation Data Set | ||||
| ) | 3.040 | 3.127 | 3.116 | 2.807 |
| ) | 0.360 | 0.304 | 0.275 | 0.272 |
| Test Data Set | ||||
| ) | 2.207 | 2.313 | 2.244 | 1.969 |
| ) | 0.388 | 0.317 | 0.280 | 0.253 |
References
- Wang, J.; Guo, T.; Chen, M.; Qu, Z.; Liu, X.; Wang, X. Numerical Simulation of Deflagration Fracturing in Shale Gas Reservoirs Considering the Effect of Stress Wave Impact and Gas Drive. Int. J. Rock Mech. Min. Sci. 2023, 170, 105478. [Google Scholar] [CrossRef]
- Wang, E.; Zhu, H. Constitutive and FEM-DFN Model of Complex Fractures in Shale Explosive Fracturing. In Proceedings of the 6th Complex Oil and Gas Engineering Technology Innovation Forum, Chengdu, China, 23–25 May 2024. [Google Scholar] [CrossRef]
- Qi, E.; Xiong, F.; Zhang, Y.; Wang, L.; Xue, Y.; Fu, Y. Gas Fracturing Simulation of Shale-Gas Reservoirs Considering Damage Effects and Fluid–Solid Coupling. Water 2024, 16, 1278. [Google Scholar] [CrossRef]
- Meng, H.; Ge, H.; Yao, Y.; Shen, Y.; Wang, J.; Bai, J.; Zhang, Z. A New Insight into Casing Shear Failure Induced by Natural Fracture and Artificial Fracture Slip. Eng. Fail. Anal. 2022, 137, 106287. [Google Scholar] [CrossRef]
- Ismail, A.; Azadbakht, S. Experimental and Numerical Methods for Hydraulic Fracturing at Laboratory Scale: A Review. Geosciences 2025, 15, 142. [Google Scholar] [CrossRef]
- Page, J.C.; Miskimins, J.L. A Comparison of Hydraulic and Propellant Fracture Propagation in a Shale Gas Reservoir. J. Can. Pet. Technol. 2009, 48, 26–30. [Google Scholar] [CrossRef]
- Wang, J.; Elsworth, D.; Cao, Y.; Liu, S. Reach and Geometry of Dynamic Gas-Driven Fractures. Int. J. Rock Mech. Min. Sci. 2020, 129, 104287. [Google Scholar] [CrossRef]
- Wu, F.; Pu, C.; Chen, D.; Xie, X. Test Study of Oil Well Breakdown Pressure under Blasting Loading. Chin. J. Rock Mech. Eng. 2009, 28, 3430–3434. [Google Scholar]
- Jiang, K.; Deng, S.; Li, H. Experimental Study on Methane Deflagration Fracturing Technology. J. China Coal Soc. 2023, 48, 4297–4307. [Google Scholar] [CrossRef]
- Wang, X. Numerical Simulation of Fracture Propagation in Deflagration Fracturing of Shale Reservior; China University of Petroleum (East China): Qingdao, China, 2023. [Google Scholar]
- Sanchez-Gonzalez, A.; Godwin, J.; Pfaff, T.; Ying, R.; Leskovec, J.; Battaglia, P.W. Learning to Simulate Complex Physics with Graph Networks. In Proceedings of the 37th International Conference on Machine Learning, Online, 12–18 July 2020. [Google Scholar]
- Yang, S.; He, X.; Zhu, B. Learning Physical Constraints with Neural Projections. Adv. Neural Inf. Process. Syst. 2020, 33, 5178–5189. [Google Scholar]
- Horie, M.; Mitsume, N. Physics-Embedded Neural Networks: Graph Neural PDE Solvers with Mixed Boundary Conditions. In Proceedings of the 36th International Conference on Neural Information Processing System, New Orleans, LA, USA, 28 November–9 December 2022; Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., Oh, A., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2022; Volume 35, pp. 23218–23229. [Google Scholar]
- Rubanova, Y.; Sanchez-Gonzalez, A.; Pfaff, T.; Battaglia, P. Constraint-Based Graph Network Simulator. arXiv 2021, arXiv:2112.09161. [Google Scholar]
- Zhang, W.; Bao, Z.; Jiang, S.; He, J. An Artificial Neural Network-Based Algorithm for Evaluation of Fatigue Crack Propagation Considering Nonlinear Damage Accumulation. Materials 2016, 9, 483. [Google Scholar] [CrossRef]
- Miller, R.L.; Moore, B.; Viswanathan, H.; Srinivasan, G. Image Analysis Using Convolutional Neural Networks for Modeling 2D Fracture Propagation. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017; pp. 979–982. [Google Scholar] [CrossRef]
- Moore, B.A.; Rougier, E.; O’Malley, D.; Srinivasan, G.; Hunter, A.; Viswanathan, H. Predictive Modeling of Dynamic Fracture Growth in Brittle Materials with Machine Learning. Comput. Mater. Sci. 2018, 148, 46–53. [Google Scholar] [CrossRef]
- Wang, Y.; Oyen, D.; Guo, W.; Mehta, A.; Scott, C.B.; Panda, N.; Fernández-Godino, M.G.; Srinivasan, G.; Yue, X. StressNet—Deep Learning to Predict Stress with Fracture Propagation in Brittle Materials. npj Mater. Degrad. 2021, 5, 6. [Google Scholar] [CrossRef]
- Zhou, X.P.; Feng, K. MPNN Based Graph Networks as Learnable Physics Engines for Deformation and Crack Propagation in Solid Mechanics. Int. J. Solids Struct. 2024, 291, 112695. [Google Scholar] [CrossRef]
- Alhemdi, A.; Gu, M. Optimizing Unconventional Hydraulic Fracturing Design Using Machine Learning and Artificial Intelligent. In Proceedings of the SPE Western Regional Meeting; SPE: Bakersfield, CA, USA, 2022. [Google Scholar] [CrossRef]
- Yang, X.; Guo, T.; Yu, M.; Chen, M. Optimization of Engineering Parameters of Deflagration Fracturing in Shale Reservoirs Based on Hybrid Proxy Model. Geoenergy Sci. Eng. 2023, 231, 212318. [Google Scholar] [CrossRef]
- Kuang, T.; Liu, J.; Yin, Z.; Jing, H.; Lan, Y.; Lan, Z.; Pan, H. Fast and Robust Prediction of Multiphase Flow in Complex Fractured Reservoir Using a Fourier Neural Operator. Energies 2023, 16, 3765. [Google Scholar] [CrossRef]
- Yuan, B.; Zhao, M.; Dai, C.; Zhang, W.; Wu, S.; Fan, T. A Data-Driven Dynamic Intelligent Characterization Method for Fracture Propagation in Horizontal Well Fracturing. Drill. Prod. Technol. 2025, 48, 138–146. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Fu, Z.; Xu, W.; Liu, S. Physics-Informed Kernel Function Neural Networks for Solving Partial Differential Equations. Neural Netw. 2024, 172, 106098. [Google Scholar] [CrossRef]
- Li, S.; Zhao, M.; Wang, Y.; Rao, Y. A New Numerical Method for Dem –Block and Particle Model. Int. J. Rock Mech. Min. Sci. 2004, 41, 414–418. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, M.; Li, S.; Wang, J.G. Stochastic Structural Model of Rock and Soil Aggregates by Continuum-Based Discrete Element Method. Sci. China Technol. Sci. 2005, 48, 95–106. [Google Scholar] [CrossRef]
- Ma, Z.S.; Feng, C.; Liu, T.P.; Li, S.H. A GPU Accelerated Continuous-Based Discrete Element Method for Elastodynamics Analysis. Adv. Mater. Res. 2011, 320, 329–334. [Google Scholar] [CrossRef]
- Feng, C.; Li, S.; Zhou, D.; Zhang, Q. Numerical Analysis of Damage and Crack Process of Rock under Explosive Loading. Chin. J. Geotech. Eng. 2014, 36, 1262–1270. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Xu, K.; Li, C.; Tian, Y.; Sonobe, T.; Kawarabayashi, K.; Jegelka, S. Representation Learning on Graphs with Jumping Knowledge Networks. In Proceedings of the 35th International Conference on Machine, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; van den Berg, R.; Titov, I.; Welling, M. Modeling Relational Data with Graph Convolutional Networks. In European Semantic Web Conference; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. Stat 2017, 1050, 10-48550. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. ACM Trans. Graph. (Tog) 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Kendall, A.; Gal, Y.; Cipolla, R. Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
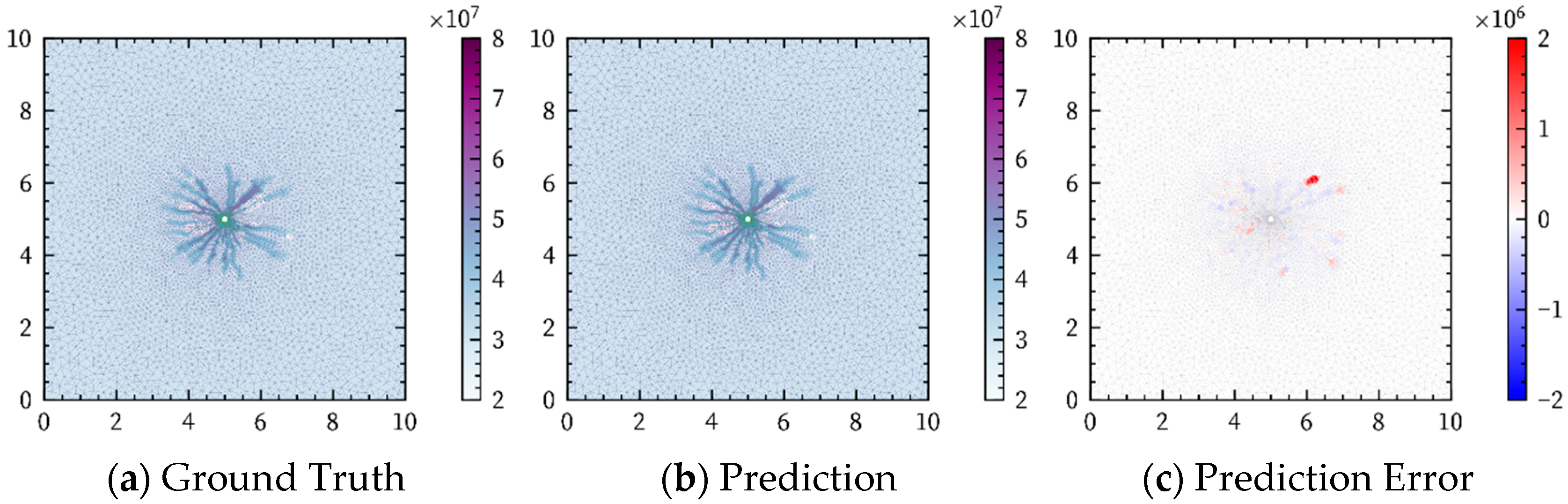
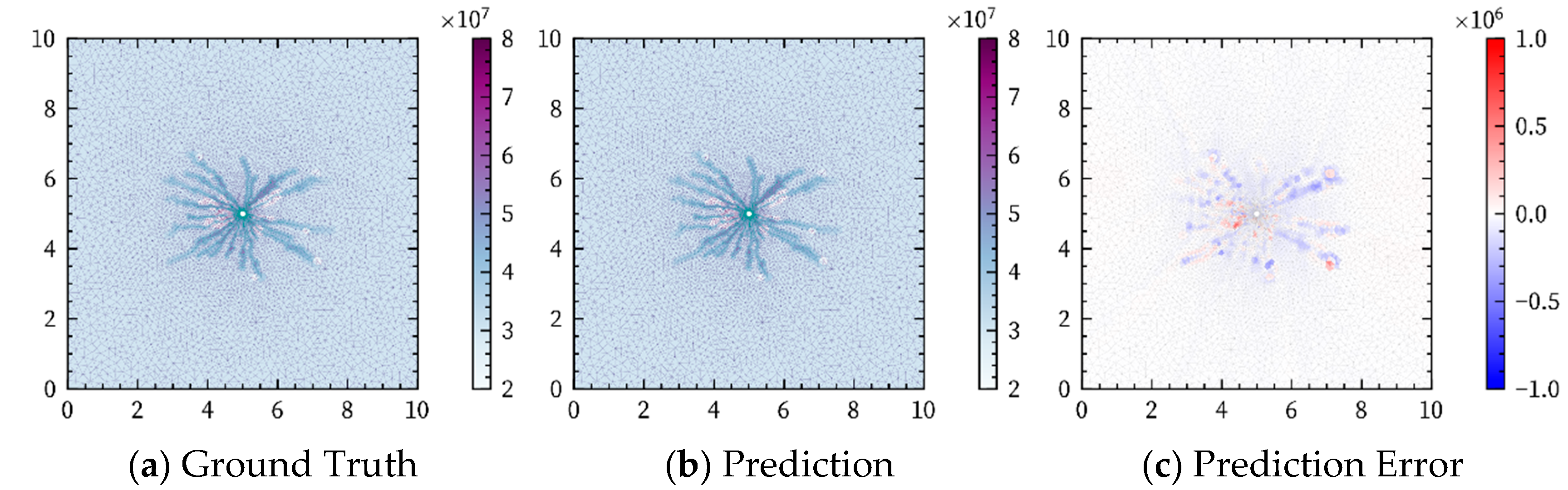
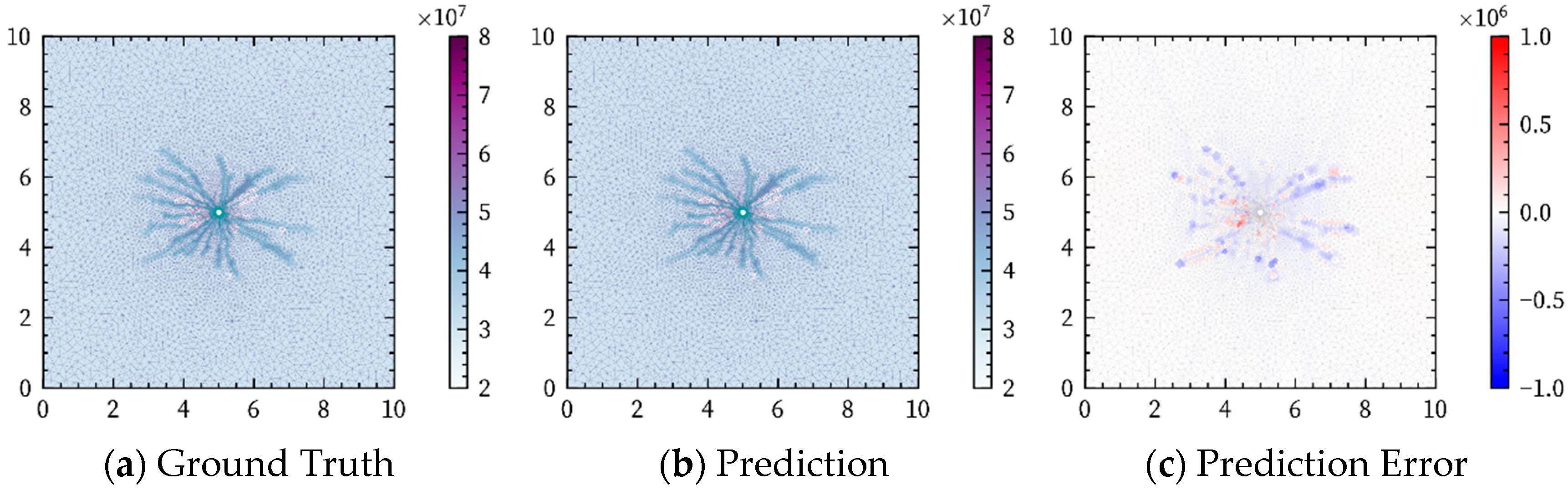
| Feature Type | Description | Symbol |
|---|---|---|
| Node-Level | Fluid pressure at the previous time step | |
| Distance from the wellbore | ||
| Angle between the line connecting the node and the wellbore center and the direction of maximum horizontal stress | ||
| Minimum distance between a node and the nearest fracture path | ||
| Relative angle between a node and the adjacent fracture path | ||
| Average fracture width in node neighborhood, | ||
| Edge-Level | Equivalent fracture width | |
| Edge length | ||
| Edge orientation | ||
| Fluid pressure difference on edge | ||
| Coupled pressure-width term | ||
| Projected pressure difference along fracture direction |
| Parameter | Value |
|---|---|
| Model Length | 10 m |
| Model Width | 10 m |
| Wellbore Radius | 0.08 m |
| Rock Density | 2600 kg⋅m−3 |
| Elastic Modulus | 40 GPa |
| Poisson’s Ratio | 0.2 |
| Cohesive Strength | 30 MPa |
| Tensile Strength | 10 MPa |
| Internal Friction Angle | 45° |
| Charge Density | 50 kg⋅m−3 |
| Detonation Velocity | 400 m⋅s−1 |
| Detonation Heat | 3 × 107 J⋅kg−1 |
| 50 MPa | |
| 40 MPa |
| Layers | MSE | MAPE | ||||
|---|---|---|---|---|---|---|
| MLP | GCN | Proposed | MLP | GCN | Proposed | |
| 2 | 1.181% | 1.879% | 0.433% | |||
| 3 | 1.036% | 1.286% | 0.538% | |||
| 4 | 0.863% | 0.651% | 0.456% | |||
| 5 | 1.134% | 1.387% | 0.533% | |||
| 6 | 0.868% | 1.239% | 0.449% | |||
| 7 | 0.674% | 2.297% | 0.388% | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Gao, T.; Guo, T.; Wang, H.; Zhou, J. Prediction of Fluid Pressure Dynamics in Deflagration Fracturing for Unconventional Reservoir Stimulation Based on Physics-Guided Graph Neural Network. Energies 2025, 18, 6144. https://doi.org/10.3390/en18236144
Yang X, Gao T, Guo T, Wang H, Zhou J. Prediction of Fluid Pressure Dynamics in Deflagration Fracturing for Unconventional Reservoir Stimulation Based on Physics-Guided Graph Neural Network. Energies. 2025; 18(23):6144. https://doi.org/10.3390/en18236144
Chicago/Turabian StyleYang, Xin, Tian Gao, Tiankui Guo, Haiyang Wang, and Jinfeng Zhou. 2025. "Prediction of Fluid Pressure Dynamics in Deflagration Fracturing for Unconventional Reservoir Stimulation Based on Physics-Guided Graph Neural Network" Energies 18, no. 23: 6144. https://doi.org/10.3390/en18236144
APA StyleYang, X., Gao, T., Guo, T., Wang, H., & Zhou, J. (2025). Prediction of Fluid Pressure Dynamics in Deflagration Fracturing for Unconventional Reservoir Stimulation Based on Physics-Guided Graph Neural Network. Energies, 18(23), 6144. https://doi.org/10.3390/en18236144







