Low-Carbon Economic Dispatch of Agricultural Park Integrated Energy Systems Based on Improved Multi-Objective Grey Wolf Optimizer
Abstract
1. Introduction
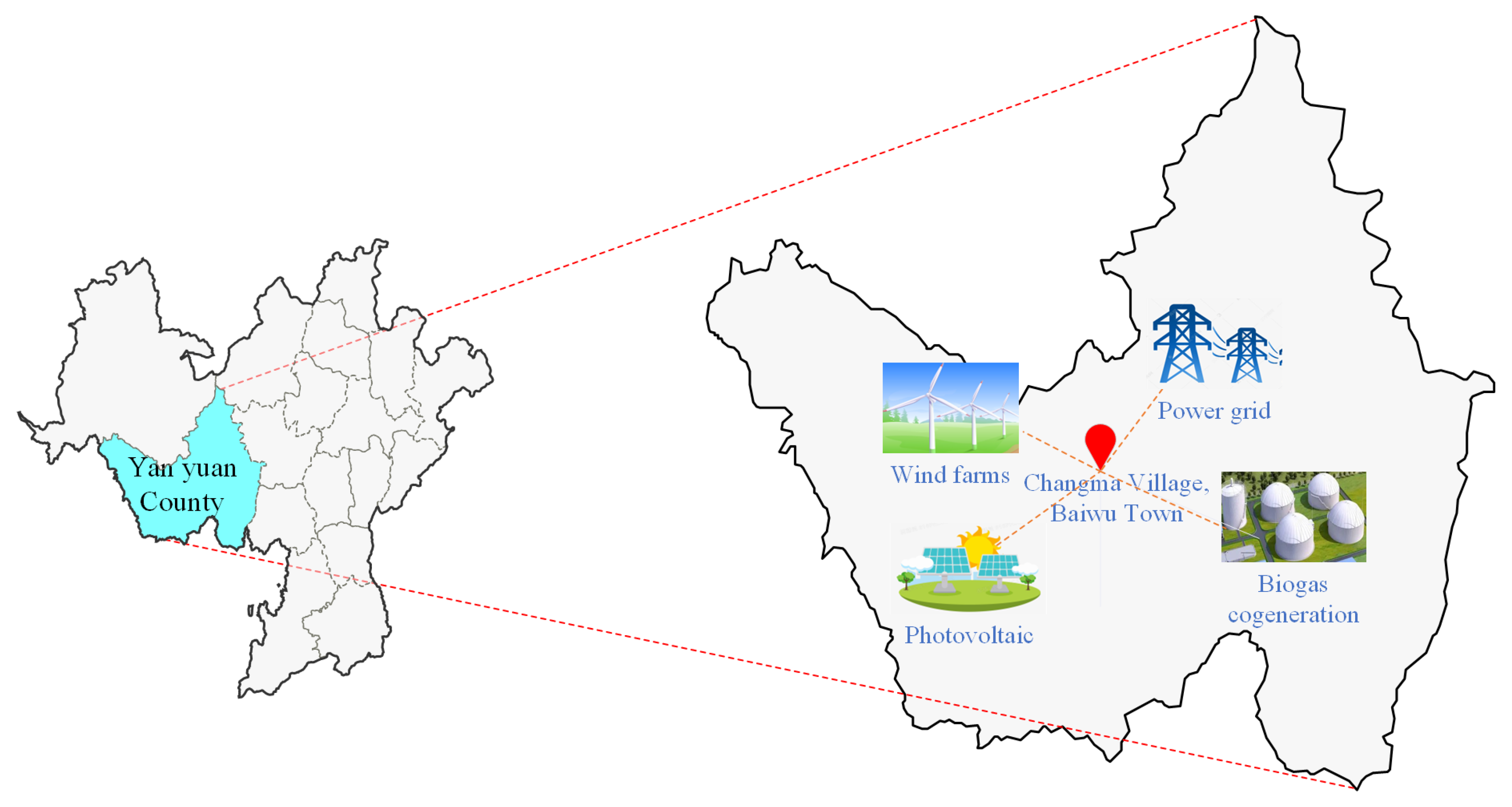
2. Site Selection of Integrated Energy System in Agricultural Park
2.1. Wind Resources in Yanyuan County, Liangshan Prefecture
2.2. Photovoltaic Resources in Yanyuan County, Liangshan Prefecture
2.3. Biomass Resources in Yanyuan County, Liangshan Prefecture
2.4. Liangshan Prefecture Yanyuan County Agricultural Park
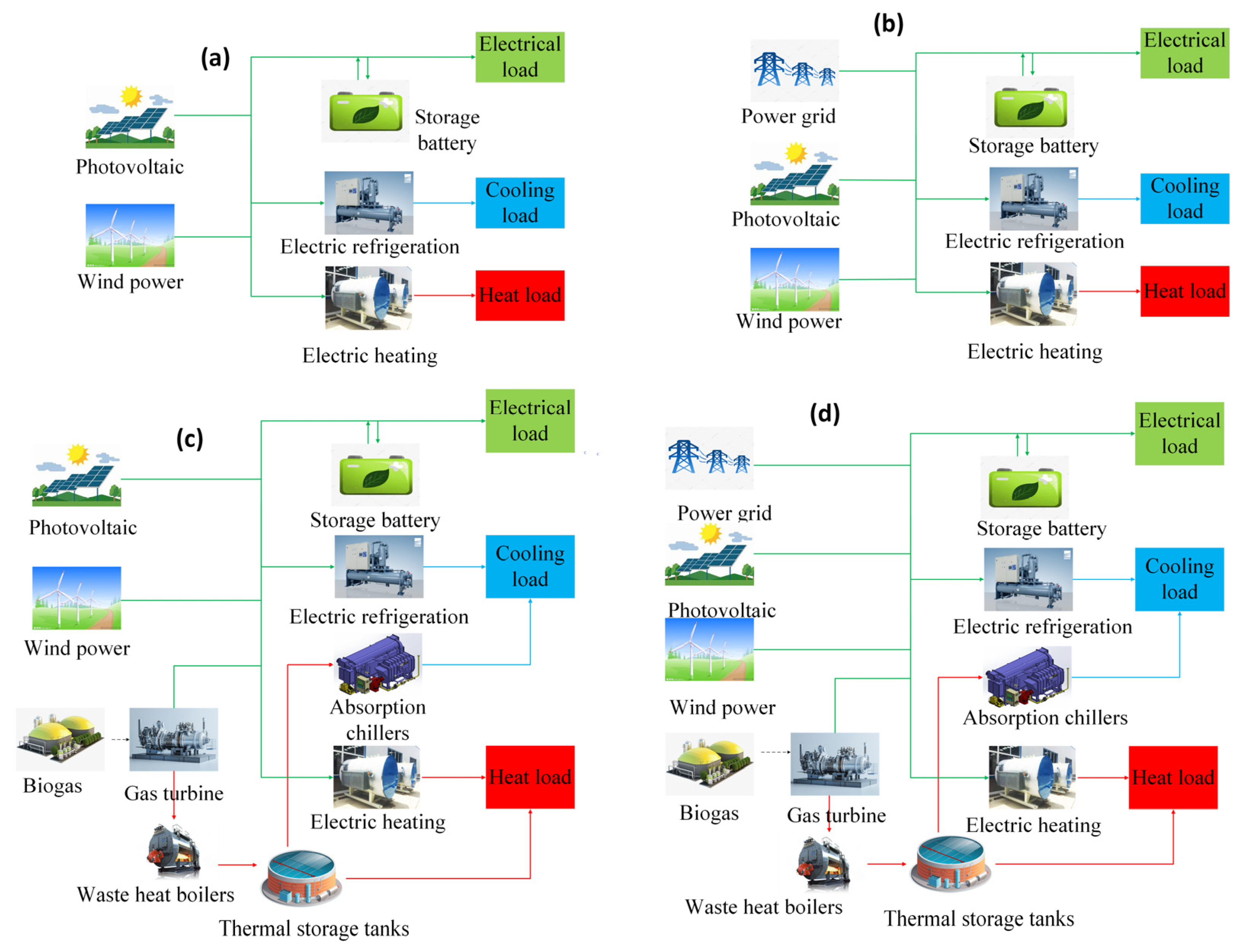
2.5. Multi-Energy Complementary Integrated Energy System Application Scenarios
3. Energy Management Strategy
4. Modeling of Integrated Energy System
4.1. Wind Power Generation
4.2. Photovoltaic Power Generation
4.3. Biogas Cogeneration
4.3.1. Biogas Gas Turbine
4.3.2. Waste Heat Recovery Boiler
4.3.3. Biogas Digester
4.4. Electric Heating and Electric Refrigeration Equipment
4.5. Absorption Chiller
4.6. Energy Storage Equipment
5. Multi-Objective Optimization Operation Model
5.1. Objective Function
5.1.1. Operating Cost Objective
- (1)
- Equipment energy supply and maintenance cost
- (2)
- Equipment conversion and maintenance cost
- (3)
- Start-up and shutdown cost
- (4)
- Cost of power usage with the grid
5.1.2. Environmental Cost Objective
5.2. Constraint Conditions
5.2.1. Energy Conservation Constraints
- Electric Energy Balance
- 2.
- Thermal Energy Balance
- 3.
- Cooling Energy Balance
5.2.2. Non-Conservative Constraint Conditions
- (1)
- Wind and Photovoltaic Output Constraints
- (2)
- Biogas Cogeneration Output Constraints
- (3)
- Electric Heating Equipment Constraint
- (4)
- Electric Refrigeration Equipment Constraint
- (5)
- Absorption Chiller Constraint
- (6)
- Battery Operation Constraints
- (7)
- Thermal Energy Storage Constraints
6. Improved Multi-Objective Grey Wolf Optimizer
6.1. Basic Concept of Grey Wolf Optimizer (GWO)
- α (Alpha) wolf: the leader responsible for decision-making and guidance, representing the best solution.
- β (Beta) wolf: assists the α wolf in decision-making and management, representing the second-best solution.
- δ (Delta) wolf: follows α and β wolves, supervises subordinate wolves, and represents the third-best solution.
- ω (Omega) wolf: the lowest-ranking members that follow all higher levels, mainly responsible for exploration and position updating, representing the remaining candidate solutions.
- (1)
- Encircling Prey Stage
- (2)
- Hunting Prey Stage
- (3)
- Attacking Prey Stage
6.2. Improved Multi-Objective Grey Wolf Optimizer
- (1)
- Pareto dominance-based multi-objective extension
- (2)
- Dynamic elite archiving mechanism
- (3)
- Diversified leadership wolf selection strategy
- α (minimum-cost solution):
- β (minimum-emission solution):
- δ (compromise solution):
- (4)
- Exponential decay-based convergence factor
6.3. Benchmark Test and Performance Companions
6.3.1. Benchmark Test and Verification
6.3.2. Performance Companions and Analysis
- (1)
- The initial value of standard MOGWO algorithm is fully initialized randomly from 0 to the maximum output power. The improved random initialization in this study is based on a random fluctuation of ±20% before optimization. This mechanism enhances the population diversity while maintaining solution feasibility.
- (2)
- The standard MOGWO selects three leader wolves (α, β, δ) using roulette wheel selection in the least-crowded regions. In the improved method, a multi-criteria leader selection strategy is proposed: α-wolf represents the non-dominated solution with the best cost performance, β-wolf represents the best carbon emission solution, and δ-wolf is determined using a normalized aggregation function combining α and β wolves, thus balancing both objectives and convergence diversity.
- (3)
- In the standard MOGWO algorithm, the alpha value is set as a linear convergence factor α = 2 − 2tT. In the improved method, a nonlinear dynamic weight coefficient α = 2 − 2(t/T)3 is adopted. This enables a broader exploration in the early iterations and a faster exploitation in later stages.
7. Operation Optimization Process and Simulation Results
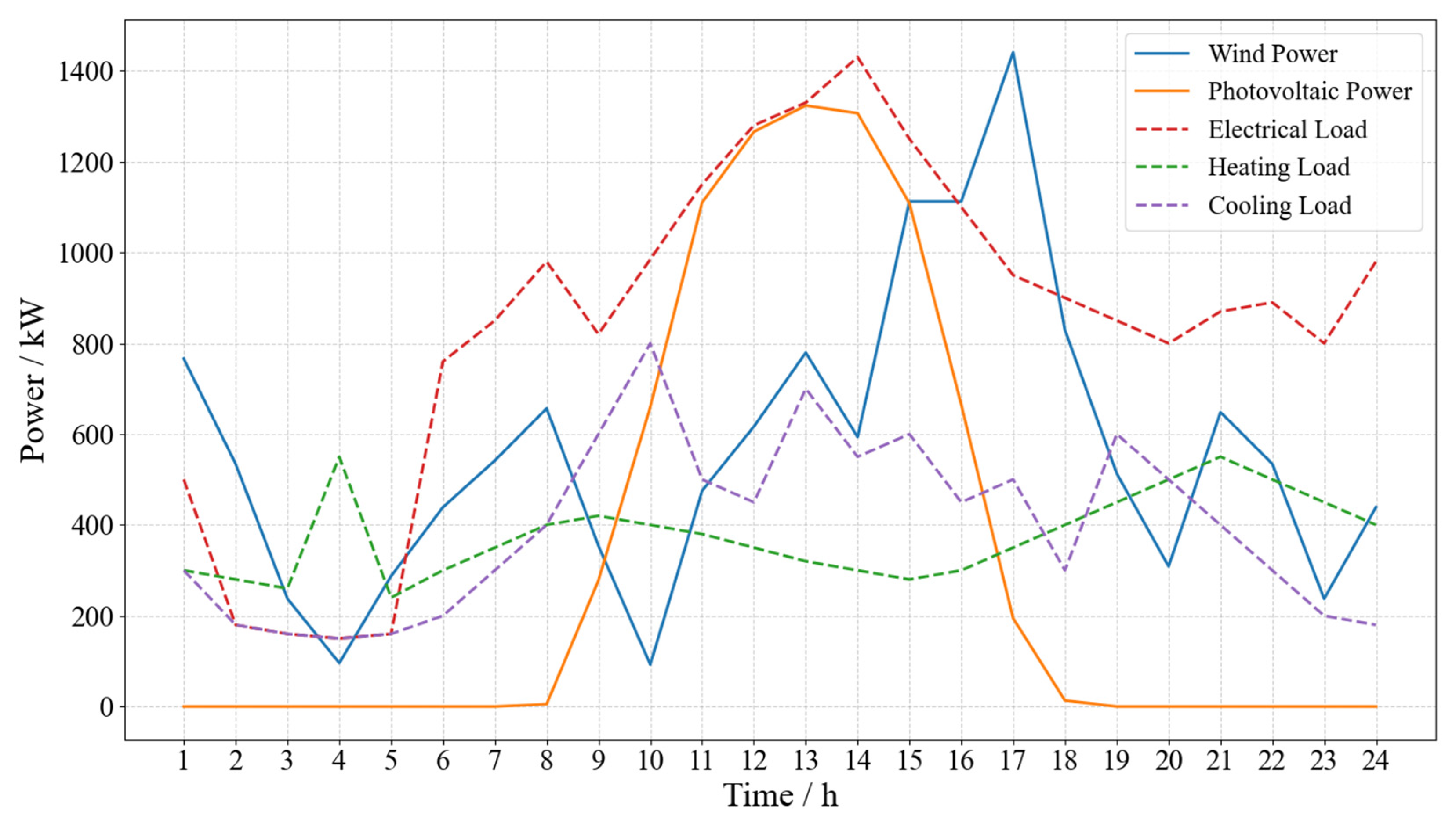
7.1. Basic Data and Parameters
7.2. Optimization Process
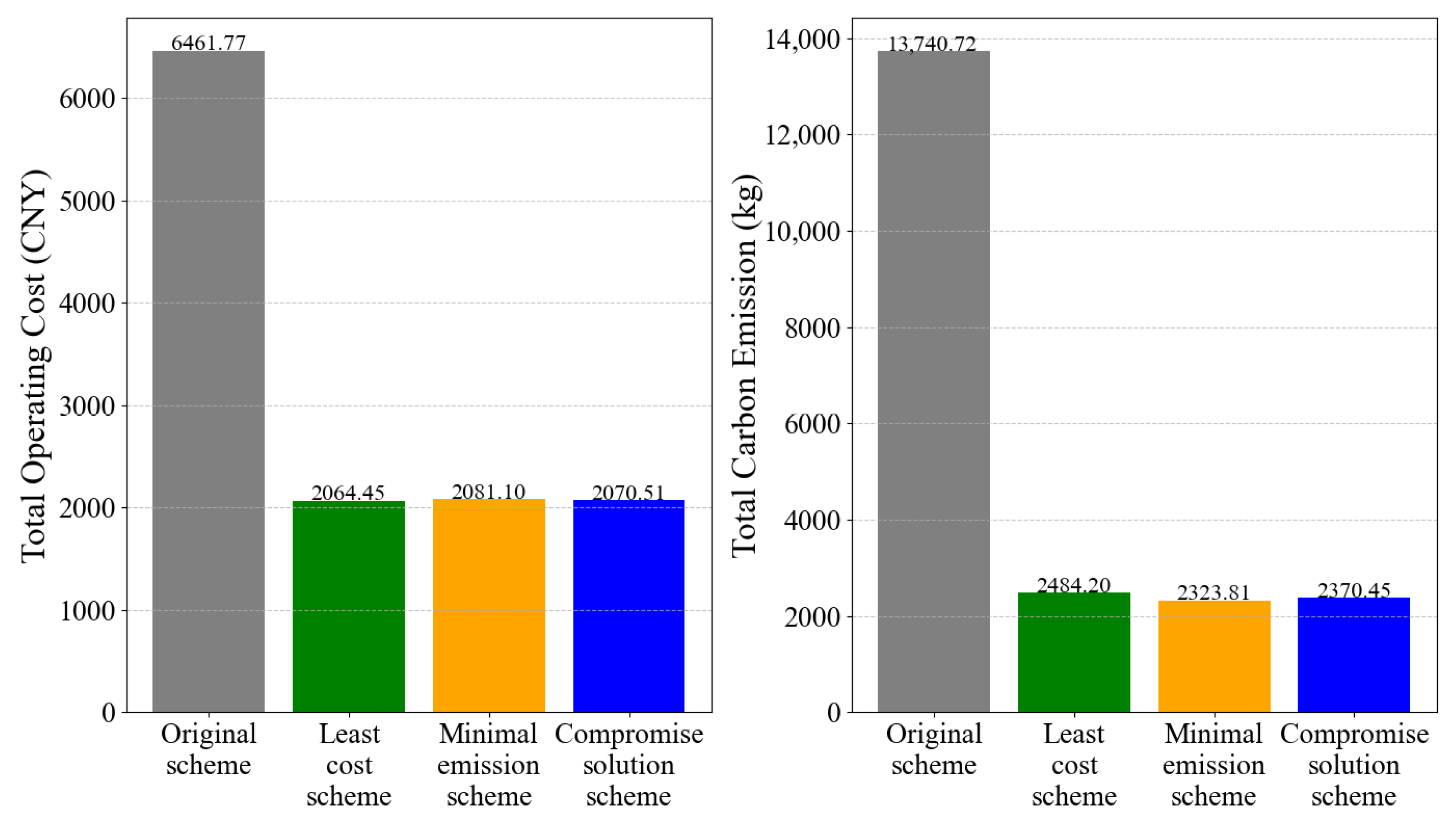
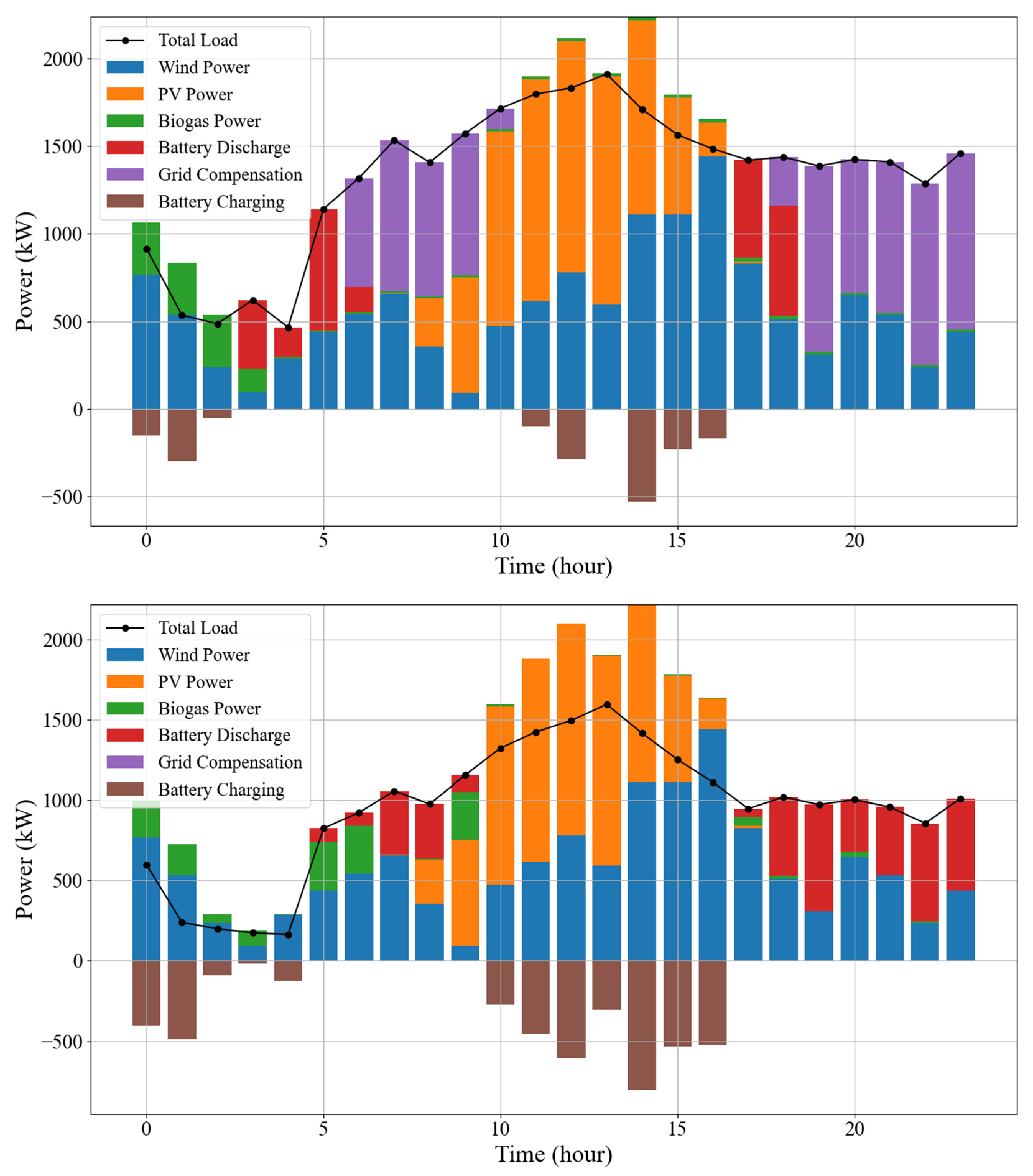
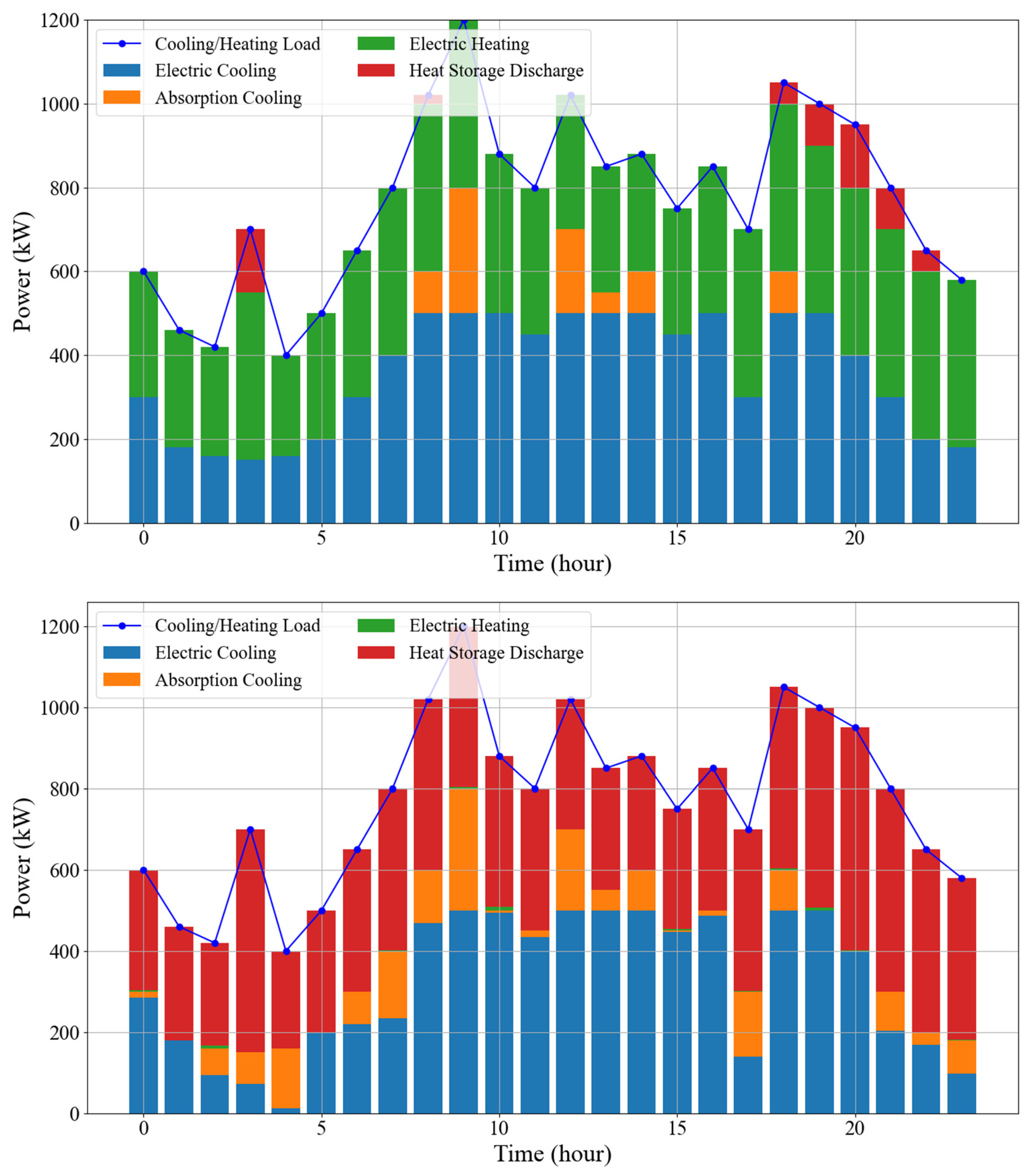
7.3. Simulation Results
7.4. Sensitivity Analysis
8. General Analysis Framework
- (1)
- The solar radiation intensity, temperature and wind speed data are inputted. The local energy sources generate clean electricity and supply it to various energy equipment. The gas turbine is selectively started based on whether the demand for cold, heat and electricity is met.
- (2)
- When the output of local clean power exceeds the local load, the surplus power is stored in the batteries. Otherwise, when the output is less than the load demand, the batteries will make up for the energy shortage. In the case when the sum of local clean power and battery discharging power is still cannot meet the load demand, the gas turbine will start, and the waste heat from the gas turbine will be stored in the heat storage tank through a boiler. Moreover, the local power grid can also be connected to offer power compensation when required.
- (3)
- A mathematical model of the integrated energy system is built using the energy management modes of Step (2). The integrated energy system includes photovoltaic power station, wind farm, biogas cogeneration, electricity-to-heat conversion units, electricity-to-cooling conversion units, absorption refrigeration machines, batteries, heat storage tanks, and heat, cold, and electricity loads, etc.
- (4)
- A multi-objective operation optimization model is established based on the comprehensive energy system in Step (3). The model is constructed with the O&M costs and carbon emissions as the objectives, and the balance of cooling, heating and electricity as well as the power ratings of energy equipment are the constraints.
- (5)
- Based on the user-defined weather conditions (temperature, solar radiation intensity, wind speed, etc.) and the demand from the local loads, the multi-objective optimization model in Step (4) is finally used to obtain the optimal equipment configuration scheme to simultaneously reduce the O&M costs and carbon emissions.

9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Available online: https://www.gov.cn/zhengce/202501/content_7000493.htm (accessed on 22 January 2025).
- Sulewski, P.; Wąs, A. Agriculture as Energy Prosumer: Review of Problems, Challenges, and Opportunities. Energies 2024, 17, 6447. [Google Scholar] [CrossRef]
- Nikolić, D.; Jovanović, S.; Jurišević, N.; Nikolić, N.; Radulović, J.; Velemir Radović, M.; Grujić, I. Sustainable Design in Agriculture—Energy Optimization of Solar Greenhouses with Renewable Energy Technologies. Energies 2025, 18, 416. [Google Scholar] [CrossRef]
- Liu, H.; Ye, S.; Yin, C.; Wang, L.; Zhang, C. Cooperative Game-Theoretic Scheduling for Low-Carbon Integrated Energy Systems with P2G–CCS Synergy. Energies 2025, 18, 3942. [Google Scholar] [CrossRef]
- Available online: https://wap.reportway.org/article/34349.html (accessed on 22 January 2025).
- MacDonald, S.; Winner, B.; Smith, L.; Juillerat, J.; Belknap, S. Bridging the rural efficiency gap: Expanding access to energy efficiency upgrades in remote and high energy cost communities. Energy Effic. 2020, 13, 503–521. [Google Scholar] [CrossRef]
- Saidmamatov, O.; Tetreault, N.; Bekjanov, D.; Khodjaniyazov, E.; Ibadullaev, E.; Sobirov, Y.; Adrianto, L.R. The Nexus between Agriculture, Water, Energy and Environmental Degradation in Central Asia—Empirical Evidence Using Panel Data Models. Energies 2023, 16, 3206. [Google Scholar] [CrossRef]
- Monsberger, C.; Reuter, S.; Ackerl, F.; Mayr, B.; Fina, B.; Mauthner, B. The Role of Renewable Gas Energy Communities in Austria’s Energy Transformation. Energies 2025, 18, 4863. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, S. Economic Analysis of Biofuel Production in Agrophotovoltaic Systems Using Building-Integrated Photovoltaics in South Korea. Energies 2025, 18, 1949. [Google Scholar] [CrossRef]
- Yang, W.; Xia, Y.; Yu, X.; Zhang, H.; Lin, X.; Ma, H.; Du, Y.; Dong, H. Optimal Dispatch of Agricultural Integrated Energy System with Hybrid Energy Storage. Energies 2022, 15, 9131. [Google Scholar] [CrossRef]
- Ahmad, R.; Farzaneh, H. Techno-economic analysis and dynamic power simulation of a hybrid solar-wind-battery system for power supply in rural areas in Pakistan. Clean. Energy Syst. 2024, 8, 100127. [Google Scholar] [CrossRef]
- Liang, W.; Wang, S.; Li, X.; Li, X.; Xu, K. Optimization method of low carbon park integrated energy system based on multi-agent game. Electr. Power Syst. Res. 2025, 243, 111484. [Google Scholar] [CrossRef]
- Li, X.; Zhang, F.; Huang, Y.; Zhang, G. Bi-Level Sustainability Planning for Integrated Energy Systems Considering Hydrogen Utilization and the Bilateral Response of Supply and Demand. Sustainability 2025, 17, 7637. [Google Scholar] [CrossRef]
- Chen, M.; Wei, J.; Yang, X.; Fu, Q.; Wang, Q.; Qiao, S. Multi-objective optimization of multi-energy complementary systems integrated biomass-solar-wind energy utilization in rural areas. Energy Convers. Manag. 2025, 323, 119241. [Google Scholar] [CrossRef]
- Wang, T.; Wang, Q.; Zhang, C. Research on the Optimal Operation of a Novel Renewable Multi-Energy Complementary System in Rural Areas. Sustainability 2021, 13, 2196. [Google Scholar] [CrossRef]
- Wei, C.; Yuan, L.; Xin, H.; Hailong, Z.; Yong, Y.; Jianbin, C. Multi-objective optimal scheduling method for integrated energy systems in facility agricultural industrial parks considering local consumption of wind and photovoltaic power. Electr. Power Constr. 2021, 42, 20–27. [Google Scholar]
- Yu, X.; Song, Y.; Sun, R. Distributed cooperative electricity-carbon trading for multi-park integrated energy systems. Sustain. Energy Grids Netw. 2025, 43, 101683. [Google Scholar] [CrossRef]
- Dardon, J.D.A.; Farzaneh, H. Techno-economic analysis of a hybrid photovoltaic-wind-biomass-battery system for off-grid power in rural Guatemala. Util. Policy 2024, 88, 101762. [Google Scholar] [CrossRef]
- Winsly, B.W.; Ramalingam, V.K.; Santhappan, J.S.; Maria, A.J.; Chokkalingam, M.P.; Rajendran, V. Optimal sizing and techno-economic-environmental evaluation of biomass-solar-wind-grid hybrid energy system: A case study of an institute in South India. Energy Convers. Manag. 2025, 325, 119352. [Google Scholar] [CrossRef]
- El Mestari, W.; Cheggaga, N.; Adli, F.; Benallal, A.; Ilinca, A. Tuning Parameters of Genetic Algorithms for Wind Farm Optimization Using the Design of Experiments Method. Sustainability 2025, 17, 3011. [Google Scholar] [CrossRef]
- Vahidi, J.; Golmaei, S.M. Optimizing Construction Scheduling Using the Sine Cosine Algorithm (SCA) with Building Information Modeling (BIM). Results Eng. 2025, 28, 107100. [Google Scholar] [CrossRef]
- Wu, M.; Du, P.; Jiang, M.; Goh, H.H.; Zhu, H.; Zhang, D.; Wu, T. An integrated energy system optimization strategy based on particle swarm optimization algorithm. Energy Rep. 2022, 8, 679–691. [Google Scholar] [CrossRef]
- Zheng, Q.; Yue, C.; Zhang, S.; Yao, C.; Zhang, Q. Optimal Allocation of Water Resources in Canal Systems Based on the Improved Grey Wolf Algorithm. Sustainability 2024, 16, 3635. [Google Scholar] [CrossRef]
- Gao, Y.; Hu, Z.; Chen, G. The “Yanyuan Model” of clean energy in Liangshan, Sichuan: Responding to the era’s “green expectations”. Bus. Manag. 2023, 8, 48–49. [Google Scholar]
- Available online: https://www.sc.chinanews.com.cn/cjbd/2023-11-01/198049.html (accessed on 1 November 2023).
- Available online: https://fgw.sc.gov.cn/sfgw/c106099/2022/1/29/7650e2495f6d4fd48e17560783b76791.shtml (accessed on 29 January 2022).
- Available online: http://www.chinapower.com.cn/tynfd/bwfd/20241127/269145.html (accessed on 23 November 2024).
- Wang, P.; Zhang, L.; Jiang, Y.; Luo, W.; Chen, Z.; Hai, H.; Xiong, Z. Current situation and countermeasures of comprehensive utilization of straw in Yanyuan County. Sichuan Agric. Sci. Technol. 2023, 12, 79–82. [Google Scholar]
- Available online: http://www.yanyuan.gov.cn/zfxxgk/zfxxgknr/tzgg_31066/202106/t20210617_1939943.html (accessed on 26 June 2018).
- Available online: http://www.yanyuan.gov.cn/mlzd/yygk/202211/t20221128_2376356.html (accessed on 29 April 2025).
- Available online: http://www.yanyuan.gov.cn/zfxxgk/zfxxgknr/zfgzbg/202406/t20240604_2685962.html (accessed on 4 June 2024).
- Available online: http://www.yanyuan.gov.cn/zt/xj/lygk/zrzy/gtkjghbz/xjgtkjztgh/202309/t20230906_2541420.html (accessed on 19 November 2024).
- Sun, Y.; Yu, Q.; Wang, X.; Gao, S.; Sun, G. Extraction of Basic Features and Typical Operating Conditions of Wind Power Generation for Sustainable Energy Systems. Sustainability 2025, 17, 6577. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Y.; Yang, Y.; Mao, T. Thermodynamic performance analysis and optimization of a solar-assisted combined cooling, heating and power system. Energy 2016, 115, 49–59. [Google Scholar] [CrossRef]
- Liu, Z.; Cui, Y.; Wang, J.; Yue, C.; Agbodjan, Y.S.; Yang, Y. Multi-objective optimization of multi-energy complementary integrated energy systems considering load prediction and renewable energy production uncertainties. Energy 2022, 254, 124399. [Google Scholar] [CrossRef]
- Basrawi, M.F.B.; Yamada, T.; Nakanishi, K.; Katsumata, H. Analysis of the performances of biogas-fuelled micro gas turbine cogeneration systems (MGT-CGSs) in middle-and small-scale sewage treatment plants: Comparison of performances and optimization of MGTs with various electrical power outputs. Energy 2012, 38, 291–304. [Google Scholar] [CrossRef]
- Wu, D.; Han, Z.; Liu, Z.; Li, P.; Ma, F.; Zhang, H.; Yin, Y.; Yang, X. Comparative study of optimization method and optimal operation strategy for multi-scenario integrated energy system. Energy 2021, 217, 119311. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, X.; Fu, L.; Jiang, S. Superconducting hydrogen-electricity multi-energy system for transportation hubs: Modeling, technical study and economic-environmental assessment. Appl. Energy 2025, 401, 126823. [Google Scholar] [CrossRef]
- Aldaliee, A.A.; Mansor, N.N.; Mokhlis, H.; Ramasamy, A.K.; Awalin, L.J. Pareto-Based Optimization of PV and Battery in Home-PV-BES-EV System with Integrated Dynamic Energy Management Strategy. Sustainability 2025, 17, 7364. [Google Scholar] [CrossRef]
- Tuan, D.H.; Tran, D.T.; Nguyen Ngoc Thanh, V.; Huynh, V.V. Load Frequency Control Based on Gray Wolf Optimizer Algorithm for Modern Power Systems. Energies 2025, 18, 815. [Google Scholar] [CrossRef]
- Coronado-Mendoza, A.; Camas-Náfate, M.; Artal-Sevil, J.S.; Domínguez-Navarro, J.A. Optimum Design of a Photovoltaic Inverter System Based on GA, PSO and GWO Algorithms with a MPPT Sliding Mode Control. Energies 2025, 18, 1911. [Google Scholar] [CrossRef]
- Huang, H.; Shen, Q.; Liu, W.; Peng, Y.; Zhu, S.; Bao, R.; Mo, L. Optimal Scheduling of a Hydropower–Wind–Solar Multi-Objective System Based on an Improved Strength Pareto Algorithm. Sustainability 2025, 17, 7140. [Google Scholar] [CrossRef]
- Ma, Z.; Jen, C.T.; Aazami, A. Time-Dependent Vehicle Routing Optimization Incorporating Pollution Reduction Using Hybrid Gray Wolf Optimizer and Neural Networks. Sustainability 2025, 17, 4829. [Google Scholar] [CrossRef]
- Zhang, H.; Sui, X.; Sui, P.; Wei, L.; Huang, Y.; Yang, Z.; Yang, H. Coil Parameter Optimization Method for Wireless Power Transfer System Based on Crowding Distance Division and Adaptive Genetic Operators. Energies 2024, 17, 3289. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, J.; Zhi, H.; Zhao, J.; Chang, X.; Zhang, S.; Guo, X.; Wang, T. An Integrated Electricity–Gas–Heat Energy System Based on the Synergy of Long- and Short-Term Energy Storage. Energies 2025, 18, 55. [Google Scholar] [CrossRef]
- Liu, Y. Analysis of Factors Affecting Power Generation in Photovoltaic Power Generation Systems. Sichuan Hydropower 2022, 41, 27–30. [Google Scholar]
- Ye, Y.; Yuan, X. Research on Wind Energy Resources and Optimal Spacing of Wind Turbines in a Typical Area of Liangshan Prefecture, Sichuan Province Based on CFD Simulation. East. Electr. Rev. 2024, 38, 28–33. [Google Scholar] [CrossRef]
- Bai, J.; Wu, X.; Chen, X.; Zhang, Z.; Fu, L.; Zhao, C.; Qing, K.; Luo, Q.; Gong, S.; Shen, B. Combined space cooling/heating and domestic hot water supply driven by data center waste heat: Complementary energy conservation, economic capacity optimization and generic analysis framework. Build. Environ. 2025, 283, 113402. [Google Scholar] [CrossRef]
- Zhang, T. Research on the Operation Optimization of Comprehensive Energy System Based on the Coordinated Utilization of Multiple Energy Sources in Rural Areas. Master’s Thesis, North China Electric Power University, Beijing, China, 2024. [Google Scholar] [CrossRef]
- Li, J. Research on the Near-Zero Carbon Operation Strategy of the Comprehensive Energy System in Facility Agriculture Industrial Parks. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2022. [Google Scholar] [CrossRef]
- Schyska, B.U.; Kies, A.; Schlott, M.; Von Bremen, L.; Medjroubi, W. The sensitivity of power system expansion models. Joule 2021, 5, 2606–2624. [Google Scholar] [CrossRef]

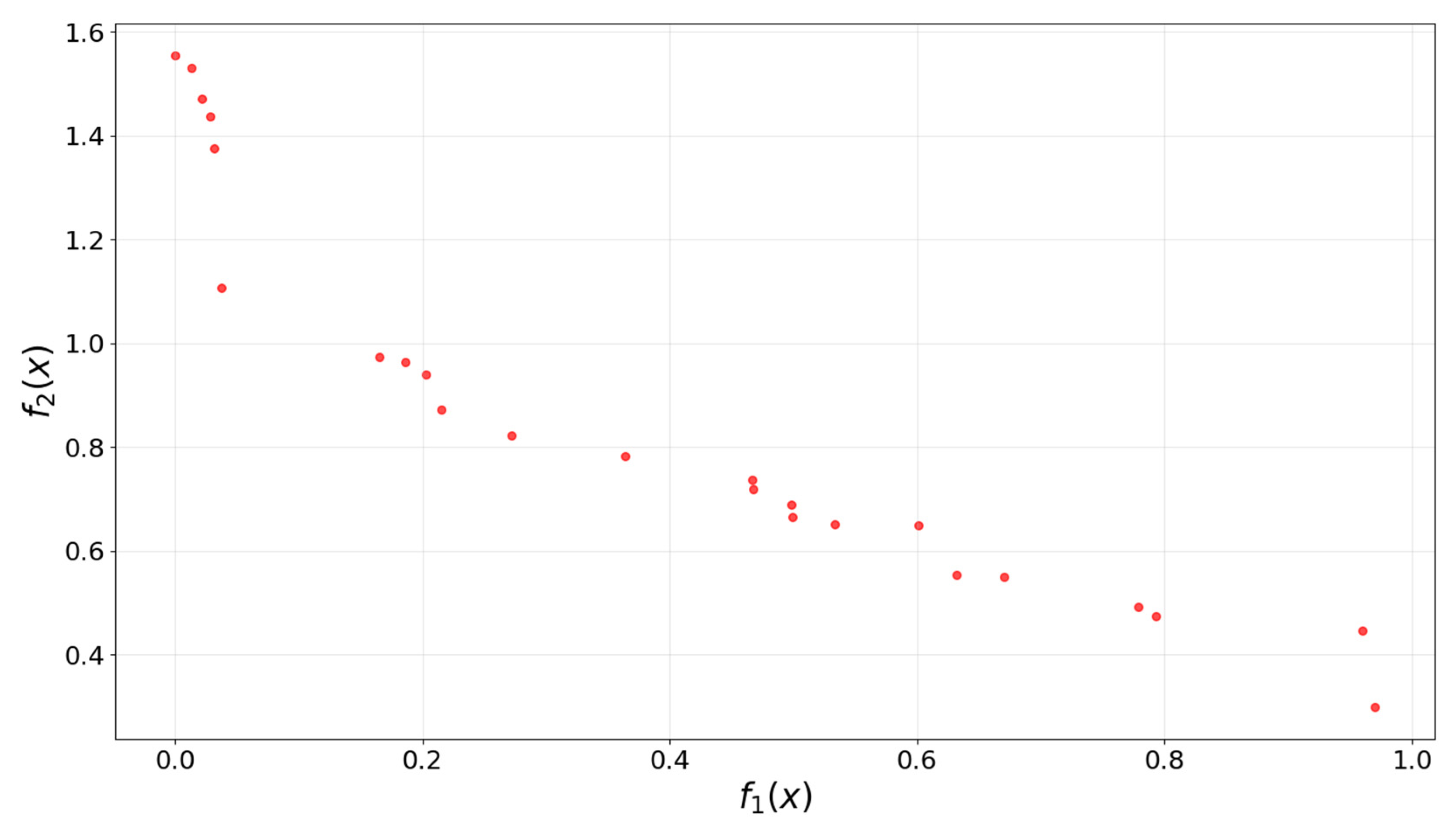
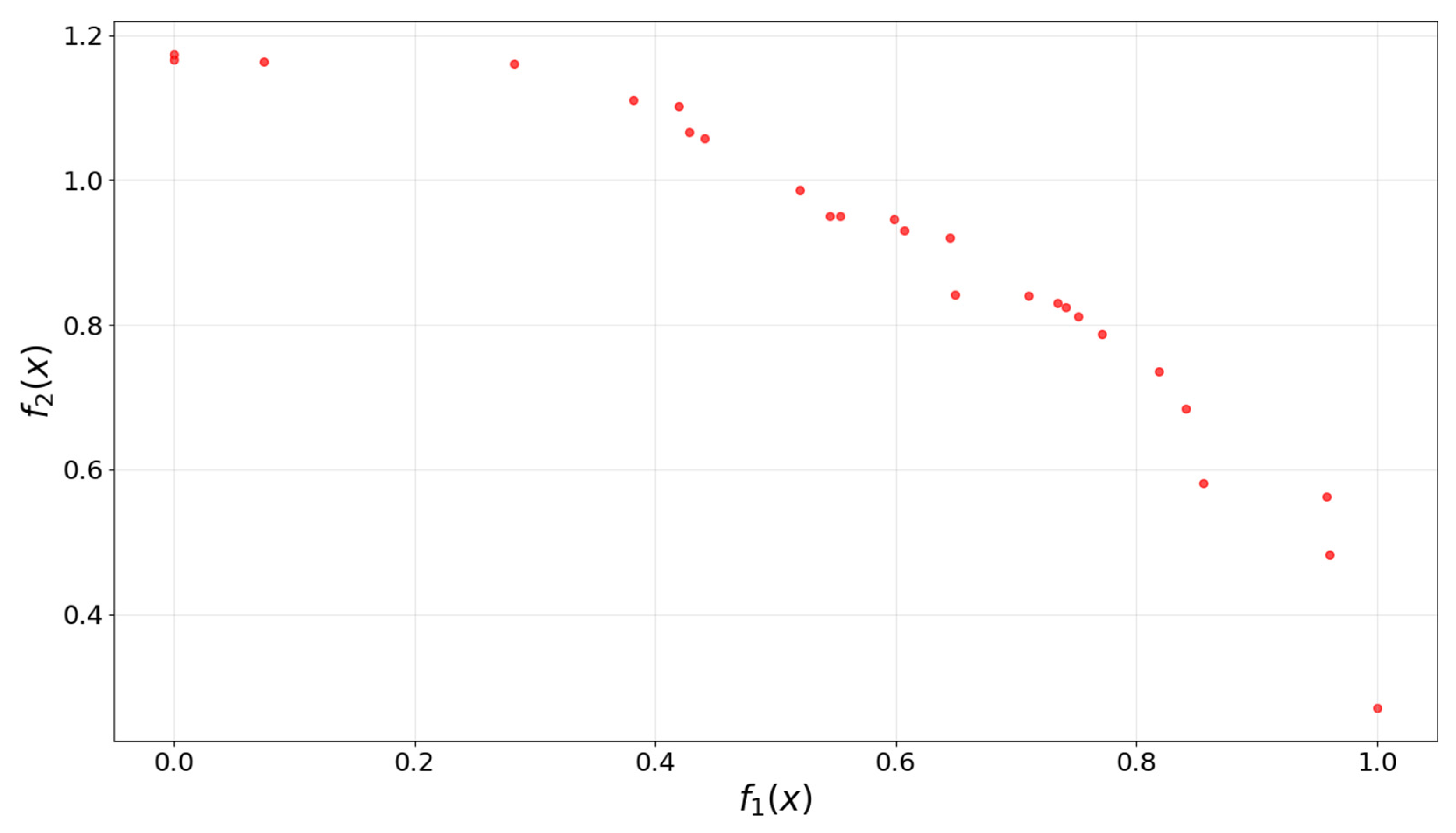
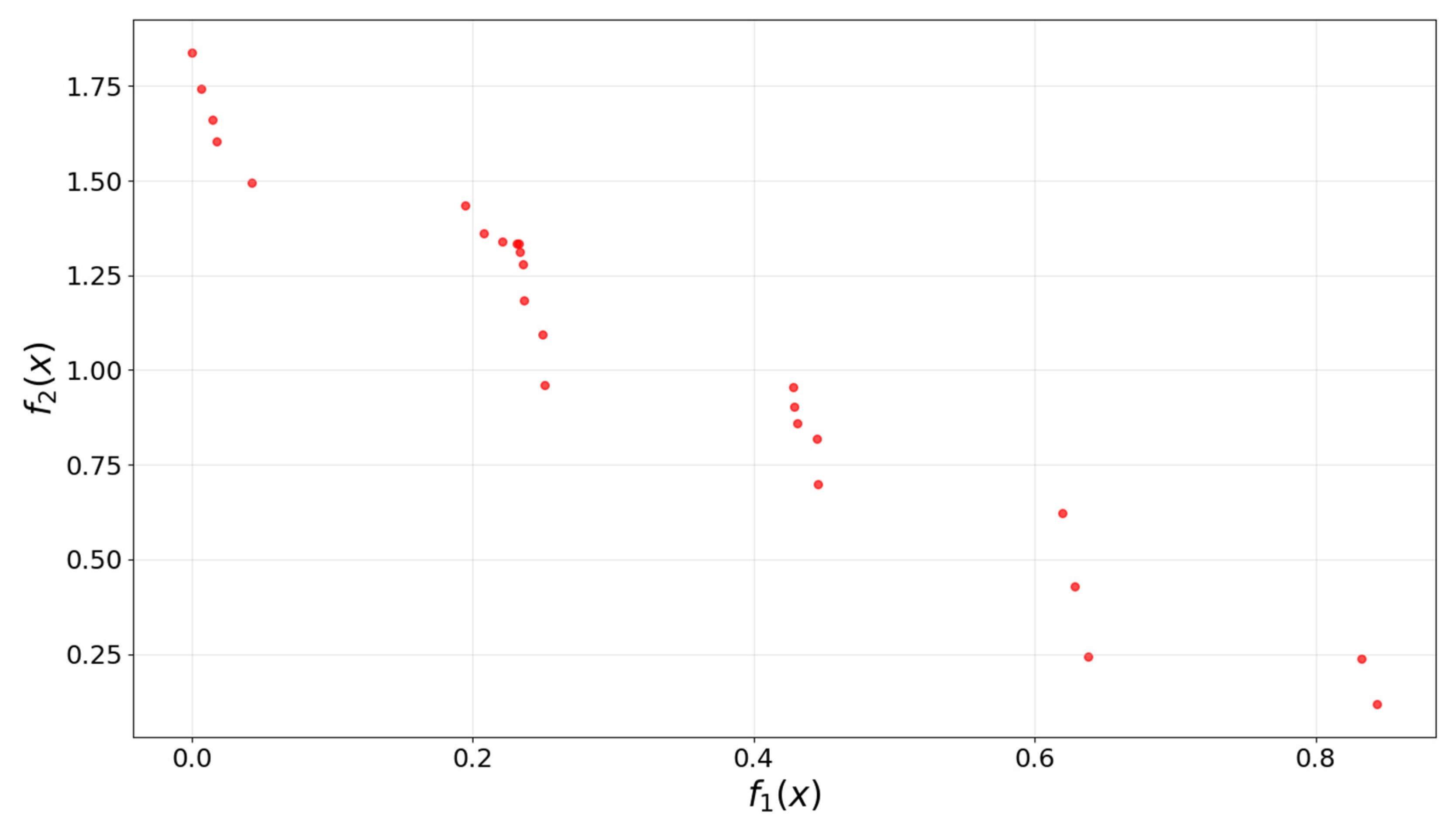

| Test Function | Pareto Solution Set Size | f1 Range | f2 Range | Front Shape |
|---|---|---|---|---|
| ZDT1 | 24 | [0.000, 0.970] | [0.300, 1.555] | Concave |
| ZDT2 | 26 | [0.000, 1.000] | [0.270, 1.174] | Convex |
| ZDT3 | 25 | [0.000, 0.843] | [0.117, 1.839] | Discontinuous |
| Algorithm | HV | Spacing | Pareto Solution Set Size |
|---|---|---|---|
| Standard MOGWO | 191,807.966 | 0.095 | 13.433 |
| Improved MOGWO | 206,743.318 | 0.081 | 16.533 |
| Ablation_Init | 172,536.407 | 0.105 | 14.700 |
| Ablation_Leaders | 178,799.677 | 0.095 | 15.400 |
| Ablation_aFactor | 146,749.461 | 0.119 | 11.233 |
| Equipment | Parameter | Value |
|---|---|---|
| Photovoltaic Power | Maximum output power | 2000 kW |
| Wind Power | Maximum output power | 2000 kW |
| Biogas Combined Heat and Power | Rated power output | 300 kW |
| Maximum heating efficiency | 0.62 | |
| Maximum power generation efficiency | 0.38 | |
| Waste heat recovery efficiency | 0.9 | |
| Heat exchange efficiency | 0.9 | |
| Electric Heating | Thermal efficiency | 0.85 |
| Rated thermal power | 500 kW | |
| Electric Cooling | Cooling efficiency | 3 |
| Maximum cooling output power | 500 kW | |
| Absorption Chiller | Refrigeration efficiency | 1.2 |
| Maximum cooling output power | 500 kW | |
| Battery Energy Storage | Rated capacity | 5000 kWh |
| Charging/discharging efficiency | 0.93 | |
| Thermal Storage Tank | Rated capacity | 5000 kWh |
| Charging/discharging efficiency | 0.9 |
| Energy Equipment | Cost (CNY/kW) |
|---|---|
| Photovoltaic Power (CPV) | 0.052 |
| Wind Power (CWT) | 0.039 |
| Biogas Combined Heat and Power (CBCHP) | 0.09 |
| Electric Heating Equipment (CEB) | 0.084 |
| Electric Cooling Equipment (CEC) | 0.084 |
| Absorption Chiller (CABC) | 0.084 |
| Battery Energy Storage (CBS) | 0.036 |
| Thermal Storage Tank (CTST) | 0.024 |
| Item | Before Optimization | After Optimization | Power Change | Change Rate |
|---|---|---|---|---|
| Biogas power generation | 1332.35 kW | 1615.86 kW | +283.51 kW | +21.28% |
| Electric heating equipment | 8852.63 kW | 43.99 kW | −8808.64 kW | −99.50% |
| Electric cooling equipment | 2876.67 kW | 2544.74 kW | −331.93 kW | −11.54% |
| Total electric load | 31,854.33 kW | 22,713.76 kW | −9140.57 kW | −28.69% |
| Battery charging | 1821.43 kW | 4626.98 kW | +2805.54 kW | +154.03% |
| Battery discharging | 2582.59 kW | 4145.49 kW | +1562.90 kW | +60.52% |
| Grid compensation | 8185.93 kW | 4.50 kW | −8181.43 kW | −99.95% |
| Item | Before Optimization | After Optimization | Power Change | Change Rate |
|---|---|---|---|---|
| Electric cooling equipment | 8630 kW | 7634.21 kW | −995.79 kW | −11.54% |
| Absorption chiller | 850 kW | 1845.79 kW | +995.79 kW | +117.15% |
| Electric heating equipment | 8410 kW | 41.79 kW | −8368.21 kW | −99.50% |
| Heat released from storage | 620 kW | 8988.21 kW | +8368.21 kW | +1349.71% |
| Parameter | Before Optimization | After Optimization | Change Rate |
|---|---|---|---|
| Cgrid | 63.3% | 0.1% | −63.2% |
| CEB | 11.5% | 0.2% | −11.3% |
| CWT | 11% | 0.343% | +23.3% |
| CPV | 4.8% | 14.9% | +10.1% |
| CEC | 3.7% | 10.3% | +6.6% |
| CBS | 2.5% | 15.3% | +12.8% |
| CBCHP | 1.9% | 7% | +5.1% |
| CABC | 1.1% | 7.5% | +6.4% |
| CTST | 0.2% | 10.4% | +10.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, Q.; Chen, X.; Shen, B.; Fu, L. Low-Carbon Economic Dispatch of Agricultural Park Integrated Energy Systems Based on Improved Multi-Objective Grey Wolf Optimizer. Energies 2025, 18, 6138. https://doi.org/10.3390/en18236138
Pu Q, Chen X, Shen B, Fu L. Low-Carbon Economic Dispatch of Agricultural Park Integrated Energy Systems Based on Improved Multi-Objective Grey Wolf Optimizer. Energies. 2025; 18(23):6138. https://doi.org/10.3390/en18236138
Chicago/Turabian StylePu, Qianxi, Xiaoyuan Chen, Boyang Shen, and Lin Fu. 2025. "Low-Carbon Economic Dispatch of Agricultural Park Integrated Energy Systems Based on Improved Multi-Objective Grey Wolf Optimizer" Energies 18, no. 23: 6138. https://doi.org/10.3390/en18236138
APA StylePu, Q., Chen, X., Shen, B., & Fu, L. (2025). Low-Carbon Economic Dispatch of Agricultural Park Integrated Energy Systems Based on Improved Multi-Objective Grey Wolf Optimizer. Energies, 18(23), 6138. https://doi.org/10.3390/en18236138








