Waste Heat Recovery in a Transcritical Carbon Dioxide Vapor Compression Cycle with Thermoelectric Generators

Abstract

Thermoelectric generators are a great alternative for waste heat energy harvesting in several technological fields. Vapor compression refrigeration systems present great potential for waste heat energy harvesting as they dissipate heat in a condenser/gas cooler from the refrigerant to the ambient. This heat can be harvested by utilizing a thermoelectric generator. The objective of this study is to evaluate the energy harvesting potential of thermoelectric generators in transcritical vapor compression cycles and their effect on cycle performance. A computational model is used to simulate a transcritical carbon dioxide refrigeration cycle with the inclusion of a thermoelectric generator between the compressor and the gas cooler. The energy harvested by the generator is calculated, and the effect on the vapor compression system is quantified. The results show that by including the thermoelectric generator, two positive effects are obtained: the electrical energy generated by the thermoelectric system positively enhances the efficiency of the cycle, and the heat extracted in the generator leaves room for further cooling in the gas cooler, producing an increase in cooling capacity that also enhances efficiency. The results show an increase in the coefficient of performance that ranges between 3.74 and 12.14% for different working conditions.

1. Introduction

Waste heat recovery has emerged as a central strategy in the pursuit of more sustainable energy systems and an emissions-free future. Industrial processes, power generation, and thermal energy conversion technologies collectively reject vast quantities of heat into the environment. Estimates suggest that more than 50% of global primary energy consumption is ultimately lost as waste heat, with recovery potential ranging from low-grade (<100 °C) to high-grade (>400 °C) sources [1,2]. Even partial exploitation of these streams could substantially reduce fossil fuel demand and mitigate greenhouse gas emissions. As such, waste heat recovery is increasingly recognized as a cornerstone of the energy transition and a means to enhance overall energy efficiency.

Within this context, vapor compression refrigeration systems (VCRs) play a dual role. On one hand, they are indispensable technologies, providing critical services for food preservation, healthcare, industrial processes, and climate control; on the other hand, they represent a significant energy burden, with vapor compression systems alone accounting for approximately 20% of global electricity consumption [3]. These systems inherently reject large amounts of heat to the environment, particularly at the compressor discharge line and condenser (gas cooler for transcritical systems). Harnessing this low-grade waste heat would not only improve system sustainability but could also contribute to reducing operational costs and peak electricity demand.

A promising approach for this purpose is thermoelectric generation, which relies on the Seebeck effect to directly convert temperature gradients into electricity [4]. Thermoelectrics are attractive for integration with VCRs due to their compactness, reliability, and ability to operate under transient conditions without moving parts. However, the field of thermoelectric generator (TEG) integration in refrigeration systems remains largely unexplored, with only a handful of studies addressing this potential.

Rachmanita et al. (2021) explored the potential of converting condenser waste heat (60 to 70 °C) from cold storage units into electricity using TEGs. The study used a water-cooling system for the cold side consisting of the water fluid, water block, pump, mini radiator, and a fan. However, the necessary energy used to power the fans and the water pump was not considered. The researchers managed to obtain up to 1.52 W of electrical power when the hot side of the thermoelectric device was at 110 °C, and enhanced average efficiency by 2% [5].

Attar et al. (2021) explore the introduction of a TEG as a de-superheating system located after the compressor in a R134a refrigeration cycle. The study remarks that the output power of the TEG unit is found to be sufficient for driving the fan of the TEG air-cooling heat sink, obtaining a passive de-superheating system. The authors report an increase in the coefficient of performance (COP) ranging from 17% to 32%, depending on the condenser and evaporator loads, by further cooling the refrigerant with the aid of the proposed desuperheater [6].

Roungbungrud et al. (2022) developed a stand-alone TEG that utilizes heat from the refrigerant exiting the condenser and is self-cooled by the condensate water from a split-type air-conditioning system. This design enhances the energy efficiency of the VCR by converting waste heat into electricity, reducing overall energy consumption and increasing the COP by 3% [7].

Mona et al. (2022) investigated the feasibility of harvesting energy from a split-type air-conditioning system that uses R22 as a refrigerant. The study obtains a limited power output between 3.15 and 4.28 mW with their proposed TEG configuration [8].

Wiriyasart et al. (2023) used a closed-loop heat sink TEG in a refrigeration system. The system utilized a concentric-tube heat exchanger to capture waste heat from the discharge line for producing the hot reservoir in the TEG. The cold fluid was produced by the refrigeration system itself, which can be detrimental as the cooling of the refrigeration system is not used for its original purpose. The proposed approach hinders the effective cooling capacity of the refrigerator and could result in a counterproductive system. The authors state that with the proposed approach, the system reduces energy consumption by approximately 23% [9].

Abdulhamed et al. (2023) aimed to develop TEGs to capture waste heat from the filter dryer receiver of an air-conditioning unit. The researchers obtained 0.2 W of output power and suggest that this otherwise wasted heat could be used to power low-power devices such as emergency signs in a building [10].

Nandanwar et al. (2023) examined the integration of TEGs alongside phase change materials into VCRs. The proposed configuration introduces the phase change material between the condenser and the expansion valve, subcooling the refrigerant and providing a hot side for the TEG. The cold side was served by an aluminum vessel carrying the condensed water yield accumulated from the evaporator coils. The results show an improvement in the COP between 4 and 7% with the novel combination of phase change materials, TEGs, and VCRs [11].

Recently, Sabbaghi et al. (2025) assessed a new integrated system combining an organic Rankine cycle and a VCR that contained a TEG unit. The system aimed to optimize energy and exergy efficiencies, economic viability, and environmental sustainability, contributing to hydrogen production through sustainable energy sources. The proposed hybrid system is able to produce 145.5 kW of cooling, 513.6 kW of heat, and 37.93 kW of electricity, showing the potential for TEGs in combination with VCRs [12].

These few studies show the potential to harvest waste heat in VCRs with the use of TEGs and the promising combination of technologies. It is worth remarking that, within the literature, most of the work involves an active cooling of the cold side of the thermoelectric module (TEM), which results in auxiliary consumption that is generally not considered for calculating enhanced efficiency. Aranguren et al. (2018) demonstrated that up to a 40% reduction in net energy generated is directly related to the auxiliary consumption of a TEG [13]. Auxiliary consumption has been shown to be a critical factor in thermoelectric generation, and the use of passive heat exchangers, such as heat pipes or thermosyphons, is considered the best option in order to eliminate the extra consumption and increase net energy generation.

In addition, all the referenced work has been performed in condensing vapor compression systems, and no research has been performed on transcritical systems. Transcritical cycles reject heat to the ambient above the critical point and make use of a gas cooler instead of a condenser to dissipate that heat. The main refrigerant that undergoes this particular cycle is carbon dioxide (CO₂); when ambient temperature exceeds a certain value, CO₂ VCRs must operate under transcritical conditions above the critical point [14].

Driven by the F-Gas regulation of the European Parliament and of the Council for Fluorinated Greenhouse Gases, the use of CO₂ as a natural refrigerant has drastically risen in the past few years, and with it, the use of transcritical VCRs [15]. The number of retail sites using transcritical CO₂ in Europe reached 95,600 in 2024, a 33% increase compared to 2023, when there were around 71,800 sites. Specifically for the industrial sector, sites using CO₂ systems in Europe grew from approximately 3300 in 2023 to 4900 in 2024, a growth of about 48% [16].

As a refrigerant, carbon dioxide has great qualities such as zero ozone depletion potential, almost negligible global warming potential, plus it is non-toxic, non-flammable, and widely available. Due to its rising popularity, several studies have focused on improving the efficiency of transcritical CO₂ VCRs. The main strategy is the use of hybrid configurations to boost the COP, such as mechanical subcooling, thermoelectric subcooling, economizers, boosters, and ejectors.

Llopis et al. (2015) performed a theoretical analysis to assess how mechanical subcooling affects operating parameters and energy use in a transcritical VCR. They found that the subcooling cycle shifts the optimal gas-cooler pressure and increases COP significantly, particularly at high ambient temperatures. The study concludes that mechanical subcooling is a viable method to improve the performance of transcritical CO₂ systems up to 20% [17].

Gullo et al. (2016) aimed to assess the energy and environmental performance of various CO₂ booster supermarket refrigeration systems operating in warm climates. They found that enhanced CO₂ booster systems with parallel compression or mechanical subcooling could achieve competitive energy performance while reducing total equivalent warming impact. The study concludes that optimized CO₂ architectures are suitable for warm-climate applications, reducing total equivalent warming impact by at least 9.6% [18].

Gullo et al. (2017) evaluated the performance of a transcritical CO₂ booster refrigeration plant equipped with multiple ejectors and integrated air-conditioning in a supermarket environment. The researchers conducted modeling and experimental analyses to measure how the multi-ejector arrangement and integrated air-conditioning load affect system compressor work, COP, and cooling capacity under varied ambient conditions. Energy savings between 15.6% and 27.3% could be accomplished with the multi-ejector concept proposed [19].

Catalán-Gil et al. (2020) focused on how different economizer arrangements affect the performance of CO₂ booster refrigeration systems. The authors found that certain arrangements improved compressor efficiency and overall COP, which allowed for obtaining energy savings up to 8.5% [20].

Casi et al. (2022) experimentally evaluated a transcritical CO₂ refrigeration plant equipped with a thermoelectric subcooler combined with an internal heat exchanger. Results showed COP and cooling capacity improvements of up to 22.4% at optimal operation, demonstrating the feasibility of thermoelectric subcooling for small-scale systems [21].

Several hybrid configurations have been studied over the past years to boost the efficiency of transcritical CO₂ VCRs. However, the integration of TEGs in transcritical VCRs to boost the COP has not yet been studied, although the potential for energy recovery is vast, and the number of CO₂ VCRs keeps rising.

The following manuscript aims to study, for the first time, the integration of a TEG in a transcritical CO₂ VCR between the compressor and the gas cooler. The outlet of the compressor corresponds to the highest temperature point of the cycle just before the heat rejection phase in the gas cooler. Including a TEG in this location would ensure the highest performance of the TEG and aid heat rejection before entering the gas cooler.

The main objective is to quantify the increase in the COP and analyze the effect of the inclusion of a TEG in the refrigeration cycle through a computational model. In addition, the proposed TEG utilizes passive heat exchangers for the cold side in order to eliminate auxiliary consumption, as this has been shown to be critical in TEGs. Section 2 describes the computational model that has been developed for this work, which consists of a transcritical CO₂ VCR model and a TEG model that work together; in Section 3, the obtained results are presented; and in Section 4, the conclusions are drawn.

2. Methodology

A computational model is developed to simulate the behavior of a transcritical CO₂ VCR with the inclusion of a TEG between the compressor and the gas cooler. The model is able to solve the thermodynamic cycle, the TEG, and obtain the global COP of the combined solution. The model is divided into 2 submodels that work together: the transcritical CO₂ VCR submodel explained in Section 2.1, and the TEG submodel described in Section 2.2. The model sequence is further explained in Section 2.3.

2.1. Transcritical CO₂ VCR Submodel

The transcritical CO₂ VCR submodel simulates a single-stage VCR that uses CO₂ as a refrigerant in a transcritical state. It is capable of calculating the pressure, temperature, and enthalpy of the main thermodynamic points, mass flow rate of CO₂ through the installation, electrical consumption of the compressor, cooling capacity produced at the evaporator, and the COP of the VCR. A schematic of the CO₂ VCR system is presented in Figure 1: point 1 corresponds to the outlet of the evaporator; point 2 represents the inlet of the compressor; point 3 represents the outlet of the compressor and the inlet of the TEG; point 4 corresponds to the outlet of the TEG and the inlet of the gas cooler (when no TEG is included point 3 and 4 are the same); point 5 represents the outlet of the gas cooler and the inlet to the back-pressure valve; point 6 is located at the outlet of the back-pressure valve and corresponds to the inlet to the deposit; point 7 represents the outlet of the deposit and the inlet to the expansion valve that controls the superheating on the evaporator; and point 8 corresponds to the exit of the expansion valve and inlet to the evaporator.

For the vapor compression model, steady-state conditions are considered. Pressure losses are negligible in comparison with the high pressures of transcritical CO₂ VCRs and, therefore, pressure losses alongside the circuit are not considered. Lastly, the pipes and the expansion valves are considered adiabatic; hence, no heat losses are considered for those components.

The inputs needed for the VCR submodel are the evaporation level ($T_{evap}$), useful superheating ($USH$), non-useful superheating ($NUSH$), gas-cooler pressure ($P_{gc}$), and ambient temperature ($T_{amb}$). The submodel is coded in MATLAB 2024a and makes use of Refprop V9.1 to obtain the thermodynamic properties of the cycle. In addition, the outputs from the TEG submodel are used for the resolution of the thermodynamic cycle. Ambient temperature is fixed at 30 °C, useful superheating is set to 4 K, and non-useful superheating is set to 6 K.

Firstly, the evaporation pressure level ($P_{evap}$) is obtained using the evaporation temperature at a saturated state, which corresponds to the pressure of points 1, 2, and 8. Pressure drops in the evaporator are supposed to be negligible in comparison with the high working pressures of CO₂. The pressure of points 3, 4, 5, 6, and 7 corresponds to the gas-cooler pressure, which is set to a constant value and controlled by the back-pressure valve. The temperature of point 1 is obtained by adding the useful superheating to the evaporation temperature (Equation (1)). Then, the inlet of the compressor is obtained by adding the non-useful superheating of the cycle (Equation (2)).

$$T_1=T_{evap}+USH$$

(1)

$$T_2=T_1+NUSH$$

(2)

where the volumetric efficiency of the compressor is represented by $R_v$; the global efficiency is represented by $R_g$; and the volumetric capacity is represented by $V_g$. The volumetric capacity of the hermetic compressor is 1.1 cm³ and works at 2900 rpm. The compressor was experimentally characterized from data obtained in previous work, and the experimental expressions used for its calculation are listed in Equations (3)–(5) [22]. The experimental coefficients $a_0-a_3$, $b_0-b_3$, and $c_0-c_3$ are listed in

Table 1. Experimental coefficients for the compressor characterization: ${\mathrm{P}}_{\mathrm{g}\mathrm{c}}$ (bar) = [60–100], ${\mathrm{T}}_2$ (°C) = [60–110], and ${\mathrm{T}}_{\mathrm{a}\mathrm{m}\mathrm{b}}$ (°C) = [21–35].

Volumetric Efficiency (${\mathit{R}}_{\mathit{v}}$)	Global Efficiency (${\mathit{R}}_{\mathit{g}}$)	Discharge Temperature (${\mathit{T}}_3$)
$a_0=0.997746299637375$	$b_0=0.483249140074624$	$c_0=11.70078013773214$
$a_1=-0.003305417995612$	$b_1=0.000149946856172$	$c_1=0.828771963340796$
$a_2=0.001806359923658$	$b_2=0.001454611396738$	$c_2=0.590547039298177$
$a_3=-0.000209827908659$	$b_3=0.000128243018925$	$c_3=0.426135218164438$
$Max. Deviation=5.2\%$	$Max. Deviation=6.4\%$	$Max. Deviation=2.8\%$

. The experimental data range for characterization and the maximum deviation are included in the table. T3 corresponds to the discharge temperature of the compressor before entering the TEG.

$$R_v=a_0+a_1·P_{gc}+a_2·T_2+a_3·T_{amb}$$

(3)

$$R_g=b_0+b_1·P_{gc}+b_2·T_2+b_3·T_{amb}$$

(4)

$$T_3=c_0+c_1·P_{gc}+c_2·T_2+c_3·T_{amb}$$

(5)

The geometrical volumetric flow rate of the refrigerant (${\dot{V}}_{ref}$) is obtained by Equation (6), and the mass flow rate of the refrigerant (${\dot{M}}_{ref}$) is obtained by Equation (7), which takes into consideration the volumetric efficiency and the specific volume at the inlet of the compressor ($V_2$). Then, the electrical consumption of the compressor (${\dot{W}}_{comp}$) is obtained by Equation (8), where $h_{3s}$ corresponds to the enthalpy at the outlet of the compressor for an isentropic process, and $h_2$ corresponds to the enthalpy at the inlet of the compressor.

$${\dot{V}}_{ref}=V_g·rpm$$

(6)

$${\dot{M}}_{ref}=V_{ref}·R_v/V_2$$

(7)

$${\dot{W}}_{comp}={\dot{M}}_{ref}·(h_{3s}-h_2)/R_g$$

(8)

The mass flow rate of the refrigerant (${\dot{M}}_{ref}$), the gas-cooler pressure ($P_{gc}$), and the temperature at the inlet of the TEG ($T_3$) are used as inputs for the TEG submodel. The TEG submodel calculates the outlet temperature of the refrigerant after the TEG (T4) and the power generated by the TEG (${\dot{W}}_{teg}$), amongst other values (the TEG submodel is further explained in Section 2.2). The gas cooler was also experimentally characterized with data from previous work [22]; the efficiency ($E_{gc}$) is calculated as a function of the gas-cooler pressure and the mass flow rate according to Equation (9). The experimental coefficients are presented in

Table 2. Experimental coefficients for the efficiency of the gas cooler: ${\mathrm{P}}_{\mathrm{g}\mathrm{c}}$ (bar) = [60–100] and ${\dot{M}}_{ref}$ (°C) = [6.3–18.7].

Efficiency of the Gas Cooler (${\mathit{E}}_{\mathit{g}\mathit{c}}$)
$d_0=0.90299$
$d_1=0.0015020964$
$d_2=0.0018220024$
$d_3=-0.0000081906$
$d_4=-0.0001224563$
$Max. Deviation=0.7\%$

, alongside the experimental data range and the maximum deviation.

$$E_{gc}=d_0+d_1·P_{gc}+d_2·{\dot{M}}_{ref}+d_3·{P_{gc}}^2+d_4·{{\dot{M}}_{ref}}^2$$

(9)

Using the efficiency of the gas cooler, the outlet temperature of the gas cooler, and ambient temperature, point 5 is calculated using Equation (10). Lastly, the enthalpies of points 6, 7, and 8 are the same, completing the thermodynamic cycle. The cooling capacity (${\dot{Q}}_0$) is obtained by Equation (11) and the COP by Equation (12). The electrical power generated by the TEG reduces the total energy demand of the refrigeration cycle, aiding efficiency and enhancing the COP. For the base cycle, the COP is calculated by dividing the cooling capacity by the power consumption of the compressor. In the case of the cycle with the TEG, the power generated by the TEG is subtracted from the denominator as the net power energy consumption is lower.

$$T_5=T_4-E_{gc}·(T_4-T_{amb})$$

(10)

$${\dot{Q}}_0={\dot{M}}_{ref}·(h_1-h_8)$$

(11)

$$COP={\dot{Q}}_0/({\dot{W}}_{comp}-{\dot{W}}_{teg})$$

(12)

2.2. TEG Submodel

The TEG submodel simulates a TEG that harvests heat from a constant flow of CO₂ and uses the ambient as the cold reservoir. It obtains the power generated by the TEMs, heat rates, temperature distribution at the TEG, and outlet temperature of the refrigerant. The TEG is subdivided into several TEG blocks. Each block consists of one copper-plate heat exchanger for the refrigerant, two thermoelectric modules, and two passive heat exchangers (heat pipes). A schematic of one TEG block is shown in Figure 2.

For the TEG model, steady-state conditions are considered. Temperature-dependent thermoelectric properties are taken into account for both the p and the n legs. In addition, the four thermoelectric effects alongside Fourier’s law of heat transfer are considered.

The generation submodel is based on the finite differences implicit method for one-dimensional heat transfer; it is coded in MATLAB and is based on a previous model in which the main outputs are calculated with a maximum deviation of 8% [23]. It is based on a thermal–electrical analogy to simulate the system, and each block of the TEG is discretized in 16 nodes, as shown in the schematic of Figure 3. The resistances showcased in the schematic correspond to thermal resistances of the different elements of the TEG.

The hot refrigerant is represented by node 1, and the surrounding ambient air corresponds to node 16. The copper-plate heat exchanger corresponds to node 2, and the cold-side heat pipes are represented by node 15. The TEMs are represented from nodes 3 to 14; nodes 3 and 14 define the ceramic plates; and between nodes 2 and 13, the thermoelectric materials and junctions are represented. From Rn_1,2 to Rn_9,10, the n-type leg is divided into 9 equal-length segments, and from Rp_1,2 to Rp_9,10, the p-type leg is divided into 9 equal-length segments in order to precisely represent the change in thermoelectric properties with temperature. The TEMs are bismuth telluride commercial modules from Marlow Industries with 127 thermocouples (TG12-8) and are connected to their optimum load resistance value, which is determined by the model.

The heat exchanger for the hot side consists of a copper plate in which an internal channel was machined to allow the CO₂ to flow through. Seen in Figure 4. The thermal resistance of the copper-plate heat exchanger for the hot side is obtained using the area and the heat transfer coefficient, as in Equation (13). The heat exchange area ($A_{hot\_hx}$) corresponds to 0.004 m², and the heat transfer coefficient is calculated using the Gnielinski correlation for internal forced convection ($h$), which was shown to be accurate for transcritical CO₂ [21,24].

$$R_{hot\_hx}=1/(A_{hot\_hx} · h)$$

(13)

The thermal contact resistances for both the hot and the cold side ($R_{hot\_cont}$ and $R_{cold\_cont}$) follow Equation (14). The area of the thermal interface material ($A_{tim}$) is the same as the area of the TEM, 40 × 40 mm, and the thermal impedance of the thermal interface material ($Z_{tim}$) was obtained experimentally from previous experimental data and is equal to 0.000056 m²K/W [25].

$$R_{hot\_cont} =R_{cold\_cont}=Z_{tim}/A_{tim}$$

(14)

The heat-pipe-based heat exchanger for the cold side consists of 4 copper water heat-pipe tubes with a length of 400 mm. The heat pipes are embedded in an aluminum plate on one end, and the rest are covered with aluminum fins. The cold heat exchanger is depicted in Figure 5. The heat exchanger was experimentally characterized in previous studies for a different application [26]. The thermal resistance of the proposed heat pipes barely changes with ambient temperature or heat flux; therefore, a constant value of 0.61 K/W was used for the computational model.

The Peltier, Seebeck, Thomson, and Joule effects that occur between nodes 3 and 13, alongside Fourier’s law, are introduced by Equations (15)–(19).

$${\alpha }_{AB}=dE/dT={\alpha }_A-{\alpha }_B$$

(15)

$${\dot{Q}}_{Peltier}=\pm {\pi }_{AB}=\pm IT({\alpha }_A-{\alpha }_B)$$

(16)

$${\dot{Q}}_{Thomson}=-\sigma \overrightarrow{I} (\overrightarrow{∆T})$$

(17)

$${\dot{Q}}_{Joule}=R_o{I}^2$$

(18)

$$\rho c_p{\displaystyle \frac{\partial T}{\partial t}}=k\left({\displaystyle \frac{{\partial }^{2}T}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}T}{\partial y^2}}+{\displaystyle \frac{{\partial }^{2}T}{\partial z^2}}\right)+\overrightarrow{q}$$

(19)

Table 3. Physical dimensions, materials, and thermal resistances obtained during the simulations.

	Dimensions	Materials	Thermal Resistance
Hot HX	56 × 56 × 12 mm3	Copper	0.052–0.174 K/W
Cold HX	75 × 400 × 12 mm3	Copper and Aluminum	0.612 K/W
TEMs	40.1 × 44.7 × 3.6 mm3	Bi2Te3 and Ceramic	1.175–1.243 K/W

collects the dimensions, materials, and thermal resistances obtained during the simulations of the main elements of the TEG: hot-side heat exchanger, cold-side heat exchanger, and thermal resistance. The thermal resistance for the hot heat exchanger changes drastically depending on the mass flow rate moved by the compressor and the temperature of the refrigerant within the TEG block. For TEMs, slight changes can be appreciated, as depending on the temperature, the thermal properties of the materials slightly shift.

The main outputs from the transcritical CO₂ VCR submodel that are used as inputs for the TEG submodel are the discharge temperature of compressor ($T_3$) and the mass flow rate of the refrigerant (${\dot{M}}_{ref}$). In addition, the ambient temperature and the gas-cooler pressure need to be introduced as inputs (already introduced for the CO₂ VCR submodel).

The TEG submodel simulates one TEG block at a time. In the first step, temperatures are supposed for each node of the TEG and the thermal–electrical analogy is solved. Heat fluxes and power generation are calculated, and the temperature distribution is obtained for the next step. When the difference between temperatures in the previous step and the actual one is lower than a tolerance value in each node ($Tol. = 0.001 °\mathrm{C}$), the TEG block is solved. To obtain the maximum output power of the TEG, the model also includes an internal loop where the load resistance is increased until maximum output power is obtained.

2.3. Model Sequence

The interaction between the models is further depicted in the flowchart diagram of Figure 6 and explained below.

The computational model starts with the input parameters of the vapor compression cycle: evaporation temperature ($T_{evap}$), useful superheating ($USH$), non-useful superheating ($NUSH$), gas-cooler pressure ($P_{gc}$), and ambient temperature ($T_{amb}$). The first part of the vapor compression cycle submodel is solved by calculating point 1, point 2, and point 3 of the cycle, as explained in Section 2.1.

After calculating point 3, the TEG submodel is already capable of solving the generator. The TEG is solved block by block. To start with, for the first TEG block, the inlet temperature of the first block is obtained by introducing the outlet temperature of the compressor ($T_3$). In addition, the load resistance of each TEM is set to its initial value. Lastly, the outlet temperature of the TEG block is set to the inlet temperature in order to initialize the iterative process.

The TEG block is calculated as described in Section 2.2, via an iterative process and by solving the thermal–electrical analogy of the generator. Heat fluxes, power generation, and temperature distribution are obtained for the TEG block. To obtain the optimum output power of the TEMs, the model also includes another loop. In this loop, the load resistance is increased until the output power starts decreasing in comparison with the last load resistance. Then, the model takes the last load resistance as the optimum resistance for that particular case, and the maximum power output of the TEG block is obtained.

If the TEG is composed of several blocks, the outlet temperature of the previous block is introduced as the inlet temperature for the following one, repeating this process until the last block is calculated. When the last block is calculated, the outlet temperature of the last TEG block corresponds to the outlet temperature of the whole TEG and the inlet of the gas cooler ($T_4$), finishing the calculation of the TEG submodel.

Finally, the second part of the vapor compression cycle can be calculated as described in Section 2.1. With both submodels solved, the main variables are collected, and the next case can be solved. The model is generally used to simulate several cases with different evaporation temperatures, pressure levels, number of TEG blocks, etc.

3. Results

The computational model is utilized to quantify the inclusion of the TEG in a transcritical CO₂ VCR. To fairly compare the effect of the TEG, a baseline needs to be obtained for the transcritical CO₂ VCR; for that, the computational model is used to simulate the behavior of the base cycle for the transcritical VCR, outlined in Section 3.1. In Section 3.2, the TEG is included, and the effect of the generation system on the transcritical VCR is quantified.

The COP of the transcritical CO₂ cycles changes drastically as the pressure of the gas cooler is modified. For that, most systems use a back-pressure valve to modify the pressure to its optimum point. Therefore, the model is tested for different gas-cooler pressures to obtain the optimal point for both the base cycle and the cycle with TEG.

3.1. Transcritical CO₂ VCR Base Cycle

The base cycle will serve as a baseline to compare the inclusion of the TEG in the transcritical CO₂ VCR cycle. The COP, cooling capacity, and optimum gas-cooler pressure will be compared and analyzed.

To obtain information over a range that can be applied to different applications, the evaporation level is modified between 0 and −30 °C, which covers beverage coolers, refrigerators (household or commercial), chillers, and freezers (household or commercial).

To capture the effect of the gas-cooler pressure in the COP, the pressure is modified in 1-bar intervals up to 94 bar.

The rest of the input parameters are set to a constant value to limit the scope of this study. Ambient temperature is set to 30 °C to ensure that the cycle works over the transcritical point. The useful superheating for the system is set to 4 K, which is widespread for commercial refrigerators. Lastly, the non-useful superheating is set to 6 K, which has been measured in various experimental systems in previous studies [21,27].

Figure 7 shows the results obtained for the base cycle simulations. The COP is represented as a function of the gas-cooler pressure for four different evaporation levels: 0, −10, −20, and −30 °C. The optimum value for the gas-cooler pressure for each evaporation temperature is collected in

Table 4. Optimum COP values for the base transcritical cycle.

Evaporation Level (°C)	COP	Qo (W)	Gas-Cooler Pressure (bar)
$0$	$1.92$	764.6	$82$
$-10$	$1.44$	586.1	$80$
$-20$	$1.08$	431.6	$81$
$-30$	$0.82$	306.8	$81$

, alongside COP and cooling capacity.

3.2. Transcritical CO₂ VCR with TEG

As mentioned in Section 2.2, the TEG is modeled as subsequent TEG blocks. Each block consists of one hot-side copper-plate heat exchanger, two TEMs, and two cold-side heat-pipe-based heat exchangers. The number of TEG blocks is also considered an input parameter for the computational model, and it changes from 1 to 10 so the effect of a smaller or larger TEG can be captured with the computational model. The larger TEG that is modeled consists of 10 TEG blocks, comprising the following: 10 hot-side copper-plate heat exchangers, 20 TEMs, and 20 cold-side heat-pipe base heat exchangers.

3.2.1. COP

Firstly, the COP is compared between the base cycle and the cycle with TEG. Figure 8 shows the COP of the cycle as a function of the gas-cooler pressure for the base cycle and the cycle with the maximum number of blocks simulated (10 TEG blocks).

The COP is enhanced at every evaporation temperature and at every gas-cooler pressure. By the inclusion of the TEG, COP is increased by 12.14, 6.95, 4.76, and 3.74% for evaporation levels of 0, −10, −20, and −30 °C, respectively. The COP increase is found to happen due to two different factors: firstly, the energy generated by the thermoelectric generator enhances energy efficiency of the cycle as it decreases the total consumption of the cycle; and secondly, the TEG rejects heat into the ambient, letting the refrigerant enter the gas cooler at a lower temperature and allowing the gas cooler to further cool the refrigerant, thus increasing the specific cooling capacity of the cycle.

Another important remark is that the optimum gas-cooler pressure decreases between 2 and 5 bar depending on the evaporation level. In addition, due to the lower outlet temperature of the gas cooler, the cycle is able to work under stable conditions for lower values of the gas-cooler pressure. This effect seems to be greater for lower evaporation temperatures, in this case, 0 and −10 °C.

Figure 9 shows the effect of a smaller or larger TEG in comparison with the base cycle. The straight line corresponds to the COP of the base cycle at its optimum gas-cooler pressure, which was introduced in Section 3.1. Each point of the cycle with TEG is represented for its optimum gas-cooler pressure, which changes as the number of TEG blocks is modified. The optimum gas-cooler pressure drops as the number of TEG blocks increases.

Firstly, the COP is increased by including any number of TEG blocks for every evaporation level. It is clear to see that the larger the TEG, the greater the increase in COP. As the number of TEG blocks increases, the enhancement in the COP obtained by adding each block is lower than the previous one. This can be explained by the fact that each TEG block introduced has a lower inlet temperature and, thus, lower generation potential. The cooling of the refrigerant produced in each TEG block also decreases as the number of TEG blocks rises; therefore, the positive effect on the gas cooler is also less noticeable.

3.2.2. Power Generated

Figure 10 showcases the total power generated by the TEG as a function of the gas-cooler pressure with the maximum number of TEG blocks (10 TEG blocks). The highlighted circles represent the value for the optimum COP of the gas-cooler pressure. Greater values for the power generated with the TEG are obtained for greater gas-cooler pressures. However, those gas-cooler pressures result in lower total COP of the VCR.

Power generated by the TEG is larger for higher values of the gas-cooler pressure due to an increase in outlet temperature of the compressor, thus raising the hot-side temperature of the TEMs. The other value that affects power generation is the mass flow rate of the compressor, which decreases as the gas-cooler pressure rises due to an increase in the pressure ratio of the compressor. In this case, in terms of power generation, the higher temperature compensates for the lower mass flow rate of the compressor, and power generation rises alongside gas-cooler pressure.

It is important to state that the optimum value for the COP is obtained for gas-cooler pressures that are not optimum from the power-generation perspective. This clearly shows that the focus should be on obtaining the maximum COP for the combined system and not maximizing power generation, which would result in a counterproductive system with lower COP.

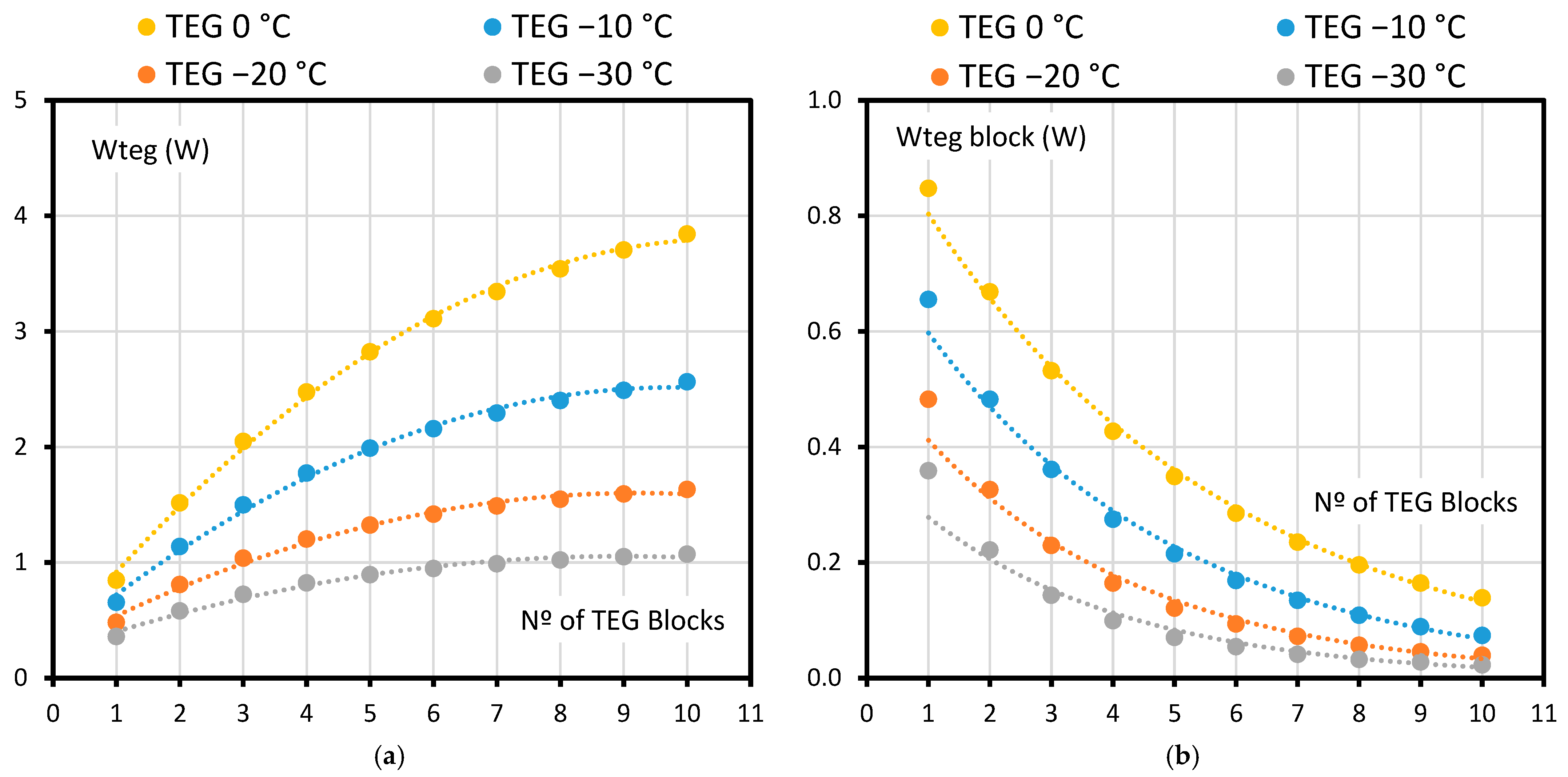
The power generated by the TEG changes as the number of TEG blocks is increased. Figure 11 shows that behavior clearly: graph (a) represents the total power generated by the TEG as the number of blocks increase; and (b) represents the power generated in each TEG block. Each data point depicted in these graphs corresponds to the value of gas-cooler pressure that maximizes the COP for each number of TEG blocks (as in Figure 9). The power generated by the TEG is greater for higher evaporation temperatures; this is explained by the fact that, for higher evaporation temperatures, the compressor is able to move a higher mass flow rate, resulting in a greater potential of heat to be harvested. It is important to note that the power generated by the last TEG blocks is really low as the input temperature becomes closer to ambient temperature, decreasing the harvesting potential of the latest TEGs.

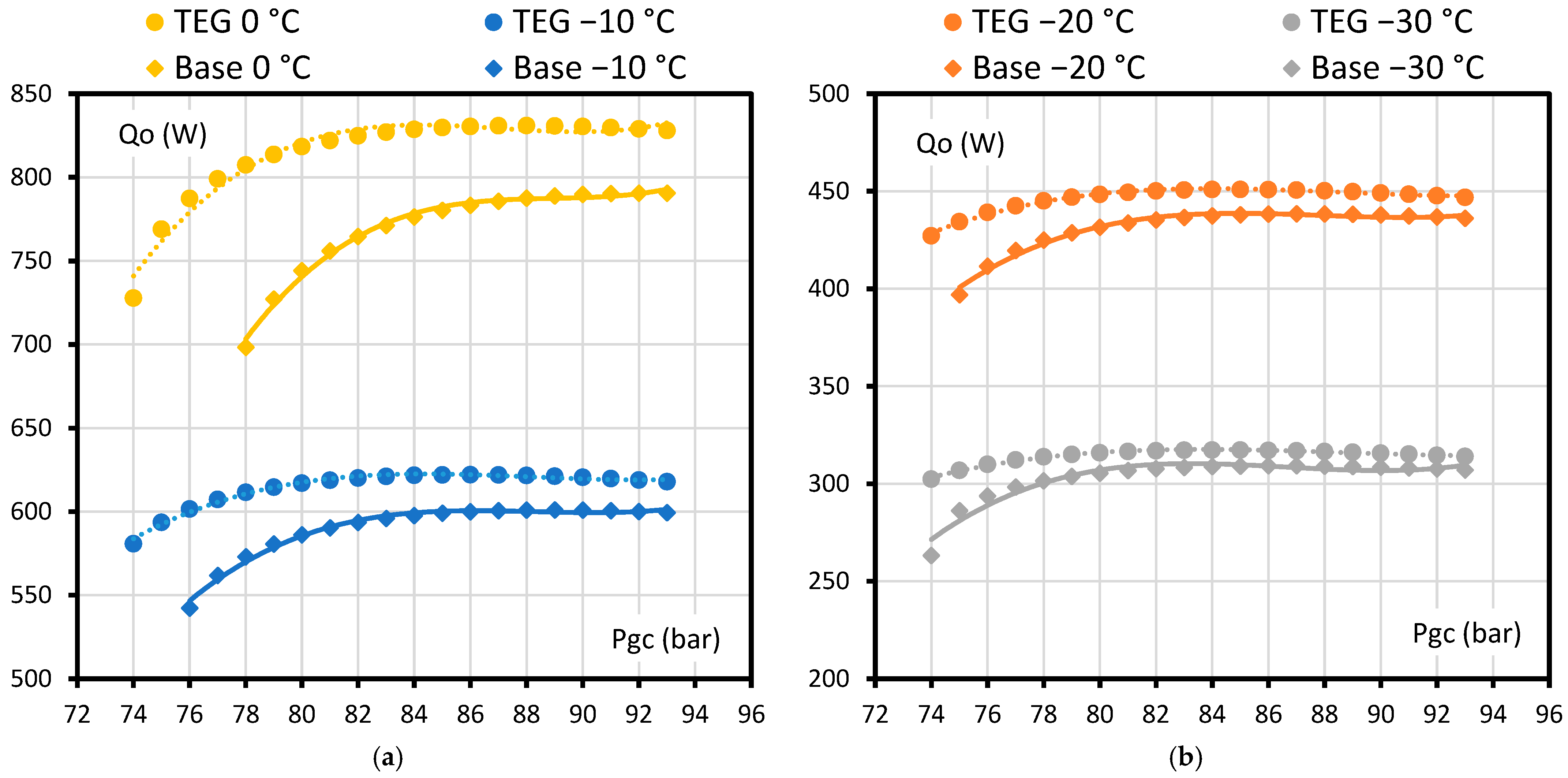
3.2.3. Cooling Capacity

The last discussed parameter is cooling capacity, which is also critical in the design process of refrigeration systems. Figure 12 depicts the cooling capacity of the system as a function of the gas-cooler pressure for the four evaporation levels that have been modeled (0, −10, −20, and −30 °C) with the maximum number of TEG blocks simulated (10 TEG blocks).

The cooling capacity of the VCR is increased by including the TEG for every evaporation level when compared with the base cycle. Larger increases in cooling capacity are obtained for the higher-evaporation-level temperatures.

As gas-cooler pressure increases, the specific cooling capacity increases between points 1 and 8. However, the mass flow rate is reduced due to an increase in the compression ratio. In terms of cooling capacity, when high gas-cooler pressures are simulated, the increase in specific cooling capacity does not compensate for the reduction in mass flow rate. This results in a decrease in the cooling capacity when the gas-cooler pressure is too high; notably, for higher gas-cooler pressures, neither the COP nor the cooling capacity is at maximum.

3.3. General Effect of the TEG

In this section, a global comparison is presented between the base cycle and the inclusion of the TEG. The results are collected in

Table 5. Global comparison of the inclusion of the TEG with 10 blocks in a transcritical CO₂ VCR.

	Base					With TEG							Comparison
Tevap (°C)	COP (/)	Q0 (W)	Pgc (Bar)	Mref (kg/h)	T5 (°C)	COP (/)	Mref (kg/h)	Pgc (Bar)	Wteg (W)	Effi. (%)	Mref (kg/h)	T5 (°C)	∆COP (%)	∆Qo (%)	∆Pgc (Bar)
$0$	1.919	765	82	19.67	32.76	2.153	20.11	77	3.74	1.02	20.11	30.96	12.14%	4.51%	−5
$-10$	1.440	586	80	14.40	31.73	1.540	14.60	77	2.56	0.86	14.60	30.48	6.95%	3.61%	−3
$-20$	1.083	432	80	10.33	31.29	1.135	10.47	77	1.69	0.71	10.47	30.28	4.76%	2.54%	−3
$-30$	0.825	307	81	7.25	31.11	0.856	7.32	79	1.16	0.59	7.32	30.20	3.74%	2.69%	−2

and commented on below. The table collects data for the four evaporation temperatures and compares the COP, cooling capacity, optimum gas-cooler pressure, mass flow rate, and outlet temperature of the gas cooler for both cases. In addition, the power generated by the TEG and the efficiency are included, as well as the comparison between the COP, cooling capacity, and optimum gas-cooler pressure. The efficiency corresponds to the global efficiency of the 10 TEG blocks.

The table clearly shows that the COP is enhanced by the inclusion of the TEG at every evaporation level, the increase of which ranges between 3.74 and 12.14%. The enhancement in the COP is obtained by two different factors: firstly, the power generated by the TEG decreases the necessary energy for the VCR; and secondly, the heat extracted at the TEG allows for further cooling in the gas cooler, increasing the specific cooling capacity of the cycle. In addition, the cooling capacity is enhanced between 2.69 and 4.51%, and the optimum gas-cooler pressure (value that maximizes COP) decreases between 2 and 5 bar.

4. Conclusions

In this work, the inclusion of a thermoelectric generator is studied for a transcritical carbon dioxide refrigeration system. The generator is to be located between the compressor and the gas cooler to take advantage of the high temperatures of the refrigerant. The proposed TEG does not include any moving parts, and ensures a long-term use of the combined system with simple system integration.

A computational model is used to quantify the effect of the thermoelectric generator and its impact on the refrigeration cycle. The computational model consists of two submodels that work together to solve the thermodynamic cycle and the generator.

The transcritical carbon dioxide vapor compression refrigeration system is solved from a thermodynamic approach using Refprop V9.1 to calculate properties while considering negligible pressure losses. The pipes and the expansion valves are considered adiabatic. In addition, a characterization of the compressor and gas cooler is used for further accuracy. The thermoelectric generator is solved by the finite difference method, taking into consideration the heat exchangers, the four thermoelectric effects, Fourier’s law, and the temperature-dependent thermoelectric properties. Both models assume steady-state conditions, are coded in Matlab, and work together to solve the complete vapor compression system with a thermoelectric generator.

The model is used to test the vapor compression system with and without the generator in order to quantify the effect of the inclusion of the thermoelectric system. The system is modeled for four evaporation temperatures: 0, −10, −20, and −30 °C. In addition, the gas-cooler pressure is modified to obtain optimum efficiency for each working condition and present a fair comparison.

By the inclusion of the thermoelectric generator, improvements of 12.14, 6.95, 4.76, and 3.74% are obtained for the coefficient of performance for evaporation temperatures of 0, −10, −20, and −30 °C, respectively. This enhancement in the efficiency is obtained due to two effects: firstly, the electrical energy generated by the thermoelectric system reduces the energy consumption of the refrigeration system; and secondly, the heat extracted at the thermoelectric generator leaves room for further cooling at the gas cooler, which results in a lower outlet temperature of the gas cooler and, thus, an increase in the specific cooling capacity of the cycle.

The cooling capacity of the system is also increased by 4.51, 3.61, 2.54, and 2.69% for evaporation temperatures of 0, −10, −20, and −30 °C, respectively. This enhancement in cooling capacity is a great result, as not only does the efficiency of the facility increase but also its capabilities.

When including the generator, the optimum value for the gas-cooler pressure that maximizes the coefficient of performance is found to decrease. Optimum gas-cooler pressure is reduced between 2 and 5 bars in comparison with the base cycle. This is also considered a positive outcome as it lowers the pressure requirements for the cycle components.

In conclusion, this work studies for the first time the inclusion of a thermoelectric generator in a transcritical vapor compression refrigeration cycle. The results show an improvement in the coefficient of performance up to 12.14%, an increase in the cooling capacity up to 4.51%, and a reduction in the optimum working pressure of up to 5 bar.

Regarding future work, thermal optimization of the heat exchangers, dimensions optimization of the TEMs, control integration strategies, or an economic analysis are possible future lines of research. This work serves as a first step in the integration of thermoelectric generators for transcritical vapor compression systems, showing great results that could be experimentally proven for future work.