Experimental Investigation of Equivalent Friction Coefficient Between Rope–Drum Mechanism and Pulley Transmission Loss for High-Altitude Wind Power Generation Systems
Abstract
1. Introduction
2. Structural Design and Working Principle of Test Bench
2.1. Structural Module Design
- (1)
- Loading module
- (2)
- Power module
- (3)
- Test module
- (4)
- Data Acquisition module
- (5)
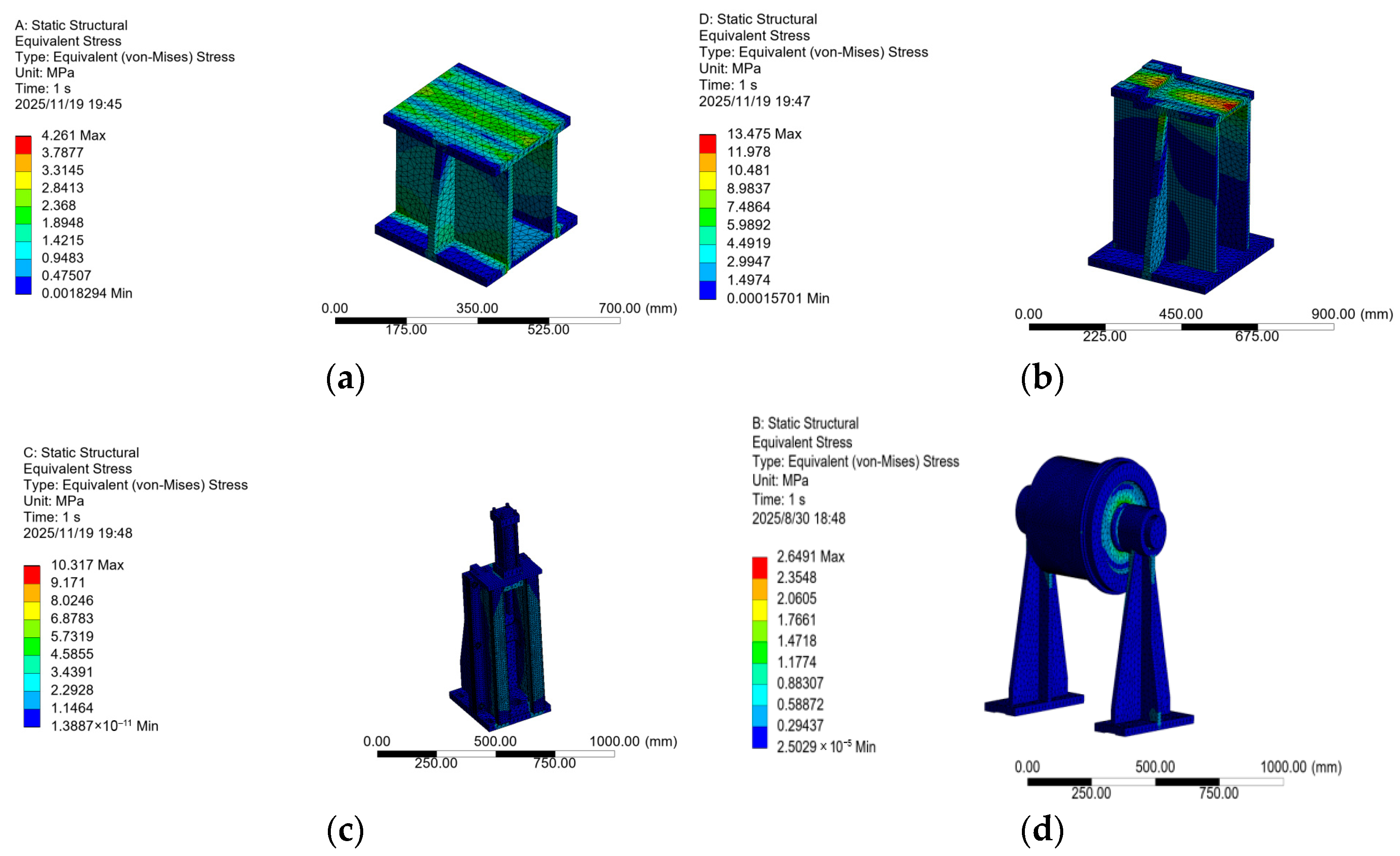
- Main load components analysis
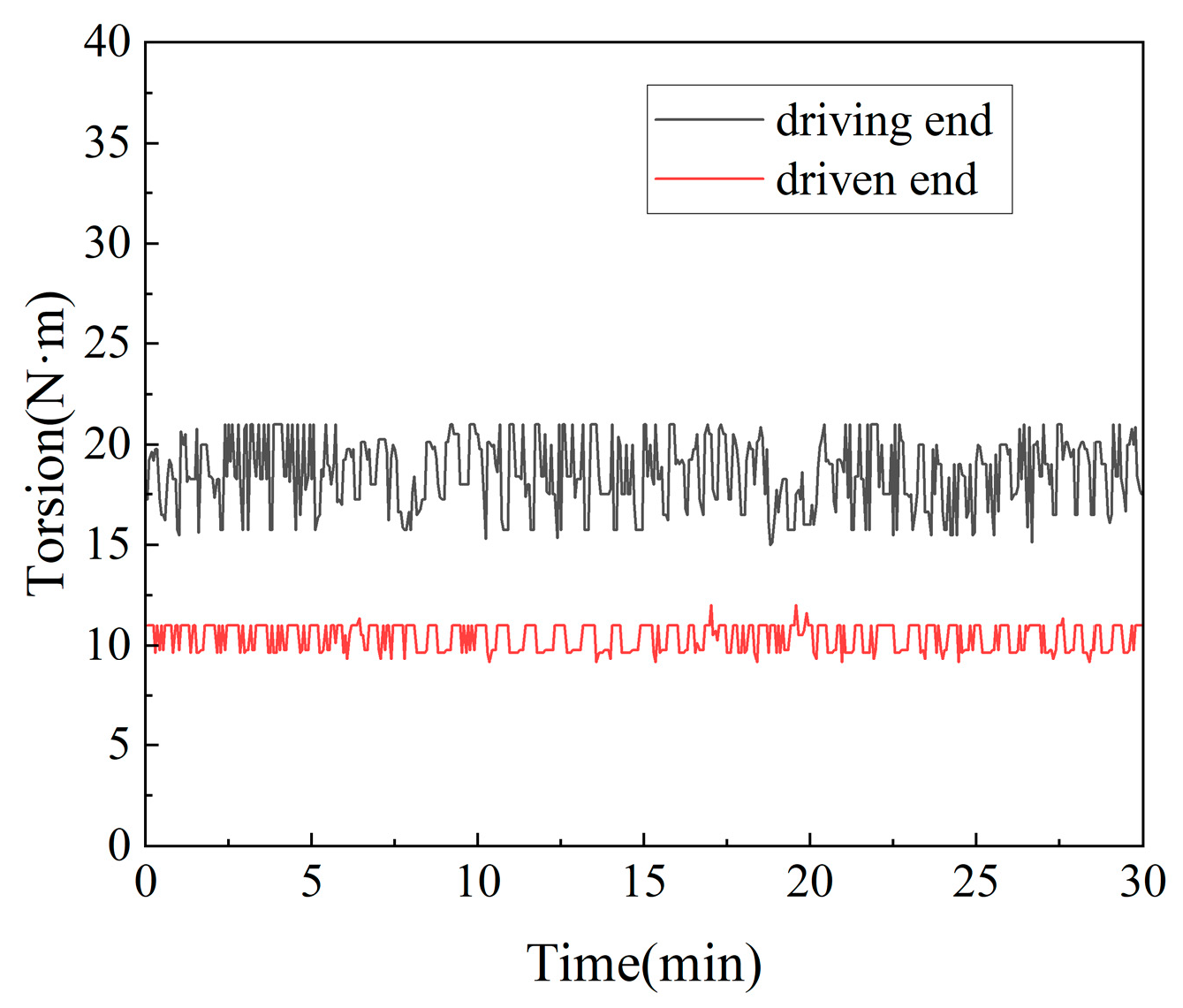
2.2. Working Principle
3. Equivalent Friction Coefficient Experiment
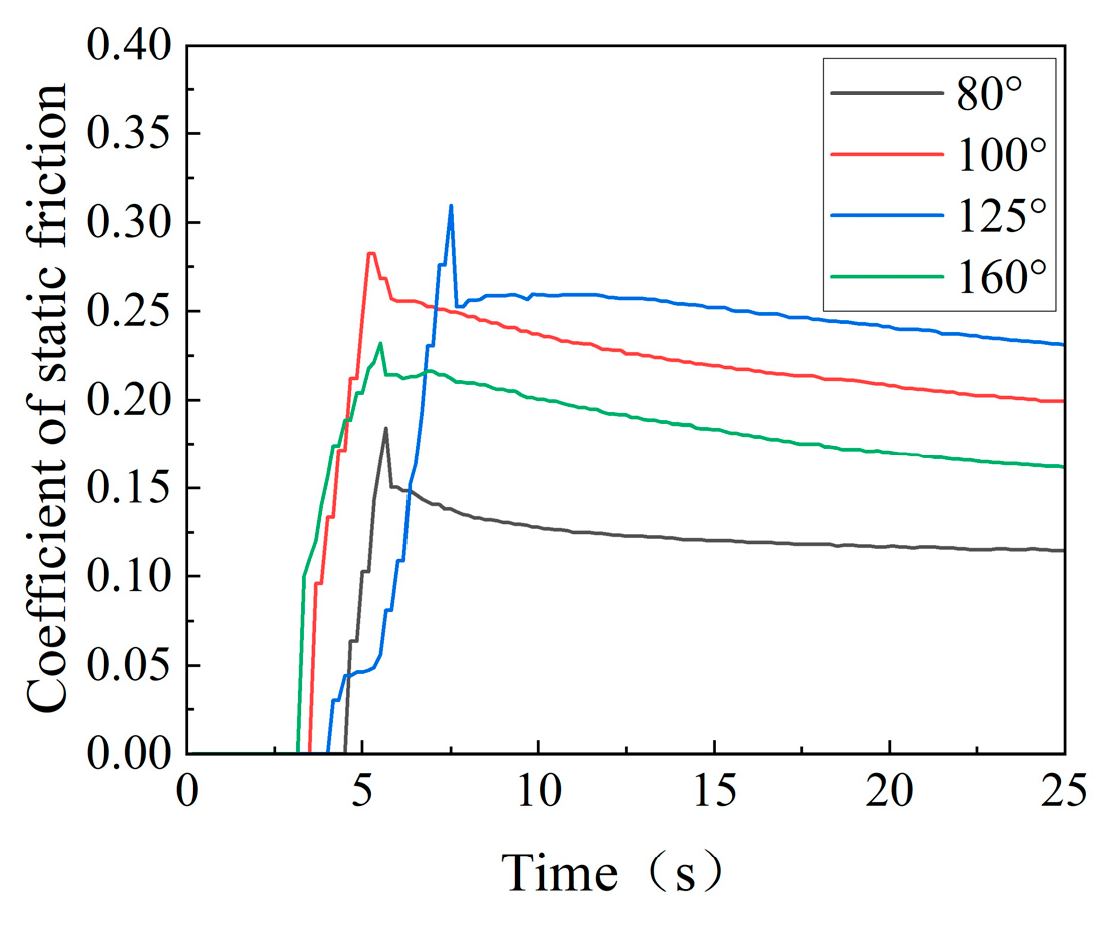
3.1. Influence of Contact Angle on Equivalent Friction Coefficient
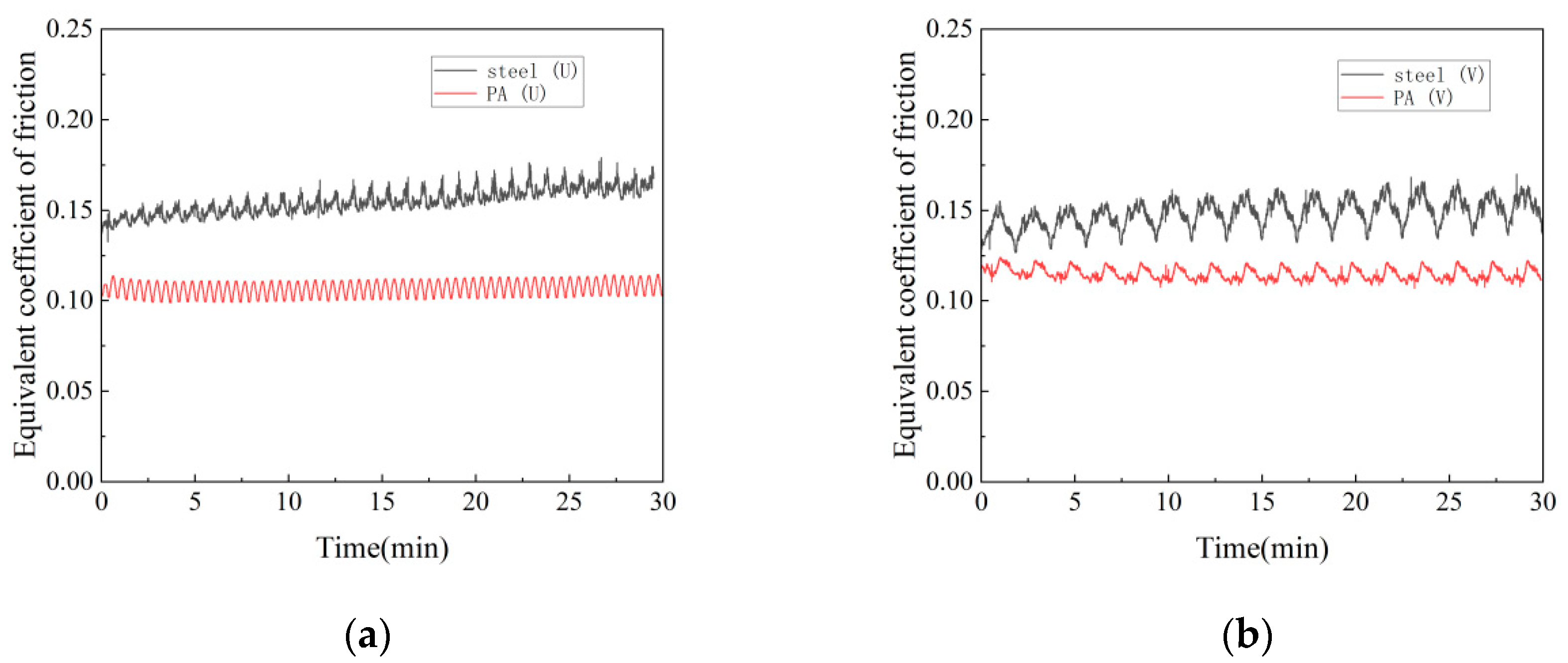
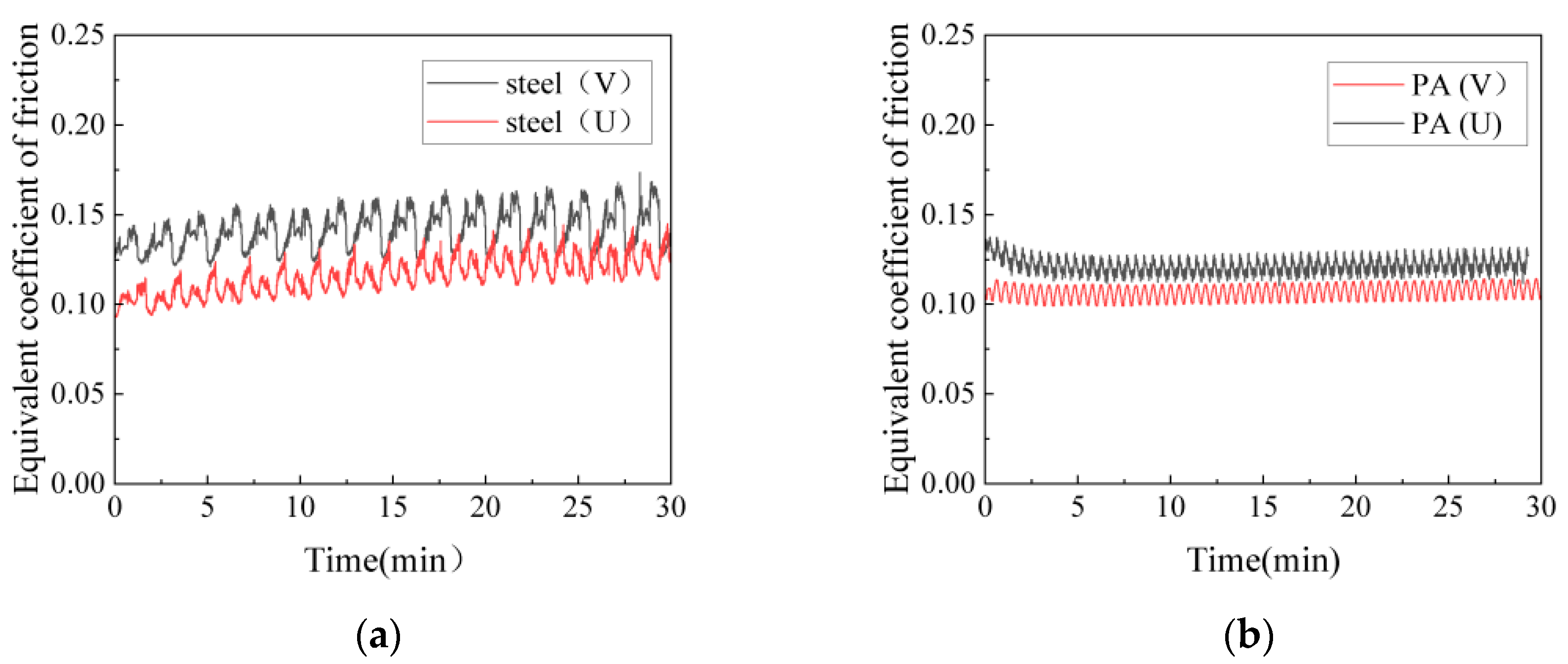
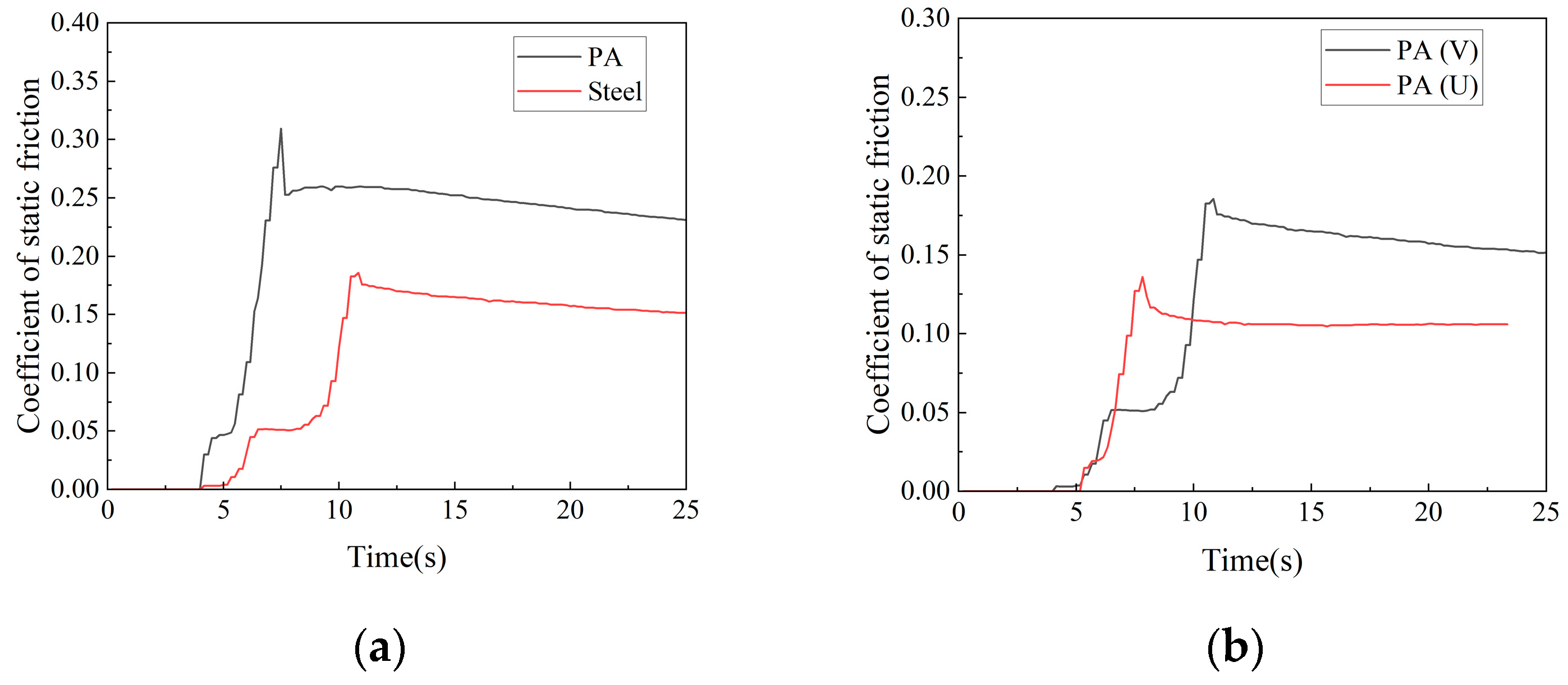
3.2. Influence of Gasket Material and Groove Type on Equivalent Friction Coefficient
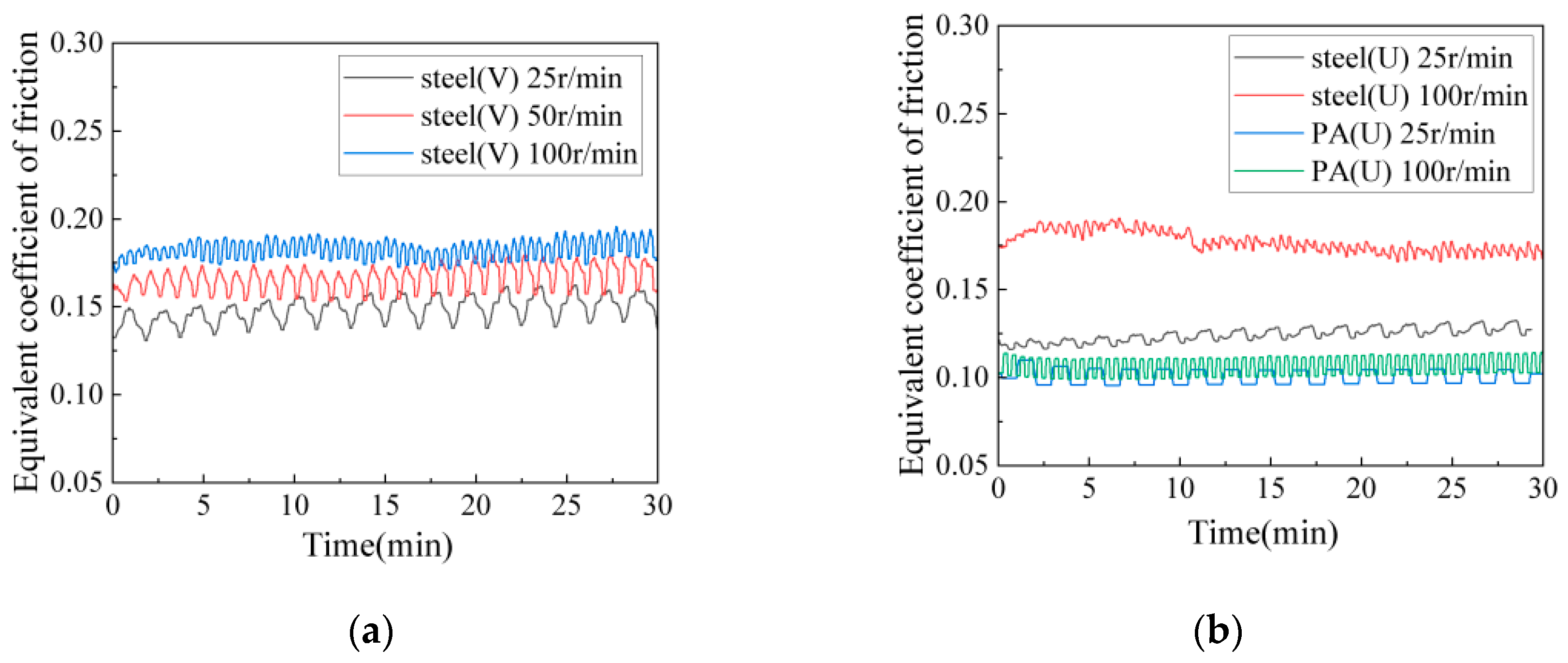
3.3. Influence of Rotational Speed on Equivalent Friction Coefficient
3.4. Static Friction Coefficient
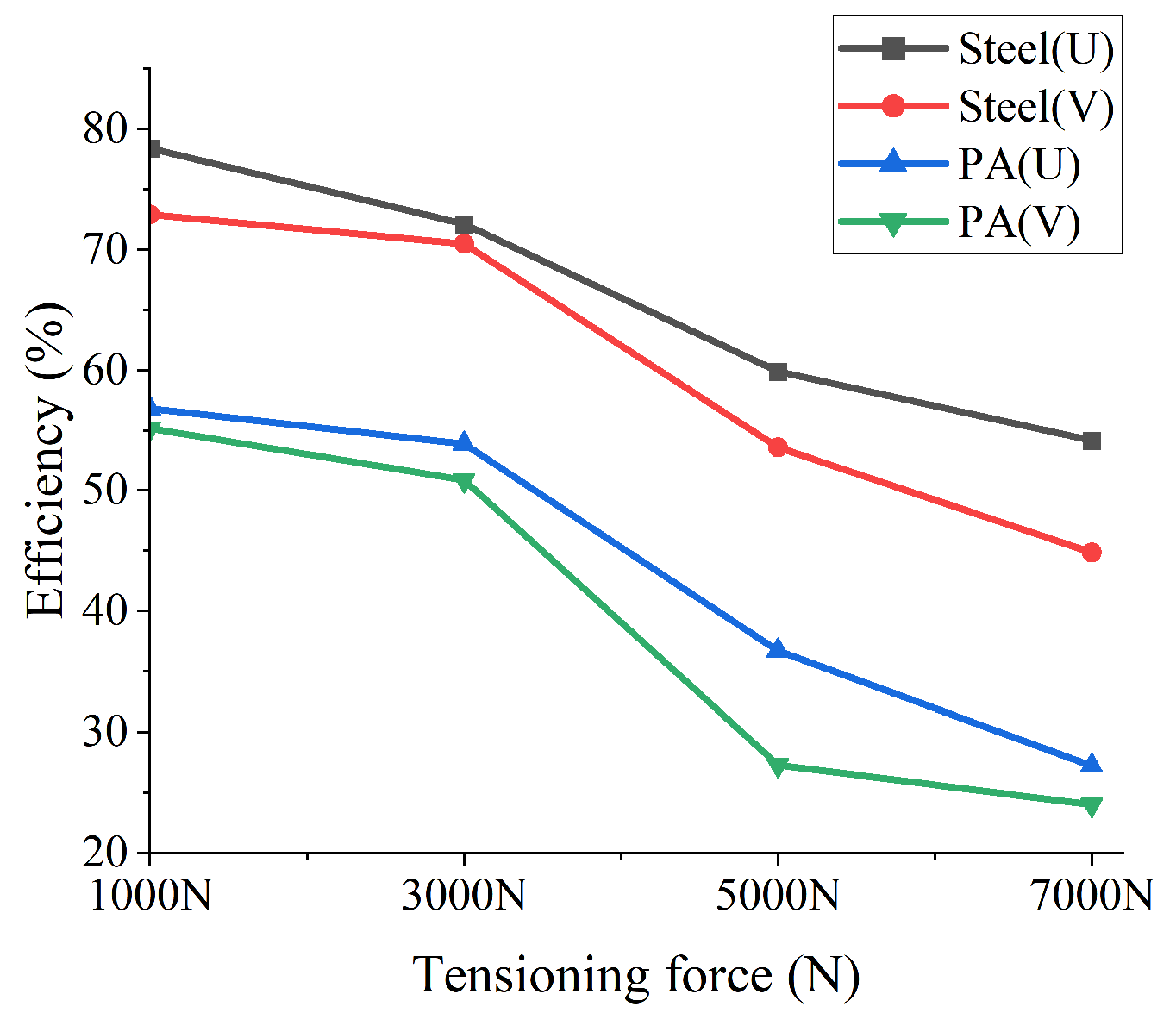
4. Pulley Transmission Loss Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Archer, C.L.; Caldeira, K. Global assessment of high-altitude wind power. Energies 2009, 2, 307–319. [Google Scholar] [CrossRef]
- Kheiri, M.; Victor, S.; Rangriz, S.; Karakouzian, M.M.; Bourgault, F. Aerodynamic performance and wake flow of crosswind kite power systems. Energies 2022, 15, 2449. [Google Scholar] [CrossRef]
- Ren, G.; Liu, J.; Wan, J.; Guo, Y.; Yu, D. Overview of wind power intermittency: Impacts, measurements, and mitigation solutions. Appl. Energy 2017, 204, 47–65. [Google Scholar] [CrossRef]
- Ali, Q.S.; Kim, M.H. Design and performance analysis of an airborne wind turbine for high-altitude energy harvesting. Energy 2021, 230, 120829. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, K.; Chen, Z.; Xu, H.; Shi, H. Mechanical characterization of large diameter UHMWPE ropes under quasi-static tensile loading: An experimental study. Structures 2024, 69, 107447. [Google Scholar] [CrossRef]
- Ye, H.; Li, W.; Lin, S.; Ge, Y.; Han, F.; Sun, Y. Experimental investigation of spooling test on the multilayer oceanographic winch with high-performance synthetic fibre rope. Ocean. Eng. 2021, 241, 110037. [Google Scholar] [CrossRef]
- Ye, H.; Li, W.; Zhang, H.; Lin, S.; Zhang, D.; Ge, Y.; Li, Z. Experimental evaluation of dimension-stable synthetic fibre rope under investigation of spooling test on the multilayer winch drum. Ocean. Eng. 2023, 279, 114585. [Google Scholar] [CrossRef]
- Xu, S.; Wang, S.; Liu, H.; Zhang, Y.; Li, L.; Soares, C.G. Experimental evaluation of the dynamic stiffness of synthetic fibre mooring ropes. Appl. Ocean. Res. 2021, 112, 102709. [Google Scholar] [CrossRef]
- Han, G.; Tao, X.; Li, X.; Jiang, W.; Zuo, W. Study of the mechanical properties of ultra-high molecular weight polyethylene fiber rope. J. Eng. Fibers Fabr. 2016, 11, 155892501601100103. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, X.; Xie, J.; Wu, R.; Huang, H.; He, W.; Wu, Z. A novel fiber-reinforced polymer rope: Concept design and experimental evaluation. Eng. Struct. 2024, 305, 117775. [Google Scholar] [CrossRef]
- Schumann, P.; Zöllner, R.; Schmidt, T. A new model and alternative solutions for the description of double layered flexible elements wrapped around a cylinder. Mech. Mach. Theory 2022, 172, 104823. [Google Scholar] [CrossRef]
- Mao, S.; Tao, J.; Xie, J.; Xu, S.; Chen, L.; Yu, H.; Liu, C. A data-driven approach for modifying the rope dynamics model of the flexible hoisting system. J. Low Freq. Noise Vib. Act. Control. 2023, 42, 1055–1070. [Google Scholar] [CrossRef]
- Kim, J.W.; Joo, B.S.; Jang, H. The effect of contact area on velocity weakening of the friction coefficient and friction instability: A case study on brake friction materials. Tribol. Int. 2019, 135, 38–45. [Google Scholar] [CrossRef]
- Li, G.; Li, W.; Ye, H.; Li, H.; Ge, Y.; Lin, S. Experimental study on cyclic-bend-over-sheave (CBOS) characteristics of an HMPE fibre rope under dynamic loading. Appl. Ocean. Res. 2023, 138, 103642. [Google Scholar] [CrossRef]
- Torres Charry, G.; Gómez Mendoza, J.B. An experimental test bench for cable-driven transmission. Machines 2021, 9, 83. [Google Scholar] [CrossRef]
- Hrabovský, L.; Učeň, O.; Kudrna, L.; Čepica, D.; Frydrýšek, K. Laboratory device detecting tensile forces in the rope and coefficient of friction in the rope sheave groove. Machines 2022, 10, 590. [Google Scholar] [CrossRef]
- Hrabovský, L.; Fries, J.; Kudrna, L.; Gaszek, J. Determination of the Coefficient of Friction in a Pulley Groove by the Indirect Method. Coatings 2022, 12, 606. [Google Scholar] [CrossRef]
- Chang, X.; Peng, Y.; Zhu, Z.; Cheng, D.Q.; Lu, H.; Tang, W.; Chen, G.A. Tribological behavior and mechanical properties of transmission wire rope bending over sheaves under different sliding conditions. Wear 2023, 514, 204582. [Google Scholar] [CrossRef]
- Chang, X.; Peng, Y.; Zhu, Z.; Lu, H.; Tang, W.; Zhang, X. Sliding friction and wear characteristics of wire rope contact with sheave under long-distance transmission conditions. Materials 2022, 15, 7092. [Google Scholar] [CrossRef]
- Nakazawa, D.; Watanabe, S.; Fukui, D.; Fujii, A.; Miyakawa, K. Elevator Rope Tension Analysis with Uneven Groove Wear of Sheave. J. Phys. Conf. Ser. 2018, 1048, 012006. [Google Scholar] [CrossRef]
- Zhao, T.; Qi, Z.; Wang, G.; Wang, T.; Xu, J. An analysis method for rope-driven multibody systems with pulley blocks. J. Mech. Sci. Technol. 2024, 38, 6471–6487. [Google Scholar] [CrossRef]
- Bukvić, M.; Milojević, S.; Gajević, S.; Đorđević, M.; Stojanović, B. Production Technologies and Application of Polymer Composites in Engineering: A Review. Polymers 2025, 17, 2187. [Google Scholar] [CrossRef] [PubMed]
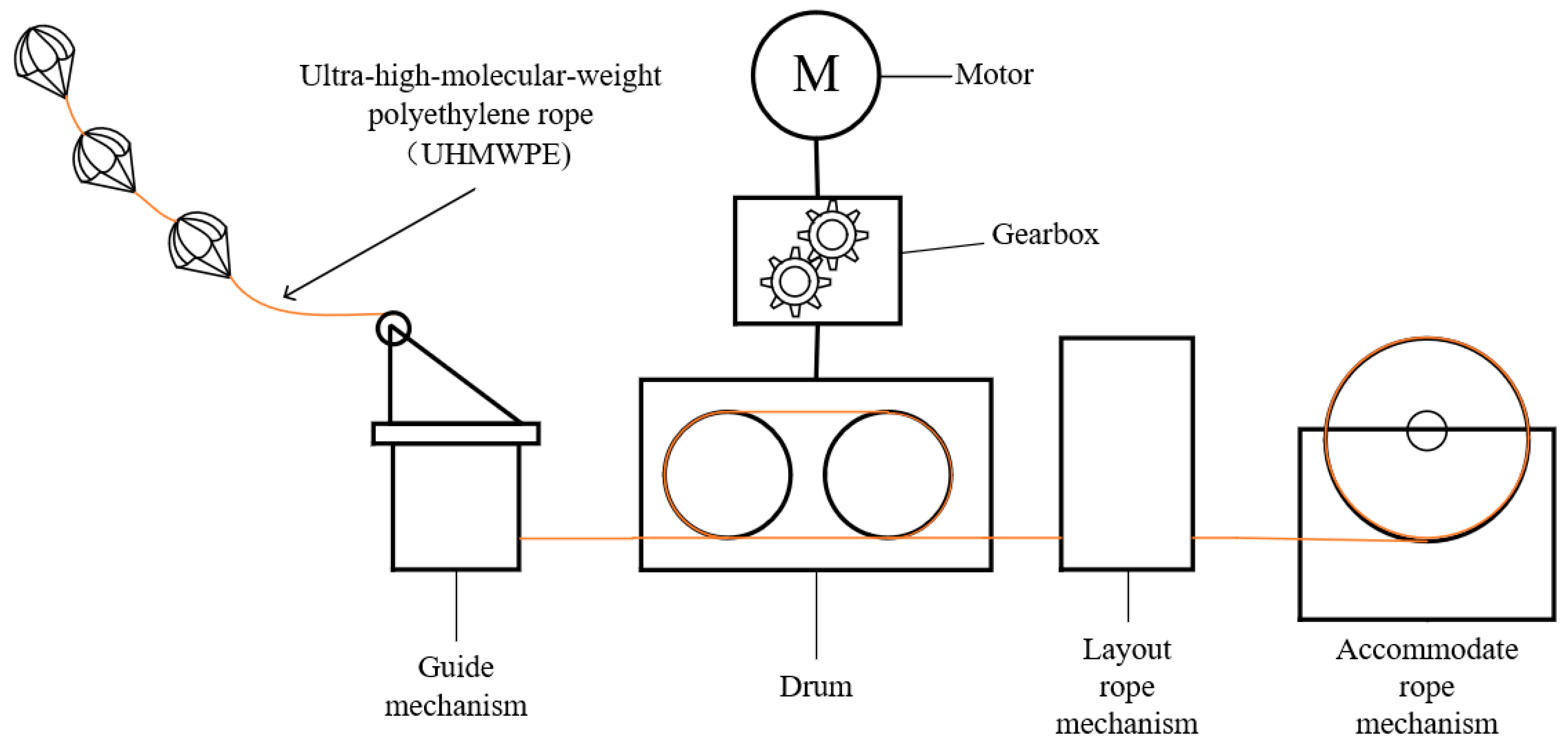
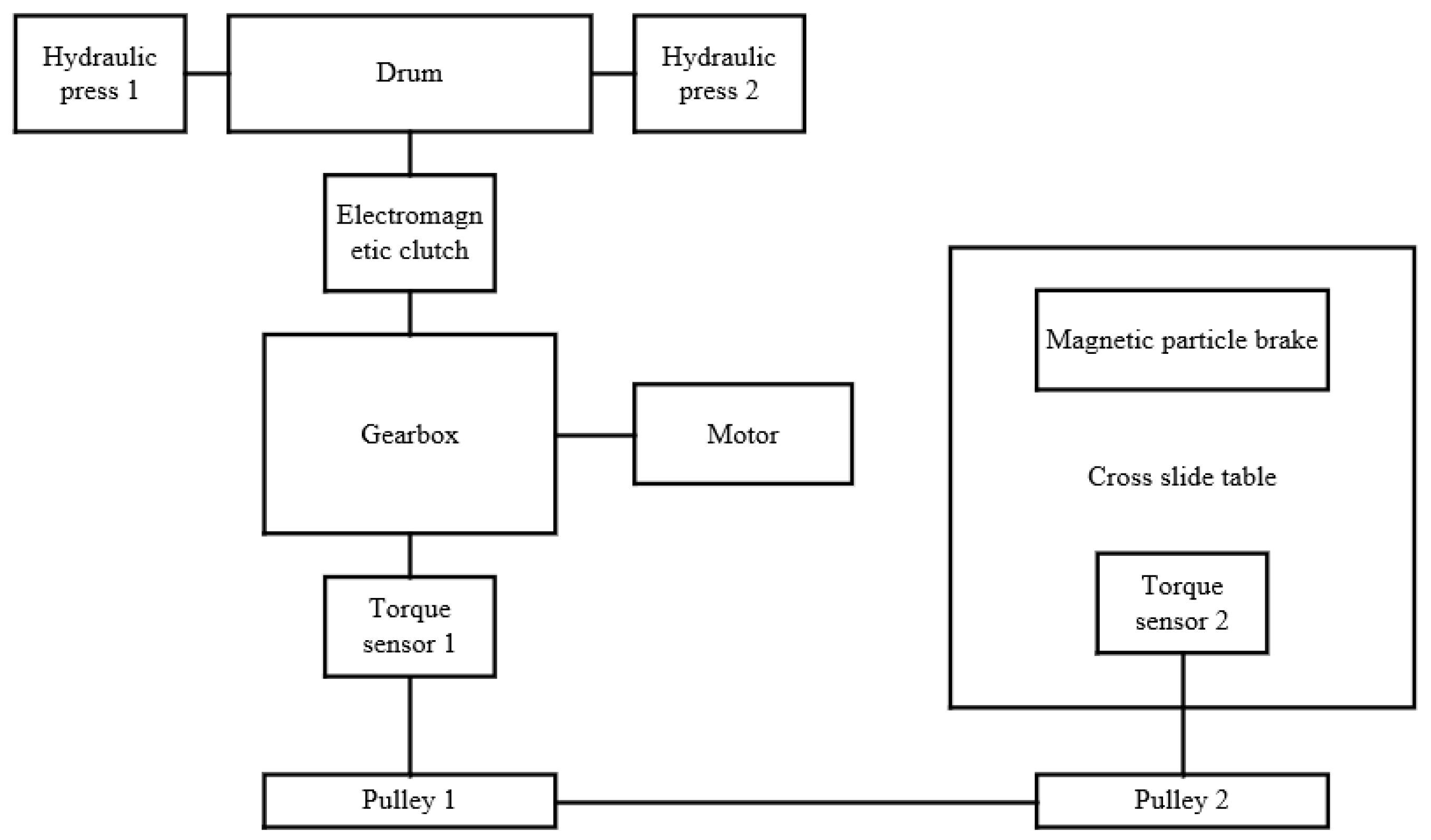
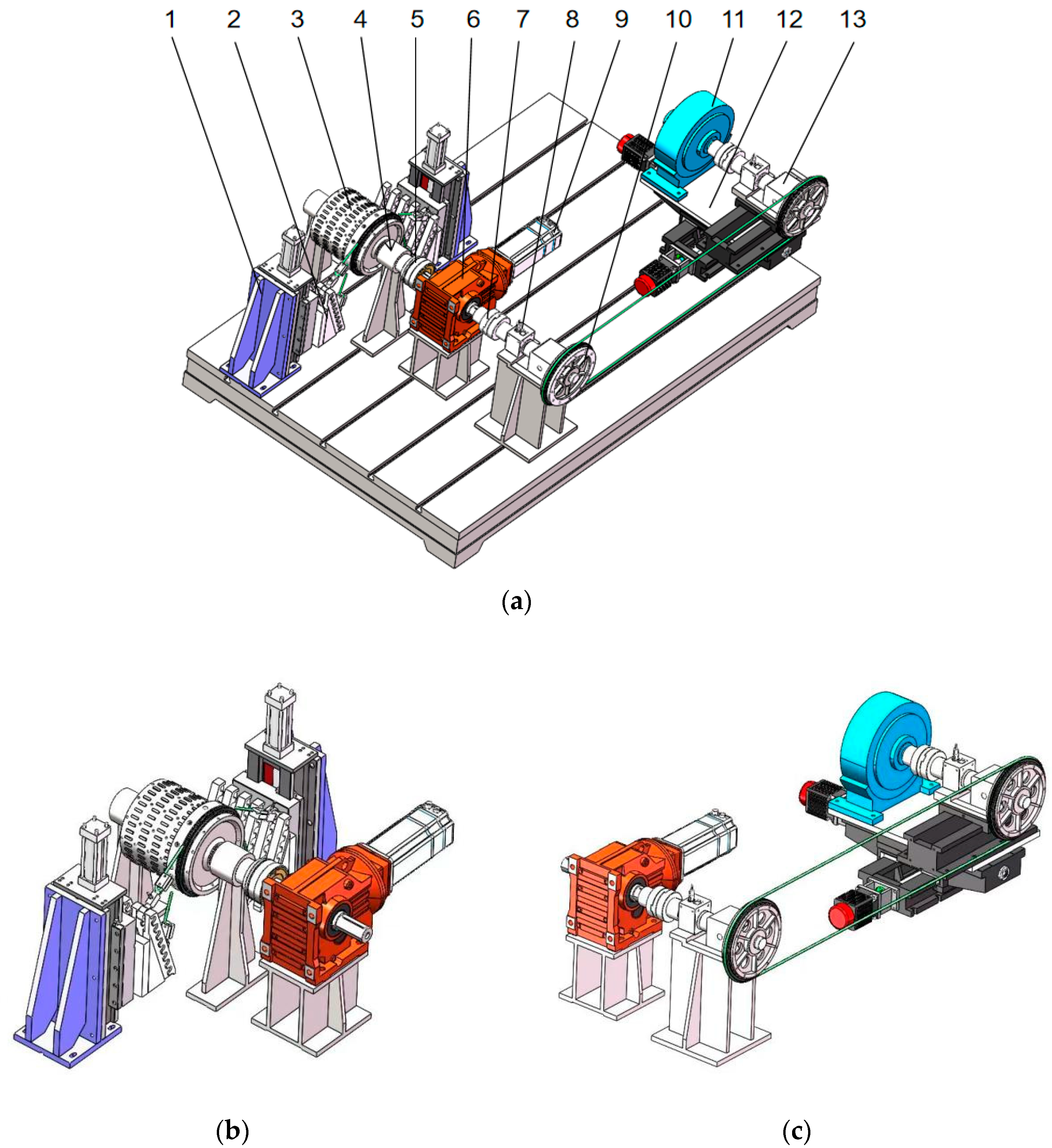
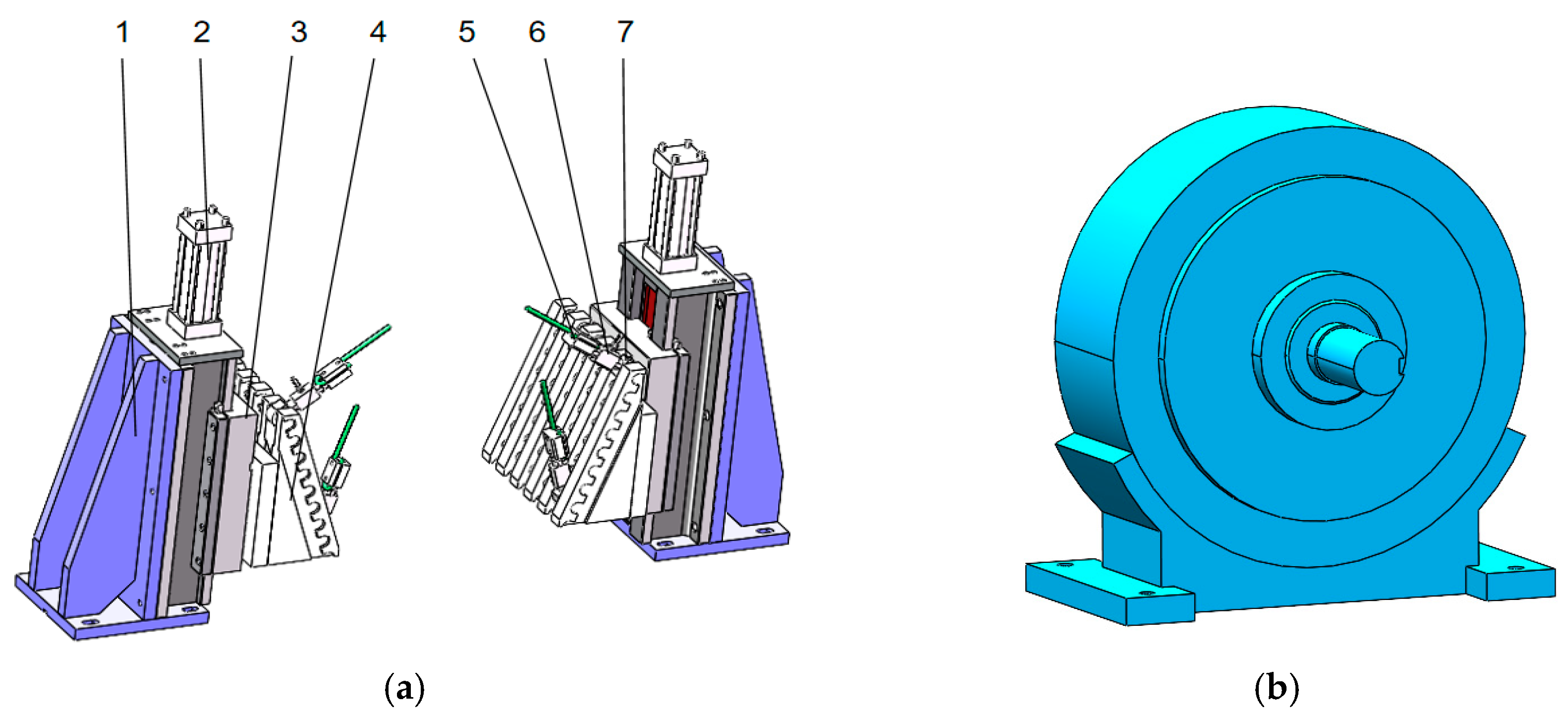
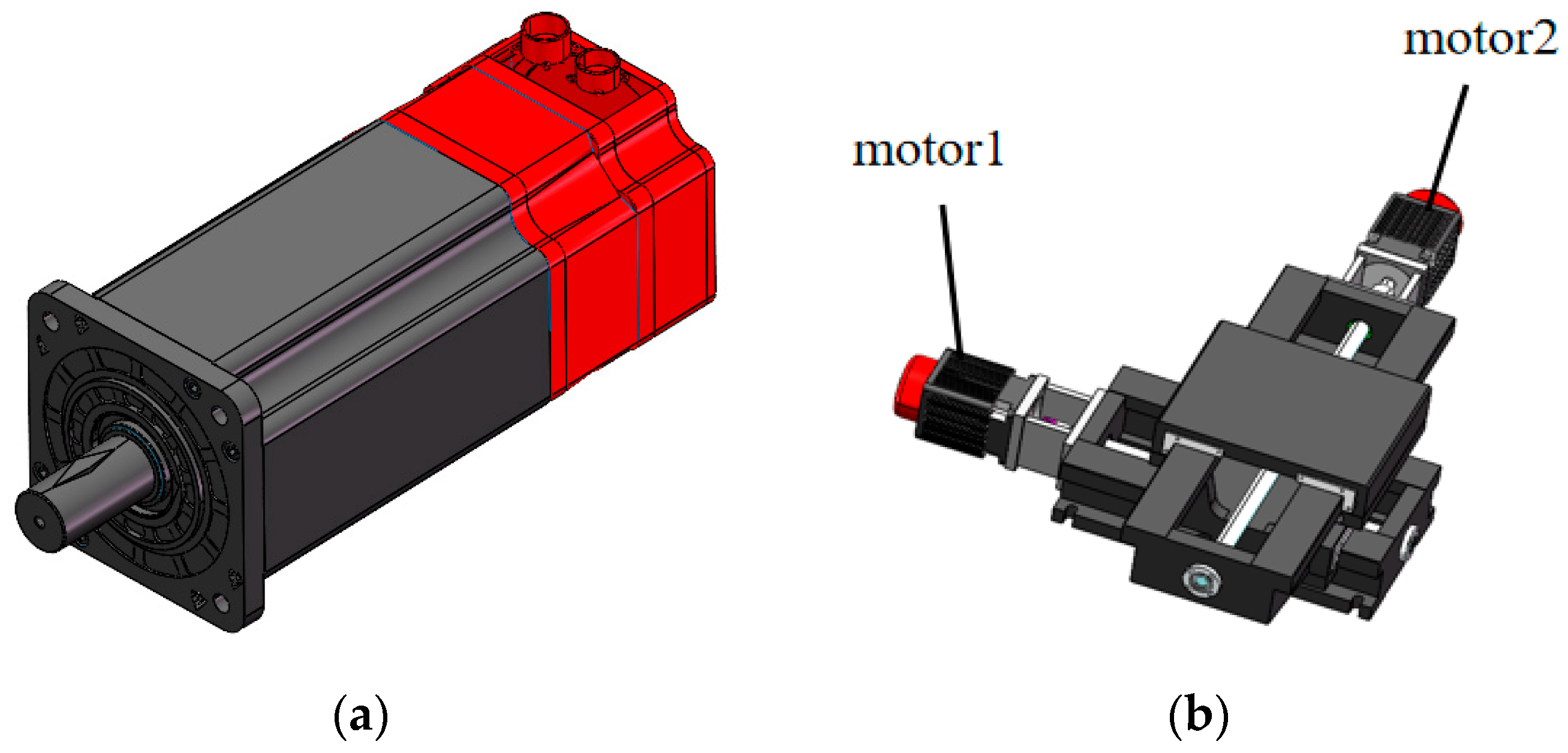
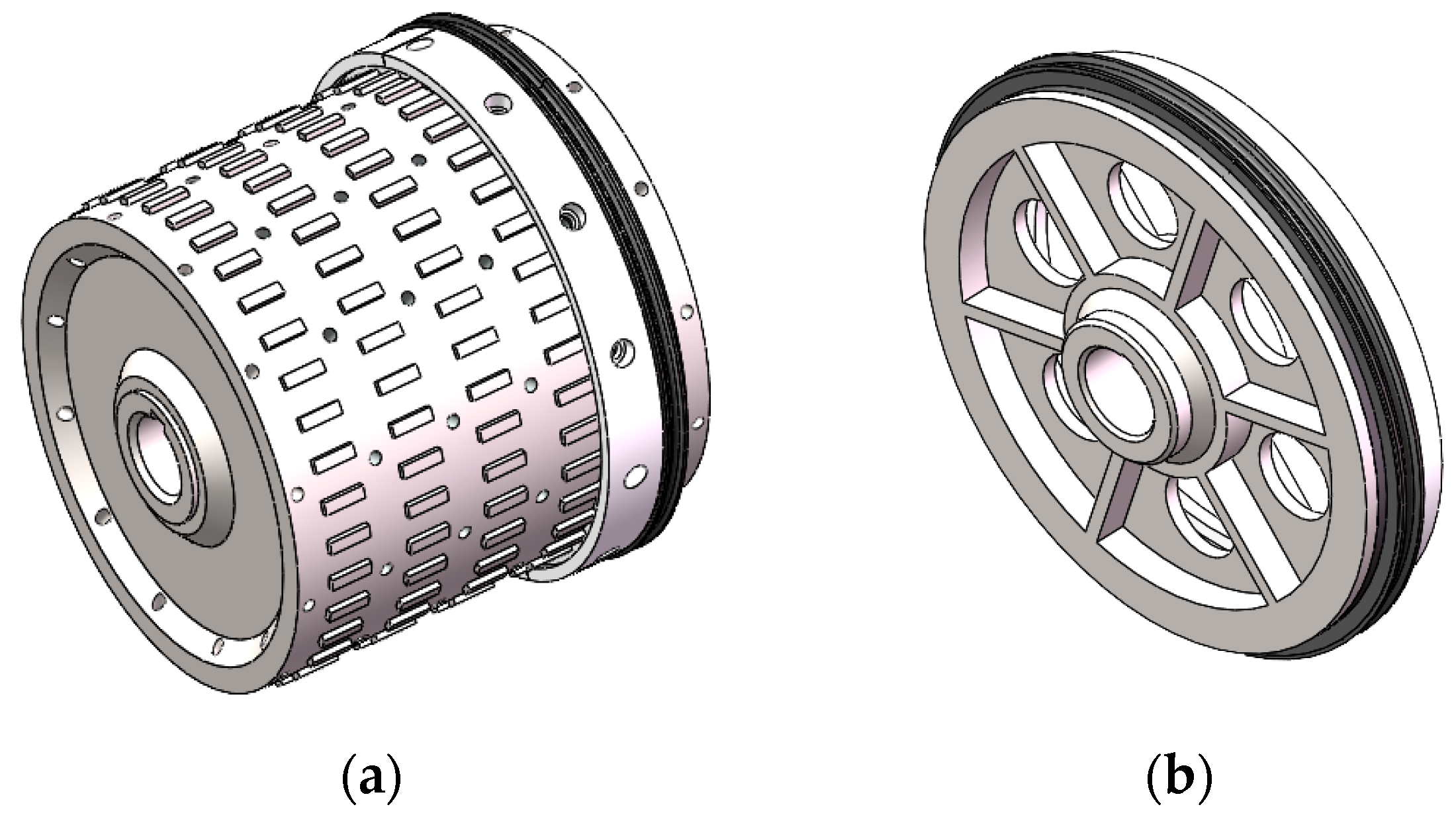
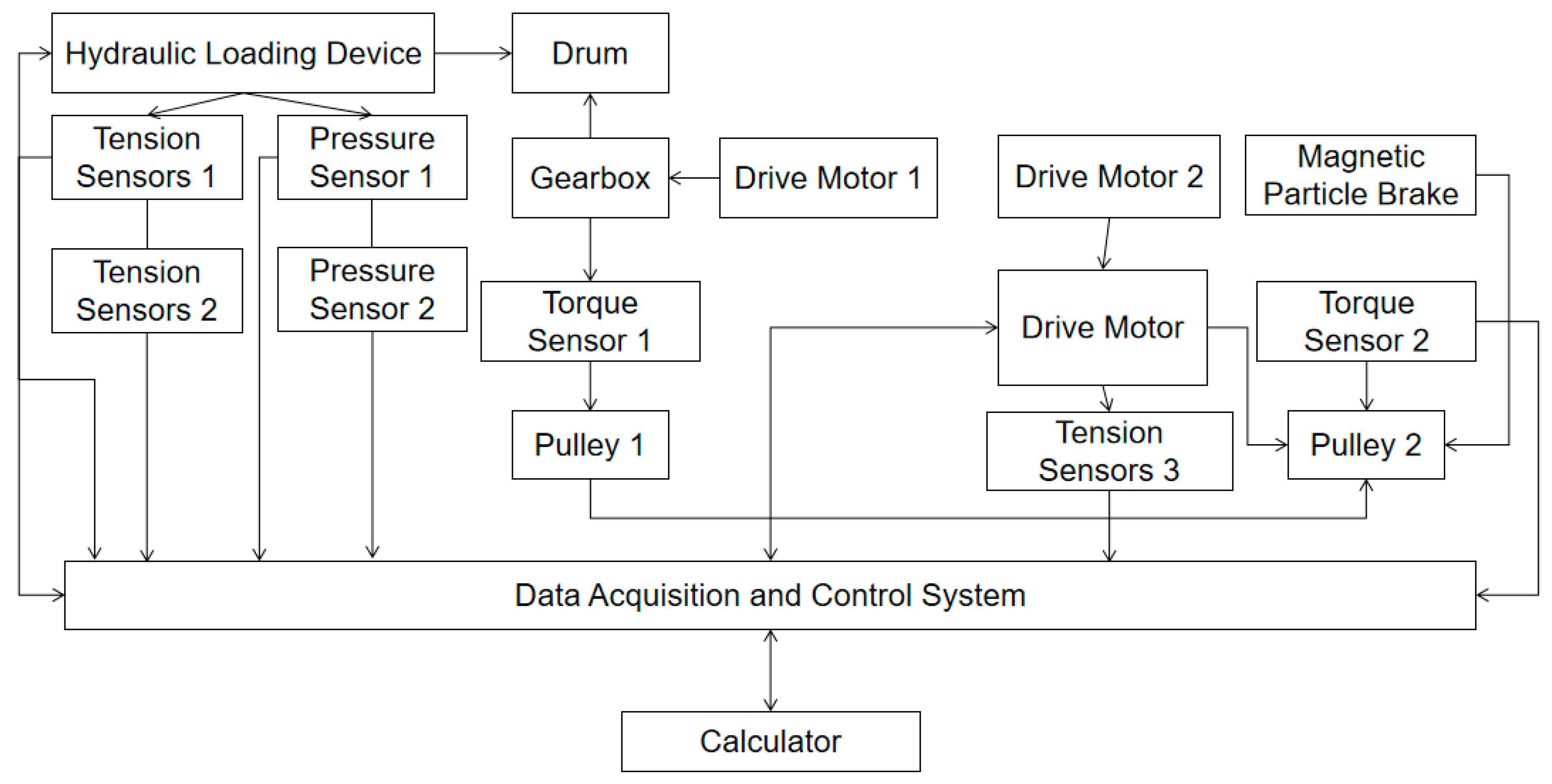
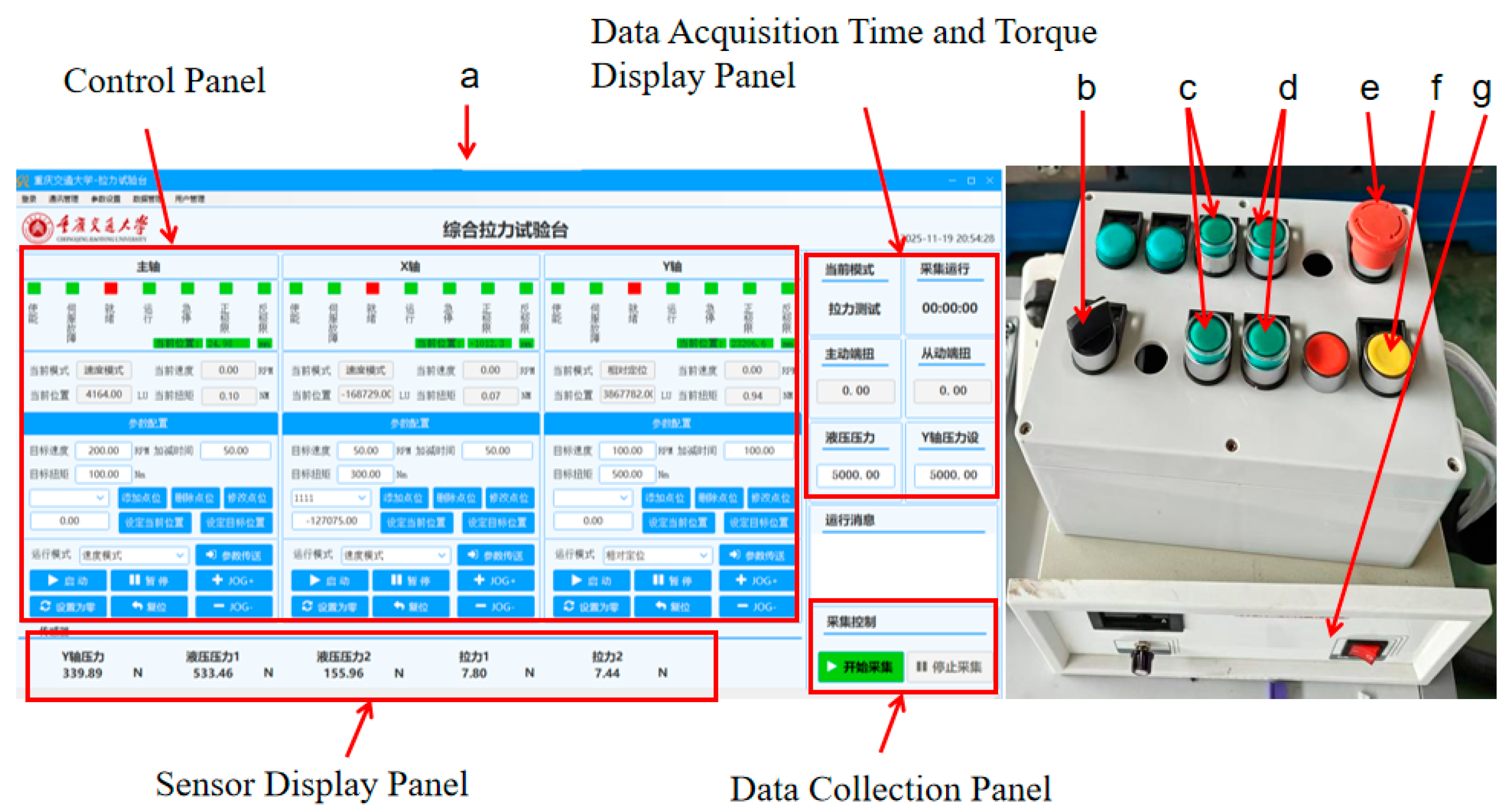






| Equipment Name | Model | Technical Specifications/Parameters |
|---|---|---|
| Servo Motor (Innovance Technology Co., Ltd., Suzhou, China) | MS1H3-55C15CD | Rated power: 5.5 kW; Rated speed: 1500 rpm; |
| Gearbox (LinoDa Transmission Technology Co., Ltd. Hangzhou, China) | K97-47.93 | Gear ratio: 47.93; Transmission efficiency: >95% |
| Speed and Torque Sensor (Bengbu Dayang Sensing System Engineering Co., Ltd., Bengbu, China) | DYN-200 | Range: ±1000 N·m Accuracy: 0.1% of full scale |
| Tension Sensor (Bengbu Dayang Sensing System Engineering Co., Ltd., Bengbu, China) | DYLY-101 | Range: ±10,000 N; Accuracy: 0.03% of full scale |
| Magnetic Powder Brake (Haibo Hua Technology Co., Ltd., Beijing, China) | CZ-100 | Rated torque: 1000 N·m; Slip power: 18 kW |
| Electromagnetic Clutch (Jietai Transmission Machinery Manufacturing Co., Ltd., Tianjin, China) | DLY0-100A | Operating voltage: 24 V; Transmission torque: 1000 N·m |
| Test Project | Controlled/Varied Parameters | Levels/Range |
|---|---|---|
| Friction coefficient measurement test | Gasket material | Steel, Polyamide (PA) |
| Groove type | U-groove, V-groove | |
| Rotational speed | 25, 50, 100 r/min | |
| Contact angle | 80°, 100°, 125°, 160° | |
| Transmission loss test | Gasket material | Steel, Polyamide (PA) |
| Groove type | U-groove, V-groove | |
| Rotational speed | 100, 150, 200 r/min | |
| Tension force | 1000, 3000, 5000, 7000 N | |
| Load condition | No-load, Load | |
| Deviation angle | 0°, 3° |
| Parameter | Value |
|---|---|
| Diameter/mm | 10 |
| Density/(g/cm3) | 0.97 |
| Tensile strength/kN | 60 |
| Modulus of elasticity/GPa | 110 |
| Item | Value |
|---|---|
| Tensile strength of materials (MPa) | 460 |
| Yield strength of material (MPa) | 250 |
| Density (kg/m−3) | 7850 |
| Modulus of elasticity (MPa) | 2 × 105 |
| Pine-to-cedar ratio | 0.3 |
| Characteristics | Steel Materials | PA Material |
|---|---|---|
| Hardness | HRC 45–60 | ~100 R Scale |
| Surface roughness | Ra 0.4–1.6 μm | Ra 0.2–0.8 μm |
| Tensioning Force [N] | Gasket Material | Groove Type | Efficiency |
|---|---|---|---|
| 1000 | Steel | U | 78.4% |
| 3000 | 72.0% | ||
| 5000 | 59.9% | ||
| 7000 | 54.2% | ||
| 1000 | V | 72.9% | |
| 3000 | 70.5% | ||
| 5000 | 53.6% | ||
| 7000 | 44.9% | ||
| 1000 | PA | U | 56.8% |
| 3000 | 53.5% | ||
| 5000 | 36.7% | ||
| 7000 | 27.2% | ||
| 1000 | V | 55.2% | |
| 3000 | 50.9% | ||
| 5000 | 27.3% | ||
| 7000 | 24.0% |
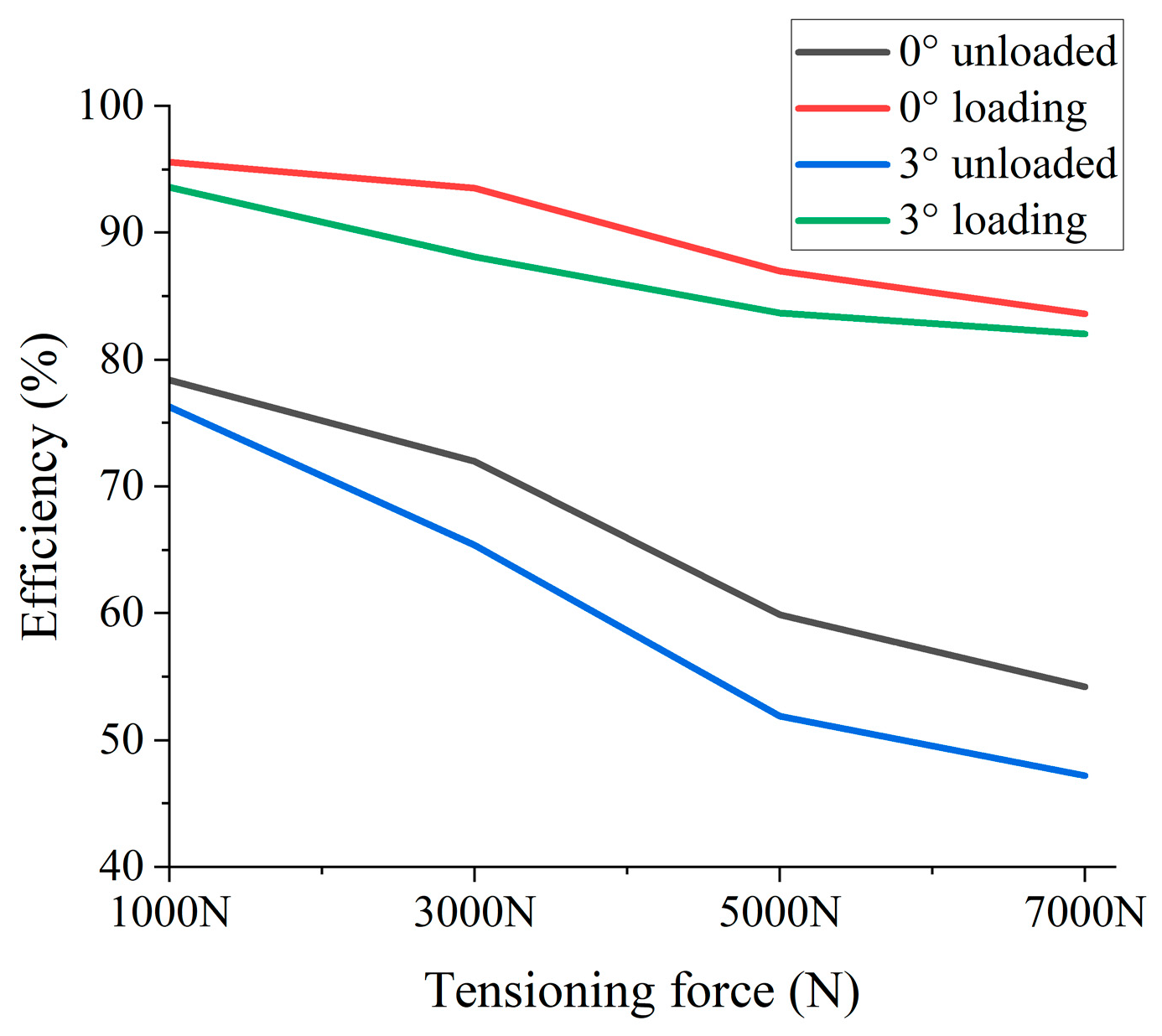
| Tensioning Force [N] | No Deviation Angle/Deviation Angle | No-Load/Load | Efficiency |
|---|---|---|---|
| 1000 | 0° | No-load | 78.4% |
| 3000 | 72.0% | ||
| 5000 | 59.9% | ||
| 7000 | 54.2% | ||
| 1000 | Load | 95.6% | |
| 3000 | 93.5% | ||
| 5000 | 87.0% | ||
| 7000 | 83.6% | ||
| 1000 | 3° | No-load | 76.3% |
| 3000 | 65.4% | ||
| 5000 | 51.9% | ||
| 7000 | 47.2% | ||
| 1000 | Load | 93.6% | |
| 3000 | 88.1% | ||
| 5000 | 83.7% | ||
| 7000 | 82.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, D.; Shuai, W.; Song, A.; Xu, X.; Jia, H.; Luo, J. Experimental Investigation of Equivalent Friction Coefficient Between Rope–Drum Mechanism and Pulley Transmission Loss for High-Altitude Wind Power Generation Systems. Energies 2025, 18, 6079. https://doi.org/10.3390/en18236079
Liang D, Shuai W, Song A, Xu X, Jia H, Luo J. Experimental Investigation of Equivalent Friction Coefficient Between Rope–Drum Mechanism and Pulley Transmission Loss for High-Altitude Wind Power Generation Systems. Energies. 2025; 18(23):6079. https://doi.org/10.3390/en18236079
Chicago/Turabian StyleLiang, Dong, Wei Shuai, Ao Song, Xiangyang Xu, Hanjie Jia, and Jiayuan Luo. 2025. "Experimental Investigation of Equivalent Friction Coefficient Between Rope–Drum Mechanism and Pulley Transmission Loss for High-Altitude Wind Power Generation Systems" Energies 18, no. 23: 6079. https://doi.org/10.3390/en18236079
APA StyleLiang, D., Shuai, W., Song, A., Xu, X., Jia, H., & Luo, J. (2025). Experimental Investigation of Equivalent Friction Coefficient Between Rope–Drum Mechanism and Pulley Transmission Loss for High-Altitude Wind Power Generation Systems. Energies, 18(23), 6079. https://doi.org/10.3390/en18236079






