Research on Power Supply Restoration in Flexible Interconnected Distribution Networks Considering Wind–Solar Uncertainties
Abstract
1. Introduction
- Thoroughly considers wind and solar power output uncertainties by establishing a Beta distribution model for photovoltaic generation and a Weibull distribution model for wind power, and employs confidence-level-adaptive chance-constrained programming to transform the stochastic optimization problem into a tractable second-order cone programming problem, enabling flexible trade-offs between restoration effectiveness and operational reliability.
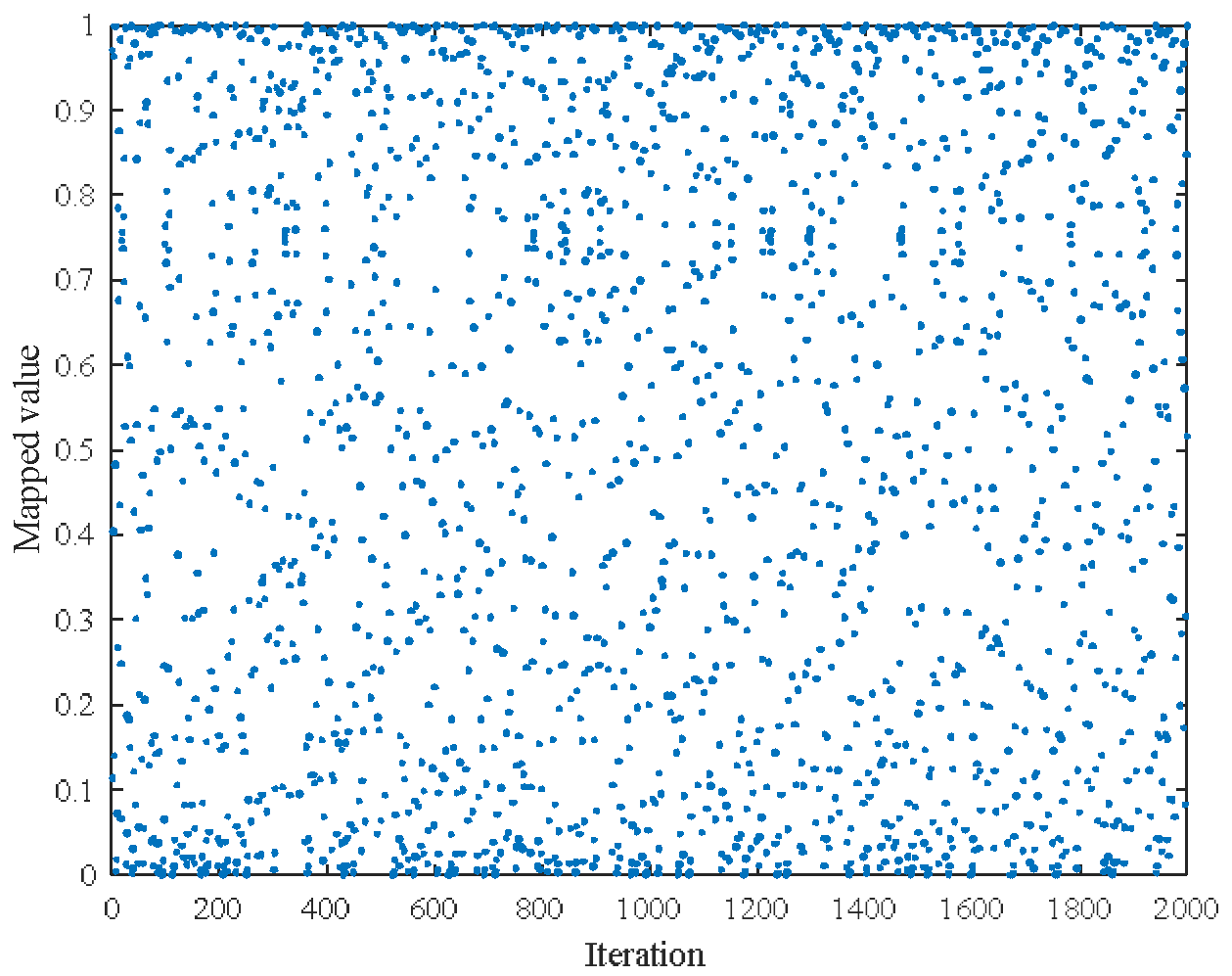
- Population initialization is implemented using logistic chaotic mapping, the golden sine strategy is introduced to enhance exploration capability, and dynamic weight coefficients are designed to improve exploitation capability, achieving faster convergence speed and higher solution quality. This is integrated with MISOCP to construct a bi-level hybrid optimization framework for solving the power supply restoration problem of distribution networks with E-SOP, where the outer layer handles discrete restoration decisions and the inner layer ensures the global optimality of continuous power flow variables.
- Proposes a coordinated E-SOP control model that integrates energy storage system operation with dual-VSC power regulation under fault conditions. Under the E-SOP distribution network topology, the proposed model significantly improves post-fault restoration effectiveness through flexible power flow control and energy buffering capabilities and achieves efficient distributed generation integration by coordinating uncertain renewable outputs with controllable energy storage.
2. Control Analysis of E-SOP
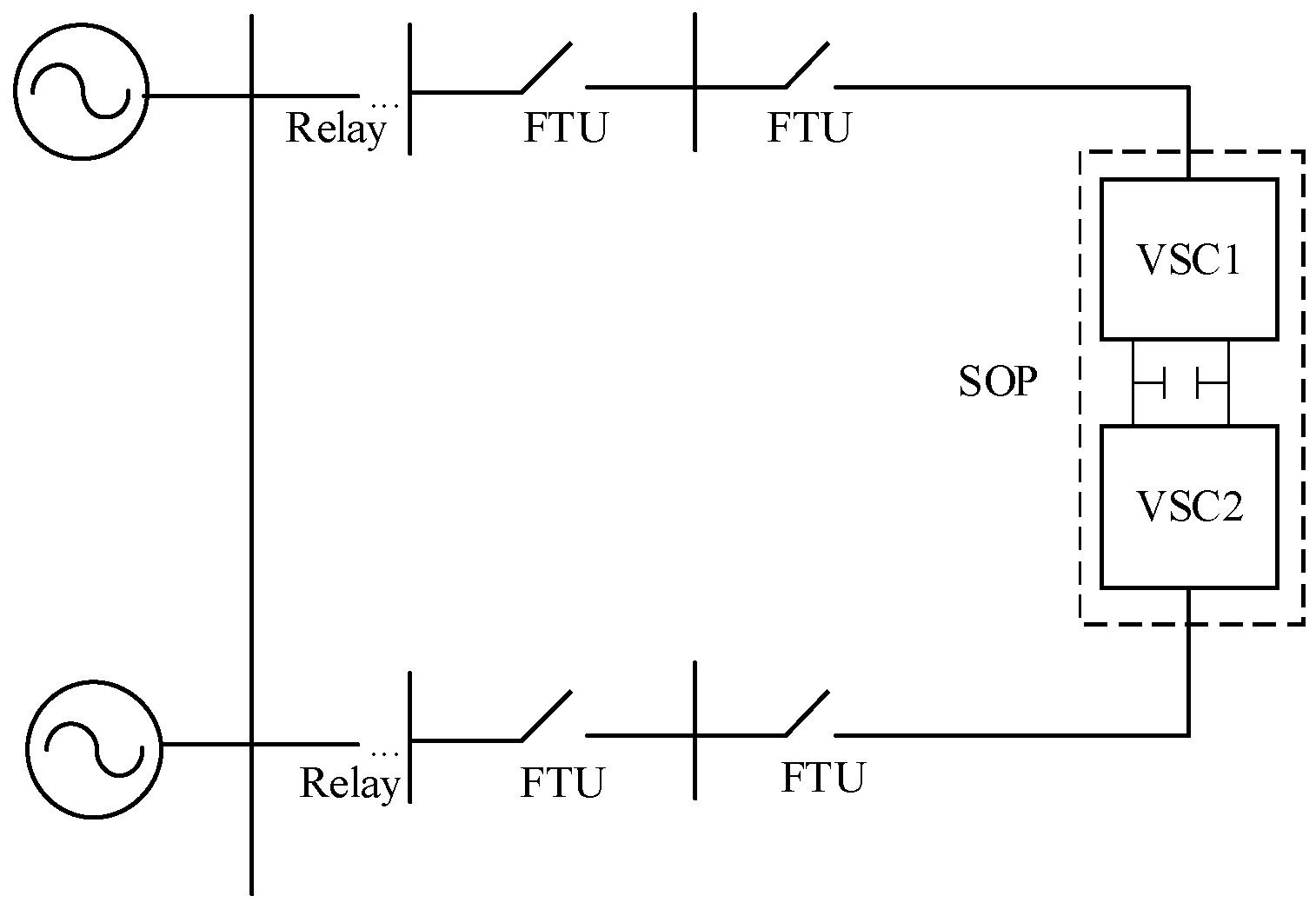
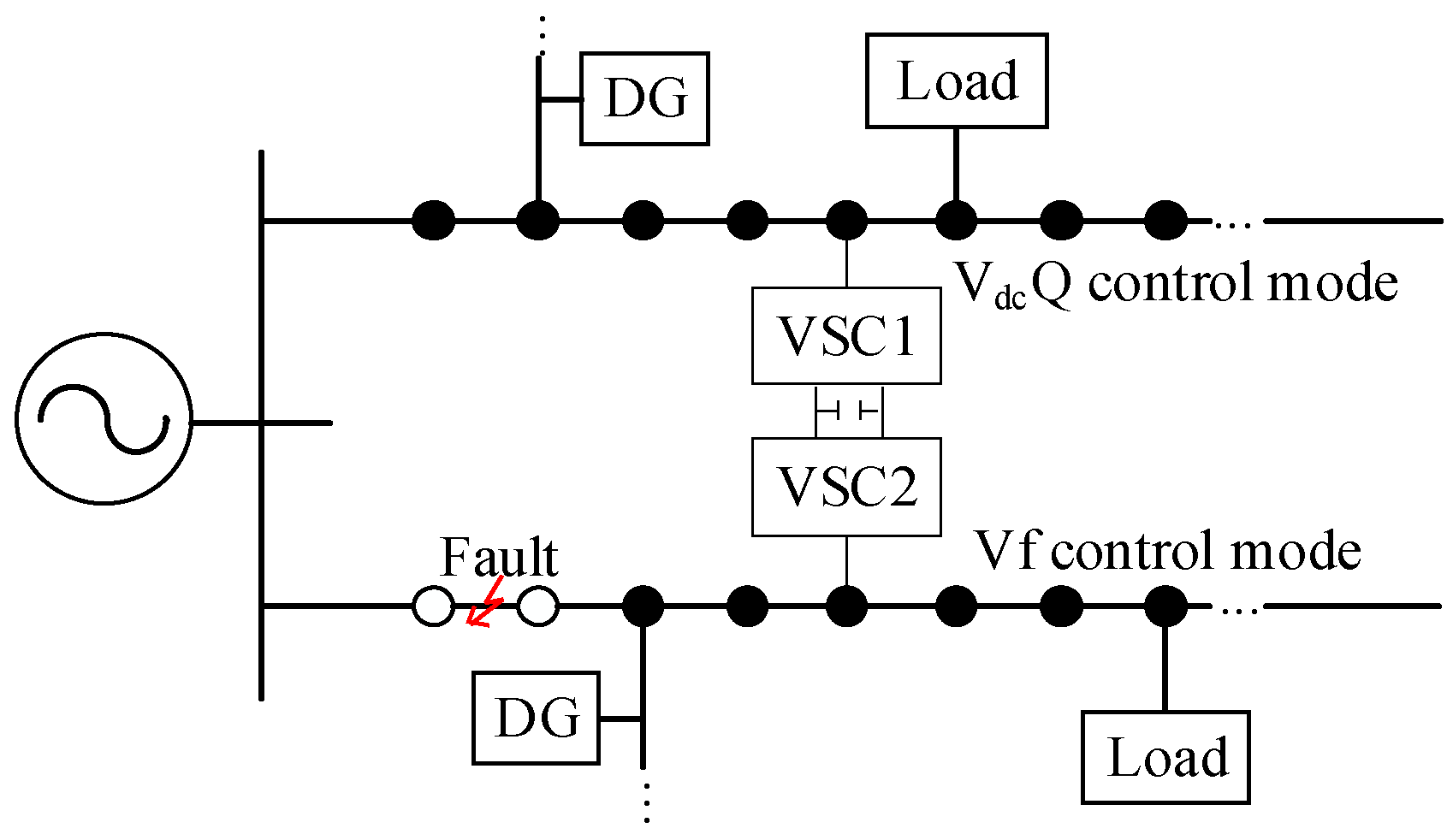
2.1. Control Strategy of SOP
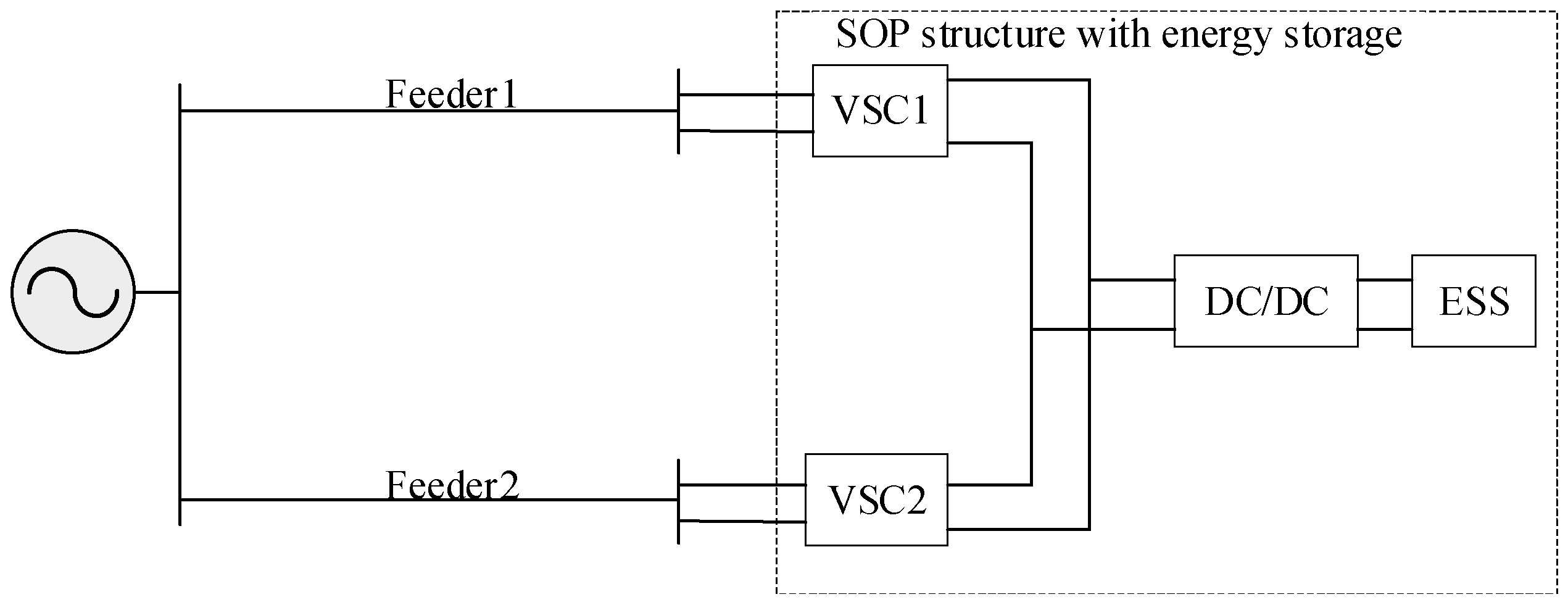
2.2. Mathematical Model of E-SOP
2.3. Mathematical Model of SOP
3. Distribution Network Model Analysis Based on Wind–Solar Uncertainty
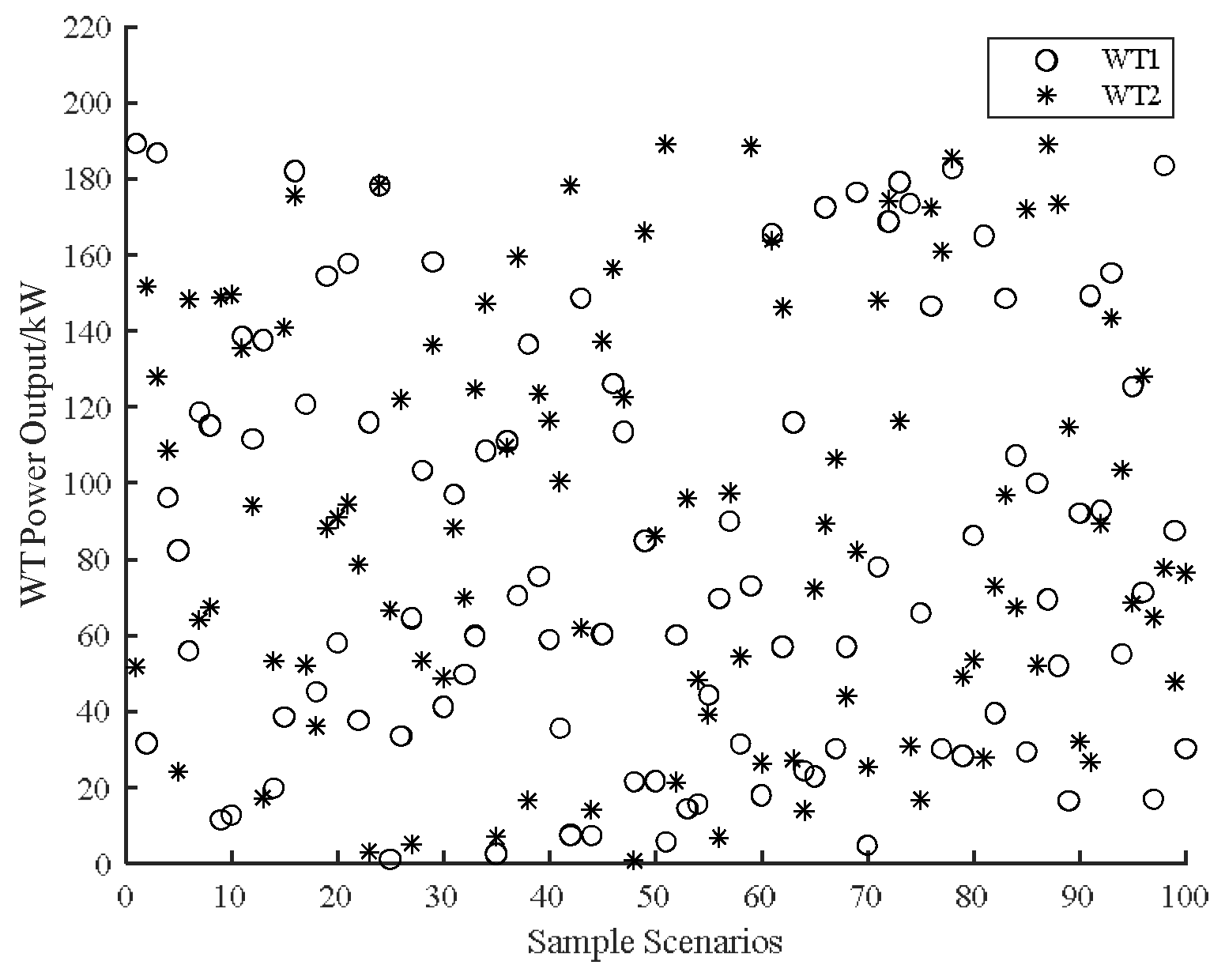
3.1. Photovoltaic Uncertainty Model
3.2. Wind Power Uncertainty Model
3.3. Objective Function
3.4. Constraints
- (1)
- Power Flow Constraints
- (2)
- Wind–Solar Power Output Constraints
- (3)
- System Security Operation Constraints
- (4)
- SOP Operation Constraints
- (5)
- ESS Constraints
4. Solution Based on Hybrid Optimization Algorithm
4.1. Improved Dung Beetle Optimization Algorithm
- (1)
- Rolling Behavior(unobstructed mode)
- (2)
- Rolling Behavior(obstructed mode)
- (3)
- Breeding Behavior
- (4)
- Foraging Behavior
- (5)
- Stealing Behavior
- (1)
- Logistic Chaotic Mapping
- (2)
- Golden Sine Strategy
- (3)
- Dynamic Weight Coefficient for Position Update
4.2. Second-Order Cone Programming and Chance-Constrained Programming
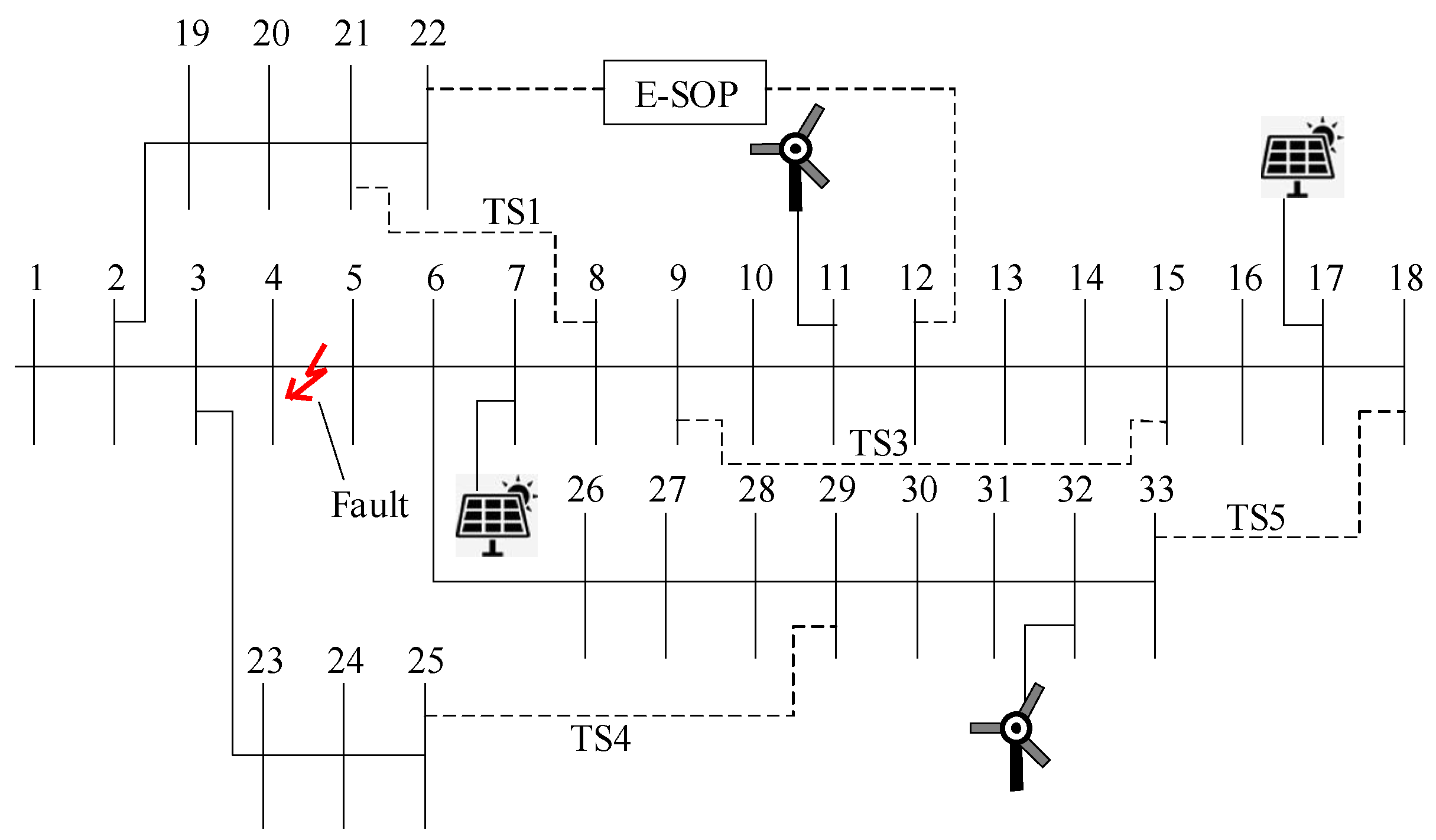
4.3. Analysis of Distribution Network Fault Restoration Model
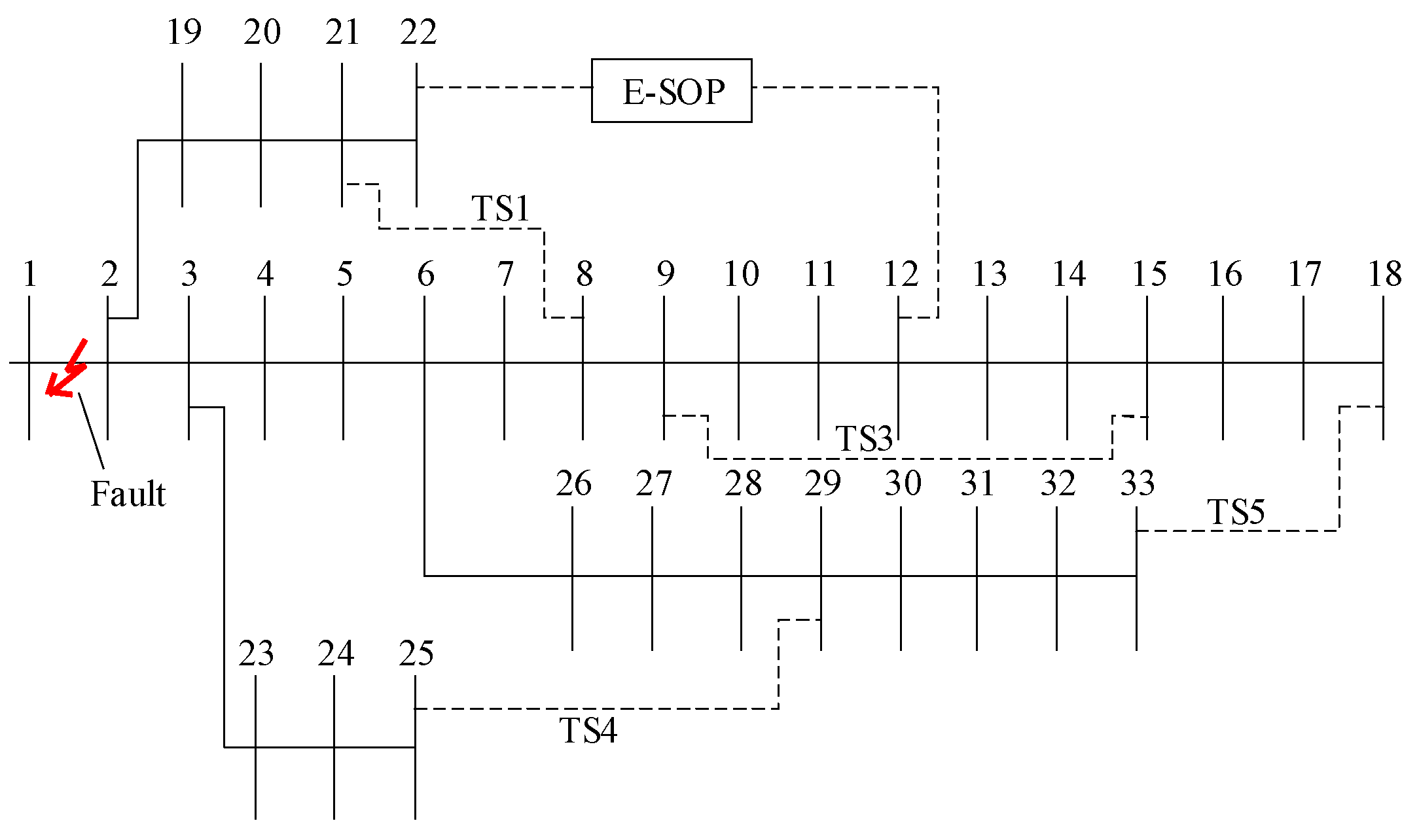
5. Case Study
5.1. Case Study 1
5.2. Case Study 2
6. Conclusions
- (1)
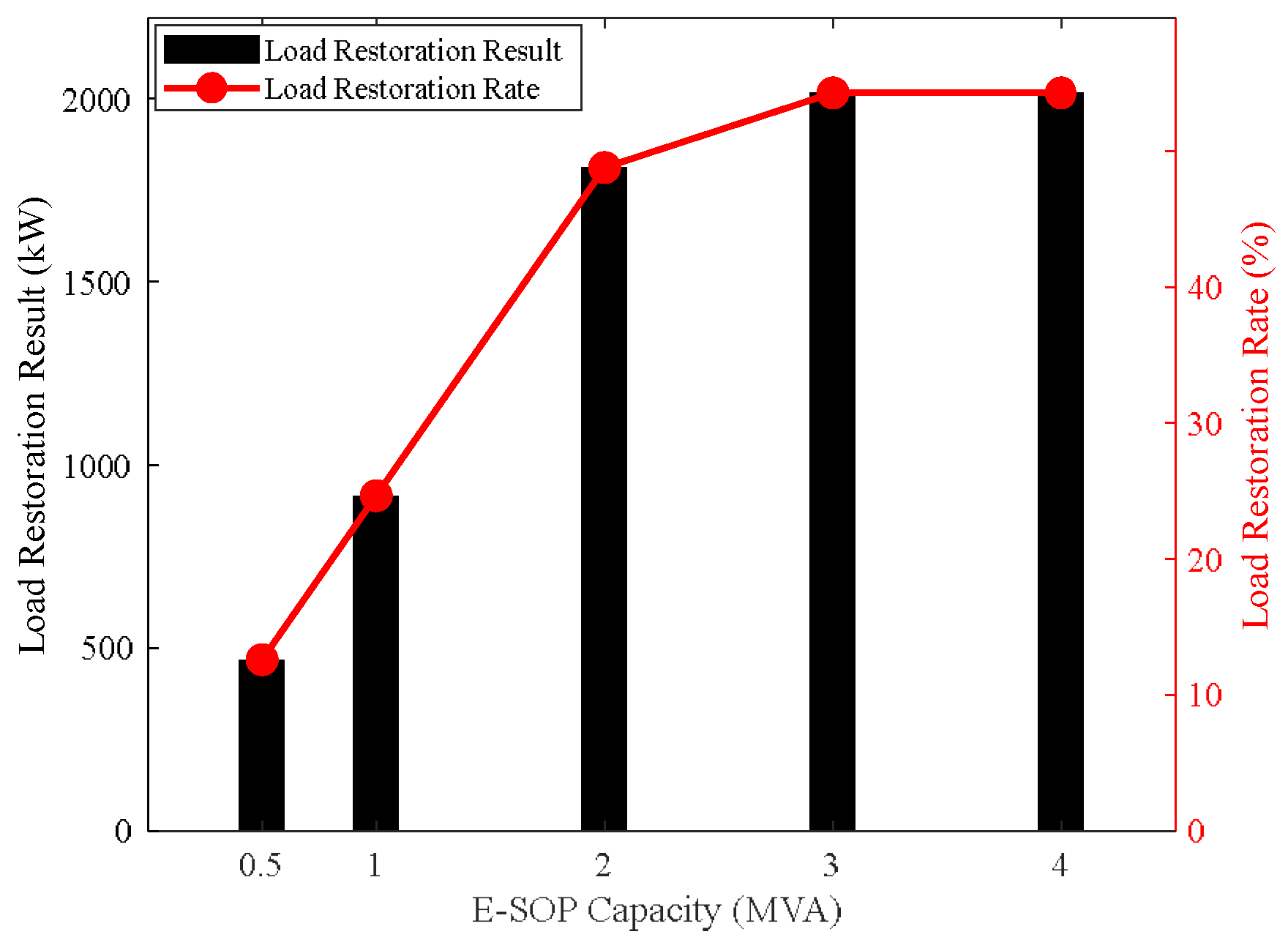
- As a flexible regulation device, E-SOP can effectively enhance the power supply restoration capability of FIDN.
- (2)
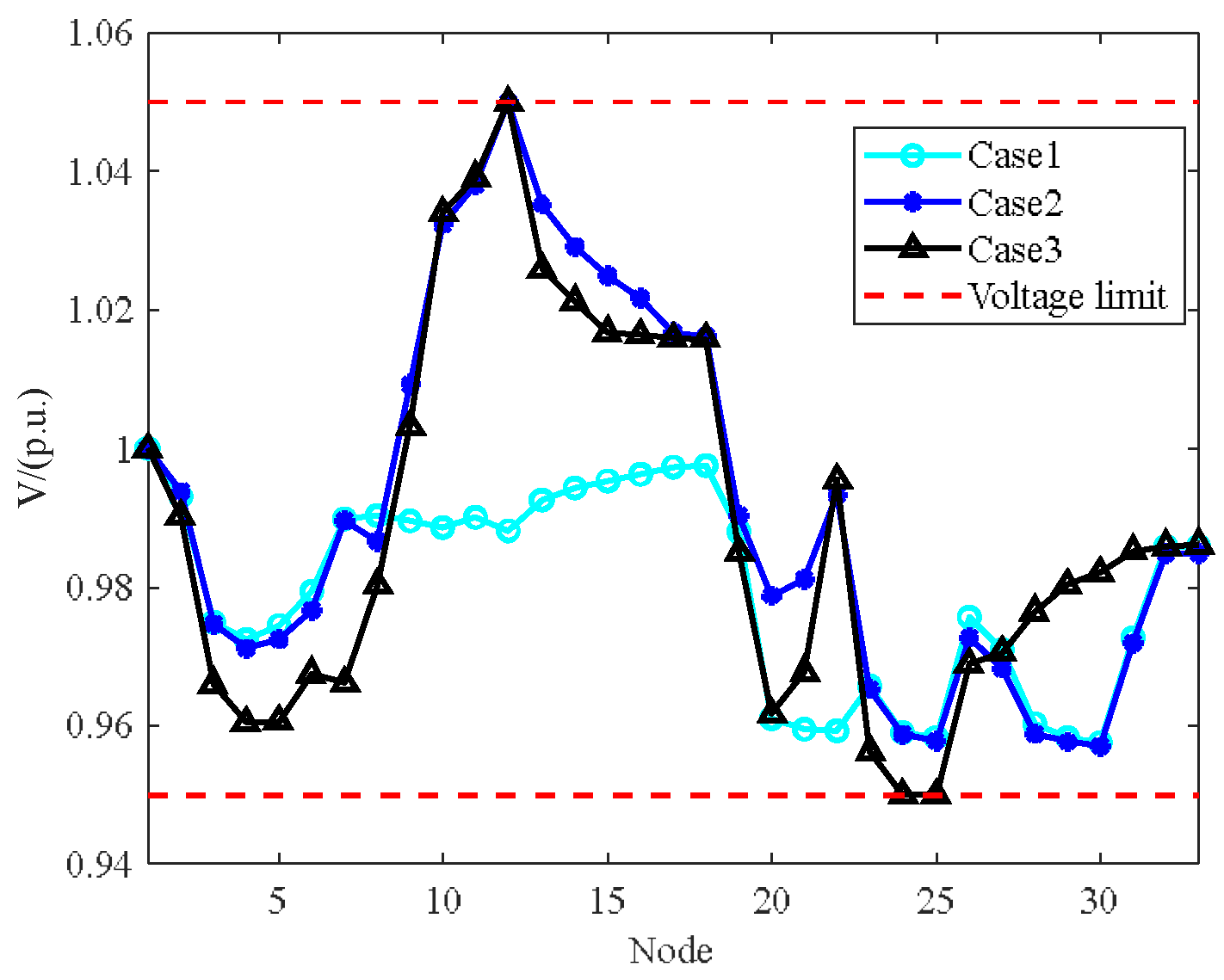
- Without considering wind–solar uncertainty, the hybrid algorithm combining improved dung beetle optimization and MISOCP outperforms both the tie switch power supply and network reconfiguration methods, and the proposed method demonstrates better voltage control capability.
- (3)
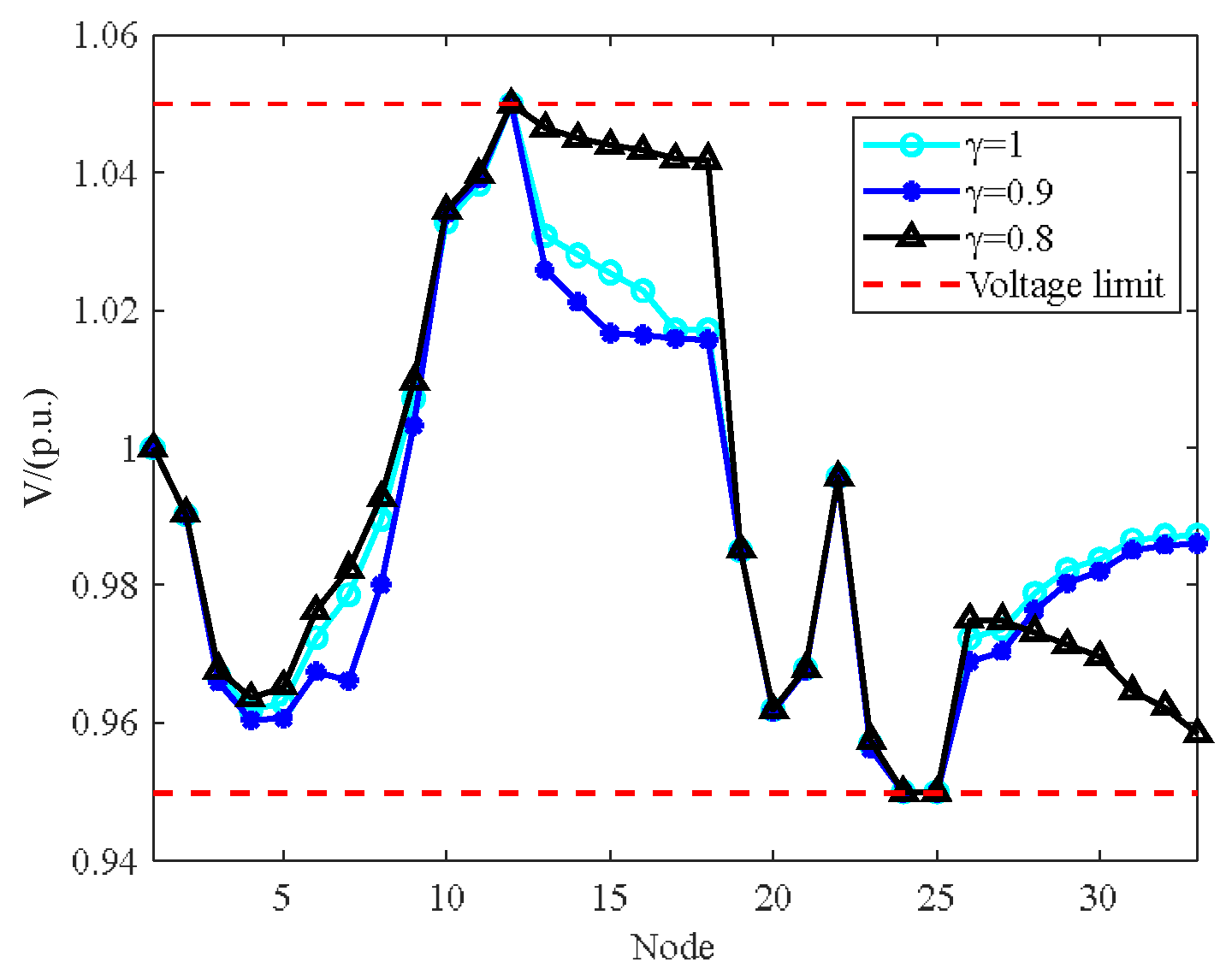
- After considering wind–solar uncertainty, the power supply restoration effectiveness of the distribution network decreases, and the voltage control effect deteriorates as the confidence level decreases. Different E-SOP capacities and confidence levels both affect load restoration results. Therefore, in practical distribution network power supply restoration problems, E-SOP capacity and confidence level should be set according to actual needs to maximize restoration effectiveness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jia, Y.; Wan, C.; Cui, W.; Song, Y.; Ju, P. Peer-to-peer energy trading using prediction intervals of renewable energy generation. IEEE Trans. Smart Grid 2023, 14, 1454–1465. [Google Scholar] [CrossRef]
- Duong, M.Q.; Le, T.; Tran, T.H.; Le, T.M.C.; Tran, N.T.N. Challenge of modern photovoltaic systems under large-scale forms to distribution grid in preinstallation and operation: Vietnam study case evaluation. In Performance Enhancement and Control of Photovoltaic Systems; Elsevier: Amsterdam, The Netherlands, 2024; pp. 259–283. [Google Scholar]
- El-Khatib, M.F.; Sabry, M.N.; El-Sebah, M.I.A.; Maged, S.A. Hardware-in-the-loop testing of simple and intelligent MPPT control algorithm for an electric vehicle charging power by photovoltaic system. ISA Trans. 2023, 137, 656–669. [Google Scholar] [CrossRef]
- El-Khatib, M.F.; Sabry, M.N.; Maged, S.A. Experimental Modeling of a New Multi-Degree-of-Freedom Fuzzy Controller Based Maximum Power Point Tracking from a Photovoltaic System. Appl. Syst. Innov. 2022, 5, 114. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, G.; Pang, D.; Wang, Y.; Yu, B.; Wang, Z. Optimal operation of flexible interconnected distribution grids based on improved virtual synchronous control techniques. Front. Energy Res. 2024, 12, 1356227. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiong, W.; Yuan, X.; Zou, X. A fault recovery strategy of flexible interconnected distribution network with SOP flexible closed-loop operation. Int. J. Electr. Power Energy Syst. 2022, 142, 108360. [Google Scholar] [CrossRef]
- Zare, A.; Chung, C.Y.; Zhan, J.; Faried, S.O.A. Distributionally Robust Chance-Constrained MILP Model for Multistage Distribution System Planning With Uncertain Renewables and Loads. IEEE Trans. Power Syst. 2018, 33, 5248–5262. [Google Scholar] [CrossRef]
- Chen, X.Y.; Tang, W.; Chen, Y.; Bai, M.; Cong, P. Chance Constrained Programming Based Fault Recovery of Distribution Network Containing Photovoltaic Generations. Power Syst. Technol. 2014, 38, 99–106. [Google Scholar]
- Liu, S.C.; Zhou, B.X.; Song, J.; Hao, T. Multi-objective fault restoration considering the randomness of the output of distributed generator. Electr. Meas. Instrum. 2018, 55, 123–128. [Google Scholar]
- Zhang, S.; Fang, Y.; Zhang, H.; Cheng, H.; Wang, X. Maximum hosting capacity of photovoltaic generation in SOP-based power distribution network integrated with electric vehicles. IEEE Trans. Ind. Inform. 2022, 18, 8213–8224. [Google Scholar] [CrossRef]
- Li, P.; Ji, J.; Ji, H.R.; Song, G.; Wang, C.; Wu, J. Self-healing oriented supply restoration method based on the coordination of multiple SOPs in active distribution networks. Energy 2020, 195, 116968. [Google Scholar] [CrossRef]
- Xiong, M.; Yang, X.; Zhang, Y.; Wu, H.; Lin, Y.; Wang, G. Reactive power optimization in active distribution systems with soft open points based on deep reinforcement learning. Int. J. Electr. Power Energy Syst. 2024, 155, 109601. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.Z.; Thomas, L.; Jenkins, N. Optimal operation of soft open points in medium voltage electrical distribution networks with distributed generation. Appl. Energy 2016, 184, 427–437. [Google Scholar] [CrossRef]
- Hu, Y.F.; Qian, F.; Li, H.L.; Liu, S.; Zhang, Q. Island fault recovery method of distribution network based on flexible interconnection device with energy storage. Distrib. Util. 2024, 41, 21–27. [Google Scholar]
- Yu, Y.W.; Yuan, X.F.; Xiong, W. A Power Supply Restoration Method for the Flexible Interconnected Distribution Network with Multi-Terminal Soft Open Point. Power Syst. Clean Energy 2021, 37, 75–82+90. [Google Scholar]
- Song, Y.; Sun, C.B.; Li, P.; Yuan, K.; Song, G.; Wang, C. SOP Based Supply Restoration Method of Active Distribution Networks Using Soft Open Point. Proc. CSEE 2018, 38, 4390–4398+4639. [Google Scholar]
- Yong, L.; Feng, L.; Xuebo, Q. Day-Ahead and Intra-Day Optimization of Flexible Interconnected Distribution System with Self-Energy Storage Based on the Grid-Side Resource Coordination. Trans. China Electrotech. Soc. 2024, 39, 758–773+923. [Google Scholar]
- Li, Z.Y.; Huang, J.H.; Zhao, W.; Zeng, R. Distributionally Robust Allocation of Multi-terminal E-SOP for Enhancing Distribution Network Resilience. J. Glob. Energy Interconnect. 2024, 7, 541–549. [Google Scholar]
- Bloemink, J.M.; Green, T.C. Increasing distributed generation penetration using soft normally-open points. In Proceedings of the 2010 IEEE Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Huang, Z.T.; Xu, Y.H.; Ye, X.J. Optimal planning of soft open point integrated with energy storage system considering operation flexibility of active distribution network. Electr. Power Eng. Technol. 2023, 42, 143–153. [Google Scholar]
- Karaki, S.H.; Chedid, R.B.; Ramadan, R. Probabilistic performance assessment of autonomous solar-wind energy conversion systems. IEEE Trans. Energy Convers. 1999, 14, 766–772. [Google Scholar] [CrossRef]
- Luo, F.; Bu, Q.S.; Ye, Z.G.; Yuan, Y.; Gao, L.; Lv, P. Dynamic Reconstruction Strategy of Distribution Network Based on Uncertainty Modeling and Impact Analysis of Wind and Photovoltaic Power. IEEE Access 2024, 12, 64069–64078. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Sharafi, J.; Khedmati, Y.; Shabani, M.M. Image steganography based on a new hybrid chaos map and discrete transforms. J. Light-Electronoptic 2021, 226 Pt 2, 22. [Google Scholar] [CrossRef]
- Zhang, W.K.; Liu, S. Improved sparrow search algorithm based on adaptive t-distribution and golden sine and its application. Microelectron. Comput. 2022, 39, 17–24. [Google Scholar]
- Xu, Q.S.; He, Q.; Wei, K.Y. Modified Ant Lion Optimizer Based Coverage Optimization of Wireless Sensor Network. Chin. J. Sens. Actuators 2019, 32, 266–275. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, UK, 1975. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Yu, W.S.; Li, M.; You, R. Power flow optimization Study on active distribution network based on three-terminal SOP with energy storage system. Acta Energiae Solaris Sin. 2022, 43, 101–110. [Google Scholar]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1402–1407. [Google Scholar] [CrossRef]
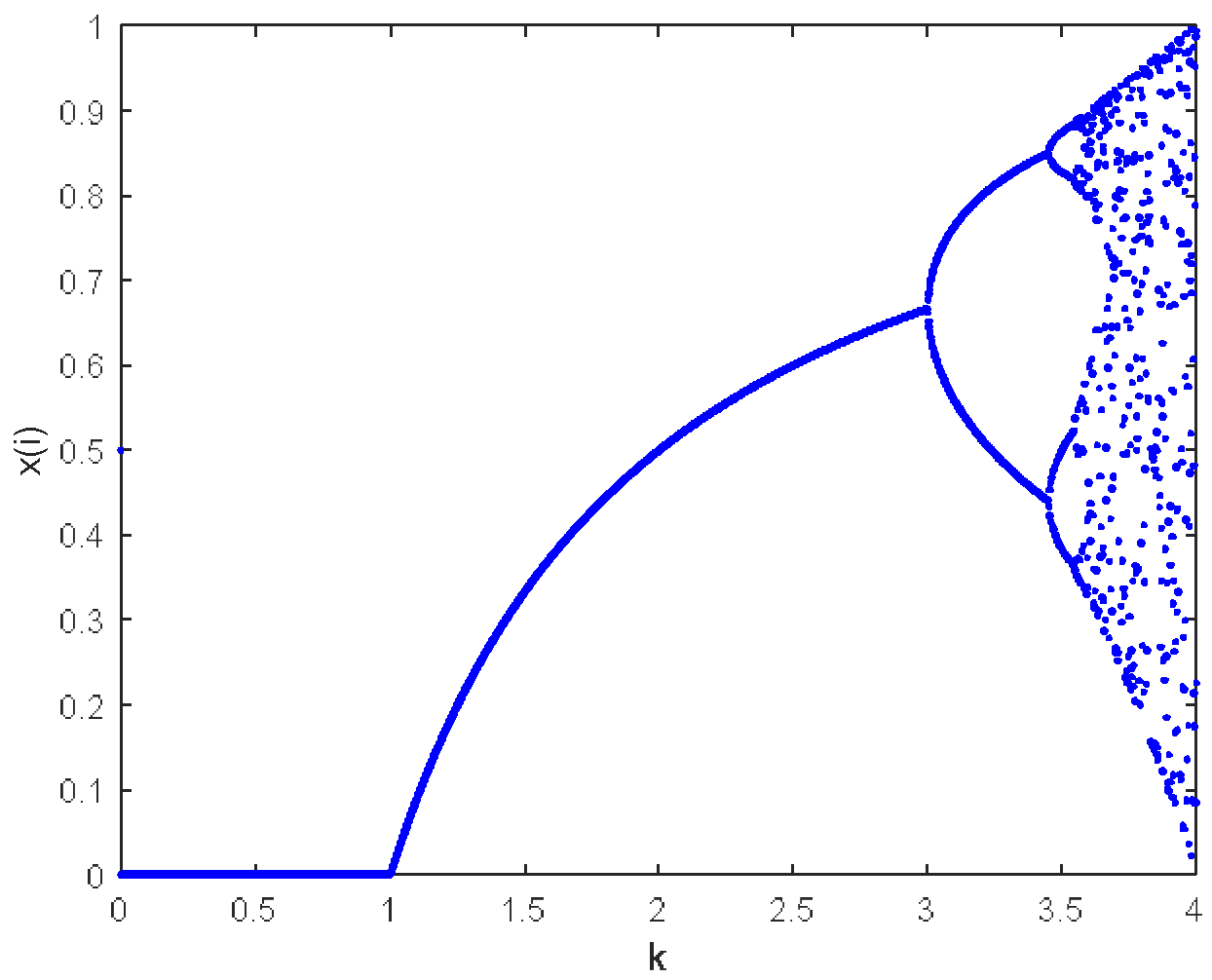

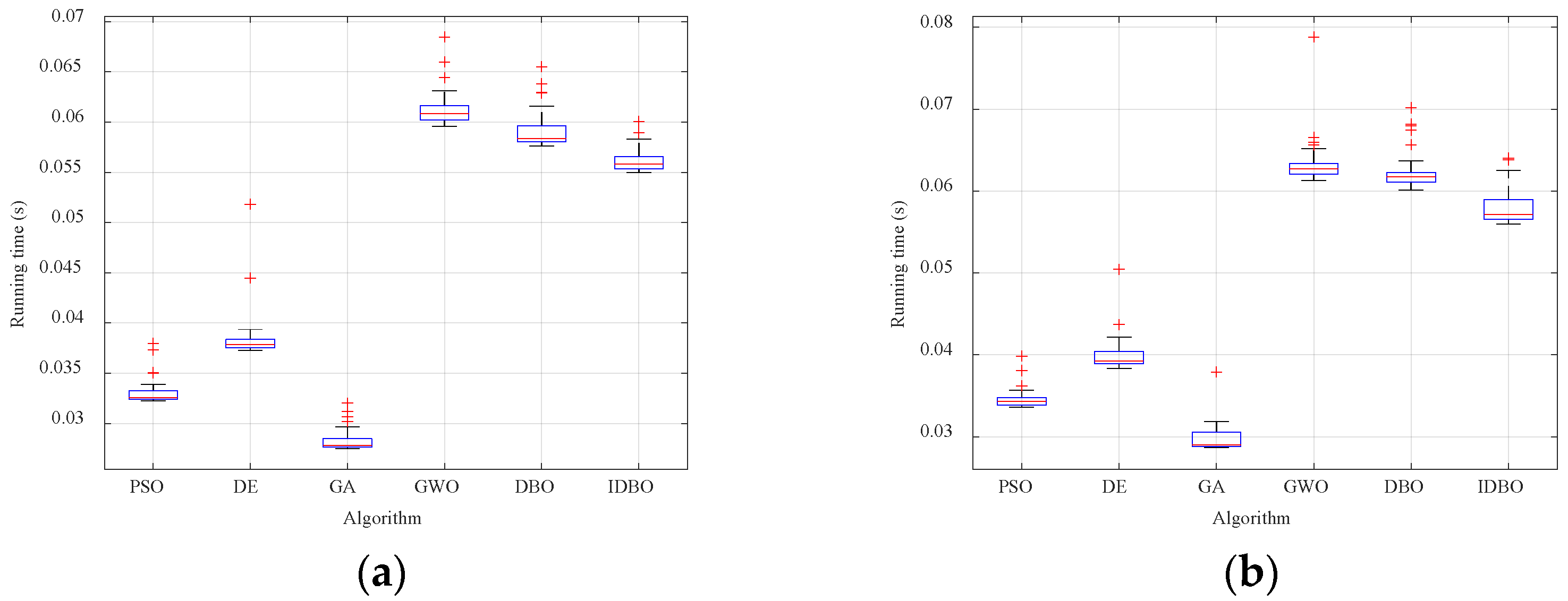
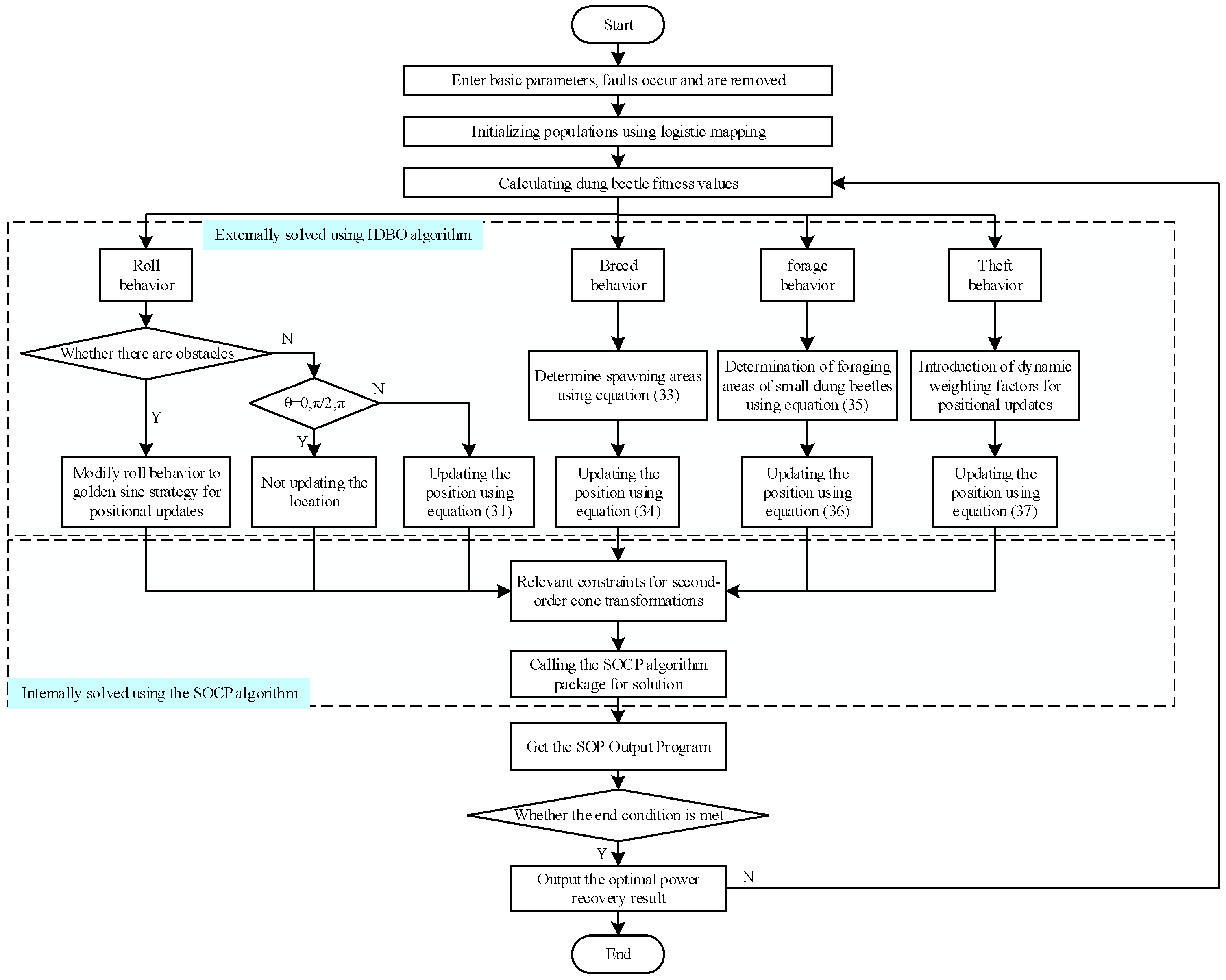

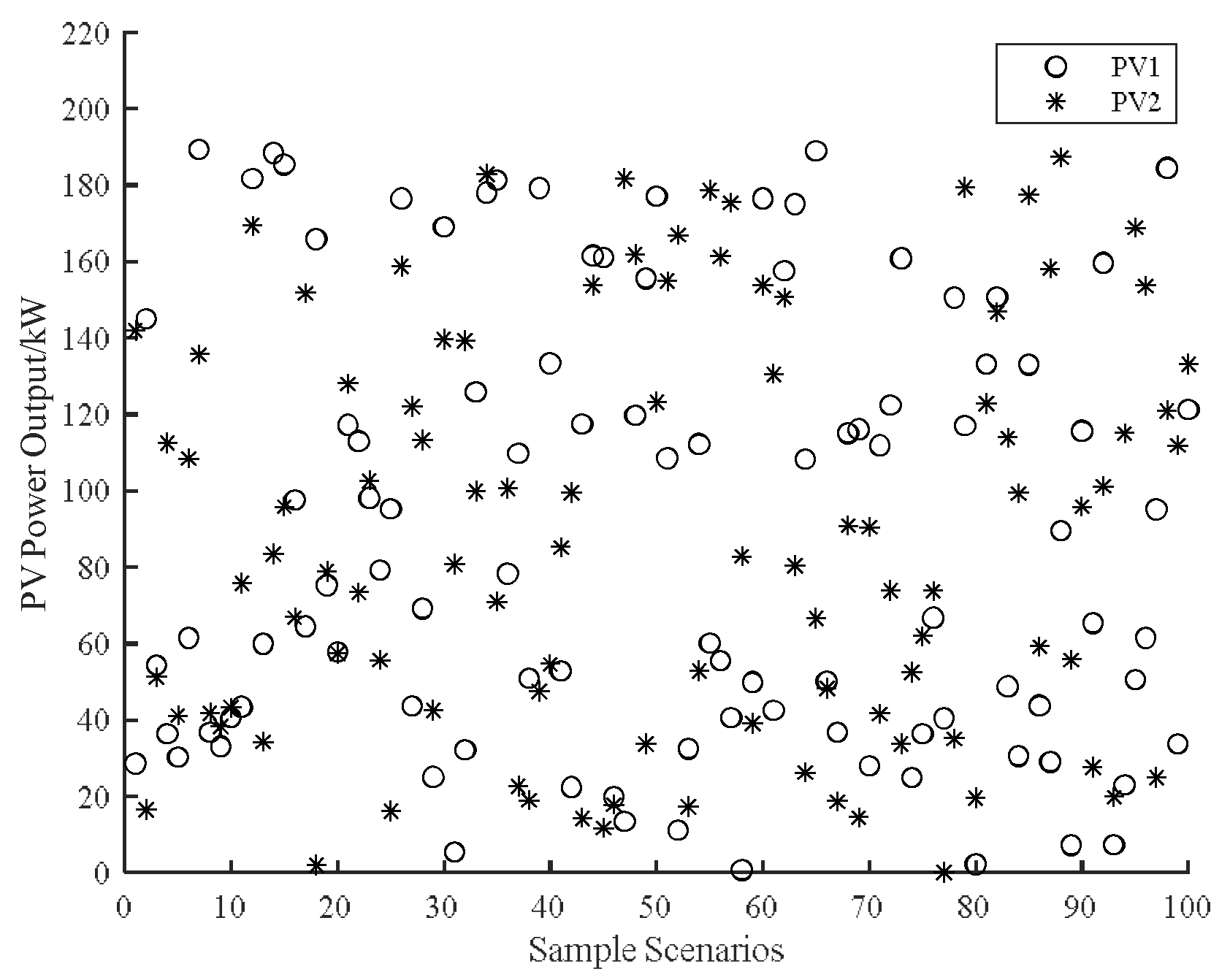
| Algorithm Name | Core Mechanism | Advantages |
|---|---|---|
| Improved Dung Beetle Optimization (IDBO) | Based on DBO, integrated with Logistic chaotic mapping for initialization, golden sine strategy for exploration, and dynamic weights for exploitation | Fast convergence, excellent population diversity, resistance to local optima, and adaptability to complex problems |
| Standard Dung Beetle Optimization (DBO) | Simulates the behaviors of dung beetles: ball-rolling (global search), dancing (local search), and reproduction (population update) | Simple principle, few parameters for easy implementation, and high efficiency in global exploration |
| Particle Swarm Optimization (PSO) | Simulates group collaboration; updates position and velocity based on personal best (pbest) and global best (gbest) | Fast convergence, simple iteration, and good adaptability to continuous variable optimization |
| Differential Evolution (DE) | Generates offspring from parent individuals via three steps: mutation, crossover, and selection, based on parent difference | Strong global optimization capability and good stability in solving nonlinear problems |
| Genetic Algorithm (GA) | Simulates biological evolution; iteratively optimizes the population through selection, crossover, and mutation operations | High robustness, adaptability to discrete/mixed variable problems, and easy parallelization |
| Grey Wolf Optimizer (GWO) | Simulates grey wolf group hunting; updates population position under the guidance of α, β, and δ wolves | Stable convergence, few parameters, and outstanding exploration capability for multimodal problems |
| Method | Evaluation Index | |||
|---|---|---|---|---|
| Best Value | Mean Value | Average Runtime/s | ||
| FSphere | IDBO | 0 | 0 | 0.056 |
| DBO | 8.93 × 10−251 | 2.30 × 10−183 | 0.059 | |
| PSO | 5.62 × 10−5 | 2 × 10−3 | 0.033 | |
| DE | 1.12 × 10−6 | 3.78 | 0.038 | |
| GA | 1.89 × 102 | 5.95 × 102 | 0.028 | |
| GWO | 3.52 × 10−48 | 5.26 × 10−46 | 0.061 | |
| FSchwefel | IDBO | 0 | 0 | 0.058 |
| DBO | 2.15 × 10−132 | 1.30 × 10−95 | 0.062 | |
| PSO | 7.23 × 10−4 | 4.97 × 10−3 | 0.034 | |
| DE | 6.34 × 10−7 | 1.51 × 10−3 | 0.040 | |
| GA | 4.72 | 7.69 | 0.029 | |
| GWO | 9.70 × 10−29 | 1.63 × 10−27 | 0.063 | |
| E-SOP Capacity | Load Restoration Results/kW | Load Restoration Rate/% |
|---|---|---|
| 0.5 MVA | 467.21 | 12.58 |
| 1 MVA | 915.01 | 24.63 |
| 2 MVA | 1812.74 | 48.80 |
| 3 MVA | 2017.94 | 54.32 |
| 4 MVA | 2017.94 | 54.32 |
| Method | Restored Load/kW | Load Restoration Rate/% | Partially or Fully De-Energized Nodes |
|---|---|---|---|
| Case1 | 1085.0 | 50.82 | 5,7–9,13–18,33 |
| Case2 | 1485.0 | 69.56 | 5,9,13–18,33 |
| Case3 | 1734.7 | 85.05 | 8,30,31 |
| Method | Confidence Level | Restored Load/kW | Load Restoration Rate/% |
|---|---|---|---|
| Without Uncertainty | 1085.0 | 50.82 | |
| Case1 | 0.9 | 1029.32 | 48.21 |
| 0.8 | 916.79 | 42.94 | |
| Without Uncertainty | 1485.0 | 69.56 | |
| Case2 | 0.9 | 1408.79 | 65.99 |
| 0.8 | 1140.39 | 53.41 | |
| Without Uncertainty | 1734.73 | 85.05 | |
| Case3 | 0.9 | 1457.03 | 70.90 |
| 0.8 | 1376.19 | 66.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Wang, C.; Qiu, W.; Xiao, H.; Hu, W. Research on Power Supply Restoration in Flexible Interconnected Distribution Networks Considering Wind–Solar Uncertainties. Energies 2025, 18, 6051. https://doi.org/10.3390/en18226051
Jiang L, Wang C, Qiu W, Xiao H, Hu W. Research on Power Supply Restoration in Flexible Interconnected Distribution Networks Considering Wind–Solar Uncertainties. Energies. 2025; 18(22):6051. https://doi.org/10.3390/en18226051
Chicago/Turabian StyleJiang, Lin, Canbin Wang, Wei Qiu, Hui Xiao, and Wenshan Hu. 2025. "Research on Power Supply Restoration in Flexible Interconnected Distribution Networks Considering Wind–Solar Uncertainties" Energies 18, no. 22: 6051. https://doi.org/10.3390/en18226051
APA StyleJiang, L., Wang, C., Qiu, W., Xiao, H., & Hu, W. (2025). Research on Power Supply Restoration in Flexible Interconnected Distribution Networks Considering Wind–Solar Uncertainties. Energies, 18(22), 6051. https://doi.org/10.3390/en18226051






