Hybrid Demand Forecasting in Fuel Supply Chains: ARIMA with Non-Homogeneous Markov Chains and Feature-Conditioned Evaluation

Abstract

In the context of growing data availability and increasing complexity of demand patterns in retail fuel distribution, selecting effective forecasting models for large collections of time series is becoming a key operational challenge. This study investigates the effectiveness of a hybrid forecasting approach combining ARIMA models with dynamically updated Markov Chains. Unlike many existing studies that focus on isolated or small-scale experiments, this research evaluates the hybrid model across a full set of approximately 150 time series collected from multiple petrol stations, without pre-clustering or manual selection. A comprehensive set of statistical and structural features is extracted from each time series to analyze their relation to forecast performance. The results show that the hybrid ARIMA–Markov approach significantly outperforms both individual statistical models and commonly applied machine learning methods in many cases, particularly for non-stationary or regime-shifting series. In 100% of cases, the hybrid model reduced the error compared to both baseline models—the median RMSE improvement over ARIMA was 13.03%, and 15.64% over the Markov model, with statistical significance confirmed by the Wilcoxon signed-rank test. The analysis also highlights specific time series features—such as entropy, regime shift frequency, and autocorrelation structure—as strong indicators of whether hybrid modeling yields performance gains. Feature-conditioning analyses (e.g., lag-1 autocorrelation, volatility, entropy) explain when hybridization helps, enabling a feature-aware workflow that selectively deploys model components and narrows parameter searches. The greatest benefits of applying the hybrid model were observed for time series characterized by high variability, moderate entropy of differences, and a well-defined temporal dependency structure—the correlation values between these features and the improvement in hybrid performance relative to ARIMA and Markov models reached 0.55–0.58, ensuring adequate statistical significance. Such approaches are particularly valuable in enterprise environments dealing with thousands of time series, where automated model configuration becomes essential. The findings position interpretable, adaptive hybrids as a practical default for short-horizon demand forecasting in fuel supply chains and, more broadly, in energy-use applications characterized by heterogeneous profiles and evolving regimes.

1. Introduction

Accurate short-term demand forecasting is a fundamental requirement for inventory control and distribution planning in modern fuel supply chains. In the case of diesel fuel, which is commonly used across industrial, commercial, and transport sectors, forecasting plays a pivotal role in ensuring timely replenishment, improving dispatch and routing decisions, optimizing delivery schedules, reducing logistical costs, and improving energy efficiency. A well-tuned forecasting system enables fuel suppliers to prevent stockouts and overstocking, minimize waste, and reduce CO₂ emissions related to suboptimal transport planning. These aspects are especially important in the context of Vendor-Managed Inventory (VMI), where suppliers are responsible for planning deliveries to multiple fuel stations. From a systems perspective, these operational improvements connect directly to energy-use efficiency and sustainability targets in the transport segment.

However, forecasting fuel demand at the station level is particularly challenging due to the stochastic nature of consumption patterns, local events, external shocks (e.g., price changes, weather), and irregular customer behavior. A single supplier may be required to generate forecasts for hundreds of stations, each characterized by a distinct time series with varying statistical properties. These may include differences in trend components, seasonal cycles, variance structures, noise levels, and autocorrelation dynamics. As a result, no single forecasting method is universally effective across all series. This creates a pressing need for automated and adaptive forecasting systems that can dynamically adjust to the characteristics of each time series. Such systems align with current developments in Artificial Intelligence in energy systems design and control, where scalable, data-driven methods are expected to enhance reliability and operational resilience. Moreover, the feature–performance relationships identified in this study can be operationalized as a lightweight pre-screening stage, enabling selective deployment of forecasting components and narrower parameter searches. This has the practical effect of reducing computational load in large-scale settings, which is increasingly relevant given the growing energy and cost footprint of routine model retraining.

Traditional statistical methods, such as ARIMA (AutoRegressive Integrated Moving Average) or exponential smoothing, offer interpretable and well-studied frameworks for time series modelling. However, they may struggle to capture regime shifts, nonlinearity, or irregularity in fuel demand. On the other hand, machine learning approaches, including neural networks or gradient boosting models, often require large amounts of data and substantial tuning effort and may lack robustness across diverse time series profiles. Moreover, such methods frequently operate as “black boxes,” making them less transparent for practical decision-making.

To overcome the limitations of individual models, hybrid forecasting approaches have gained increasing attention in recent years. These methods aim to combine the strengths of different models to achieve higher accuracy and robustness. In this study, we propose a dynamic hybrid model that combines an ARIMA component with a stochastic model based on discrete-time Markov chains, designed specifically for fuel demand forecasting. The hybridization is implemented through a weighted combination of forecasts, where the weighting parameter (denoted as α) is optimized in a moving time window by minimizing forecasting error. This approach allows the model to adjust dynamically to changing time series characteristics and data regimes, leveraging the strengths of each component at the right time.

Importantly, the hybrid model does not assume a fixed weighting scheme. Instead, the α parameter is updated iteratively, depending on the recent forecasting performance of the ARIMA and Markov models. This structure raises a natural research question In other words, do certain characteristics of diesel consumption profiles favour ARIMA-based modelling, while others suggest stronger reliance on Markov dynamics? Therefore, the objectives of this study are twofold:

• To evaluate the forecasting accuracy of the hybrid ARIMA–Markov model compared to its standalone components across a large set of real-world diesel demand time series.
• To investigate how statistical features of the time series (e.g., seasonality strength, volatility, entropy, autocorrelation) affect the effectiveness of hybridization and under what conditions the hybrid model significantly outperforms its individual counterparts, thereby informing feature-guided model selection in energy-system applications.

The contribution of this work is both methodological and practical. From a methodological perspective, we present a forecasting framework that automatically adapts to diverse time series without manual tuning. From a practical standpoint, the findings can support model selection automation for fuel supply chain operators by indicating, in advance, which series are likely to benefit from hybridization. Moreover, the results have implications for understanding the relationship between time series characteristics and forecasting model performance in high-stakes applications such as fuel logistics. The approach also connects to sustainability analysis in practice by enabling reductions in emergency deliveries and improved truck loading, which are proximate levers for CO₂ mitigation in distribution operations.

The remainder of the article is structured as follows. In Section 2, we review relevant literature on hybrid forecasting models and their application in logistics and energy sectors. Section 3 describes the individual models (ARIMA and Markov) chains and outlines proposed methodology with the hybridization mechanism. Section 4 presents the dataset, feature engineering process, and experimental methodology the empirical results, including forecasting error comparisons and correlation analysis between time series features and the hybrid model’s behavior. Finally, last section concludes the study, discusses practical implications, and suggests directions for future research.

2. Related Works

Literature from recent decades describes a wide range of methods for forecasting demand in various fields, from engineering to economics. Classic statistical approaches include regression models, moving averages, exponential smoothing, and time series analysis methods such as the ARIMA autoregressive model and its seasonal variant, SARIMA. Research confirms the effectiveness of these statistical models in many areas, from retail sales to the fuel and energy sectors [1]. For example, ARIMA/SARIMA models have been successfully used to forecast retail and energy demand [1]. On the other hand, the rapid development of artificial intelligence (AI) techniques has brought machine learning-based methods to forecasting. These include expert systems, fuzzy logic, neural networks, and hybrid approaches integrating multiple AI techniques. Neural networks (including deep ones, such as LSTM) have gained particular popularity—their adaptability often allows them to outperform traditional models in terms of forecast accuracy for complex, nonlinear demand patterns [2]. Research shows that nonlinear machine learning models can produce smaller forecast errors than classic ARIMA models [3]. In practice, however, effectiveness depends on the nature of the data—for example, for products with stable demand, LSTM networks may be better, but with clear seasonality, traditional statistical models can be competitive [4].

In response to the limitations of individual forecasting methods, researchers have increasingly explored the combination of different models to leverage their complementary strengths. These hybrid forecasting models are based on the premise that each method possesses certain advantages but also inherent weaknesses—thus, their integration may enhance the overall forecasting performance [5]. As early as in the pioneering work of Bates and Granger (1969), combining forecasts from two independent models resulted in lower error variance compared to using either model alone [6]. Since then, many researchers have followed this path, proposing increasingly creative hybrid solutions. Notably, hybrid models have achieved top ranks in international forecasting competitions. For instance, the winning approach in the renowned M4 competition was a hybrid that combined classical exponential smoothing methods with a recurrent neural network (RNN) [7]. The author proves that on average, combining different methods yields more accurate forecasts than using them individually. Hybridization can be implemented in several ways. In the parallel structure, each model produces its own forecast independently, and the results are then aggregated—typically using a weighted average [8]. This principle underlies the classic Bates–Granger method, where forecasts from two separate models are averaged [6]. A second type is the sequential structure, in which the output of one model becomes the input for another. This idea was introduced in [5], where the author proposed combining the ARIMA model with an artificial neural network (ANN) in a serial framework: ARIMA is first used to model the linear structure in the data, and then the ANN approximates the nonlinear components from the residuals [5]. Since then, numerous variants of such serial hybrids have been proposed and tested on diverse datasets, enhancing the original architecture [9]. The literature reports a broad range of hybrid combinations, particularly those that integrate ARIMA with nonlinear models such as artificial neural networks (ANN), support vector machines (SVM/LSSVM), or granular computing networks [10]. These hybrids have demonstrated strong performance across various domains, including wind speed prediction, crude oil price forecasting, tourism demand, precipitation modeling, network traffic analysis, epidemic spread, energy consumption, and water demand forecasting [11]. Frequently, hybrid models outperform individual methods. For instance, in [12] the authors proposed a hybrid forecasting architecture that sequentially combines ARIMA and artificial neural networks (ANN) to enhance predictive accuracy. In this framework, the original data is first modeled using ARIMA, and the resulting residuals are then passed to the ANN for secondary learning. A distinctive feature of the approach is a classification step that groups ARIMA outputs into three categories before feeding them into the neural network. Experimental results on benchmark datasets demonstrate that the proposed hybrid model outperforms conventional forecasting methods in most cases. In [13] authors addressed the challenge of forecasting financial time series characterized by high nonlinearity and nonstationarity. They proposed a hybrid model combining signal decomposition (CEEMDAN), complexity analysis (Sample Entropy), and predictive modeling (ARIMA for high-frequency components and CNN-LSTM for low-frequency ones). The model’s architecture separates signal components based on complexity, applies tailored models to each, and aggregates forecasts to reconstruct the final signal. Experimental results showed superior accuracy compared to standalone models, answering the research question of how to effectively integrate statistical and deep learning techniques in financial forecasting. In [14] the authors tackled the problem of improving the accuracy of crude oil price forecasting in the South African context. Recognizing the limitations of purely linear models like ARIMA in capturing nonlinear dynamics, they proposed two hybrid models: ARIMA-GRNN and ARIMA-ANN-based ELM. In both cases, the ARIMA model was first fitted to capture the linear structure, and its residuals were then modeled using neural networks to account for nonlinearities. The models were evaluated on monthly data from 2021 to 2023, covering different periods (pre-, during-, and post-COVID-19). The results showed that the ARIMA-ANN-based ELM model achieved the highest accuracy (lowest RMSE and MAE) across the full sample, outperforming both the base ARIMA and the ARIMA-GRNN models. Similarly, in work [15] a hybrid ARIMA–LSTM model for short-term vehicle speed prediction using data from intelligent transportation systems has been proposed. The model first applies ARIMA to capture linear patterns, then uses LSTM to model residuals representing nonlinear dynamics. Results on real-world traffic sensor data showed that the hybrid approach achieved lower prediction errors (MAE, RMSE) than either method alone. The study highlights how hybrid architectures can improve short-term forecasting accuracy in traffic applications, particularly under dynamic and nonlinear conditions. Hybrid approaches are also emerging in supply chain applications. Babai et al. (2021), after comparing SARIMA and LSTM models for retail sales data, proposed a hybrid method that trains both models on clusters of stores with similar sales profiles—potentially combining the advantages of both statistical and neural techniques [16]. Similarly, Sun et al. (2018) proposed a hybrid scheme for forecasting fuel demand at petrol stations, combining a clustering algorithm with a decision tree model [17]. Their method first groups daily fuel sales trajectories into clusters of similar shape, and then a decision tree predicts the future day’s cluster membership and estimates demand accordingly. Experimental results demonstrated that this approach outperformed three benchmark methods by a considerable margin [17].

Markov chains represent a distinct class of forecasting tools, particularly useful in situations where the future state depends primarily on the current state, rather than on the full historical path of the process. In the context of demand forecasting, this means modelling a sequence of events in which, for example, the demand in the next period depends mainly on the current period’s demand. Although Markovian methods have not been as widely used in demand forecasting as ARIMA models or neural networks, several studies indicate their applicability. Tsiliyannis (2018) proposed Markov chain-based models for forecasting product returns in reverse logistics (remanufacturing) and demonstrated their real-time effectiveness [18]. His method outperformed traditional linear regression models in estimating upcoming return volumes, particularly in accurately predicting sudden spikes and drops in the return flow [18]. Markov chains have also been applied in urban transportation. For instance, Zhou et al. (2018) used a Markov model to predict bicycle demand in a bike-sharing system [19]. Their model estimated the probabilities of bike rentals and returns at individual stations and proved more suitable than traditional approaches such as gravity models in capturing the unique dynamics of each station [16]. In other words, in systems characterized by high demand irregularity and limited memory of historical data, the Markov approach may better represent the current state of demand compared to models requiring long time series. Markov models have also achieved success in finance. Wiliński (2019) introduced a financial market forecasting model based on a Markov chain with a variable transition matrix (a so-called heterogeneous Markov chain) [20]. This allowed transition probabilities between states to be adjusted according to changing market conditions. Such an approach addresses the problem of non-stationarity unlike classic Markov chains with fixed probabilities, models with variable (context-sensitive) transition matrices are better equipped to handle trends or structural changes in demand data [20]. A broader review of the literature on Hidden Markov Models (HMMs) confirms their wide range of applications in engineering from machine condition prognosis to market modelling [21]. Overall, while applications of Markov chains in demand forecasting are still relatively limited, there is growing evidence that they can effectively complement or even replace traditional methods in environments characterized by high volatility and nonlinear demand patterns. In such cases, Markov models especially those with dynamic transition matrices offer an appealing alternative due to their interpretability and capacity to capture short-term demand dependency patterns [20,21].

The characteristics of the forecasted time series play a crucial role in selecting an appropriate forecasting method. Nevertheless, relatively few studies have systematically examined the relationship between data features and the performance of specific forecasting techniques. In recent years, however, research efforts have emerged to address this gap. Bandara et al. (2020) introduced the concept of leveraging similarities between time series by applying various clustering algorithms to group series with similar characteristics [22]. For each cluster, they trained a global LSTM forecasting model. This “divide and forecast” approach led to improved accuracy training separate neural networks on more homogeneous data segments resulted in better forecasting performance than using a single model across the entire heterogeneous dataset. In another line of research, Kang et al. (2017) proposed a method for visualizing and analyzing multiple time series simultaneously by mapping them into a feature space [23]. Each series was characterized by a set of indicators (e.g., spectral entropy, trend strength, seasonal strength, seasonal period, first-order autocorrelation, and Box-Cox transformation parameter) and then represented as a point on a two-dimensional plane. This enabled the identification of “zones” in the feature space and an assessment of which forecasting methods performed best for series with specific properties. Their results demonstrated that forecasting performance varied depending on the characteristics of the series—certain techniques yielded lower errors in highly seasonal areas, while others performed better when strong trends were present. Similarly, in [24] the authors examined forecasting model selection based on time series characteristics. They tested both subjective (expert-based) and algorithmic (automated feature-based) model selection approaches, ultimately proposing a hybrid method that combined both strategies. This yielded promising results, suggesting that a combined selection mechanism may offer advantages over either approach alone. Another important factor influencing forecasting performance is the length of the available historical data. Qin et al. (2019) analyzed the impact of time series length on the accuracy of ARIMA models [25]. Their findings showed that ARIMA’s forecasting performance deteriorates significantly with very short series. This observation confirms the intuitive notion that the shorter the series, the greater the forecast uncertainty. This should be considered when selecting forecasting methods for instance, deep learning models typically require longer sequences for training, while statistical models can sometimes operate on shorter samples, albeit with reduced precision [25]. In summary, recent studies suggest that accounting for time series characteristics such as trend, seasonality, volatility, history length, value distribution, or autocorrelation can significantly enhance forecasting model selection and improve prediction accuracy. Product groups or phenomena with different temporal profiles may require tailored approaches. Therefore, the development of automatic time series classification methods and hybrid forecasting strategies that adapt to the specific structure of the data appears to be a promising direction for further research. This is particularly relevant in practical domains such as logistics and business, where demand patterns are highly diverse and often irregular.

Demand forecasting plays a particularly important role in the logistics of fuel supply accurately predicting fuel demand at petrol stations enables the optimization of inventory levels and delivery routes while preventing shortages or surpluses, ultimately reducing costs and enhancing customer satisfaction. Despite its importance, literature reviews indicate that the fuel sector has not yet received sufficient attention in the context of advanced forecasting methods. For example, in their comprehensive review of demand forecasting techniques in the energy sector, Mystakidis et al. (2021) noted that only a handful of studies have focused on demand forecasting for fuel stations [26]. Similarly, Sun et al. emphasized that this issue remains underexplored compared to other industries [17]. In practice, fuel companies still often rely on traditional techniques (e.g., linear forecasts based on historical sales data), while other industries are increasingly adopting machine learning and hybrid approaches. Nonetheless, early signs of change are emerging. As previously mentioned, the study by Sun et al. (2018) demonstrated that the use of artificial intelligence algorithms (clustering combined with decision trees) can significantly improve fuel demand forecasting accuracy compared to classical approaches [17]. Other studies likewise suggest that “intelligent” forecasting methods can reduce errors and operational costs in the energy sector, translating into higher profitability [27]. It is therefore reasonable to expect that in the coming years, machine learning techniques including neural networks and hybrid approaches will be increasingly adopted in the fuel industry and in broader logistics applications. These techniques offer the ability to account for complex demand patterns (e.g., the influence of weather, holidays, promotional campaigns, or macroeconomic trends) far more effectively than simple models. Thus, demand forecasting long recognized as a core element of supply chain management is evolving toward a greater integration of statistical techniques with artificial intelligence. The literature indicates that hybrid approaches, when appropriately matched to the nature of the data, can yield the most significant benefits in terms of reducing forecast errors and supporting business decision-making [27]. The specific challenges faced by the fuel sector such as high daily demand volatility at stations, the impact of random factors, and logistical constraints represent a promising area for the application of advanced forecasting methods and highlight the need for further research in this domain.

3. Methodological Framework

3.1. Basics of Forecasting with Markov Chains

3.1.1. Homogeneous Markov Chains

Markov chains represent a relatively straightforward yet effective tool for modelling processes in which the future state depends solely on the present one, without regard to the sequence of events that led to it. In the context of a petrol station, this means that demand at a given day or hour is primarily determined by demand during the preceding day or hour, rather than by sales patterns observed weeks or months earlier. Cyclical fluctuations in demand can be incorporated by designing an appropriate state structure within the Markov chain, thereby capturing, for instance, peaks in sales during weekends, holidays, or other specific periods. Unlike more advanced forecasting approaches, such as neural networks, Markov chains are relatively easy to interpret and communicate, which facilitates their acceptance and trust among station staff. The essential element of modelling with Markov chains lies in the definition of states and the transition probabilities between them. If latent patterns in the data can be expressed in terms of states and their transitions, then Markov chains can efficiently detect and represent such structures.

A Markov process is defined as a sequence of random variables in which the probability of the next event depends exclusively on the current state. For the purposes of the present analysis, only Markov processes defined on a discrete state space—that is, Markov chains—will be considered. Let us denote by:

$$X=\left(X_0,X_1,\dots ,X_t,\dots ,X_{t_{max}}\right)$$

(1)

a sequence of discrete random variables. The value of the variable $X_t$ will be called the state of the chain $s_k$ at the moment t. The finite set of all possible states is called the state space $S$, which can be expressed as:

$$s\in S,\hspace{1em}\hspace{0.33em}S=\left\{s_1,s_2,\dots ,s_{k-1,}{s}_k\right\},k<\mathrm{\infty }$$

(2)

It is assumed that the set of states $S$ is calculable. The discrete timestamps used in the considered problem can be defined as follows:

$$tϵT,T=\left\{\mathrm{1,2},\dots ,t_{max}\right\},t_{max}\le \mathrm{\infty }$$

(3)

Definition 1. 

A sequence of random variables X is a Markov chain if the Markov property holds:

$$\mathbb{P}\left(X_{t+1}=s_{t+1} |{ X}_t=s_t,X_{t-1}=s_{t-1},\dots ,X_0=s_0\right)=\mathbb{P}\left(X_{t+1}=s |{ X}_t=s_t\right) \forall tϵT \wedge \forall s_0, \dots ,s_t{,s}_{t+1}\in S$$

(4)

Thus, in a Markov chain, the conditional distribution at time $t+1$ depends only on the state at time $t$, and not on the full trajectory of past states.

Definition 2. 

Let $\mathcal{P}$ denote a transition matrix of dimension $(k\times k)$ with elements $\{p_{ij}:i,j=1,\dots ,k\}$. A sequence of random variables $(X_0,X_1,\dots )$, taking values in a finite state space $S=\{s_1,s_2,\dots ,s_{k-1},s_k\}$, is a Markov chain with transition matrix $\mathcal{P}$ if, for every $t$ and for any $i,j\in \{1,\dots ,k\}$, the following condition is satisfied:

$$p_{ij}=\mathcal{P}\left(X_{t+1}=s_j |{ X}_t=s_i\right)$$

(5)

Here, $p_{ij}$ represents the conditional probability of transitioning from state $s_i$ at time $t$ to state $s_j$ at time $t+1$. The elements of the transition matrix satisfy:

$$\forall tϵT:p_{ij}=\mathcal{P}\left(X_{t+1}=s_j|X_t=s_i\right)$$

(6)

$$p_{ij}\ge 0,\hspace{1em}\hspace{0.33em}\forall i,j\in \{1,\dots k\}$$

(7)

$$\forall i:\sum _{j\in \{1,\dots k\}}{p}_{ij}=1$$

(8)

Definition 3. 

The Markov chain is homogeneous when, for each time stamp, it is described by the same transition matrix script $\mathcal{P}$. The transition matrix is fixed and does not depend on time.

The specification of the initial state is also crucial in the construction of a Markov chain. Formally, the initial state is the random variable $X_0$. Consequently, the process is typically initiated with a probability distribution over the state space.

Definition 4. 

The initial distribution ${\pi }_0\left(s_i\right)$ is defined as the probability vector:

$${\pi }_0\left(s_i\right)=\left[{\pi }_0\left(s_1\right),{\pi }_0\left(s_2\right), \dots ,{\pi }_0\left(s_k\right)\right]=\mathcal{P}\{\left(X_0=s_i\right):\forall s_i\in S\}$$

(9)

The distribution of the forecasted state one step ahead is then given by:

$${\mathrm{\pi }}_{t + 1}={\mathrm{\pi }}_{t }·\mathcal{P}$$

(10)

Note that the ${\mathrm{\pi }}_{t + 1}$ or ${\mathrm{\pi }}_t$ are the row vectors; thus, the following recursive formulation applies:

$$\begin{array}{ccc}& {\pi }_1={\pi }_0\cdot \mathcal{P},\hspace{1em}\hspace{0.33em}{\pi }_2={\pi }_1\cdot \mathcal{P}={\pi }_0\cdot {\mathcal{P}}^2,\hspace{1em}\hspace{0.33em}{\pi }_3={\pi }_2\cdot \mathcal{P}={\pi }_0\cdot {\mathcal{P}}^3,\dots ,\hspace{1em}\hspace{0.33em}{\pi }_{t+1}={\pi }_0\cdot {\mathcal{P}}^{t+1}& \end{array}$$

(11)

In practice, most applications of Markov chains assume fixed transition probabilities over time, i.e., homogeneous Markov chains (HMCs). However, this assumption may not hold in systems influenced by human behaviour, such as fuel demand, where patterns vary substantially across time horizons (for example, across seasons or phases of business cycles [27]). For this reason, in the subsequent analysis we adopt heterogeneous or non-homogeneous Markov chains, in which the transition matrix varies with time. Although such models lack a classical stationary distribution, they are nevertheless highly effective in forecasting contexts characterized by dynamic and time-dependent changes. Numerous methods and applications of heterogeneous Markov chains have been reported in the scientific literature, highlighting their practical usefulness [28,29].

3.1.2. Non-Homogeneous Markov Chains

In real-world systems, data describing stochastic processes such as demand are inherently discrete in nature yet derived from continuous observations, meaning that abrupt fluctuations may occur. This evolving behavior often departs from the assumptions underlying homogeneous Markov chains. When random variation plays a relatively minor role, it is common practice to derive the empirical distribution of observations, as expressed by Equation (11). By subsequently observing the process at a later time $t+\tau$ and recording the number of transitions between states, a transition matrix $\mathcal{P}\left(\tau \right)$ can be constructed that satisfies the following relationship:

$${\pi }_{t+\tau }={\pi }_t\cdot \mathcal{P}\left(\tau \right)$$

(12)

The matrix:

$$\mathcal{P}\left(\tau \right)=\{p_{\tau ,i,j}{\}}_{(i,j\in S)}$$

(13)

is referred to as the transition matrix at time $\tau$, where $\tau \in [1,\dots ,n]$ and $n$ denotes the length of the forecast horizon.

In the case of non-homogeneous Markov chains, the Markov property remains valid, although the transition probabilities may vary over time [20]. Such heterogeneous formulations are particularly suitable for short-term forecasting, where the transition matrices for successive steps are known or can be estimated in advance. This makes it possible to trace the evolution of the probability distribution of states while accounting for temporal changes in $P\left(\tau \right)$ at each iteration. Short-term forecasting does not require a stationary distribution, since it focuses on predicting state transitions within a limited future horizon. Further theoretical treatments of non-homogeneous Markov chains can be found in [30,31].

In the present analysis the transition matrix was re-estimated for each new data window, using a rolling analysis approach applied individually to every time series. Each time a new demand observation from the verification period was added to the learning set $T$, a new transition matrix was computed and used to generate the next state forecast. The resulting forecasted state was subsequently transformed into a point forecast of demand, as described below.

For the implementation of Markov chains in forecasting, the definition of the state space for each time series was a crucial step. The number of states was determined analogously to the procedure used for histogram construction. Each state represents a specific range of demand values, with the width of an interval $X_w$ calculated as:

$$X_w={\displaystyle \frac{\mathrm{m}\mathrm{a}\mathrm{x}\left(X\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(X\right)}{\sqrt{N}}}$$

(14)

where $\mathrm{m}\mathrm{a}\mathrm{x}\left(X\right)$ and $\mathrm{m}\mathrm{i}\mathrm{n}\left(X\right)$ denote the maximum and minimum values in the series $X$, and $N$ represents the number of observations. This formula implies that the width of each interval is proportional to the data range divided by the square root of the sample size, leading to narrower intervals for longer series. Although this approach is less conventional, it is particularly useful in modelling fuel demand, where high variability may otherwise produce states with negligible or zero probability of occurrence.

Each demand interval is thus assigned to a unique state from the state space $S=\{s_1,s_2,\dots ,s_k\}$, as illustrated conceptually in Figure 1.

From Equation (10), the forecasted state probability distribution ${\pi }_{t+1}$ can be derived. The corresponding point forecast of demand for the next period was then computed as follows:

$$Y_{t+1}^P=\sum _{j=1}^k{\pi }_{t+1}\left(s_j\right)\cdot {\widehat{X}}_j$$

(15)

where:

• ${\pi }_{t+1}\left(s_j\right)$ denotes the forecasted probability of the time series being in state $s_j$,
• ${\widehat{X}}_j$ represents the midpoint of the demand interval assigned to that state.

This formulation assumes that the expected future demand corresponds to the weighted mean of state midpoints, where the weights are given by the forecasted probabilities of each state. Using this procedure, forecasts for all time series were obtained iteratively for each period within the verification horizon.

3.2. Fundamentals of Forecasting with ARIMA Models

ARIMA models are grounded in the concept of autocorrelation, that is, the correlation between a variable and its own past values. The fundamental characteristic of ARIMA models lies in the assumption that the value of a variable at time $t$ can be expressed as a linear combination of its previous values at moments $t-1, t-2,\dots ,t-p$, augmented by a random error component. Within this class of models, three fundamental types can be distinguished:

• Autoregressive models (AR);
• Moving Average models (MA);
• Combined Autoregressive–Moving Average models (ARMA).

In general form, an autoregressive model of order $p$ may be represented as:

$$Y_t={\phi }_0+{\phi }_1{Y}_{t-1}+{\phi }_2{Y}_{t-2}+\cdots +{\phi }_p{Y}_{t-p}+e_t$$

(16)

where

• $Y_t, Y_{t-1}, Y_{t-2}, Y_{t-p}$—the value of the variable, respectively, at the time $t, t -1, t-2, t-p$;
• ${\phi }_0, {\phi }_1, {\phi }_2, {\phi }_p$—model parameters;
• $e_t$—value of random component at the period $t$;
• $p$—order lag.

The lag parameter $p$ determines the number of previous time steps considered when estimating the variable’s current value. When the random errors from preceding periods are correlated, the process is modelled using a moving average (MA) structure, defined as:

$$\begin{array}{cccc}& Y_t={\vartheta }_0-{\vartheta }_1{e}_{t-1}-{\vartheta }_2{e}_{t-2}-\cdots -{\vartheta }_q{e}_{t-q}+e_t& & \end{array}$$

(17)

where:

• $e_t,e_{t-1},e_{t-2},\dots ,e_{t-q}$ represent the model residuals at times $t,t-1,t-2,\dots ,t-q$;
• ${\vartheta }_0,{\vartheta }_1,{\vartheta }_2,\dots ,{\vartheta }_q$ are the model parameters;
• and $q$ denotes the order of the moving average.

To achieve a better fit to historical data, the autoregressive and moving average components are often combined, forming the ARMA model, which incorporates both $p$ and $q$ parameters. The general form of an ARMA($p,q$) model is given by:

$$Y_t={\varphi }_0+{\varphi }_1{Y}_{t-1}+{\varphi }_2{Y}_{t-2}+\cdots +{\varphi }_p{Y}_{t-p}+e_t-{\vartheta }_0-{\vartheta }_1{e}_{t-1}-{\vartheta }_2{e}_{t-2}-\cdots -{\vartheta }_q{e}_{t-q}$$

(18)

This formulation enables the model to simultaneously capture both the persistence of the time series (through autoregressive terms) and the influence of random shocks (through moving average terms).

4. Research Design

4.1. Methodology Framework

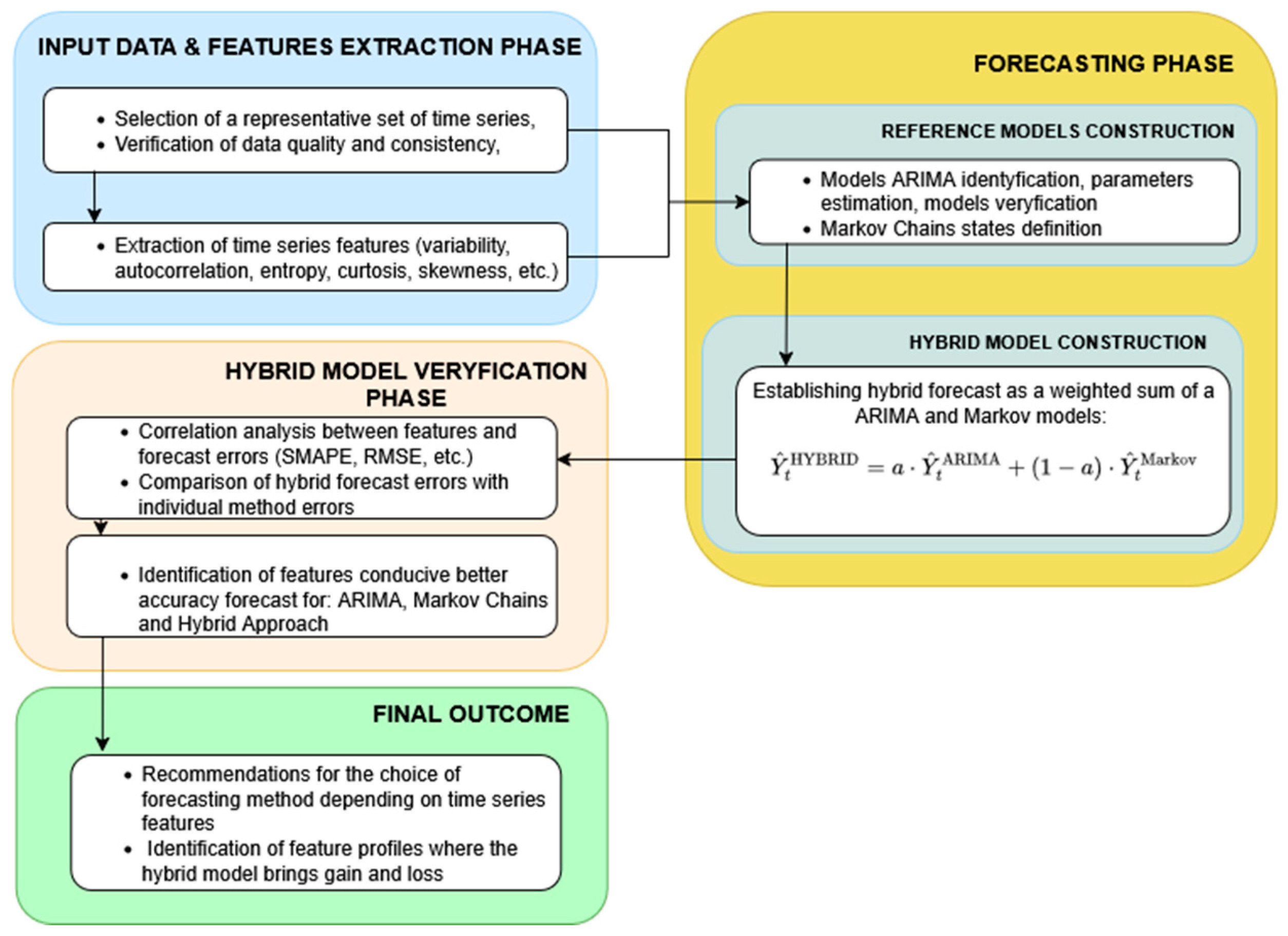
The methodological framework proposed in this study aims to investigate and evaluate a hybrid forecasting approach that integrates deterministic and stochastic modelling principles. The design of the method reflects the assumption that no single model can adequately capture all aspects of complex temporal behavior, particularly in the case of fuel demand, where both regular seasonal patterns and irregular fluctuations coexist. To address this challenge, the proposed framework combines the predictive strength of an ARIMA model, which captures linear temporal dependencies, with a Markov-based component that represents probabilistic state transitions and stochastic dynamics. Importantly, the hybrid model does not rely on a fixed weighting scheme. Instead, the contribution of each component is governed by an adaptive coefficient $\alpha$, which is updated iteratively according to the recent forecasting performance of both models. This adaptive mechanism introduces an additional layer of learning, allowing the hybrid structure to respond dynamically to changing time series characteristics.

In order to achieve aims of the research, the methodological pipeline was structured into four principal phases, as illustrated in the accompanying schematic diagram (see Figure 2):

• Input data and feature extraction phase, which involves loading, preprocessing, and quantifying descriptive characteristics of the analyzed time series;
• Forecasting phase, in which the hybrid ARIMA–Markov model is trained and applied within a rolling prediction framework;
• Hybrid model verification phase, where model performance is assessed using multiple accuracy metrics and comparative analysis; and

• Final outcome, which synthesizes the empirical findings and interprets the behavior of the adaptive weighting parameter $\alpha$ in the context of time series features.

This multi-stage structure provides a coherent methodological foundation for exploring both the predictive efficiency and the interpretability of the proposed hybrid approach.

In the first stage of the study, a representative set of time series was selected, representing the daily consumption of diesel fuel at petrol stations. The data were obtained from a telemetry system monitoring the fuel levels in storage tanks. Before proceeding with further analyses, all time series were subjected to a cleaning and validation process—outliers were removed, any missing values were filled in, and the data were transformed into a uniform format suitable for further modeling.

Next, a set of statistical features describing the structural properties of each series was extracted. The analyzed features included measures of variability (such as standard deviation and coefficient of variation), autocorrelation (the value of the autocorrelation function at lag 1), entropy as a measure of the randomness of the time series, as well as kurtosis and skewness, which characterize the distribution of values. In addition, selected indicators of complexity and non-linearity were considered.

The feature extraction was intended not only to gain a better understanding of the data characteristics but also to enable further analysis of how these features influence forecast accuracy. The list of features considered in the study is presented in

Table 1. List of time series features.

No.	Feature Name	Brief Description
1	Skewness	Measures the asymmetry of the value distribution relative to the mean. Helps detect deviations from symmetrical distributions that may affect forecast quality.
2	Kurtosis	Describes the ‘peakedness’ of the distribution. High values indicate heavy tails and potential presence of outliers.
3	Variance	A classical measure of total variability in the series. High variance suggests volatile behavior, which can be harder to model.
4	Standard Deviation	An intuitive complement to variance. Indicates the spread of observations around the mean—useful for understanding demand amplitude.
5	Coefficient of Variation (CV)	Relative variability (std/mean), independent of scale. Enables comparisons across series with different demand levels.
6	Local Std Deviation Variability (Heteroskedasticity)	Calculated as std of moving std. Indicates whether the volatility itself changes over time—a signal of heteroskedasticity.
7	ACF(1)	First-lag autocorrelation. Shows whether observations are highly dependent on the previous day—relevant for assessing linear structure.
8	Mean ACF(1:7)	Average autocorrelation for lags 1 to 7. Highlights persistence of temporal dependencies beyond immediate lags.
9	PACF(1)	Partial autocorrelation at lag 1. Shows direct linear dependency, removing the influence of earlier lags.
10	Mean PACF(1:7)	Average partial autocorrelation from lags 1 to 7. Indicates the depth of direct dependencies in the series.
11	Seasonality Strength (Max ACF ≥ 1)	Maximum ACF value for lags ≥ 1. High value indicates strong seasonality, which can guide model selection (e.g., seasonal methods).
12	Absolute Value ACF(1)	Autocorrelation of absolute values. Captures nonlinear dependencies related to amplitude—useful for detecting ARCH/GARCH-like behavior.
13	Entropy of Differences	Measures the complexity of value changes. Higher entropy implies more unpredictable, irregular behavior.
14	Number of Regime Shifts	Number of significant shifts in local means (e.g., >1 std). Useful for identifying structural breaks and sudden regime changes.
15	Variance of Local Means	Indicates whether local averages are stable over time. High values suggest shifting trends, complicating forecasting.

.

In the second phase, three categories of forecasting models were developed: the ARIMA model, the Markov model, and the hybrid ARIMA–Markov model. In parallel, Markov chain models were built by transforming the time series into sequences of discrete demand states and estimating transition matrices within each moving window, thereby forming heterogeneous Markov chains capable of reflecting local regime changes. Finally, the hybrid model linearly combined the forecasts from both components according to the adaptive weighting formula described in the following section, where the detailed implementation of the forecasting phase is presented.

In the third stage, the forecasting accuracy of each of the three models was evaluated. For each time series and each model, ex-post errors values were calculated (such as MAE, SMAPE, RMSE). Based on these metrics, a correlation analysis was then performed to examine the relationships between the previously extracted time series features and the obtained forecasting errors. The analysis was conducted independently for the ARIMA model, the Markov chain model, and the hybrid model. The objective was to identify which data features contribute to high forecasting accuracy for a given model, as well as to determine when and for which types of time series the hybrid model outperforms the individual approaches. Particular attention was paid to identifying those time series profiles for which the application of the hybrid approach yields the greatest forecasting benefits.

In the final phase of the study, conclusions were drawn and practical recommendations were formulated regarding the selection of forecasting methods based on the characteristics of time series. Based on the conducted analyses, guidelines were proposed to identify those types of series for which the hybrid model offers a significant improvement over individual methods. The study also highlighted the potential for implementing these findings in decision support systems in fuel logistics, particularly in adaptive forecasting modules that automatically select the appropriate forecasting method depending on the current characteristics of the data.

4.2. Hybrid Forecasting Framework Based on ARIMA–Markov Chains Linear Combination

Time series of fuel demand, including diesel fuel, are characterized by high levels of variability, seasonality, and the presence of local anomalies—such as sudden surges or drops resulting from promotional campaigns, weather changes, or the specific location of the fuel station. In practice, no single forecasting method proves universally effective. Forecasting accuracy in complex, dynamic systems can often be improved by combining models that capture different aspects of temporal behavior. The proposed forecasting framework integrates a classical ARIMA model with a Markov chain-based stochastic model, using a dynamic linear combination mechanism to balance their relative influence over time. The main purpose of this hybrid approach is to exploit both the deterministic structure captured by ARIMA and the stochastic transitions modelled by the Markov process, while allowing the relationship between the two to adapt dynamically as new data become available.

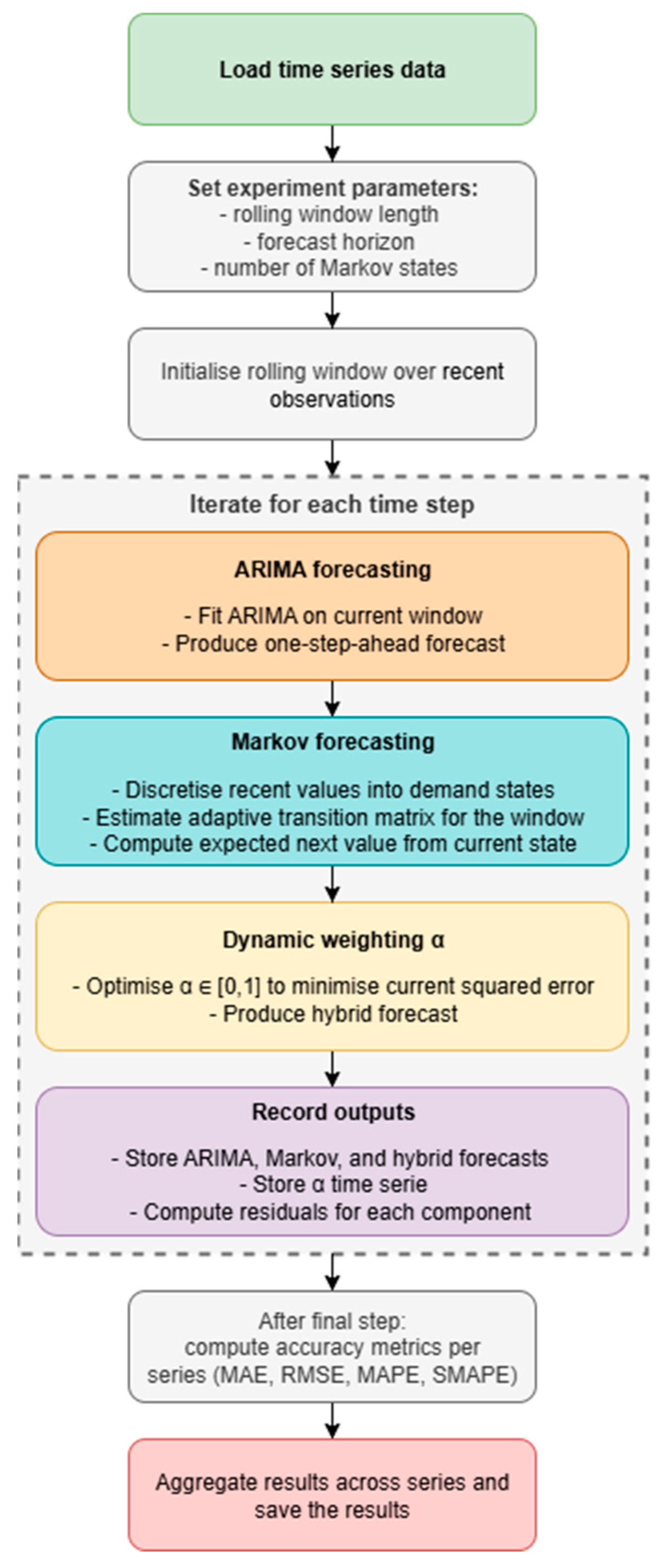
The framework follows a rolling forecasting scheme, in which both models are re-estimated on a moving training window. This approach enables the forecasting system to remain responsive to evolving data patterns, such as changes in demand levels or structural breaks in the time series. The flowchart for the hybrid ARIMA–Markov linear-combination pipeline is presented at Figure 3.

The input data consist of multiple time series, each representing a distinct object or observation category, such as fuel demand at an individual station. Once the data are prepared, the model parameters are specified, including the size of the rolling training window, the forecasting horizon (typically one step ahead), and the number of discrete states used to represent the Markov process.

The forecasting procedure is performed iteratively across all time series, allowing model parameters to be updated continuously as new observations become available. At each iteration, an ARIMA model is fitted to the most recent data segment, producing a one-step-ahead forecast ${\widehat{y}}_{t+1}^{ARIMA}$. The corresponding residuals: $e_t^{ARIMA}=y_t-{\widehat{y}}_t^{ARIMA}$ is retained as a measure of model performance and an indicator of potential non-linear behavior not captured by the autoregressive structure.

In parallel, a Markov chain model is constructed using recent observations. The values within the training window are discretized into a finite number of bins, each representing a distinct system state. Transitions between these states form a transition probability matrix, where each element $p_{ij}$ denotes the probability of moving from state $s_i$ to state $s_j$. Given this matrix, the expected next-period value is obtained as the probability-weighted average of the state midpoints (see Equation (19)), yielding the one-step-ahead Markov forecast ${\widehat{y}}_t^{MARKOV}$. This component captures stochastic and local change patterns that complement the deterministic behaviour represented by the ARIMA model.

A main element of the framework is the dynamic linear combination of the ARIMA and Markov forecasts. Instead of using a fixed weighting scheme, an optimal coefficient ${\alpha }_t$ is determined at each time step by solving a constrained optimisation problem that minimises the mean squared forecasting error:

$$\underset{{\alpha }_t}{\mathrm{m}\mathrm{i}\mathrm{n}}(y_t-[{\alpha }_t·{\widehat{y}}_t^{ARIMA}+(1-{\alpha }_t)·{\widehat{y}}_t^{MARKOV}]{)}^2$$

(19)

subject to $0\le {\alpha }_t\le 1$. The formulation ensures a convex combination of both forecasts. This procedure allows the model to adaptively adjust the relative influence of each component, assigning greater weight to the one that performs better within the current rolling window.

The final hybrid forecast is expressed as:

$${\widehat{Y}}_{t+1}^{HYBRID}={\alpha }_t·{\widehat{Y}}_{t+1}^{ARIMA}+\left(1-{\alpha }_t\right)·{\widehat{Y}}_{t+1}^{MARKOV}$$

(20)

This formulation may be interpreted as a form of online learning, where the combination rule evolves continuously in response to recent forecasting performance.

Once all rolling windows have been processed, the forecasting performance is assessed using standard accuracy metrics, including Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE), and Symmetric Mean Absolute Percentage Error (SMAPE).

The SMAPE (Symmetric Mean Absolute Percentage Error) metric was used in the conducted study as the primary forecast error indicator in the correlation analysis, replacing the traditional MAPE (Mean Absolute Percentage Error). The choice of SMAPE was motivated by several important considerations, which are outlined below. SMAPE divides the absolute forecast error not by the actual value (as in the case of MAPE), but by the arithmetic mean of the actual and predicted values. As a result, this metric treats positive and negative errors in a more symmetric manner, regardless of the direction of the forecast deviation. Unlike MAPE, which deteriorates when the actual value Y_t→0 (since dividing by values close to zero leads to infinite or extremely large errors), SMAPE mitigates this problem because the denominator is not based solely on the actual value. Additionally, SMAPE is expressed as a percentage, which enables intuitive interpretation and facilitates the comparison of errors across time series with different scales. In the context of the analyzed fuel demand time series, significant fluctuations in daily consumption were observed in some cases, the values were very low (e.g., weekend drops in demand), which made MAPE unstable and sensitive to extreme values. MAPE can lead to disproportionately high error values when denominators are close to zero. In contrast, SMAPE remains stable even in the presence of small or zero values, does not favor models that consistently underpredict, and provides a more reliable basis for comparing the accuracy of different models.

For each time series and model variant (ARIMA, Markov, and hybrid), the results are summarized and compared. The analysis includes both quantitative evaluation of accuracy and qualitative examination of the time-varying coefficient ${\alpha }_t$. These adaptive weights provide insight into the relative importance of deterministic and stochastic components over time and across different demand profiles, offering a deeper understanding of how the hybrid model adapts to varying data characteristics.

5. Results for the Case Study

5.1. Dataset Characteristics

The data used in the study comes from 147 different gas stations and represents the historical daily demand for diesel fuel in the period from 1 January 2023 to 31 December 2023. The observed time series values are in liters. The analyzed time series are characterized by high volatility due to the large number of factors affecting the demand for diesel fuel at gas stations (day of the week, seasonality, weather, location, etc.). In order to analyze the characteristics of the time series, a defined set of features was determined for each of them (see Table 1). On this basis, a preliminary assessment and similarity of the series can be made in order to create demand profiles, which will enable the development of recommendations for selecting the most effective forecasting model.

To provide an aggregated visualization of the structure of the analyzed time series in terms of their statistical properties, a Principal Component Analysis (PCA) was conducted. This technique allows for dimensionality reduction in multivariate data while retaining as much of the total variance of the original variables as possible. Each time series was represented in a 15-dimensional feature space describing its structure (e.g., measures of variability, autocorrelation, entropy, skewness, kurtosis, etc.). As part of the PCA procedure, all features were first standardized (mean equal to 0, standard deviation equal to 1) to eliminate the influence of differences in scale among the variables. Then, a covariance matrix was computed, from which the eigenvalues and corresponding eigenvectors were extracted. These eigenvectors define the new axes of the principal components—PCA1, PCA2, and so on—which are linear combinations of the original features. The data were then projected onto these new axes, transforming them into the PCA coordinate space. A scatter plot in the space of the first two principal components (PCA1 and PCA2), presented in Figure 4, enables a visual assessment of the dispersion of the analyzed series in the feature space.

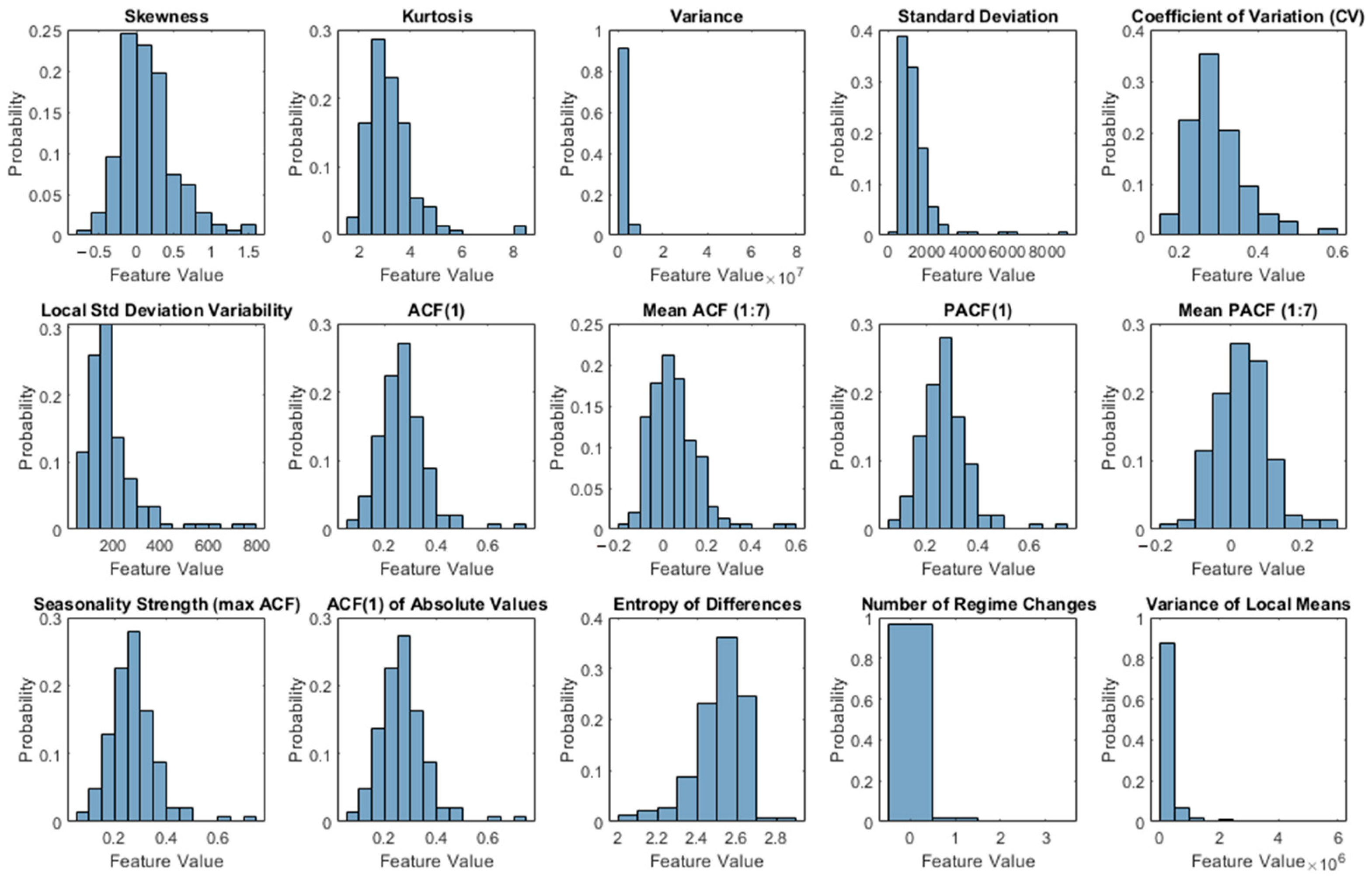
The first principal component (PCA1) explains 39% of the total variance, while the second component (PCA2) accounts for 25.5%, resulting in a cumulative explained variance of over 64% in two dimensions. This allows for an efficient and dimensionally reduced presentation of the structure of the studied population of time series. The analysis of the plot suggests that most of the time series are concentrated in the central region of the principal component space, indicating a relative homogeneity of the dataset in terms of structural characteristics. However, some series exhibit more extreme values along PCA1 or PCA2, potentially representing outliers or specific types of demand patterns (e.g., noticeably higher variability, strong seasonality, or low autocorrelation). The distributions of all analyzed characteristics in the entire time series set are presented in Figure 5.

Based on Figure 5 one can conclude that the variability (measured, by variance, standard deviation, and variation coefficient) as well as local heteroskedasticity (local standard deviation variability) indicate significant differences between time series, manifested in the presence of long distribution tails. This suggests the existence of series with substantially higher dynamics than the average. It is also worth noting the distribution of the number of regime changes and variance of local means, which in most cases take low values but also highlight the presence of series with distinct jumps or trend shifts. The seasonality characteristic (maximum ACF calculated based on 30 lags) reveals a diverse strength of cyclical patterns, which may be relevant when selecting an appropriate forecasting model. Overall, the observed feature distributions confirm the existence of both typical and atypical time series within the dataset, which justifies the use of a hybrid approach capable of adapting to the local properties of the data.

5.2. Detailed Forecasting Results

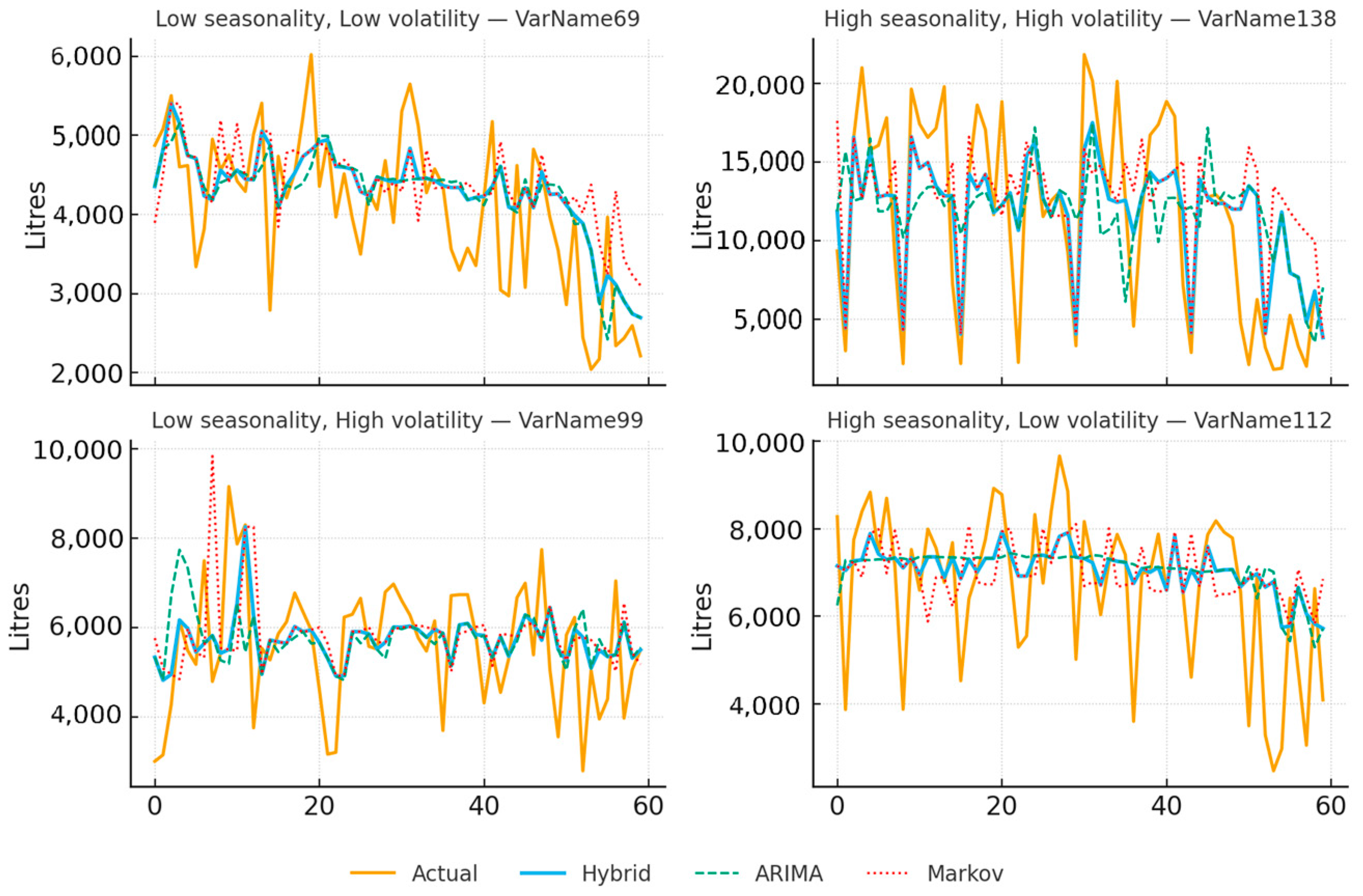
This section illustrates the forecasting behavior of the proposed approach on selected examples before turning to aggregate evidence. Given the large number of time series analyzed and the rolling-window estimation scheme (which generates a distinct model at each verification step), an exhaustive display of all trajectories is impractical. Instead, representative cases are shown to convey typical dynamics and error patterns; the subsequent subsections summarizes performance across all series using aggregated statistics and distributional comparisons.

Figure 6 presents four representative series chosen to span contrasting regimes of seasonality (low vs. high) and volatility (low vs. high). For each panel, the last 60 verification points are shown with actuals (solid), hybrid (solid, emphasized), ARIMA (dashed), and Markov (red, dotted). Across regimes, the hybrid trajectory typically adheres more closely to the actual demand path than either baseline, particularly around local turning points and short-lived deviations, while ARIMA tends to smooth transitions and the Markov component captures discrete shifts with greater sensitivity. These examples are intended to illustrate the qualitative behavior of the models under different signal conditions rather than to provide definitive evidence.

The remainder of the analysis reports aggregated results: distributional plots of error metrics, per-series improvements of the Hybrid model relative to its ARIMA and Markov baselines, rank-based comparisons, and conditioning analyses that relate hybrid gains to measurable time-series properties. This structure provides a balanced view of typical performance, heterogeneity across series, and the conditions under which hybridization offers the greatest benefit.

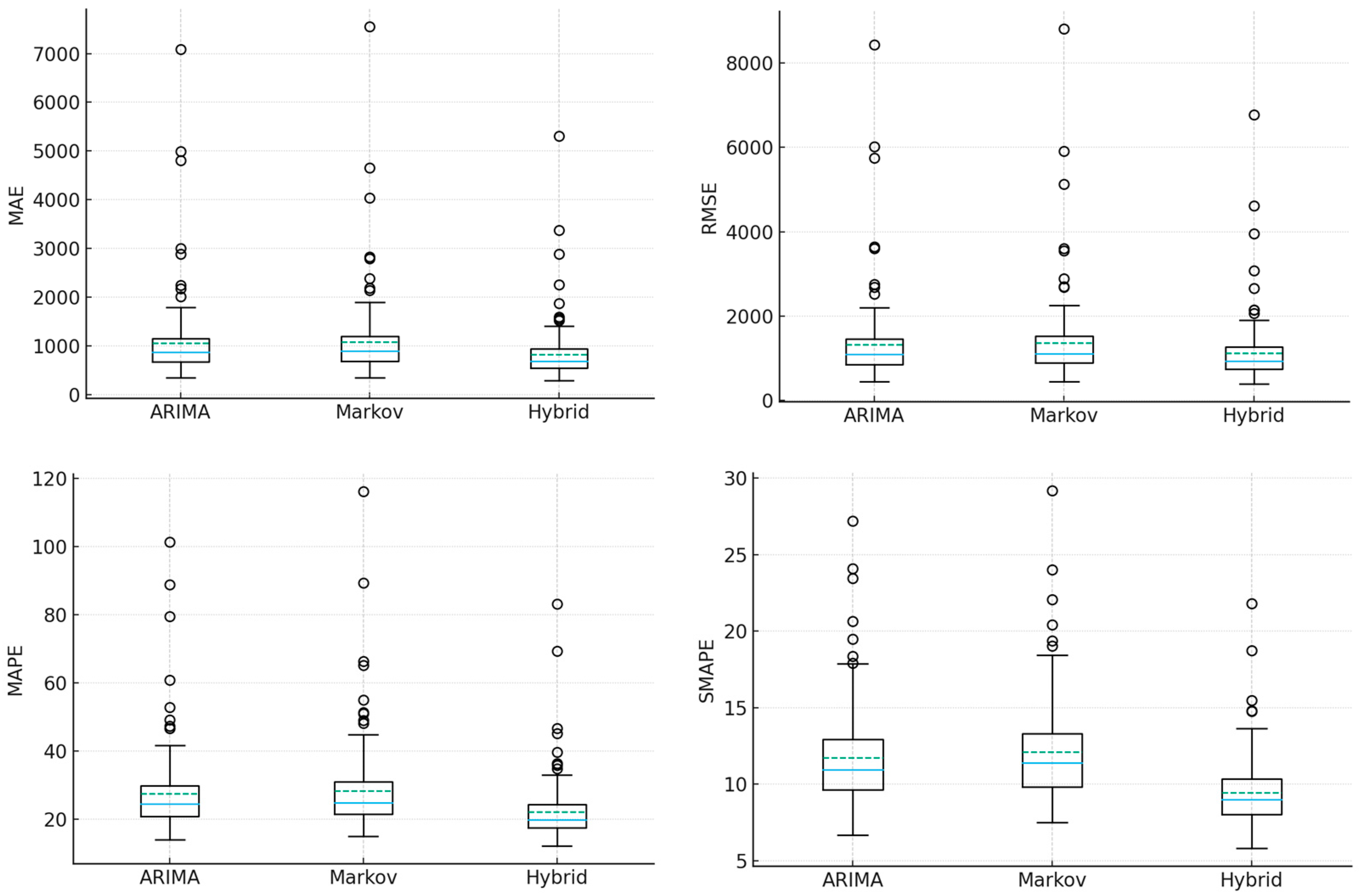
Aggregate performance was evaluated by summarizing errors across all series and contrasting the Hybrid specification with ARIMA and Markov baselines via distributional, per-series, and rank-based comparisons. Figure 7 presents the distribution of forecast errors for MAE, RMSE, MAPE, and SMAPE across models.

The hybrid model achieves consistently lower central errors and tighter interquartile ranges (IQR) than both baselines. For MAE, the median error is 693.97 with an IQR of 552.20–940.71, compared with ARIMA (874.99, IQR 678.84–1156.26) and Markov (897.10, IQR 692.71–1201.16). A similar pattern is observed for RMSE (Hybrid: 933.27, IQR 739.65–1260.46; ARIMA: 1089.64, 844.59–1451.11; Markov: 1104.13, 883.16–1525.86). The advantage also holds for percentage-based measures: MAPE (Hybrid median 19.85 vs. ARIMA 24.56 and Markov 24.90) and SMAPE (Hybrid 9.00 vs. ARIMA 10.96, Markov 11.38). These results indicate that the hybrid approach reduces both typical error magnitude and dispersion across heterogeneous demand profiles.

Hybrid improves upon ARIMA in 100% of cases (147/147 series), with a median error reduction of 18.67% (IQR 16.53–21.83%). Relative to Markov chain approach, hybrid model again improves 100% of series, with a median reduction of 20.54% (IQR 18.42–24.34%). An analogous analysis for RMSE yields consistent conclusions: hybrid model improves over ARIMA in 100% of series (median reduction 13.03%, IQR 11.21–16.13%) and over Markov in 100% of series (median reduction 15.64%, IQR 13.65–18.90%). Paired Wilcoxon signed-rank tests indicated statistically significant improvements of the Hybrid model over both ARIMA and Markov across all series (maximum $p\text{-}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}=7.15\times {10}^{-26}$, $N=147$).

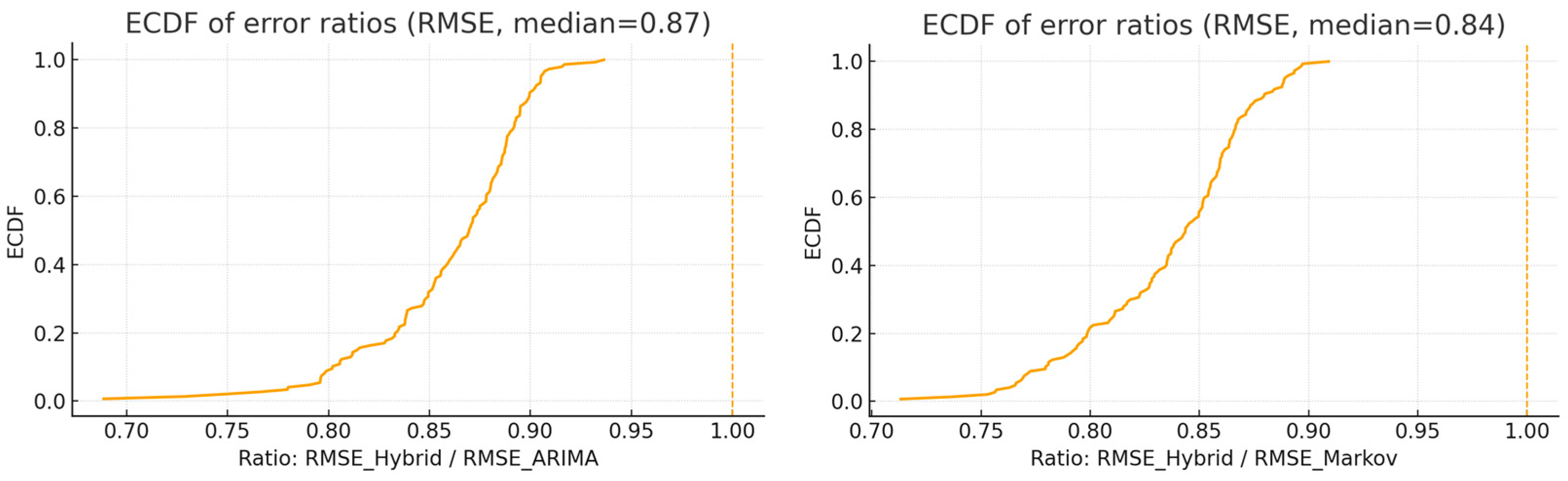
As a further analysis, an empirical cumulative distribution function (ECDF) comparison was conducted to assess relative error levels across all series (see Figure 8). The ECDF, which plots the cumulative proportion of observations up to a given value, was applied to the ratios ${\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{H}\mathrm{y}\mathrm{b}\mathrm{r}\mathrm{i}\mathrm{d}}/{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{A}\mathrm{R}\mathrm{I}\mathrm{M}\mathrm{A}}$ and ${\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{H}\mathrm{y}\mathrm{b}\mathrm{r}\mathrm{i}\mathrm{d}}/{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{M}\mathrm{a}\mathrm{r}\mathrm{k}\mathrm{o}\mathrm{v}}$. Values below 1.0 indicate that the hybrid model attains a lower error than the respective baseline.

The ECDF for ${\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{H}\mathrm{y}\mathrm{b}\mathrm{r}\mathrm{i}\mathrm{d}}/{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{A}\mathrm{R}\mathrm{I}\mathrm{M}\mathrm{A}}$ lies entirely to the left of 1.0, demonstrating improvement for all series. The curve rises steeply around its centre, indicating concentrated gains rather than effects driven by a small number of outliers. Quantitatively, the median RMSE reduction relative to ARIMA equals 13.03% (IQR 11.21–16.13%), corresponding to a median ratio of approximately 0.87. An analogous pattern is observed for the comparison with Markov: the ECDF of ${\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{H}\mathrm{y}\mathrm{b}\mathrm{r}\mathrm{i}\mathrm{d}}/{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{M}\mathrm{a}\mathrm{r}\mathrm{k}\mathrm{o}\mathrm{v}}$ also lies fully left of 1.0, with a median reduction of 15.64% (IQR 13.65–18.90%) and a median ratio near 0.84. These curves therefore indicate universal (all-series) and consistent (narrow IQRs) benefits of the hybrid approach over both baselines.

5.3. Correlation Analysis

Based on the accuracy results obtained from all models (ARIMA, Markov chains, Hybrid Model) expressed by the SMAPE error, Spearman’s correlation coefficients were calculated between SMAPE for each time series and the corresponding feature values. Additionally, in order to obtain information on which features may positively influence the benefits of using the hybrid model, a new variable was defined using the following formula:

$${Imp}^{{SMAPE}_{ARIMA}}={SMAPE}_{ARIMA}-{SMAPE}_{HYBRID}$$

(21)

$${Imp}^{{SMAPE}_{MARKOV}}={SMAPE}_{MARKOV}-{SMAPE}_{HYBRID}$$

(22)

These variables $(Imp.SMAP{E}_{ARIMA}, Imp.SMAP{E}_{Markov})$ describe the relative improvement in the accuracy of forecasts obtained from the hybrid model compared to the errors obtained from ARIMA models and Markov chains used separately. This also made it possible to determine which features of the series have a positive impact on the benefits of hybridization. The matrix with correlation coefficient values for all pairs is shown in Figure 9.

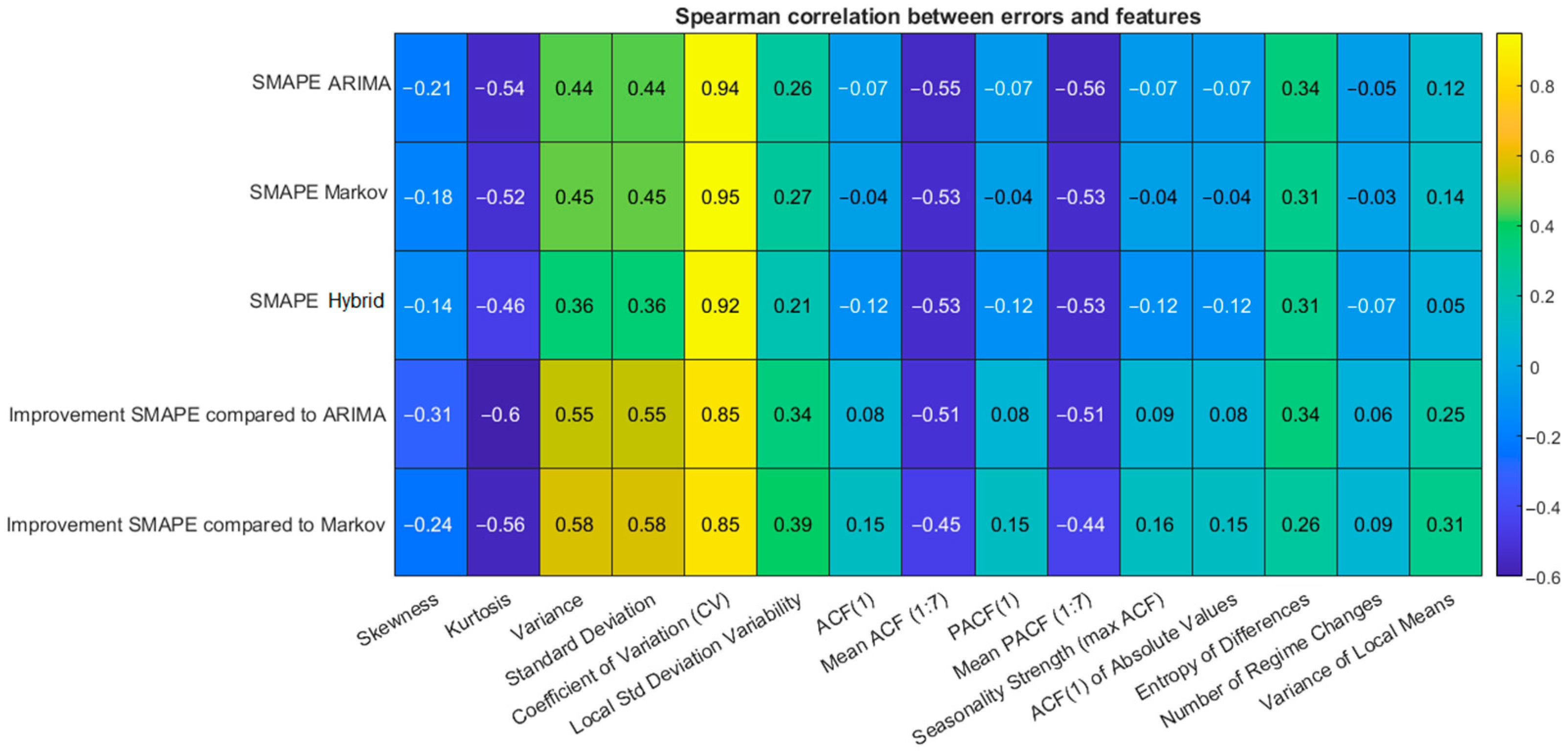
In Figure 4, the Spearman correlation matrix is presented between analyzed time series statistical features and the forecasting errors (SMAPE) obtained from the ARIMA, the Markov chain, and the hybrid model. Additionally, the matrix includes the correlation between the features and the relative improvement in the hybrid model’s performance compared to each of the base models. The analysis revealed that the strongest positive correlations with forecasting errors (across all three models) are observed for features describing both global and local variability: variance, standard deviation, coefficient of variation (CV), and variability of local standard deviation (heteroskedasticity). This indicates that greater instability in the time series translates into increased forecasting difficulty, regardless of the method used. On the other hand, features characterizing the distribution structure of the data, such as kurtosis and skewness, show negative correlations with forecasting errors, particularly in the case of the ARIMA model. This suggests that such models perform better with series that have more symmetric and less heavy-tailed distributions. Particular attention should be paid to features related to the temporal dependence structure, such as the mean ACF (1:7) and mean PACF (1:7), which measure the average strength of lagged dependencies in the time series. These features exhibit consistent negative correlations with the forecasting errors of all models (ranging from approximately −0.51 to −0.56), indicating that the presence of strong temporal dependencies improves forecasting accuracy. In other words, the models perform better on time series that exhibit regularity and cyclic behavior in demand patterns. The entropy of differences, interpreted as a measure of complexity and unpredictability, shows a moderate positive correlation with forecasting errors (up to 0.34 for the ARIMA model). High entropy may indicate the presence of chaotic or irregular changes in the series, which lead to increased forecast error. Conversely, a series with low entropy in its differences is easier to predict due to reduced random fluctuations. The analysis of correlations between the features and the performance improvement of the hybrid model (compared to ARIMA and Markov) suggests that the greatest benefits of hybridization occur for time series characterized by high variability, but also in cases where entropy is moderate and the structure of temporal dependencies is well defined. These correlations reach values around 0.55–0.58, indicating statistically meaningful relationships.

In order to determine which of the designated correlation coefficient values are statistically significant, a Student’s t-test was performed.

Table 2. p-values from significance testing of Spearman correlations between input features and forecasting accuracy (α = 0.05).

	Skewness	Kurtosis	Variance	Standard Deviation	Coefficient of Variation (CV)	Local std. Deviation Variability	ACF (1)	Mean ACF (1:7)	PACF (1)	Mean PACF (1:7)	Seasonality Strength (max ACF)	ACF(1) of Absolute Values	Entropy of Differences	Number of Regime Changes	Variance of Local Means
SMAPE ARIMA model	0.011	0	0	0	0	0.002	0.381	0	0.385	0	0.396	0.381	0	0.585	0.142
SMAPE MARKOV model	0.029	0	0	0	0	0.001	0.612	0	0.624	0	0.641	0.612	0	0.733	0.097
SMAPE HYBRID model	0.100	0	0	0	0	0.012	0.150	0	0.153	0	0.148	0.150	0	0.386	0.510
Improvement SMAPE compared to ARIMA model	0	0	0	0	0	0	0.335	0	0.329	0	0.288	0.335	0	0.508	0.002
Improvement SMAPE compared to Markov	0.003	0	0	0	0	0	0.065	0	0.062	0	0.048	0.065	0.001	0.258	0

shows the corresponding p-values. An alpha value of 0.05 was adopted as the significance level.

For most of the analyzed relationships, the p-values are lower than the adopted significance level of α = 0.05, which confirms that the values of the calculated correlation coefficients for the selected features are statistically significant. Statistical significance has been particularly confirmed for features such as: Entropy of differences, Mean PACF(1:7), Mean ACF(1:7), as well as global and local variability measures—including variance, standard deviation, coefficient of variation (CV), and local standard deviation variability. All these features show significant associations (p < 0.001), confirming their relevance in the context of forecasting difficulty. In the case of the hybrid model, statistically significant correlations are observed for the majority of features, which may indicate its ability to adapt to a wide range of structural properties of time series data.

6. Conclusions

This study introduced a dynamic hybrid forecasting framework that linearly combines an ARIMA component with a discrete-time Markov chain, with the combining weight updated adaptively in a rolling window. Using daily diesel demand from 147 stations, the approach was benchmarked against its standalone constituents. Across all series and error metrics, the Hybrid specification delivered consistent and practically meaningful improvements: central errors were reduced and interquartile ranges tightened relative to both ARIMA and Markov baselines. Empirical cumulative distribution analyses showed error ratios below unity for every series, and paired non-parametric tests confirmed statistical significance. These results indicate that hybridization enhances both accuracy and reliability in short-horizon fuel demand forecasting.

From an energy-systems perspective, the gains are operationally relevant. More accurate short-term forecasts can stabilize Vendor-Managed Inventory operations, reduce safety stocks and emergency replenishments, improve vehicle routing and load factors, and thereby curb transport-related CO₂ emissions and costs. Because the framework remains lightweight and interpretable, it lends itself to deployment in industrial settings where transparency and rapid retraining are essential.

The analysis also clarified when hybridization helps. Conditioning on time-series characteristics showed that stronger short-range dependence (e.g., higher lag-1 autocorrelation) and the coexistence of seasonality with moderate-to-high volatility are favorable regimes. In these settings, the adaptive weighting exploits linear predictability through ARIMA while the Markov component absorbs residual regime shifts. Correlation analyses were consistent with this mechanism: measures of temporal dependence were negatively associated with forecast errors across all models, whereas variability and entropy increased difficulty; the Hybrid’s advantage over each baseline generally grew with variability provided that dependency structure was not overwhelmed by noise.

An additional advantage is computational: by exploiting the observed associations between features and accuracy gains, many routine fits can be avoided or warm-started (e.g., constrained ARIMA orders, adaptive state binning, or reduced retraining frequency). This not only shortens wall-clock time but also lowers the energy demand of continuous forecasting operations—an aspect aligned with sustainable computing in energy logistics.

Methodologically, the framework balances interpretability and adaptivity without resorting to data-hungry “black boxes”. The study reports sufficient implementation detail (rolling re-estimation, feature extraction, and model selection procedures) to enable reproduction and transfer to related fuels or energy commodities. This makes the approach a pragmatic candidate for AI in energy systems design and control, particularly where many heterogeneous demand profiles must be forecast concurrently.

There are limitations that open avenues for future work. First, only univariate, one-step-ahead point forecasts were considered; extensions to multi-horizon, probabilistic, and intraday settings would broaden applicability. Second, the state discretization in the Markov layer was data-driven but fixed within windows; learned or adaptive partitions may capture non-linearities more effectively. Third, only endogenous information was used; integrating exogenous drivers (prices, weather, calendar effects) and explicit regime-detection could further stabilize performance during structural breaks. Finally, linking forecast distributions directly with downstream inventory and routing optimization would close the loop from prediction to decision, supporting system-level objectives such as cost and emission minimization.

In summary, the proposed ARIMA–Markov hybrid provides consistent accuracy gains across a heterogeneous set of real-world demand profiles while retaining operational simplicity and transparency. The evidence supports hybridization as a robust default for short-term forecasting in fuel logistics and, more broadly, in energy-use contexts characterized by meaningful temporal structure and non-trivial variability.