LCL Grid-Connected Inverter Resonance Feedforward-Active Damping Hybrid Control Strategy for Mitigating Weak Grid Resonance and Harmonic Currents

Abstract

In weak grid inverter grid-connected systems, the presence of grid impedance and voltage harmonic disturbances can cause distortion in the grid-connected current. While traditional voltage full-feedforward methods reduce steady-state error, they compromise current quality and may even threaten system instability. To address these issues, an improved grid voltage feedforward approach is proposed. This involves incorporating resonant feedforward into the feedforward channel to counteract grid impedance effects while preserving the system’s open-loop gain, increasing system margin, and enhancing stability. Additionally, the Proportional–Integral (PI) controller is modified to an active damping method using quasi-proportional resonant and harmonic compensation controllers. This enhances harmonic suppression while reducing sensor usage. Finally, the effectiveness of the proposed control strategy was validated through simulation experiments and a hardware-in-the-loop simulation platform based on RT-LAB.

1. Introduction

New energy industries such as photovoltaic power generation play a crucial role in addressing energy shortages and environmental pollution, holding significant importance for national power and energy development [1]. Grid-connected inverters serve as the critical interface between distributed power sources and the grid, with their performance directly impacting power quality and system stability. LCL filters are widely adopted as output filters for grid-connected inverters due to their exceptional high-frequency harmonic attenuation capability within a compact inductive volume, serving as a vital tool for power quality control [2].

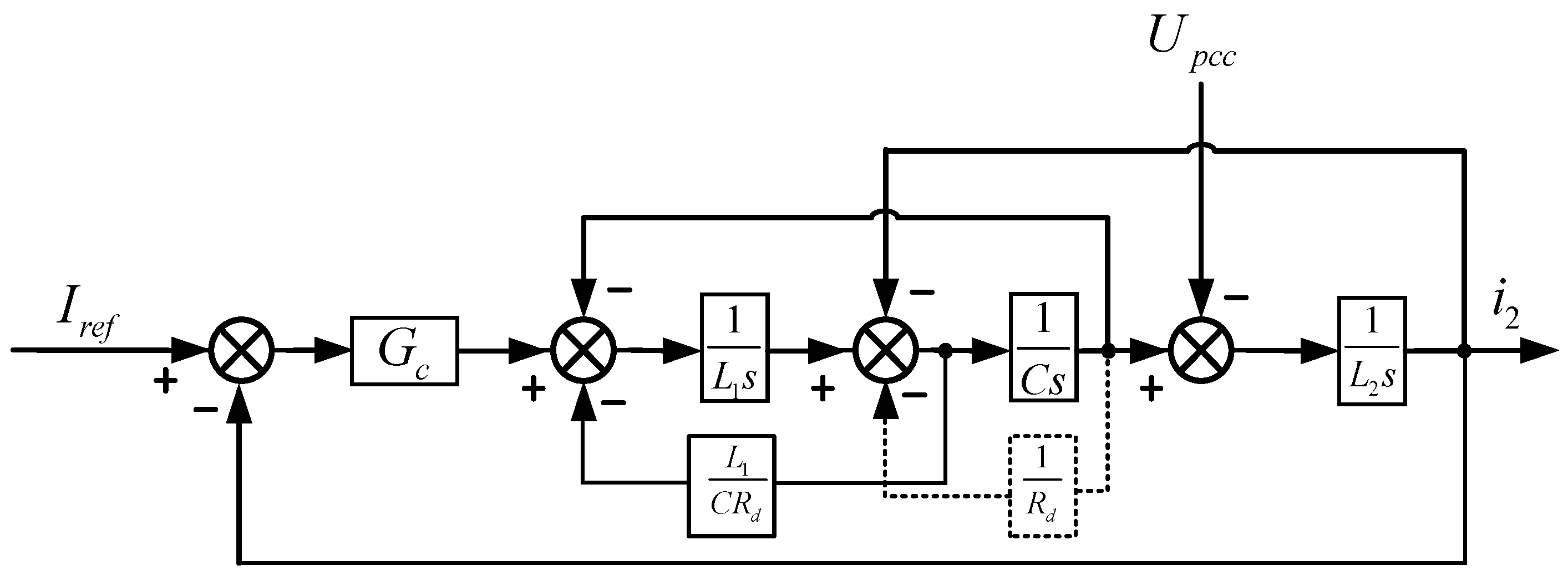
However, as a third-order passive system, the LCL filter exhibits an inherent resonance peak at its resonant frequency. This inherently high-amplitude resonance spike may cause system instability [3]. To address resonance issues, passive damping (PD) methods were initially widely adopted [4], involving the series or parallel connection of physical resistors in the filter capacitor or inductor branches [5]. Although this approach is simple to design and highly reliable, the introduction of resistors causes additional power losses, reducing overall system efficiency—particularly during rated power operation—which contradicts the fundamental requirement for efficient operation in renewable energy systems [6]. Furthermore, damping resistors also affect the filter’s high-frequency attenuation characteristics and suffer from issues such as heat generation and aging [7].

In recent years, active damping (AD) technology has emerged as a solution to the inherent limitations of passive damping and has become a research hotspot [8]. Capacitive current feedback active damping, in particular, has gained widespread application due to its advantages in terms of simple engineering implementation, minimal energy dissipation, and preservation of low-frequency gain without affecting filtering [9]. Active damping strategies based on state observers [10] or advanced multivariable control methods [11] have also been applied to resonance suppression, further enhancing system robustness and dynamic response performance. Furthermore, techniques such as quasi-proportional resonance controllers [12] and repetitive control [13] can effectively suppress specific subharmonics and enhance the quality of grid-injected current.

In practical engineering applications, however, particularly in ‘weak grid’ scenarios involving long-distance transmission, the background impedance of the power grid cannot be ignored. Grid impedance interacts with LCL filters, altering the system’s original resonant characteristics. This can degrade the performance of controllers designed based on rated parameters and may even trigger stability issues [14]. Furthermore, background voltage harmonics (such as the 5th and 7th harmonics) present in the grid can enter the system through common coupling points. This causes distortion in the grid-connected current, making it difficult to meet grid connection standards [15]. To suppress grid voltage disturbances, traditional approaches typically use full feed-forward techniques for grid voltage. While this method effectively reduces steady-state error, the positive feedback effect it introduces significantly diminishes phase margin under weak grid conditions. When grid reactance is high, this can easily trigger system instability [16]. To enhance the robustness of the feedforward loop, Reference [17] proposes a virtual impedance-based feedforward control strategy that improves system stability to some extent, although the design process is relatively complex. Reference [18] employs a second-order differential phase-differential term of the grid-connected current as feedforward to suppress the filter’s intrinsic resonant frequency. While this approach provides superior system stability and resistance to interference, it is significantly impacted by noise.

Traditional proportional–integral controllers are widely used in current-loop controller design for three-phase systems due to their ability to achieve dead-heavy tracking of DC signals in synchronous rotating coordinates [7]. However, their performance is limited in single-phase systems or for specific harmonic suppression. Proportional-resonant controllers can provide infinite gain at specific frequencies (e.g., the fundamental frequency) in stationary coordinates, enabling dead-heavy tracking of AC signals at that frequency [19]. Nevertheless, ideal PR controllers are sensitive to grid frequency deviations and struggle to suppress specific harmonics [20]. To address this issue, quasi-proportional resonance controllers and multi-resonance controllers have been proposed. By incorporating resonance terms at multiple frequency points (e.g., the fundamental frequency and the 5th and 7th harmonics), these controllers can effectively suppress multiple specific harmonics, significantly improving grid-connected current quality [21]. However, the performance of quasi-proportional resonators and multi-resonance controllers still depends heavily on accurate tracking of the power grid frequency. Furthermore, when the power grid frequency fluctuates or background harmonic interference occurs, setting the parameters for multiple resonance peaks becomes more complicated [22].

Based on the above analysis, significant progress has been made in existing research on resonance damping, grid disturbance feedforward compensation and harmonic suppression for LCL grid-connected inverters. However, challenges remain. Firstly, most strategies address individual issues (e.g., damping resonance or suppressing harmonics) in isolation, rather than using a composite control scheme that can address resonance stability, grid impedance disturbances and multi-frequency harmonic problems simultaneously. Secondly, while some complex control strategies (e.g., fully adaptive control) are highly robust, they rely on precise sensors and complex online algorithms, which limits their engineering applicability. For example, Reference [23] uses an adaptive improved feedforward strategy that adjusts the feedforward policy dynamically based on grid impedance variations. While this improves the robustness of the grid-connected system, it necessitates extensive state estimation and a large number of high-precision sensors, resulting in significant costs. Finally, balancing simplicity, cost-effectiveness and high system performance remains a critical optimisation challenge.

To address grid distortion and system instability caused by grid impedance and voltage harmonics in weak grids, this paper proposes a composite control strategy. Its core innovations are: First, an improved resonant feedforward control is introduced. By incorporating a resonant element into the feedforward channel, it actively counteracts the negative effects of grid impedance. This approach maintains the system’s high-frequency open-loop gain and reduces steady-state error while significantly enhancing stability margins. Second, replacing the traditional PI controller with a quasi-proportional resonant and harmonic compensator. This design achieves both efficient active damping and excellent specific harmonic suppression capability without requiring additional sensors, effectively improving grid-connected current quality and reducing system costs. Through Matlab/Simulink simulations, the proposed strategy demonstrates excellent stability and superior dynamic performance.

2. LCL Grid-Connected Inverter Mathematical Model

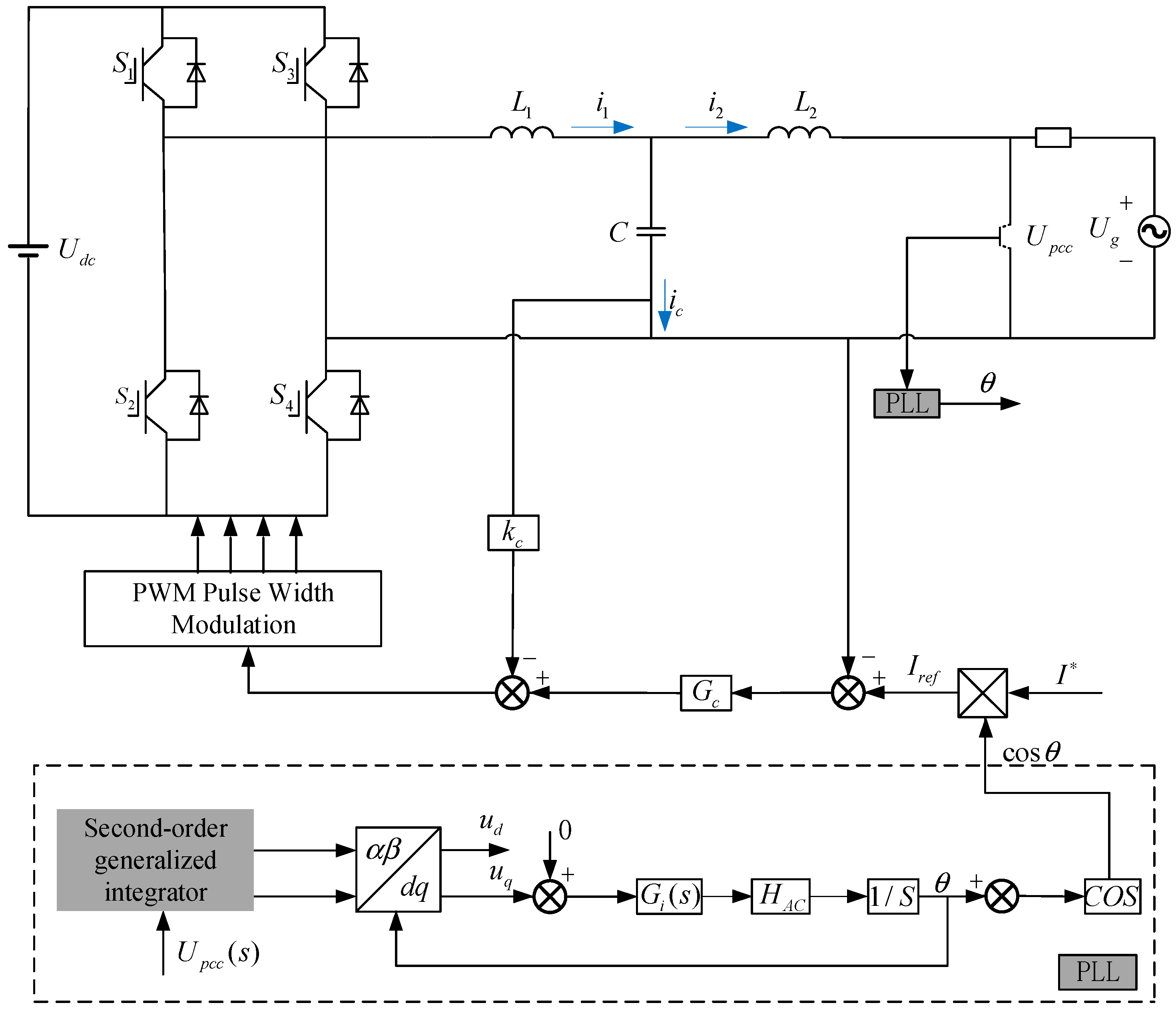
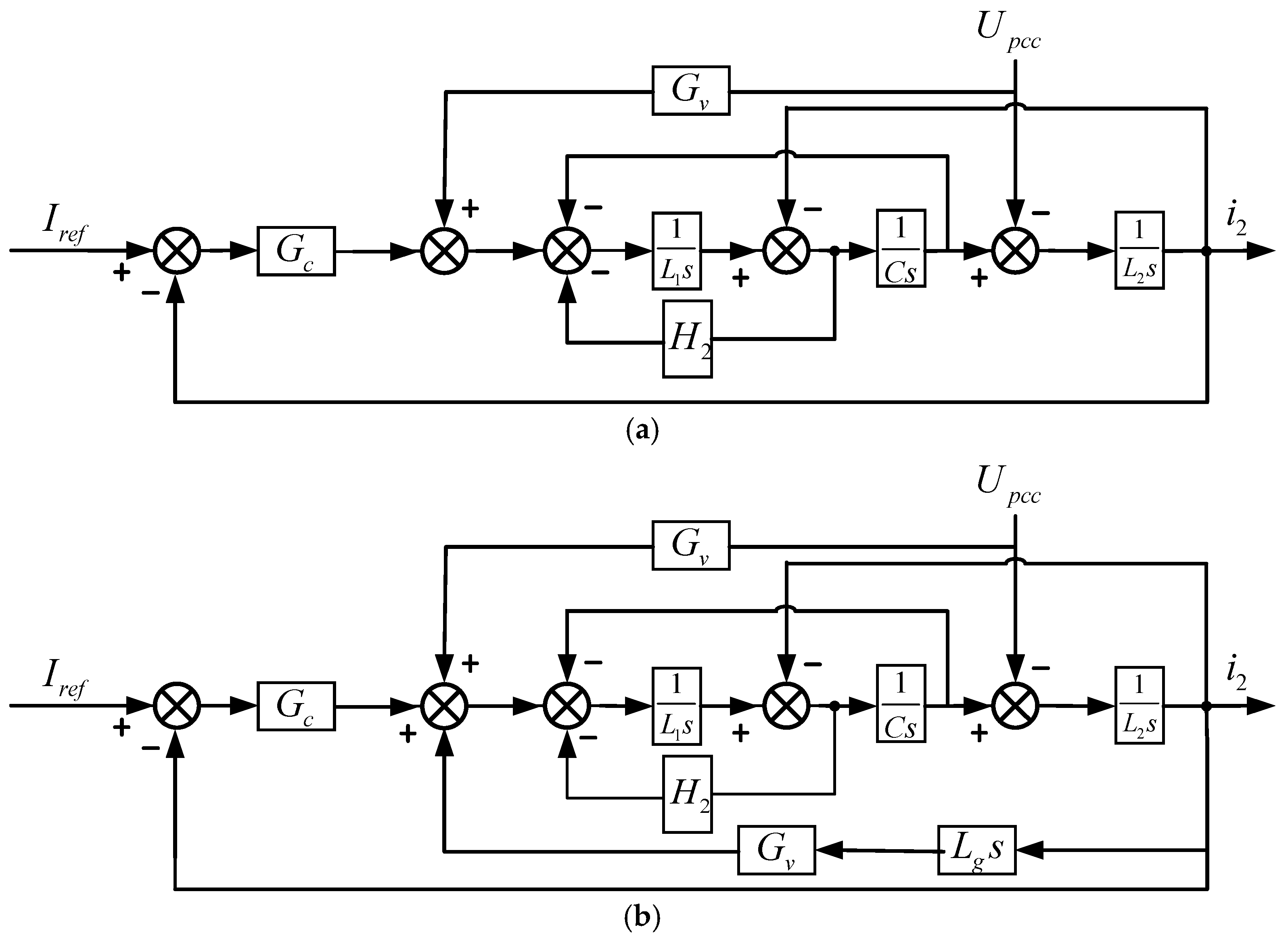
Figure 1 shows the main circuit and control schematic of a single-phase voltage-type grid-connected inverter. The main circuit comprises an inverter full-bridge circuit formed by four switching devices. $U_{dc}$ represents the DC-side input voltage. The inverter-side inductor $L_1$, filter capacitor C, and grid-side inductor $L_2$ collectively form an LCL filter. $U_g$ denotes the grid voltage, and $X_L$ represents the grid impedance. The control section primarily consists of a phase-locked loop (PLL) module for sampling and current-loop control. Within the PLL module, the second-order generalized integrator outputs quantities in the $\alpha \beta$ coordinate system with a 90-degree phase difference. These are transformed into quantities in the $dq$ rotating coordinate system via coordinate transformation. Following processing by the PI controller and integrator, phase information is output—namely, the fundamental phase $\theta$ of the grid voltage. Simultaneously, the grid current reference value $I^{\ast }$ is combined with this phase $\theta$ to synthesize the reference current Iref. Additionally, $i_1$, $i_c$, and $i_2$ represent the inverter-side inductive current, capacitive current, and grid-side inductive current, respectively. $G_c$ denotes the current outer-loop controller, and $U_{pcc}$ indicates the common coupling point voltage. Kc is the capacitor current feedback gain for active damping implementation. Given the numerous advantages of single-polarity double-frequency modulation—including low switching losses and reduced harmonic content—the inverter employs this modulation scheme.

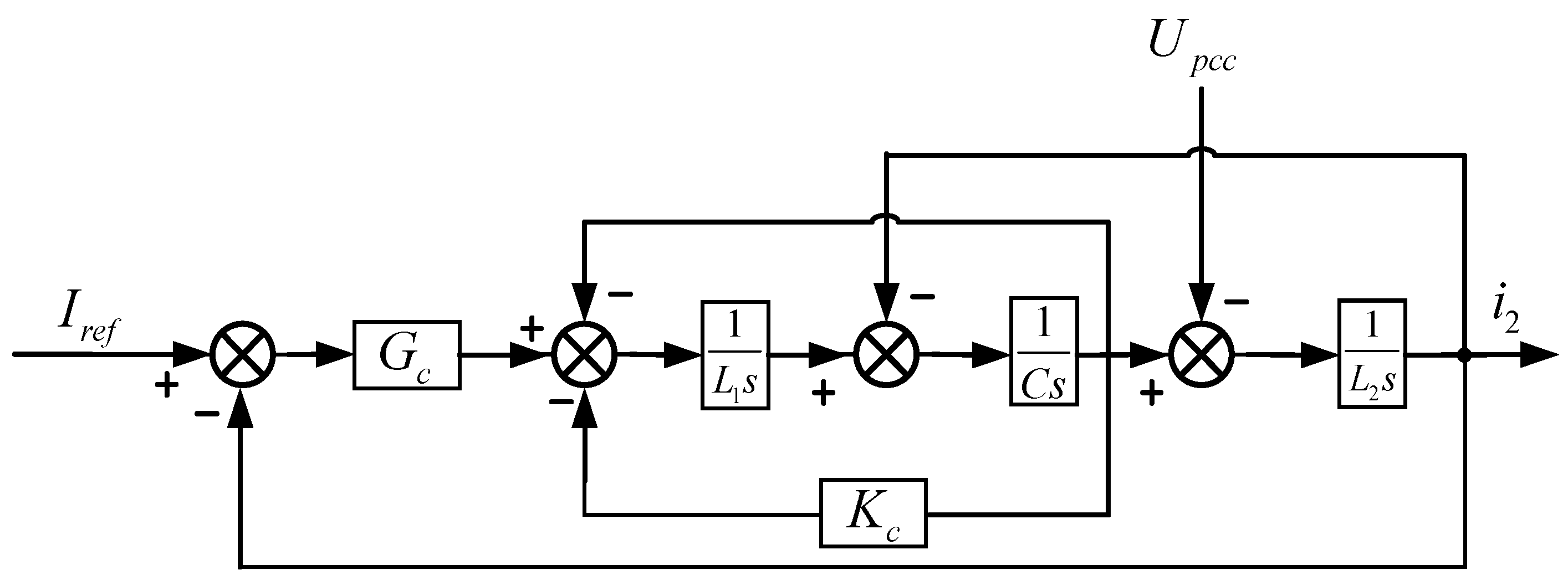
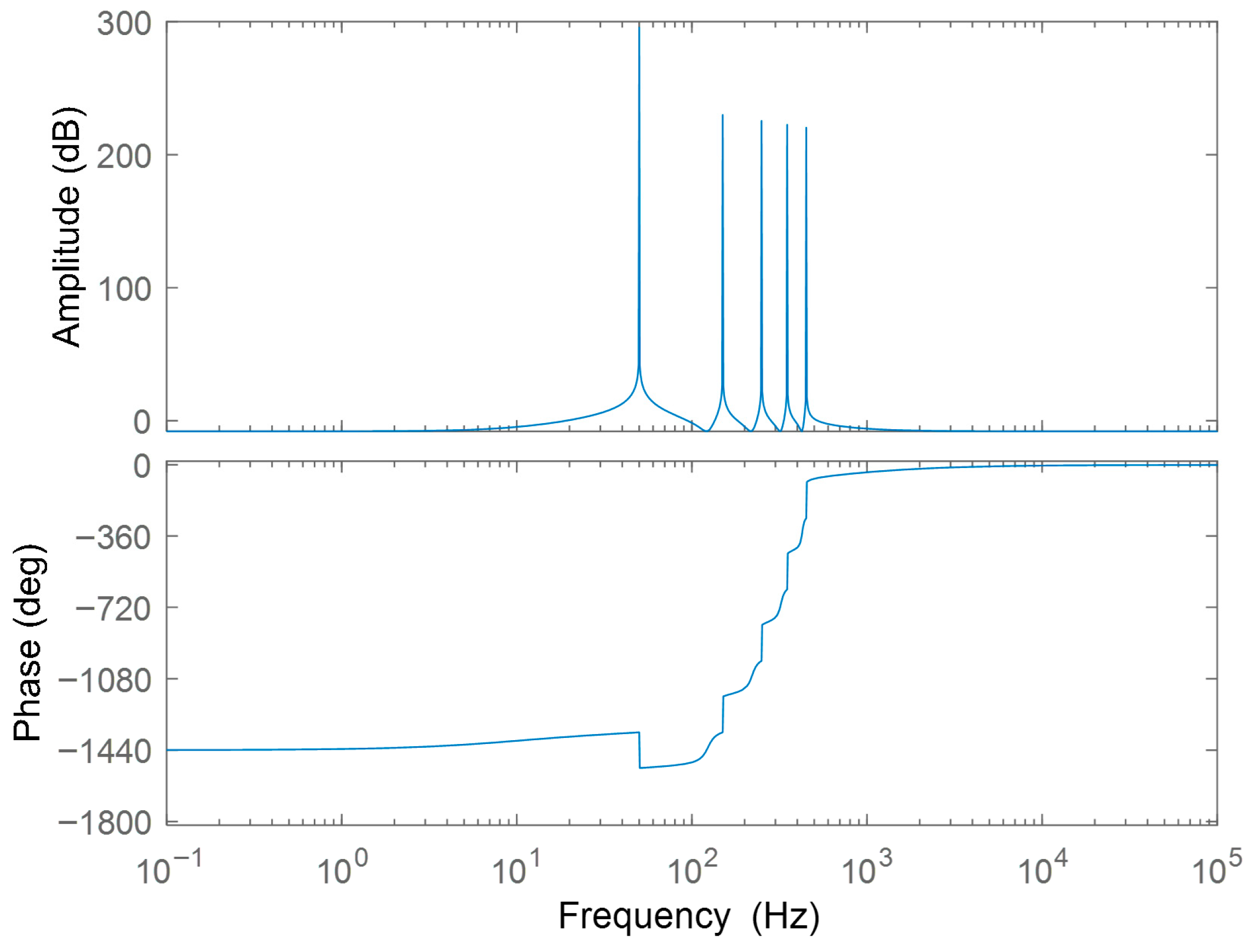
Figure 2 illustrates the basic control block diagram without considering active damping and grid impedance, which involves delay equivalence issues. Reference [21] proposes employing a compensator based on the equal-area method to eliminate the impact caused by system delay. Once the system is fully compensated, the delay can be equivalently represented as a proportional element with a gain of 1. Since the switching frequency of this model significantly exceeds the open-loop cutoff frequency, the equivalent transfer function $K_{pwm}$ from the modulation wave to the inverter side of the full-bridge inverter circuit can be approximated as:

$$K_{pwm}={\displaystyle \frac{U_{dc}}{U_{tri}}}$$

(1)

In the formula: $U_{dc}$ represents the amplitude of the DC-side voltage; $U_{tri}$ denotes the amplitude of the single-pole double-frequency triangular carrier wave. In this paper, the $K_{pwm}$ of the inverter and the current controller have undergone normalization processing, denoted as $G_c$.

From the control block diagram in Figure 2, the transfer function $G_{r-2}$ between the input current $i_2$ and the current reference value $I_{ref}$ can be derived as follows:

$$G_{r-2}(s)={\displaystyle \frac{i_2(s)}{I_{ref}(s)}}={\displaystyle \frac{G_c}{L_1{L}_{2}C{s}^3+K_c{L}_{2}C{s}^s+(L_1+L_2)s}}$$

(2)

where $f_r$ is the resonant frequency of the LCL filter, which is typically set to 10 times the fundamental frequency of the power grid and less than 0.5 times the sampling frequency, and ${\omega }_r$ is the corresponding resonant angular frequency satisfying ${\omega }_r=2\pi f_r$. The expression for $f_r$ is:

$$f_r={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{L_1+L_2}{L_1{L}_{2}C}}}$$

(3)

According to Figure 2, under grid voltage disturbance conditions, the transfer function $G_{r-v}\left(s\right)$ of the output current $i_2$ with respect to the common coupling point voltage $U_{pcc}$ is:

$$G_{r-v}(s)={\displaystyle \frac{i_2(s)}{-U_{pcc}(s)}}={\displaystyle \frac{G_1}{1+G_{r-2}}}$$

(4)

Among them:

$$G_1(s)={\displaystyle \frac{s^2{L}_{1}C+1}{s^3{L}_1{L}_{2}C+s(L_1+L_2)}}$$

(5)

From the system equivalent control block diagram and Equations (2) and (3), the expression for the grid-connected current $i_2$ is given by:

$$i_2(s)=G_{r-2}(s)I_{ref}(s)-G_{r-v}(s)U_{pcc}(s)$$

(6)

Equation (2) lacks a quadratic damping term, rendering it incapable of suppressing the resonant effects introduced by the filter. In Equation (6), the grid-connected current is influenced by the coupling point voltage, which in turn is affected by grid impedance and harmonics. Therefore, it is necessary to investigate methods for suppressing grid background harmonics.

3. Suppression of Harmonic Distortions in Power Grids

3.1. Active Damping Analysis

In LCL inverters, the inherent resonance generated by the filter significantly impacts the system. Current solutions generally fall into two categories: passive damping and active damping. Passive damping achieves damping by connecting capacitors in series or parallel with the filter’s inductors or capacitors. However, this method often involves substantial losses and low system efficiency, so passive damping is rarely used alone. Active damping simulates the effects of six passive damping configurations (as shown in Figure 3) by introducing virtual resistances into the control system. Among these six damping approaches, capacitor-paralleled resistors yield the most effective results. Therefore, this paper proposes an active damping control scheme using capacitor-paralleled virtual impedance to suppress resonance spikes. This approach simultaneously preserves the filter’s gain across both low and high frequency bands, ensuring rapid response and high stability.

Virtual Resistor Active Damping is an advanced control technique that simulates the behavior of physical resistors through control algorithms. Its core principle involves selecting a state variable within the system that is closely related to resonant dynamics (such as the capacitive current or capacitive voltage of an LCL filter). This variable is processed through a carefully designed active damping function (typically a proportional or proportional-derivative element), and the processed signal is fed back as a correction term to the modulating wave or the output of the preceding controller. This process effectively injects a damping term into the control system that opposes the direction of energy flow at the resonant frequency. Consequently, it achieves effective suppression of the inherent resonant peaks in the LCL filter without requiring actual physical resistors.

This method is widely adopted primarily due to its multiple significant advantages. First, it achieves damping effects through pure software algorithms without adding any hardware, fundamentally eliminating the additional power loss and heat generation issues associated with passive damping resistors, thereby significantly improving system efficiency. Second, the method features a clear principle and straightforward implementation. Typically, it only requires adding a feedback loop for a state variable to the existing control structure, making it easy to program within digital controllers and highly practical. Finally, unlike the fixed characteristics of passive damping, the “resistance value” (i.e., damping gain) of the virtual resistor can be adjusted or optimized online based on system operating conditions, endowing the control system with stronger adaptive capabilities. For these reasons, the active damping method using virtual resistors has become a mainstream and highly efficient solution in both academia and industry for suppressing LCL resonance and enhancing the stability of grid-connected inverters.

As shown in Figure 4, the damping effect is achieved through the control section after equivalent transformation via the control block diagram using a capacitor–parallel–resistor configuration. First, active damping control is applied to the information about to be sampled by advancing the introduction point to the control section. However, since the damping coefficient kd contains a second-order differential term at this point and differentiation amplifies noise, and discrete differentiation weakens active damping due to error terms. Therefore, the tap point is advanced to counteract noise interference from the second-order derivative term. After equivalent transformation, capacitive current feedback control is employed to enhance system damping.

Applying an equivalent transformation to the control block diagram converts the physical model of capacitive parallel virtual resistors into an active damping method incorporating capacitive current feedback into the control system. As illustrated in Figure 4, module $L_1/C{R}_d$ in the feedback channel is derived from this transformation; here, R_d represents the virtual resistor’s resistance value. This transformation eliminates the need for direct differentiator usage, which is associated with high-frequency noise, and converts the implementation of active damping into a proportional link. The module introduces a zero into the open-loop transfer function of the system, which effectively counteracts the resonant pole generated by the LCL filter. This provides sufficient damping to suppress resonance spikes and enhance system stability. The gain value can be adjusted according to the desired damping ratio and filter parameters.

3.2. Analysis of Grid Background Harmonic Suppression

Harmonic compensation (HC) possesses the characteristic of responding only to specific harmonic orders without affecting the dynamics of the Proportional Resonant (PR) controller. Furthermore, PR technology can be successfully applied to current control in grid converter applications, where the requirement is to synchronize the current with a constant grid frequency and compensate for low-order harmonics. Therefore, the PR + HC controller is suitable for AD control of LCL-type grid-connected inverters. The following are the PR + HC controller formulas:

$$G_{pr}(s)=K_p+{\displaystyle \frac{2K_{i}s}{s^2+{\omega }_0^2}}$$

(7)

$$G_{hc}(s)={\displaystyle \sum _{a=3,5,7,9}{K}_{ah}\frac{s}{s^2+{({\omega }_a\cdot h)}^2}}$$

(8)

$$\begin{array}{ll}{H}_{AC}=& K_p+{\displaystyle \frac{2K_{i}s}{s^2+{\omega }_0^2}}+{\displaystyle \frac{K_{ih}\cdot s}{s^2+{(2\pi \cdot 150)}^2}}+{\displaystyle \frac{K_{ih}\cdot s}{s^2+{(2\pi \cdot 250)}^2}}\\ & +{\displaystyle \frac{K_{ih}\cdot s}{s^2+{(2\pi \cdot 350)}^2}}+{\displaystyle \frac{K_{ih}\cdot s}{s^2+{(2\pi \cdot 450)}^2}}\end{array}$$

(9)

Equation (8) represents the transfer function of the PR controller, where $K_p$ denotes the proportional gain; $K_i$ represents the integral gain of the fundamental resonance term; ${\omega }_0=2\pi f_0$, where ${\omega }_0$ is the fundamental angular frequency, and $f_0$ is the fundamental frequency, i.e., 50 Hz. Equation (9) represents the transfer function of the HC controller, composed of multiple resonance terms. $K_{ih}$ denotes the integral gain of the harmonic compensation resonance term, a represents the harmonic compensation order, and h denotes the harmonic order, where $a=h$. When $K_p = 0.4$, $K_i = 300$, and $K_{ih}= 300$, the Bode diagram of the harmonic compensation function $H_{AC}$ in Equation (10) is shown in Figure 5.

4. Improved Control Strategy Combining Resonant Feedforward with Quasi-Proportional Resonance and Harmonic Compensation Controller

4.1. Traditional Voltage Feedforward

Under actual weak grid conditions, grid impedance cannot be neglected due to factors such as long transmission lines, as it affects the quality of grid-connected current. Considering that grid impedance exhibits resistive-inductive characteristics, and resistive properties are beneficial to system stability, we only consider the purely inductive grid impedance Lg. As shown in Equation (6), the coupling point voltage significantly affects the system’s grid-connected current. To eliminate the impact of coupling point voltage carrying grid disturbances on the inverter’s grid-connected current, a traditional approach involves adding a full feedforward loop for grid voltage to compensate for grid voltage disturbances, as illustrated in Figure 6. This shifts the grid impedance voltage from the control block diagram to the regulator. Under equivalent feedforward control, the system’s open-loop transfer function is derived as:

$$G_q={\displaystyle \frac{G_c}{s^3{L}_1(L_2+L_g)C+s^2{k}_{d}C(L_2+L_g)+s(L_1+L_2)}}$$

(10)

Plot the corresponding system Bode diagrams for zero-voltage feedforward and full-voltage feedforward. Figure 7a shows the amplitude-frequency characteristic curve of the grid-connected inverter coupling point without feedforward, while Figure 7b shows the amplitude-frequency characteristic curve of the grid-connected inverter coupling point with full feedforward.

Figure 7a shows the amplitude-frequency characteristic curves of the grid-connected inverter coupling point without feedforward. As the grid impedance increases from $L_g=1 \mathrm{m}\mathrm{H}$ to $L_g=5 \mathrm{m}\mathrm{H}$, to the final value of $L_g=10 \mathrm{m}\mathrm{H}$, the corresponding phase margin remains substantial and the system remains stable. However, the gain at the system fundamental frequency decreases from an initial 42 dB to a final 20 dB, significantly affecting the system gain. Figure 7b shows the amplitude-frequency characteristic curve of the grid-connected inverter coupling point with full feedforward. It is evident that without grid impedance, the system stability margin is 45 degrees, ensuring system stability. However, when the grid impedance $L_g=1 \mathrm{m}\mathrm{H}$, the phase margin drops to 5.6 degrees. When grid impedance is $L_g=5 \mathrm{m}\mathrm{H}$ and $L_g=10 \mathrm{m}\mathrm{H}$, there is no phase margin and the system becomes unstable. This demonstrates that traditional full feedforward causes the resonant angular frequency of the LCL filter to decrease rapidly under high grid inductive reactance, shifting the resonant conjugate pole to the left and drastically reducing the system stability margin, severely impacting system stability. However, its gain does not decrease with impedance.

4.2. Improved Resonance Feedforward Strategy

Although traditional full feedforward does not affect system gain when grid impedance increases, it causes the resonant angular frequency of the LCL filter to decrease rapidly when grid inductance is high. The impact of grid inductance significantly reduces the system’s stability margin. Therefore, Building upon the work in [21], this paper proposes incorporating a resonant element into the voltage positive feedback channel. This resonant loop, essentially a second-order generalized integrator for fundamental extraction, preserves the original characteristics at low-order harmonics while introducing attenuation for higher-order harmonics. The expression for the introduced second-order resonant element $G_v$ is:

$$G_v={\displaystyle \frac{k_r{w}_{c}s}{s^2+2k_r{w}_{c}s+w_c^2}}$$

(11)

In the equation: ${\omega }_c$ denotes the extraction angular velocity, and $K_r$ represents the resonance coefficient.

As shown in Figure 8a, the resonant feedforward control block diagram incorporates a resonant element into the existing full feedforward channel at the coupling point. Then, through the equivalent transformation of the control block diagram as shown in Figure 8b, the improved coupling point voltage feedforward is decomposed into grid voltage and grid impedance. These components are separately fed forward through the resonant link to the controller. Finally, the open-loop transfer function $G_{g-open}$ of the improved resonant feedforward can be derived from the control block diagram as follows:

$$G_{g-open}={\displaystyle \frac{G_c}{s^3{L}_1(L_2+L_g)C+s^2{k}_{d}C(L_2+L_g)+s(L_1+L_2+L_g)-s{L}_g{G}_v}}$$

(12)

The resonant feedforward control block diagram to be introduced at this point is as follows:

4.3. Proportional Resonance and Harmonic Compensation Controller Combined with Enhanced Resonance Feedforward

Weak power grids often experience higher levels of voltage harmonics and grid noise, which can compromise inverter stability and interference immunity. PI controllers may fail to effectively suppress these disturbances, leading to increased output current fluctuations or degraded overall system performance. Meanwhile, ideal proportional resonance (PR) controllers are overly sensitive to grid parameters, making PR implementation challenging in practice. Therefore, quasi-proportional resonance (QPR) is commonly employed. Its cutoff frequency ${\omega }_c$ primarily influences the bandwidth at the resonance frequency ${\omega }_0$ Controlling ${\omega }_v$ regulates the resonance point bandwidth, while adjusting $K_p$ and $K_r$ optimizes system dynamic performance. In power systems, when supply voltage fluctuates or loads undergo sudden changes, the rectifier output current often contains harmonic components at 3rd, 5th, 7th, etc. These harmonics degrade current quality. To address this, harmonic compensation controllers are introduced based on QPR. These controllers detect and compensate for specific harmonic orders without affecting the dynamic performance of the PR controller, responding only to targeted harmonic frequencies. This effectively reduces harmonic content in the current and enhances current quality. Furthermore, PR technology can be successfully applied to current control in grid converter applications, where the requirement is to synchronize the current with a constant grid frequency and compensate for low-order harmonics. The transfer function of the PR + HC controller is:

$$\begin{array}{ll}{H}_{AC}=& K_p+{\displaystyle \frac{2K_{i}s}{s^2+{\omega }_0^2}}+{\displaystyle \frac{K_{ih}\cdot s}{s^2+{(2\pi \cdot 150)}^2}}+{\displaystyle \frac{K_{ih}\cdot s}{s^2+{(2\pi \cdot 250)}^2}}\\ & +{\displaystyle \frac{K_{ih}\cdot s}{s^2+{(2\pi \cdot 350)}^2}}+{\displaystyle \frac{K_{ih}\cdot s}{s^2+{(2\pi \cdot 450)}^2}}\end{array}$$

(13)

In the formula: $K_p$ is the proportional coefficient; n is the multiple of the harmonic frequency relative to the fundamental frequency (including 3rd, 5th, and 7th harmonics).

The improved resonant feedforward can suppress resonance issues caused by grid impedance, reduce steady-state errors in grid-connected currents, and mitigate the impact of weak grid inductance on grid-connected current stability. However, it lacks sufficient capability to suppress low-frequency harmonics in the grid, resulting in higher low-order harmonic content in the system. In contrast, the introduced multi-resonant controller demonstrates strong suppression capability for low-order harmonics in grid voltage. This paper simultaneously employs the improved resonant feedforward and multi-resonance controllers to enhance grid-connected current stability and mitigate the impact of low-order harmonics on the system under weak grid conditions. Applying the multi-resonant controller HC [12] yields the system’s open-loop transfer function. Figure 9 shows its corresponding Bode plot. Without active damping, the open-loop Bode plot exhibits an extremely high resonance peak at the resonant frequency, accompanied by a sharp phase jump. The system suffers from insufficient phase margin and poor stability. After incorporating capacitive current feedback, the Bode plot shows critical improvements: the resonance peak is effectively suppressed, and the curve becomes smoother. The phase jump also moderates, phase margin increases significantly, and system stability is restored. Building upon this, the integration of QPR and harmonic compensation controllers primarily impacts the low-frequency range: Substantially boosting low-frequency gain enhances reference tracking accuracy, enabling zero steady-state error control. Simultaneously addressing steady-state errors in grid-injection current improves harmonic suppression capability.

5. Simulation and Results Analysis

To validate the improvement in grid-connected current quality achieved by the control strategy proposed in this paper, a single-phase LCL grid-connected inverter simulation model was constructed in Matlab (R2022a)/Simulink. Its model parameters are shown in

Table 1. Key System Parameters.

Parameters	Value	Parameters	Value
Rated Power	5 kw	Inductance L1 (mH)	0.8
DC voltage	400 V	Capacitance C (μF)	10
Rated AC Current (RMS)	22.73 A	Inductance L2 (mH)	0.12
Switching frequency	10 kHz	Multivibrator Proportional Coefficient	20
Maximum rated current on the AC side	32 A	Current Outer Loop Resonance Coefficient	1000
Traditional PI Current Outer Loop kp	12	Resonant feedforward coefficient	0.5
Traditional PI Current Outer Loop Ki	10,000

:

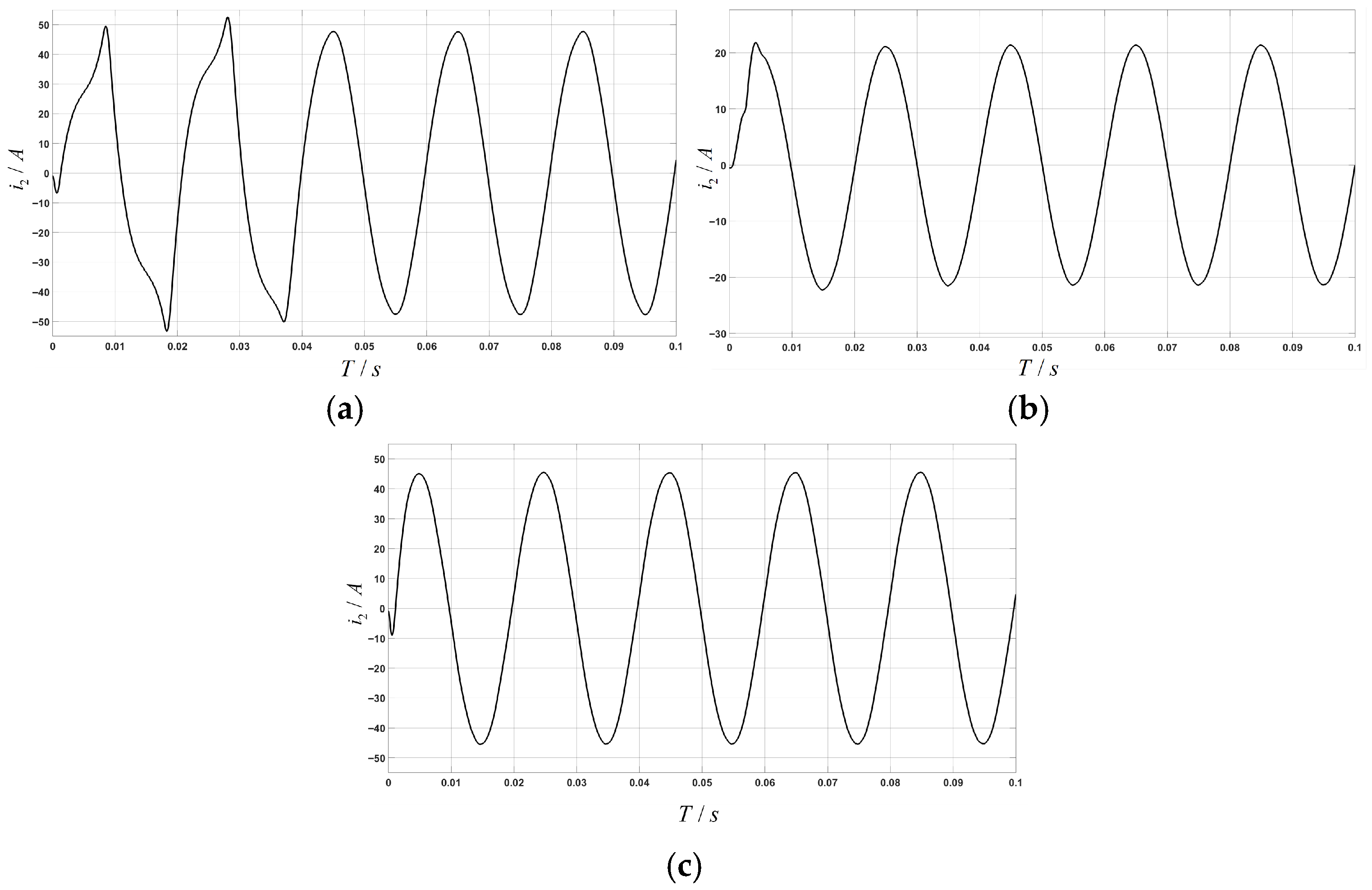
To simulate the higher-order harmonics present in real power grids, 3rd, 5th, and 7th harmonic components were introduced in series into the grid, with their respective amplitudes set at 10%, 6%, and 3% of the fundamental wave amplitude. Current performance under various operating conditions was verified against the background of odd-order harmonics in the grid. As shown in Figure 10 both control strategies produce favorable current waveforms when grid impedance $L_g=0 \mathrm{m}\mathrm{H}$. 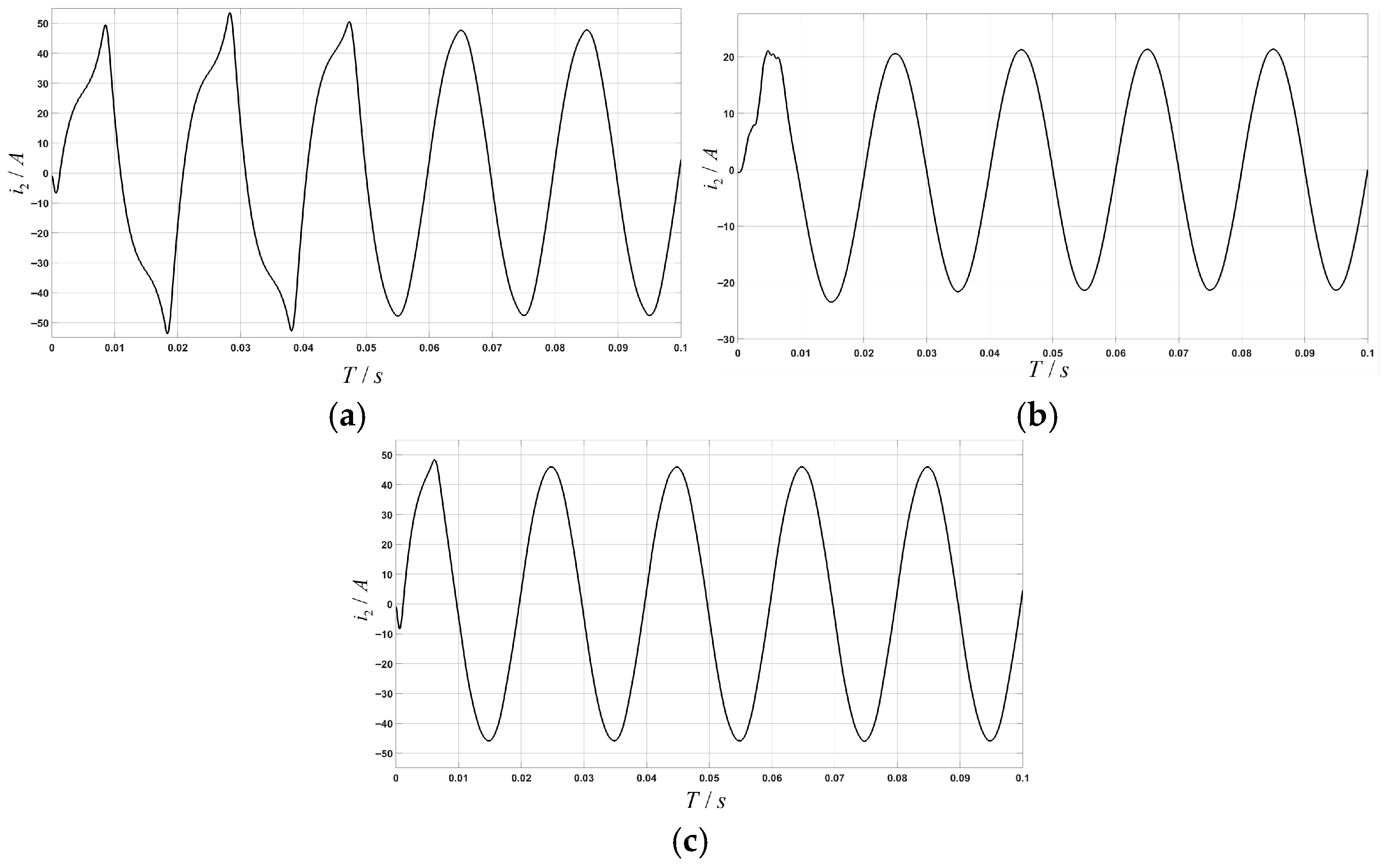Figure 11 compares traditional full feedforward control with improved feedforward control at $L_g=5 \mathrm{m}\mathrm{H}$. Traditional full feedforward exhibits significant harmonics during the first two cycles, improving after 0.04 s but still showing waveform distortion and residual harmonics. 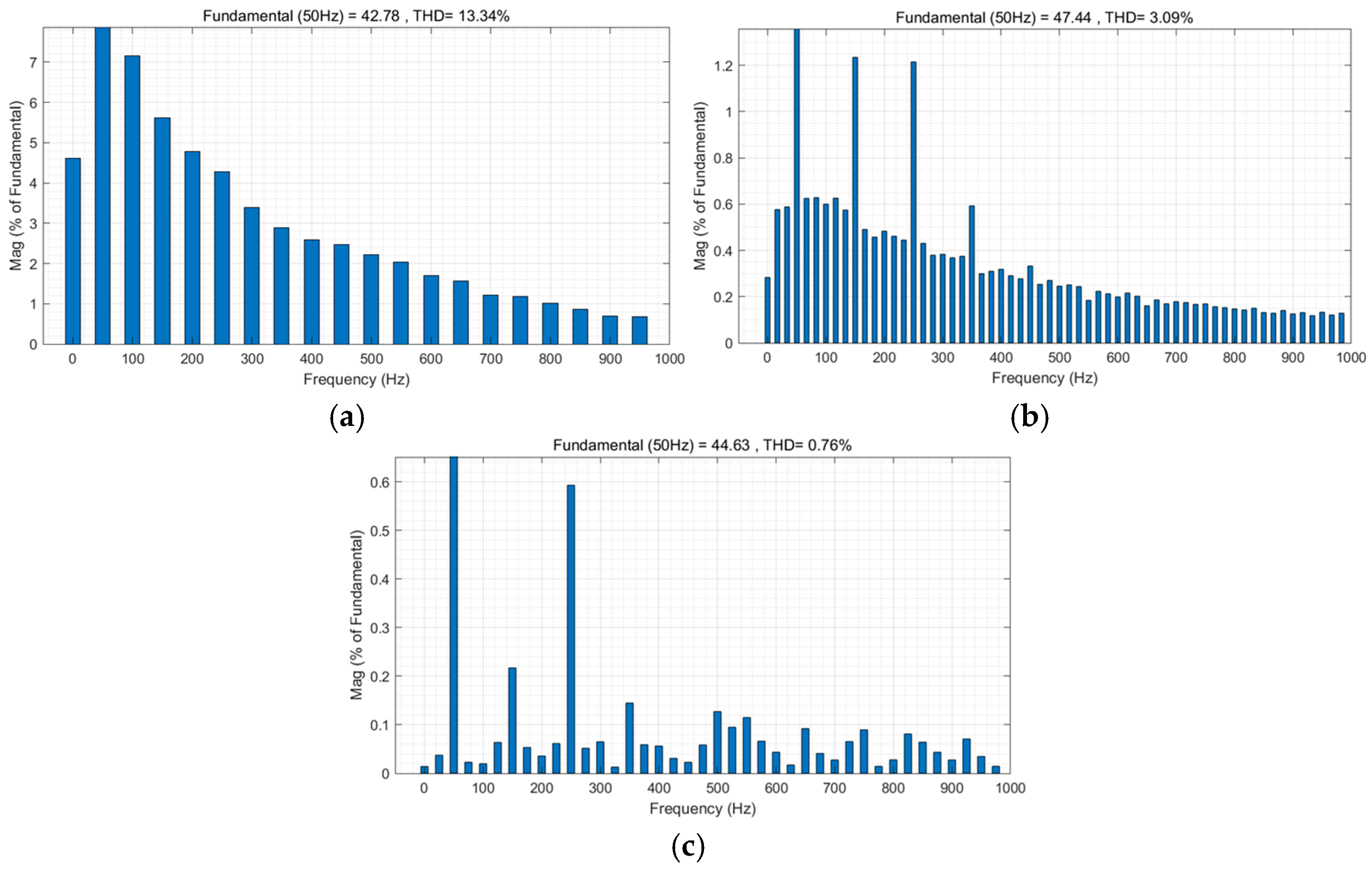Figure 12 presents the comparative waveforms of both control strategies at $L_g=10 \mathrm{m}\mathrm{H}$. It is evident that the traditional feedforward control exhibits severe grid-connected current distortion with significant harmonics, and substantial errors exist between the current amplitude and the reference value.

Table 2. Grid-Connected Current THD under Different Control Strategies at Various Grid Impedances.

Control Strategy	Grid-Connected Current Harmonic Distortion (THD) (%)
	Lg = 0 mH	Lg = 5 mH	Lg = 10 mH
Traditional Full Feedforward Control	2.45	3.75	13.34
Adaptive Resonant Feedforward Control	2.4	2.1	3.64
Improved Composite Control	1.80	1.35	0.76

presents the grid-connected current Total Harmonic Distortion (THD) for different control strategies under varying grid impedances. The adaptive resonant feedforward control data regarding its impact on grid-connected current harmonic content is referenced from [23].

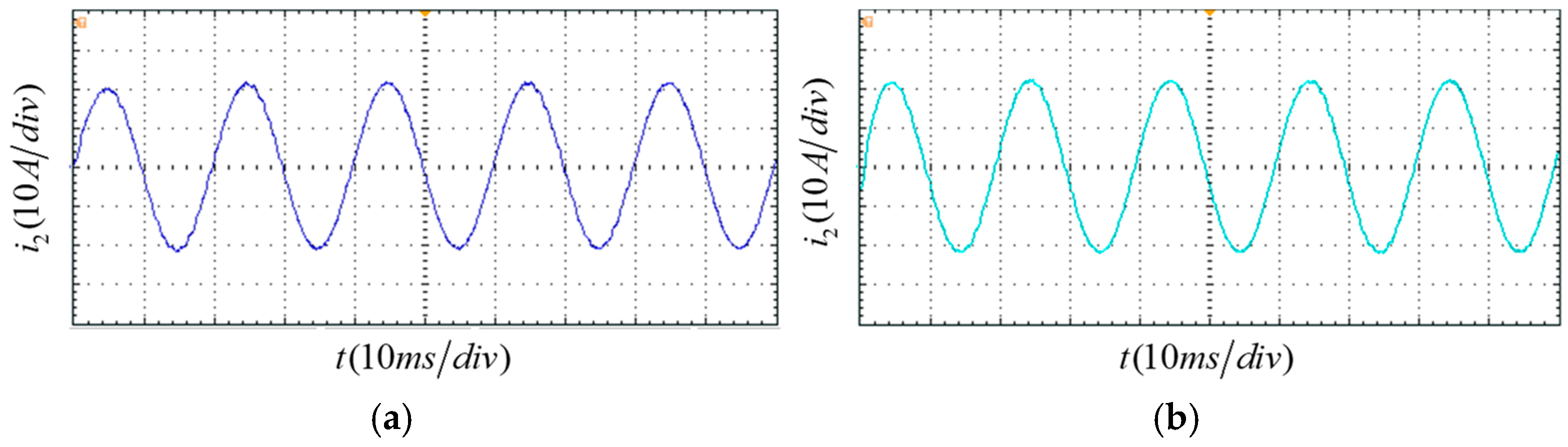
As shown in Figure 10, under ideal grid impedance conditions (Lg = 0 mH), the grid-connected current waveforms of the three control strategies exhibit distinct performance gradients. While the traditional full feedforward control (a) maintains a basic sinusoidal shape, it displays noticeable high-frequency ripples and zero-crossing distortion, revealing an insufficient capability to suppress switching noise. The adaptive active damping control strategy (b) further refines dynamic response, achieving reduced overshoot and oscillations through real-time parameter adjustment. The improved composite control strategy (c) produces a nearly perfect sinusoidal waveform. Its smooth, flat curve validates the optimisation effect of the feed-forward component and highlights the precise suppression capability of the multiresonance controller for specific harmonics. This stepwise improvement in performance conclusively demonstrates that the proposed composite control strategy can achieve a leap from ‘basic stability’ to ‘high-quality output’, even under severe grid conditions, thus laying a solid foundation for outstanding subsequent performance under weak grid conditions.

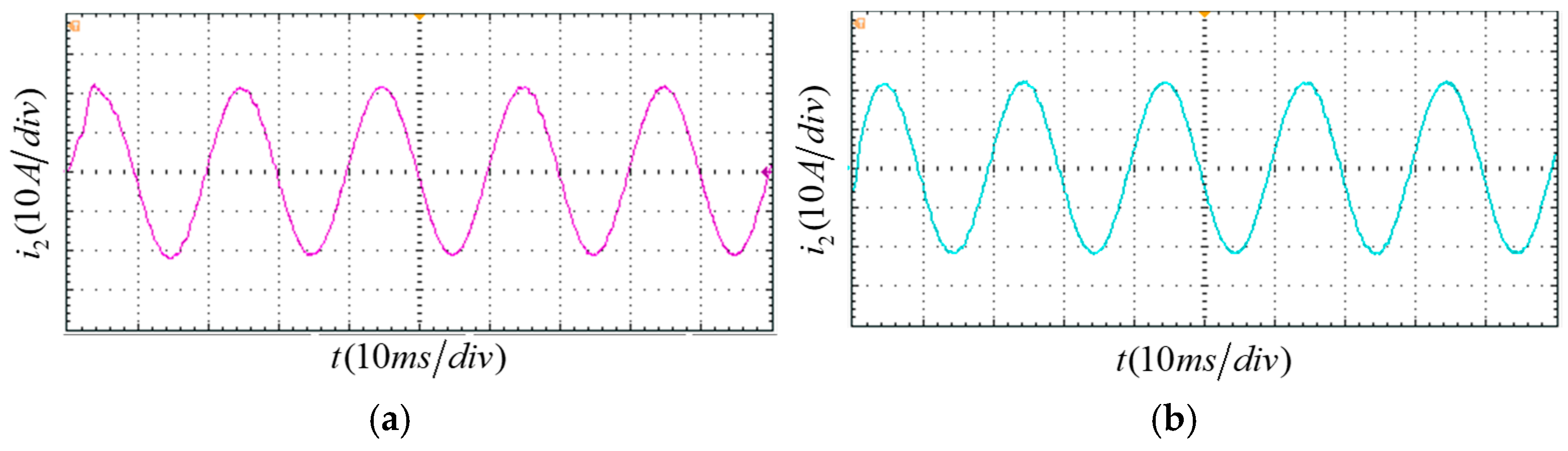
As shown in Figure 11, under the moderately weak grid condition with grid impedance Lg = 5 mH, the differences in performance between the three control strategies become much more pronounced. The waveform of the traditional full feedforward control (a) shows pronounced distortion, with oscillations at the zero-crossing point and flat-top distortion at current peaks. The adaptive active damping control strategy (b) achieves satisfactory steady-state performance under weak grid conditions; however, its limitations become apparent when compared with the improved feedforward strategy (c). The adaptive approach exhibits a relatively slower dynamic response during transient conditions, with a noticeable phase lag in current tracking observed during periods of grid disturbance. In contrast, the enhanced composite control strategy (c) maintains an almost ideal sinusoidal waveform. Its smooth curve profile and precise zero-crossing characteristics demonstrate the effective overcoming of the negative impact of grid impedance by the synergistic effect of the improved resonant feedforward and multi-resonant controllers. This approach ensures system stability while delivering superior power quality.

As shown in Figure 12, under the extreme weak grid condition with grid impedance Lg = 10 mH, the performance differences between the three control strategies become critical. Traditional full feedforward control (a) has become completely unstable, resulting in severe non-linear distortion of the waveform. It has lost its sinusoidal characteristics and shows significant amplitude decay and phase shift, indicating that the control system can no longer properly track the reference command. The adaptive active damping control strategy (b) produces a stable sinusoidal waveform, but noticeable current overshoot occurs during transient periods, especially when responding to sudden changes in load. This phenomenon, accompanied by low-frequency oscillations during recovery, indicates limitations in the system’s dynamic response capability. Furthermore, close inspection reveals minor harmonic distortions near the current peaks, suggesting that specific harmonic components are not being adequately suppressed. In contrast, the enhanced composite control strategy (c) maintains excellent sinusoidal waveform characteristics under such severe conditions, exhibiting only slight smoothing at the peak. This fully demonstrates the strong adaptability of the enhanced resonant feedforward mechanism to grid impedance variations, and the outstanding performance of the multi-resonant controller in maintaining system stability and current quality under extreme conditions.

As illustrated in Figure 12, the enhanced control strategy incorporates a resonant component within the feedforward loop. This element reduces grid impedance at frequencies beyond the fundamental frequency, while maintaining the disturbance cancellation capability of the fundamental feedforward. Consequently, the original and improved grid-connected current waveforms both exhibit favourable characteristics. This paper performs Fourier decomposition on these waveforms and compares their harmonic content with that of traditional and adaptive feedforward control. 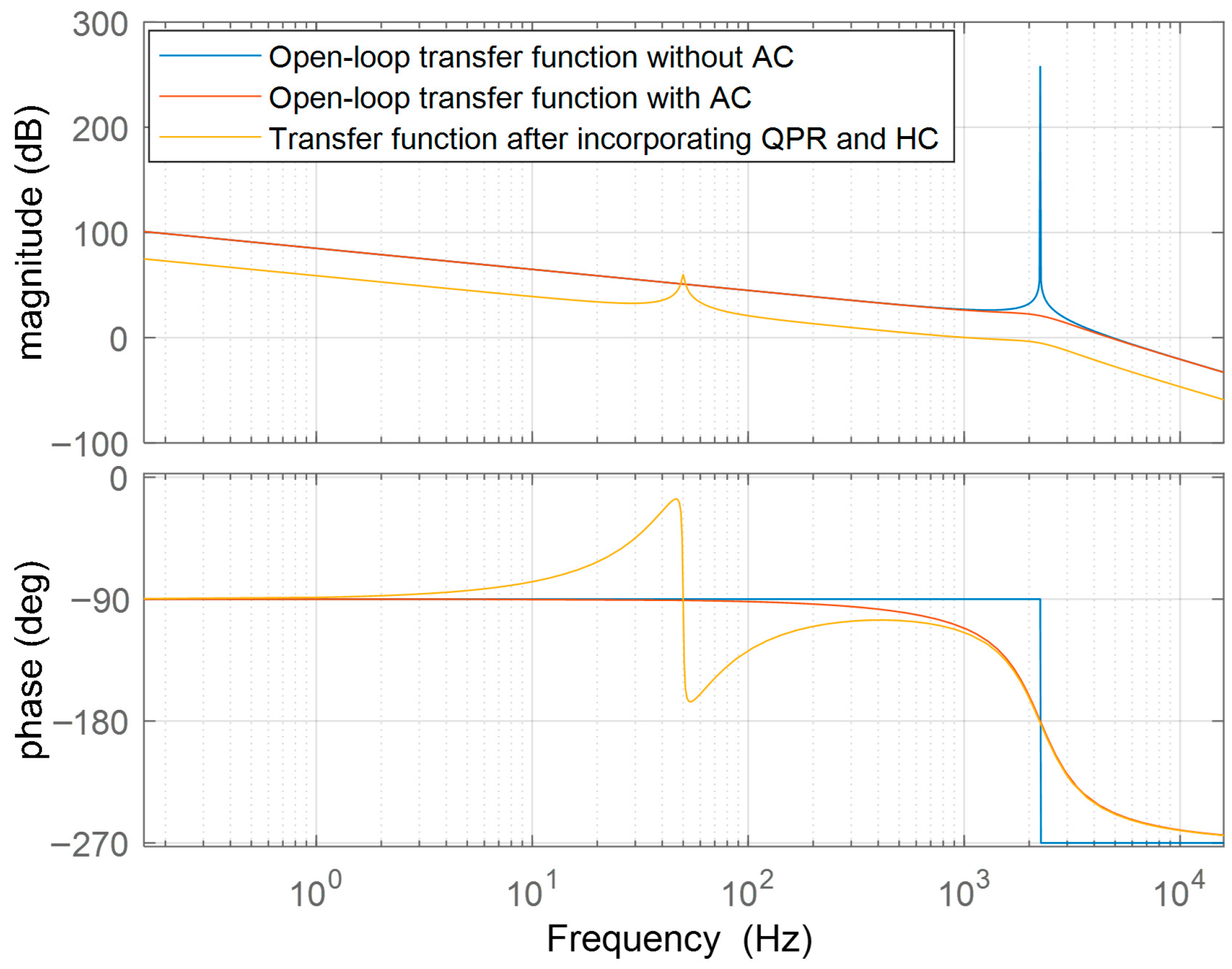As illustrated in Figure 13c, the enhanced feedforward control strategy demonstrates exceptional performance, even under the stringent condition of a 10 mH grid impedance. Not only does this strategy significantly reduce the amplitude error of the grid-connected current to 0.26 A, it also achieves excellent harmonic suppression: the sixth harmonic content is suppressed to 0.1%, while all other harmonics are controlled below 0.2%. Consequently, the total harmonic distortion (THD) falls well below the 5% grid connection standard. This exceptional performance is due to the innovative integration of resonant elements into the traditional feedforward architecture. This approach effectively suppresses high-frequency harmonics induced by grid impedance and completely eliminates disturbance waves. It achieves a unified balance between precise control and robust disturbance immunity. Compared to traditional full-feedforward strategies (a) and adaptive strategies (b), this approach strikes a superior balance between control accuracy, harmonic suppression depth and engineering practicality, providing a reliable technical solution for delivering high-quality grid-connected power.

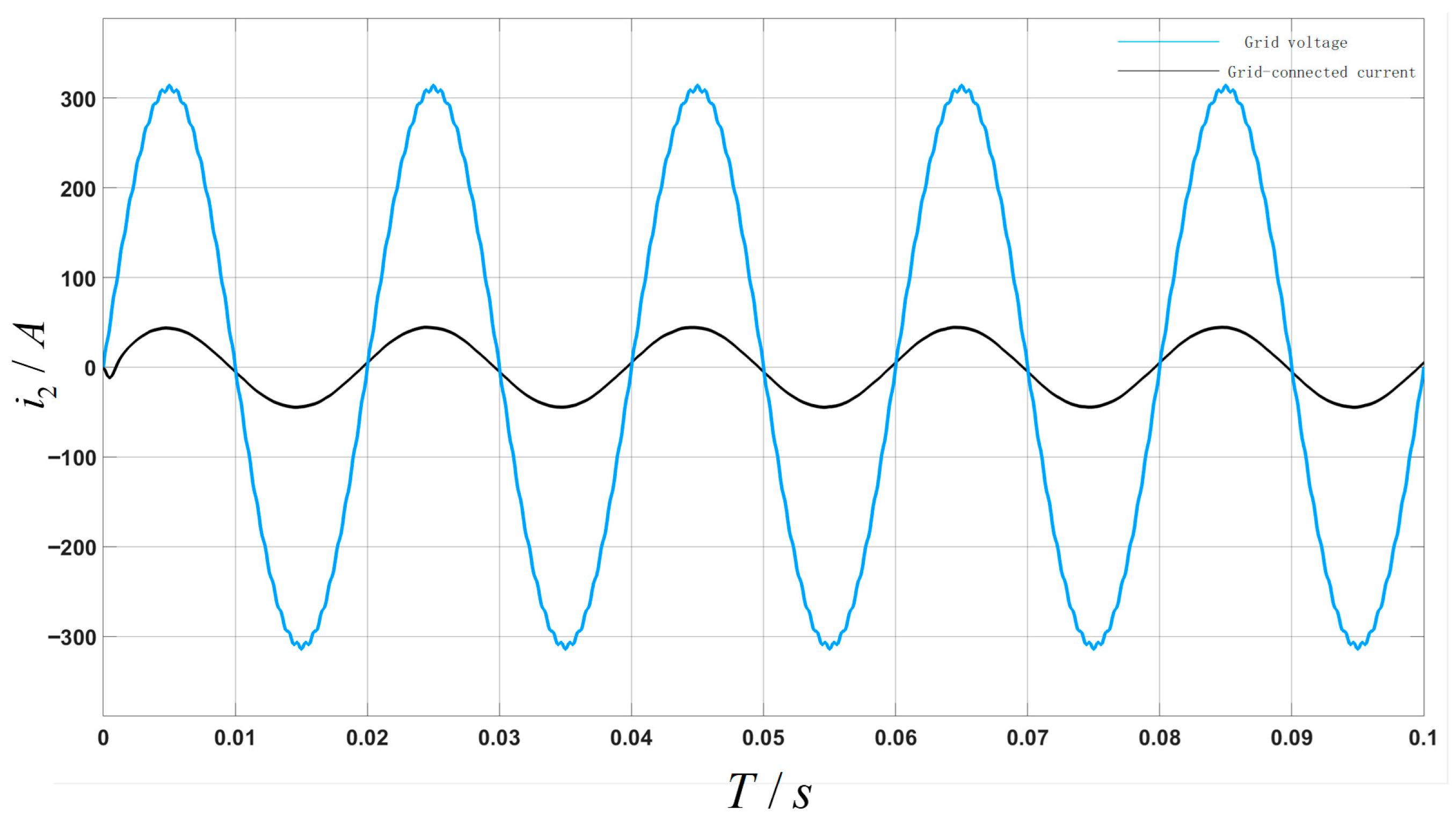
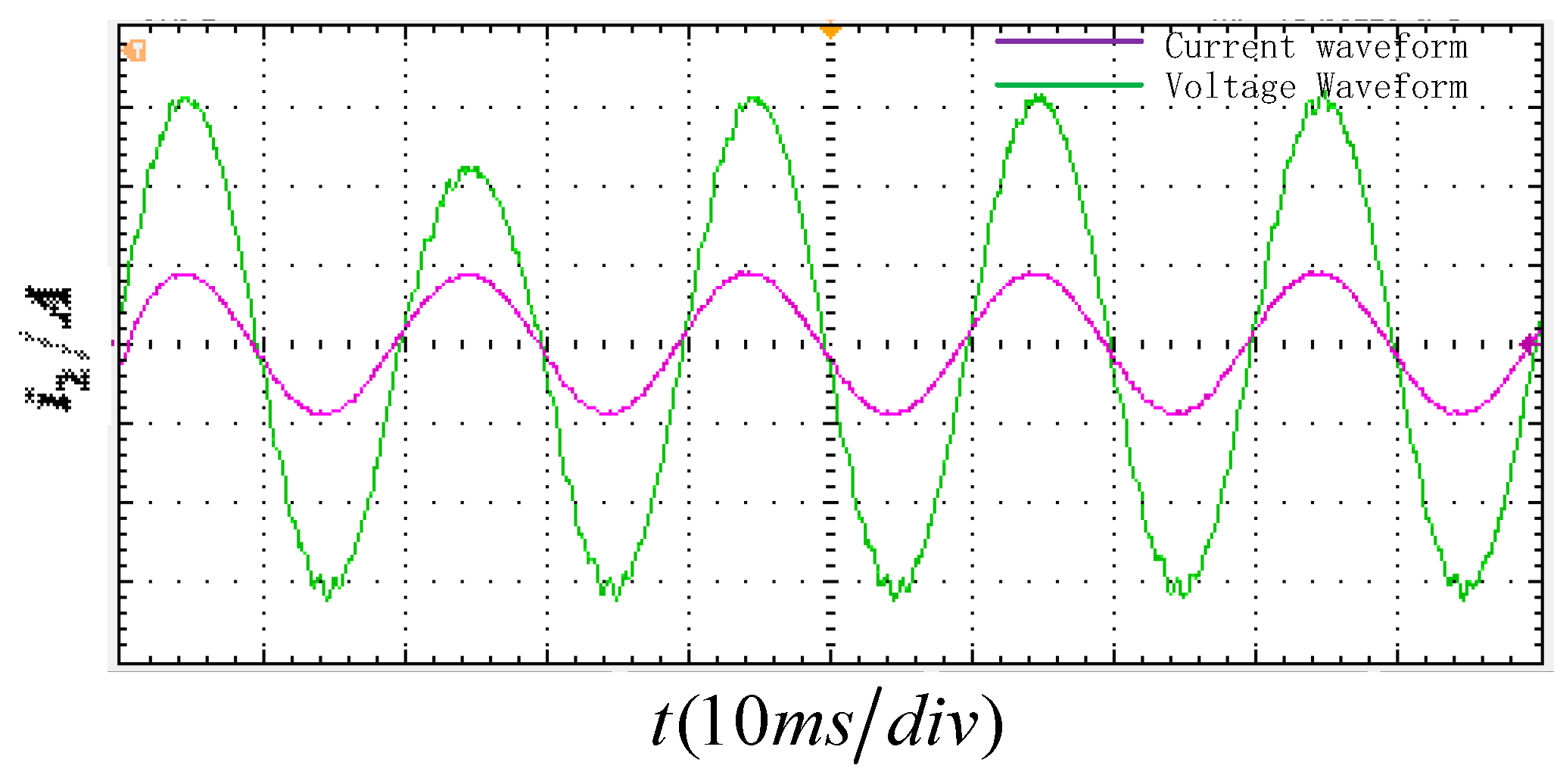
Figure 14 shows the dynamic response waveform of the system during a grid voltage sag fault, following the implementation of the improved feedforward and multi-resonance control composite strategy. The simulation results show that, when the grid voltage suddenly sags, the grid-connected current rapidly and smoothly transitions to the new reference value with no noticeable oscillations or instability occurring throughout the transient process. The current waveform maintains good sinusoidal quality during dynamic regulation, with low harmonic distortion and a rapid transition to a new stable state within milliseconds. The excellent dynamic performance of the system validates the proposed control strategy. The enhanced resonant feedforward effectively senses and compensates for grid voltage disturbances, significantly improving the speed of the system’s response and its immunity to disturbances. Meanwhile, the multi-resonance controller effectively suppresses harmonic components during transients, ensuring precise current tracking and waveform quality. These results demonstrate that the proposed strategy exhibits excellent dynamic performance and robustness when confronted with severe disturbances, such as grid faults.

Figure 15 shows the dynamic response waveform of the grid-connected current when 33rd-harmonic disturbances are injected into the power grid following the implementation of an improved control strategy. Unlike in the voltage dip scenario, this waveform primarily demonstrates the suppression capability of the control strategy for specific high-frequency harmonics: after 33rd harmonic injection, the grid-connected current maintains a well-defined sinusoidal waveform without any noticeable high-frequency oscillations or waveform distortion. This suggests that the multiresonance controller in the proposed strategy has significant filtering effects on higher-order harmonics. The enhanced feedforward channel works with the resonant controller to eliminate the impact of background grid harmonics on current tracking accuracy. This ensures steady-state performance and power quality for the system under high-frequency disturbances, demonstrating the strategy’s ability to suppress harmonics across multiple frequency bands.

6. Hardware-in-the-Loop Experimental Results

To further validate the correctness and effectiveness of the voltage control method for single-phase grid-connected inverters proposed in this paper, a hardware-in-the-loop semi-physical simulation experiment was conducted using the RT-LAB simulation platform. The voltage fault conditions during the experiment matched the simulation settings. The RT-LAB semi-physical simulation platform is shown in Figure 16.

Figure 17b shows the improved feedforward control strategy, which demonstrates outstanding dynamic performance with a rapid current response and precise tracking. Its proactive compensation mechanism enables it to rapidly suppress disturbances. While it exhibits slight waveform adjustments, it responds highly efficiently to system variations, making it particularly suitable for grid-connected applications that demand high dynamic performance.

Figure 18b shows the test waveform of the improved feedforward control strategy, which demonstrates its core advantages even when confronted with the greater challenges posed by l = 5. Compared to adaptive active damping (a), which is robust but may exhibit conservative responses, the improved feedforward control achieves a faster dynamic response, enabling swift tracking of command changes. Its key value lies in proactively compensating for system disturbances through a forward-looking mechanism, thereby demonstrating greater adaptability and disturbance rejection potential under complex operating conditions. Although the steady-state waveform exhibits slight ripples, these precisely reflect the controller’s active and rapid processing of system dynamics.

Even under the stringent condition of increased inductance to L = 10, the improved feed-forward control strategy shown in Figure 19b demonstrates superior adaptability to changes in performance compared to the adaptive active damping strategy shown in Figure 19a. Its waveform response is fast and precise, demonstrating the unique ability of the feedforward mechanism to overcome system inertia caused by high inductance. Despite the more complex operating conditions, this strategy effectively suppresses disturbances through proactive compensation, ensuring rapid system stabilisation.

Figure 20 illustrates the dynamic response of the grid-connected current during a sudden voltage dip. As can be seen, at the instant of the voltage drop and recovery, the current fluctuates briefly before stabilising rapidly, which demonstrates the exceptional dynamic response and disturbance rejection capability of the control strategy. Throughout the sustained voltage dip, the current maintains an excellent sinusoidal waveform, which validates the method’s robustness and stable operation under severe conditions.

The improved feedforward control strategy proposed in this paper, based on the aforementioned hardware-in-the-loop experiments, demonstrates superior dynamic response performance, enhanced disturbance rejection capability and excellent operational stability under various inductance conditions and voltage sag scenarios.

7. Conclusions and Outlook

This paper proposes a hybrid control strategy combining an improved resonant feedforward controller with a proportional multiresonant controller. It aims to address multiple challenges faced by LCL grid-connected inverters in weak grid environments, including inherent resonance, grid impedance, and background harmonics. Simulation results validate the effectiveness of this strategy. This section will delve into these results and analyze the advantages, underlying mechanisms, and applicability of the proposed method.

7.1. Synergistic Effects of Composite Control Strategies

This study focuses on recognising the limitations of single-control approaches and seeking a synergistic solution. The simulation results show that the proposed composite strategy outperforms traditional full-feedforward and single-improvement methods when it comes to addressing grid impedance variations and background harmonic interference. This advantage stems from the effective complementarity of the two control methods.

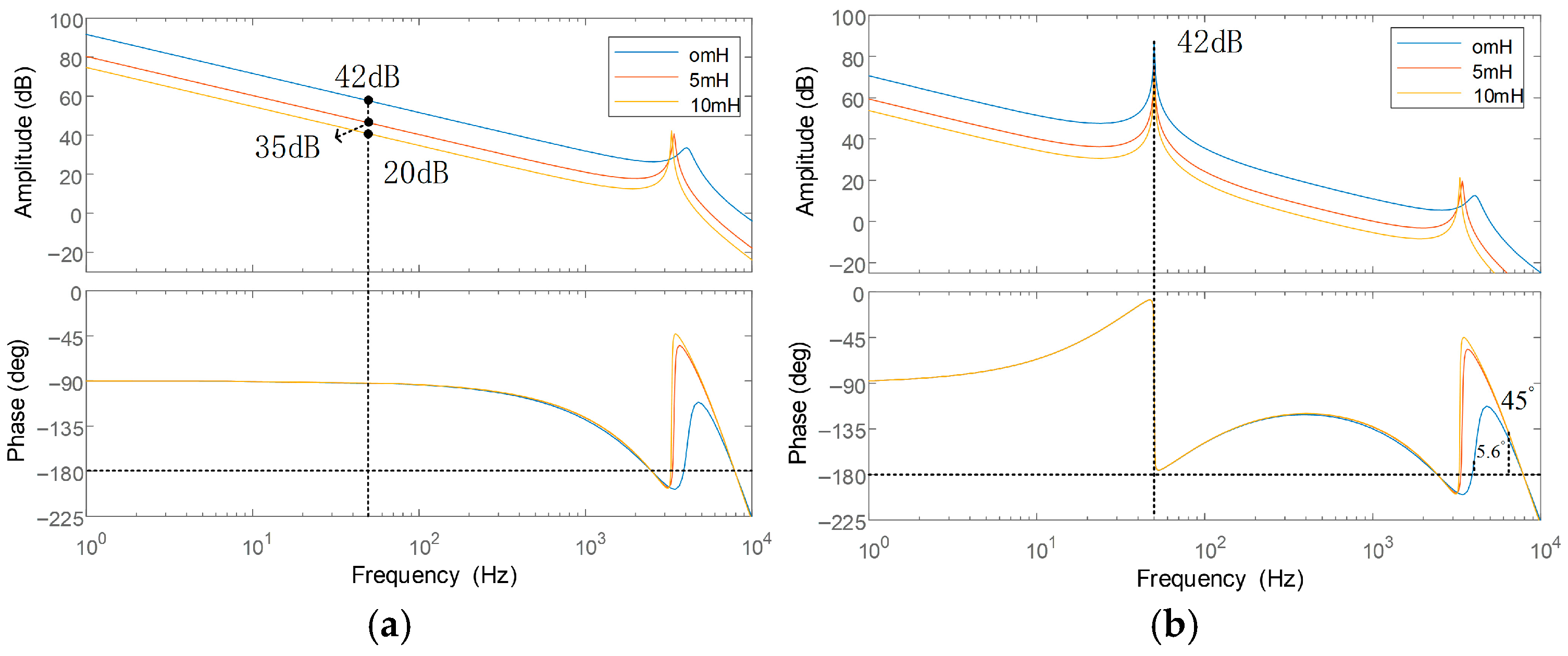
The role of improved resonant feedforward: As illustrated in Figure 9 and Table 2, improved resonant feedforward effectively addresses the issue of significant system stability deterioration caused by increased grid impedance in traditional full feedforward control (as depicted in Figure 7). The key lies in its precise compensation of feedforward at specific frequencies (primarily fundamental frequencies). This offsets voltage drops caused by grid impedance at these frequencies, maintaining the system’s reference tracking accuracy (i.e., the fundamental gain remains constant regardless of impedance changes). It also avoids introducing additional phase lag across the entire frequency band, thereby ensuring the system’s stability margin under weak grid conditions. Figure 9 confirms this, showing the system maintaining sufficient phase margin under varying grid impedances.

The role of the proportional multiharmonic controller: As shown in Table 2 and Figure 14, the total harmonic distortion (THD) of the grid-connected current is significantly lower under the composite control strategy than under traditional methods. There is particularly effective suppression of higher-order harmonics, such as the sixth harmonic. This is primarily due to the high gain provided by the proportional multiresonance controller at characteristic harmonic frequencies, such as the fundamental frequency and the 3rd, 5th and 7th harmonics. This enables zero-steer tracking of the command current and effective suppression of harmonic disturbances of the same order in the grid voltage. Consequently, it compensates for the limitations of using improved feedforward alone to suppress low-order harmonics present in the grid background.

7.2. Performance Comparison with Traditional and Advanced Control Strategies

The THD data in Table 2 provides an intuitive performance comparison. Compared to the traditional full feedforward control method, the proposed method optimises THD from 2.45% to 1.80% under weak grid conditions (Lg = 0 mH), demonstrating superior steady-state performance even in the absence of grid impedance influence. However, as grid impedance increases to Lg = 10 mH, the traditional method becomes unstable, causing THD to surge to 13.34%. In contrast, the proposed method optimises THD further to 0.76%, fully demonstrating its effectiveness and robustness under severe weak grid conditions.

The proposed approach demonstrates comparable competitiveness to the advanced active control method. At 10 mH, the THD of the proposed method is 0.76%, which is lower than that of the active control strategy (3.64%). This shows that, despite not using complex online parameter identification and adaptive adjustment mechanisms, combining a carefully designed fixed-parameter resonant feedforward with a multi-resonant controller efficiently and robustly suppresses specific disturbances (impedance and characteristic subharmonics) while keeping the control system simple. This provides a valuable solution for balancing control performance and system complexity in engineering practice.

7.3. Compared with Adaptive Control

To further validate the superiority of the proposed strategy, it was compared with an adaptive feedforward control strategy. When the grid impedance increased to 10 mH under severe conditions, the total harmonic distortion (THD) of the grid-connected current under adaptive control reached 3.09%. While adaptive control can theoretically adapt to changes in the system through online parameter adjustment, this result suggests that its performance in practical applications may be limited by the accuracy of parameter identification, the speed of convergence and the complexity of the algorithm. Performance may degrade or become unstable under strong disturbances. In contrast, the improved fixed-parameter resonant feedforward and quasi-proportional multi-resonance composite control strategy achieves a significantly lower THD of 0.76%, eliminating the need for complex online identification or adaptive adjustment mechanisms. This demonstrates that the strategy effectively locks onto and suppresses critical disturbances caused by grid impedance and background harmonics of a specific order through its carefully designed fixed control structure. Consequently, it provides a more reliable and robust solution in extremely weak grid conditions. Therefore, this strategy strikes a better balance between control performance, system complexity, and engineering feasibility, offering a highly practical alternative for addressing weak grid challenges.

7.4. Dynamic Performance and Robustness Analysis

Figure 14 and Figure 15 demonstrate the superiority of the proposed strategy by showing how it responds dynamically to changes. During both the reference current jump and the grid impedance step changes, the system recovers stability rapidly within one cycle, with minimal overshoot and oscillation. This performance stems from two key factors. Firstly, enhanced resonant feedforward maintains the system’s stability margin, providing a foundation for a fast dynamic response. Secondly, the proportional gain in the proportional-resonant controller ensures sufficient bandwidth, enabling a quick response to changes in commands and effective suppression of disturbances.

7.5. Limitations and Future Prospects

This study validated through simulation the significant advantages of the proposed improved composite control strategy in enhancing grid-connected current quality, suppressing resonance, and strengthening system stability. It provides valuable theoretical references and solutions for high-performance control of LCL grid-connected inverters.

Looking ahead, this research can be deepened in the following directions: Exploring the integration of advanced algorithms such as adaptive control and artificial intelligence with feedforward multiresonance control can enhance the robustness and adaptability of this strategy in complex dynamic power grid environments. Finally, promoting the application of this strategy in multi-machine parallel systems of large-scale renewable energy power plants will provide key technical support for achieving the safe and stable grid integration of high-penetration renewable energy.