A Comparative Study of Machine Learning Models for PV Energy Prediction in an Energy Community
Abstract
1. Introduction
1.1. Background
1.2. Review of Related Work and Contribution
2. Materials and Methods
2.1. Data
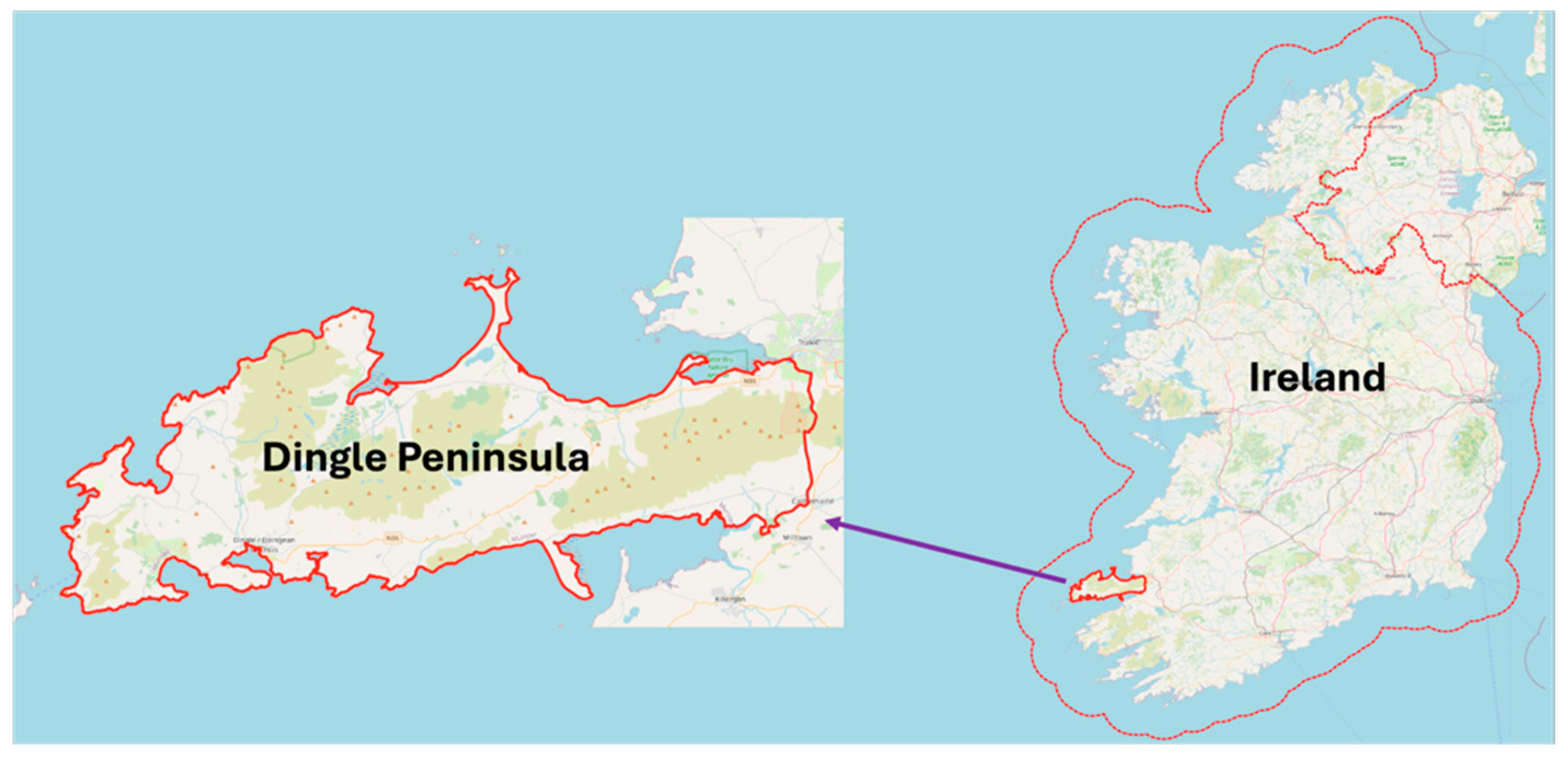
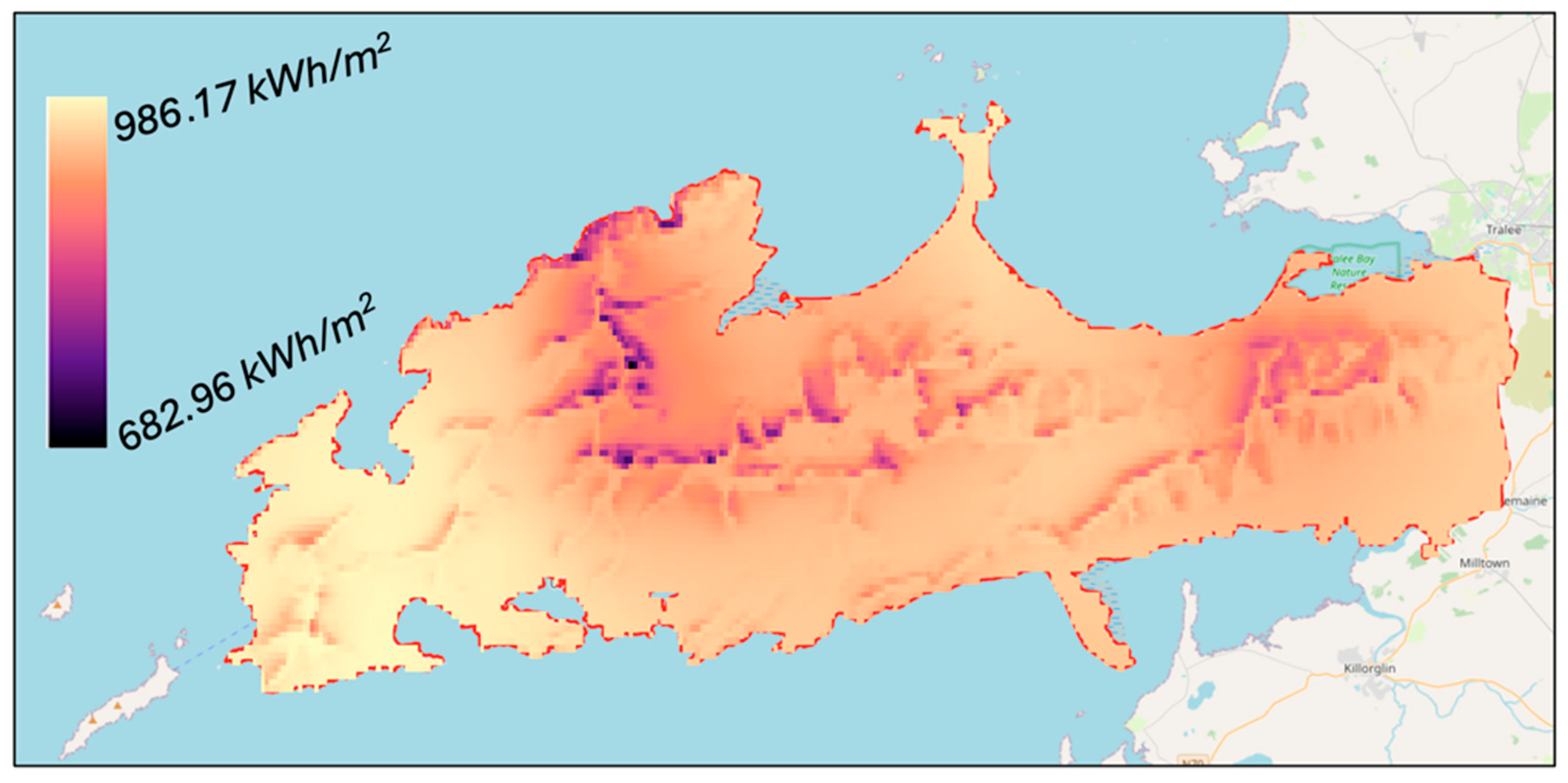
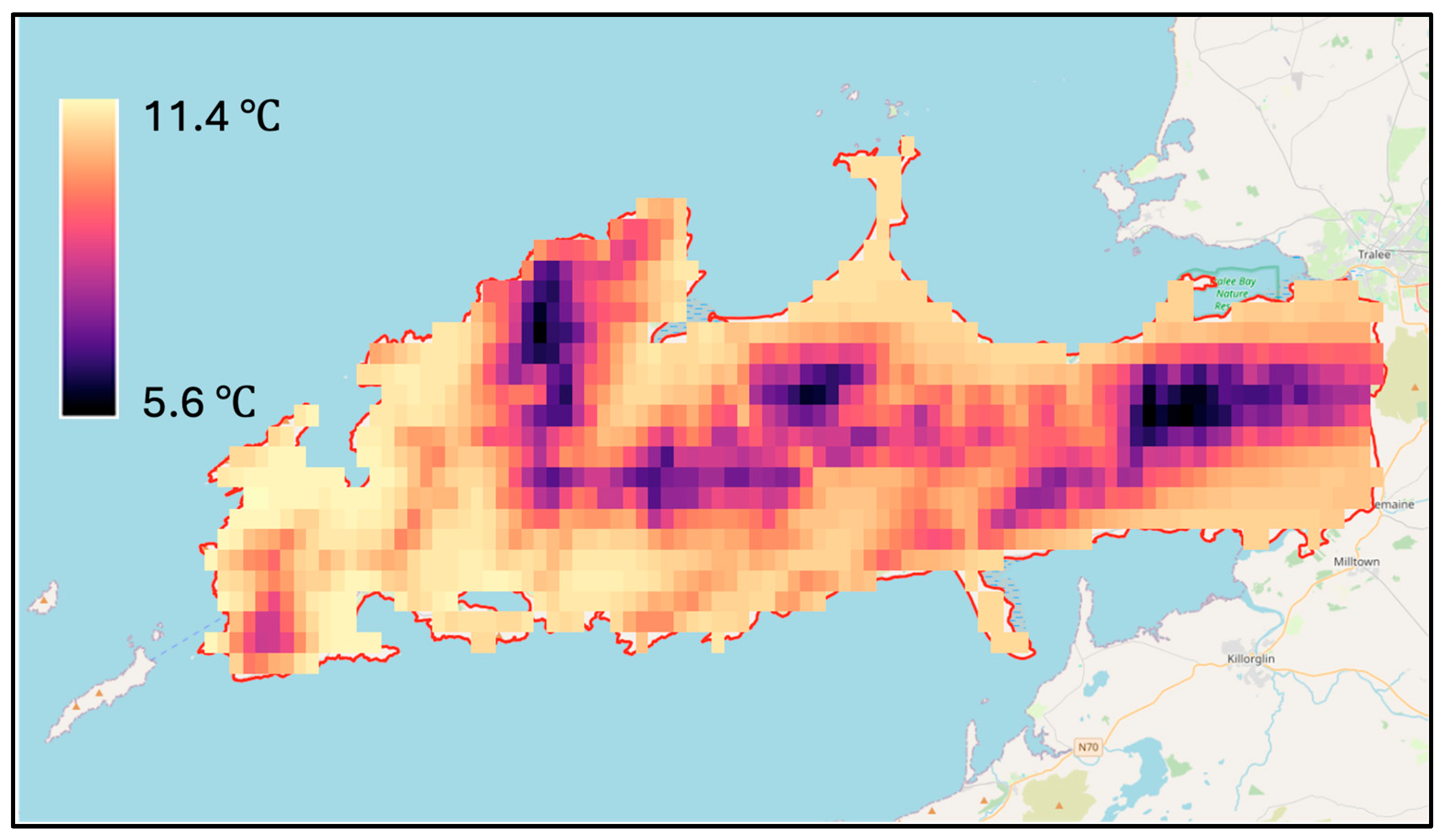
2.1.1. Study Area
2.1.2. Dataset Exploration
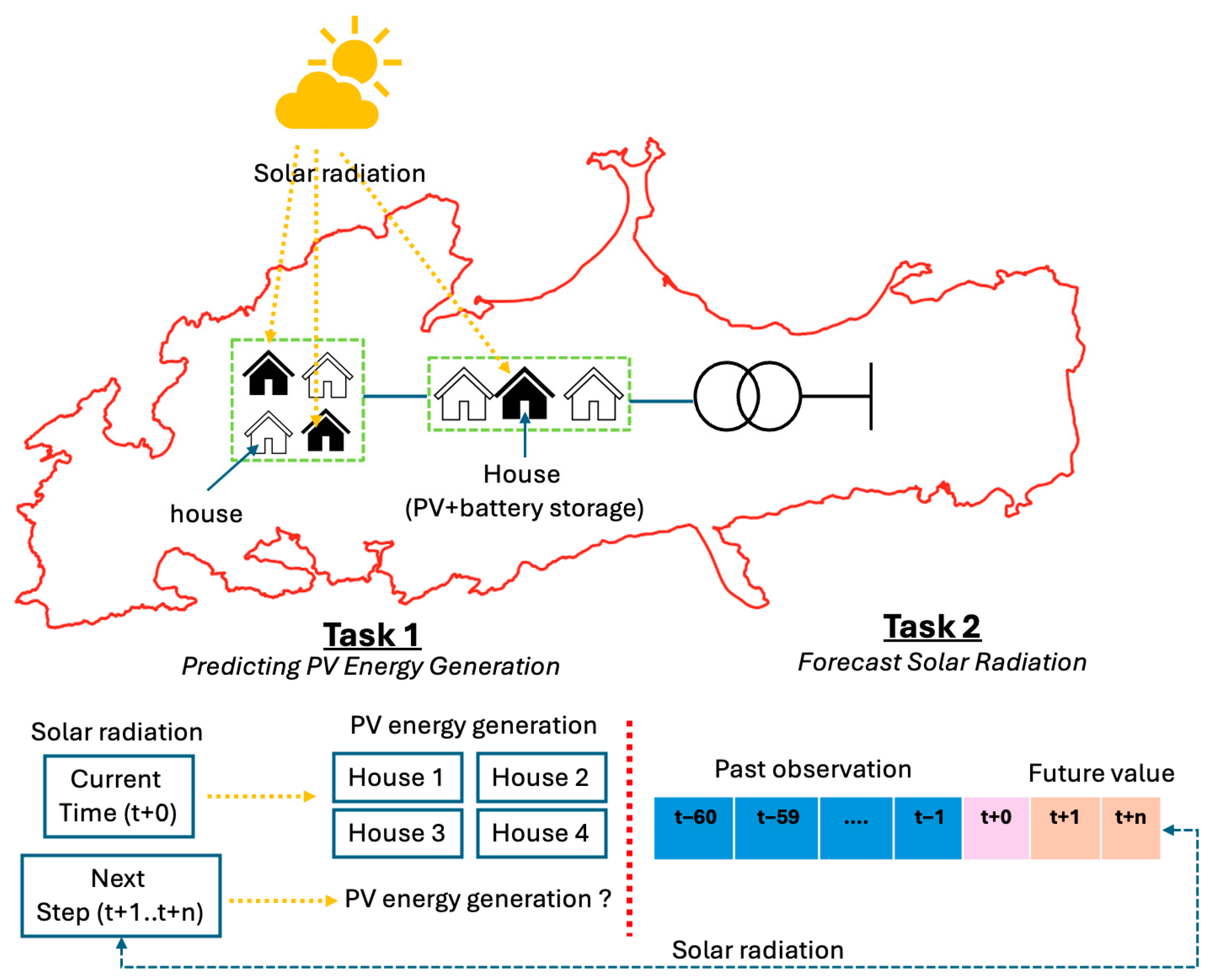
2.2. Model
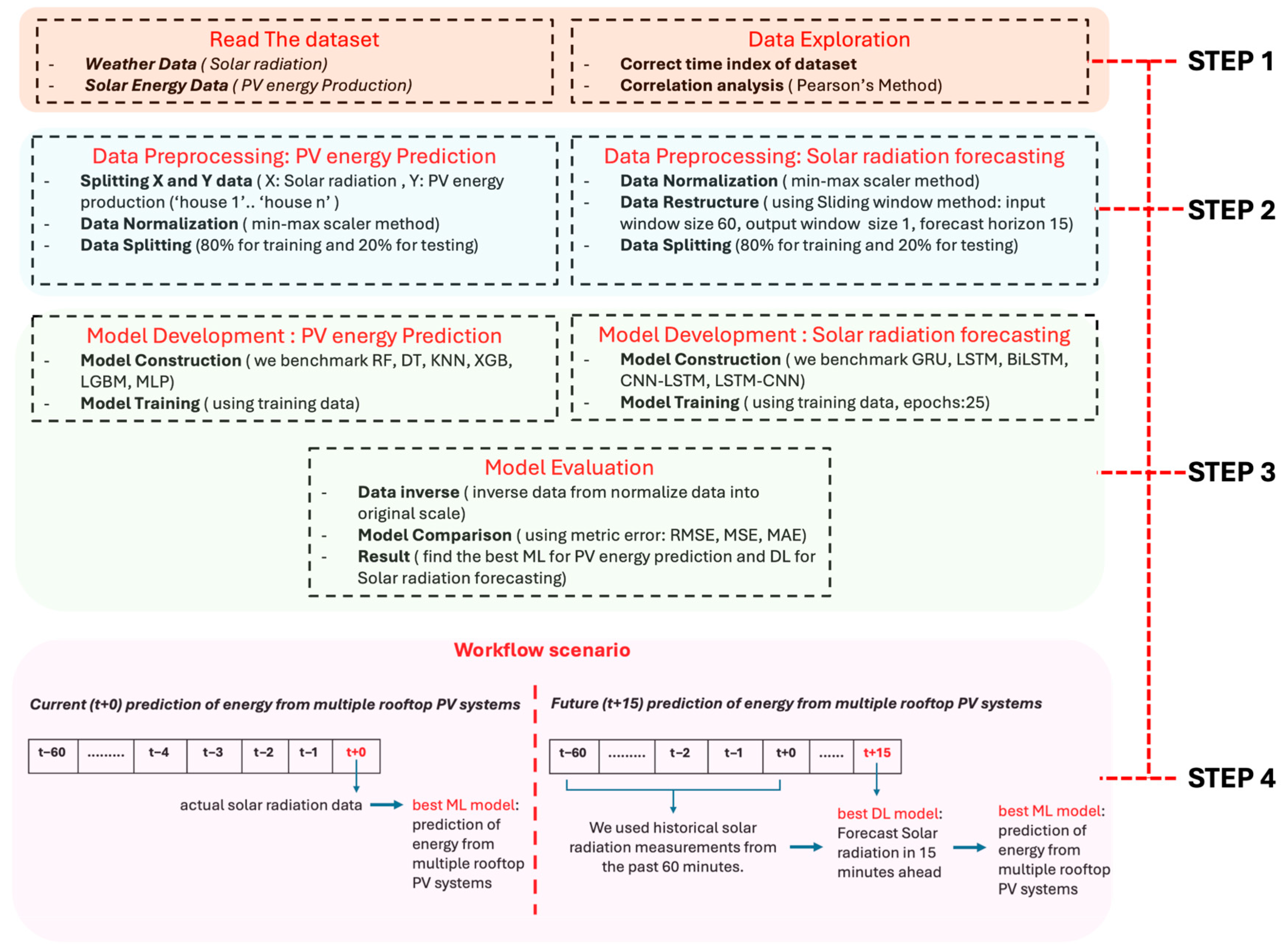
2.3. Proposed Workflow
3. Results and Discussion
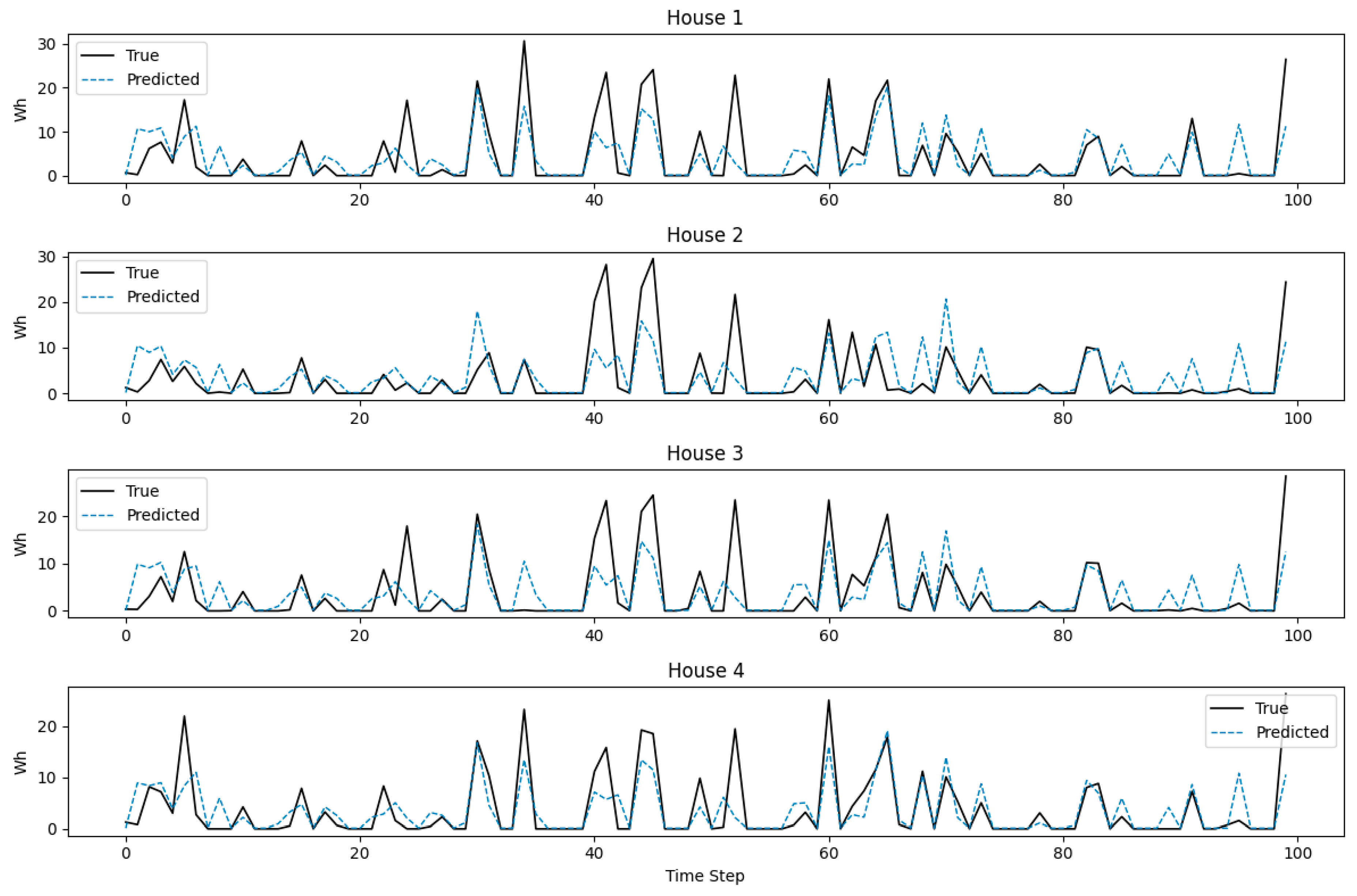
3.1. Predicting PV Energy Generation
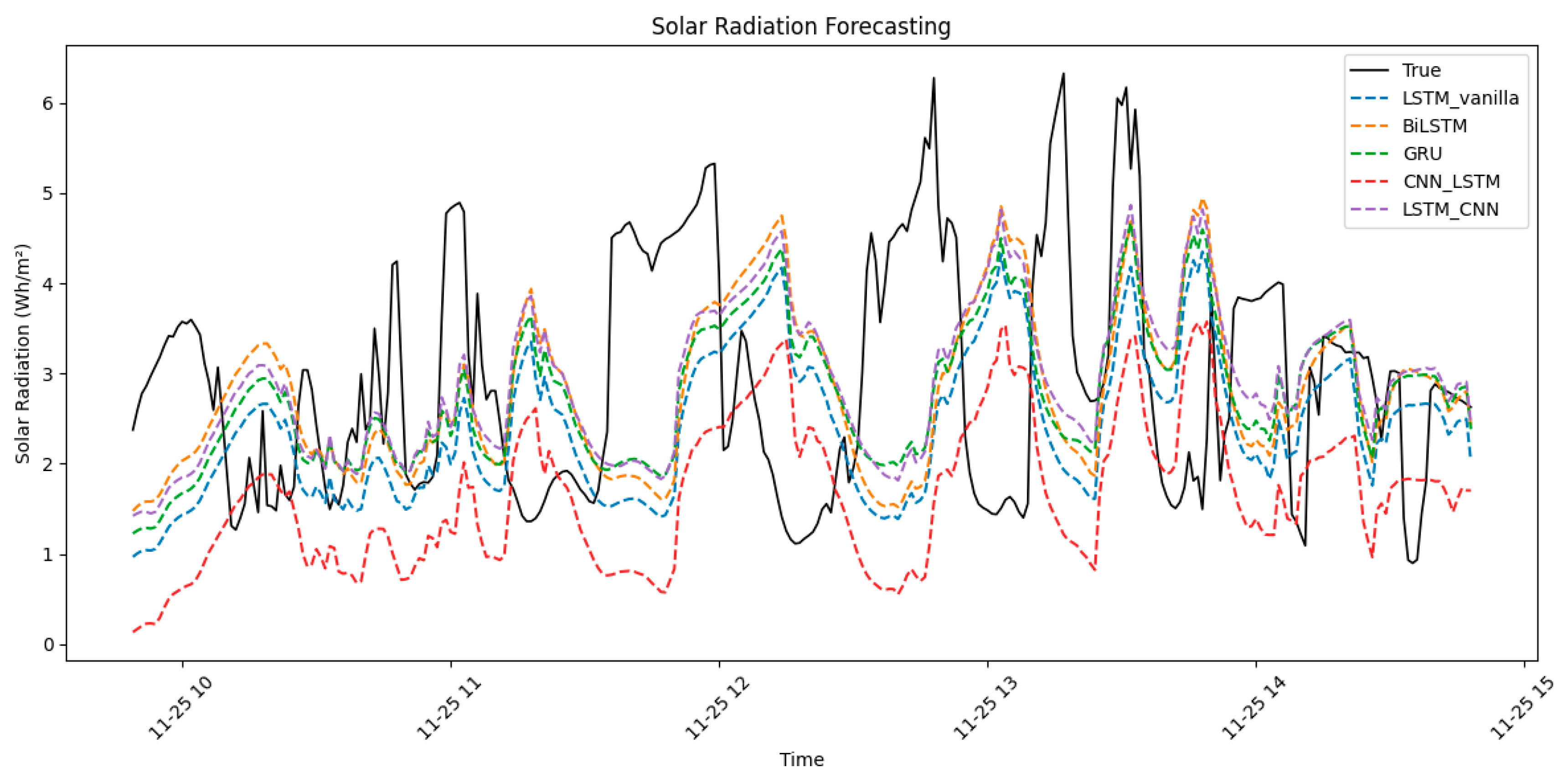
3.2. Solar Irradiation Forecasting (Minutes Ahead)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IRENA | International Renewable Energy Agency |
| PV | Photovoltaic |
| CNN-LSTM | Convolutional Neural Network—Long Short-Term Memory |
| LSTM-CNN | Long Short-Term Memory—Convolutional Neural Network |
| Wh | Watt-hour |
| GW | Gigawatt |
| RMSE | Root Mean Square Error |
| MSE | Mean Square Error |
| MAE | Mean Absolute Error |
| KNN | K-Nearest Neighbors |
| MLP | Multilayer Perceptron |
| GRU | Gated Recurrent Unit |
References
- International Renewable Energy Agency. Renewable Power Generation Costs in 2024. Available online: https://www.irena.org (accessed on 2 November 2025).
- Trivedi, R.; Bahloul, M.; Saif, A.; Patra, S.; Khadem, S. Comprehensive Dataset on Electrical Load Profiles for Energy Community in Ireland. Sci. Data 2024, 11, 621. [Google Scholar] [CrossRef]
- Coignard, J.; Janvier, M.; Debusschere, V.; Moreau, G.; Chollet, S.; Caire, R. Evaluating forecasting methods in the context of local energy communities. Int. J. Electr. Power Energy Syst. 2021, 131, 106956. [Google Scholar] [CrossRef]
- Gaboitaolelwe, J.; Zungeru, A.M.; Yahya, A.; Lebekwe, C.K.; Vinod, D.N.; Salau, A.O. Machine Learning Based Solar Photovoltaic Power Forecasting: A Review and Comparison. IEEE Access 2023, 11, 40820–40845. [Google Scholar] [CrossRef]
- Lari, A.J.; Sanfilippo, A.P.; Bachour, D.; Perez-Astudillo, D. Using Machine Learning Algorithms to Forecast Solar Energy Power Output. Electronics 2025, 14, 866. [Google Scholar] [CrossRef]
- Singh, U.; Singh, S.; Gupta, S.; Alotaibi, M.A.; Malik, H. Forecasting rooftop photovoltaic solar power using machine learning techniques. Energy Rep. 2025, 13, 3616–3630. [Google Scholar] [CrossRef]
- Suanpang, P.; Jamjuntr, P. Machine Learning Models for Solar Power Generation Forecasting in Microgrid Application Implications for Smart Cities. Sustainability 2024, 16, 6087. [Google Scholar] [CrossRef]
- Aouidad, H.I.; Bouhelal, A. Machine learning-based short-term solar power forecasting: A comparison between regression and classification approaches using extensive Australian dataset. Sustain. Energy Res. 2024, 11, 1–21. [Google Scholar] [CrossRef]
- Shah, A.; Viswanath, V.; Gandhi, K.; Patil, N.M. Predicting Solar Energy Generation with Machine Learning based on AQI and Weather Features. arXiv 2024, arXiv:2408.12476. [Google Scholar] [CrossRef]
- Hayajneh, A.M.; Alasali, F.; Salama, A.; Holderbaum, W. Intelligent Solar Forecasts: Modern Machine Learning Models and TinyML Role for Improved Solar Energy Yield Predictions. IEEE Access 2024, 12, 10846–10864. [Google Scholar] [CrossRef]
- Nastić, F.; Jurišević, N.; Nikolić, D.; Končalović, D. Harnessing open data for hourly power generation forecasting in newly commissioned photovoltaic power plants. Energy Sustain. Dev. 2024, 81, 101512. [Google Scholar] [CrossRef]
- Dimitropoulos, N.; Mylona, Z.; Marinakis, V.; Kapsalis, P.; Sofias, N.; Primo, N.; Maniatis, Y.; Doukas, H. Comparative analysis of AI-based models for short-term photovoltaic power forecasting in energy cooperatives. Intell. Decis. Technol. 2022, 15, 691–705. [Google Scholar] [CrossRef]
- Dimitropoulos, N.; Sofias, N.; Kapsalis, P.; Mylona, Z.; Marinakis, V.; Primo, N.; Doukas, H. Forecasting of short-term PV production in energy communities through Machine Learning and Deep Learning algorithms. In Proceedings of the IISA 2021-12th International Conference on Information, Intelligence, Systems and Applications, Chania, Crete, Greece, 12–14 July 2021. [Google Scholar] [CrossRef]
- Capotosto, T.; di Fazio, A.R.; Perna, S.; Conte, F.; Iannello, G.; de Falco, P. Day-ahead Forecast of PV Systems and End-Users in the Contest of Renewable Energy Communities. In Proceedings of the 2022 AEIT International Annual Conference, Rome, Italy, 3–5 October 2022. [Google Scholar] [CrossRef]
- Mazzeo, D.; Herdem, M.S.; Matera, N.; Bonini, M.; Wen, J.Z.; Nathwani, J.; Oliveti, G. Artificial intelligence application for the performance prediction of a clean energy community. Energy 2021, 232, 120999. [Google Scholar] [CrossRef]
- Rajendran, S.S.P.; Gebremedhin, A. Deep learning-based solar power forecasting model to analyze a multi-energy microgrid energy system. Front. Energy Res. 2024, 12, 1363895. [Google Scholar] [CrossRef]
- De Paola, A.; Musiari, E.; Fortunati, L.; Gregori, F.; Anselmi, G.P.; Andreadou, N.; Kotsakis, E.; Fulli, G. An Open-Source IT Tool for Energy Forecast of Renewable Energy Communities. IEEE Access 2025, 13, 69619–69630. [Google Scholar] [CrossRef]
- Dattola, F.; Iaquinta, P.; Iusi, M.; Federico, D.; Greco, R.; Talerico, M.; Coscarella, V.; Legato, L.; Pellegrino, I.; Bergamaschi, S.; et al. PRECEDE: Climate and Energy Forecasts to Support Energy Communities with Deep Learning Models. In Proceedings of the 2024 IEEE International Conference on Big Data (BigData 2024), Washington, DC, USA, 15–18 December 2024; pp. 4650–4658. [Google Scholar] [CrossRef]
- Solargis. Solar Resource Maps & GIS Data For 200+ Countries. Available online: https://solargis.com/resources/free-maps-and-gis-data?locality=ireland (accessed on 12 August 2025).
- Bamisile, O.; Acen, C.; Cai, D.; Huang, Q.; Staffell, I. The environmental factors affecting solar photovoltaic output. Renew. Sustain. Energy Rev. 2024, 208, 115073. [Google Scholar] [CrossRef]
- Agrawal, R. Fundamentals of Machine Learning. In Machine Learning for Healthcare, 1st ed.; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Dao, T.C.T.; Nguyen, L.N.T.; Nguyen, T.-D.; Le, M.-V.; French, I.T.; Doan, V.-T.; Vo, V.H.K.; Tran, N.C.; Pham, D.-H.; et al. Solar Radiation Forecasting Based on Random Forest and XGBoost. In Proceedings of the 2024 7th International Conference on Green Technology and Sustainable Development, GTSD 2024, Ho Chi Minh City, Vietnam, 25–26 July 2024; pp. 136–140. [Google Scholar] [CrossRef]
- Azman, M.A.; Jantan, H.; Bahrin, U.F.M.; Kadir, E.A. Solar Power Production Forecasting Model Using Random Forest Algorithm. In Lecture Notes in Networks and Systems; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2024; pp. 135–144. [Google Scholar] [CrossRef]
- Lahouar, A.; Slama, J.B.H. Day-ahead load forecast using random forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar] [CrossRef]
- Dong, Y.; Ma, X.; Fu, T. Electrical load forecasting: A deep learning approach based on K-nearest neighbors. Appl. Soft Comput. 2021, 99, 106900. [Google Scholar] [CrossRef]
- Aksan, F.; Suresh, V.; Janik, P. Optimal Capacity and Charging Scheduling of Battery Storage through Forecasting of Photovoltaic Power Production and Electric Vehicle Charging Demand with Deep Learning Models. Energies 2024, 17, 2718. [Google Scholar] [CrossRef]
- Aksan, F.; Suresh, V.; Janik, P. PV Generation Prediction Using Multilayer Perceptron and Data Clustering for Energy Management Support. Energies 2025, 18, 1378. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The Performance of LSTM and BiLSTM in Forecasting Time Series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data 2019), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Ye, X.; Xiong, X.; Li, T. Photovoltaic Power Forecasting Model based on Random Forest and BiLSTM Neural Network. In Proceedings of the IEEE Advanced Information Technology, Chongqing, China, 15–17 March 2024; pp. 1345–1348. [Google Scholar] [CrossRef]
- Mazen, F.M.A.; Shaker, Y.; Seoud, R.A.A. Forecasting of Solar Power Using GRU–Temporal Fusion Transformer Model and DILATE Loss Function. Energies 2023, 16, 8105. [Google Scholar] [CrossRef]
- Aksan, F.; Li, Y.; Suresh, V.; Janik, P. CNN-LSTM vs. LSTM-CNN to Predict Power Flow Direction: A Case Study of the High-Voltage Subnet of Northeast Germany. Sensors 2023, 23, 901. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. Photovoltaic power forecasting based LSTM-Convolutional Network. Energy 2019, 189, 116225. [Google Scholar] [CrossRef]
- Meng, M.; Song, C. Daily photovoltaic power generation forecasting model based on random forest algorithm for north china in winter. Sustainability 2020, 12, 2247. [Google Scholar] [CrossRef]
- Guan, L.; Zou, L. Study on solar power prediction model by random forest method based on a numerical weather prediction model. Authorea 2024. Preprint. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Pham, M.-H.; Phap, V.M.; Do, Q.-H.; Nguyen, N.-T.; Nguyen, D.-T.; Nguyen, T.N. Forecasting of solar power generation in Vietnam deploying a simple GRU model. In Proceedings of the 2023 IEEE Asia Meeting on Environment and Electrical Engineering, EEE-AM 2023, Hanoi, Vietnam, 13–15 November 2023. [Google Scholar] [CrossRef]
- Elmousaid, R.; Drioui, N.; Elgouri, R.; Agueny, H.; Adnani, Y. Ultra-short-term global horizontal irradiance forecasting based on a novel and hybrid GRU-TCN model. Results Eng. 2024, 23, 102817. [Google Scholar] [CrossRef]
- Streamlit. A Faster Way to Build and Share Data Apps. Available online: https://streamlit.io/ (accessed on 9 October 2025).



| Model | Implementation | Key Hyperparameters |
|---|---|---|
| Random Forest [22,23,24] | RandomForest wrapped in MultiOutputRegressor | n_estimators = 200, random_state = 42 |
| XGBoost [22] | XGB wrapped in MultiOutputRegressor | n_estimators = 200, random_state = 42, learning_rate = 0.1, max_depth = 15 |
| K-Nearest Neighbors [25] | KNeighbors wrapped in MultiOutputRegressor | n_neighbors = 5 |
| LightGBM | LGBM wrapped in MultiOutputRegressor | n_estimators = 200, random_state = 42, learning_rate = 0.1, max_depth = 15 |
| Decision Tree [26] | DecisionTree wrapped In MultiOutputRegressor | max_depth = 10, random_state = 42 |
| Multilayer Perceptron [27] | Keras Sequential | Input = X_train.shape [1], hidden layers: 128 (ReLU), 64 (ReLU), output = y_train.shape [1], optimizer = Adam, loss = MSE, metric = MAE |
| Model | Architecture | Key Layer & Parameters | Compiler | Fitting |
|---|---|---|---|---|
| LSTM [28] | Sequential | Input: (timesteps, 1) LSTM (64 units, activation = tanh) Dense (output steps) | Optimizer: Adam, Loss: MSE, Metric: MAE | Validation split: 0.1, Epochs: 25, Batch size: 32 |
| Bidirectional LSTM [29] | Sequential | Input: (timesteps, 1) Bidirectional LSTM (64 units, activation = tanh) Dense (output steps) | Optimizer: Adam, Loss: MSE, Metric: MAE | Validation split: 0.1, Epochs: 25, Batch size: 32 |
| GRU [30] | Sequential | Input: (timesteps, 1) GRU (64 units, activation = tanh) Dense (output steps) | Optimizer: Adam, Loss: MSE, Metric: MAE | Validation split: 0.1, Epochs: 25, Batch size: 32 |
| CNN-LSTM [31] | Sequential | Input: (timesteps, 1) Conv1D (filters = 64, kernel size = 3, activation = relu) MaxPooling1D (pool size = 2), LSTM (unit = 64, activation = tanh), Dense (output steps) | Optimizer: Adam, Loss: MSE, Metric: MAE | Validation split: 0.1, Epochs: 25, Batch size: 32 |
| LSTM-CNN [31,32] | Sequential | Input: (timesteps, 1) LSTM (unit = 64, activation = tanh), Conv1D (filters = 64, kernel size = 3, activation = relu), GlobalMaxPooling1D(), Dense (output steps) | Optimizer: Adam, Loss: MSE, Metric: MAE | Validation split: 0.1, Epochs: 25, Batch size: 32 |
| House Number | RMSE | |||||
|---|---|---|---|---|---|---|
| Random Forest | XGBoost | KNN | LightGBM | Decision Tree | MLP | |
| 1 | 5.5813 | 5.6587 | 5.9904 | 5.6583 | 5.6472 | 5.6892 |
| 2 | 5.4729 | 5.5478 | 5.8806 | 5.5475 | 5.5387 | 5.5823 |
| 3 | 5.5181 | 5.5958 | 5.916 | 5.5971 | 5.5885 | 5.6303 |
| 4 | 4.8391 | 4.9055 | 5.2124 | 4.905 | 4.8967 | 4.9373 |
| House Number | MSE | |||||
|---|---|---|---|---|---|---|
| Random Forest | XGBoost | KNN | LightGBM | Decision Tree | MLP | |
| 1 | 31.1507 | 32.0214 | 35.885 | 32.016 | 31.8912 | 32.3669 |
| 2 | 29.9529 | 30.7776 | 34.581 | 30.7748 | 30.677 | 31.1617 |
| 3 | 30.4495 | 31.3129 | 34.9996 | 31.3275 | 31.2316 | 31.6999 |
| 4 | 23.4172 | 24.0643 | 27.1691 | 24.0589 | 23.9772 | 24.3774 |
| House Number | MAE | |||||
|---|---|---|---|---|---|---|
| Random Forest | XGBoost | KNN | LightGBM | Decision Tree | MLP | |
| 1 | 2.9768 | 3.0344 | 3.097 | 3.0336 | 3.0255 | 3.226 |
| 2 | 2.9321 | 2.9875 | 3.049 | 2.9871 | 2.9803 | 3.2937 |
| 3 | 2.9335 | 2.9952 | 3.0505 | 2.9953 | 2.989 | 3.2631 |
| 4 | 2.5726 | 2.6221 | 2.6927 | 2.6219 | 2.6168 | 2.8214 |
| Model | RMSE | MSE | MAE |
|---|---|---|---|
| LSTM | 0.689 | 0.475 | 0.435 |
| Bidirectional LSTM | 0.626 | 0.391 | 0.27 |
| GRU | 0.611 | 0.373 | 0.238 |
| CNN-LSTM | 1.299 | 1.688 | 1.194 |
| LSTM-CNN | 0.622 | 0.387 | 0.327 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aksan, F.; Pawlica, A.; Suresh, V.; Janik, P. A Comparative Study of Machine Learning Models for PV Energy Prediction in an Energy Community. Energies 2025, 18, 5980. https://doi.org/10.3390/en18225980
Aksan F, Pawlica A, Suresh V, Janik P. A Comparative Study of Machine Learning Models for PV Energy Prediction in an Energy Community. Energies. 2025; 18(22):5980. https://doi.org/10.3390/en18225980
Chicago/Turabian StyleAksan, Fachrizal, Anna Pawlica, Vishnu Suresh, and Przemysław Janik. 2025. "A Comparative Study of Machine Learning Models for PV Energy Prediction in an Energy Community" Energies 18, no. 22: 5980. https://doi.org/10.3390/en18225980
APA StyleAksan, F., Pawlica, A., Suresh, V., & Janik, P. (2025). A Comparative Study of Machine Learning Models for PV Energy Prediction in an Energy Community. Energies, 18(22), 5980. https://doi.org/10.3390/en18225980








