An Efficient Method for Simulating High-Velocity Non-Darcy Gas Flow in Fractured Reservoirs Based on Diffusive Time of Flight
Abstract
1. Introduction
2. Methodology
- The reservoir temperature is constant during the simulation.
- The effect of gravity on gas flow is neglected to simplify the model and focus on pressure-driven flow behavior.
- The effect of pressure on matrix and fracture permeability is ignored.
- Single-phase gas flow is assumed, with no adsorption or desorption effects, to maintain modeling simplicity.
- No-flow boundary conditions are imposed on all outer boundaries of the reservoir.
2.1. Derivation of the Eikonal Equation for Pressure Front Propagation
2.2. Dimensional Reduction of the Flow Problem Along the τ Direction
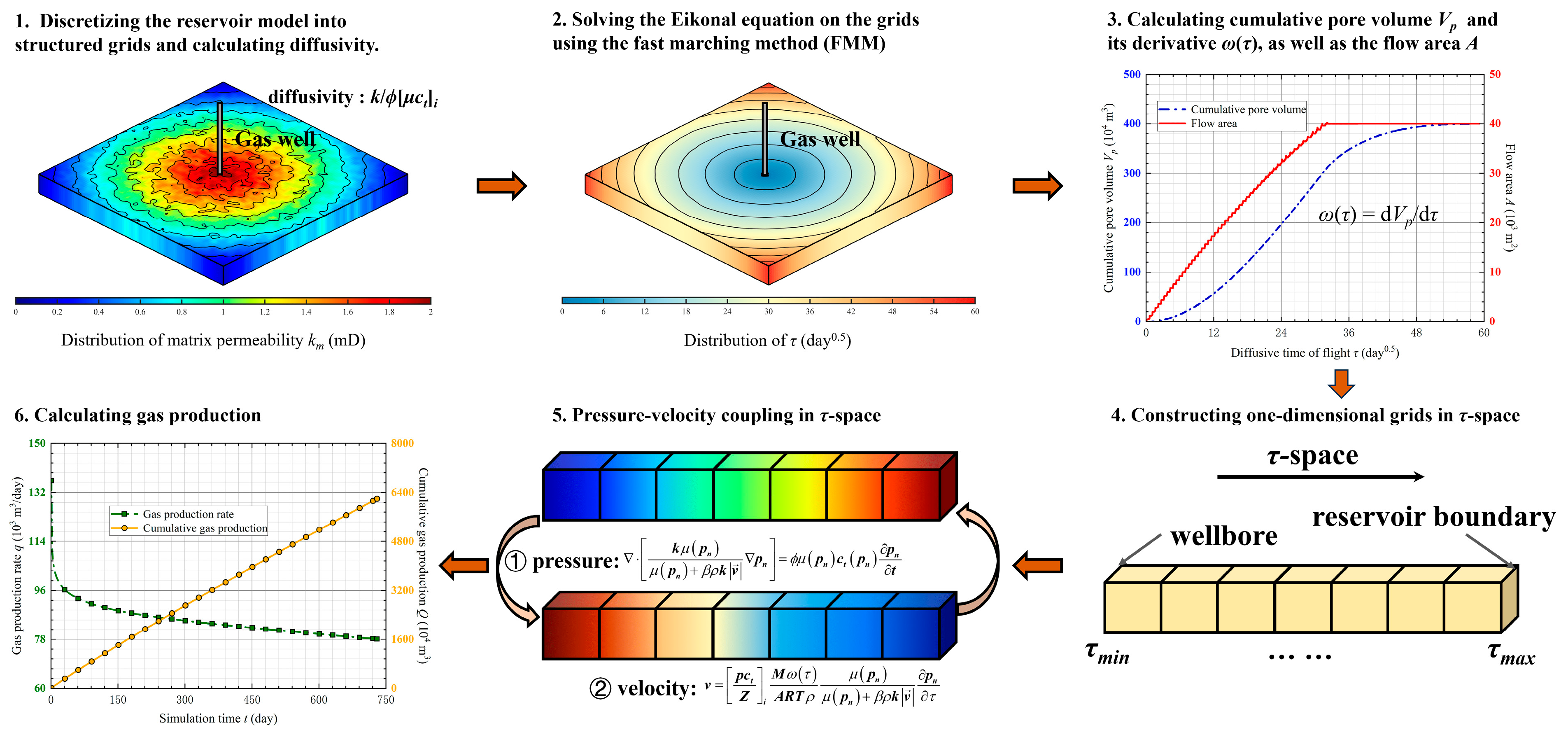
2.3. Numerical Framework of the Proposed Method
- 1.
- Grid discretization and diffusivity calculation. Discretizing the reservoir model into structured grids, each grid is assigned physical properties such as porosity (ϕ), permeability (k), and rock compressibility (cr). The diffusivity is then calculated in each grid as α = k/ϕ[μct]i, which serves as the key parameter for solving the Eikonal equation.
- 2.
- Determination of τ distribution. By solving the Eikonal equation numerically on the grids using the fast marching method (FMM), the τ value for each grid is calculated, thus obtaining the spatial distribution of τ.
- 3.
- Calculation of Vp, A, ω(τ). For each τ value, summing the pore volumes of all grids with τ values less than or equal to the given τ yields the corresponding cumulative pore volume Vp. The value of ω(τ) is then obtained as the derivative dVp/dτ. In addition, the flow area A is computed as the total cross-sectional area of the iso-τ surface corresponding to the given τ.
- 4.
- Construction of one-dimensional grids in τ-space. The range of τ values, from the minimum value at the wellbore (typically τmin = 0) to the maximum value corresponding to the τ required for the pseudo-pressure disturbance to propagate to the reservoir boundary, is discretized into a series of segments. This results in a set of one-dimensional grids in τ-space.
- 5.
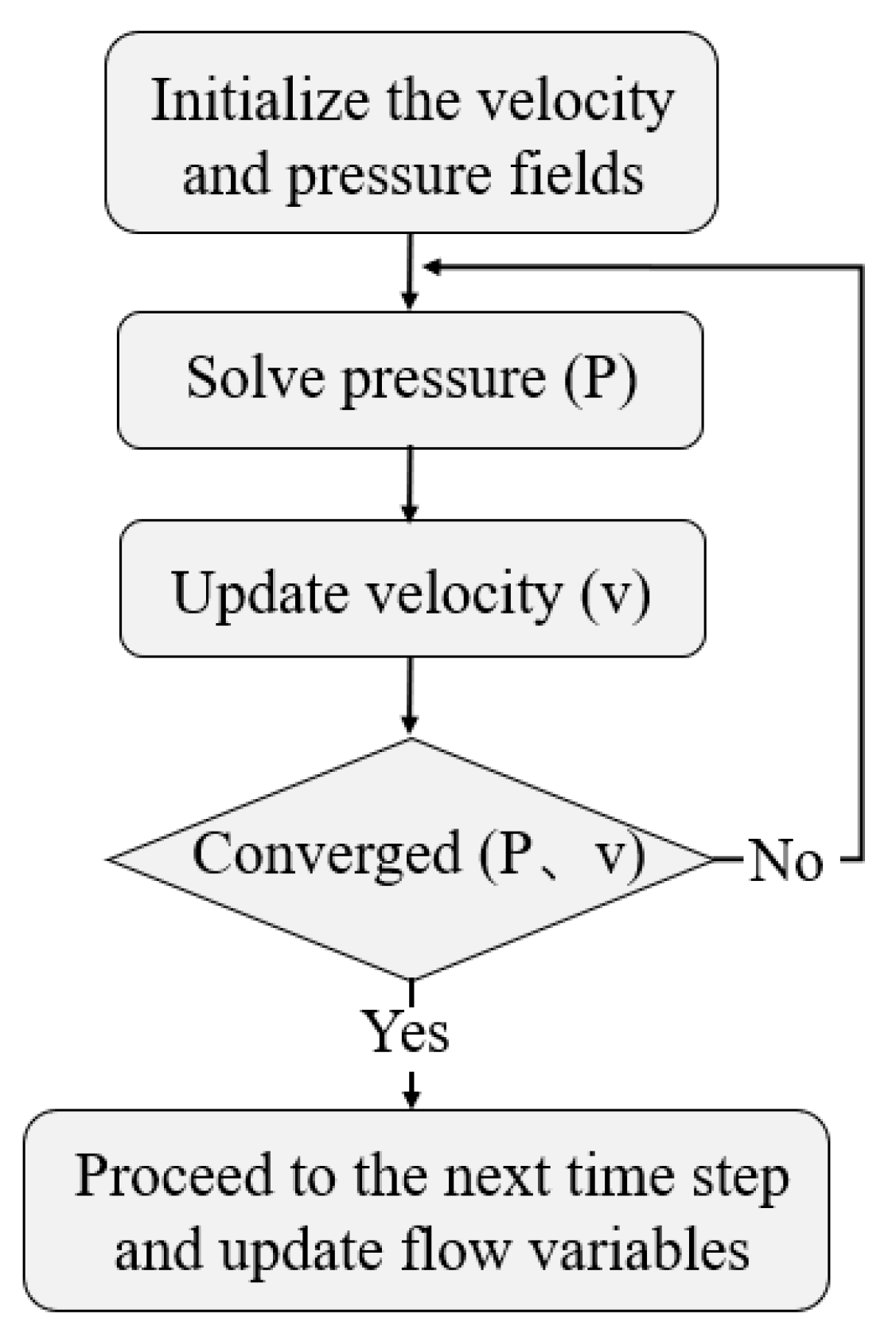
- Pressure–velocity coupling in τ-space. The one-dimensional flow equation and the velocity equation (i.e., Equations (18) and (21)) are solved on the discrete grids constructed in step 4 to simulate high-velocity non-Darcy gas flow. At each time step, the simulation starts with the initial velocity. For the first time step, the initial gas velocity is assumed to be 0. For all subsequent time steps, the initial gas velocity is set equal to the gas velocity from the previous time step. With the initial velocity given, Equation (18) is first solved to calculate the pseudo-pressure. The result is then used in Equation (21) to update the velocity. The updated velocity is then used in Equation (18) again to recalculate the pseudo-pressure. The iteration proceeds until the differences in pressure and velocity between two iterations are below a given threshold. Once this condition is met, the simulation moves on to the next time step. To ensure rapid and stable convergence of this nonlinear coupling, the Newton–Raphson iteration method is employed. The iteration continues until the relative change in the velocity field is satisfactory.Sensitivity tests show that tightening the tolerance to 10−5 changes the production rate by less than 0.3% but increases computation time significantly; therefore, 10−4 is adopted as an optimal balance between accuracy and efficiency. This iterative procedure updates the velocity and pressure fields until convergence is achieved, ensuring the numerical stability of the nonlinear coupling in Equation (18). The detailed computational workflow of this pressure–velocity coupling algorithm is illustrated in Figure 2.
- 6.
- Gas production calculation. The one-dimensional flow equations are solved along the τ grids to calculate the gas production rates.
3. Validation
4. Results and Discussion
4.1. Effects of Flow and Reservoir Parameters on Non-Darcy Gas Transport
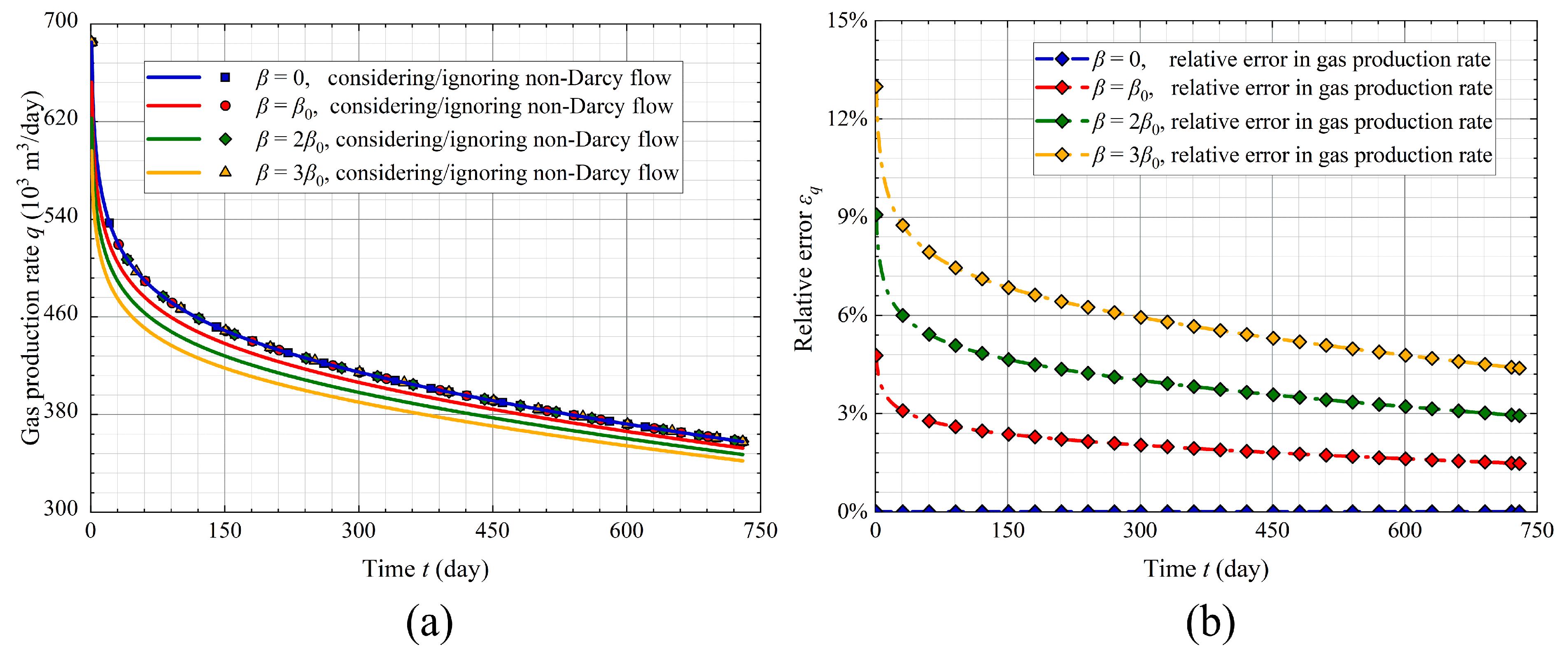
4.1.1. Forchheimer Coefficient
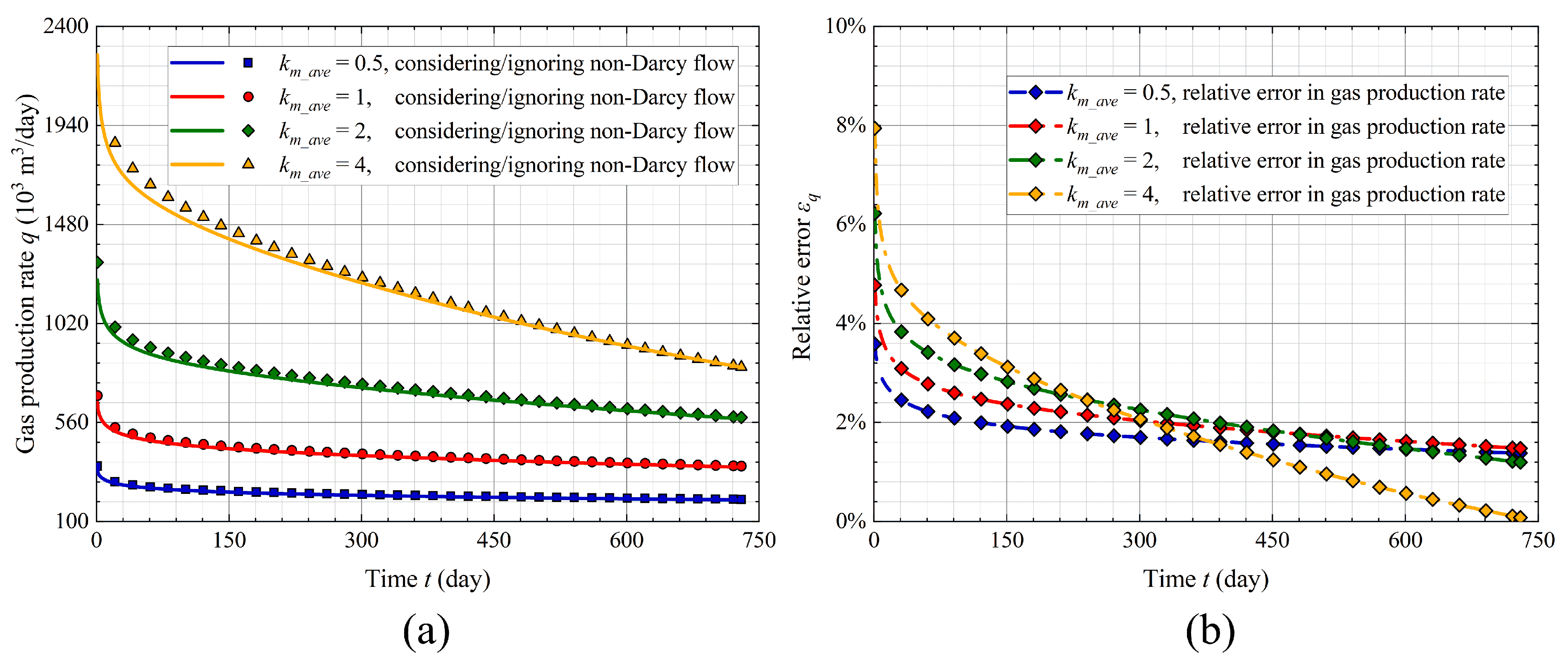
4.1.2. Average Matrix Permeability
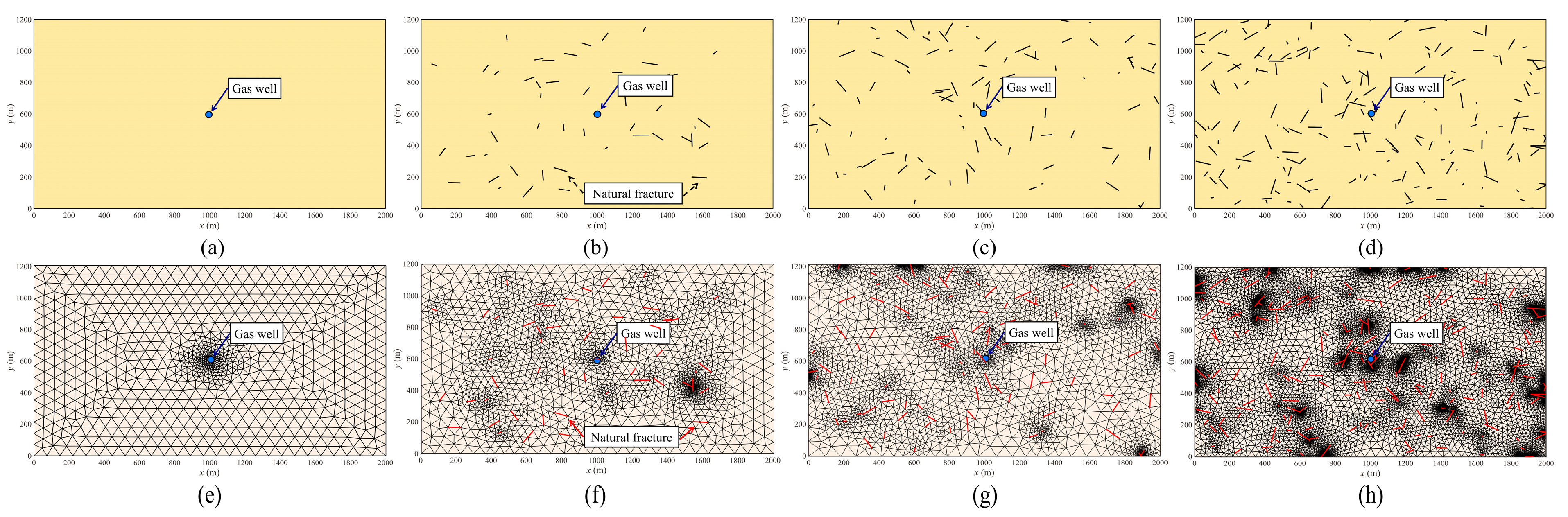
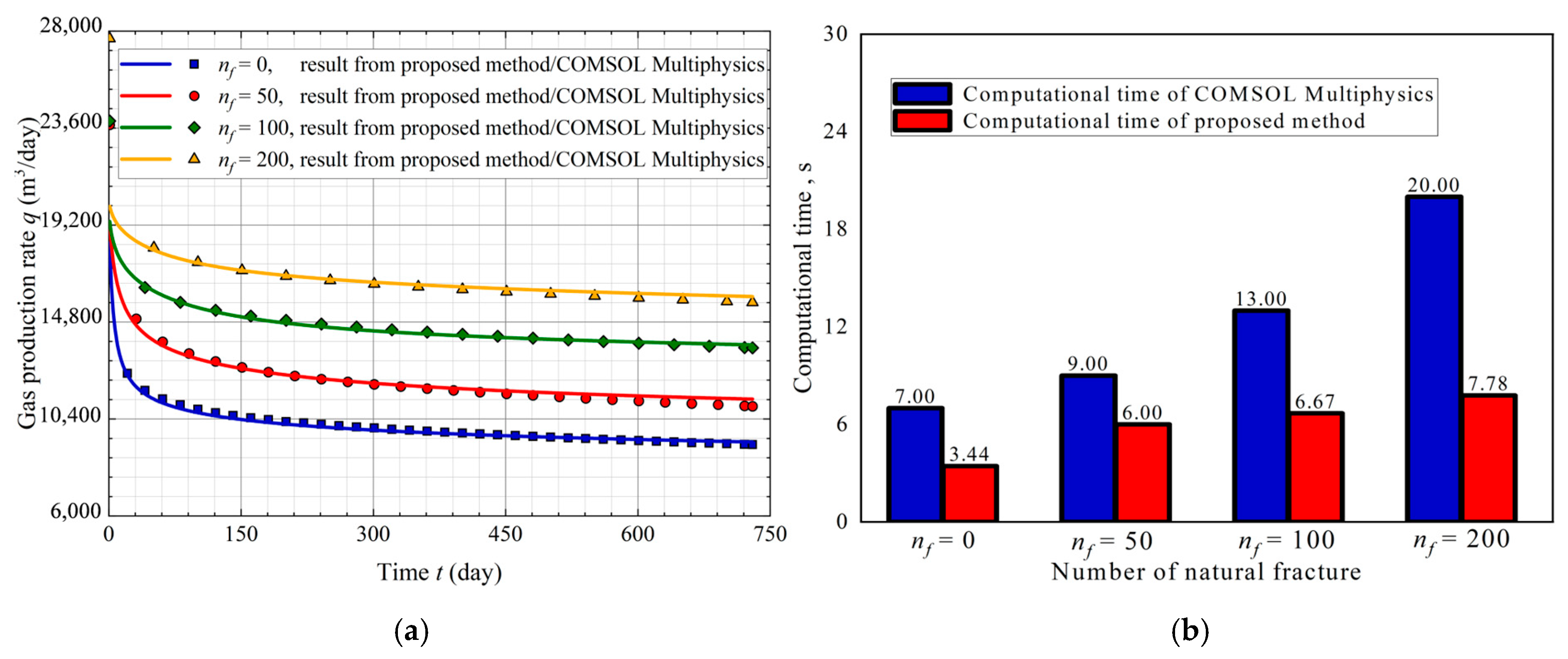
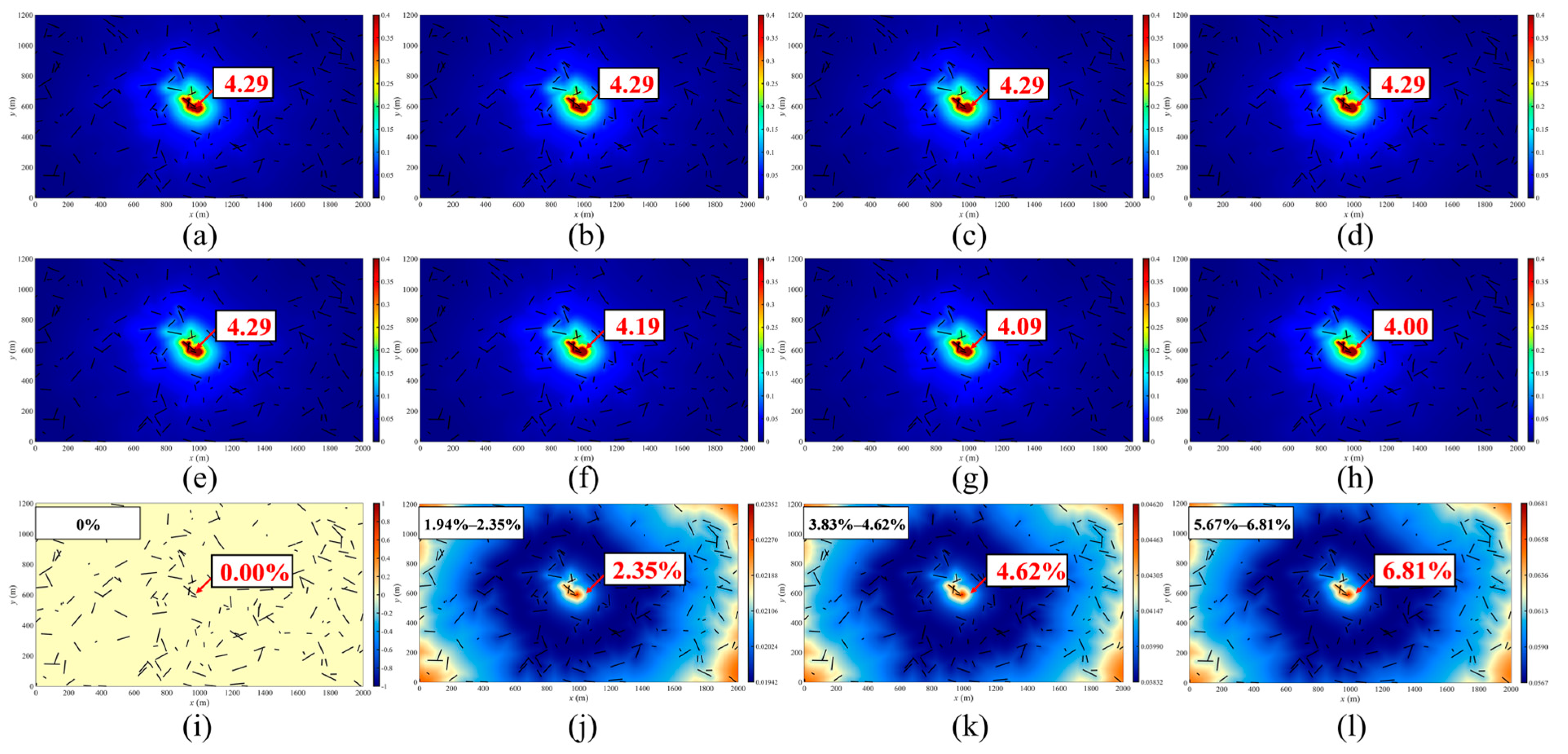
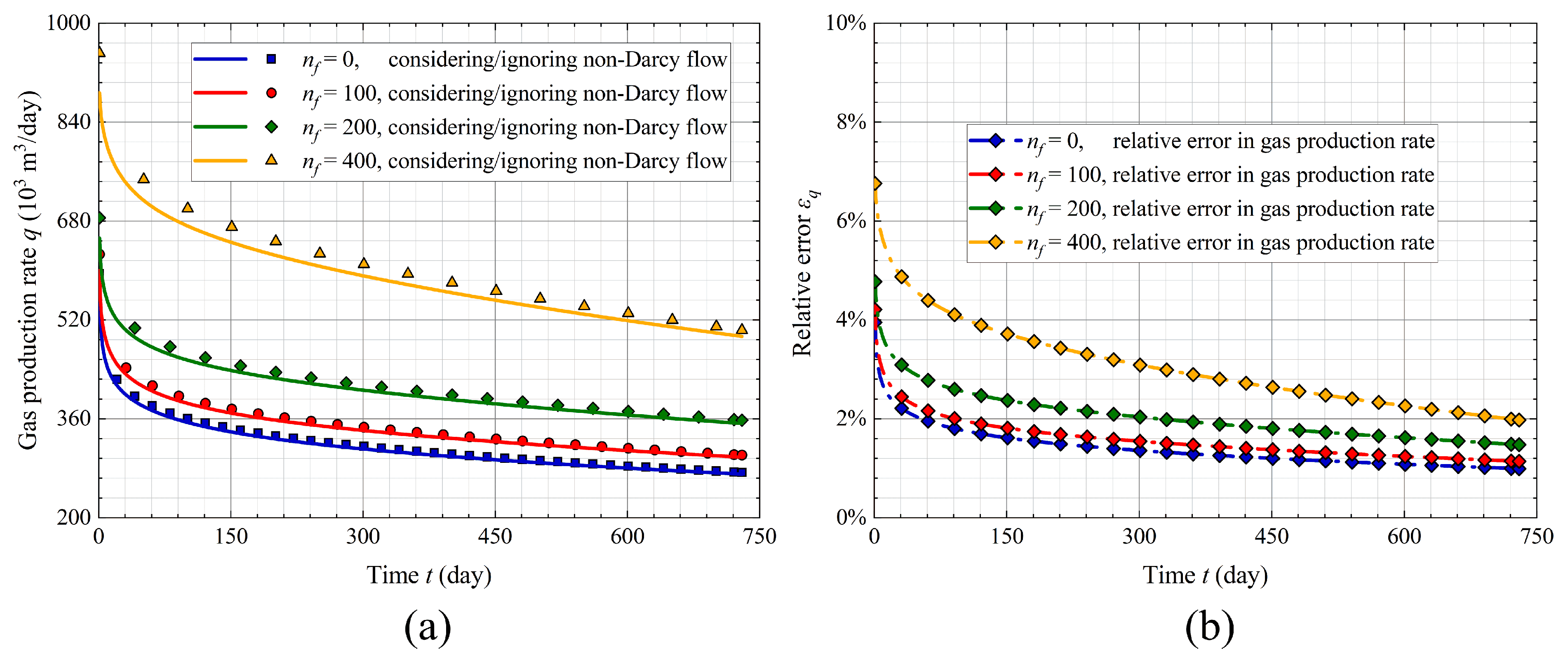
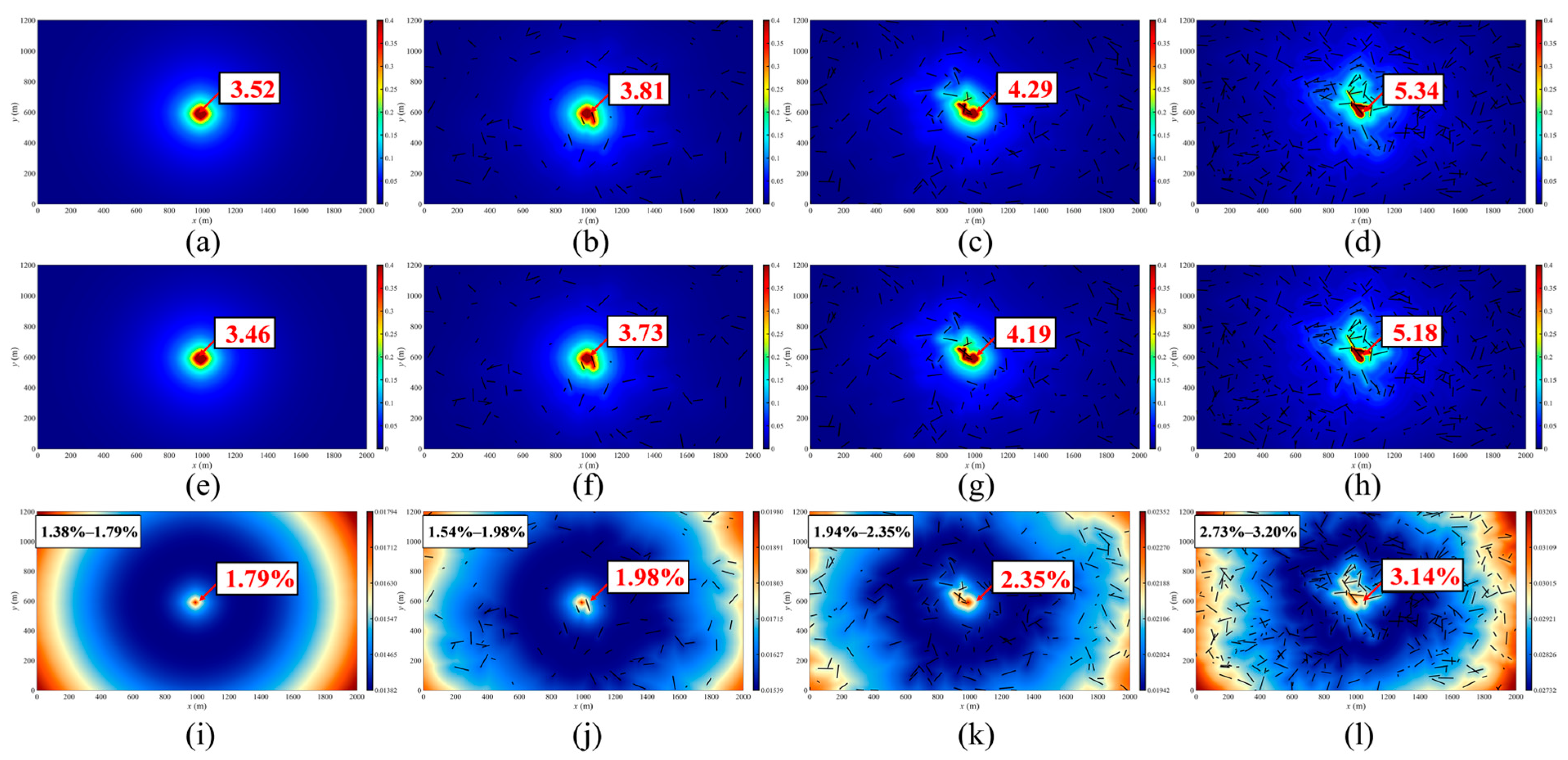
4.1.3. Number of Natural Fractures
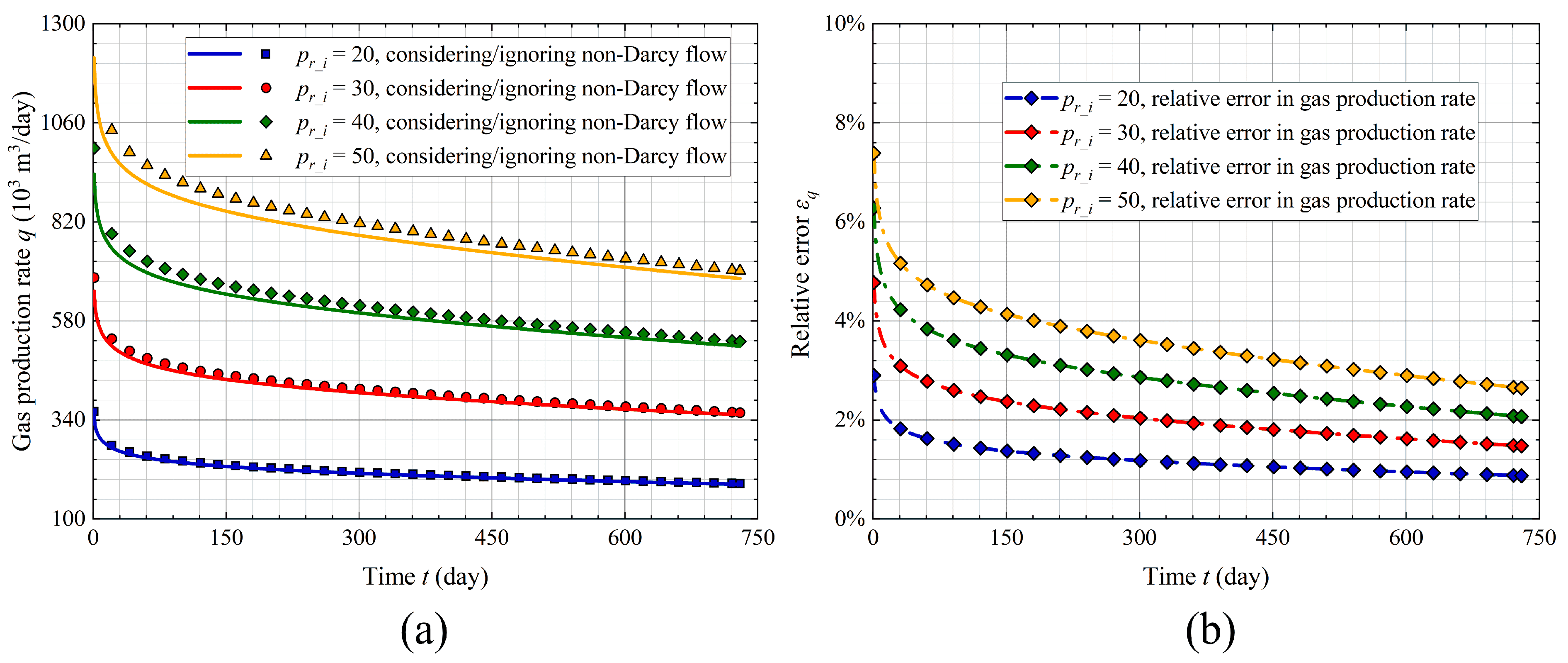
4.1.4. Initial Reservoir Pressure
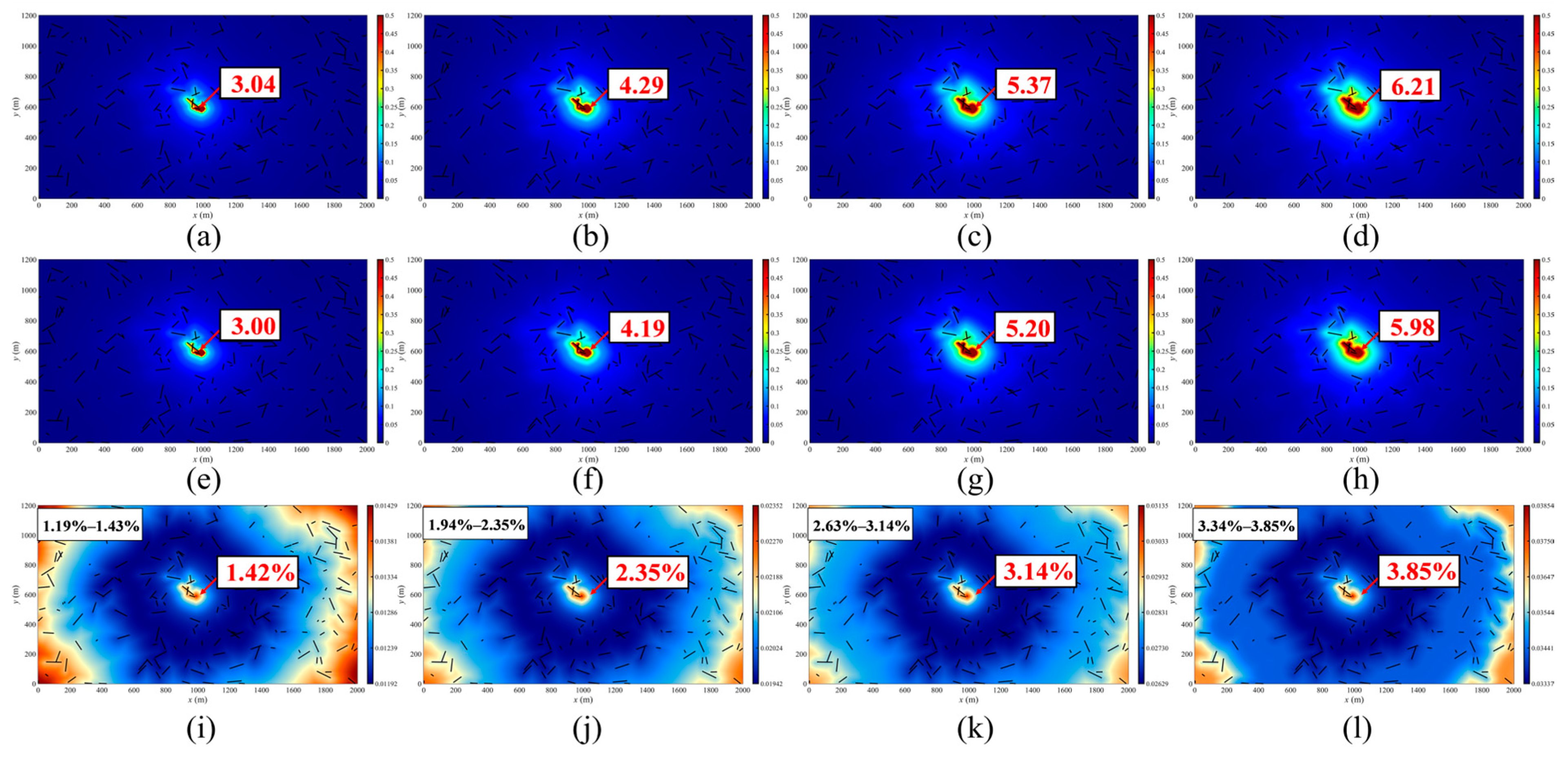
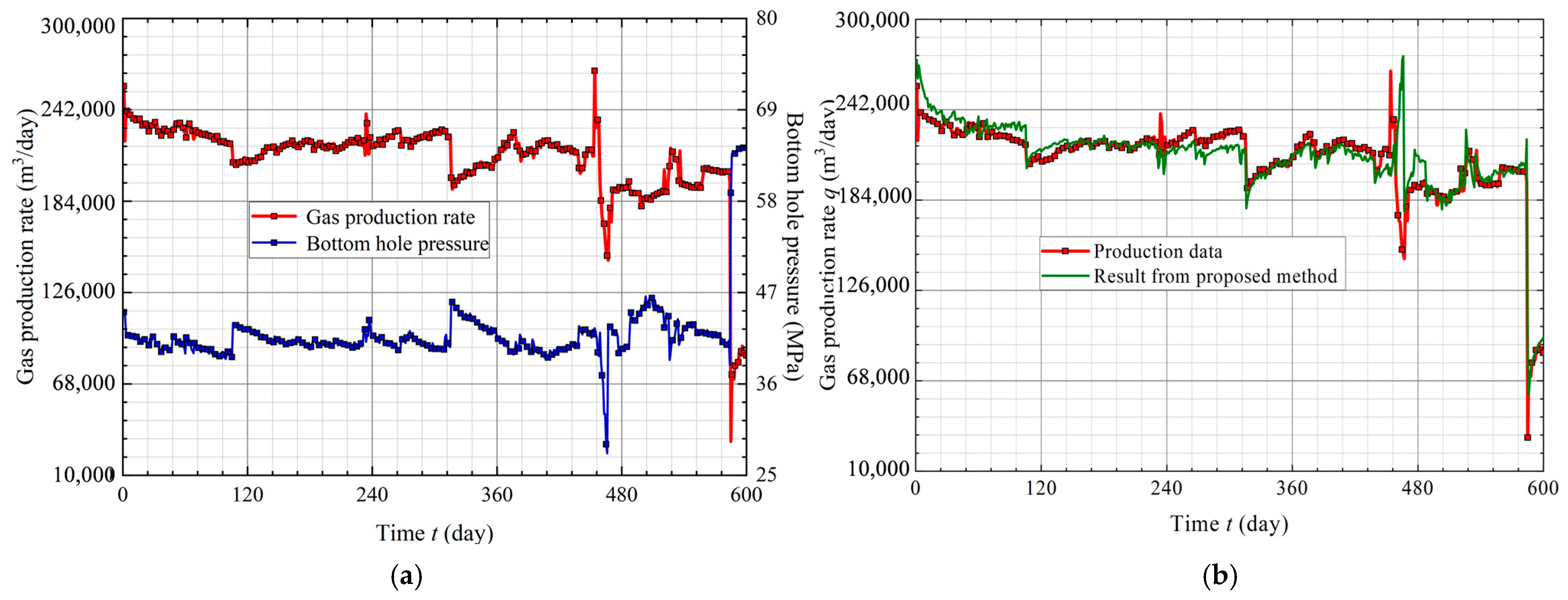
4.2. Field Case Demonstration
5. Recommendations and Conclusions
- 1.
- In this work, the gas continuity equation is transformed into a linear form using the definition of normalized pseudo-pressure and pseudo-time, effectively accounting for the pressure dependence of gas properties. Based on this transformed equation, the Eikonal equation is derived to determine the spatial distribution of the diffusive time of flight (DTOF), which characterizes the propagation of pseudo-pressure disturbances through the reservoir.
- 2.
- By using DTOF as a spatial coordinate, the proposed method allows the pseudo-pressure and velocity to be solved in a one-dimensional domain instead of the original three-dimensional Cartesian space. This approach simplifies the numerical procedure and enables fast simulation of high-velocity non-Darcy gas flow in complex heterogeneous and fractured reservoirs.
- 3.
- The proposed method can accurately capture gas production performance while significantly reducing computational time compared to the conventional numerical approaches, and this computational advantage becomes increasingly evident in more complex fracture scenarios.
- 4.
- In high-velocity gas reservoirs, the flow resistance caused by the effect of non-Darcy flow becomes significant, which leads to a noticeable reduction in gas velocity and production rate. Ignoring this effect can result in significant overestimation of gas recovery. Therefore, it is necessary to incorporate non-Darcy flow in gas production simulations to ensure reliable results.
- 5.
- The effect of non-Darcy flow on gas production and velocity becomes more significant with increasing Forchheimer coefficient, number of natural fractures, and initial reservoir pressure, as these factors lead to higher flow velocities. In comparison, under high matrix permeability, the effect of non-Darcy flow is significant at the early production stage but decreases quickly due to rapid pressure decline.
- 6.
- As reflected in the non-Darcy correction term βρ||, the effect of non-Darcy flow depends not only on gas velocity but also on gas density (highly sensitive to pressure). Therefore, both velocity and pressure should be considered when evaluating the effect of non-Darcy flow in gas reservoir simulations.
- 7.
- The proposed method effectively captures the nonlinear behavior of high-velocity non-Darcy gas flow, though several simplifications remain, including the Darcy-based τ-field, single-phase flow, and 2D configuration. While current validation focuses on production rates and computational efficiency, future work will incorporate detailed analysis of local non-Darcy characteristics—particularly the nonlinear velocity–pressure relationship—to further verify the physical accuracy of the model. These aspects will be systematically addressed in future multiphase and 3D model extensions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | flow area enclosed by the iso-τ contour at a given τ, m2 |
| divergence of a vector field in the (τ, φ, λ) coordinate | |
| c | compressibility, MPa−1 |
| h | the local distances corresponding to unit changes in each direction of the (τ, φ, λ) coordinate |
| J | local volume scaling factor in the (τ, φ, λ) coordinate |
| k | permeability, mD |
| M | gas molar mass, g/mol |
| p | pressure, MPa |
| q | gas production rate, m3/day |
| R | universal gas constant, J/(mol·K) |
| position vector in the original Cartesian coordinate | |
| T | reservoir temperature, K |
| t | time, day |
| gas flow velocity, m/day | |
| VP | cumulative pore volume, m3 |
| Z | compressibility factor |
| τ | diffusive time of flight required for a pressure disturbance from a well to propagate to a specific location in the reservoir, day0.5 |
| β | Forchheimer coefficient, m−1 |
| ρ | gas density, kg/m3 |
| μ | gas viscosity, mPa·s |
| ϕ | porosity |
| α | diffusivity, m2/day |
| ω(τ) | derivative of the pore volume along the τ direction, m3/ day0.5 |
| ε | relative error |
| Subscripts | |
| Darcy | ignoring the non-Darcy flow |
| f | fracture |
| g | gas |
| i | initial state |
| m | matrix |
| Non-Darcy | considering the non-Darcy flow |
| n | normalized pseudo |
| q | gas production rate |
| r | reservoir |
| t | total |
| v | velocity |
Appendix A. Fast Marching Method for Solving the Eikonal Equation
- (1)
- Determine the initial grids (cells) and assign them a τ value, then label the initial grids (cells) as the frozen grids (cells). (Generally, the τ of the initial grids is set to 0).
- (2)
- Find the grids adjacent to the frozen grids (cells) and label the adjacent grids (cells) as the pre-frozen grids (cells).
- (3)
- Calculate the τ value of all pre-frozen matrix and fracture grids using Equations (A6)–(A8) and Equations (A9)–(A12), respectively. Then compare the τ values of all pre-frozen grids (cells) and label the grid (cell) with the smallest τ value as the frozen grid (cell).
- (4)
- Repeat steps 2 to 3 until all grids (cells) are labeled as frozen grids (cells).
References
- Holditch, S.A.; Morse, R.A. The effects of non-Darcy flow on the behavior of hydraulically fractured gas wells (includes associated paper 6417). J. Pet. Technol. 1976, 28, 1169–1179. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, Y.S.; Fakcharoenphol, P. Non-Darcy displacement in linear composite and radial aquifer during CO2 sequestration. Int. J. Oil Gas Coal Technol. 2014, 7, 244–262. [Google Scholar] [CrossRef]
- Liu, X.; Geng, S.; Sun, J.; Li, Y.; Guo, Q.; Zhan, Q. Novel coupled hydromechanical model considering multiple flow mechanisms for simulating underground hydrogen storage in depleted low-permeability gas reservoir. Int. J. Hydrogen Energy 2024, 85, 526–538. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, L.; Cao, Z.; Liu, J.; Xue, E.; Wang, P.; Cao, X.; Liu, Y. Thermo-mechanical degradation and fracture evolution in low-permeability coal subjected to cyclic heating–cryogenic cooling. Phys. Fluids 2025, 37, 086617. [Google Scholar] [CrossRef]
- Cao, Z.; Xiong, Y.; Xiong, Y. Diffusion Evolution Rules of Grouting Slurry in Mining-induced Cracks in Overlying Strata. Rock Mech. Rock Eng. 2025, 58, 6493–6512. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, D.T. Effects of non-Darcy flow and penetrating ratio on performance of horizontal wells with multiple fractures. In Proceedings of the SPE Unconventional Resources Conference Canada, Calgary, AB, Canada, 5–7 November 2013. [Google Scholar]
- Zhang, W.; Dai, B.; Liu, Z.; Zhou, C. A pore-scale numerical model for non-Darcy fluid flow through rough-walled fractures. Comput. Geotech. 2017, 87, 139–148. [Google Scholar] [CrossRef]
- Forchheimer, P. Wasserbewegung durch Boden. Z. Ver. Dtsch. Ing. 1901, 45, 1782–1788. [Google Scholar]
- Friedel, T.; Voigt, H.D. Investigation of non-Darcy flow in tight-gas reservoirs with fractured wells. J. Pet. Sci. Eng. 2006, 54, 112–128. [Google Scholar] [CrossRef]
- Mustapha, H.; de Langavant, L.; Giddins, M.A. Darcy and non-Darcy flows in fractured gas reservoirs. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, United Arab Emirates, 14–16 September 2015. [Google Scholar]
- Fan, M.; McClure, J.; Han, Y.; Ripepi, N.; Westman, E.; Gu, M.; Chen, C. Using an experiment/simulation-integrated approach to investigate fracture-conductivity evolution and non-Darcy flow in a proppant-supported hydraulic fracture. SPE J. 2019, 24, 1912–1928. [Google Scholar] [CrossRef]
- Berawala, D.S.; Andersen, P.Ø. Numerical investigation of Non-Darcy flow regime transitions in shale gas production. J. Pet. Sci. Eng. 2020, 190, 107114. [Google Scholar] [CrossRef]
- Jaber, A.K.; Al-Jawad, S.N.; Alhuraishawy, A.K. A review of proxy modeling applications in numerical reservoir simulation. Arabian J. Geosci. 2019, 12, 701. [Google Scholar] [CrossRef]
- Rios, V.S.; Avansi, G.D.; Schiozer, D.J. Practical workflow to improve numerical performance in time-consuming reservoir simulation models using submodels and shorter period of time. J. Pet. Sci. Eng. 2020, 195, 107547. [Google Scholar] [CrossRef]
- Wang, J.G.; Kabir, A.; Liu, J.; Chen, Z. Effects of non-Darcy flow on the performance of coal seam gas wells. Int. J. Coal Geol. 2012, 93, 62–74. [Google Scholar] [CrossRef]
- Kulkarni, K.N.; Datta-Gupta, A.; Vasco, D.W. A streamline approach for integrating transient pressure data into high-resolution reservoir models. SPE J. 2001, 6, 273–282. [Google Scholar] [CrossRef]
- Zhang, Y.; Bansal, N.; Fujita, Y.; Datta-Gupta, A.; King, M.J.; Sankaran, S. From streamlines to Fast Marching: Rapid simulation and performance assessment of shale-gas reservoirs by use of diffusive time of flight as a spatial coordinate. SPE J. 2016, 21, 1883–1898. [Google Scholar] [CrossRef]
- Fujita, Y.; Datta-Gupta, A.; King, M.J. A comprehensive reservoir simulator for unconventional reservoirs that is based on the fast marching method and diffusive time of flight. SPE J. 2016, 21, 2276–2288. [Google Scholar] [CrossRef]
- Teng, B. Simulation model size reduction using volume of investigation by fast marching method. J. Pet. Sci. Eng. 2020, 191, 107183. [Google Scholar] [CrossRef]
- Chen, H.; Li, A.; Terada, K.; Datta-Gupta, A. Rapid simulation of unconventional reservoirs by multidomain multiresolution modeling based on the diffusive time of flight. SPE J. 2023, 28, 1083–1096. [Google Scholar] [CrossRef]
- Ghedan, S.G.; Aljawad, M.S.; Poettmann, F.H. Compressibility of natural gases. J. Pet. Sci. Eng. 1993, 10, 157–162. [Google Scholar] [CrossRef]
- Zimmerman, R.W. Compressibility of Sandstones; Elsevier: New York, NY, USA, 1991. [Google Scholar]
- Al-Hussainy, R.; Ramey, H.J., Jr.; Crawford, P.B. The flow of real gases through porous media. J. Pet. Technol. 1966, 18, 624–636. [Google Scholar] [CrossRef]
- Lee, W.J.; Rollins, J.B.; Spivey, J.P. Pressure-Transient Testing; SPE Textbook Series; Society of Petroleum Engineers: Richardson, TX, USA, 2003. [Google Scholar]
- Kim, J.U.; Datta-Gupta, A.; Brouwer, R.; Haynes, B. Calibration of high-resolution reservoir models using transient pressure data. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar]
- Xie, J.; Yang, C.; Gupta, N.; King, M.J.; Datta-Gupta, A. Depth of investigation and depletion in unconventional reservoirs with fast-marching methods. SPE J. 2015, 20, 831–841. [Google Scholar] [CrossRef]
- Li, Q.; Teng, B. Rapid Numerical Simulation of Heat Transfer in Fractured Geothermal Reservoirs Based on Dynamic Thermal Influence Volume. SPE J. 2025, 30, 3029–3047. [Google Scholar] [CrossRef]
- Sethian, J.A. Fast Marching Methods. SIAM Rev. 1999, 41, 199–235. [Google Scholar] [CrossRef]
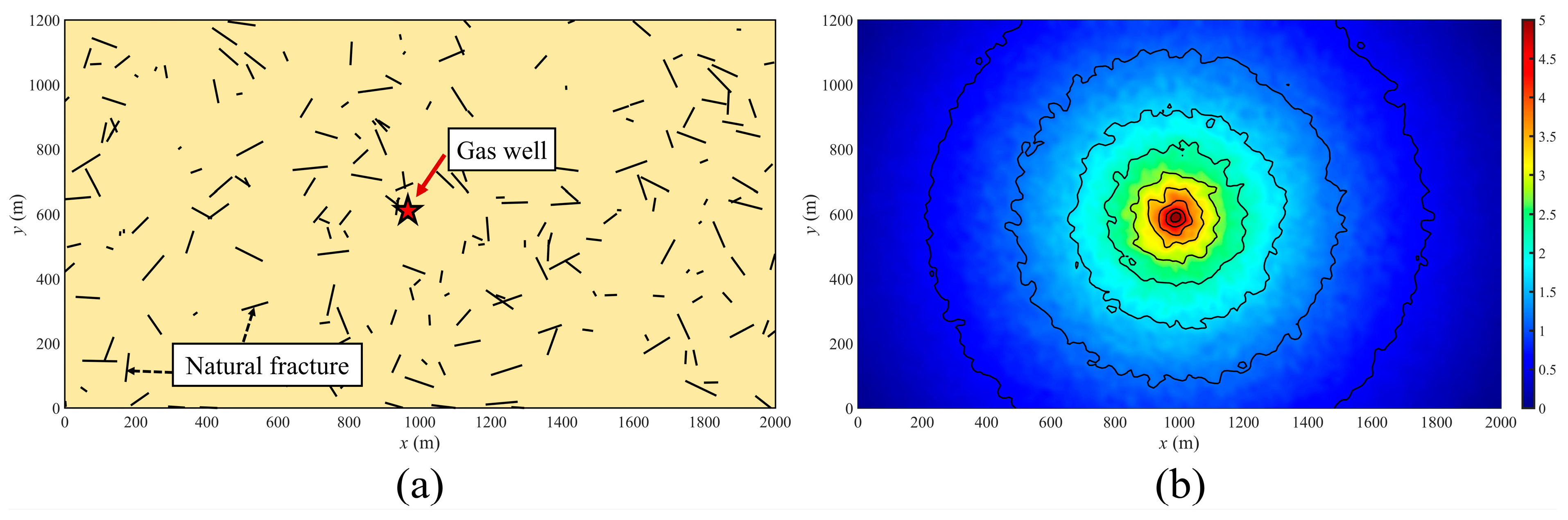

| Property | Values | Property | Values |
|---|---|---|---|
| Initial reservoir pressure pini (MPa) | 30 | Reservoir temperature T (°C) | 65 |
| Bottom-hole pressure Pbh (MPa) | 5 | Compressibility of matrix cm (MPa−1) | 1.2 × 10−3 |
| Gas molar mass Mmg (g/mol) | 16.043 | Universal gas constant R (J/mol·K) | 8.314 |
| Property | Values | Property | Values |
|---|---|---|---|
| Initial reservoir pressure pini (MPa) | 30 | Reservoir temperature T (°C) | 65 |
| Bottom-hole pressure Pbh (MPa) | 5 | Compressibility of the matrix cm (MPa−1) | 1.2 × 10−3 |
| Compressibility of natural fracture cf (MPa−1) | 1.2 × 10−3 | Natural fracture width wf (m) | 1 × 10−2 |
| Matrix porosity ϕm | 0.4 | Natural fracture ϕnf | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, J.; Li, Q.; Liu, J.; Zhou, W.; Teng, B. An Efficient Method for Simulating High-Velocity Non-Darcy Gas Flow in Fractured Reservoirs Based on Diffusive Time of Flight. Energies 2025, 18, 5891. https://doi.org/10.3390/en18225891
Bai J, Li Q, Liu J, Zhou W, Teng B. An Efficient Method for Simulating High-Velocity Non-Darcy Gas Flow in Fractured Reservoirs Based on Diffusive Time of Flight. Energies. 2025; 18(22):5891. https://doi.org/10.3390/en18225891
Chicago/Turabian StyleBai, Jingjin, Qingquan Li, Jiazheng Liu, Wenzhuo Zhou, and Bailu Teng. 2025. "An Efficient Method for Simulating High-Velocity Non-Darcy Gas Flow in Fractured Reservoirs Based on Diffusive Time of Flight" Energies 18, no. 22: 5891. https://doi.org/10.3390/en18225891
APA StyleBai, J., Li, Q., Liu, J., Zhou, W., & Teng, B. (2025). An Efficient Method for Simulating High-Velocity Non-Darcy Gas Flow in Fractured Reservoirs Based on Diffusive Time of Flight. Energies, 18(22), 5891. https://doi.org/10.3390/en18225891






