Investigation of Gas Evolution on Nickel Wire Electrodes During Alkaline Water Electrolysis
Abstract
1. Introduction
2. Materials and Methods
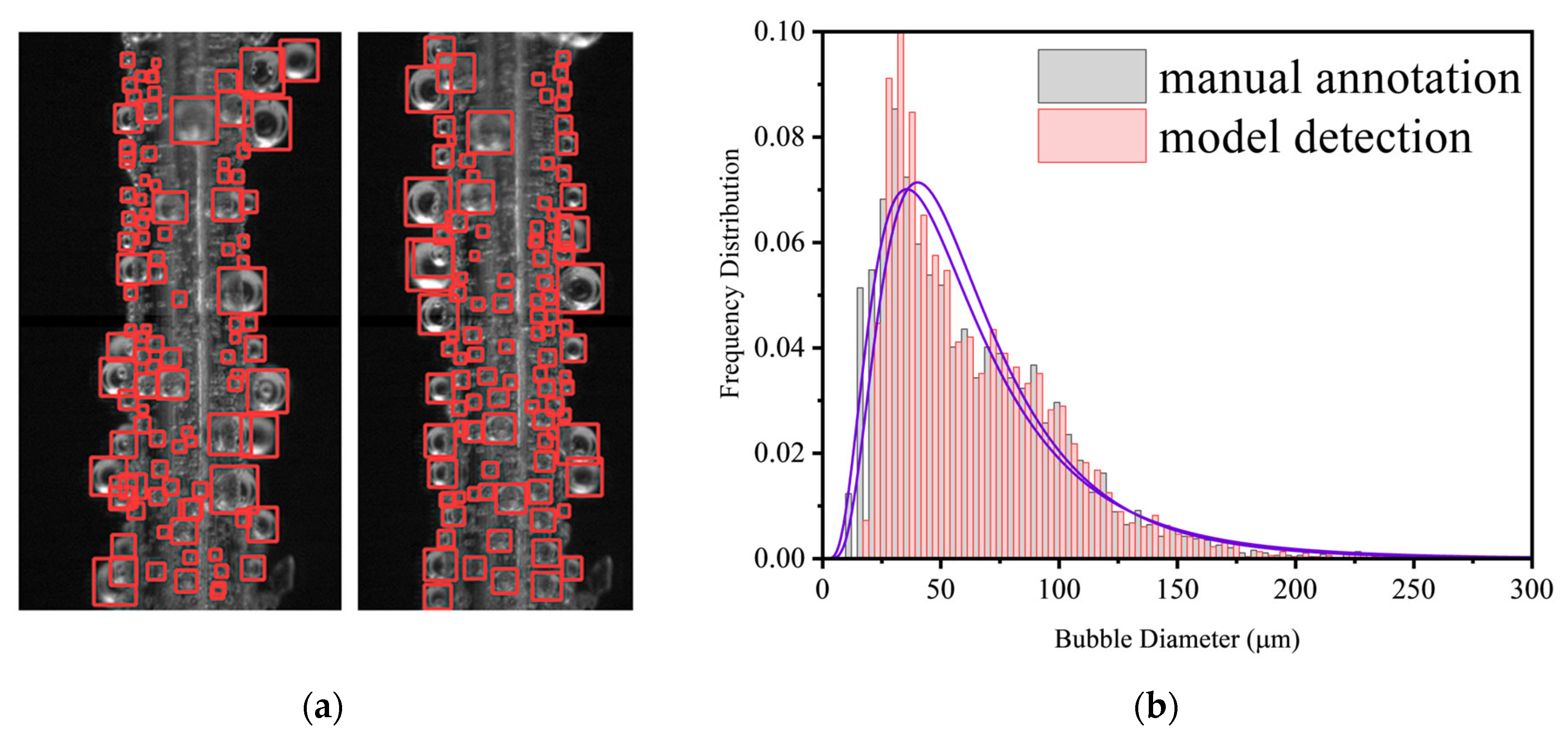
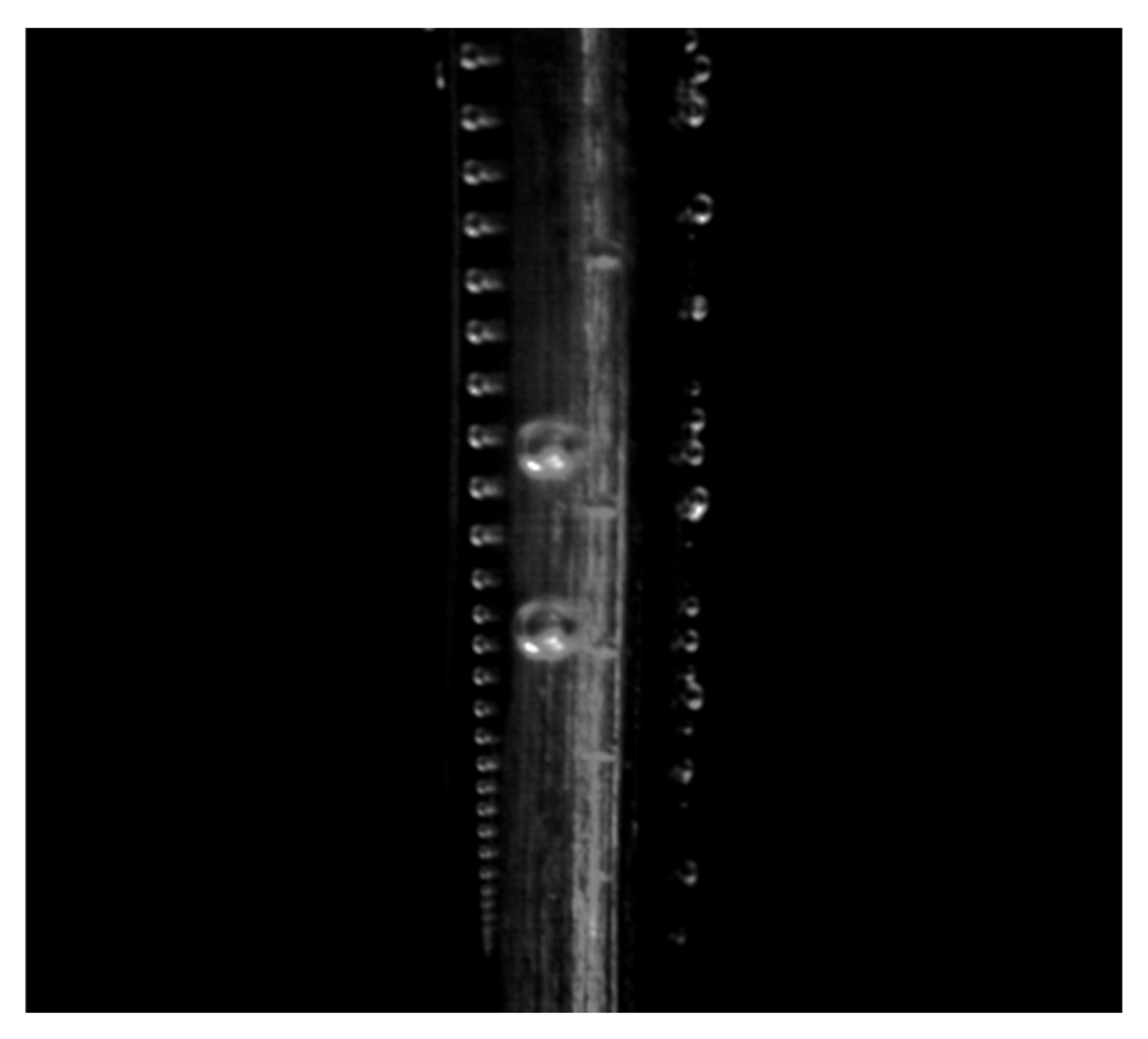
2.1. Visual Observation
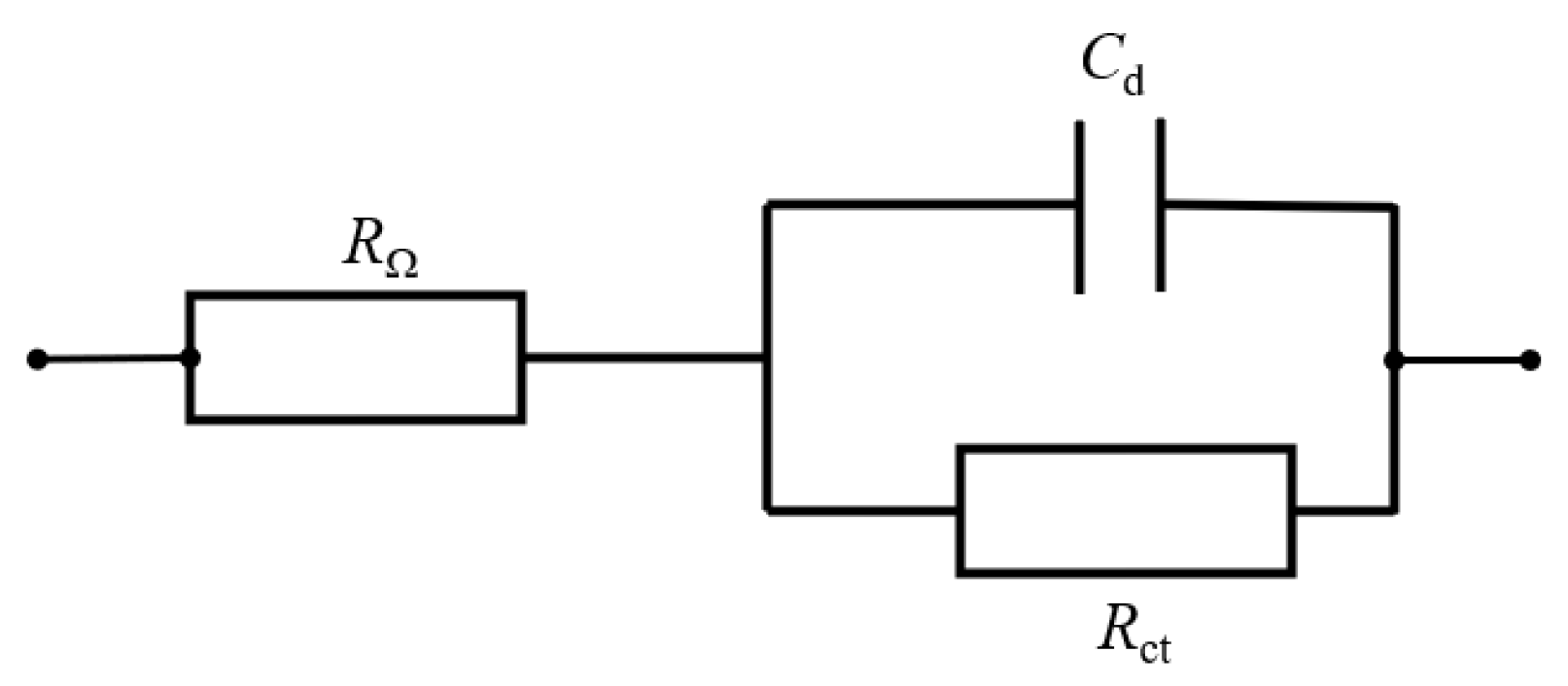
2.2. Electrochemical Characterization
3. Results
3.1. Oxygen Evolution Behavior on Vertical Nickel Wire Electrodes
3.1.1. Growth and Detachment Modes
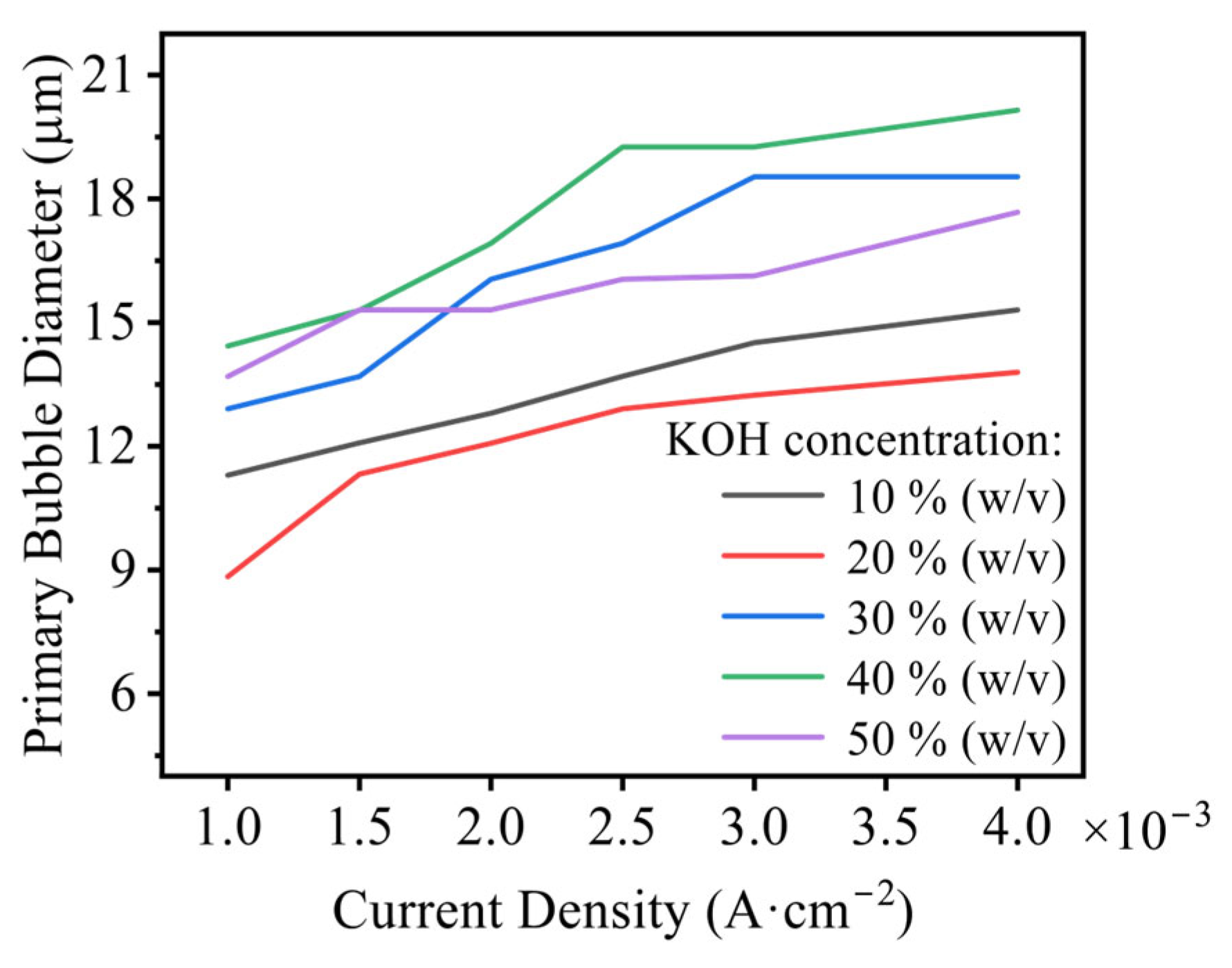
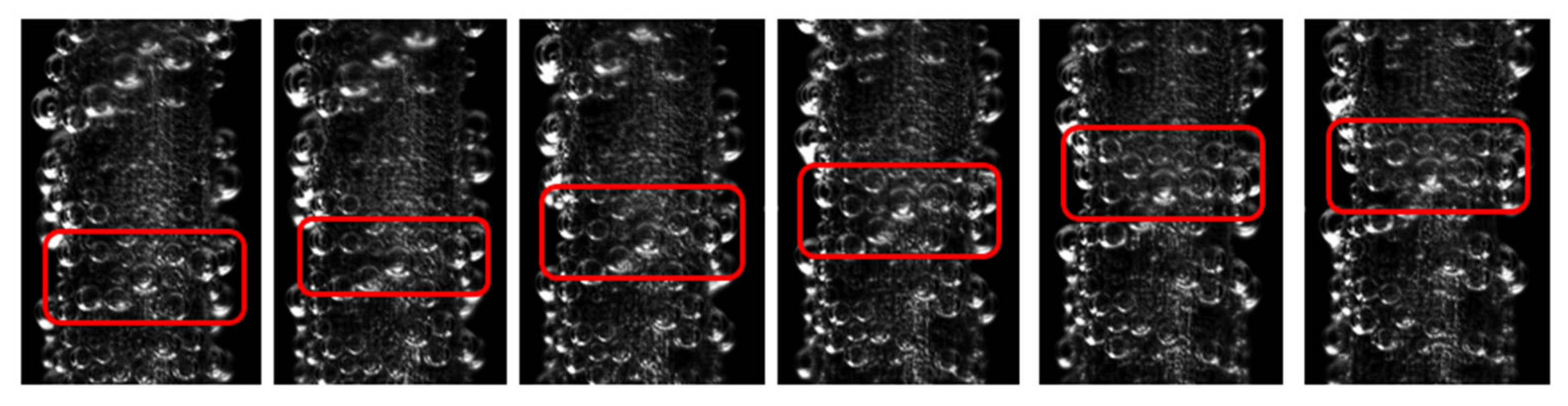
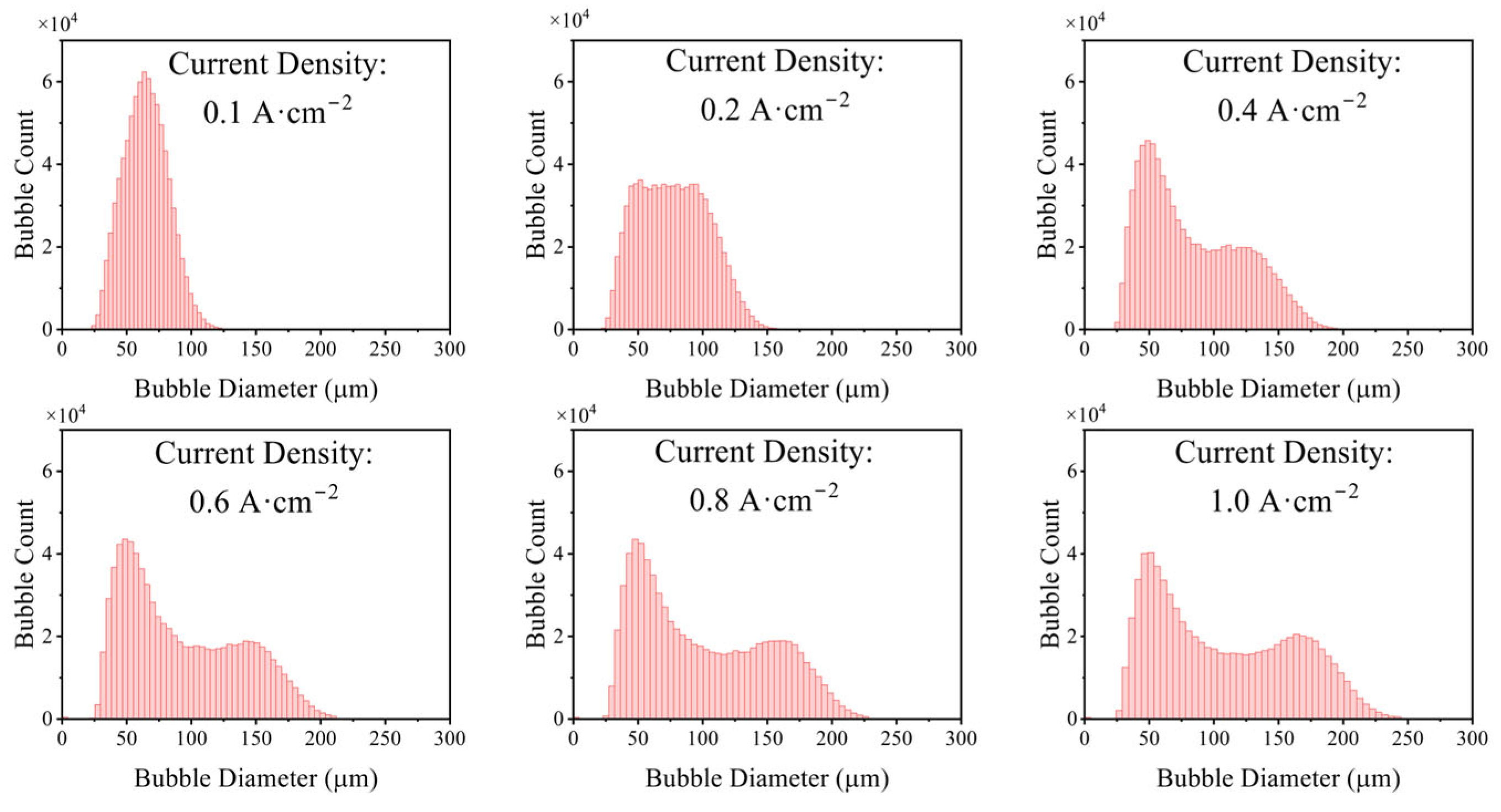
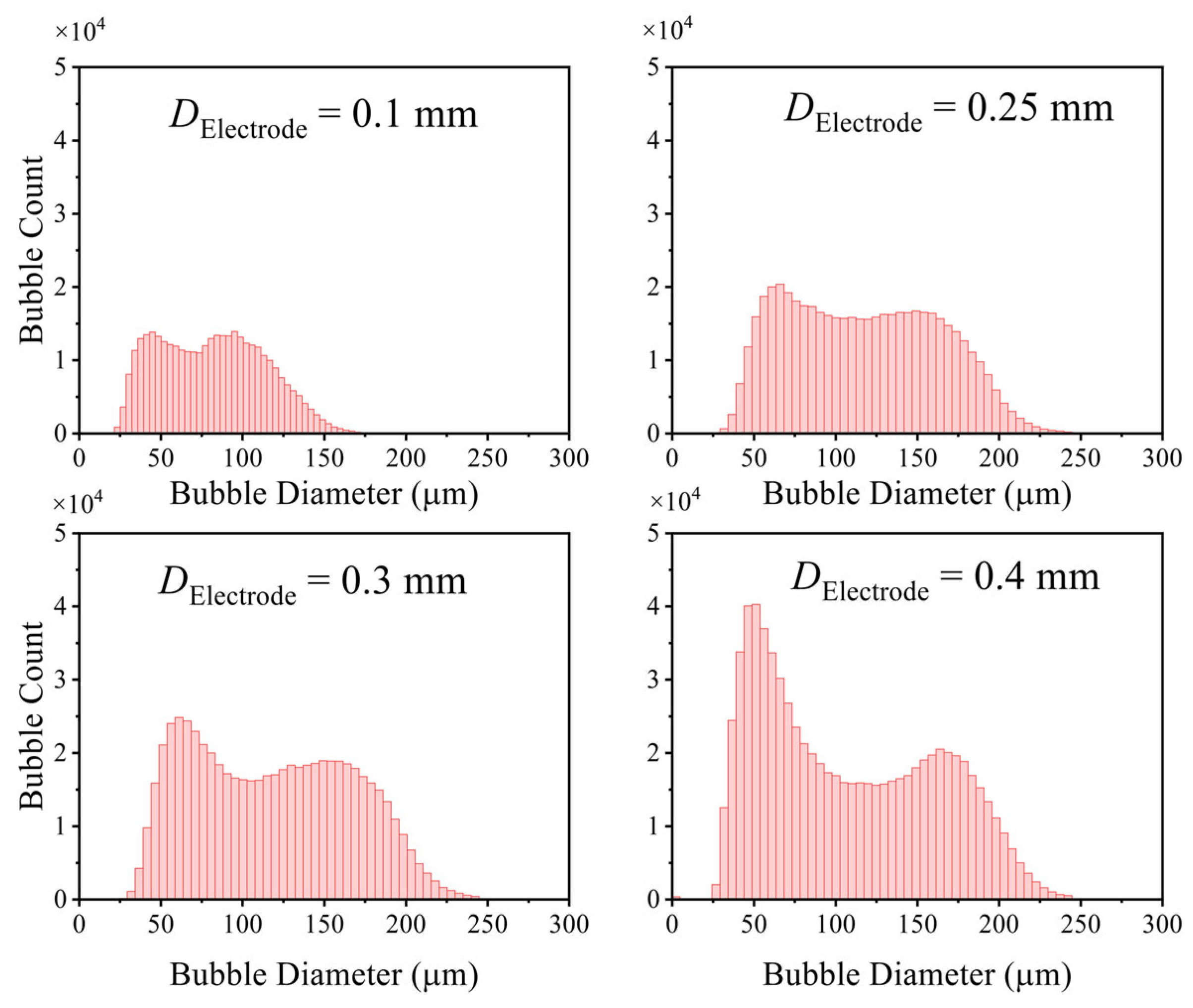
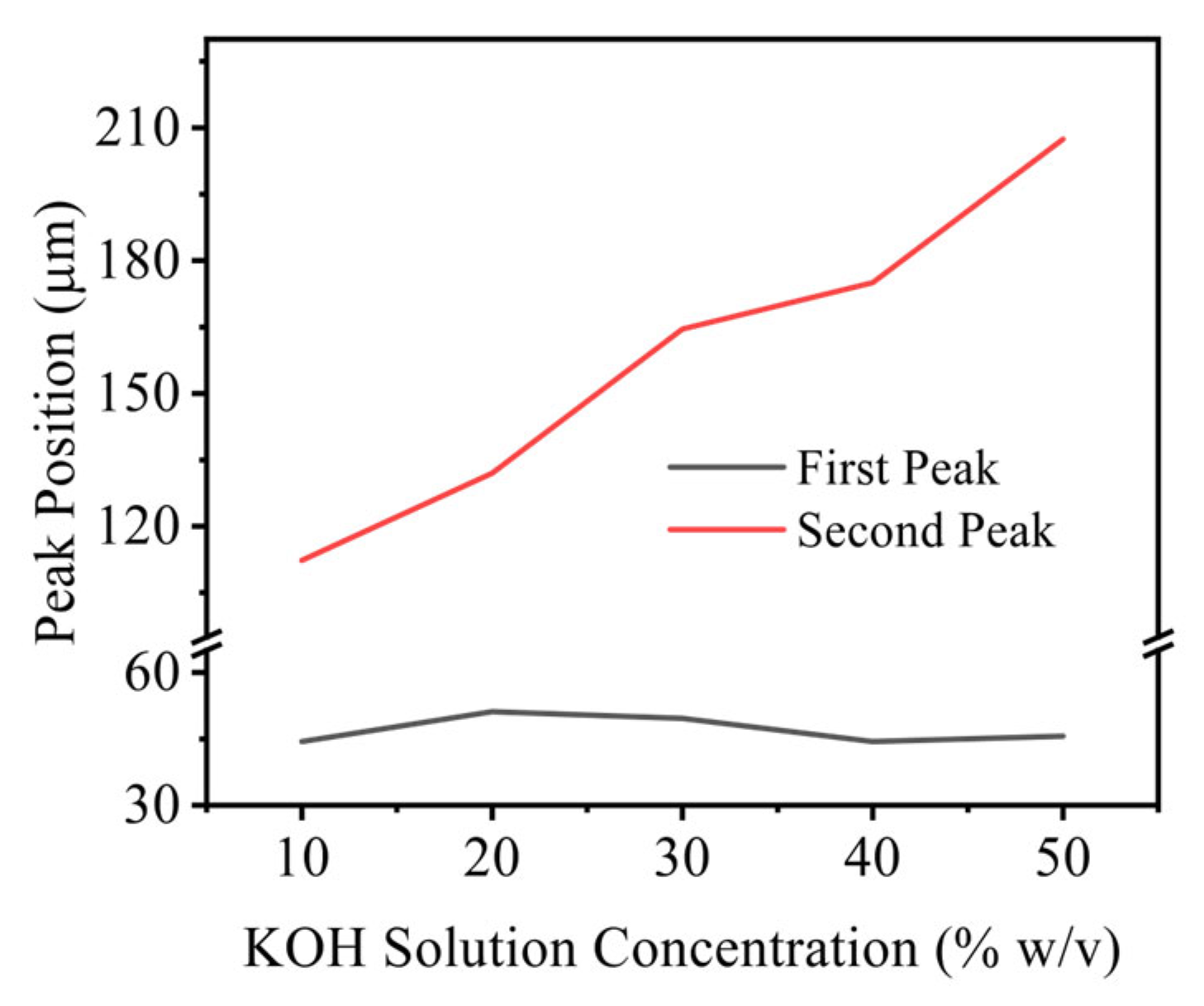
3.1.2. Influence of Electrolytic Parameters
3.2. Influence of Gas Evolution on Electrolytic Performance
3.2.1. OER Performance Under Varying Operating Conditions
3.2.2. Correlation Between Gas Evolution and OER Performance
4. Conclusions
- Bubble evolution modes were classified. Under very low current density (0.001 A·cm−2), isolated bubbles complete growth and detachment independently, and detachment diameter increases with current density. At higher current densities, surface coverage by bubbles increases and bubbles manifest as an attached bubble layer plus free bubble groups: bubbles in the layer grow via diffusion and coalescence, whereas free bubbles grow predominantly via coalescence.
- Effects of current density, electrode diameter, and KOH concentration were revealed. Increasing current density thickens the bubble layer and transforms the bubble size distribution from unimodal to bimodal, with the two peaks attributable to the attached layer and the free bubble population, respectively. Increasing wire diameter raises both the number and size of bubbles in the attached layer and increases the number and size of free bubbles, due to larger active areas (more nucleation sites) and reduced curvature (stronger adhesion and more available growth space), which delays detachment. With increasing KOH concentration, the mean bubble diameter within the attached layer remains essentially constant because nucleation sites are saturated; the number of small/medium bubbles in the layer increases as higher viscosity weakens the sweeping action of bubble clusters. In contrast, the average size of free bubbles increases while their number decreases, as higher viscosity slows bubble rise, prolongs residence near the electrode, and promotes coalescence.
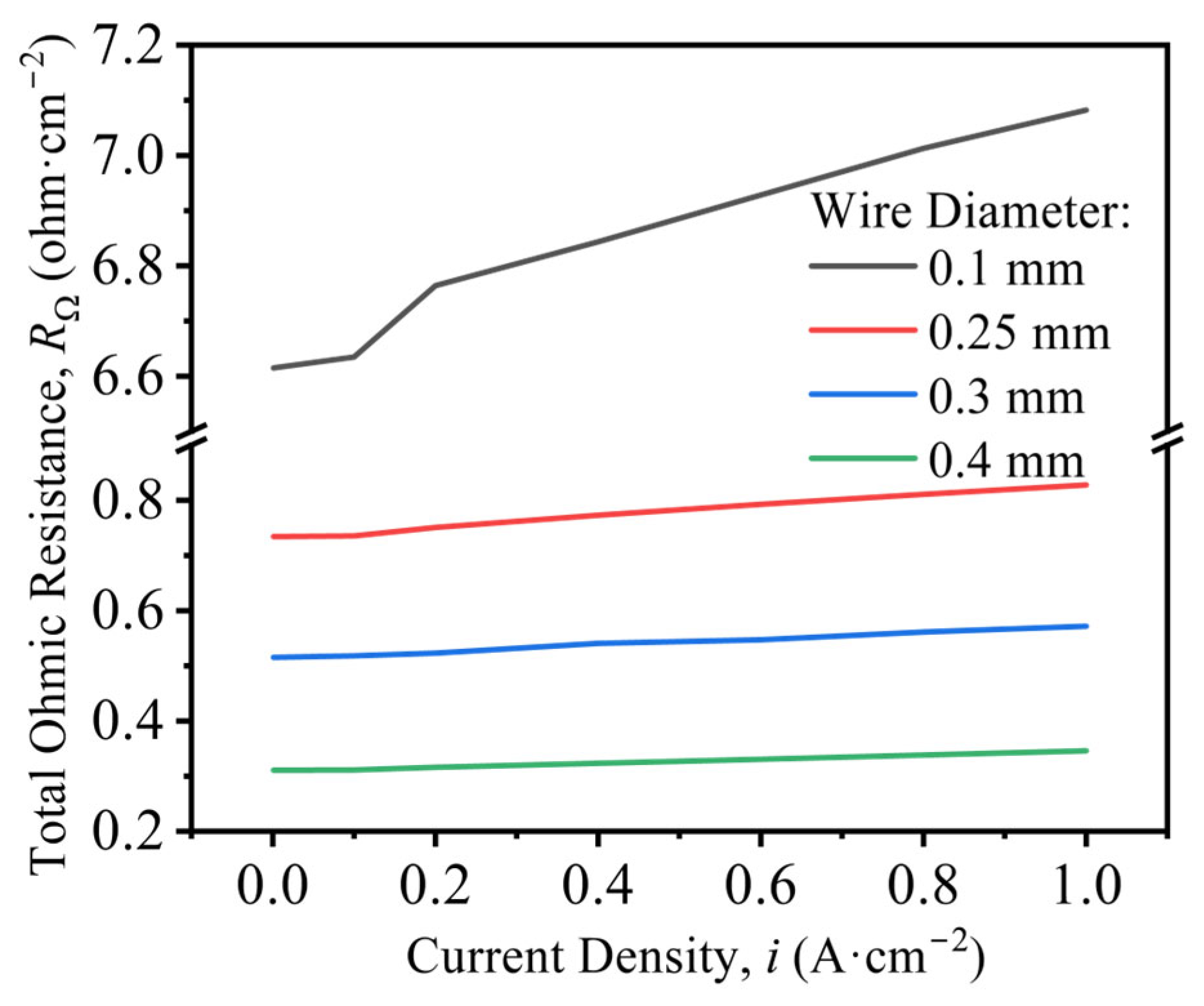
- Larger wire diameters improve OER performance, reflected by lower overpotentials and smaller Tafel slopes. The effect of KOH concentration is non-monotonic: performance is optimal at 30% (w/v) KOH, where both overpotential and Tafel slope reach minimum, consistent with industrial practice. The bubble-induced overpotential, ΔEbub, increases with current density. Electrodes of smaller diameter exhibit higher areal bubble coverage and inferior activation-controlled performance. Dispersed bubbles elevate the solution resistance; correlation analysis demonstrates a linear relationship between total bubble volume and bubble-induced ohmic resistance, Rbub.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yin, Y.; Pang, J.; Huang, D.; Wu, D.; Dou, Q. Current Situation and Development of Large-Scale Water Electrolysis Hydrogen Production Technology. Guangdong Chem. Ind. 2022, 49, 97–98+57. [Google Scholar] [CrossRef]
- Beijing Jinzhengzongheng Information Consulting Co., Ltd. China Hydrogen Energy Industry Development Blue Book (2023); Beijing Jinzhengzongheng Information Consulting Co., Ltd.: Beijing, China, 2023; pp. 1–82. Available online: https://max.book118.com/html/2025/0102/8103033120007014.shtm (accessed on 22 September 2025).
- Yu, H.; Shao, Z.; Hou, M.; Yi, B.; Duan, F.; Yang, Y. Research Progress and Development Suggestions on Water Electrolysis for Hydrogen Production. Strateg. Study CAE 2021, 23, 146–152. [Google Scholar] [CrossRef]
- Sebbahi, S.; Assila, A.; Belghiti, A.A.; Laasri, S.; Kaya, S.; Hlil, E.K.; Rachidi, S.; Hajjaji, A. A Comprehensive Review of Recent Advances in Alkaline Water Electrolysis for Hydrogen Production. Int. J. Hydrog. Energy 2024, 82, 583–599. [Google Scholar] [CrossRef]
- Chi, J.; Yu, H.M. Water Electrolysis Based on Renewable Energy for Hydrogen Production. Chin. J. Catal. 2018, 39, 390–391. [Google Scholar] [CrossRef]
- Grigoriev, S.A.; Fateev, V.N.; Bessarabov, D.G.; Millet, P. Current Status, Research Trends, and Challenges in Water Electrolysis Science and Technology. Int. J. Hydrog. Energy 2020, 45, 26036–26058. [Google Scholar] [CrossRef]
- Bashkatov, A.; Hossain, S.S.; Mutschke, G.; Yang, X.; Rox, H.; Weidinger, I.M.; Eckert, K. On the Growth Regimes of Hydrogen Bubbles at Microelectrodes. Phys. Chem. Chem. Phys. 2022, 24, 26738–26752. [Google Scholar] [CrossRef]
- Ward, C.A.; Balakrishnan, A.; Hooper, F.C. On the Thermodynamics of Nucleation in Weak Gas-Liquid Solutions. J. Fluids Eng. 1970, 92, 695–701. [Google Scholar] [CrossRef]
- Struyven, F.; Sellier, M.; Mandin, P. Review: Interactions Between Electrogenerated Bubbles and Microfluidic Phenomena. Int. J. Hydrog. Energy 2023, 48, 32607–32630. [Google Scholar] [CrossRef]
- Lubetkin, S.D. Why Is It Much Easier to Nucleate Gas Bubbles Than Theory Predicts? Langmuir 2003, 19, 2575–2587. [Google Scholar] [CrossRef]
- Brandon, N.P.; Kelsall, G.H. Growth Kinetics of Bubbles Electrogenerated at Microelectrodes. J. Appl. Electrochem. 1985, 15, 475–484. [Google Scholar] [CrossRef]
- Lubetkin, S.D. The Fundamentals of Bubble Evolution. Chem. Soc. Rev. 1995, 24, 243–250. [Google Scholar] [CrossRef]
- Taqieddin, A.; Nazari, R.; Rajic, L.; Alshawabkeh, A. Review—Physicochemical Hydrodynamics of Gas Bubbles in Two-Phase Electrochemical Systems. J. Electrochem. Soc. 2017, 164, E448–E459. [Google Scholar] [CrossRef]
- Jin, L.; Cheng, Z.; Deng, L.; Sun, T.; Gao, Z.; Yang, L.; Li, F.; He, G.; Geng, Z.; Zhang, C. Electrode Morphology and Structural Engineering Accelerates Bubble Detachment Dynamics in NiFe Porous Electrodes for Alkaline Water Electrolysis. Electrochim. Acta 2025, 535, 146670. [Google Scholar] [CrossRef]
- Ikeda, H.; Misumi, R.; Kojima, Y.; Haleem, A.A.; Kuroda, Y.; Mitsushima, S. Microscopic High-Speed Video Observation of Oxygen Bubble Generation Behavior and Effects of Anode Electrode Shape on OER Performance in Alkaline Water Electrolysis. Int. J. Hydrog. Energy 2022, 47, 11116–11127. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.; Wu, H.; Shi, Y. Experimental Investigation and Analysis for the Bubble Size Distribution During Alkaline Water Electrolysis by Using a Wire Electrode. DeCarbon 2024, 5, 100052. [Google Scholar] [CrossRef]
- Zhang, D.K.; Zeng, K. Evaluating the Behavior of Electrolytic Gas Bubbles and Their Effect on the Cell Voltage in Alkaline Water Electrolysis. Ind. Eng. Chem. Res. 2012, 51, 13825–13832. [Google Scholar] [CrossRef]
- Araújo, F.; Costa Neto, R.; Moita, A.S. Alkaline Water Electrolysis: Ultrasonic Field and Hydrogen Bubble Formation. Int. J. Hydrog. Energy 2024, 78, 594–603. [Google Scholar] [CrossRef]
- Song, Q.; Xue, Z.; Liu, C.; Qiao, X.; Liu, L.; Huang, C.; Liu, K.; Li, X.; Lu, Z.; Wang, T. General Strategy to Optimize Gas Evolution Reaction via Assembled Striped-Pattern Superlattices. J. Am. Chem. Soc. 2020, 142, 1857–1863. [Google Scholar] [CrossRef]
- Sides, P.J. Phenomena and Effects of Electrolytic Gas Evolution. In Modern Aspects of Electrochemistry; Springer: Boston, MA, USA, 1986; Volume 18, pp. 303–354. [Google Scholar] [CrossRef]
- Haverkort, J.W.; Aghdam, A.S.; Craye, E.J.B. The Optimal Electrode Hole Size in Zero-Gap Alkaline Water Electrolysis: A Combined Electrochemical, Theoretical, and Bubble Imaging Approach. Int. J. Hydrog. Energy 2025, 171, 150919. [Google Scholar] [CrossRef]
- Yin, W.; Yuan, L.; Huang, H.; Cai, Y.; Pan, J.; Sun, N.; Zhang, Q.; Shu, Q.; Gu, C.; Zhuang, Z.; et al. Strategies to Accelerate Bubble Detachment for Efficient Hydrogen Evolution. Chin. Chem. Lett. 2024, 35, 108351. [Google Scholar] [CrossRef]
- Fogaça, W.; Ikeda, H.; Misumi, R.; Kuroda, Y.; Mitsushima, S. Enhancement of Oxygen Evolution Reaction in Alkaline Water Electrolysis by Lorentz Forces Generated by an External Magnetic Field. Int. J. Hydrog. Energy 2024, 61, 1274–1281. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Z.; Guo, Z. Water Electrolysis Enhanced by Super Gravity Field for Hydrogen Production. Int. J. Hydrog. Energy 2010, 35, 3198–3205. [Google Scholar] [CrossRef]
- Bakker, M.M.; Vermaas, D.A. Gas Bubble Removal in Alkaline Water Electrolysis with Utilization of Pressure Swings. Electrochim. Acta 2019, 319, 148–157. [Google Scholar] [CrossRef]
- Zhao, P.; Gong, S.; Zhang, C.; Chen, S.; Cheng, P. Roles of Wettability and Wickability on Enhanced Hydrogen Evolution Reactions. ACS Appl. Mater. Interfaces 2024, 16, 27898–27907. [Google Scholar] [CrossRef]
- Hodges, A.; Renz, S.; Lohmann-Richters, F.; Al-Musawi, A.; Jupke, A.; Lehnert, W.; Swiegers, G.F.; Wallace, G.G. Critical Analysis of Published Physical Property Data for Aqueous Potassium Hydroxide. Collation into Detailed Models for Alkaline Electrolysis. J. Chem. Eng. Data 2023, 68, 1485–1506. [Google Scholar] [CrossRef]
- Gilliam, R.J.; Graydon, J.W.; Kirk, D.W.; Thorpe, S.J. A Review of Specific Conductivities of Potassium Hydroxide Solutions for Various Concentrations and Temperatures. Int. J. Hydrog. Energy 2007, 32, 359–364. [Google Scholar] [CrossRef]
- See, D.M.; White, R.E. Temperature and Concentration Dependence of the Specific Conductivity of Concentrated Solutions of Potassium Hydroxide. J. Chem. Eng. Data 1997, 42, 1266–1268. [Google Scholar] [CrossRef]
- Khalighi, F.; Vreman, A.W.; Tang, Y.; Deen, N.G. Solutal Marangoni Effects on Growing Hydrogen and Oxygen Bubbles in Alkaline Water Electrolysis. Chem. Eng. Sci. 2025, 311, 121577. [Google Scholar] [CrossRef]
- Lu, X.; Yadav, D.; Ma, B.; Ma, L.; Jing, D. Rapid Detachment of Hydrogen Bubbles for Electrolytic Water Splitting Driven by Combined Effects of Marangoni Force and the Electrostatic Repulsion. J. Power Sources 2024, 599, 234217. [Google Scholar] [CrossRef]

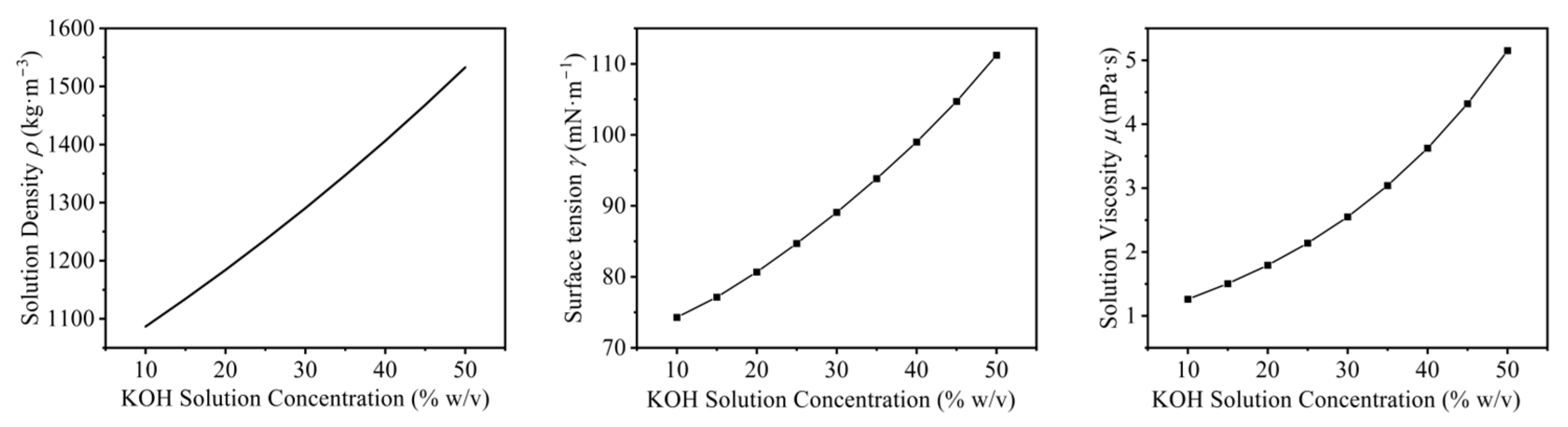


| Item Name | Specification | Manufacturer Information |
|---|---|---|
| Electrolytic Cell | Customized 250 mL Container | Custom-made, Tianjin, China |
| Electrochemical Workstation | Reference 3000 | Gamry Instruments, Warminster, PA, USA |
| High-Speed Camera | Phantom | Ametek, Inc., Berwyn, PA, USA |
| Imaging Lens | 2X FMOUNT | Navitar, Inc., Rochester, NY, USA |
| Nickel Wire | Purity 99.99%/Diameter 0.1~0.4 mm | Shenghang Research Institute of Metal Materials, Shenyang, China |
| Mercuric Oxide Electrode | R0501 | Shanghai Ledun Industrial Co., Ltd., Shanghai, China |
| Potassium Hydroxide Solution | 10% and 50% (w/v) | Shanghai Aladdin Biochemical Technology Co., Ltd., Shanghai, China |
| Potassium Hydroxide Solution | 20% and 40% (w/v) | Shanghai Macklin Biochemical Technology Co., Ltd., Shanghai, China |
| Potassium Hydroxide Solution | 30% (w/v) | Anhui Zesheng Technology Co., Ltd., Hefei, China |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zeng, J.; An, Y.; Duan, Y.; Song, Q. Investigation of Gas Evolution on Nickel Wire Electrodes During Alkaline Water Electrolysis. Energies 2025, 18, 5888. https://doi.org/10.3390/en18225888
Liu J, Zeng J, An Y, Duan Y, Song Q. Investigation of Gas Evolution on Nickel Wire Electrodes During Alkaline Water Electrolysis. Energies. 2025; 18(22):5888. https://doi.org/10.3390/en18225888
Chicago/Turabian StyleLiu, Junxu, Jingxin Zeng, Yuhang An, Yuanyuan Duan, and Qiang Song. 2025. "Investigation of Gas Evolution on Nickel Wire Electrodes During Alkaline Water Electrolysis" Energies 18, no. 22: 5888. https://doi.org/10.3390/en18225888
APA StyleLiu, J., Zeng, J., An, Y., Duan, Y., & Song, Q. (2025). Investigation of Gas Evolution on Nickel Wire Electrodes During Alkaline Water Electrolysis. Energies, 18(22), 5888. https://doi.org/10.3390/en18225888






