High-Performance Reservoir Simulation with Wafer-Scale Engine for Large-Scale Carbon Storage
Abstract
1. Introduction
2. Background
2.1. Speed Versus Accuracy in Reservoir Simulations
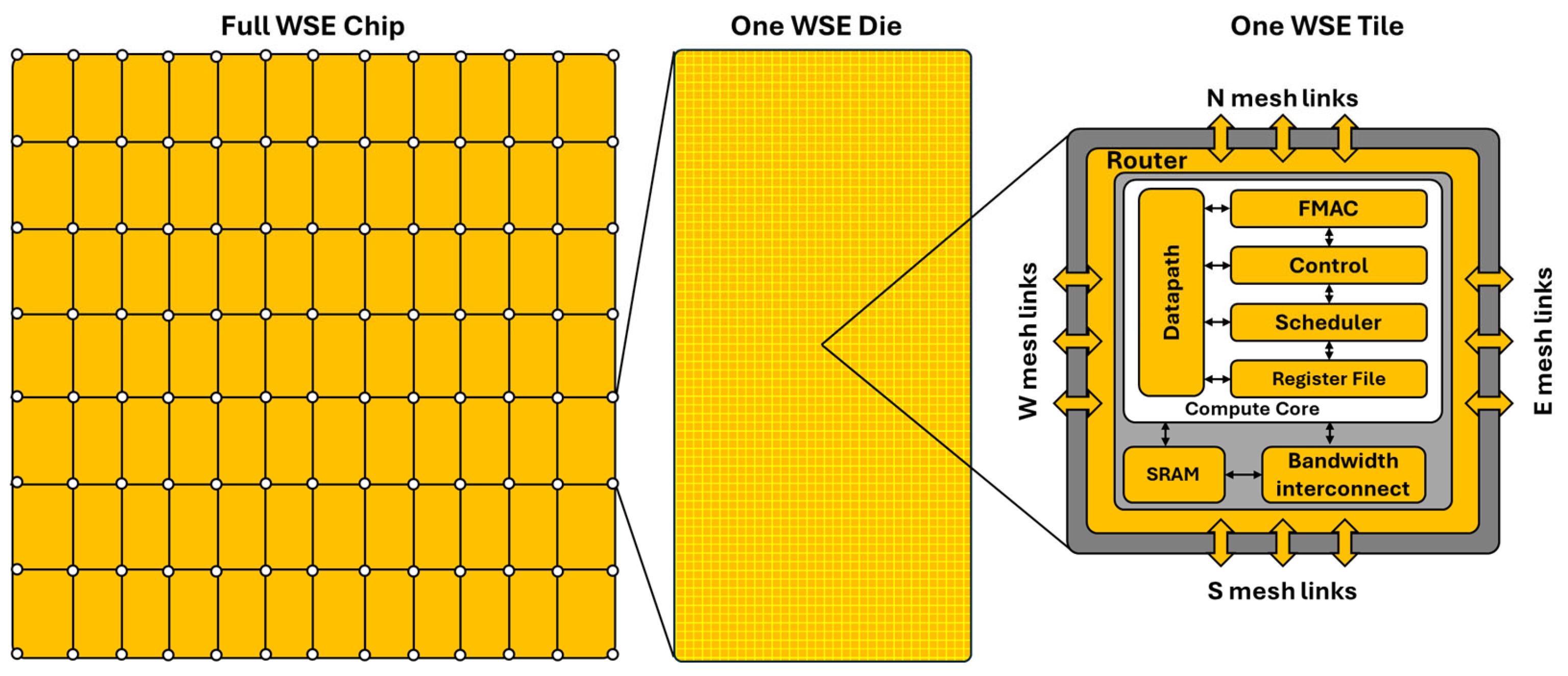
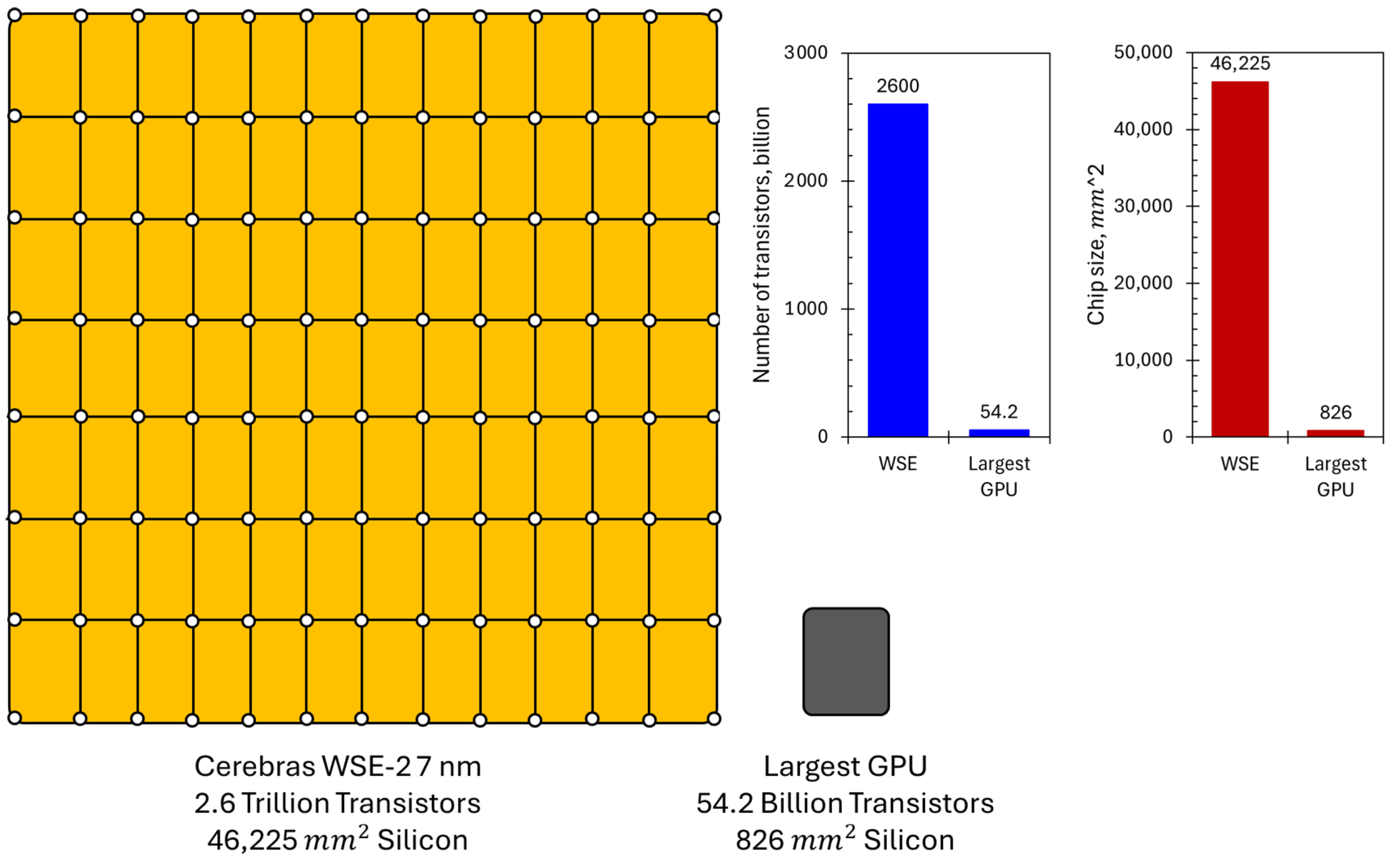
2.2. Wafer-Scale Computing
3. Methodology
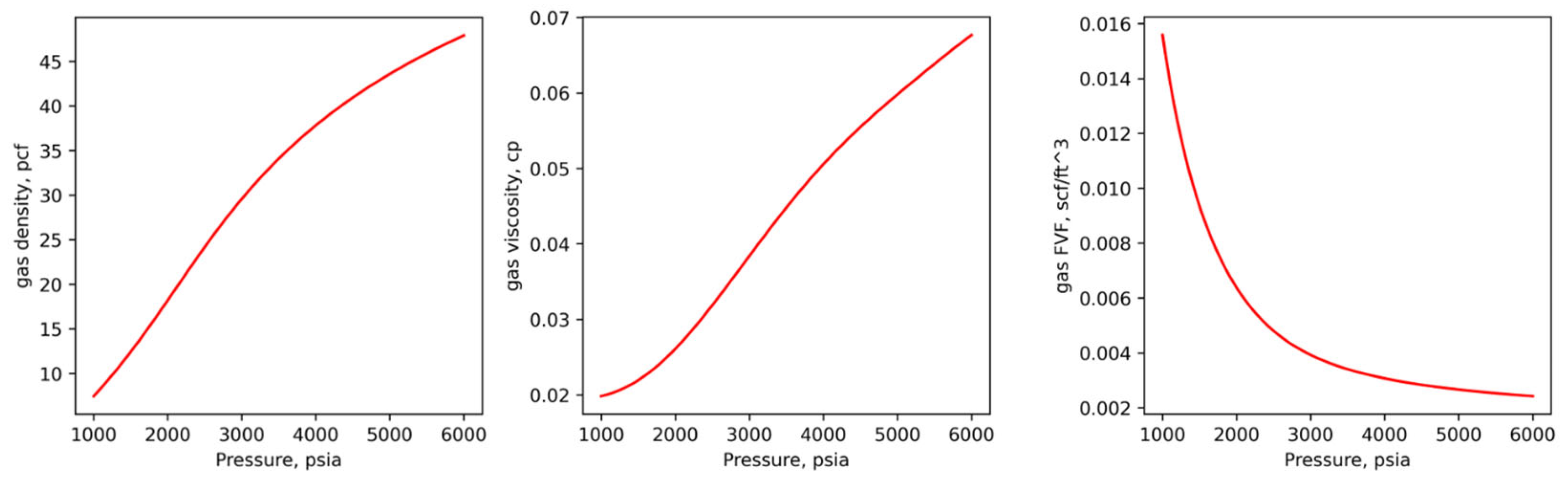
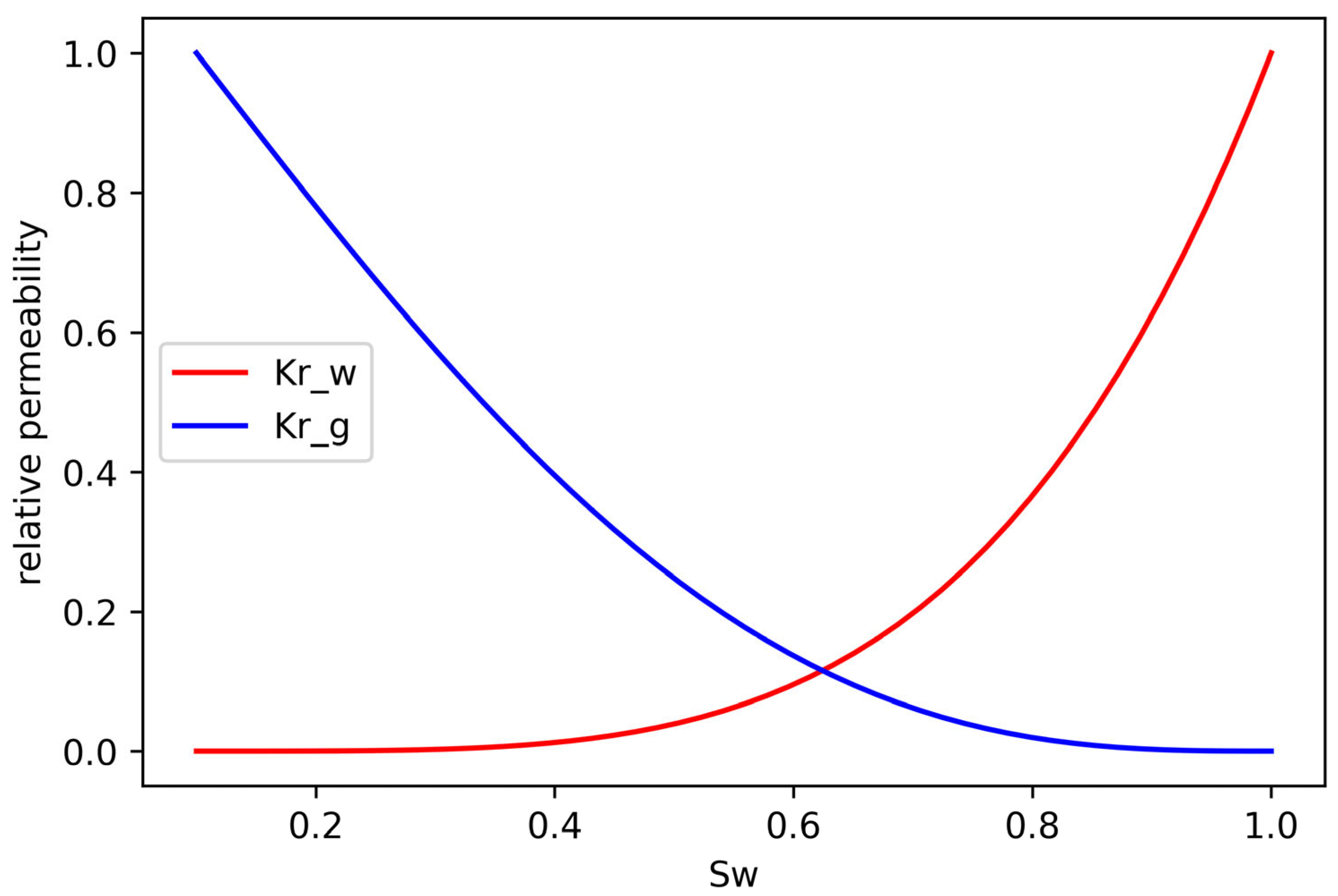
3.1. Physics-Based Mathematical Model
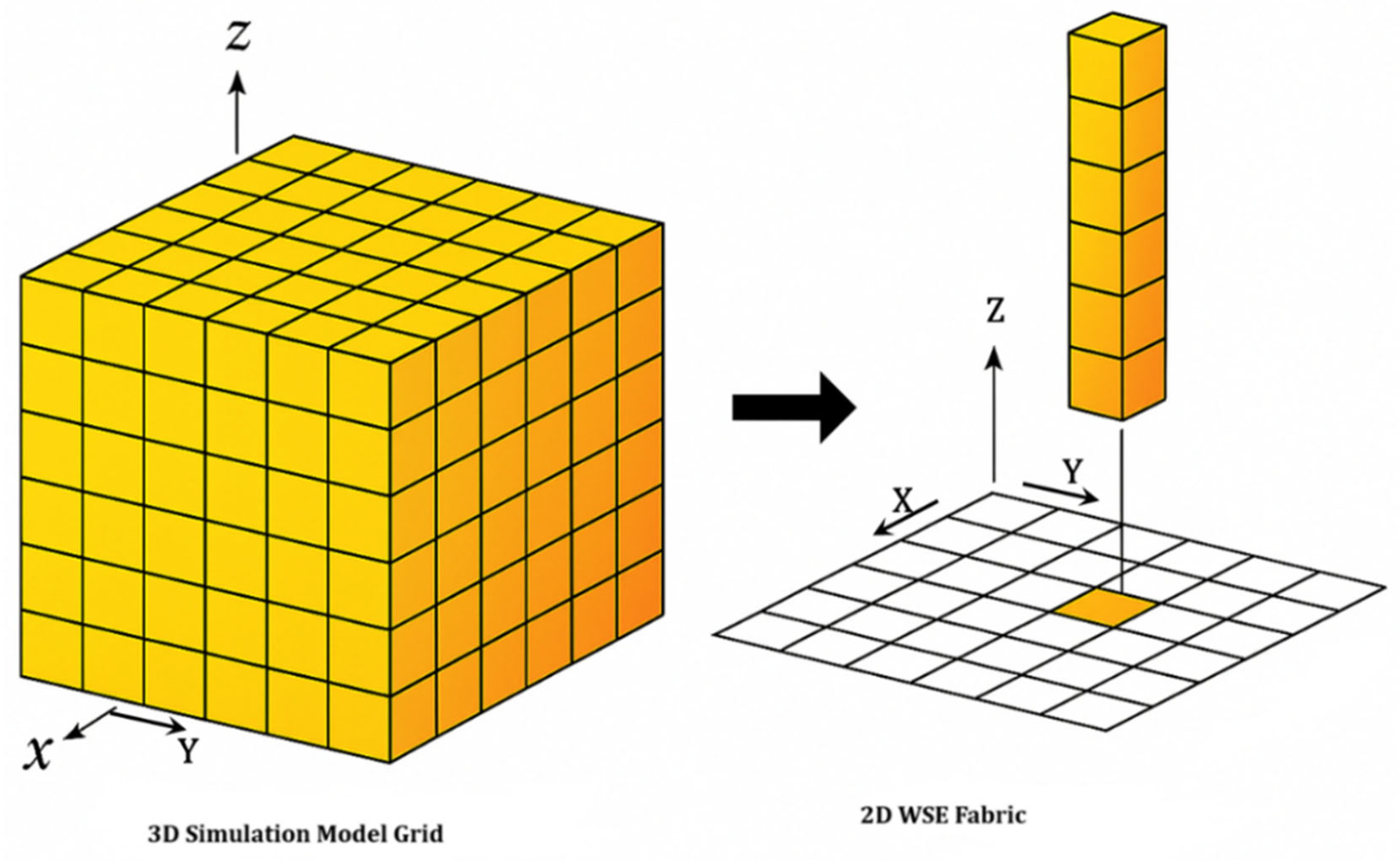
3.2. Implementation on the WSE
3.3. Design of Benchmark Studies
4. Results and Performance Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Model Validation
| Parameter | Value |
|---|---|
| Max. Relative Permeability of Gas | 1.0 |
| Max. Relative Permeability of Water | 1.0 |
| Corey Exponent of Gas | 3.5 |
| Corey Exponent of Water | 3.5 |
| Porosity | 0.2 |
| Matrix Permeability | 9.0 × 10−13 m2 |
| Gas Viscosity | 2.3 × 10−5 Pa s |
| Water Viscosity | 5.5 × 10−4 Pa s |
| Total Flow Rate | 2.5 × 10−7 m3/s |
| Domain Length | 0.1 m |
| Domain Width | 1.0 m |
| Domain Thickness | 0.002 m |

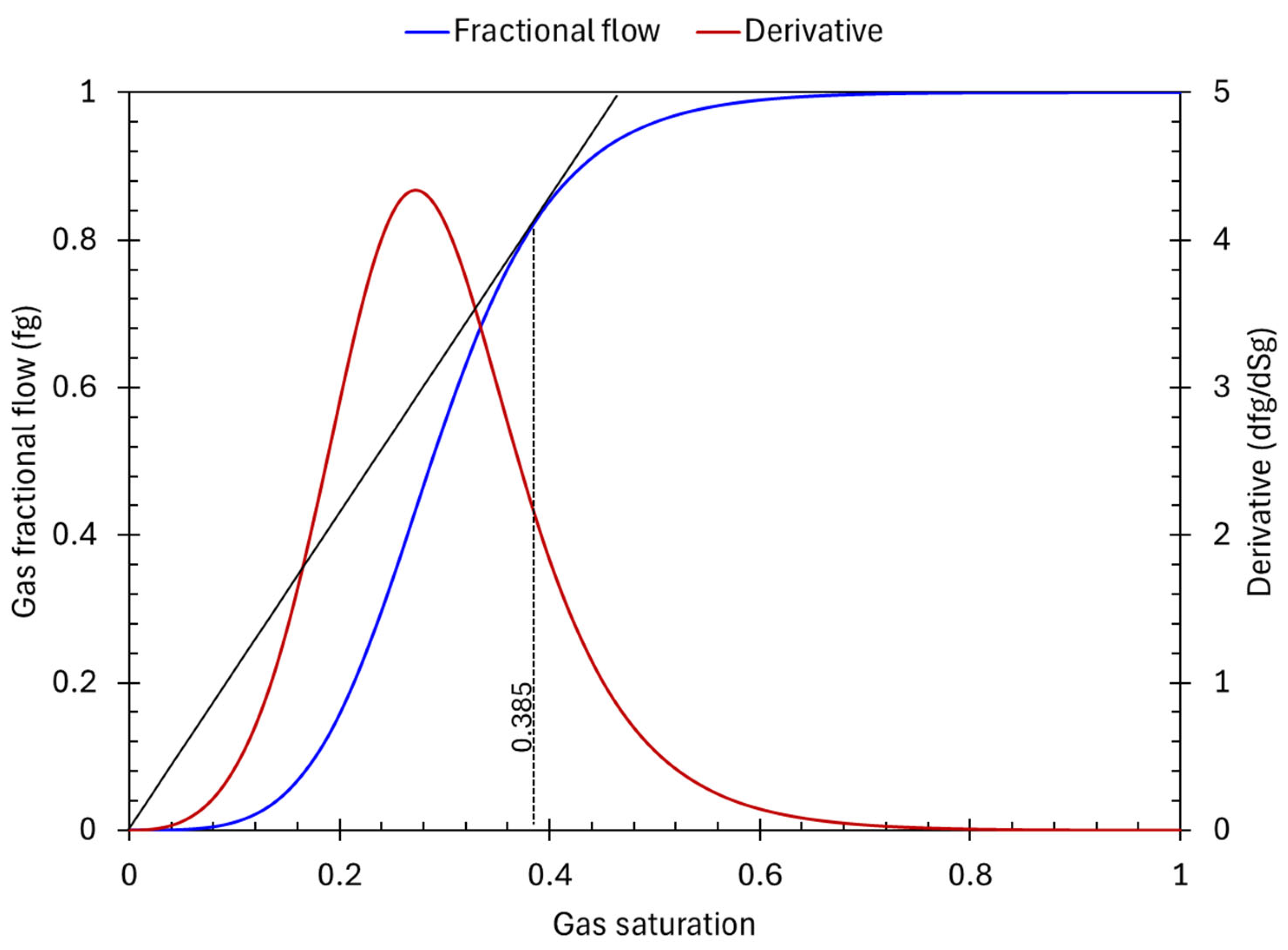
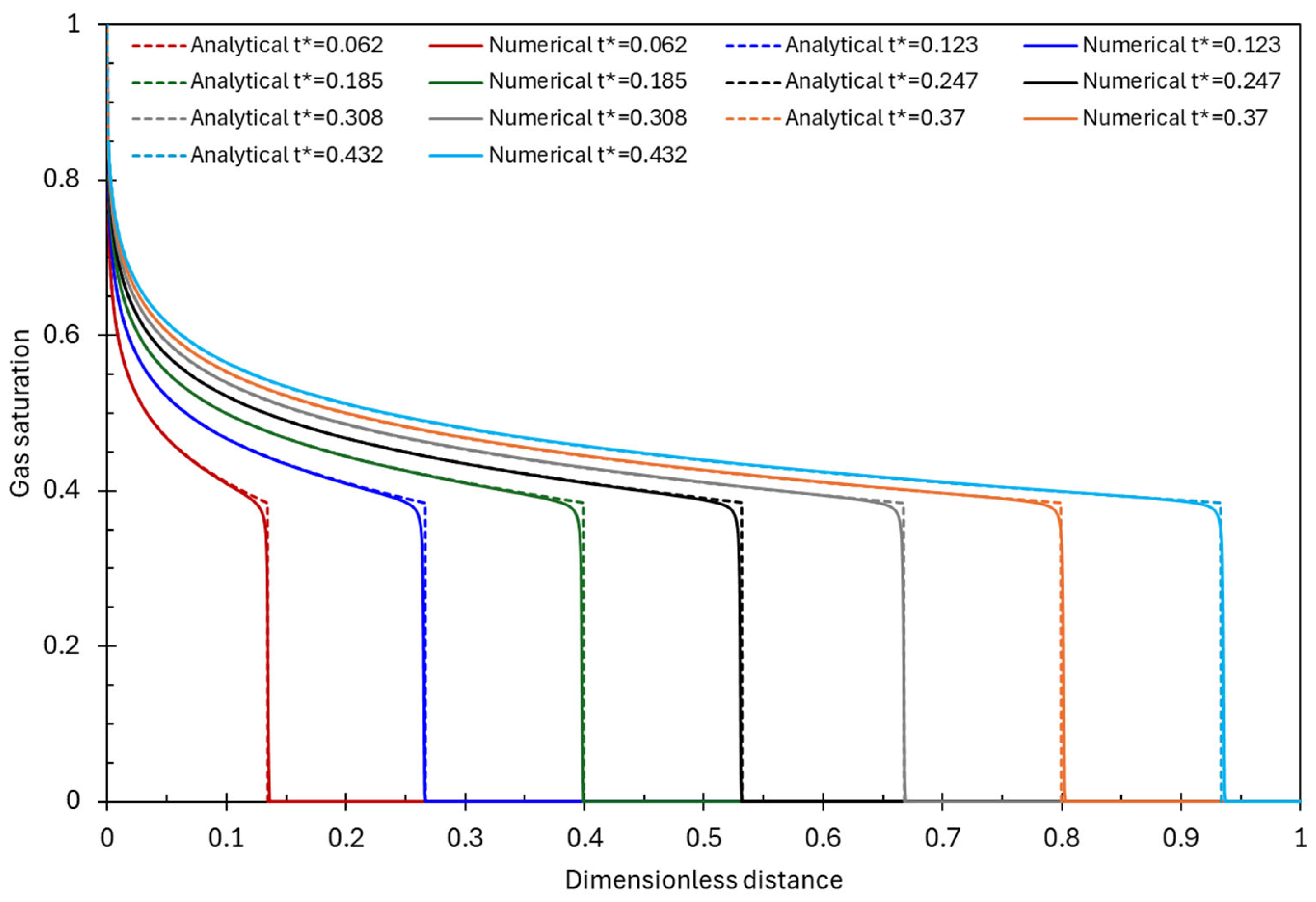
References
- Wang, Y.; Jin, Y.; Pang, H.; Lin, B. Upscaling for Full-Physics Models of CO2 Injection Into Saline Aquifers. SPE J. 2025, 30, 3065–3082. [Google Scholar] [CrossRef]
- Khalaf, M.; Liu, G.; Dilmore, R.; Lackey, G.; Mehana, M.; Cunha, L.; Strazisar, B. Reservoir Dynamics in Proposed Operational Scenarios Where CO2-EOR Fields Are Transitioned From CO2-Flood Enhanced Oil Recovery to Dedicated Carbon Storage: A Field Case Study; US DOE National Energy Technology Laboratory: Pittsburgh, PA, USA, 2025. [Google Scholar] [CrossRef]
- Sun, A.Y. Optimal Carbon Storage Reservoir Management through Deep Reinforcement Learning. Appl. Energy 2020, 278, 115660. [Google Scholar] [CrossRef]
- Du, H.; Zhao, Z.; Cheng, H.; Yan, J.; He, Q. Modeling Density-Driven Flow in Porous Media by Physics-Informed Neural Networks for CO2 Sequestration. Comput. Geotech. 2023, 159, 105433. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Corey, A.T. The Interrelation between Gas and Oil Relative Permeability. Prod. Mon. 1954, 19, 38–41. [Google Scholar]
- Bauer, R.A.; Will, R.; Greenberg, S.E.; Whittaker, S.G. Illinois Basin–Decatur Project. In Geophysics and Geosequestration; Cambridge University Press: Cambridge, UK, 2019; pp. 339–370. [Google Scholar]
- DataShare, C. Illinois Basin—Decatur Project Dataset. Available online: https://co2datashare.org/dataset/illinois-basin-decatur-project-dataset (accessed on 15 September 2025).
- Koo, C.; Park, S.; Hong, T.; Park, H.S. An Estimation Model for the Heating and Cooling Demand of a Residential Building with a Different Envelope Design Using the Finite Element Method. Appl. Energy 2014, 115, 205–215. [Google Scholar] [CrossRef]
- Harish, V.S.K.V.; Kumar, A. Reduced Order Modeling and Parameter Identification of a Building Energy System Model through an Optimization Routine. Appl. Energy 2016, 162, 1010–1023. [Google Scholar] [CrossRef]
- Sun, Q.; Teng, R.; Li, H.; Xin, Y.; Ma, H.; Zhao, T.; Chen, Q. Generalized Frequency-Domain Analysis for Dynamic Simulation and Comprehensive Regulation of Integrated Electric and Heating System. Appl. Energy 2024, 372, 123817. [Google Scholar] [CrossRef]
- Service, R.F. Exascale Computers Show off Emerging Science. Science 2023, 382, 864–865. [Google Scholar] [CrossRef]
- Peherstorfer, B.; Willcox, K. Dynamic Data-Driven Reduced-Order Models. Comput. Methods Appl. Mech. Eng. 2015, 291, 21–41. [Google Scholar] [CrossRef]
- Lucia, D.J.; Beran, P.S.; Silva, W.A. Reduced-Order Modeling: New Approaches for Computational Physics. Prog. Aerosp. Sci. 2004, 40, 51–117. [Google Scholar] [CrossRef]
- Trifonov, V.; Illarionov, E.; Voskresenskii, A.; Petrosyants, M.; Katterbauer, K. Hybrid Solver with Deep Learning for Transport Problem in Porous Media. Discov. Geosci. 2025, 3, 33. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, X.; Zhu, H.; Tang, Z.; Zhao, X.; Zhang, F.; Sepehrnoori, K. Engineering Factor Analysis and Intelligent Prediction of CO2 Storage Parameters in Shale Gas Reservoirs Based on Deep Learning. Appl. Energy 2025, 377, 124642. [Google Scholar] [CrossRef]
- Zhang, Y.-F.; Qu, M.-L.; Yang, J.-P.; Foroughi, S.; Niu, B.; Yu, Z.-T.; Gao, X.; Blunt, M.J.; Lin, Q. Prediction of CO2 Storage Efficiency and Its Uncertainty Using Deep-Convolutional GANs and Pore Network Modelling. Appl. Energy 2025, 381, 125142. [Google Scholar] [CrossRef]
- San, O.; Maulik, R. Extreme Learning Machine for Reduced Order Modeling of Turbulent Geophysical Flows. Phys. Rev. E 2018, 97, 042322. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, L.; Xu, J.; Wang, Z.; Yuan, J.; Tan, A.C.C. A Reduced Order Modeling-Based Machine Learning Approach for Wind Turbine Wake Flow Estimation from Sparse Sensor Measurements. Energy 2024, 294, 130772. [Google Scholar] [CrossRef]
- Zhong, Z.; Sun, A.Y.; Jeong, H. Predicting CO2 Plume Migration in Heterogeneous Formations Using Conditional Deep Convolutional Generative Adversarial Network. Water Resour. Res. 2019, 55, 5830–5851. [Google Scholar] [CrossRef]
- Mo, S.; Zabaras, N.; Shi, X.; Wu, J. Deep Autoregressive Neural Networks for High--Dimensional Inverse Problems in Groundwater Contaminant Source Identification. Water Resour. Res. 2019, 55, 3856–3881. [Google Scholar] [CrossRef]
- Tang, M.; Liu, Y.; Durlofsky, L.J. A Deep-Learning-Based Surrogate Model for Data Assimilation in Dynamic Subsurface Flow Problems. J. Comput. Phys. 2020, 413, 109456. [Google Scholar] [CrossRef]
- Wen, G.; Li, Z.; Azizzadenesheli, K.; Anandkumar, A.; Benson, S.M. U-FNO—An Enhanced Fourier Neural Operator-Based Deep-Learning Model for Multiphase Flow. Adv. Water Resour. 2022, 163, 104180. [Google Scholar] [CrossRef]
- Jin, Z.L.; Liu, Y.; Durlofsky, L.J. Deep-Learning-Based Surrogate Model for Reservoir Simulation with Time-Varying Well Controls. J. Pet. Sci. Eng. 2020, 192, 107273. [Google Scholar] [CrossRef]
- Sun, A.Y.; Yoon, H.; Shih, C.-Y.; Zhong, Z. Applications of Physics-Informed Scientific Machine Learning in Subsurface Science: A Survey. In Knowledge-Guided Machine Learning; Chapman and Hall/CRC: Boca Raton, FL, USA, 2022; pp. 111–132. [Google Scholar]
- Yanchun, L.; Deli, J.; Suling, W.; Ruyi, Q.; Meixia, Q.; He, L. Surrogate Model for Reservoir Performance Prediction with Time-Varying Well Control Based on Depth Generative Network. Pet. Explor. Dev. 2024, 51, 1287–1300. [Google Scholar] [CrossRef]
- Vo Thanh, H.; Yasin, Q.; Al-Mudhafar, W.J.; Lee, K.K. Knowledge-Based Machine Learning Techniques for Accurate Prediction of CO2 Storage Performance in Underground Saline Aquifers. Appl. Energy 2022, 314, 118985. [Google Scholar] [CrossRef]
- Etienam, C.; Juntao, Y.; Said, I.; Ovcharenko, O.; Tangsali, K.; Dimitrov, P.; Hester, K. A Novel A.I Enhanced Reservoir Characterization with a Combined Mixture of Experts—NVIDIA Modulus Based Physics Informed Neural Operator Forward Model. arXiv 2024, arXiv:2404.14447. [Google Scholar]
- Pachalieva, A.; O’Malley, D.; Harp, D.R.; Viswanathan, H. Physics-Informed Machine Learning with Differentiable Programming for Heterogeneous Underground Reservoir Pressure Management. Sci. Rep. 2022, 12, 18734. [Google Scholar] [CrossRef]
- Illarionov, E.; Temirchev, P.; Voloskov, D.; Kostoev, R.; Simonov, M.; Pissarenko, D.; Orlov, D.; Koroteev, D. End-to-End Neural Network Approach to 3D Reservoir Simulation and Adaptation. J. Pet. Sci. Eng. 2022, 208, 109332. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, Z.; Qiao, Y.; Xiang, T.; Loy, C.C. Domain Generalization: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 4396–4415. [Google Scholar] [CrossRef]
- Goswami, S.; Kontolati, K.; Shields, M.D.; Karniadakis, G.E. Deep Transfer Operator Learning for Partial Differential Equations under Conditional Shift. Nat. Mach. Intell. 2022, 4, 1155–1164. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-Informed Machine Learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- He, X.; Zhu, W.; Kwak, H.; Yousef, A.; Hoteit, H. Deep Learning-Assisted Bayesian Framework for Real-Time CO2 Leakage Locating at Geologic Sequestration Sites. J. Clean. Prod. 2024, 448, 141484. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, M.; Xia, X.; Tian, Z.; Qin, X.; Cai, J. Lattice Boltzmann Prediction of CO2 and CH4 Competitive Adsorption in Shale Porous Media Accelerated by Machine Learning for CO2 Sequestration and Enhanced CH4 Recovery. Appl. Energy 2024, 370, 123638. [Google Scholar] [CrossRef]
- Mack, C.A. Fifty Years of Moore’s Law. IEEE Trans. Semicond. Manuf. 2011, 24, 202–207. [Google Scholar] [CrossRef]
- Theis, T.N.; Wong, H.-S.P. The End of Moore’s Law: A New Beginning for Information Technology. Comput. Sci. Eng. 2017, 19, 41–50. [Google Scholar] [CrossRef]
- Hu, Y.; Lin, X.; Wang, H.; He, Z.; Yu, X.; Zhang, J.; Yang, Q.; Xu, Z.; Guan, S.; Fang, J.; et al. Wafer-Scale Computing: Advancements, Challenges, and Future Perspectives [Feature]. IEEE Circuits Syst. Mag. 2024, 24, 52–81. [Google Scholar] [CrossRef]
- Lauterbach, G. The Path to Successful Wafer-Scale Integration: The Cerebras Story. IEEE Micro 2021, 41, 52–57. [Google Scholar] [CrossRef]
- Van Essendelft, D.; Almolyki, H.; Shi, W.; Jordan, T.; Wang, M.-Y.; Saidi, W.A. Record Acceleration of the Two-Dimensional Ising Model Using High-Performance Wafer Scale Engine. arXiv 2024, arXiv:2404.16990. [Google Scholar] [CrossRef]
- Woo, M.; Jordan, T.; Schreiber, R.; Sharapov, I.; Muhammad, S.; Koneru, A.; James, M.; Van Essendelft, D. Disruptive Changes in Field Equation Modeling: A Simple Interface for Wafer Scale Engines. arXiv 2022, arXiv:2209.13768. [Google Scholar] [CrossRef]
- Hock, A. Accelerating AI and HPC for Science at Wafer-Scale with Cerebras Systems. In Proceedings of the Argonne Training Program on Extreme-Scale Computing (ATPESC); 2022. Available online: https://extremecomputingtraining.anl.gov/wp-content/uploads/sites/96/2022/11/ATPESC-2022-Track-1-Talk-8-Hock-Cerebras-for-ATPESC.pdf (accessed on 15 September 2025).
- Sai, R.; Jacquelin, M.; Hamon, F.; Araya-Polo, M.; Settgast, R.R. Massively Distributed Finite-Volume Flux Computation. In Proceedings of the SC ’23 Workshops of The International Conference on High Performance Computing, Network, Storage, and Analysis, Denver, CO, USA, 12–17 November 2023; ACM: New York, NY, USA, 2023; Volume 1, pp. 1713–1720. [Google Scholar]
- Kim, H.; Rezkalla, M.; Sun, A.; VanEssendelft, D.; Shih, C.; Liu, G.; Siriwardane, H. WSE (Wafer Scale Engine) Applications for CCS (Carbon Capture and Storage). In Proceedings of the 2024 FECM/NETL Carbon Management Research Project Review Meeting, Pittsburgh, PA, USA, 5–9 August 2024; Available online: https://netl.doe.gov/sites/default/files/netl-file/24CM/24CM_CTS2_6_Shih.pdf (accessed on 15 September 2025).
- Fenghour, A.; Wakeham, W.A.; Vesovic, V. The Viscosity of Carbon Dioxide. J. Phys. Chem. Ref. Data 1998, 27, 31–44. [Google Scholar] [CrossRef]
- Rocki, K.; Van Essendelft, D.; Sharapov, I.; Schreiber, R.; Morrison, M.; Kibardin, V.; Portnoy, A.; Dietiker, J.F.; Syamlal, M.; James, M. Fast Stencil-Code Computation on a Wafer-Scale Processor. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Atlanta, GA, USA, 9–19 November 2020; pp. 1–14. [Google Scholar]
- PSC Neocortex. Available online: https://www.psc.edu/resources/neocortex/ (accessed on 15 September 2025).
- Van Essendelft, D.; Wingo, P.; Jordan, T.; Smith, R.; Saidi, W. A System Level Compiler for Massively-Parallel, Spatial, Dataflow Architectures. arXiv 2025, arXiv:2506.15875. [Google Scholar] [CrossRef]
- van der Vorst, H.A. Bi-CGSTAB: A Fast and Smoothly Converging Variant of Bi-CG for the Solution of Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1992, 13, 631–644. [Google Scholar] [CrossRef]
- Naguib, H.M.; Hou, G.; Chen, S.; Yao, H. Mechanisms and Optimal Reaction Parameters of Accelerated Carbonization of Calcium Silicate. Kuei Suan Jen Hsueh Pao/J. Chinese Ceram. Soc. 2019, 47. [Google Scholar] [CrossRef]
- GEOS Verification of CO2 Core Flood Experiment with Buckley-Leverett Solution. Available online: https://geosx-geosx.readthedocs-hosted.com/en/latest/docs/sphinx/advancedExamples/validationStudies/carbonStorage/buckleyLeverett/Example.html#id1 (accessed on 1 January 2025).
- Ekechukwu, G.K.; de Loubens, R.; Araya-Polo, M. LSTM-Driven Forecast of CO2 Injection in Porous Media. arXiv 2022, arXiv:2203.05021. [Google Scholar] [CrossRef]
- Buckley, S.E.; Leverett, M.C. Mechanism of Fluid Displacement in Sands. Trans. AIME 1942, 146, 107–116. [Google Scholar] [CrossRef]


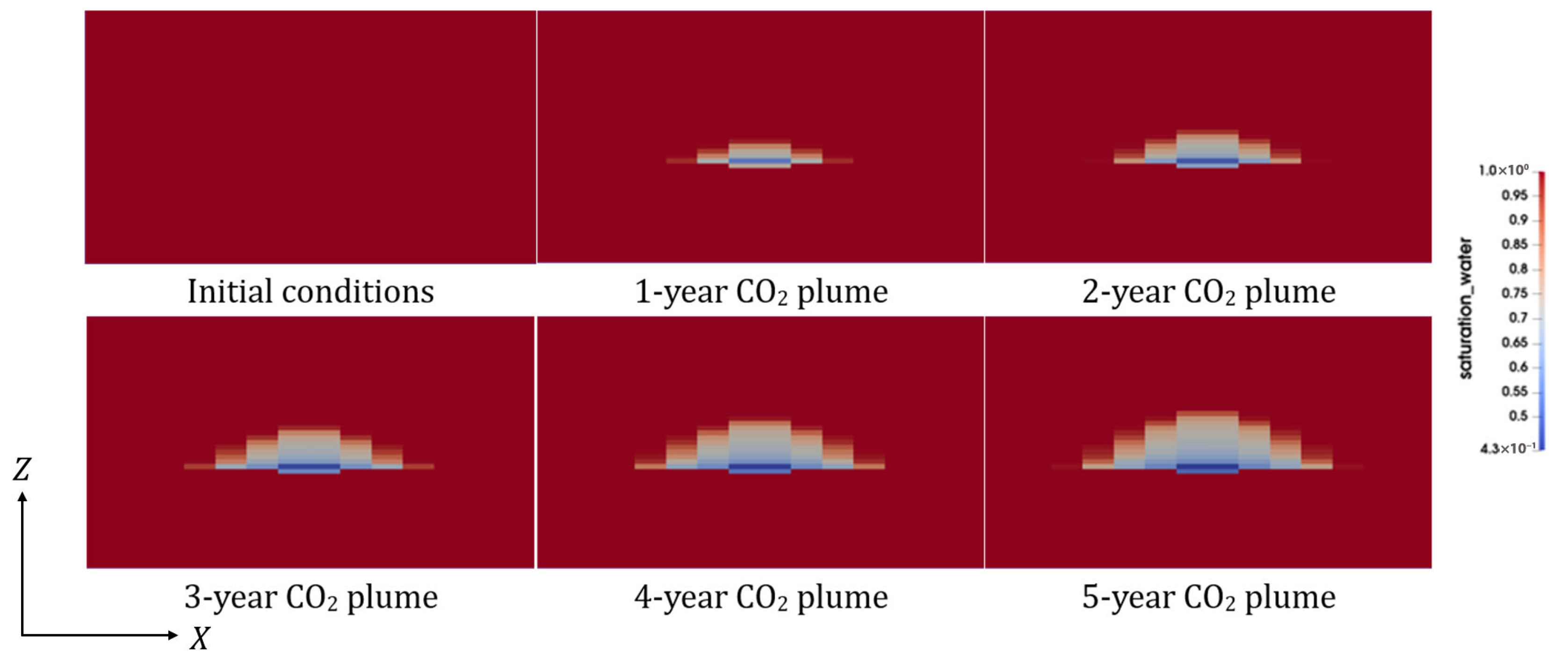
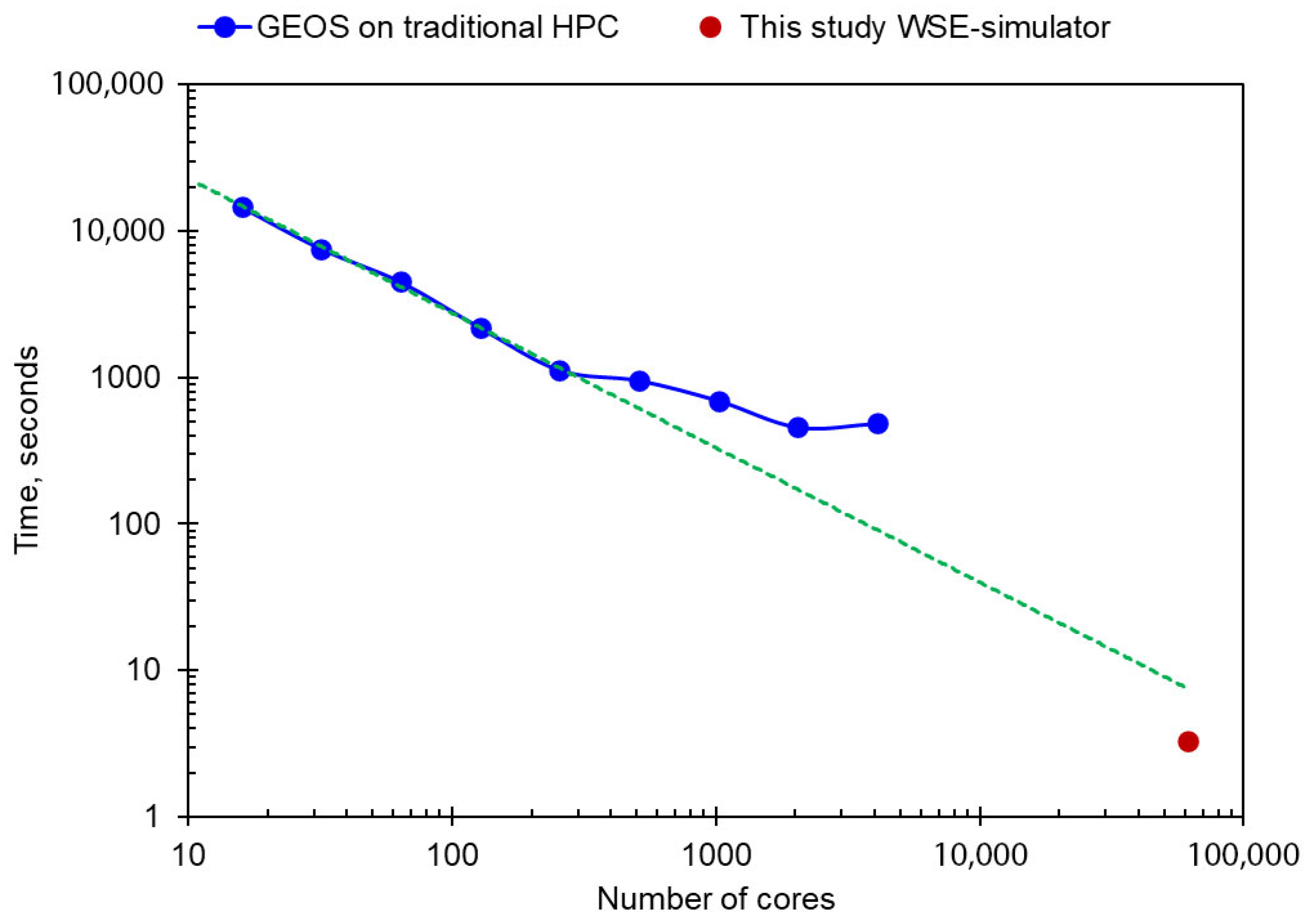
| Parameter | Base Mesh | Refined Mesh |
|---|---|---|
| Grid resolution | 124 × 124 × 108 | 248 × 248 × 108 |
| Total number of grid cells | 1.66 million | 6.64 million |
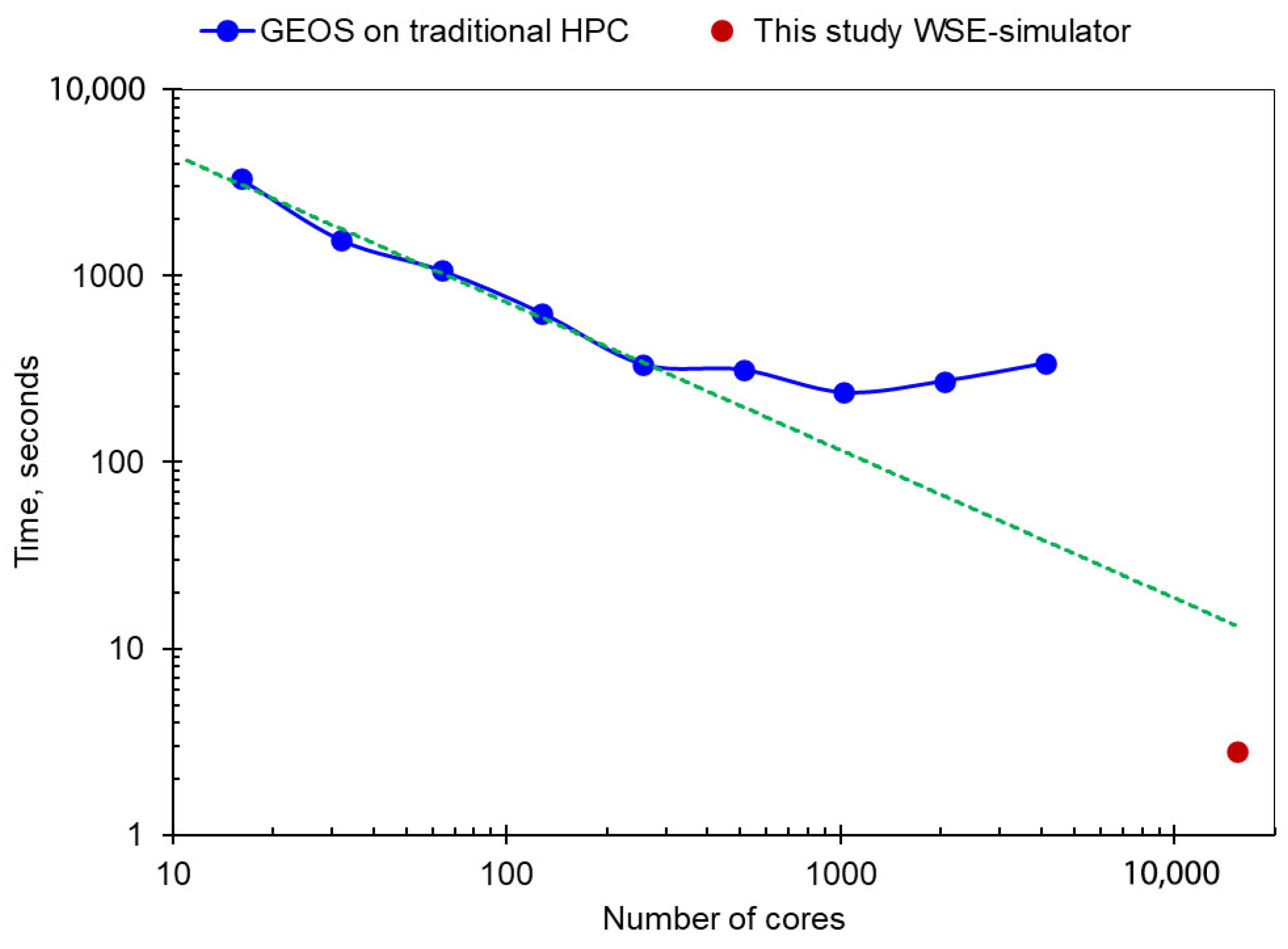
| Runtime of this study simulator on WSE | 2.82 s | 3.28 s |
| Runtime of GEOS on traditional HPC | 334 s | 1123 s |
| Speedup of this study simulator | 118× | 342× |
| Number of cores used on WSE | 15,376 (1.8% of full WSE capacity) | 61,504 (7.2% of full WSE capacity) |
| Feature | Full-Physics Simulators | ML Simulators | WSE-Based Simulator |
|---|---|---|---|
| Approach | Solves PDEs using numerical methods | Learn patterns from data | Solves PDEs using finite difference on WSE hardware |
| Accuracy | High (physics-based) | Variable (depends on training data) | High (physics-based) |
| Speed | Slow (hours to days) | Fast (seconds to minutes) | Super-fast (seconds) |
| Data requirement | Moderate (reservoir description) | Very high (large datasets) | Moderate (reservoir description) |
| Generalizability | High (physics-based) | Low–medium (limited to trained domains) | High (physics-based) |
| Hardware | CPU/GPU | GPU/TPU | WSE (Wafer-Scale Engine) |
| Limitations | Long runtimes | Requires training, limited physics insights | Legacy simulator needs to be adapted to run on WSE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalaf, M.; Kim, H.; Sun, A.Y.; Van Essendelft, D.; Shih, C.Y.; Liu, G.; Siriwardane, H. High-Performance Reservoir Simulation with Wafer-Scale Engine for Large-Scale Carbon Storage. Energies 2025, 18, 5874. https://doi.org/10.3390/en18225874
Khalaf M, Kim H, Sun AY, Van Essendelft D, Shih CY, Liu G, Siriwardane H. High-Performance Reservoir Simulation with Wafer-Scale Engine for Large-Scale Carbon Storage. Energies. 2025; 18(22):5874. https://doi.org/10.3390/en18225874
Chicago/Turabian StyleKhalaf, Mina, Hyoungkeun Kim, Alexander Y. Sun, Dirk Van Essendelft, Chung Yan Shih, Guoxiang Liu, and Hema Siriwardane. 2025. "High-Performance Reservoir Simulation with Wafer-Scale Engine for Large-Scale Carbon Storage" Energies 18, no. 22: 5874. https://doi.org/10.3390/en18225874
APA StyleKhalaf, M., Kim, H., Sun, A. Y., Van Essendelft, D., Shih, C. Y., Liu, G., & Siriwardane, H. (2025). High-Performance Reservoir Simulation with Wafer-Scale Engine for Large-Scale Carbon Storage. Energies, 18(22), 5874. https://doi.org/10.3390/en18225874





