Multi-Criteria-Based Key Transmission Section Identification and Prevention–Emergency Coordinated Optimal Control Strategy
Abstract
1. Introduction
- Considering the topological, power flow, and voltage importance of transmission lines. A comprehensive index is proposed to accurately identify the critical lines of the system.
- The initial transmission section of the critical lines is subsequently identified via the cut-set search and power flow consistency verification. The distribution of the power flow impact after critical line faults is analyzed through the Theil index, then a multi-criteria-based method is proposed to identify key transmission sections among initial transmission sections.
- Considering the coupling relationship between prevention control and emergency control, an optimal model for prevention–emergency coordinated control of key transmission sections is established. By introducing a constraint relaxation factor, the aforementioned model is decomposed, and the golden section method is then employed to update the constraint relaxation factor, thereby searching for the optimal coordinated control solution of the system.
2. Key Transmission Section Identification Considering Multiple Criteria
2.1. Critical Line Identification
2.1.1. Topological Criticality
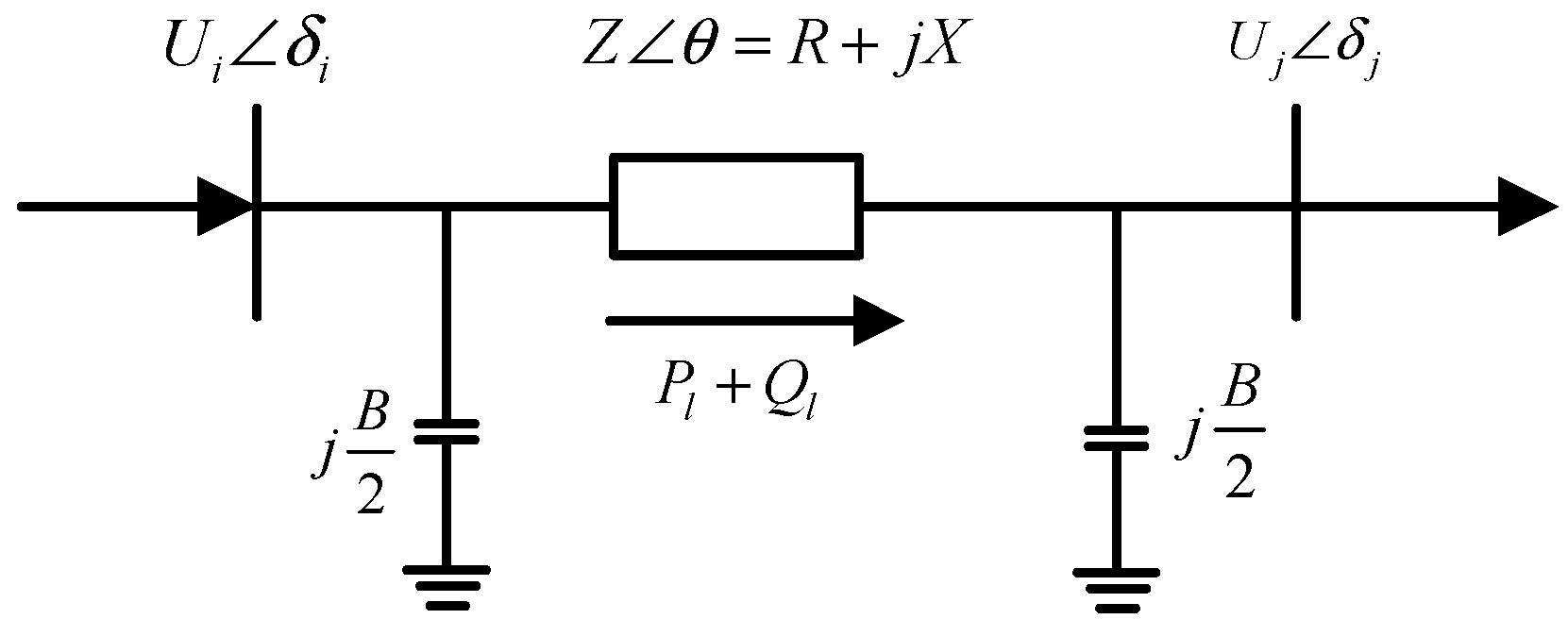
2.1.2. Power Flow Criticality
2.1.3. Voltage Criticality
2.2. Key Transmission Section Identification Method
2.2.1. Initial Transmission Section Identification
| Algorithm 1: DFS-based Cut-set Generation Algorithm |
| Input: System’s undirected adjacency matrix M, critical line l, maximum number n within a cut-set, k = 1 |
| Output: Initial transmission section set S(l) of critical line l 1: for i = 1 to n do 2: Generate all possible combinations of n − 1 lines from the system 3: Count the number of all combinations and denote as h 4: for j = 1 to h do 5: Integrate the j-th combination with critical line l to form candidate set s(k) 6: Remove all lines in s(k) from M to obtain modified graph M’ 7: Starting from any generator node, perform DFS traversal on M’ 8: If at least one load node is unreachable then 9: If all power flow directions are consistent then 10: Add s(k) to S(l) 11: end if 12: end if 13: j = j + 1 14: k = k + 1 15: end for 16: i = i + 1 17: end for |
| 18: Return S(l) |
2.2.2. Key Transmission Section Identification
- Step 1: Based on the initial transmission section set of the critical line , calculate the Theil index of power flow impact rate after the critical line l fault for each initial transmission section;
- Step 2: From the initial transmission section set , retain section set where the value of ranks in the top A%;
- Step 3: On the basis of , retain section set where the value of ranks in the bottom A%;
- Step 4: From Ω2, select section Ω3 with the smallest value and form t section Ω3 with the critical line as the key transmission section of the system.
3. Prevention–Emergency Coordinated Control of Key Transmission Sections
3.1. Coordinated Optimization Model
3.1.1. Objective Function
3.1.2. Constraints
- (1)
- Load Rate Constraints
- (2)
- System Power Balance Constraint;
- (3)
- Operational Security Constraints
- (4)
- Power Adjustment Balance Constraint
3.2. Solution Method
3.2.1. Model Partitioning
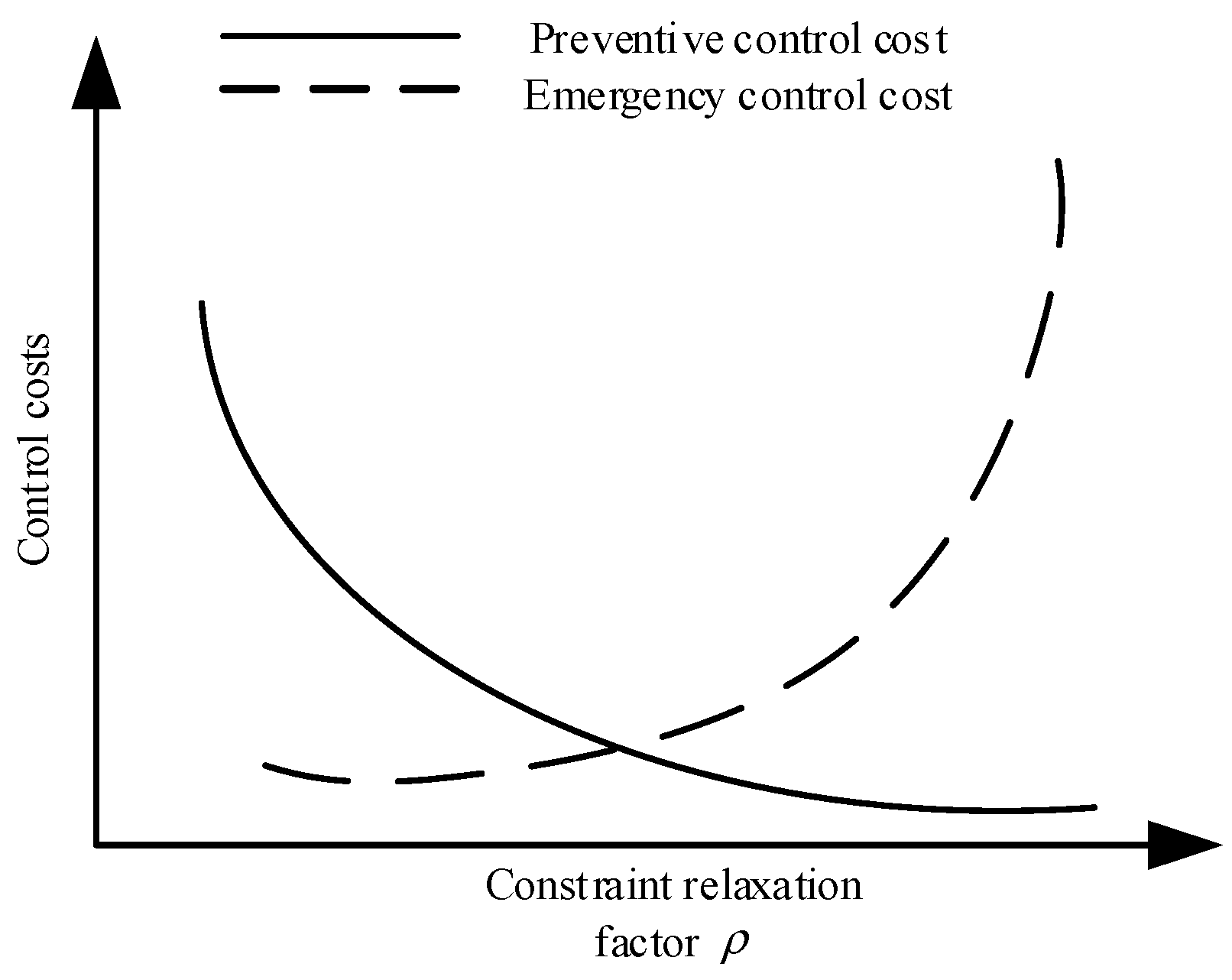
3.2.2. Solution Strategy Based on the Golden Section Method
- Step 1: Set the iteration number to = 1, the termination criterion to = 0.001, and the initial search interval for the constraint relaxation factor to .
- Step 2: Select the optimal division points as follows: and .
- Step 3: Solve the optimization model based on .
- (a)
- Solve the prevention control model based on , obtain the system state after prevention control, and calculate the prevention control cost
- (b)
- Based on the system state after prevention control, solve the emergency control model for the system under anticipated faults, and calculate the emergency control cost
- (c)
- Calculate the total cost of coordinated control as
- Step 4: Update the factor interval : if , set ; otherwise, set ;
- Step 5: Termination check: if , terminate the iteration and output the optimal control cost; otherwise, continue the iteration.
4. Case Study
4.1. Analysis and Evaluation of Identification Results
4.1.1. Analysis and Evaluation of Critical Line Identification Methods
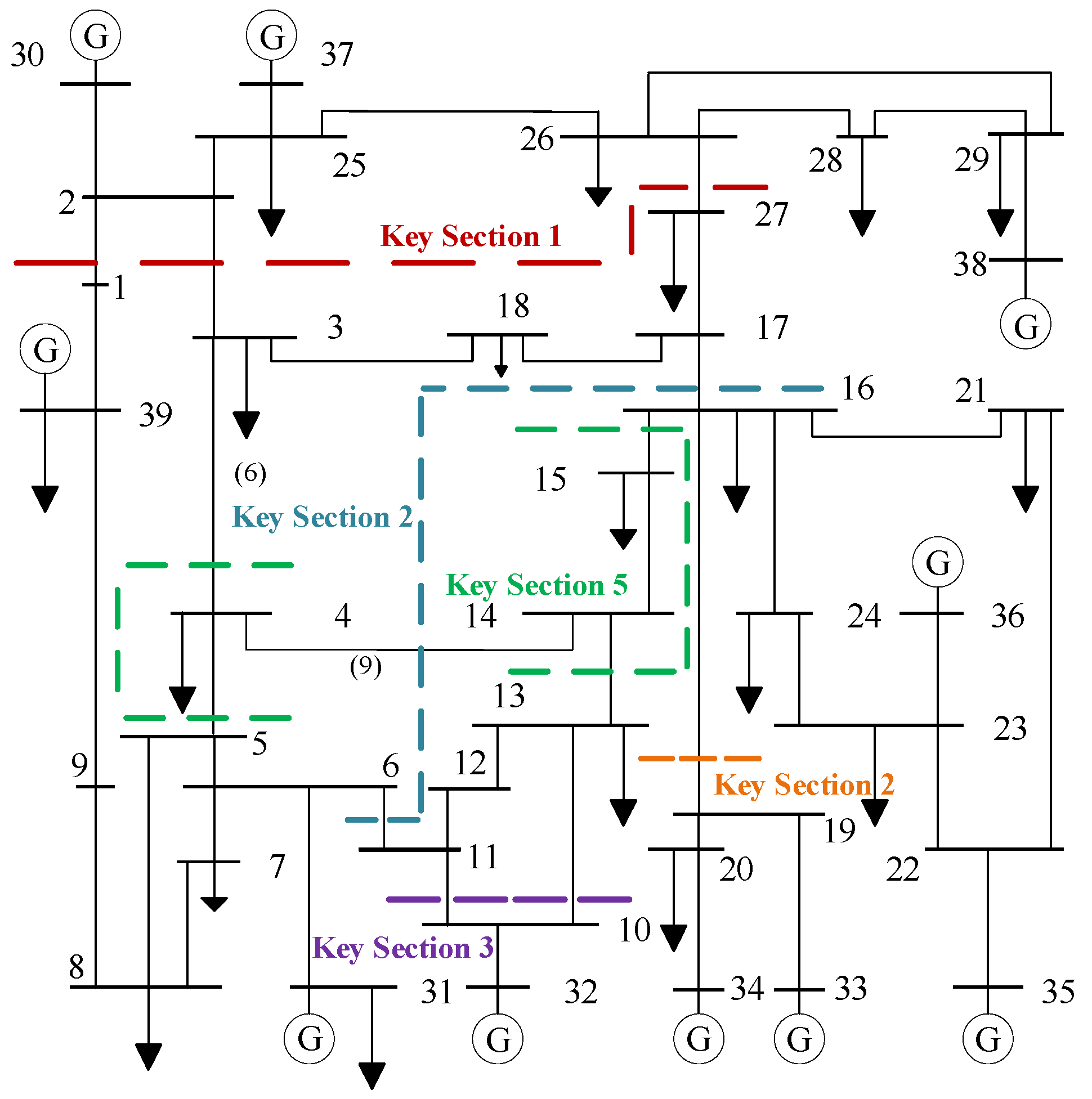
4.1.2. Analysis of Key Transmission Section Identification Results
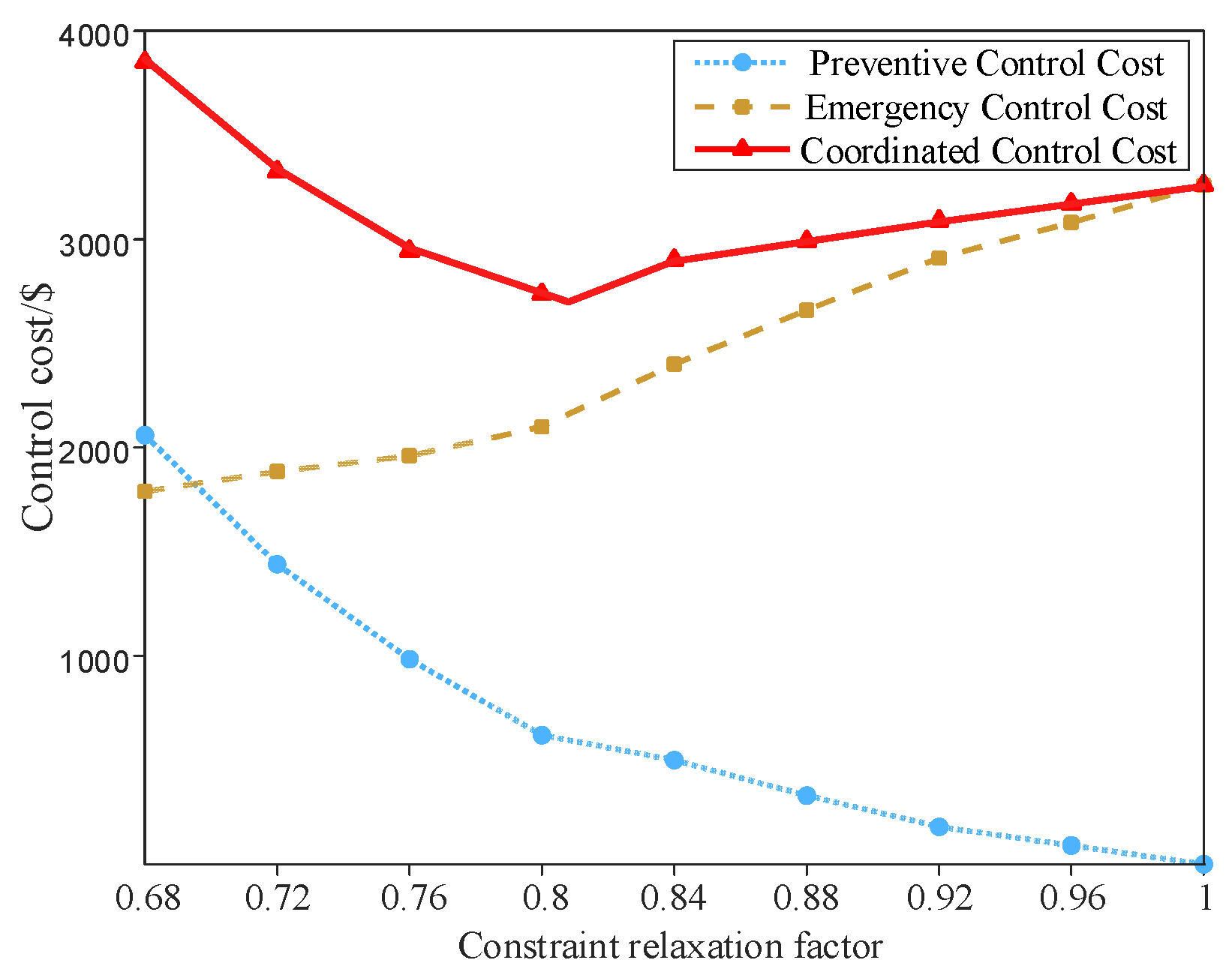
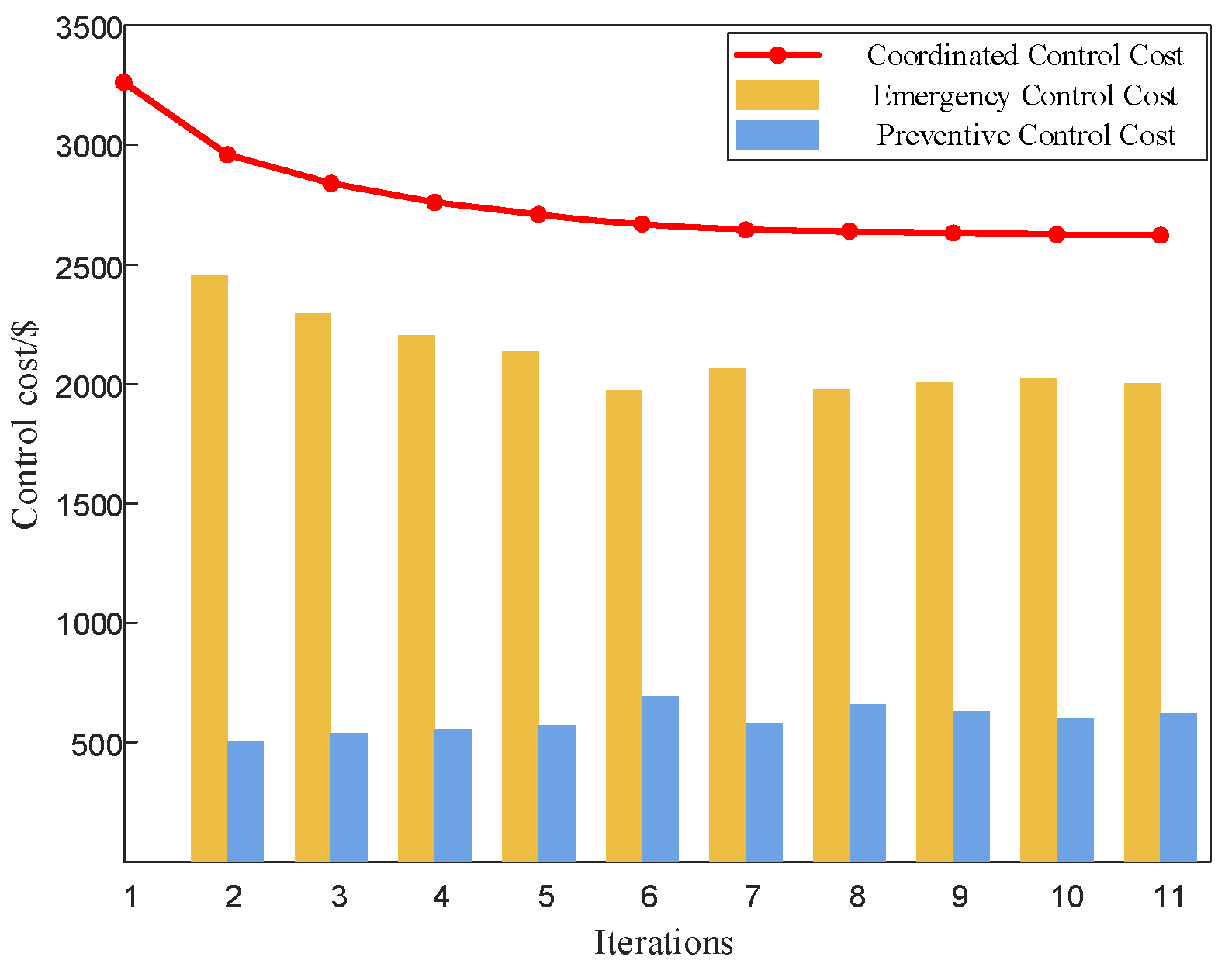
4.2. Analysis of Prevention–Emergency Coordinated Control Results
5. Conclusions
- (1)
- The critical line characteristics established in this paper by considering the topological, power flow, and voltage characteristics of transmission lines can identify the critical lines in the system more accurately.
- (2)
- By using the Theil index of power flow impact rate to analyze the impact on the initial transmission sections after critical line faults, the multi-strategy identification method for key transmission sections proposed in this paper can accurately identify the key transmission sections with strong internal electrical correlation from the initial transmission sections.
- (3)
- The coordinated optimal control strategy proposed in this paper for key transmission sections can effectively achieve the optimal coordinated control of prevention control and emergency control, reduce the total coordinated control cost of the system, and significantly improve the system’s safety.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.; Pandey, A.; Goswami, P.; Pentayya, P.; Kazi, F. Analysis of Mumbai Grid Failure Restoration on Oct 12, 2020: Challenges and Lessons Learnt. IEEE Trans. Power Syst. 2022, 37, 4555–4567. [Google Scholar] [CrossRef]
- Chen, C.; Hu, Y.; Meng, X.; Yu, J. Cascading Failures in Power Grids: A Load Capacity Model with Node Centrality. Complex Syst. Model. Simul. 2024, 4, 1–14. [Google Scholar] [CrossRef]
- Haes Alhelou, H.; Hamedani-Golshan, M.E.; Njenda, T.C.; Siano, P. A Survey on Power System Blackout and Cascading Events: Research Motivations and Challenges. Energies 2019, 12, 682. [Google Scholar] [CrossRef]
- Lin, W.; Yang, Z.; Yu, J.; Jin, L.; Li, W. Tie-Line Power Transmission Region in a Hybrid Grid: Fast Characterization and Expansion Strategy. IEEE Trans. Power Syst. 2020, 35, 2222–2231. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, B.; Zhang, Z. An electrical betweenness approach for vulnerability assessment of power grids considering the capacity of generators and load. Phys. A Stat. Mech. Its Appl. 2011, 390, 4692–4701. [Google Scholar] [CrossRef]
- Luo, G.; Shi, D.; Chen, J. Automatic identification of transmission sections based on complex network theory. IET Gener. Transm. Distrib. 2014, 8, 1203–1210. [Google Scholar] [CrossRef]
- Fan, B.; Shu, N.; Li, Z.; Li, F. Critical Nodes Identification for Power Grid Based on Electrical Topology and Power Flow Distribution. IEEE Syst. J. 2023, 17, 4874–4884. [Google Scholar] [CrossRef]
- Sun, J.; Liu, J.; Li, C.; Zhi, N. An identification method for vulnerable lines based on combination weighting method and GraphSAGE algorithm. Int. J. Electr. Power Energy Syst. 2023, 149, 109035. [Google Scholar] [CrossRef]
- Chen, B.; Chen, X.; Chen, H. Efficient algorithm for finding k shortest paths based on re-optimization technique. Transp. Res. Part. E Logist. Transp. Rev. 2019, 133, 101819. [Google Scholar] [CrossRef]
- Guo, J.; Fu, Y.; Li, Z.; Shahidehpour, M. Direct calculation of line outage distribution factors. IEEE Trans. Power Syst. 2009, 24, 1633–1634. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J.; Xiong, X.; Chen, J. A Post-Contingency Power Flow Control Strategy for AC/DC Hybrid Power Grid Considering the Dynamic Electrothermal Effects of Transmission Lines. IEEE Access 2019, 7, 65288–65302. [Google Scholar] [CrossRef]
- Wang, C.; Feng, C.; Zeng, Y.; Zhang, F. Improved Correction Strategy for Power Flow Control Based on Multi-Machine Sensitivity Analysis. IEEE Access 2020, 8, 82391–82403. [Google Scholar] [CrossRef]
- Mazzi, N.; Zhang, B.; Kirschen, D.S. An Online Optimization Algorithm for Alleviating Contingencies in Transmission Networks. IEEE Trans. Power Syst. 2018, 33, 5572–5582. [Google Scholar] [CrossRef]
- Zhao, X.; Ling, X.; Yan, M.; Dong, Y.; He, M.; Zhao, Y. Identification of Critical Transmission Sections Considering N-K Contingencies Under Extreme Events. Energies 2025, 18, 4342. [Google Scholar] [CrossRef]
- Gou, B.; Zhang, H. Fast real-time corrective control strategy for overload relief in bulk power systems. IET Gener. Transm. Distrib. 2013, 7, 1508–1515. [Google Scholar] [CrossRef]
- Amusan, O.; Shi, S.; Wu, D.; Liao, H. Structural Vulnerability Analysis of Interdependent Electric Power and Natural Gas Systems. Energies 2023, 16, 6918. [Google Scholar] [CrossRef]
- Chen, Y.; Nan, L.; He, C.; Wang, Y. Transmission Interconnections Identification for Electricity System Considering Impacts of Natural Gas Systems. IEEE Trans. Smart Grid 2023, 14, 1920–1932. [Google Scholar] [CrossRef]
- Wang, Z.; He, J.; Nechifor, A.; Zhang, D.; Crossley, P. Identification of Critical Transmission Lines in Complex Power Networks. Energies 2017, 10, 1294. [Google Scholar] [CrossRef]
- Qiu, G.; Liu, Y.; Liu, J.; Zhao, J.; Wang, L.; Liu, T.; Gao, H. Analytic Deep Learning-based Surrogate Model for Operational Planning With Dynamic TTC Constraints. IEEE Trans. Power Syst. 2021, 36, 3507–3519. [Google Scholar] [CrossRef]
- Yuan, H.; Xu, Y. Preventive-Corrective Coordinated Transient Stability Dispatch of Power Systems with Uncertain Wind Power. IEEE Trans. Power Syst. 2020, 35, 3616–3626. [Google Scholar] [CrossRef]
- Yang, L.; Li, C. Identification of Vulnerable Lines in Smart Grid Systems Based on Improved Agglomerative Hierarchical Clustering. IEEE Access 2023, 11, 13554–13563. [Google Scholar] [CrossRef]
- Zhou, B.; Cai, Y.; Zang, T.; Wu, J.; Li, X.; Dong, S. Reliability Optimization Method for Gas–Electric Integrated Energy Systems Considering Cyber–Physical Interactions. Energies 2023, 16, 5187. [Google Scholar] [CrossRef]

| Line | |||||
|---|---|---|---|---|---|
| 1 | 1 | 0.7948 | 0.7301 | 2.5249 | |
| 2 | 0.9619 | 0.4009 | 0.7903 | 2.1531 | |
| 3 | 0.4409 | 0.7692 | 0.8037 | 2.0138 | |
| 4 | 0.3242 | 0.8696 | 0.7727 | 1.9665 | |
| 5 | 0.1418 | 1 | 0.7537 | 1.8955 | |
| 6 | 0.6789 | 0.5089 | 0.7008 | 1.8886 | |
| 7 | 0.5479 | 0.5268 | 0.7428 | 1.8175 | |
| 8 | 0.5836 | 0.4020 | 0.8108 | 1.7964 | |
| 9 | 0.2188 | 0.9721 | 0.5493 | 1.7402 | |
| 10 | 0.4596 | 0.4934 | 0.6829 | 1.7259 |
| Initial Transmission Sections | |||
|---|---|---|---|
| , , | 1.1361 | 0.1359 | 0.4250 |
| , , | 1.1676 | 0.1044 | 0.4575 |
| , , , , | 1.1809 | 0.0911 | 0.5615 |
| Key Sections | TTC | |
|---|---|---|
| Proposed Method | 1224 MW | |
| Reference [14] | 1068 MW 2035 MW 1724 MW |
| Anticipated Fault | Fault Type | Probability |
|---|---|---|
| 2 × 10−2 | ||
| 1.1 × 10−2 | ||
| 9.6 × 10−3 | ||
| 4.4 × 10−3 | ||
| 8.6 × 10−5 |
| Parameters | Symbol | Value |
|---|---|---|
| Cost of increase power | 5 $/MW | |
| Cost of decrease power | 5 $/MW | |
| Cost of load cut | 1000 $/MW | |
| Cost of generator cut | 100 $/MW | |
| Maximum load rate | 1 | |
| Ramp rate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; He, C.; Zhang, H.; Nan, L.; Liu, T.; Gao, J.; Wang, B.; Ye, X.; Sun, X. Multi-Criteria-Based Key Transmission Section Identification and Prevention–Emergency Coordinated Optimal Control Strategy. Energies 2025, 18, 5871. https://doi.org/10.3390/en18225871
Peng X, He C, Zhang H, Nan L, Liu T, Gao J, Wang B, Ye X, Sun X. Multi-Criteria-Based Key Transmission Section Identification and Prevention–Emergency Coordinated Optimal Control Strategy. Energies. 2025; 18(22):5871. https://doi.org/10.3390/en18225871
Chicago/Turabian StylePeng, Xinyu, Chuan He, Honghao Zhang, Lu Nan, Tianqi Liu, Jian Gao, Biao Wang, Xi Ye, and Xinwei Sun. 2025. "Multi-Criteria-Based Key Transmission Section Identification and Prevention–Emergency Coordinated Optimal Control Strategy" Energies 18, no. 22: 5871. https://doi.org/10.3390/en18225871
APA StylePeng, X., He, C., Zhang, H., Nan, L., Liu, T., Gao, J., Wang, B., Ye, X., & Sun, X. (2025). Multi-Criteria-Based Key Transmission Section Identification and Prevention–Emergency Coordinated Optimal Control Strategy. Energies, 18(22), 5871. https://doi.org/10.3390/en18225871








