Optimized Defense Resource Allocation for Coupled Power-Transportation Networks Considering Information Security
Abstract
1. Introduction
- (1)
- We formulated a tri-level DAC model as a Stackelberg game, casting cybersecurity planning in coupled transport–power networks as multi-agent sequential decision-making.
- (2)
- We designed a hybrid KKT-reduced solution framework that combines KKT optimality conditions with IIE to tackle the computational challenges of tri-level optimization.
- (3)
- We adopted three evaluation metrics—maximum voltage deviation (MVD), root-mean-square (RMS) voltage deviation, and voltage qualification rate (VQR)—to quantify the synergy between defense allocation and corrective operation, with effectiveness validated in simulation studies.
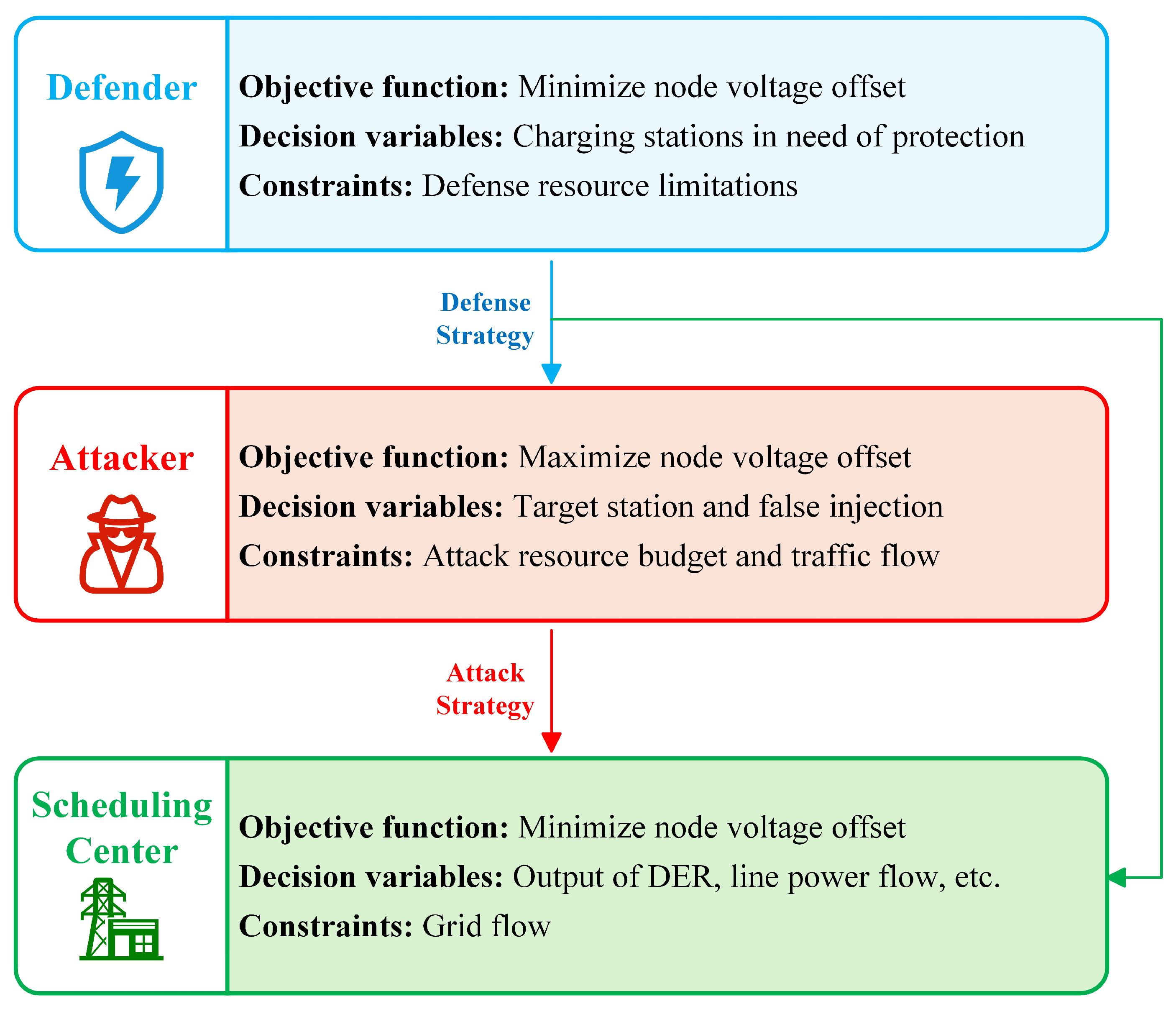
2. A Tri-Level Defense–Attack–Correction Optimization Formulation in a Stackelberg Framework
3. Formulation
3.1. Objective
3.2. Constraints
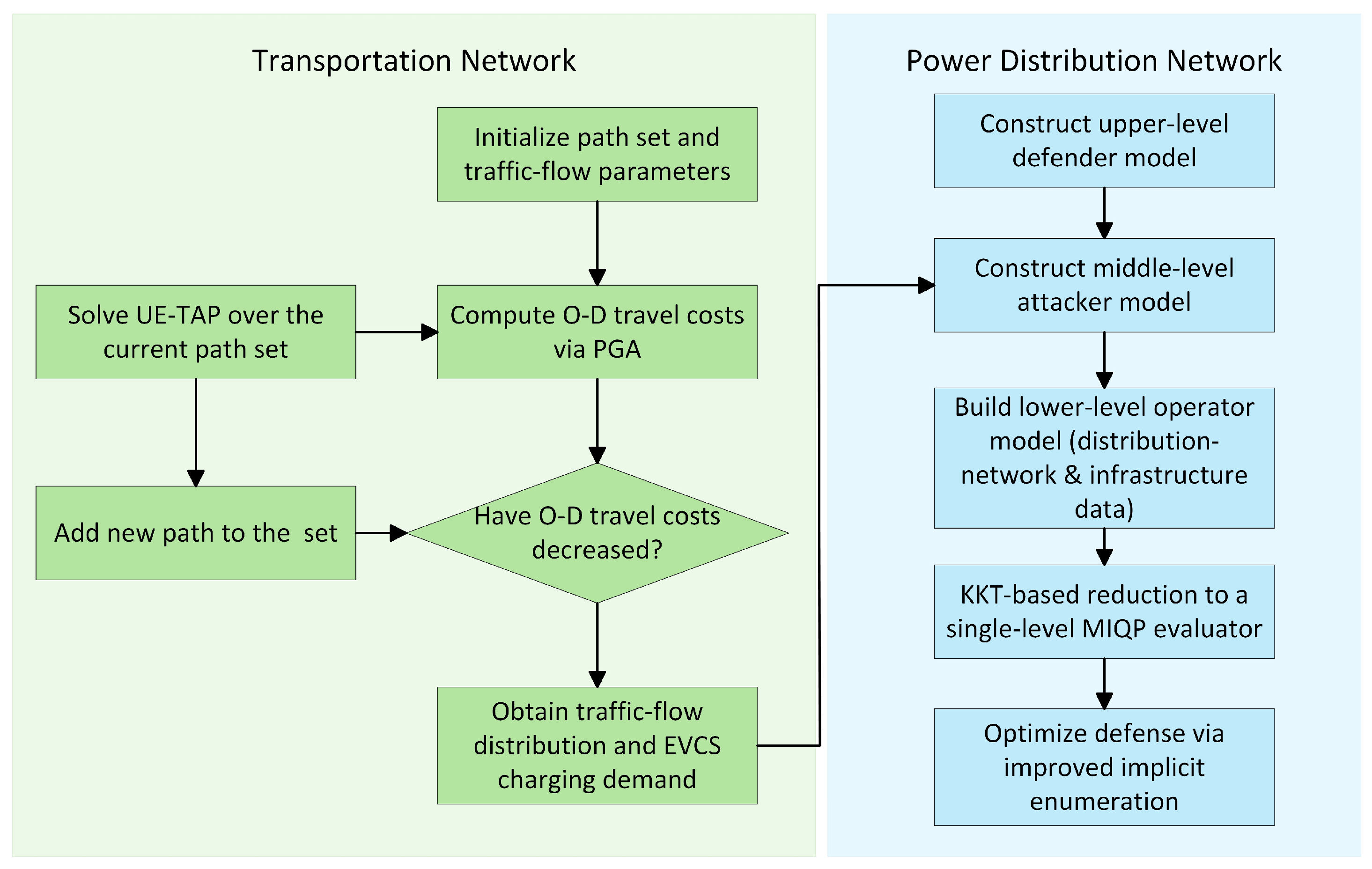
4. Model Solution Method
4.1. Construction of the Bi-Level Optimization Model
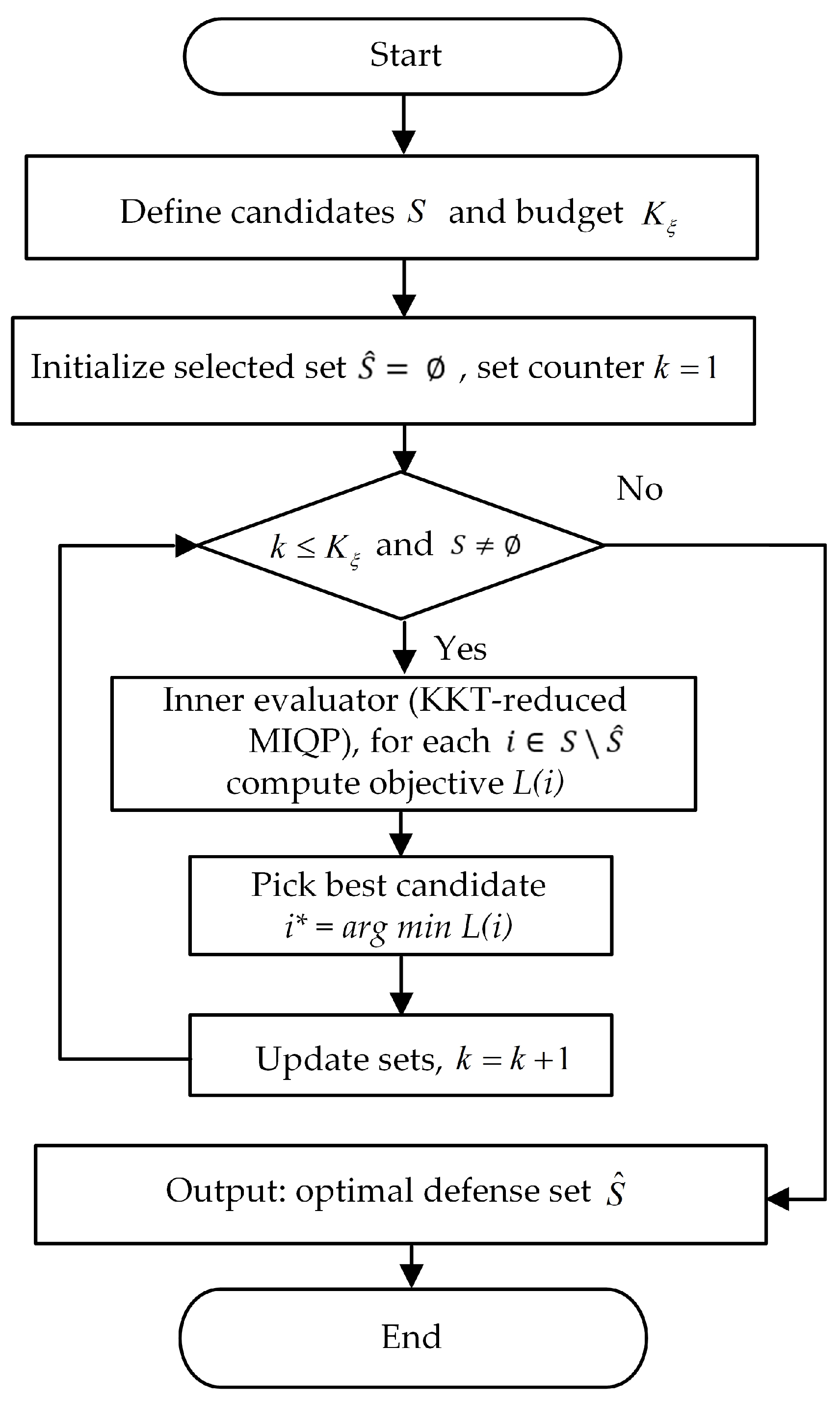
4.2. Solution Method Based on the Improved Implicit Enumeration Algorithm
4.3. Node Voltage Evaluation Index
- Maximum Node Voltage Deviation.
- 2.
- Root Mean Square (RMS) of Node Voltage Deviation.
- 3.
- Bus-Voltage Qualification Rate (VQR).
5. Case Study
5.1. Parameter Settings for the Case Study
5.2. Analysis of Defense Resource Allocation Effectiveness
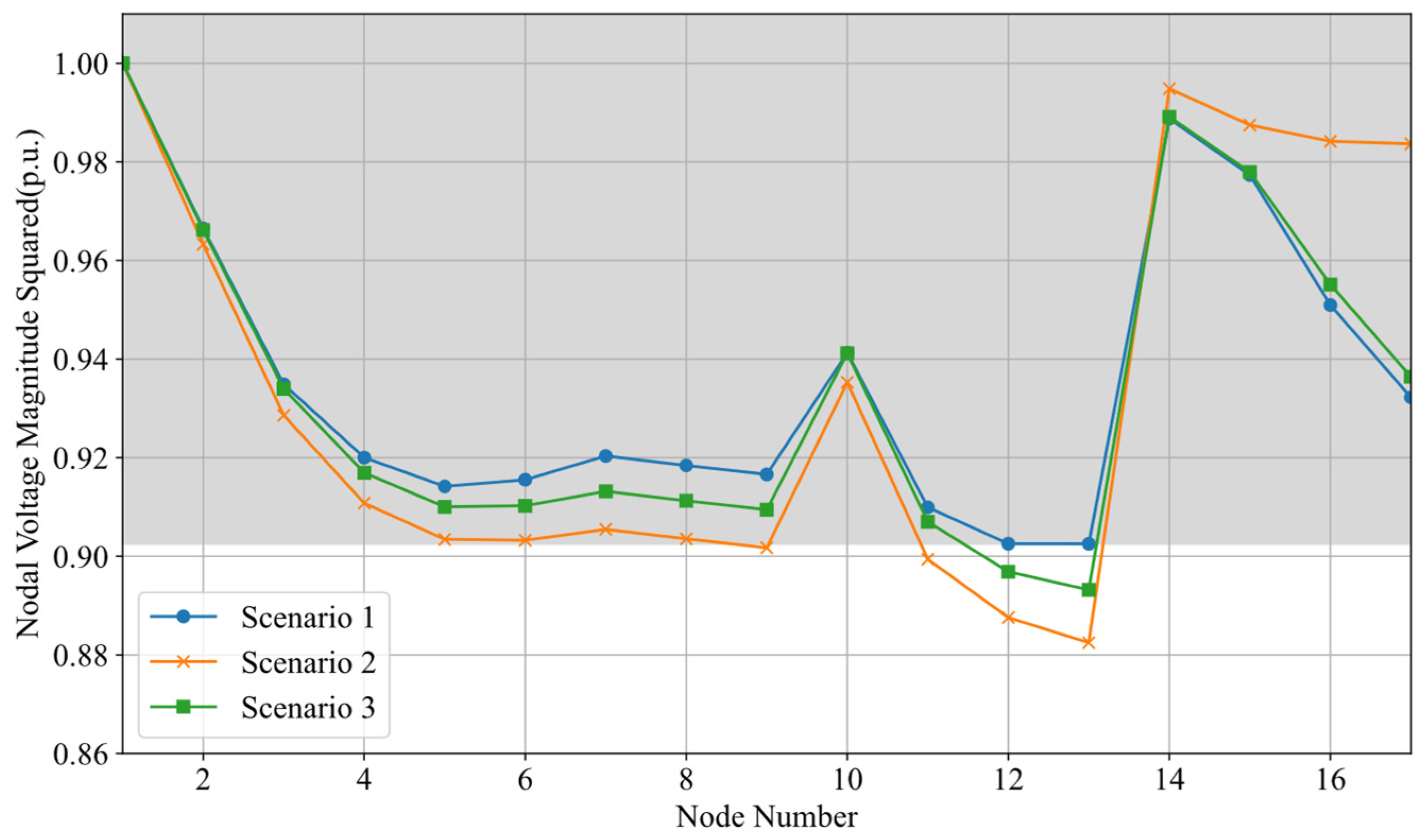
5.3. Analysis of the Impact of DESS and PV on Defense Resource Allocation
5.4. Analysis of the Superiority of the Improved Implicit Enumeration Algorithm
- Quality and search effort (Table 7).
- Complexity perspective.
- Runtime and memory (Table 8).
- Measurement protocol.
5.5. Comparison with Column-and-Constraint Generation
6. Conclusions
- (i)
- Frequency-aware resilience. Extend the DAC architecture to frequency stability by modeling convex proxies for system frequency response—nadir, rate of change in frequency, and automatic generation control/area control error—and co-optimize DESS and EV fast-frequency-response headroom together with hardening of frequency-critical telemetry and control channels.
- (ii)
- Uncertainty and co-design. Develop multi-period, uncertainty-aware scheduling that couples traffic-demand and PV-output variability with adversarial perturbations, while jointly designing detection and defense via robust state estimation and anomaly aware reweighting.
- (iii)
- Scalability and validation. Scale the framework to city-scale, unbalanced three-phase networks using decomposition, parallelization, and learning-guided pruning; release open benchmarks, a reference solver, and digital-twin co-simulation to enable reproducible validation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EVCS | Electric vehicle charging station |
| EV | Electric vehicle |
| V2G | Vehicle-to-grid |
| FDIA | False data injection attack |
| UE-TAP | User-equilibrium traffic assignment |
| DAD | Defense–attack–defense |
| C&CG | Column-and-constraint generation |
| PV | Photovoltaic |
| KKT | Karush–Kuhn–Tucker |
| IIE | Improved implicit enumeration |
| MVD | Maximum voltage deviation |
| RMS | Root-mean-square |
| VQR | Voltage qualification rate |
| DESS | Distributed energy storage systems |
| MIP | Bi-level mixed-integer program |
| MIQP | Mixed-integer quadratic programming |
| CE | Complete enumeration |
| DER | Distributed energy resources |
| p.u. | Per-unit |
| PV VAR | Reactive power from PV inverters |
| Wall | Wall-clock time |
| RSS | Resident set size |
| DAC | Defense–attack–correction |
References
- Acharya, S. Cybersecurity of Electric Vehicle Charging. Doctoral Dissertation, New York University Tandon School of Engineering, Brooklyn, NY, USA, 2022. [Google Scholar]
- Qian, T.; Fang, M.; Hu, Q.; Shao, C.; Zheng, J. V2Sim: An Open-Source Microscopic V2G Simulation Platform in Urban Power and Transportation Network. arXiv 2024. [Google Scholar] [CrossRef]
- Ribas Monteiro, L.F.; Rodrigues, Y.R.; Zambroni De Souza, A.C. Cybersecurity in Cyber–Physical Power Systems. Energies 2023, 16, 4556. [Google Scholar] [CrossRef]
- Wang, B.; Dehghanian, P.; Wang, S.; Mitolo, M. Electrical Safety Considerations in Large-Scale Electric Vehicle Charging Stations. IEEE Trans. Ind. Appl. 2019, 55, 6603–6612. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, T.; Chen, T.; Hu, Q.; Chen, H.; Hu, X.; Jiang, Z. A High-Resolution Electric Vehicle Charging Transaction Dataset with Multidimensional Features in China. Sci. Data 2025, 12, 643. [Google Scholar] [CrossRef]
- Babu, P.R.; Palaniswamy, B.; Reddy, A.G.; Odelu, V.; Kim, H.S. A Survey on Security Challenges and Protocols of Electric Vehicle Dynamic Charging System. Secur. Priv. 2022, 5, e210. [Google Scholar] [CrossRef]
- Antoun, J.; Kabir, M.E.; Moussa, B.; Atallah, R.; Assi, C. A Detailed Security Assessment of the EV Charging Ecosystem. IEEE Netw. 2020, 34, 200–207. [Google Scholar] [CrossRef]
- Fraiji, Y.; Ben Azzouz, L.; Trojet, W.; Saidane, L.A. Cyber Security Issues of Internet of Electric Vehicles. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Subran, A.K.; Sankaran, S.; Sutraye, P.; Nishad, A.K. Threat Modeling and Attack Simulation of Charging Infrastructures in Electric Vehicles. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24–28 June 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Sepehrzad, R.; Faraji, M.J.; Al-Durra, A.; Sadabadi, M.S. Enhancing Cyber-Resilience in Electric Vehicle Charging Stations: A Multi-Agent Deep Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2024, 25, 18049–18062. [Google Scholar] [CrossRef]
- Qian, T.; Ming, W.; Shao, C.; Hu, Q.; Wang, X.; Wu, J.; Wu, Z. An Edge Intelligence-Based Framework for Online Scheduling of Soft Open Points with Energy Storage. IEEE Trans. Smart Grid 2024, 15, 2934–2945. [Google Scholar] [CrossRef]
- Gorzałczany, M.B.; Rudziński, F. Detection and Localization of False Data Injection Attacks in Smart Grids Applying an Interpretable Fuzzy Genetic Machine Learning/Data Mining Approach. Energies 2025, 18, 1568. [Google Scholar] [CrossRef]
- Radhoush, S.; Vannoy, T.; Liyanage, K.; Whitaker, B.M.; Nehrir, H. Distribution System State Estimation and False Data Injection Attack Detection with a Multi-Output Deep Neural Network. Energies 2023, 16, 2288. [Google Scholar] [CrossRef]
- Kausar, F.; Deo, S.; Hussain, S.; Ul Haque, Z. Federated Deep Learning Model for False Data Injection Attack Detection in Cyber Physical Power Systems. Energies 2024, 17, 5337. [Google Scholar] [CrossRef]
- Alcaraz, C.; Lopez, J.; Wolthusen, S. OCPP Protocol: Security Threats and Challenges. IEEE Trans. Smart Grid 2017, 8, 2452–2459. [Google Scholar] [CrossRef]
- Ghafouri, M.; Kabir, E.; Moussa, B.; Assi, C. Coordinated Charging and Discharging of Electric Vehicles: A New Class of Switching Attacks. ACM Trans. Cyber-Phys. Syst. 2022, 6, 1–26. [Google Scholar] [CrossRef]
- Kabir, M.E.; Ghafouri, M.; Moussa, B.; Assi, C. A Two-Stage Protection Method for Detection and Mitigation of Coordinated EVSE Switching Attacks. IEEE Trans. Smart Grid 2021, 12, 4377–4388. [Google Scholar] [CrossRef]
- Wei, F.; Lin, X. Cyber-Physical Attack Launched from EVSE Botnet. IEEE Trans. Power Syst. 2024, 39, 3603–3614. [Google Scholar] [CrossRef]
- Soykan, E.U.; Bagriyanik, M.; Soykan, G. Disrupting the Power Grid via EV Charging: The Impact of the SMS Phishing Attacks. Sustain. Energy Grids Netw. 2021, 26, 100477. [Google Scholar] [CrossRef]
- Acharya, S.; Mieth, R.; Karri, R.; Dvorkin, Y. False Data Injection Attacks on Data Markets for Electric Vehicle Charging Stations. Adv. Appl. Energy 2022, 7, 100098. [Google Scholar] [CrossRef]
- Nasr, T.; Torabi, S.; Bou-Harb, E.; Fachkha, C.; Assi, C. Power Jacking Your Station: In-Depth Security Analysis of Electric Vehicle Charging Station Management Systems. Comput. Secur. 2022, 112, 102511. [Google Scholar] [CrossRef]
- Bo, X.; Qu, Z.; Wang, L.; Dong, Y.; Zhang, Z.; Wang, D. Active Defense Research against False Data Injection Attacks of Power CPS Based on Data-Driven Algorithms. Energies 2022, 15, 7432. [Google Scholar] [CrossRef]
- Aljohani, T.; Almutairi, A. A Comprehensive Survey of Cyberattacks on EVs: Research Domains, Attacks, Defensive Mechanisms, and Verification Methods. Def. Technol. 2024, 42, 31–58. [Google Scholar] [CrossRef]
- Liberati, F.; Garone, E.; Di Giorgio, A. Review of Cyber-Physical Attacks in Smart Grids: A System-Theoretic Perspective. Electronics 2021, 10, 1153. [Google Scholar] [CrossRef]
- Qian, T.; Liang, Z.; Shao, C.; Guo, Z.; Hu, Q.; Wu, Z. Unsupervised Learning for Efficiently Distributing EVs Charging Loads and Traffic Flows in Coupled Power and Transportation Systems. Appl. Energy 2025, 377, 124476. [Google Scholar] [CrossRef]
- Smith, M.D.; Paté-Cornell, M.E. Cyber Risk Analysis for a Smart Grid: How Smart Is Smart Enough? A Multiarmed Bandit Approach to Cyber Security Investment. IEEE Trans. Eng. Manag. 2018, 65, 434–447. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, Y.; Li, Y.; Li, Z.; Yao, W.; Shi, X. Robust Substation Enhancement Strategy for Allocating the Defensive Resource against the Cyber-Attacks on IEDs. IEEE Trans. Ind. Inform. 2024, 20, 3539–3550. [Google Scholar] [CrossRef]
- Tang, X.; Sun, R.; Tan, Y.; Zhao, Y. IED-Attacks Oriented Robust Optimization Model of Defender-Attacker-Defender forMultiple Substations. Proc. CSU-EPSA 2024, 36, 124–134. [Google Scholar]
- Wen, J.; Gan, W.; Chu, C.-C.; Jiang, L.; Luo, J. Robust Resilience Enhancement by EV Charging Infrastructure Planning in Coupled Power Distribution and Transportation Systems. IEEE Trans. Smart Grid 2025, 16, 491–504. [Google Scholar] [CrossRef]
- Shan, X.G.; Zhuang, J. A Game-Theoretic Approach to Modeling Attacks and Defenses of Smart Grids at Three Levels. Reliab. Eng. Syst. Saf. 2020, 195, 106683. [Google Scholar] [CrossRef]
- Qian, T.; Liang, Z.; Chen, S.; Hu, Q.; Wu, Z. A Tri-Level Demand Response Framework for EVCS Flexibility Enhancement in Coupled Power and Transportation Networks. IEEE Trans. Smart Grid 2025, 16, 598–611. [Google Scholar] [CrossRef]
- Shao, C.-W.; Li, Y.-F. Optimal Defense Resources Allocation for Power System Based on Bounded Rationality Game Theory Analysis. IEEE Trans. Power Syst. 2021, 36, 4223–4234. [Google Scholar] [CrossRef]
- Liang, Z.; Qian, T.; Shao, C.; Hu, Q.; Wu, Z.; Xu, Q.; Zheng, J. A Strategic EV Charging Networks Planning Framework for Intercity Highway With Time-Expanded User Equilibrium. IEEE Trans. Smart Grid 2025. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, B.; Jin, X.; Luo, Y.; Song, M.; Ye, Y.; Hu, Q.; Chen, Q.; Zambroni, A.C. Mitigating Power Grid Impact from Proactive Data Center Workload Shifts: A Coordinated Scheduling Strategy Integrating Synergistic Traffic—Data—Power Networks. Appl. Energy 2025, 377, 124697. [Google Scholar] [CrossRef]
- Dong, Z.; Tian, M.; Tang, M.; Liang, J. Power Generation Allocation of Cyber–Physical Power Systems from a Defense–Attack–Defense Perspective. Int. J. Electr. Power Energy Syst. 2024, 156, 109690. [Google Scholar] [CrossRef]
- Zhao, Z.; Shang, Y.; Qi, B.; Wang, Y.; Sun, Y.; Zhang, Q. Research on Defense Strategies for Power System Frequency Stability under False Data Injection Attacks. Appl. Energy 2024, 371, 123711. [Google Scholar] [CrossRef]
- Drake, D.; Mavikumbure, H.S.; Cobilean, V.; Manic, M. Cyber-Physical Security Trends of EV Charging Systems: A Survey. In Proceedings of the IECON 2024—50th Annual Conference of the IEEE Industrial Electronics Society, Chicago, IL, USA, 3–6 November 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Ren, L.; Binyuan, Y.; Hengdao, G.; Junrong, L.; Yihua, Z.; Yun, F.; Liang, T.; Zeyuan, Z. Research on Relay Setting Attack Defense in Power Systems Based on a Three-Layer Optimization Model. Front. Energy Res. 2024, 12, 1502078. [Google Scholar] [CrossRef]
- Li, X.; Li, W.; Wang, N.; Li, L.; Gong, X. Resilience Enhancement by Line Hardening for Communication Routing Considering Renewable Energy Sources in Cyber-physical Power Systems. IET Renew. Power Gener. 2024, 18, 2477–2495. [Google Scholar] [CrossRef]
- Wang, F.; Zhuge, C.; Chen, A. Data-Driven Vulnerability Analysis of Shared Electric Vehicle Systems to Cyberattacks. Transp. Res. Part D Transp. Environ. 2024, 135, 104379. [Google Scholar] [CrossRef]
- Naderi, E.; Asrari, A.; Fajri, P. False Data Injection Cyberattacks Targeting Electric Vehicles in Smart Power Distribution Systems. In Proceedings of the 2024 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 19–21 June 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Elshazly, A.A.; Elgarhy, I.; Eltoukhy, A.T.; Mahmoud, M.; Eberle, W.; Alsabaan, M.; Alshawi, T. False Data Injection Attacks on Reinforcement Learning-Based Charging Coordination in Smart Grids and a Countermeasure. Appl. Sci. 2024, 14, 10874. [Google Scholar] [CrossRef]
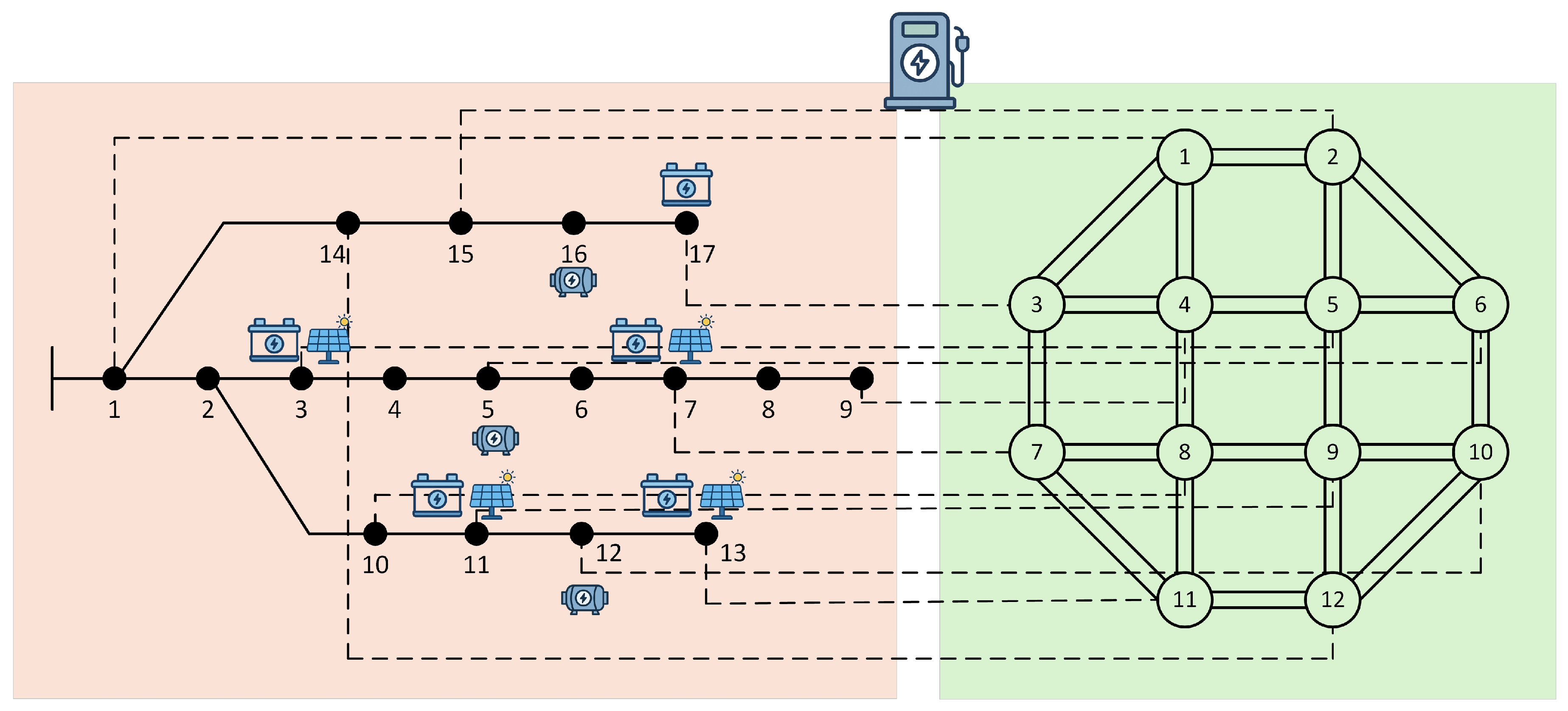
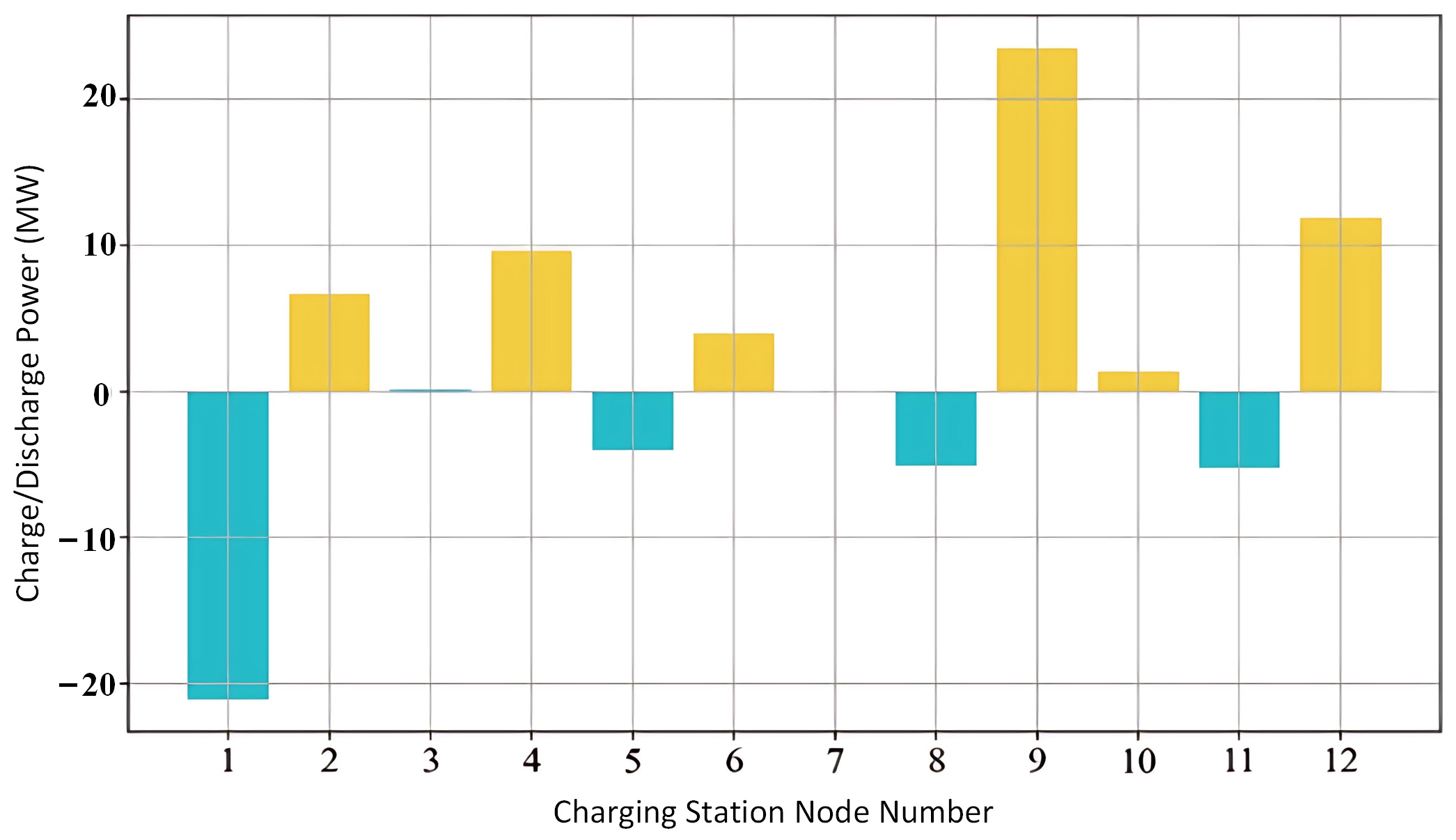
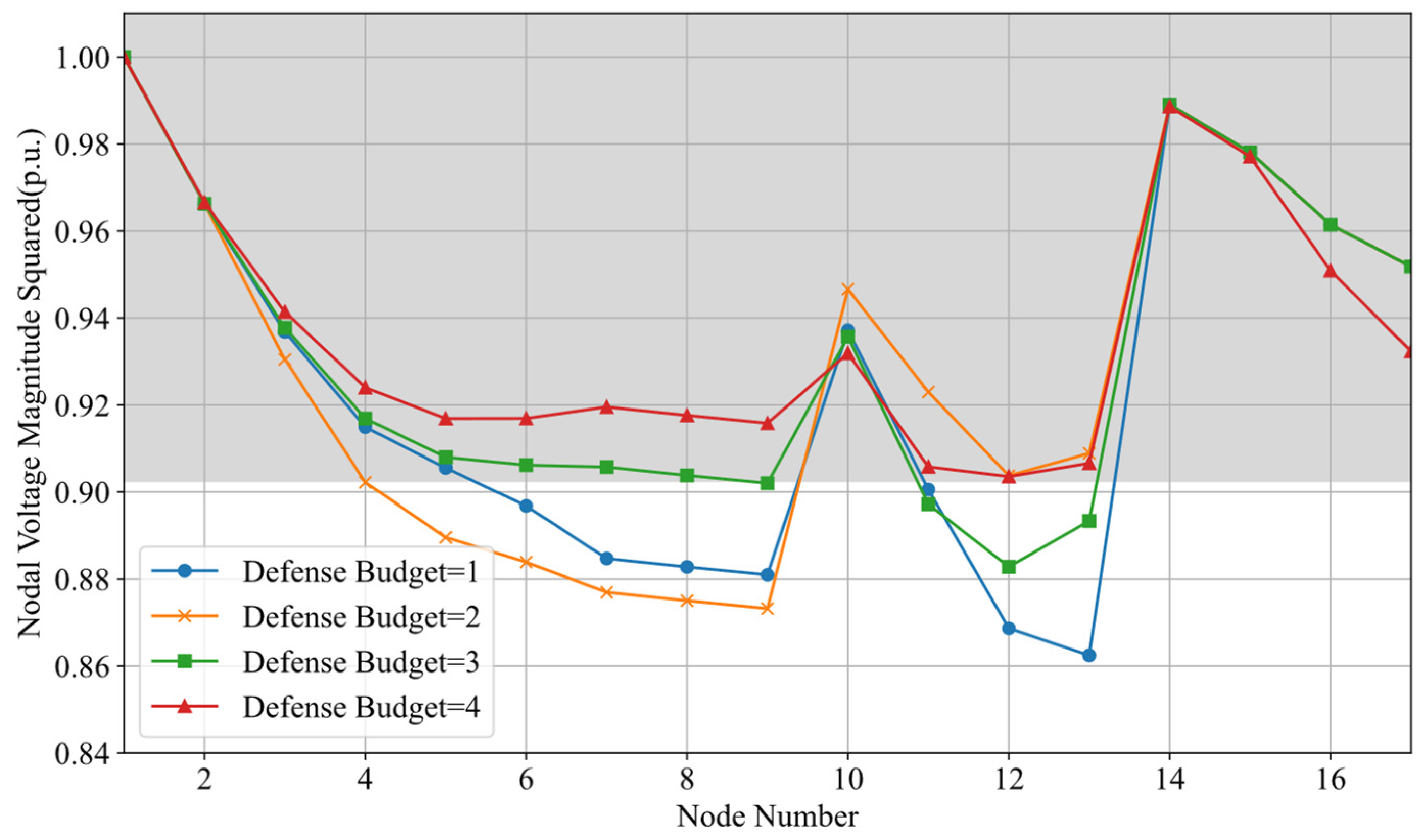

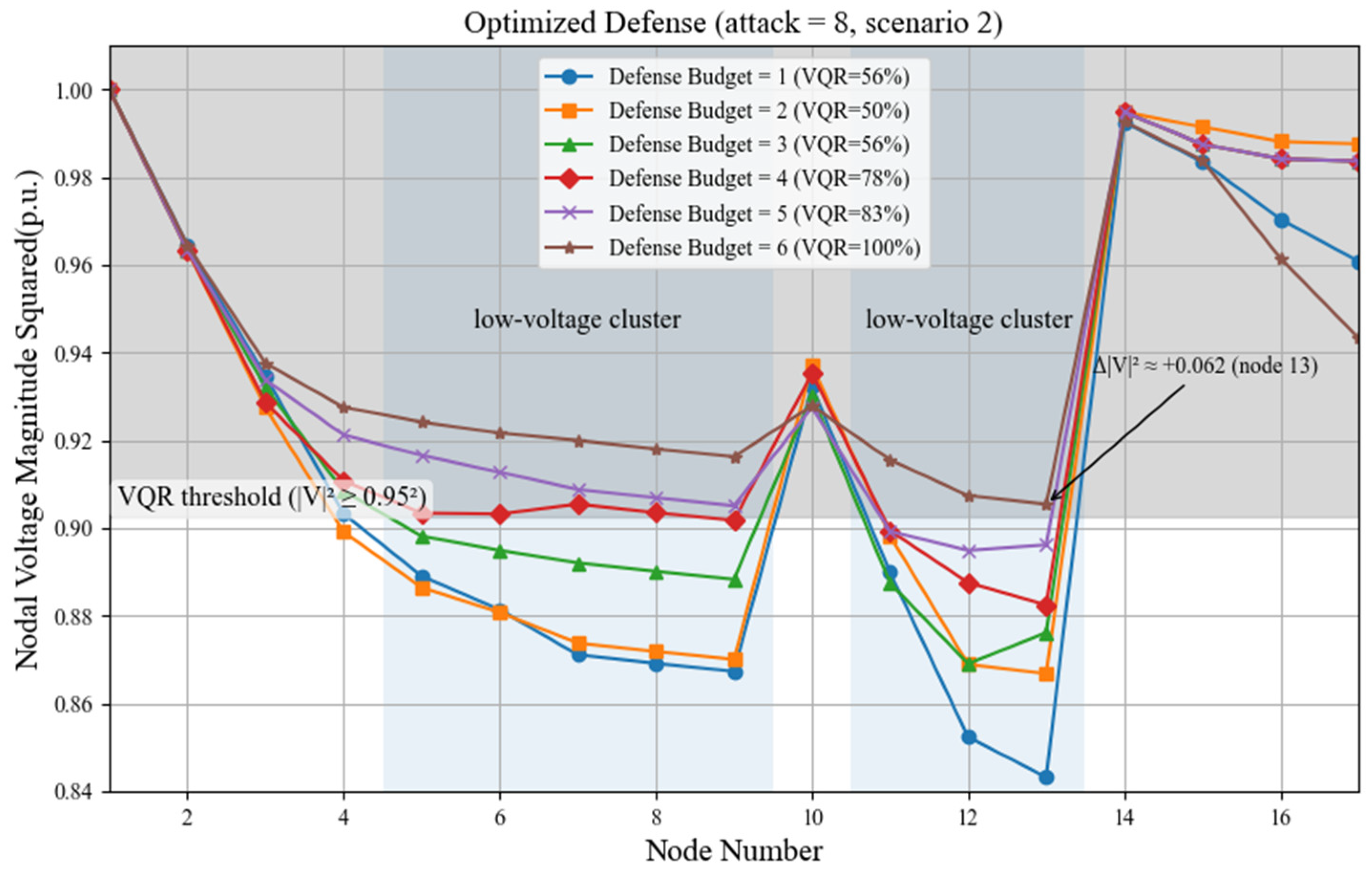
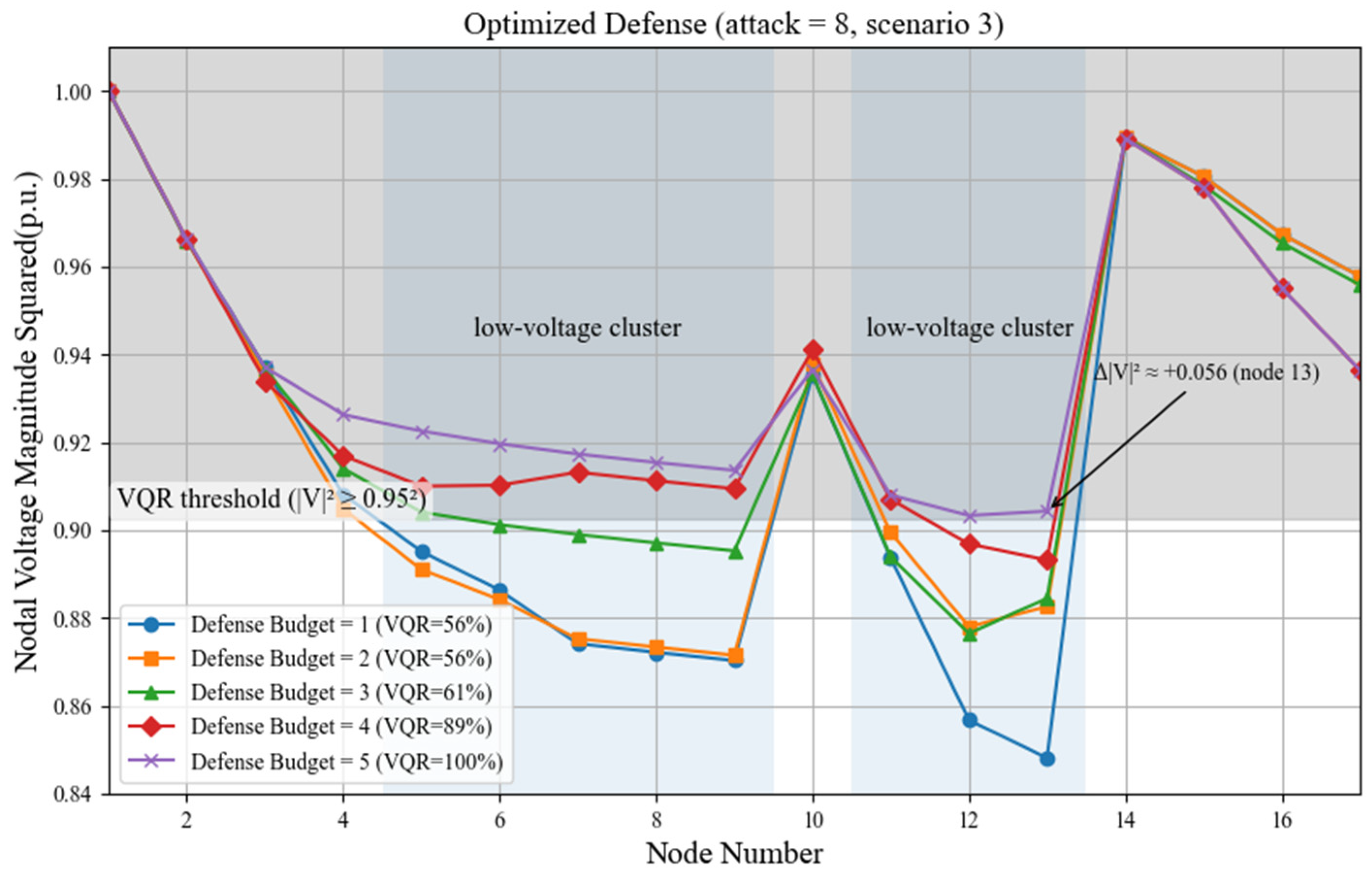
| Transportation Node | Distribution Bus | Transportation Node | Distribution Bus |
|---|---|---|---|
| 1 | 1 | 7 | 7 |
| 2 | 15 | 8 | 10 |
| 3 | 17 | 9 | 11 |
| 4 | 9 | 10 | 12 |
| 5 | 3 | 11 | 13 |
| 6 | 5 | 12 | 14 |
| Defense Resource Budget | Protected EVCS | Attacked EVCS | MVD (p.u.) | RMS (p.u.) | VQR |
|---|---|---|---|---|---|
| 1 | 4 | 1, 7, 8, 10, 11, 12 | 0.1006 | 0.0439 | 61.11% |
| 2 | 4, 11 | 1, 6, 7, 8, 10, 12 | 0.0948 | 0.0423 | 66.67% |
| 3 | 4, 7, 11 | 1, 6, 8, 9, 10, 12 | 0.0897 | 0.0390 | 77.78% |
| 4 | 4, 7, 10, 11 | 1, 2, 3, 6, 9, 12 | 0.0787 | 0.0354 | 100.00% |
| Scenario Number | DESS | PV |
|---|---|---|
| 1 | √ | √ |
| 2 | √ | 50% Reduction |
| 3 | 50% Reduction | √ |
| Defense Resource Budget | Protected EVCS | MVD (p.u.) | RMS (p.u.) | VQR |
|---|---|---|---|---|
| 1 | 4 | 0.1050 | 0.0462 | 55.56% |
| 2 | 4, 11 | 0.0947 | 0.0435 | 50.00% |
| 3 | 4, 7, 11 | 0.0891 | 0.0392 | 83.33% |
| 4 | 4, 7, 10, 11 | 0.0793 | 0.0356 | 100.00% |
| Defense Resource Budget | Protected EVCS | MVD (p.u.) | RMS (p.u.) | VQR |
|---|---|---|---|---|
| 1 | 4 | 0.1101 | 0.0489 | 55.56% |
| 2 | 4, 11 | 0.0967 | 0.0464 | 55.56% |
| 3 | 4, 7, 11 | 0.0955 | 0.0430 | 55.56% |
| 4 | 4, 7, 10, 11 | 0.0884 | 0.0392 | 77.78% |
| 5 | 4, 6, 7, 10, 11 | 0.0818 | 0.0369 | 83.33% |
| 6 | 4, 6, 7, 9, 10, 11 | 0.0767 | 0.0341 | 100% |
| Defense Resource Budget | Protected EVCS | MVD (p.u.) | RMS (p.u.) | VQR |
|---|---|---|---|---|
| 1 | 4 | 0.1083 | 0.0474 | 55.56% |
| 2 | 4, 11 | 0.0957 | 0.0449 | 55.56% |
| 3 | 4, 7, 11 | 0.0931 | 0.0409 | 61.11% |
| 4 | 4, 7, 10, 11 | 0.0842 | 0.0374 | 88.88% |
| 5 | 4, 6, 7, 10, 11 | 0.0789 | 0.0352 | 100.00% |
| Defense Resource Budget | Solution Method | Protected EVCS | Attacked EVCS | VQR | Outer Evaluations |
|---|---|---|---|---|---|
| 1 | CE | 4 | 1, 7, 8, 10, 11, 12 | 61.11% | 12 |
| IIE | 4 | 1, 7, 8, 10, 11, 12 | 61.11% | 12 | |
| 2 | CE | 7, 11 | 1, 4, 6, 8, 10, 12 | 61.11% | 66 |
| IIE | 4, 11 | 1, 6, 7, 8, 10, 12 | 66.67% | 23 | |
| 3 | CE | 4, 7, 11 | 1, 6, 8, 9, 10, 12 | 77.78% | 220 |
| IIE | 4, 7, 11 | 1, 6, 8, 9, 10, 12 | 77.78% | 33 | |
| 4 | CE | 4, 7, 10, 11 | 1, 2, 3, 6, 9, 12 | 100.00% | 495 |
| IIE | 4, 7, 10, 11 | 1, 2, 3, 6, 9, 12 | 100.00% | 42 |
| Run | Algo | Wall (s) | CPU (s) | Outer Evals | Peak RSS (MB) |
|---|---|---|---|---|---|
| 1 | CE | 878.356 | 2511.781 | 495 | 209.7 |
| IIE | 80.105 | 321.203 | 42 | 191.3 | |
| 2 | CE | 794.627 | 2686.250 | 495 | 209.8 |
| IIE | 212.322 | 211.297 | 42 | 190.3 | |
| 3 | CE | 924.665 | 2882.203 | 495 | 209.6 |
| IIE | 71.797 | 279.812 | 42 | 192.3 | |
| Avg. | CE | 865.880 | 2693.410 | 495 | 209.7 |
| IIE | 121.410 | 270.770 | 42 | 191.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liang, W.; Li, J.; Xiong, Y.; Li, Y.; Hu, Q.; Qian, T.; Yue, J. Optimized Defense Resource Allocation for Coupled Power-Transportation Networks Considering Information Security. Energies 2025, 18, 5855. https://doi.org/10.3390/en18215855
Liu Y, Liang W, Li J, Xiong Y, Li Y, Hu Q, Qian T, Yue J. Optimized Defense Resource Allocation for Coupled Power-Transportation Networks Considering Information Security. Energies. 2025; 18(21):5855. https://doi.org/10.3390/en18215855
Chicago/Turabian StyleLiu, Yuheng, Wenteng Liang, Jie Li, Yufeng Xiong, Yan Li, Qinran Hu, Tao Qian, and Jinyu Yue. 2025. "Optimized Defense Resource Allocation for Coupled Power-Transportation Networks Considering Information Security" Energies 18, no. 21: 5855. https://doi.org/10.3390/en18215855
APA StyleLiu, Y., Liang, W., Li, J., Xiong, Y., Li, Y., Hu, Q., Qian, T., & Yue, J. (2025). Optimized Defense Resource Allocation for Coupled Power-Transportation Networks Considering Information Security. Energies, 18(21), 5855. https://doi.org/10.3390/en18215855








