The Role of Double-Φ Floating Semi-Submersible Vertical Axis Wind Turbines in Suppressing the Gyroscopic Effect
Abstract
1. Introduction
2. Methodology
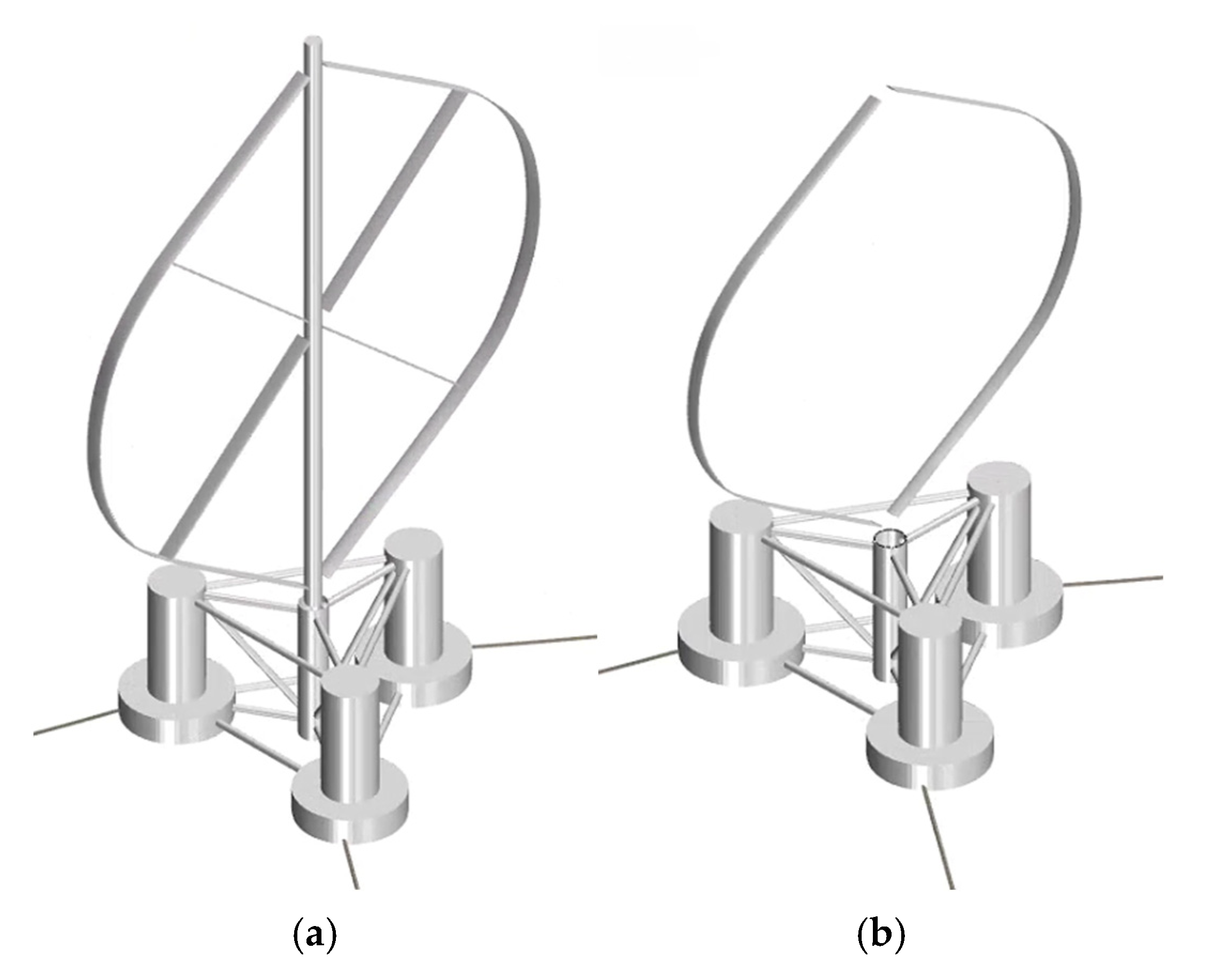
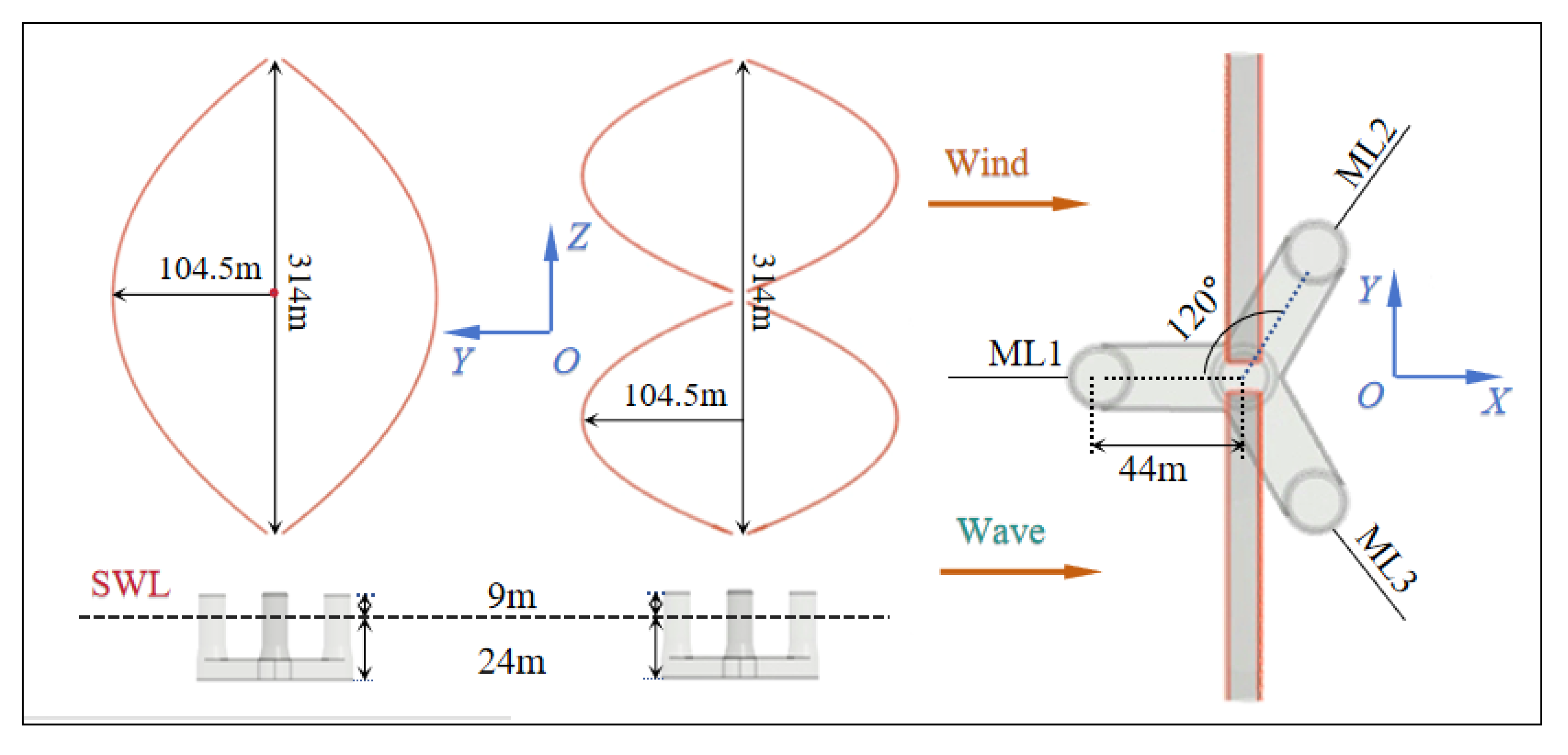
2.1. Model Setup
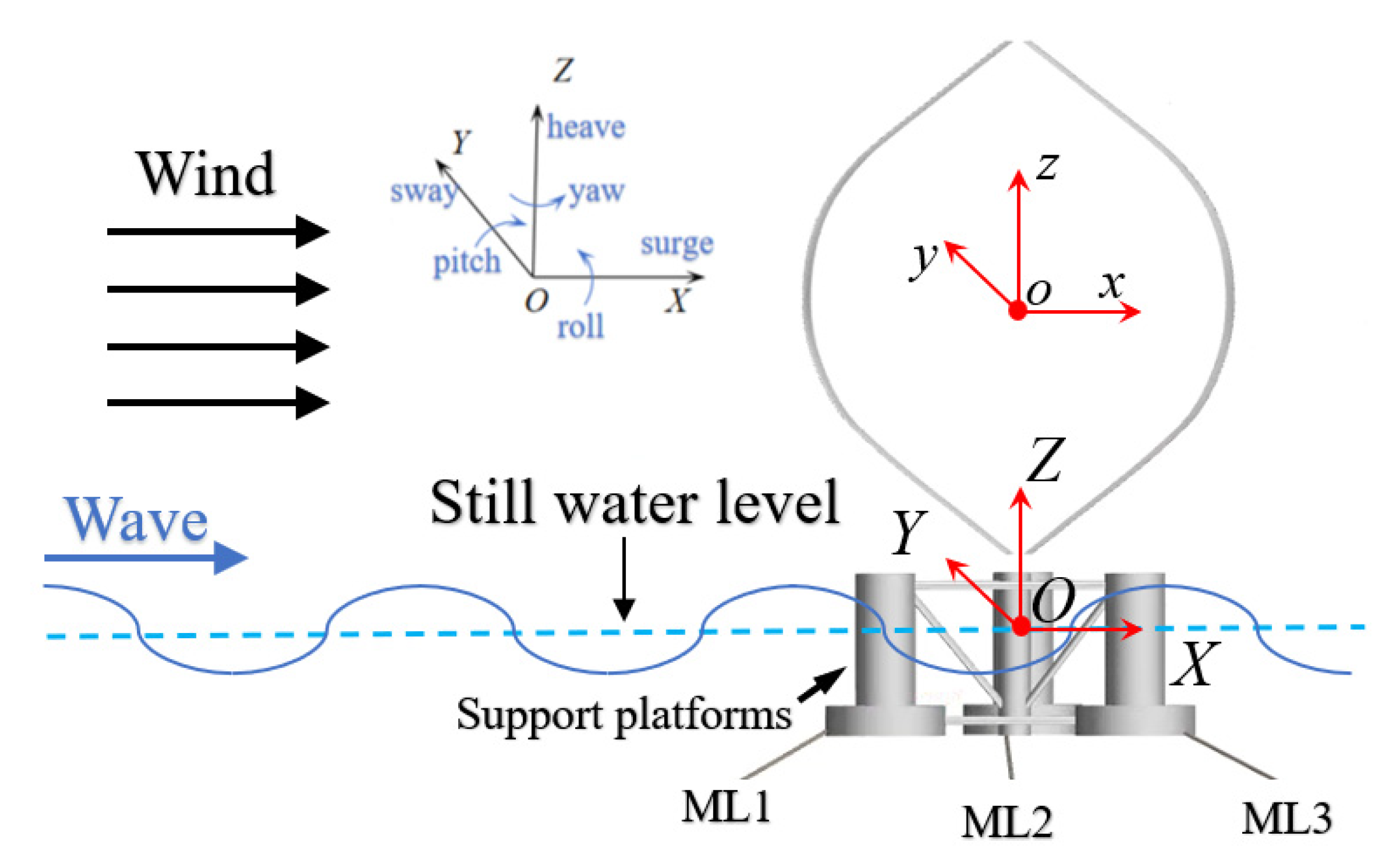
2.2. Parameter Definitions
2.3. CFD Numerical Method
2.3.1. Governing Equations and Turbulence Model
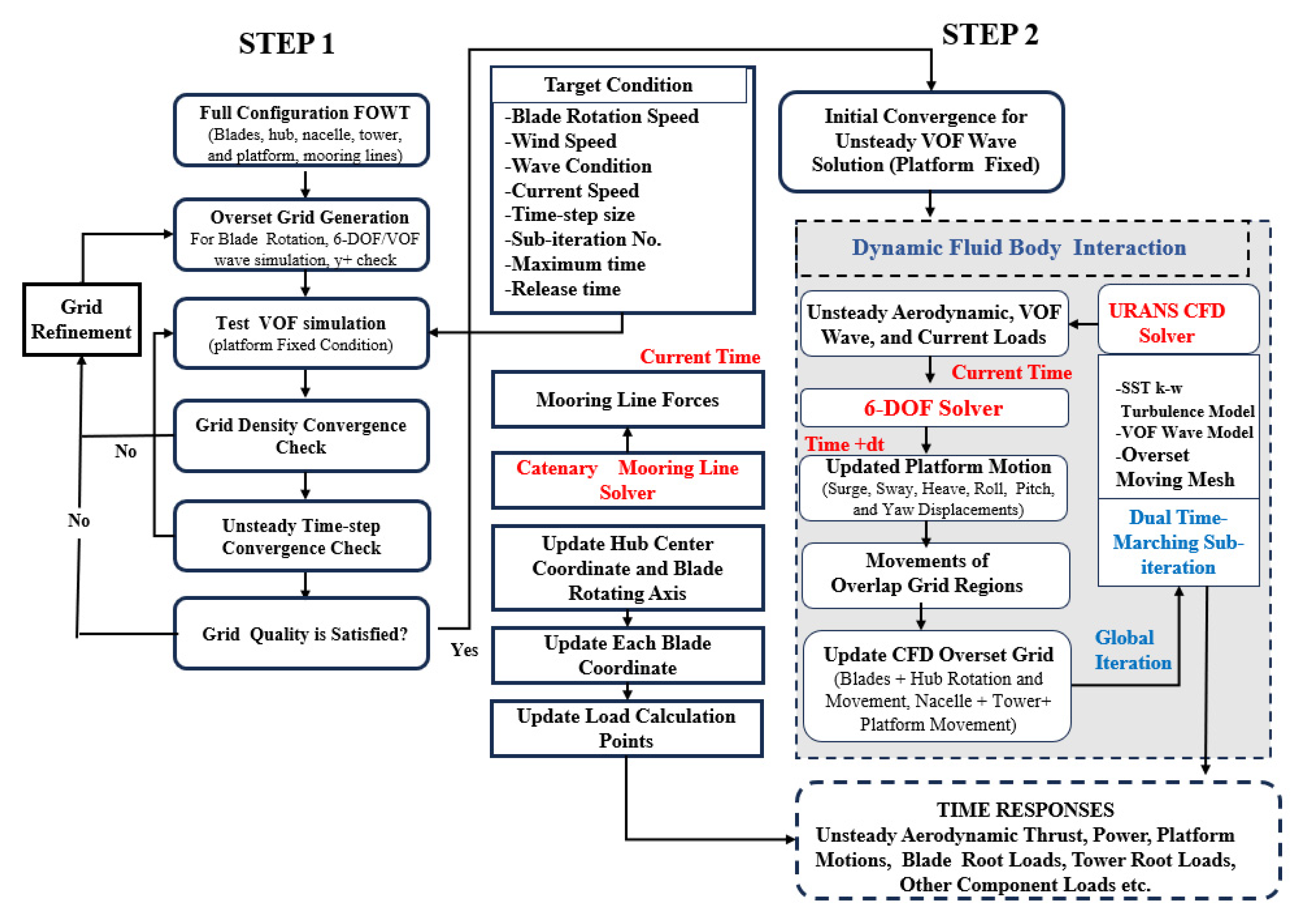
2.3.2. Implementation of FOVWT Motions
2.4. Validation of Effectiveness
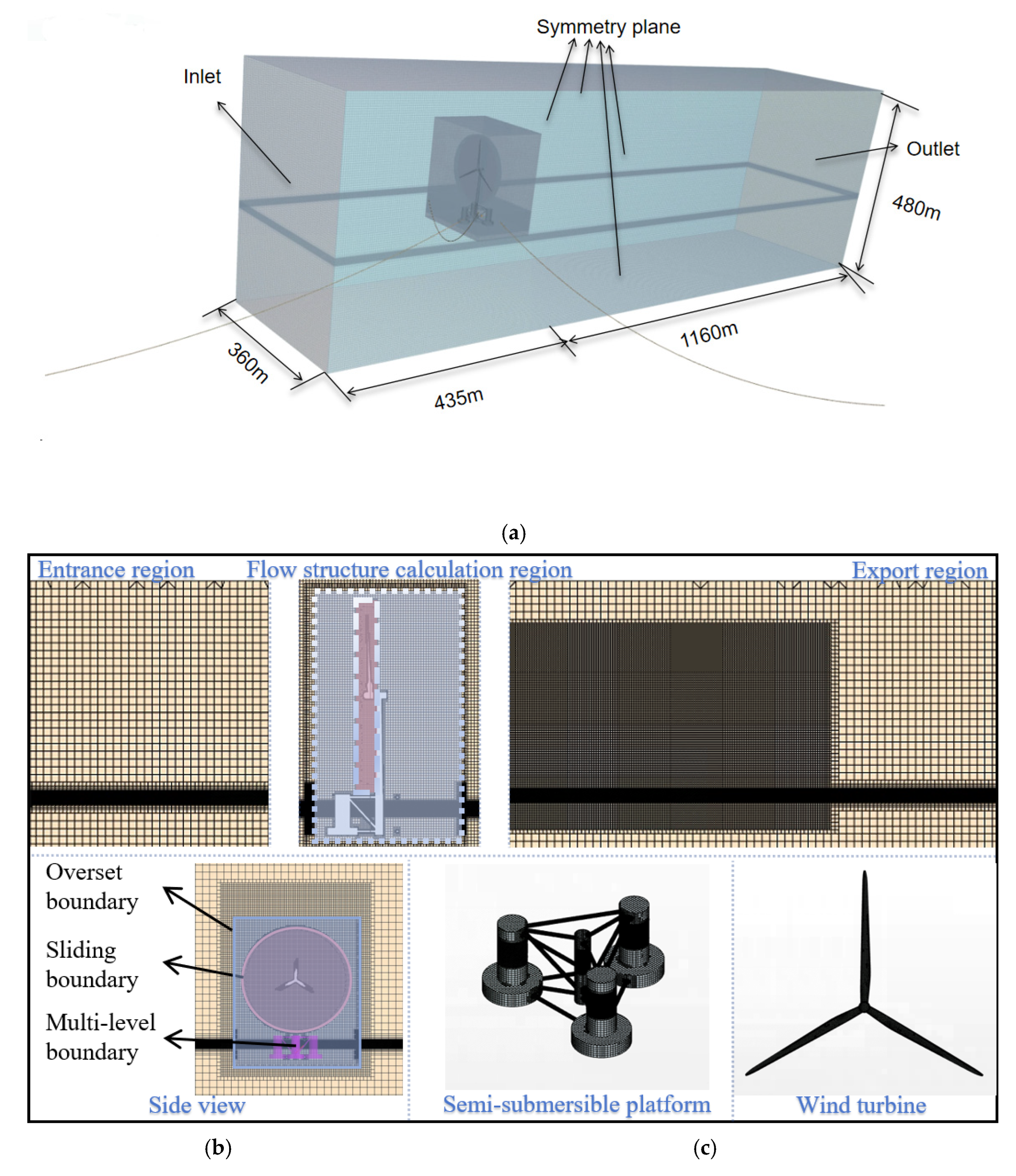
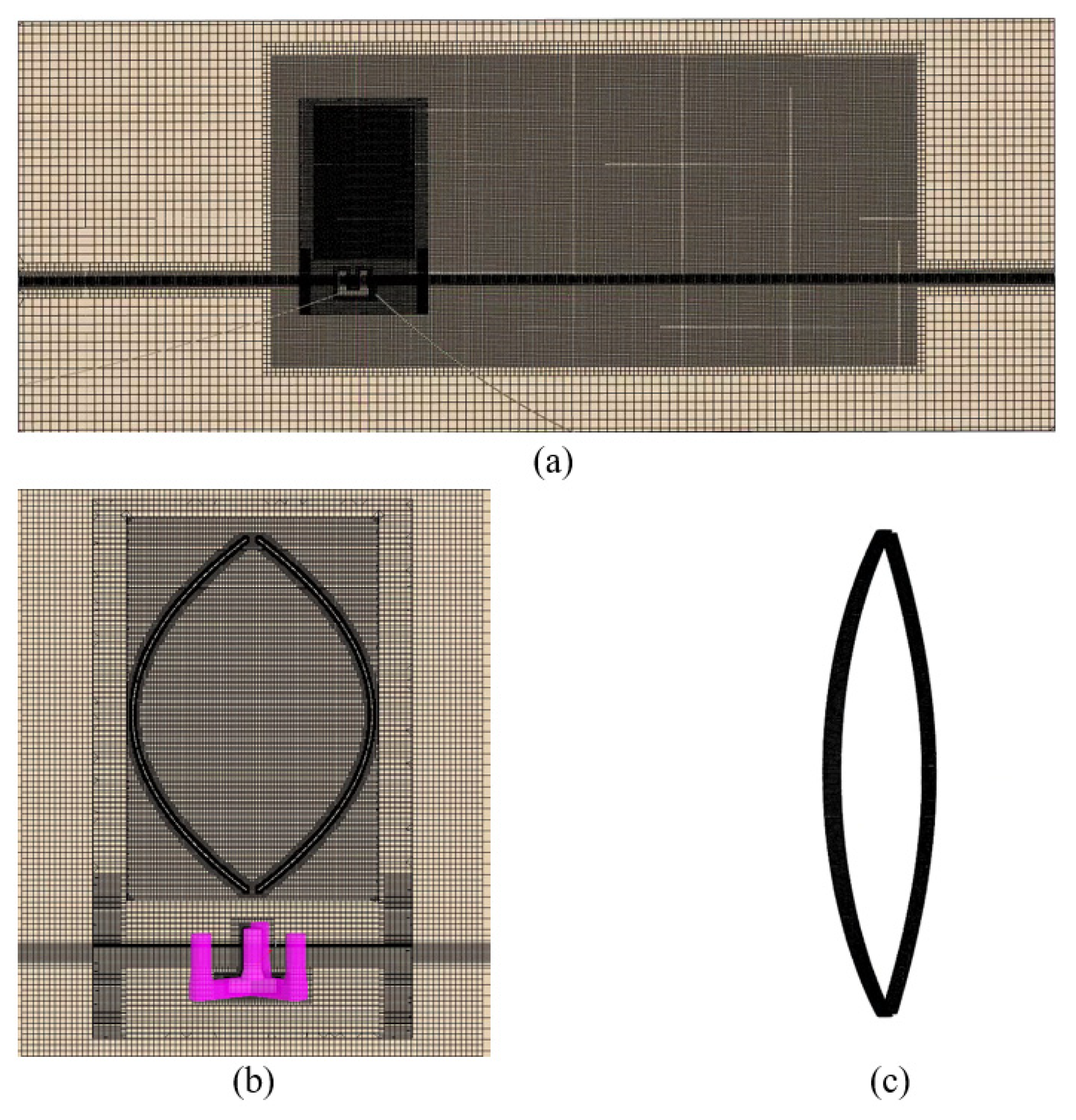
2.4.1. Mesh Generation
2.4.2. Boundary Conditions
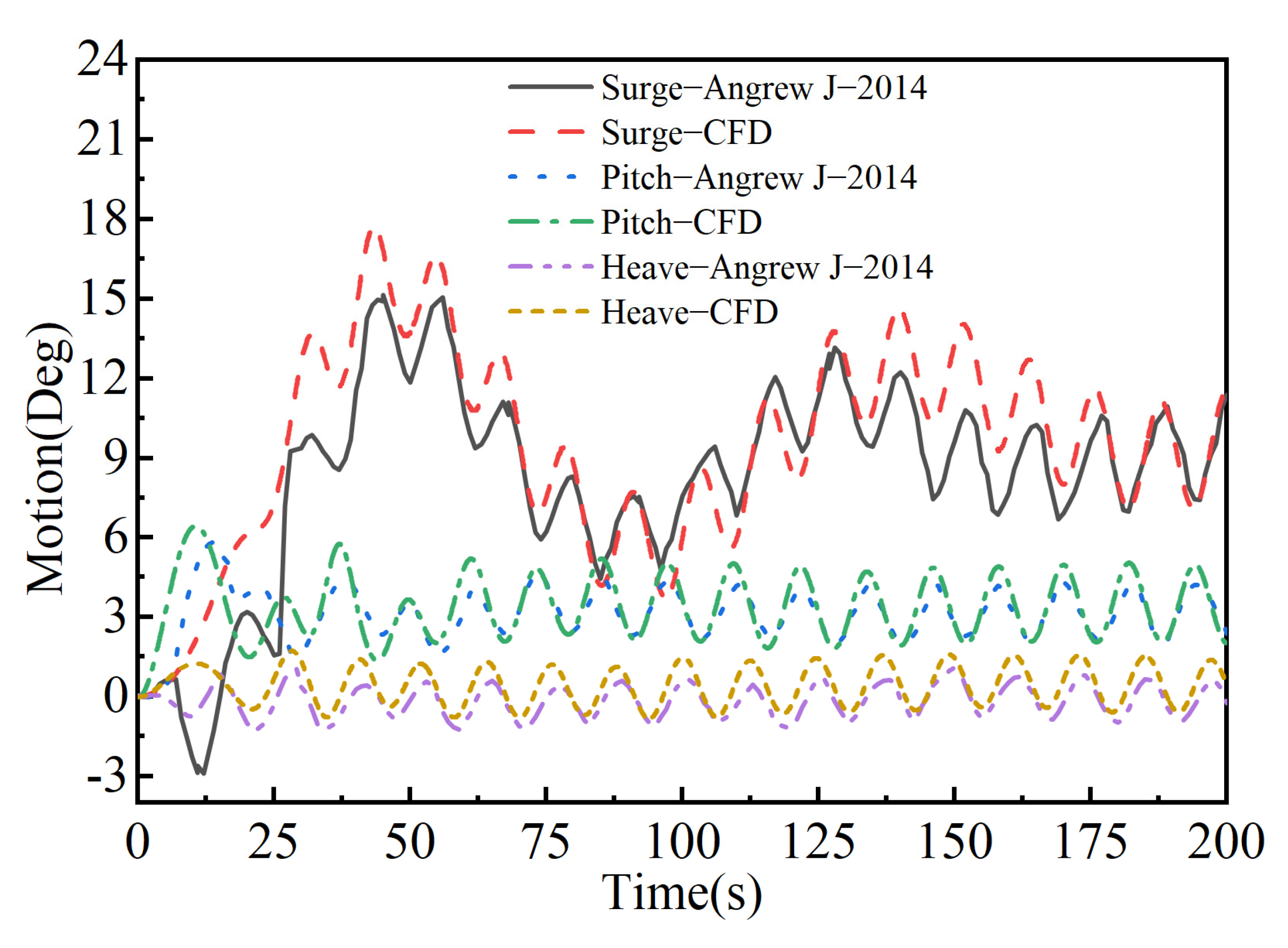
2.4.3. Result Validation
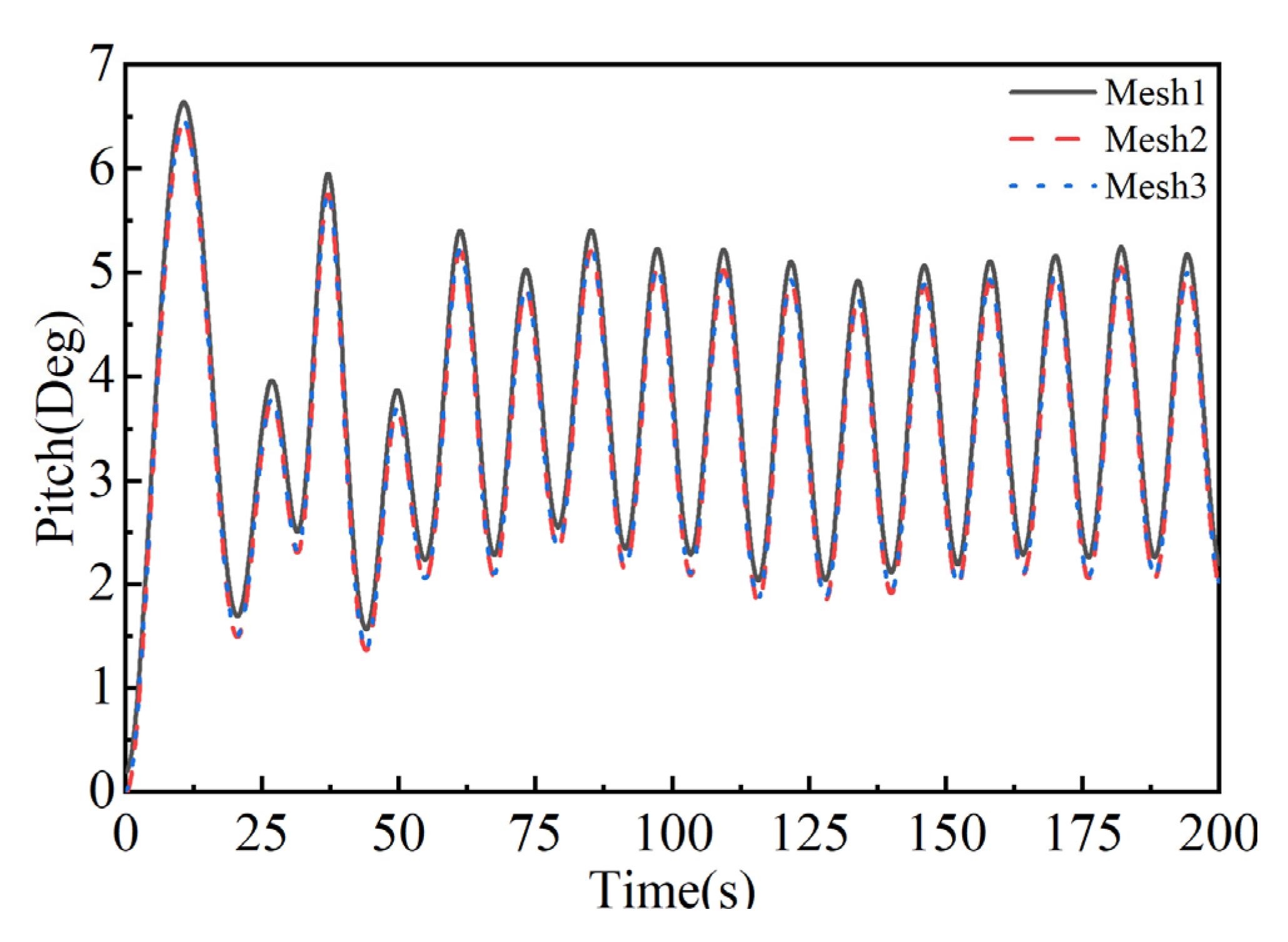
2.4.4. Mesh Independence Verification
3. Comparison of Pitch Performance Between Double-Φ and Single-Φ Rotors
3.1. Parameters of the FOWT
3.2. Suppression Effect of Structural Modification
3.2.1. Simulation Cases
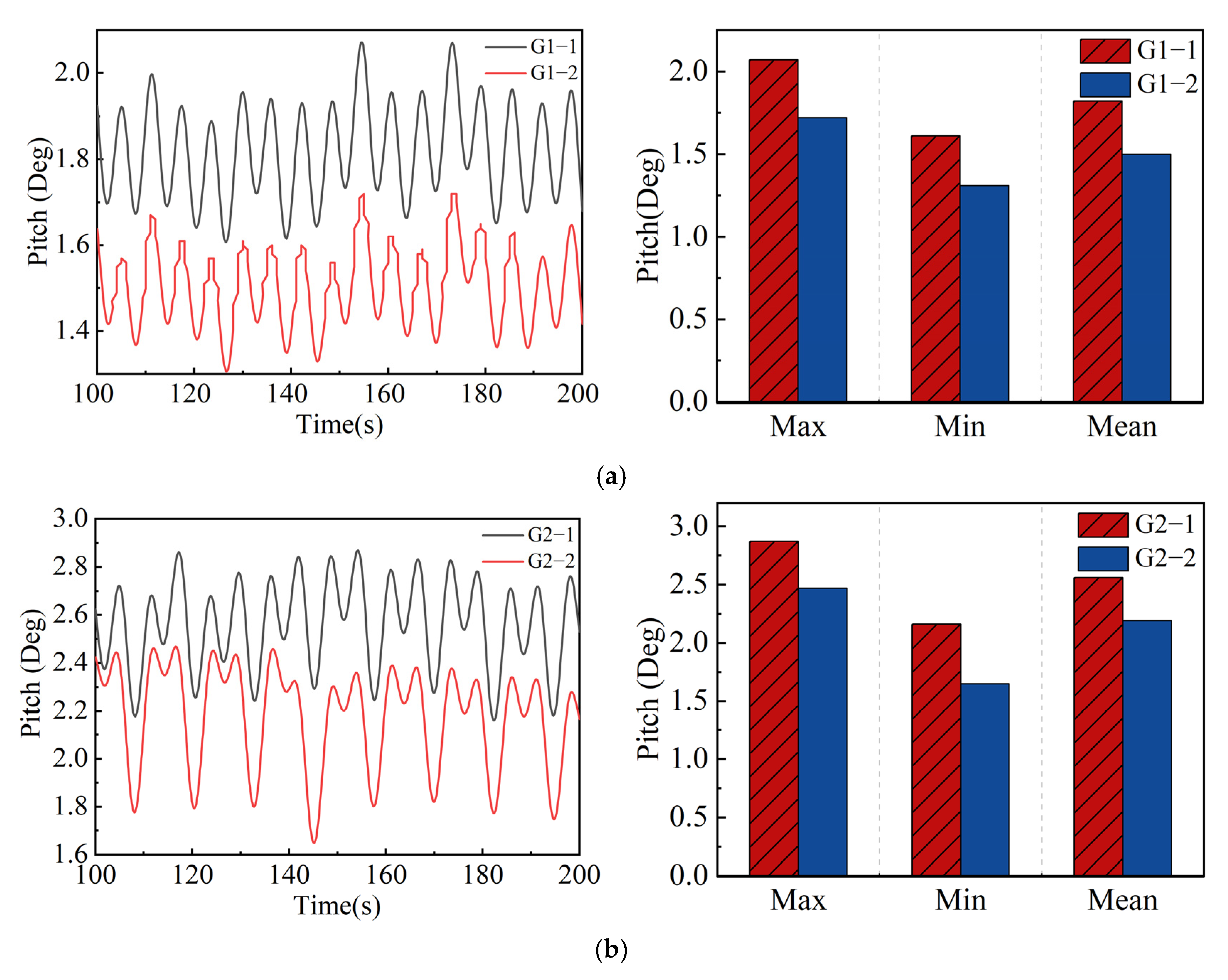
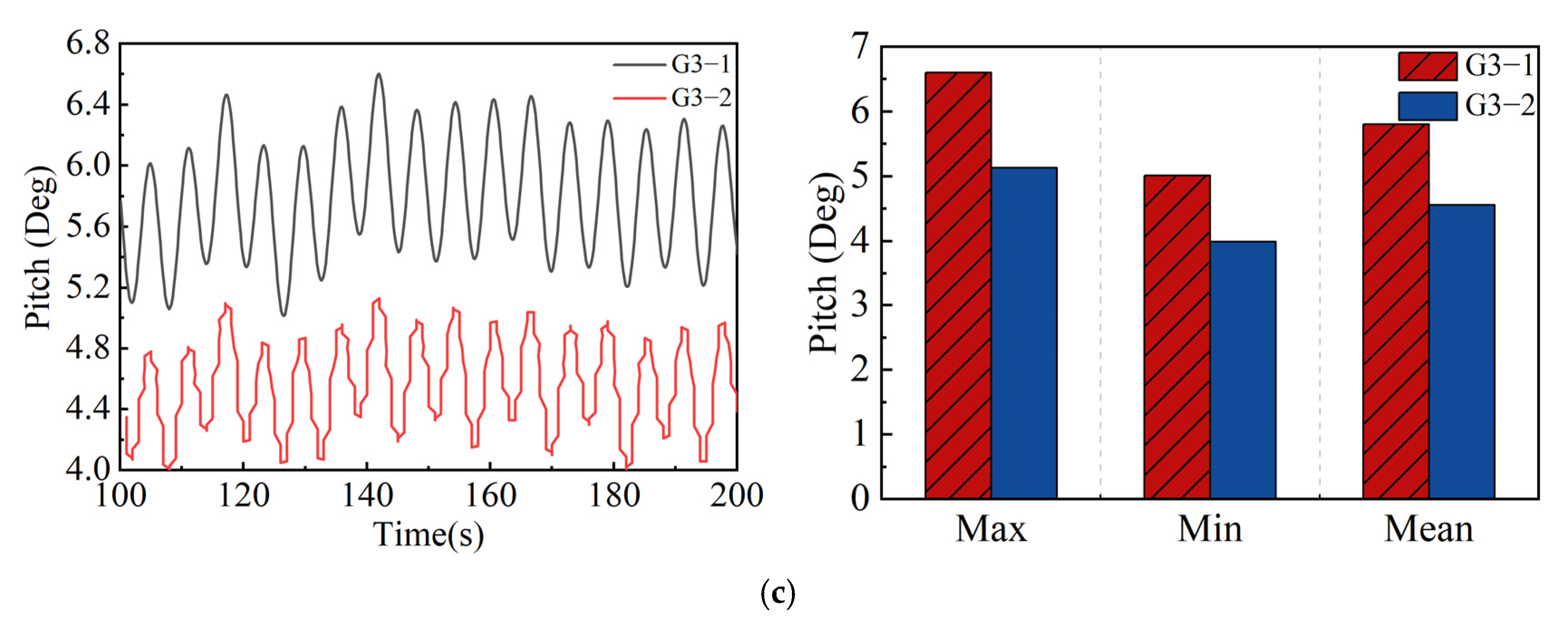
3.2.2. Motion Analysis Under Different Operating Conditions
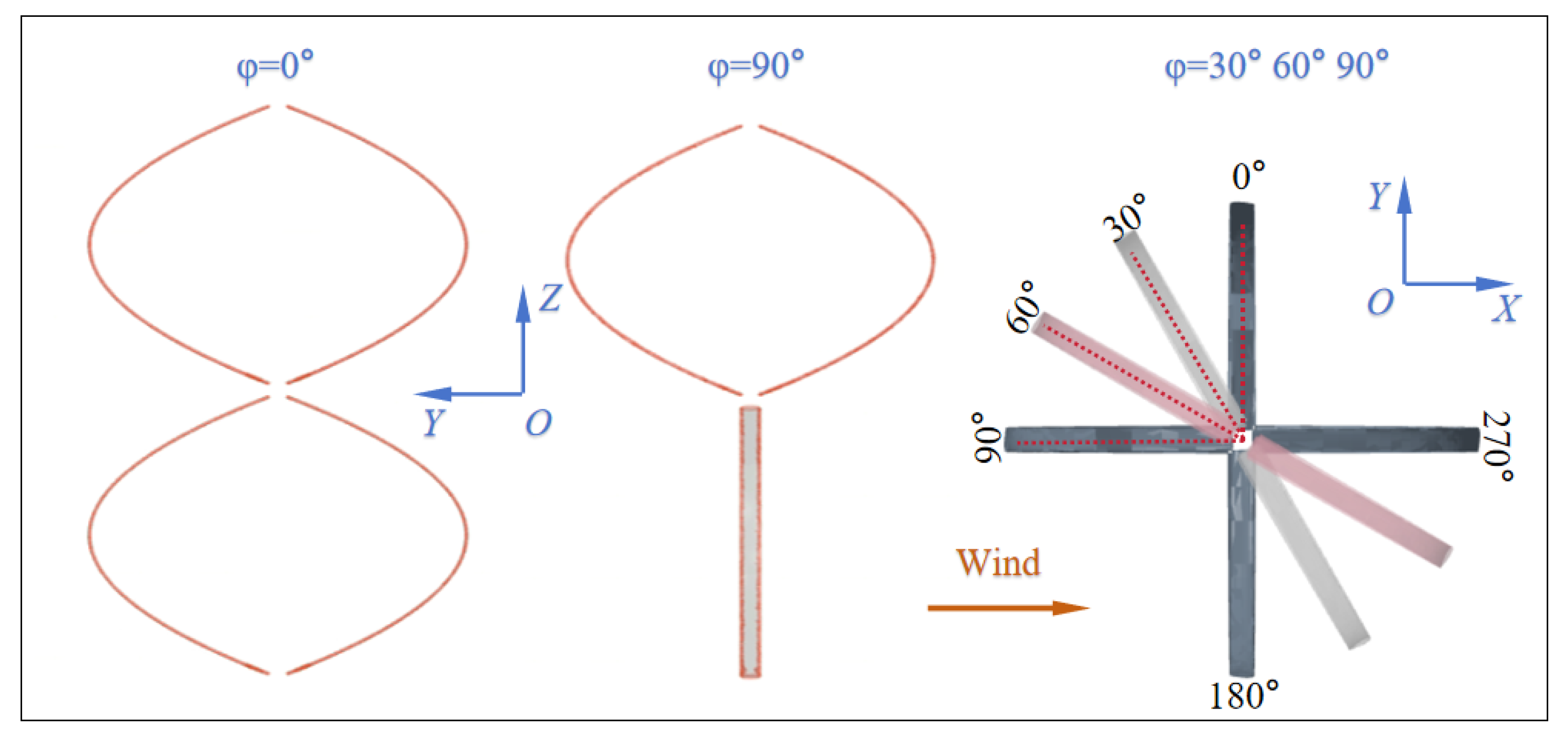
3.3. Suppression Effect of Varying Installation Angle
3.3.1. Simulation Case
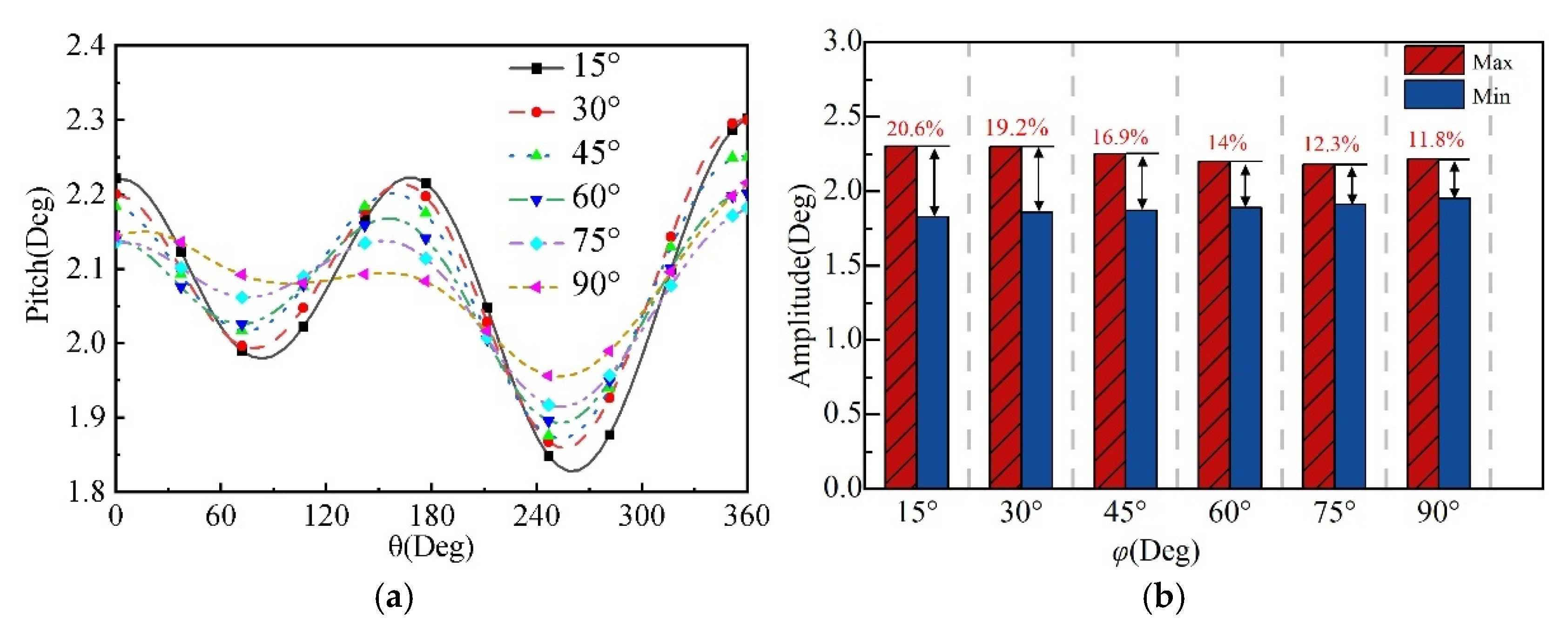
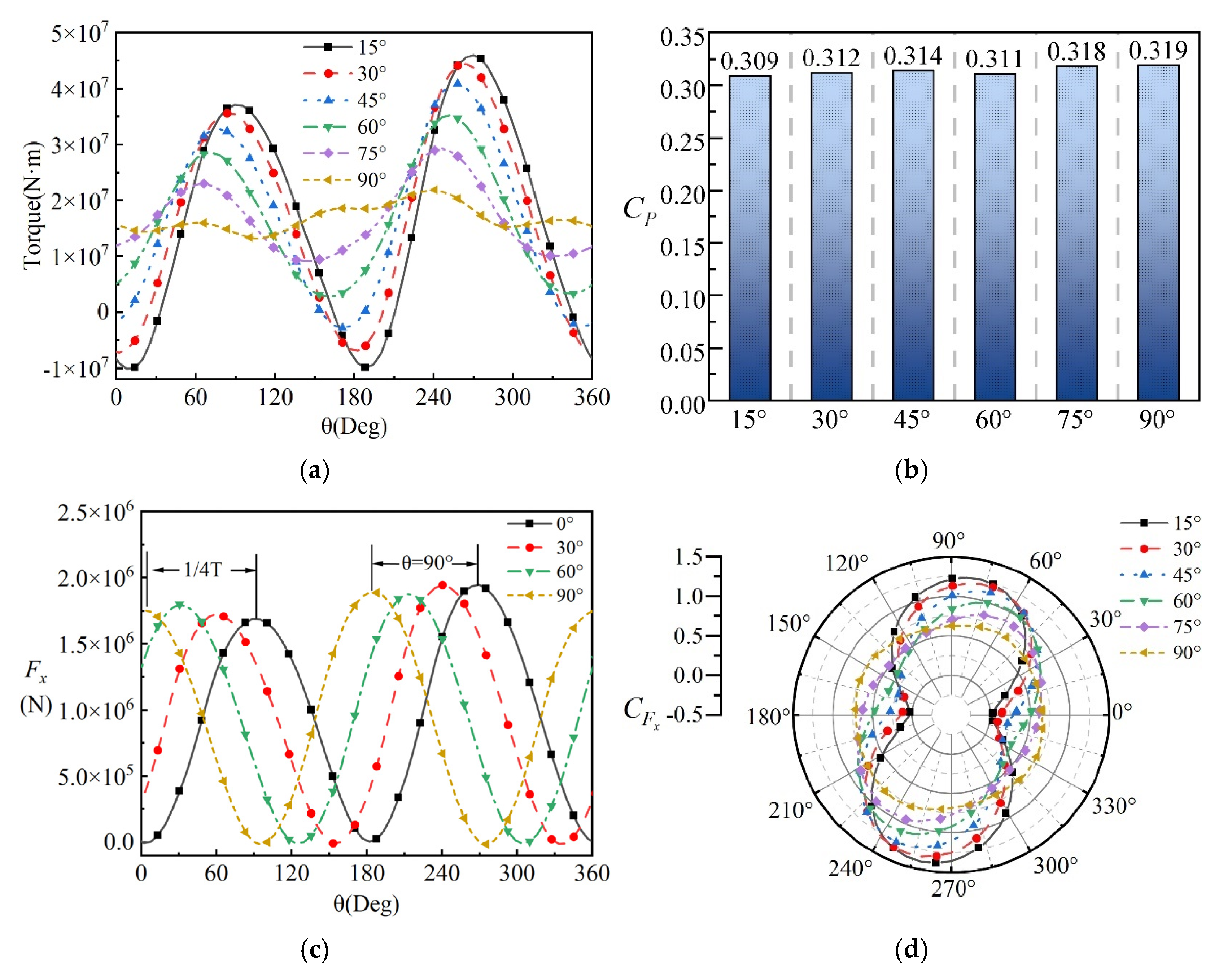
3.3.2. Motion Analysis of Wind Turbines Under Different Installation Angles
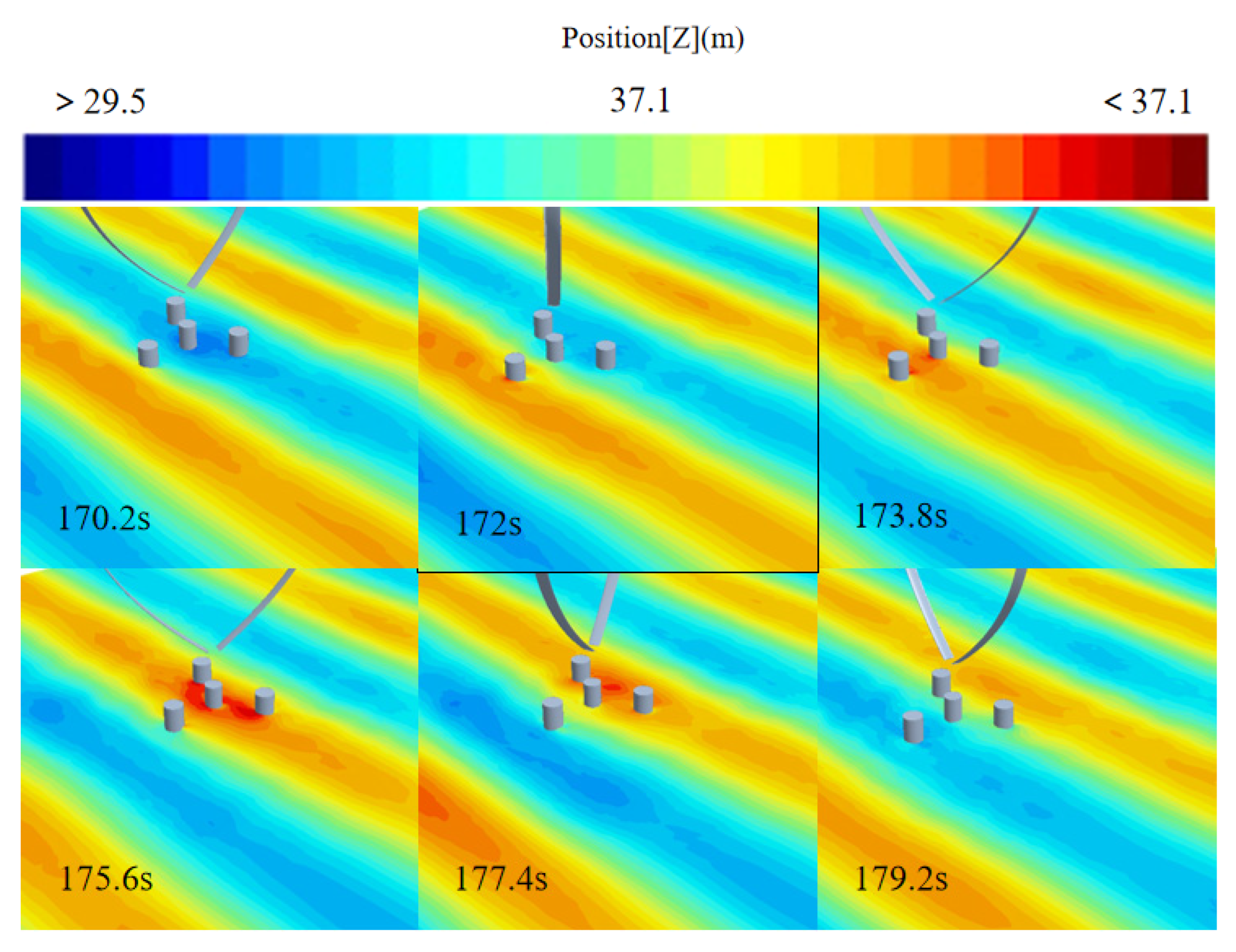
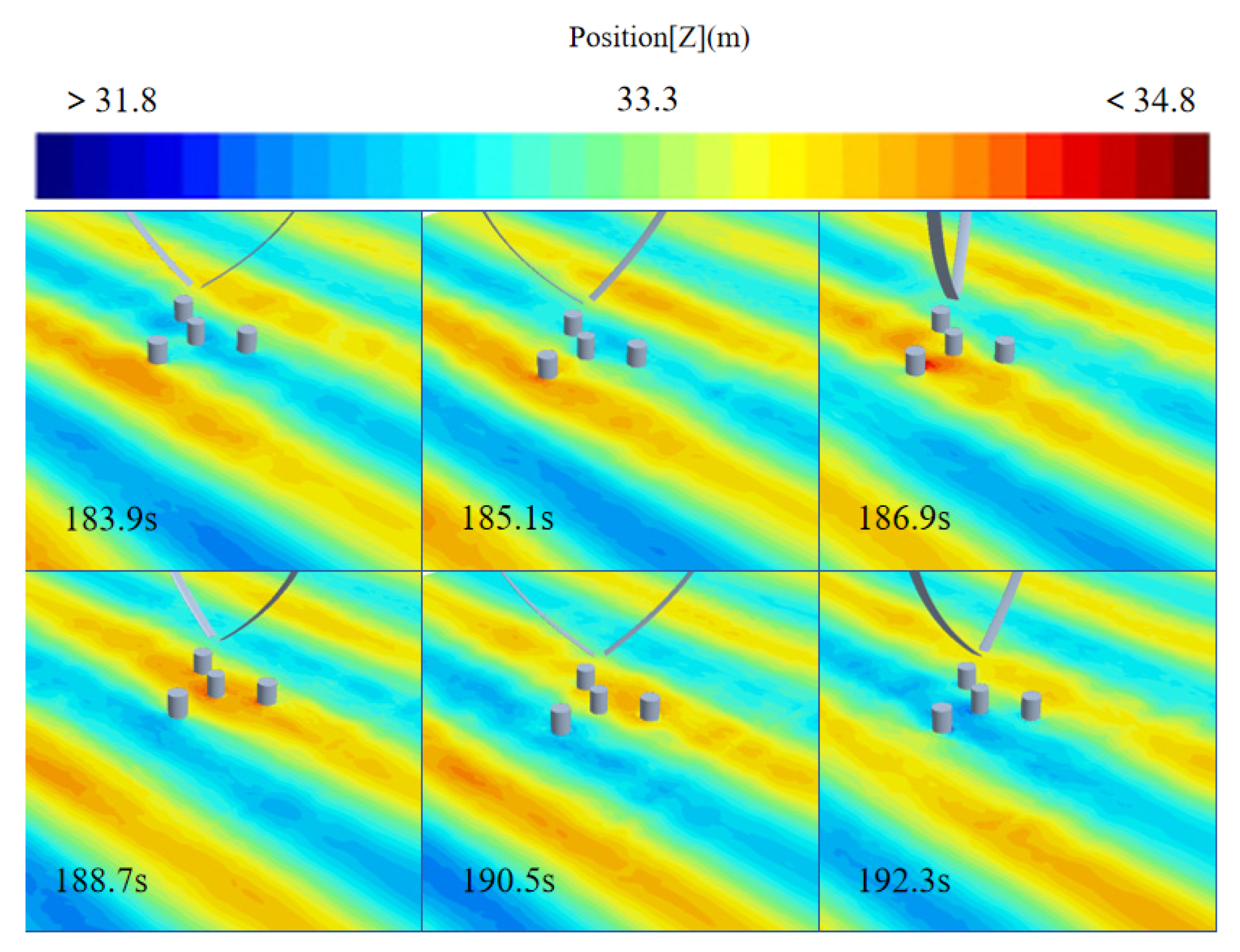
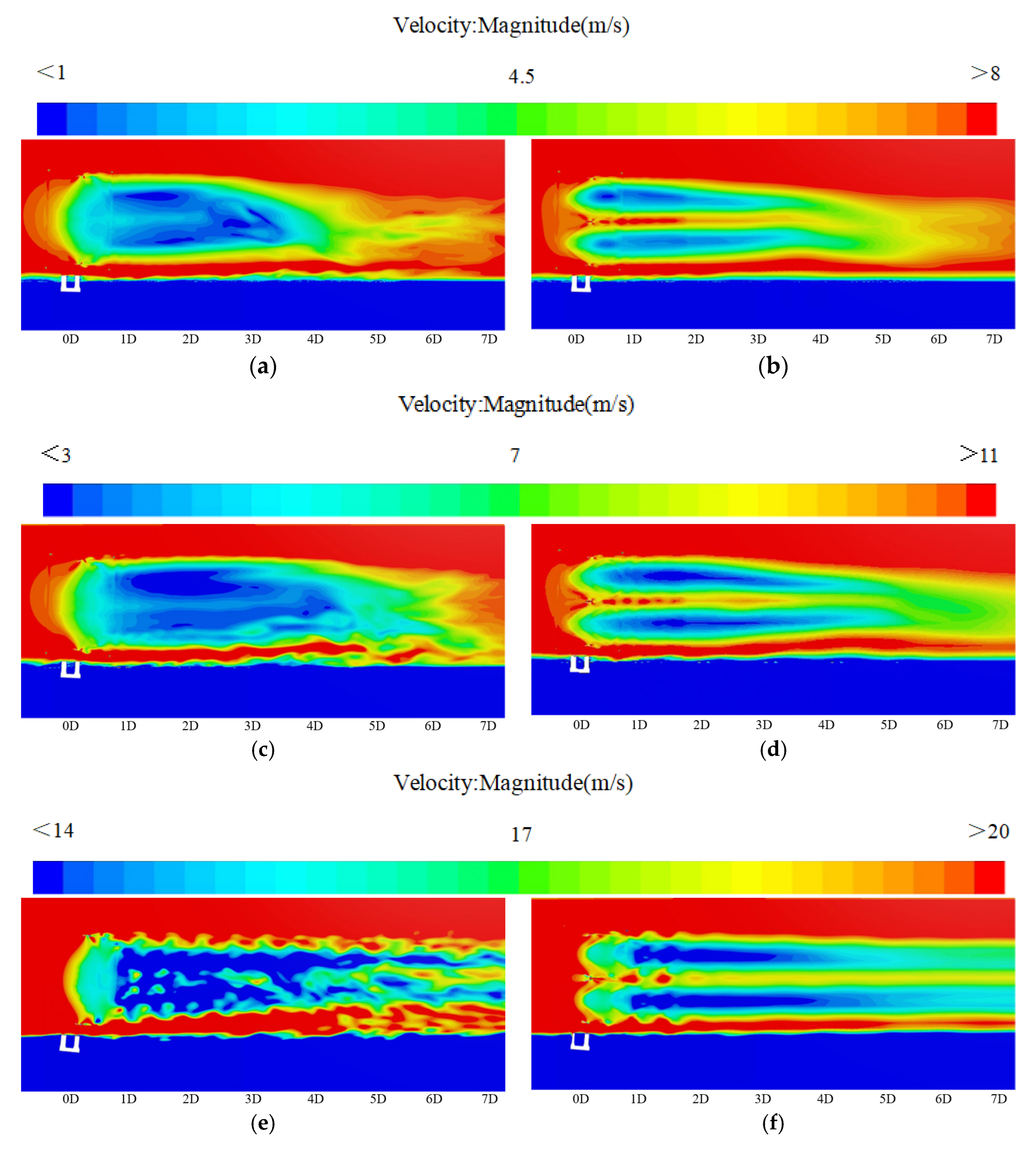
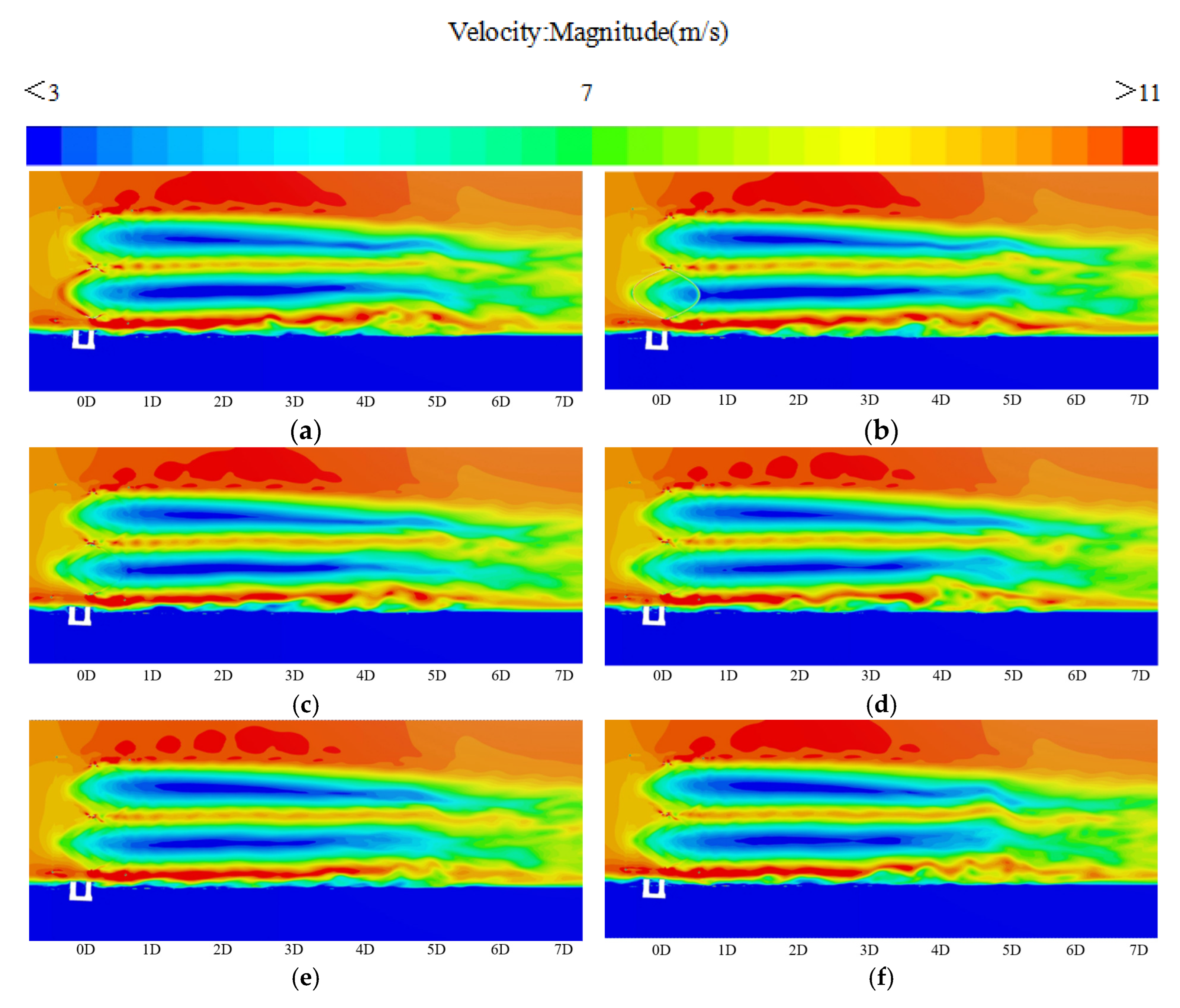
3.4. Wake Analysis of the Floating Wind Turbine
3.4.1. Effect of Rotor Configuration on Wake Characteristics
3.4.2. Effect of Installation Angle
4. Results and Discussion
- 1.
- Under rated wind–wave conditions, the double- configuration significantly reduces pitch responses induced by rotor gyroscopic effects. In extreme sea states, the peak pitch angle is reduced by approximately 22%, accompanied by a notable decrease in axial loads, demonstrating that the double- structure effectively attenuates the amplification of the platform instability caused by gyroscopic moments.
- 2.
- Changing the rotor misalignment angle likewise weakens the gyroscopic effect. As the misalignment increases, the pitch response diminishes. Specifically, when comparing 15° with 90°, the pitch motion amplitude drops from 20.6% to 11.8%, with the turbine power output being nearly unaffected. This is mainly attributed to the cancelation of thrust peaks and troughs within a cycle at larger misalignment angles, which mitigates the periodic load fluctuations driven by gyroscopic effects.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Achakulwisut, P.; Erickson, P.; Guivarch, C.; Schaeffer, R.; Brutschin, E.; Pye, S. Global fossil fuel reduction pathways under different climate mitigation strategies and ambitions. Nat. Commun. 2023, 14, 5425. [Google Scholar] [CrossRef] [PubMed]
- REN21 M J. Renewables 2023 Global Status Report Collection, Renewables in Energy Supply. 2023. Available online: https://energypedia.info/wiki/Publication_-_Renewables_2023_Global_Status_Report_collection,_Renewables_in_Energy_Supply (accessed on 28 October 2025).
- Global Overview, Renewables 2024. Available online: https://www.iea.org/reports/renewables-2024/global-overview (accessed on 28 October 2025).
- Desalegn, B.; Gebeyehu, D.; Tamrat, B. Wind energy conversion technologies and engineering approaches to enhancing wind power generation: A review. Heliyon 2022, 8, e11263. [Google Scholar] [CrossRef] [PubMed]
- Didane, D.H.; Rosly, N.; Zulkafli, M.F.; Shamsudin, S.S. Performance evaluation of a novel vertical axis wind turbine with coaxial contra-rotating concept. Renew. Energy 2018, 115, 353–361. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, K.; Zhao, G. The influencing factors and hierarchical relationships of offshore wind power industry in China. Environ. Sci. Pollut. Res. 2021, 28, 52329–52344. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Liu, Z.; Zhang, Y. A review of platform designs for floating offshore wind turbines. Chin. J. Ship Res. 2024, 19, 21–31. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, S.Y.; Tan, G.; Deng, Y.; Zhang, Y.; Wang, Y.; Wang, Z. Vibration mitigation of spar-buoy floating wind turbines using a nonlinear energy sink. Ocean Eng. 2024, 304, 117883. [Google Scholar] [CrossRef]
- Wang, B.; Gao, X.; Li, Y.; Liu, L.; Li, H. Dynamic response analysis of a semi-submersible floating wind turbine based on different coupling methods. Ocean Eng. 2024, 297, 116948. [Google Scholar] [CrossRef]
- Ren, Y.; Shi, W.; Venugopal, V.; Zhang, L.; Li, X. Experimental study of tendon failure analysis for a TLP floating offshore wind turbine. Appl. Energy 2024, 358, 122633. [Google Scholar] [CrossRef]
- Sirigu, M.; Ghigo, A.; Petracca, E.; Giorgi, G.; Bracco, G. Fatigue assessment of a new concept for a floating barge with pendulum for offshore wind turbines in MOST. J. Phys. Conf. Ser. 2024, 2767, 62024. [Google Scholar] [CrossRef]
- Edwards, E.C.; Holcombe, A.; Brown, S.; Ransley, E.; Hann, M.; Greaves, D. Evolution of floating offshore wind platforms: A review of at-sea devices. Renew. Sustain. Energy Rev. 2023, 183, 113416. [Google Scholar] [CrossRef]
- Jeong, M.; Loth, E.; Qin, C.; Selig, M.; Johnson, N. Aerodynamic rotor design for a 25 MW offshore downwind turbine. Appl. Energy 2024, 353, 122035. [Google Scholar] [CrossRef]
- Koragappa, P.; Verdin, P.G. Design and optimisation of a 20 MW offshore wind turbine blade. Ocean Eng. 2024, 305, 117975. [Google Scholar] [CrossRef]
- Mehta, M.; Zaaijer, M.; von Terzi, D. Drivers for optimum sizing of wind turbines for offshore wind farms. Wind. Energy Sci. 2024, 9, 141–163. [Google Scholar] [CrossRef]
- Huanqiang, Z.; Xiaoxia, G.; Hongkun, L.; Qiansheng, Z.; Xiaoxun, Z.; Yu, W.; Fei, Z. Investigation of a new 3D wake model of offshore floating wind turbines subjected to the coupling effects of wind and wave. Appl. Energy 2024, 365, 123189. [Google Scholar] [CrossRef]
- Wenfeng, L.; Zhenzhou, Z.; Yige, L.; Huiwen, L.; Shangshang, W.; Ali, K.; Guodan, D.; Yan, L.; Yuanzhuo, M. Investigation of dynamic wake model of a floating offshore wind turbine under heave, surge and pitch motion. Renew. Energy 2025, 254, 123665. [Google Scholar] [CrossRef]
- Wang, T.; Cai, C.; Gao, X.; Sun, X.; Guo, N.; Hu, Z.; Zheng, J.; Wang, D.; Peng, C.; Li, Q. Study on wake interactions of tandem floating offshore wind turbines under different yaw conditions using actuator line method. Energy 2025, 337, 138486. [Google Scholar] [CrossRef]
- Mian, H.; Messmer, T.; Stoevesandt, B.; Siddiqui, M. Coherent flow structures in the wake of a model floating wind turbine under pitch and roll motions. Energy 2025, 335, 138212. [Google Scholar] [CrossRef]
- Abbas, N.J.; Jasa, J.; Zalkind, D.S.; Wright, A.; Pao, L. Control co-design of a floating offshore wind turbine. Appl. Energy 2024, 353, 122036. [Google Scholar] [CrossRef]
- Du, X.; Liang, J.; Muro, J.L.; Qian, G.; Burlion, L.; Bilgen, O. Development of a control co-design optimization framework with aeroelastic-control coupling for floating offshore wind turbines. Appl. Energy 2024, 372, 123728. [Google Scholar] [CrossRef]
- Liu, J.; Cai, C.; Song, D.; Zhong, X.; Shi, K.; Chen, Y.; Cheng, S.; Huang, Y.; Jiang, X.; Li, Q. Nonlinear model predictive control for maximum wind energy extraction of semi-submersible floating offshore wind turbine based on simplified dynamics model. Energy 2024, 311, 133356. [Google Scholar] [CrossRef]
- Ghigo, A.; Faraggiana, E.; Giorgi, G.; Mattiazzo, G.; Bracco, G. Floating Vertical Axis Wind Turbines for offshore applications among potentialities and challenges: A review. Renew Sustain. Energy Rev. 2024, 193, 114302. [Google Scholar] [CrossRef]
- Bhutta, M.M.A.; Hayat, N.; Farooq, A.U.; Ali, Z.; Jamil, S.R.; Hussain, Z. Vertical axis wind turbine—A review of various configurations and design techniques. Renew Sustain. Energy Rev. 2012, 16, 1926–1939. [Google Scholar] [CrossRef]
- Borg, M.; Collu, M.; Kolios, A. Offshore floating vertical axis wind turbines, dynamics modelling state of the art. Part II: Mooring line and structural dynamics. Renew Sustain. Energy Rev. 2014, 39, 1226–1234. [Google Scholar] [CrossRef]
- Liu, Q.; Huang, H.; Iglesias, G.; Wang, J.; Bashir, M. Fully coupled aero-hydrodynamic analysis of floating vertical axis wind turbines in staggered configurations. Energy 2025, 337, 138679. [Google Scholar] [CrossRef]
- Martin, J.B. Plasticity: Fundamentals and General Results; McGraw-Hill: Columbus, OH, USA, 1975. [Google Scholar]
- Al-Solihat, M.K.; Nahon, M.; Behdinan, K. Dynamic modeling and simulation of a spar floating offshore wind turbine with consideration of the rotor speed variations. J. Dyn. Syst. Meas. Control 2019, 141, 081014. [Google Scholar] [CrossRef]
- Høeg, C.E.; Zhang, Z. The influence of gyroscopic effects on dynamic responses of floating offshore wind turbines in idling and operational conditions. Ocean Eng. 2021, 227, 108712. [Google Scholar] [CrossRef]
- Greenwood, D.T. Principles of Dynamics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1965. [Google Scholar]
- Pezeshki, H.; Pavlou, D.; Adeli, H.; Siriwardane, S. Gyroscopic effects of the spinning rotor-blades assembly on dynamic response of offshore wind turbines. J. Wind Eng. Ind. Aerodyn. 2024, 247, 105698. [Google Scholar] [CrossRef]
- Liu, Z.; Tu, Y.; Wang, W.; Qian, G. Numerical analysis of a catenary mooring system attached by clump masses for improving the wave-resistance ability of a spar buoy-type floating offshore wind turbine. Appl. Sci. 2019, 9, 1075. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, B.; Tian, X.; Li, X.; Dong, Y.; Wang, M.; Peng, Z. Experimental study on mitigating vibration of floating offshore wind turbine using tuned mass damper. Ocean Eng. 2023, 288, 115974. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, T.; Hu, Z.; Ma, G. Study on characteristics and optimal layout of components in shallow water mooring system of floating wind turbine. Appl. Sci. 2022, 12, 10137. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.; Zhang, J.; Guan, D.; Chen, H.; Lu, T. Experiment investigations of pitch motions for a semi-submersible wind turbine with the passive gyro stabilizers. Appl. Ocean Res. 2025, 163, 104757. [Google Scholar] [CrossRef]
- Cayuela-Padilla, S.; M’zOughi, F.; Garrido, I.; Garrido, A.J. Design and stability analysis of a new six-floater oscillating water column-based floating offshore wind turbine platform. Sci. Rep. 2024, 14, 16191. [Google Scholar] [CrossRef]
- Zhao, H.; Wei, K.; Yang, W. Further study of heave plate designs for enhancing motion control of floating offshore wind turbines. Ocean Eng. 2025, 327, 121016. [Google Scholar] [CrossRef]
- Salic, T.; Charpentier, J.F.; Benbouzid, M.; Le Boulluec, M. Control strategies for floating offshore wind turbine: Challenges and trends. Electronics 2019, 8, 1185. [Google Scholar] [CrossRef]
- Ha, K.; Truong, H.V.A.; Dang, T.D.; Ahn, K.K. Recent control technologies for floating offshore wind energy system: A review. Int. J. Precis. Eng. Manuf. Green Technol. 2021, 8, 281–301. [Google Scholar] [CrossRef]
- Ai, S.; Su, J.; Meng, W.; Yan, Y. Integrated control of blade pitch and generator speed for floating wind turbines. Ocean Eng. 2024, 300, 117080. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, Y.; Cai, C.; Wu, X.; Zhang, Y.; Kong, D.; Liu, J.; Sun, X.; Zhong, X.; Li, Q. Cyclic pitch control for aerodynamic load reductions of floating offshore wind turbines under pitch motions. Energy 2024, 309, 132945. [Google Scholar] [CrossRef]
- Wang, S.; Xiao, J.; Chen, S.; Ji, R.; Wang, K. Rotational speed prediction for rated power operation of a horizontal axis tidal turbine under surging motion conditions. Ocean Eng. 2025, 339, 122206. [Google Scholar] [CrossRef]
- Yin, M.; Ji, R.; Zhu, R.; Xu, S.; Sun, K.; Zhang, J.; Zhang, Y.; Reabroy, R. Performance and wake prediction of a ducted tidal stream turbine in yaw misalignment using the lattice Boltzmann method. Energy Convers. Manag. 2026, 347, 120574. [Google Scholar] [CrossRef]
- Abdallah, A.; William, M.A.; Moharram, N.A.; Zidane, I.F. Boosting H-Darrieus vertical axis wind turbine performance: A CFD investigation of J-Blade aerodynamics. Results Eng. 2025, 27, 106358. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.-H. Fully coupled aero-hydrodynamic analysis of a semi-submersible FOWT using a dynamic fluid body interaction approach. Renew. Energy 2016, 92, 244–261. [Google Scholar] [CrossRef]
- Goupee, A.J.; Koo, B.J.; Kimball, R.W.; Lambrakos, K.F.; Dagher, H.J. Experimental comparison of three floating wind turbine concepts. J. Offshore Mech. Arct. Eng. 2014, 136, 020906. [Google Scholar] [CrossRef]
- CD-adapco. STAR-CCM+, v13.02; Documentation; CD-adapco: Melville, NY, USA, 2018. [Google Scholar]
- Dong, K.; Wang, X.; Zhang, D.; Liu, L.; Feng, D. CFD Research on the Hydrodynamic Performance of Submarine Sailing near the Free Surface with Long-Crested Waves. J. Mar. Sci. Eng. 2022, 10, 90. [Google Scholar] [CrossRef]
- Zhao, B.; Jiang, H.; Sun, J.; Zhang, D. Research on the Hydrodynamic Performance of a Pentamaran in Calm Water and Regular Waves. Appl. Sci. 2023, 13, 4461. [Google Scholar] [CrossRef]
- Wang, S.; Tang, J.; Li, C.; Ji, R.; Fernandez-Rodriguez, E. Performance evaluation and fast prediction of a pitched horizontal-axis tidal turbine under wave-current conditions using a variable-speed control strategy. J. Fluids Struct. 2025, 133, 104265. [Google Scholar] [CrossRef]
- Huang, H.; Liu, Q.; Yue, M.; Miao, W.; Wang, P.; Li, C. Fully coupled aero-hydrodynamic analysis of a biomimetic fractal semi-submersible floating offshore wind turbine under wind-wave excitation conditions. Renew. Energy 2023, 203, 280–300. [Google Scholar] [CrossRef]


| Symbol | Parameter |
|---|---|
| (m/s) | Free-stream wind velocity |
| () | Rotor swept area |
| (m) | Rotor radius |
| Number of blades | |
| (rad/s) | Angular velocity |
| (°) | Blade installation angle |
| (N) | Axial thrust |
| (N) | Lateral force |
| Tip speed ratio | |
| (Nm) | Rotor torque |
| /(kg/m3) | Air density |
| Parameter | Numerical Result | Reference Value [46] | Error |
|---|---|---|---|
| Surge | 119 | 113 | 5.3% |
| Sway | 114 | 112 | 1.7% |
| Heave | 17.9 | 17.5 | 2.3% |
| Roll | 26.2 | 26.9 | 2.6% |
| Pitch | 27.5 | 26.8 | 2.6% |
| Yaw | 79.8 | 82.3 | 3.0% |
| Case | Fluid Region (Million) | Rotating Region (Million) | Total Grid (Million) |
|---|---|---|---|
| Mesh1 | 340 | 650 | 990 |
| Mesh2 | 420 | 800 | 1220 |
| Mesh3 | 420 | 980 | 1500 |
| Item | Value | |
|---|---|---|
| Cut-in wind speed (m/s) | 4 | |
| Cut-out wind speed (m/s) | 25 | |
| Rated wind speed (m/s) | 10 | |
| Rotor speed (rad/s) | 0.508 | |
| Blade airfoil | NACA0018 | |
| Single- configuration | Rotor diameter (m) | 209 |
| Rotor height (m) | 314 | |
| Blade chord length (m) | 10.45 | |
| Number of blades | 2 | |
| Double- configuration | Rotor diameter (m) | 104.5 |
| Rotor height (m) | 157 | |
| Blade chord length (m) | 5.225 | |
| Number of blades | 2 | |
| Item | Value |
|---|---|
| Pontoon angle (°) | 120 |
| Central column height (m) | 33 |
| Side column height (m) | 32 |
| Mass (kg) | 2.360 × 107 |
| Center of gravity (x, y, z) (m) | (−0.02, 0.00, −7.94) |
| Center of buoyancy (x, y, z) (m) | (0.00, 0.00, −14.24) |
| Roll moment of inertia, Ixx (kg·m2) | 2.670 × 1010 |
| Pitch moment of inertia, Iyy (kg·m2) | 2.660 × 1010 |
| Yaw moment of inertia, Izz(kg·m2) | 1.640 × 1010 |
| Displacement volume (m3) | 2.350 × 104 |
| Draft (m) | 22 |
| Item | Value |
|---|---|
| Number of mooring lines | 3 |
| Angle between adjacent lines (°) | 120 |
| Length of each mooring line (m) | 1259 |
| Mooring radius (m) | 1230 |
| Water depth (m) | 333.27 |
| Mass per unit length (kg·m) | 108.36 |
| Axial stiffness (N/m) | 902,000 |
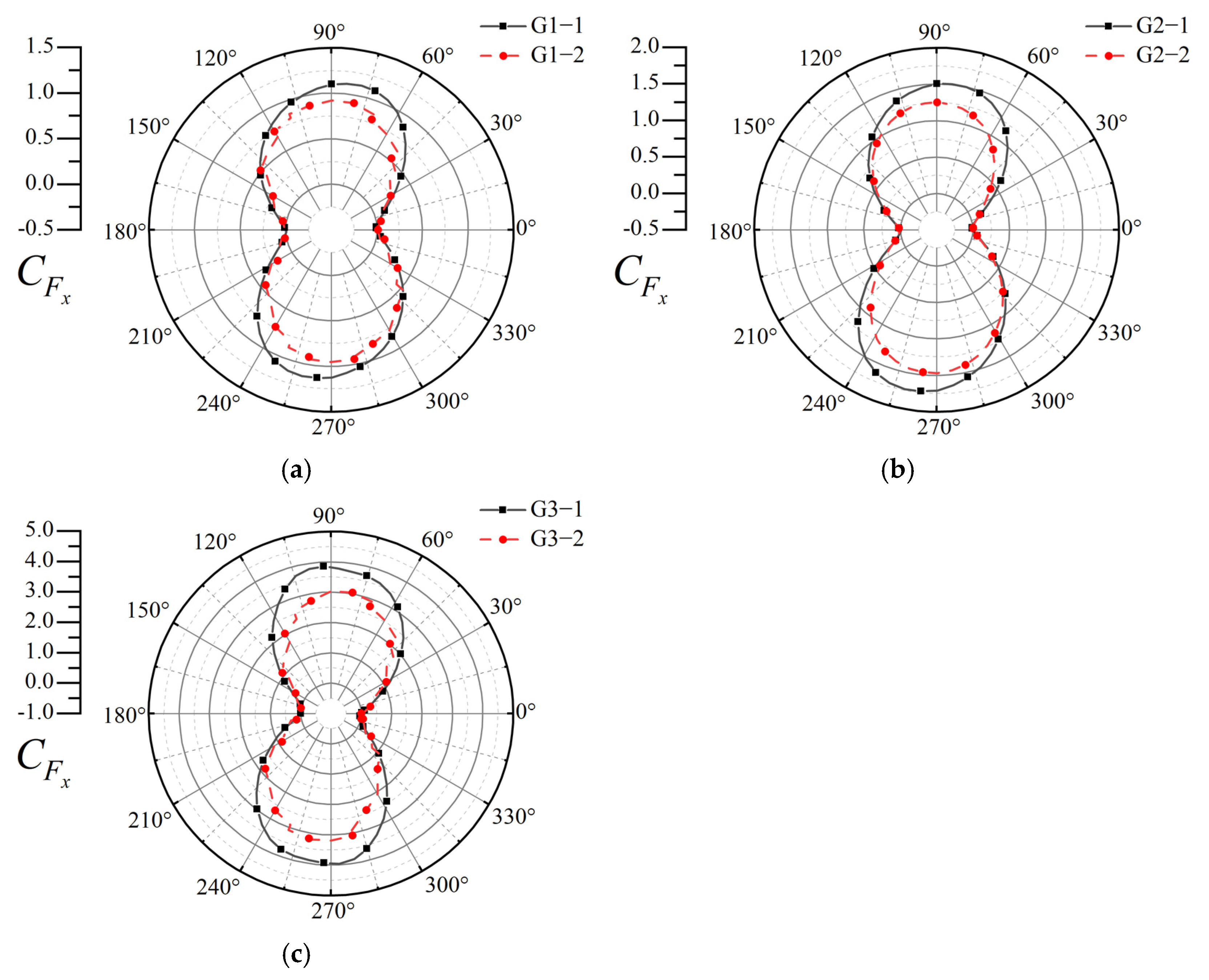
| Case | Wave Height (m) | Peak Period (s) | Wind Speed (m/s) | Turbine Configuration |
|---|---|---|---|---|
| G1-1 | 3.02 | 10.73 | 8 | Single- |
| G1-2 | Double- | |||
| G2-1 | 7.58 | 12.1 | 10 | Single- |
| G2-2 | Double- | |||
| G3-1 | 7.58 | 12.1 | 20 | Single- |
| G3-2 | Double- |
| Case | Pitch (°) | ||
|---|---|---|---|
| Max | Min | Mean | |
| G1-1 | 2.07 | 1.61 | 1.82 |
| G1-2 | 1.72 | 1.31 | 1.50 |
| G2-1 | 2.87 | 2.16 | 2.56 |
| G2-2 | 2.47 | 1.65 | 2.19 |
| G3-1 | 6.60 | 5.01 | 5.80 |
| G3-2 | 5.13 | 3.99 | 4.56 |
| Case | Wave Height (m) | Period (s) | Wind Speed (m/s) | Double-Φ VAWT Installation Angles |
|---|---|---|---|---|
| G2-2 | 7.58 | 12.1 | 10 | 15° 30° 45° 60° 75° 90° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Wang, Z.; Zhang, W.; Zhao, B. The Role of Double-Φ Floating Semi-Submersible Vertical Axis Wind Turbines in Suppressing the Gyroscopic Effect. Energies 2025, 18, 5847. https://doi.org/10.3390/en18215847
Jiang J, Wang Z, Zhang W, Zhao B. The Role of Double-Φ Floating Semi-Submersible Vertical Axis Wind Turbines in Suppressing the Gyroscopic Effect. Energies. 2025; 18(21):5847. https://doi.org/10.3390/en18215847
Chicago/Turabian StyleJiang, Jin, Zhengyang Wang, Weijie Zhang, and Binbin Zhao. 2025. "The Role of Double-Φ Floating Semi-Submersible Vertical Axis Wind Turbines in Suppressing the Gyroscopic Effect" Energies 18, no. 21: 5847. https://doi.org/10.3390/en18215847
APA StyleJiang, J., Wang, Z., Zhang, W., & Zhao, B. (2025). The Role of Double-Φ Floating Semi-Submersible Vertical Axis Wind Turbines in Suppressing the Gyroscopic Effect. Energies, 18(21), 5847. https://doi.org/10.3390/en18215847






