Metaheuristic-Based Control Parameter Optimization of DFIG-Based Wind Energy Conversion Systems Using the Opposition-Based Search Optimization Algorithm
Abstract
1. Introduction
1.1. Research Gaps
1.2. Motivation
- Improve energy conversion efficiency and minimize power losses under variable wind conditions.
- Enhance dynamic stability by reducing oscillations and settling times.
- Lower computational burden, enabling faster adaptation and real-time control.
1.3. Research Contribution
2. Literature Review
2.1. PI Controller Tuning in DFIG Systems
2.2. Metaheuristic Optimization Techniques for PI Tuning
2.3. Hybrid and Advanced Control Strategies
2.4. Emerging Techniques in Intelligent Control
2.5. Owl Search Optimization (OSO) and Other Metaheuristics
3. Proposed Methodology
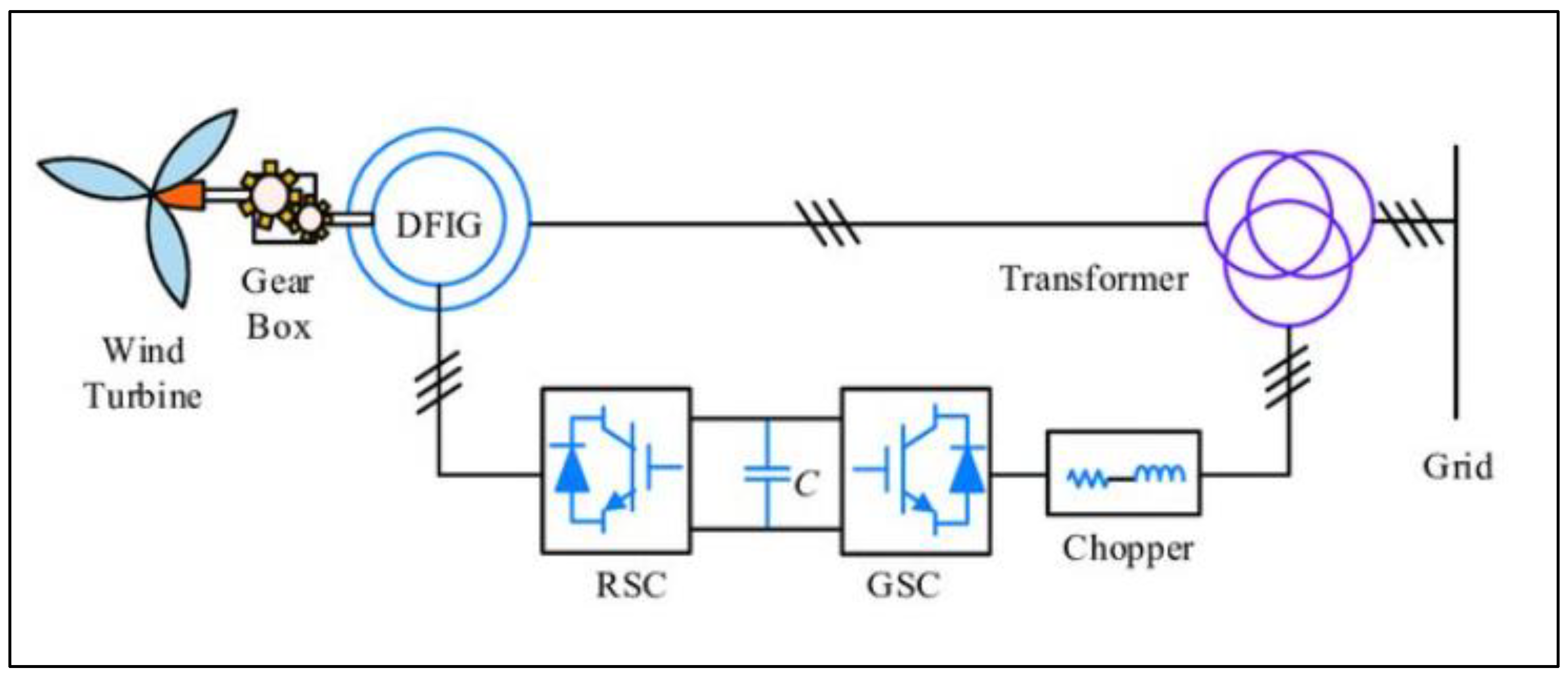
3.1. Model Development of DFIG-Based Wind Energy Conversion
- Rotor-Side Converter (RSC). The RSC regulates the power flow—both active and reactive—between the rotor and the grid by adjusting the generator slip. A 3-phase IGBT-based voltage source inverter (VSI) connects to the rotor of the induction generator through slip rings. Using vector control, the system can also control torque and flux independently [19].
- DC-Link Capacitor. The DC capacitor will be an electrolytic capacitor that performs as an energy buffer between the RSC and GSC. It acts as an energy buffer between the RSC and GSC, smoothing power transfer and stabilizing voltage [16].
3.2. Operation of Back-to-Back Converter
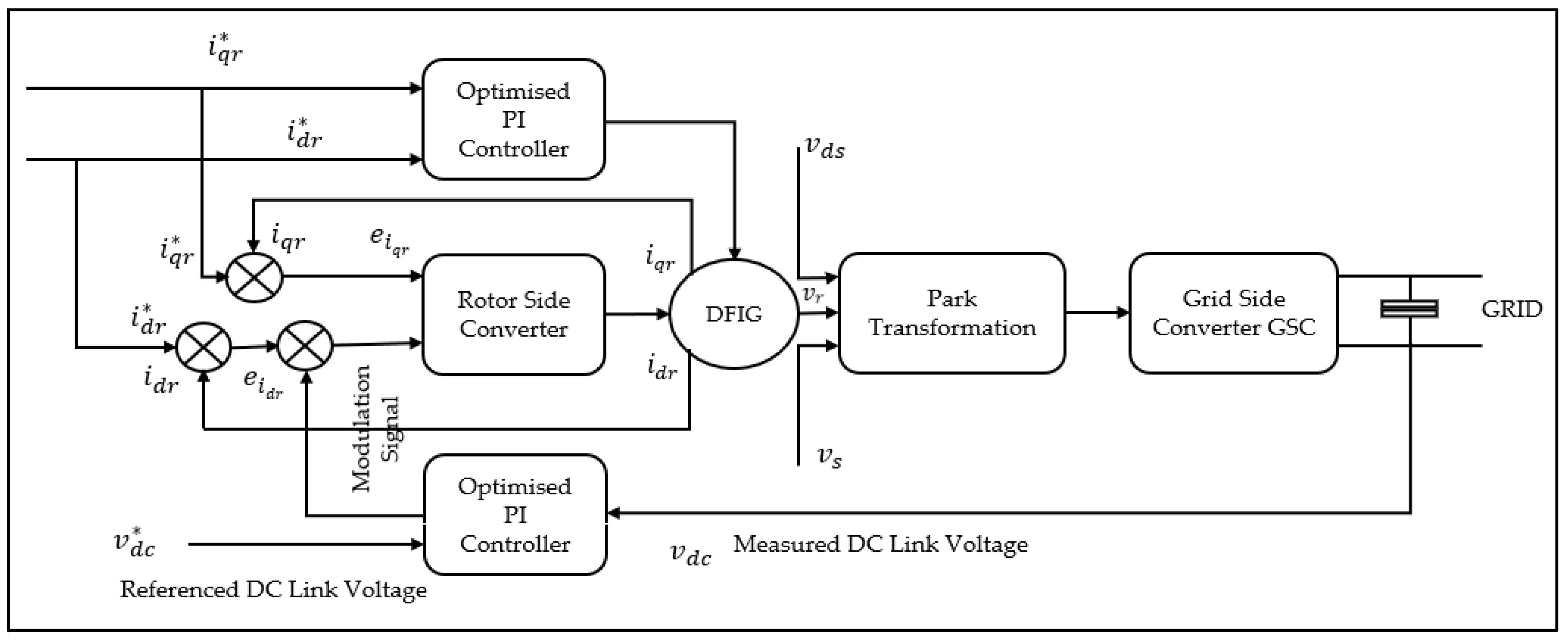
3.3. Control Structure of the DFIG Converter
3.3.1. RSC Control
3.3.2. GSC Control
3.4. Mathematical Equations and Performance Metrics
3.5. PI Controller Optimization Problem
- ITAE: integral of time-weighted absolute error.
- OS: percentage overshoot.
- : settling time.
- : converter power losses.
- : weighting factors reflecting control priorities.
3.6. Owl Search Optimization (OSO) Algorithm for PI Tuning
- Initialization: Generate candidate solutions (, ) within defined bounds.
- Fitness Evaluation: Compute the objective function J for each solution.
- Position Update: Adapt search based on exploration–exploitation balance.
- Selection: Retain the best candidates.
- Termination: Stop the process when the algorithm reaches the maximum iterations or meets the convergence criteria.
- Fewer iterations to reach convergence.
- Reduced computational overhead (no crossover/mutation as in GA).
- Faster adaptation to disturbances compared to SA.
4. Study of Other Optimization Algorithms
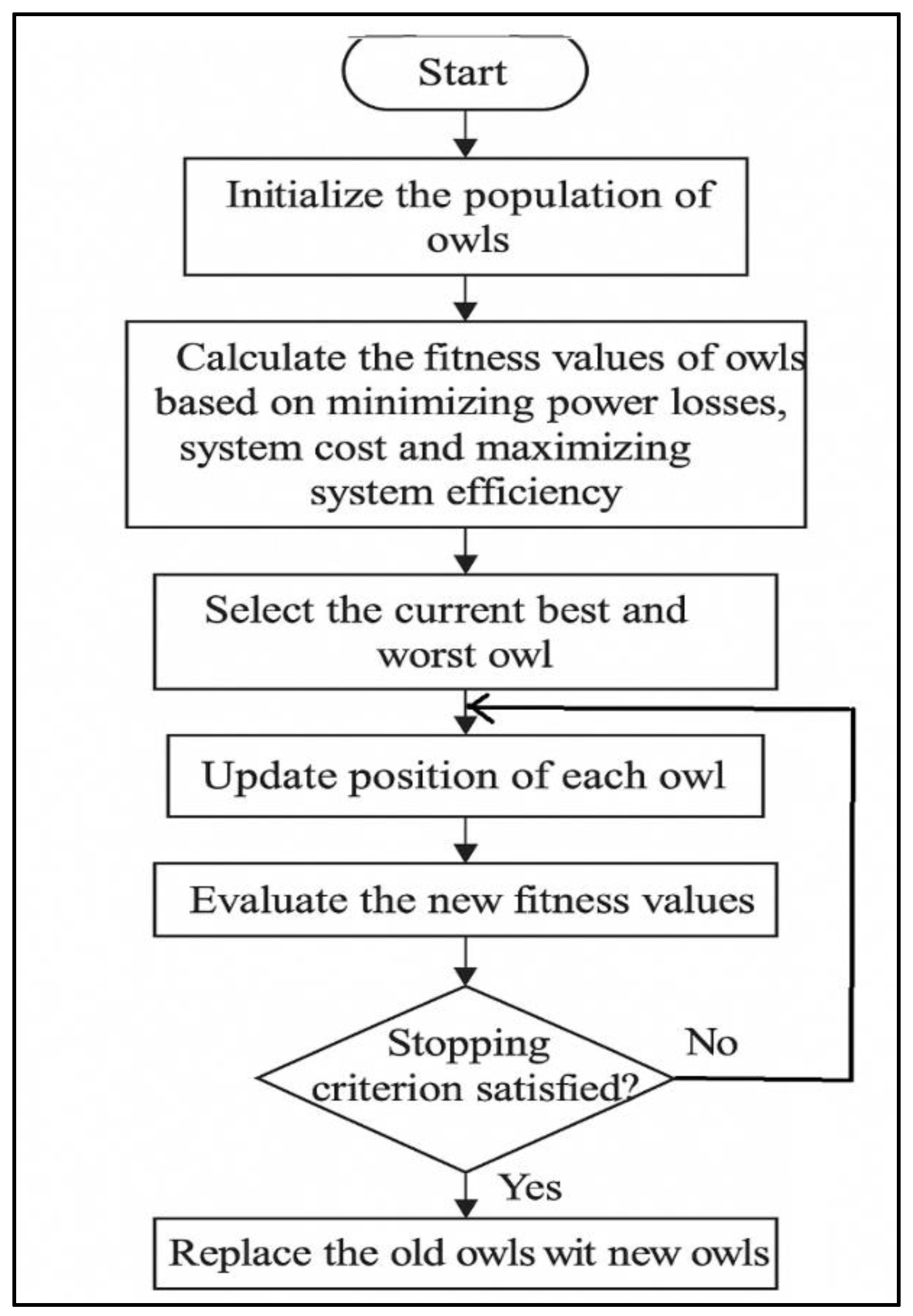
4.1. Optimization Using Owl Search Optimization
4.1.1. Algorithm of Owl Search Optimization
4.1.2. Flowchart of Owl Search Optimization
4.1.3. Computational Efficiency
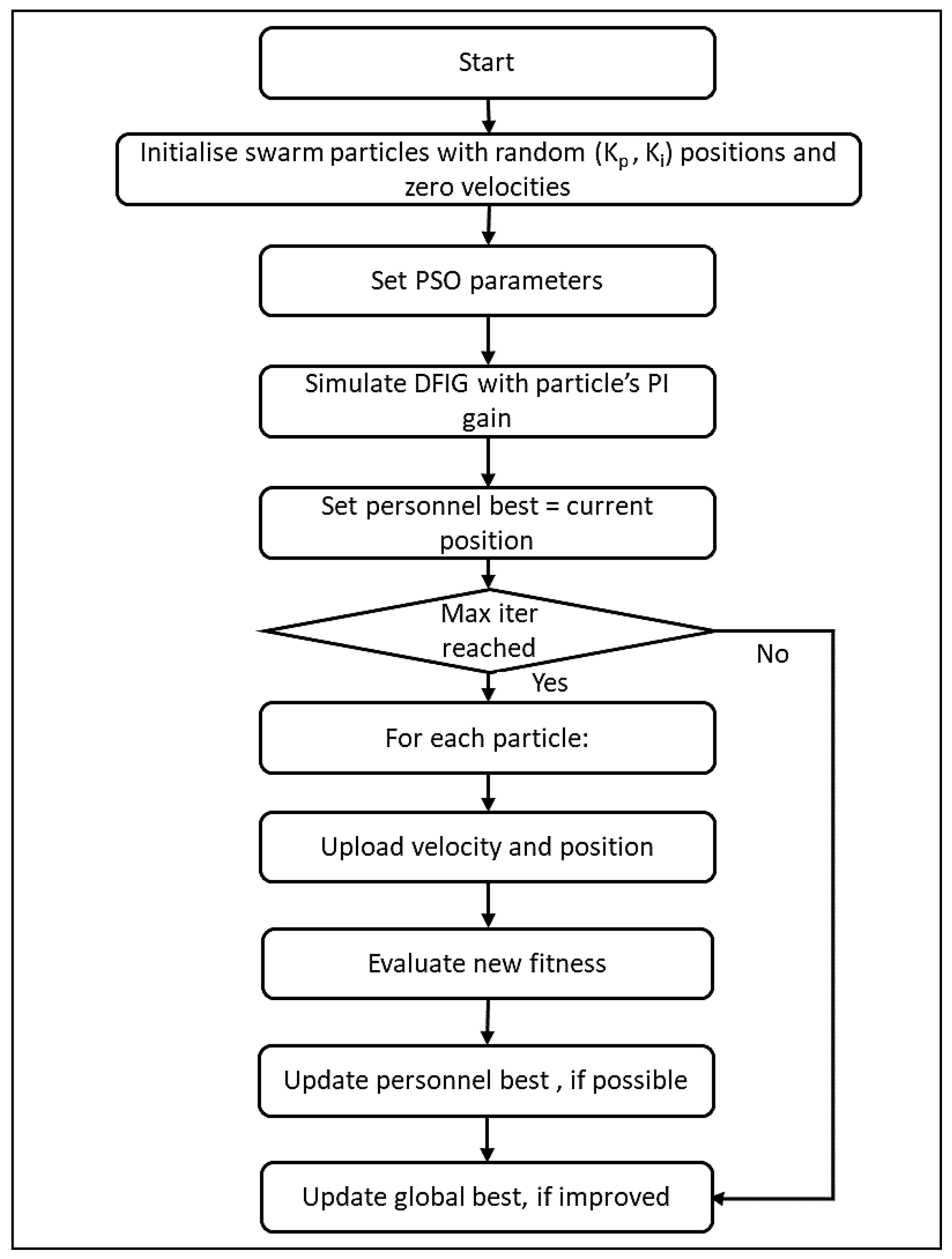
4.2. Particle Swarm Optimization (PSO)
4.2.1. Algorithm of Particle Swarm Optimization
4.2.2. Flowchart of Particle Swarm Optimization
4.3. Genetic Algorithm (GA)
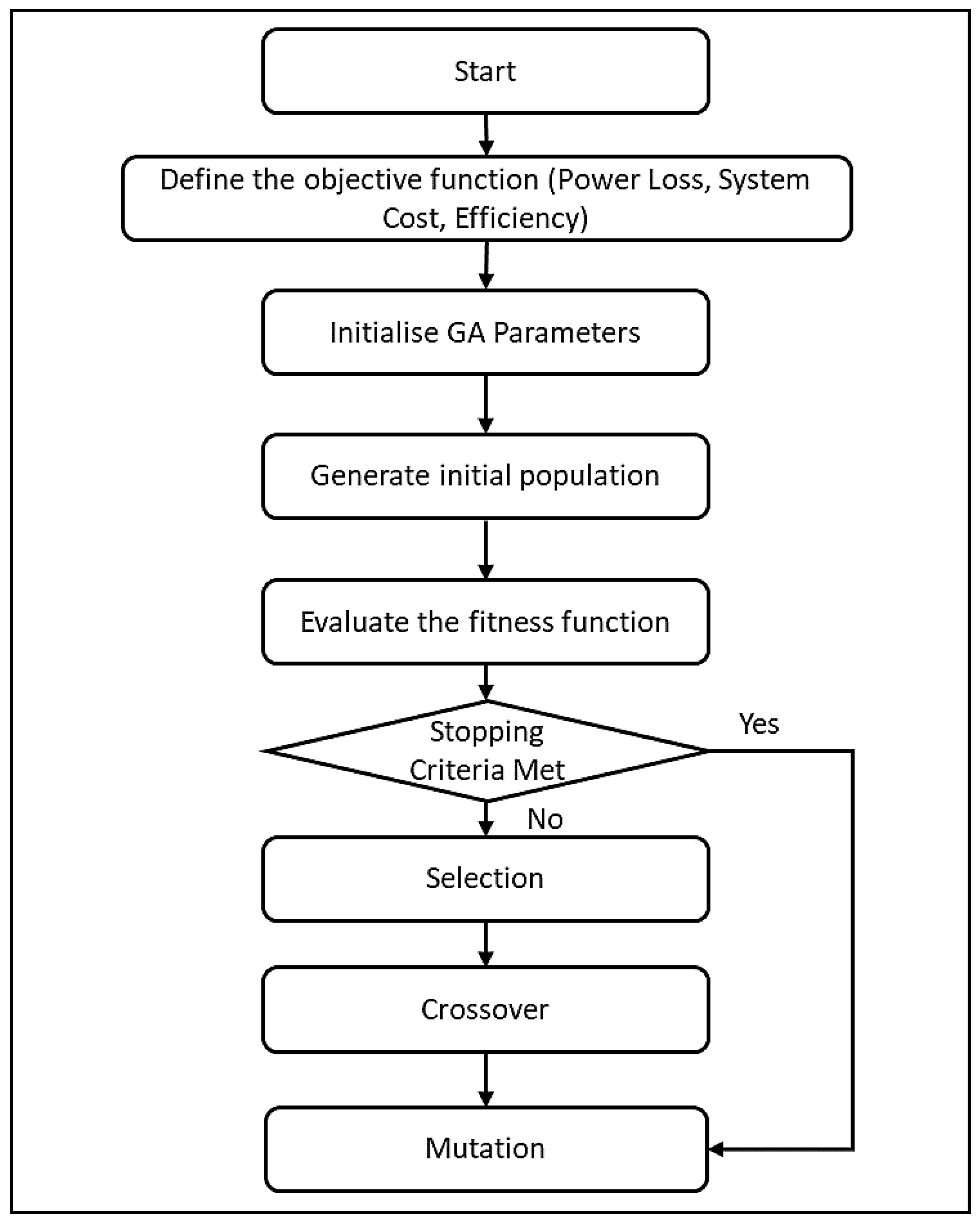
4.3.1. Flowchart of Genetic Algorithm
4.3.2. Algorithm of Genetic Algorithm (GA)
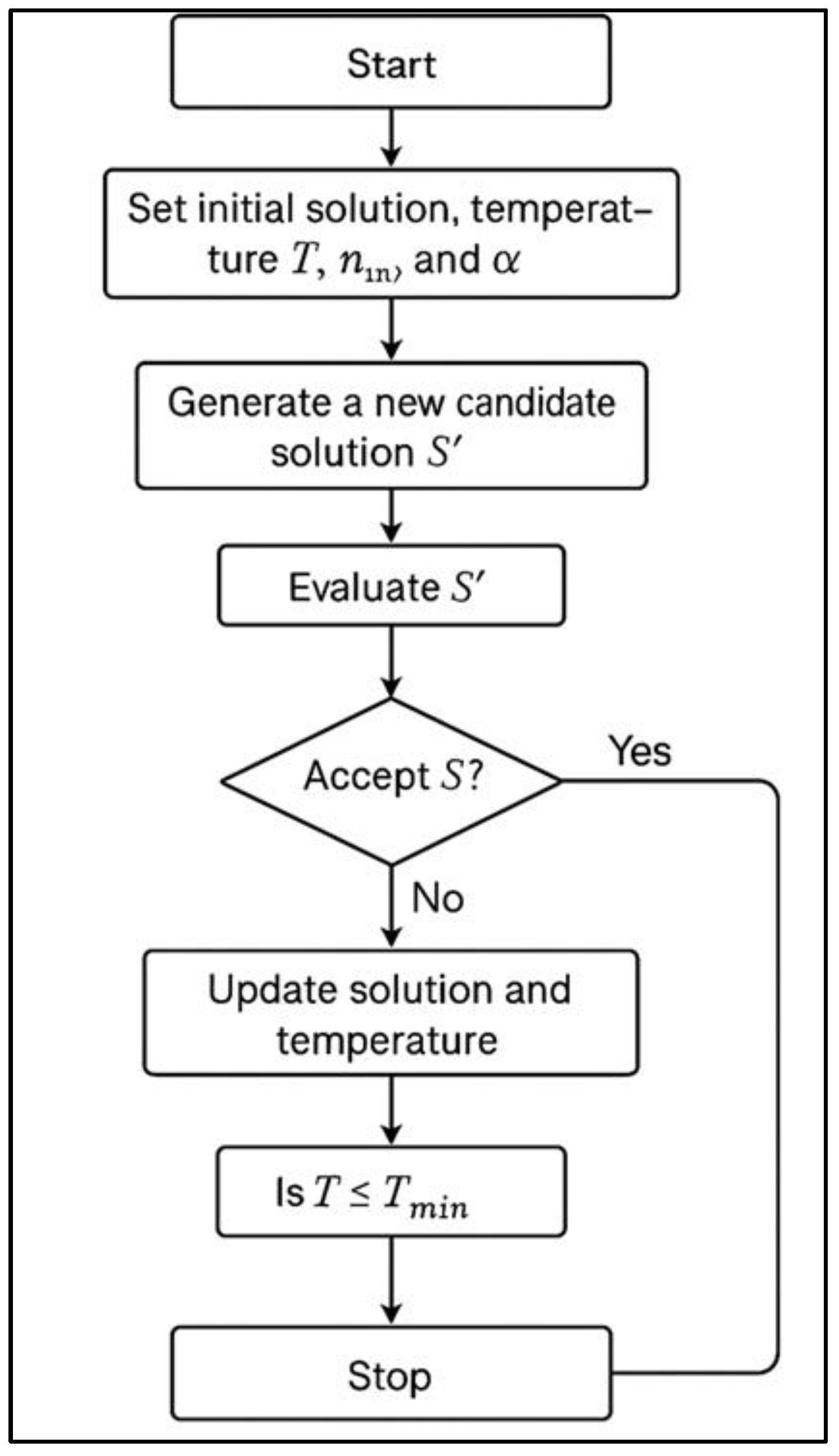
4.4. Simulated Annealing (SA)
4.4.1. Algorithm of Simulated Annealing (SA)
4.4.2. Flowchart of Simulated Annealing
4.5. Comparisons of the Studied Algorithm Structures
5. Simulation and Results
5.1. Simulation Setup
5.2. DFIG Model Verification
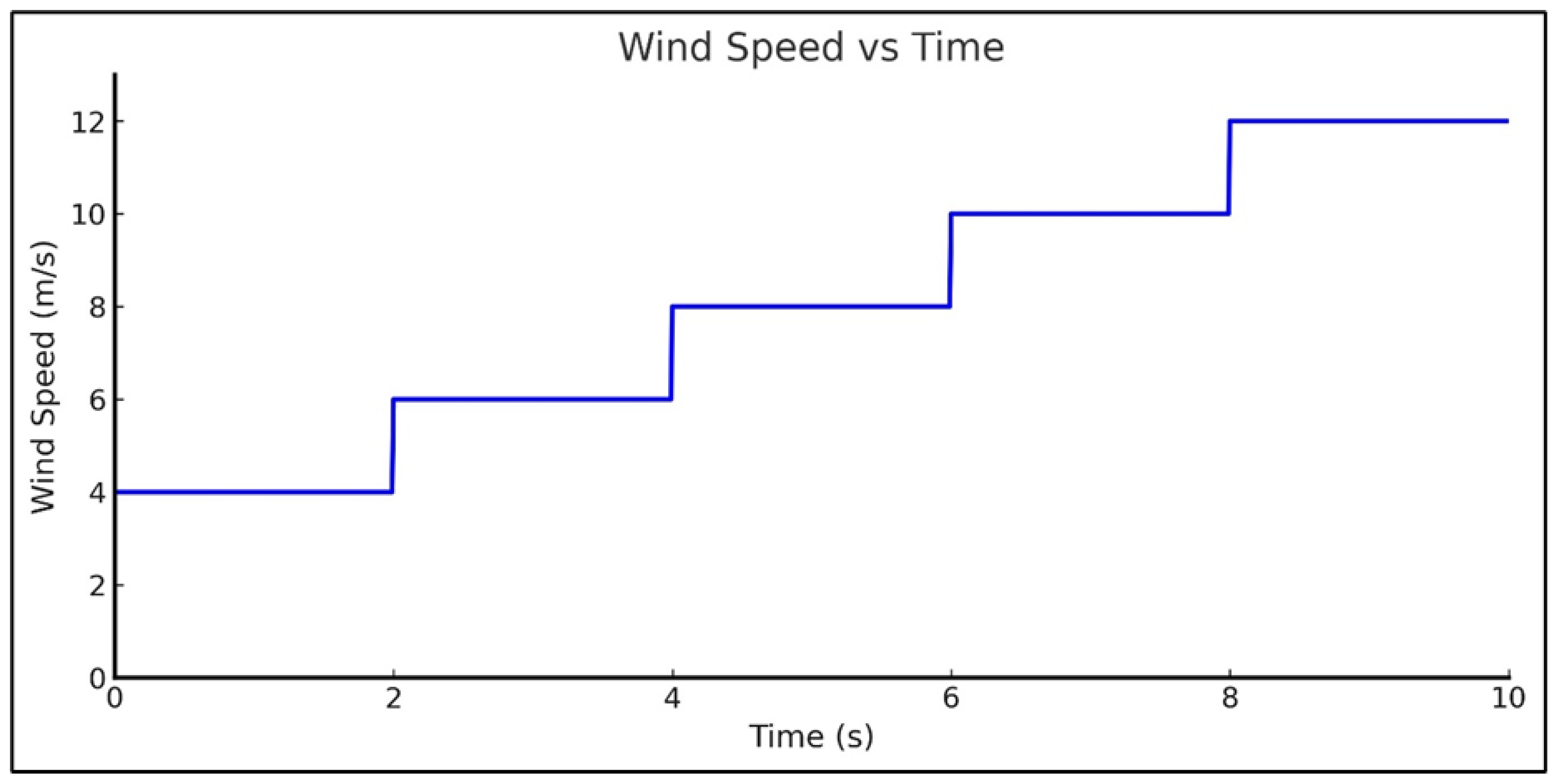
5.3. Simulation Analysis Under Step-Changing Wind Speed Inputs (4–12 m/s)
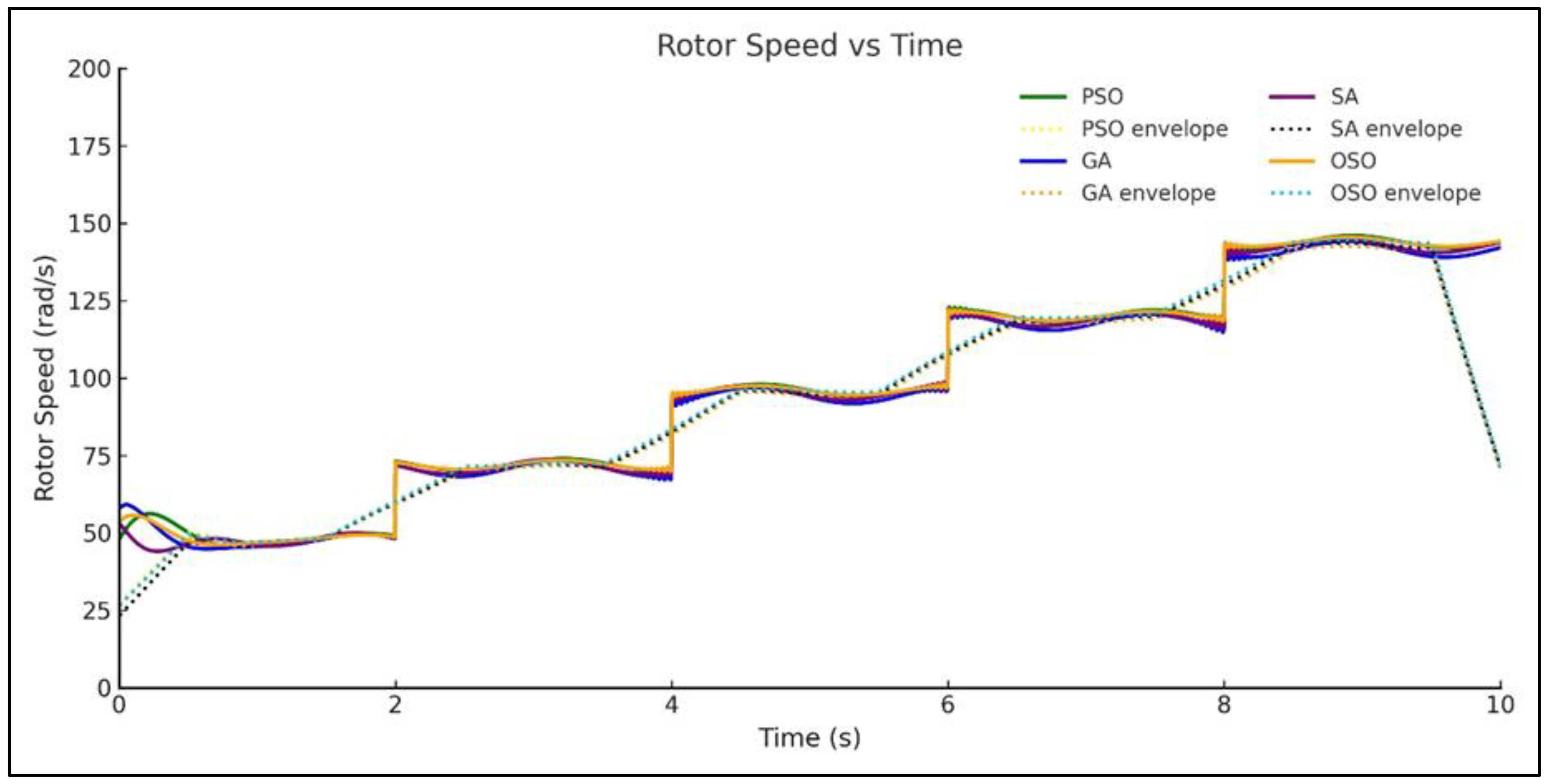
5.3.1. Rotor Speed Response
5.3.2. DC-Link Voltage Stability
5.3.3. Active Power Dynamics
5.3.4. Stator Current Quality
5.3.5. Electromagnetic Torque Response
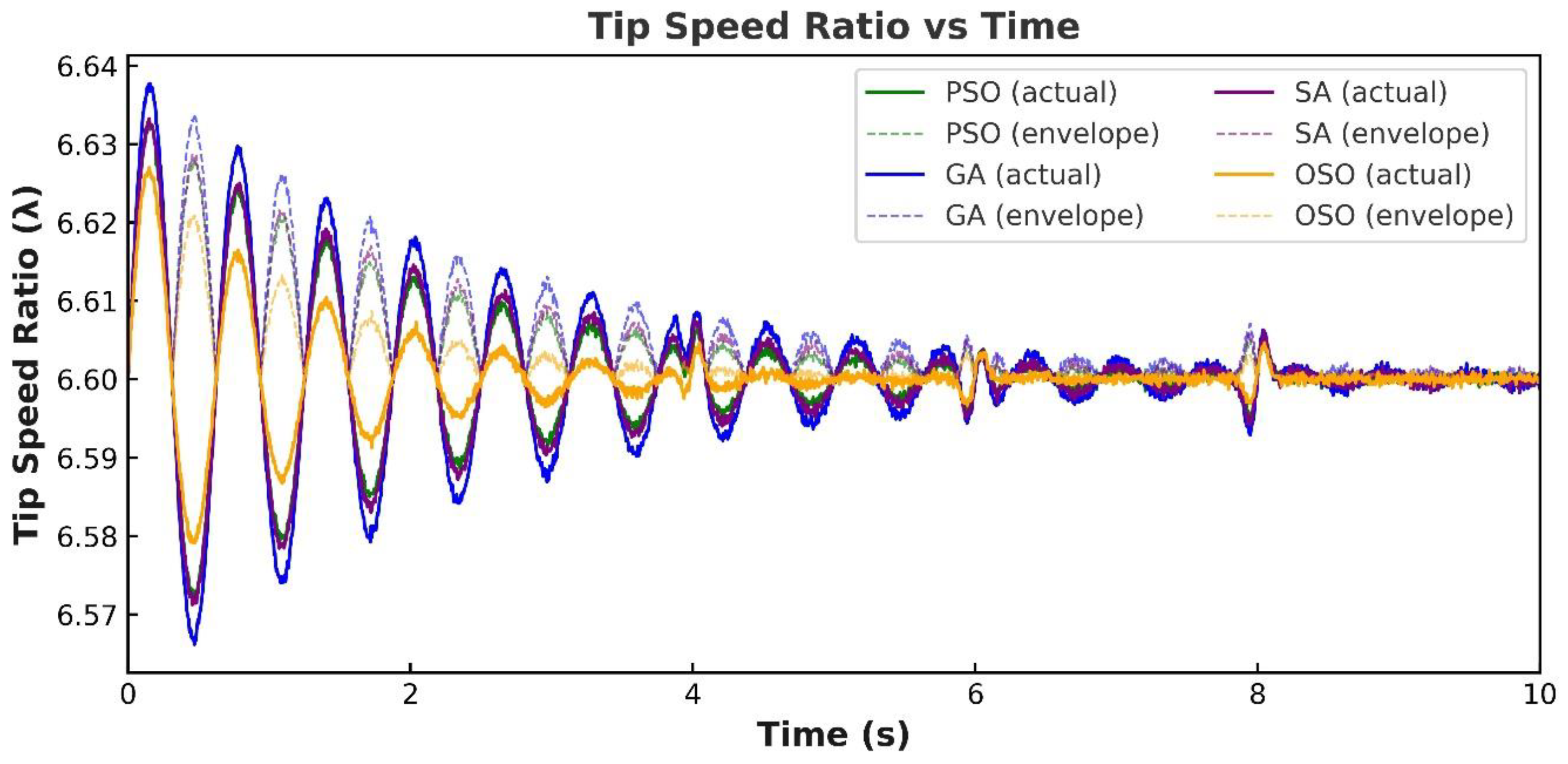
5.3.6. Tip Speed Ratio (TSR) Under Step-Changing Wind Speed Conditions
5.4. Simulation Analysis on Variable Wind Speed Scenario from 4 m/s to 12 m/s
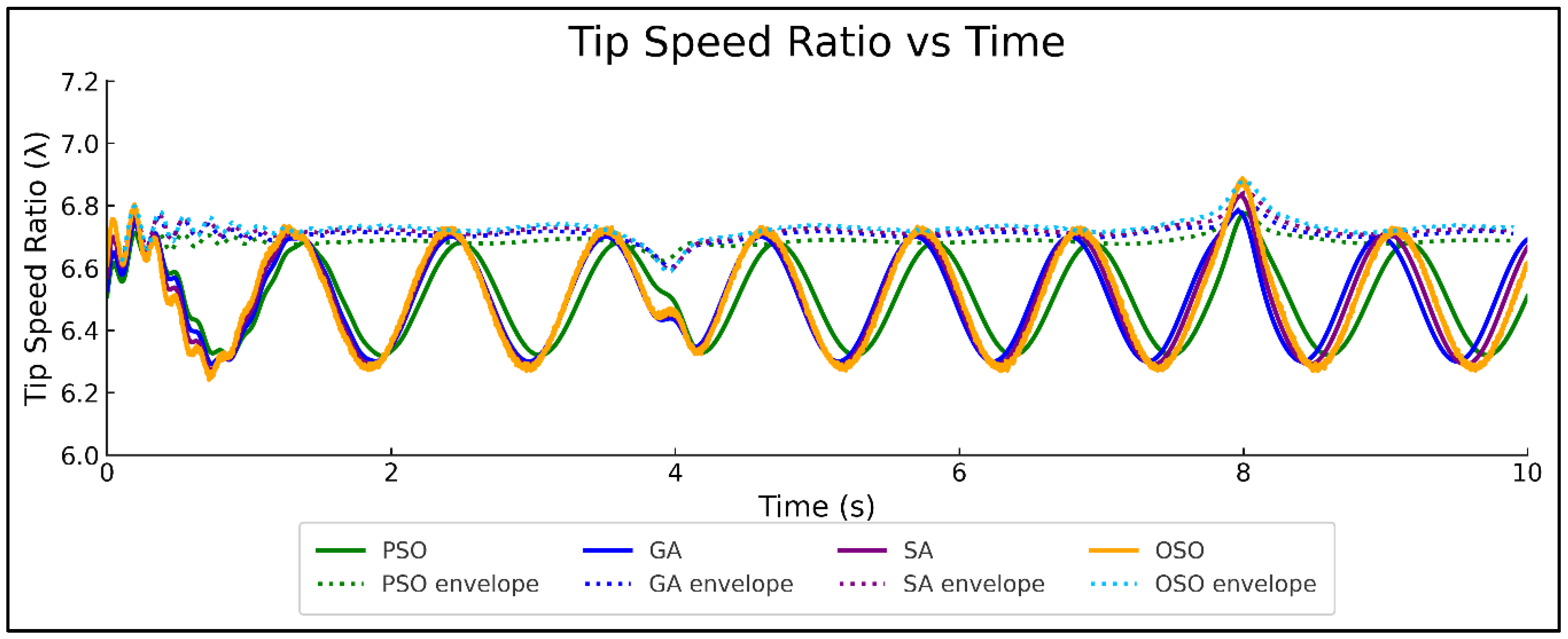
5.4.1. Tip-Speed Ratio (TSR)
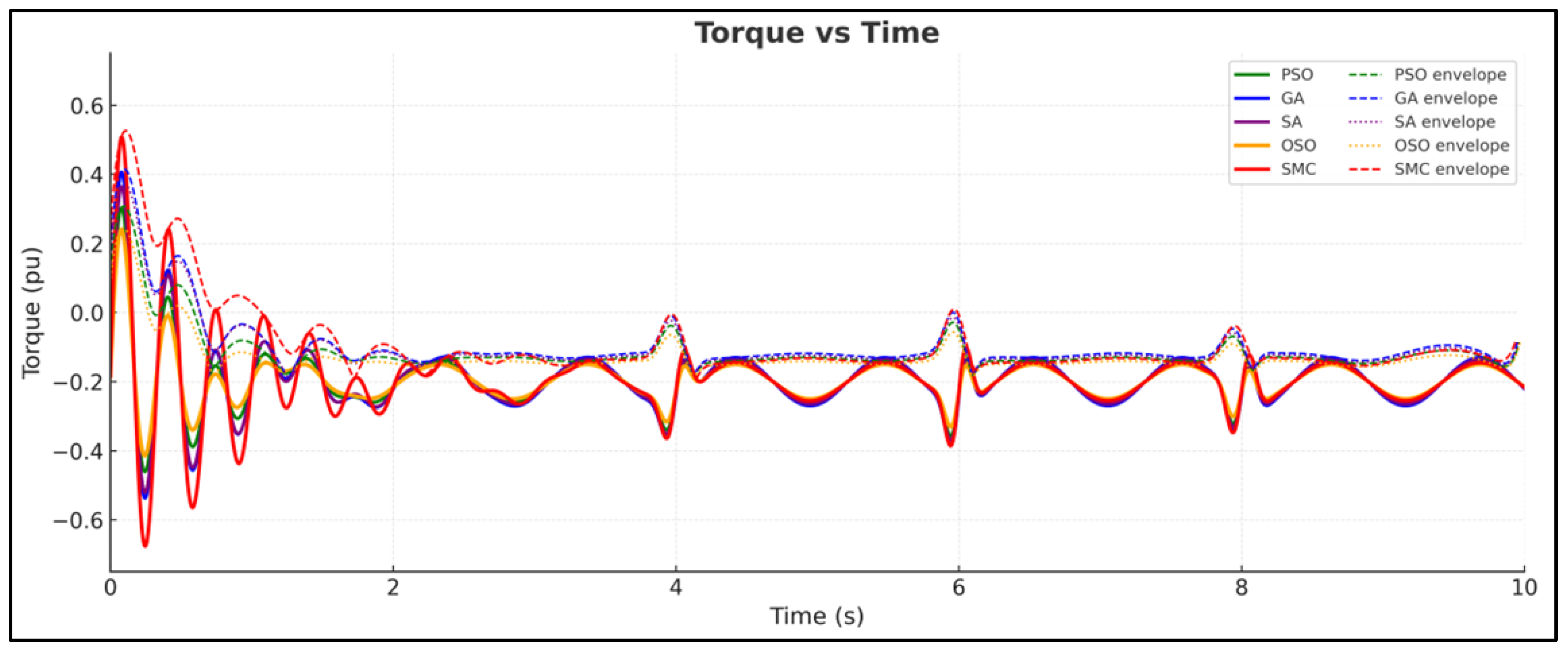
5.4.2. Torque vs. Time
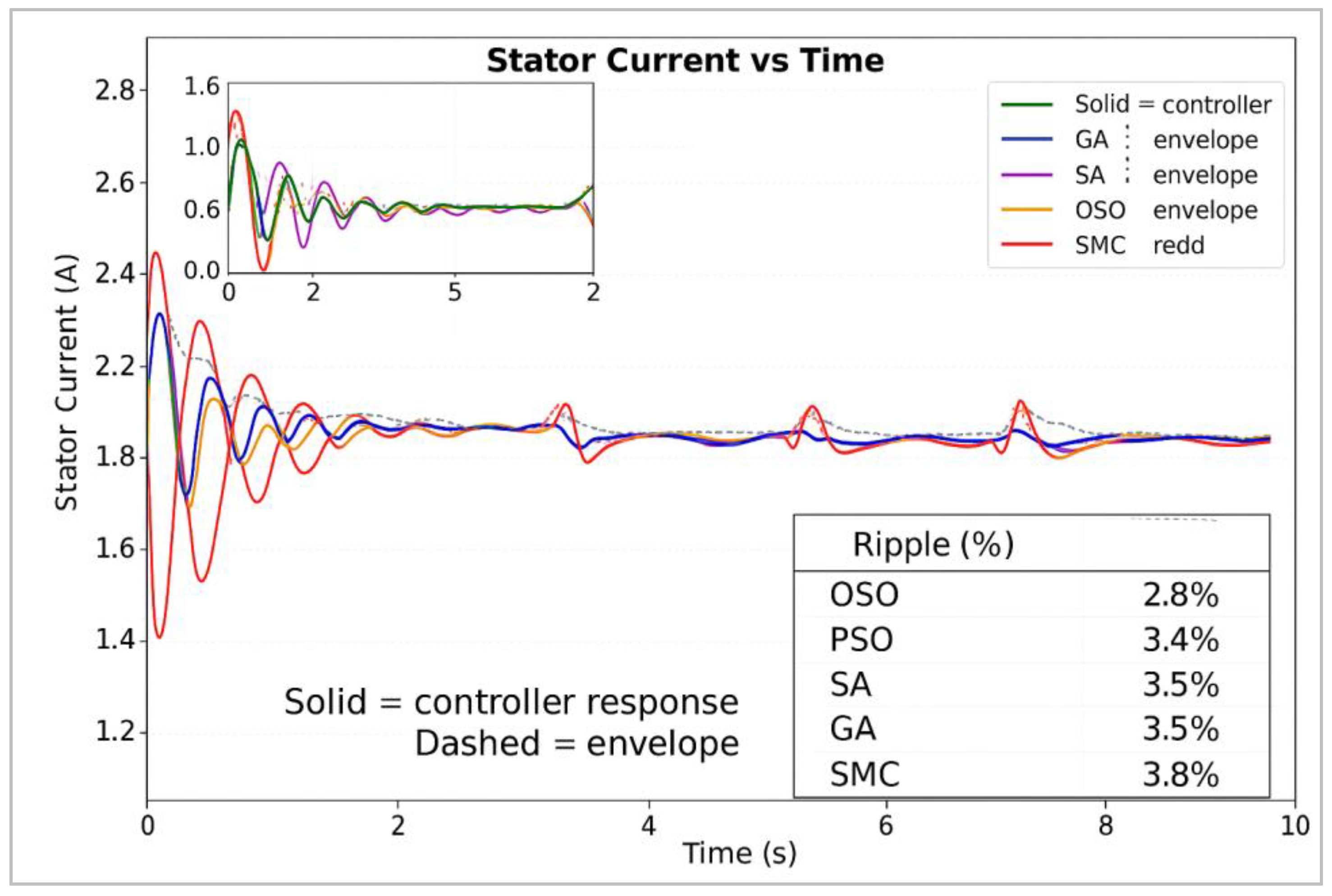
5.4.3. Stator Current vs. Time
5.4.4. Rotor Speed vs. Time
5.4.5. DC-Link Voltage vs. Time
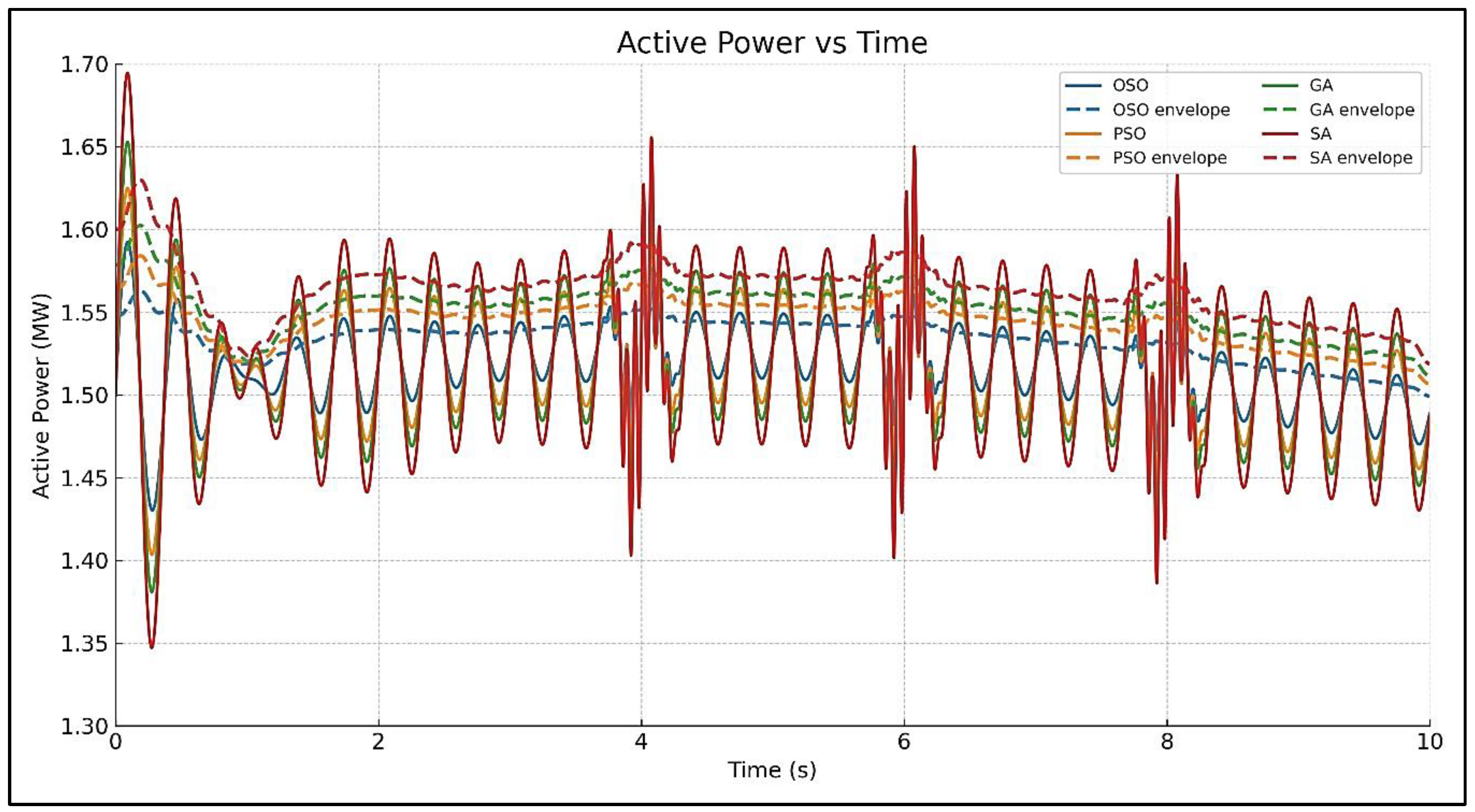
5.4.6. Active Power vs. Time
6. Simulation Analysis Discussion
6.1. Step Wind Speed Change
6.2. Variable Wind Speed Ramp
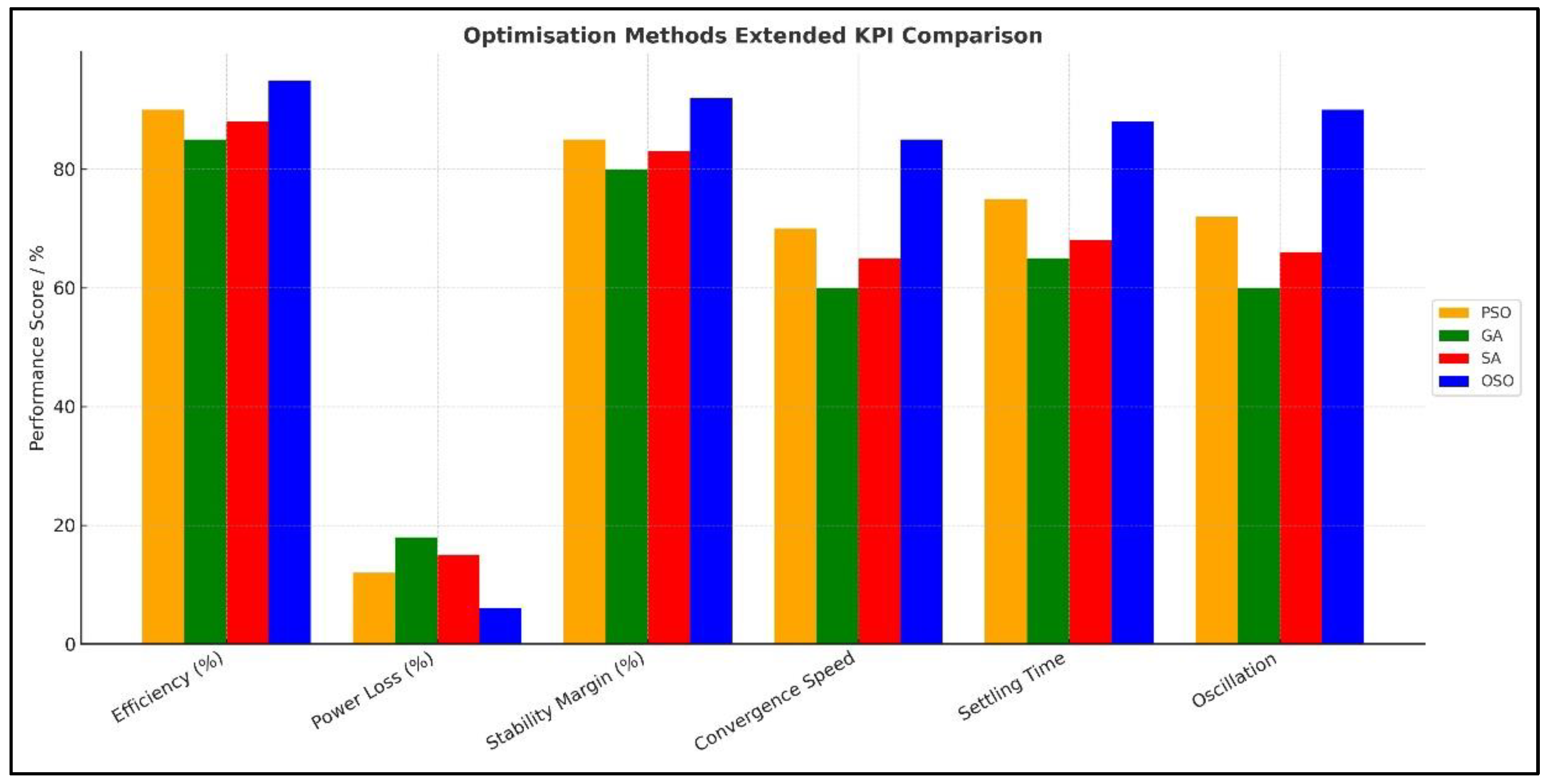
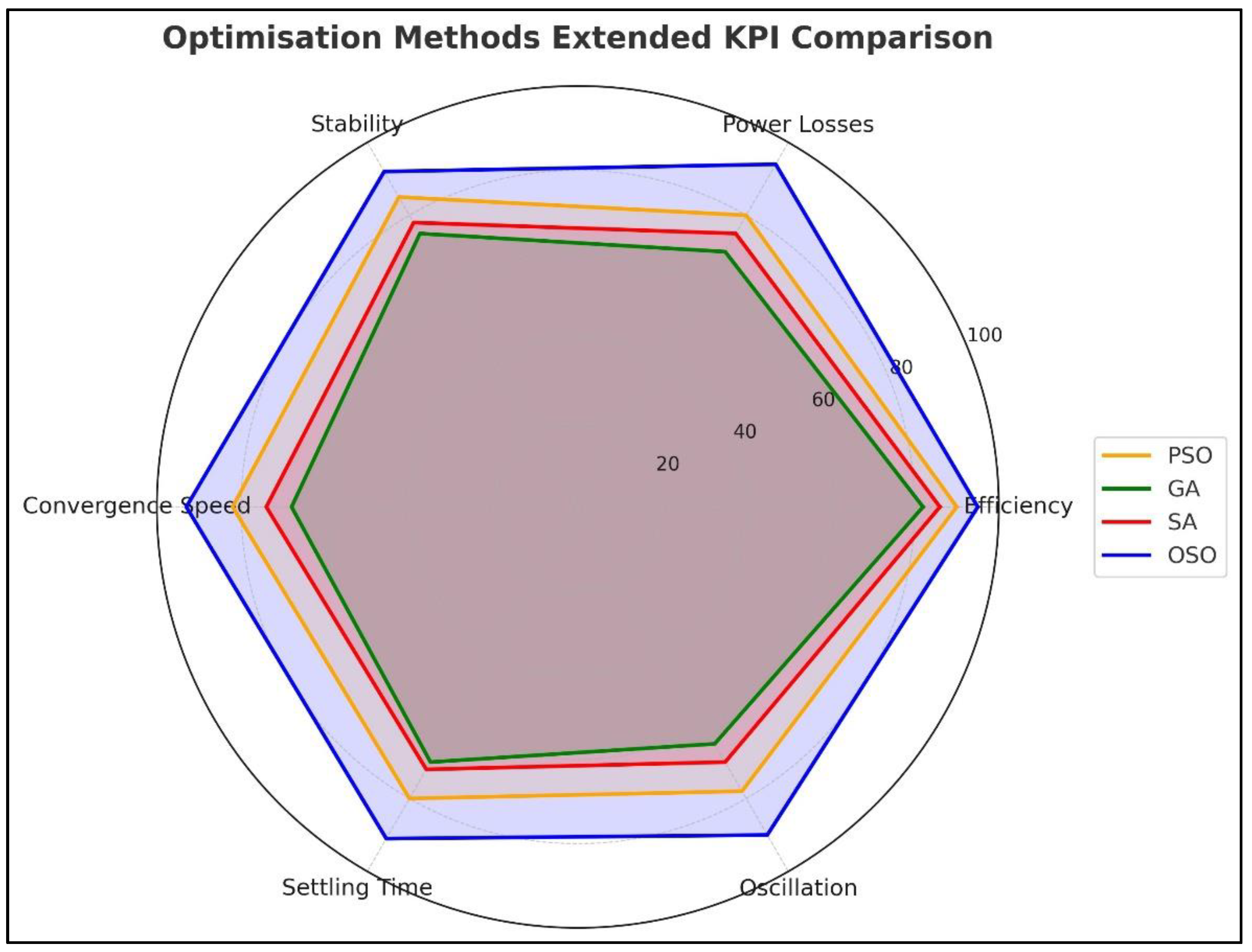
6.3. Key Performance Indices
6.4. Sensitivity Analysis
7. Conclusions
- Dynamic response: OSO achieved the lowest rise and settling times, with effective suppression of oscillations and overshoot.
- Ripple suppression: OSO minimized DC-link voltage and stator current ripples, reducing RMS ripple values by about 20–30% compared to GA and SA.
- Harmonic quality and PQ indices: OSO delivered the lowest stator current THD (~2.8%) and maintained a high power factor (>0.96), ensuring grid-friendly operation.
- LVRT/FRT performance: OSO provided superior fault ride-through capability, with stable DC-link headroom and rapid post-disturbance recovery.
8. Future Work
- Hardware-in-the-Loop (HIL) and Experimental Validation: Extending the study beyond simulations to FPGA- or DSP-based HIL platforms and real testbed implementation.
- Extended Grid Disturbances: Incorporating imbalanced faults, harmonic-rich weak grids, and multi-machine interactions to evaluate robustness further.
- Hybrid Optimization Frameworks: Investigating OSO in combination with adaptive control or reinforcement learning for enhanced adaptability under extreme conditions.
- Scalability Studies: Applying OSO to large-scale wind farms with multi-turbine coordination, including wake effects and grid-code compliance.
- Cyber-Physical Resilience: Evaluating the resilience of OSO-based controllers under communication delays, cyberattacks, and uncertainties in sensor measurements.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nwagu, C.N.; Ujah, C.O.; Kallon, D.V.V.; Aigbodion, V.S. Integrating solar and wind energy into the electricity grid for improved power accessibility. Unconv. Resour. 2025, 5, 100129. [Google Scholar] [CrossRef]
- Duranay, Z.B.; Güldemir, H.; Coşkun, B. The Role of Wind Turbine Siting in Achieving Sustainable Energy Goals. Processes 2024, 12, 2900. [Google Scholar] [CrossRef]
- Ullah, F.; Zhang, X.; Khan, M.; Mastoi, M.S.; Munir, H.M.; Flah, A.; Said, Y. A comprehensive review of wind power integration and energy storage technologies for modern grid frequency regulation. Heliyon 2024, 10, e30466. [Google Scholar] [CrossRef]
- Li, S. Reactive power limit of wind farm with doubly-fed induction generators and its asymmetric P-Q dependence. Int. J. Electr. Power Energy Syst. 2025, 169, 110819. [Google Scholar] [CrossRef]
- Kebede, M.G.; Tuka, M.B. Power Control of Wind Energy Conversion System with Doubly Fed Induction Generator. J. Energy 2022, 2022, 8679053. [Google Scholar] [CrossRef]
- Alhato, M.M.; Ibrahim, M.N.; Rezk, H.; Bouallègue, S. An Enhanced DC-Link Voltage Response for Wind-Driven Doubly Fed Induction Generator Using Adaptive Fuzzy Extended State Observer and Sliding Mode Control. Mathematics 2021, 9, 963. [Google Scholar] [CrossRef]
- Izanlo, A.; Abdollahi, S.E.; Gholamian, S.A. A New Method for Design and Optimization of DFIG for Wind Power Applications. Electr. Power Components Syst. 2020, 48, 1523–1536. [Google Scholar] [CrossRef]
- e Mustafa, F.; Ahmed, I.; Basit, A.; Alqahtani, M.; Khalid, M. An adaptive metaheuristic optimization approach for Tennessee Eastman process for an industrial fault tolerant control system. PLoS ONE 2024, 19, e0296471. [Google Scholar] [CrossRef] [PubMed]
- Xiang, X.; Diao, R.; Bernadin, S.; Foo, S.Y.; Sun, F.; Ogundana, A.S. An Intelligent Parameter Identification Method of DFIG Systems Using Hybrid Particle Swarm Optimization and Reinforcement Learning. IEEE Access 2024, 12, 44080–44090. [Google Scholar] [CrossRef]
- Manjunath, T.G.; Kusagur, A. Analysis of Different Meta Heuristics Method in Intelligent Fault Detection of Multilevel Inverter with Photovoltaic Power Generation Source. Int. J. Power Electron. Drive Syst. 2018, 9, 1214–1222. [Google Scholar] [CrossRef]
- Huang, W.; Hu, B.; Shao, C.; Li, W.; Wang, X.; Xie, K.; Chung, C.Y. Power System Reliability Evaluation Based on Sequential Monte Carlo Simulation Considering Multiple Failure Modes of Components. J. Mod. Power Syst. Clean Energy 2024, 13, 202–214. [Google Scholar] [CrossRef]
- Elnaghi, B.E.; Abelwhab, M.N.; Abdel-Kader, F.E.S.A.; Ismaiel, A.M.; Mohammed, R.H.; Dessouki, M.E. Experimental Validation of Second-Order Adaptive Fuzzy Logic Controller for Grid-Connected DFIG Wind Power Plant. IEEE Access 2023, 11, 135255–135271. [Google Scholar] [CrossRef]
- Aguilar, M.E.B.; Coury, D.V.; Reginatto, R.; Monaro, R.M. Multi-objective PSO applied to PI control of DFIG wind turbine under electrical fault conditions. Electr. Power Syst. Res. 2020, 180, 106081. [Google Scholar] [CrossRef]
- Guediri, A.; Touil, S. Optimization Using a Genetic Algorithm Based on DFIG Power Supply for the Electrical Grid. Int. J. Eng. 2022, 35, 121–129. [Google Scholar] [CrossRef]
- Yang, K.; Cho, K. Simulated Annealing Algorithm for Wind Farm Layout Optimization: A Benchmark Study. Energies 2019, 12, 4403. [Google Scholar] [CrossRef]
- Puchalapalli, S.; Singh, B. A Novel Control Scheme for Wind Turbine Driven DFIG Interfaced to Utility Grid. IEEE Trans. Ind. Appl. 2020, 56, 2925–2937. [Google Scholar] [CrossRef]
- Gholami, A.; Sahab, A.; Tavakoli, A.; Alizadeh, B. DFIG-Based Wind Energy System Robust Optimal Control by Using of Novel LMI-Based Adaptive MPC. IETE J. Res. 2023, 69, 3467–3476. [Google Scholar] [CrossRef]
- Jain, M.; Maurya, S.; Rani, A.; Singh, V. Owl search algorithm: A novel nature-inspired heuristic paradigm for global optimization. J. Intell. Fuzzy Syst. 2018, 34, 1573–1582. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Lin, Y.; Zhang, Z.; Gong, X. Dynamic Equivalent Modeling for Wind Farms With DFIGs Using the Artificial Bee Colony With K-Means Algorithm. IEEE Access 2020, 8, 173723–173731. [Google Scholar] [CrossRef]
- Ngom, I.; Mboup, A.B.; Thiaw, L.; Skander-Mustapha, S.; Belkhodja, I.S. An improved control for DC-link fluctuation during voltage dip based on DFIG. In Proceedings of the 2018 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–22 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Cheng, T.; Wu, J.; Wang, H.; Zheng, H. Dynamic Optimization of Rotor-Side PI Controller Parameters for Doubly-Fed Wind Turbines Based on Improved Recurrent Neural Networks Under Wind Speed Fluctuations. IEEE Access 2023, 11, 102713–102726. [Google Scholar] [CrossRef]
- Sai, B.S.V.; Chatterjee, D.; Mekhilef, S.; Wahyudie, A. An SSM-PSO Based MPPT Scheme for Wind Driven DFIG System. IEEE Access 2022, 10, 78306–78319. [Google Scholar] [CrossRef]
- Abood, S.; Annamalai, A.; Khalid, I.; Chouikha, M.; Al-Zuhairi, H.A. AI-Based Hybrid Control for Optimizing Doubly-Fed Induction Generators in Wind Turbines. Int. J. Intell. Eng. Syst. 2025, 18, 439–459. [Google Scholar] [CrossRef]
- Jayabarathi, T.; Raghunathan, T.; Gandomi, A.H. The Bat Algorithm, Variants and Some Practical Engineering Applications: A Review. In Nature-Inspired Algorithms and Applied Optimization; Springer: Cham, Switzerland, 2018; pp. 313–330. [Google Scholar] [CrossRef]
- Ali, S.Q.; Hasanien, H.M.; Al-Ammar, E.A. Application of an Adaptive Artificial Neural Network Controller for Improving the Dynamic Response of Doubly Fed Induction Generators-Based Wind Farm. J. Bioinform. Intell. Control 2013, 2, 83–91. [Google Scholar] [CrossRef]
- Nasim, F.; Khatoon, S.; Ibraheem; Urooj, S.; Shahid, M.; Ali, A.; Nasser, N. Hybrid ANFIS-PI-Based Optimization for Improved Power Conversion in DFIG Wind Turbine. Sustainability 2025, 17, 2454. [Google Scholar] [CrossRef]
- Kaur, G.; Arora, S. Chaotic whale optimization algorithm. J. Comput. Des. Eng. 2018, 5, 275–284. [Google Scholar] [CrossRef]
- Zhou, S.; Rong, F.; Ning, X. Optimization Control Strategy for Large Doubly-Fed Induction Generator Wind Farm Based on Grouped Wind Turbine. Energies 2021, 14, 4848. [Google Scholar] [CrossRef]
- Behara, R.K.; Saha, A.K. Deep Q-Network Reinforcement Learning-Based Rotor Side Control System of a Grid Integrated DFIG Wind Energy System Under Variable Wind Speed Conditions. IEEE Access 2024, 12, 184179–184205. [Google Scholar] [CrossRef]
- Amiri, F.; Eskandari, M.; Moradi, M.H. Improved Load Frequency Control in Power Systems Hosting Wind Turbines by an Augmented Fractional Order PID Controller Optimized by the Powerful Owl Search Algorithm. Algorithms 2023, 16, 539. [Google Scholar] [CrossRef]
- Alazzam, H.; Al-Adwan, A.; Abualghanam, O.; Alhenawi, E.; Alsmady, A. An Improved Binary Owl Feature Selection in the Context of Android Malware Detection. Computers 2022, 11, 173. [Google Scholar] [CrossRef]
- Aris, N.A.; Ikram, R.R.R.; Zamli, K.Z. Comparison of Four Metaheuristics for Cost-Effective Virtual Learning Resource Optimisation. In Proceedings of the 2025 IEEE International Conference on Industry 4.0, Artificial Intelligence, and Communications Technology (IAICT), Bali, Indonesia, 3–5 July 2025; IEEE: Piscataway, NJ, USA, 2025; pp. 498–502. [Google Scholar] [CrossRef]
- Bekakra, Y.; Attous, D.B. Optimal tuning of PI controller using PSO optimization for indirect power control for DFIG based wind turbine with MPPT. Int. J. Syst. Assur. Eng. Manag. 2014, 5, 219–229. [Google Scholar] [CrossRef]
- El Kafazi, I.; Boubii, C.; Rafia, H.; Bannari, R.; El Bhiri, B. MPC-PSO of a DFIG and comparison with PI controller. In Proceedings of the 2023 5th Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Türkiye, 14–16 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Aguilar, M.E.B.; Coury, D.V.; Reginatto, R.; Monaro, R.M.; de Godoy, P.T.; Jahn, T.G. Multi-Objective PSO for Control-Loop Tuning of DFIG Wind Turbines with Chopper Protection and Reactive-Current Injection. Energies 2023, 17, 28. [Google Scholar] [CrossRef]
- Rodríguez-Pajarón, P.; Bayo, A.H.; Milanović, J.V. Forecasting voltage harmonic distortion in residential distribution networks using smart meter data. Int. J. Electr. Power Energy Syst. 2022, 136, 107653. [Google Scholar] [CrossRef]
- Echiheb, F.; Elkafazi, I.; Bossoufi, B.; El Bhiri, B.; Almalki, M.M.; Alghamdi, T.A.H. Nonlinear robust sliding mode—Backstepping hybrid control for WECS-theoretical design and experimental evaluation. Heliyon 2024, 10, e31767. [Google Scholar] [CrossRef] [PubMed]
- Boudjema, Z.; Meroufel, A.; Djerriri, Y.; Bounadja, E. Fuzzy sliding mode control of a doubly fed induction generator for wind energy conversion. Carpathian J. Electron. Comput. Eng. 2013, 6, 7–14. Available online: https://www.researchgate.net/publication/280320513_Fuzzy_sliding_mode_control_of_a_doubly_fed_induction_generator_for_wind_energy_conversion (accessed on 15 September 2025).








| Method | Strengths | Limitations | Reference |
|---|---|---|---|
| PI controller (manual tuning) | Simple structure, fast response, widely adopted | Poor adaptability to nonlinearities, parameter variations, and grid disturbances; instability under dynamic conditions | [9,11,20] |
| Gradient-based methods | Straightforward implementation, effective for small-scale problems | Susceptible to local optima, low robustness, and unsuitable for high-dimensional nonlinear DFIG systems | [7,12] |
| Particle swarm optimization (PSO) | Fast convergence, widely applied in wind energy systems | Premature convergence, local trapping, and reduced efficiency under dynamic wind variations | [13] |
| Genetic algorithm (GA) | Good global search ability, robust for nonlinear problems | Higher oscillations, longer settling times, and higher computational cost | [14] |
| Simulated annealing (SA) | Strong exploration, avoids premature convergence, stable in some conditions | Slow convergence, heavy computational burden, and limited real-time applicability | [15] |
| Owl search optimization (OSO) (proposed) | Balanced exploration–exploitation, strong global optimization, adaptive control, minimal oscillations | Application to DFIG power converter optimization remains underexplored | [18] |
| Algorithm | Type | Computational Complexity | Strengths | Limitations | Suitability for DFIG PI Tuning |
|---|---|---|---|---|---|
| PSO | Swarm Intelligence | O(N·I), where N = particles, I = iterations | Fast convergence, simple to implement, suitable for continuous parameter tuning | Prone to premature convergence, performance degrades under highly dynamic conditions | Adequate but limited robustness in real-time wind variability |
| GA | Evolutionary Computation | O(N·I·C), where C = crossover/mutation operations | Strong exploration capability, good for complex/nonlinear search spaces | Slow convergence, high computational burden, sensitive to parameter settings | Useful for offline optimization, less practical for real-time tuning |
| SA | Probabilistic Search | O(I), where I = iterations | Escapes local minima using probabilistic acceptance, simple structure | Slow convergence, performance depends on cooling schedule, single-solution trajectory limits exploration | Provides robustness but lacks efficiency for fast-changing wind environments |
| OSO | Nature-Inspired Metaheuristic | O(N·I) | Strong balance of exploration and exploitation, avoids premature convergence, faster than GA and SA, simpler than PSO | Relatively new; fewer theoretical guarantees and limited benchmarking in power systems | Highly suitable for real-time PI tuning due to fast convergence, low computation, and adaptability |
| Metric | OSO (Orange) | PSO (Green) | SA (Purple) | GA (Blue) |
|---|---|---|---|---|
| Rotor Speed (Rise, Settling, Overshoot) | <1.0 s, <1.2 s, <2% | =1.1 s, <1.3 s, 3% | =1.3 s, ≈1.6 s, 4% | =1.5 s, ≈1.8 s, 6% |
| DC-Link Voltage (Vdc) (Ripple RMS, Peak–Peak, Recovery) | =0.3%, =0.6%, <0.8 s | =0.35%, =0.8%, =1.0 s | =0.45%, =1.2%, =1.3 s | =0.55%, =1.5%, =1.6 s |
| Active Power (P) (Rise, Overshoot, Ripple Peak–Peak) | =1.3 s, <2.5%, =0.05 p.u. | =1.4 s, =3%, =0.07 p.u. | =1.6 s, =3.8%, =0.1 p.u. | =1.8 s, =5%, =0.15 p.u. |
| Stator Current (Steady Ripple, THD, PF) | =0.05 A, =2.8%, >0.96 | =0.07 A, =3.2%, ≈0.96 | =0.1 A, =3.9%, ≈0.95 | =0.12 A, =4.6%, ≈0.93 |
| Electromagnetic Torque (Mean, Overshoot, Localized ripples) | =−0.25 p.u., <8%, Minimal | =−0.25 p.u., =10%, Small | =−0.25 p.u., =12%, Moderate | =−0.25 p.u., =15%, pronounced |
| Tip Speed Ratio (λ) (Centered, Ripples) | =6.5, Tight convergence, small ripple | =6.5, Moderate ripple | =6.6, Slightly higher ripple | =6.7, largest deviations |
| LVRT/FRT (0.2–0.5 p.u. sag, 150–300 ms) (Recovery) | Fastest, current limiting effective, DC headroom secure | Good, slightly higher inrush | Moderate, longer current limiting | Slowest, high overshoot, weak current limiting |
| Metric | OSO (Orange) | PSO (Green) | SA (Purple) | GA (Blue) |
|---|---|---|---|---|
| Dynamic Response Rise Time (s)/Settling Time (s)/Overshoot (%) | 1.3/1.5/4–5% | 1.8/2.2/7–8% | 1.6/2.0/6–7% | 1.0/1.2/<3% |
| Steady-State Ripple Vdc (RMS/Peak–Peak %)/Current (RMS/Peak–Peak %) | 0.35/0.8; 3.2/6.5 | 0.55/1.3; 4.6/8.2 | 0.42/1.0; 3.9/7.1 | 0.28/0.6; 2.8/5.2 |
| Harmonics and PQ Indices THD (%)/Power Factor | 2.8/0.98 | 4.6/0.94 | 3.9/0.95 | 3.2/0.97 |
| LVRT/FRT Performance | Survives 0.3 p.u. sag, recovers ≈ 180 ms (moderate oscillations) | Struggles at 0.2–0.3 p.u. sag, >250 ms recovery, poor damping | Handles 0.3 p.u. sag, recovers ≈ 220 ms, moderate overshoot | Tolerates 0.2 p.u. sag, recovers < 150 ms, minimal overshoot |
| Convergence Statistics Time (s)/Mean Objective | 1.8/0.035 ± 0.004 | 2.5/0.049 ± 0.006 | 2.1/0.041 ± 0.005 | 2.2/0.038 ± 0.003 |
| Computational Cost (N × Iter)/Wall-time (s) | 20 × 40 = 800/1.1 | 30 × 40 = 1200/1.9 | 25 × 45 = 1125/1.6 | 20 × 30 = 600/0.9 |
| Controller Type | THD (%) | Settling Time (s) | Overshoot (%) | Implementation Complexity | Remarks/Source | Torque Response Observations |
|---|---|---|---|---|---|---|
| OSO–PI (Proposed) | 2.8 | 1.2 | 6.5 | Low | Fast adaptation, robust stability | Smooth torque recovery |
| Sliding-Mode Control (SMC) | 3.8 | 1.8 | 7.0 | High | Chattering, requires full model | High robustness during disturbances. However, its high-frequency chattering introduces visible harmonic content in the torque waveform |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behara, K.; Behara, R.K. Metaheuristic-Based Control Parameter Optimization of DFIG-Based Wind Energy Conversion Systems Using the Opposition-Based Search Optimization Algorithm. Energies 2025, 18, 5843. https://doi.org/10.3390/en18215843
Behara K, Behara RK. Metaheuristic-Based Control Parameter Optimization of DFIG-Based Wind Energy Conversion Systems Using the Opposition-Based Search Optimization Algorithm. Energies. 2025; 18(21):5843. https://doi.org/10.3390/en18215843
Chicago/Turabian StyleBehara, Kavita, and Ramesh Kumar Behara. 2025. "Metaheuristic-Based Control Parameter Optimization of DFIG-Based Wind Energy Conversion Systems Using the Opposition-Based Search Optimization Algorithm" Energies 18, no. 21: 5843. https://doi.org/10.3390/en18215843
APA StyleBehara, K., & Behara, R. K. (2025). Metaheuristic-Based Control Parameter Optimization of DFIG-Based Wind Energy Conversion Systems Using the Opposition-Based Search Optimization Algorithm. Energies, 18(21), 5843. https://doi.org/10.3390/en18215843






