Abstract
The increasing adoption of high-performance DC motor control in embedded systems has driven the development of cost-effective solutions that extend beyond traditional software-based optimization techniques. This work presents a refined hardware-centric approach implementing real-time particle swarm optimization (PSO) directly executed on STM32 microcontroller for DC motor speed control, departing from conventional simulation-based parameter-tuning methods. Novel hardware-optimized composition of an interval type-2 fuzzy logic controller (FLC) and a PID controller is developed, designed for resource-constrained embedded systems and accounting for processing delays, memory limitations, and real-time execution constraints typically overlooked in non-experimental studies. The hardware-in-the-loop implementation enables real-time parameter optimization while managing actual system uncertainties in controlling DC micro-motors. Comprehensive experimental validation against conventional PI, PID, and PIDF controllers, all optimized using the same embedded PSO methodology, reveals that the proposed FT2-PID controller achieves superior performance with 28.3% and 56.7% faster settling times compared to PIDF and PI controllers, respectively, with significantly lower overshoot at higher reference speeds. The proposed hardware-oriented methodology bridges the critical gap between theoretical controller design and practical embedded implementation, providing detailed analysis of hardware–software co-design trade-offs through experimental testing that uncovers constraints of the low-cost microcontroller platform.
1. Introduction
Rising demands in green energy generation, electric vehicles [1], transportation, construction, consumer electronics, and industrial automation are bolstering demand for high-performance, robust and high-quality motors. Direct Current (DC) motors, even though they are one of the oldest electric motor designs, are still more than relevant in modern industry. Their market is experiencing steady growth, attributed to a broad range of application areas such as robotics, military, spacecraft [2], medical equipment, agriculture [3] and unmanned monitoring systems [4]. DC micro-motors are widely employed in robotic manipulators and mobile platforms, where small-scale actuators enable fine motion control; in biomedical devices such as infusion pumps, prosthetic limbs, and surgical tools that demand reliability and smooth operation; and in aerospace applications, including unmanned aerial vehicles and satellite mechanisms, where weight and efficiency are critical. The global push for sustainable practices, along with the rise of electric vehicles, further drives DC motor adoption due to their advantages: low noise, low cost, favorable speed–torque characteristics, fast dynamic response, high power-to-weight ratio, and overall performance relative to cost.
Yet open-loop methods are still used for controlling brushed and brushless DC motors. Despite their simplicity, such systems suffer from limited accuracy in dynamic or unpredictable conditions, are highly sensitive to external disturbances and load variations, and lack adaptability to changing conditions. Wear and tear cannot be compensated automatically, requiring manual tuning. Consequently, these limitations have increasingly motivated the adoption of closed-loop control [5]. The presence of a feedback loop provides enhanced precision, accuracy, and adaptability to varying conditions. Disturbances can be compensated, and stable performance is maintained, even in dynamic environments. Additionally, robustness is achieved, which is essential in robotics, automation, electric vehicles, medical equipment, and computer numerical control machines. Sensorless DC motor controllers offer simplicity and cost-effectiveness [6,7], but they perform poorly at low speeds and exhibit jitter or cogging. Rapid load changes further reduce control accuracy. In contrast, sensored closed-loop controllers provide smooth operation, enhanced stability, and precise response even under disturbances [8,9]. Consequently, sensored schemes have become the preferred choice in modern applications. Reliable performance is ensured, while accurate and precise control may be achieved even at low speeds.
Traditionally, the most common control methods, used in the majority of studies, are the PI and PID controllers [10,11,12]. These conventional controllers are well-established techniques for nonlinear system control, mainly due to their simple architecture and the easily managed control algorithm. However, PID controllers are sensitive to measurement errors and noise, causing crucial performance deterioration, instabilities and undesired oscillations [13]. Additionally, derivative filtering is proposed in [14,15,16], significantly enhancing robustness and improving stability. Parallel and coupling PID controllers were proposed in [17], while in [18] an approach using backstepping sliding mode control was demonstrated. Observer-based nonlinear controllers have also been employed in [19,20], providing immunity to measurement noise.
In recent years, much research has been performed on artificial intelligence (AI) control methods. Embedded artificial intelligence is impacting the future of every industry and every human being. Autonomous cars, robots, virtual nursing assistants, diagnosis of diseases, virtual tutors in education and customer services are some current and future applications. The main advantage of AI controllers is their robustness [21], capable of overcoming the uncertainty of conventional control methods and providing better system response [22,23]. Commonly implemented methods use structures based on neural networks, fuzzy logic, genetic algorithms or even hybrid approaches. Fuzzy logic controllers (FLC) for DC motor control have been employed in [24,25], towards improved controller’s performance. The problem of disturbances has been addressed in [26]. FLCs’ superiority over conventional PID controllers has been experimentally validated in [27]. Novel neural network controllers were examined in [28,29,30], while recently [22,31] genetic algorithm approaches were demonstrated. The robustness of neuro-adaptive controller was experimentally proved in [32]. In [33] a hybrid controller, consisting of a parallel combination of sliding mode and neurofuzzy controllers, was proposed.
Fuzzy logic controllers execute the control process by utilizing linguistic expressions along with the processes of fuzzification, rule base, and defuzzification [34]. These controllers provide an excellent way of dealing with imprecision and nonlinearity in complex control situations [35]. Despite the apparent advantages of Type-1 FLCs, it has been proved that they are not capable of fully handling the impact of uncertainties [36,37]. In recent studies interval Type-2 FLCs outperformed IT1-FLCs [38,39,40] mainly attributed to the crisp values of their membership grades in IT1-FLCs. While the membership functions of Type-1 FLCs are certain, the membership functions of Type-2 FLCs are fuzzy themselves. Type-2 FLCs have primary membership functions (PMFs), which might be any value in the interval [0, 1]. Moreover, in PMFs there are secondary membership functions (SMF), defining the probability of PMFs. The latter leads to an increased computational burden and as a result zero or unity SMFs are developed. The combination of a conventional PID and a fuzzy system led to the creation of Fuzzy-PID (FPID) [41,42,43]. Adaptive fuzzy controllers were presented in [44,45], providing robustness and improved control performance. In this paper, a composition of an interval Type-2 FLC and a PID controller is proposed to manage uncertainties in controlling the DC micro-motor under study. PID controller parameters are dynamically set by fuzzy sets, improving performance, robustness and system response.
In recent literature numerous efforts in closed-loop DC motor control development have been conducted, either by means of simulations [46,47,48], or in experimental configurations [49,50,51]. The former approaches, even though valuable to prove the conceptual design, use either low-cost development boards, which have hardware constraints and especially memory limitations, or expensive FPGA development boards which are considered as “overkill” for these type of applications. On the other hand, modern families of microcontrollers (e.g., like STM32 provided by STMicroelectronics), keep pace with emerging trends and remain at the forefront of embedded systems development, providing an ideal balance between cost, performance, scalability and dependability as presented in [52,53,54].
Although a few control algorithms applied on experimental setup have been suggested, the amount of research analyzing practical difficulties and limitations either at the hardware or software level, while proposing a clear methodology and design optimization techniques, is limited. Considering cases, in which readymade solutions are costly or insufficient due to custom application specifications, a low cost, fully flexible, customizable and parametrised prototype should be built. Based on the aforementioned factors, the key contributions of this paper are:
- Present refined hardware-in-the-loop approach, integrating real-time PSO directly on STM32 microcontroller, with comprehensive hardware–software co-design analysis highlighting constraints and trade-offs.
- Develop novel optimized hybrid FT2-PID controller tailored for embedded platforms.
- Validate the proposed FT2-PID controller against PI, PID, and PIDF controllers, showing significantly faster settling times and reduced overshoot at higher reference speeds.
- Address critical hardware limitations, including processing time, memory constraints, and real-time execution challenges, being overlooked in theoretical studies.
To the best of the authors’ knowledge, similar efforts offering this level of technical detail are not found in the research literature. In this paper, an adaptive FT2-PID controller is especially designed and experimentally implemented for coreless DC micro-motor (though the procedure can be easily applied to other DC motor types). Prioritizing cost and simplicity, hardware limitations and components selection are presented in detail. The proposed controller is compared with PI, PID and PID with D filtering controllers, all tuned using embedded real-time PSO algorithm [55]. Discrete reference speed cases are investigated not only to present the robustness of the controller under investigation but also to compare the microcontroller performance and resources needed. Emphasis is being given to microcontroller’s system-level characteristics and to hardware considerations for the prototype design. Parameters such as pulse width modulation (PWM) bit resolution, interrupt time selection for speed measurements, encoder’s resolution, experimental speed data filtering are also examined and pointed out. Finally, the design and the level of goodness of a microcontroller embedded adaptive FT2-PID is discussed.
The structure of this paper is as follows. A brief theory of DC micro-motor is presented in Section 2, while the control strategies are discussed in Section 3. Prototype design and development is described in Section 4. Section 5 presents the software development considering hardware limitations. The derived results are reported and commented in Section 6 and ultimately Section 7 serves to conclude the work.
2. Brief DC Micro-Motor Theory Overview
DC micro-motors are miniature motors that offer compact size, high efficiency, and precise control. Their small dimensions ranging from a few millimeters to centimeters and lightweight construction make them ideal for robotics, medical devices, and embedded systems where space and efficiency are critical. Figure 1 presents the equivalent circuit and the investigated micro-motor.
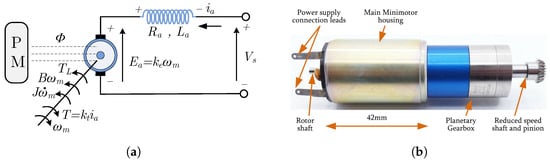
Figure 1.
DC micro-motor: (a) equivalent circuit and (b) investigated micro-motor.
The armature winding has resistance and inductance , with supply voltage applied. The back-emf is induced as the armature rotates through the magnetic field, proportional to angular velocity , which represents the rate of change of shaft position. The rotational speed (), expressed in revolutions per minute (rpm), is related to the angular velocity () using the equation below:
The back-emf coefficient () is fundamentally related to the permanent magnet flux () through the motor construction, and can be expressed as:
where P is the number of pole pairs and Z is the number of conductors. For a given motor design with fixed magnetic flux, remains constant. The back-emf is given by:
The armature current is determined by the supply voltage, armature resistance, inductance, and back-emf:
The back-emf coefficient () reflects the motor’s design and permanent magnet flux, relating angular velocity to induced voltage. The torque constant (), which links armature current to electromagnetic torque, is numerically equal to in consistent SI units, a relationship that arises from the conservation of energy in electromechanical conversion. The mechanical dynamics of the motor are described by the following set of equations, where is the viscous damping coefficient, denotes the moment of inertia of the rotor, and represents the load torque:
By combining the electrical and mechanical equations, the following differential equations are obtained, which fully describe the system dynamics:
Upon applying the Laplace transform to Equations (7) and (8) assuming zero load torque (), the transfer function of the motor is derived, which relates the motor speed to the applied input voltage:
This represents the nominal motor dynamics without external loading. The complete system response including load torque disturbances is illustrated in the block diagram of Figure 2. In this diagram, the supply voltage () serves as the input, while the micro-motor’s rotational speed () serves as the output. Accurate modeling of the motor necessitates identifying six parameters: , , , , , and . The specific parameter values for the DC micro-motor utilized in this work are provided in Table A1.
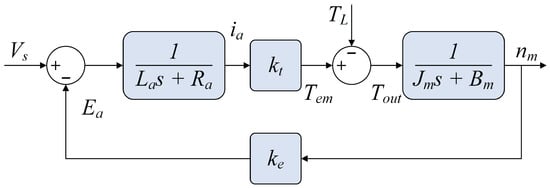
Figure 2.
Block diagram representation of the DC motor transfer function including load disturbance.
3. Control Strategies
3.1. Closed-Loop Control for Micro-Motor Speed Regulation
The objective of the controller under study is to regulate the DC micro-motor speed to a specified reference value by employing a closed-loop negative feedback control system. Negative feedback is utilized to ensure system stability by opposing deviations from the reference speed, thereby driving the error toward zero. In the context of this study, the controller employs two inputs to determine the control action: the error and the change in error. The error is expressed as the difference between the measured rotational speed () and the reference rotational speed ().
Respectively, the change in error, which describes how the error changes over time, is calculated as:
The controller processes the error signal to generate the control signal . To interface with the DC micro-motor, a converter is incorporated between the controller and the motor, translating the control signal into the appropriate input voltage . This converter reconciles the voltage and current mismatches, ensuring the control signals are properly scaled to meet the power requirements and drive the micro-motor. The converter dynamics can be approximated as a first-order system with transfer function:
where is the converter gain and is its effective time constant, capturing the conversion delay. The negative feedback structure dynamically adjusts the control action based on the deviation between the reference and measured micro-motor speed, thereby minimizing the error signal . The measured speed itself may differ slightly from the actual motor speed due to sensor dynamics and filtering; this can also be modeled as a first-order system:
where is the sensor gain and represents the effective time constant including measurement lag. This closed-loop mechanism compensates for external disturbances, system nonlinearities, and load variations, ensuring accurate and stable speed regulation. Additionally, the feedback system enhances the motor’s response to dynamic changes in speed, improving steady-state accuracy and robustness against fluctuations.
Figure 3 presents the schematic of the negative feedback control loop used. The diagram illustrates the interconnections between key system components, including the controller, converter, DC micro-motor, and speed sensor. This closed-loop configuration ensures motor speed control by continuously comparing the reference speed with the measured speed.
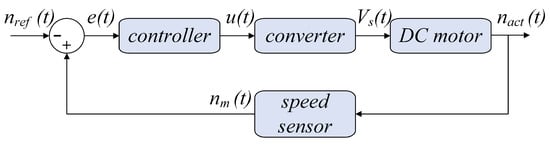
Figure 3.
Schematic of the negative feedback control loop for regulating DC micro-motor’s speed.
3.2. PI, PID, and PIDF Controllers
Proportional-integral (PI) controllers are widely adopted in industrial applications due to their simplicity and effectiveness. The PI controller combines proportional and integral control actions, with transfer function:
The proportional term provides immediate response to error, while the integral term eliminates steady-state offset. However, the PI controller lacks response to the rate of change of error, which can result in slower dynamics in rapidly changing systems. The proportional-integral-derivative (PID) controller adds a derivative term that responds to error rate of change, improving transient response and reducing overshoot:
Conventional PID controllers frequently struggle to handle the intricate dynamics of DC motors, leading to suboptimal performance [56]. While the derivative term improves the system’s responsiveness and stability, it can also amplify high-frequency noise, resulting in oscillations or unwanted vibrations in the control signal. To address these challenges, a derivative filter can be introduced. This filter smooths the high-frequency components of the derivative term, reducing the controller’s sensitivity to noise and mitigating undesirable oscillations. The resulting controller, known as the Proportional-Integral-Derivative-Filter controller (PIDF), is mathematically expressed as:
Here, N represents the filter coefficient, which determines how much high-frequency noise is filtered out from the derivative term, while the proportional and integral terms continue to provide their fundamental control actions. The filter is typically employed to avoid undesirable oscillations or instability caused by noise amplification in the derivative term. The value of N creates a trade-off between noise suppression and the controller’s responsiveness. In this work, the filter coefficient N is treated as a design parameter. Its specific value is determined through optimization along with the PID gains, ensuring optimal system performance. Table 1 summarizes the advantages and disadvantages of selecting small or large values of N.

Table 1.
Advantages and disadvantages of filter coefficient value selection [14,15,16] for the derivative filter component.
The PIDF controller is particularly effective in DC motor control applications where precise speed regulation is required despite fluctuations in load or noise in the feedback signal. By incorporating a derivative filter, it suppresses high-frequency noise that can otherwise destabilize the control loop. This controller strikes a balance between rapid error correction and maintaining stability, enabling the controller to achieve accurate motor operation while adapting to changes in reference speed or system disturbances. Figure 4 shows the structure of the examined controllers.
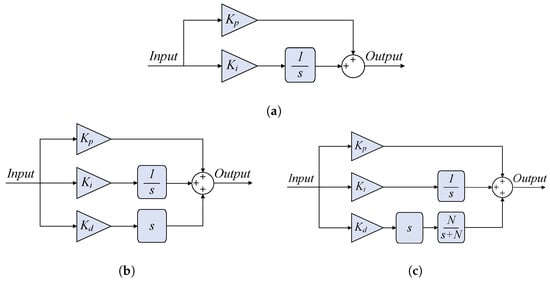
Figure 4.
Structure of the controllers under study: (a) PI (b) PID (c) PIDF.
3.3. FT2-PID Controller
Fuzzy logic is a computational model based on approximate reasoning rather than fixed, exact rules. It manages uncertainty and imprecision, making it effective in complex control systems. Unlike traditional controllers that require precise mathematical models, fuzzy logic handles ambiguity, imprecise measurements, and noisy data. Using linguistic variables and fuzzy rules, it adapts well to systems with nonlinearities and disturbances, where conventional methods like PID may falter.
In essence, fuzzy logic control operates through three key stages: fuzzification, inference, and defuzzification. During fuzzification, precise input values are transformed into fuzzy representations using membership functions (MFs) that describe the degree of membership within a given range, typically [0, 1]. Complete membership in a fuzzy set is denoted by 1, while 0 reflects no membership. In the inference stage, a rule base consisting of conditional relationships is applied to the fuzzified inputs. These relationships define how the inputs correspond to the outputs, with the inference engine processing them to generate the corresponding fuzzy outputs. In this work, the process follows the Mamdani fuzzy inference system, which combines these rules to derive fuzzy control actions. Finally, in the defuzzification phase, the fuzzy outputs are translated into a precise, crisp value, which serves as the final control signal, enabling accurate system control.
Interval Type-2 Fuzzy Logic (IT2-FL) extends traditional fuzzy logic by introducing an additional dimension of uncertainty within its membership functions. While Type-1 fuzzy logic employs precise membership grades to map input values to fuzzy sets, IT2-FL utilizes interval-valued membership functions to account for uncertainties inherent in real-world data. This framework captures both the primary membership values and their associated uncertainties, thereby enabling a more nuanced representation of vagueness and imprecision.
Uncertainty in these sets is characterized using key parameters. The mean () represents the central value of the membership function, serving as the core membership value around which the fuzzy set’s membership degrees vary. The standard deviation () quantifies the spread of membership values around the mean, with larger indicating greater uncertainty. The delta () represents the uncertainty interval, describing the deviation in the mean membership value. Figure 5 shows IT2 Gaussian membership functions, with the left image representing uncertainty in the mean and the right image depicting uncertainty in the standard deviation.
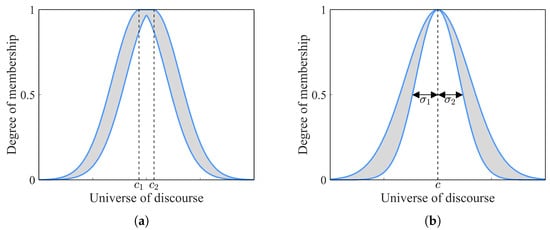
Figure 5.
Gaussian IT2 MFs with: (a) uncertainty in the mean (b) uncertainty in the standard deviation.
In this work uncertainty in the mean is used, with the centers of each membership function expressed as:
where and represent the centers of each MF, is the mean, and is the uncertainty in the mean. The standard deviation is assumed to remain the same across both membership functions. The membership function of an interval type-2 fuzzy set defined over the input domain F and output domain G can be expressed as:
where and are secondary membership intervals that account for the uncertainty in the primary memberships and , respectively. These fuzzy sets are defined over the domains F and G, which represent the input and output spaces, respectively. The relationship between inputs and outputs is governed by a set of fuzzy rules, commonly represented as . A typical rule is formulated as:
where are interval type-2 fuzzy sets associated with the inputs, and represents the output fuzzy set. These rules form a rule base that enables the inference process, ultimately producing a fuzzy output that is defuzzified into a crisp control signal.
The IT2-FLC structure is illustrated in Figure 6. The diagram demonstrates the process by which crisp inputs are transformed into fuzzy values, processed through the inference system, and subsequently converted back into crisp outputs. The arrows illustrate the transfer of information across these stages. In this study, an interval Type-2 Fuzzy Logic-based PID controller is implemented, integrating the adaptive capabilities of interval Type-2 Fuzzy Logic (IT2-FL) with the proven effectiveness of the PID control framework. The proposed controller dynamically adjusts the proportional (), integral (), and derivative () gains through a Type-2 fuzzy inference system. This enables real-time adaptation of the control parameters to varying system conditions, ensuring robust and precise control. The proposed structure of the FT2-PID controller is depicted in Figure 7.
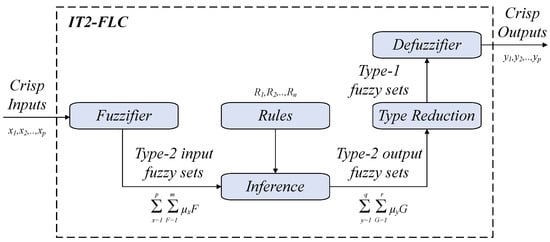
Figure 6.
Block diagram of the IT2-FLC structure.
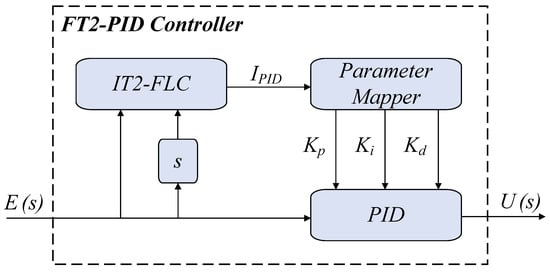
Figure 7.
Proposed FT2-PID controller structure.
The proposed IT2-FLC accepts two inputs: the error (e) and the change in error (). The output of the controller is a scalar value referred to as the PID Tuning Index (). The input and output ranges were determined through iterative experimental tuning: error spans ±1000 rpm to encompass maximum expected deviations during transient operation, change-in-error spans ±100 rpm to capture typical rate-of-change values during speed transitions, and the tuning index range of [−10, 10] provides sufficient resolution for mapping to discrete PID parameter sets while remaining computationally efficient. The input variables error and change in error use three membership functions each: N, M, and P, resulting in a compact rule base with 9 rules. The output variable PID tuning index employs five membership functions: VL, L, M, H, and VH to provide finer granularity for smoother transitions between PID parameter sets and more refined control action. The standard deviation () is set to 250 for the error and 25 for the change in error MFs, while the delta () values are 62.5 and 6.25, respectively. Gaussian membership functions were selected over triangular functions due to their smoother gradients, which provide more refined control transitions and better represent uncertainty in the Type-2 fuzzy framework, despite their higher computational cost. MFs and the inference system surface are depicted in Figure 8. The rule base governing the IT2-FLC is presented in Table 2.
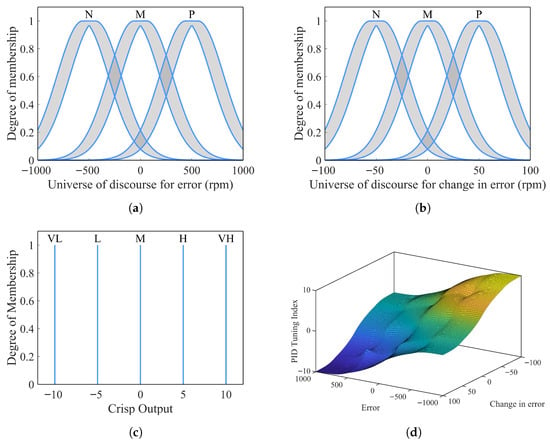
Figure 8.
Membership functions of the IT2-FLC: (a) error, (b) change in error, (c) PID tuning index, and (d) the control surface of the inference system.

Table 2.
The developed Fuzzy Association Matrix (FAM) for IT2-FLC.
The proposed control strategy implements a fuzzy gain-scheduling approach, where the IT2-FLC outputs a scheduling variable () that selects from 10 pre-optimized PID parameter sets. Unlike continuously adaptive controllers that compute gains in real-time, this architecture uses PSO to simultaneously optimize all parameter sets (30 variables for PID: 10 sets of , , ) through testing on the physical motor via the microcontroller. Once optimized, these sets are stored in memory and selected at runtime through fuzzy inference and table lookup, providing computationally efficient adaptive control.
Since lies within the range , parameter mapping is required to determine the appropriate PID gains (, , and ). The absolute value is utilized, ensuring symmetric controller behavior: deviations of equal magnitude above or below the reference speed select the same parameter set. As shown in Table 3, is divided into 10 intervals, each corresponding to a unique PID parameter set that is dynamically selected at runtime. The PSO-optimized parameter values are presented in Section 6.

Table 3.
Parameter mapping based on PID Tuning Index.
4. Prototype Design and Development
The hardware system’s topology, as shown in Figure 9, illustrates the interconnected components necessary for the control and operation of the DC micro-motor. At the heart of the system, a microcontroller functions as the central processing unit, responsible for acquiring, processing, and transmitting various signals. The microcontroller interfaces with a rotary encoder, which monitors the micro-motor’s speed and delivers real-time feedback. Given the micro-motor’s higher voltage and current demands compared to the microcontroller, a dedicated power supply and a robust motor driver circuit are included to ensure proper operation of the motor. The system’s capability to monitor motor performance is enhanced by an oscilloscope, which facilitates the acquisition of speed and current data. Since the oscilloscope operates in the analog domain, a digital-to-analog converter (DAC) is employed to bridge the gap between the digital signals generated by the microcontroller and the analog signals required by the oscilloscope.
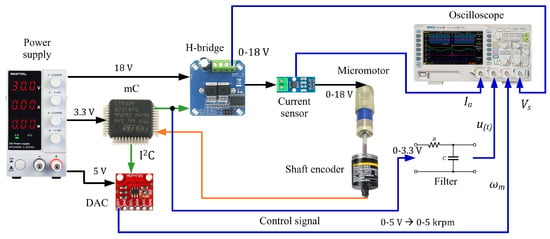
Figure 9.
Hardware architecture overview.
Furthermore, the system incorporates multiple power supplies to meet the diverse power requirements of the various components. A dedicated power supply is allocated for the DC micro-motor, while two buck converters provide 5 V and 12 V to power the peripheral devices, ensuring stable and efficient operation of the entire system. The following sections will delve into the specifics of each hardware module, offering a comprehensive analysis of their design considerations, operational principles, and role within the overall system architecture. Figure 10 shows the experimental testbench setup.

Figure 10.
Experimental testbench for DC micro-motor control and data acquisition.
4.1. Microcontroller
The selection of the microcontroller was based on several critical criteria: (a) external hardware interrupts for speed measurement, as the encoder generates square pulses, (b) software interrupts, required not only for speed measurement but also for the controller’s time-discrete actions, (c) sufficient number of general-purpose digital input/output pins, including at least one output pin with PWM capability, (d) fast processing and enough memory to meet the application requirements, (e) low cost and market availability. Considering these factors, the STM32F103C8 from STMicroelectronics was selected. The detailed microcontroller specifications are presented in Table 4.

Table 4.
Microcontroller specifications.
4.2. Power Supply
The NPS306W digital DC power supply is selected for its capacity to provide stable and sufficient power for the coreless DC micro-motor, with a maximum output of 30 V and 6 A. In addition, two buck-boost voltage regulation modules supply the necessary 5 V and 12 V for peripheral components. These regulated power levels are essential for powering the DAC, current sensor, motor driver, and rotary encoder, which together support the motor’s control and monitoring.
4.3. Driver, Sensors, and Peripherals
DC motors demand high voltage and current, whereas microcontrollers operate on low-power signals. To address this mismatch, the BTS7960 H-bridge motor driver is used to convert the low-power signals from the microcontroller into high-power signals capable of driving the motor. The BTS7960 is well-suited for the application, as it supports bidirectional motor control, operates within the required voltage and current range, and can handle a PWM frequency of up to 25 kHz, all while maintaining cost-effectiveness and wide availability. For precise monitoring of the motor’s speed, the OMRON E6A2-CW5C rotary encoder is integrated into the system, providing 200 pulses per rotation to accurately measure the rotational speed. Data acquisition is a critical aspect of system performance evaluation, and for this purpose, the RIGOL DS1054Z oscilloscope is selected. With four channels, a 50 MHz bandwidth, and a sampling rate of 1 GS/s, the oscilloscope is used to capture and display both the microcontroller’s control signals and the motor’s real-time speed and current characteristics. In addition, the ACS712 Hall-effect current sensor is chosen to measure the motor’s current, providing data for visual representation on the oscilloscope. This sensor measures currents up to 5 A with a sensitivity of 185 mV per ampere. Since the microcontroller generates only digital signals, a 10-bit MCP4725 digital-to-analog converter (DAC) is employed to convert the digital data into analog signals for oscilloscope visualization. The hardware components used are summarized in Table 5.

Table 5.
Summary of hardware components.
5. Software Development Considering Hardware Limitations
5.1. Software Development Philosophy
The control strategy for the micro-motor system is implemented through a modular software architecture, comprising four main routines: (a) the control loop routine, which includes PI, PID, PIDF, and FT2-PID control strategies, (b) the PSO tuning routine, (c) the Encoder Pulse Interrupt Service Routine (ISR), triggered by the rising edges of the encoder’s square pulses, and (d) the Time Interval ISR, executed at predefined intervals to filter and perform calculations on speed measurement data. Two initialization routines were developed for variable setup and interrupt configuration. The PSO routine is divided into two main subroutines: parameter initialization and objective calculation. The software was implemented in C using STM32CubeIDE, leveraging the STM32F103C8 microcontroller’s features. In particular, the platform’s customizable Pulse Width Modulation (PWM) generation capabilities streamlined the development of the examined DC micro-motor control algorithms. The software implementation is schematically represented in the flowchart in Figure 11.
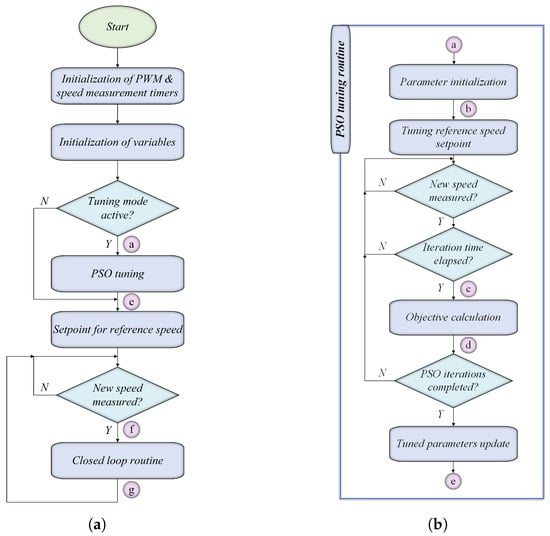
Figure 11.
Software architecture flowchart for (a) main control algorithm and (b) PSO tuning routine.
5.2. Main Flowchart
The main program routine begins with the initialization of timers and variables, followed by setting the micro-motor’s reference speed. When tuning mode is enabled, the program executes the PSO tuning routine; otherwise, it proceeds directly to the setpoint of reference speed. When a new speed measurement is available, the program initiates the closed-loop control routine. The workflow of the main routine is depicted in Figure 11a.
5.3. PSO Tuning Routine
Particle Swarm Optimization (PSO) is a population-based optimization algorithm where each particle represents a candidate solution. Each particle’s movement is guided by its personal best position and the swarm’s global best position, enabling collective exploration of the solution space. In this study, PSO minimizes the settling time as the objective function. The position and velocity of each particle are progressively modified through iterative updates, following the equations outlined below:
where
- denotes the position of the i-th particle at time t;
- represents the velocity of the i-th particle at time t;
- w is the inertia weight, which adjusts the influence of the particle’s prior velocity;
- and are the cognitive and social coefficients, which determine the weight given to the personal best and global best positions in influencing the particle’s movement, respectively;
- and have random values, uniformly distributed between 0 and 1, adding stochastic behavior to the algorithm;
- refers to the best position found by the i-th particle during its search;
- represents the best position found by the entire swarm.
The PSO tuning routine is illustrated in Figure 11b. The Parameter Initialization Subroutine, shown in Figure 12a, initializes particle positions and velocities within defined bounds for the parameters being optimized. The tuning reference speed is set to 2750 rpm. During execution, the Objective Calculation subroutine, depicted in Figure 12b, evaluates each particle’s fitness by measuring system settling time, which guides updates to personal and global best positions. This iterative process continues until the specified number of iterations is completed, after which the optimized parameters are applied. The PSO parameters were selected based on literature guidelines and refined through experimental testing. The selected population size and iterations balance optimization quality with computational constraints on the STM32 microcontroller. The cognitive and social coefficients follow standard practice for balanced exploration, while inertia weight varies from 0.2 to 0.9 for gradual convergence. These parameters demonstrated consistent convergence across optimization runs. Table 6 summarizes the parameter values used in the PSO routine:
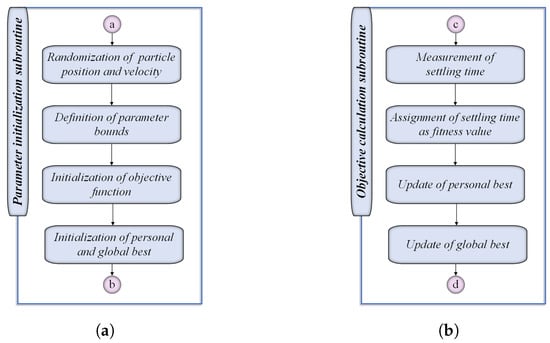
Figure 12.
PSO tuning subroutines (a) parameter initialization and (b) objective calculation.

Table 6.
PSO parameter values used in this work.
5.4. Closed-Loop Routine
The closed-loop routine, illustrated in Figure 13, is integral to the precise control of the micro-motor within this system. The process begins with the continuous reading of the motor’s speed, which provides real-time feedback to the system. Upon receiving the latest speed measurement, the routine retrieves the latest tuned controller parameters, ensuring that the controller operates with the optimal settings. Following this, the controller performs the necessary calculations based on the error between the reference and measured speeds. The computed control signal is then subjected to saturation limits to prevent excessive control actions that could destabilize the system. Finally, a PWM control signal is generated from the control signal. This signal is sent to the motor driver to adjust the motor’s voltage, thereby achieving the desired speed. This iterative process ensures accurate and responsive speed control, balancing performance and stability throughout operation.
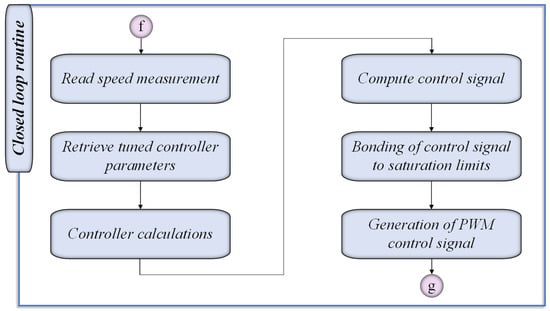
Figure 13.
Closed-loop routine flowchart.
STM32F103C8 offers fully customizable PWM pulse generation. PWM is utilized to control the micro-motor’s voltage with a specific degree of accuracy, facilitating the adjustment of micro-motor speed. The characteristics of the PWM signal, specifically its resolution and frequency, are determined by the microcontroller’s clock speed and the chosen resolution. The relationship governing this dependency is expressed in Equation (22):
Here, is the frequency of the PWM signal, represents the clock frequency of the microcontroller, and n denotes the bit resolution of the PWM. The bit resolution defines the granularity of the voltage control, while the PWM frequency is related to how smoothly the motor operates. Table 7 presents the achievable PWM frequencies for various bit resolutions, assuming a clock speed of 72 MHz.

Table 7.
Correlation between PWM resolution and frequency.
The motor driver used in this system is capable of operating at frequencies as high as 25 kHz. To ensure compatibility while maintaining adequate resolution, a 12-bit resolution and a PWM frequency of 17.578 kHz are chosen. The resolution of the voltage control step is calculated using Equation (23), where is the nominal voltage of the micro-motor, and corresponds to the resolution scale:
For an 18 V micro-motor operating with 12-bit resolution, the voltage step is determined as follows:
This voltage step value influences the motor’s speed control precision. The relationship between the control speed step and the voltage step is described in Equation (25), where is the nominal speed of the motor:
By substituting the nominal speed of 5000 rpm and the voltage step of 4.39 mV, the control speed step is calculated as:
This calculated speed step of 1.22 rpm ensures that the system can provide sufficiently fine control over the micro-motor’s operation. The selected values balance the requirements for precision and system compatibility with the motor driver hardware.
5.5. Interrupt Services Routines
This category of routines manages two program interrupts, namely the Encoder Pulse ISR and the Time Interval ISR, which are both employed for measuring the speed of the DC micro-motor (Figure 14).
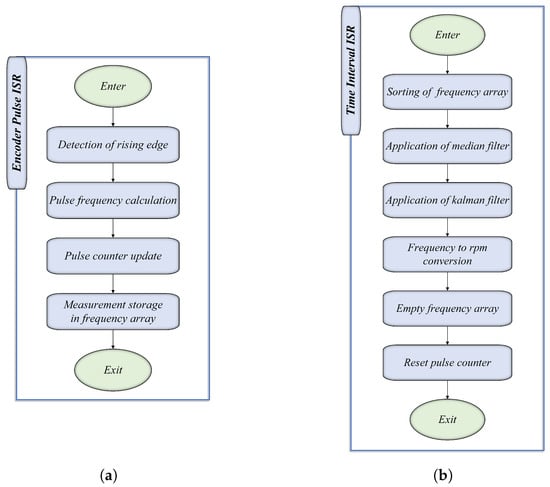
Figure 14.
Flowchart of the software routines for (a) Encoder Pulse ISR and (b) Time Interval ISR.
5.5.1. Speed Measurement Methodology
Figure 15 illustrates the proposed speed measurement principle. The rotary encoder produces square pulses which are directly proportional to the angular displacement of the micro-motor shaft. These pulses form the foundation for determining the micro-motor’s speed over a defined time interval, denoted as . During this interval, interrupts are triggered by the rising edges of the encoder’s pulse signal. Each interrupt represents a discrete event that is processed by the microcontroller, which measures the elapsed time between consecutive rising edges. The microcontroller records the number of clock cycles () occurring between two rising edges. This count is used to calculate the frequency of encoder pulses () for a given speed as:
where is the clock frequency of the microcontroller. Given the encoder’s resolution () representing the number of pulses per full micro-motor revolution, the rotational speed () is calculated as:
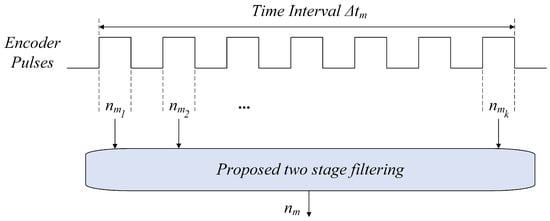
Figure 15.
Schematic of proposed speed measurement methodology.
5.5.2. Time Interval
During the time interval , the microcontroller calculates and stores multiple speed measurements. At the end of the interval, the collected data is processed, and a new speed measurement is obtained. Increasing this interval allows capturing more pulses, which enhances the accuracy of the calculated rotational speed. However, this comes at the expense of control responsiveness, as the controller updates only after each new measurement is available. Conversely, a shorter interval provides more frequent updates, enabling faster response to system changes, but may reduce accuracy due to fewer captured pulses. Thus, selecting represents a critical balance between measurement accuracy and control responsiveness, requiring careful optimization based on application requirements. Table 8 summarizes the benefits and drawbacks of selecting small or large time interval values. Figure 16 illustrates the correlation between the selected time interval and the number of encoder pulses, based on the equation:
where is the number of encoder pulses generated within the time interval period. For this work, a of 2 ms is chosen based on trial and error, as it strikes a balance between measurement accuracy and control responsiveness.

Table 8.
Advantages and disadvantages of selecting small or large .
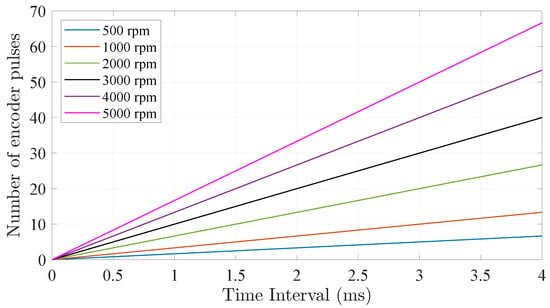
Figure 16.
Number of encoder pulses generated for different time intervals and micro-motor speeds.
5.5.3. Proposed Two-Stage Filtering Method
Raw data obtained from the rotary encoder often exhibit noise, particularly under dynamic conditions. To address this, a two-stage filtering method is proposed, combining a median filter with a Kalman filter. In the initial stage, raw data speed measurements are processed through the median filter () to eliminate outliers and suppress sporadic noise. Following the initial median filtering stage, the signal undergoes further processing using a Kalman filter. This stage enhances the reliability of the speed estimation by reducing the effect of high-frequency noise. The Kalman filter estimates the speed () using the following recursive equations:
where
- K: Kalman gain, determining the weight of the new measurement;
- P: Estimate error covariance;
- Q: Process noise covariance;
- R: Measurement noise covariance;
- : Estimated speed at the current time step k;
- : Measured speed after the median filter at time step k.
The parameters listed in Table 9 were selected to optimize the performance of the Kalman filter in suppressing noise while preserving the responsiveness of the speed estimation process. The selection process was carried out through an iterative trial-and-error procedure, where different parameter sets were experimentally evaluated until a satisfactory trade-off between estimation stability and dynamic responsiveness was achieved. These parameters strike a balance between sensitivity to dynamic changes and the stability of the estimated output. To evaluate the effectiveness of the proposed filtering approach, a step voltage was applied to the micro-motor, enabling a direct comparison between raw sensor data, single-stage Kalman filtering, and the proposed two-stage filtering method. As illustrated in Figure 17a, the proposed method significantly attenuates noise and provides substantially improved signal quality, resulting in a more stable and accurate speed estimation. The applied step voltage is shown in Figure 17b for reference.

Table 9.
Selected Kalman filter parameters in this work.
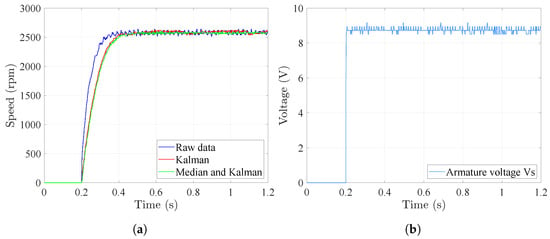
Figure 17.
Speed measurements for step voltage. (a) Comparison between raw data, Kalman filtering, and the proposed two-stage filtering method. (b) Depicts the step input voltage.
6. Results and Discussion
6.1. Real-Time PSO Tuning
The Particle Swarm Optimization (PSO) algorithm was employed for real-time tuning of all evaluated controllers. The target speed for all controllers was set at 2750 rpm to ensure uniformity in performance assessment across different control strategies. The fitness function minimizes the settling time, defined as the time required for the motor speed to reach and remain within 2% of the target speed following a step command. The PSO algorithmic parameters were presented in Table 6. The PSO tuning was conducted experimentally on the physical motor system, with the microcontroller executing the optimization algorithm in real-time. The algorithm utilized a population size of 6 particles across 100 iterations, where each fitness evaluation necessitated approximately 0.9 s of motor operation to assess settling time performance, yielding a total tuning duration of 9 min. This constitutes a one-time commissioning procedure wherein the optimized parameters are permanently stored in non-volatile memory.
The convergence times presented in Figure 18 indicate the point at which each controller’s PSO algorithm reached convergence, defined as the inability to achieve further reduction in the settling time objective function. The results indicate that the PI and PID controllers achieve convergence within 30 s, highlighting their computational efficiency and simplicity. In contrast, the PIDF and FT2-PID controllers exhibit significantly longer convergence times, requiring approximately 7 min and 5 min, respectively. This disparity is attributed to the increased complexity of these controllers and the higher number of variables involved in their parameter optimization processes. Notably, the FT2-PID controller simultaneously optimized 30 parameters representing all PID gain values across the complete range of intervals through a unified PSO optimization process to ensure globally optimal settling time performance.
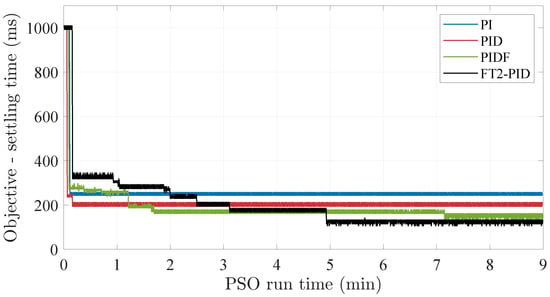
Figure 18.
PSO convergence times for PI, PID, PIDF, and FT2-PID controllers at target speed of 2750 rpm.
Table 10 presents the optimized parameters for the PI, PID, and PIDF controllers. For the FT2-PID controller, parameter tuning follows a different approach due to its adaptive nature. The controller utilizes the IT2-FLC framework described in Section 5 to dynamically adjust the PID gains (, , ) according to the PID Tuning Index (), which varies between . Each interval corresponds to a specific parameter set as defined in Table 3, with the PSO-optimized values for all intervals detailed in Table 11.

Table 10.
PSO tuning results for PI, PID, and PIDF controllers.

Table 11.
PSO tuning results for FT2-PID controller based on .
6.2. Memory Usage and Analysis
The memory usage of the microcontroller was evaluated after uploading the control algorithms for all controllers, as well as during the Particle Swarm Optimization (PSO) real-time tuning. The results, presented in Table 12 and Table 13, highlight SRAM and Flash memory usage for the different controllers.

Table 12.
Memory requirements for DC micro-motor control.

Table 13.
Memory requirements for PSO real-time tuning.
Table 12 presents the memory requirements for all controllers. The FT2-PID controller exhibits the highest memory consumption, requiring 3.20 KB of SRAM and 32.39 KB of Flash memory. This increased memory demand is primarily due to the higher computational complexity associated with fuzzy type-2 logic and additional tuning parameters. Table 13 shows the memory usage during PSO real-time tuning. SRAM usage increases by more than 145% for all controllers compared to standard operation. The FT2-PID controller, again, demands the most memory, with 7.86 KB of SRAM and 41.69 KB of Flash memory. These results suggest that the microcontroller’s memory is sufficient for all tested controllers in both standard operation and PSO real-time tuning. However, the significant rise in memory consumption during PSO tuning highlights the need for efficient resource management when deploying optimization techniques on embedded systems.
SRAM usage directly affects real-time performance due to its role in storing temporary variables, stack operations, and intermediate computations during controller execution. Flash memory, although less critical to runtime performance, shows notable consumption by the FT2-PID controller. During PSO real-time tuning operation, the FT2-PID controller utilizes approximately 65% of available Flash memory and 39% of available SRAM.
Figure 19 provides a visual comparison of SRAM and Flash memory usage across all controllers. The FT2-PID controller consistently demonstrates the highest memory consumption in both SRAM and Flash categories. These findings highlight the trade-offs between advanced control performance and resource utilization, which must be carefully considered during system design. While all tested controllers are suitable for implementation on the selected microcontroller, the FT2-PID controller is the most resource-intensive. Future work could explore memory optimization techniques for fuzzy type-2 controllers, aiming to reduce memory usage while maintaining system performance and efficiency.
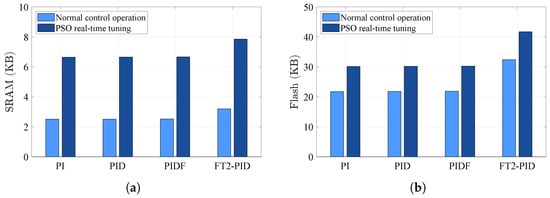
Figure 19.
Memory consumption comparison between SRAM and Flash for all controllers. (a) Shows SRAM memory consumption, and (b) shows Flash memory consumption.
6.3. CPU Load Analysis
The CPU load was evaluated for all controllers to assess the computational demand imposed by each control algorithm. The outcomes are summarized in Table 14, which details the CPU load percentage at various motor speeds. Two configurations were analyzed: PI, PID, and PIDF controllers, and the FT2-PID controller. The data reveal that the CPU load increases with motor speed for all controllers. The FT2-PID controller exhibits a significantly higher CPU load compared to the PI, PID, and PIDF configurations. At a motor speed of 5000 rpm, the FT2-PID controller requires approximately 69.14% of the CPU resources, whereas the PI, PID, and PIDF controllers demand only 11.73%. This substantial difference of approximately 57.41% can be attributed to the added complexity of the fuzzy type-2 control logic and the associated computations required for its real-time operation.

Table 14.
CPU load at various micro-motor speeds.
At 1500 rpm, the CPU load for the FT2-PID controller is 57.72%, while the PI, PID, and PIDF controllers demand only 3.70%. This represents an increase of 54.02% in CPU load for the FT2-PID controller, further emphasizing the computational overhead associated with the fuzzy type-2 control algorithm. Similarly, at 3000 rpm, the FT2-PID controller consumes 61.11% of CPU resources, which is approximately 54.32% more than the 6.79% required by the other controllers. Figure 20 visually represents the CPU load variation with motor speed for all controllers. The FT2-PID controller’s computational overhead becomes evident as the motor speed increases, showcasing a steeper curve compared to the PI, PID, and PIDF controllers. The figure emphasizes the trade-offs between control complexity and computational efficiency, particularly for high-speed operations where the CPU is under significant load.
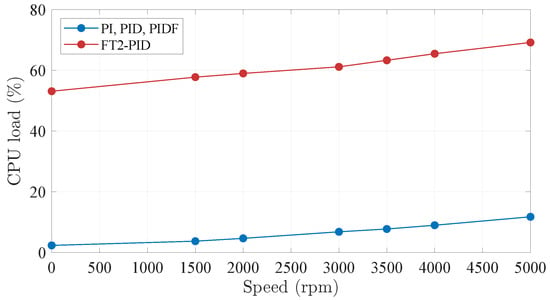
Figure 20.
CPU load for different steady state speeds.
The increasing CPU load with motor speed highlights the importance of selecting computationally efficient algorithms, especially for high-speed applications. The PI, PID, and PIDF controllers demonstrate significantly lower CPU load across all tested speeds, making them more suitable for resource-constrained environments. However, the FT2-PID controller, despite its higher computational demand, offers the potential for superior control performance, particularly in systems requiring robust handling of uncertainties. These results underscore the trade-offs between computational resource utilization and control algorithm complexity. While the FT2-PID controller provides advanced features such as enhanced robustness and adaptability, its implementation on resource-limited microcontrollers necessitates careful consideration of CPU usage. This is particularly critical in applications where multiple tasks must run concurrently, as the high CPU load could limit the availability of processing power for other real-time operations.
In future work, optimization of the FT2-PID algorithm could be explored to reduce its computational burden without compromising control performance. Techniques such as approximate inference methods or precomputed rule bases may help achieve a balance between advanced control capabilities and efficient resource usage.
6.4. Controller Performance Evaluation
The performance of the designed controllers is evaluated across a series of experimental conditions to assess their behavior under varying reference speeds. The conditions are presented in Table 15, which provides an overview of the different test cases, corresponding reference speeds, and the controllers used.

Table 15.
Overview of experimental cases and controllers.
6.4.1. Experimental Cases
The experimental evaluation is conducted across three reference speeds representing progressively demanding operating conditions. The reference speed defines the desired motor speed in revolutions per minute (rpm) that each controller must achieve and maintain. By testing all controllers at three distinct target speeds, their performance can be systematically compared under varying operational demands.
Three experimental cases are defined with reference speeds of 2000 rpm, 2750 rpm, and 3500 rpm, corresponding to low, medium, and high-speed operating conditions, respectively. For each case, the controllers’ speed regulation performance is evaluated using three key metrics: rise time, overshoot, and settling time. These metrics collectively characterize the transient response behavior and provide quantitative insight into each controller’s ability to achieve rapid, stable, and accurate speed control.
6.4.2. Experimental Results: Current, Voltage, and Speed
Figure 21, Figure 22 and Figure 23 present the experimental results for the armature current, armature voltage, and motor speed for all four controllers, tested at the three different target speeds: 2000 rpm, 2750 rpm, and 3500 rpm under no-load conditions. These figures offer a comparative view of how each controller regulates the motor’s current, voltage, and speed under varying reference speed conditions.
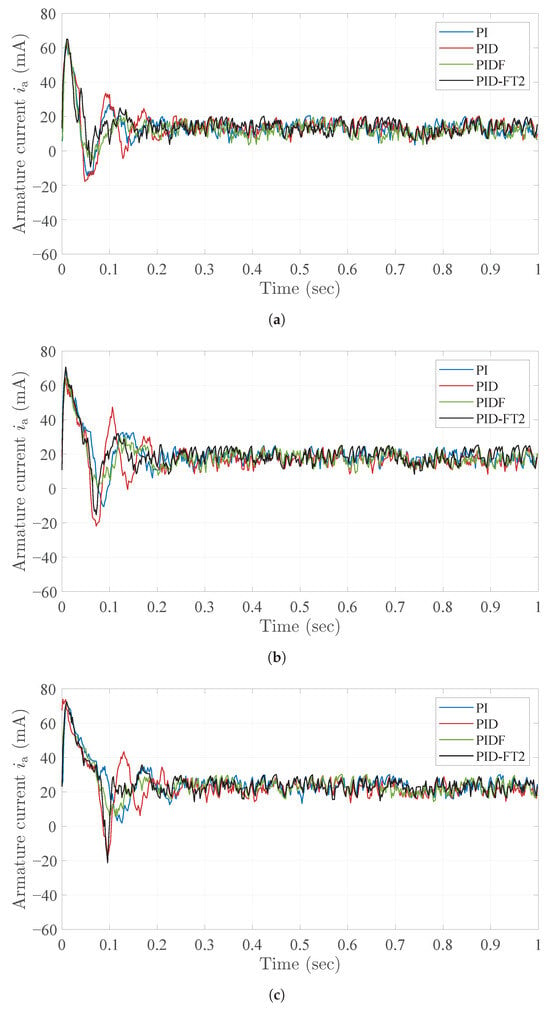
Figure 21.
Armature current experimental results for different reference speeds. Shows the response (a) for 2000 rpm, (b) for 2750 rpm, and (c) for 3500 rpm.
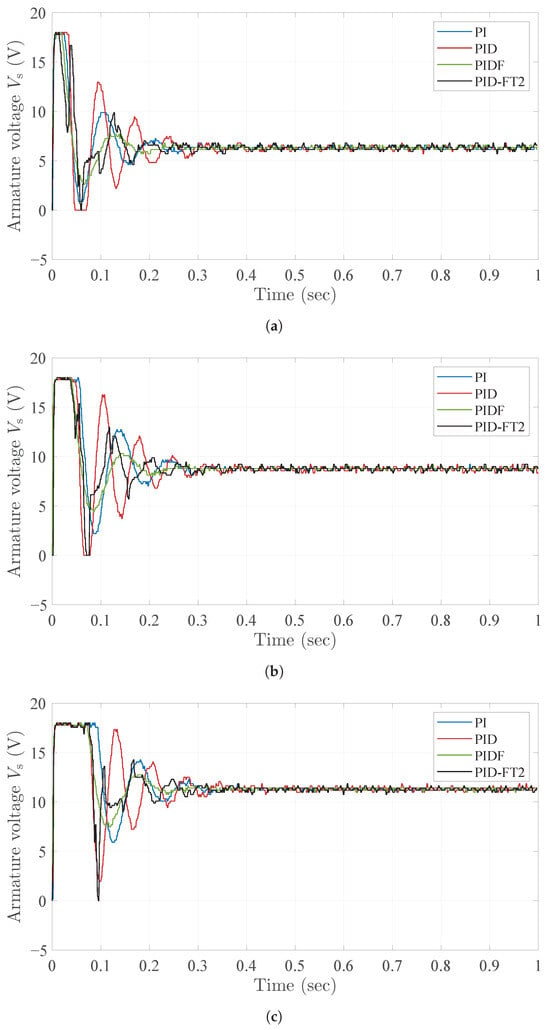
Figure 22.
Armature voltage experimental results for different reference speeds. Shows the response (a) for 2000 rpm, (b) for 2750 rpm, and (c) for 3500 rpm.
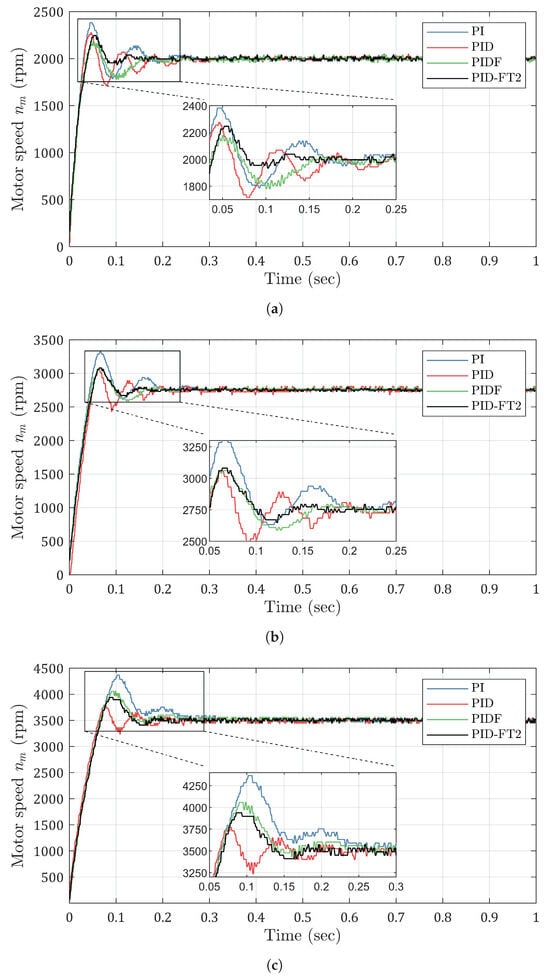
Figure 23.
Motor speed experimental results for different reference speeds. Shows the response (a) for 2000 rpm, (b) for 2750 rpm, and (c) for 3500 rpm.
6.4.3. Controller Performance Metrics
To quantify the performance of each controller in regulating the speed of DC micro-motors, key metrics such as rise time, overshoot and settling time are analyzed across three experimental cases. These metrics provide critical insight into the responsiveness, stability, and accuracy of the controllers in achieving precise motor speed control.
6.4.4. Rise Time
The rise time for different controllers at various reference speeds is shown in Table 16. This metric measures the time taken for the system to respond from 10% to 90% of the final value. For DC micro-motors, achieving low rise times is essential to ensure rapid speed adjustments and minimize delays in response.

Table 16.
Rise time for examined controllers.
In case 1 at a reference speed of 2000 rpm, the PI controller achieves the shortest rise time of 22.7 ms, followed closely by the PID controller at 24.3 ms. The PIDF and FT2-PID controllers exhibit slightly higher rise times of 26.1 ms and 29.7 ms, respectively. For DC micro-motors, these differences reflect varying trade-offs between fast response and robustness. As the reference speed increases to 3500 rpm in case 3, all controllers exhibit a rise in response time due to the increased demand on motor dynamics. The FT2-PID controller records the longest rise time of 53.5 ms, approximately 2.3% slower than the PIDF controller at 52.3 ms. These results underline the need for carefully selecting controllers based on specific performance requirements.
6.4.5. Overshoot
Overshoot values for different controllers at various reference speeds are shown in Table 17. In DC micro-motor applications, minimizing overshoot is critical to prevent mechanical damage and ensure stable operation.

Table 17.
Overshoot for examined controllers.
In case 1, the PI controller exhibits the highest overshoot at 19.00%, whereas the PIDF controller achieves the lowest value at 9.00%. The FT2-PID controller maintains an overshoot of 12.00%, balancing between responsiveness and stability. The PIDF controller exhibits higher overshoot of 16.00% compared to 8.00% for PID at higher speeds, attributable to the optimized filter coefficient N = 57.4 prioritizing settling time performance over transient overshoot damping. At higher speeds, the FT2-PID controller demonstrates remarkable consistency, with overshoot values increasing marginally to 12.50% in case 3.
6.4.6. Settling Time
The settling time for different controllers at various reference speeds is presented in Table 18. Settling time is defined as the duration required for the motor speed to stabilize within 2% of the target value.

Table 18.
Settling time for examined controllers.
In case 1, the FT2-PID controller demonstrates the fastest stabilization, achieving a settling time of 104 ms. This represents a 28.3% improvement over the PIDF controller and a 56.7% improvement over the PI controller. These results are particularly significant for DC micro-motor applications where rapid stabilization is critical to prevent operational delays. At higher reference speed (case 3), the FT2-PID controller maintains its superior performance with a settling time of 167 ms, compared to 225 ms for PIDF and 313 ms for PI. This consistent advantage across operating speeds demonstrates the FT2-PID controller’s robust capability for precise speed control under varying operating conditions.
6.4.7. Summary
The performance metrics, rise time, overshoot and settling time, illustrate distinct advantages and trade-offs among the controllers for DC micro-motor applications. The experimental results reveal that no single controller excels across all performance metrics simultaneously, necessitating careful consideration of application-specific priorities.
The FT2-PID controller emerges as the most balanced option, excelling in rapid stabilization and consistently maintaining low overshoot values. It achieves the fastest settling times across all test cases and maintains consistent overshoot values of 12.00–12.50% regardless of reference speed. However, this enhanced settling performance entails a trade-off of 5–31% slower rise times relative to simpler controllers. The CPU load analysis shows that the FT2-PID controller demands about 55% greater computational resources compared to conventional controllers, consistent with its superior steady-state regulation capability.
While the PI controller achieves the fastest rise time, its pronounced overshoot and slower settling behavior reduce its suitability for precision motor control. Its fixed-parameter structure also leads to noticeable performance degradation at higher operating speeds. The PID controller, with moderate rise times and low overshoot, provides a reliable compromise for applications requiring general-purpose control. The PIDF controller shows excellent performance in reducing overshoot at lower reference speeds, making it an attractive option for systems prioritizing stability. However, its longer settling times especially at higher speeds reveal some limitations.
These findings establish the FT2-PID controller as the optimal choice for achieving both precision and robust performance in DC micro-motor systems, particularly where settling time and steady-state accuracy are critical such as in precision positioning, robotics, and automated manufacturing. The STM32F103C8 platform limitations directly influenced these trade-offs by constraining fuzzy system complexity for real-time performance.
7. Conclusions
In this paper, the experimental implementation of speed control for a coreless DC motor using a low-cost microcontroller was presented, employing real-time Particle Swarm Optimization executed directly on the STM32 microcontroller rather than through offline simulation. A novel hardware-optimized composition of Interval Type-2 Fuzzy Logic Controller and PID controller was developed and evaluated against conventional PI, PID, and PIDF controllers through comprehensive experimental validation, addressing critical hardware limitations and practical feasibility constraints.
The hardware-in-the-loop implementation enabled real-time parameter optimization while managing actual system uncertainties. The experimental results demonstrated that the FT2-PID controller achieved substantially faster settling times compared to PI, PID, and PIDF controllers, with significantly lower overshoot consistency at higher reference speeds. However, these performance gains came with inherent trade-offs in computational requirements and initial response characteristics, reflecting fundamental hardware–software co-design considerations in real-time control system implementation.
The implementation addressed practical hardware constraints including PWM resolution and frequency trade-offs, minimum achievable voltage and speed control steps, control loop timing optimization balancing controller responsiveness against shaft encoder measurement accuracy, and speed filtering methodology combining averaging and Kalman techniques. Additionally, comprehensive resource utilization analysis quantified memory consumption and processor load for all examined controllers. These constraints directly influenced controller design decisions, demonstrating that successful embedded implementation requires hardware-aware design explicitly accounting for digital resolution limitations, temporal dependencies, and computational resource management typically abstracted in simulation-based studies. The hardware-in-the-loop PSO optimization executed on the microcontroller with the physical motor enabled simultaneous tuning of all controller parameters under actual operating conditions, ensuring the optimized gains respected implementation constraints while bridging the gap between theoretical controller design and practical embedded realization.
For future work, further optimization of the FT2-PID algorithm could reduce computational burden without compromising control efficacy. Comparative studies with other modern control approaches, such as adaptive neural controllers or neuro-fuzzy hybrid controllers, could provide deeper insights into hardware–software co-design trade-offs on resource-constrained platforms. Extended experimental validation under varying mechanical loads, external disturbances, and motor parameter variations would provide comprehensive robustness analysis. Testing across different motor types and sizes would demonstrate the generalizability of the proposed hardware-centric implementation methodology. By addressing these future directions, the gap between advanced theoretical control strategies and their practical embedded implementation can be further narrowed, enabling wider adoption of sophisticated control techniques in cost-effective industrial applications.
Author Contributions
Conceptualization, N.V.C. and Y.L.K.; methodology, Y.L.K.; software, N.V.C.; validation, N.V.C. and Y.L.K.; formal analysis, N.V.C.; investigation, N.V.C. and Y.L.K.; resources, Y.L.K.; data curation, N.V.C.; writing—original draft preparation, N.V.C.; writing—review and editing, Y.L.K.; visualization, Y.L.K.; supervision, Y.L.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Coreless DC micro-motor technical characteristics according to manufacturer datasheet (Faulhaber 2842 S 018 C).
Table A1.
Coreless DC micro-motor technical characteristics according to manufacturer datasheet (Faulhaber 2842 S 018 C).
| Quantity | Symbol | Value | Unit |
|---|---|---|---|
| Rated power | 6.19 | W | |
| Efficiency | 74 | % | |
| Nominal voltage | 18 | V | |
| Terminal resistance | 12.5 | ||
| Rotor inductance | 1300 | H | |
| Back-EMF constant | 3.52 | mV/rpm | |
| Torque constant | 0.03 | ||
| Rotor inertia | J | 14 | g·cm2 |
| Mechanical time constant | 15 | ms | |
| No-load current | 33 | mA | |
| Current constant | 0.03 | ||
| Friction torque | 0.156 | oz·in | |
| Stall torque | 7.193 | oz·in | |
| No-load speed | 5000 | rpm | |
| Rated speed | 2500 | rpm | |
| Speed constant | 284 | rpm/V | |
| Slope of n-T curve | 106 | rpm/mNm | |
| Angular acceleration | rad/s2 |
References
- Cheng, M.; Sun, L.; Buja, G.; Song, L. Advanced electrical machines and machine-based systems for electric and hybrid vehicles. Energies 2015, 8, 9541–9564. [Google Scholar] [CrossRef]
- Praveen, R.; Ravichandran, M.; Achari, V.S.; Raj, V.J.; Madhu, G.; Bindu, G. A novel slotless Halbach-array permanent-magnet brushless DC motor for spacecraft applications. IEEE Trans. Ind. Electron. 2011, 59, 3553–3560. [Google Scholar] [CrossRef]
- Wang, T.; Du, W.; Zeng, L.; Su, L.; Zhao, Y.; Gu, F.; Liu, L.; Chi, Q. Design and Testing of an End-Effector for Tomato Picking. Agronomy 2023, 13, 947. [Google Scholar] [CrossRef]
- Lee, D.H. Combined sensor–sensorless control of PMDC motor for HD camera of unmanned monitoring system. J. Electr. Eng. Technol. 2020, 15, 27–35. [Google Scholar] [CrossRef]
- Tajdari, F.; Ebrahimi Toulkani, N. Implementation and intelligent gain tuning feedback–based optimal torque control of a rotary parallel robot. J. Vib. Control 2022, 28, 2678–2695. [Google Scholar] [CrossRef]
- Karnavas, Y.L.; Topalidis, A.S.; Drakaki, M. Development of a low cost brushless DC motor sensorless controller using dsPIC30F4011. In Proceedings of the 2018 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; pp. 1–4. [Google Scholar]
- Sun, L. A new method for sensorless control of brushless DC motor. Clust. Comput. 2019, 22, 2793–2800. [Google Scholar] [CrossRef]
- Lee, D.H. Balanced parallel instantaneous position control of PMDC motors with low-cost position sensors. J. Power Electron. 2020, 20, 834–843. [Google Scholar] [CrossRef]
- Ghder Soliman, W.; Rama Koti Reddy, D. Microprocessor based prototype design of a PMDC motor with its system identification and PI controller design. SN Appl. Sci. 2019, 1, 1–8. [Google Scholar] [CrossRef]
- Sankardoss, V.; Geethanjali, P. Parameter estimation and speed control of a PMDC motor used in wheelchair. Energy Procedia 2017, 117, 345–352. [Google Scholar] [CrossRef]
- Bao, D.; Shen, H.; Ding, W.; Yuan, H.; Guo, Y.; Song, Z.; Gong, T. Research on the High Stability of an Adaptive Controller Based on a Neural Network for an Electrolysis-Free-Capacitor Motor Drive System. Energies 2025, 18, 2076. [Google Scholar] [CrossRef]
- Kecskés, I.; Burkus, E.; Király, Z.; Odry, Á.; Odry, P. Competition of motor controllers using a simplified robot leg: Pid vs fuzzy logic. In Proceedings of the 2017 Fourth International Conference on Mathematics and Computers in Sciences and in Industry (MCSI), Corfu, Greece, 24–27 August 2017; pp. 37–43. [Google Scholar]
- Sankardoss, V.; Geethanjali, P. Design and low-cost implementation of an electric wheelchair control. IETE J. Res. 2021, 67, 657–666. [Google Scholar] [CrossRef]
- Yang, S.K. A new anti-windup strategy for PID controllers with derivative filters. Asian J. Control 2012, 14, 564–571. [Google Scholar] [CrossRef]
- Huba, M.; Vrančič, D. Comparing filtered PI, PID and PIDD control for the FOTD plants. IFAC-PapersOnLine 2018, 51, 954–959. [Google Scholar] [CrossRef]
- Vrančić, D.; Huba, M. High-order filtered PID controller tuning based on magnitude optimum. Mathematics 2021, 9, 1340. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, Z. Improvements of direct current motor control and motion trajectory algorithm development for automated guided vehicle. Adv. Mech. Eng. 2019, 11, 1687814018824937. [Google Scholar] [CrossRef]
- Xue, J.; Chen, J.; Stancu, A.; Wang, X.; Li, J. Spatial Trajectory Tracking of Wall-Climbing Robot on Cylindrical Tank Surface Using Backstepping Sliding-Mode Control. Micromachines 2023, 14, 548. [Google Scholar] [CrossRef] [PubMed]
- Chu, H.; Gao, B.; Gu, W.; Chen, H. Low-speed control for permanent-magnet DC torque motor using observer-based nonlinear triple-step controller. IEEE Trans. Ind. Electron. 2016, 64, 3286–3296. [Google Scholar] [CrossRef]
- Humaidi, A.J.; Kasim Ibraheem, I. Speed control of permanent magnet DC motor with friction and measurement noise using novel nonlinear extended state observer-based anti-disturbance control. Energies 2019, 12, 1651. [Google Scholar] [CrossRef]
- Ahmad, N.S. Robust H∞-fuzzy logic control for enhanced tracking performance of a wheeled mobile robot in the presence of uncertain nonlinear perturbations. Sensors 2020, 20, 3673. [Google Scholar] [CrossRef]
- Ganzaroli, C.A.; de Carvalho, D.F.; Coimbra, A.P.; do Couto, L.A.; Calixto, W.P. Comparative Analysis of the Optimization and Implementation of Adjustment Parameters for Advanced Control Techniques. Energies 2022, 15, 4139. [Google Scholar] [CrossRef]
- Tuna, M.; Fidan, C.B.; Kocabey, S.; Gorgulu, S. Effective and reliable speed control of permanent magnet DC (PMDC) motor under variable loads. J. Electr. Eng. Technol. 2015, 10, 2170–2178. [Google Scholar] [CrossRef][Green Version]
- Murugananth, G.R.; Vijayan, S. Development of fuzzy controlled chopper drive for permanent magnet DC motor. J. Vib. Control 2015, 21, 555–562. [Google Scholar] [CrossRef]
- Çorapsiz, M.R. Performance analysis of speed control of PMDC motor using fuzzy logic controller. East. Anatol. J. Sci. 2017, 3, 16–29. [Google Scholar]
- Velagic, J.; Galijasevic, A. Design of fuzzy logic control of permanent magnet DC motor under real constraints and disturbances. In Proceedings of the 2009 IEEE Control Applications,(CCA) & Intelligent Control, (ISIC), St. Petersburg, Russia, 8–10 July 2009; pp. 461–466. [Google Scholar]
- Odry, Á.; Fullér, R.; Rudas, I.J.; Odry, P. Fuzzy control of self-balancing robots: A control laboratory project. Comput. Appl. Eng. Educ. 2020, 28, 512–535. [Google Scholar] [CrossRef]
- Kumar, N.S.; Sadasivam, V.; Asan Sukriya, H. A comparative study of PI, fuzzy, and ANN controllers for chopper-fed DC drive with embedded systems approach. Electr. Power Components Syst. 2008, 36, 680–695. [Google Scholar] [CrossRef]
- Guan, X.; Lou, S.; Li, H.; Tang, T. Intelligent control of quad-rotor aircrafts with a STM32 microcontroller using deep neural networks. Ind. Robot Int. J. Robot. Res. Appl. 2021, 48, 700–709. [Google Scholar] [CrossRef]
- Prakash, R.; Vasanthi, R. Speed control of DC-DC converter fed DC motor using robust adaptive intelligent controller. J. Vib. Control 2015, 21, 3107–3120. [Google Scholar] [CrossRef]
- Öztürk, N.; Celik, E. Speed control of permanent magnet synchronous motors using fuzzy controller based on genetic algorithms. Int. J. Electr. Power Energy Syst. 2012, 43, 889–898. [Google Scholar] [CrossRef]
- Nizami, T.K.; Chakravarty, A.; Mahanta, C. Design and implementation of a neuro-adaptive backstepping controller for buck converter fed PMDC-motor. Control Eng. Pract. 2017, 58, 78–87. [Google Scholar] [CrossRef]
- Elmas, C.; Ustun, O. A hybrid controller for the speed control of a permanent magnet synchronous motor drive. Control Eng. Pract. 2008, 16, 260–270. [Google Scholar] [CrossRef]
- Erenturk, K. MATLAB-based GUIs for fuzzy logic controller design and applications to PMDC motor and AVR control. Comput. Appl. Eng. Educ. 2005, 13, 10–25. [Google Scholar] [CrossRef]
- Li, D.; Ranjitkar, P. A fuzzy logic-based variable speed limit controller. J. Adv. Transp. 2015, 49, 913–927. [Google Scholar] [CrossRef]
- Hagras, H.A. A hierarchical type-2 fuzzy logic control architecture for autonomous mobile robots. IEEE Trans. Fuzzy Syst. 2004, 12, 524–539. [Google Scholar] [CrossRef]
- Mendel, J.M. Uncertain rule-based fuzzy systems. In Introduction and New Directions; Springer: Cham, Switzerland, 2017; Volume 684. [Google Scholar]
- Karnavas, Y.L.; Chatzipapas, N.V. Interval Type-2 Fuzzy Logic Controller Development for Coreless DC Micromotor Speed Control Applications. In Proceedings of the Fourth International Conference on Communication, Computing and Electronics Systems, Coimbatore, India, 15–16 September 2022; Springer: Singapore, 2023; pp. 755–767. [Google Scholar]
- Hassani, H.; Zarei, J. Interval Type-2 fuzzy logic controller design for the speed control of DC motors. Syst. Sci. Control Eng. 2015, 3, 266–273. [Google Scholar] [CrossRef]
- Buyukyildiz, C.; Saritas, I. Sensorless brushless DC motor control using type-2 fuzzy logic. Int. J. Intell. Syst. Appl. Eng. 2020, 8, 184–190. [Google Scholar] [CrossRef]
- Shi, Q.; Lam, H.K.; Xiao, B.; Tsai, S.H. Adaptive PID controller based on Q-learning algorithm. CAAI Trans. Intell. Technol. 2018, 3, 235–244. [Google Scholar] [CrossRef]
- Mahmud, M.; Motakabber, S.; Alam, A.Z.; Nordin, A.N. Adaptive PID controller using for speed control of the BLDC motor. In Proceedings of the 2020 IEEE International Conference on Semiconductor Electronics (ICSE), Kuala Lumpur, Malaysia, 28–29 July 2020; pp. 168–171. [Google Scholar]
- Shokouhandeh, H.; Jazaeri, M. An enhanced and auto-tuned power system stabilizer based on optimized interval type-2 fuzzy PID scheme. Int. Trans. Electr. Energy Syst. 2018, 28, e2469. [Google Scholar] [CrossRef]
- Chiu, C.H. Adaptive fuzzy control strategy for a single-wheel transportation vehicle. IEEE Access 2019, 7, 113272–113283. [Google Scholar] [CrossRef]
- Rigatos, G.G. Adaptive fuzzy control of DC motors using state and output feedback. Electr. Power Syst. Res. 2009, 79, 1579–1592. [Google Scholar] [CrossRef]
- Dhinakaran, P.; Manamalli, D. Novel strategies in the Model-based Optimization and Control of Permanent Magnet DC motors. Comput. Electr. Eng. 2015, 44, 34–41. [Google Scholar] [CrossRef]
- Ahmed, S.; Amin, A.A.; Wajid, Z.; Ahmad, F. Reliable speed control of a permanent magnet DC motor using fault-tolerant H-bridge. Adv. Mech. Eng. 2020, 12, 1687814020970311. [Google Scholar] [CrossRef]
- Shen, Y.; Yao, X.; Liu, S. Research on the drive control of the Disk Coreless BLDC motor based on the soft switching inverter. In Proceedings of the 2020 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), Harbin, China, 25–27 December 2020; pp. 1019–1022. [Google Scholar]
- Alset, U.; Apte, A.; Mehta, H. Implementation of Fuzzy Logic based High Performance Speed Control System for PMDC motor using ATMEGA-328P-PU Micro-controller. In Proceedings of the 2020 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 2–4 July 2020; pp. 1–5. [Google Scholar]
- Soliman, W.G.; Rama Koti Reddy, D.; Reddy, D.A. Microprocessor-based performance indices analysis of individual systems distributed motion control strategies. SN Appl. Sci. 2020, 2, 26. [Google Scholar] [CrossRef]
- Mishra, P.; Banerjee, A.; Ghosh, M. FPGA-based real-time implementation of quadral-duty digital-PWM-controlled permanent magnet BLDC drive. IEEE/ASME Trans. Mechatronics 2020, 25, 1456–1467. [Google Scholar] [CrossRef]
- Chaber, P.; Ławryńczuk, M. Fast analytical model predictive controllers and their implementation for STM32 ARM microcontroller. IEEE Trans. Ind. Inform. 2019, 15, 4580–4590. [Google Scholar] [CrossRef]
- Shan, X.; Li, M.; Yan, H.; Wang, Q.; Lan, Z. Design and implementation of the electrically powered wheelchair controller based on STM32. In Proceedings of the 2015 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 2–5 August 2015; pp. 1484–1488. [Google Scholar]
- Rhouma, A.; Hafsi, S.; Bouani, F. Global optimization in robust fractional control of uncertain fractional order systems: A thermal application using the stm32 microcontroller. Electronics 2022, 11, 268. [Google Scholar] [CrossRef]
- Sharaf, A.M.; Elgammal, A.A. Novel AI-based soft computing applications in motor drives. In Power Electronics Handbook; Elsevier: Amsterdam, The Netherlands, 2018; pp. 1261–1302. [Google Scholar]
- Mostafa, J.; Serdar, E.; Davut, I.; Mohit, B.; Ievgen, Z. Efficient DC motor speed control using a novel multi-stage FOPD(1 + PI) controller optimized by the Pelican optimization algorithm. Sci. Rep. 2024, 14, 22442. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).