Control of Drum Shear Electric Drive Using Self-Learning Artificial Neural Networks

Abstract

The objective of this work was to study the possibility of upgrading the control system of the drum shear mechanism by using neural network PI controllers to improve the efficiency of the sheet-metal cutting process. The developed detailed model of the mechanism, including a dual DC electric drive with three subordinate control loops for the voltage of the thyristor converter, current and speed of the motors, a 6-mass kinematic system with viscoelastic connections as well as a model of the metal cutting process, made it possible to uncover that the interaction of electric drives with the mechanical part leads to significant speed fluctuations during the cutting process, which worsens the quality of the sheet-metal edge. A modified system of current and speed controllers with built-in three-layer fitting neural networks as nonlinear components of proportional-integral channels is proposed. An algorithm for the fast learning of neural controllers using the gradient descent method in each cycle of calculating the controller signal is also proposed. The developed neuro-regulators make it possible to reduce the amplitude of speed fluctuations during the cutting process by four times, ensuring the effective damping of oscillations and reducing the duration of transient processes to 0.1 s.

1. Introduction

Hot rolling plays a critical role in modern metallurgical production, enabling the continuous manufacture of high-quality steel products that meet increasingly stringent technical and economic requirements. The process is fundamental not only for achieving precise geometrical dimensions and superior mechanical properties, but also for ensuring material efficiency across industries such as construction, automotive, and heavy engineering. As rolling production evolves to accommodate higher production speeds and tighter tolerances, the reliability and control of individual components within the rolling mill become ever more significant.

A hot strip rolling mill is a complex system that requires sophisticated regulations in order to obtain a constant thickness of the strip at the exit of the mill.

Among these components, drum shears are essential for segmenting and trimming the metal slabs during the hot rolling process. Their operation is crucial to maintaining the integrity of the rolled products by ensuring that cuts are executed with high accuracy and consistency. The effective control of drum shears contributes directly to minimizing dimensional deviations and material losses, thereby optimizing the overall process efficiency and reducing operational costs.

However, drum-type shears are an electromechanical object with a complex mechanical part in which fluctuations inevitably occur, affecting the accuracy of the cutting process and the product’s quality. Optimizing this component of the rolling mill can increase the efficiency of the production process.

One of the ways to solve such a problem could be the use of modern neural network technologies. Quite a lot of examples are already known in this area.

In the article written by Voronin S. [1], the practical implementation of the Industrial Internet of Things (IIoT) concept was considered to monitor the technical condition of electromechanical equipment exemplified by a plate mill 5000. The main problem addressed by the research was the significant (up to three times) difference in loads between the motors of the top and bottom rolls, causing the overheating of the more heavily loaded motor, thus shortening the service life of the insulation and premature failures. The authors proposed an approach based on the development of object-oriented digital twins—state monitors created using open-source software.

In the research by Ke, L. and co-authors [2], a complex analysis of the process of cutting 40 Mn strip steel on flying shears using finite element methods was presented. The authors performed a kinematic study of the flying shears mechanism and created a plane strain FEM-model using the Johnson–Cook constitutive model.

In the research by Ling-yun, Q. and co-authors [3], a complex analysis of the process of cutting high-strength pipe steels of X100 grade on hot-rolling flying shears using three-dimensional modeling by the finite element method was presented. The authors developed a detailed FE model that considered the kinematics of the blades including an elastic-plastic model of the steel strip material and rigid models of the cutting edges and feed rollers.

Considerable attention is currently being paid to the prospects of the modernization of shear mechanisms using variable-frequency electric drives of alternating current.

The article by Maklakov A.S. et al. [4] considered modern achievements in the field of network connection schemes of alternating current regenerative electric drives (AC REDs) for rolling mills, which play a key role in metallurgical production due to their reliability, efficiency, and high power.

The article by Ng [5] presented a practical application of direct torque control (DTC) technology for the modernization of the flying shear system at a metallurgical enterprise. The research was motivated by frequent failures of the existing system, which led to unplanned production downtime.

In the article by Solomon M.-G. and Gaiceanu, M. [6], the problem of energy consumption optimization of the flying shear system for high-efficiency lines for transverse cutting of metal strips was investigated. Their main attention was paid to the complex dynamic mode of operation of a vector-controlled asynchronous motor.

However, in the reviewed literature, there are no works devoted to the improvement of the quality of the existing DC electric drives of drum shears. Further development of existing DC electric drives of drum shears is possible due to the improvement of control systems in heavy-duty production conditions.

The purpose of this work was to substantiate the possibility of improving the technical characteristics of the DC electric drives of drum shears by using adaptive control systems based on the use of ANNs.

In the article by Kaminski and Tarczewski [7], the growing application of neural network technologies in electric drive systems was considered, covering three key areas: control, estimation of variable states, and diagnostics. The authors analyzed modern trends and prospects for the use of artificial intelligence in electrical engineering systems, focusing on electric machines and power electronics.

The modern scientific literature widely demonstrates research on the application of technologies related to ANNs for controlling electric drives of various types.

The article by Cheng, M. et al. [8] considered the development of a self-learning nonlinear controller for the high-precision positioning of an air-suspension micro-table driven by a voice coil motor (VCM) based on a combination of a nonlinear PID-structure and a neural network that dynamically adjusts the weight parameters of the controller depending on the current system error.

In the article written by Li, L. [9], the application of a high-level neural network algorithm for controlling a supercapacitor tram system is investigated. The author’s main attention was paid to the development of an adaptive neuro-fuzzy inference system (ANFIS), which allows for the limitations of traditional fuzzy controllers to be overcome.

In another study, Lin, R. and co-authors [10] solved the actual problem of accounting for the velocity-dependent hysteresis characteristics of the voice coil motor (VCM), which significantly affects the positioning accuracy in precision systems. The authors proposed an innovative approach that combines the VCM transfer function with the NARX neural network model, which makes it possible to effectively describe nonlinear hysteresis that changes depending on the frequency of the input signal.

In the article written by Zhang, A. et al. [11], the development and control of a rotary series-elastic actuator (SEA) using an innovative neural network approach was researched. The main contribution of the work was the proposed neural network model predictive control (NNMPC), which uses a simplified nonlinear autoregressive neural network with the ReLU activation function (ReLU-NARX NN) to approximate the dynamics of the system.

In the study of Hamad A. [12], the author presented an innovative algorithm for the adaptive speed control of the reluctance motor (VRM) using bi-channel single-layer neural networks. A feature of this approach is the use of a neuron network, where each node functions as an independent controller at a local operating point, which collectively allows for effective control of the system’s nonlinear behavior.

In article [13], the application of hybrid fuzzy neural network (FNN) for the self-learning control of brushless DC motors (BLDC) was considered. FNN combines fuzzy logic and neural networks, which allows the system to adaptively adjust weighting coefficients and membership functions of the input parameters during operation.

The article by Lin, Y. et al. [14] considered the improvement of the vector control system of a permanent magnet synchronous motor (PMSM) using the backpropagation (BP) algorithm in a neural network. The results of the research demonstrated the perspective of using neural network technologies to improve the performance of PMSM control systems.

The research performed by Schenke, M. et al. [15] developed a new method of controlling the torque of a permanent magnet synchronous motor (PMSM) using reinforcement learning (RL), which solves the key problem of the safe online training of a controller on a real drive without the need for prior knowledge of the object model.

During their research, Aydemir, M. and Okumus, H.I. [16] solved the current problem of the accurate determination of stator flux linkage in a reluctance motor using an innovative neural network approach. The authors suggested using a nonlinear neural autoregressive network with exogenous inputs (NARX) to estimate flux linkage, which allows for the elimination of the influence of changes in phase resistance in real-time.

The article by Selvaraj, A. and Thottungal, R. [17] presented an improved drive of a brushless direct current (BLDC) motor controlled through a neural network adaptive system model reference adaptive control (MRAC). The authors proposed a hybrid algorithm combining MRAC with an artificial neural network (ANN), which provides the real-time intelligent adaptation of parameters.

Article [18] presented an innovative approach to the control of capacitorless PMSM drives, which have complex nonlinear dynamics due to the absence of buffer elements. The authors developed a neural network adaptive control system based on the BP neural network, which solves problems such as DC bus voltage instability and weak resistance to disturbances.

In the study of Lin, F.-J. and co-authors [19], an intelligent servo drive control system based on a permanent magnet assisted synchronous reluctance motor (PMASynRM) was developed; the basis of the proposed solution is a hybrid algorithm combining intelligent backstepping control with a recurrent wavelet-fuzzy neural network (RWFNN).

In the article by Penthala, T. and Kaliaperumal, S. [20], the problem of controlling induction (asynchronous) motors (IMs) with the use of predictive control methods, in particular, model predictive torque control (MPTC), was considered. To optimize the system, the authors integrated a cascaded artificial neural network (ANN) into the MPFC, which automatically adapted the control parameters without the need for the manual selection of weighting coefficients.

The article written by Said, M. et al. [21] considered an innovative approach to improving direct torque control for doubly fed induction motors based on the use of an artificial neural network. The proposed solution makes it possible to eliminate hysteresis comparators and switching tables from the structure of the control system, replacing them with a neural network algorithm, which makes it possible to achieve more integrated and effective control.

The study by Benayad, N. et al. [22] considered the improvement of direct torque control (DTC) for a squirrel-cage induction motor (SCIM) using artificial intelligence. The authors proposed replacing the classic PI-controllers with an artificial neural network (ANN), which allows for the implementation of fundamentally new control qualities: high dynamics, smooth operation, stability, and robustness.

The article by Hamil, A. et al. [23] carried out a comparative analysis of three speed control methods of a DC motor in electric vehicles: a classical proportional-integral (PI) controller, a fuzzy logic controller (FLC), and a neural network approach (ANN). The most promising was the use of artificial neural networks, whose abilities to learn and adapt make it possible to optimally adjust control parameters in real-time.

The article by Shmidt and Dadenkov [24] presented a method for synthesizing a neural network controller for controlling the angular velocity of a DC motor by using the DeepLearning4j library. The authors developed an approach that allows a neural network to be trained on a control object model with a modified calculation of the loss function, which provides flexible adjustment of the transient processes’ quality.

The article by Gartlib, E.A et al. [25] proposed an innovative approach for the compensation of shock loads in the rolling mill by integrating a neural network algorithm into the main drive control system. The use of a predictive neural network control system made it possible to effectively reduce the kinetic torque arising during the process of metal rolling.

The article by Kozlova, L.P et al. [26] presented a neural network algorithm for controlling the servo drives of the joints of the lower limbs of the exoskeleton, designed to compensate for stochastic external disturbances, the uncertainty of the parameters of the dynamic model, and nonlinear factors (friction, elasticity). The neural network control system has the ability to learn and adapt, allowing for effective work with nonlinear objects without precise knowledge of their structure.

In the article by Belov, M.P. et al. [27], they investigated the work of neural network controllers for electric drives of an optical-mechanical complex, represented in the form of a three-mass system, taking into account nonlinear factors such as elasticity, backlash, and dry friction as well as external disturbances. To identify the dynamic system, a neural network model based on radial basis functions (RBFs) was used, which made it possible to synthesize effective control algorithms.

In the article by Gangula, S.D. et al. [28], they proposed an innovative neuro-adaptive control system for a PMDC motor with a buck converter, combining a backstepping controller and a self-learning neural network based on Zernike polynomials (ZRNN). It was shown that the application of this solution eliminated speed fluctuations at start-up and ensured stable operation under 600% load jumps.

Thus, the completed review of the modern scientific literature confirms the feasibility of using ANNs for controlling complex electromechanical systems.

The purpose of this work was to modify the control system of the drum shears’ electric drive by introducing controllers based on ANNs, which will ensure an increase in the efficiency of this mechanism, taking into account operational features such as a branched mechanical system and shock loads at the moment of strip metal cutting.

In order to achieve the set purpose, it was necessary to solve a number of tasks:

• Develop a detailed model of the mechanical system of drum shears;
• Develop a model of the electric drive of this mechanism based on known technical documentation and specification data of individual units;
• Compare the results obtained in the model with available recorded transient processes;
• Develop a block diagram of the system of electric drive controllers using ANNs, which can be implemented without modifying the power part of the electrical equipment;
• Develop a method of training for neural networks in the composition of electric drive coordinate controllers to ensure an increase in the dynamic accuracy of the drum shears’ mechanism.

2. Materials and Methods

2.1. Mathematical Modeling of the Mechanical System of Drum Shears

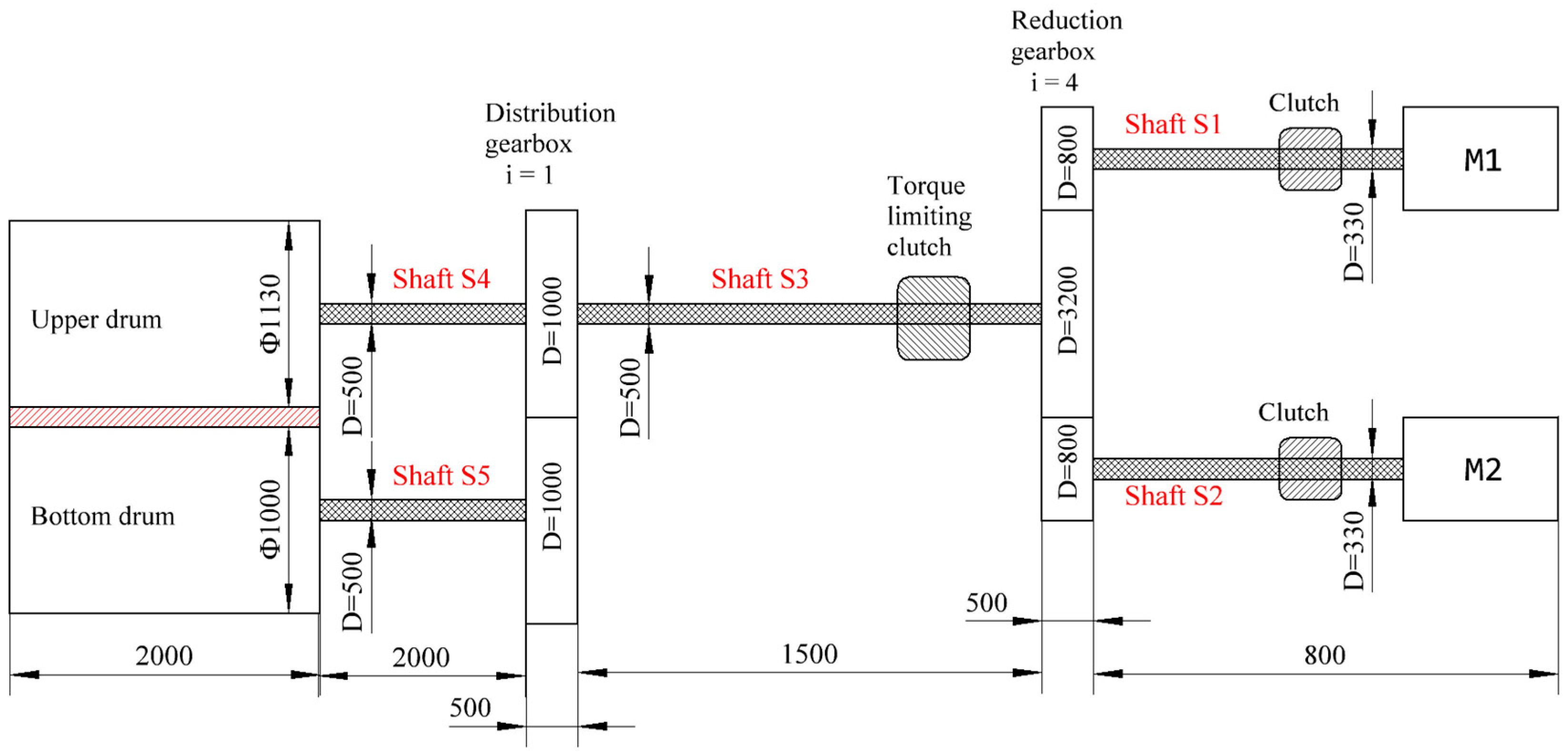
Drum shears with an inclined upper blade were installed between the roughing and finishing mills of hot rolling mill “1700” in sheet rolling shop 1 of JSC Qarmet, Republic of Kazakhstan, Temirtau, and were used for cutting the front and rear ends of the strip plate. Figure 1 shows the technological flowchart and layout of the electromechanical equipment of the drum shears under the conditions of JSC Qarmet.

Technical characteristics of the drum shears are given in

Table 1. Technical and technological data of the drum shears.

Parameters	Units	Value
Thickness of the strip plate	mm	$20 ÷$ 45
Width of the strip plate	mm	$700 ÷$ 1550
Speed	m/s	$0.58 ÷$ 2
Temperature	$℃$	900
Maximum specific cutting work at 900 °C	kg·mm/mm3	4
Inclination of the upper blade (single bevel)		1/28.4
Calculated cutting force	tons	350
Maximum calculated torque from the cutting force (on the drive shaft)	ton·m	150
The diameter of the drums along the edges of the blades:
Upper	mm	1130/1020
Lower	mm	1000
$\mathrm{Cutting} \mathrm{onset} \mathrm{angle} {\sigma }_{\mathrm{M}\mathrm{A}\mathrm{X}}=45 \mathrm{m}\mathrm{m}$ on the lower drum		28°
Cutting end angle		8°
Rolling rhythm (minimum)	s	45

.

The shears were driven by two direct current electric motors of the P19-75-7K type with the characteristics—1750 kW, 190 rpm, through a cylindrical gearbox. Technical characteristics of the drive motor are given in

Table 2. Technical characteristics of the drive motor of the drum shears.

Parameters	Value
Type	P19-75-7K
Rated power, kW	1750
Rotational frequency, rpm	190
Voltage, V	600
Rated current, A	2980
Rated torque, N·m	92,000
The number of pole pairs	8
The number of the armature winding paths	16
Bus resistance, Ohm	0.001
Armature circuit resistance, Ohm	0.0263
Armature circuit inductance, mH	3.653
EMF coefficient at Φ = ΦH, AeF	28
Moment of inertia of the drive, kgm2	6000

.

Based on the available technical documentation, the layout of the main mechanical equipment of the drum flying shears installed on the hot rolling mill “1700” of the sheet rolling shop 1 of JSC Qarmet was developed; this is presented in Figure 2.

The asymmetry of this design, due to the different diameters of the drums of flying shears, stands out particularly.

One of the important features of the electromechanical systems of hot rolling mills are the presence of elastic connections [29].

The drum drive is a multi-mass electromechanical system where the kinematic transmission plays the role of an elastic link. Such systems are classified as systems with first-order elasticities [29].

The following assumptions are used for the analysis of such systems [29]:

• Elements of the system to which forces and torques are applied are considered absolutely rigid and not subject to deformation.
• The mass of elastic links is either neglected or taken into account as a part of the equivalent masses.
• The ratio between the torque (force) and deformation remains constant (i.e., the elastic link has constant stiffness).
• Deformation of elastic elements follows Hooke’s law and is linear.
• Wave processes arising during deformation can be neglected.

The calculated six-mass kinematic diagram of the mechanical part of the drum shears is shown in Figure 3.

In the diagram in Figure 3, the following notations are used:

J11, J12 are the rotational masses that take into account the moments of inertia of the drive electric motors D1 and D2 and the distributed moments of inertia of the corresponding shafts S1 and S2, which can be calculated according to the following formulas:

$${{\displaystyle J}}_{11}={{\displaystyle J}}_{m1}+{\displaystyle \frac{1}{2}}{{{\displaystyle J}}_{s1}}_{,}$$

(1)

$${{\displaystyle J}}_{12}={{\displaystyle J}}_{m2}+{\displaystyle \frac{1}{2}}{{{\displaystyle J}}_{s2}}_{,}$$

(2)

where [cs1, bs1] is the visco-elastic element modeling shaft 1; [cs2, bs2] is the visco-elastic element modeling shaft 2;

J2 is the flywheel mass of the reduction gearbox, taking into account the moment of inertia of the gearbox itself and the distributed moments of inertia of shafts S1, S2, and S3:

$${{\displaystyle J}}_2={{\displaystyle J}}_{G3.2}+{\displaystyle \frac{1}{2}}{{\displaystyle J}}_{s3}+{\displaystyle \frac{\left({{\displaystyle J}}_{s1}+{{\displaystyle J}}_{s2}+2{{\displaystyle J}}_{G0.8}\right)}{2}}\cdot {{\displaystyle i}}^2,$$

(3)

where [cs3, bs3] is the visco-elastic element modeling shaft 3.

J3 is the flywheel mass of the distribution gearbox, which takes into account the moment of inertia of the gearbox itself and the distributed moments of inertia of shafts S3, S4, and S5:

$${{\displaystyle J}}_3=2{{\displaystyle J}}_{G1.0}+{\displaystyle \frac{1}{2}}\left({{\displaystyle J}}_{s3}+{{\displaystyle J}}_{s4}+{{\displaystyle J}}_{s5}\right),$$

(4)

where J4, J5 are the flywheel masses that take into account the moments of inertia of drums D1 and D2 and the distributed moments of inertia of the corresponding shafts S4 and S5, which can be calculated according to the following formulas:

$${{\displaystyle J}}_4={{\displaystyle J}}_{DU}+{\displaystyle \frac{1}{2}}{{{\displaystyle J}}_{s4}}_{,}$$

(5)

$${{\displaystyle J}}_5={{\displaystyle J}}_{DB}+{\displaystyle \frac{1}{2}}{{{\displaystyle J}}_{s5}}_{,}$$

(6)

where [cs4, bs4] is the visco-elastic element modeling shaft 4; [cs5, bs5] is the visco-elastic element modeling shaft 5; Tm1, Tm2 are the driving electromagnetic torques created by the first and second drive motors, respectively; TNLm1, TNLm2 are the idling resistance torques of the first and second drive motors, respectively; TE1, TE2 are the elastic torques created by torsion of shaft 1 and 2, respectively; TNL2 is the resistance torque created by friction forces in the reduction gearbox; TE3 is the elastic torque created by torsion of shaft 3; TNL3 is the resistance torque created by frictional forces in the distribution gearbox; TNL4, TNL5 are the friction resistance torques in the bearings of the upper and lower drums, respectively; TE4, TE5 are the elastic torques created by torsion shaft 4 and 5, respectively.

Based on the diagram shown in Figure 3, it is easy to write down the motion equations of individual masses of the kinematic scheme:

$$\left\{\begin{array}{l}{{\displaystyle J}}_{11}{\displaystyle \frac{d{{\displaystyle \omega }}_{11}}{dt}}={{\displaystyle T}}_{m1}-{{\displaystyle T}}_{NLm1}-{{\displaystyle T}}_{E1}\hfill \\ {{\displaystyle J}}_{12}{\displaystyle \frac{d{{\displaystyle \omega }}_{12}}{dt}}={{\displaystyle T}}_{m2}-{{\displaystyle T}}_{NLm2}-{{\displaystyle T}}_{E2}\hfill \\ {\displaystyle \frac{{{\displaystyle J}}_2}{i}}{\displaystyle \frac{d{{\displaystyle \omega }}_2}{dt}}=\left({{\displaystyle T}}_{E1}+{{\displaystyle T}}_{E2}\right)\cdot i-{{\displaystyle T}}_{NL2}-{{\displaystyle T}}_{E3}\hfill \\ {{\displaystyle J}}_3{\displaystyle \frac{d{{\displaystyle \omega }}_3}{dt}}={{\displaystyle T}}_{E3}-{{\displaystyle T}}_{NL3}-{{\displaystyle T}}_{E4}-{{\displaystyle T}}_{E5}\hfill \\ {{\displaystyle J}}_4{\displaystyle \frac{d{{\displaystyle \omega }}_4}{dt}}={{\displaystyle T}}_{E4}-{{\displaystyle T}}_{NL4}-{{\displaystyle T}}_{L4}\hfill \\ {{\displaystyle J}}_5{\displaystyle \frac{d{{\displaystyle \omega }}_5}{dt}}={{\displaystyle T}}_{E5}-{{\displaystyle T}}_{NL5}-{{\displaystyle T}}_{L5}\hfill \\ {{\displaystyle T}}_{E1}={{\displaystyle b}}_{s1}\left({{\displaystyle \omega }}_{11}-{{\displaystyle \omega }}_2\right)+{{\displaystyle c}}_{s1}\left({{\displaystyle \phi }}_{11}-{{\displaystyle \phi }}_2\right)\hfill \\ {{\displaystyle T}}_{E2}={{\displaystyle b}}_{s2}\left({{\displaystyle \omega }}_{12}-{{\displaystyle \omega }}_2\right)+{{\displaystyle c}}_{s2}\left({{\displaystyle \phi }}_{12}-{{\displaystyle \phi }}_2\right)\hfill \\ {{\displaystyle T}}_{E3}={{\displaystyle b}}_{s3}\left({{\displaystyle \omega }}_2-{{\displaystyle \omega }}_3\right)+{{\displaystyle c}}_{s3}\left({{\displaystyle \phi }}_2-{{\displaystyle \phi }}_3\right)\hfill \\ {{\displaystyle T}}_{E4}={{\displaystyle b}}_{s4}\left({{\displaystyle \omega }}_3-{{\displaystyle \omega }}_4\right)+{{\displaystyle c}}_{s4}\left({{\displaystyle \phi }}_3-{{\displaystyle \phi }}_4\right)\hfill \\ {{\displaystyle T}}_{E5}={{\displaystyle b}}_{s5}\left({{\displaystyle \omega }}_3-{{\displaystyle \omega }}_5\right)+{{\displaystyle c}}_{s5}\left({{\displaystyle \phi }}_3-{{\displaystyle \phi }}_5\right)\hfill \end{array}\right.,$$

(7)

2.2. Determination of the Parameters of the Mathematical Model of the Mechanical Part of the Drum Flying Shears

The moment of inertia of the mass J is determined by the mass distribution relative to the axis of rotation. For standard machine elements (motor rotor, clutch, brake pulley), the values of moments of inertia are given in the reference literature.

The moment of inertia of a solid cylinder:

$$J=\rho \cdot {\displaystyle \frac{\pi }{32}}\cdot {{\displaystyle D}}^4\cdot l,$$

(8)

where r is the density, kg/m³; for steel r = 7800 kg/m³; D is the outer diameter, m; l is the length, m.

For the most common parts, the moment of inertia can be calculated using the expression:

$$J=K\cdot m\cdot {{\displaystyle R}}^2,$$

(9)

where m is the mass of the part, kg; R is the outer radius, m; K is the coefficient: K = 0.6 for the brake pulley; K = 0.64 for the gear wheels; K = 0.7 for the drums; K = 0.44 for the clutches.

The elastic properties of the parts are estimated by stiffness (or compliance) coefficients for the corresponding type of deformation.

The stiffness coefficient (or stiffness) characterizes the load required for unit deformation.

During the torsion of a round solid shaft of length l:

$$c={\displaystyle \frac{G\cdot \frac{\pi }{32}\cdot {{\displaystyle D}}^4}{l}},$$

(10)

where D is the diameter of the shaft, m; G is the shear modulus, Pa, G = 0.4 E; E is the modulus of elasticity of steel, Pa; E = 200,000 MPa = 2 × 10¹¹ Pa.

The coefficient of elastic viscous friction, which characterizes the energy dissipated due to internal viscoelastic losses of the material during torsional vibrations, is proportional to the stiffness coefficient c. This proportionality factor η is the coefficient of internal friction (or loss). Typical values for steel are η = 0.001–0.005.

Using data from Table 1 and Table 2 as well as the dimensions of the equipment from Figure 2, we calculated the numerical values of the elements of the computational scheme in Figure 3. The obtained results are shown in

Table 3. Parameters of the mathematical model of the mechanical part of the drum flying shears.

No.	Element	Designation	Value, kgm2
1	Moment of inertia of shafts 1 and 2 taking into account the clutch	JS1, JS2	8
2	The moment of inertia of the shaft 3 taking into account the torque-limiting clutch	JS3	79
3	Moment of inertia of shafts 4 and 5 taking into account the coupling	JS4, JS5	105.3
4	Gear wheel D = 800 mm	JG0.8	156.83
5	Gear wheel D = 320 mm	JG3.2	40,150
6	Gear wheel D = 1000 mm	JG1.0	382.9
7	The moment of inertia of the upper drum	JDU	1657.8
8	The moment of inertia of the lower drum	JDB	1531.5
9	Stiffness coefficients of shafts 1 and 2	cs1, cs2	1.1643 × 108
10	Stiffness coefficients of shaft 3	cs3	3.2725 × 108
11	Stiffness coefficients of shafts 4 and 5	cs4, cs5	2.4544 × 108
12	Viscous friction coefficients of shafts 1 and 2	bs1, bs2	1.1643 × 105
13	Viscous friction coefficients of shaft 3	bs3	3.2725 × 105
14	Viscous friction coefficients of shafts 4 and 5	bs4, bs5	2.4544 × 105

.

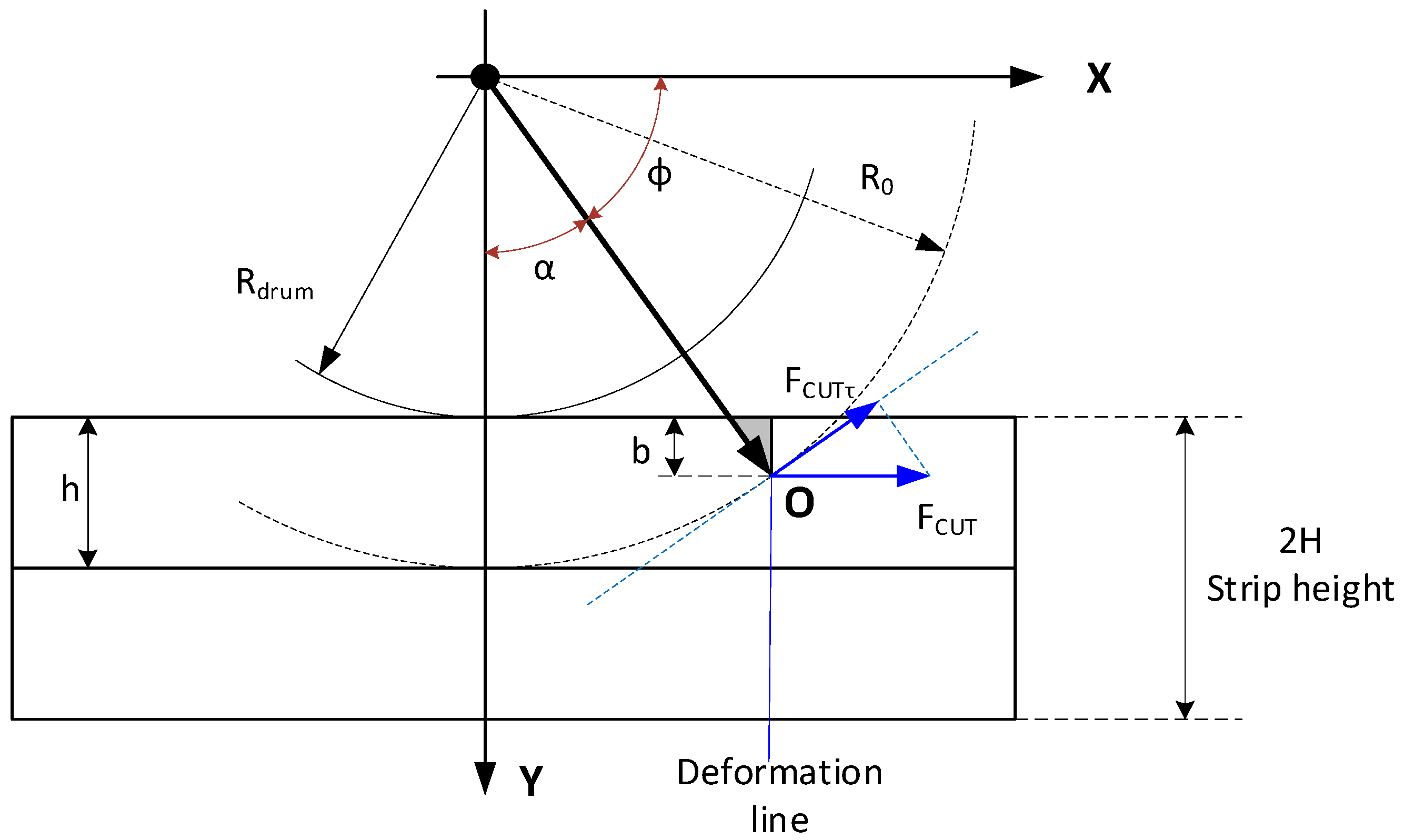
Figure 4 shows the diagram of the mutual arrangement of the drum and the cut strip during elastic deformation of the metal.

In Figure 4, the following notations are used: h is half the height of the metal strip; the full height of the strip is processed by two drums, m; R_DRUM, R0 are the radius of the drum and radius of the cutting edge (taking into account the protruding part of the blade), respectively, m; ϕ is the angle describing the current position of the drum, rad; X and Y are the axes of the coordinate system in which the movement of the drum is considered; O is the position of the cutting edge of the blade at the angle of rotation ϕ; b is the height of the destruction area; F_CUT, F_CUTτ are the cutting force and its projection on the tangential surface to the surface of the drum at point O.

When metal is cut, the destruction area is a sheared surface, shown in Figure 4 as the gray area.

Let us assume that the destruction occurs only by shear, then, with the perpendicular impact of the force, the ratio between the cutting force and the material characteristics is:

$$\mathrm{F}={\mathrm{S}}_{\mathrm{CUT}} {\mathsf{\tau }}_{\mathrm{shift}}$$

(11)

where S_CUT is the destruction area of the material; τ_shift is the material shear stress at working temperature.

The surface area of destruction can be calculated as

$${\mathrm{S}}_{\mathrm{CUT}}=\mathrm{b}·\mathrm{t}$$

(12)

where t is the width of the workpiece (or the cut line length); b is the height of the destruction area.

However, in real conditions, cutting does not occur strictly perpendicular to the sheared surface but occurs along a certain shear (or cutting) angle α. This leads to the fact that the effective cutting length is increasing, and the force applied in the direction of the cut depends on this angle. As a result, the equation for calculating the cutting force is written as:

$$F={\displaystyle \frac{b\cdot t\cdot {{\displaystyle \tau }}_{shift}}{\sin \left(\alpha \right)}},$$

(13)

where b is the height of the destruction area, which determines which part of the cross-section is subjected to shear destruction; t is the width of the workpiece (or the cut line length); τ_shift is the critical shear stress at which material rupture begins. During hot rolling, this value is determined by the temperature and condition of the material; α is the shear angle (or cutting angle), which is determined by the geometry of the contact between the cutting edge and the workpiece.

This equation allows us to estimate the required cutting force, which should be developed by the flying shears to correctly perform the cut, based on the geometric dimensions of the workpiece, the working value of the shear stress τ_shift (taking into account the temperature conditions of the material), and the shear angle α.

In practice, additional empirical coefficients or corrections can be introduced to take into account factors such as non-ideal cutting conditions, the influence of process dynamics, the accuracy of the shear blade clearance, etc. The choice of a specific model depends on the details of the technological process and the equipment used.

It is quite complicated to determine one universal value of shear stress τ_shift for different kinds of steel, since it depends on many factors such as the temperature, the steel composition, microstructure, deformation rate, degree of deformation, and specific test conditions. However, in engineering practice, approximate values based on experimental data are often used for approximate calculations.

For steel with a fully formed austenite structure (which is typical for temperatures of about 900 °C), typical values of the critical shear stress can be in the range of 20–30 MPa.

As the temperature increases, the critical shear stress τ_shift exponentially decreases, especially in the recrystallization interval (700–1000 °C). This is due to a decrease in the strength of interatomic bonds and an increase in the mobility of dislocations. The chemical composition of steel also affects the structure, phase state, and plastic deformation resistance. Carbon and alloying elements increase the strength and hardness of steel, increasing the value of critical shear stresses τ_shift. According to [30,31], the value of critical shear stress τ_shift for mild steel in the temperature range of 700–1000 °C decreases from 60 to 15 MPa. For alloyed steel 42CrMo, the value of critical shear stress τ_shift decreases from 300 to 80 MPa.

In the considered model, we took the value of the critical shear stress to be equal to 20 MPa. This value is indicative and can be adjusted depending on the specific conditions of the hot rolling process and the composition of the steel.

For more accurate calculations, it is recommended to rely on experimental data for a specific type of steel and processing conditions.

Based on geometric considerations, we can write down the necessary expressions based on the diagram in Figure 4.

Metal cutting begins when the cutting edge of the blade touches the metal strip’s surface. This event occurs when the projection of the vector R₀ on the vertical axis is equal to the radius of the drum R_DRUM. In order to determine the angle at which metal cutting begins; we used the following equality:

$$\left({{\displaystyle R}}_D+h\right)\cdot \sin \left(\phi \right)={{\displaystyle R}}_D\to {{\displaystyle \phi }}_{start}=\arcsin \left({\displaystyle \frac{{{\displaystyle R}}_D}{{{\displaystyle R}}_D+h}}\right),$$

(14)

During the drum rotation, the height of the destruction area b increases and can be calculated using the expression

$$b={{\displaystyle Y}}_0-{{\displaystyle R}}_D=\left({{\displaystyle R}}_D+h\right)\cdot \sin \left(\phi \right)-{{\displaystyle R}}_D,$$

(15)

where Y₀ is the coordinate of the cutting point O along the vertical axis.

It should be noted that before the rotation angle reaches the value φ_start as well as after passing the point φ = 180 degrees, metal cutting does not occur, and the height of the destruction area b should be considered zero.

Finally, to calculate the cutting force and the resistance torque created by this force, we can write the following expressions:

$${{\displaystyle F}}_{CUT}={\displaystyle \frac{b\cdot t\cdot {{\displaystyle \tau }}_{shift}}{\cos \left(\frac{\pi }{2}-\phi \right)}},$$

(16)

$${{\displaystyle T}}_{CUT}={{\displaystyle F}}_{CUT}\cdot {{\displaystyle R}}_0\cdot \cos \left({\displaystyle \frac{\pi }{2}}-\phi \right),$$

(17)

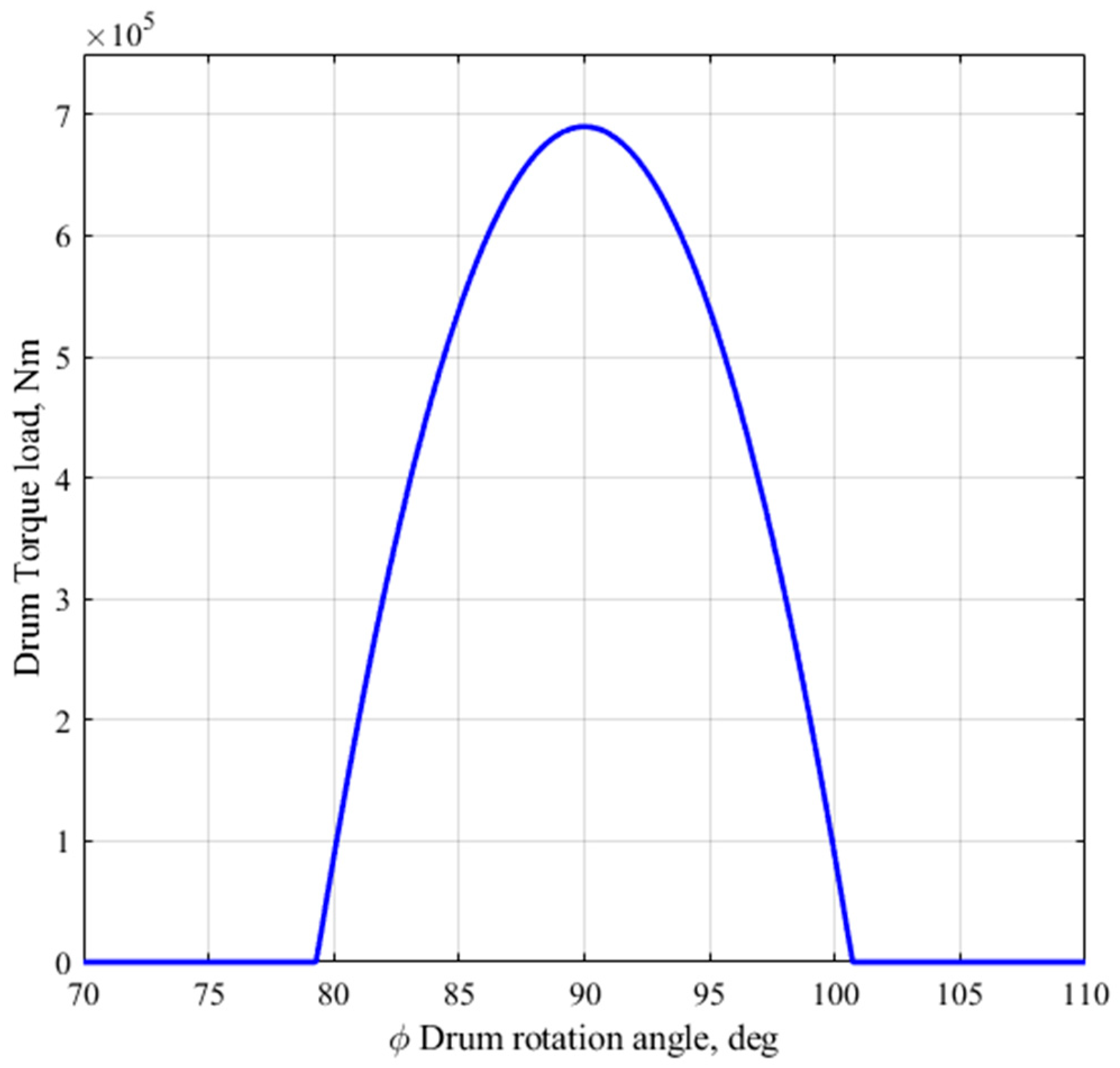
Using the above expressions, we can calculate the dependence of the resistance torque of the drum flying shears for the conditions of hot rolling mill “1700” in sheet rolling shop 1 of JSC Qarmet.

The obtained results are presented in Figure 5.

2.3. Mathematical Modeling of a Reversible Thyristor Direct Current Electric Drive

When modeling a direct current motor with independent excitation, the following general assumptions are used:

(1)

The excitation current has a constant value;

(2)

The value of saturation both along the contour of the main magnetic flux and along the dissipation circuit is neglected;

(3)

The influence of the eddy current circuit is neglected;

(4)

The machine is fully compensated (i.e., the influence of the armature reaction is absent).

The system of equations of a direct current motor in the canonical form has a well-known form [29]:

$$\left\{\begin{array}{l}{L}_{\mathsf{\Sigma }}{\displaystyle \frac{d{I}_A}{dt}}=U_A-k\mathsf{\varphi }·\mathsf{\omega }-I_A{R}_{\mathsf{\Sigma }}\hfill \\ J{\displaystyle \frac{d\omega }{dt}}=k\mathsf{\varphi }·I_A-TL\hfill \end{array}\right.,$$

(18)

where L_Σ is the total inductance of the armature circuit, H; R_Σ is total active resistance of the armature circuit, Ohm; U_A is the armature voltage, V; I_A is the armature current, A; ω is the angular speed of the armature, 1/s; J is the moment of inertia of the armature, kg∙m²; kϕ is the motor flux coefficient, V s; TL is the resistance torque of the electric drive, N∙m.

Also, in this work, we neglected the discreteness of the adjustable thyristor converter, using average values modeling.

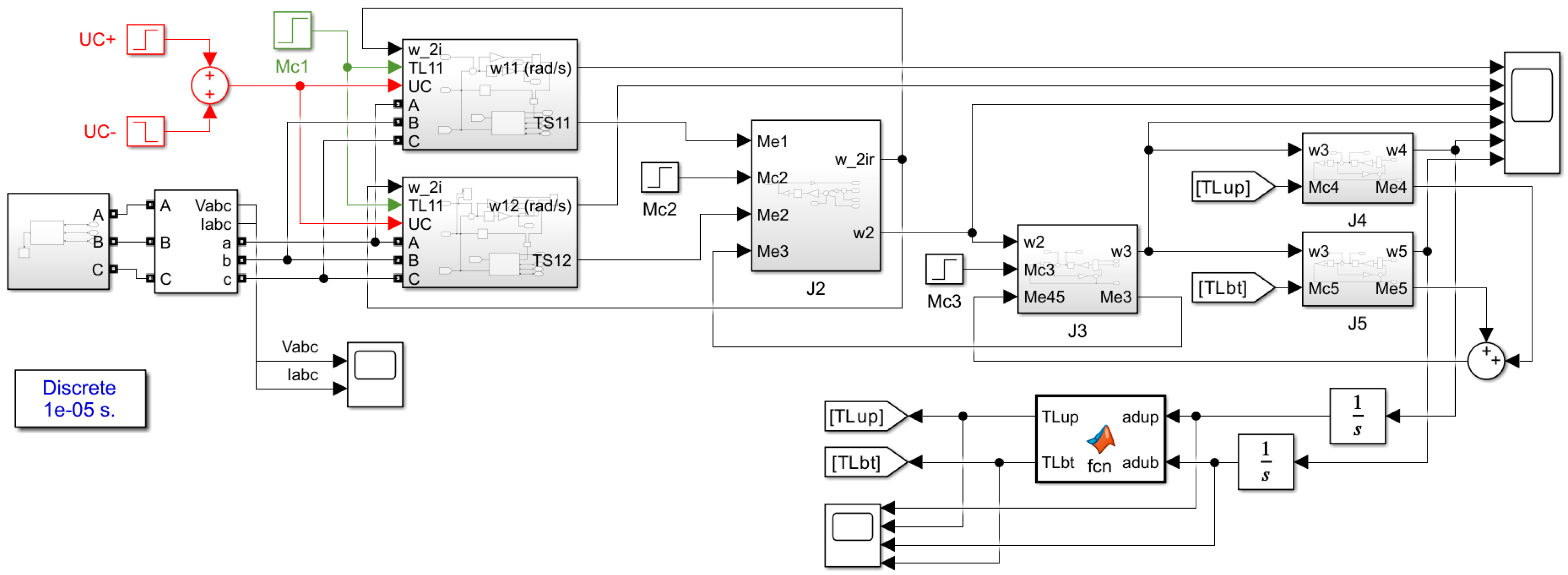
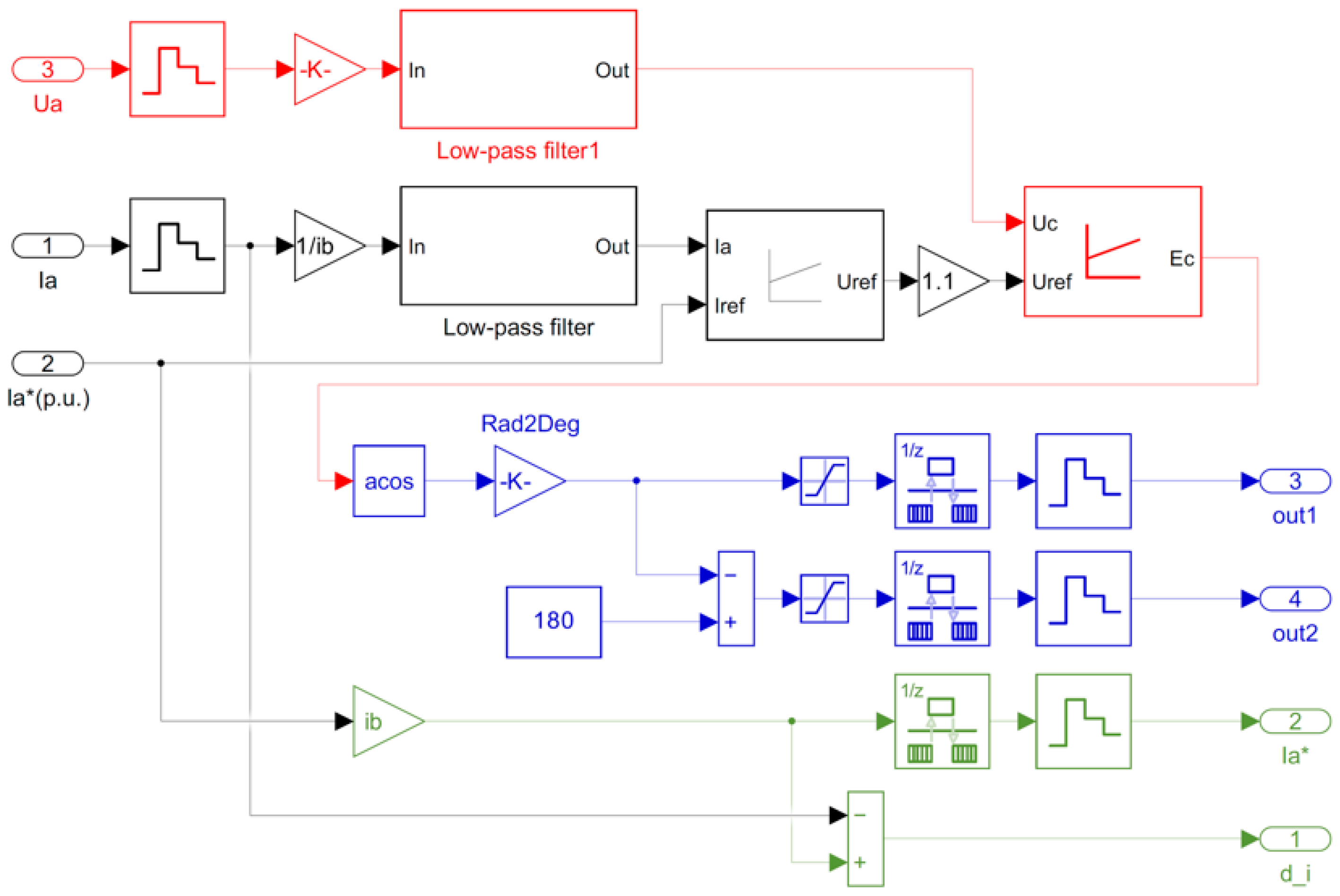
As the speed control system of the electric drive of the drum flying shears of the finishing group, a multi-circuit control system was used to ensure a wide range of speed control while maintaining the optimal energy, mass, and economic parameters of the electric drive. The model of the system is shown in Figure 6.

As a basic model of a direct current electric drive with a multi-circuit system of subordinate control, a block of a 4-quadrant three-phase reversible electric drive from the MATLAB 2024a, Simscape\Electrical library was used (Figure 7).

Adjustment of the controllers ensures that the current circuit corresponds to the modular optimum, and the speed circuit to the symmetrical optimum.

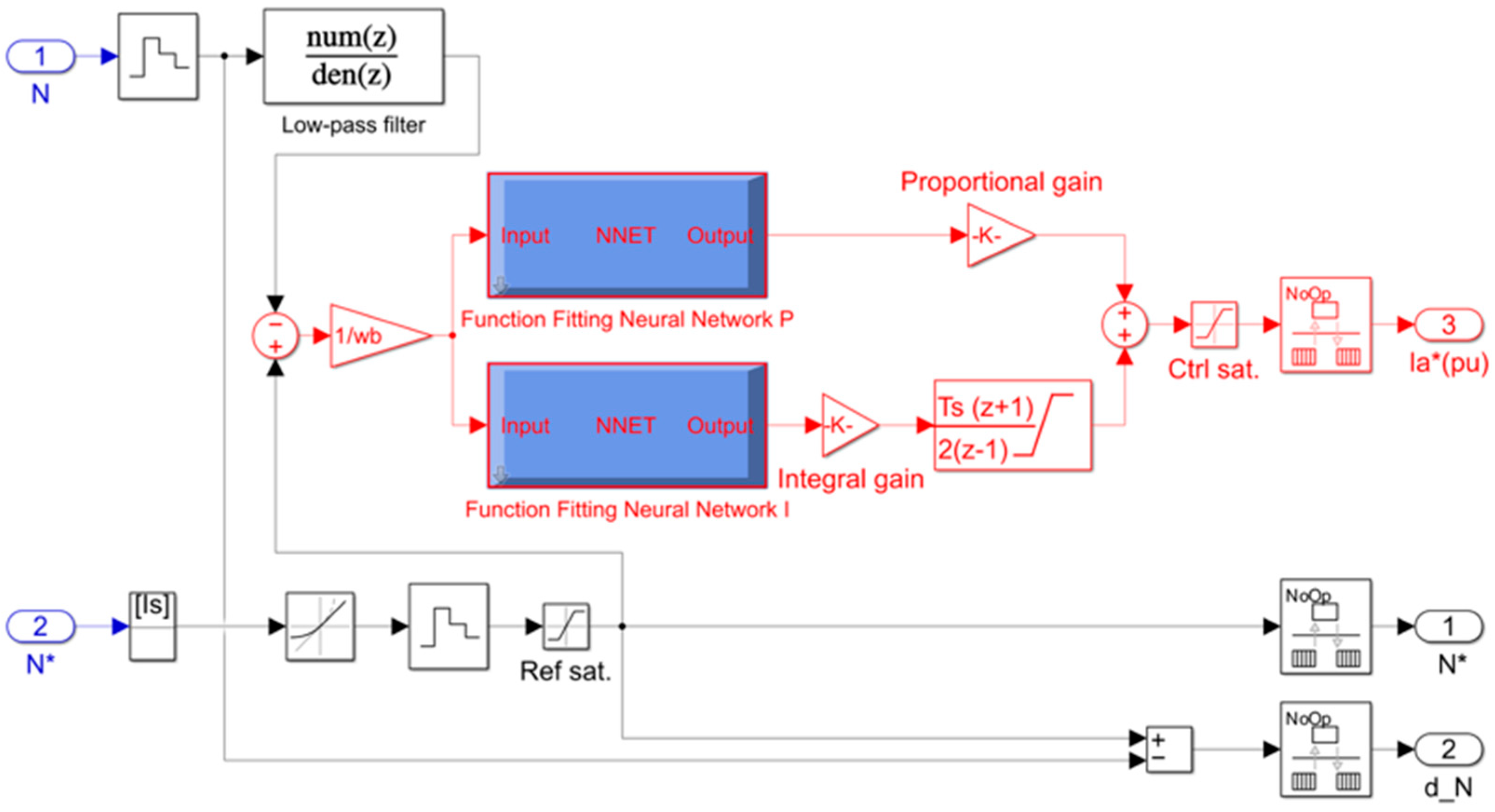
Considering the features of the electric drives of flying shear motors, this model, in addition to the current and speed circuits, was supplemented with a third internal circuit for voltage control of the thyristor converter (Figure 8).

Such a controller provides stabilization of the equivalent gain of the thyristor converter in the intermittent current mode and additionally reduces the fluctuation of the current circuit.

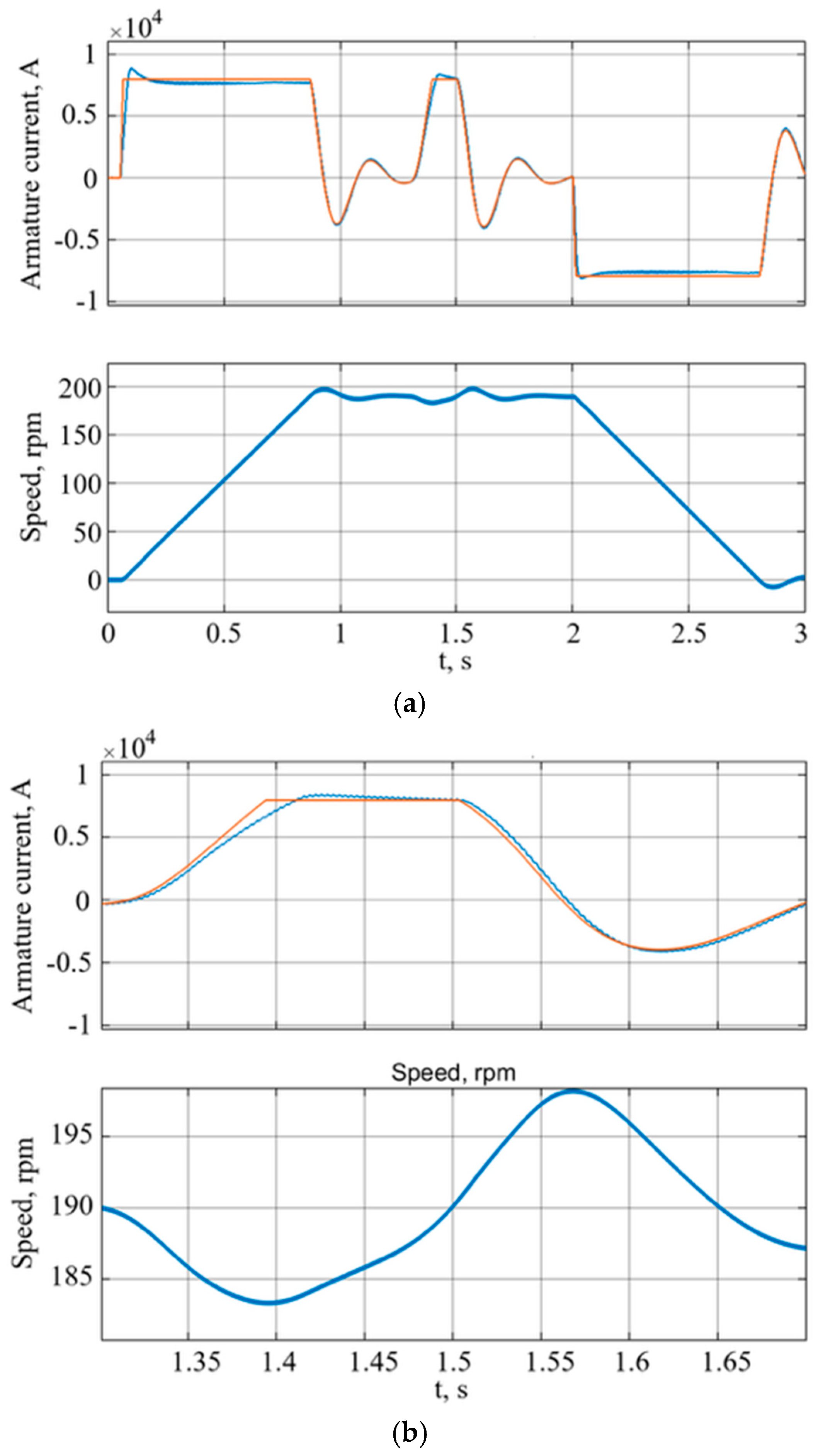
The interaction of the electric drives, configured in this way, and the elastic multi-mass mechanical part of the drum shears, led to the appearance of noticeable oscillating speeds during the cutting process (in the range of 182–199 rpm, the range of the oscillating angular speed is Δω₁ = 17 rpm). This led to the saturation of the speed controller and the operation of electric drives with the maximum permissible current during most of this process as well as the prolongation of the oscillatory process up to 1 s, which was five times longer than the duration of the cutting process itself (Figure 9).

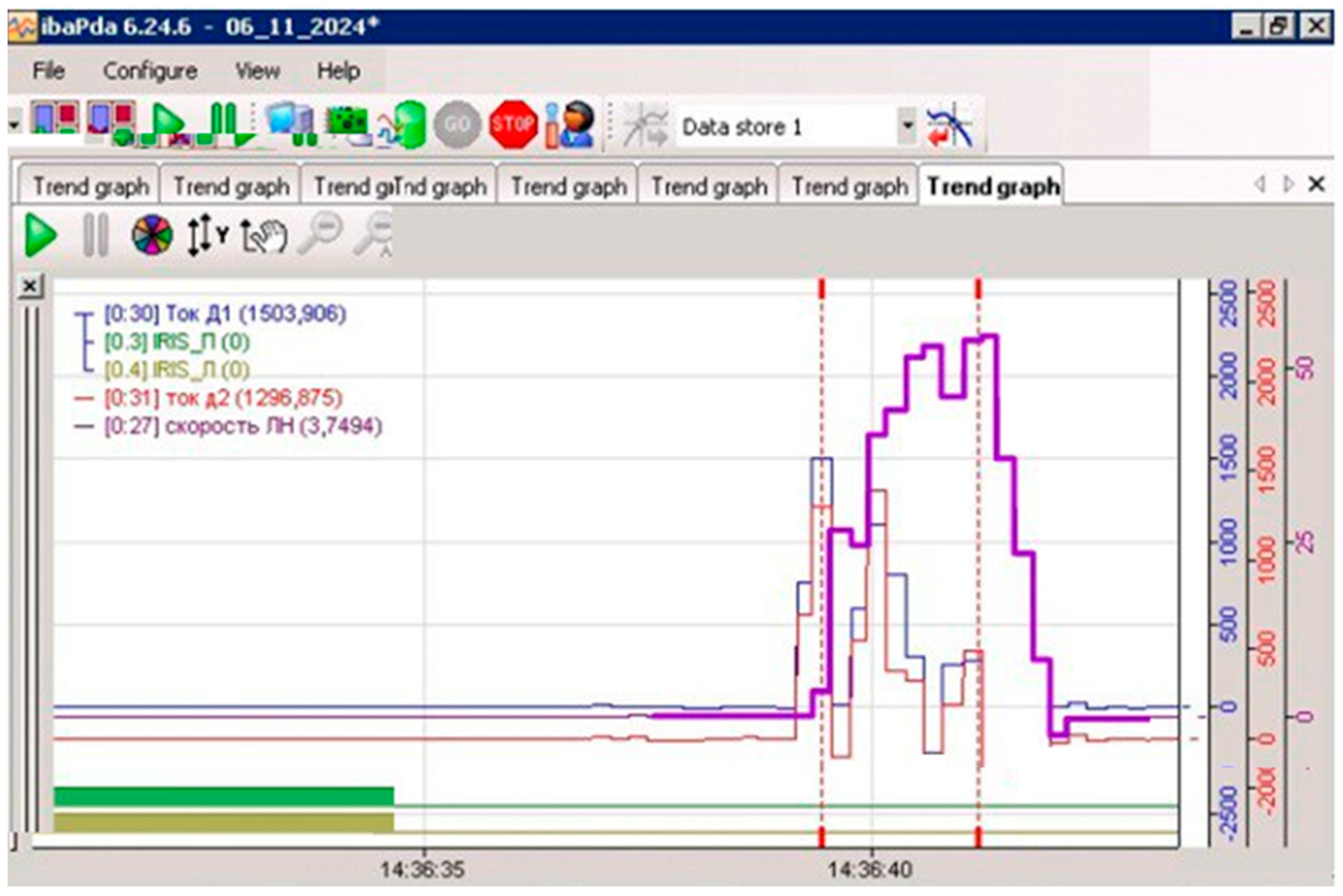
The adequacy of the developed mathematical model of the multi-mass mechanical system of drum shears was confirmed by the results of the experimental studies. Figure 10 shows the graph of the angular velocity of the drum shears, obtained by the registration devices of the rolling mill.

The red dash lines in Figure 10 show the interval of cutting the metal strip.

Taking into account that the purpose of the dispatching system of the rolling mill is to evaluate the performance of the equipment and not the exact measurement for research work, it can be stated that the graphs presented in Figure 9 and Figure 10 are quite close in absolute value and by nature of the processes, and the developed model described the electric drive of the drum shears quite accurately.

The developed electromechanical model corresponds to the fundamental principles traditionally applied in the analysis of dynamic processes in both induction and DC drives. It accurately reproduces transient electromagnetic and mechanical interactions and reflects the coupling between electrical, magnetic, and mechanical subsystems. Such an approach ensures not only high computational efficiency, but also strong physical interpretability of the results, which is essential for the design of intelligent control systems based on artificial neural networks.

Moreover, comparable research directions have been presented in [32,33,34,35,36,37], where scholars focused on the development, identification, and verification of dynamic electromagnetic and energy models of induction machines under diverse operating and power supply conditions. These studies collectively enrich the theoretical basis for modeling complex electromechanical processes, particularly in systems affected by voltage asymmetry, harmonics, and nonlinear loads.

In particular, Yevheniia, K. et al. [33] introduced and experimentally validated a dynamic electromagnetic model of an asynchronous motor operating under poor-quality electric power conditions. Their results clearly demonstrated how voltage imbalance and harmonic distortion lead to torque pulsations and nonuniform magnetic flux distribution, highlighting the importance of compensatory control algorithms for maintaining motor stability. Furthermore, Tetiana, S. et al. [34] examined the electromagnetic compatibility between rail circuits and traction supply systems, revealing fundamental mechanisms of electromagnetic interference propagation. The findings from this study can be directly extended to high-power industrial electric drives operating in electromagnetically active environments.

Also, Romashykhin, I. et al. [35] proposed an innovative energy-based parameter identification method for induction machines, enabling the accurate determination of equivalent circuit parameters and dynamic coefficients. This approach significantly increases the precision of digital simulations, providing a strong methodological foundation for adaptive control system design. In addition, Chenchevoi, V. et al. [36] developed comprehensive mathematical models describing energy conversion in induction motor–generator systems featuring parametric asymmetry. Their research expanded the analytical framework for studying autonomous electromechanical complexes, where deviations from symmetry influence both steady-state and transient performance.

Furthermore, Tryputen, N. et al. [37] demonstrated the feasibility of employing physical modeling techniques for validating and optimizing automatic control systems of thermal and electromechanical objects. Their methodological approach proved effective for verifying control system adaptability and robustness, offering valuable insights that can also be applied to the validation of ANN-based and self-learning controllers for industrial electric drives.

Taken together, these studies [32,33,34,35,36,37] provide a solid theoretical and experimental foundation that complements the modeling approach developed in this work. They confirm the scientific relevance of integrating energy-based methods, electromagnetic compatibility analysis, and intelligent control paradigms into the comprehensive modeling and optimization of electric drives.

3. Application of ANN in Controllers of the Reversible Thyristor Electric Drive of Drum Shears

Artificial neural networks (ANNs) can be used as elements of proportional-integral current and speed controllers of the electric drive of drum shears to improve the quality of transient processes. Such neural networks are usually built, instead of amplifiers, into the channels of proportional, integral, and differentiating components of controllers, while keeping the dynamic (integrator and differentiator) parts of the controller unchanged. Therefore, such ANNs are characterized by a small number of neurons in the hidden layer (5–10), since in fact they form a certain nonlinear dependence between the value of error and the output values of individual components, which most often have the form of functions close to a hyperbolic tangent or an arctangent with a variable compression ratio along the axis of abscissa.

Traditionally, the training of ANNs includes the calculation of the root mean square error on a certain test interval with the subsequent adjustment of the weight coefficients of the network by the method of backpropagation of the error using the Levenberg–Marquardt algorithm or gradient descent method.

However, for the class of considered objects, a different approach can be applied—a fast-learning algorithm. The idea is as follows. The simplest three-layer ANN of the integral and proportional components of the controller are generated as a set of matrices of a given configuration with random weight coefficients of hidden layer neurons w2i, w2p and output neurons w3i, w3p:

% Initialization
w2i = rand(1,5)*3.5;
w3i = rand(5,1)*3.5;
w2p = rand(1,5)*3.5;
w3p = rand(5,1)*3.5;

Furthermore, using the control object model and/or the set of normalized experimental data, the error $ei=Iref-Ia$ is calculated in each cycle of calculations of the output signal of the controller and the response of the model. Since the synthesized controller was designed to achieve an error equal to zero, this error was also used to adjust the weight coefficients by the method of error backpropagation. The difference in ANN training of the integral and proportional components lies in the area of operation of these components: the integral is activated only near (−0.05–+0.05) the set value $Iref$. It should be noted that when using a hyperbolic tangent as an activation function of neurons of the hidden layer and the output neuron $S\left(x\right)$, the gradient descent method is based on a simple relationship $S’\left(x\right)=1-S{\left(x\right)}^2$, which leads to a simple formula for calculating the amount of correction of the weight coefficients [38]:

$${\displaystyle \frac{\partial E}{\partial w_{jk}}}=-\left(t_k-e_k\right)\left(1+S\left({\displaystyle {\sum }_j{w}_{jk}\cdot e_j}\right)\right)\left(1-S\left({\displaystyle {\sum }_j{w}_{jk}\cdot e_j}\right)\right)\cdot e_j,$$

(19)

where ${\displaystyle \frac{\partial E}{\partial w_{jk}}}$ is the partial derivative of the total RMS error or instantaneous error value by the selected weighting coefficient $w_{jk}$; $\left(t_k-e_k\right),e_j$ are distributed proportionally to the weight coefficients of errors at the output of the output layer neurons and hidden layer neurons.

Also, unlike the traditional approach, the learning factor was set to an order less—alpha = 0.01–0.05. Below, in Algorithm 1, the core of the formalized program in matrix form, which implements the described procedures for the synthesis of an ANN current controller (the “*” operator for matrices denotes a cross product, “.*” denotes element wise multiplication).

Algorithm 1 Procedures for the learning of an ANN current controller

% Controller ei = Iref − Ia; y3i = Krti * tanh(w3i * tanh(w2i * ei)); y3ii = y3ii + y3i*dt; if abs(y3ii) > 1         y3ii = sign(y3ii); end y3p = Krtp * tanh(w3p * tanh(w2p * ei)); y3s = y3p + y3ii; if abs(y3s) > 1         y3s = sign(y3s); end % Object—model of aperiodic units (thyristor converter and armature with EMF) in finite increments U = 0.5*((U*Tu + Ku*y3s*dt)/(Tu + dt) + (U*(Tu − dt) + Ku*y3s*dt)/Tu); ed = ed + Kf/Jd*Ia*dt; Ia = 0.5*((Ia*Ta + (U − ed)*dt)/(Ta + dt) + (Ia*(Ta − dt) + (U − ed)*dt)/Ta); % Learning—Error Back Propagation with Scaled Conjugate Gradient for w2i, w3i er = Iset − Ia*kot; e2 = w3’ * er; s3 = tanh(e2); Sx3 = (1 + s3) .* (1 − s3); dE3 = −(er .* (Sx3 .* o2)’); w3 = w3 − alfa * dE3; e1 = w2’ * e2; s2 = tanh(e1); Sx2 = (1 + s2) .* (1 − s2); dE2 = −(e2 .* (Sx2 .* s2)’);         w2 = w2 − alfa * dE2;

For the proportional component, parameter adjustment is carried out similarly.

Such procedures can be implemented using single-chip controllers. In particular, we conducted a study of the training and operation procedure of the neural network type selected in this paper on an Intel Galileo Gen. 2 controller from the Arduino family. The training procedure described above in Appendix A was performed quite quickly: we deliberately increased the number of epochs to 1000 and 10,000 and obtained the average computation time for a network with 10 hidden-layer neurons as 61–62 ms/1000 epochs and 599–601 ms/10,000 epochs (i.e., approximately 0.06 ms/epoch); for 3 neurons—0.02 ms/epoch; and for 2 neurons—0.014 ms/epoch. The network operation procedure requires even fewer processor resources (no more than 10% of the training procedure). Considering that the sampling period of a motor drive controller is typically 0.001–0.01 s, the feasibility of implementing such a regulator is beyond doubt.

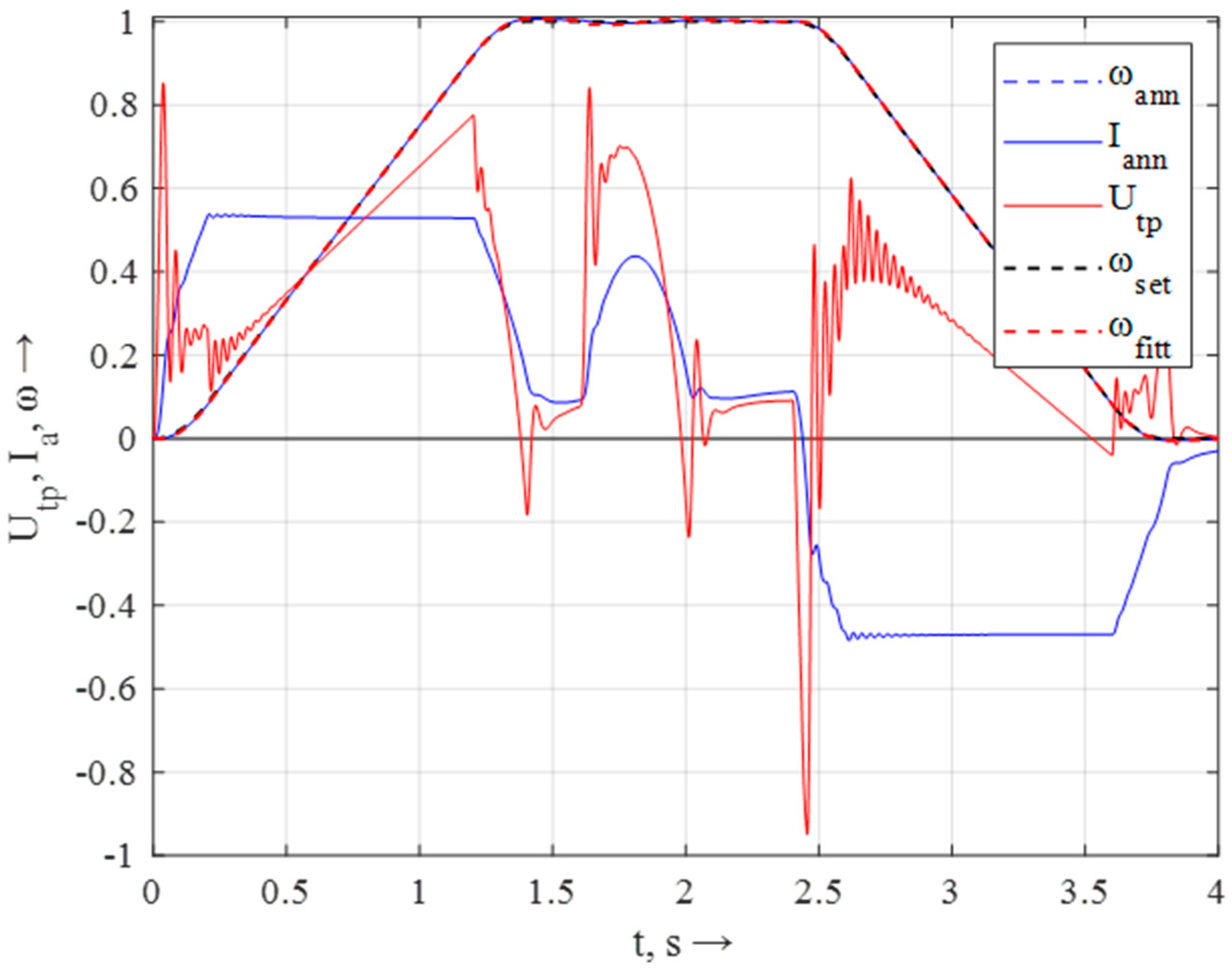
As a result of repeating such a procedure for 10–100 epochs, we obtained the settings of the current and speed controllers that provided a following response to an S-tachogram (Figure 11).

It is important to note that the training procedure can be activated at any time, and if the networks have already been trained, then an additional training procedure will be performed.

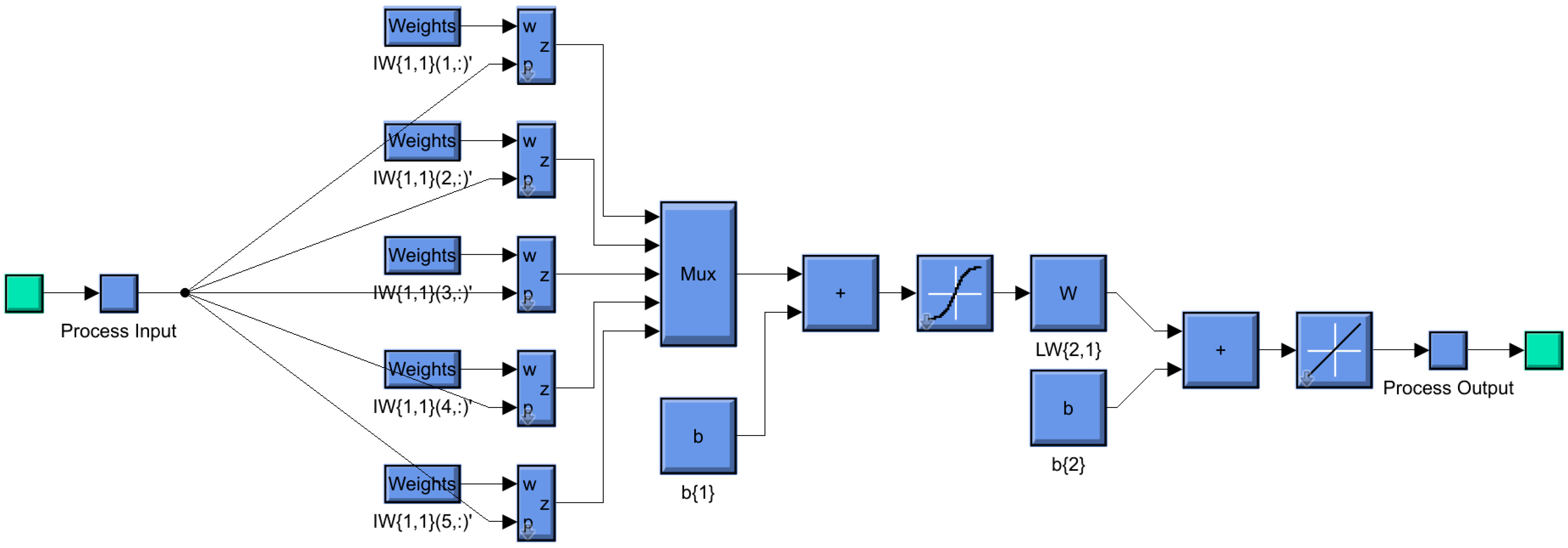
For system research, the obtained neural networks can also be transformed into typical MATLAB 2024a with Simulink subsystems, for example, using the nftool package, which provides the selection of the ANN with the fitting neural network architecture (Figure 12), describing the tabular nonlinear dependence. Next, the obtained blocks were implemented in the current and speed controllers of the thyristor converter-motor (TC-M) model (Figure 13 shows the speed controller with the elements necessary for the functioning of the regulation switch).

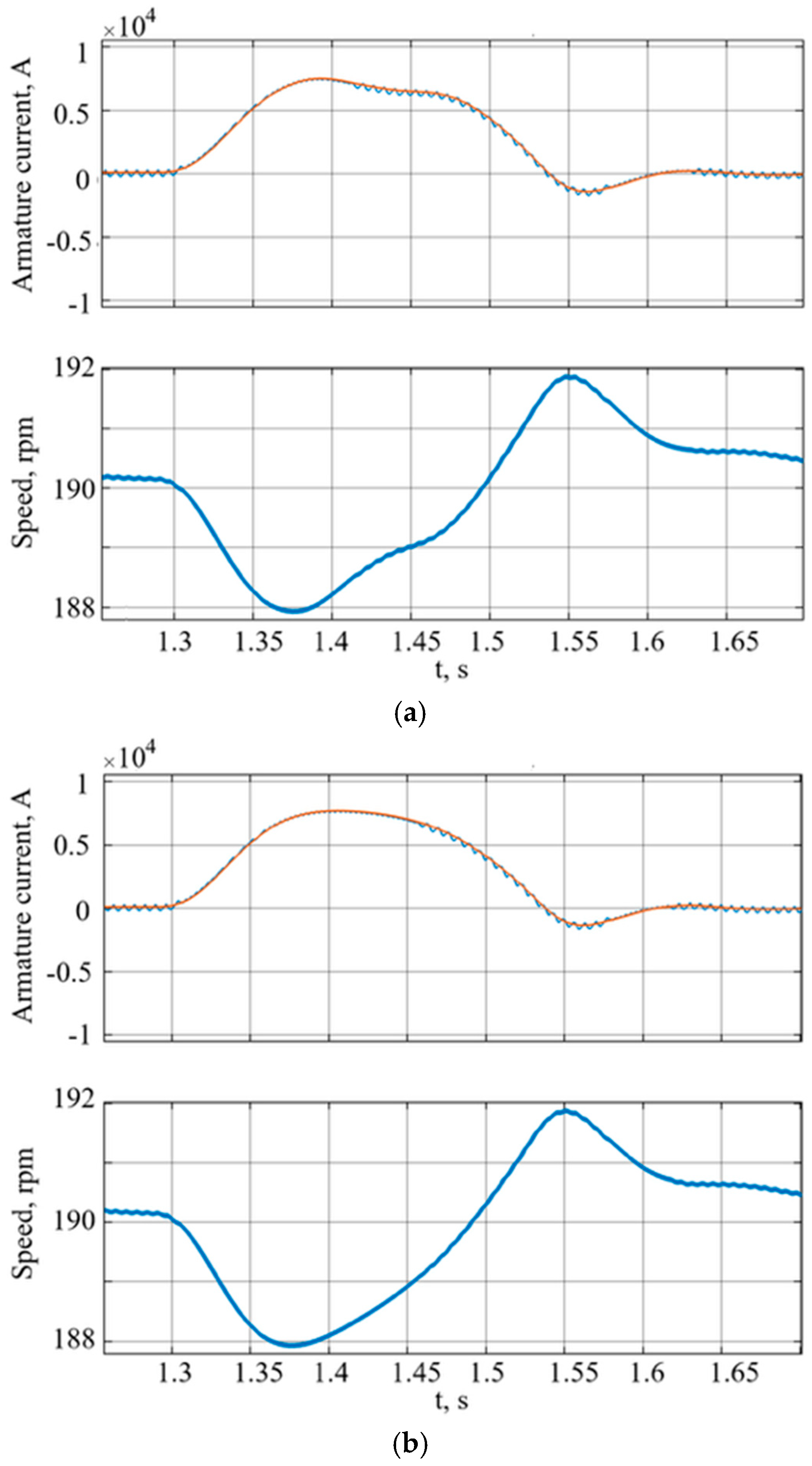
Modeling of the transient processes showed that controllers with implemented neural networks make it possible to significantly improve the quality of the transient processes of speed and current in electric drives of the drum shears’ mechanism (Figure 14).

Speed and current controllers with built-in neural networks made it possible to limit speed fluctuations during cutting in the range from 188 to 192 rpm. Other static and dynamic indicators are shown in

Table 4. Comparison of the static and dynamic indicators in basic and updated systems.

System	${\mathit{\omega }}_{\mathbf{min}},\mathit{r}\mathit{p}\mathit{m}$	${\mathit{\omega }}_{\mathbf{max}},\mathit{r}\mathit{p}\mathit{m}$	$\mathbf{\Delta }\mathit{\omega },\mathit{r}\mathit{p}\mathit{m}$	${\mathit{t}}_{\mathit{c}\mathit{u}\mathit{t}\mathit{t}\mathit{i}\mathit{n}\mathit{g}},\mathit{s}$
PI	182	199	17	0.45
ANN-PI	188	192	4	0.3

.

The range of angular velocity oscillations decreased almost four times: Δω₂ = 4 rpm compared with Δω₁ = 17 rpm in a system with classic controllers. During the cutting process, the speed controller does not enter the saturation mode, which provides the damping of oscillations in the mechanical part of the drum shears and the end of the transient process within 0.1 s after the end of the cutting process. Even when the cutting force was increased by 10%, only the shape of the current graph changed without changing the overall duration of the transient process and the amplitude of the speed oscillation.

4. Discussion

This paper presents the synthesis of a closed-loop control system for a drum shear electric drive employing a self-learning neural network PID controller. In the controller design, the influence of the six-mass mechanical subsystem with elastic couplings and viscous damping was taken into account. The study also considered the formation of impact loads that occur during the operation of the drum shear.

The actual values of the stiffness and internal viscous friction coefficients of industrial equipment may differ from the calculated ones. However, this discrepancy does not significantly affect the training process of the neural network controllers or the performance of the closed-loop control system.

The temperature and chemical composition of the steel can substantially influence the magnitude of impact loads and the absolute values of the dynamic control performance of the drum shear. Nevertheless, under varying load conditions, the neural network control system consistently demonstrated superior regulation characteristics compared to conventional PID controllers.

It is also worth noting that the proposed neural network control architecture does not alter the order of astaticism in the speed and current control loops. At the same time, it is known that fractional-order integral–differential controllers can not only increase the order of astaticism, but also simultaneously improve several other dynamic performance indices of the control system.

The study had certain limitations. The effects of measurement noise on the training and operation of neural network controllers were not addressed. However, existing signal-filtering techniques can effectively mitigate this issue. In addition, insufficient attention was paid to the hardware implementation aspects of the proposed neural network control system. Nevertheless, the hardware realization of neural networks does not impose high computational demands on microcontrollers, especially when compared with fractional-order integral–differential controllers.

Future research will focus on developing a neural-network-based control system with an increased order of astaticism, where the neural network will be used to approximate fractional-order integral controllers using HIL-experimental research.

5. Conclusions

The detailed analysis of the dynamics of the drum shears performed in the research required a sufficiently deep analysis of the work of the mechanical part of the object under study, including the features of the resistance forces formation, considering elastic connections and viscous losses in the multi-mass mechanical part. Also, most of the features of 4-quadrant thyristor converters were taken into account including the not so commonly used 3-circuit subordinate regulation system with an additional converter voltage stabilization circuit. Indeed, such an analysis was performed with a number of generally accepted assumptions, particularly those that do not consider wave processes during the deformation of parts and changes in viscosity coefficients depending on temperature and speed. A more accurate analysis of shock loads can be performed, for example, with the help of the FEM software package. However, at this stage of the research—the development of the modernization concept of the electric drive control system—the authors consider the consideration of such effects as redundant, and the accepted assumptions to be acceptable.

At the same time, it turned out during the research that the obtained results arose from supplementing the controllers with some nonlinear dependencies with characteristics close to the hyperbolic tangent or arctangent. Further research in this direction will probably make it possible to develop an even more effective method for the synthesis of such controllers.

It should also be noted that the proposed controllers do not change the order of astaticism of the speed and current circuits. At the same time, it is known that fractional-order integral–differentiating controllers can not only increase the order of astaticism, but also simultaneously improve a number of other dynamic indicators of the system [31]. Therefore, in the future, a comparative analysis of the architecture of the control system proposed in this work and one built using the apparatus of fractional-integral calculus is assumed.