Energy Symbiosis in Isolated Multi-Source Complementary Microgrids: Diesel–Photovoltaic–Energy Storage Coordinated Optimization Scheduling and System Resilience Analysis
Abstract
1. Introduction
- Limitations of existing review literature. Although recent reviews have advanced the understanding of microgrid coordination, most have primarily focused on binary structures such as PV–storage or wind–diesel systems. Comparatively fewer studies have examined the more practical three-component diesel–PV–storage systems in engineering applications. In addition, the applicability of current reviews is often limited to grid-connected systems, with relatively less attention paid to islanded scenarios that involve unique challenges such as frequency stability and black-start modes [4]. Methodologically, many studies treat optimization scheduling and resilience assessment separately, leaving the intrinsic connection between them underexplored [5].
- Challenges in three-way synergistic research. Despite significant progress, at least three unresolved issues remain. (1) A universal capacity allocation criterion is lacking. For instance, empirical studies on Hawaii’s microgrid suggest optimal diesel–PV–storage ratios between 1:1.5:0.8 and 1:2.1:2.2, yet no consistent theoretical explanation has been provided for such variations. (2) The universality of synergistic control strategies requires further validation, as comparative analyses (e.g., across 10 isolated microgrids in Africa) indicate that the same control method can lead to ±15% differences in economic outcomes [6]. (3) Current resilience assessment frameworks are often simplified, with metrics such as the System Average Interruption Duration Index (SAIDI) unable to fully capture resilience characteristics across multiple time scales [7].
- Relationship between symbiosis and resilience. Although the concept of energy symbiosis has been introduced, its quantitative link to system resilience is not yet well established. First, no unified indicator system exists for measuring the degree of symbiosis, making cross-study comparisons challenging [8]. Second, the pathways through which symbiosis enhances resilience remain insufficiently clarified. For example, simulation studies suggest that economically optimal scheduling can also reduce frequency deviations by up to 20%, yet the underlying mechanisms are rarely analyzed from a resilience perspective. Finally, the post-fault recovery capacity of synergistic scheduling remains underexplored, limiting its practical application in resilience-oriented design [9].
2. Analysis of Energy Symbiosis Mechanisms
2.1. The Symbiotic Foundation of Diesel, PV, and Energy Storage
2.2. Comparative Analysis of Collaborative Optimization Scheduling Methods
2.3. Symbiosis Quantification Index
| Indicators/Models | Core Variables | Decision Impact |
|---|---|---|
| ECI [41] | Pdiesel, PPV | Assess the complementarity of existing systems and provide guidance on capacity expansion. |
| Pareto optimization [42] | Ccost, R, E | Balancing cost, reliability, and environmental friendliness during the design phase |
3. System Resilience Analysis
3.1. Resilience Definition and Assessment Framework
3.2. Analysis of the Characteristics of Scheduling Strategies’ Impact on Resilience
3.3. Balancing the Resilience and Economic Viability of Multi-Source Complementary Microgrids
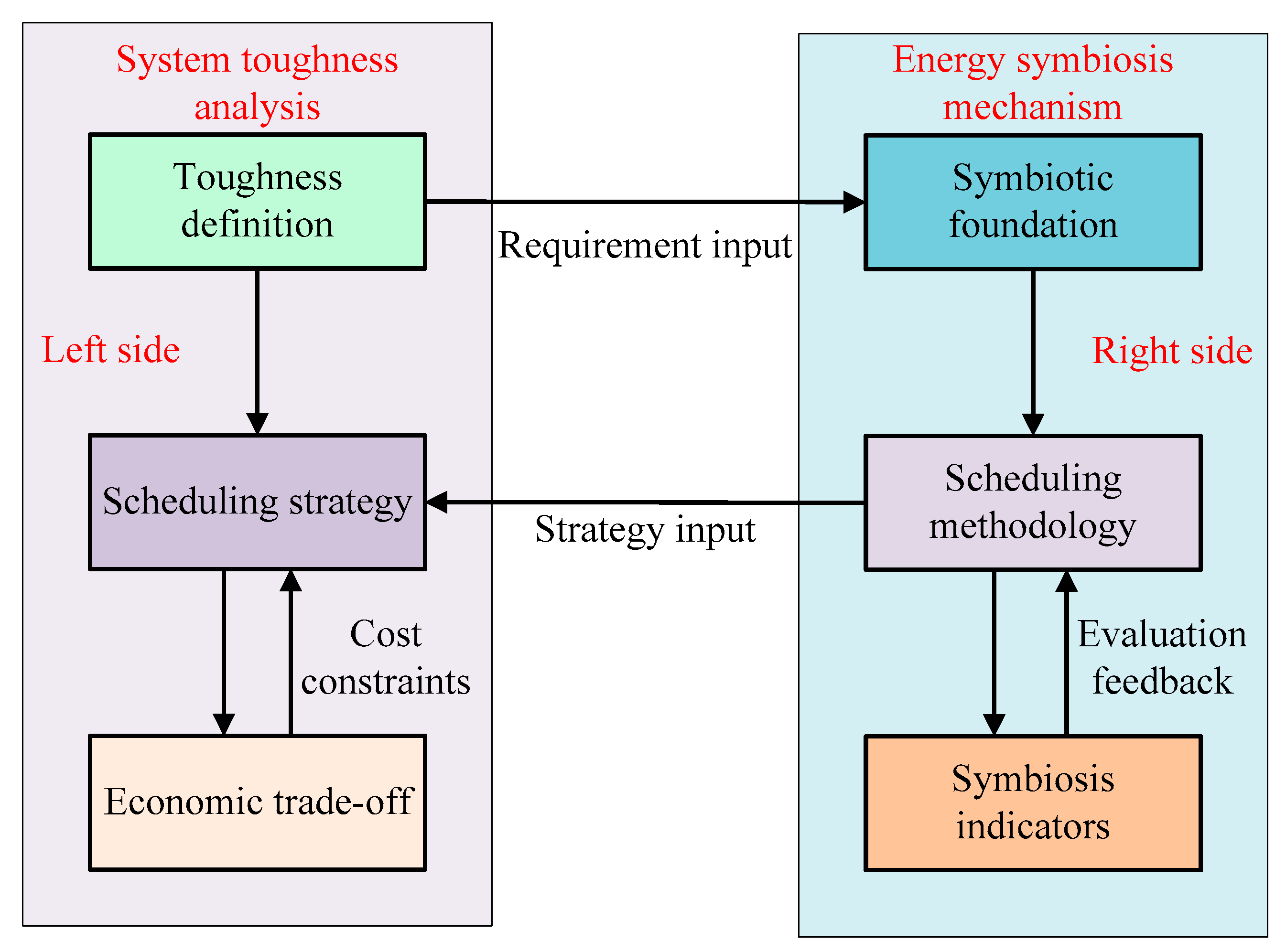
4. Synergistic Design Paradigm of Symbiosis Degree and Resilience Threshold
4.1. Design Framework for Symbiotic Microgrid Scheduling
4.2. Case Study: Island Hospital Microgrid in Southeast Asia
5. Challenges and Future Directions
5.1. Core Challenges
5.2. Breakthrough Path
5.3. Proposed Framework for Future Research
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| PV | PV |
| ESS | Energy Storage Systems |
| LCOE | Levelized Cost of Energy |
| ζ | Integrating the Dynamic Coordination Degree |
| ECI | Energy Complementarity Index |
| IEA | International Energy Agency |
| PCS | Power Conversion System |
| DOD | Depth of Discharge |
| SOC | State of Charge |
| MAF | Mutual Aid Factor |
| SE | Symbiotic Entropy |
| MPC | Model Predictive Control |
| MAS | Multi-agent Systems |
| DRL | Deep Reinforcement Learning |
| VSG | Virtual Synchronous Generator |
References
- Kreishan, M.Z.; Fotis, G.P.; Vita, V.; Ekonomou, L. Distributed Generation Islanding Effect on Distribution Networks and End User Loads Using the Load Sharing Islanding Method. Energies 2016, 9, 956. [Google Scholar] [CrossRef]
- Llanos, J.; Olivares, D.E.; Simpson-Porco, J.W.; Kazerani, M.; Saez, D. A Novel Distributed Control Strategy for Optimal Dispatch of Isolated Microgrids Considering Congestion. IEEE Trans. Smart Grid 2019, 10, 6595–6606. [Google Scholar] [CrossRef]
- Van Der Zant, H.F.; Pillet, A.-C.; Schaap, A.; Stark, S.J.; De Weijer, T.A.; Cahyaningwidi, A.A.; Lehner, B.A.E. The Energy Park of the Future: Modelling the Combination of Wave-, Wind- and Solar Energy in Offshore Multi-Source Parks. Heliyon 2024, 10, e26788. [Google Scholar] [CrossRef]
- Ghahramani, M.; Habibi, D.; Ghamari, S.; Aziz, A. Optimal Operation of an Islanded Hybrid Energy System Integrating Power and Gas Systems. IEEE Access 2024, 12, 196591–196608. [Google Scholar] [CrossRef]
- Liu, J.; Qin, C.; Yu, Y. Enhancing Distribution System Resilience with Proactive Islanding and RCS-Based Fast Fault Isolation and Service Restoration. IEEE Trans. Smart Grid 2020, 11, 2381–2395. [Google Scholar] [CrossRef]
- Wang, R.; Li, K.; Chen, P.; Tang, H. Multiple Subpopulation Salp Swarm Algorithm with Symbiosis Theory and Gaussian Distribution for Optimizing Warm-up Strategy of Fuel Cell Power System. Appl. Energy 2025, 393, 126050. [Google Scholar] [CrossRef]
- Liu, X.; Hou, K.; Jia, H.; Zhao, J.; Mili, L.; Mu, Y.; Rim, J.; Lei, Y. A Resilience Assessment Approach for Power System from Perspectives of System and Component Levels. Int. J. Electr. Power Energy Syst. 2020, 118, 105837. [Google Scholar] [CrossRef]
- Sun, C.; Joos, G.; Ali, S.Q.; Paquin, J.N.; Rangel, C.M.; Jajeh, F.A.; Novickij, I.; Bouffard, F. Design and Real-Time Implementation of a Centralized Microgrid Control System with Rule-Based Dispatch and Seamless Transition Function. IEEE Trans. Ind. Appl. 2020, 56, 3168–3177. [Google Scholar] [CrossRef]
- Oh, S.; Chae, S.; Neely, J.; Baek, J.; Cook, M. Efficient Model Predictive Control Strategies for Resource Management in an Islanded Microgrid. Energies 2017, 10, 1008. [Google Scholar] [CrossRef]
- Lu, Z.; Yu, X.; Xu, F.; Jing, L.; Cheng, X. Multi-Objective Optimal Scheduling of Islanded Microgrid Based on ISSA. J. Renew. Sustain. Energy 2025, 17, 25301. [Google Scholar] [CrossRef]
- Rauniyar, M.; Bhujel, N.; Aryal, T.; Cicilio, P.; Tamrakar, U.; Fourney, R.; Moradi Rekabdarkolaee, H.; Shirazi, M.; Hansen, T.M.; Tonkoski, R. Experimental Validation of a Diesel Genset Frequency Dynamics Model for Use in Remote Area Power Systems. IEEE Access 2024, 12, 86319–86332. [Google Scholar] [CrossRef]
- Zhong, C.; Zhao, H.; Liu, Y.; Liu, C. Model Predictive Secondary Frequency Control of Island Microgrid Based on Two-Layer Moving-Horizon Estimation Observer. Appl. Energy 2024, 372, 123721. [Google Scholar] [CrossRef]
- Ban, C.; Huang, S.; Xiong, L.; Zhou, Y.; Wang, Q.; Song, R.; Wang, L.; Li, F. Distributed Model Predictive Control Based on Bus Voltage Derivative and SoC Dynamic Model for Shipboard DC Microgrids. Electronics 2024, 13, 2880. [Google Scholar] [CrossRef]
- Vuić, L.; Hivziefendić, J.; Sarić, M.; Osmić, J. Voltage and Frequency Control of Solar–Battery–Diesel Based Islanded Microgrid. J. Electr. Eng. 2023, 74, 442–453. [Google Scholar] [CrossRef]
- Zhang, J.; Li, K.-J.; Wang, M.; Lee, W.-J.; Gao, H.; Zhang, C.; Li, K. A Bi-Level Program for the Planning of an Islanded Microgrid Including CAES. IEEE Trans. Ind. Appl. 2016, 52, 2768–2777. [Google Scholar] [CrossRef]
- Chen, W.; Chen, Y. Two-Step Measurement of Water–Energy–Food Symbiotic Coordination and Identification of Key Influencing Factors in the Yangtze River Basin. Entropy 2021, 23, 798. [Google Scholar] [CrossRef]
- Rodrigues, Y.; Monteiro, M.; Abdelaziz, M.; Wang, L.; De Souza, A.Z.; Ribeiro, P. Improving the Autonomy of Islanded Microgrids through Frequency Regulation. Int. J. Electr. Power Energy Syst. 2020, 115, 105499. [Google Scholar] [CrossRef]
- Hong, Y.-Y.; Lai, Y.-Z.; Chang, Y.-R.; Lee, Y.-D.; Lin, C.-H. Optimizing Energy Storage Capacity in Islanded Microgrids Using Immunity-Based Multiobjective Planning. Energies 2018, 11, 585. [Google Scholar] [CrossRef]
- Zhang, T.; Yue, D.; Yu, L.; Dou, C.; Xie, X. Joint Energy and Workload Scheduling for Fog-Assisted Multimicrogrid Systems: A Deep Reinforcement Learning Approach. IEEE Syst. J. 2023, 17, 164–175. [Google Scholar] [CrossRef]
- Xie, P.; Jia, Y.; Lyu, C.; Wang, H.; Shi, M.; Chen, H. Optimal Sizing of Renewables and Battery Systems for Hybrid AC/DC Microgrids Based on Variability Management. Appl. Energy 2022, 321, 119250. [Google Scholar] [CrossRef]
- Goldfarb, D.; Todd, M.J. Chapter II linear programming. Handb. Oper. Res. Manag. Sci. 1989, 1, 73–170. [Google Scholar] [CrossRef]
- McCarl, B.A.; Moskowitz, H.; Furtan, H. Quadratic programming applications. Omega 1977, 5, 43–55. [Google Scholar] [CrossRef]
- Liu, Z.; Reynolds, A. Robust multiobjective nonlinear constrained optimization with ensemble stochastic gradient sequential quadratic programming-filter algorithm. SPE J. 2021, 26, 1964–1979. [Google Scholar] [CrossRef]
- Banihabib, R.; Fadnes, F.S.; Assadi, M. Techno-Economic Optimization of Microgrid Operation with Integration of Renewable Energy, Hydrogen Storage, and Micro Gas Turbine. Renew. Energy 2024, 237, 121708. [Google Scholar] [CrossRef]
- Abualigah, L.; Elaziz, M.A.; Khasawneh, A.M.; Alshinwan, M.; Ibrahim, R.A. Meta-heuristic optimization algorithms for solving real-world mechanical engineering design problems: A comprehensive survey, applications, comparative analysis, and results. Neural Comput. Appl. 2022, 34, 4081–4110. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- An, S.; Chen, M.; Wei, Z.; Qiu, F. Optimal Configuration of Energy Storage Microgrid Based on Chaos Optimization Multi-Objective Genetic Algorithm. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 5118–5124. [Google Scholar]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar] [CrossRef]
- Bertsimas, D.; Tsitsiklis, J. Simulated annealing. Stat. Sci. 1993, 8, 10–15. [Google Scholar] [CrossRef]
- Wang, Z.; Rangaiah, G.P. Application and analysis of methods for selecting an optimal solution from the Pareto-optimal front obtained by multiobjective optimization. Ind. Eng. Chem. Res. 2017, 56, 560–574. [Google Scholar] [CrossRef]
- Fadoul, F.F.; Çağlar, R. Integrating Bayesian Inference and Neural ODEs for Microgrids Dynamics Parameters Estimation. Sustain. Energy Grids Netw. 2024, 39, 101498. [Google Scholar] [CrossRef]
- Qin, B.; Wang, M.; Zhang, G.; Zhang, Z. Impact of renewable energy penetration rate on power system frequency stability. Energy Rep. 2022, 8, 997–1003. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, D.Z. An effective hybrid optimization strategy for job-shop scheduling problems. Comput. Oper. Res. 2001, 28, 585–596. [Google Scholar] [CrossRef]
- Guo, L.; Guo, Z.; Li, X.; Wang, C.; Hong, C.; Zhang, Y. Consensus-Based Distributed Coordinated Control for Islanded DC Microgrids. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Zhu, Y.; Xu, Z.; Zhao, J.; Han, K.; Qian, J.; Li, W. Development and application of an integrated MPC technology. IFAC Proc. Vol. 2008, 41, 6962–6967. [Google Scholar] [CrossRef]
- Yan, J.; Li, L.; Zhao, F.; Zhang, F.; Zhao, Q. A multi-level optimization approach for energy-efficient flexible flow shop scheduling. J. Clean. Prod. 2016, 137, 1543–1552. [Google Scholar] [CrossRef]
- Ma, C.; Sun, J.; Huang, J.; Wang, K. Transient Stability Enhancement Strategy for Islanded Microgrids Based on Energy Storage–Virtual Synchronous Machine Control. Energies 2023, 16, 6390. [Google Scholar] [CrossRef]
- Faraji, M.; Saeed Mahdavi, M.; Nurmanova, V.; Gharehpetian, G.B.; Bagheri, M. Coordinated Control of Flywheel and Battery Energy Storage Systems for Frequency Regulation in Diesel Generator-Based Microgrid. IEEE Access 2025, 13, 65980–65996. [Google Scholar] [CrossRef]
- Sachs, J.; Sawodny, O. A Two-Stage Model Predictive Control Strategy for Economic Diesel-PV-Battery Island Microgrid Operation in Rural Areas. IEEE Trans. Sustain. Energy 2016, 7, 903–913. [Google Scholar] [CrossRef]
- Zhao, B.; Qiu, H.; Qin, R.; Zhang, X.; Gu, W.; Wang, C. Robust Optimal Dispatch of AC/DC Hybrid Microgrids Considering Generation and Load Uncertainties and Energy Storage Loss. IEEE Trans. Power Syst. 2018, 33, 5945–5957. [Google Scholar] [CrossRef]
- Kang, W.; Guan, Y.; Danang Wijaya, F.; Kondorura Bawan, E.; Priyo Perdana, A.; Vasquez, J.C.; Guerrero, J.M. Community Microgrid Planning in Lombok Island: An Indonesian Case Study. Front. Energy Res. 2023, 11, 1209875. [Google Scholar] [CrossRef]
- Bai, B.; Wang, K.; Bu, L.; Liu, S.; Cheng, M.; Yue, C. Feasibility Evaluation for a Multi-Energy Microgrid Case Study in China. In Proceedings of the 2019 IEEE PES Asia-pacific Power and Energy Engineering Conference (APPEEC), Macau, China, 1–4 December 2019; pp. 1–5. [Google Scholar]
- Xiao, J.; Wang, P.; Setyawan, L. Hierarchical Control of Hybrid Energy Storage System in DC Microgrids. IEEE Trans. Ind. Electron. 2015, 62, 4915–4924. [Google Scholar] [CrossRef]
- Anzalchi, A.; Pour, M.M.; Sarwat, A. A Combinatorial Approach for Addressing Intermittency and Providing Inertial Response in a Grid-Connected PV System. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Arora, A.; Bhadu, M.; Kumar, A. Simultaneous Damping and Frequency Control in AC Microgrid Using Coordinated Control Considering Time Delay and Noise. Trans. Inst. Meas. Control 2024, 46, 2436–2463. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Lu, Z. Multi-Objective Load Dispatch for Microgrid with Electric Vehicles Using Modified Gravitational Search and Particle Swarm Optimization Algorithm. Appl. Energy 2022, 306, 118018. [Google Scholar] [CrossRef]
- Phan, Q.A.; Scully, T.; Breen, M.; Murphy, M.D. Facilitating High Levels of Wind Penetration in a Smart Grid through the Optimal Utilization of Battery Storage in Microgrids: An Analysis of the Trade-Offs between Economic Performance and Wind Generation Facilitation. Energy Convers. Manag. 2020, 206, 112354. [Google Scholar] [CrossRef]
- Lin, Q.; Uno, H.; Ogawa, K.; Kanekiyo, Y.; Shijo, T.; Arai, J.; Matsuda, T.; Yamashita, D.; Otani, K. Field Demonstration of Parallel Operation of Virtual Synchronous Controlled Grid-Forming Inverters and a Diesel Synchronous Generator in a Microgrid. IEEE Access 2022, 10, 39095–39107. [Google Scholar] [CrossRef]
- Zai, W.; Wang, J.; Li, G. A Drone Scheduling Method for Emergency Power Material Transportation Based on Deep Reinforcement Learning Optimized PSO Algorithm. Sustainability 2023, 15, 13127. [Google Scholar] [CrossRef]
- Arsalis, A.; Georghiou, G.E.; Papanastasiou, P. Recent Research Progress in Hybrid PV–Regenerative Hydrogen Fuel Cell Microgrid Systems. Energies 2022, 15, 3512. [Google Scholar] [CrossRef]
- Sanjalawe, Y.; Al-E’mari, S.; Fraihat, S.; Makhadmeh, S. AI-driven job scheduling in cloud computing: A comprehensive review. Artif. Intell. Rev. 2025, 58, 197. [Google Scholar] [CrossRef]
- Kurkure, Y.; Sharma, S.; Wang, X.; Papka, M.E.; Lan, Z. CQSim+: Symbiotic Simulation for Multi-Resource Scheduling in High-Performance Computing. In Proceedings of the 39th ACM SIGSIM Conference on Principles of Advanced Discrete Simulation, Santa Fe, NM, USA, 23–26 June 2025; pp. 154–164. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, R.; Zhou, X.; Tan, R.; Wen, Y.; Yan, Y.; Wang, Z. Adaptive capacity provisioning for carbon-aware data centers: A digital twin-based approach. IEEE Trans. Sustain. Comput. 2025, 10, 730–743. [Google Scholar] [CrossRef]
- Yan, J.; Liu, S.; Yan, Y.; Liu, Y.; Han, S.; Zhang, H. How to choose mobile energy storage or fixed energy storage in high proportion renewable energy scenarios: Evidence in China. Appl. Energy 2024, 376, 124274. [Google Scholar] [CrossRef]
- Zhao, X.G.; Chen, H.; Hu, S.; Zhou, Y. The impact of carbon quota allocation and low-carbon technology innovation on carbon market effectiveness: A system dynamics analysis. Environ. Sci. Pollut. Res. 2023, 30, 96424–96440. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, J.; Yang, J.; Zhao, J. Deep multi-fidelity bayesian data fusion for probabilistic distribution system voltage estimation with high penetration of pvs. IEEE Trans. Power Syst. 2023, 39, 3661–3672. [Google Scholar] [CrossRef]
- Hwang, S.; Tongsopit, S.; Kittner, N. Transitioning from diesel backup generators to PV-plus-storage microgrids in California public buildings. Sustain. Prod. Consum. 2023, 38, 252–265. [Google Scholar] [CrossRef]
- Levin, T.; Bistline, J.; Sioshansi, R.; Cole, W.J.; Kwon, J.; Burger, S.P. Energy storage solutions to decarbonize electricity through enhanced capacity expansion modelling. Nat. Energy 2023, 8, 1199–1208. [Google Scholar] [CrossRef]
- Yang, B.; Liu, Z.; Yang, S.; Cui, C.; Deng, S. Research on the optimal allocation method of PV micro-grid energy storage capacity based on empirical modal decomposition. J. Phys. Conf. Ser. 2023, 2503, 012013. [Google Scholar] [CrossRef]
- Banihashemi, S.A.; Khalilzadeh, M. Time-cost-quality-environmental impact trade-off resource-constrained project scheduling problem with DEA approach. Eng. Constr. Archit. Manag. 2021, 28, 1979–2004. [Google Scholar] [CrossRef]
- Gorman, W. The quest to quantify the value of lost load: A critical review of the economics of power outages. Electr. J. 2022, 35, 107187. [Google Scholar] [CrossRef]
- Hua, H.; Du, C.; Chen, X.; Kong, H. Optimal dispatch of multiple interconnected-integrated energy systems considering multi-energy interaction and aggregated demand response for multiple stakeholders. Appl. Energy 2024, 376, 124256. [Google Scholar] [CrossRef]
- Zhang, F.; Maroulis, S. Experience is not enough: A dynamic explanation of the limited adaptation to extreme weather events in public organizations. Glob. Environ. Change 2021, 70, 102358. [Google Scholar] [CrossRef]
- Shi, J.; Hu, J.; Yue, Y.; Xue, X.; Liang, W.; Li, Z. Outage probability for OTFS based downlink LEO satellite communication. IEEE Trans. Veh. Technol. 2022, 71, 3355–3360. [Google Scholar] [CrossRef]
- Wang, Y.; Rousis, A.O.; Strbac, G. A three-level planning model for optimal sizing of networked microgrids considering a trade-off between resilience and cost. IEEE Trans. Power Syst. 2021, 36, 5657–5669. [Google Scholar] [CrossRef]
- Himmiche, S.; Marangé, P.; Aubry, A.; Pétin, J.-F. Robustness Evaluation Process for Scheduling under Uncertainties. Processes 2023, 11, 371. [Google Scholar] [CrossRef]
- Cañizares, J.C.; Copeland, S.M.; Doorn, N. Making Sense of Resilience. Sustainability 2021, 13, 8538. [Google Scholar] [CrossRef]
- Setyadi, A.; Pawirosumarto, S.; Damaris, A. Rethinking Sustainable Operations: A Multi-Level Integration of Circularity, Localization, and Digital Resilience in Manufacturing Systems. Sustainability 2025, 17, 6929. [Google Scholar] [CrossRef]
- Sha, Y.; Ma, Q.; Xu, C.; Tan, X.; Yan, J.; Zhang, Y. Research on the balance optimization of investment demand and investment capability of power grid enterprises. Energy Rep. 2023, 9, 943–950. [Google Scholar] [CrossRef]
- Ham, D.H. Safety-II and resilience engineering in a nutshell: An introductory guide to their concepts and methods. Saf. Health Work 2021, 12, 10–19. [Google Scholar] [CrossRef]
- Stanković, A.M.; Tomsovic, K.L.; De Caro, F.; Braun, M.; Chow, J.H. Methods for analysis and quantification of power system resilience. IEEE Trans. Power Syst. 2022, 38, 4774–4787. [Google Scholar] [CrossRef]
- Alexopoulos, K.; Anagiannis, I.; Nikolakis, N.; Chryssolouris, G. A quantitative approach to resilience in manufacturing systems. Int. J. Prod. Res. 2022, 60, 7178–7193. [Google Scholar] [CrossRef]
- Wei, W.; Yang, R.; Gu, H.; Zhao, W.; Chen, C.; Wan, S. Multi-objective optimization for resource allocation in vehicular cloud computing networks. IEEE Trans. Intell. Transp. Syst. 2021, 23, 25536–25545. [Google Scholar] [CrossRef]
- Bragolusi, P.; D’Alpaos, C. The valuation of buildings energy retrofitting: A multiple-criteria approach to reconcile cost-benefit trade-offs and energy savings. Appl. Energy 2022, 310, 118431. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, Z.; Li, X. Neural dynamic fault-tolerant scheme for collaborative motion planning of dual-redundant robot manipulators. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 11189–11201. [Google Scholar] [CrossRef]
- Malik, A.; Kushwah, R. Energy-efficient scheduling in IoT using Wi-Fi and ZigBee cross-technology. J. Supercomput. 2023, 79, 10977–11006. [Google Scholar] [CrossRef]
- Lei, X.; Cheng, L.; Ye, L.; Zhang, L.; Kim, J.S. Integration of the generalized complementary relationship into a lumped hydrological model for improving water balance partitioning: A case study with the Xinanjiang model. J. Hydrol. 2023, 621, 129569. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, Z.; Ye, H.; Ren, B.; Xu, Y.; Liu, Y. Frequency response modeling and equivalent inertial estimation of induction machine. Energy Rep. 2022, 8, 554–564. [Google Scholar] [CrossRef]
- Carreño, E.A.; Alberto, A.V.P.; de Souza, C.A.M.; de Mello, H.L.; Henriques-Pons, A.; Anastacio Alves, L. Considerations and Technical Pitfalls in the Employment of the MTT Assay to Evaluate Photosensitizers for Photodynamic Therapy. Appl. Sci. 2021, 11, 2603. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, J.; Xu, H.; Yang, M.; Liu, W. Improving full-chain process synergy of multi-energy complementary distributed energy system in cascade storage and initiative management strategies. Energy Convers. Manag. 2024, 322, 119120. [Google Scholar] [CrossRef]
- Kamnarn, U.; Yodwong, J.; Piyawongwisal, P.; Wutthiwai, P. Design and simulation of DC distributed power supply with power balance control technique. Int. J. Power Electron. Drive Syst. (IJPEDS) 2022, 13, 460–469. [Google Scholar] [CrossRef]
- AlMahri, S.; Santiago, R.; Lee, D.W.; Ramos, H.; Alabdouli, H. Evaluation of the dynamic response of triply periodic minimal surfaces subjected to high strain-rate compression. Addit. Manuf. 2021, 46, 102220. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, J.; Zhang, Q.; Zhang, Z.; Winstead, V.; Yu, D. A composite power decoupling method for a PV inverter with optimized energy buffer. IEEE Trans. Ind. Appl. 2021, 57, 3877–3887. [Google Scholar] [CrossRef]
- Parri, J.; Patara, F.; Sampietro, S.; Vicario, E. A framework for model-driven engineering of resilient software-controlled systems. Computing 2021, 103, 589–612. [Google Scholar] [CrossRef]
- Krumhansl, K.A.; Dowd, M.; Wong, M.C. Multiple metrics of temperature, light, and water motion drive gradients in eelgrass productivity and resilience. Front. Mar. Sci. 2021, 8, 597707. [Google Scholar] [CrossRef]
- Zhang, P.; Qian, Y.; Qian, Q. Multi-objective optimization for materials design with improved NSGA-II. Mater. Today Commun. 2021, 28, 102709. [Google Scholar] [CrossRef]
- Morstyn, T.; Farrell, N.; Darby, S.J.; McCulloch, M.D. Using peer-to-peer energy-trading platforms to incentivize prosumers to form federated power plants. Nat. Energy 2018, 3, 94–101. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2010, 58, 158–172. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A. Virtual synchronous machines—Classification of implementations and analysis of equivalence to droop controllers for microgrids. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Meegahapola, L.; Sguarezi, A.; Bryant, J.S.; Gu, M.; Conde Duque, E.R.; Cunha, R.B.A. Power System Stability with Power-Electronic Converter Interfaced Renewable Power Generation: Present Issues and Future Trends. Energies 2020, 13, 3441. [Google Scholar] [CrossRef]
- Dreidy, M.; Mokhlis, H.; Mekhilef, S. Inertia response and frequency control techniques for renewable energy sources: A review. Renew. Sustain. Energy Rev. 2017, 69, 144–155. [Google Scholar] [CrossRef]
- Huang, X.; Lu, D.; Ricciuto, D.M.; Hanson, P.J. A model-independent data assimilation (MIDA) module and its applications in ecology. Geosci. Model Dev. Discuss. 2021, 14, 5217–5238. [Google Scholar] [CrossRef]
- Nie, X.; Min, C.; Pan, Y.; Li, Z.; Królczyk, G. An Improved Deep Neural Network Model of Intelligent Vehicle Dynamics via Linear Decreasing Weight Particle Swarm and Invasive Weed Optimization Algorithms. Sensors 2022, 22, 4676. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, B.; Hou, M.; Duan, G.R. Practical prescribed-time stabilization of a class of nonlinear systems by event-triggered and self-triggered control. IEEE Trans. Autom. Control 2023, 69, 3426–3433. [Google Scholar] [CrossRef]
- Quintero-Durán, M.J.; Candelo-Becerra, J.E.; González-Niño, M.E.; Hernández-Moreno, S.A.; Váz, R.F. Synchronverter Control Strategy: A Review of Different Improvements and Applications. Energies 2025, 18, 3574. [Google Scholar] [CrossRef]
- Alsiraji, H.A.; Guerrero, J.M. A new hybrid virtual synchronous machine control structure combined with voltage source converters in islanded ac microgrids. Electr. Power Syst. Res. 2021, 193, 106976. [Google Scholar] [CrossRef]
- Omar, N.; Monem, M.A.; Firouz, Y.; Salminen, J. Lithium iron phosphate based battery–Assessment of the aging parameters and development of cycle life model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar] [CrossRef]
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.P.; Hansen, T.M.; Tonkoski, R. Virtual Inertia: Current Trends and Future Directions. Appl. Sci. 2017, 7, 654. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Constrained model predictive control. In Model Predictive Control; Springer: London, UK, 2007; pp. 177–216. [Google Scholar]
- Scattolini, R. Architectures for distributed and hierarchical model predictive control–a review. J. Process Control 2009, 19, 723–731. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Nawaz, S.; Lezaun, J.; Valenzuela, J.M.; Renforth, P. Broaden research on ocean alkalinity enhancement to better characterize social impacts. Environ. Sci. Technol. 2023, 57, 8863–8869. [Google Scholar] [CrossRef]
- Gabrel, V.; Murat, C.; Thiele, A. Recent advances in robust optimization: An overview. Eur. J. Oper. Res. 2014, 235, 471–483. [Google Scholar] [CrossRef]
- Gorissen, B.L.; Yanıkoğlu, İ.; Den Hertog, D. A practical guide to robust optimization. Omega 2015, 53, 124–137. [Google Scholar] [CrossRef]
- Alavi, H.S.; Churchill, E.F.; Wiberg, M.; Lalanne, D.; Dalsgaard, P. Introduction to human-building interaction (hbi) interfacing hci with architecture and urban design. ACM Trans. Comput.-Hum. Interact. (TOCHI) 2019, 26, 1–10. [Google Scholar] [CrossRef]
- Carrión, M.; Arroyo, J.M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Lasseter, R.H. Smart distribution: Coupled microgrids. Proc. IEEE 2011, 99, 1074–1082. [Google Scholar] [CrossRef]
- Kochańczyk, M.; Lipniacki, T. Pareto-based evaluation of national responses to COVID-19 pandemic shows that saving lives and protecting economy are non-trade-off objectives. Sci. Rep. 2021, 11, 2425. [Google Scholar] [CrossRef]
- Wang, G.; Tan, Z.; Tan, Q.; Yang, S.; Lin, H.; Ji, X.; Gejirifu, D.; Song, X. Multi-Objective Robust Scheduling Optimization Model of Wind, Photovoltaic Power, and BESS Based on the Pareto Principle. Sustainability 2019, 11, 305. [Google Scholar] [CrossRef]
- Joshal, K.S.; Gupta, N. Microgrids with Model Predictive Control: A Critical Review. Energies 2023, 16, 4851. [Google Scholar] [CrossRef]
- Huang, X.; Yang, F.; Zheng, J.; Feng, C.; Zhang, L. Personalized human resource management via HR analytics and artificial intelligence: Theory and implications. Asia Pac. Manag. Rev. 2023, 28, 598–610. [Google Scholar] [CrossRef]
- Nawaz, N.; Arunachalam, H.; Pathi, B.K.; Gajenderan, V. The adoption of artificial intelligence in human resources management practices. Int. J. Inf. Manag. Data Insights 2024, 4, 100208. [Google Scholar] [CrossRef]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Bui-Ngoc, T.; Nguyen, T.; Nguyen-Quang, M.T.; Shiau, J. Predicting load–displacement of driven PHC pipe piles using stacking ensemble with Pareto optimization. Eng. Struct. 2024, 316, 118574. [Google Scholar] [CrossRef]
- Gupta, S.; Basumatary, K.; Shukla, A.; Gonzalez-Longatt, F. Real-Time Co-Simulation Platform for Grid-Forming BSS Using RTDS and FPGA. In Proceedings of the 2024 IEEE International Conference on Power System Technology (PowerCon), Kathmandu, Nepal, 4–6 November 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Demir, G.; Chatterjee, P.; Pamucar, D. Sensitivity analysis in multi-criteria decision making: A state-of-the-art research perspective using bibliometric analysis. Expert Syst. Appl. 2024, 237, 121660. [Google Scholar] [CrossRef]
- Gu, X.; Liang, B. Design and implementation of brake control algorithm HIL test platform for civil aircraft. J. Phys. Conf. Ser. 2025, 3118, 012019. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, P.; Liu, X.; Zhang, X.; Hong, L.; Cao, Z. Risk assessment of highway structures in natural disaster for the property insurance. Nat. Hazards 2020, 104, 2663–2685. [Google Scholar] [CrossRef]
- Laimon, M. Renewable energy curtailment: A problem or an opportunity? Results Eng. 2025, 26, 104925. [Google Scholar] [CrossRef]
- Maletič, D.; Maletič, M.; Al-Najjar, B.; Gomišček, B. An Analysis of Physical Asset Management Core Practices and Their Influence on Operational Performance. Sustainability 2020, 12, 9097. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, L.; Zhu, W.; Bao, X.; Liu, C. Robust model predictive control for optimal energy management of island microgrids with uncertainties. Energy 2018, 164, 1229–1241. [Google Scholar] [CrossRef]
- Rajamand, S. Load frequency control and dynamic response improvement using energy storage and modeling of uncertainty in renewable distributed generators. J. Energy Storage 2021, 37, 102467. [Google Scholar] [CrossRef]
- Gautam, M. Deep Reinforcement Learning for Resilient Power and Energy Systems: Progress, Prospects, and Future Avenues. Electricity 2023, 4, 336–380. [Google Scholar] [CrossRef]
- Manshadi, S.D.; Khodayar, M.E. Resilient operation of multiple energy carrier microgrids. IEEE Trans. Smart Grid 2015, 6, 2283–2292. [Google Scholar] [CrossRef]
- Youssef, A.-R.; Mallah, M.; Ali, A.; Shaaban, M.F.; Mohamed, E.E.M. Enhancement of Microgrid Frequency Stability Based on the Combined Power-to-Hydrogen-to-Power Technology under High Penetration Renewable Units. Energies 2023, 16, 3377. [Google Scholar] [CrossRef]

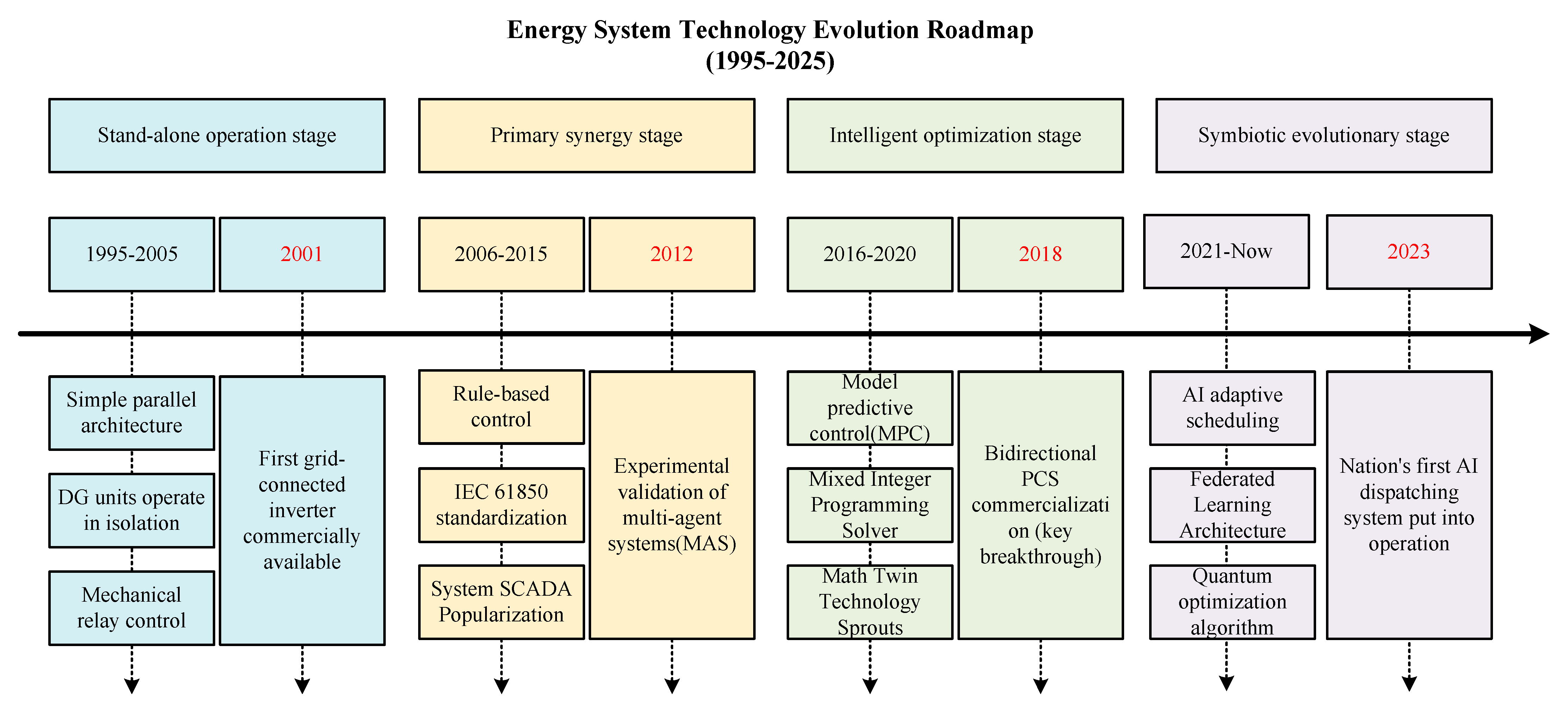
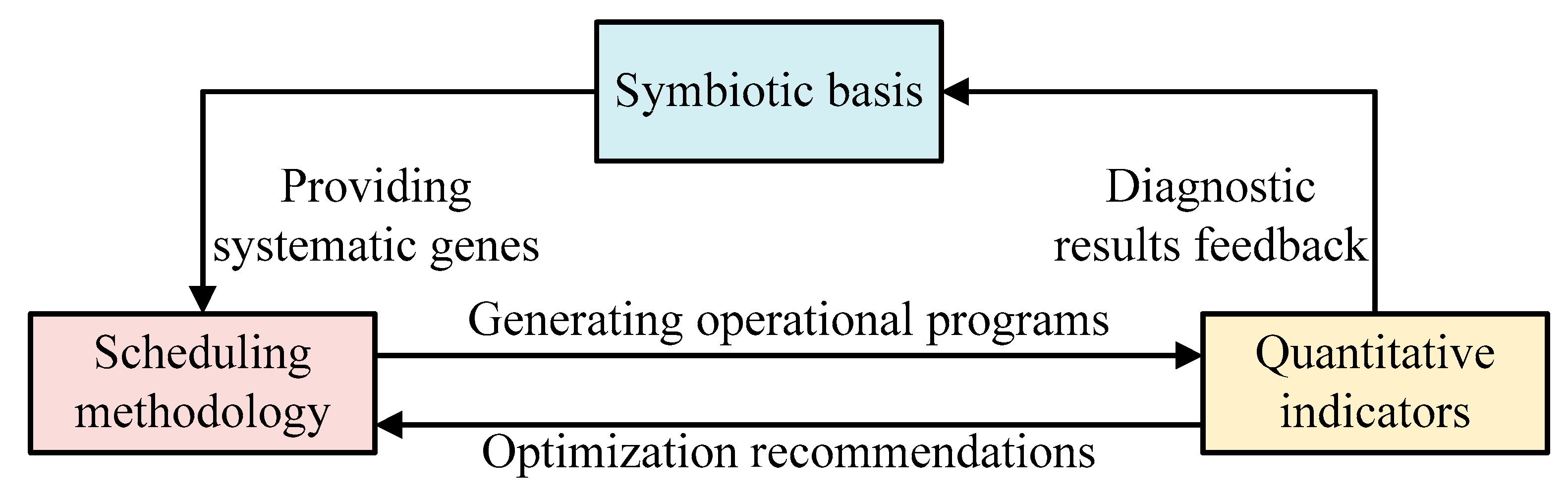
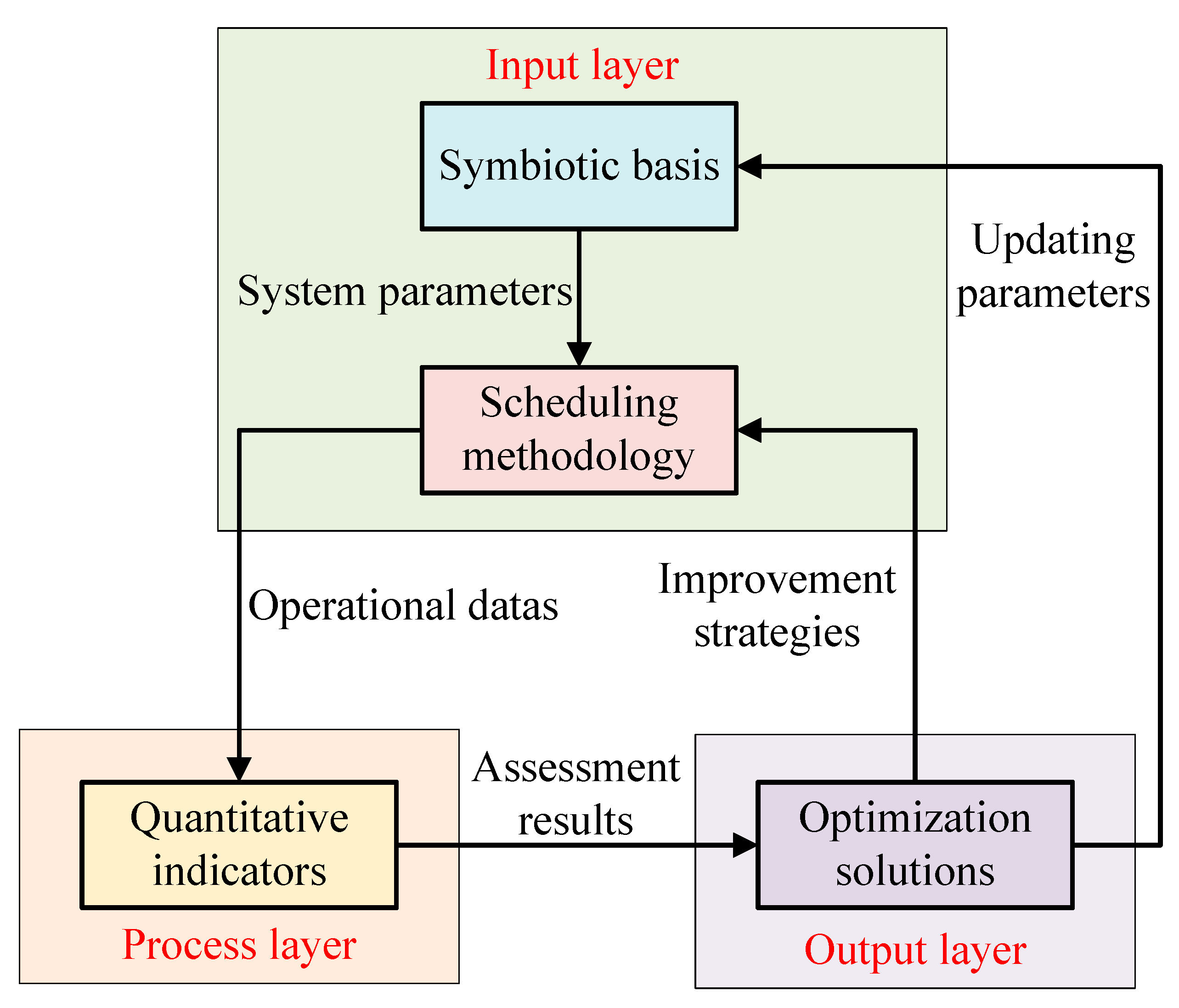

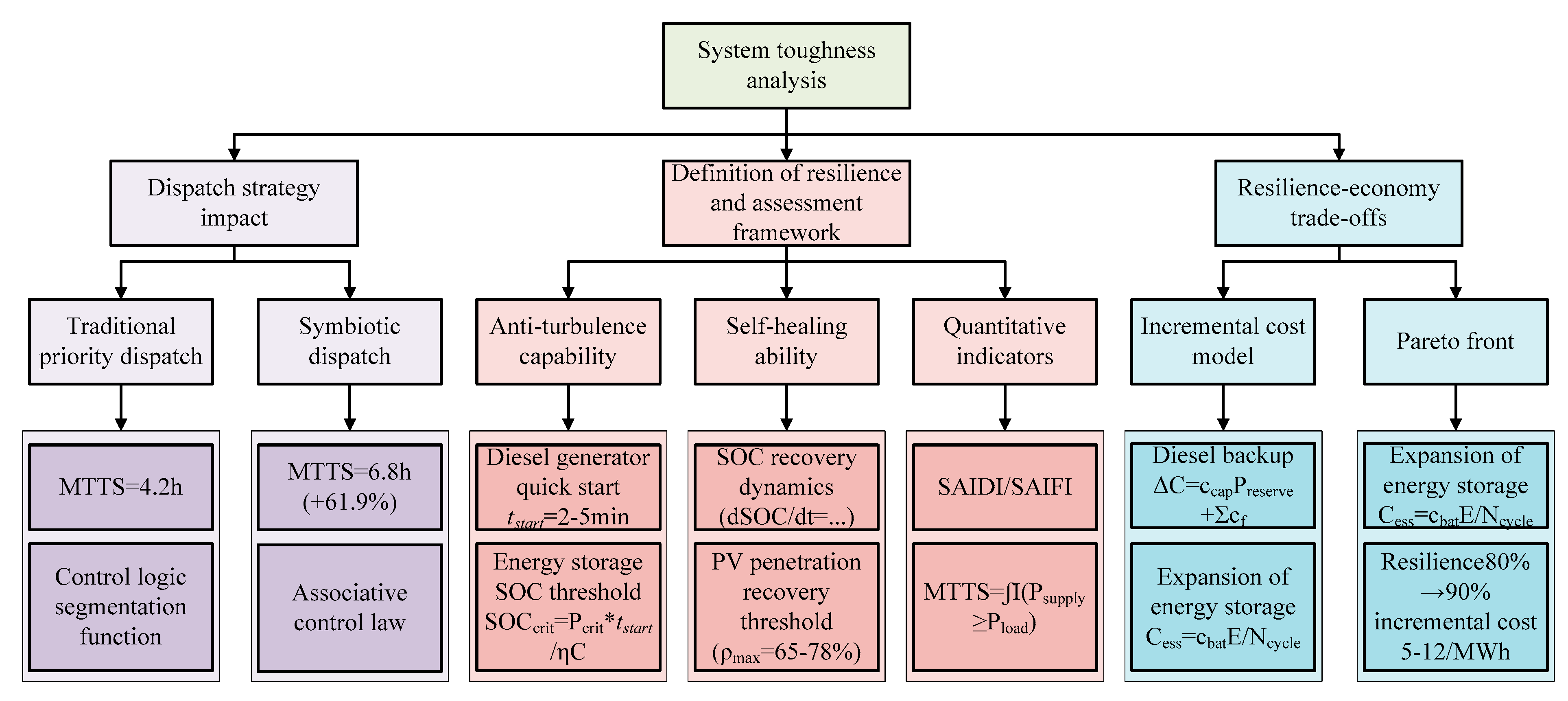
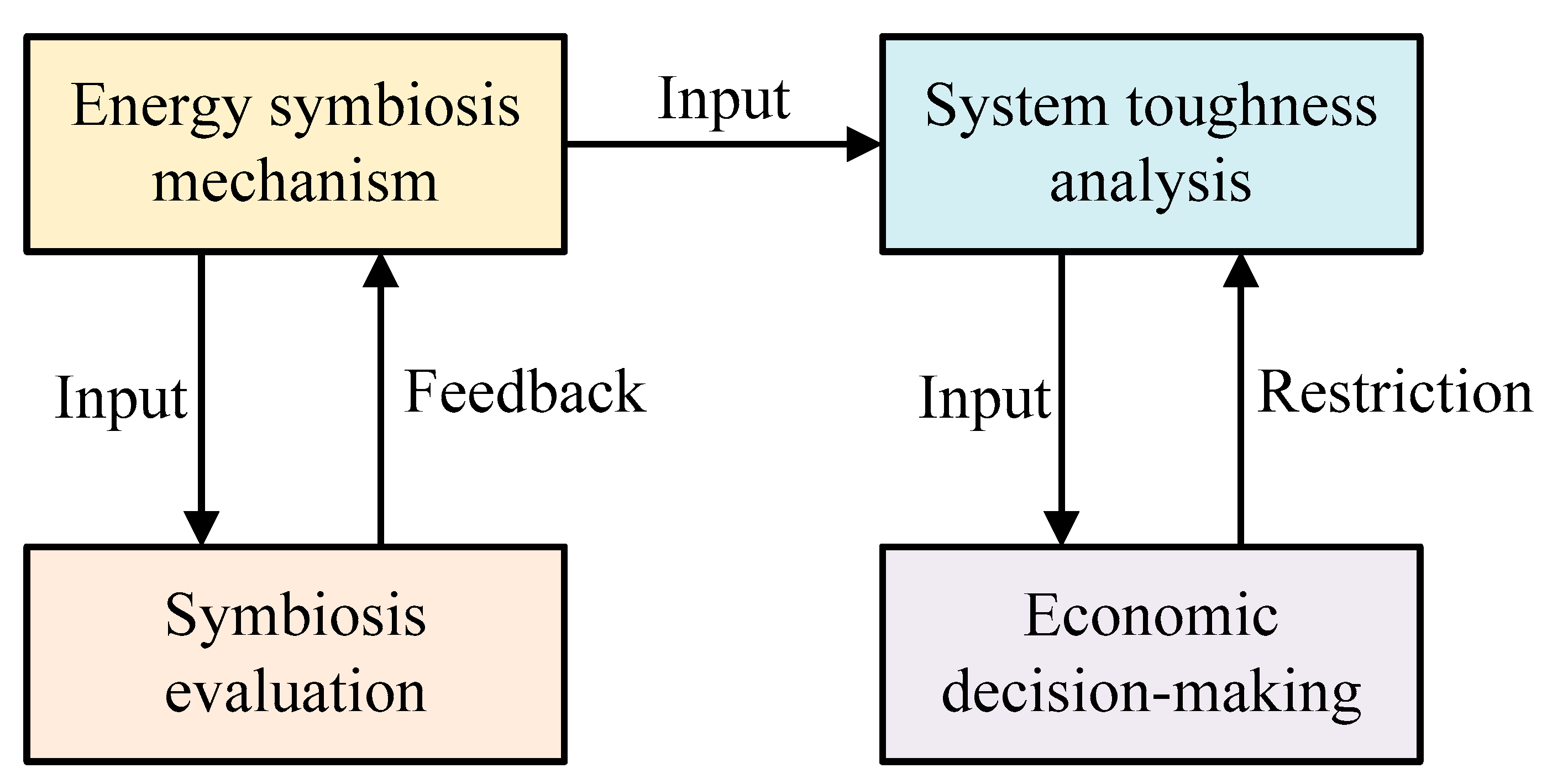


| Component | Core Strengths | Limitations | Synergistic Effect |
|---|---|---|---|
| Diesel generator set | Fast power support, inertia response | High fuel costs, carbon emissions | Providing stability, backup power |
| PV | Zero cost, clean energy | Intermittent, diurnal periodicity | Reducing fuel consumption, relying on energy storage smoothing |
| Energy storage | Millisecond response, energy space-time transfer | Limited capacity, life decay | Smoothing fluctuations, frequency modulation and peak shaving |
| Indicator | Optimization Direction | Regulatory Measures |
|---|---|---|
| MAF | Improving diesel compensation efficiency | Increased diesel ramp rate and energy storage power response speed |
| SE | Maintain moderate coordination and orderliness | Adjusting the proportion of energy output (such as PV limitation) |
| Method Type | Representative Algorithm | Computational Complexity | Topological Adaptability | Typical Application Scenarios | Limitations |
|---|---|---|---|---|---|
| Rule-based strategy [8] | Priority control | O(RlogR) | ★★★★☆ | Emergency backup control | Unable to handle multiple goal conflicts |
| MPC [9] | Rolling optimization | O(H·N3) | ★★★★★ | PV fluctuation mitigation | Requires Accurate system models |
| MAS [17] | Game theory algorithms | O(I·N) | ★★☆☆☆ | Distributed architecture | Heavy Communication burden |
| Meta-heuristic algorithm [18] | Particle swarm optimization algorithm (PSO) | O(I·N) | ★★★★☆ | Parameter optimization | Parameter sensitivity |
| Mixed integer programming [19] | Branch-and-cut | O(2m·poly(N)) | ★★★☆☆ | Capacity planning | Computational time |
| Capability Dimension | Key Formula | Core Variables | Engineering Significance |
|---|---|---|---|
| Anti-disturbance [45,46,47] | Diesel starts equation, SOC critical value | tstart, SOCcrit | Ensure uninterrupted power supply to critical loads after a failure |
| Self-healing [48] | SOC recovery dynamics [50] | Pcharge,λload | The speed at which the evaluation system recovers from disturbances |
| Quantitative indicators [49] | MTTS, ρmax | Power supply time, frequency deviation [50] | Guidance on system planning and threshold settings for operation |
| Expression | Control Target | Key Variables | Design Inspiration |
|---|---|---|---|
| Energy storage cooperative control law [50] | Smooth out fluctuations + frequency adjustment | kp | Parameters should be selected based on the accuracy of PV predictions. |
| Diesel power distribution [51] | Ensure continuity of power supply | The energy storage capacity must cover the demand during the diesel start-up delay period. |
| Strategy Type | Interference Immunity | Self-Healing Ability | Economic Efficiency |
|---|---|---|---|
| Traditional scheduling [52] | Reliance on diesel generators, slow response (minutes) | SOC recovery depends on human intervention | High fuel costs |
| Symbiotic scheduling [53] | Energy storage with millisecond response + diesel backup | Automatic charging to restore SOC when there is excess PV power [54] | Reduce diesel fuel consumption by 20–40% |
| Plan | Core Formula | Design Variable | Optimization Objective |
|---|---|---|---|
| Diesel backup [58] | ΔCdiesel | Preserve, Pidle | Reduce no-load loss costs |
| Energy storage expansion [59] | Cess, Ncycle | ΔSOC, E | Extend cycle life and reduce cost per kilowatt hour |
| PV over-allocation [60] | ρ, Light rejection ratio | Balancing excess revenue and curtailment losses |
| Phase | Key Issue | Dependencies | Decision Output |
|---|---|---|---|
| Definition and assessment [61,62] | How resilient does the system need to be | None (top-level design input) | MTTS, ρmax target value |
| Scheduling strategy [63] | How to dynamically achieve resilience | Based on indicators and dynamic models | Cooperative control law parameters (kp, ki) [64] |
| Economic trade-offs [65,66] | How much does it cost to achieve resilience | Indicator constraints + strategy costs | Optimal ratio of energy storage/diesel/PV [67] |
| Evaluation Dimensions | Symbiotic Indicators | Resilience Index | Interaction Coefficient β | Typical Influence Patterns |
|---|---|---|---|---|
| Power balance [82] | ECI | MTTS | 0.82 | ECI = 0.8 → MTTS = 6h ± 0.5 |
| Dynamic response [83] | ζ | Frequency deviation Δf | −0.75 | ζ 0.6 → 0.7, Δf↓0.15 Hz |
| Energy buffer [84] | SOC recovery rate | Failure recovery rate | 0.91 | Rate ≥ Recovery rate at 5%/h >90% |
| Stage | Input | Output | Tools/Methods |
|---|---|---|---|
| Requirements analysis | Load curve, meteorological data | Resilience indicator requirements (MTTS, etc.) | Spectral clustering algorithm [114] |
| Symbiosis Design | ECI/ζ target value | Capacity allocation plan | Pareto optimization [115] |
| Resilience verification | Topological parameters, control strategies | Fault recovery rate, Δfmax | RTDS real-time simulation [116] |
| Parameter iteration | Performance Evaluation Report | Weighting coefficient adjustment plan | Sensitivity analysis [117] |
| Hardware implementation | Final design parameters | Equipment Selection List, Control Parameters | HIL test platform [118] |
| Indicator | Diesel-Only Backup | Diesel–PV–ESS Symbiosis | Improvement |
|---|---|---|---|
| MTTS | 48 h | 76 h | + 58% |
| Fault recovery rate | 79% | 92% | +13% |
| Voltage deviation | ±6.5% | ±4.0% | −38% |
| Frequency deviation | ±0.55 Hz | ±0.30 Hz | −45% |
| Diesel runtime share | 100% | 65% | −35% |
| Fuel consumption (3 days) | 20,000 L | 14,400 L | −28% |
| Equivalent LCOE | 0.168 USD/kWh | 0.144 USD/kWh | −14% |
| CO2 emissions | baseline | –18% reduction | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Cao, S.; Li, R.; Xu, W. Energy Symbiosis in Isolated Multi-Source Complementary Microgrids: Diesel–Photovoltaic–Energy Storage Coordinated Optimization Scheduling and System Resilience Analysis. Energies 2025, 18, 5741. https://doi.org/10.3390/en18215741
Wang J, Cao S, Li R, Xu W. Energy Symbiosis in Isolated Multi-Source Complementary Microgrids: Diesel–Photovoltaic–Energy Storage Coordinated Optimization Scheduling and System Resilience Analysis. Energies. 2025; 18(21):5741. https://doi.org/10.3390/en18215741
Chicago/Turabian StyleWang, Jialin, Shuai Cao, Rentai Li, and Wei Xu. 2025. "Energy Symbiosis in Isolated Multi-Source Complementary Microgrids: Diesel–Photovoltaic–Energy Storage Coordinated Optimization Scheduling and System Resilience Analysis" Energies 18, no. 21: 5741. https://doi.org/10.3390/en18215741
APA StyleWang, J., Cao, S., Li, R., & Xu, W. (2025). Energy Symbiosis in Isolated Multi-Source Complementary Microgrids: Diesel–Photovoltaic–Energy Storage Coordinated Optimization Scheduling and System Resilience Analysis. Energies, 18(21), 5741. https://doi.org/10.3390/en18215741






