Effects of Operational Parameters on Heat Extraction Efficiency in Medium-Deep Geothermal Systems: THM Coupling Numerical Simulation

Abstract

Amid the global energy transition, geothermal energy, as a clean, stable, and renewable energy source, serves as a core direction for energy structure optimization. The development of medium-deep geothermal reservoirs is dominated by thermo–hydro–mechanical (THM) multi-physics coupling effects, yet the quantitative regulation laws of their operational parameters remain unclear. In this study, a numerical model for geothermal extraction considering THM multi-physics coupling was established. Using the single-factor variable method, simulations were conducted within the set parameter ranges of injection–production pressure difference, well spacing, and injection temperature. The spatiotemporal evolution characteristics of the temperature field, the dynamic temperature–pressure responses at the midpoint of injection–production wells and production wells, and efficiency indicators, such as instantaneous heat extraction power and cumulative heat extraction, were analyzed and quantified. The results show that a larger pressure difference accelerates the expansion of the cold zone in the reservoir, which improves short-term heat extraction efficiency but increases the risk of long-term thermal depletion; a smaller well spacing leads to higher initial heat production power but results in lower long-term cumulative heat extraction due to rapid heat consumption; within the normal temperature range of 16–24 °C, the injection temperature has a negligible impact on heat extraction efficiency. This study clarifies the regulatory laws of operational parameters and provides theoretical support for well pattern design and injection–production process optimization in medium-deep geothermal development.

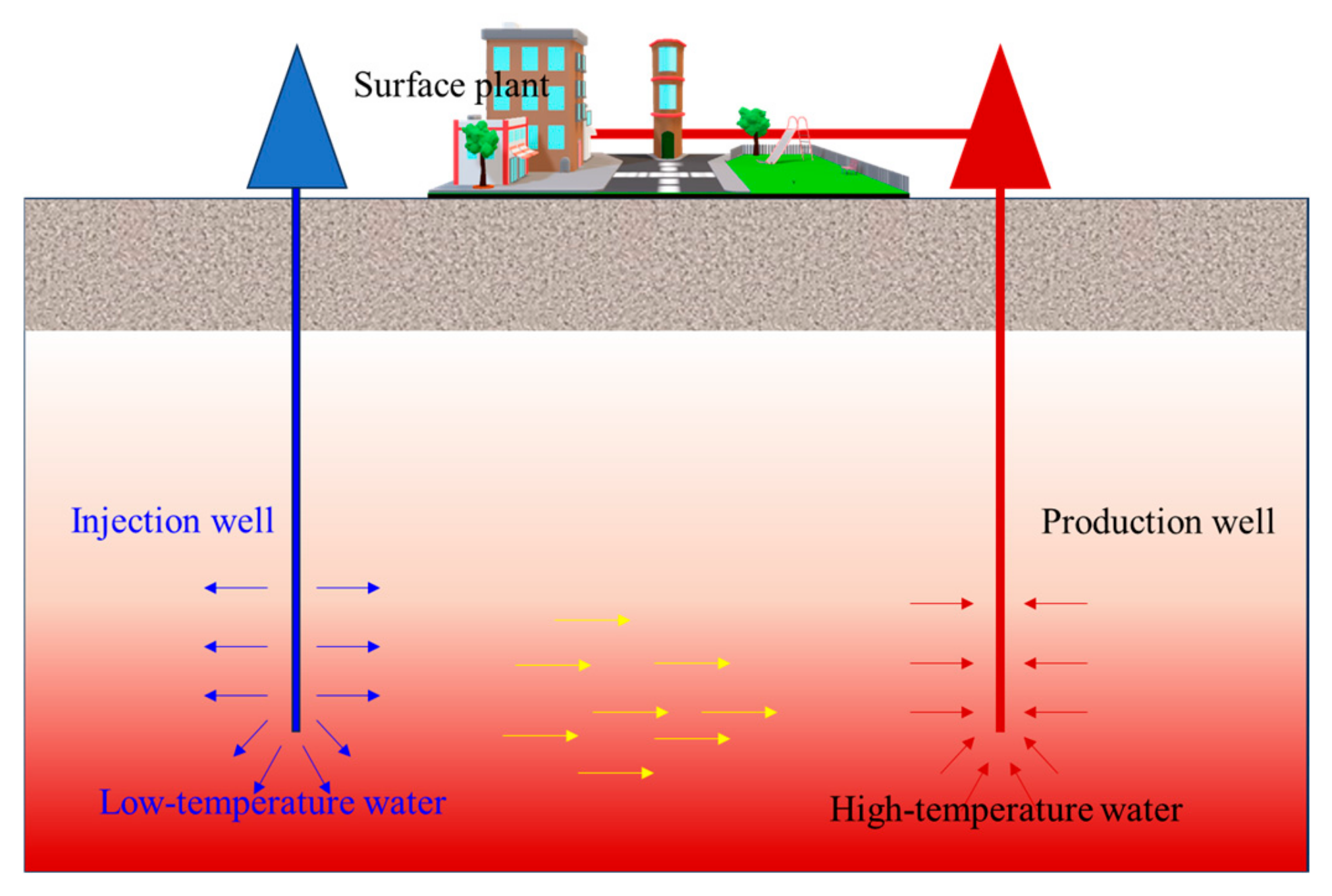
1. Introduction

Under the context of the global energy transition and “dual carbon” goals, geothermal energy, as a clean, stable, and sustainable renewable energy source, occupies a core position in the optimization of energy structures [1,2,3,4,5,6,7,8]. Key indicators, such as heat extraction efficiency (including instantaneous heat production power, cumulative heat extraction, and thermal depletion cycle), in geothermal system development directly determine the economic feasibility of projects and energy benefits. Injection–production pressure difference (driving fluid seepage), well spacing (affecting the spatial scope of heat exchange), and injection temperature (determining the temperature difference for heat exchange) are the core controllable parameters influencing heat extraction efficiency [9,10,11], and their action mechanisms require quantification [12]. Clarifying the correlation mechanism between operational parameters and heat extraction efficiency under the “thermo–hydro–mechanical (THM) multi-physics coupling” of geothermal reservoirs, improving the theoretical system of numerical simulation for geothermal development, and providing a quantitative basis for well pattern design (well spacing) and injection–production process optimization (pressure difference, injection temperature) in medium-deep geothermal development are of great significance for reducing development costs and extending the effective production cycle of reservoirs.

In this study, ‘medium-deep geothermal reservoirs’ refers to hydrothermal or engineered systems typically located at depths between 1500 and 3000 m. While the fundamental thermo–hydro–mechanical (THM) coupling principles explored here are highly relevant to enhanced geothermal systems (EGS), the specific model and parameters in this work are primarily configured for the analysis of a permeable medium-deep reservoir, and thus the terms are related in context but not used interchangeably. During geothermal extraction, the working fluid flows within high-temperature rock masses, and this flow process is subject to the coupling effects of the temperature field, seepage field, and stress field (thermal–hydrologic–mechanical, THM). The theory of THM multi-physics coupling serves as the core foundation for the numerical simulation of geothermal reservoirs. Early scholars conducted extensive pioneering work on the establishment and simplification of coupling equations for saturated/unsaturated and homogeneous/heterogeneous media. The origin of THM coupling theory can be traced back to the porous elasticity theory proposed by Biot [13] in the 1950s, which, for the first time, quantified the correlation between fluid flow and solid skeleton deformation in porous media, laying a mechanical foundation for the subsequent development of coupling models. In 1984, Noorishad et al. [14], based on Biot’s consolidation theory, specifically derived the THM coupling formulas and finite element discretization format for fractured rock masses, breaking through the limitations of homogeneous media. Furthermore, with the principles of consolidation and thermoelasticity as the core, they established the basic coupling equations for saturated porous media. Although water–rock heat exchange and thermally induced changes in mechanical parameters were not incorporated, this work still provided important references for simplified coupling models. For the completeness of the model, Hart et al. [15] constructed a fully coupled mechanical–thermal–hydraulic (MTH) model for saturated porous media under dynamic loading, systematically proposing fluid mass balance, mixture momentum balance, and energy balance equations, and clarifying the mathematical relationships for the collaborative evolution between fields. Mctigue [16], based on mixture theory, proposed the fully coupled theory of saturated porous thermoelastic media under the assumption of small temperature fluctuations, providing a theoretical basis for coupling simulations in medium–low-temperature scenarios. H.H. Vaziri [17] established a THM coupling model for the oil sand heating process and developed a specialized calculation program; he further constructed a coupling model of non-isothermal, single-phase seepage and nonlinear elastic deformation, which was solved using the finite element method, providing a reference for the simulation of mechanical responses during long-term extraction of geothermal reservoirs. In terms of the refinement of medium characterization, international research mainly focuses on two mainstream approaches: the equivalent continuous medium and the dual-medium approach. Rutqvist [18] adopted the porous homogeneous medium method to derive the governing equations of four software programs in the field of nuclear waste disposal, providing theoretical support for the coupled simulation of fractured rock masses.

The regulatory mechanisms of operational parameters, such as injection–production pressure difference, well spacing, and injection temperature, are central to the economic viability of geothermal development. Regarding well spacing optimization, 3D coupling simulations [19,20,21] have shown that a well spacing of 800 m can balance the production temperature, reservoir lifespan, and total heat production. Studies [22,23,24] have confirmed that within the spacing range of 200–500 m, every 100 m increase in spacing can raise the production well temperature by 8–12 °C over 30 years, and this design must be coordinated with fracture aperture. Li et al. [25] designed a geothermal development case based on the embedded discrete fracture model (EDFM), quantified the influence of well spacing on the spatiotemporal evolution of pressure and temperature fields, and further verified the importance of spacing optimization. For the impact of injection–production pressure difference, research focusing on the “pressure-seepage-heat efficiency” dynamic balance [26,27,28] has indicated that pressure difference affects heat extraction efficiency by regulating the range of fracture stimulation zones, and it exhibits a positive correlation with the improvement of permeability. Zhang et al. [29] proposed a mesoscopic THM damage model, analyzed the mechanism of thermal stress in hot dry rock (HDR) fracturing, and pointed out that an excessively high pressure difference accelerates the expansion of cold zones and shortens the thermal depletion cycle. It is a widely accepted consensus that the temperature difference between the injected fluid and the reservoir determines the driving force for heat exchange. Relevant simulations [30,31,32,33] have shown that heat exchange efficiency is relatively high when the fluid velocity is 0.7 m/s and the flow rate is 20–26 m³/h; however, these studies lack sensitivity analysis of small temperature differences in the normal temperature range of 15–35 °C. Li et al. [34] established a multi-field coupling model, analyzed the interaction of thermo–chemical effects under fracture width and stress gradient, and provided insights for parameter synergistic optimization, but did not incorporate the regulatory mechanism of injection temperature. Multi-parameter synergistic research remains a gap: Existing studies mainly focus on single-factor analysis, exploring the correlation between individual parameters and field evolution. A synergistic optimization framework linking “injection–production pressure difference–well spacing-injection temperature” has not yet been established, making it difficult to directly guide engineering practice.

To address the issues of insufficient sensitivity analysis of normal-temperature injection parameters, unclear long-term effects of medium-short well spacing, lack of a multi-parameter synergistic framework, and insufficient analysis of key locations, this study takes medium-deep geothermal reservoirs as the research object, establishes a fully coupled THM model, and conducts single-factor and long-term simulations. It quantifies the influences of injection–production pressure difference, well spacing, and injection temperature on heat extraction efficiency, focuses on capturing the temperature–pressure evolution at the midpoint of injection–production wells and production wells, reveals the coupling mechanism, proposes directions for parameter optimization, and provides theoretical support for medium-deep geothermal development. While the single-factor simulations aim to isolate and quantify the effects of individual parameters, the coupling mechanisms revealed in this study lay the foundation for future multi-parameter synergistic design.

2. Mathematical Model and Numerical Method

2.1. Description of Physical Problem and Model Assumptions

This study conducts numerical simulations on the heat extraction process in Enhanced Geothermal Systems (EGS) or medium-deep geothermal reservoirs. The core physical scenario is shown in Figure 1, where a two-dimensional rectangular reservoir model is considered. In this model, low-temperature fluid is injected into the high-temperature rock mass through the injection well. The injection of fluid disrupts the original equilibrium state. On one hand, the low-temperature fluid flows toward the production well driven by the pressure difference and is heated through heat exchange (convection and conduction) with the high-temperature rock during migration; on the other hand, the injected fluid changes the pore pressure field and temperature field of the reservoir, thereby inducing significant stress and deformation in the rock mass.

While single-factor simulations are employed in this study to clearly isolate and quantify the individual effect of each operational parameter, the primary novelty lies in revealing the underlying thermo–hydro–mechanical (THM) multi-physics coupling mechanisms (e.g., how pressure-difference-induced rock deformation dynamically alters permeability and consequently accelerates thermal convection). These insights, often obscured in complex multi-parameter optimization, provide a crucial theoretical foundation for future synergistic parameter design. Furthermore, the assumptions of a 2D geometry and homogeneous isotropic media are adopted to reduce computational cost while capturing the primary THM coupling mechanisms. These assumptions are reasonable for preliminary design and parameter sensitivity analysis, particularly in large-scale reservoirs where horizontal flow dominates. However, in highly heterogeneous or fractured reservoirs, 3D effects and anisotropy may significantly influence fluid pathways and heat transfer. Therefore, the current model is most applicable to conceptual design and parameter screening, while site-specific applications should incorporate geological heterogeneity and 3D structural features.

By establishing a fully coupled THM numerical model, this study systematically analyzes how key operational parameters (such as well spacing, injection–production pressure difference, injection temperature, and formation temperature) affect the heat production temperature of the production well through the aforementioned coupling mechanism, thus providing a theoretical basis for optimizing geothermal extraction strategies.

To construct a solvable mathematical model, the following basic assumptions are made on the premise of ensuring the authenticity of physical processes:

(1)

Porous medium assumption: The reservoir rock is simplified as a homogeneous, isotropic, and continuous porous medium, and its mechanical behavior follows a linear elastic constitutive relation.

(2)

Fluid flow assumption: The working fluid is single-phase liquid water, and its flow obeys Darcy’s law, with the influence of gravity neglected.

(3)

Thermodynamic assumption: At the representative elementary volume (REV) scale of the porous medium, the solid skeleton and pore fluid instantly reach a state of local thermal equilibrium, i.e., their temperatures are equal.

(4)

Coupling mechanism assumption: Porosity and permeability are dynamically varying field variables, and their evolution is a function of effective stress and temperature change, which are described using the corresponding poroelastic and thermoelastic models.

(5)

Initial condition assumption: The model is initially in a state of hydrostatic pressure distribution, uniform temperature field, and stress equilibrium.

2.2. Governing Equations and Multi-Physics Coupling Mechanism

2.2.1. Governing Equation of Stress Field

The rock in the formation is regarded as an ideal elastic porous medium, and its stress is mainly composed of two parts: effective stress and pore pressure. The constitutive equation can be expressed as follows:

$${\sigma }_{ij}={\sigma }_{eff}+\alpha p{\delta }_{ij}$$

(1)

where σ_ij is the stress tensor, MPa; σ_eff is the effective stress, MPa; α is the Biot coefficient, which can be expressed as α = 1 − K/K_s; K is the bulk modulus of the rock, K = E/3(1 − 2ν), MPa; K_s is the bulk modulus of the rock’s solid skeleton, MPa; E is the Young’s modulus, MPa; ν is the Poisson’s ratio; p is the pore pressure, MPa; and δ_ij is the Kronecker delta.

After considering temperature, formation deformation mainly consists of three components: stress-induced deformation, temperature-induced deformation, and pore pressure-induced deformation. Its strain can be expressed as follows:

$${\epsilon }_{ij}={\displaystyle \frac{1}{2G}}{\sigma }_{ij}-\left({\displaystyle \frac{1}{6G}}-{\displaystyle \frac{1}{9K}}\right){\sigma }_{ik}{\delta }_{ij}+{\displaystyle \frac{\alpha }{3K}}\Delta p{\delta }_{ij}+{\displaystyle \frac{{\alpha }_{\mathrm{T}}\Delta T}{3}}{\delta }_{ij}$$

(2)

By combining Equations (1) and (2), the governing equation of the stress field can be expressed as follows:

$$G{u}_{i.kk}+{\displaystyle \frac{G}{1-2v}}{u}_{k,ki}-{\alpha }_{T}K{T}_{,j}-\alpha p_{,j}+f_{,j}=0$$

(3)

2.2.2. Governing Equation of Seepage Field

Fluid flow in the formation follows Darcy’s law. Neglecting the influence of gravity, the fluid flow can be expressed as follows:

$$q_{\mathrm{w}}=-{\displaystyle \frac{k}{\mu }}𝛻p$$

(4)

where q_w is the Darcy seepage velocity vector of the fluid, m; μ is the viscosity coefficient of the fluid, Pa·s; and k is the permeability, Pa·s.

Fluid in the rock matrix is mainly stored in pores, so the fluid mass per unit volume of the rock matrix can be expressed as follows:

$$m={\rho }_{\mathrm{w}}\varphi$$

(5)

where φ is the porosity of the rock matrix.

By combining Equations (4) and (5), the following expression can be derived:

$${\displaystyle \frac{\partial {\rho }_{\mathrm{w}}\varphi }{\partial t}}-𝛻\cdot ({\displaystyle \frac{k}{\mu }}{\rho }_{\mathrm{w}}𝛻p)=Q_{\mathrm{s}}$$

(6)

Porosity can be expressed as follows:

$$\phi =1-(1-{\phi }_0)exp\left[-{\displaystyle \frac{1}{K_s}}(p-p_0)+{\alpha }_T(T-T_0)-({\epsilon }_V-{\epsilon }_{V0})\right]$$

(7)

In Equation (7), −1/K_s(p − p₀) represents the influence of liquid pressure on porosity, and α_T(T − T₀) represents the influence of temperature on porosity.

The evolution of permeability depends on porosity, and the relationship between them can be expressed as follows:

$${\displaystyle \frac{k}{k_0}}={\left({\displaystyle \frac{\phi }{{\phi }_0}}\right)}^3$$

(8)

Thus, the evolution equation of permeability can be obtained as follows:

$$k=k_0{\left\{{\displaystyle \frac{1}{{\phi }_0}}-{\displaystyle \frac{(1-{\phi }_0)}{{\phi }_0}}exp\left[-{\displaystyle \frac{1}{K_s}}(p-p_0)+{\alpha }_T(T-T_0)-({\epsilon }_V-{\epsilon }_{V0})\right]\right\}}^3$$

(9)

By differentiating Equation (7) with respect to time, the following expression can be derived:

$${\displaystyle \frac{\partial \phi }{\partial t}}=-(1-{\phi }_0)(-{\displaystyle \frac{1}{K_s}}{\displaystyle \frac{\partial p}{\partial t}}+{\alpha }_T{\displaystyle \frac{\partial T}{\partial t}}-{\displaystyle \frac{\partial {\epsilon }_V}{\partial t}})exp\left[-{\displaystyle \frac{p-p_0}{K_s}}+{\alpha }_T(T-T_0)-{\epsilon }_V\right]$$

(10)

By combining Equations (6) and (10), the governing equation of the seepage field can be obtained as follows:

$$\begin{array}{l}{\rho }_{\mathrm{w}}(1-{\phi }_0){\displaystyle \frac{1}{K_s}}exp\left[-{\displaystyle \frac{p-p_0}{K_s}}+{\alpha }_T(T-T_0)-{\epsilon }_V\right]{\displaystyle \frac{\partial p}{\partial t}}-𝛻\cdot ({\displaystyle \frac{k}{u}}{\rho }_{\mathrm{w}}𝛻p)\\ ={\rho }_{\mathrm{w}}(1-{\phi }_0){\alpha }_{T}exp\left[-{\displaystyle \frac{p-p_0}{K_s}}+{\alpha }_T(T-T_0)-{\epsilon }_V\right]{\displaystyle \frac{\partial T}{\partial t}}\\ -{\rho }_{\mathrm{w}}(1-{\phi }_0)exp\left[-{\displaystyle \frac{p-p_0}{K_s}}+{\alpha }_T(T-T_0)-{\epsilon }_V\right]{\displaystyle \frac{\partial {\epsilon }_V}{\partial t}}+Q_{\mathrm{s}}\end{array}$$

(11)

Let $S=(1-{\phi }_0){\displaystyle \frac{1}{K_s}}exp\left[-{\displaystyle \frac{p-p_0}{K_s}}+{\alpha }_T(T-T_0)-{\epsilon }_V\right]$ be defined; then, the governing equation of the seepage field can be simplified into the form of a water storage model:

$${\rho }_{\mathrm{w}}S{\displaystyle \frac{\partial p}{\partial t}}-𝛻\cdot ({\displaystyle \frac{k}{\mu }}{\rho }_{\mathrm{w}}𝛻p)={\rho }_{\mathrm{w}}S{\alpha }_T{K}_s{\displaystyle \frac{\partial T}{\partial t}}-{\rho }_{\mathrm{w}}S{K}_s{\displaystyle \frac{\partial {\epsilon }_V}{\partial t}}+Q_{\mathrm{s}}$$

(12)

In Equation (12), S is the storage coefficient. Both the influence of temperature on the seepage field (${\rho }_{\mathrm{w}}S{\alpha }_T{K}_s{\displaystyle \frac{\partial T}{\partial t}}$) and the influence of the stress field on the seepage field (${\rho }_{\mathrm{w}}S{K}_s{\displaystyle \frac{\partial {\epsilon }_V}{\partial t}}$) are reflected in the source–sink term of the water storage model.

2.2.3. Governing Equation of Temperature Field

Fluid flow in the formation complies with the first law of thermodynamics. The temperature field during groundwater migration can be divided into two parts: the rock skeleton and the fluid. The temperature field of the rock skeleton can be expressed as follows:

$${\displaystyle \frac{\partial \left[{\rho }_{\mathrm{s}}{c}_{\mathrm{s}}(1-\varphi )\Delta T_{\mathrm{s}}\right]}{\partial t}}=T_{\mathrm{s}}{\alpha }_{\mathrm{T}}(1-\varphi )K{\displaystyle \frac{\partial {\epsilon }_V}{\partial t}}+𝛻\cdot \left[{\lambda }_{\mathrm{s}}(1-\varphi )𝛻T_{\mathrm{s}}\right]+(1-\varphi )Q_{\mathrm{ts}}$$

(13)

where ρₛ is the density of the rock skeleton, kg/m³; cₛ is the specific heat capacity of the rock skeleton, J/(kg·K); Tₛ is the temperature of the rock, K; λₛ is the thermal conductivity coefficient of the rock skeleton, W/(m·K); and Qₜₛ is the heat source of the rock skeleton, J.

The temperature field of the fluid can be expressed as follows:

$${\displaystyle \frac{\partial ({\rho }_{\mathrm{w}}{c}_{\mathrm{w}}\varphi \Delta T_{\mathrm{w}})}{\partial t}}=-𝛻\cdot ({\rho }_{\mathrm{w}}{c}_{\mathrm{w}}{q}_{\mathrm{w}}{T}_{\mathrm{w}})+𝛻\cdot \left[{\lambda }_{\mathrm{w}}\varphi 𝛻T_{\mathrm{w}}\right]+\varphi Q_{\mathrm{tw}}$$

(14)

where c_w is the specific heat capacity of the fluid, J/(kg·K); T_w is the temperature of the fluid, K; λ_w is the thermal conductivity coefficient of the fluid, W/(m·K); and Qₜ_w is the heat source of the fluid, J.

The governing equation of the formation temperature field can be expressed as follows:

$$\begin{array}{l}{\displaystyle \frac{\partial \left[{\rho }_{\mathrm{s}}{c}_{\mathrm{s}}(1-\varphi )\Delta T_s+{\rho }_{\mathrm{w}}{c}_{\mathrm{w}}\varphi \Delta T_{\mathrm{w}}\right]}{\partial t}}=T_{\mathrm{s}}{\alpha }_{\mathrm{T}}(1-\varphi )K{\displaystyle \frac{\partial {\epsilon }_V}{\partial t}}-𝛻\cdot ({\rho }_{\mathrm{w}}{c}_{\mathrm{w}}{q}_{\mathrm{w}}{T}_{\mathrm{w}})\\ +𝛻\cdot \left[{\lambda }_{\mathrm{s}}(1-\varphi )𝛻T_{\mathrm{s}}+{\lambda }_{\mathrm{w}}\varphi 𝛻T_{\mathrm{w}}\right]+\left[(1-\varphi )Q_{\mathrm{ts}}+\varphi Q_{\mathrm{tw}}\right]\end{array}$$

(15)

When the rock skeleton and the fluid are in a state of thermal equilibrium, the governing equation of the temperature field can be simplified as follows:

$$\begin{array}{l}{\displaystyle \frac{\partial \left[\left({\rho }_s{c}_s-{\rho }_s{c}_s\varphi +{\rho }_w{c}_w\varphi \right)\Delta T\right]}{\partial t}}=T{\alpha }_T(1-\varphi )K{\displaystyle \frac{\partial {\epsilon }_V}{\partial t}}-𝛻\cdot ({\rho }_w{c}_w{q}_{w}T)\\ +𝛻\cdot \left[\left({\lambda }_s-{\lambda }_s\varphi +{\lambda }_w\varphi \right)𝛻T\right]+\left[Q_{Ts}-\varphi Q_{Ts}+\varphi Q_{Tw}\right]\end{array}$$

(16)

By rearranging the terms of Equation (16), the following expression can be obtained:

$$\begin{array}{l}{\displaystyle \frac{\partial \left[\left({\rho }_s{c}_s-{\rho }_s{c}_s\varphi +{\rho }_w{c}_w\varphi \right)\Delta T\right]}{\partial t}}-T{\alpha }_T(1-\varphi )K{\displaystyle \frac{\partial {\epsilon }_V}{\partial t}}+𝛻\cdot ({\rho }_w{c}_w{q}_{w}T)\\ -𝛻\cdot \left[\left({\lambda }_s-{\lambda }_s\varphi +{\lambda }_w\varphi \right)𝛻T\right]=\left[Q_{Ts}-\varphi Q_{Ts}+\varphi Q_{Tw}\right]\end{array}$$

(17)

In Equation (17), the first term on the left side represents the rate of change of thermal energy, the second term on the left side represents the heat change caused by rock mass deformation, the third term on the left side represents the heat change caused by thermal convection, the fourth term on the left side represents the heat change caused by thermal conduction, and the right side represents the source–sink term.

2.3. Multi-Field Coupling Relationships

Geothermal energy extraction mainly involves the stress field, the seepage field, and the temperature field. In the stress field, the effects of stress, pore pressure, temperature, and body force on rock deformation are considered. In the seepage field, the focus is on the effects of rock mass thermal expansion and rock mass deformation on seepage. In the temperature field, the primary considerations are the effects of rock mass deformation, thermal diffusion, and thermal convection. In the interaction among various physical fields, rock mass deformation and porosity evolution caused by the stress field affect the seepage field and the temperature field. The pore pressure in the seepage field acts on the stress field, and the resulting thermal convection influences the evolution of the temperature field. Thermal expansion in the temperature field leads to rock mass deformation, and thermal convection affects the evolution of the seepage field.

3. Model Validation and Simulation Scheme

The thermo–hydro–mechanical (THM) multi-physics coupling model established in this study is implemented using the commercial finite element software COMSOL Multiphysics 6.2. This software possesses robust multi-physics coupling analysis capabilities, enabling accurate description of the interaction mechanisms among heat transfer, fluid seepage, and rock mass deformation in geothermal reservoirs, thus providing a reliable numerical simulation platform for quantifying the effects of operational parameters on heat extraction efficiency.

3.1. THM Model Validation

To ensure the accuracy and reliability of the numerical model, model validation is first conducted before carrying out systematic parameter studies. A 2D model with dimensions of 1 m × 0.4 m is constructed. The initial temperature of the model is set to 10 °C, and the initial pore pressure is set to 1 × 10⁵ Pa. The temperature of the upper boundary of the model is set to 60 °C, the pore pressure of the upper boundary is set to 0, and a uniform load of 100 kPa is applied. The other boundaries are considered impermeable and thermally insulated, with normal displacement constrained. The main parameters of the model are listed in

Table 1. Calculation parameter settings.

Parameter	Value	Parameter	Value
Rock Density	2000 kg/m3	Elastic Modulus	6 × 107 Pa
Poisson’s Ratio	0.4	Permeability Coefficient	4 × 10−6 m/s
Biot Coefficient	1	Storage Coefficient	2 × 10−9 1/Pa
Porosity	0.2	Rock Thermal Conductivity Coefficient	1.2 W/(m⋅K)
Rock Specific Heat Capacity	800 J/(kg⋅K)	Expansion Coefficient	1.5 × 10−5 1/K
Water Density	1000 kg/m3	Water Thermal Conductivity Coefficient	0.58 W/(m⋅K)

.

Bai Bing [35] et al. derived the governing equations for thermo–hydro–mechanical (THM) coupling in porous media under one-dimensional conditions based on the Fourier transform and found that the time-dependent changes in temperature and pressure can be expressed as follows:

$$p\left(x,t\right)={\displaystyle \frac{2}{h}}{\displaystyle \sum }_{n=0}^{\infty }{\displaystyle \frac{1}{\xi }}\left({\varphi }_{12}{e}^{-{\gamma }_{11}{\xi }^{2}t}+{\varphi }_{11}{e}^{-{\gamma }_{22}{\xi }^{2}t}\right)\sin \xi \left(h-x\right)$$

(18)

$$\theta \left(x,t\right)={\theta }_a+{\displaystyle \frac{2}{h}}{\displaystyle \sum }_{n=0}^{\infty }{\displaystyle \frac{1}{\xi }}\left({\varphi }_{22}{e}^{-{\gamma }_{11}{\xi }^{2}t}+{\varphi }_{21}{e}^{-{\gamma }_{22}{\xi }^{2}t}\right)\sin \xi \left(h-x\right)$$

(19)

Three heights in the model (z = 0.25 m, 0.50 m, and 0.75 m) were selected to calculate the time-dependent changes in temperature and pore pressure, and the correlation between the THM model established in this study and the theoretical solutions was compared and analyzed. As shown in Figure 2, it is evident that for the THM coupling problem, the theoretical solutions and numerical simulation results exhibit an extremely high correlation. At different heights, the Pearson correlation coefficients of the temperature and pore pressure results obtained by the two methods are all greater than 0.997. Generally, when the Pearson correlation coefficient is greater than 0.8, two sets of data can be considered to have a high correlation. It can be observed from Figure 2 that the THM model established in this study shows a faster rate of temperature increase and pore pressure decrease than the theoretical solutions. This is because permeability is set as a constant in the theoretical solutions, whereas in the model of this study, permeability is variable, preferential seepage paths are formed during the seepage process, resulting in an increase in permeability. The root mean square error (RMSE) between the numerical and theoretical temperature results is 1.8 K, and for pore pressure, it is 0.015 MPa, representing relative errors of less than 2% and 3%, respectively. These quantitative metrics confirm the high accuracy and reliability of the proposed THM model.

3.2. Geometric Model Construction

This study adopts a two-dimensional planar model for simulation to simplify computational complexity while ensuring the representativeness of the model. The planar dimensions of the model are set to 240 m (length) × 160 m (width), and the diameter of both the injection wellbore and production wellbore is set to 0.2 m. During the numerical calculation process, the finite element discretization method is adopted for mesh generation of the computational domain. A quadrilateral structured mesh is selected as the mesh type, and mesh refinement is performed on the areas around the wellbore to improve the calculation accuracy of fluid flow and heat exchange near the wellbore. The minimum element size in the refined regions around the wells was set to 0.05 m, gradually transitioning to a maximum element size of 2 m in the outer regions of the reservoir. This strategy ensures a balance between computational efficiency and resolution of critical near-wellbore physics.

The initial well spacing (distance between the centers of the injection well and production well) is set to 80 m. The coordinates of the injection well are (80 m, 80 m), and those of the production well are (160 m, 80 m). The determination of the model boundary range is based on the “no boundary effect” principle, that is, ensuring the outer boundary of the model is sufficiently far from the injection–production wells to avoid interference of boundary conditions on fluid flow and heat transfer inside the reservoir.

3.3. Setting of Initial Conditions and Boundary Conditions

3.3.1. Initial Conditions

The initial state parameters of the geothermal reservoir are set with reference to the actual geological conditions of medium-high temperature geothermal fields.

Initial water pressure: The initial pore water pressure of the reservoir is uniformly set to 20 MPa, corresponding to a reservoir depth of approximately 2000 m (calculated based on a hydrostatic pressure gradient of 10 MPa/km), which is consistent with the reservoir depth range of conventional deep geothermal development.

Initial stress state: The initial in situ stress of the reservoir is set as a self-weight stress field. The vertical stress is determined by the weight of the overlying rock formations (calculated based on a rock density of 2700 kg/m³ and a gravitational acceleration of 9.8 m/s²). Based on a reservoir depth of 2000 m, the vertical stress is set to 54 MPa.

Initial temperature: The initial temperature of the entire reservoir is uniformly set to 230 °C, which is consistent with the temperature characteristics of medium-high temperature geothermal reservoirs. The main parameter settings of the model are shown in

Table 2. Model parameter settings.

Parameter	Symbol	Unit	Value
Young’s Modulus of Geothermal Reservoir	E	GPa	17
Young’s Modulus of Geothermal Reservoir Skeleton	Es	GPa	48
Poisson’s Ratio of Geothermal Reservoir	v	/	0.35
Rock Density	ρs	kg/m3	2600
Water Density	ρw	kg/m3	1000
Dynamic Viscosity	μ	Pa·s	1.00 × 10−3
Initial Porosity	φ0	/	0.01
Initial Permeability	k0	m2	1.00 × 10−18
Specific Heat Capacity of Rock	cs	J/(kg·K)	1000
Specific Heat Capacity of Water	cw	J/(kg·K)	4200
Thermal Expansion Coefficient	αT	K−1	1.00 × 10−5
Thermal Conductivity Coefficient of Rock Mass	λs	W/(m·K)	2.50
Thermal Conductivity Coefficient of Fluid	λw	W/(m·K)	0.58

.

3.3.2. Boundary Conditions

To simulate the actual environment of a closed geothermal reservoir, the model’s boundary conditions are set as follows to ensure consistency with on-site engineering conditions:

Flow boundary: The outer boundary of the model is a no-flow boundary. The injection–production pressure difference is achieved by applying fixed pressure boundary conditions to the injection well and production well, respectively.

Thermal boundary: The outer boundary of the model is an adiabatic (no heat flux) boundary. This assumption simulates a closed geothermal reservoir with minimal heat loss to the surroundings, which is consistent with deep geothermal systems where the reservoir is surrounded by low-conductivity rock formations. The fluid temperature at the injection well is set according to the simulation conditions.

Mechanical boundary: The bottom of the model constrains vertical (y-direction) displacement; the left and right sides constrain horizontal (x-direction) displacement to simulate confining pressure; and the top boundary applies a load equivalent to the gravity of the overlying rock formations.

3.4. Design of Single-Factor Parameter Simulation Scheme

To quantitatively analyze the influence of operational parameters on the heat extraction efficiency of the geothermal system, this study adopts the single-factor variable method to design the simulation scheme. Specifically, other parameters are fixed constant, while only the target parameter is adjusted. By comparing the heat extraction efficiency under different parameter values, the influence law of each parameter is clarified. The selected key operational parameters and their level settings are as follows:

3.4.1. Simulation Scheme for Injection–Production Pressure Difference

The injection–production pressure difference directly determines the fluid seepage velocity in the reservoir, thereby affecting heat transfer efficiency. This study sets five levels of injection–production pressure difference, covering low, medium, and high pressure difference ranges. The specific levels are 4 MPa, 6 MPa, 8 MPa, 10 MPa, and 12 MPa. During the simulation, the well spacing is fixed at 80 m, the injection temperature at 20 °C, and the simulation duration at 30 a. The focus is on analyzing the influence of the injection–production pressure difference on the evolution of the temperature field and heat extraction efficiency.

3.4.2. Simulation Scheme for Injection Temperature

The temperature difference between the injected fluid and the reservoir is the driving force for heat exchange, which directly affects heat extraction efficiency. This study sets five levels of injection temperature, covering the range from normal temperature to medium temperature injection. The specific levels are 16 °C, 18 °C, 20 °C, 22 °C, and 24 °C. During the simulation, the well spacing is fixed at 80 m, the injection–production pressure difference at 8 MPa, and the simulation duration at 30 a. By comparing the variation trend of the production well outlet temperature under different injection temperatures, the sensitivity of heat extraction efficiency to injection temperature is quantified.

3.4.3. Simulation Scheme for Well Spacing

Well spacing is a key parameter affecting the fluid flow path and heat exchange efficiency between injection and production wells. In this study, a well spacing of 80 m was selected as the baseline case for the majority of the simulations presented in this work (e.g., the analysis of reservoir evolution in Section 4.1 and the investigation of injection temperature in Section 4.3). This baseline value was chosen as a representative spacing found in many engineered geothermal systems, providing a common reference for comparing the effects of other parameters.

To systematically investigate the sensitivity of heat extraction efficiency to this specific parameter, a single-factor sensitivity analysis was conducted. Four levels of well spacing were designed: 60 m, 70 m, 80 m, and 90 m. This range was selected to cover typical well spacing configurations from relatively tight to moderate, allowing for the examination of trends and the identification of potential trade-offs between short-term efficiency and long-term sustainability. During these sensitivity simulations, all other parameters (injection–production pressure difference: 8 MPa, injection temperature: 20 °C, initial reservoir temperature at 230 °C) were held constant to isolate the effect of well spacing.

4. Simulation Results

4.1. Evolution of Reservoir Temperature and Pore Pressure

Based on the simulation scheme designed in Section 3, this section selects a typical working condition (well spacing: 80 m, injection–production pressure difference: 8 MPa, injection temperature: 20 °C, initial reservoir temperature: 230 °C) to simulate the 30-year thermal extraction process. Focusing on the simulation results of this benchmark parameter combination, this section systematically analyzes the attenuation law of the reservoir temperature field, the migration characteristics of high-temperature regions, and the evolution trend of the distribution gradient of the pore pressure field with the progress of extraction. It also reveals the multi-field coupling coordinated evolution mechanism of the geothermal reservoir, laying a foundation for subsequent parameter sensitivity analysis.

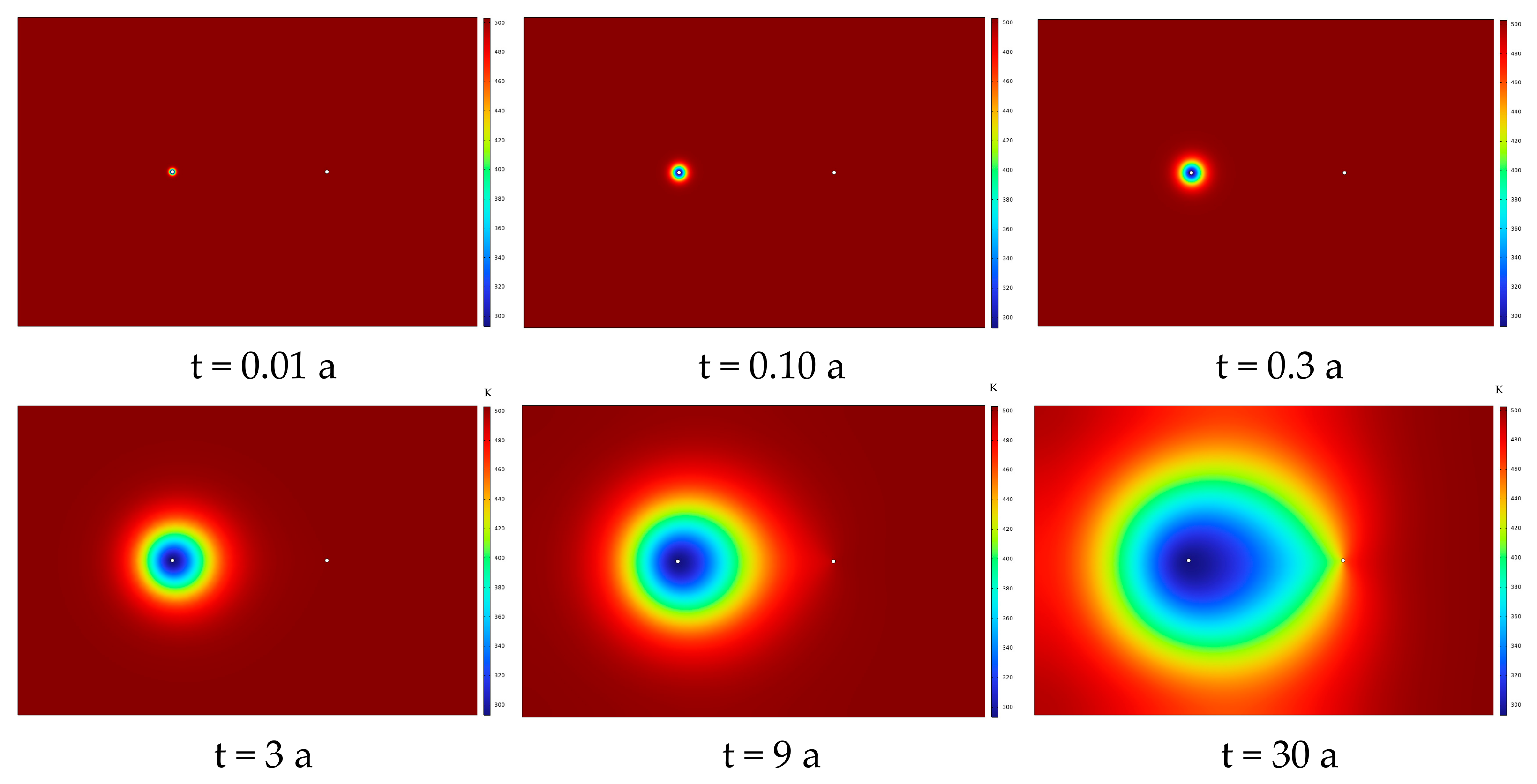
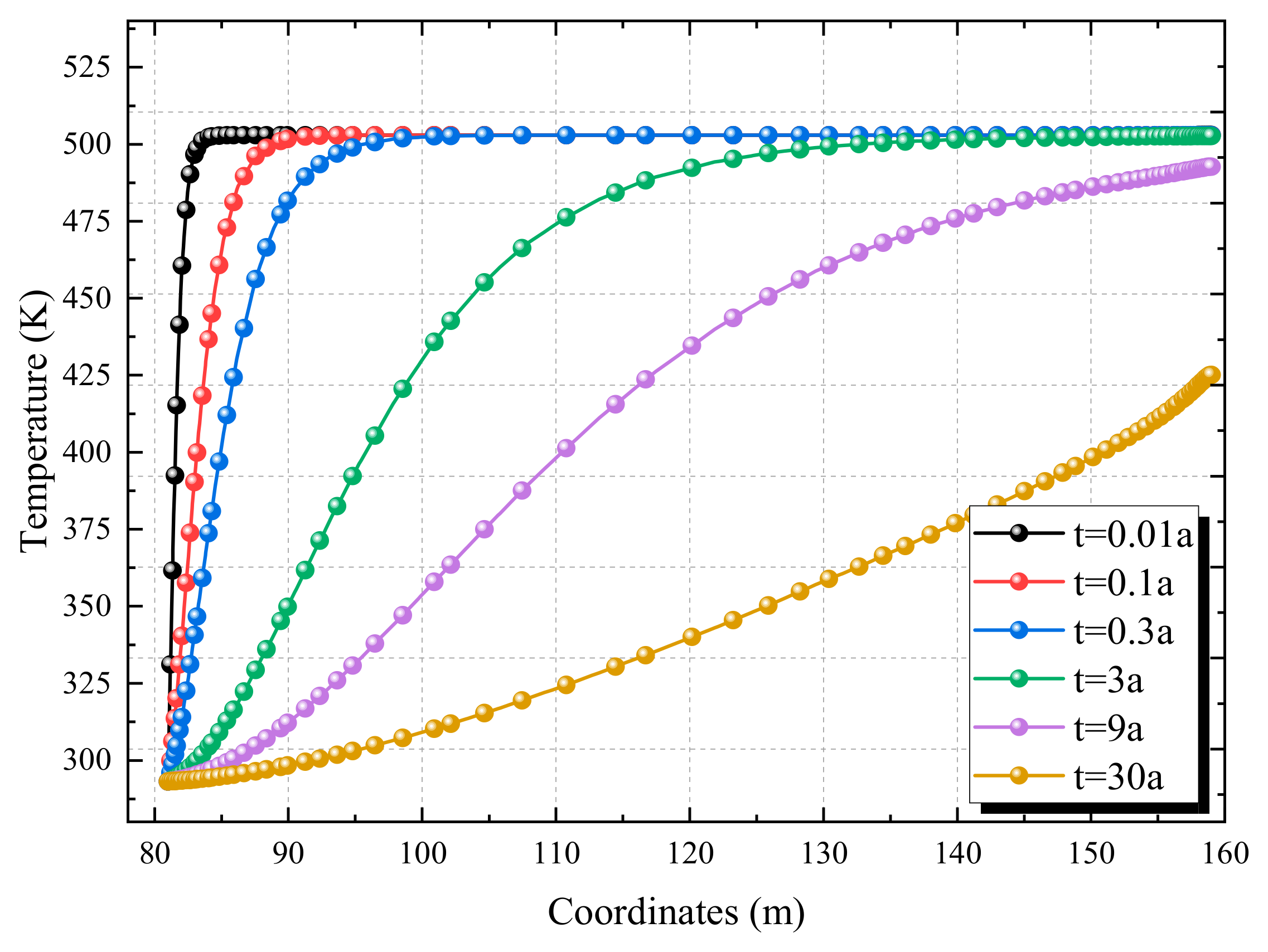
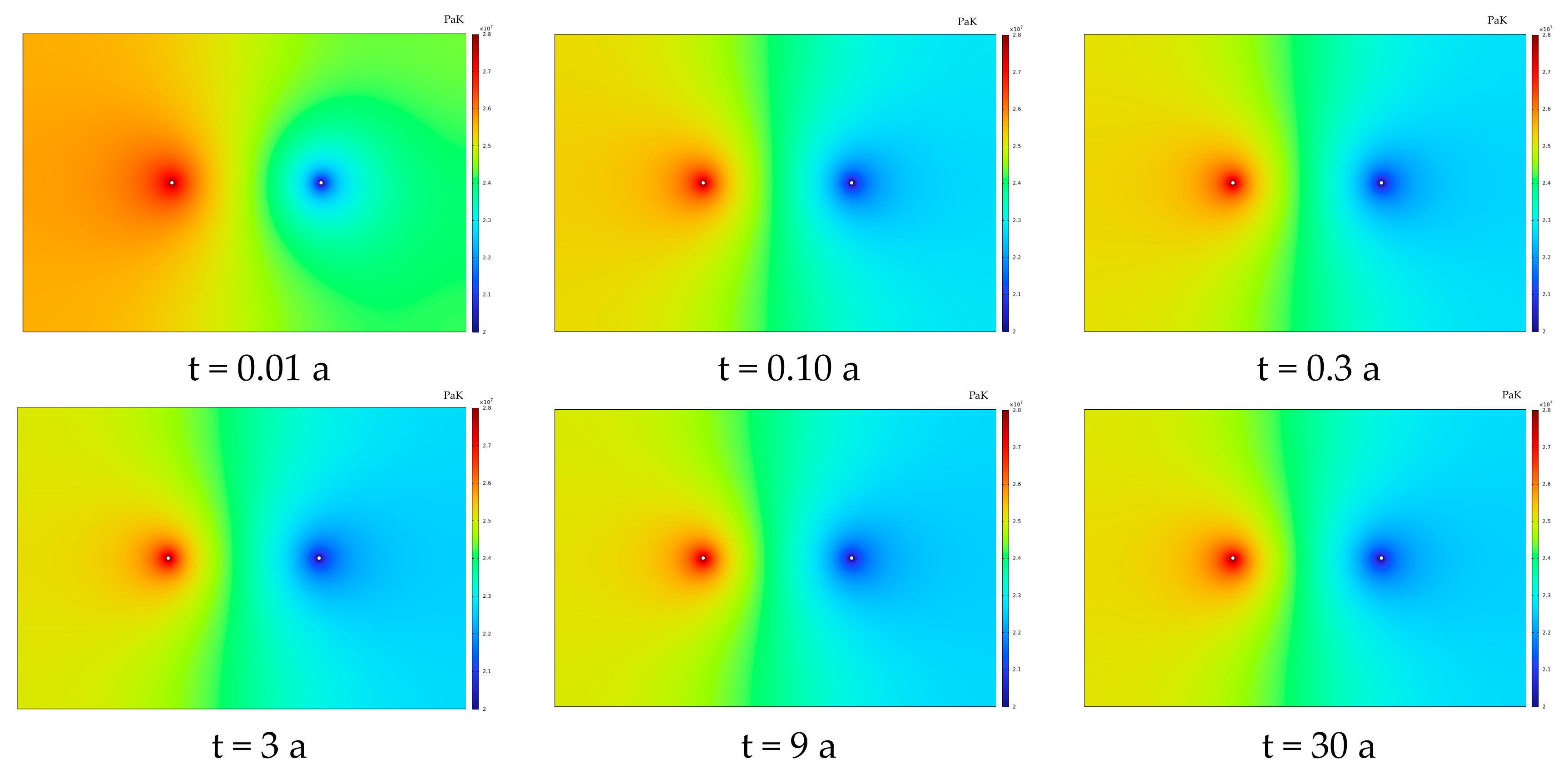
As can be seen from Figure 3 and Figure 4, the injection well (at the 80 m coordinate) continuously injects low-temperature water (20 °C). As the extraction time increases, the cold water gradually advances toward the production well (at the 160 m coordinate), showing an obvious process of “cold zone expansion—high-temperature zone compression”.

In the early extraction stage (t = 0.01~0.3 a): At t = 0.01 a, only the temperature near the injection well (80~83 m) drops rapidly to around 300 K, while the area beyond 90 m still maintains the initial high temperature of the reservoir; at t = 0.3 a, the cold zone has advanced to 100 m, the temperature in the 80~100 m interval decreases significantly, and the area beyond 100 m remains a high-temperature zone. During this stage, the cold water advances at the fastest speed, which reflects the strong fluid seepage and thermal convection driven by the injection–production pressure difference in the early extraction stage.

In the middle extraction stage (t = 3~9 a): At t = 3 a, the cold zone advances to 120 m; at t = 9 a, the cold zone further expands to 145 m. The advancement speed of cold water slows down at this stage. This is because after the reservoir temperature decreases, the thermal convection efficiency declines, and the cold water front is dominated by heat conduction, so the advancement rate shifts from “seepage control” to “heat conduction control”.

In the late extraction stage (t = 30 a): The cold zone almost runs through the entire interval between the injection and production wells (80~160 m), and only a small amount of high-temperature zone remains near 150~160 m. This indicates that the cold water has approached the production well and most areas of the reservoir have been cooled.

From the analysis of absolute temperature values and distribution gradients, the temperature field presents an evolution law of “sharp drop in the early stage—slow drop in the middle stage—stabilization in the late stage”. The initial high temperature of the reservoir continuously decreases during the extraction process; at t = 30 a, the temperature in most areas between the injection and production wells drops to 300~400 K, with only the terminal area remaining above 400 K. In the early extraction stage (e.g., t = 0.01 a), the temperature gradient in the 80~90 m interval is extremely large (jumping from 300 K to 500 K); as time goes by, the gradient gradually flattens (e.g., at t = 30 a, the temperature in the 80~160 m interval slowly rises from 300 K to 425 K), which reflects the transformation of the geothermal reservoir from “strong temperature heterogeneity” to “weak temperature heterogeneity”.

The evolution of the temperature field directly reflects the timeliness and sustainability of heat extraction. In the short term (0~3 a): The cold water advances rapidly, the high-temperature zone has a large range, and the heat extraction efficiency is high (the outlet temperature of the production well is high, and the heat production power is large). In the middle term (3~9 a): The high-temperature zone is compressed but still maintains a certain scale; the heat extraction efficiency gradually decreases with the advancement of cold water, but it still has development value. In the long term (9~30 a): The high-temperature zone is greatly reduced, and the heat extraction efficiency decreases significantly. It is necessary to consider the risk of reservoir “thermal depletion” or extend the effective extraction cycle by adjusting parameters such as well spacing and injection–production pressure difference.

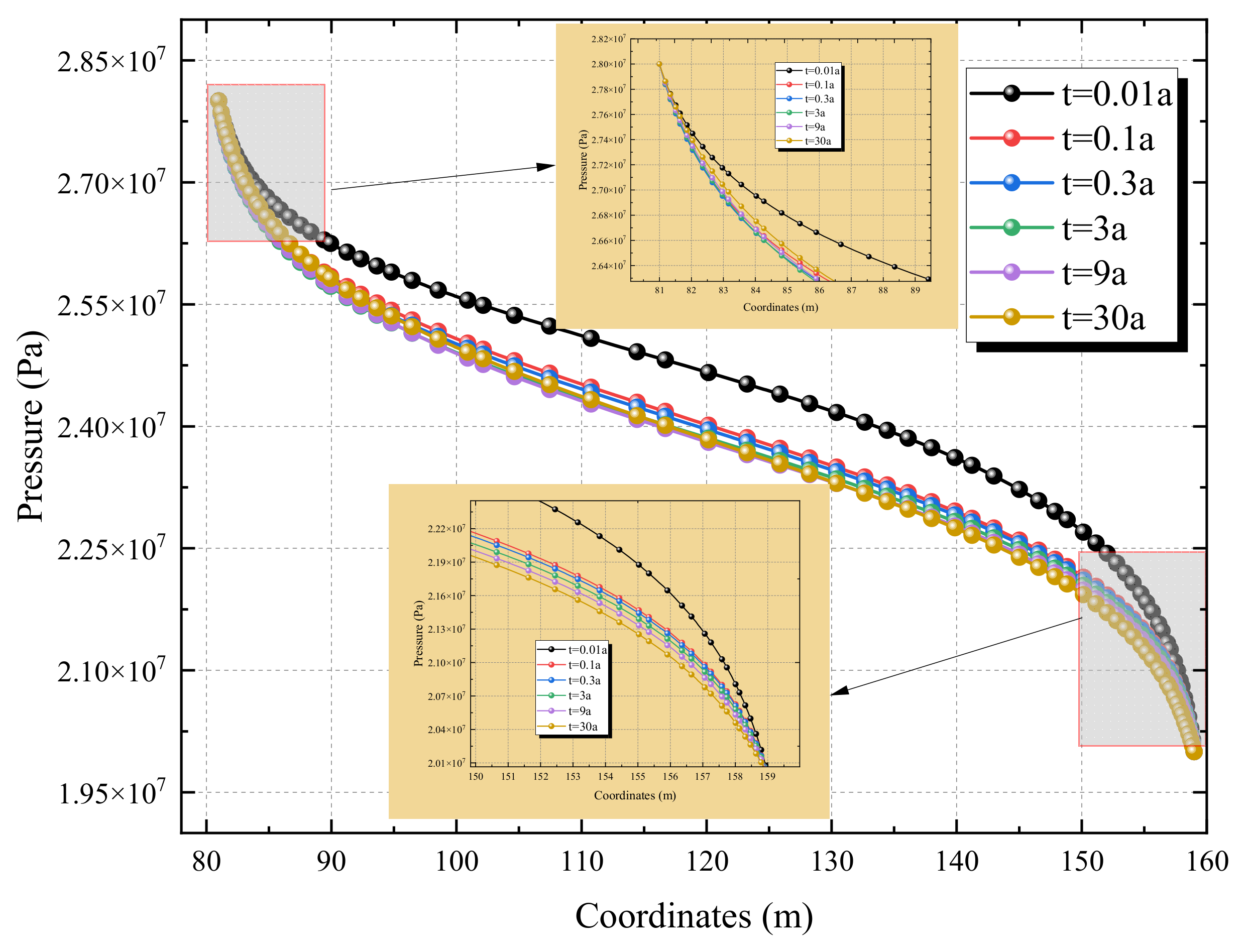
From the perspective of the overall trend (Figure 5 and Figure 6), the pore water pressure shows a monotonically decreasing characteristic along the line connecting the injection and production wells (80→160 m), which is a direct reflection of fluid seepage from the injection well to the production well driven by the injection–production pressure difference.

Near the injection well (80~90 m, enlarged view at the top-left corner): After the extraction enters the stable stage (t > 0.01 a), the pressure gradient is extremely steep in the early stage (t = 0.1 a), which reflects the process of “rapid pressure relief—seepage initiation” of the fluid near the injection well; in the later stage (t = 9 a, 30 a), the gradient gradually flattens, indicating that the seepage field near the injection well gradually stabilizes.

Near the production well (150~160 m, enlarged view at the bottom-right corner): Throughout the entire extraction cycle, the pressure curve shows an obvious “steep drop” characteristic in the early stage, which reflects the rapid disturbance of local pressure caused by the production extraction of the production well; in the later stage, the curve tends to be flat, indicating that the seepage field near the production well also gradually reaches dynamic equilibrium.

There is strong coupling between the evolution of the pore water pressure field and the temperature field (analyzed in the previous section), and the intrinsic mechanism can be revealed from the following two aspects: (1) Seepage-driven thermal convection: In the early stage, a large pressure gradient leads to a high fluid seepage velocity, which further causes the rapid advancement of the cold water front (corresponding to the rapid temperature drop in the 80~100 m area in the temperature field); in the later stage, a small pressure gradient results in a low seepage velocity, leading to a decline in thermal convection efficiency (corresponding to the attenuation of heat extraction efficiency in the temperature field). (2) Synergy between pressure attenuation and thermal depletion: Under long-term extraction, the continuous decrease in pressure and the continuous attenuation of temperature occur simultaneously, which reflects the dual consumption of “fluid–heat” in the reservoir and ultimately leads to a gradual decline in heat extraction efficiency with extraction time.

4.2. Influence of Injection–Production Pressure Difference on Heat Extraction Efficiency of Geothermal Systems

As the core dynamic parameter driving fluid seepage in geothermal reservoirs, the magnitude of the pressure difference directly determines the seepage velocity and migration path of fluids in the reservoir and significantly changes the spatiotemporal distribution characteristics of the geothermal reservoir temperature field through the thermo–hydro–mechanical (THM) multi-field coupling effect. To intuitively reveal the macroscopic regulation law of the injection–production pressure difference on the geothermal reservoir temperature field, this section conducts specialized simulations under the working conditions of injection–production pressure differences of 4 MPa, 6 MPa, 8 MPa, 10 MPa, and 12 MPa based on the thermo–hydro–mechanical coupled numerical model, with the well spacing fixed at 80 m, injection temperature at 20 °C, and initial reservoir temperature at 230 °C. Through the post-processing module of COMSOL Multiphysics, the temperature field contour maps of the geothermal reservoir under different injection–production pressure differences are output, which intuitively present the distribution differences and evolution trends of the temperature field from the spatial scale. This provides macroscopic visual support for the subsequent dynamic evolution analysis of temperature at key locations of injection–production wells and the quantitative analysis of heat extraction efficiency (Figure 7).

The expansion rate of the low-temperature zone (blue-green zone) in the temperature field shows a positive correlation with the injection–production pressure difference, which reflects the direct driving effect of the pressure difference on fluid seepage velocity:

Early extraction stage (t = 0.1 a): Under all pressure differences, the cold zone is confined to the vicinity of the injection well, with no significant difference (since seepage has just started, the driving effect of the pressure difference has not been fully manifested).

Middle extraction stage (t = 6 a): The larger the pressure difference, the wider the expansion range of the cold zone. For example, the radius of the blue low-temperature zone under 12 MPa is much larger than that under 4 MPa, which indicates that a high pressure difference drives fluid to seep rapidly and significantly improves thermal convection efficiency.

Late extraction stage (t = 30 a): Under high pressure differences (e.g., 12 MPa, 10 MPa), the cold zone almost penetrates the entire area between the injection and production wells; under low pressure differences (e.g., 4 MPa), the range of the cold zone is relatively small. This shows that high pressure differences accelerate the extraction of reservoir heat, while low pressure differences delay the thermal depletion process.

At the same time node, the response of the temperature field to the injection–production pressure difference presents a “stepwise sensitivity” characteristic: From 4 MPa to 12 MPa, for every 2 MPa increase, the “magnitude and rate” of cold zone expansion are significantly enhanced. For example, at t = 6 a, the cold zone range under 8 MPa is approximately 1.2 times that under 6 MPa, and the range under 12 MPa is approximately 1.3 times that under 8 MPa. This reflects the “marginal effect” of pressure difference on thermal convection—the larger the pressure difference, the more significant the promoting effect of unit pressure increment on cold zone expansion.

The evolutionary differences of the temperature field directly correspond to two types of development strategies: “short-term high efficiency” and “long-term stability”.

High pressure differences (e.g., 10 MPa, 12 MPa): The cold zone expands rapidly, and the heat extraction efficiency is high in the short term (0~6 a), which is suitable for development scenarios pursuing “rapid heat production”. However, the reservoir is prone to thermal depletion in the long term (>30 a), so it is necessary to plan well pattern adjustment or reservoir reinjection in advance.

Low pressure differences (e.g., 4 MPa, 6 MPa): The cold zone expands slowly, and the efficiency is low in the short term, but stable heat production can still be maintained in the long term (>30 a). This is suitable for geothermal projects oriented to “long-term sustainable development”, especially for scenarios with high requirements for heat production stability.

In summary, by regulating fluid seepage velocity, the injection–production pressure difference significantly affects the spatiotemporal evolution of the geothermal reservoir temperature field: the larger the pressure difference, the faster the cold zone expands, and the higher the short-term heat extraction efficiency, but the higher the long-term thermal depletion risk; the smaller the pressure difference, the slower the cold zone expands, and the lower the short-term efficiency, but the better the long-term sustainability. This law provides a visual and quantitative basis for the optimal design of pressure differences in geothermal systems.

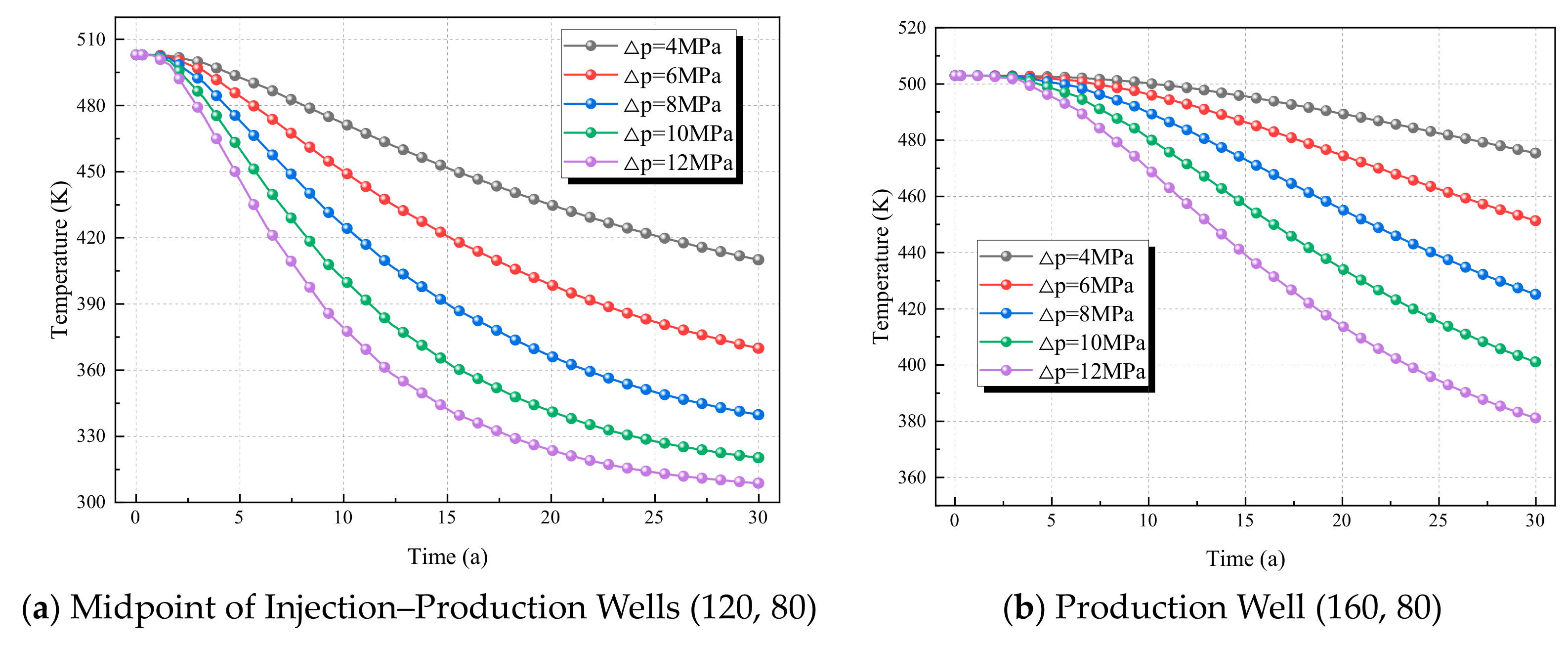
To further quantify the dynamic regulatory effect of the injection–production pressure difference on the geothermal reservoir seepage field, the midpoint of the injection–production wells (120, 80) and the production well (160, 80) are selected as key monitoring points: the former can reflect the average seepage and heat exchange status of the area between the injection and production wells, while the latter directly reflects the pressure response characteristics of the heat extraction terminal. Based on the thermo–hydro–mechanical coupled simulation results under different injection–production pressure differences (4 MPa, 6 MPa, 8 MPa, 10 MPa, 12 MPa), the pore water pressure time-series data of the two monitoring points are extracted. The influence law of pressure difference on the evolution of pore water pressure at key locations is intuitively presented through line charts, laying a theoretical foundation for the seepage field for the subsequent quantitative analysis of heat extraction efficiency and total heat extraction.

As can be seen from Figure 8, under all pressure differences, the temperature of the production well decreases continuously over time, which reflects the continuous heat extraction process of the geothermal reservoir. The larger the injection–production pressure difference, the faster the temperature drop rate. For example:

−

Under Δp = 12 MPa (purple curve): The temperature drops from approximately 500 K to below 450 K after 30 years, showing the fastest drop rate;

−

Under Δp = 4 MPa (gray curve): The temperature only drops to around 475 K after 30 years, with the slowest drop rate.

A larger pressure difference leads to a faster fluid seepage velocity, and the cold water front advances more rapidly toward the production well, resulting in a rapid attenuation of the production well temperature.

As can be seen from Figure 8, consistent with the production well, the temperature at the midpoint decreases continuously over time, but the drop amplitude is more pronounced (within the same time period, the midpoint temperature is 10–50 K lower than that of the production well). It also follows the law that “the larger the pressure difference, the faster the temperature drops”. For example:

−

Under Δp = 12 MPa (purple curve): The temperature drops sharply from approximately 500 K to around 300 K after 30 years;

−

Under Δp = 4 MPa (gray curve): The temperature drops to around 410 K after 30 years, and the attenuation rate is much lower than that under high-pressure difference conditions.

The midpoint is located between the injection and production wells, serving as the core area for fluid seepage and thermal convection. The heat exchange of the cold water front is more direct here, so the temperature attenuation is more intense than that at the production well. The significantly higher temperature attenuation rate at the midpoint of the injection–production wells reflects that “the area between the injection and production wells is the core action zone for heat extraction”, and the thermal convection effect of fluid seepage is more prominent in this middle area.

High pressure differences (e.g., 10 MPa, 12 MPa) can quickly reduce the reservoir temperature and improve short-term heat extraction efficiency (with high outlet temperature of the production well and large heat production power), whereas low pressure differences (e.g., 4 MPa, 6 MPa) result in slow temperature attenuation and low reservoir heat consumption rate, leading to a longer “effective cycle” for long-term heat extraction, which is suitable for development scenarios pursuing stable heat production. In summary, by regulating the fluid seepage velocity, the injection–production pressure difference significantly affects the temperature evolution at key locations of the geothermal reservoir: the larger the pressure difference, the faster the temperature drops, and the higher the short-term heat extraction efficiency, but the higher the long-term thermal depletion risk. Moreover, the temperature attenuation at the midpoint of the injection–production wells is more intense than that at the production well, making it the core response zone of the thermo–hydro coupling effect. This law provides a quantitative basis for the optimal design of the injection–production pressure difference in geothermal systems (balancing short-term efficiency and long-term stability).

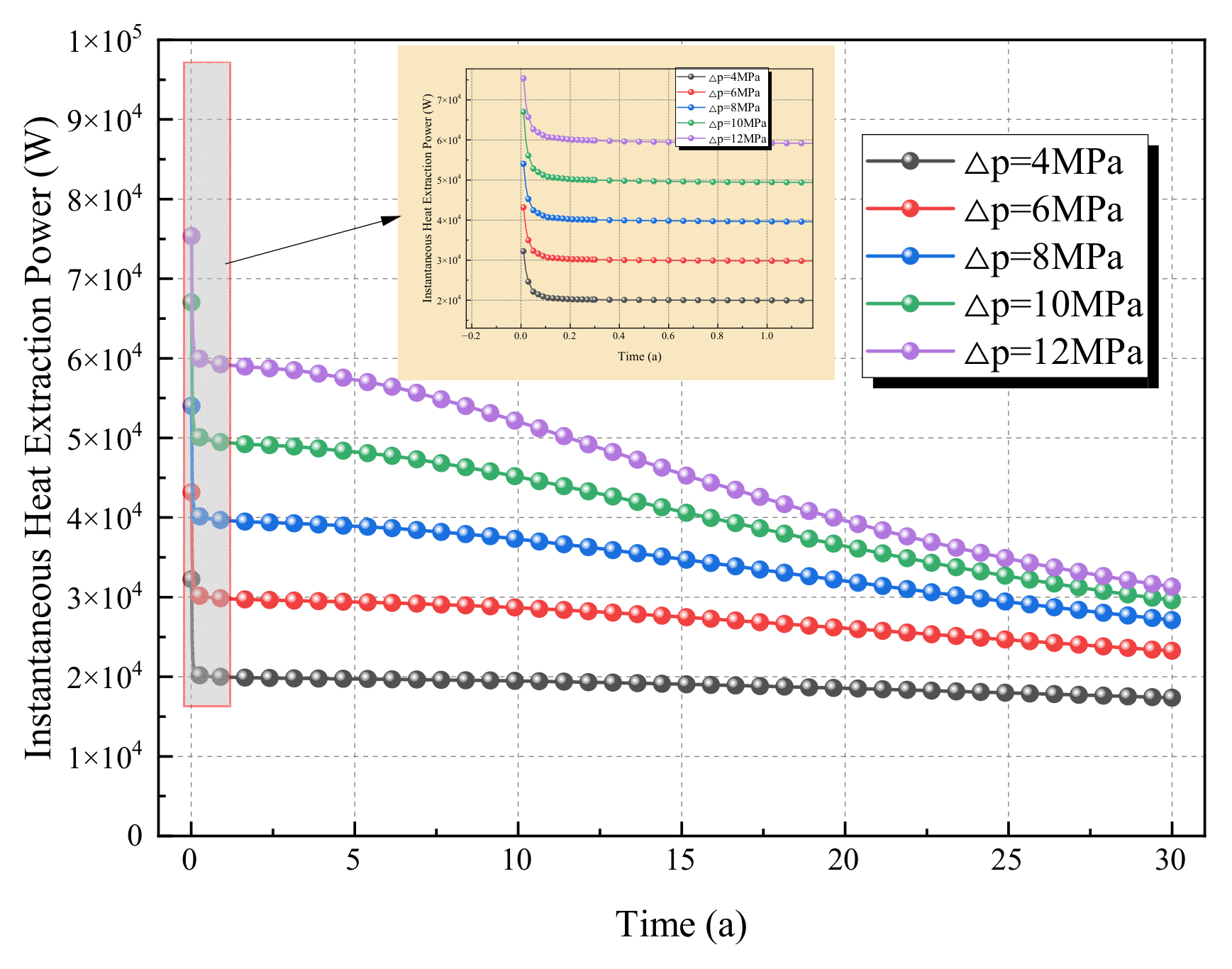
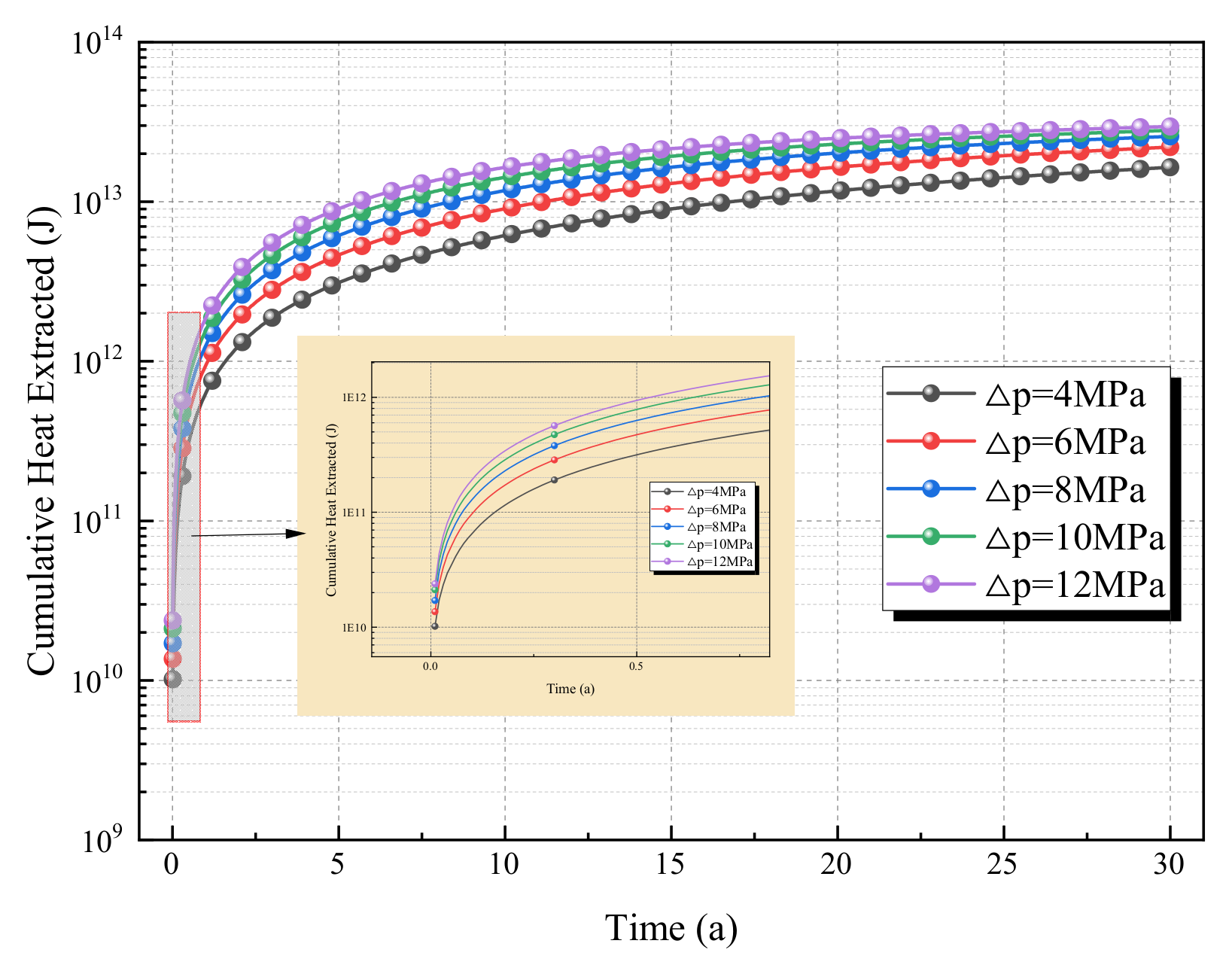
To quantify the dynamic regulatory effect of the injection–production pressure difference on heat extraction efficiency, instantaneous heat extraction power (reflecting the heat production intensity at a certain moment, unit: W) and cumulative heat extraction (reflecting the total heat gain during the extraction cycle, unit: J) are selected as core evaluation indicators. Based on the thermo–hydro–mechanical coupled simulation results under different injection–production pressure differences (4 MPa, 6 MPa, 8 MPa, 10 MPa, 12 MPa), time-series data are extracted and variation curves are plotted to intuitively present the dynamic fluctuation characteristics of heat extraction power and the cumulative evolution law of heat extraction. This provides key data support for the subsequent optimal design of the injection–production pressure difference and the quantitative evaluation of heat extraction efficiency.

As can be seen from Figure 9 and Figure 10, the instantaneous power under all pressure differences continuously attenuates, yet the power under high pressure differences remains consistently higher than that under low pressure differences. For instance, after 30 years, the power under Δp = 12 MPa is approximately 3 × 10⁴ W, while it is only about 1.5 × 10⁴ W under Δp = 4 MPa. This indicates that the “short-term heat production advantage” of high pressure differences can be maintained over the long term, but the attenuation rate is faster; low pressure differences result in lower heat production intensity but better stability.

The cumulative heat extraction continuously increases over time and gradually approaches saturation. The cumulative amount under high pressure differences (10 MPa, 12 MPa) is eventually significantly higher than that under low pressure differences (4 MPa, 6 MPa). For example, after 30 years, the cumulative heat extraction under Δp = 12 MPa is close to 2.9 × 10¹³ J, while it is approximately 1.6 × 10¹³ J under Δp = 4 MPa.

4.3. Influence of Injection Temperature on Heat Extraction Efficiency of Geothermal Systems

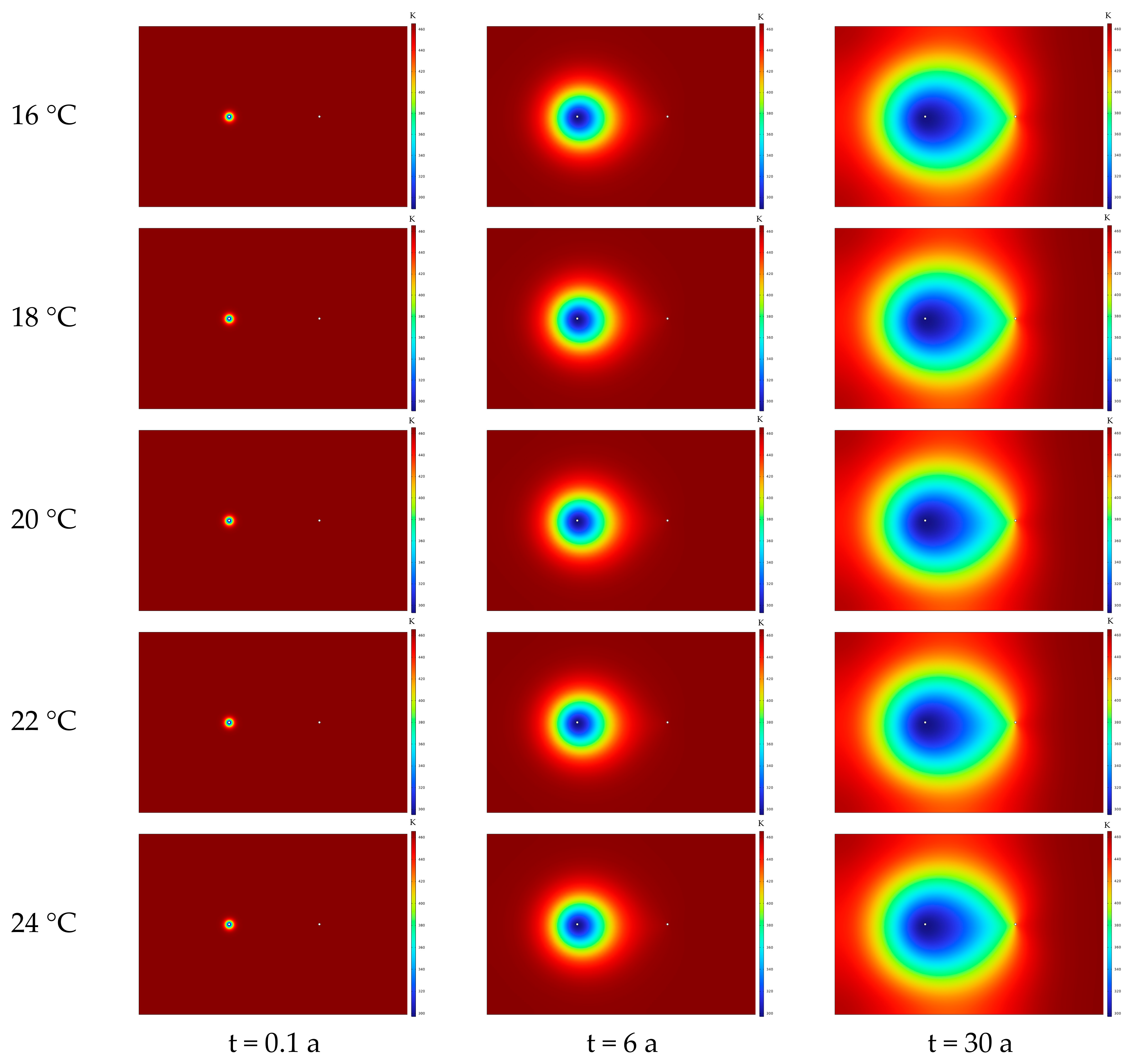
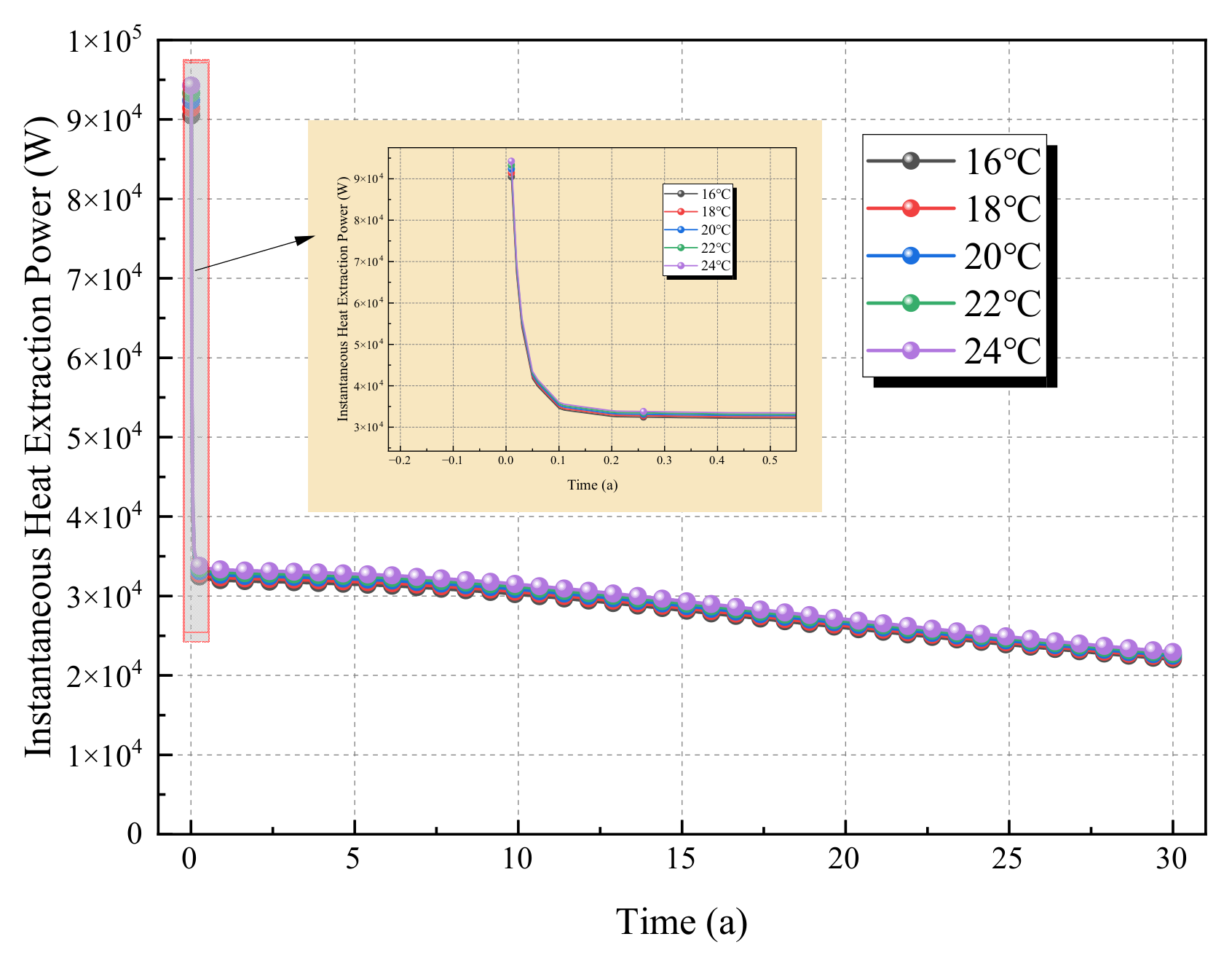
To clarify the macroscopic regulation mechanism of injection temperature on the heat exchange process in geothermal reservoirs, this section conducts thermo–hydro–mechanical (THM) coupled simulations with an injection temperature gradient (16 °C, 18 °C, 20 °C, 22 °C, 24 °C). The selection of 16 °C, 18 °C, 20 °C, 22 °C, and 24 °C as injection temperatures is due to their proximity to the normal temperature range, which facilitates the exploration of heat extraction response laws of geothermal systems under normal temperature injection conditions in practical engineering. Through temperature field contour maps of the geothermal reservoir under different injection temperatures, the influence laws of injection temperature on the range of thermal convection and the degree of high-temperature zone compression are intuitively revealed from the spatial scale.

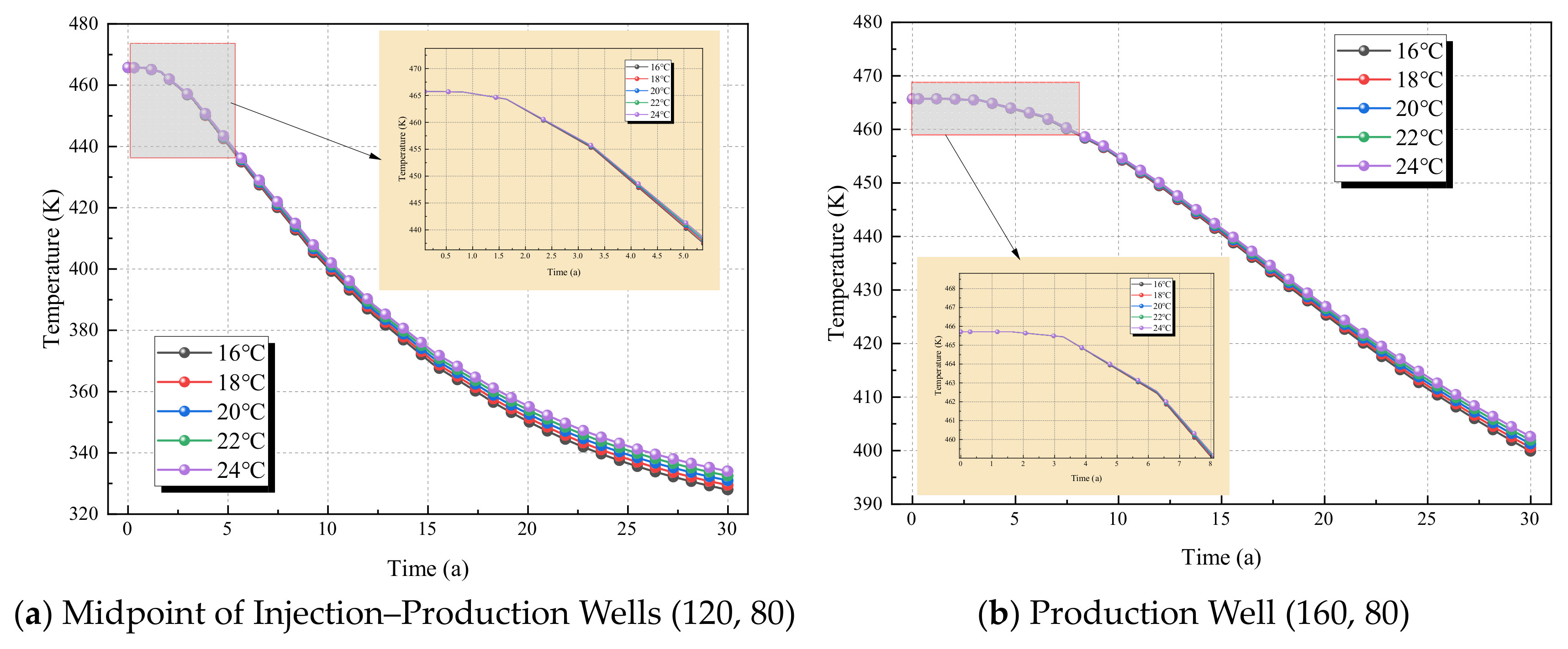
To further quantify the dynamic regulatory effect of injection temperature on the geothermal reservoir temperature field, the midpoint of the injection–production wells (120, 80) and the production well (160, 80) are selected as key monitoring points: the former reflects the average heat exchange status of the area between the injection and production wells, while the latter directly embodies the temperature response characteristics of the heat extraction terminal. Based on the THM coupled simulation results under different injection temperatures (16 °C, 18 °C, 20 °C, 22 °C, 24 °C), temperature time-series data of the two monitoring points are extracted, and the influence law of injection temperature on the temperature evolution at key locations is intuitively presented through line charts.

As can be seen from Figure 11 and Figure 12, the under all injection temperatures, the midpoint temperature decreases continuously over time, and the lower the injection temperature, the faster the temperature drop rate. For example, under 16 °C (gray curve), the temperature drops from approximately 460 K to 330 K after 30 years, while under 24 °C (purple curve), it only drops from 460 K to around 340 K during the same period. The temperature evolution of the production well (160, 80) follows the same law as the midpoint: the temperature decreases continuously over time, but the production well temperature is always higher than the midpoint temperature (the production well temperature is 20–50 K higher than the midpoint temperature at the same time). For instance, after 30 years, the production well temperature under 16 °C is approximately 400 K, while the midpoint temperature is only 330 K.

The temperature difference between the injection temperature and the initial reservoir temperature is the core driving force for thermal convection—the lower the injection temperature, the larger the temperature difference, and the stronger the thermal convection. This is manifested as rapid expansion of the cold zone in the temperature field (contour maps) and rapid temperature attenuation at key locations (curve charts), resulting in high short-term heat extraction efficiency but a higher risk of long-term reservoir “thermal depletion”. For “short-term high-efficiency heat production”, a low injection temperature of 16–18 °C is preferred to quickly improve heat extraction power using a large temperature difference, whereas for “long-term stable heat production”, a high injection temperature of 22–24 °C is selected to delay thermal depletion and prolong the effective extraction cycle by reducing the temperature difference.

In summary, through the coupling mechanism of “temperature difference–thermal convection”, injection temperature significantly affects the temperature evolution at key locations of the geothermal reservoir: Lower injection temperatures lead to higher short-term heat extraction efficiency but poorer long-term stability, whereas higher injection temperatures result in lower short-term efficiency but better long-term sustainability.

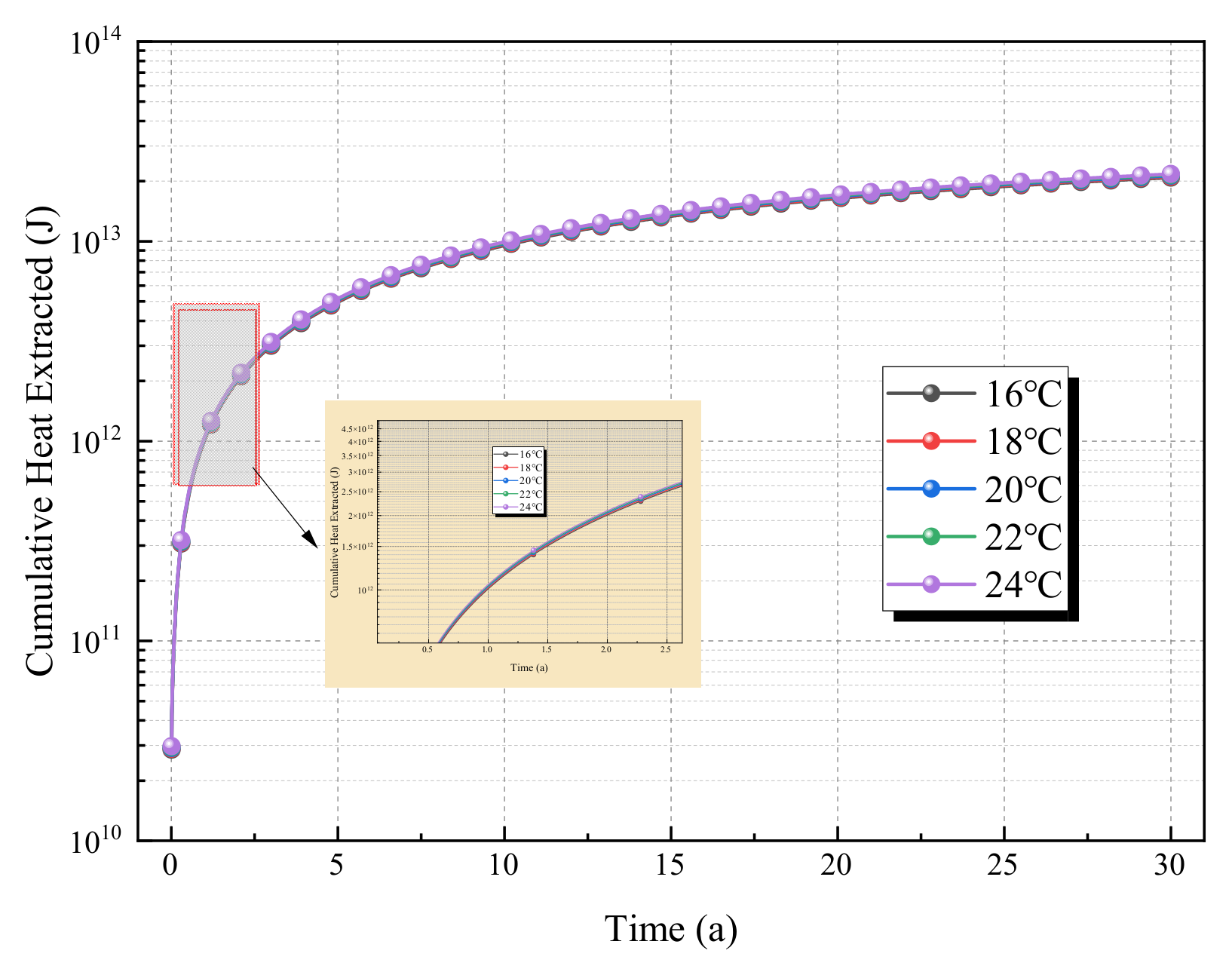
These two figures present the evolution laws of heat extraction efficiency under different injection temperatures (16 °C, 18 °C, 20 °C, 22 °C, 24 °C) from the perspectives of long-term heat gain and instantaneous heat production intensity, respectively (Figure 13 and Figure 14). Under all injection temperatures, the cumulative heat extraction continuously increases over time and gradually approaches saturation. The overlapping curves indicate that within the normal temperature range of 16–24 °C, the regulatory effect of injection temperature on long-term cumulative heat extraction is extremely weak. The temperature difference between the injection temperature (16–24 °C) and the initial reservoir temperature is sufficiently large, so thermal convection is dominated by the “strong temperature difference between the high reservoir temperature and normal injection temperature” rather than minor differences in injection temperature (e.g., only an 8 °C difference between 16 °C and 24 °C), leading to the convergence of long-term cumulative heat extraction.

The initial heat extraction power is high, followed by continuous attenuation. The overlapping curves show that within the 16–24 °C range, the influence of injection temperature on the dynamic evolution of instantaneous heat production intensity is consistent. In the early extraction stage, the strong temperature difference drives rapid fluid seepage, and the thermal convection efficiency reaches a relatively high level; the marginal impact of minor changes in injection temperature (16–24 °C) on the “seepage–thermal convection” coupling process is negligible. Therefore, the initial peak value and attenuation trend of instantaneous power both show overlap.

Within the normal temperature range of 16–24 °C, due to the sufficiently large temperature difference with the high reservoir temperature, the regulatory effect of injection temperature on heat extraction efficiency (cumulative heat extraction, instantaneous power) is extremely insignificant, as reflected by overlapping curves. This means that in practical engineering, if the injection water is at normal temperature (e.g., groundwater, surface water), there is no need to overemphasize its minor temperature fluctuations; the optimization of heat extraction efficiency should focus more on core parameters such as injection–production pressure difference and well spacing. The “insensitivity” of injection temperature within this range also provides flexibility in the selection of injection water for geothermal projects—as long as normal temperature conditions are met, stable heat extraction effects can be achieved.

4.4. Influence of Well Spacing on Heat Extraction Efficiency of Geothermal Systems

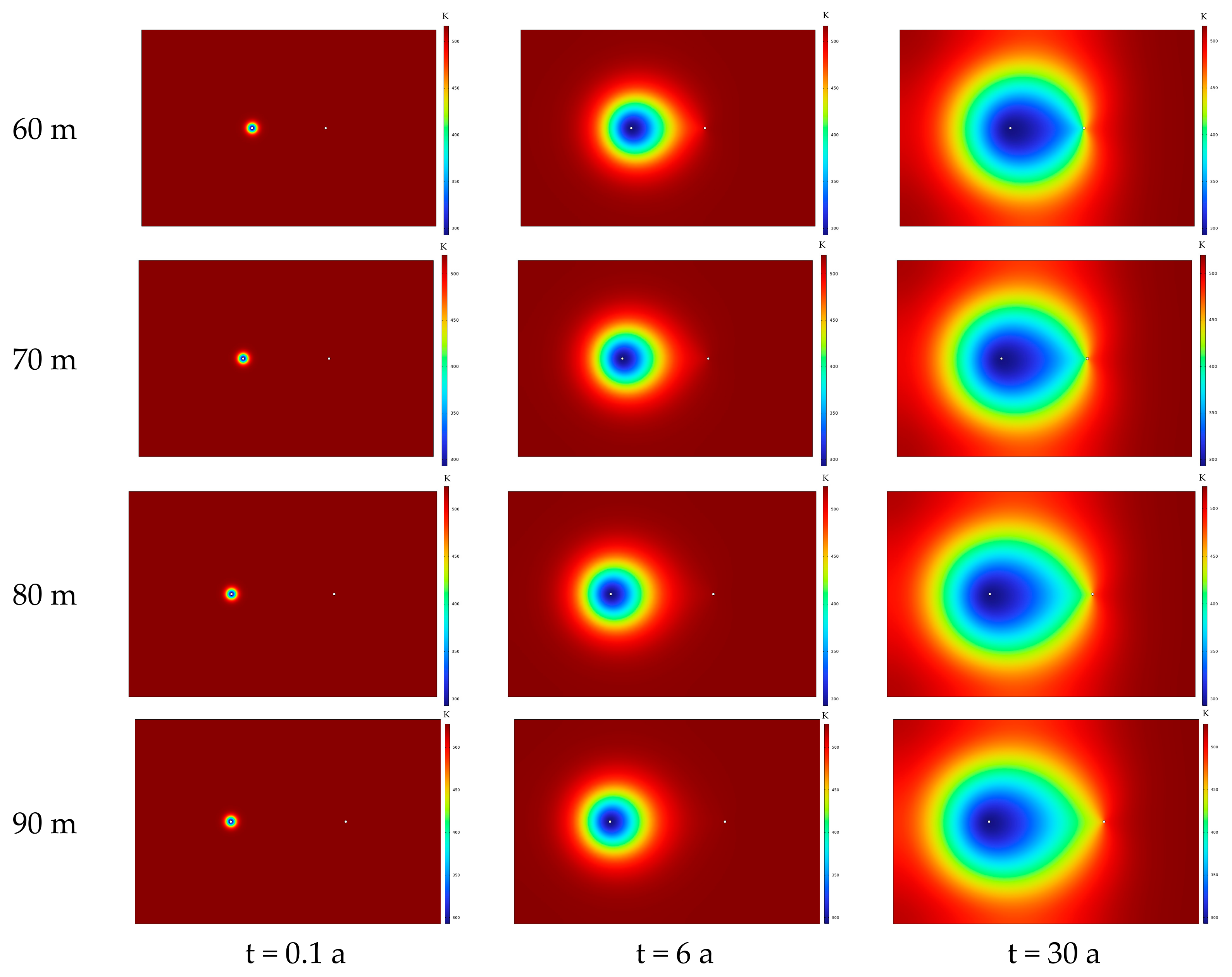
To quantify the macroscopic regulation mechanism of well spacing on heat transfer and thermal convection processes in geothermal reservoirs, this section focuses on the spatial coupling effect between well spacing and the geothermal reservoir temperature field. THM coupled simulations are conducted with a fixed injection temperature of 20 °C, a fixed injection–production pressure difference of 8 MPa, and a well spacing gradient (60 m, 70 m, 80 m, 90 m).

As can be seen from Figure 15 and Figure 16 the well spacing directly affects the range of thermal convection between injection and production wells and the expansion rate of the cold zone:

-

Early extraction stage (t = 0.1 a): Under all well spacings, the cold zone is confined to the vicinity of the injection well, with no significant differences (thermal convection has just started, and the spatial effect of well spacing has not been fully manifested).

-

Middle extraction stage (t = 6 a): The smaller the well spacing, the wider the expansion range of the cold zone. For example, the radius of the blue low-temperature zone at a well spacing of 60 m is significantly larger than that at 90 m, indicating that smaller well spacing results in shorter seepage paths between injection and production wells, higher thermal convection efficiency, and faster advancement of the cold water front.

-

Late extraction stage (t = 30 a): The cold zone at a well spacing of 60 m almost penetrates the entire area between the injection and production wells, while the cold zone range at 90 m is relatively small. This shows that smaller well spacing leads to faster reservoir heat consumption and a more rapid thermal depletion process.

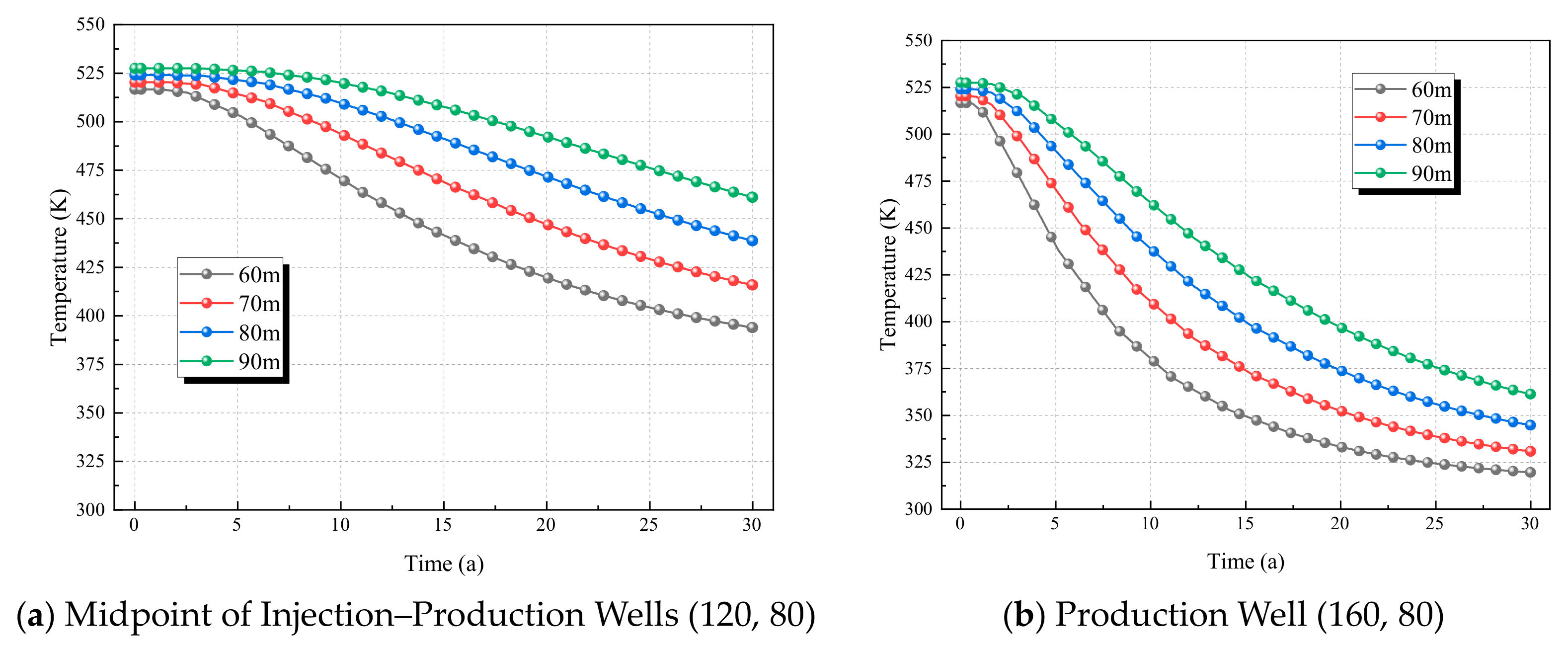
Under all well spacings, the midpoint temperature decreases continuously over time, and the smaller the well spacing, the faster the temperature drop rate. For example, at a well spacing of 60 m (gray curve), the temperature drops from approximately 525 K to below 400 K after 30 years, while at 90 m (green curve), it only drops from 525 K to around 450 K during the same period. The production well follows the same law as the midpoint: the temperature decreases continuously over time, but the production well temperature is always higher than the midpoint temperature (the production well temperature is 20–50 K higher than the midpoint temperature at the same time). For instance, after 30 years, the production well temperature at a well spacing of 60 m is approximately 325 K, while the midpoint temperature is only below 400 K.

In summary, well spacing is a core spatial parameter for regulating the heat extraction efficiency of geothermal systems: smaller well spacing leads to higher short-term heat extraction efficiency but poorer long-term stability; larger well spacing results in lower short-term efficiency but better long-term sustainability. This law provides a quantitative basis for the “optimized spacing design” of geothermal well patterns.

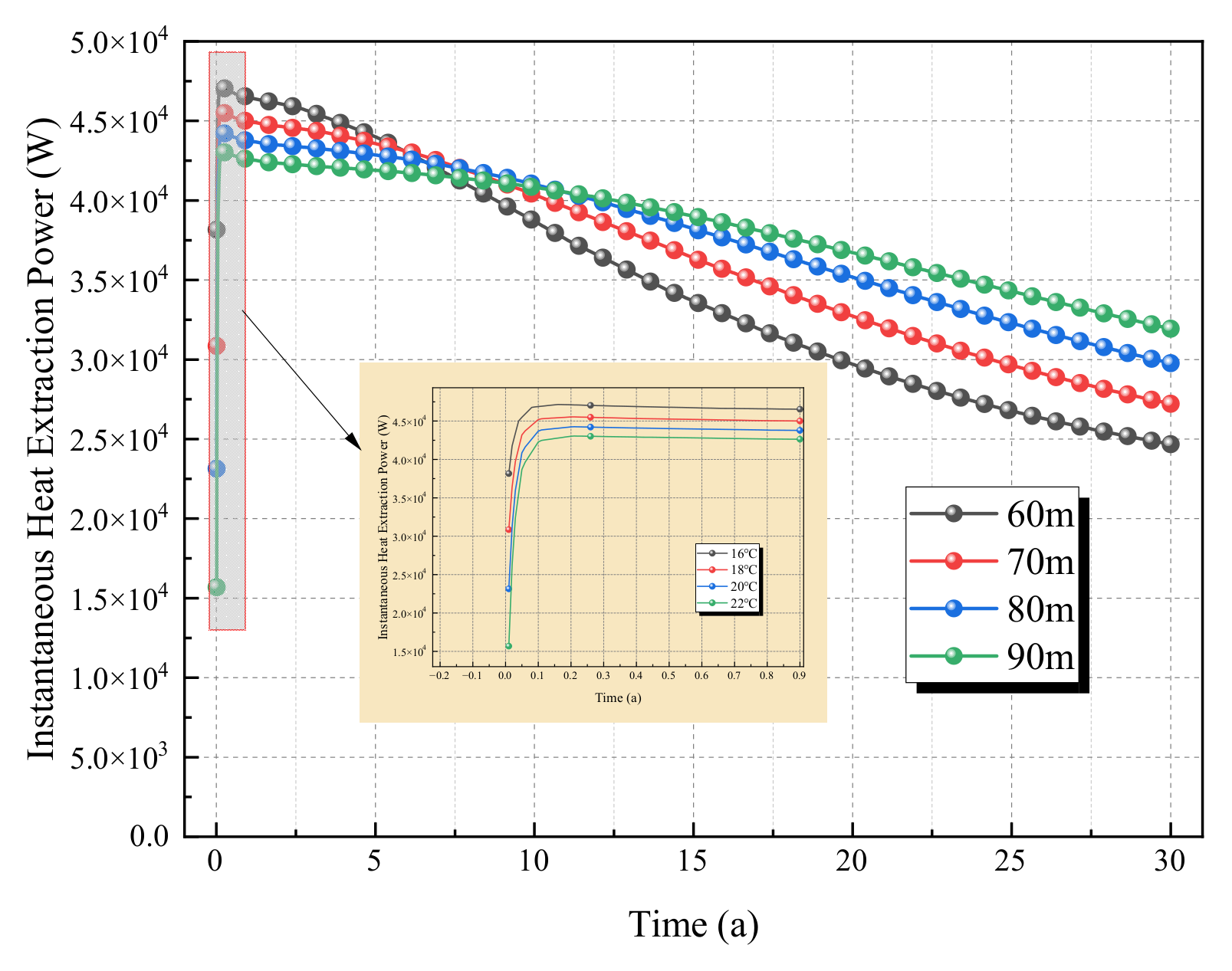
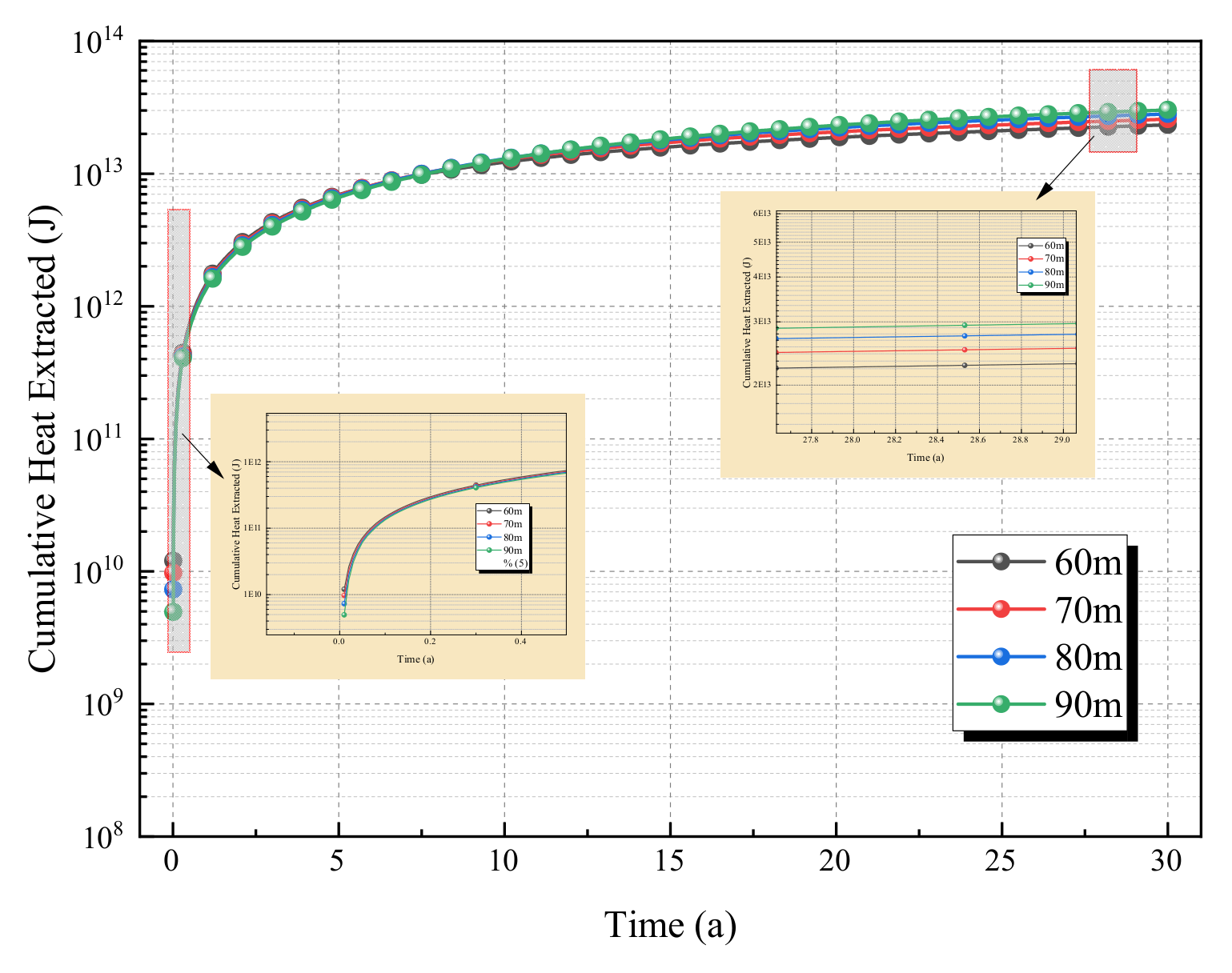
As can be seen from Figure 17 and Figure 18 the smaller well spacing leads to a higher initial peak of instantaneous power and faster attenuation. For example, at a well spacing of 60 m (gray curve), the initial power can reach 4.75 × 10⁴ W, but it rapidly attenuates to approximately 3 × 10⁴ W after 30 years; in contrast, at 90 m (green curve), the initial power is about 4.45 × 10⁴ W, with relatively gentle attenuation. Mechanism: Smaller well spacing results in shorter seepage paths between injection and production wells, a stronger driving force for thermal convection, and higher initial heat production power; however, rapid reservoir heat consumption leads to rapid power attenuation. The “short-term heat production advantage” of small well spacing diminishes rapidly over time, while the “long-term stability” of large well spacing becomes more prominent.

The cumulative heat extraction continuously increases over time and gradually approaches saturation. The final cumulative amount at large well spacing (90 m) is significantly higher than that at small well spacing (60 m). For example, after 30 years, the cumulative heat extraction at 90 m is close to 2.97 × 10¹³ J, while it is approximately 2.21 × 10¹³ J at 60 m. Growth rate: In the early stage (0–5 years, enlarged view), the cumulative amount at small well spacing increases extremely rapidly, while the growth at large well spacing is relatively slow. In the later stage (10–30 years), the growth of the cumulative amount at small well spacing tends to stagnate (due to thermal depletion), while large well spacing still maintains stable growth and eventually surpasses the cumulative amount at small well spacing. Mechanism: The high instantaneous power at small well spacing drives the rapid rise of cumulative amount in the early stage; however, the reservoir heat is quickly exhausted, leading to stagnant growth in the later stage; large well spacing results in slow reservoir heat consumption, sustainable long-term growth, and ultimately higher total gain.

In summary, by regulating the “intensity of thermal convection and the rate of reservoir heat consumption”, well spacing exhibits the law of “high short-term efficiency but rapid long-term attenuation for small well spacing, and moderate short-term performance but higher long-term total gain for large well spacing” in terms of both instantaneous heat production intensity and long-term heat accumulation.

5. Conclusions

In this study, a two-dimensional thermo–hydro–mechanical (THM) multi-field coupled numerical model for medium-deep geothermal reservoirs was established. The single-factor variable method was used to analyze the influences of injection–production pressure difference, well spacing, and injection temperature on heat extraction efficiency. The key conclusions are as follows:

(1)

The injection–production pressure difference dominates thermal convection and thermal depletion: A larger pressure difference leads to faster fluid seepage and more rapid cold zone advancement, improving short-term heat extraction power; additionally, rock mass deformation further accelerates seepage. However, high pressure differences accelerate heat consumption, increasing the risk of long-term thermal depletion.

(2)

Well spacing determines the spatiotemporal balance of heat extraction: Small well spacing results in short seepage paths, leading to high initial heat production power but rapid heat consumption and low long-term cumulative heat extraction; large well spacing leads to moderate short-term heat production but stable long-term output, making it suitable for long-term development.

(3)

The sensitivity of injection temperature within the normal temperature range of 16–24 °C is negligible: Within this range, different injection temperatures have little impact on the temperature drop at key locations, instantaneous power, and cumulative heat extraction. Thermal convection is dominated by strong temperature differences, providing greater flexibility in the selection of water sources in engineering.