Voltage Control for DC Microgrids: A Review and Comparative Evaluation of Deep Reinforcement Learning
Abstract
1. Introduction
- It provides a survey of various state-of-the-art model-based, model-free, and hybrid voltage control techniques.
- It proposes BO-DRL-based solutions for voltage control of a DC/DC buck converter with an input LC filter.
- It proposes recommendations for future research, particularly those that employ machine learning and data-driven control algorithms.
2. Background of the Study
2.1. Cause of Voltage Instability
- Intermittent generation: The fluctuating nature of RES causes mismatch between generation and demand, leading to voltage instability [16]. For example, PV output depends on weather conditions like temperature and solar irradiance.
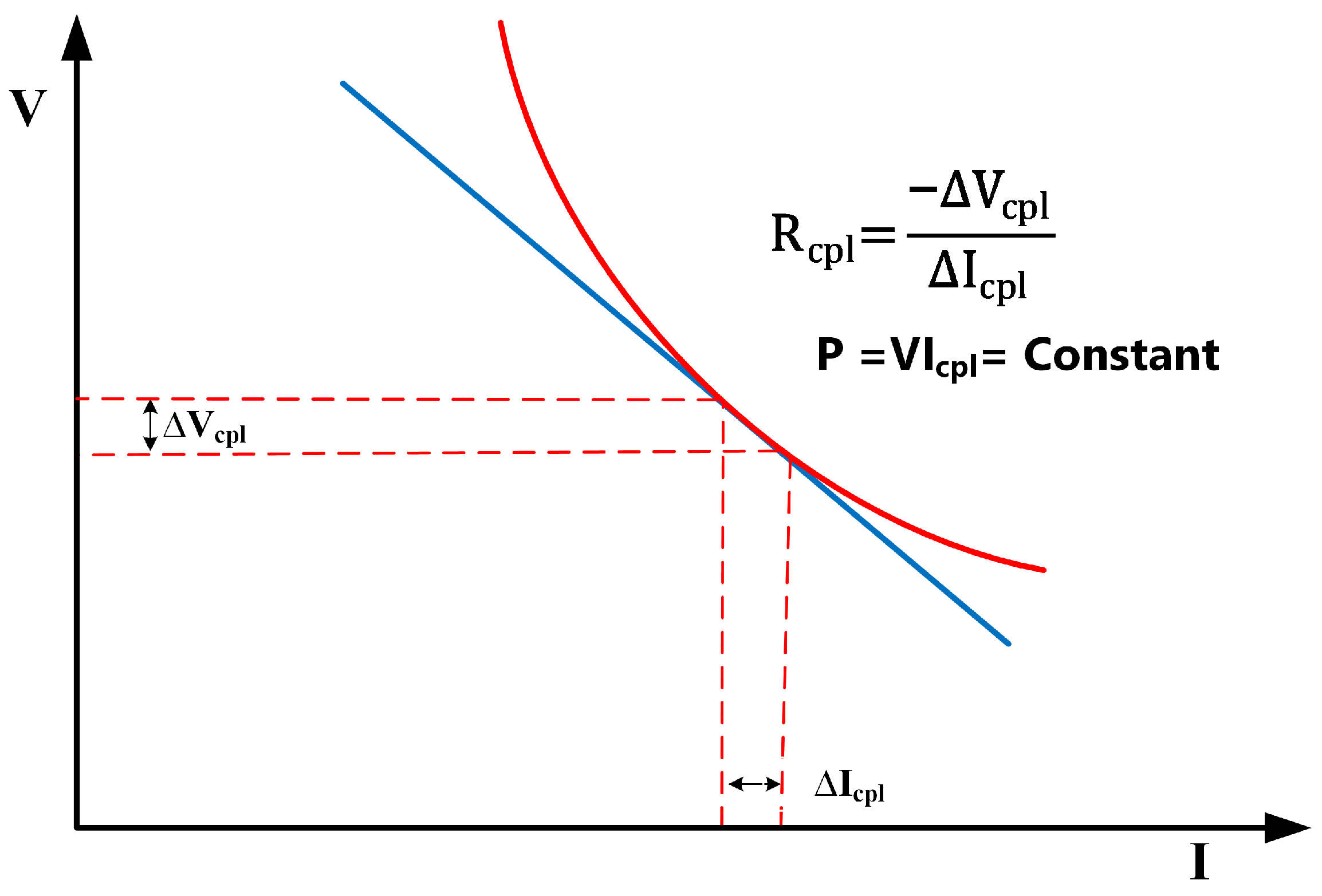
- CPL are nonlinear loads characterized by negative incremental impedance [17]. They maintain constant power consumption despite DC bus voltage fluctuates. DC load regulated by DC/DC converters often exhibits CPL behavior, which can destabilize the system. Voltage instability caused by CPL has been extensively studied [18,19]. Figure 2 illustrates this negative incremental impedance behavior.
- Pulse power loads (PPL) draw large current in short durations, potentially causing voltage instability due to their high-power characteristics [20]. They are common in onboard MG of electric ships, particularly for systems like sonar and radar.
- Faults and aging can alter system dynamics, posing the risk of instability and poor performance. Additional challenges related to the operation, control, and protection of DC MGs are reported in [21].
- Filters, such as commonly used LC types, improve power quality, but can reduce the damping ratio of DC MG, increasing the risk of instability [22].
2.2. DC Microgrid Control
3. Model-Based Techniques
3.1. Sliding Mode Control
3.2. Adaptive Droop Control
3.3. Model Predictive Control
3.4. Passivity-Based Control
3.5. Active Disturbance Control
3.6. H-Infinity Control
4. Model-Free Techniques
4.1. Fuzzy Logic Control
4.2. Data-Driven Control
4.2.1. Artificial Neural Network
4.2.2. Local Model Networks
4.2.3. Model-Free Adaptive Control
4.2.4. Deep Reinforcement Learning
5. Hybrid Control Techniques
5.1. Metaheuristic Optimization Algorithms
5.2. Physics-Informed Neural Networks
6. A Case Study of DC/DC Converter with LC Filter
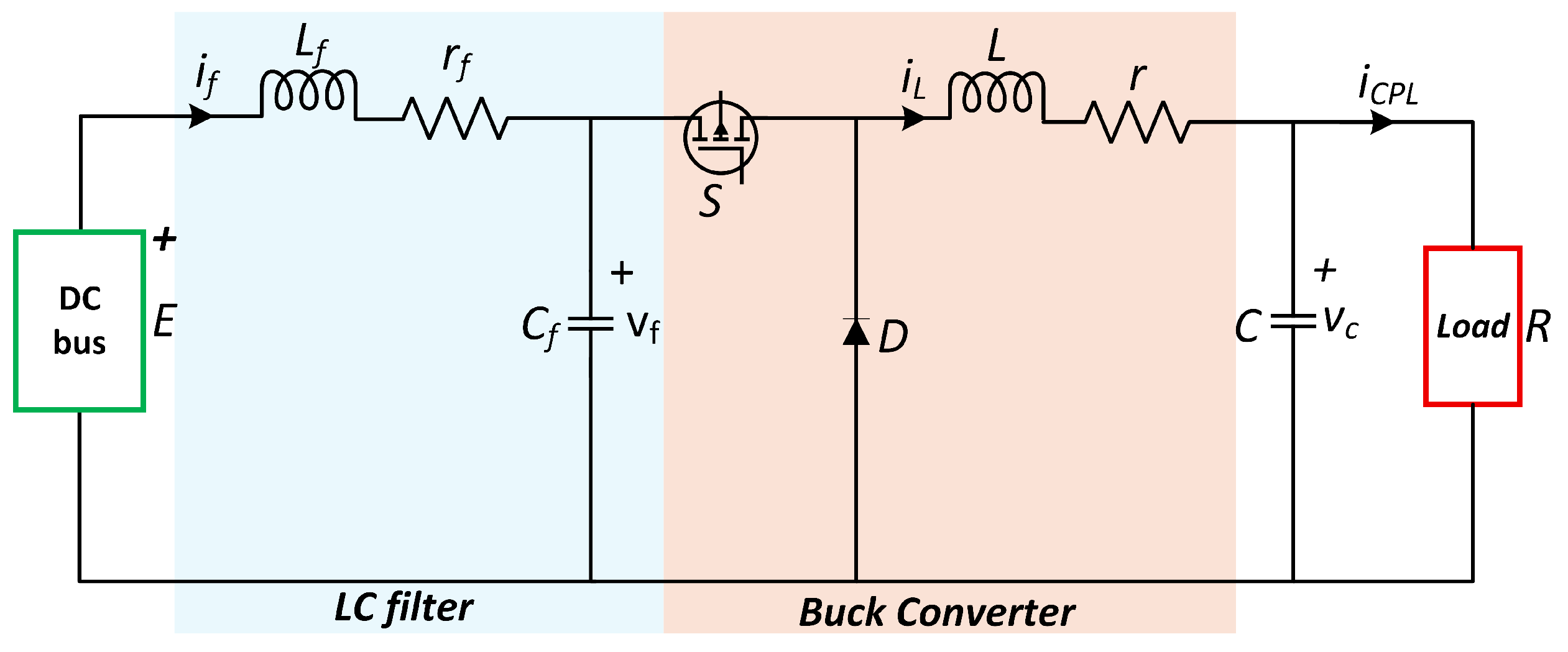
6.1. System Model
6.2. DRL Algorithms
6.2.1. PPO
6.2.2. TD3
6.3. DRL Controller Design
6.3.1. State Space
6.3.2. Action Space
6.3.3. Reward Function
6.3.4. Hyperparameter Optimization
| Algorithm 1 Bayesian optimization |
|
6.4. Simulation Results
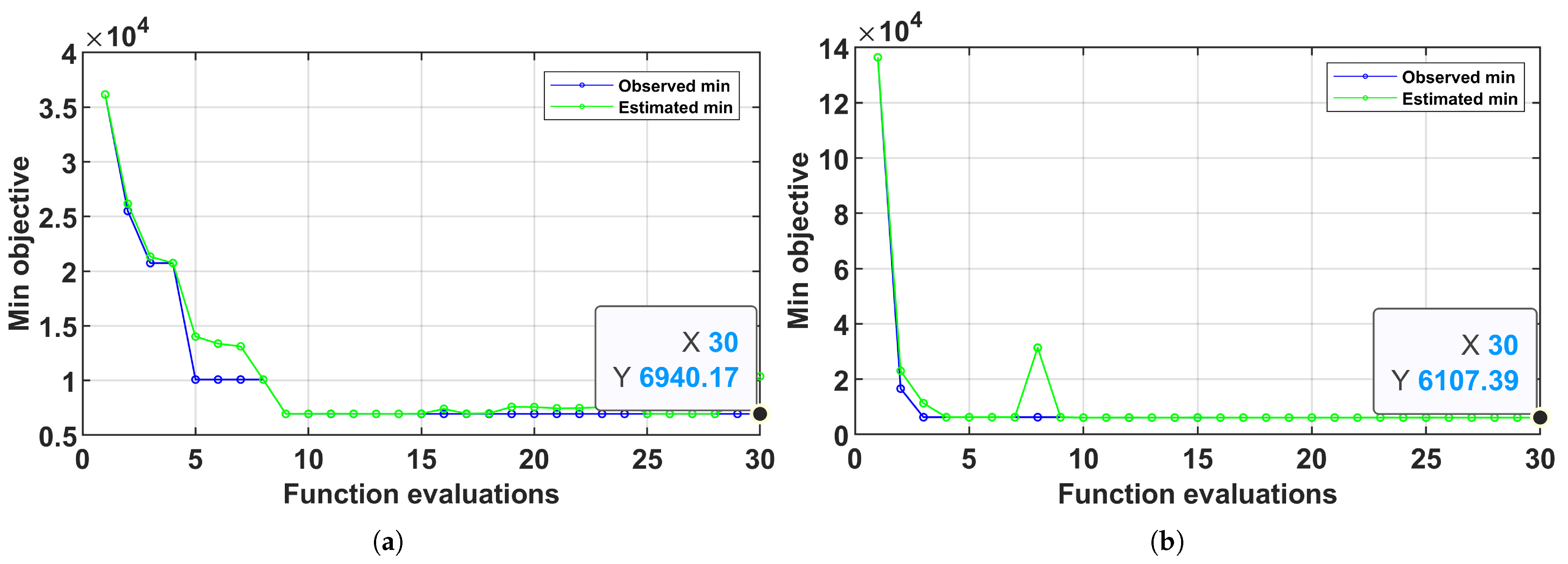
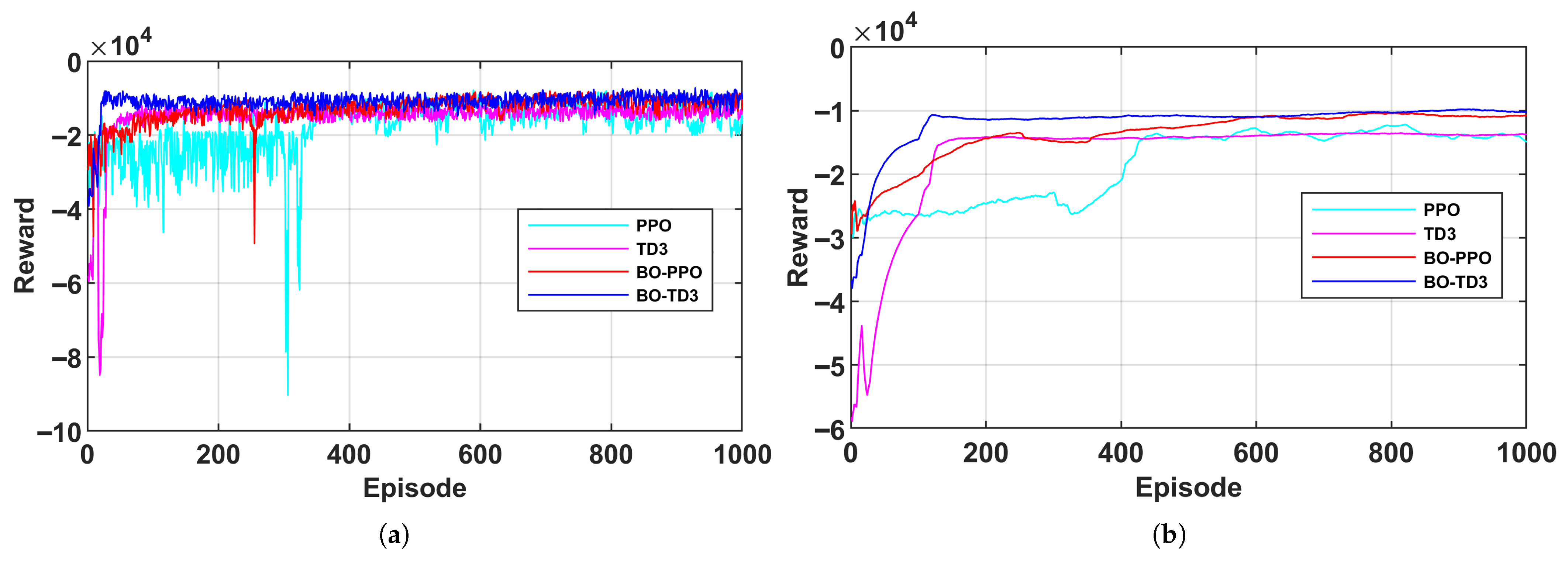
6.4.1. Training and Optimization Results
6.4.2. Comparative Evaluation Under Dynamic Conditions
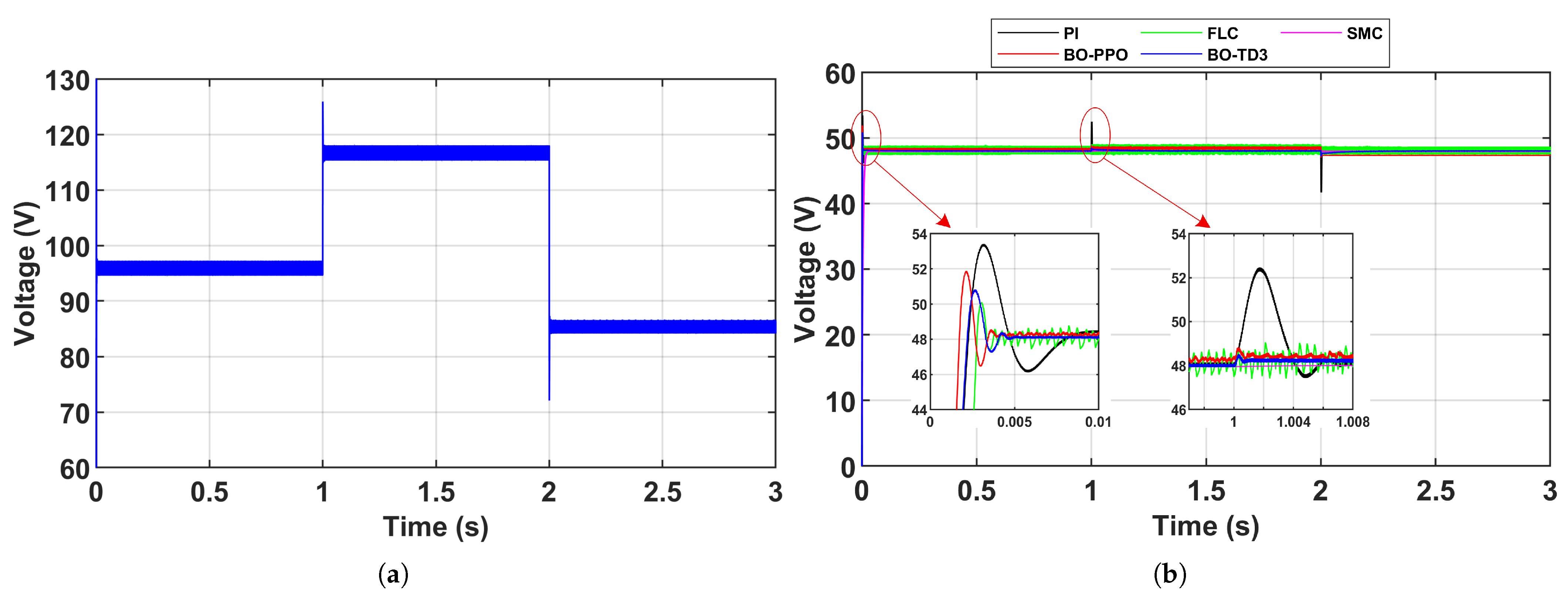
Scenario 1–Varying Reference Voltage
Scenario 2–Supply Disturbance
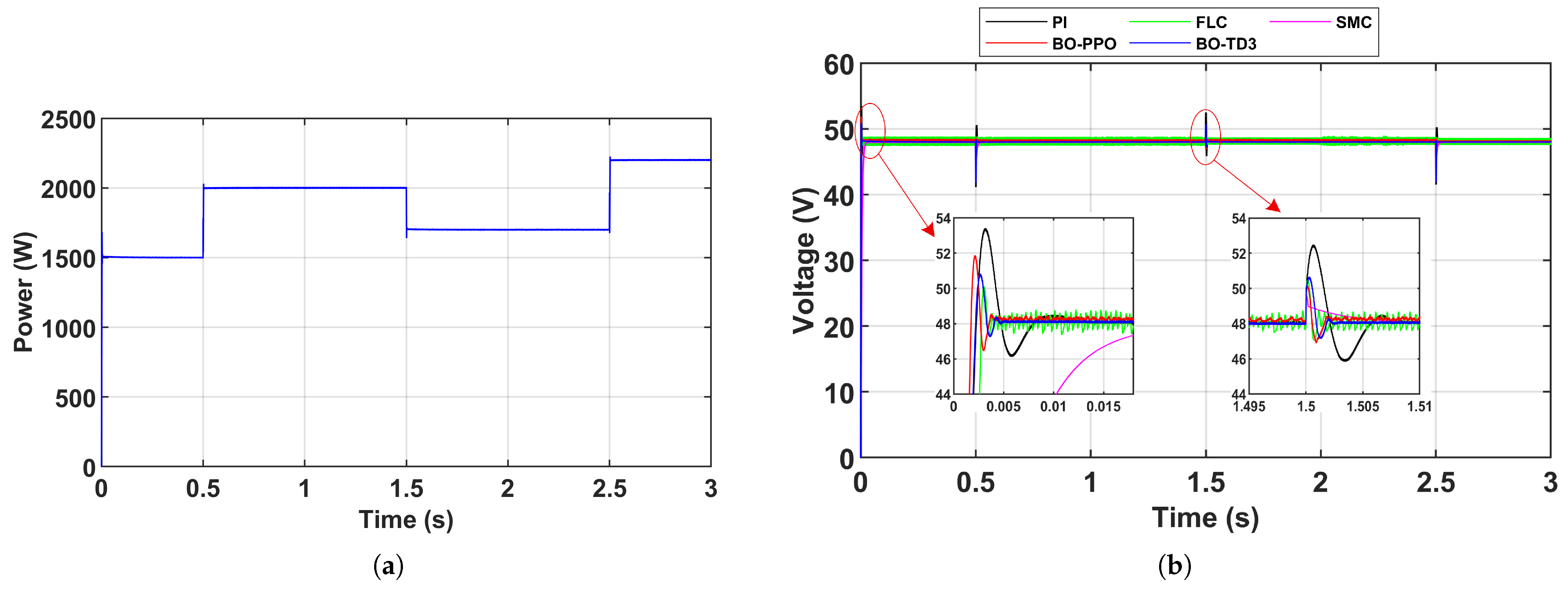
Scenario 3–Load Disturbance
7. Challenges and Future Works
- Traditional control approaches often struggle under system disturbances, such as the integration of new DER/ESD or system reconfiguration. These events frequently alter DC MG dynamics. Advanced control strategies like DRL can be trained to continuously adapt their control actions, maintaining stability under high perturbations.
- Data-driven control methods, while offering flexibility and reduced model dependency, often lack interpretability due to their black-box nature. Hybrid control strategies that combine data-driven and physics-based models–such as Model-based reinforcement learning (MBRL) and Physics-informed reinforcement learning (PIRL) should be further explored to balance flexibility, interpretability, and explainability while enhancing voltage stability under uncertainty.
- As MG continue to increase in scale and complexity (multiple DER, diverse loads and interconnection with other MG), the need for more adaptable and flexible control schemes becomes apparent. It is recommended to investigate and develop Multi-agent deep reinforcement learning (MADRL) frameworks. This will enable scalable and coordinated control across large-scale MG systems, allowing for robust autonomous decision-making and enhanced operational resilience.
- To ensure the practical applicability and reliability of the proposed control algorithms, future research should incorporate real-time experimental validation. This could be achieved by establishing Hardware-in-the-loop (HIL) test environments, for initial system integration and controller testing, and Power hardware-in-the-loop (PHIL) to assess performance with actual power-level components.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADRC | Active Disturbance Rejection Control |
| ANFIS | Adaptive Neuro Fuzzy Inference System |
| ANN | Artificial Neural Network |
| BO | Bayesian Optimization |
| CPL | Constant Power Load |
| DDC | Data Driven Control |
| DDPG | Deep Deterministic Policy Gradient |
| DER | Distributed Energy Resources |
| DQN | Deep Q Network |
| DRL | Deep Reinforcement Learning |
| ESD | Energy Storage Devices |
| HESS | Hybrid Energy Storage Systems |
| HIL | Hardware-in-the-loop |
| IoT | Internet of Things |
| LLC | Local Linear Controller |
| LLM | Local Linear Model |
| MADRL | Multi Agent Deep Reinforcement Learning |
| MDP | Markov Decision Process |
| MFAC | Model Free Adaptive Control |
| MOA | Metaheuristic Optimization Algorithm |
| MPC | Model Predictive Control |
| PBC | Passivity Based Control |
| PEMFC | Proton Exchange Membrane Fuel Cell |
| PHIL | Power Hardware-in-the-loop |
| PI | Proportional Integral controller |
| PIRL | Physics Informed Reinforcement Learning |
| PPL | Pulse Power Load |
| PPO | Proximal Policy Optimization |
| PSO | Particle Swarm Optimization |
| RES | Renewable Energy Sources |
| SMC | Sliding Mode Control |
| SOC | State of Charge |
| TRPO | Trust Region Policy Optimization |
Appendix A. Additional Tables
| Control Method | Reference | Year | Proposed Method | Main Contribution | Limitation |
|---|---|---|---|---|---|
| SMC | [33] | 2023 | Adaptive SMC | Improving voltage stability in a buck converter feeding CPLs | Complexity in design |
| [34] | 2023 | HM-GFTSMC | Improving voltage stability in a buck converter | Proving stability can be challenging in a complex MG scenario. | |
| [35] | 2024 | HOSMC-PID | Improving large signal stability in a DC MG | Proving stability can be challenging in a complex MG scenario. | |
| [40] | 2022 | RBFNN estimation-based Adaptive SMC | Improving voltage stability in a PEMFC. | Increased complexity. | |
| Adaptive Droop Control | [42] | 2019 | Hierarchical adaptive droop and supervisory control | Improving voltage stability and load power sharing in a DC MG with multi-energy storage devices. | The effectiveness of the proposed technique has not been validated against existing approaches. |
| [43] | 2020 | Adaptive distributed droop | Improving DC bus voltage stability | Stability challenges in a large-scale system | |
| [44] | 2023 | Adaptive droop + consensus control | DC MG power smoothing and voltage control | Difficulty in tuning parameters. | |
| [46] | 2022 | Droop index control | Improving voltage stability. | Performance may be sensitive to droop index. | |
| MPC | [53] | 2021 | FCS–MPC | Voltage control and power allocation optimization for DC MG with HESS | Prediction at each control cycle can be computationally intensive. |
| [54] | 2020 | Fast distributed MPC | Improving voltage stability | High computational cost. | |
| [55] | 2021 | Hybrid MPC | Improving voltage stability of a boost converter interfaced with CPLs | Prediction at each control cycle can be computationally intensive. | |
| [56] | 2022 | MPC combined with Kalman Observer | Enhancing voltage stability of an interleaved boost converter | Increased sensitivity to model accuracy. | |
| PBC | [59] | 2019 | PBC | DC MG voltage regulation | Performance under varying load conditions has not been investigated. |
| [10] | 2019 | Decentralized PBC | Improving voltage stability | Performance depends on model accuracy | |
| [60] | 2024 | IDA-PBC + SMRC | Improving voltage stability | Parameter uncertainties have not been considered. | |
| [61] | 2021 | Adaptive PBC | Voltage regulation in a buck-boost converter | Performance depends on the accuracy of the system model. | |
| ADRC | [64] | 2015 | ADRC | Improving performance of a flywheel energy storage system. | Not specified |
| [65] | 2017 | Time-scale droop control based on ADRC | Time-scale voltage droop control robust to uncertainties and external disturbances. | Performance depends on model accuracy. | |
| [66] | 2019 | Modified ADRC | Comparison of ADRC techniques for suppressing disturbances in a boost converter. | Evaluation is based on average model. | |
| H∞ | [68] | 2019 | H∞ | Enhancing voltage stability. | Choosing appropriate weighting functions is challenging. |
| [70] | 2023 | Loop-shaping H∞ | Robust voltage control of DC MG. | Performance not validated against other methods. |
| Control Method | Reference | Year | Proposed Method | Main Contribution | Limitation |
|---|---|---|---|---|---|
| FLC | [76] | 2020 | SCA-HS tuned Type II Fuzzy | Enhancing voltage stability in a boost converter feeding CPLs. | Performance is often sensitive to the choice of optimization parameters and fuzzy rule base. |
| [77] | 2020 | iSIT2-FPI + SMC | The authors proposed an SMC-based model-free FLC. | Relatively complex to implement. | |
| [78] | 2020 | Fuzzy-PI dual mode | The authors combined FLC with PI to enhance dynamic response and restrain fluctuations of the bus voltage. | Tuning scaling gains is necessary whenever the system dynamic changes. | |
| [80] | 2019 | ANFIS | Improving transient and steady-state responses of a flyback converter using FLC and neural network | Training ANFIS requires high-quality data. High computational cost | |
| ANN | [87] | 2022 | CCSNN | The authors proposed an EMS to enhance power sharing among CESS, as well as maintain bus voltage stability. | It is computationally intensive to tune CC hyperparameters and train a neural network. |
| [88] | 2020 | HBSANN | Proposed an HBSANN-based power management strategy. Improving the voltage regulation of a DC MG | It requires high quality training data | |
| [89] | 2021 | DNN | Proposed a supervised deep learning aided-sensorless controller | Risk of overfitting | |
| [90] | 2021 | ANN–approximate dynamic programming | Improving voltage stability under variable load and input voltage conditions. | Requires high-quality data | |
| LMN | [91] | 2019 | LMN + LLC | Identification of a DC/DC converter’s dynamics directly from measured data. Developed a voltage controller based on the identified model. | Performance was not evaluated against robust control methods. |
| MFAC | [96] | 2023 | MFAC | Design a pseudo-gradient estimation algorithm based on I/O data. Improving voltage stability in a BDC. | Pseudo-gradient estimation methods may introduce systematic errors due to the approximation process. |
| [99] | 2021 | Model-free iSIT2-FPI | Improving voltage regulation in a stand-alone shipboard DC MG. | Increased complexity. | |
| DRL | [108] | 2023 | PID+DDPG | Enhancing the voltage stability of a buck converter | Performance is partially dependent on model accuracy. |
| [109] | 2022 | DQN | Improving the voltage stability of a buck converter | Handles only discrete actions. | |
| [114] | 2024 | TD3 | Optimizing parameters of a PI controller. | Performance was tested under light load conditions. | |
| [116] | 2020 | DDPG | Voltage stabilization of IoT-based buck converter feeding CPLs. | The paper does not discuss training or simulation results. | |
| [117] | 2023 | Integral RL | Improving voltage stability in an interleaved boost converter. | The paper does not discuss training or simulation results. |
| Control Method | Reference | Year | Proposed Method | Main Contribution | Limitation |
|---|---|---|---|---|---|
| MOAs | [119] | 2020 | GA-tuned PID | Improving voltage stability and performance of a fuel cell | Poor parameter tuning can influence effectiveness of the algorithm. |
| [120] | 2021 | PSO-tuned PI | Improving voltage stability in a buck-boost converter. | Performance in the presence of disturbances has not been evaluated. | |
| [121] | 2023 | QOAOA | Improving efficiency of a cascaded boost converter. | Performance with varying load conditions is not discussed. | |
| [122] | 2023 | SSA-PSO | Improving voltage stability in a PV-powered MG. | The proposed method is not compared with other established methods. | |
| PINNs | [127] | 2024 | PINN | Estimating SOH of a lithium-ion battery. | Difficulty in handling high-dimensional nonlinear models. |
| [128] | 2024 | PINN | Enhancing stability in a buck converter. | Difficulty in handling high-dimensional converter dynamics. |
References
- Arshad, R.; Mininni, G.M.; De Rosa, R.; Khan, H.A. Enhancing climate resilience of vulnerable women in the Global South through power sharing in DC microgrids. Renew. Energy 2024, 237, 121495. [Google Scholar] [CrossRef]
- Xu, X.; Xia, J.; Hong, C.; Sun, P.; Xi, P.; Li, J. Optimization of cooperative operation of multiple microgrids considering green certificates and carbon trading. Energies 2025, 18, 4083. [Google Scholar] [CrossRef]
- Cagnano, A.; De Tuglie, E.; Mancarella, P. Microgrids: Overview and guidelines for practical implementations and operation. Appl. Energy 2020, 258, 114039. [Google Scholar] [CrossRef]
- e Ammara, U.; Zehra, S.S.; Nazir, S.; Ahmad, I. Artificial neural network-based nonlinear control and modeling of a DC microgrid incorporating regenerative FC/HPEV and energy storage system. Renew. Energy Focus 2024, 49, 100565. [Google Scholar] [CrossRef]
- Ojo, K.E.; Saha, A.K.; Srivastava, V.M. Microgrids’ control strategies and real-time monitoring systems: A comprehensive review. Energies 2025, 18, 3576. [Google Scholar] [CrossRef]
- Eyimaya, S.E.; Altin, N.; Nasiri, A. Optimization of photovoltaic and battery storage sizing in a DC microgrid using LSTM networks based on load forecasting. Energies 2025, 18, 3676. [Google Scholar] [CrossRef]
- Derakhshan, S.; Shafiee-Rad, M.; Shafiee, Q.; Jahed-Motlagh, M.R.; Sahoo, S.; Blaabjerg, F. Decentralized voltage control of autonomous DC microgrids with robust performance approach. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5508–5520. [Google Scholar] [CrossRef]
- Eydi, M.; Ghazi, R.; Buygi, M.O. A decentralized control method for proportional current-sharing, voltage restoration, and SOCs balancing of widespread DC microgrids. Int. J. Electr. Power Energy Syst. 2024, 155, 109645. [Google Scholar] [CrossRef]
- Rizk, H.; Chaibet, A.; Kribèche, A. Model-based control and model-free control techniques for autonomous vehicles: A technical survey. Appl. Sci. 2023, 13, 6700. [Google Scholar] [CrossRef]
- Cucuzzella, M.; Lazzari, R.; Kawano, Y.; Kosaraju, K.C.; Scherpen, J.M.A. Robust passivity-based control of boost converters in DC microgrids. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 8435–8440. [Google Scholar] [CrossRef]
- Santoni, C.; Zhang, Z.; Sotiropoulos, F.; Khosronejad, A. A data-driven machine learning approach for yaw control applications of wind farms. Theor. Appl. Mech. Lett. 2023, 13, 100471. [Google Scholar] [CrossRef]
- Modu, B.; Abdullah, M.P.; Sanusi, M.A.; Hamza, M.F. DC-based microgrid: Topologies, control schemes, and implementations. Alex. Eng. J. 2023, 70, 61–92. [Google Scholar] [CrossRef]
- Ashok Kumar, A.; Amutha Prabha, N. A comprehensive review of DC microgrid in market segments and control technique. Heliyon 2022, 8, e11694. [Google Scholar] [CrossRef]
- Xu, Q.; Vafamand, N.; Chen, L.; Dragicevic, T.; Xie, L.; Blaabjerg, F. Review on advanced control technologies for bidirectional DC/DC converters in DC microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1205–1221. [Google Scholar] [CrossRef]
- Ekanayake, U.N.; Navaratne, U.S. A survey on microgrid control techniques in islanded mode. J. Electr. Comput. Eng. 2020, 2020, 6275460. [Google Scholar] [CrossRef]
- Bukar, A.L.; Modu, B.; Abdullah, M.P.; Hamza, M.F.; Almutairi, S.Z. Peer-to-peer energy trading framework for an autonomous DC microgrid using game theoretic approach. Renew. Energy Focus 2024, 51, 100636. [Google Scholar] [CrossRef]
- Patel, R.; Chudamani, R. Stability analysis of the main converter supplying a constant power load in a multi-converter system considering various parasitic elements. Eng. Sci. Technol. Int. J. 2020, 23, 1118–1125. [Google Scholar] [CrossRef]
- Rahimian, M.M.; Mohammadi, H.R.; Guerrero, J.M. Constant power load issue in DC/DC multi-converter systems: Past studies and recent trends. Electr. Power Syst. Res. 2024, 235, 110851. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Akhbari, A.; Rahimi, M.; Andresen, B.; Khooban, M.H. Reducing impact of constant power loads on DC energy systems by artificial intelligence. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4974–4978. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; Yu, Y.; Yang, R. Coordinated control and optimal flow of shipboard MVDC system for adapting to large pulsed power load. Electr. Power Syst. Res. 2023, 221, 109354. [Google Scholar] [CrossRef]
- Kumar, K.; Kumar, P.; Kar, S. A review of microgrid protection for addressing challenges and solutions. Renew. Energy Focus 2024, 49, 100572. [Google Scholar] [CrossRef]
- Tavagnutti, A.A.; Bosich, D.; Pastore, S.; Sulligoi, G. A reduced order model for the stable LC-filter design on shipboard DC microgrids. In Proceedings of the 2023 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Venice, Italy, 29–31 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Al-Ismail, F.S. A critical review on DC microgrids voltage control and power management. IEEE Access 2024, 12, 30345–30361. [Google Scholar] [CrossRef]
- Li, F.; Tu, W.; Zhou, Y.; Li, H.; Zhou, F.; Liu, W.; Hu, C. Distributed secondary control for DC microgrids using two-stage multi-agent reinforcement learning. Int. J. Electr. Power Energy Syst. 2025, 164, 110335. [Google Scholar] [CrossRef]
- Saleem, O.; Rizwan, M. Performance optimization of LQR-based PID controller for DC-DC buck converter via iterative-learning-tuning of state-weighting matrix. Int. J. Numer. Model. Electron. Netw. Devices Fields 2019, 32, e2572. [Google Scholar] [CrossRef]
- Sheikhi Jouybary, H.; Arab Khaburi, D.; El Hajjaji, A.; Mpanda Mabwe, A. Optimal sliding mode control of modular multilevel converters considering control input constraints. Energies 2025, 18, 2757. [Google Scholar] [CrossRef]
- Peng, C.; Xie, C.; Zou, J.; Jiang, X.; Zhu, Y. A feedback linearization sliding mode decoupling and fuzzy anti-surge compensation based coordinated control approach for PEMFC air supply system. Renew. Energy 2024, 237, 121760. [Google Scholar] [CrossRef]
- Ullah, Q.; Busarello, T.D.C.; Brandao, D.I.; Simões, M.G. Design and performance evaluation of SMC-based DC–DC converters for microgrid applications. Energies 2023, 16, 4212. [Google Scholar] [CrossRef]
- Obeid, H.; Petrone, R.; Chaoui, H.; Gualous, H. Higher order sliding-mode observers for state-of-charge and state-of-health estimation of lithium-ion batteries. IEEE Trans. Veh. Technol. 2023, 72, 4482–4492. [Google Scholar] [CrossRef]
- Muhammad, R.; Muhammad, A.; Bhatti, A.I.; Minhas, D.M.; Ahmed, B.A. Mathematical modeling and stability analysis of DC microgrid using SM hysteresis controller. Int. J. Electr. Power Energy Syst. 2018, 95, 507–522. [Google Scholar] [CrossRef]
- Cucuzzella, M.; Lazzari, R.; Trip, S.; Rosti, S.; Sandroni, C.; Ferrara, A. Sliding mode voltage control of boost converters in DC microgrids. Control Eng. Pract. 2018, 73, 161–170. [Google Scholar] [CrossRef]
- Mathew, K.K.; Abraham, D.M. Particle swarm optimization based sliding mode controllers for electric vehicle onboard charger. Comput. Electr. Eng. 2021, 96, 107502. [Google Scholar] [CrossRef]
- Mustafa, G.; Ahmad, F.; Zhang, R.; Haq, E.U.; Hussain, M. Adaptive sliding mode control of buck converter feeding resistive and constant power load in DC microgrid. Energy Rep. 2023, 9, 1026–1035. [Google Scholar] [CrossRef]
- Balta, G.; Güler, N.; Altin, N. Global fast terminal sliding mode control with fixed switching frequency for voltage control of DC–DC buck converters. ISA Trans. 2023, 143, 582–595. [Google Scholar] [CrossRef]
- Roy, T.K.; Oo, A.M.T.; Ghosh, S.K. Designing a high-order sliding mode controller for photovoltaic- and battery energy storage system-based DC microgrids with ANN-MPPT. Energies 2024, 17, 532. [Google Scholar] [CrossRef]
- Li, X.; Wang, M.; Dong, C.; Jiang, W.; Xu, Z.; Wu, X.; Jia, H. A robust autonomous sliding-mode control of renewable DC microgrids for decentralized power sharing considering large-signal stability. Appl. Energy 2023, 339, 121019. [Google Scholar] [CrossRef]
- Derakhshannia, M.; Moosapour, S.S. RBFNN based fixed time sliding mode control for PEMFC air supply system with input delay. Renew. Energy 2024, 237, 121772. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, K.; Chi, S.; Lyu, L.; Ma, H.; Wang, K. The bidirectional DC/DC converter operation mode control algorithm based on RBF neural network. In Proceedings of the 2019 IEEE PES International Conference on Innovative Smart Grid Technologies Asia (ISGT Asia), Chengdu, China, 21–24 May 2019. [Google Scholar] [CrossRef]
- Chen, X.; Shen, W.; Dai, M.; Cao, Z.; Jin, J.; Kapoor, A. Robust adaptive sliding-mode observer using RBF neural network for lithium-ion battery state of charge estimation in electric vehicles. IEEE Trans. Veh. Technol. 2016, 65, 1936–1947. [Google Scholar] [CrossRef]
- Xiao, X.; Lv, J.; Chang, Y.; Chen, J.; He, H. Adaptive sliding mode control integrating with RBFNN for proton exchange membrane fuel cell power conditioning. Appl. Sci. 2022, 12, 3132. [Google Scholar] [CrossRef]
- Zhang, H.; Sinha, R.; Golmohamadi, H.; Chaudhary, S.K.; Bak-Jensen, B. Autonomous control of electric vehicles using voltage droop. Energies 2025, 18, 2824. [Google Scholar] [CrossRef]
- Yuan, M.; Fu, Y.; Mi, Y.; Li, Z.; Wang, C. Hierarchical control of DC microgrid with dynamical load power sharing. Appl. Energy 2019, 239, 1–11. [Google Scholar] [CrossRef]
- Kumar, R.; Pathak, M.K. Distributed droop control of DC microgrid for improved voltage regulation and current sharing. IET Renew. Power Gener. 2020, 14, 2499–2506. [Google Scholar] [CrossRef]
- Li, X.; Li, P.; Ge, L.; Wang, X.; Li, Z.; Zhu, L.; Guo, L.; Wang, C. A unified control of super-capacitor system based on bi-directional DC-DC converter for power smoothing in DC microgrid. J. Mod. Power Syst. Clean Energy 2023, 11, 938–949. [Google Scholar] [CrossRef]
- Rehmat, A.; Alam, F.; Nasir, M.; Zaidi, S.S. Robust hierarchical non-linear droop control design for the PV based islanded microgrid. In Proceedings of the 19th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 11–15 January 2022; pp. 620–628. [Google Scholar] [CrossRef]
- Thogaru, R.B.; Naware, D.; Mitra, A.; Chaudhary, J. Resiliency-driven approach of DC microgrid voltage regulation based on droop index control for high step-up DC-DC converter. Int. Trans. Electr. Energy Syst. 2022, 2022, 3676438. [Google Scholar] [CrossRef]
- Guo, Z.; Zuo, D.; Liu, X.; Zhang, Z.; Ma, J.; Meng, F.; Fang, Y. Dual tracking model-free predictive control for three-level neutral-point clamped inverters. Electr. Power Syst. Res. 2025, 249, 112054. [Google Scholar] [CrossRef]
- Murillo-Yarce, D.; Riffo, S.; Restrepo, C.; González-Castaño, C.; Garcés, A. Model predictive control for stabilization of DC microgrids in island mode operation. Mathematics 2022, 10, 3384. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, J.; Zhai, J.; Yang, L.; Qian, X.; Tao, Z. Continuous-control-set model predictive control strategy for MMC-UPQC under non-ideal conditions. Energies 2025, 18, 2946. [Google Scholar] [CrossRef]
- Babqi, A.J.; Alamri, B. A comprehensive comparison between finite control set model predictive control and classical proportional-integral control for grid-tied power electronics devices. Acta Polytech. Hung. 2021, 18, 67–87. [Google Scholar] [CrossRef]
- Diaz Franco, F.; Vu, T.V.; Gonsulin, D.; Vahedi, H.; Edrington, C.S. Enhanced performance of PV power control using model predictive control. Sol. Energy 2017, 158, 679–686. [Google Scholar] [CrossRef]
- Villalón, A.; Rivera, M.; Salgueiro, Y.; Muñoz, J.; Dragičević, T.; Blaabjerg, F. Predictive control for microgrid applications: A review study. Energies 2020, 13, 2454. [Google Scholar] [CrossRef]
- Ni, F.; Zheng, Z.; Xie, Q.; Xiao, X.; Zong, Y.; Huang, C. Enhancing resilience of DC microgrids with model predictive control based hybrid energy storage system. Int. J. Electr. Power Energy Syst. 2021, 128, 106738. [Google Scholar] [CrossRef]
- Marepalli, L.K.; Gajula, K.; Herrera, L. Fast distributed model predictive control for DC microgrids. In Proceedings of the 21st IEEE Workshop on Control and Modeling for Power Electronics (COMPEL 2020), Aalborg, Denmark, 9–12 November 2020. [Google Scholar] [CrossRef]
- Karami, Z.; Shafiee, Q.; Sahoo, S.; Yaribeygi, M.; Bevrani, H.; Dragičević, T. Hybrid model predictive control of DC-DC boost converters with constant power load. IEEE Trans. Energy Convers. 2021, 36, 1347–1356. [Google Scholar] [CrossRef]
- Tan, B.; Li, H.; Zhao, D.; Liang, Z.; Ma, R.; Huangfu, Y. Finite-control-set model predictive control of interleaved DC-DC boost converter based on Kalman observer. eTransportation 2022, 11, 100158. [Google Scholar] [CrossRef]
- Kao, C.Y.; Khong, S.Z.; van der Schaft, A. On the converse passivity theorems for LTI systems. In Proceedings of the IFAC World Congress, IFAC-PapersOnLine, Berlin, Germany, 11–17 July 2020; pp. 6422–6427. [Google Scholar] [CrossRef]
- Acevedo, D.M.; Parraguez-Garrido, I.; Gil-Gonzalez, W.; Montoya, O.D.; Gonzalez-Castano, C. Adaptive passivity-based control for DC motor speed regulation in DC-DC converter-fed systems. IEEE Access 2025, 13, 131957–131966. [Google Scholar] [CrossRef]
- Sun, J.; Lin, W.; Hong, M.; Loparo, K.A. Voltage regulation of DC-microgrid with PV and battery: A passivity method. In Proceedings of the IFAC Workshop on Control of Smart Grid and Renewable Energy Systems (CSGRES), IFAC-PapersOnLine, Jeju, Republic of Korea, 10–12 June 2019; pp. 753–758. [Google Scholar] [CrossRef]
- Martínez, L.; Fernández, D.; Mantz, R. Passivity-based control for an isolated DC microgrid with hydrogen energy storage system. Int. J. Hydrogen Energy 2024, 67, 1262–1269. [Google Scholar] [CrossRef]
- Soriano-Rangel, C.A.; He, W.; Mancilla-David, F.; Ortega, R. Voltage regulation in buck-boost converters feeding an unknown constant power load: An adaptive passivity-based control. IEEE Trans. Control Syst. Technol. 2021, 29, 395–402. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Hao, F.; Guo, J.; Yu, Z.; Ye, J. Output voltage control of LLC resonant converter based on improved linear active disturbance rejection control. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 3555–3564. [Google Scholar] [CrossRef]
- Chang, X.; Li, Y.; Zhang, W.; Wang, N.; Xue, W. Active disturbance rejection control for a flywheel energy storage system. IEEE Trans. Ind. Electron. 2015, 62, 991–1001. [Google Scholar] [CrossRef]
- Yang, N.; Gao, F.; Paire, D.; Miraoui, A.; Liu, W. Distributed control of multi-time scale DC microgrid based on ADRC. IET Power Electron. 2017, 10, 329–337. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, A. Active disturbance rejection control of DC–DC boost converter: A review with modifications for improved performance. IET Power Electron. 2019, 12, 2095–2107. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, X.; Zhang, Y.; Zhang, Q. Event-triggered H-infinity pitch control for floating offshore wind turbines. IEEE Trans. Sustain. Energy 2025, 16, 1329–1339. [Google Scholar] [CrossRef]
- Rigatos, G.; Zervos, N.; Siano, P.; Abbaszadeh, M.; Wira, P.; Onose, B. Nonlinear optimal control for DC industrial microgrids. Cyber-Phys. Syst. 2019, 5, 231–253. [Google Scholar] [CrossRef]
- Mehdi, M.; Jamali, S.Z.; Khan, M.O.; Baloch, S.; Kim, C.H. Robust control of a DC microgrid under parametric uncertainty and disturbances. Electr. Power Syst. Res. 2020, 179, 106074. [Google Scholar] [CrossRef]
- Ruchi, S.; Avirup, M.; Shyam, K. Robust control of an islanded DC microgrid using H-infinity loop-shaping design considering parametric uncertainties. In Proceedings of the TENCON 2023—IEEE Region 10 Conference, Chiang Mai, Thailand, 31 October–3 November 2023; pp. 1082–1087. [Google Scholar] [CrossRef]
- Al Sumarmad, K.A.; Sulaiman, N.; Wahab, N.I.A.; Hizam, H. Energy management and voltage control in microgrids using artificial neural networks, PID, and fuzzy logic controllers. Energies 2022, 15, 303. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Durairaj, S.; Padmavathi, S. A performance evaluation of a fuzzy logic controller-based photovoltaic-fed multi-level inverter for a three-phase induction motor. J. Frankl. Inst. 2021, 358, 7394–7412. [Google Scholar] [CrossRef]
- Dumitrescu, C.; Ciotirnae, P.; Vizitiu, C. Fuzzy logic for intelligent control system using soft computing applications. Sensors 2021, 21, 2617. [Google Scholar] [CrossRef]
- Belman-Flores, J.M.; Rodríguez-Valderrama, D.A.; Ledesma, S.; García-Pabón, J.J.; Hernández, D.; Pardo-Cely, D.M. A review on applications of fuzzy logic control for refrigeration systems. Appl. Sci. 2022, 12, 1302. [Google Scholar] [CrossRef]
- Bhosale, R.; Agarwal, V. Fuzzy logic control of the ultracapacitor interface for enhanced transient response and voltage stability of a DC microgrid. IEEE Trans. Ind. Appl. 2019, 55, 712–720. [Google Scholar] [CrossRef]
- Farsizadeh, H.; Gheisarnejad, M.; Mosayebi, M.; Rafiei, M.; Khooban, M.H. An intelligent and fast controller for DC/DC converter feeding CPL in a DC microgrid. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1104–1108. [Google Scholar] [CrossRef]
- Khooban, M.H.; Gheisarnejad, M.; Farsizadeh, H.; Masoudian, A.; Boudjadar, J. A new intelligent hybrid control approach for DC-DC converters in zero-emission ferry ships. IEEE Trans. Power Electron. 2020, 35, 5832–5841. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, S.; Wang, J.; Zhang, L. Bus voltage stabilization control of photovoltaic DC microgrid based on fuzzy-PI dual-mode controller. J. Electr. Comput. Eng. 2020, 2020, 2683052. [Google Scholar] [CrossRef]
- Rodriguez, M.; Arcos-Aviles, D.; Martinez, W. Fuzzy logic-based energy management for isolated microgrid using meta-heuristic optimization algorithms. Appl. Energy 2023, 335, 120771. [Google Scholar] [CrossRef]
- Shahid, M.A.; Abbas, G.; Hussain, M.R.; Asad, M.U.; Farooq, U.; Gu, J.; Balas, V.E.; Uzair, M.; Awan, A.B.; Yazdan, T. Artificial intelligence-based controller for DC-Dc flyback converter. Appl. Sci. 2019, 9, 5108. [Google Scholar] [CrossRef]
- Al-Hitmi, M.A.; Islam, S.; Muyeen, S.M.; Iqbal, A.; Thomas, K.; Abdullah, A.K.M.; Ben-brahim, L. An ANN-based distributed secondary controller used to ensure accurate current sharing in DC microgrid. AEU Int. J. Electron. Commun. 2025, 201, 156002. [Google Scholar] [CrossRef]
- Zhao, S.; Blaabjerg, F.; Wang, H. An overview of artificial intelligence applications for power electronics. IEEE Trans. Power Electron. 2021, 36, 4633–4658. [Google Scholar] [CrossRef]
- Han, Y.; Liao, Y.; Ma, X.; Guo, X.; Li, C.; Liu, X. Analysis and prediction of the penetration of renewable energy in power systems using artificial neural network. Renew. Energy 2023, 215, 118914. [Google Scholar] [CrossRef]
- Lopez-Garcia, T.B.; Coronado-Mendoza, A.; Domínguez-Navarro, J.A. Artificial neural networks in microgrids: A review. Eng. Appl. Artif. Intell. 2020, 95, 103894. [Google Scholar] [CrossRef]
- Saadatmand, S.; Shamsi, P.; Ferdowsi, M. The voltage regulation of a buck converter using a neural network predictive controller. In Proceedings of the 2020 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 6–7 February 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Khan, H.S.; Mohamed, I.S.; Kauhaniemi, K.; Liu, L. Artificial neural network-based voltage control of DC/DC converter for DC microgrid applications. In Proceedings of the 2021 6th IEEE Workshop on the Electronic Grid (eGRID), New Orleans, LA, USA, 8–10 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Singh, P.; Anwer, N.; Lather, J.S. Energy management and control for direct current microgrid with composite energy storage system using combined cuckoo search algorithm and neural network. J. Energy Storage 2022, 55, 105689. [Google Scholar] [CrossRef]
- Singh, P.; Lather, J.S. Dynamic power management and control for low voltage DC microgrid with hybrid energy storage system using hybrid bat search algorithm and artificial neural network. J. Energy Storage 2020, 32, 101974. [Google Scholar] [CrossRef]
- Akpolat, A.N.; Dursun, E.; Kuzucuoglu, A.E. Deep learning-aided sensorless control approach for PV converters in DC nanogrids. IEEE Access 2021, 9, 106641–106654. [Google Scholar] [CrossRef]
- Dong, W.; Li, S.; Fu, X.; Li, Z.; Fairbank, M.; Gao, Y. Control of a buck DC/DC converter using approximate dynamic programming and artificial neural networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1760–1768. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Miranian, A.; Escaño, J.M.; Rakhshani, E.; Shariati, N.; Pouresmaeil, E. A data-driven based voltage control strategy for DC-DC converters: Application to DC microgrid. Electronics 2019, 8, 493. [Google Scholar] [CrossRef]
- She, B.; Li, F.; Cui, H.; Zhang, J.; Bo, R. Fusion of model-free reinforcement learning with microgrid control: Review and vision. IEEE Trans. Smart Grid 2023, 14, 3232–3245. [Google Scholar] [CrossRef]
- Hartmann, B.; Nelle, O. On the smoothness in local model networks. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3573–3578. [Google Scholar] [CrossRef]
- Novak, J.; Chalupa, P.; Bobal, V. Local model networks for modelling and predictive control of nonlinear systems. In Proceedings of the 23rd European Conference on Modelling and Simulation (ECMS 2009), Madrid, Spain, 9–12 June 2009; European Council for Modelling and Simulation: Kingston upon Thames, UK, 2009; pp. 557–562. [Google Scholar] [CrossRef][Green Version]
- Hou, Z.; Xiong, S. On model-free adaptive control and its stability analysis. IEEE Trans. Autom. Control 2019, 64, 4555–4569. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, D.; Peng, Z.; Liu, L. Model-free adaptive control for ultracapacitor based three-phase interleaved bidirectional DC–DC converter. IET Power Electron. 2023, 16, 2696–2707. [Google Scholar] [CrossRef]
- Yu, W.; Wang, R.; Bu, X.; Hou, Z. Model free adaptive control for a class of nonlinear systems with fading measurements. J. Frankl. Inst. 2020, 357, 7743–7760. [Google Scholar] [CrossRef]
- Saeid, A.H.; Babak, N.-M. Active stabilization of a microgrid using model free adaptive control. In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Mosayebi, M.; Sadeghzadeh, S.M.; Gheisarnejad, M.; Khooban, M.H. Intelligent and fast model-free sliding mode control for shipboard DC microgrids. IEEE Trans. Transp. Electrif. 2021, 7, 1662–1671. [Google Scholar] [CrossRef]
- Yue, J.; Liu, Z.; Su, H. Model-free composite disturbance rejection control for dynamic wireless charging system based on online parameter identification. IEEE Trans. Ind. Electron. 2024, 71, 7777–7785. [Google Scholar] [CrossRef]
- Yue, J.; Liu, Z.; Su, H. Data-driven adaptive extended state observer-based model-free disturbance rejection control for DC–DC converters. IEEE Trans. Ind. Electron. 2024, 71, 7745–7755. [Google Scholar] [CrossRef]
- Cai, Q.; Luo, X.Q.; Wang, P.; Gao, C.; Zhao, P. Hybrid model-driven and data-driven control method based on machine learning algorithm in energy hub and application. Appl. Energy 2022, 305, 117913. [Google Scholar] [CrossRef]
- Dan, Y.; Zhong, H.; Wang, C.; Wang, J.; Fei, Y.; Yu, L. A graph deep reinforcement learning-based fault restoration method for active distribution networks. Energies 2025, 18, 4420. [Google Scholar] [CrossRef]
- Wolgast, T.; Niese, A. Approximating energy market clearing and bidding with model-based reinforcement learning. IEEE Access 2024, 12, 145106–145117. [Google Scholar] [CrossRef]
- Bachiri, K.; Yahyaouy, A.; Gualous, H.; Malek, M.; Bennani, Y.; Makany, P.; Rogovschi, N. Multi-agent DDPG based electric vehicles charging station recommendation. Energies 2023, 16, 6067. [Google Scholar] [CrossRef]
- Zandi, O.; Poshtan, J. Voltage control of a quasi Z-source converter under constant power load condition using reinforcement learning. Control Eng. Pract. 2023, 135, 105499. [Google Scholar] [CrossRef]
- Shakya, A.K.; Pillai, G.; Chakrabarty, S. Reinforcement learning algorithms: A brief survey. Expert Syst. Appl. 2023, 231, 120495. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, X.; Ma, H. A novel proportion-integral-differential controller based on deep reinforcement learning for DC/DC power buck converters. In Proceedings of the 2021 IEEE 1st International Power Electronics and Application Symposium (PEAS), Shanghai, China, 13–15 November 2021. [Google Scholar] [CrossRef]
- Cui, C.; Yan, N.; Huangfu, B.; Yang, T.; Zhang, C. Voltage regulation of DC-DC buck converters feeding CPLs via deep reinforcement learning. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1777–1781. [Google Scholar] [CrossRef]
- Shi, X.; Chen, N.; Wei, T.; Wu, J.; Xiao, P. A reinforcement learning-based online-training AI controller for DC-DC switching converters. In Proceedings of the 2021 6th International Conference on Integrated Circuits and Microsystems (ICICM 2021), Nanjing, China, 22–24 October 2021; pp. 435–438. [Google Scholar] [CrossRef]
- Marahatta, A.; Rajbhandari, Y.; Shrestha, A.; Phuyal, S.; Thapa, A.; Korba, P. Model predictive control of DC/DC boost converter with reinforcement learning. Heliyon 2022, 8, e11416. [Google Scholar] [CrossRef]
- Ye, J.; Guo, H.; Zhao, D.; Wang, B.; Zhang, X. TD3 algorithm based reinforcement learning control for multiple-input multiple-output DC–DC converters. IEEE Trans. Power Electron. 2024, 39, 12729–12742. [Google Scholar] [CrossRef]
- Rajamallaiah, A.; Karri, S.P.K.; Shankar, Y.R. Deep reinforcement learning based control strategy for voltage regulation of DC-DC buck converter feeding CPLs in DC microgrid. IEEE Access 2024, 12, 17419–17430. [Google Scholar] [CrossRef]
- Muktiadji, R.F.; Ramli, M.A.M.; Milyani, A.H. Twin-delayed deep deterministic policy gradient algorithm to control a boost converter in a DC microgrid. Electronics 2024, 13, 433. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Farsizadeh, H.; Khooban, M.H. A novel nonlinear deep reinforcement learning controller for DC-DC power buck converters. IEEE Trans. Ind. Electron. 2021, 68, 6849–6858. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Khooban, M.H. IoT-based DC/DC deep learning power converter control: Real-time implementation. IEEE Trans. Power Electron. 2020, 35, 13621–13630. [Google Scholar] [CrossRef]
- Qie, T.; Zhang, X.; Xiang, C.; Yu, Y.; Iu, H.H.C.; Fernando, T. A new robust integral reinforcement learning based control algorithm for interleaved DC/DC boost converter. IEEE Trans. Ind. Electron. 2023, 70, 3729–3739. [Google Scholar] [CrossRef]
- Tomar, V.; Bansal, M.; Singh, P. Metaheuristic algorithms for optimization: A brief review. Eng. Proc. 2023, 59, 238. [Google Scholar] [CrossRef]
- Kumar, S.; Krishnasamy, V.; Neeli, S.; Kaur, R. Artificial intelligence power controller of fuel cell based DC nanogrid. Renew. Energy Focus 2020, 34, 120–128. [Google Scholar] [CrossRef]
- Vadi, S.; Gurbuz, F.B.; Bayindir, R.; Sagiroglu, S. Optimization of PI based buck-boost converter by particle swarm optimization algorithm. In Proceedings of the 9th International Conference on Smart Grid (icSmartGrid), Setubal, Portugal, 29 June–1 July 2021; pp. 295–301. [Google Scholar] [CrossRef]
- Hema, S.; Sukhi, Y. Deep learning-based FOPID controller for cascaded DC-DC converters. Comput. Syst. Sci. Eng. 2023, 46, 1503–1519. [Google Scholar] [CrossRef]
- AL-Wesabi, I.; Fang, Z.; Farh, H.M.H.; Dagal, I.; Al-Shamma’a, A.A.; Al-Shaalan, A.M.; Yang, K. Hybrid SSA-PSO based intelligent direct sliding-mode control for extracting maximum photovoltaic output power and regulating the DC-bus voltage. Int. J. Hydrogen Energy 2024, 51, 348–370. [Google Scholar] [CrossRef]
- Nanyan, N.F.; Ahmad, M.A.; Hekimoğlu, B. Optimal PID controller for the DC-DC buck converter using the improved sine cosine algorithm. Results Control Optim. 2024, 14, 100352. [Google Scholar] [CrossRef]
- Farea, A.; Yli-Harja, O.; Emmert-Streib, F. Understanding physics-informed neural networks: Techniques, applications, trends, and challenges. AI 2024, 5, 1534–1557. [Google Scholar] [CrossRef]
- Stiasny, J.; Chatzivasileiadis, S. Physics-informed neural networks for time-domain simulations: Accuracy, computational cost, and flexibility. Electr. Power Syst. Res. 2023, 224, 109748. [Google Scholar] [CrossRef]
- Huang, B.; Wang, J. Applications of physics-informed neural networks in power systems—A review. IEEE Trans. Power Syst. 2023, 38, 572–588. [Google Scholar] [CrossRef]
- Wang, F.; Zhai, Z.; Zhao, Z.; Di, Y.; Chen, X. Physics-informed neural network for lithium-ion battery degradation stable modeling and prognosis. Nat. Commun. 2024, 15, 48779. [Google Scholar] [CrossRef]
- Hui, P.; Cui, C.; Lin, P.; Ghias, A.M.Y.M.; Niu, X.; Zhang, C. On physics-informed neural network control for power electronics. arXiv 2024, arXiv:2406.15787. [Google Scholar] [CrossRef]
- Lee, J.S.; Lee, G.Y.; Park, S.S.; Kim, R.Y. Impedance-based modeling and common bus stability enhancement control algorithm in DC microgrid. IEEE Access 2020, 8, 211224–211234. [Google Scholar] [CrossRef]
- Hao, W.; Han, H.; Liu, Z.; Sun, Y.; Su, M.; Hou, X.; Yang, P. A stabilization method of LC input filter in DC microgrids feeding constant power loads. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017. [Google Scholar]
- Pang, S.; Nahid-Mobarakeh, B.; Pierfederici, S.; Huangfu, Y.; Luo, G.; Gao, F. Research on LC filter cascaded with buck converter supplying constant power load based on IDA-passivity-based control. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 4992–4997. [Google Scholar] [CrossRef]
- Firdous, N.; Din, N.M.U.; Assad, A. An imbalanced classification approach for establishment of cause-effect relationship between heart-failure and pulmonary embolism using deep reinforcement learning. Eng. Appl. Artif. Intell. 2023, 126, 107004. [Google Scholar] [CrossRef]
- Rehman, A.U.; Ullah, Z.; Qazi, H.S.; Hasanien, H.M.; Khalid, H.M. Reinforcement learning-driven proximal policy optimization-based voltage control for PV and WT integrated power system. Renew. Energy 2024, 227, 120590. [Google Scholar] [CrossRef]
- Del Rio, A.; Jimenez, D.; Serrano, J. Comparative analysis of A3C and PPO algorithms in reinforcement learning: A survey on general environments. IEEE Access 2024, 12, 146795–146806. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Li, Z. A TD3-based multi-agent deep reinforcement learning method in mixed cooperation-competition environment. Neurocomputing 2020, 411, 206–215. [Google Scholar] [CrossRef]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. arXiv 2018, arXiv:1802.09477. [Google Scholar] [CrossRef]
- Wang, S.; Duan, J.; Shi, D.; Xu, C.; Li, H.; Diao, R.; Wang, Z. A data-driven multi-agent autonomous voltage control framework using deep reinforcement learning. IEEE Trans. Power Syst. 2020, 35, 4644–4654. [Google Scholar] [CrossRef]
- Liessner, R.; Schmitt, J.; Dietermann, A.; Bäker, B. Hyperparameter optimization for deep reinforcement learning in vehicle energy management. In Proceedings of the ICAART 2019-Proceedings of the 11th International Conference on Agents and Artificial Intelligence, Prague, Czech Republic, 19–21 February 2019; SciTePress: Setúbal, Portugal, 2019; pp. 134–144. [Google Scholar] [CrossRef]
- Victoria, A.H.; Maragatham, G. Automatic tuning of hyperparameters using Bayesian optimization. Evolving Syst. 2021, 12, 217–223. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- MohammadNoor, I.; Fadi, S.; Ali Bou, N.; Aleksander, E.; Abdallah, S. Bayesian optimization with machine learning algorithms towards anomaly detection. In Proceedings of the IEEE Global Communications Conference, Abu Dhabi, United Arab Emirates, 9–13 December 2018; p. 90. [Google Scholar] [CrossRef]
- Eimer, T.; Lindauer, M.; Raileanu, R. Hyperparameters in Reinforcement Learning and How to Tune Them. arXiv 2023, arXiv:2306.01324. [Google Scholar] [CrossRef]

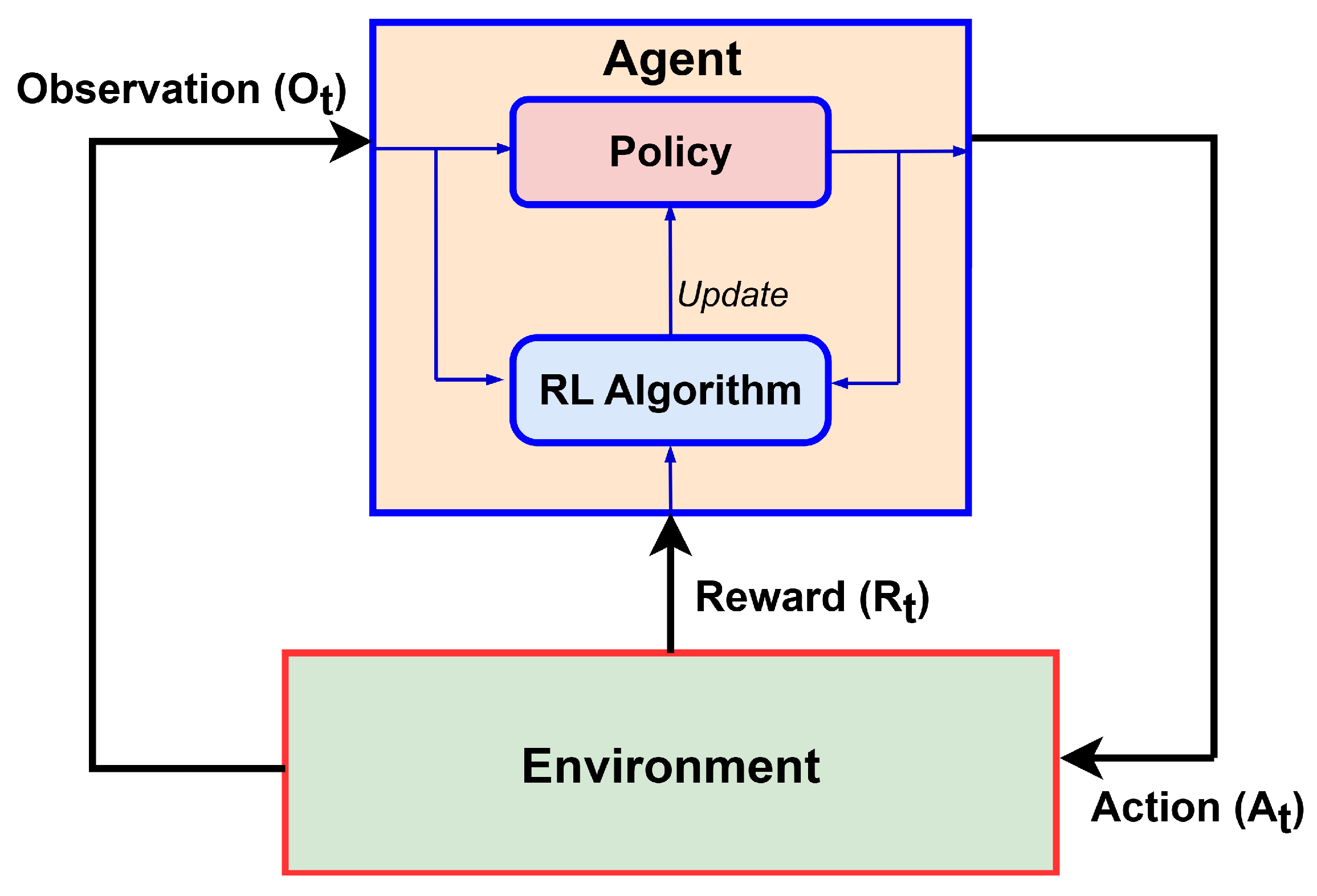



| Learning Policy | Key Features | Agent | Type | Action |
|---|---|---|---|---|
| On-policy | Learning is based on the current policy. Exploration is limited to the current policy. Suitable when the environment is relatively stable and the agent can explore safely. | State-action-reward-state-action (SARSA) | value-based | discrete |
| Policy gradient (PG) | policy-based | discrete or continuous | ||
| Actor critic (AC) | actor-critic | discrete or continuous | ||
| Trust region policy optimization (TRPO) | actor-critic | discrete or continuous | ||
| Proximal Policy optimization (PPO) | actor-critic | discrete or continuous | ||
| Off-policy | Learn from different policies. Explore more broadly through behavior policy. Suitable for complex environment | Q-learning | value-based | discrete |
| Deep Q-network (DQN) | value-based | discrete | ||
| Double DQN (DDQN) | value-based | discrete | ||
| Deep deterministic policy gradient (DDPG) | actor-critic | continuous | ||
| Twin-delay deep deterministic policy gradient (TD3) | actor-critic | continuous | ||
| Soft actor-critic (SAC) | actor-critic | continuous | ||
| Asynchronous advantage actor-critic (A3C) | actor-critic | discrete or continuous |
| Category | Strengths | Limitations |
|---|---|---|
| Model-based | High accuracy and fast response when the system model is known. Stability can be guaranteed analytically. Facilitates optimal and predictive control. | Requires system model and parameters. Limited adaptability to uncertainties. Requires re-modeling in the event of system changes. |
| Model-free | Does not require an explicit system model. High adaptability and flexibility. Robust to parameter variations and uncertainties. | Lacks analytical stability guarantees. High computational cost during training. Requires high-quality data. |
| Hyperparameter | PPO | TD3 |
|---|---|---|
| Minibatch size (m) | [50, 400] | [50, 400] |
| Discount factor () | [0.9, 1] | [0.9, 1] |
| Actor learning rate () | ||
| Critic learning rate () | ||
| Number of epochs (k) | [1, 10] | [1, 10] |
| Target smooth model standard deviation () | – | [0.1, 0.5] |
| Entropy loss function (w) | [0.01, 0.1] | – |
| Metrics | PI | FLC | SMC | BO-PPO | BO-TD3 |
|---|---|---|---|---|---|
| Rise time (s) | 0.0016 | 0.0021 | 0.0090 | 0.0012 | 0.0016 |
| Settling time (s) | 0.0070 | 0.1398 | 0.0161 | 0.0033 | 0.0032 |
| Overshoot (%) | 11.27 | 5.41 | 0.03 | 7.42 | 5.95 |
| Metrics | PI | FLC | SMC | BO-PPO | BO-TD3 |
|---|---|---|---|---|---|
| RMSE | 0.0826 | 0.3462 | 0.1754 | 0.2798 | 0.0780 |
| MAE | 0.0706 | 0.2907 | 0.0889 | 0.2707 | 0.0650 |
| MAPE | 0.147 | 0.6057 | 0.1853 | 0.5639 | 0.1355 |
| IAE | 0.0095 | 0.0392 | 0.0120 | 0.0365 | 0.0088 |
| Metrics | PI | FLC | SMC | BO-PPO | BO-TD3 |
|---|---|---|---|---|---|
| RMSE | 0.8363 | 0.9832 | 1.2592 | 0.8676 | 0.7775 |
| MAE | 0.1039 | 0.3408 | 0.1038 | 0.4680 | 0.0750 |
| MAPE | 0.2165 | 0.7100 | 0.2163 | 0.9749 | 0.1562 |
| IAE | 0.3117 | 1.0223 | 0.3115 | 1.4039 | 0.2248 |
| Metrics | PI | FLC | SMC | BO-PPO | BO-TD3 |
|---|---|---|---|---|---|
| RMSE | 0.8437 | 0.9671 | 1.2679 | 0.7627 | 0.7942 |
| MAE | 0.1013 | 0.2980 | 0.1249 | 0.2356 | 0.0620 |
| MAPE | 0.2111 | 0.6208 | 0.2603 | 0.4909 | 0.1292 |
| IAE | 0.3040 | 0.8939 | 0.3748 | 0.7069 | 0.1860 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammad, S.; Obeid, H.; Hammou, A.; Hinaje, M.; Gualous, H. Voltage Control for DC Microgrids: A Review and Comparative Evaluation of Deep Reinforcement Learning. Energies 2025, 18, 5706. https://doi.org/10.3390/en18215706
Muhammad S, Obeid H, Hammou A, Hinaje M, Gualous H. Voltage Control for DC Microgrids: A Review and Comparative Evaluation of Deep Reinforcement Learning. Energies. 2025; 18(21):5706. https://doi.org/10.3390/en18215706
Chicago/Turabian StyleMuhammad, Sharafadeen, Hussein Obeid, Abdelilah Hammou, Melika Hinaje, and Hamid Gualous. 2025. "Voltage Control for DC Microgrids: A Review and Comparative Evaluation of Deep Reinforcement Learning" Energies 18, no. 21: 5706. https://doi.org/10.3390/en18215706
APA StyleMuhammad, S., Obeid, H., Hammou, A., Hinaje, M., & Gualous, H. (2025). Voltage Control for DC Microgrids: A Review and Comparative Evaluation of Deep Reinforcement Learning. Energies, 18(21), 5706. https://doi.org/10.3390/en18215706







