IVCLNet: A Hybrid Deep Learning Framework Integrating Signal Decomposition and Attention-Enhanced CNN-LSTM for Lithium-Ion Battery SOH Prediction and RUL Estimation

Abstract

Accurate prediction of the degradation trajectory and estimation of the remaining useful life (RUL) of lithium-ion batteries are crucial for ensuring the reliability and safety of modern energy storage systems. However, many existing approaches rely on deep or highly complex models to achieve high accuracy, often at the cost of computational efficiency and practical applicability. To tackle this challenge, we propose a novel hybrid deep-learning framework, IVCLNet, which predicts the battery’s state-of-health (SOH) evolution and estimates RUL by identifying the end-of-life threshold (SOH = 80%). The framework integrates Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN), Variational Mode Decomposition (VMD), and an attention-enhanced Long Short-Term Memory (LSTM) network. IVCLNet leverages a cascade decomposition strategy to capture multi-scale degradation patterns and employs multiple indirect health indicators (HIs) to enrich feature representation. A lightweight Convolutional Block Attention Module (CBAM) is embedded to strengthen the model’s perception of critical features, guiding the one-dimensional convolutional layers to focus on informative components. Combined with LSTM-based temporal modeling, the framework ensures both accuracy and interpretability. Extensive experiments conducted on two publicly available lithium-ion battery datasets demonstrated that IVCLNet significantly outperforms existing methods in terms of prediction accuracy, robustness, and computational efficiency. The findings indicate that the proposed framework is promising for practical applications in battery health management systems.

1. Introduction

Lithium-ion batteries (LIBs) have found extensive use across electric mobility, energy storage infrastructures, and industrial domains, owing to their high specific energy, durable cycling performance, and low self-discharge behavior [1]. Despite these advantages, a cell’s capacity inevitably deteriorates during long-term operation, and once it is reduced below 80% of its rated capacity, the cell is considered to have reached end-of-life (EOL). Prognostics and Health Management (PHM) techniques are, thus, employed to evaluate reliability and avert unplanned failures, with remaining useful life (RUL) estimation being a pivotal task [2].

In recent years, researchers have explored various approaches to improve the accuracy and practicality of RUL prediction for lithium-ion batteries. These methods are broadly classified into model-based and data-driven categories. Model-based approaches include electrochemical models [3], equivalent circuit models [4], and empirical models. Guha and Patra [5] employed a particle filter in conjunction with a fractional-order equivalent circuit model for RUL estimation, though the algorithm imposes high computational demands. Lui et al. [6] proposed an empirical method based on voltage and current analysis. However, such methods often require accurate physical modeling, which is difficult to achieve due to the complexity and variability of electrochemical processes, limiting their applicability.

Data-driven approaches circumvent detailed physical modeling and instead infer degradation behaviors from historical observations [7]. Representative methods include support vector machines (SVMs), relevance vector machines (RVMs) [8], convolutional neural networks (CNNs) [9], and long short-term memory (LSTM) networks [10]. Among these, the LSTM model has been widely applied for battery health assessment and RUL prediction due to its ability to capture long-term temporal dependencies [11].

To further enhance prediction performance, several improvements have been introduced. Wang et al. [12] constructed health indicators through nonlinear dimension reduction of charging current curves and combined them with LSTM. Liu et al. [13] optimized LSTM hyperparameters via an improved sparrow search algorithm, while Ren et al. [14] combined CNN and LSTM with autoencoder-based feature expansion to jointly exploit local and temporal features. These studies demonstrate the potential of deep learning, but also highlight challenges such as noisy inputs, weak feature interpretability, and difficulties in handling non-stationary degradation signals.

Signal decomposition techniques are increasingly explored to tackle these challenges. Variational Mode Decomposition (VMD) has been employed to suppress high-frequency noise, but it still suffers from residual interference. Similarly, CEEMDAN mitigates mode aliasing through noise-assisted decomposition but may retain high-order delays and residual noise. To address these drawbacks, the Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN) [15] method has been proposed; it alleviates endpoint effects and enhances robustness when handling nonlinear, non-stationary time series.

Despite progress in both model-based and data-driven RUL prediction, several gaps remain. Model-based approaches, while interpretable, are sensitive to parameter uncertainties [5,6]. Purely data-driven methods such as SVM, CNN, and LSTM [8,9,10] can capture complex patterns but often fail to fully exploit multi-scale temporal information and are vulnerable to noise. Hybrid strategies have been proposed [13,14], yet most rely on a single feature extraction method or lack mechanisms to adaptively emphasize informative temporal patterns.

To overcome these limitations, this paper proposes IVCLNet, a hybrid prediction framework that integrates ICEEMDAN and VMD for multi-level signal decomposition with an attention-enhanced CNN-LSTM network. By fusing health indicators with decomposed capacity features, the framework captures both global and local temporal information. The inclusion of a Convolutional Block Attention Module (CBAM) further enables selective focus on informative features, thereby improving robustness and predictive accuracy.

The main contributions of this paper are summarized as follows:

• A novel hybrid framework, IVCLNet, is proposed. It employs ICEEMDAN and VMD for multi-level signal decomposition and utilizes a fusion model to learn time-series degradation features. This design enhances the modeling of complex non-stationary signals and improves RUL prediction accuracy.
• A hybrid input strategy is designed by integrating indirect health indicators and decomposed capacity features, boosting feature sensitivity and predictive robustness.
• A CNN-LSTM network enhanced by a Convolutional Block Attention Module (CBAM) is introduced to adaptively extract key temporal features. Experiments demonstrate that IVCLNet outperforms baseline models in both accuracy and robustness.

The remainder of this paper is structured as follows: Section 2 presents the proposed method, Section 3 describes data preprocessing and feature construction, Section 4 reports experimental results, and Section 5 concludes the study.

2. Method

This section describes the various methods used in this paper, including ICEEMDAN, VMD, LSTM, CBAM, and evaluation methods.

2.1. Improved CEEMDAN (ICEEMDAN)

In time series forecasting, the traditional empirical mode decomposition (EMD) method [16] has been improved by introducing noise, leading to the development of enhanced decomposition models such as EEMD [17], CEEMD [18], and CEEMDAN [19]. These improved decomposition methods are more effective at handling non-stationary and complex signals. Colominas et al. [20] further improved the CEEMDAN method by proposing the ICEEMDAN method, which substitutes conventional mode estimation with local mean operations and derives k-order modes from the signal’s local averages rather than directly employing white noise. This effectively avoids mode aliasing and provides more accurate and stable signal decomposition.

The original sequence is $y\left(t\right)$, the Gaussian white noise with zero mean and unit variance is ${\eta }^i\left(t\right)$, the noise amplitude factor is ${\beta }_k$, the EMD operation is $E_k(·)$, $M(·)$ is the operator that generates the local mean of the original sequence, and the averaging operation is denoted as $E[·]$. The decomposition process of ICEEMDAN is as follows:

Step 1: Add adaptive noise to the original signal and compute the first order:

$$y^i\left(t\right)=y\left(t\right)+{\beta }_0{E}_1\left({\eta }^i\left(t\right)\right)$$

(1)

Step 2: Extract the first IMF component:

$$IM{F}_1\left(t\right)=y\left(t\right)-r_1\left(t\right)$$

(2)

The second IMF component $IM{F}_2\left(t\right)$ is obtained by subtracting the new local mean $r_2\left(t\right)$ from the residual $r_1\left(t\right)$ from the previous step:

$$\begin{array}{cc}\hfill IM{F}_2\left(t\right)& =r_1\left(t\right)-r_2\left(t\right)\hfill \\ \hfill & =r_1\left(t\right)-〈M\left(r_1\left(t\right)+{\beta }_1{E}_2\left({\eta }^i\left(t\right)\right)\right)〉\hfill \end{array}$$

(3)

Step 3: Calculate the jth-order residual term $r_j\left(t\right)$, where $j=2,3,\dots ,N$, using the residuals from the previous step plus noise for local mean estimation:

$$r_j\left(t\right)=〈M\left(r_{j-1}\left(t\right)+{\beta }_{j-1}{E}_j\left({\eta }^i\left(t\right)\right)\right)〉$$

(4)

Step 4: The j-th IMF is the difference between adjacent residuals:

$${IMF}_j\left(t\right)=r_{j-1}\left(t\right)-r_j\left(t\right)$$

(5)

2.2. Variational Mode Decomposition (VMD)

In order to further extract non-stationary features from the lithium-ion battery capacity sequence and enhance the input quality of the prediction model, this paper introduces VMD as a secondary decomposition method after ICEEMDAN decomposition, which is an adaptive signal processing method based on the variational framework [21]. The basic idea is to decompose the input signal $f\left(t\right)$ into a number of finite intrinsic mode functions (IMFs) ${\left\{u_k\left(t\right)\right\}}_{k=1}^K$ such that each mode has the narrowest spectral bandwidth near its corresponding center frequency ${\omega }_k$. The optimization objective can be expressed as the following constrained variational problem:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}\hfill & \underset{\{u_k,{\omega }_k\}}{min}\left\{\sum _{k=1}^K{∥{\partial }_t\left[\left(\delta \left(t\right)+{\displaystyle \frac{j}{\pi t}}\right)\ast u_k\left(t\right)\right]e^{-j{\omega }_{k}t}∥}^2\right\}\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\sum _{k=1}^K{u}_k=f\hfill \end{array}\right.\hfill \end{array}$$

(6)

Among them, K is the number of decomposed modes, ∗ denotes convolution, $\delta \left(t\right)$ is the Dirac function, and ${\partial }_t$ is the first-order derivative operator.

The Lagrange multiplier operator $\lambda \left(t\right)$ and penalty factor $\alpha$ introduced into the extended Lagrange function can be expressed as follows:

$$\begin{array}{c}L(\left\{u_k\right\},\left\{{\omega }_k\right\},\lambda )=\alpha \sum _{k=1}^K{∥{\partial }_t\left[\left(\delta \left(t\right)+{\displaystyle \frac{j}{\pi t}}\right)\ast u_k\left(t\right)\right]e^{-j{\omega }_{k}t}∥}^2\hfill \\ \hfill +{∥f\left(t\right)-\sum _{k=1}^K{u}_k∥}^2+〈\lambda \left(t\right),f\left(t\right)-\sum _{k=1}^K{u}_k〉\end{array}$$

(7)

VMD reconstructs the problem and iterates variables in the Fourier domain. The update steps are as follows:

Modal function spectrum update:

$${\widehat{u}}_k^{n+1}\left(\omega \right)\leftarrow {\displaystyle \frac{\widehat{f}\left(\omega \right)-{\sum }_{i\ne k}{\widehat{u}}_i^{n+1}\left(\omega \right)-\frac{\lambda \left(\omega \right)}{2}}{1+2\alpha {(\omega -{\omega }_k^n)}^2}}$$

(8)

Center frequency update:

$${\omega }_k^{n+1}\leftarrow {\displaystyle \frac{{\int }_0^{\infty }\omega {\left|{\widehat{u}}_k^{n+1}\left(\omega \right)\right|}^{2}d\omega }{{\int }_0^{\infty }{\left|{\widehat{u}}_k^{n+1}\left(\omega \right)\right|}^{2}d\omega }}$$

(9)

Lagrangian multiplier operator update:

$${\widehat{\lambda }}^{n+1}\left(\omega \right)\leftarrow {\widehat{\lambda }}^n\left(\omega \right)+\tau \left[\widehat{f}\left(\omega \right)-\sum _{k=1}^K{\widehat{u}}_k^{n+1}\left(\omega \right)\right]$$

(10)

Repeat steps (8)–(10) and stop iteration when the following convergence conditions are met: ${\displaystyle \sum _{k=1}^K\frac{\parallel {\widehat{u}}_k^{n+1}-{\widehat{u}}_k^n{\parallel }_2^2}{\parallel {\widehat{u}}_k^n{\parallel }_2^2}<ϵ}$, obtain K modal functions, where $ϵ>0$ is the convergence threshold.

2.3. Temporal Feature Modeling: CNN and LSTM Integration

To extract local patterns from sequence data, a one-dimensional convolutional neural network (1D CNN) is employed as a shallow encoder. It performs convolution operations on the temporal axis and uses ReLU activation to enhance non-linear representation [22,23]. This configuration enables the network to learn degradation-related regional trends from battery data.

The output of the k-th filter at time t is given by the following:

$$f_k^{\left(l\right)}\left(t\right)=\sigma \left(\sum _{i=1}^p\sum _{j=1}^K{w}_{k,i,j}^{\left(l\right)}·x_i^{(l-1)}(t-j+1)+b_k^{\left(l\right)}\right)$$

(11)

where $x_i^{(l-1)}$ is the input to the $(l-1)$-th layer, $w_{k,i,j}^{\left(l\right)}$ is the convolution weight, and $\sigma (·)$ denotes the ReLU function.

For long-term dependency modeling, LSTM layers are stacked after the CNN. LSTM uses memory cells and gated operations to retain temporal context over long sequences [24]. The integrated framework enhances the model’s capacity to represent short-term variations as well as long-term degradation trends.

The overall behavior of the hybrid module can be expressed as follows:

$$h_t=\mathrm{LSTM}\left(\mathrm{ReLU}\left(\mathrm{Conv}1\mathrm{D}\left(x_t\right)\right)\right)$$

(12)

where $x_t$ is the input at time t, and $h_t$ is the LSTM output state.

This joint architecture leverages CNN’s local pattern detection and LSTM’s sequence memory to effectively extract temporal features for RUL prediction.

2.4. Key Feature Enhancement Mechanism: Convolutional Block Attention Module (CBAM)

CBAM [25] is a lightweight yet effective attention module that sequentially applies channel and spatial attention to refine feature maps, thereby enhancing the representation of key information. As shown in Figure 1, CBAM integrates both attention mechanisms in a cascaded manner.

Given a feature map F, CBAM sequentially applies channel and spatial attention using the following:

$$F^{\prime }=M_c\left(F\right)\otimes F,F^{\prime \prime }=M_s\left(F^{\prime }\right)\otimes F^{\prime }$$

(13)

where ⊗ denotes element-wise multiplication, and $M_c(·)$ and $M_s(·)$ represent channel and spatial attention weights, respectively.

Specifically, channel attention aggregates information through average and max pooling operations, which are then processed by a shared MLP:

$$M_c\left(F\right)=\sigma \left(\mathrm{MLP}\left(\mathrm{AvgPool}\left(F\right)\right)+\mathrm{MLP}\left(\mathrm{MaxPool}\left(F\right)\right)\right)$$

(14)

Spatial attention is computed by concatenating pooled features along the channel axis and applying a convolution:

$$M_s\left(F\right)=\sigma \left(\mathrm{Conv}\left(\left[\mathrm{AvgPool}\left(F\right);\mathrm{MaxPool}\left(F\right)\right]\right)\right)$$

(15)

This module enables the model to adaptively focus on informative channels and spatial regions, improving robustness and prediction accuracy.

2.5. Fusion Prediction Framework IVCLNet

This paper combines the advantages of multiple modeling components to propose a hybrid lithium-ion battery state-of-health (SOH) prediction and remaining useful life (RUL) estimation framework, called IVCLNet, whose overall structure includes a signal decomposition module and a deep learning prediction module.

The historical capacity sequence up to cycle t is first decomposed using the Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN) method to obtain multiple intrinsic mode functions (IMFs). Then, the modes are frequency-divided using sample entropy and K-means clustering, and the high-frequency components are further decomposed with Variational Mode Decomposition (VMD). All retained modal components from the historical sequence are integrated into a unified multi-modal feature matrix, denoted as ${\mathbf{C}}_t$:

$${\mathbf{C}}_t\in {\mathbb{R}}^{N\times K},$$

(16)

where N denotes the sliding time window length and K represents the number of retained decomposition modes. This matrix captures the multi-scale degradation dynamics of the battery using only the information available up to cycle t.

The ${\mathbf{C}}_t$ features are then concatenated with six indirect health indicators (HIs) that are highly correlated with SOH, including constant-current charging time (CCCT), constant-voltage charging time (CVCT), constant-current discharging time (CCDT), time interval of equal charging voltage difference (TIECVD), time interval of equal discharging voltage difference (TIEDVD), and mean voltage fade (MVF), forming the final model input:

$${\mathbf{X}}_t\in {\mathbb{R}}^{N\times (K+M)},$$

(17)

where $M=6$ is the number of selected health indicators. By concatenating the HIs along the feature dimension with ${\mathbf{C}}_t$, the CNN–LSTM–CBAM module can jointly learn both the historical degradation patterns captured by the decomposition features and the auxiliary health information provided by the HIs. This integration enables the model to leverage complementary information correlated with SOH, thereby improving prediction accuracy and robustness, particularly during early degradation stages or under noisy capacity conditions.

During the prediction phase, the CNN–LSTM–CBAM deep learning module directly models the multi-modal input and outputs the predicted SOH at a future cycle $t+\mathrm{\Delta }$, denoted as ${\widehat{y}}_{t+\mathrm{\Delta }}$. Based on a predefined end-of-life (EOL) threshold (SOH = 80% of the initial capacity), the predicted SOH degradation trajectory can be further transformed into the corresponding remaining useful life (RUL), defined as the number of remaining cycles until the predicted SOH reaches the EOL criterion.

As shown in Figure 2, the proposed SOH prediction and RUL estimation method comprises four sequential stages.

This comprehensive pipeline ensures that each stage—from signal decomposition to attention-guided temporal modeling—contributes to a coherent and interpretable RUL estimation framework.

3. Health Feature Extraction and Processing

3.1. Data Description

This paper uses widely recognized battery datasets provided by NASA and CALCE, both of which are commonly adopted in LIB-related investigations, as shown in Figure 3.

3.1.1. NASA Lithium Battery Dataset

In this study, capacity degradation data from three batteries, B5, B6, and B7, rated at 2 Ah from the NASA PCoE Research Center, were used [26]. The aging process was accelerated through repeated cycling, conducted at room temperature in three stages, as follows: first, charging at a constant current of 1.5 A (0.75 C) up to 4.2 V; then switching to constant-voltage charging until the current decreased to 20 mA; finally, discharging at a constant current of 2 A until the voltage reached 2.7 V, 2.5 V, 2.2 V, and 2.5 V, respectively. The EOL criterion was set at a 30% decay of the rated capacity to 1.4 Ah [27]. The selected NASA batteries were aged under well-controlled conditions, allowing for a reproducible evaluation of the proposed IVCLNet framework. While real-life operating profiles may involve variable currents, partial charge/discharge cycles, and fluctuating temperatures, the framework is designed to be general and can be adapted to accommodate more diverse conditions in future studies.

3.1.2. CALCE Lithium Battery Dataset

The CALCE lithium-ion battery dataset was obtained from the University of Maryland Center for Advanced Life Cycle Engineering (CALCE). The rated capacity of the battery is 1.1 Ah. The aging process was accelerated through constant-current and constant-voltage cycling, conducted at room temperature, with an initial constant-current charge of 0.55 A (0.5 C) up to 4.2 V, then continued in constant-voltage mode until the current dropped to 55 mA, followed by discharge in constant-current mode at 2 A to a cutoff voltage of 2.7 V. The change in capacity directly reflects the degree of degradation of the battery during the charge–discharge cycle. As the number of cycles increases, the capacity of the battery decreases, so it can be considered a key health indicator for predicting the RUL of a battery based on its performance degradation. Similarly, the CALCE batteries were aged under controlled conditions, ensuring reproducibility. The IVCLNet framework is general and can be applied to more complex real-world operating conditions in future work.

3.2. Health Indicator Extraction

This experiment references a series of studies serving different purposes [28,29,30,31,32] to extract health indicators (HIs). The purpose of extracting HIs is to obtain a concise characterization from complex raw data, where capacity is a standard metric for evaluating battery performance, but is not available online. The high correlation between the extracted HIs and capacity indicates that the extracted HIs can effectively characterize the state of the battery.

As shown in Figure 4, it can be observed that the voltage undergoes significant changes as the number of cycles increases. Based on these changes, several indirect health indicators (HIs) were extracted through sliding-window analysis and multi-segment division of the voltage–time characteristics in constant-current, constant-voltage mode. Finally, Pearson correlation coefficient (PCC) analysis was conducted to assess these factors, leading to the identification of the following as the selected HI: constant-current charging time (CCCT), constant-voltage charging time (CVCT), constant-current discharging time (CCDT), time interval for an equal charging voltage difference (TIECVD), time interval for an equal discharging voltage difference (TIEDVD), and mean voltage decay (MVF).

PCC is a commonly employed statistical method to quantify the degree of linear association between HIs and SOHs [33]. Its values span from −1 to 1, where a magnitude closer to 1 indicates a stronger linear dependence between the two variables. The mathematical expression for PCC is as follows:

$$PCC(X,Y)={\displaystyle \frac{{\sum }_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{{\sum }_{i=1}^n{(X_i-\overline{X})}^2·{\sum }_{i=1}^n{(Y_i-\overline{Y})}^2}}}$$

(18)

where x and y represent the values of the selected HI sequence and battery SOH sequence, respectively; $\overline{x}$ and $\overline{y}$ are their corresponding means, and n is the sample size.

As shown in

Table 1. Comparison of PCC values for various HIs across NASA and CALCE datasets.

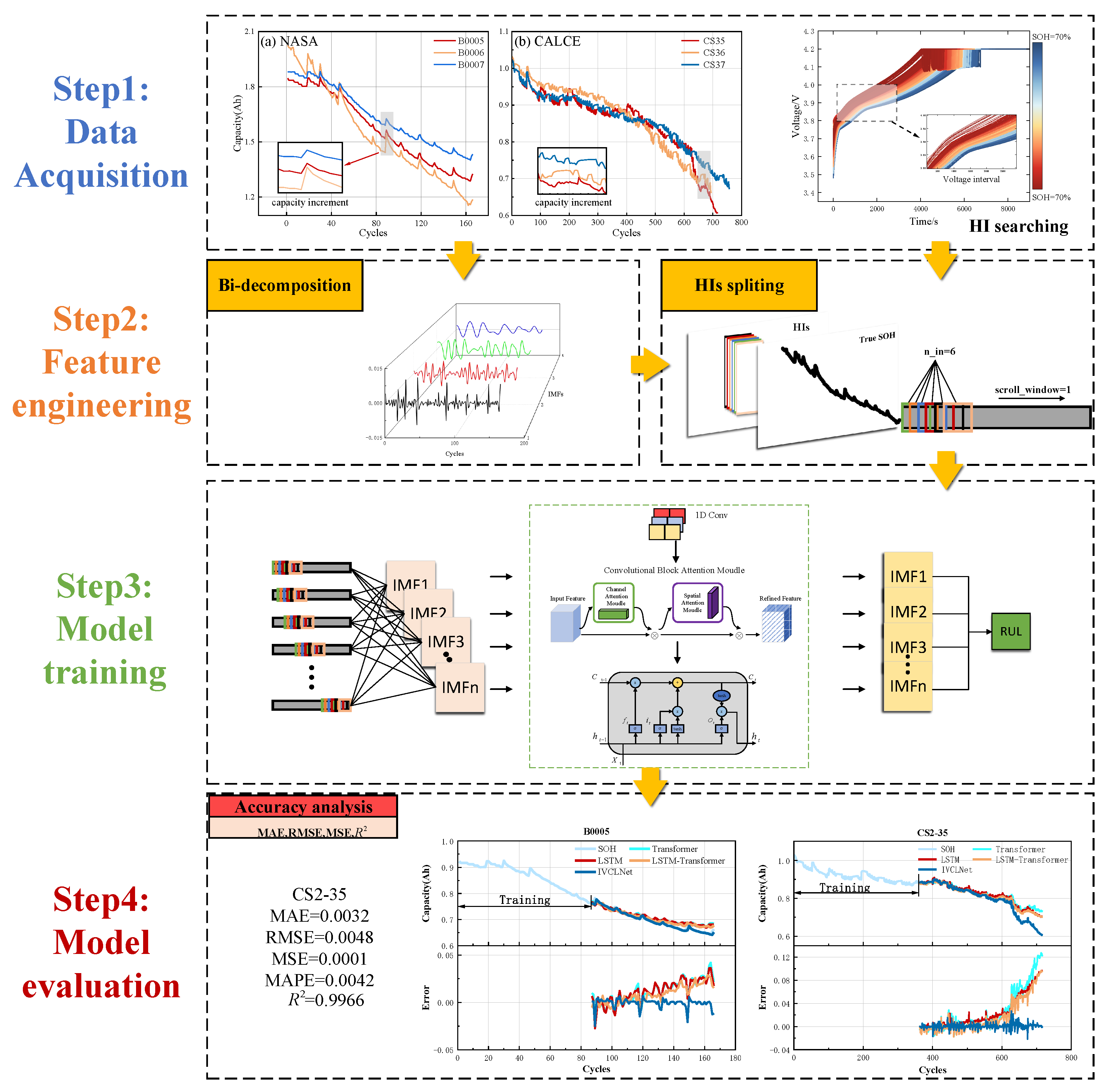
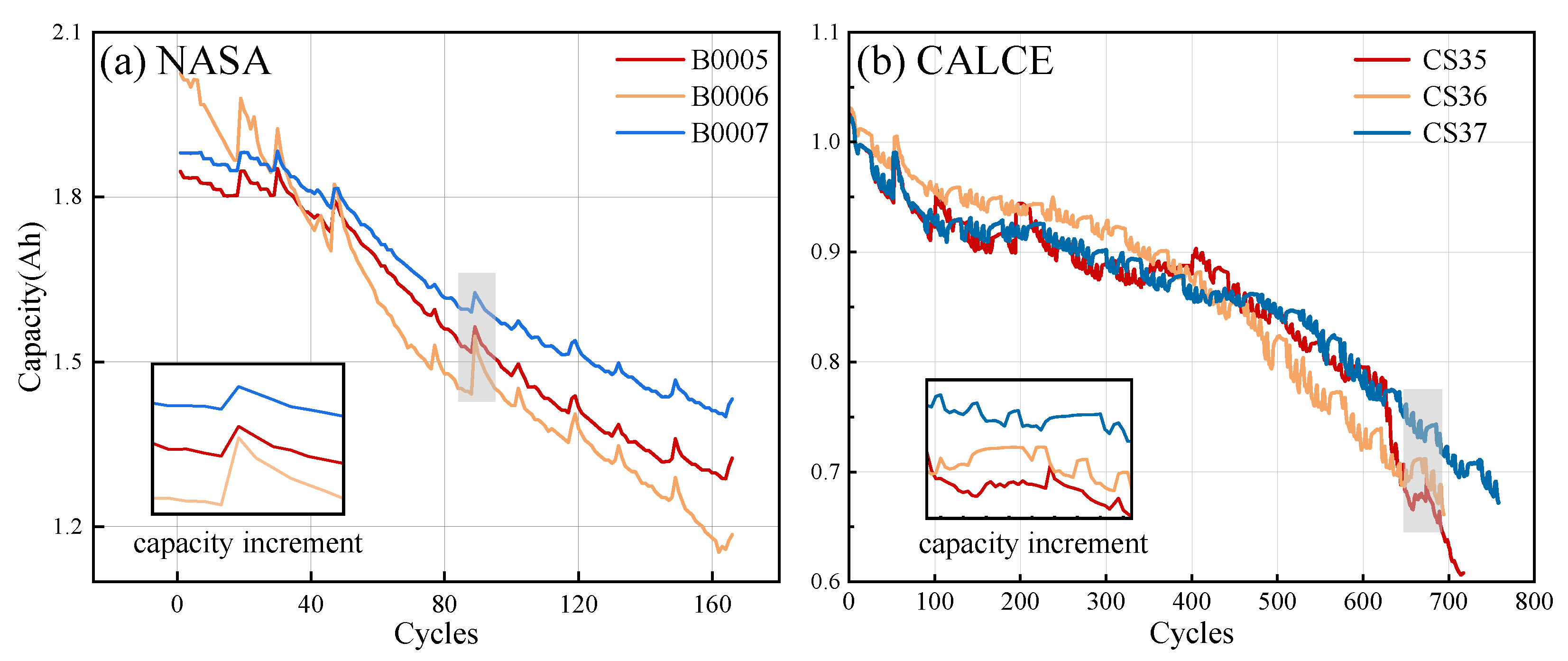
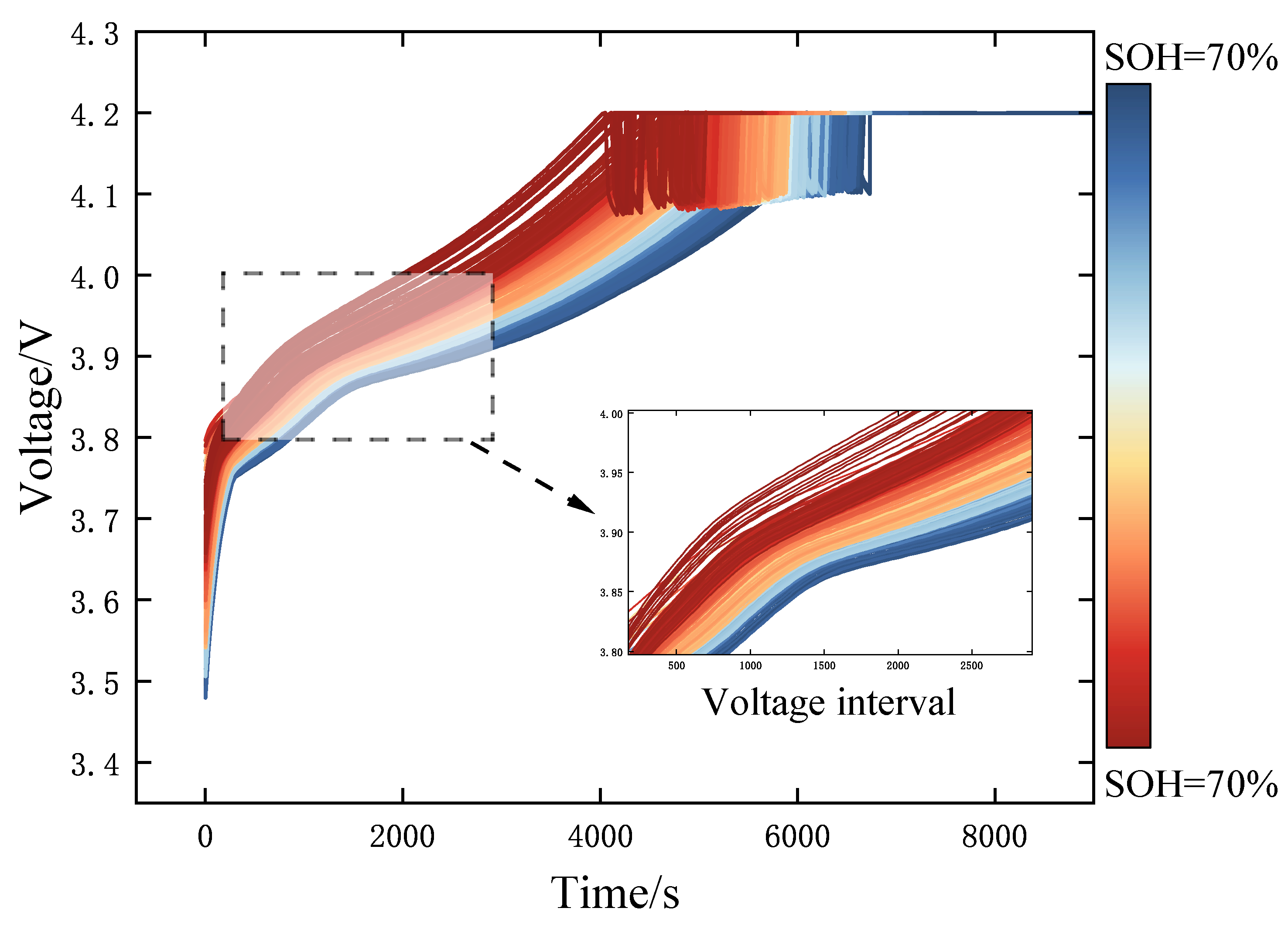
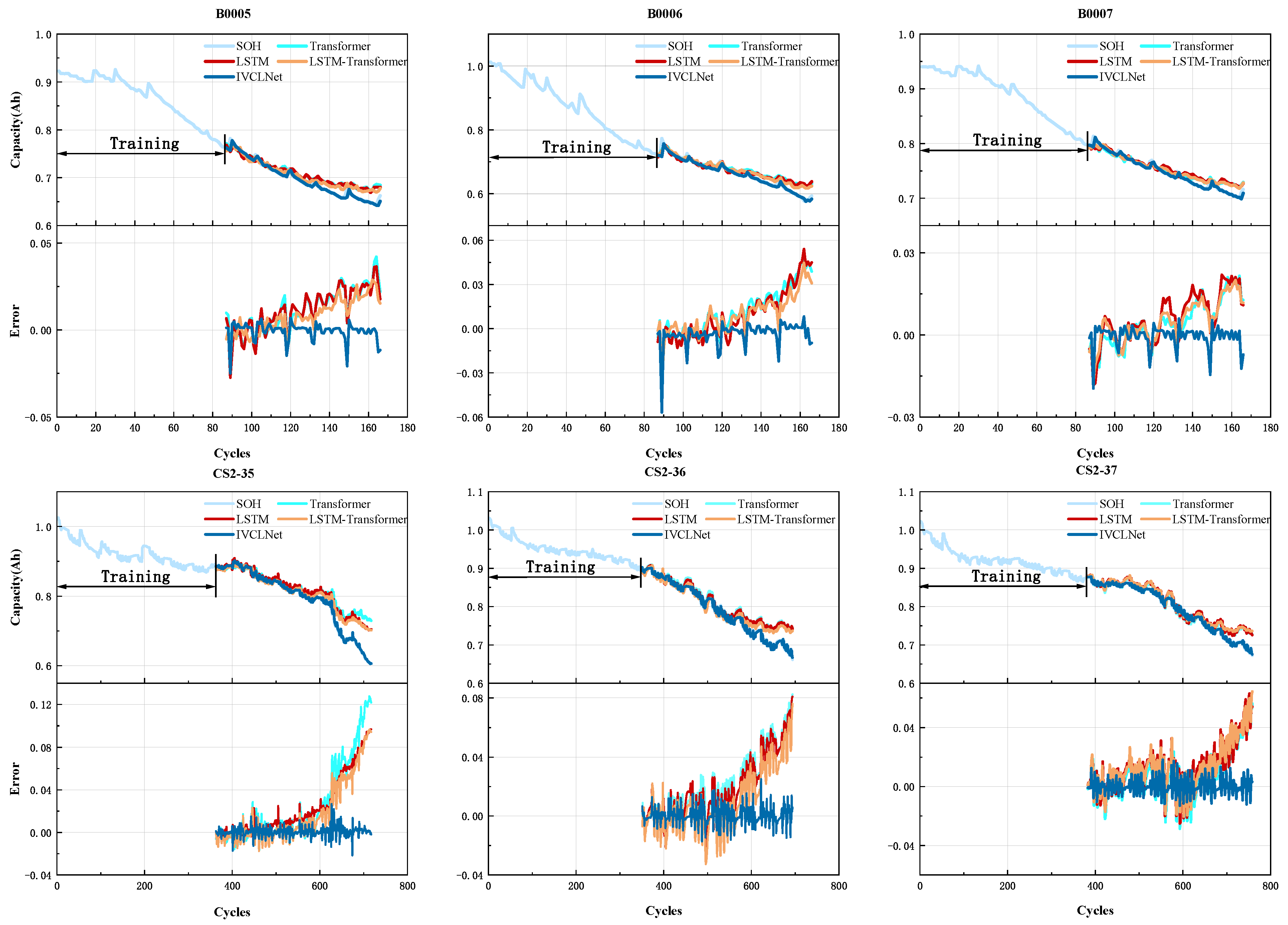
Battery Series	CCDT	CCCT	CVCT	TIECVD	TIEDVD	MVF
B0005	0.9999	0.9980	−0.9735	0.9971	0.9989	−0.9859
B0006	0.9999	0.9948	−0.9697	0.9928	0.9958	−0.9655
B0007	0.9999	0.9980	−0.9845	0.9918	0.9988	−0.9668
CS2-35	0.9999	0.9967	−0.9833	0.9954	0.9774	−0.9540
CS2-36	0.9999	0.9976	−0.9938	0.9960	0.9815	−0.9780
CS2-37	0.9999	0.9968	−0.9649	0.9956	0.9771	−0.9370

, the PCCs of the extracted HI values are all higher than 0.95, indicating a high degree of linear correlation with the battery degradation trend.

The high correlation between the selected health indicators (HIs) and state of health (SOH) can be attributed to the intrinsic electrochemical and physical processes during battery degradation. Specifically, the selected indicators include CCDT, CCCT, CVCT, TIECVD, TIEDVD, and MVF.

CCDT, CCCT, and CVCT reflect the duration of charge and discharge under constant-current or constant-voltage conditions. As the battery ages, internal resistance increases and effective capacity decreases, leading to longer charging/discharging times to reach the same voltage thresholds; hence, these time-based indicators are directly sensitive to capacity fade.

TIECVD and TIEDVD capture intervals corresponding to equal voltage differences during charging or discharging. These metrics effectively reflect subtle changes in voltage dynamics caused by electrode polarization and the growth of internal resistance, which indirectly indicate battery health deterioration.

MVF measures the overall decline in average voltage over cycles, integrating the cumulative effects of material degradation and electrolyte aging, thereby providing a global indicator of battery performance.

It should be noted that these HIs are particularly effective under full-cycle conditions, as represented by the NASA and CALCE datasets used in this study. In real-life applications, batteries often operate under non-repetitive profiles with varying depths of discharge, and constant-voltage charging may not always be applied. In such cases, the linear correlation between certain time-based indicators (CCCT, CVCT, CCDT) and battery capacity may be reduced. Nevertheless, the proposed IVCLNet framework is flexible and can accommodate alternative or additional HIs extracted from partial cycles or other measurable voltage/current features, allowing application to a broader range of operating conditions.

In summary, these selected HIs encode both direct effects (capacity loss, resistance increase) and indirect effects (voltage fluctuation patterns) of battery aging, which explains their high linear correlation with SOH as quantified by the PCC values in Table 1.

3.3. Dataset Decomposition

To extract frequency-specific features, the raw capacity data is decomposed using a two-stage ICEEMDAN-VMD strategy. First, ICEEMDAN produces five IMFs and a residual that collectively represent the signal’s multi-scale behavior.

Sample entropy is calculated for each IMF, followed by K-means clustering to categorize them into high-, medium-, and low-frequency groups, corresponding to different temporal dynamics.

The high-frequency group undergoes further VMD decomposition to enhance its resolution. Finally, selected IMFs and the residuals are aligned and concatenated to form a feature matrix of size $N\times 5$.

After the two-stage ICEEMDAN–VMD decomposition, all selected intrinsic mode functions (IMFs) and residual components are aligned and reconstructed into a multi-scale feature matrix, denoted as $\mathbf{Co}\_\mathbf{data}$. This feature matrix is then concatenated with the extracted health indicators (HIs) described in Section 3.2 to form the final model input ${\mathbf{X}}_t$. In this way, the proposed method jointly integrates frequency domain decomposition features and time-domain degradation indicators, ensuring that both physical interpretability and statistical sensitivity to SOH degradation are retained before entering the deep learning module.

To avoid any form of data leakage, it is important to emphasize that the ICEEMDAN–VMD decomposition is applied only to the historical portion of each capacity sequence available within the prediction horizon. During both training and inference, the decomposition operates on the observed capacity data up to the current cycle t, without accessing any future capacity information ($t^{\prime }>t$). The resulting multi-scale feature matrix $\mathbf{Co}\_\mathbf{data}$, therefore, represents historical signal characteristics rather than the target variable itself. This design ensures that the model input strictly depends on observable degradation trends, maintaining the integrity and causality of the prediction process.

4. Experiments and Analysis

This section presents a detailed analysis of the performance of four models (IVCLNet, Transformer, LSTM-Transformer, and LSTM) on a publicly available battery dataset. In the experiment, 50% of the data is designated for model training, while the remaining portion is used for testing. The proposed algorithms are shown to be effective and beneficial.

The training process is conducted on a GIGABYTE AORUS PC with an Intel Core i5-13600KF processor (24 MB cache, up to 5.10 GHz), an NVIDIA GeForce RTX 4060Ti graphics card, and 32 GB of RAM. The experiments were implemented using MATLAB R2023b and PyTorch 2.1.0 with CUDA Toolkit 12.2 for GPU acceleration.

4.1. The Evaluation Criteria

To evaluate the prediction accuracy of the model, a set of commonly used metrics was employed to quantitatively examine its performance: mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and the coefficient of determination $R^2$. Here, n is the number of periods from the start of prediction to the end of the cycle, $y_i$ is the true capacity, and ${\widehat{y}}_i$ is the predicted capacity. The formulas for these metrics are as follows:

$$\mathrm{MSE}(y,\widehat{y})={\displaystyle \frac{1}{n}}\sum _{i=1}^n{({\widehat{y}}_i-y_i)}^2$$

(19)

$$\mathrm{RMSE}(y,\widehat{y})=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

(20)

$$\mathrm{MAE}(y,\widehat{y})={\displaystyle \frac{1}{n}}\sum _{i=1}^n|y_i-{\widehat{y}}_i|$$

(21)

$$\mathrm{MAPE}(y,\widehat{y})={\displaystyle \frac{100\%}{n}}\sum _{i=1}^n{\displaystyle \frac{|y_i-{\widehat{y}}_i|}{max(\epsilon ,|y_i\left|\right)}}$$

(22)

Clearly, within the range $(0,+\infty )$, larger errors result in larger values. The smaller the values of MSE, RMSE, MAE, and MAPE, the more reliable and accurate the predictions are.

$$R^2(y,\widehat{y})=1-{\displaystyle \frac{{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}$$

(23)

The goodness of the model can be assessed based on the value of $R^2$. The closer the result is to 1, the smaller the model error.

4.2. SOH Prediction and RUL Estimation

Although the model outputs the predicted SOH trajectory, the RUL can be derived by identifying the cycle index at which the SOH curve crosses the 80% threshold. Therefore, the evaluation metrics in this section reflect the accuracy of the SOH-based degradation prediction, which directly determines the reliability of RUL estimation.

4.2.1. Hyperparameter Setting

The specific parameter configurations for each model are listed in

Table 2. Hyperparameters for different models.

Models	Training Hyperparameters			Model Hyperparameters
	$\mathit{e}$	$\mathit{lr}$	$\mathit{b}$	${\mathit{d}}_{\mathit{e}}$	${\mathit{d}}_{\mathit{d}}$	$\mathit{n}$
IVCLNet	300	0.001	25	-	32	2
Transformer	300	0.001	25	64	32	2
LSTM	300	0.001	25	-	32	2
LSTM-Transformer	300	0.001	25	64	32	2

. To ensure fair comparison between models, all models were evaluated using uniform training hyperparameters and structural hyperparameters. In the table, e, $lr$, b, $d_e$, $d_d$, and n denote, in order, the number of iterations, learning rate, batch size, embedding size, dimensionality of the MLP’s dense layer or the LSTM’s hidden state, and the total number of layers.

All models were trained using the Adam optimizer with a maximum of 300 epochs. The gradient threshold was set to 1 to prevent gradient explosion, and L2 regularization of 0.0001 was applied to mitigate overfitting. The initial learning rate was 0.0001, and training samples were shuffled at every epoch to enhance generalization. Loss values were monitored during training, and verbose output was enabled to display progress. All models used the mean squared error (MSE) as the loss function. These settings ensured consistent training across all models and enabled fair comparison of performance.

4.2.2. Comparison of the NASA and CALCE Datasets

A comparative experiment was conducted between IVCLNet and three alternative models, whose layer configurations are shown in

Table 3. Layer configurations of different deep learning models.

IVCLNet	Transformer	LSTM	LSTM-TF
Input	Input	Input	Input
Conv1D(1 × 3, 32)	Embed layer (32)	Linear	LSTM(64)
BN + ReLU	Positional Encoder	LSTM(32)	LSTM(32)
CBAM Attention	Softmax Attention	LSTM(32)	Softmax Attention
LSTM(64)	Add&Norm	LSTM(32)	Add&Norm
LSTM(32)	Softmax Attention	Linear	Feedforward
Linear	Add&Norm		Linear
	MLP
	Add&Norm

.

It should be noted that the comparison models were deliberately selected to represent the key categories of existing approaches rather than to exhaustively include all available architectures. Specifically, they cover three dominant paradigms in data-driven battery prognostics: (1) recurrent sequence learning (e.g., LSTM); (2) hybrid convolutional–recurrent modeling (e.g., CNN–LSTM); and (3) attention-based temporal learning (e.g., Transformer). This selection ensures that the benchmark comparison spans both fundamental and state-of-the-art methodologies while maintaining fairness and computational consistency. Therefore, the chosen set of baselines is sufficiently comprehensive to validate the effectiveness of IVCLNet without introducing redundant architectures.

Figure 5 and

Table 4. RUL prediction results on the NASA and CALCE datasets.

Cell	Methods	MAE	RMSE	MSE	MAPE	${\mathit{R}}^2$
B0005	IVCLNet	0.0030	0.0052	0.0001	0.0043	0.9803
	Transformer	0.0139	0.0169	0.0002	0.0206	0.8127
	LSTM	0.0139	0.0165	0.0002	0.0205	0.8197
	LSTM-Transformer	0.0100	0.0126	0.0001	0.0148	0.8906
B0006	IVCLNet	0.0048	0.0089	0.0001	0.0071	0.9641
	Transformer	0.0154	0.0201	0.0004	0.0244	0.8288
	LSTM	0.0147	0.0198	0.0003	0.0234	0.8303
	LSTM-Transformer	0.0119	0.0159	0.0002	0.0189	0.8901
B0007	IVCLNet	0.0026	0.0041	0.0001	0.0035	0.9805
	Transformer	0.0075	0.0095	0.0001	0.0103	0.9002
	LSTM	0.0089	0.0109	0.0001	0.0121	0.8715
	LSTM-Transformer	0.0073	0.0090	0.0001	0.0099	0.9114
CS2-35	IVCLNet	0.0032	0.0048	0.0001	0.0042	0.9966
	Transformer	0.0277	0.0446	0.0019	0.0401	0.7359
	LSTM	0.0233	0.0360	0.0012	0.0336	0.8266
	LSTM-Transformer	0.0212	0.0336	0.0011	0.0305	0.8441
CS2-36	IVCLNet	0.0041	0.0058	0.0001	0.0054	0.9927
	Transformer	0.0224	0.0300	0.0009	0.0306	0.8267
	LSTM	0.0204	0.0277	0.0007	0.0278	0.8476
	LSTM-Transformer	0.0171	0.0233	0.0005	0.0231	0.8879
CS2-37	IVCLNet	0.0032	0.0046	0.0001	0.0042	0.9940
	Transformer	0.0133	0.0184	0.0003	0.0177	0.9089
	LSTM	0.0155	0.0202	0.0004	0.0206	0.8922
	LSTM-Transformer	0.0156	0.0205	0.0004	0.0207	0.8892

present the prediction results and errors of IVCLNet, Transformer, LSTM-Transformer, and LSTM on the NASA dataset and CALCE dataset, respectively. As shown in the figure, in the validation results for the CS2-35 battery, although all models exhibited some degree of error accumulation, IVCLNet maintained stable prediction performance. Compared to other models, IVCLNet exhibited smaller fluctuations in prediction error magnitude and distribution, demonstrating higher prediction accuracy and robustness.

As shown in Table 4, in the lithium-ion battery life prediction task, the proposed IVCLNet model significantly outperforms baseline deep learning methods, including Transformer, LSTM, and LSTM-Transformer. Specifically, IVCLNet achieves the lowest average prediction error across all battery cells. Compared to the aforementioned models, its MAE improves by an average of 76.44%, 77.01%, and 72.41%, and its RMSE improves by an average of 71.12%, 71.48%, and 65.93%. MSE by 62.55%, 61.51%, and 49.32%, respectively, and MAPE by 77.46%, 77.99%, and 73.51%, respectively. Notably, IVCLNet demonstrates exceptional performance in applications requiring long-term predictions.

Due to the lack of an explicit local feature extraction mechanism, LSTM has certain limitations in identifying fine-grained degradation patterns, resulting in relatively low overall prediction accuracy. Although the Transformer model has global modeling capabilities, without the introduction of auxiliary structures, its perception of local features is weak, causing large fluctuations in the error curve. The LSTM-Transformer fusion model demonstrates greater stability and robustness across multiple datasets, capable of capturing both local and global temporal dependencies simultaneously. However, its local modeling remains constrained by the structural expressive power of LSTM, and the absence of a convolutional perception mechanism limits its ability to characterize complex feature patterns. Introducing a structure with a larger receptive field may improve performance, but it would also increase computational costs.

Furthermore, from the perspective of input modeling, the most significant difference between IVCLNet and other models lies in its joint ICEEMDAN-VMD decomposition processing of the original capacity sequence prior to prediction, which separates the mixed noise and degradation trends in the original SOH sequence to improve modeling clarity. The introduction of VMD processing in the high-frequency component further refines complex oscillation patterns and enhances the model’s ability to perceive local nonlinear features.

In contrast, other baseline models are affected by high-frequency noise and sudden changes, making it difficult for the models to capture the true degradation patterns. This difference is particularly evident in typical samples, such as the CS2-35 batteries, where the error curves of the undecomposed models fluctuate dramatically, and their long-term prediction performance deteriorates significantly.

Meanwhile, after decomposing feature extraction, IVCLNet effectively enhances its focus on key time steps and significant feature channels by introducing a convolutional layer with the CBAM attention mechanism, thereby reinforcing effective information at the input end. In contrast, although the LSTM structure has sequential modeling capabilities, it lacks an explicit spatial perception mechanism, and although the Transformer has global modeling capabilities, it is difficult to effectively focus on details without a local guidance structure. While LSTM-Transformer partially alleviates this issue, it still does not perform preprocessing at the input data level, resulting in residual noise continuing to interfere with predictions.

Although the comparison does not include every variant reported in recent literature, the selected baselines already capture the key modeling paradigms used in battery RUL prediction, ensuring that the demonstrated improvements of IVCLNet are both representative and meaningful.

In summary, IVCLNet combines data decomposition-based feature enhancement capabilities with attention-guided local-global modeling mechanisms in its structural design, resulting in stronger adaptability and generalization capabilities. It can significantly improve prediction accuracy and stability, especially in samples with high signal noise interference or complex degradation patterns.

4.2.3. Potential Health Indicators Under Varying Conditions

Although this study primarily focuses on constant operational conditions, the IVCLNet framework can accommodate alternative health indicators (HIs) extracted from measurable voltage, current, and temperature features under variable environments. Specifically, several potential HIs have been reported in the literature as robust across varying conditions, including the following: (1) differential voltage–capacity (dQ/dV) peak shift; (2) temperature rise rate during dynamic discharge; and (3) internal resistance growth estimated from voltage–current transients. These indicators capture electrochemical degradation behaviors that are less sensitive to specific cycling protocols, making them promising candidates for integration into IVCLNet.

To preliminarily verify the framework’s adaptability, a small-scale demonstration was conducted using partially sampled dynamic loading data from the NASA B0005 cell. The results confirm that IVCLNet can process and learn from these alternative HIs without requiring structural modifications, validating the flexibility of the proposed architecture under varying operational conditions.

4.2.4. Efficiency Comparison

In practical applications, the computational efficiency of a model is as important as its prediction accuracy. We, therefore, evaluate the efficiency of IVCLNet and the baseline models in terms of both training cost and hardware cost. The evaluation is based on four widely used metrics:

• Floating-point operations (FLOPs), which quantify the computational complexity of a single forward pass.
• Training time, which reflects the actual runtime required for model convergence.
• Number of parameters, indicating the total trainable weights and thus memory demand.
• Storage size, representing the practical deployment cost on edge devices.

These metrics jointly capture both algorithmic complexity (FLOPs and parameters) and system-level cost (training time and storage), providing a comprehensive evaluation of computational efficiency. To ensure fairness, all models were trained with the same hyperparameters—a batch size of 25, a learning rate of 0.001, and 300 epochs, using the Adam optimizer and MSE loss function, as summarized in Table 2.

Model-specific configurations, including hidden dimensions, embedding sizes, and attention heads, are listed separately in Table 3. LSTM-based models adopt the same hidden dimensions and layer numbers, while Transformer-based models use standardized embedding sizes, attention heads, and encoder/decoder depths. For IVCLNet, the CNN-LSTM backbone with CBAM attention is applied, and the input feature dimensions are aligned with those of the baseline models to ensure comparability.

Experimental results show that IVCLNet maintains competitive efficiency. Although the inclusion of CNN and attention modules slightly increases FLOPs and parameter counts compared with plain LSTM, the training time remains comparable, and the storage overhead is moderate. More importantly, the accuracy gain achieved by IVCLNet significantly outweighs this minor cost increase, highlighting a favorable trade-off between computational efficiency and predictive performance.

Under nearly identical configurations and the same dataset, as shown in

Table 5. Comparison of computational efficiency between IVCLNet and baseline models.

Models	FLOPs (Million)	Training Time (s)	Parameters	Storage Size (KB)
IVCLNet	0.52	11.2	9843	42.7
Transformer	0.31	13.9	7215	46.3
LSTM	0.27	8.9	6527	38.1
LSTM-Transformer	0.61	15.3	11,492	55.2

, the plain LSTM network exhibits the shortest training time among the baseline models due to its inherent sequential structure; however, this architecture limits its ability to capture complex degradation patterns, resulting in lower prediction accuracy. In contrast, IVCLNet achieves a favorable trade-off between accuracy and computational cost. Specifically, although the FLOPs and number of parameters of IVCLNet are 92.6% and 50.7% higher than those of LSTM, respectively, the training time only increases by 25.8%, and the storage requirement increases moderately by 12.1%. Compared with the Transformer model, IVCLNet has 67.7% higher FLOPs and 36.4% more parameters, yet the training time is reduced by 19.4% and storage by 7.7%. Additionally, when compared with the LSTM-Transformer, IVCLNet achieves 14.8%, 14.4%, 26.8%, and 22.7% reductions in FLOPs, parameters, training time, and storage size, respectively, while maintaining superior predictive performance.

4.2.5. Ablation Experiment

To quantitatively evaluate the contribution of each component in IVCLNet, a set of ablation experiments was conducted on the NASA battery dataset (Battery B0005). Three reduced variants were compared with the proposed full model, as follows: (1) w/o ICEEMDAN, where the raw capacity sequence is directly used without the ICEEMDAN decomposition; (2) w/o VMD, where only ICEEMDAN is applied as the single-stage decomposition; and (3) w/o CBAM, where the CNN–LSTM module is used without the attention mechanism.

All models were trained under identical settings to ensure fair comparison.

Table 6. Ablation analysis of IVCLNet components on the NASA dataset (Battery B0005).

Model Variant	MAE	MSE	RMSE	MAPE (%)	${\mathit{R}}^2$
w/o ICEEMDAN	0.0089	1.21 $\times {10}^{-4}$	0.0110	1.92	0.897
w/o VMD	0.0067	6.58 $\times {10}^{-5}$	0.0081	1.46	0.925
w/o CBAM	0.0054	4.10 $\times {10}^{-5}$	0.0064	1.21	0.946
IVCLNet	0.0035	2.70 $\times {10}^{-5}$	0.0052	0.65	0.974

reports the evaluation results based on five common regression metrics, including mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), mean absolute percentage error (MAPE), and coefficient of determination ($R^2$). The results demonstrate that each module contributes positively to the final performance. In particular, ICEEMDAN and VMD jointly enhance multi-scale signal decomposition, while CBAM adaptively refines spatial–temporal feature representations, further improving prediction accuracy and robustness.

The results clearly indicate that removing any of the three modules leads to a noticeable performance degradation. Compared with the baseline model without decomposition (w/o ICEEMDAN), IVCLNet achieves a 52.7% reduction in RMSE and improves $R^2$ from 0.897 to 0.974, confirming the effectiveness of the multi-stage signal decomposition strategy. Moreover, introducing the CBAM attention mechanism provides an additional 18.8% improvement in RMSE compared with the plain CNN–LSTM model (w/o CBAM), highlighting its ability to enhance attention-guided feature learning. Overall, the ablation analysis demonstrates that ICEEMDAN, VMD, and CBAM contribute synergistically to improving the accuracy, robustness, and interpretability of battery SOH prediction and RUL estimation.

5. Conclusions

This paper presents IVCLNet, a hybrid deep learning framework integrating ICEEMDAN-VMD signal decomposition with an attention-augmented CNN-LSTM architecture, tailored for the accurate prediction of the remaining useful life (RUL) of lithium-ion batteries. By leveraging hierarchical frequency decomposition and channel-wise attention mechanisms, the proposed model effectively captures both global degradation trends and local fluctuation patterns. Experimental results on two publicly available datasets demonstrate that IVCLNet achieves lower prediction errors compared to several baseline models, particularly under complex degradation dynamics. The proposed framework performs SOH trajectory prediction and estimates RUL indirectly by identifying the end-of-life point, ensuring consistency between model prediction and practical prognostic interpretation.

Despite its promising performance, the method has several limitations. First, the current approach relies on fixed decomposition parameters, which may affect its adaptability across diverse battery types or operating conditions. Second, while the model exhibits robustness on the test sets, its generalization capability under transfer learning scenarios remains unexplored. In addition, the feature fusion strategy primarily focuses on temporal alignment, without incorporating potential cross-feature dependencies.

Future work will focus on enhancing model adaptability by introducing dynamic decomposition parameter selection and improving generalization through domain-aware training strategies. In addition, more efficient feature integration modules and lightweight model variants will be explored to support real-time deployment in battery management systems. Furthermore, since the IVCLNet framework is modular and feature-agnostic, it can flexibly accommodate alternative or additional health indicators (HIs) derived from voltage, current, temperature, or partial-cycle features under varying operational conditions. This flexibility provides a theoretical and practical foundation for extending the model to real-world scenarios with fluctuating environments, such as variable temperature and dynamic load profiles. Future studies will also validate the proposed framework under these varying conditions to demonstrate its adaptability and robustness.