Using Approximation-Based Global Optimization Algorithm superEGO for Analyzing Wind Energy Potential
Abstract
1. Introduction
2. Advancements in Poland’s Wind Energy Market
2.1. Wind Energy in Poland
2.2. Wind Energy in the Pomeranian Voivodeship
3. Methodology
3.1. Fitting the Statistical Distribution for WS
3.2. Parameter Estimation for the WD Using MLE
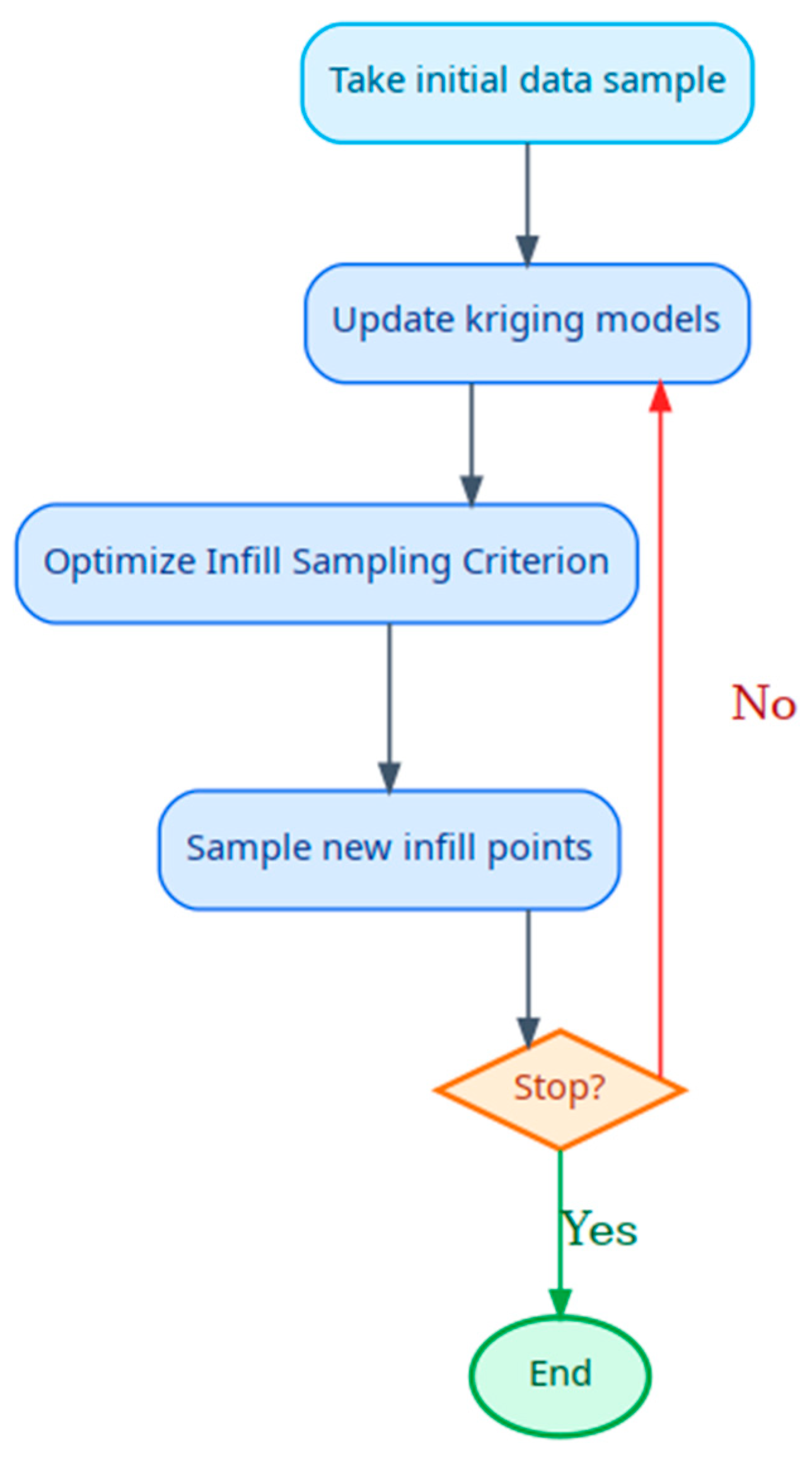
3.3. SEGO Algorithm
4. Results
5. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nihal, A.; Areche, F.O.; Araujo, V.G.S.; Ober, J. Synergistic evaluation of energy security and environmental sustainability in BRICS geo-political entities: An integrated index framework. Equilib. Q. J. Econ. Econ. Policy 2024, 19, 793–839. [Google Scholar] [CrossRef]
- Igliński, B.; Pietrzak, M.B.; Kiełkowska, U.; Skrzatek, M.; Gajdos, A.; Zyadin, A.; Natarajan, K. How to meet the Green Deal objectives—Is it possible to obtain 100% RES at the regional level in the EU? Energies 2022, 15, 2296. [Google Scholar] [CrossRef]
- Niță, D.; Stoicuța, N.; Nițescu, A.; Dobre-Baron, O.; Isac, C. Constructing a quantification tool of the progress towards the green economy: Aggregation perspective. Equilib. Q. J. Econ. Econ. Policy 2024, 19, 1139–1184. [Google Scholar] [CrossRef]
- Uddin, G.S.; Abdullah-Al-Baki, C.; Donghyun, P.; Ahmed, A.; Shu, T. Social benefits of solar energy: Evidence from Bangladesh. Oeconomia Copernic. 2023, 14, 861–897. [Google Scholar] [CrossRef]
- Igliński, B.; Flisikowski, K.; Pietrzak, M.B.; Kiełkowska, U.; Skrzatek, M.; Zyadin, A.; Natarajan, K. Renewable energy in the Pomeranian voivodeship—institutional, economic, environmental and physical aspects in light of EU energy transformation. Energies 2021, 14, 8221. [Google Scholar] [CrossRef]
- Jakubelskas, U.; Skvarciany, V. Circular economy practices as a tool for sustainable development in the context of renewable energy: What are the opportunities for the EU? Oeconomia Copernic. 2023, 14, 833–859. [Google Scholar] [CrossRef]
- Balcerzak, A.; Uddin, G.S.; Dutta, A.; Pietrzak, M.B.; Igliński, B. Energy mix management: A new look at the utilization of renewable sources from the perspective of the global energy transition. Equilib. Q. J. Econ. Econ. Policy 2024, 19, 379–390. [Google Scholar] [CrossRef]
- Janowski, M. Generacja wiatrowa w KSE—diagnoza funkcjonowania w latach 2010–2018. Elektroenerg. Współczesność Rozw. 2019, 2, 18–24. [Google Scholar]
- Olabi, A.G.; Abdelkareem, M.A. Renewable energy and climate change. Renew. Sustain. Energy Rev. 2022, 158, 112111. [Google Scholar] [CrossRef]
- Brodny, J.; Tutak, M. The level of implementing sustainable development goal “Industry, innovation and infrastructure” of Agenda 2030 in the European Union countries: Application of MCDM methods. Oeconomia Copernic. 2023, 14, 47–102. [Google Scholar] [CrossRef]
- European Commission. REPowerEU. Available online: https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal/repowereu-affordable-secure-and-sustainable-energy-europe_en (accessed on 24 February 2025).
- Założenia do Aktualizacji Polityki Energetycznej Polski do 2040 r. Available online: https://www.gov.pl/web/klimat/zalozenia-do-aktualizacji-polityki-energetycznej-polski-do-2040-r (accessed on 24 February 2025).
- Chang, L.; Saydaliev, H.B.; Meo, M.S.; Mohsin, M. How renewable energy matter for environmental sustainability: Evidence from top-10 wind energy consumer countries of European Union. Sustain. Energy Grids Netw. 2022, 31, 100716. [Google Scholar] [CrossRef]
- REN21. Renewables 2024 Global Status Report—Renewables in Energy Supply. Paris, France. 2024. Available online: https://www.ren21.net/gsr-2024/ (accessed on 1 December 2024).
- Chaurasiya, P.K.; Ahmed, S.; Warudkar, V. Study of different parameters estimation methods of Weibull distribution to determine wind power density using ground based Doppler SODAR instrument. Alex. Eng. J. 2018, 57, 2299–2311. [Google Scholar] [CrossRef]
- Guedes, K.S.; De Andrade, C.F.; Rocha, P.A.; Mangueira, R.S.; Moura, E.P. Performance analysis of metaheuristic optimization algorithms in estimating the parameters of several wind speed distributions. Appl. Energy 2020, 268, 114952. [Google Scholar] [CrossRef]
- Gungor, A.; Gokcek, M.; Uçar, H.; Arabacı, E.; Akyüz, A. Analysis of wind energy potential and Weibull parameter estimation methods: A case study from Turkey. Int. J. Environ. Sci. Technol. 2020, 17, 1011–1020. [Google Scholar] [CrossRef]
- Wind Energy in Poland Report. 2024. Available online: https://psew.pl/wp-content/uploads/2024/06/Wind-energy-in-Poland-Report-2024-2.pdf (accessed on 30 November 2024).
- Carta, J.A.; Ramirez, P.; Velazquez, S. A review of wind speed probability distributions used in wind energy analysis: Case studies in the Canary Islands. Renew. Sustain. Energy Rev. 2009, 13, 933–955. [Google Scholar] [CrossRef]
- Celik, A.N. A statistical analysis of wind power density based on the Weibull and Rayleigh models at the southern region of Turkey. Renew. Energy 2004, 29, 593–604. [Google Scholar] [CrossRef]
- Elmahdy, E.E.; Aboutahoun, A.W. A new approach for parameter estimation of finite Weibull mixture distributions for reliability modeling. Appl. Math. Model. 2013, 37, 1800–1810. [Google Scholar] [CrossRef]
- Mathew, S. Wind Energy: Fundamentals, Resource Analysis and Economics; Springer: Berlin/Heidelberg, Germany, 2006; Volume 1. [Google Scholar]
- Akdag, S.A.; Dinler, A. A new method to estimate Weibull parameters for wind energy applications. Energy Convers. Manag. 2009, 50, 1761–1766. [Google Scholar] [CrossRef]
- Stevens, M.J.M.; Smulders, P.T. The estimation of the parameters of the Weibull wind speed distribution for wind energy utilization purposes. Wind Eng. 1979, 3, 132–145. [Google Scholar]
- Justus, C.; Hargraves, W.; Mikhail, A.; Graber, D. Methods for estimating wind speed frequency distributions. J. Appl. Meteorol. 1978, 17, 350–353. [Google Scholar] [CrossRef]
- Jowder, F.A. Wind power analysis and site matching of wind turbine generators in Kingdom of Bahrain. Appl. Energy 2009, 86, 538–545. [Google Scholar] [CrossRef]
- George, F. A comparison of shape and scale estimators of the two-parameter Weibull distribution. J. Mod. Appl. Stat. Methods 2014, 13, 3. [Google Scholar] [CrossRef]
- Chang, T.P. Performance comparison of six numerical methods in estimating Weibull parameters for wind energy application. Appl. Energy 2011, 88, 272–282. [Google Scholar] [CrossRef]
- Chang, T.P. Wind energy assessment incorporating particle swarm optimization method. Energy Convers. Manag. 2011, 52, 1630–1637. [Google Scholar] [CrossRef]
- Rocha, P.A.C.; De Sousa, R.C.; De Andrade, C.F.; da Silva, M.E.V. Comparison of seven numerical methods for determining Weibull parameters for wind energy generation in the northeast region of Brazil. Appl. Energy 2012, 89, 395–400. [Google Scholar] [CrossRef]
- Arslan, T.; Bulut, Y.M.; Yavuz, A.A. Comparative study of numerical methods for determining Weibull parameters for wind energy potential. Renew. Sustain. Energy Rev. 2014, 40, 820–825. [Google Scholar] [CrossRef]
- Usta, I. An innovative estimation method regarding Weibull parameters for wind energy applications. Energy 2016, 106, 301–314. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Chi, D. Wind energy potential assessment for the site of Inner Mongolia in China. Renew. Sustain. Energy Rev. 2013, 21, 215–228. [Google Scholar] [CrossRef]
- Usta, I.; Arik, I.; Yenilmez, I.; Kantar, Y.M. A new estimation approach based on moments for estimating Weibull parameters in wind power applications. Energy Convers. Manag. 2018, 164, 570–578. [Google Scholar] [CrossRef]
- Tosunoglu, F. Accurate estimation of T year extreme wind speeds by considering different model selection criterions and different parameter estimation methods. Energy 2018, 162, 813–824. [Google Scholar] [CrossRef]
- Seo, S.; Oh, S.D.; Kwak, H.Y. Wind turbine power curve modeling using maximum likelihood estimation method. Renew. Energy 2019, 136, 1164–1169. [Google Scholar] [CrossRef]
- Alrashidi, M.; Rahman, S.; Pipattanasomporn, M. Metaheuristic optimization algorithms to estimate statistical distribution parameters for characterizing wind speeds. Renew. Energy 2020, 149, 664–681. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A. Application of differential evolution for wind speed distribution parameters estimation. Wind Eng. 2021, 45, 1544–1556. [Google Scholar] [CrossRef]
- Gökçek, M.; Bayülken, A.; Bekdemir, Ş. Investigation of wind characteristics and wind energy potential in Kirklareli, Turkey. Renew. Energy 2007, 32, 1739–1752. [Google Scholar] [CrossRef]
- Saxena, B.K.; Rao, K.V.S. Estimation of wind power density at a wind farm site located in Western Rajasthan region of India. Procedia Technol. 2016, 24, 492–498. [Google Scholar] [CrossRef]
- Aydin, O.; Igliński, B.; Krukowski, K.; Siemiński, M. Analyzing wind energy potential using efficient global optimization: A case study for the City Gdańsk in Poland. Energies 2022, 15, 3159. [Google Scholar] [CrossRef]
- Siah, E.S.; Sasena, M.; Volakis, J.L.; Papalambros, P.Y.; Wiese, R.W. Fast parameter optimization of large-scale electromagnetic objects using DIRECT with Kriging metamodeling. IEEE Trans. Microw. Theory Tech. 2004, 52, 276–285. [Google Scholar] [CrossRef]
- Sasena, M.J. Flexibility and Efficiency Enhancements for Constrained Global Design Optimization with Kriging Approximations. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2002. [Google Scholar]
- Aydin, L.; Aydin, O.; Artem, H.S.; Mert, A. Design of dimensionally stable composites using efficient global optimization method. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 156–168. [Google Scholar] [CrossRef]
- Open Weather Map. Available online: openweathermap.org (accessed on 24 October 2021).
- Roustant, O.; Ginsbourger, D.; Deville, Y. DiceKriging, DiceOptim: Two R packages for the analysis of computer experiments by kriging-based metamodeling and optimization. J. Stat. Softw. 2012, 51, 1–55. [Google Scholar] [CrossRef]
- Scrucca, L. GA: A Package for Genetic Algorithms in R. J. Stat. Softw. 2013, 53, 1–37. [Google Scholar] [CrossRef]
- Mullen, K.; Ardia, D.; Gil, D.L.; Windover, D.; Cline, J. DEoptim: An R package for global optimization by differential evolution. J. Stat. Softw. 2011, 40, 1–26. [Google Scholar] [CrossRef]
- Husmann, K.; Lange, A.; Spiegel, E. The R Package Optimization: Flexible Global Optimization with Simulated-Annealing. 2017. Available online: https://cran.r-project.org/web/packages/optimization/vignettes/vignette_master.pdf (accessed on 23 October 2025).
- Bharani, R.; Sivaprakasam, A. A meteorological data set and wind power density from selective locations of Tamil Nadu, India: Implication for installation of wind turbines. Total Environ. Res. Themes 2022, 22, 423–424. [Google Scholar] [CrossRef]
- WINDExchange: Small Wind Guidebook. Wind Exchange. Available online: https://windexchange.energy.gov/small-wind-guidebook (accessed on 12 September 2024).
- Royal Academy of Engineering. Wind Turbine Power Calculations. RWE Npower Renewables, Mechanical and Electrical Engineering Power Industry; Royal Academy of Engineering: London, UK, 2010. [Google Scholar]
- Penn State University. Wind Energy and Power Calculations. Available online: https://www.e-education.psu.edu/emsc297/node/649 (accessed on 30 June 2025).
- Balcerzak, A.P.; Uddin, G.S.; Igliński, B.; Pietrzak, M.B. Global energy transition: From the main determinants to economic challenges. Equilib. Q. J. Econ. Econ. Policy 2023, 18, 597–608. [Google Scholar] [CrossRef]
- Zheng, M.; Feng, G.-F.; Chang, C.P. Is green finance capable of promoting renewable energy technology? Empirical investigation for 64 economies worldwide. Oeconomia Copernic. 2023, 14, 483–510. [Google Scholar] [CrossRef]
- Zinecker, M.; Pěnčík, J.; Kocmanová, A.; Meluzín, T.; Balcerzak, A.P.; Pietrzak, M.B. Exploring the approaches towards support of academic entrepreneurship: Evidence from an emerging market. Technol. Econ. Dev. Econ. 2024, 30, 1890–1919. [Google Scholar] [CrossRef]
- Tasabat, S.E.; Ozkan, T.K.; Aydin, O. Addressing the Weaknesses of Multi-Criteria Decision-Making Methods Using Python; Peter Lang Publishing Group: New York, NY, USA, 2024; pp. 20–21. [Google Scholar]

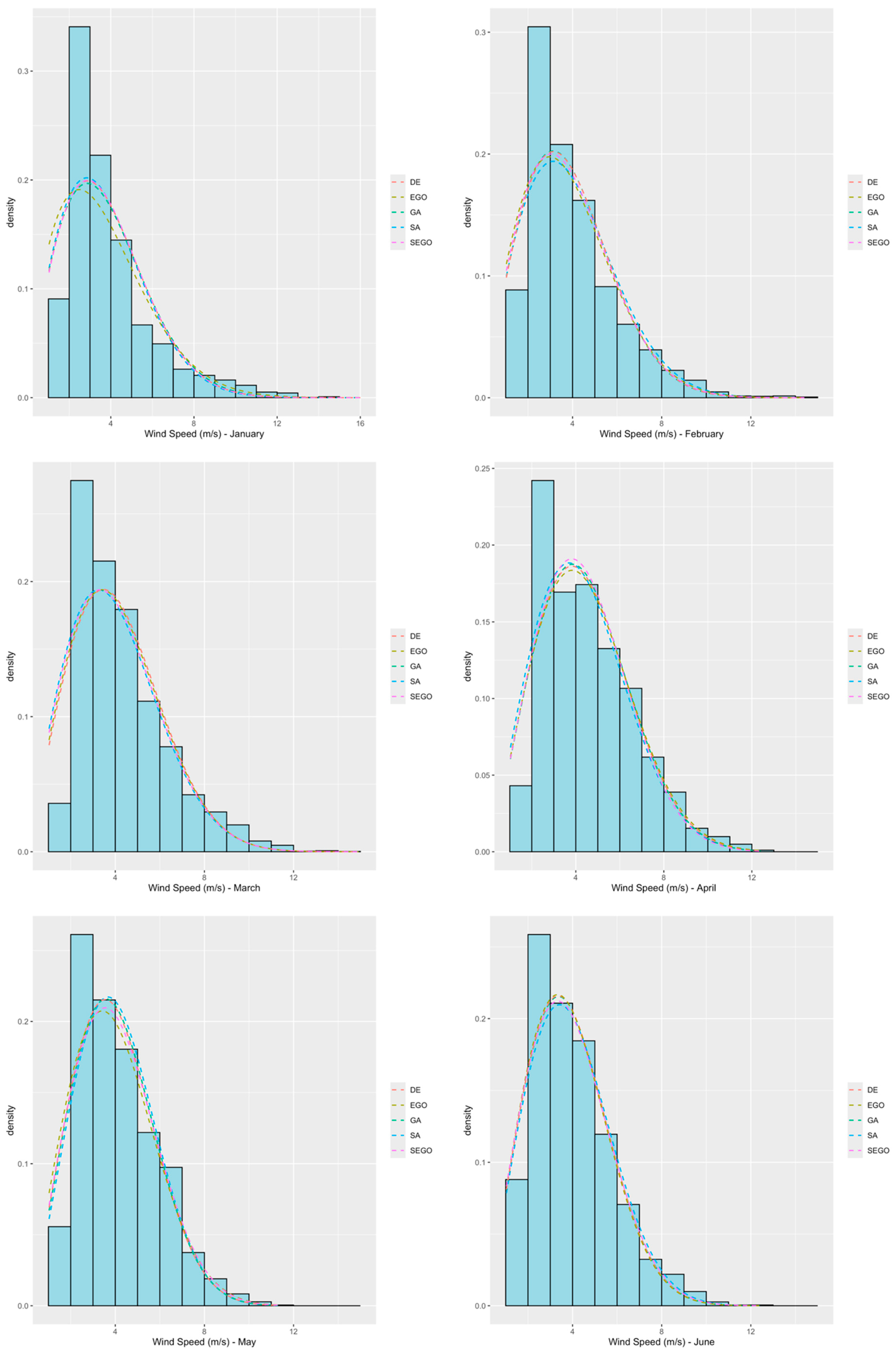
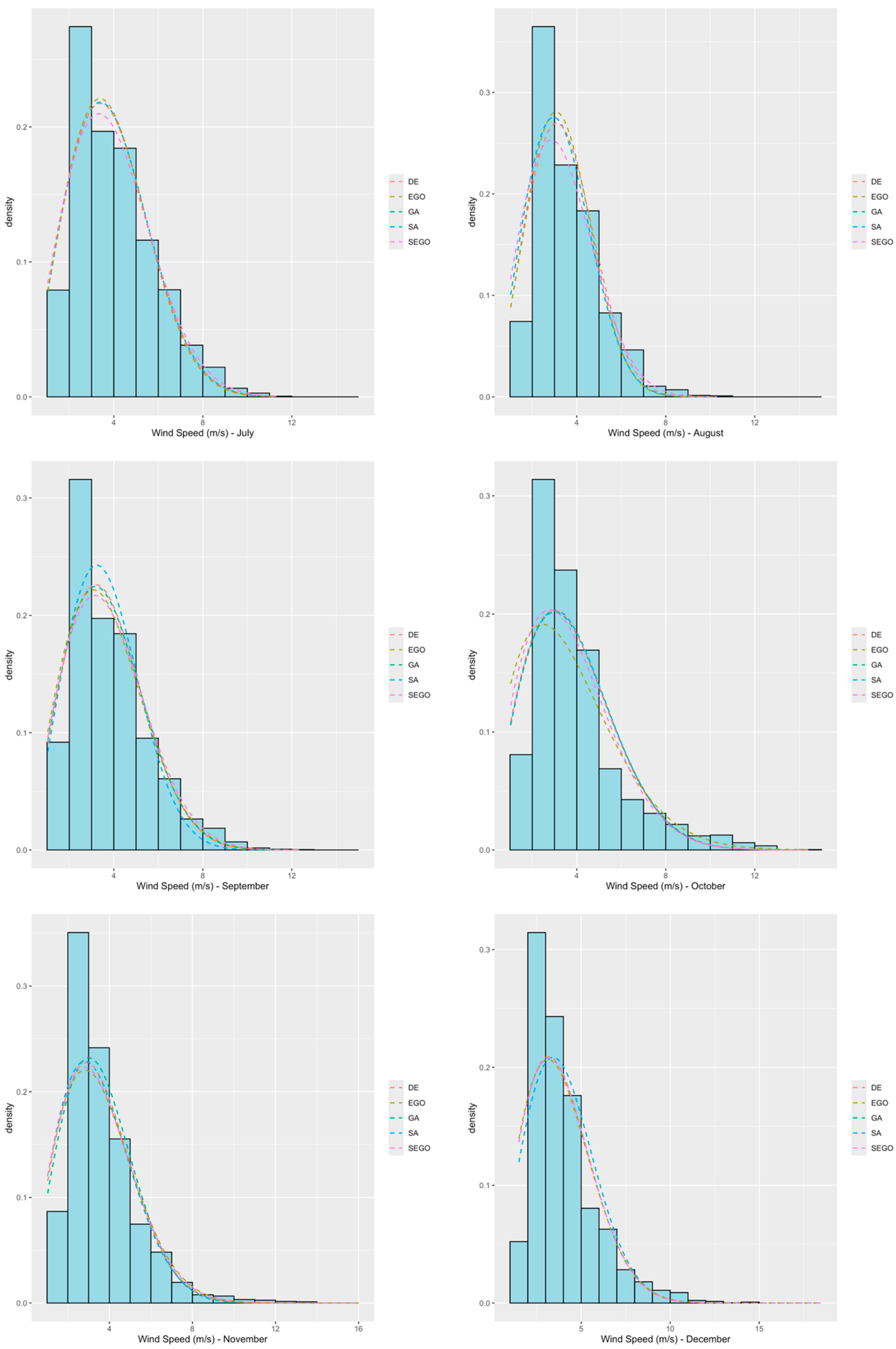
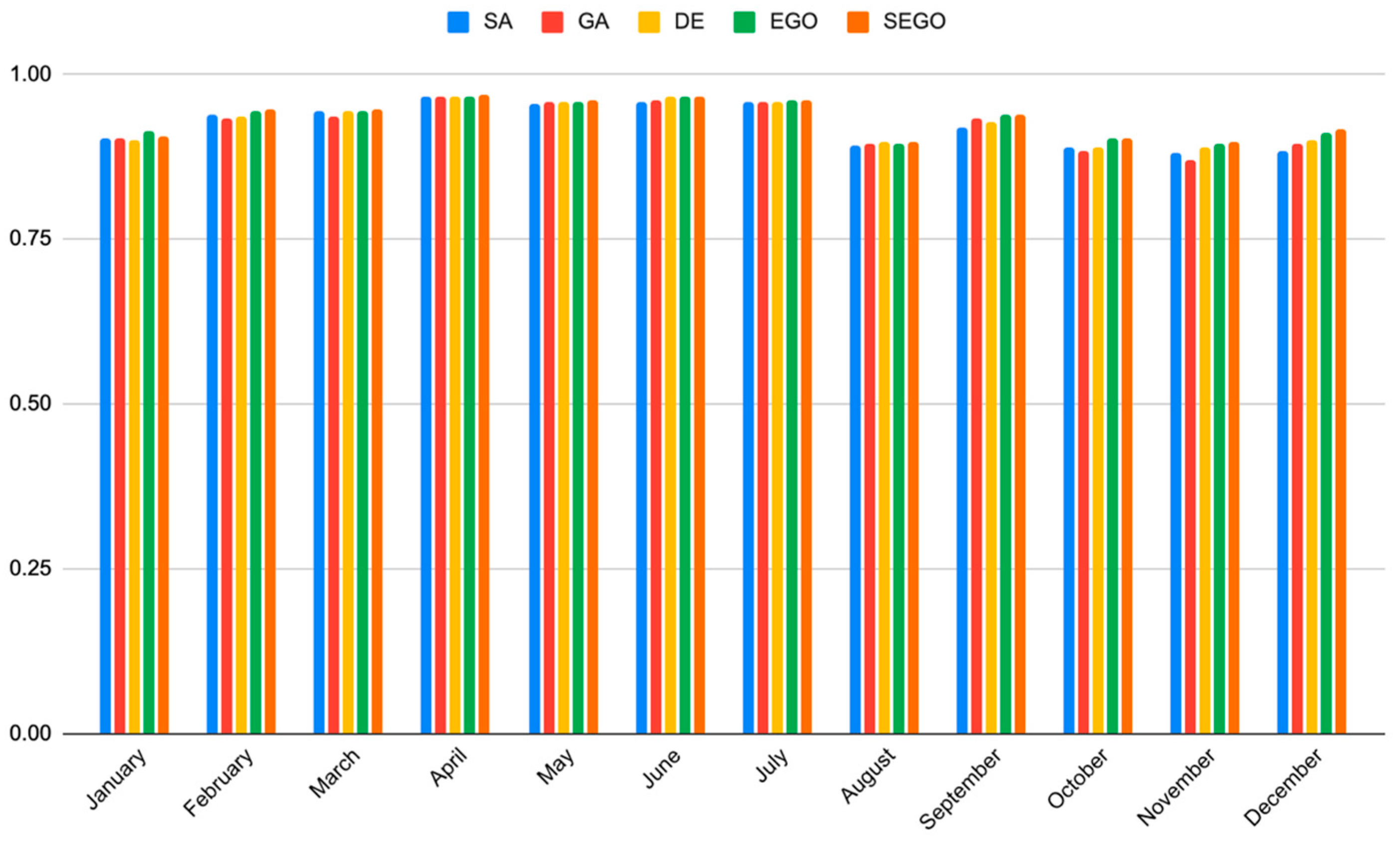

| Month | Average WS (m/s) | Min. Temperature (Average–Celsius °) | Max. Temperature (Average–Celsius °) |
|---|---|---|---|
| January | 2.72 | −1.21 | 1.94 |
| February | 2.87 | −0.58 | 2.77 |
| March | 3.15 | 2.33 | 5.39 |
| April | 3.51 | 6.15 | 9.61 |
| May | 3.17 | 10.66 | 14.39 |
| June | 3.02 | 15.65 | 19.24 |
| July | 3.12 | 16.76 | 19.96 |
| August | 2.38 | 17.17 | 20.85 |
| September | 2.68 | 13.29 | 16.52 |
| October | 2.77 | 8.29 | 11.25 |
| November | 2.83 | 4.27 | 6.86 |
| December | 3.19 | 1.86 | 4.48 |
| Month | SA | GA | DE | EGO | SEGO | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| k | c | k | c | k | C | k | c | k | c | |
| January | 1.93 | 4.15 | 1.91 | 4.23 | 1.93 | 4.21 | 1.72 | 4.11 | 1.94 | 4.21 |
| February | 2.00 | 4.42 | 2.06 | 4.32 | 2.06 | 4.33 | 1.96 | 4.28 | 2.01 | 4.30 |
| March | 2.06 | 4.51 | 2.15 | 4.64 | 2.15 | 4.64 | 2.12 | 4.60 | 2.08 | 4.54 |
| April | 2.20 | 4.86 | 2.26 | 4.98 | 2.24 | 4.98 | 2.22 | 5.02 | 2.28 | 4.92 |
| May | 2.44 | 4.56 | 2.38 | 4.50 | 2.36 | 4.48 | 2.23 | 4.46 | 2.31 | 4.53 |
| June | 2.25 | 4.44 | 2.27 | 4.35 | 2.27 | 4.34 | 2.26 | 4.31 | 2.23 | 4.36 |
| July | 2.31 | 4.35 | 2.30 | 4.35 | 2.30 | 4.35 | 2.32 | 4.31 | 2.21 | 4.38 |
| August | 2.48 | 3.64 | 2.53 | 3.78 | 2.53 | 3.78 | 2.59 | 3.70 | 2.26 | 3.69 |
| September | 2.41 | 4.04 | 2.24 | 4.13 | 2.26 | 4.13 | 2.17 | 4.09 | 2.17 | 4.18 |
| October | 2.02 | 4.25 | 2.00 | 4.25 | 2.00 | 4.22 | 1.72 | 4.11 | 1.92 | 4.10 |
| November | 2.09 | 3.86 | 2.21 | 3.96 | 2.11 | 3.91 | 2.04 | 3.94 | 2.05 | 3.91 |
| December | 2.24 | 4.45 | 2.13 | 4.28 | 2.13 | 4.28 | 2.09 | 4.27 | 2.12 | 4.29 |
| Month | SA | GA | DE | EGO | SEGO | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | |
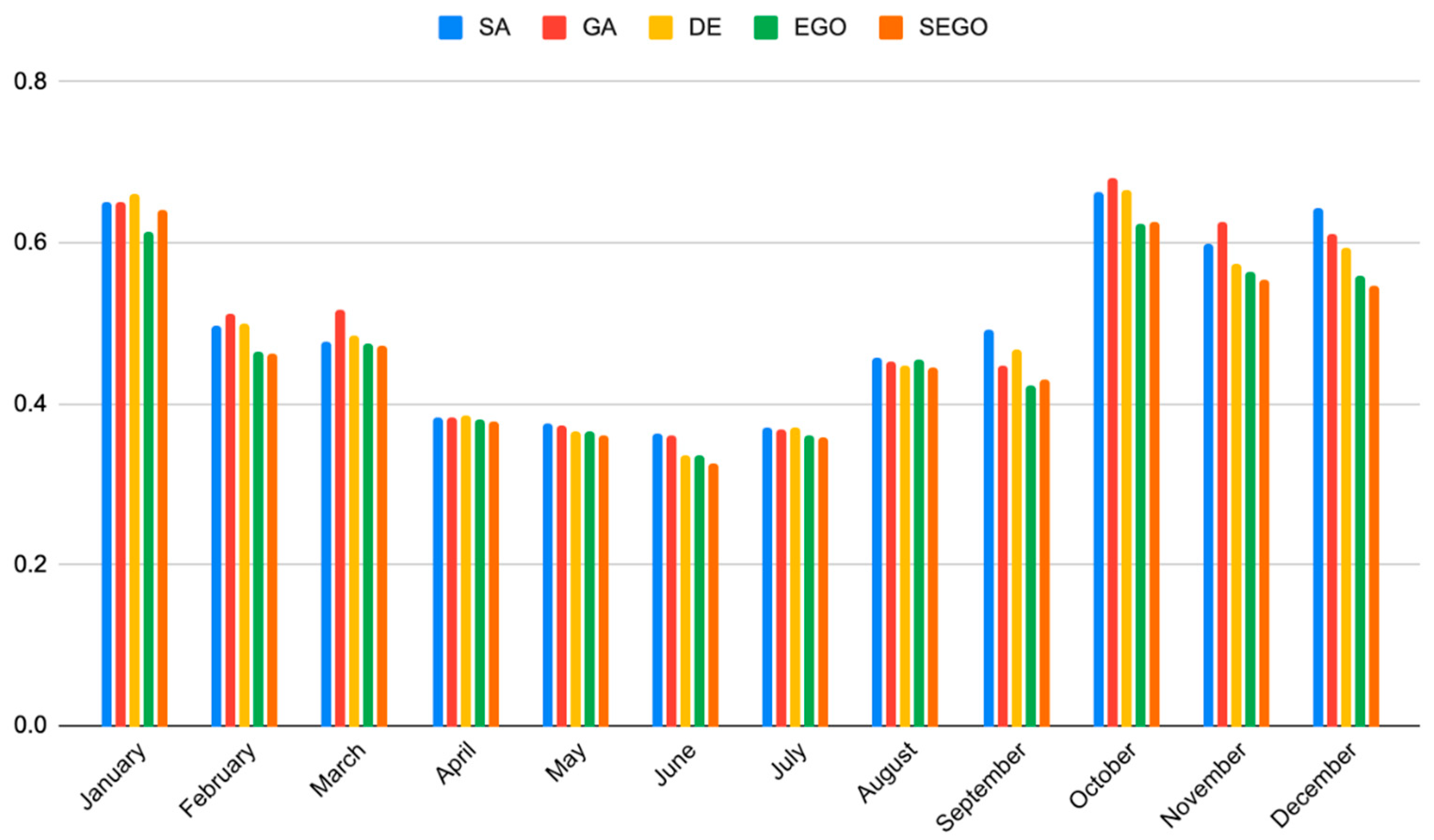
| January | 0.6512 | 0.9022 | 0.6496 | 0.9027 | 0.6616 | 0.8990 | 0.6136 | 0.9132 | 0.6413 | 0.9051 |
| February | 0.4967 | 0.9373 | 0.5130 | 0.9331 | 0.5007 | 0.9363 | 0.4650 | 0.9451 | 0.4618 | 0.9458 |
| March | 0.4762 | 0.9451 | 0.5178 | 0.9350 | 0.4835 | 0.9434 | 0.4758 | 0.9452 | 0.4720 | 0.9460 |
| April | 0.3828 | 0.9667 | 0.3830 | 0.9667 | 0.3856 | 0.9662 | 0.3802 | 0.9671 | 0.3773 | 0.9676 |
| May | 0.3760 | 0.9560 | 0.3732 | 0.9566 | 0.3658 | 0.9583 | 0.3665 | 0.9582 | 0.3615 | 0.9593 |
| June | 0.3632 | 0.9592 | 0.3605 | 0.9598 | 0.3358 | 0.9651 | 0.3363 | 0.9650 | 0.3272 | 0.9668 |
| July | 0.3713 | 0.9567 | 0.3672 | 0.9577 | 0.3703 | 0.9570 | 0.3599 | 0.9594 | 0.3579 | 0.9598 |
| August | 0.4569 | 0.8925 | 0.4526 | 0.8945 | 0.4487 | 0.8963 | 0.4539 | 0.8939 | 0.4454 | 0.8979 |
| September | 0.4913 | 0.9182 | 0.4471 | 0.9323 | 0.4664 | 0.9263 | 0.4234 | 0.9392 | 0.4298 | 0.9392 |
| October | 0.6639 | 0.8896 | 0.6802 | 0.8841 | 0.6649 | 0.8893 | 0.6229 | 0.9028 | 0.6250 | 0.9022 |
| November | 0.5996 | 0.8805 | 0.6262 | 0.8697 | 0.5745 | 0.8903 | 0.5636 | 0.8945 | 0.5542 | 0.8979 |
| December | 0.6441 | 0.8830 | 0.6111 | 0.8946 | 0.5934 | 0.9007 | 0.5602 | 0.9115 | 0.5473 | 0.9155 |
| Parameters | Metrics | |||
|---|---|---|---|---|
| Technique | k | c | RMSE | R2 |
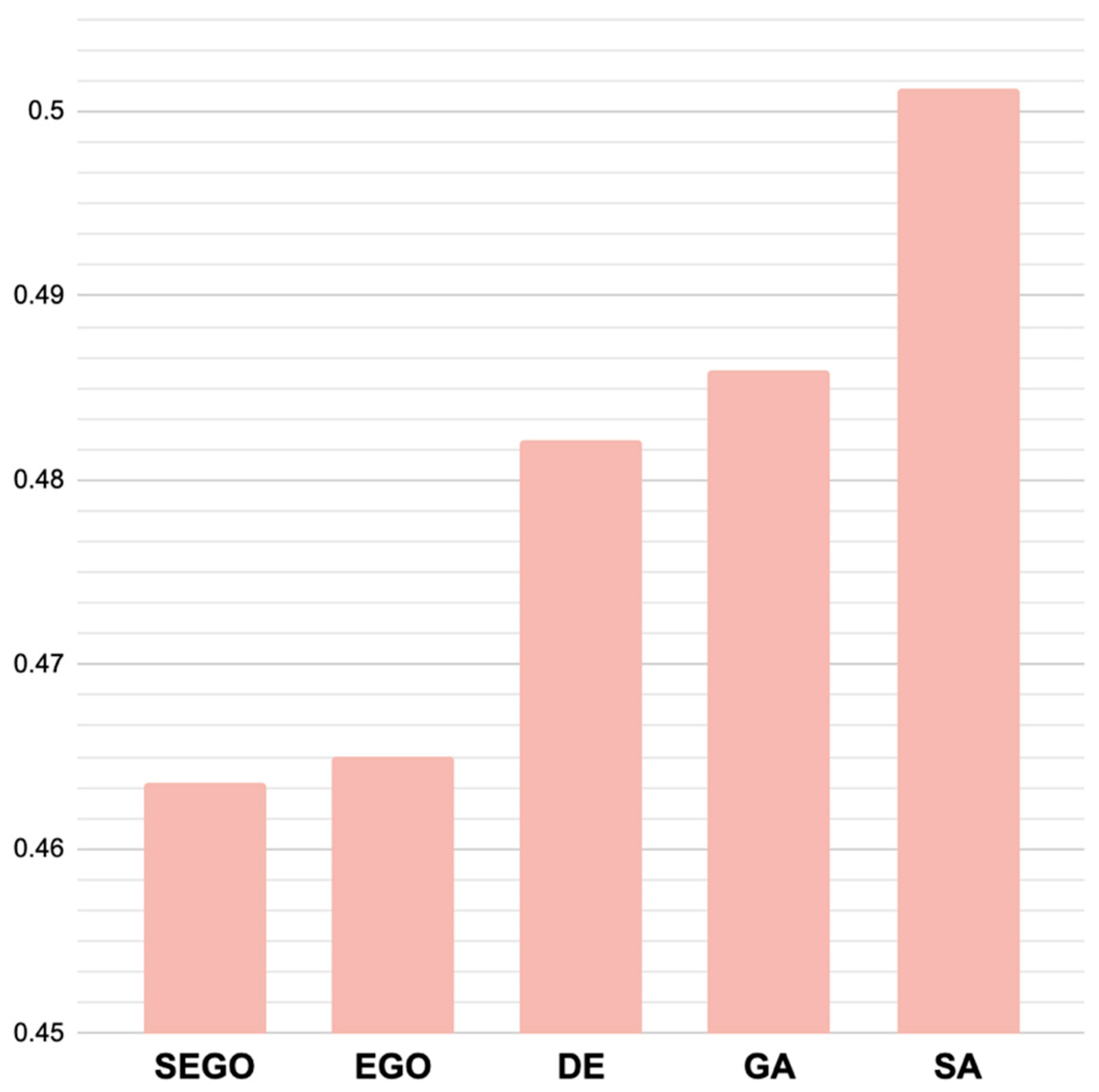
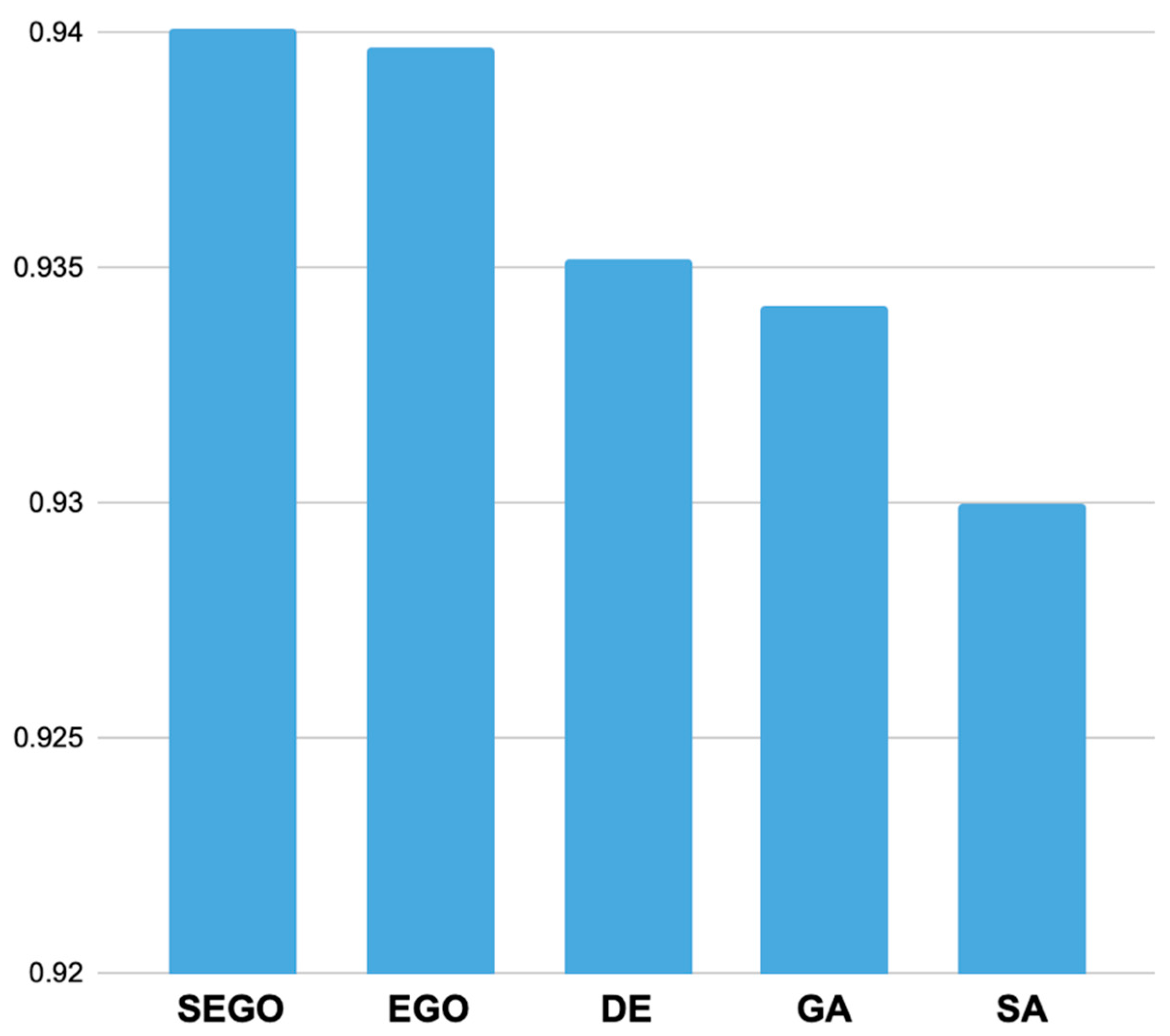
| SA | 2.16 | 4.40 | 0.501242 | 0.9300 |
| GA | 2.14 | 4.33 | 0.486022 | 0.9342 |
| DE | 2.15 | 4.33 | 0.482129 | 0.9352 |
| EGO | 2.05 | 4.25 | 0.465032 | 0.9397 |
| SEGO | 2.08 | 4.31 | 0.463599 | 0.9401 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Igliński, B.; Aydin, O.; Krajewski, J. Using Approximation-Based Global Optimization Algorithm superEGO for Analyzing Wind Energy Potential. Energies 2025, 18, 5631. https://doi.org/10.3390/en18215631
Igliński B, Aydin O, Krajewski J. Using Approximation-Based Global Optimization Algorithm superEGO for Analyzing Wind Energy Potential. Energies. 2025; 18(21):5631. https://doi.org/10.3390/en18215631
Chicago/Turabian StyleIgliński, Bartłomiej, Olgun Aydin, and Jarosław Krajewski. 2025. "Using Approximation-Based Global Optimization Algorithm superEGO for Analyzing Wind Energy Potential" Energies 18, no. 21: 5631. https://doi.org/10.3390/en18215631
APA StyleIgliński, B., Aydin, O., & Krajewski, J. (2025). Using Approximation-Based Global Optimization Algorithm superEGO for Analyzing Wind Energy Potential. Energies, 18(21), 5631. https://doi.org/10.3390/en18215631









