Integrating High-DER-Penetrated Distribution Systems into Energy Market with Feasible Region and Accompanying Strategic Bidding
Abstract
1. Introduction
- Using feasible regions that are cast by a two-stage adaptive robust optimization framework to capture detailed operational constraints of high-DER-penetrated distribution systems, distribution systems are securely integrated into the day-ahead market.
- Building on the feasible region, a joint energy-reserve bidding strategy based on the nested segmented feasible region is proposed, enhancing the distribution side’s responsiveness to market price signals and improving scheduling flexibility.
2. The Modeling of the Transmission and Distribution Side
2.1. The Day-Ahead Energy Market Model
- Unit-level constraints
- Unit power output and reserve constraints:Constraint (2) ensures that the sum of the generation output and reserve capacity of a unit remains within its allowable power output range, while constraint (3) enforces the scheduled reserve to be non-negative.
- Startup and shutdown logic constraint:Constraints (4)–(5) adopt the classic “three-binary” formulation to represent the startup and shutdown logic of thermal units.
- Minimum ON/OFF time constraints:The minimum ON and OFF time limits of units are imposed by constraints (6)–(7), which ensure that once a unit is started up or shut down, it must remain in operation or stay OFF for, respectively, no less than the minimum ON time or minimum OFF time .
- Ramping rate constraints of units:Constraints (8)–(9) represent the ramp-up and ramp-down limits of units during operation while also taking into account the ramping rates during startup and shutdown processes.
- 2.
- System-level constraints
- System power balance constraint:Constraint (10) ensures the system power balance at each time interval. The power generation from units and DER-penetrated distribution systems together support the fixed loads.
- Line flow constraints:Constraint (11) uses shift factors to calculate the power flow on transmission lines. includes the flow contribution from units, distribution systems, and fixed loads. Constraint (12) then imposes upper and lower bounds on the power flow through the line to secure operation.
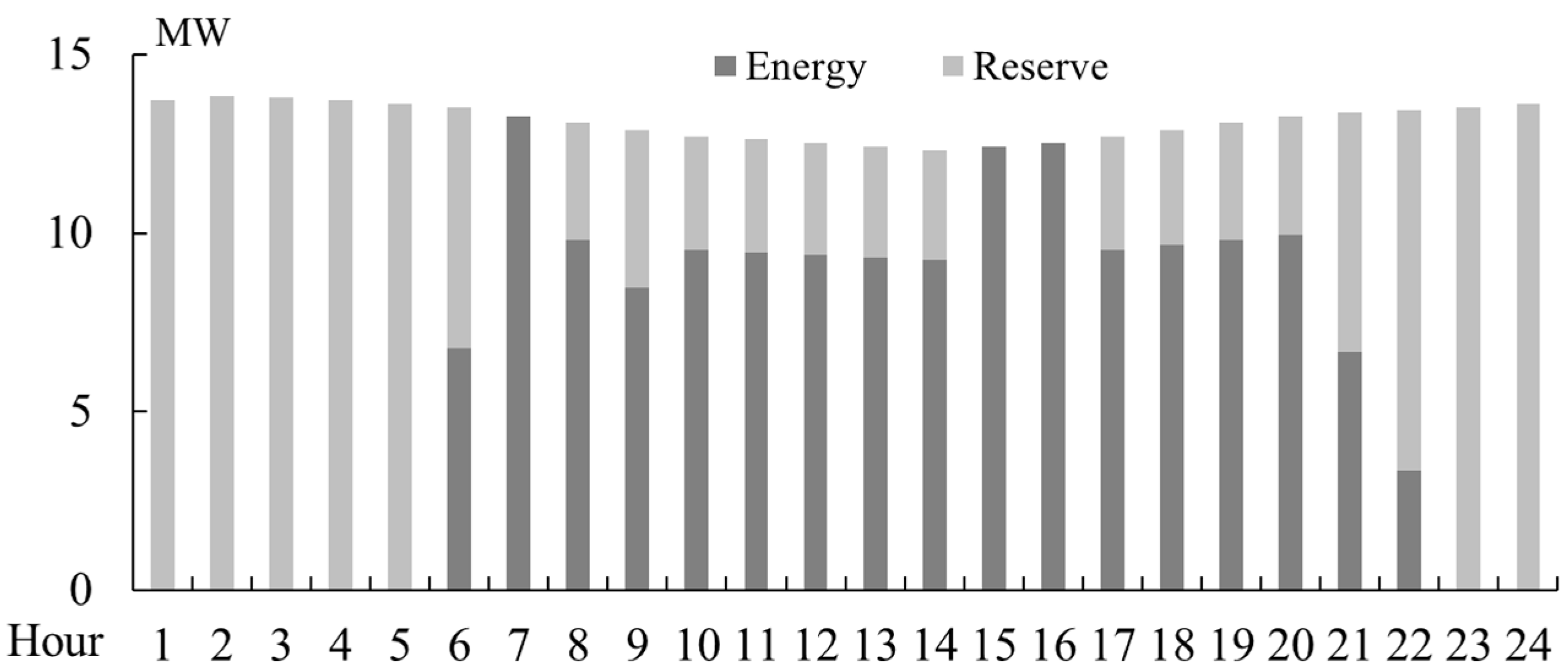
- Reserve capacity requirement constraints:Constraint (13) enforces the requirement that the total system reserve capacity provided by units and distribution systems should meet the system’s security reserve demand at each time interval. This constraint ensures that sufficient backup capacity is available to handle uncertainties such as load fluctuations or renewable generation variability.
2.2. The Operational Constraints of the Distribution System
- Active and reactive power flow on distribution lines:
- Nodal power balance constraints:
- Active and reactive power flow balance of the interconnection bus:
- Distribution line active power limit:
- Nodal voltage constraints:
- Output constraints of DERs:
- System reserve constraints:
3. The Feasible Region and the Bidding Model of the Distribution System
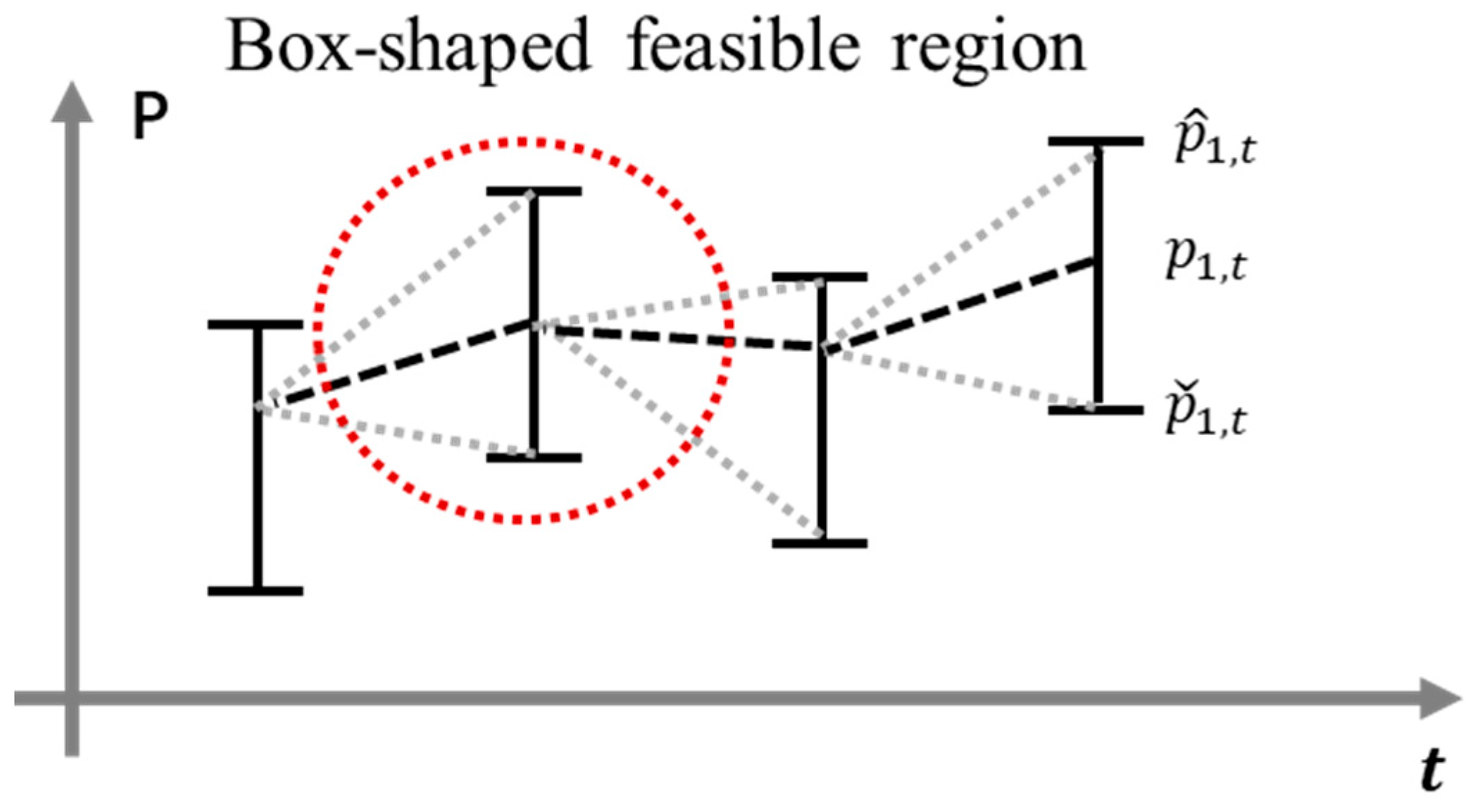
3.1. The Feasible Region of the Distribution System
3.2. The Redispatch Problem of the Distribution System
3.3. The Bidding Model of the Distribution System
4. Case Study
4.1. Test System Setup and Case Design
4.2. The Feasible Region
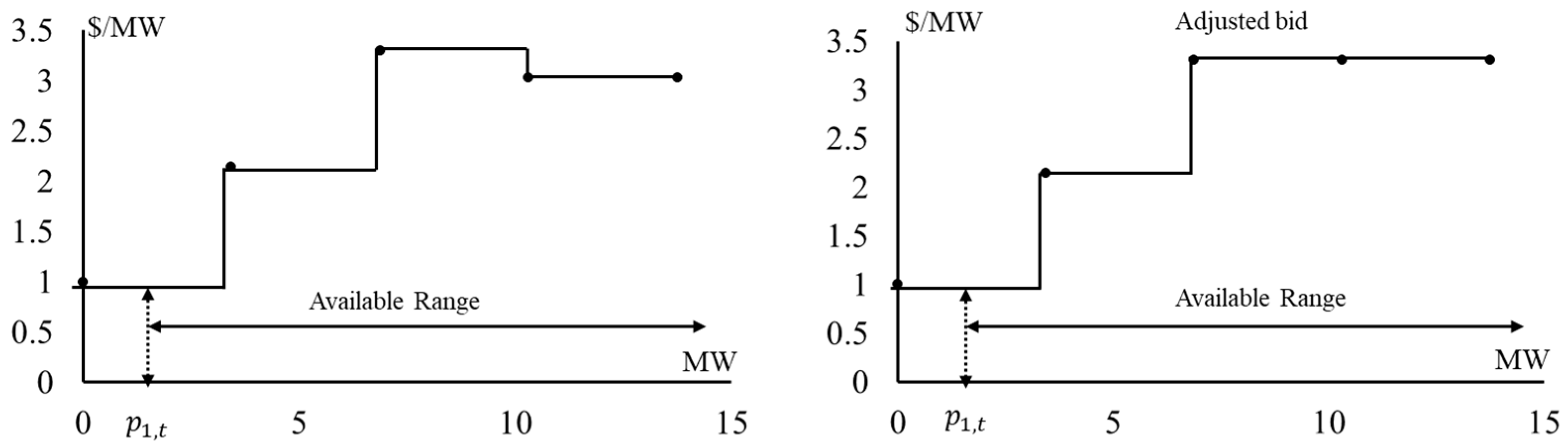
4.3. The Strategic Bidding of the Distribution System
4.4. Participating in the Day-Ahead Market
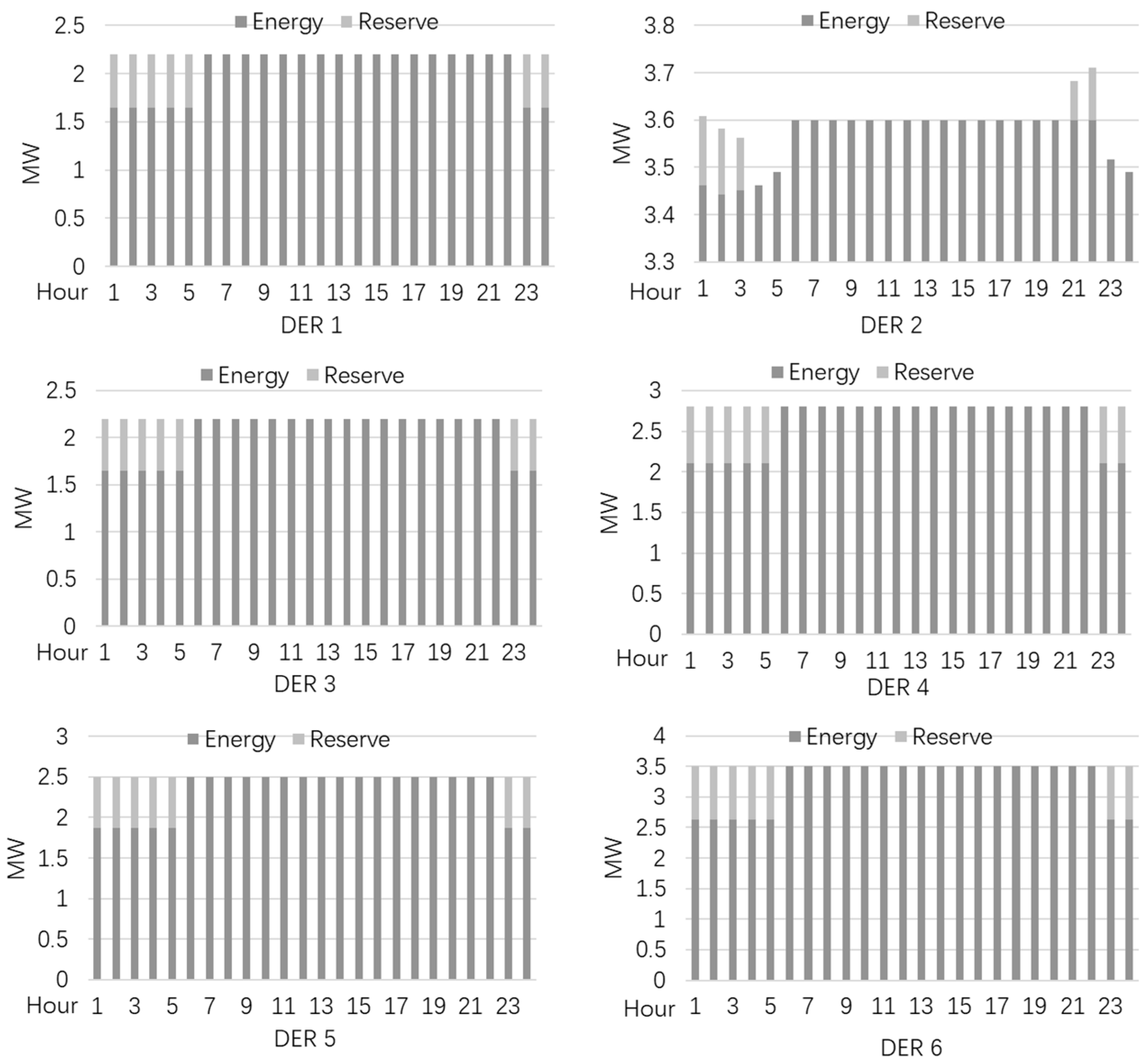
4.5. Redispatching After Market Clearing of the Day-Ahead Market
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices and sets: | |
| Index of thermal units. | |
| Index of distributed energy resources. | |
| Index of loads. | |
| , , | Indices of buses; substation bus is indexed by . |
| , | Index of hours. |
| Set of thermal units. | |
| Set of distributed systems. | |
| Set of DERs in a distributed system. | |
| Set of loads in distribution system. | |
| Set of lines in distribution system. | |
| Set of buses in distribution system. | |
| Set of loads in transmission system. | |
| Set of lines in transmission system. | |
| Set of buses in transmission system. | |
| Set of thermal units on bus . | |
| Set of distribution systems on bus . | |
| Set of loads on bus in distribution system. | |
| Set of lines in distribution system connected to bus . | |
| Set of loads on bus in transmission system. | |
| Set of hours, , where . | |
| Variables for the transmission system: | |
| Active power dispatch of unit at hour . | |
| Reserve capacity of unit at hour . | |
| Active power injection to the distribution system from substation bus at hour . | |
| Active power flow of line at hour . | |
| ON/OFF indicator of unit at hour . | |
| Binary indicator of startup action of unit at hour . | |
| Binary indicator of shutdown action of unit at hour . | |
| Parameters for the transmission system: | |
| Bidding price of unit . | |
| Bidding price of reserve capacity of unit . | |
| No-load cost of unit . | |
| Active power demand of fixed load at hour . | |
| Power flow limit of line . | |
| Active power lower/upper bound of unit . | |
| Ramp-up/down ability of unit during operation procedure. | |
| Ramp-up/down ability of unit during startup/shutdown procedure. | |
| Startup cost of unit | |
| Shift factor of bus to line . | |
| Minimum ON time of unit . | |
| Minimum OFF time of unit . | |
| Total reserve capacity requirement. | |
| Variables for the distribution system: | |
| Active power of DER at hour . | |
| Active power injection to the transmission system at hour . | |
| Active power flow of line at hour . | |
| Reactive power output of DER at hour . | |
| Reactive power injection to the transmission side at hour . | |
| Reactive power flow along line at hour . | |
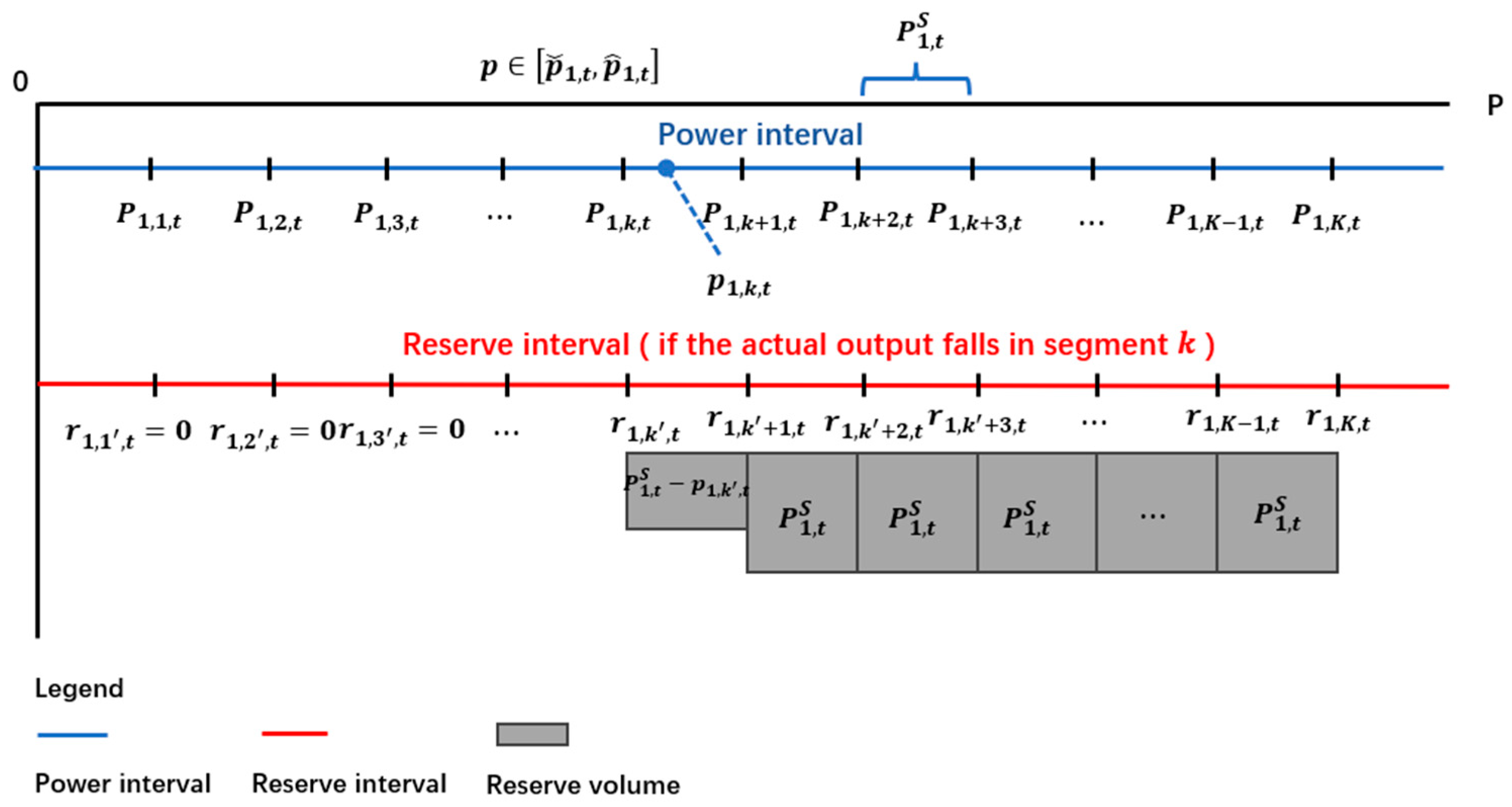
| Reserve capacity of DER at hour . | |
| Reserve capacity injection to the transmission side at hour . | |
| Voltage magnitude of bus at hour . | |
| Voltage phase angle of bus at hour . | |
| Lower boundary of substation bus active power injection at hour . | |
| Upper boundary of substation bus active power injection at hour . | |
| ON/OFF indicator of DER . | |
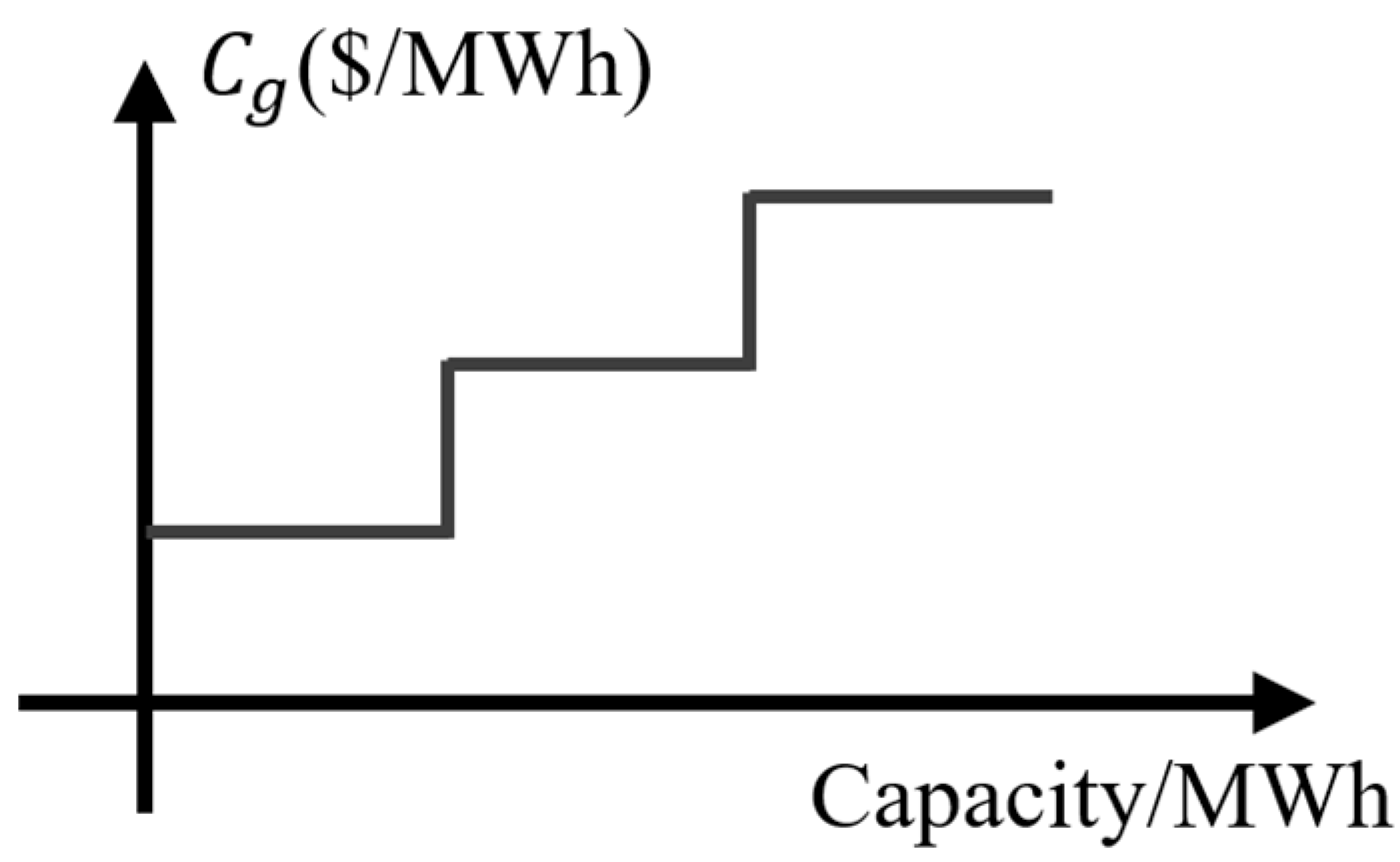
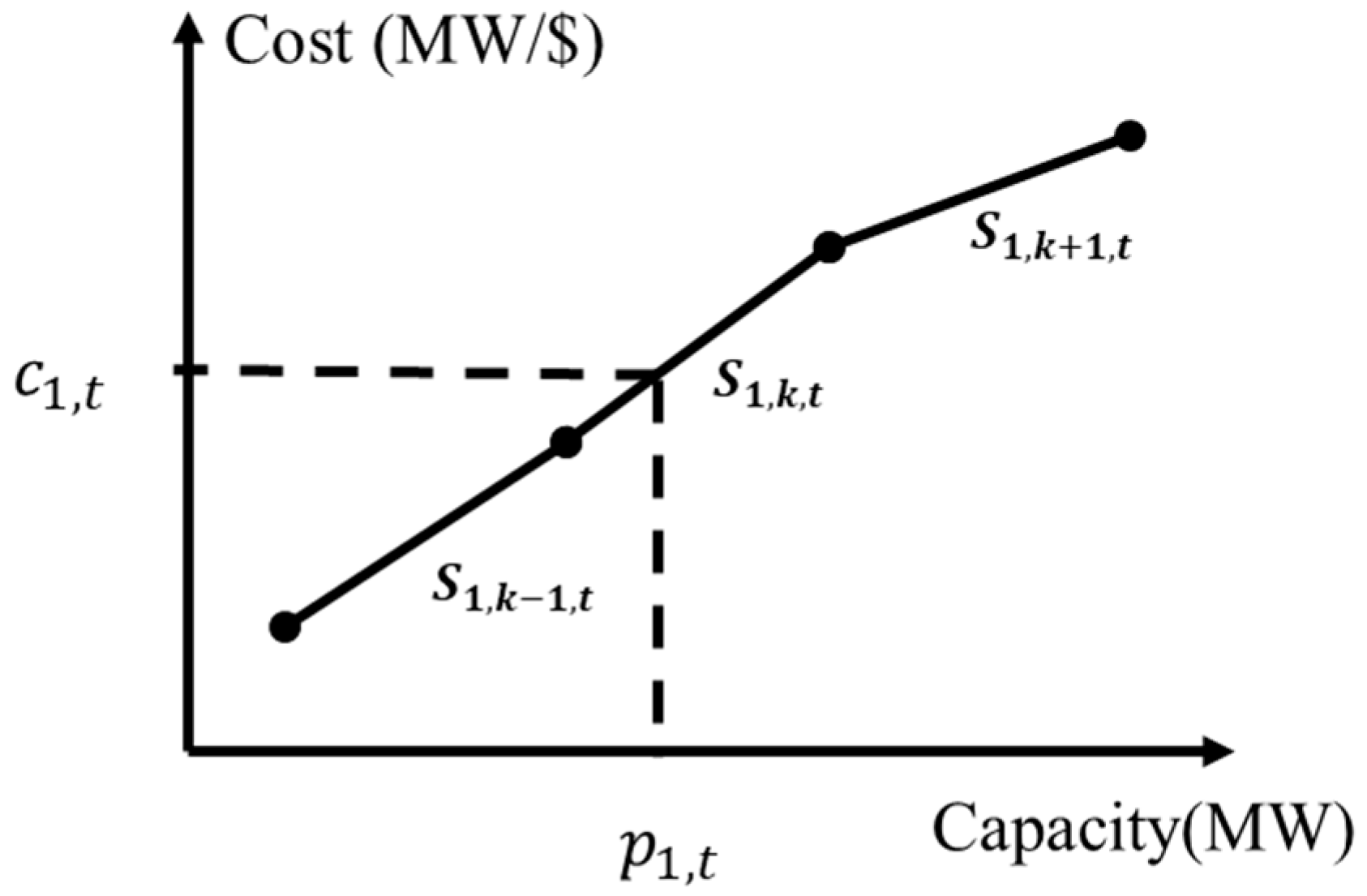
| Active power cost at hour for bus 1. | |
| Binary indicator for segment at hour . | |
| Power adjustment in segment at hour . | |
| Reserve capacity cost at hour for bus 1. | |
| Reserve capacity adjustment in segment at hour . | |
| Equivalent reserve price slope for segment at time . | |
| Uncertainty coefficient in two-stage robust optimization () | |
| Parameters for the distribution system: | |
| Bidding price of DER . | |
| Bidding price of reserve capacity of DER . | |
| The cost of DER energy output. | |
| The cost of DER reserve capacity. | |
| Susceptance of line . | |
| Conductance of line . | |
| Power flow limit of line . | |
| Active power demand of load at hour . | |
| Bound of active power injection to the transmission side. | |
| , | Active power lower and upper bound of DER . |
| Reactive power demand of load at hour . | |
| Bound of reactive power injection to the transmission side. | |
| , | Reactive power lower and upper bound of DER . |
| , | Voltage magnitude lower and upper bound of bus . |
| Number of power output segments. | |
| Maximum adjustable power/reserve range for bus 1 within a segment at hour . | |
| Lower bound of power output in segment at hour . | |
| Initial reserve capacity in segment at time . | |
| Reserve capacity in segment corresponding to energy segment at time . | |
| Marginal cost of power output in segment . | |
| Marginal cost of reserve capacity in segment . | |
| Active flag of segment . | |
| The slope of segment . | |
| The endpoint of segment . | |
| Given substation bus voltage. | |
References
- Castro, F.; Canizes, B.; Soares, J.; Almeida, J.; Vale, Z. Comprehensive framework for distribution network multi-investment expansion planning: Emissions, uncertainty, and resource remuneration integration. Energy Convers. Manag. 2024, 316, 118734. [Google Scholar] [CrossRef]
- Silva, J.; Sumaili, J.; Bessa, J.; Seca, L.; Matos, M.A.; Miranda, V.; Caujolle, M.; Goncer, B.; Sebastian-Viana, M. Estimating the Active and Reactive Power Flexibility Area at the TSO-DSO Interface. IEEE Trans. Power Syst. 2018, 33, 4741–4750. [Google Scholar] [CrossRef]
- Müller, F.; Szabó, J.; Sundström, O.; Lygeros, J. Leveraging Aggregation and Disaggregation of Energetic Flexibility from Distributed Energy Resources. IEEE Trans. Smart Grid 2019, 10, 1205–1214. [Google Scholar] [CrossRef]
- Wang, Y.; Zhong, H.; Ruan, G. A Projection-Based Approach for Distributed Energy Resources Aggregation. In Proceedings of the 2023 IEEE PES Innovative Smart Grid Technologies Europe (ISGT EUROPE), Grenoble, France, 23–26 October 2023; pp. 1–5. [Google Scholar]
- Liu, B.; Ma, J. Feasible Region for DERs in Unbalanced Distribution Networks with Uncertain Line Impedances. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023; pp. 1–5. [Google Scholar]
- Chen, Y.; Zhao, C. Improved Approximation of Dispatchable Region in Radial Distribution Networks via Dual SOCP. IEEE Trans. Power Syst. 2023, 38, 5585–5597. [Google Scholar] [CrossRef]
- Li, Z.; Huang, W.; Zheng, J.; Wu, Q. Dispatchable Region for Active Distribution Networks Using Approximate Second-Order Cone Relaxation. CSEE J. Power Energy Syst. 2023, 9, 1999–2007. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, L.; Chen, Y.; Li, J.; Yang, Y. On Accurate and Compact Model of High DER-Penetrated Sub-Transmission/Primary Distribution Systems in ISO Energy Market. IEEE Trans. Sustain. Energy 2021, 12, 810–820. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, L.; Chen, Y.; Li, J. Integrating High DER-Penetrated Distribution Systems into ISO Energy Market Clearing: A Feasible Region Projection Approach. IEEE Trans. Power Syst. 2021, 36, 2262–2272. [Google Scholar] [CrossRef]
- Wen, Y.; Hu, Z.; You, S.; Duan, X. Aggregate Feasible Region of DERs: Exact Formulation and Approximate Models. IEEE Trans. Smart Grid 2022, 13, 4405–4423. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, J.; Wang, H.; Ruiyang, J.; Li, G.; Zhou, M. On the Coordination of Transmission-Distribution Grids: A Dynamic Feasible Region Method. IEEE Trans. Power Syst. 2023, 38, 1857–1868. [Google Scholar] [CrossRef]
- Chen, X.; Dall’Anese, E.; Zhao, C.; Li, N. Aggregate Power Flexibility in Unbalanced Distribution Systems. IEEE Trans. Power Syst. 2020, 11, 258–269. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, J.; Li, G.; Wang, X.; Zhou, M. Characterizing Temporal-Coupled Feasible Region of Active Distribution Networks. IEEE Trans. Ind. Applicat. 2022, 58, 5687–5696. [Google Scholar] [CrossRef]
- Wang, C.; Xing, J.; Wang, Y.; Xu, J.; Fu, Z.; Xu, B.; Liu, H. Bidding Strategy for the Alliance of Prosumer Aggregators in the Distribution Market. Energies 2024, 17, 5006. [Google Scholar] [CrossRef]
- Chen, C.; Bose, S.; Tong, L. DSO-DERA Coordination for the Wholesale Market Participation of Distributed Energy Resources. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023. [Google Scholar]
- Mallaki, M.S.; Naderi, M.; Abedi, M.D.; Manshadi, S.B.; Gharehpetian, G. Strategic Bidding in Distribution Network Electricity Market Focusing on Competition Modeling and Uncertainties. J. Mod. Power Syst. Clean. Energy 2021, 9, 561–572. [Google Scholar] [CrossRef]
- Iria, J.; Scott, P.; Attarha, A.; Soares, F. Comparison of Network-(in)Secure Bidding Strategies to Coordinate Distributed Energy Resources in Distribution Networks. Sustain. Energy Grids Netw. 2023, 36, 101209. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, B.; Lin, Y.; Chen, Y.; Wu, L. Optimal SOC Headroom of Pump Storage Hydropower for Maximizing Joint Revenue from Day-Ahead and Real-Time Markets under Regional Transmission Organization Dispatch. J. Mod. Power Syst. Clean. Energy 2024, 12, 238–250. [Google Scholar] [CrossRef]
- Kim, H.; Kim, M. Data-Driven Virtual Power Plant Bidding Strategy in Electricity Markets Integrating Hybrid Forecasting Model and Customized Incentive Demand Response. IEEE Internet Things J. 2025, 12, 13851–13869. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, H.; Wei, R.; Li, Z. A Distributed Market-Aided Restoration Approach of Multi-Energy Distribution Systems Considering Comprehensive Uncertainties from Typhoon Disaster. IEEE Trans. Smart Grid 2025, 16, 3743–3757. [Google Scholar] [CrossRef]
- Yang, Z.; Zhong, H.; Xia, Q.; Kang, C. Solving OPF using linear approximations: Fundamental analysis and numerical demonstration. IET Gener. Transm. Distrib. 2017, 11, 4115–4125. [Google Scholar] [CrossRef]
- Chen, X.; Li, N. Leveraging Two-Stage Adaptive Robust Optimization for Power Flexibility Aggregation. IEEE Trans. Smart Grid 2021, 12, 3954–3965. [Google Scholar] [CrossRef]
- Zeng, B.; Zhao, L. Solving Two-Stage Robust Optimization Problems Using a Column-And-Constraint Generation Method. Oper. Res. Lett. 2013, 41, 457–461. [Google Scholar] [CrossRef]
- Test System Data. Available online: https://github.com/eethzhao/IEEE-118-bus-system-data-test-system- (accessed on 30 September 2025).



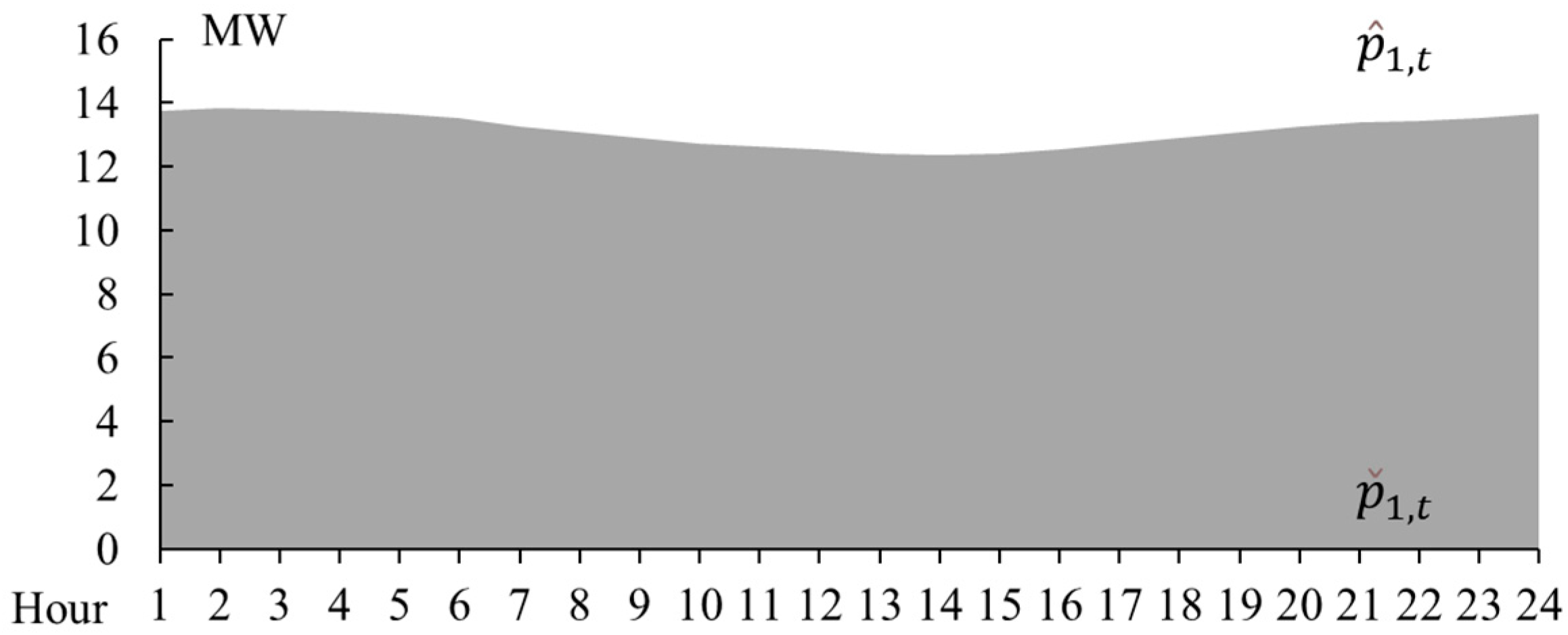
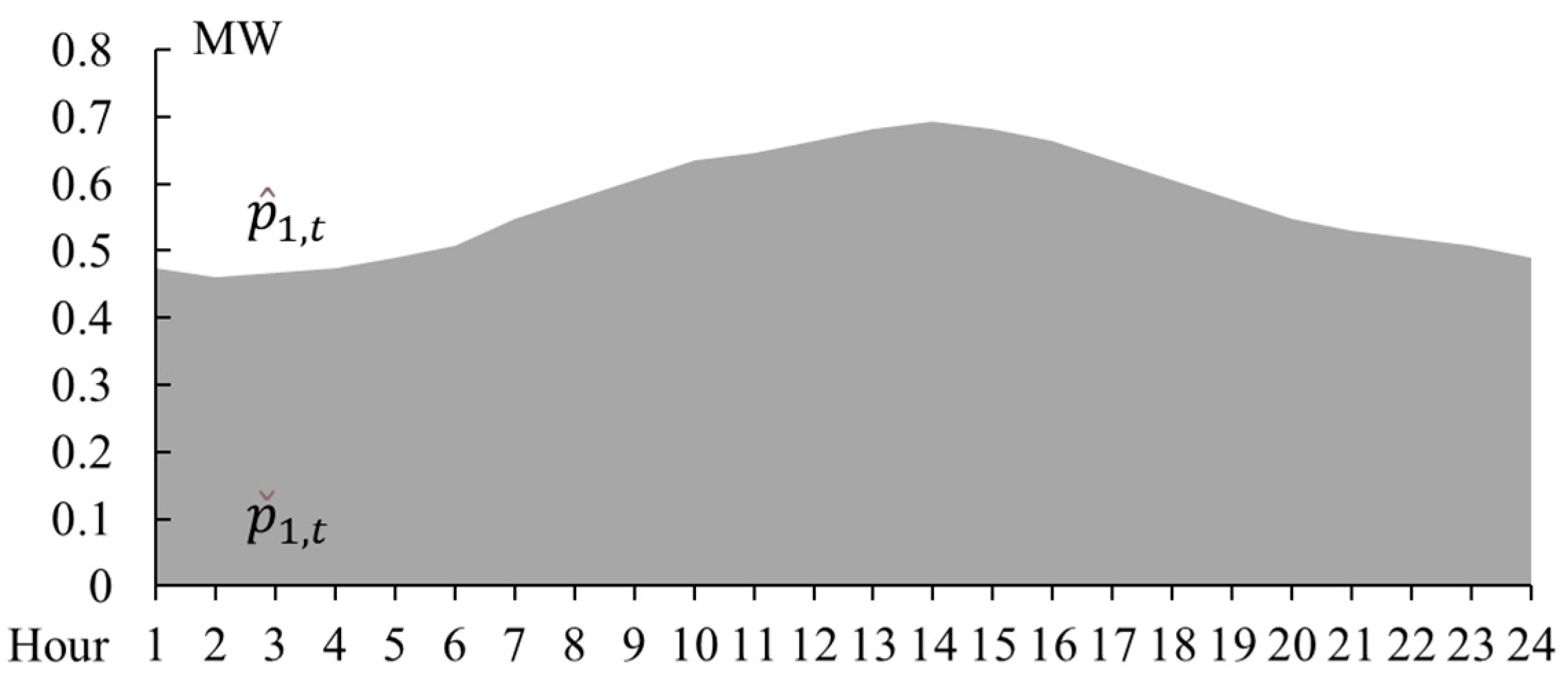
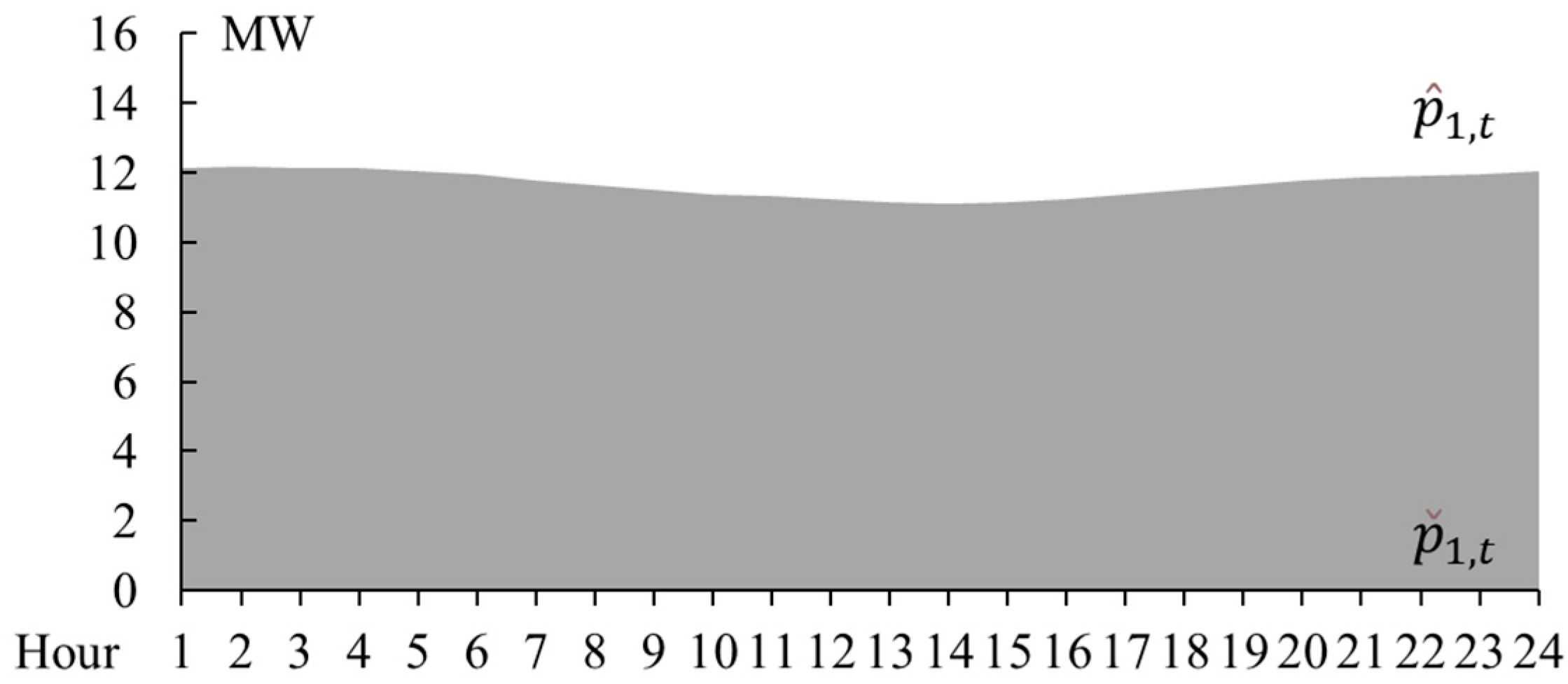
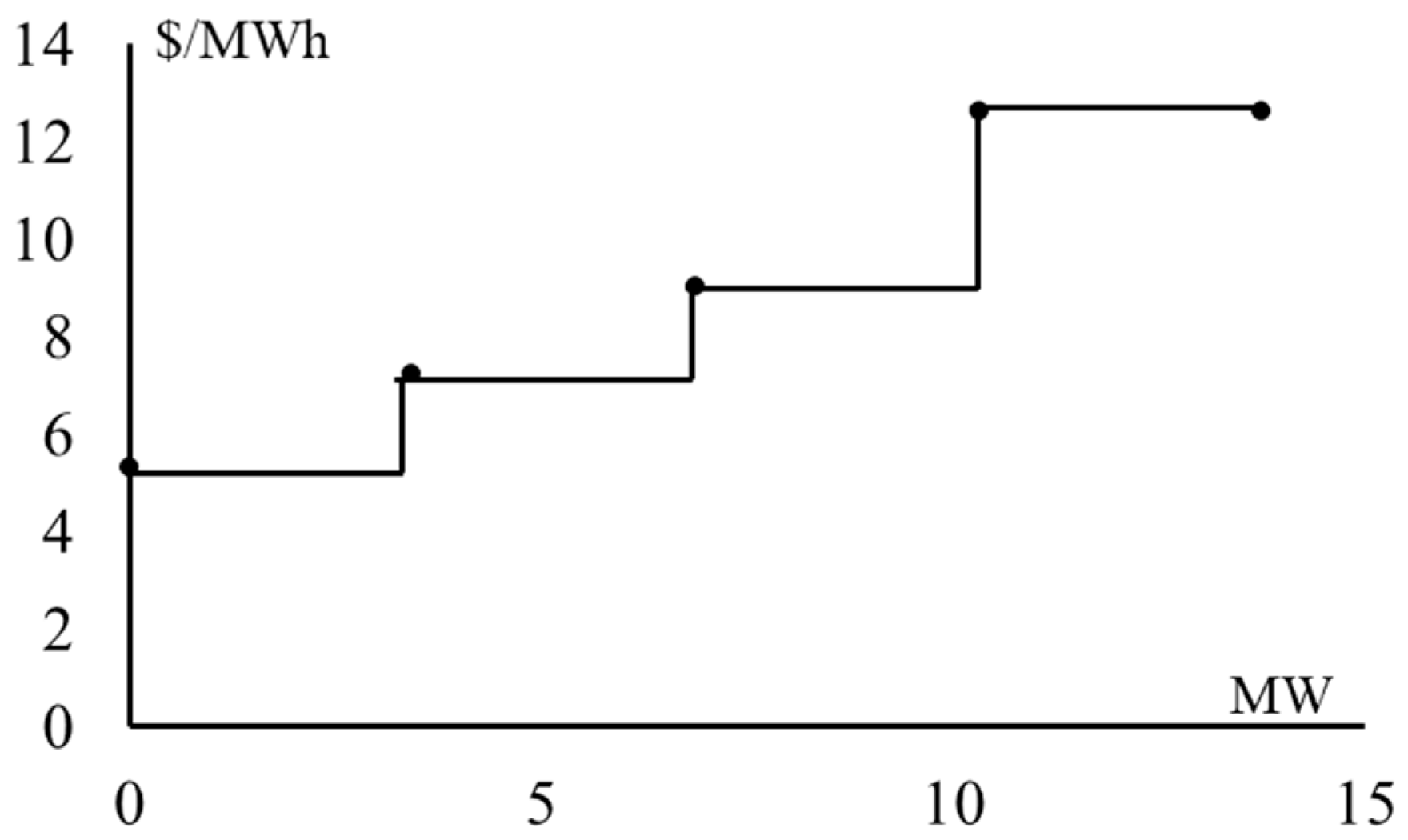

| Case | Total Cost ($) | Energy Cost ($) | Reserve Cost ($) |
|---|---|---|---|
| Participating in no market | 3,445,009 | 1,929,686 | 213,475 |
| Participating only in the energy market | 3,379,107 | 1,864,151 | 230,061 |
| Participating jointly in power and reserve markets | 3,372,904 | 1,894,777 | 186,841 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Zhao, J.; Cen, B.; Chen, Z.; Jia, Y. Integrating High-DER-Penetrated Distribution Systems into Energy Market with Feasible Region and Accompanying Strategic Bidding. Energies 2025, 18, 5630. https://doi.org/10.3390/en18215630
Zhao T, Zhao J, Cen B, Chen Z, Jia Y. Integrating High-DER-Penetrated Distribution Systems into Energy Market with Feasible Region and Accompanying Strategic Bidding. Energies. 2025; 18(21):5630. https://doi.org/10.3390/en18215630
Chicago/Turabian StyleZhao, Tianhui, Jingbo Zhao, Bingcheng Cen, Zhe Chen, and Yongyong Jia. 2025. "Integrating High-DER-Penetrated Distribution Systems into Energy Market with Feasible Region and Accompanying Strategic Bidding" Energies 18, no. 21: 5630. https://doi.org/10.3390/en18215630
APA StyleZhao, T., Zhao, J., Cen, B., Chen, Z., & Jia, Y. (2025). Integrating High-DER-Penetrated Distribution Systems into Energy Market with Feasible Region and Accompanying Strategic Bidding. Energies, 18(21), 5630. https://doi.org/10.3390/en18215630






