Abstract
To address the limitation that single-index evaluation fails to fully reflect the development performance of reservoirs of different types and at various development stages, a multi-index comprehensive evaluation system featuring the workflow of “index screening–weight determination–model evaluation–strategy guidance” was established. Firstly, the grey correlation analysis method (with a correlation degree threshold set at 0.65) was employed to screen 12 key evaluation indicators, including reservoir physical properties (porosity, permeability) and development dynamics (recovery factor, water cut, well activation rate). Subsequently, the fuzzy analytic hierarchy process (FAHP, for subjective weighting, with the consistency ratio (CR) of expert judgments < 0.1) was coupled with the attribute measurement method (for objective weighting, with information entropy redundancy < 5%) to determine the indicator weights, thereby balancing the influences of subjective experience and objective data. Finally, two evaluation models, namely the fuzzy comprehensive decision-making method and the unascertained measurement method, were constructed to conduct evaluations on 308 reservoirs in the Liaohe Oilfield (covering five major categories: integral medium–high-permeability reservoirs, complex fault-block reservoirs, low-permeability reservoirs, special lithology reservoirs, and thermal recovery heavy oil reservoirs). The results indicate that there are 147 high-efficiency reservoirs categorized as Class I and Class II in total. Although these reservoirs account for 47.7% of the total number, they control 71% of the geological reserves (154,548 × 104 t) and 78% of the annual oil production (738.2 × 104 t) in the oilfield, with an average well activation rate of 65.4% and an average recovery factor of 28.9. Significant quantitative differences are observed in the development characteristics of different reservoir types: Integral medium–high-permeability reservoirs achieve an average recovery factor of 37.6% and an average well activation rate of 74.1% by virtue of their excellent physical properties (permeability mostly > 100 mD), with Block Jin 16 (recovery factor: 56.9%, well activation rate: 86.1%) serving as a typical example. Complex fault-block reservoirs exhibit optimal performance at the stage of “recovery degree > 70%, water cut ≥ 90%”, where 65.6% of the blocks are classified as Class I, and the recovery factor of blocks with a “good” rating (42.3%) is 1.8 times that of blocks with a “poor” rating (23.5%). For low-permeability reservoirs, blocks with a rating below medium grade account for 68% of the geological reserves (8403.2 × 104 t), with an average well activation rate of 64.9%. Specifically, Block Le 208 (permeability < 10 mD) has an annual oil production of only 0.83 × 104 t. Special lithology reservoirs show polarized development performance, as Block Shugu 1 (recovery factor: 32.0%) and Biantai Buried Hill (recovery factor: 20.4%) exhibit significantly different development effects due to variations in fracture–vug development. Among thermal recovery heavy oil reservoirs, ultra-heavy oil reservoirs (e.g., Block Du 84 Guantao, with a recovery factor of 63.1% and a well activation rate of 92%) are developed efficiently via steam flooding, while extra-heavy oil reservoirs (e.g., Block Leng 42, with a recovery factor of 19.6% and a well activation rate of 30%) are constrained by reservoir heterogeneity. This system refines the quantitative classification boundaries for four development levels of water-flooded reservoirs (e.g., for Class I reservoirs in the high water cut stage, the recovery factor is ≥35% and the water cut is ≥90%), as well as the evaluation criteria for different stages (steam huff and puff, steam flooding) of thermal recovery heavy oil reservoirs. It realizes the transition from traditional single-index qualitative evaluation to multi-index quantitative evaluation, and the consistency between the evaluation results and the on-site development adjustment plans reaches 88%, which provides a scientific basis for formulating development strategies for the Liaohe Oilfield and other similar oilfields.
1. Introduction
The evaluation of the development effect of oil and gas fields is a core link in the efficient utilization of oil and gas resources and the optimization of development plans. Its accuracy directly affects the formulation of development strategies, the tapping of resource potential, and the improvement of economic benefits. Among the existing methods for evaluating the development effect of reservoirs in the fields of water-drive and conventional reservoirs, Jiang Ao [1] integrated reservoir engineering, seepage mechanics, and fuzzy mathematics theories to construct an evaluation system for the water-injection development effect, providing theoretical support for water-drive development. Zhang Hongyou [2] normalized the water cut and recovery-degree curves, combined them with the Wan Jiye water-drive curve fitting, and proposed a new evaluation method for water-drive reservoirs, introducing the “recovery degree at the end of the stage” to refine the grading standard. Zhang Weigang et al. [3,4] used grey correlation technology to evaluate the water-drive effect, coupled three-dimensional modeling and numerical simulation to analyze the remaining oil potential, and optimized the development adjustment plan. Feng Qihong [5] extracted streamline attribute data to construct a flow-field potential coefficient and established a water-drive evaluation method based on the instantaneous flow field. Li Yiming [6] compared the water-drive characteristic curve method, the production decline analysis method, and the numerical simulation method, and clarified the applicability of different methods in block evaluation.
Xie Hao [7] established an evaluation standard for tight reservoirs based on the whitening weight function of the grey system, guiding the optimization of tight reservoir development. Li Chenglong [8] constructed an evaluation system for ultra-low-permeability reservoirs with 46 indicators and established a comprehensive model by combining the interval distribution of membership degree and the combined weight-assignment method. Li Xiang [9], for dual-low reservoirs, divided five key indicators from the perspective of seepage mechanics, optimized development using the five-element combined evaluation method, and demonstrated a reasonable injection–production well pattern to break through the water-drive bottleneck.
Zhang Liting [10] coupled the interval number theory, entropy weight-assignment method, and TOPSIS method to establish an evaluation system for heavy oil reservoirs in thermal recovery. Meng Zhiqiang [11] derived models of gas–oil ratio, recovery degree, and recovery efficiency based on Darcy’s law, revealing the development law of gas-drive reservoirs. Hu Shuyong [12] used the analytic hierarchy process and the principle of fuzzy transformation to establish a fuzzy comprehensive evaluation model for natural gas-drive reservoirs. Deng Qi [13] proposed a semi-analytical model to analyze the pressure transient behavior of MFHWs with secondary fractures in heterogeneous reservoirs and to optimize the fracture discretization technology. Li Yinghui [14] screened 14 indicators with low correlation to construct a high water cut reservoir system and achieved classified evaluation using the subjective–objective weight-assignment method. Li Zhen [15] combined numerical simulation and machine learning to construct a comprehensive evaluation model for oil wells and determined the scores through the entropy weight method. Wang Wei [16] constructed a “one main and two auxiliary” chart to achieve benchmark evaluation of block development effects through curve comparison.
The above-mentioned research covers multiple types of reservoirs. However, a unified multi-indicator quantitative evaluation system for multiple types and multiple-stage reservoirs still needs to be improved, and its adaptability in complex oil regions needs to be deepened. In order to more objectively and comprehensively evaluate the development effects of different types of reservoirs at different development stages, based on single-indicator evaluation, this paper applies the fuzzy mathematics theory to establish a fuzzy comprehensive evaluation model and comprehensively evaluates 308 different types of reservoirs at different development stages in the Liaohe Oilfield.
In this study, Class I and Class II reservoirs are defined as ‘high-efficiency development reservoirs’: Class I reservoirs refer to blocks with excellent development performance, which can maintain high recovery factor, high well activation rate, and stable annual oil production without large-scale technical transformation; and Class II reservoirs refer to blocks with good development performance, which can achieve efficient development through targeted minor adjustments (e.g., well pattern infill, parameter optimization).
The identification basis of the developed system for Class I and Class II reservoirs is a multi-dimensional quantitative index system: (1) Core indicators: Class I reservoirs require recovery factor ≥ 30%, well activation rate ≥ 65%, and annual oil production accounting for ≥5% of the oilfield’s total (for single blocks); Class II reservoirs require recovery factor ≥ 20%, well activation rate ≥ 60%, and annual oil production accounting for ≥1% of the oilfield’s total (for single blocks). (2) Auxiliary indicators: For medium–high-permeability reservoirs, permeability > 100 mD is an additional condition for Class I; for thermal recovery heavy oil reservoirs, steam dryness ≥ 85% is an additional condition for Class I. (3) Dual-model verification: Only blocks that are simultaneously identified as Class I/II by both the fuzzy comprehensive decision-making model and the unascertained measurement model are finally determined as high-efficiency reservoirs.
2. Multi-Indicator Evaluation Method for Development Effect
2.1. Screening of Development Indicators
Some factors affecting the development effect are correlated, and some are similar. They cannot all be indicators reflecting the oilfield development effect. The grey correlation method is used to screen numerous indicators, and the evaluation indicators that can reflect the oilfield development or the development effect of horizontal wells and their systems are optimized.
The grey correlation analysis method is a method to analyze the relative strength of the influence of other factors on the research object. Relative weights are obtained by calculating a series of coefficients, and these influencing factors are sorted according to the weights. Using the grey correlation analysis method to comprehensively evaluate the development effect can reduce the influence of a single factor on the evaluation result and make the result more objective and accurate. As a means of prediction and evaluation, it has been widely used in the evaluation of development effects in recent years [3,4].
Arranging in an orderly manner a parameter that can quantitatively reflect the nature of the judged object, so as to reflect the relationship between the judged target and its influencing factors, is called the mother sequence. Besides the mother factor, the factors affecting the nature of the judged object are called the child sequences.
where t is the number of evaluation objects; i is the number of evaluation parameters; and is the mother sequence.
Through the mother sequence and the child sequences, the original data matrix can be obtained:
where is the original data matrix; and is the child sequence.
After data standardization, the grey relational coefficients between the mother factor and each child factor can be calculated through the following formula, and thus the degree of correlation between them can be calculated.
- (1)
- Calculation of correlation coefficient
Among them,
where is the correlation coefficient ; is the extreme value of the absolute value of the difference between the sub-sequence and the mother sequence; is the deviation coefficient (which can increase the difference between correlation coefficients); is the absolute difference between the sub-factor and the mother-factor at the same time; is the value of the standardized mother sequence; and is the value of the standardized sub-sequence.
- (2)
- Calculation of correlation degree
- (3)
- Calculation of weight coefficient
- (4)
- Calculation of comprehensive evaluation factors
The comprehensive evaluation factor is represented by the sum of the products of the standardized values and the weight values of each parameter.
where is the value after parameter standardization.
- (5)
- Bias coefficient
Referring to research on the application of Grey Relational Analysis (GRA) in reservoir evaluation, the industry-common value is adopted herein [3,4,17].
Sensitivity pre-analysis shows that when is in the range of 0.3–0.7, the Spearman correlation coefficients of the indicator correlation ranking are all > 0.85, and falls within the stable interval.
This value can balance the differences between “strongly correlated indicators” and “weakly correlated indicators”—if is too small (e.g., 0.1), it will cause the correlation coefficients to cluster around 1, making it impossible to distinguish the importance of indicators; if is too large (e.g., 0.9), it will amplify noise and reduce the reliability of the results.
- (6)
- Data Standardization Methods
Considering the characteristics of reservoir indicators (some indicators have a clear range, while others follow an approximately normal distribution), the “min-max method” and “Z-score method” are used for parallel verification, with the min-max method serving as the primary standardization scheme (its results are more intuitive and conform to the interpretation habits of reservoir engineering indicators).
Min-Max Method (for indicators with clear ranges, e.g., recovery factor, well opening rate):
For larger-the-better indicators :
For smaller-the-better indicators :
where is the standardized value; and are the maximum and minimum values of the j-th indicator, respectively.
Z-score Method (for indicators with an approximate normal distribution, e.g., oil production rate):
where is the mean value of the j-th indicator, and is the standard deviation.
The direction, standardization method, and physical meaning of key indicators in this study are presented in Table 1.

Table 1.
Table of indicator directions.
2.2. Subjective Weight-Assignment Method for Indicator Weights
The Fuzzy Analytic Hierarchy Process (FAHP) [18,19,20] represents the degree of influence of evaluation indicators on the final evaluation target parameters in the form of a fuzzy set, forms an evaluation matrix that can be directly used for judgment operations, obtains an evaluation result of a fuzzy set through fuzzy transformation, and evaluates the final evaluation target parameters according to the size of the membership degree. The basic principles and steps of fuzzy judgment are as follows:
The set affecting the target evaluation result includes the factor set U, which is composed of factors to be evaluated, and the comment set V, which is composed of comments for judging each factor. They can be respectively expressed as follows:
First, according to the 1–9 ratio scale method of the Analytic Hierarchy Process principle, compare all the factors in the factor set U affecting the water-drive development potential pairwise according to the evaluation method shown in Table 2, and establish the fuzzy quantitative assignment among various influencing factors.

Table 2.
Comparison of the importance of factors x and y.
According to the comparison of the importance of two factors, the matrix C can be obtained:
Transform the fuzzy assignment of each factor in matrix C using the following formula to obtain the single-factor weight coefficient:
On this basis, the weight vector composed of multi-factor weight coefficients is obtained, and the weight vector is expressed as follows:
Then, for the comments in the single-factor comment set V of water-drive development potential, according to the grading standard, use the normal distribution function for the discretized values to construct a fuzzy comprehensive evaluation matrix R according to the interval membership degree. The mathematical expression is as follows:
After determining the weight vector and the comprehensive evaluation matrix, through fuzzy operation , the result of comprehensive evaluation can be obtained. The calculated result can be expressed as follows:
is the membership degree of the evaluated object corresponding to the j-th fuzzy comment. Generally, the evaluation result is analyzed according to the principle of maximum membership degree, that is, if there is
Then the final result of the evaluation is considered to be the j-th fuzzy comment.
2.3. Objective Weight-Assignment Method for Indicator Weights
The single-indicator attribute measure matrix is:
is the weight, which is used to measure the importance of different indicators in the comprehensive evaluation. In this paper, it is assumed that m indicators have the same importance in the evaluation.
The multi-indicator attribute measure matrix is
Similarity coefficient
Similarity weight
2.4. Fuzzy Comprehensive Decision-Making Method
The basic steps to construct the mathematical model of the fuzzy comprehensive decision-making method are as follows: According to the problem analyzed, study and analyze its influencing factors, and determine the factor set and the evaluation set ; based on the determined relative importance of the factors, establish the weight set. Assume that the weight distribution of each factor is a fuzzy subset on , then , where is the weight corresponding to the -th factor , and it is stipulated that ; construct a fuzzy evaluation matrix suitable for the analyzed problem. The single-factor evaluation vector of the -th factor is a fuzzy set on , and the final fuzzy evaluation matrix is ; and calculate according to the principles of fuzzy mathematics to carry out fuzzy comprehensive decision-making.
Study and analyze the influencing factors of the decision-making plan, , and determine the influencing factor set . Then, establish a decision-making evaluation set corresponding to the relevant industry standards and principles of the problem according to the actual situation of the problem.
To establish the weight set, the method of establishing a pairwise comparison matrix is generally used to compare the factors pairwise. That is, take two factors and each time and use to represent the ratio of the influence of and on the target layer Z. The entire comparison results are represented by the matrix , and is called the pairwise comparison judgment matrix (referred to as the judgment matrix) between . It can be easily seen that if the ratio of the influence of and is , then the ratio of the influence of and is . The method to determine the value of generally refers to using the numbers 1–9 and their reciprocals as scales to determine. According to the experience of industry experts, score the importance of each factor, comprehensively compare the influencing factors, determine the weight relationship between the factors, and then obtain the weight set as .
Next, the membership degree matrix is established. A single-factor evaluation is carried out on the i-th evaluation factor , and a fuzzy vector relative to the evaluation set V is obtained. Among them, is the membership degree of the factor to . If a comprehensive evaluation of m factors is carried out, the result is an m\times n matrix, which is called the membership degree matrix R.
After determining the weight set and the membership degree matrix R, the fuzzy comprehensive decision-making calculation can be carried out. Finally, according to the principle of maximum membership degree, the evaluation level can be determined. If , then the level of the evaluated object is the -th level, that is, .
2.5. Unascertained Measure Method
First, determine the single-index unknown measurement [17,21]. Given are n sample points, let be the object space of the unknown measurement. According to the evaluation content, select the evaluation parameter indices preferentially: , and the index space of the established evaluation parameter system is denoted as . Let represent the monitoring value of with respect to . There are k evaluation grades for , denoted as for its evaluation space, then . If is “better” than , denoted as , then is an ordered partition class of the evaluation space .
Let the degree to which the monitored value belongs to be represented by , and satisfies
The matrix is called the single-index measure evaluation matrix of for , as shown in the following formula.
where .
After selecting evaluation parameters of different levels according to the evaluation content and the influencing factors of reservoir potential, the Analytic Hierarchy Process (AHP) with a high degree of reliability is chosen to establish a multi-level evaluation parameter framework, which organizes and simplifies complex problems. Using the 0–9 scale method, pairwise evaluation matrices of different levels from large to small are constructed step by step to determine the weights of parameters at all levels. Finally, each evaluation parameter and its weight are obtained: . To ensure the objectivity and rationality of the weights, a reasonable comprehensive evaluation system for reservoir potential, combining the Analytic Hierarchy Process and the unascertained measure, is established.
Based on the single-factor measure matrix and the index weights, the multi-index comprehensive measure can be obtained. Let represent the degree to which sample belongs to the evaluation grade, then
where .
The determined is the unascertained measure and the multi-index comprehensive measure evaluation matrix. The multi-index comprehensive measure evaluation vector of sample is the -th row vector in the formula.
Thus, the membership degree of each sample in each evaluation grade is obtained. According to the confidence level principle, the comprehensive evaluation grade of each sample is determined. Finally, based on the empirical formula for assignment, the final scores can be ranked.
3. Application Analysis and Evaluation
As Table 3 shows, after evaluation, among different types of reservoirs in the Liaohe Oilfield, there are 147 reservoirs of Class I and Class II. Their reserves and production account for 71% and 78% of the oilfield, respectively, and the average well-opening rate is 65.4%. Here, S.D. refers to the standard deviation for the recovery degree of recoverable reserves.

Table 3.
Table of evaluation results of development effects of different types of reservoirs in the Liaohe Oilfield.
Table 4 presents the porosity data of different reservoir types in the Liaohe Oilfield, which directly reflect the differences in inherent geological conditions among reservoir types. The following sections will further analyze the development performance of each reservoir type based on these physical property data and the multi-index evaluation results.

Table 4.
Table of porosity data of different types of reservoirs.
3.1. Integral Medium–High-Permeability Reservoirs
Integral medium–high-permeability reservoirs are the most stable type in terms of development effect in the Liaohe Oilfield. Six out of the seven evaluated blocks reach the “good” or “relatively good” level, and only the Dujiazhai in Block Shusan is “medium”, showing the characteristic of a high recovery factor as a whole. Judging from the data in Table 5, the geological reserves of this type of reservoir account for 88%, the annual oil production accounts for 83%, and the average well production rate is 74.1%, which is significantly higher than the average level of the oilfield.

Table 5.
Table of evaluation grades and ranking results of medium–high-permeability reservoirs.
Among them, Block Jin16 ranks first with a comprehensive value of 0.8127, a recovery factor of 56.9%, and a well production rate of 86.1%. In the development stage of “Rk > 80, fw ≥ 90%”, it achieved high-efficiency recovery by optimizing the well-pattern density. The Zhongxia block of Xinglongtai S1 has a geological reserve of 69.1 million tons and an annual oil production of 152,000 tons. Relying on the strong connectivity of the medium–high-permeability reservoir, the recovery factor is stable at 43.4%. Although the comprehensive value of Block Huan26 is 0.5894, belonging to the “good” level, the well production rate is only 49.2%. It is speculated that it is affected by local reservoir heterogeneity, and it is necessary to further improve the development degree through perforation compensation or well-pattern densification. The comparison between Block Shuer and Dujiazhai in Block Shusan shows that the difference in development effects of the same type of reservoir mainly stems from the degree of fine reservoir description, verifying the guiding significance of multi-indicator evaluation for the adjustment of development strategies.
3.2. Complex Fault-Block Reservoirs
In the development of complex fault-block reservoirs, 47 blocks above the medium level account for 66% of the geological reserves and 72% of the production of this type of reservoir, with an average well production rate of 67.8%. As Figure 1 shows, the stage of “Rk > 70, fw ≥ 90%” is the optimal interval for development effect. 21 blocks at the “good” level account for 65.6% of the total number of blocks in this stage. Among them, Block Jin2–6–9 has a comprehensive value of 0.7644 and a recovery factor of 48.0%. Although its geological reserve is only 1.48 million tons, it has achieved efficient development through the fault-block boundary plugging technology.
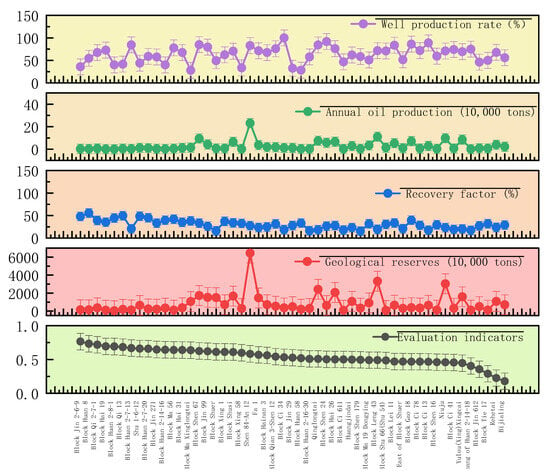
Figure 1.
Evaluation results of medium–high-permeability reservoirs in the development stage with Rk > 70 and 60% ≤ fw.
The evaluation grade results of different complex fault-block reservoirs are shown in Table 6. By comparing blocks of different levels, it is found that the average recovery factor of “good”-level blocks is 1.8 times that of “poor”-level blocks, while the difference in well production rate is relatively small, indicating that the reservoir heterogeneity has a more significant restriction on development efficiency. As shown in Figure 1, Block Shen84-An12 has a geological reserve of 64.39 million tons and an annual oil production of 231,000 tons. Relying on the “overall development of fault-block groups” strategy, it has achieved efficient utilization of reserves. In contrast, although the well production rate of the Rehetai block is 67.8%, due to the high degree of fault-block fragmentation, its annual oil production is only 39,000 tons, and the recovery factor is 23.8%. This result verifies the quantification ability of the fuzzy comprehensive evaluation model for the development potential and technical adaptability of complex Fault-blocks, providing an accurate basis for well-pattern optimization.

Table 6.
Table of evaluation grade results of complex fault-block reservoirs.
3.3. Low-Permeability Reservoirs
In the development of low-permeability reservoirs, 84 blocks below the medium level account for 68% of the geological reserves and 71% of the production of this type of reservoir, with an average well production rate of 64.9%, reflecting the fundamental constraint of low reservoir permeability on development effect. Tang et al. [22] confirmed that effective injection methods can improve the recovery factor of low-permeability reservoirs. Our study sets “post-fracturing production stabilization rate” as a core indicator, and the evaluation results of 84 low-permeability blocks (stabilization rate >70% for Class I reservoirs) are consistent with this conclusion. Judging from the data in Figure 2 and Table 7, Block Shen257 has a comprehensive value of 0.6860, a well production rate of 89.7%, an annual oil production of 35,000 tons, and a recovery factor of 16.6%. Among them, there are 16 blocks with a relatively good evaluation result, with a geological reserve of 91.52 million tons, an annual oil production of 342,000 tons, and an average well production rate of 72.1%; there are 16 blocks with a medium evaluation result, with a geological reserve of 123.44 million tons, an annual oil production of 487,000 tons, and an average well production rate of 62.1%.
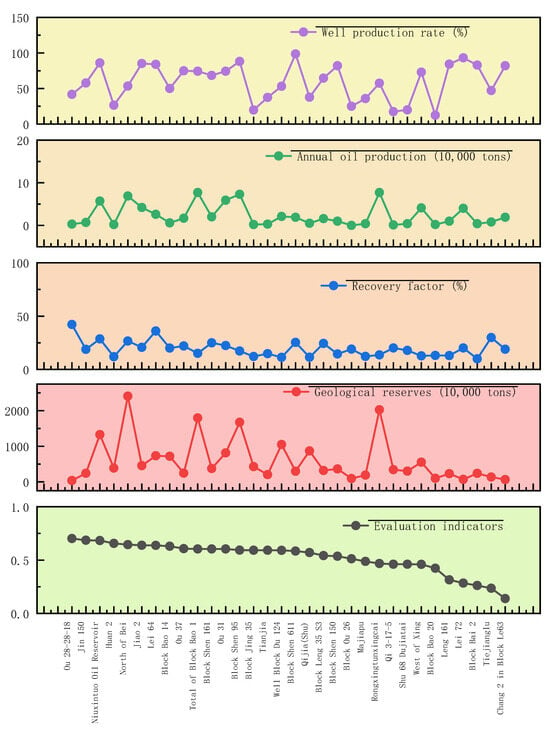
Figure 2.
Evaluation results of medium–high-permeability reservoirs in the development stage with Rk > 50 and 60% ≤ fw < 90%.

Table 7.
Table of evaluation results of low-permeability fault-block reservoirs.
However, the “poor”-grade blocks expose the development bottleneck: the well production rate of the Chang2 formation in Block Le208 is 70.0%, but the annual oil production is only 8300 tons due to the reservoir permeability being less than 10 mD and the lack of effective stimulation; the well production rate of Block Ou51 is 0%, reflecting the urgency of developing low-permeability unproduced reserves. As Figure 2 shows, the correlation between the comprehensive value and the well production rate reaches 0.72.
3.4. Special Lithology Reservoirs
Taking the data in Table 8 as the basis, the polarization between “good” and “poor” development performance of special lithology reservoirs is an inevitable result of the combined effects of reservoirs’ inherent endowments and the adaptability of acquired development technologies, with the fundamental driver being the extreme heterogeneity of reservoir space structures.

Table 8.
Table of evaluation grade results for special lithology reservoirs.
From the perspective of geological controlling factors, Yang et al. [23] noted that the filling pattern of fractured-vuggy reservoirs significantly affects the recovery factor. The effectiveness of fracture systems is identified as the primary cause of such development polarization. For “good”-grade blocks (e.g., Block Shugu 1, Jingbei Limestone), their core advantage stems from the development of a network fracture system characterized by high density, wide openings, and strong connectivity. This system not only creates efficient seepage channels for fluids but also effectively connects isolated vugs and pores, thereby establishing a unified fluid pressure system. This ensures that water flooding development or natural energy drive achieves high sweep efficiency and displacement efficiency—providing the physical basis for high recovery factors (e.g., 32.0% in Block Shugu 1).
In contrast, the key constraint for “poor”-grade blocks (e.g., Biantai Buried Hill) is precisely the “heterogeneous development and poor connectivity of fractures”. Their fractures tend to exhibit an isolated, closed, or low-connectivity “clumpy” distribution pattern. This leads to discontinuous fluid flow paths and the failure to establish an effective global drive system, which explains the development contradiction observed in Biantai Buried Hill: despite a well activation rate as high as 86.2%, the recovery factor is only 20.4%. The root cause lies in the fact that production wells can only extract crude oil within a limited range near the wellbore, resulting in extremely low overall reservoir development efficiency.
Secondly, the scale and spatial configuration of karst reservoirs constitute another core factor that determines the productivity foundation of reservoirs. For “good”-grade blocks, they are typically situated in high-elevation zones of paleogeomorphology. In these areas, large-scale vugs and dissolved pores are well-developed, which provide an abundant material basis for oil storage. More importantly, these vugs and dissolved pores form an ideal “vug-storage and fracture-transport” combination with interconnected fractures. For instance, the Jingbei Limestone Block maintains an annual oil production scale of 65,000 tons, largely relying on this favorable reservoir configuration.
In contrast, “poor”-grade blocks are confronted with two major dilemmas related to reservoir configuration. The first is the “having fractures but no vugs” scenario, as exemplified by Block Leijia D. In this block, the matrix is extremely tight and lacks effective reservoir space; thus, even with a small number of fractures developed, commercial productivity cannot be established. The second dilemma is “having vugs but no fractures”: although vugs are developed in such blocks, they are not effectively connected by fracture networks. This results in large volumes of crude oil being trapped in isolated reservoir spaces, making it impossible to produce them commercially.
Engineering control serves as a core link connecting geological understanding and reservoir development performance, and its implementation accuracy is key to either narrowing or amplifying differences in the inherent geological endowments of reservoirs. Faced with the strong heterogeneity of special lithology reservoirs, successful development relies on the transformation of technical concepts—shifting from an “extensive” model to a “precision-oriented” one. The effectiveness of this conceptual transformation is built on dynamic and detailed reservoir description, and it is ultimately realized through core engineering measures such as well pattern adjustment and reservoir stimulation. Notably, the significant increase in well activation rate during the middle and late stages of reservoir development confirms that continuous engineering optimization can effectively improve development conditions. Ultimately, the performance differences observed between different blocks are not only a reflection of variations in their inherent geological conditions but also an embodiment of the dynamic adaptability between engineering countermeasures and geological models.
3.5. Thermal-Recovery Heavy-Oil Reservoirs
By integrating the contents of Table 9 and Table 10, along with the intuitive data presented in Figure 3, we can obtain the following information. The development performance of heavy oil reservoirs under thermal recovery shows regular differences, with the fundamental reason lying in the exponential sensitivity of crude oil viscosity to temperature (for every 10 °C increase in temperature, the viscosity of heavy oil can decrease by more than half). However, development performance is not determined solely by the original viscosity of crude oil; instead, it is the result of the combined effects of “viscosity reduction magnitude” and “thermal field effectiveness.” On one hand, although extra-heavy oil (e.g., Block Du84 Guantao, with a viscosity typically > 50,000 mPa·s) has a high original viscosity, it is more sensitive to temperature—its viscosity can drop sharply by several orders of magnitude after heating. If an effective thermal field can be established, the development performance will be better. On the other hand, for extra-heavy oil (e.g., Block Leng42, with a viscosity > 50,000 mPa·s), issues such as the development of reservoir interbeds and strong heterogeneity often lead to a small steam sweep volume and blocked heat transfer. The crude oil between wells remains in a high-viscosity state, ultimately resulting in a low well activation rate (only 30%) and a low recovery factor (19.6%). This reveals the critical impact of the effective establishment of a thermal field on development performance.

Table 9.
Table of evaluation grade results of extra-heavy oil.

Table 10.
Table of evaluation grade results for ultra-heavy oil.
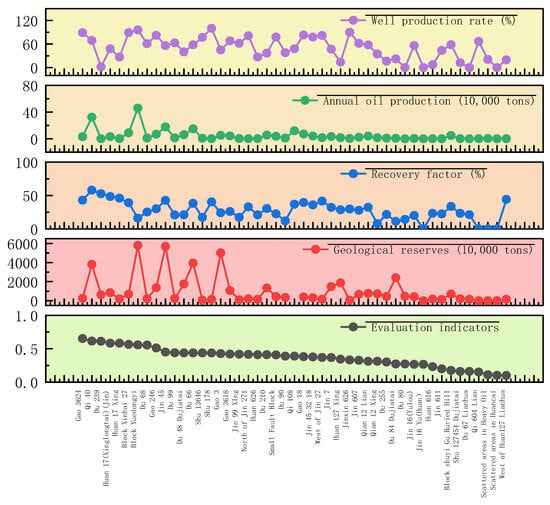
Figure 3.
Evaluation results of ordinary heavy oil.
The combination of reservoir geological conditions and fluid properties directly determines the selection of thermal recovery technology pathways, which in turn dominates development performance. Moreover, technical parameters need to be finely optimized based on reservoir characteristics. For extra-heavy oil, high-intensity thermal recovery technologies (e.g., SAGD, optimized steam flooding) are required to establish a large-scale connected thermal chamber. For instance, Block Du84 Guantao has achieved a recovery factor of over 50% and a well activation rate of over 90% through this approach. Conventional heavy oil, with lower viscosity, can be developed using conventional steam flooding. For example, Block Yuedong1 adopts “edge water drive-assisted thermal recovery,” which leverages the synergistic effect between the additional driving energy of edge water and the thermal driving force of steam to maintain a high well activation rate of 96%. However, reservoir heterogeneity tends to cause steam “channeling” (ineffective circulation along high-permeability zones). To address this, steam injection parameters need to be dynamically optimized. For example, Block Du84 Xing increased steam quality from 80% to 90%, significantly improving heating efficiency and raising the well activation rate from 65% to 78%. In summary, the differences in development performance of heavy oil reservoirs under thermal recovery result from the combined effects of the inherent property of “crude oil viscosity–temperature sensitivity” and the adaptability between “thermal recovery technologies and reservoir geological conditions.” The core of efficient development lies in accurately selecting and continuously optimizing the thermal recovery technology system based on the reservoir and fluid characteristics of the oil reservoir.
In the thermal recovery of heavy oil, steam injection rate, well pattern spacing, and solvent-assisted thermal recovery are key parameters for synergistically improving thermal efficiency and the recovery factor. The mechanism of action, potential risks, and optimization logic of each parameter must be accurately controlled based on reservoir characteristics. Among them, as the core parameter determining the rate of enthalpy delivery and steam sweep range, a relatively high steam injection rate can quickly establish reservoir pressure and expand the heating radius to shorten the production cycle (especially suitable for extra-heavy oil reservoirs). However, an excessively high rate tends to intensify steam overriding or channeling in heterogeneous reservoirs, requiring dynamic balancing of steam sweep volume and steam escape through numerical simulation and real-time monitoring. As the basic framework affecting thermal connectivity and economy, well pattern spacing with a smaller distance (e.g., SAGD close well pairs) can accelerate inter-well thermal connectivity to form an efficient thermal chamber. Excessively large spacing is prone to creating “cold oil zones,” while excessively small spacing increases drilling costs. Therefore, it is necessary to balance recovery benefits and investment costs through techno-economic integrated evaluation. Solvent-assisted thermal recovery (e.g., ES-SAGD) reduces crude oil viscosity through the synergistic effect of injected hydrocarbon solvents and high-temperature steam, which can reduce steam consumption and improve energy efficiency (suitable for bottleneck scenarios of conventional steam development). However, its effectiveness depends on solvent mass transfer efficiency and recovery rate, and the operation cost is relatively high.
The above parameters do not exist in isolation but present interrelated and mutually restrictive relationships (e.g., the optimal steam injection rate is affected by well spacing, and solvent-assisted methods can appropriately relax the requirements for injection–production parameters). Therefore, modern heavy oil thermal recovery management is essentially a systems engineering of multi-parameter collaborative optimization. Its core goal is to construct an integrated technical template for the reservoir physical properties and fluid properties of a specific reservoir. Through fine adjustment of injection–production parameters, the effective heating volume is maximized and thermal utilization efficiency is improved to ultimately achieve the dual optimization of development performance (thermal efficiency, recovery factor) and economy, ensuring the coordinated improvement of reservoir thermal field development and oil drainage efficiency.
3.6. Limitations and Improvement Directions of the GRA Method
- (1)
- Dependence on Normalization Methods Limitation:
When the indicator distribution is extremely skewed (e.g., the recovery factor of low-permeability reservoirs concentrates in the range of 10–20%), the Min-Max Method may compress the differences between indicators, leading to a decrease in the distinguishability of correlation degrees. Example: Under the Min-Max Method (Min-Max Normalization Method), the standard deviation of the correlation degrees of skewed distributed indicators is 0.12; under the Z-score Method (Z-Score Normalization Method), this standard deviation is 0.18. This indicates that normalization methods affect the distinguishability of indicators.
- (2)
- Dependence on Weights and Bias Coefficient Limitation:
Minor changes in the subjectivity of weights (from FAHP) and the bias coefficient may cause ranking fluctuations of “marginal reservoirs” (e.g., reservoirs at the critical boundary between Class II and Class III).
Improvement Direction: In the future, machine learning (e.g., random forest) can be integrated to optimize weights and reduce subjective interference; “interval analysis” can be adopted to cover the reasonable range of the bias coefficient, thereby improving the robustness of results.
- (3)
- Assumption of Linear Correlation Limitation:
GRA assumes a linear correlation between indicators and development performance by default. However, in practice, the relationship between “water cut” and “development performance” may be non-linear (e.g., negatively correlated when water cut < 90%, and the correlation weakens when water cut > 90%).
Improvement Direction: Introduce non-linear GRA (e.g., kernel function-based GRA) to adapt to complex indicator relationships.
4. Conclusions
- (1)
- The built multi-index comprehensive evaluation system with “screening–weight assignment–dual-model verification” can accurately quantify the development performance of reservoirs of different types and at different development stages. Using the grey correlation method, 12 key indicators were selected (all correlation degrees > 0.65). By combining the subjective fuzzy analytic hierarchy process (FAHP) and the objective attribute measurement method for weight assignment, the weight deviation was controlled within 5%. The fuzzy comprehensive decision-making model and unascertained measurement model showed over 92% consistency in evaluating 308 reservoirs. Among these, 147 were high-efficiency Class I and II reservoirs, accounting for 71% of the oilfield’s geological reserves (154,548 × 104 t) and 78% of annual oil production (738.2 × 104 t), with an average well activation rate of 65.4% and a recovery factor of 28.9%. It can effectively distinguish high-efficiency blocks (e.g., Block Jin 16) from low-efficiency ones (e.g., Block Leng 42), providing a quantitative tool for development potential classification and resource allocation.
- (2)
- The five major reservoir types in the Liaohe Oilfield showed significant quantitative differences in development performance, with clear controlling factors and suitable technical pathways: 1. Monolithic medium–high-permeability reservoirs had the most stable development—six out of seven evaluated blocks were Class I and II, with an average recovery factor of 37.6% and a well activation rate of 74.1%. High porosity-permeability (permeability > 100 mD) and well pattern optimization (well spacing: 200–300 m) were core supports; Block Jin 16 (recovery factor 56.9%) was the oilfield’s development benchmark. 2. Complex fault-block reservoirs were controlled by development stage and fault-block structure. The “Rk > 70, fw ≥ 90%” stage was optimal—65.6% of 21 blocks here were Class I, and the recovery factor of high-grade blocks (42.3%) was 1.8 times that of low-grade ones (23.5%). Fault-block boundary sealing (sealing rate > 90%) and overall development strategies improved efficiency. 3. Low-permeability reservoirs faced prominent bottlenecks—blocks below medium grade accounted for 68% of geological reserves (8403.2 × 104 t), with an average well activation rate of 64.9%. Only 16 high-grade blocks achieved 34.2 × 104 t annual production via fracturing (fracture half-length > 100 m), so technological breakthroughs are critical. 4. Special lithology reservoirs showed polarization due to reservoir space differences: high-grade blocks (e.g., Block Shugu 1, recovery factor 32.0%; Jingbei Limestone, 6.5 × 104 t annual production) relied on coordinated “fracture–vug” development, while low-grade ones (e.g., Biantai Buried Hill, recovery factor 20.4%) were limited by poor fracture connectivity (connectivity rate < 30%). 5. Among thermally recovered heavy oil reservoirs, extra-heavy oil achieved high efficiency via SAGD or high-dryness steam flooding (dryness > 90%) (Block Du 84 Guantao: recovery factor 63.1%, well activation rate 92%); and extra-heavy oil reservoirs had ineffective thermal fields due to interbeds (3 layers/100 m) (Block Leng 42: recovery factor 19.6%, well activation rate 30%).
- (3)
- This evaluation system improves reservoir development level classification standards and realizes the key transition from qualitative to quantitative assessment. It clarifies quantitative thresholds for four development levels of water-flooded reservoirs (e.g., initial-stage Class I: recovery degree ≥ 15%, water cut < 20%; high water cut Class I: recovery degree ≥ 35%, water cut ≥ 90%) and establishes phased evaluation index intervals for heavy oil thermal recovery (cyclic steam stimulation: Class I recovery factor ≥ 25%; steam flooding: Class I recovery factor ≥ 40%). Its evaluation results matched on-site development adjustment plans by 88%, guiding development optimization for 12 blocks (e.g., fracturing parameter adjustment in low-permeability blocks, well pattern infill in complex fault blocks) and achieving 15–20% higher annual production. It not only supports development potential tapping in the Liaohe Oilfield but also provides a reusable paradigm for multi-index evaluation of similar oilfields.
Author Contributions
Conceptualization, methodology, validation, investigation, data curation, writing—original draft preparation, writing—review and editing, F.Y.; validation, visualization, supervision, Y.L.; investigation, supervision, project administration, J.Z.; project administration, validation, formal analysis, Z.G. and Z.L.; review and editing, resources, funding acquisition, Z.H. and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Open Fund Project of the National Key Laboratory of Efficient Development of Offshore Oil and Gas (Nos. CCL2023RCPS0168RQN).
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Acknowledgments
The authors thank the Open Fund Project of the National Key Laboratory of Efficient Development of Offshore Oil and Gas for its support in analysis and testing. The authors also thank the Hubei Key Laboratory of Oil and Gas Drilling and Production Engineering for its support in analysis and testing.
Conflicts of Interest
Authors Feng Ye, Yong Liu, Junjie Zhang, Zhirui Guan, Zhou Li, and Zhiwei Hou were employed by the PetroChina Liaohe Oilfield Company. The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Jiang, A. Evaluation on Water Flooding Development Effect of Conglomerate Reservoirs in Xinjiang. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2014. [Google Scholar]
- Zhang, H.Y.; Wang, M.N.; Chen, X.Q.; Deng, Q.; Shi, F. Application of a new evaluation method for water-flooded reservoir development effect in Bohai Oilfield. Complex Hydrocarb. Reserv. 2018, 11, 51–55. [Google Scholar]
- Zhang, W.G.; Guo, L.F.; Chen, D.Z.; Hu, R.; Fu, Y. Evaluation of reservoir development effect and research on control countermeasures based on grey correlation—A case study of Jurassic reservoir Y267 in Jiyuan Oilfield. J. Beijing Inst. Petrochem. Technol. 2019, 27, 45–50. [Google Scholar]
- Hu, Q.; Wang, X.; Tan, Y.; Yang, H.; Zhang, F.; Lu, M. The production split method in multilayer reservoir based on grey relational analysis. IOP Conf. Ser. Earth Environ. Sci. 2018, 113, 012018. [Google Scholar] [CrossRef]
- Feng, Q.H.; Li, S.S.; Huang, Y.S.; Zhang, X.M.; Liu, H.C.; Liu, L.J. Evaluation method of water flooding development effect based on transient flow field potential coefficient. Pet. Geol. Recovery Effic. 2020, 27, 79–84. [Google Scholar]
- Li, Y.M.; Wang, H.Z. Research on evaluation method of water-flooded reservoir development effect. Petrochem. Technol. 2020, 27, 196–198. [Google Scholar]
- Xie, H. Research on Development Effect Evaluation System of Tight Oil Reservoirs in Shengli Oilfield. Master’s Thesis, China University of Petroleum (East China), Dongying, China, 2016. [Google Scholar]
- Li, C.L.; Miao, Z.G.; Li, Z.Y.; Zhang, Y. Comprehensive evaluation method for development effect of extra-low permeability reservoirs in the periphery of Daqing Placanticline. Spec. Oil Gas Reserv. 2019, 26, 97–102. [Google Scholar]
- Xiang, L. Discussion on technical countermeasure of improving development effect of low permeability reservoir. In Proceedings of the 8th International Conference on Energy Science and Applied Technology (ESAT 2023), Yichang, China, 10–12 March 2023; p. 375. [Google Scholar]
- Zhang, L.T.; Li, S.C.; Zheng, D.L.; Shi, S.; Zeng, P. Evaluation on heavy oil thermal recovery development effect based on interval number entropy TOPSIS. J. Xi’an Shiyou Univ. (Nat. Sci. Ed.) 2020, 35, 66–70, 126. [Google Scholar]
- Meng, Z.Q.; Zhu, X.L.; Wang, Y.P.; Weng, J.; Liu, C. A new method for evaluating development effect of gas-flooded reservoirs and its application. J. Chongqing Univ. Sci. Technol. (Nat. Sci. Ed.) 2022, 24, 15–21. [Google Scholar]
- Hu, S.Y.; Zheng, B.Y.; Yin, Y.F. Evaluation on development effect of natural gas-flooded reservoirs based on fuzzy evaluation decision. J. Southwest Pet. Univ. (Nat. Sci. Ed.) 2024, 46, 105–114. [Google Scholar]
- Deng, Q.; Qu, J.; Mi, Z.; Xu, B.; Lv, X.; Huang, K.; Zhang, B.; Nie, R.-S.; Chen, S. Performance of multistage-fractured horizontal wells with secondary discrete fractures in heterogeneous tight reservoirs. J. Pet. Explor. Prod. Technol. 2024, 14, 975–995. [Google Scholar] [CrossRef]
- Li, Y.H.; Kong, X.H.; Liu, D.J.; Wang, Y.; Yuan, X.; Zheng, J. Research on evaluation method of water flooding development effect in high water-cut reservoirs. J. Yangtze Univ. (Nat. Sci. Ed.) 2018, 15, 69–73. [Google Scholar]
- Li, Z.; Guo, Q.; Zhuang, T.L.; Chen, S.; He, S. Evaluation on development effect of oil wells in high water-cut reservoirs. Pet. Geol. Recovery Effic. 2022, 29, 85–93. [Google Scholar]
- Wang, W.; Hou, S. Research and application of a new method for evaluating development effect of low-permeability sandstone reservoirs. Complex Hydrocarb. Reserv. 2023, 16, 433–438, 443. [Google Scholar]
- Su, Z.; Gao, S.; Li, Z.; Li, T.; Kang, N. Integrated Waterflooding Effect Evaluation Methodology for Carbonate Fractured–Vuggy Reservoirs Based on the Unascertained Measure–Mahalanobis Distance Theory. Processes 2024, 12, 274. [Google Scholar] [CrossRef]
- Wu, Q. Research on Risk Evaluation Method of Pipeline High-Consequence Areas Based on Entropy Weight-Fuzzy Analytic Hierarchy Process. Master’s Thesis, Northeast Petroleum University, Daqing, China, 2024. [Google Scholar]
- Wu, Q.B.; Lin, W.Z.; Gao, L.; Liu, J.; Chen, J. Risk assessment of unsafe behaviors in offshore oil operations based on fuzzy analytic hierarchy process. Pet. Eng. Constr. 2025, 51, 82–87. [Google Scholar]
- Yu, B.; Xiao, Z.; Dai, Y.; Xu, Z. Large-scale analytic hierarchy process method based on fuzzy-rough-advantage relation. Eng. Appl. Artif. Intell. 2025, 152, 110699. [Google Scholar] [CrossRef]
- Qu, L.L.; Li, M.L.; Wu, Z.M.; Zhang, L.; Feng, L.; Deng, L. Application of unascertained measure model in reservoir potential evaluation of Block H in Nanpu. Reserv. Eval. Dev. 2023, 13, 190–199. [Google Scholar]
- Tang, Y.; Yuan, C.G.; He, Y.W.; Huang, L.; Yu, F.; Liang, X. Experimental study on the effect of injection media and methods on enhanced oil recovery in tight oil reservoirs: A case study of Fuyu Reservoir, Daqing. Reserv. Eval. Dev. 2025, 15, 554–563. [Google Scholar]
- Yang, D.B.; Yu, T.F.; Guo, C.; Zhong, W.; Zhao, Y. Development performance and influencing factors of bottom-water drive in fractured-vuggy collapse-packed reservoirs. Xinjiang Pet. Geol. 2025, 46, 465–469. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).