Next Article in Journal
Lithium-Ion Battery SOH Prediction Method Based on ICEEMDAN+FC-BiLSTM
Previous Article in Journal
Assessing Efficiency in the Circular Economy Using the Levelized Cost of Waste: A Case Study of Textile Waste Pyrolysis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 18
Issue 21
10.3390/en18215616
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Optimal Location of Charging Stations for Electric Vehicles in Distribution Networks: A Literature Review

by
David Lara Leon
1,†,
Yandi Gallego Landera
2,†,
Luis Garcia Santander
1,
Lesyani Teresa León Viltre
2,*,
Oscar Cuaresma Zevallos
3 and
Fredy Antonio Muñoz Jarpa
2
1
Departamento de Ingeniería Eléctrica, Universidad de Concepcion, Concepción 4070386, Chile
2
Departamento de Ingeniería Eléctrica y Electrónica, Universidad del Bío-Bío, Concepción 4051381, Chile
3
Electrical Engineering Department, Rio de Janeiro State University (UERJ), 524 São Francisco Xavier, Rio de Janeiro 20550-900, Brazil
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Energies 2025, 18(21), 5616; https://doi.org/10.3390/en18215616
Submission received: 10 October 2025 / Revised: 20 October 2025 / Accepted: 22 October 2025 / Published: 25 October 2025
Browse Figures
Versions Notes

Abstract

Currently, the global use of electric vehicles is still low; however, a significant increase is expected in the coming years. Determining the optimal location of charging stations in distribution systems can influence the increased adoption of this technology in transportation, as it contributes to the proper functioning of distribution networks. There are several optimization methods, which can be classified into exact, heuristic, and metaheuristic methods, each with different characteristics and applications. This article presents a literature review of the main optimization methods currently used to determine the location of charging stations in distribution systems. It concludes that metaheuristic optimization methods are the most widely used. In addition, the review identifies current research gaps, particularly the limited use of real EV demand data and the lack of stochastic approaches to represent demand variability. The main contribution of this work lies in emphasizing the importance of incorporating stochastic methods to adequately address the uncertainty of EV demand in distribution networks.

1. Introduction

The simultaneous use of renewable-based distributed generation and electric vehicles can affect the proper functioning of distribution systems, considering that both technologies are variable. Distributed generation, whether wind or photovoltaic, depends on weather conditions, while the charging of electric vehicles depends on location, time of day, vehicle type, among other factors [1,2].
Charging stations, when located without an optimization process, are often placed based on practical criteria, such as proximity to areas with economic impact, which does not always guarantee compliance with the technical requirements of the distribution network. One of the criteria for locating charging stations is proximity to shopping centers or places with high foot traffic, and technical network criteria are not taken into account. The ease of installation and cost also influence the location [3,4].
The incorrect placement of charging stations in the distribution system can cause load imbalances, increased electrical losses, and difficulties in integrating renewable distributed generation, among other negative effects. The aspects mentioned above negatively affect power quality, since parameters such as SAIFI and THD can be impacted by improper siting of charging stations in distribution systems [5]. An increase in the SAIFI value means more frequent service interruptions and a lower probability of ensuring a reliable power supply [6]. An increase in the THD value indicates greater signal distortion, which leads to problems such as overheating and risk of damage to electrical equipment, among other harmful effects.
Therefore, developing optimization models for locating charging stations in electrical systems would enable the simultaneous integration of distributed renewable generation (DRG) and electric vehicles (EVs), while meeting the technical requirements of the distribution network [4,7,8].
Although progress has been made in understanding how much DRG the grid can safely handle, it is still not well defined how many EVs can be integrated without problems. This shows that more research is needed. In addition, the current ways of deciding where to locate EV charging stations are not very efficient and make it harder for this technology to be adopted more quickly. That is why it is important to develop better planning models for locating charging stations so that both RDG and EVs can be safely integrated into the grid without exceeding its technical limits [7,9].
There are several previous articles on literature reviews related to the optimal location of charging stations in distribution networks. In [10,11,12,13], a review is conducted on the main optimization methods for determining the optimal location of charging stations, taking into account economic, technical, and environmental aspects, as well as the impacts of such location on distribution networks. However, although these studies mention some research that employs stochastic techniques to consider demand variability, no in-depth analysis of this aspect is carried out, representing a gap identified in the literature. Electric vehicles represent a variable load that depends on the time of day, the season of the year, among other factors, and accounting for this demand variation is of great importance, since the results of optimization algorithms could otherwise be inaccurate.
Taking these aspects into account, the scientific questions of this research are as follows: What are the main optimization methods employed for the location of EV charging stations in distribution networks? What research gaps remain open, and which aspects have not yet been adequately addressed? To answer these questions, the main objective of this article is to conduct a literature review of the principal optimization methods currently used to determine the optimal location of charging stations in distribution networks. In addition to providing an overview of the main optimization methods currently applied to determine the optimal location of charging stations, the main contribution of this work lies in emphasizing the importance of using stochastic methods to properly represent the variability of electric vehicle demand. This paper is organized as follows: First, the impact of charging stations on distribution networks and the technical aspects of the influence of electric vehicle demand on distribution networks are analyzed. Then, alternatives for addressing electric vehicle demand and the economic aspects of charging station location in distribution networks are examined. Subsequently, the different current optimization methods are analyzed, identifying the main limitations found in the literature. This section delves into stochastic methods to account for demand variability, which constitutes the main contribution of this work. Additionally, an analysis of the optimization of charging station location in distribution networks is presented, and the main methods employed are discussed.

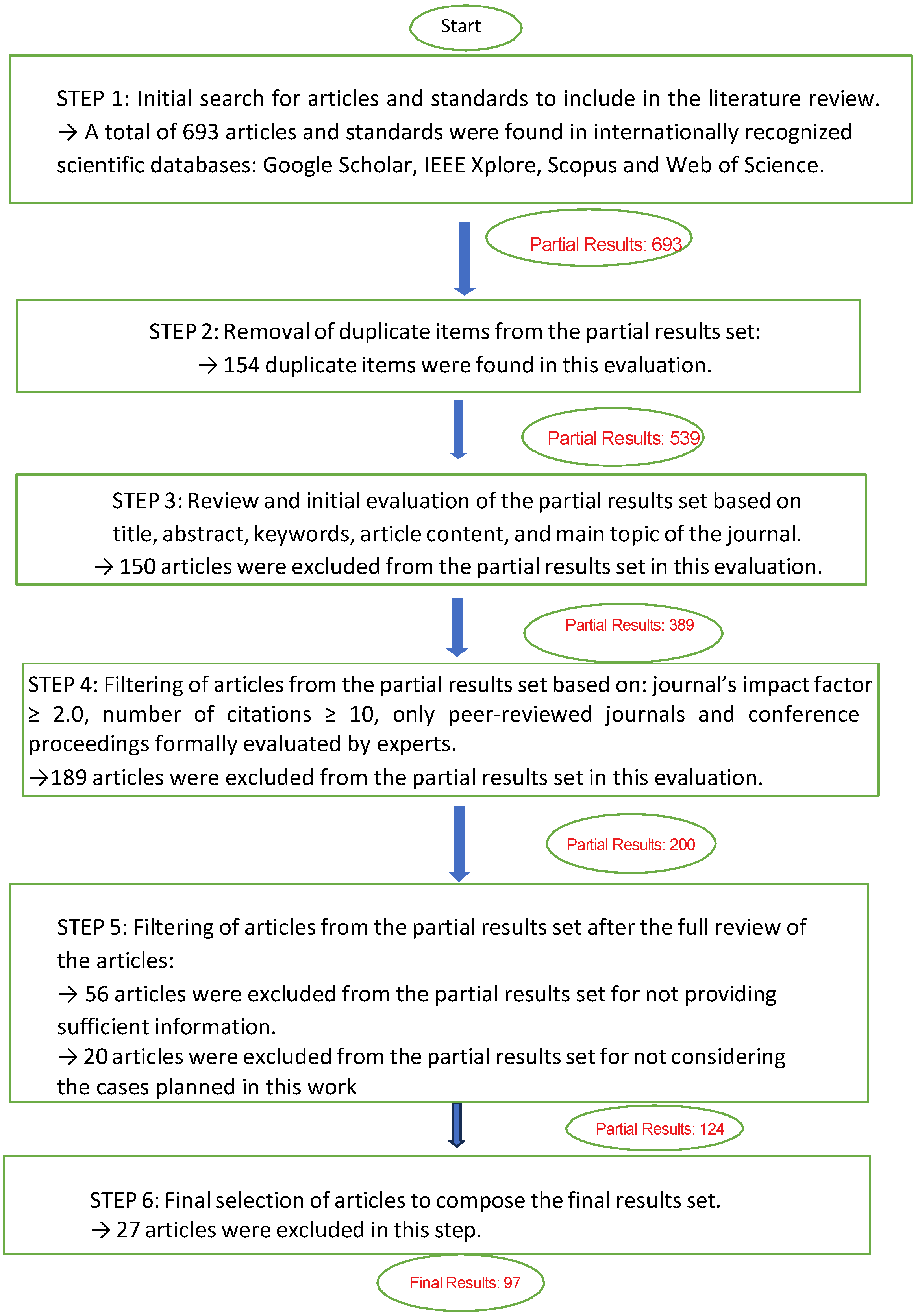
2. Methodology Used for Article Selection

The methodology followed in this review article consisted of a comprehensive search of scientific literature related to the integration of electric vehicles (EVs) in distribution networks and the optimization of charging station location. A search was conducted through the web interfaces of academic databases such as Google Scholar, IEEE Xplore, Scopus, and Web of Science, using keywords combined with Boolean operators (AND, OR), considering publications between the years 2018 and 2025. The selection of the publication year range from 2018 to 2025 was made with the aim of including only recent works that reflect the most current advances in optimization methods applied to the placement of electric vehicle charging stations. An example of the keywords used for the search is (“electric vehicle” OR “EV”) AND (“charging station” OR “charging infrastructure” OR “EVCS”) AND (optimization OR placement OR siting). The selected studies directly addressed the impact of charging stations on distribution networks, as well as the optimization methods employed for their location.
The inclusion criteria favored studies published in high-impact journals, with an impact factor greater than 2.0, at least 10 citations, and subjected to peer review, in order to ensure the inclusion of high-quality studies. Articles published in the last five years were also prioritized. Specifically, studies published between 2018 and 2025 were considered to include only recent works that reflect current advances in optimization methods. As exclusion criteria, articles not directly related to distribution systems, studies that did not present optimization models, and duplicate publications were discarded.
The articles found were recorded in an EXCEL spreadsheet, where titles, authors, year of publication, type of optimization employed, and inclusion/exclusion criteria were documented, facilitating a detailed analysis. In the initial search, 693 articles were identified. After reviewing the abstracts, 539 were selected for full reading. Finally, after applying the inclusion and exclusion criteria, a total of publications were obtained for a more detailed review. It was concluded that metaheuristic methods are the most widely used in the optimization of charging station location, and key areas for future research were identified, such as the interaction between charging stations and renewable distributed generation sources. A block diagram explaining the selection and analysis process of the main articles used in this study is presented below, showing the steps and criteria followed to identify the most relevant sources. This is shown in Figure 1.

3. Impact of Charging Stations on Distribution Networks

The high charging demand of electric vehicles on distribution networks can significantly affect the operation of these electrical systems. This high demand can cause overloads in transformers and power lines, as well as voltage drops. Additionally, charging stations, especially fast chargers, being nonlinear loads can generate harmonics, which may cause damage to equipment and distribution systems [14,15].
Using optimization methods to determine the optimal location of charging stations in the distribution network can improve electrical losses, the total installation cost and power quality measured by indicators such as THD, as well as system reliability [16,17,18].
International accords such as the Paris Agreement and the Conferences of the Parties (COP) 27–28, among others, have motivated several countries to adopt greener means of energy generation and transportation to reduce greenhouse gas (GHG) emissions and promote sustainability [3]. Various governments, companies, and private organizations are allocating resources to expand charging infrastructure, which means improving the convenience and accessibility of electric vehicle charging stations (EVCS) for users. They are implementing laws and regulations that will significantly promote the use of electric vehicles (EVs).
Furthermore, optimizing the location of charging stations can improve the utilization of existing infrastructure, reducing operational and maintenance costs while increasing the benefits of renewable energy integration [18,19,20].
To reduce the negative effects of placing charging stations in distribution networks without technical criteria, several authors use optimization methods to determine the optimal location of electric vehicle charging stations within the distribution network [17,18]. Another important solution is the design of microgrids that incorporate charging stations along with renewable energy sources [19,20,21]. Proper planning of charging station locations can reduce negative impacts on the distribution network and facilitate the increased use of electric vehicles in transportation.

3.1. Technical Aspects of the Influence of Electric Vehicle Demand on Distribution Networks

As mentioned earlier, the installation of charging stations in distribution networks can have negative effects, including overloading of transformers and power lines. Additionally, charging stations vary in charging speed (slow, semi-fast, and fast), with fast chargers imposing the greatest demands on the grid due to the demand spikes they generate in short periods [22,23].
As the number of electric vehicles increases, the energy demand at charging stations will rise, which can affect the proper functioning of electrical systems, especially during peak demand hours [24,25,26].
The ability of networks to handle this new demand also depends on the location and concentration of charging stations [27,28,29].
However, the demand from electric vehicles in distribution systems is not always negative. If properly managed, it could be used to return energy to the grid when needed. An example of this is technology like V2G (Vehicle-to-Grid). In this way, they can help balance generation and consumption [30,31,32,33,34].

Alternatives to Address Electric Vehicle Demand

Due to the high demand that charging stations can place on distribution networks, several solutions have been developed, among which the use of electrified roads (eRoads) and electric road systems (ERS) can be mentioned. This type of technology can provide a continuous energy supply to electric vehicles and is available for both trucks and smaller vehicles [1,2,35].
Additionally, this technology can reduce the need for large-capacity batteries, which has a favorable effect on the weight of electric vehicles, as well as on the pollution from battery components. On the other hand, the use of fast charging stations (FCS) also helps manage the demand caused by charging electric vehicles, especially during peak hours, although it is important to keep in mind that, since they involve non-linear loads, they can affect power quality. A combination of fast charging stations and electrified roads could help manage the demand caused by electric vehicles on distribution networks [2].
There are several international examples of projects aimed at increasing the use of electric vehicles. Among these are projects such as Electric Nation and Electric Avenue in the United Kingdom. These projects involved 700 electric vehicle owners, conducting measurements over 18 months to gather data on the charging of these electric vehicles at different locations within the electrical system [4].

3.2. Economic Aspects of Charging Station Location in Distribution Networks

The economic aspect plays an important role in the development of electric vehicles, as well as in the location of charging stations. Sometimes, the installation and maintenance costs are prioritized over technical aspects related to the operation of the grid. Many authors use the cost of infrastructure as one of the variables to optimize when determining the location of charging stations in the distribution network [36].
A focus of current research on the location of charging stations in distribution networks is the use of the total social cost model, as mentioned in [36,37]. This model takes into account not only the installation cost of charging stations but also the impact this has on the environment. On the other hand, works such as [37,38] propose objective functions that optimize the construction and operation costs of the stations, considering factors such as land price, construction expenses, and energy losses in the grid.
Other studies, such as [39], combine multiple objective functions; in this case, they optimize energy losses in the electrical grid and transportation costs for electric vehicle users. This model takes into account costs associated with waiting time at stations and travel distance, as well as the costs related to the construction and maintenance of the infrastructure.
Choosing a charging station location that considers costs not only for operators but also for users, based on detailed models of total costs, environmental impact, and user convenience, ensures that charging stations are placed in accessible locations and also meet the technical requirements of the distribution network [38].

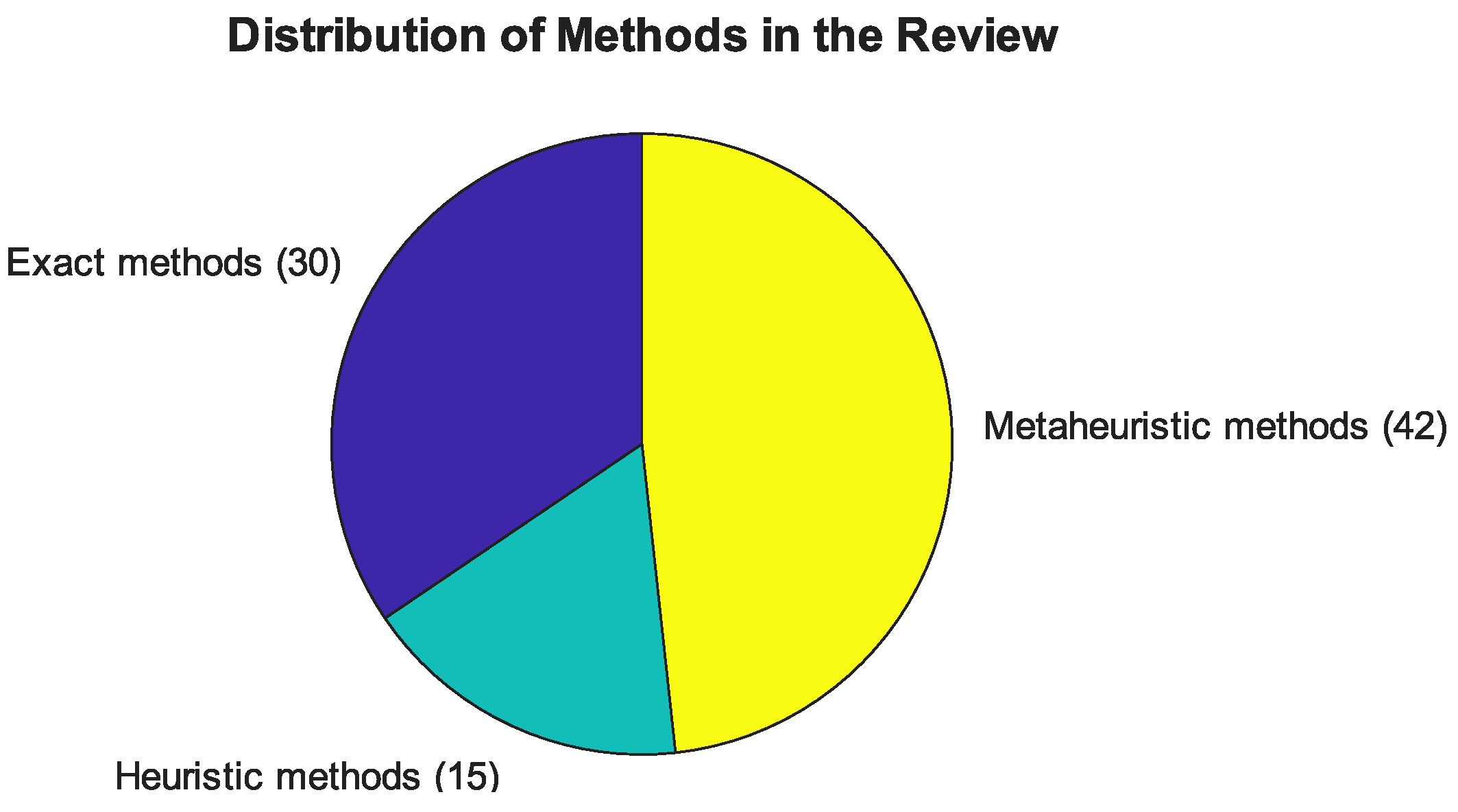
4. Optimization of the Location of Charging Stations in Distribution Networks

The site location analysis is essential to determine the optimal placement of charging stations. This analysis should include factors such as population density, proximity to frequently visited places like commercial areas, and the existing electrical grid infrastructure at that location. Multiple authors have demonstrated, through optimization methods, the optimal location of electric vehicle charging stations within the distribution network. The most commonly used optimization methods today are classified as exact, heuristic, and metaheuristic. Exact methods, including linear or integer programming, provide very precise solutions. Despite the high accuracy of exact optimization methods, they cannot be applied when the optimization problem involves multiple variables, as the methods become complicated and, therefore, impractical.
On the other hand, heuristic techniques provide solutions that are not as precise as those obtained with exact methods, but within a reasonable amount of time. One example of these is the genetic algorithm (GA) [39], which mimics natural evolutionary processes and is capable of exploring large solution spaces through selection, crossover, and mutation operations, adapting to the charging station location problems. Finally, metaheuristic techniques offer a more flexible and powerful approach to complex problems. Among them is Particle Swarm Optimization (PSO) [40,41,42], which simulates the collective behavior of moving particles to find optimal solutions; the Horse Herd Optimization (HHO) [43], a metaheuristic technique that mimics the social behavior of a herd of horses to explore solution spaces and is applied to complex optimization problems. It is based on the behavior of horses in their search for food, providing effective solutions for problems with large search spaces.
Among other metaheuristic techniques, the following can be mentioned: the Gray Wolf Optimization (GWO) [44] method, which mimics the hunting behavior and leadership hierarchy of gray wolves to explore and exploit the solution space in search of optimal solutions, inspired by the hunting behavior of wolves in packs. The Symbiotic Organisms Search (SOS) algorithm [45] mimics symbiotic interactions in nature. Likewise, the Butterfly Optimization Algorithm (BOA) [46] simulates the migration behavior of butterflies, while the Improved Bald Eagle Search Algorithm (IBESA) [37] is based on the hunting strategy of these birds. Finally, graph theory [47] is also a metaheuristic optimization technique used in distribution network problems. These techniques offer various tools to optimize the placement of charging stations, taking into account different aspects of the electrical distribution system.
Figure 2 shows a diagram that summarizes the general classification of optimization techniques and includes some corresponding examples.
To find the optimal location of electric vehicle charging stations in the distribution network, considering various variables to optimize, such as the installation costs and energy losses, among others, metaheuristic methods like Particle Swarm Optimization (PSO), Genetic Algorithms (GA), or the Gray Wolf Optimization (GWO) method are often highly effective. These methods provide a good solution to complex problems with multiple objectives.

4.1. Exact Optimization Methods

Exact methods guarantee finding the optimal solution, although they generally require high computational resources, especially in complex problems, which limits their application to simple networks. Among these techniques are mixed-integer linear programming (MILP) [48,49,50,51,52,53], quadratic programming (QP) [54,55,56], and linear programming [57,58]. Additionally, integer linear programming [59,60,61,62] and mixed nonlinear programming [63] are also considered exact methods. In these articles, a single objective function is used, although sometimes this single function combines more than one variable to optimize, as is the case of costs in [48,49,53], energy losses [48,53] or the design of efficient charging schedules [48,53]. The use of multiple objective functions is less frequent in the articles that employ this method due to the high computational complexity it generates. In [59,60,61,62,63], a single objective function is also used to optimize multiple variables.
The study in [48] uses mixed-integer linear programming to determine the optimal location and size of fast charging stations, along with the battery capacity in electric buses. In this case, a single objective function is optimized that combines costs and energy efficiency, applied to a small network. In [49], a mathematical model is presented to predict the number of required charging stations and to optimize their location, incorporating Vehicle-to-Grid (V2G) strategies in distribution networks. The authors, in a single objective function, combine minimizing costs and increasing demand coverage, using a moderately complex system. Article [52] employs mixed-integer linear programming to integrate autonomous electric vehicles and distributed energy resources into power systems. The authors also use a single objective function. Similarly, ref. [53] uses the same technique to reduce energy losses by employing a single objective function to minimize both energy losses and installation costs.
The studies presented in [54,55,56] focus on quadratic programming to design efficient charging schedules, including real-time strategies. In these cases, the single objective function combines the variables of charging efficiency and demand peaks in a moderately complex network. In contrast, refs. [57,58] apply linear programming methods to optimize charging stations that integrate renewable energy and wireless technologies, although they also use a single objective function. Other studies, such as [59,60,61,62] develop mixed-integer linear programming models to address the optimal location of stations in transportation networks, considering traffic congestion. Finally, ref. [63] uses mixed-integer nonlinear programming to optimize the location and assignment of lines in charging stations for electric buses.

4.2. Heuristic Optimization Methods

Heuristic methods are designed to find acceptable solutions in a reasonable time, although they do not guarantee the most optimal solution. These techniques are useful in networks of medium to high complexity, where exact methods would be complex to implement. These techniques include the forward sweep algorithm [64], graph theory [47], queuing theory [65,66], the geospatial approach [67], among others.
The authors of [64] use a forward and backward sweep algorithm (BFS) to analyze the behavior of power flow in a distribution network, identifying optimal locations for charging stations. However, the solution depends on the topology and size of the network and does not guarantee achieving the optimal result, especially in complex networks.
In [47], an approach based on graph theory and genetic algorithms is proposed to optimize the location of charging stations, emphasizing the improvement of accessibility and the minimization of operational costs. The quality of the solution largely depends on algorithm parameters (population, iterations, mutation rates), which may require several adjustments.
Queueing theory, applied in [65,66], allows modeling and analyzing demand at charging stations to optimize their location and reduce waiting times, addressing both integration with distributed generation and planning in urban areas. However, these articles do not take demand uncertainty into account, which could affect the accuracy of the results. Article [65] uses this technique to determine the optimal location of stations in a distributed network with renewable generation; in contrast, ref. [66] analyzes a planning model in Al Ain, the United Arab Emirates, highlighting the need to balance capacity and demand.
In [67], a geospatial approach supported by open data is presented to deploy charging stations in rural areas of Scotland to improve coverage and promote electric mobility in remote regions.

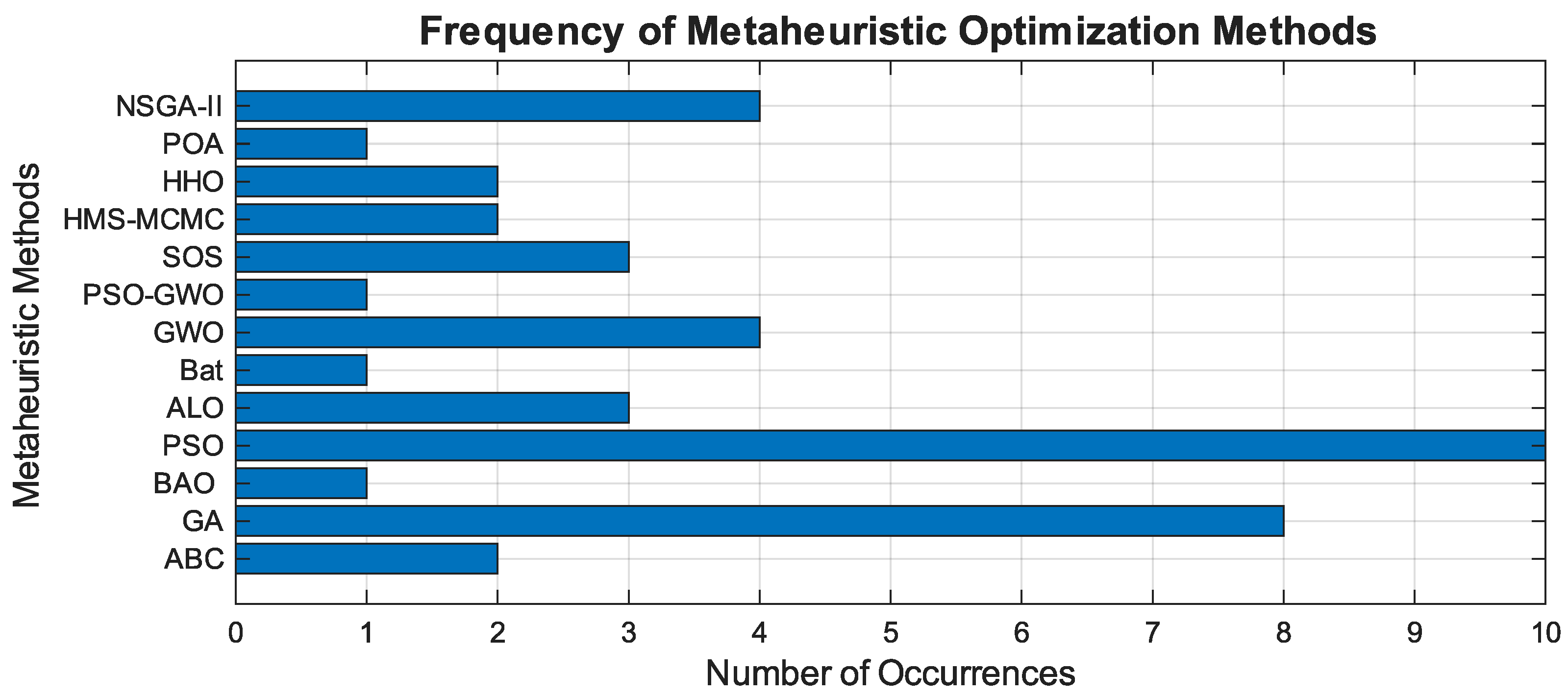
4.3. Metaheuristic Optimization Methods

Metaheuristic methods are advanced techniques inspired by natural, biological, or social phenomena, applied to complex optimization problems. Among the most notable are the Artificial Bee Colony Algorithm (ABC) [68], the Genetic Algorithm (GA) [39,69,70,71], the Butterfly Optimization Algorithm [72] and the Particle Swarm Optimization Algorithm (PSO) [40,41,73,74,75,76]. Other metaheuristic optimization methods include the Antlion Optimization (ALO) Algorithm [42], the Bat-Inspired Optimization Technique [77], Gray Wolf Optimization (GWO) [37,78,79], as well as its hybrid version PSO-GWO [44]. Methods such as the Symbiotic Organism Search (SOS) Algorithm [80,81], the Hybrid Metropolis and Sequential Monte Carlo Sampling (HMS-MCMC) Method [39], and the Horse Herd Model [43] are also included. These methods are especially useful in high-complexity networks where exact and heuristic methods may be insufficient.
In [68], the authors propose a method to determine the optimal location of fast charging stations for electric vehicles in a smart distribution network. Using the ABC algorithm, the charging station is simulated according to the IEEE 33-bus standards. The results show that the proposed method allows finding the optimal location of charging stations and can reduce the cost of implementing additional locations, ensuring adequate supply from the power system.
In [69], the authors use the Genetic Algorithm to determine the optimal location of electric vehicle charging stations in a power network. In [39], a cost-based model and a genetic algorithm are proposed to optimize the location of the stations, including variables to optimize such as installation and operational costs. The authors of [70] propose a combined approach using genetic algorithms and a fuzzy analytic hierarchy process to optimize the location and capacity of charging stations in Seoul, considering indicators such as parking index, public transport connectivity, and land use to improve station distribution, reorganizing fast and slow chargers. An important contribution of this article is the use of a real distribution system for simulations, although real measurements of electrical demand were not considered.
In [72], the Butterfly Optimization Algorithm is used to determine the optimal location of charging stations in a distribution network, as well as the appropriate capacity for each station, to minimize infrastructure and operational costs while ensuring efficient coverage for electric vehicle users. A limitation of this article is that the capacity of each charging station is assumed to be fixed, which may not reflect variations in demand.
Articles [41,74] aim to optimize the location of charging stations using PSO; however, ref. [41] introduces an improvement to the algorithm, while [74] applies it directly. In [40], PSO is used to plan the location of stations considering the total cost for stations and users, seeking to balance infrastructure and demand. In [73], PSO is applied in a more complex scenario, optimizing the location of stations along with the integration of distributed generation into the network. In [42], the Antlion algorithm is improved to optimize station location, focusing on efficiency and cost minimization. These articles do not consider demand variations, which may fluctuate even across different seasons of the year, potentially affecting the accuracy of the results.
The authors of [77] propose a technique based on the Bat Algorithm to determine the optimal location of charging stations and distributed generation (DG) in a balanced distribution system, with the main objective of minimizing energy losses. However, they do not consider demand variability in the analysis.
In [37], GWO is used to determine the optimal locations of fast charging stations in the power distribution network, considering energy losses as an optimization variable. In [78], the optimal location of fast charging stations for electric vehicles in power and transportation networks is addressed, incorporating Vehicle-to-Grid (V2G) strategies to maximize the integration of distributed resources and improve system stability. Meanwhile, article [79] proposes a multi-objective planning approach to locate fast charging stations and distributed generators in a distribution system, considering the minimization of losses, improvement of the voltage profile, and other relevant technical factors. These articles do not use real power networks and do not fully consider demand variability.
Article [44] presents a hybrid PSO-GWO version to solve optimization problems in energy systems, combining the advantages of both algorithms to improve the location of renewable energy sources in distribution networks. However, the simulations are conducted on a test system and do not use data from a real system, which limits the practical applicability of the results.
Articles [80,81] address the optimal location of charging stations using SOS. Work [80] integrates an approach based on reliability indices to ensure network stability and efficiency. In [80], V2G is incorporated to enable bidirectional interaction between electric vehicles and the grid, optimizing costs and operational stability. Meanwhile, ref. [81] focuses on minimizing network losses and improving overall efficiency through the optimal integration of charging stations. These studies highlight the capability of the SOS algorithm to tackle optimization problems in power networks with high electric vehicle penetration.
In [39], HMS-MCMC is proposed to determine the optimal location of charging stations. Article [43] uses the Horse Herd Model in a Maximum Power Point Tracking (MPPT) system for solar-powered electric vehicle charging stations, optimizing energy harvesting and efficiency under dynamic solar conditions.
Current research also considers the placement of charging stations in distribution systems together with distributed generation. The authors of [71] use the Political Optimization Algorithm (POA) to optimize the location and size of renewable distributed generators (solar, wind, and fuel cell) and electric vehicle charging stations in a distribution network. The variables to optimize are power losses and voltage profile improvement. Similarly, the authors of [82] propose an artificial intelligence (AI)-based technique for the optimal placement of Electric Vehicle Charging Stations (EVCS) and Distributed Generation (DG) in distribution networks, considering the reliability of the power system. The authors of [83] simultaneously optimize the location of EVCS, DG, and capacitors to minimize energy losses and improve voltage profile, stability, and cost, also considering the Vehicle-to-Grid function. The results are validated in IEEE 33- and 69-bus test systems. The article [84] proposes a joint planning model for distributed generation and electric vehicle charging stations using two-level programming and an intelligent algorithm, aiming to reduce losses and improve voltage, validated in IEEE systems and a real network.
Many of the articles mentioned above have limitations related to the mathematical complexity involved in working with multiple objective functions. However, there are metaheuristic optimization methods such as NSGA-II (Non-dominated Sorting Genetic Algorithm II) [85,86,87,88], which was designed to generate a set of non-dominated solutions when working with multiple objective functions simultaneously, without the need to combine them into a single function, which is advantageous when dealing with objective functions of different time scales.

4.4. Main Trends in the Use of Optimization Algorithms

Based on the reviewed literature, optimization algorithms applied to the optimal placement of electric vehicles show an evolution in their application. In 2018 and 2019, the trend was to use exact optimization methods, which are highly accurate but have the drawback of complexity when multiple variables are involved. In 2021, an increase in the use of heuristic and metaheuristic methods can be observed, although some exact methods were still applied. Subsequently, in 2022 and 2023, the predominance of metaheuristic algorithms became consolidated, with specific applications of exact techniques for particular problems. Finally, starting in 2024, a consolidated trend toward the use of metaheuristic techniques and hybrid combinations is reflected, highlighting the need for flexible methods capable of handling multiple objectives. In Table 1, the evolution in the use of optimization methods to determine the location of charging stations is shown.

4.5. Practical Applications of Optimization Methods for Charging Stations

Most current articles addressing the optimal placement of charging stations do not conduct their studies using a real distribution network, but rather employ a test network. Additionally, they do not utilize actual measurements of electric vehicle demand behavior in a real-world system. This represents a gap identified in the literature, as it is necessary to validate optimization algorithm results in real applications to ensure their practical implementation. Although some articles, such as [52,53,65,66,67,70], carry out simulations using topologies of a real distribution system, real demand measurement data is not used. In [89], the authors use the IEEE 69-bus test system to validate their algorithm, and real electric vehicle demand measurements are incorporated. In [90], although optimization algorithms are not applied to determine the optimal location, the behavior of electric vehicles is simulated in the distribution system of the Trentino-Alto Adige region in Italy. For the analysis, 411,800 individual charging sessions recorded by actual users at different charging points in the region are used, allowing for a more realistic prediction of future demand behavior. A similar analysis is carried out in [91], where the authors use a real urban area in the Czech Republic, with a park-and-ride facility connected to a local substation, to determine the optimal location of charging stations within the urban area, employing an exact optimization method with total costs as the objective function to be minimized. This demonstrates that current research remains largely at the simulation level, and future work using real operational data is required to confirm the effectiveness of the proposed methods. Therefore, this is identified as a priority line of future research.
Another limitation identified in the literature is the use of load profiles from a characteristic day for optimization, without considering load variation across different seasons of the year or the progressive growth in electric vehicle usage. The authors in [1,3,6,7,77,92] address the planning of charging station placement using demand profiles from a typical day. In [66], the authors take into account the future increase in electric vehicle use, but only over a short time horizon. In [49], it is noted that most optimization models do not integrate the uncertainty of load variation in the short and long term. The authors of [2] also highlight the importance of incorporating broader time scenarios to determine the placement of distributed generation resources (DGR) together with charging stations. In [66], the need to consider the growth in the number of electric vehicles to obtain more accurate solutions is also mentioned. Furthermore, studies such as [7,49] show how the lack of consideration of these load variations over time can negatively impact network reliability.
Nevertheless, some authors employ stochastic methods to estimate demand behavior over time. In [66], the Monte Carlo method is used to evaluate different demand scenarios in the planning of charging station locations, considering the growth in the number of electric vehicles. In [49], several stochastic techniques are analyzed to address demand variation in the future. Recent research takes into account the variability of electric vehicle demand, not only over time but also across locations. Ref. [93] uses stochastic programming and Benders decomposition to model multiple demand scenarios; Ref. [94] applies Monte Carlo methods to replicate travel patterns and estimate EV demand; Ref. [80] analyzes time series to capture the actual variability of demand throughout the day; and Ref. [95] considers the spatiotemporal distribution and different charging power levels to simulate demand under dynamic conditions. Although some current studies use stochastic methods to forecast demand, these analyses generally predict demand either in the short or long term independently. Therefore, as a future research direction, stochastic models should be developed to simultaneously integrate both short- and long-term uncertainties, enabling the generation of more realistic charging station placement solutions that account for demand variation over time.

4.6. Main Findings and Gaps Identified in the Literature

From the review of the literature on the location of electric vehicle charging stations, several important findings can be highlighted. Exact algorithms provide highly precise solutions, although they are limited to simple networks due to their high computational complexity. Heuristic methods allow for fast and acceptable solutions, while metaheuristic methods are recommended for complex problems with multiple objective functions. There is also a growing interest in integrating additional factors, such as distributed generation and Vehicle-to-Grid strategies, to improve the operation of distribution systems. Despite the increasing number of studies on the planning and optimization of charging stations, there are still limitations that affect the reliability and practical applicability of the results. Considering the classification of these methods into exact, heuristic, and metaheuristic approaches, specific limitations can be identified in each category, as well as other limitations that are generally present regardless of the type of optimization technique.

4.6.1. Gaps Detected in the Application of the Methods Under Study

1.
Limited validation in real networks
Most studies use test networks and professional software simulations, without validating results with data from real systems or actual electricity demand measurements [1,7,9,26,90]. This limits the practical applicability of the methods, as the results may not accurately reflect real operating conditions.
2.
Limited use of multi-objective optimization
Although heuristic and metaheuristic methods can handle multiple objectives, many studies employ a single objective function, combining criteria such as costs, losses, coverage, or efficiency, which reduces the ability to optimize variables with different temporal scales [11,13,85,86,87]. This limitation shows that the studies could overlook how decisions regarding one objective affect the others.
3.
Lack of consideration of demand uncertainty
Many studies do not account for demand variations across seasons or the progressive growth of electric vehicles [5,6,12,92]. This shows that the planning of charging stations may not be robust against future changes in demand, limiting the reliability of the systems.
4.
Lack of joint integration of DG and charging stations
Many studies do not jointly analyze the location and operation of charging stations alongside the presence of distributed generation in the network, which limits the applicability of the results to modern systems where DG affects losses, reliability, and power quality [48,49,52,71,82,83,84]. This emphasizes that the lack of DG-EV integration in the models reduces the ability of studies to guide decisions in real networks.
5.
Limited inclusion of V2G in charging station planning
Few studies include V2G as a variable in the problem formulation, as this increases complexity by considering bidirectional energy flows, impacts on reliability, battery degradation, and coordination with network demand [49,52,83,89]. This indicates that current assessments may underestimate the potential and risks of bidirectional charging strategies, affecting long-term planning.

4.6.2. Gaps Specific to Exact Methods

6.
High computational complexity
Exact methods require high computational resources, especially for problems with multiple variables or complex networks, which limits their use to small or simplified networks [53,61,62]. This implies that the applicability of exact methods is limited to controlled cases and not to more complex real-world scenarios.

4.6.3. Gaps Specific to Heuristic Methods

7.
Dependence on algorithm parameters
The quality of solutions depends on parameters such as population size, iterations, or mutation rates, which may require multiple adjustments and trials [37,47,74,80]. This dependency reduces reproducibility and may affect the consistency of the results.
8.
No guarantee of optimality
Heuristic methods aim to find acceptable solutions within a reasonable time, but they do not guarantee finding the optimal solution [37,39,42,72]. This reflects a trade-off between computation time and solution quality, which may limit the reliability of the optimization.

4.6.4. Gaps Specific to Metaheuristic Methods

9.
Assumed fixed station capacity
Some studies assume that the charging station capacity is constant, ignoring actual demand variations [44,70,72]. This may lead to the incorrect sizing of charging station capacity, reducing system efficiency and affecting the long-term planning of their location.
10.
Limited use of real data for simulations
Many studies conduct simulations on test networks or simplified models, without incorporating real electricity consumption measurements, which limits the practical validity of the results [8,28,80,90]. This highlights the need to validate the models with real-world data to improve reliability and practical applicability.

5. Discussion

To better grasp the current trends in research on optimization techniques applied to the location of electric vehicle charging stations, statistical graphs showing the number of publications per optimization method used are analyzed. Figure 3 presents a graph of the number of publications by optimization method, based on a sample of articles on the subject.
From the figure analysis, it can be observed that metaheuristic methods are the most commonly used for this type of application, as 42 articles correspond to some kind of metaheuristic technique. This is because these techniques are particularly suitable for problems involving more than one objective function to optimize. Placing electric vehicle charging stations in a real system, using real data, would be a complex problem for using exact methods.
Although exact methods, such as Mixed Integer Linear Programming (MILP), guarantee more precise solutions, Figure 3 shows a lower number of publications using these types of techniques compared to metaheuristic methods. This may be because exact methods demand a high computational load, making them impractical for optimization problems with multiple variables.
On the other hand, from the analysis of Figure 3, it is observed that heuristic methods have the lowest number of publications. This may be related to the fact that, although these techniques are simple and relatively fast, the solutions obtained by applying any technique from this group do not guarantee the best possible solution. For this reason, they can be less reliable in complex networks, and their application to multi-objective problems is limited.
Additionally, from Figure 3, possible research lines can be identified, such as the combination of exact methods with metaheuristic methods, taking advantage of the strengths of each technique. This highlights the fact that hybrid methods could be a promising alternative to balance solution quality and computational efficiency.
The choice of the optimization method is closely linked to the complexity of the problem to be optimized. In the reviewed articles, exact methods are mainly applied when the number of objective functions to be minimized is small. In contrast, metaheuristic techniques are used in scenarios with multiple variables, where exact methods become computationally complex. This suggests that the selection of the method directly depends on the degree of complexity of the optimization problem. Table 2 shows a summary of the selection of the optimization method considering the characteristics of the problem to be optimized and its application.

5.1. Analysis of Publications Using Metaheuristic Methods

Metaheuristic optimization methods include techniques such as the Genetic Algorithm, which is based on imitating natural selection. Another metaheuristic technique is the Particle Swarm Optimization algorithm, which mimics the social behavior of animals, such as birds or fish. The Bee Colony Algorithm follows the behavior of bees in nectar collection, using exploration and exploitation to generate solutions. The Bat Search Algorithm is inspired by the echolocation of bats, adjusting solutions through a balance between exploration and exploitation, among others. Figure 4 shows the number of publications corresponding to different metaheuristic methods.
The analysis of Figure 4 shows that the most widely used optimization methods in current articles on the topic are particle swarm optimization, genetic algorithms, the symbiotic organism search algorithm, and Gray Wolf Optimization. These techniques are especially valued in scenarios with multiple variables to optimize. This emphasizes that metaheuristic methods are preferred due to their flexibility and ability to manage competing objectives in complex network scenarios.

Main Variables to Optimize in Metaheuristic Techniques

Table 3 summarizes the main optimized variables in the sample of publications using metaheuristic optimization methods. It is important to highlight that, although some articles mention energy losses and voltage deviation within the objective functions, these magnitudes actually depend on the set of decisions adopted in the algorithm, such as the location, size, or number of charging stations. Therefore, in this work, they are included as variables to be optimized to maintain consistency with the way they are reported in the reviewed studies.
The main variables optimized in papers related to the location of charging stations in distribution networks are energy losses, voltage profile, and cost. Energy losses include factors such as efficiency, supply quality, load balance, and system reliability, which directly impact technical performance and the optimal use of energy resources. On the other hand, cost takes into account investment, operation, and maintenance costs. Most optimization efforts focus on minimizing energy losses and associated costs, as these are the most critical objectives in the management of electrical systems.
In most of the reviewed articles on the optimization of electric vehicle charging stations, it is generally observed that power quality and reliability are not directly considered, particularly through indicators such as THD, SAIFI, and SAIDI. These indicators are essential to assess the quality of the power supply and the impact of charging stations on users. However, in many cases, optimization models mainly focus on charging capacity, cost reduction, and station location, without integrating the analysis of how these decisions may affect the stability and resilience of the electrical system. This omission could be due to the implicit assumption that distribution networks already operate with adequate service quality levels and that some variables directly affect quality supply. However, including these indicators in optimization models would be highly useful, considering that charging stations, especially fast charging stations, are non-linear loads that generate harmonics and can affect power quality, particularly in distribution systems with distributed generation and multiple charging stations, as summarized in Table 4.

5.2. Advantages and Disadvantages of Optimization Techniques

In previous sections, the general classification of optimization methods into exact, heuristic, and metaheuristic methods was mentioned. When comparing these methods in terms of advantages and disadvantages, it can be said that exact optimization methods have the advantage of obtaining the most accurate solution, but they become very complex, especially when dealing with problems involving multiple variables to optimize. Moreover, their complexity increases with the number of nodes in the distribution system, charging stations, and variables to be optimized, making them poorly applicable to large systems or those with multiple objectives. They require very precise modeling of all system parameters; variations in electric vehicle demand or renewable generation can invalidate the optimal solution. On the other hand, heuristic methods are designed to find acceptable solutions within reasonable times; they have the advantage of being faster but do not guarantee an optimal solution. Heuristic methods are easier to implement and faster, but their results are not precise and become less reliable if demand changes or the network grows.
Finally, metaheuristic methods have the advantage of being very effective in problems where multiple variables are optimized. However, like heuristic methods, they have the disadvantage of not being able to find the most accurate solution. Additionally, although they handle multiple objectives, they do not guarantee the most optimal solution, and most studies are applied to test networks, limiting practical applicability. Many works also do not jointly consider reliability aspects (SAIFI) and power quality (THD), which constitutes a limitation for real-world applications. Algorithms such as genetic algorithms, particle swarm optimization, and Gray Wolf Optimization have become widely used tools in advanced optimization, demonstrating their effectiveness in a variety of applications. The incorporation of stochastic techniques allows modeling and predicting demand variability, improving the ability of heuristic and metaheuristic methods to generate more robust solutions in the face of demand uncertainties.
Based on the consulted literature, metaheuristic methods such as particle swarm optimization, genetic algorithm, symbiotic organism search, and Gray Wolf Optimization are widely used to optimize the location of charging stations in distribution networks. The main variables to optimize are commonly grouped into two categories: costs and energy losses.

6. Conclusions

After reviewing the main current articles on the location of charging stations in electrical distribution systems, it can be concluded that the most commonly used optimization methods for this application are metaheuristic methods, primarily genetic algorithms and PSO (Particle Swarm Optimization). Regarding the variables to be optimized, in most of the reviewed articles, the variables most frequently considered are cost and energy losses. Using optimization methods to select the location of charging stations in distribution systems allows compliance with technical standards and contributes to greater adoption of electric vehicles as a means of transportation. Moreover, several limitations were identified in current research on the optimization of electric vehicle charging station locations in distribution networks. Exact methods, although precise, exhibit high computational complexity when dealing with multiple variables; heuristic methods provide quick solutions but are not the most accurate; and metaheuristic methods are effective but become complex when multiple variables are involved as objective functions. Furthermore, most studies do not adequately consider demand variability over time and across different seasons, rely on test networks for simulations rather than real distribution systems, and are limited to simulated studies without practical validation of the obtained results. These limitations open opportunities for future research in this area.

Author Contributions

Conceptualization: D.L.L. and Y.G.L.; methodology: L.T.L.V. and D.L.L.; formal analysis: D.L.L., L.T.L.V. and O.C.Z.; investigation: D.L.L., Y.G.L. and L.T.L.V.; validation: O.C.Z. and D.L.L.; resources: L.T.L.V., Y.G.L. and L.G.S.; data curation: D.L.L. and F.A.M.J.; writing—original draft preparation: F.A.M.J., L.G.S. and D.L.L.; visualization: D.L.L.; supervision: D.L.L. All authors have read and agreed to the published version of the manuscript.

Funding

This work was financially supported by the Universidad del Bío-Bío through the Direction of Research (DICREA) and the Department of Electrical and Electronic Engineering.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Acknowledgments

The authors wish to thank the Universidad del Bío-Bío and its Department of Electrical and Electronic Engineering, as well as the Universidad de Concepción, for their institutional support and access to academic resources that facilitated the completion of this work.

Conflicts of Interest

The authors declare no conflicts of interest.

Nomenclature

AcronymMeaning
SAIFISystem Average Interruption Frequency Index
THDTotal Harmonic Distortion
DRGDistributed Generation Resources
EVElectric Vehicle
EVCSElectric Vehicle Charging Station
COPConferences of the Parties
GHGGreenhouse Gas
V2GVehicle to Grid
ERSEnergy Recovery System
FCSFast Charging Station
GAGenetic Algorithm
PSOParticle Swarm Optimization
HHOHorse Herd Optimization
GWOGray Wolf Optimization
SOSSymbiotic Organisms Search
BAOButterfly Optimization Algorithm
IBESAImproved Bald Eagle Search Algorithm
QPQuadratic Programming
BFSBackward/Forward Sweep
ABCArtificial Bee Colony Algorithm
ALOAnt Lion Optimizer
HMS-MCMCHybrid Metaheuristic Strategy–Markov Chain Monte Carlo
DGDistributed Generation
MPPTMaximum Power Point Tracking
BATBat Algorithm (Bat-Inspired Optimization)
POAPolitical Optimization Algorithm
NSGA-IINon-Dominated Sorting Genetic Algorithm

References

  1. Kabir, M.E.; Assi, C.; Tushar, M.H.K.; Yan, J. Optimal Scheduling of EV Charging at a Solar Power-Based Charging Station. IEEE Syst. J. 2020, 14, 4221–4231. [Google Scholar] [CrossRef]
  2. Aljumah, A.; Darwish, A.; Csala, D.; Twigg, P. A Review on the Allocation of Sustainable Distributed Generators with Electric Vehicle Charging Stations. Sustainability 2024, 16, 6353. [Google Scholar] [CrossRef]
  3. Kar, R.R.; Ganpatrao Wandhare, R. Energy Management System for Electric Vehicle Charging Stations with Photovoltaic Integration in Weak Grids. In Proceedings of the 2023 IEEE 20th India Council International Conference, INDICON 2023, Telangana, India, 17 December 2023; pp. 398–402. [Google Scholar] [CrossRef]
  4. Dumiak, M. A Road Test for Vehicle-to-Grid Tech. IEEE Spectr. 2022, 59, 21–25. [Google Scholar] [CrossRef]
  5. Khan, R.; Mehmood, K.K.; Bukhari, S.B.A.; Imran, K.; Wadood, A.; Rhee, S.B.; Park, S. An Optimization-Based Reliability Enhancement Scheme for Active Distribution Systems Utilizing Electric Vehicles. IEEE Access 2021, 9, 157247–157258. [Google Scholar] [CrossRef]
  6. Al-Muhaini, M. Electric Vehicle Markov-Based Adequacy Modeling for Electric Microgrids. IEEE Access 2020, 8, 132721–132735. [Google Scholar] [CrossRef]
  7. Pagany, R.; Ramirez Camargo, L.; Dorner, W. A review of spatial localization methodologies for the electric vehicle charging infrastructure. Int. J. Sustain. Transp. 2019, 13, 433–449. [Google Scholar] [CrossRef]
  8. Thanikanti, S.B.; Yuvaraj, T.; Hemalatha, R.; Aljafari, B.; Nwulu, N.I. Optimizing Radial Distribution System with Distributed Generation and EV Charging: A Spotted Hyena Approach. IEEE Access 2024, 12, 113422–113441. [Google Scholar] [CrossRef]
  9. Shahriar, S.; Al-Ali, A.R.; Osman, A.H.; Dhou, S.; Nijim, M. Prediction of EV charging behavior using machine learning. IEEE Access 2021, 9, 111576–111586. [Google Scholar] [CrossRef]
  10. Ahmad, F.; Marzband, M.; Iqbal, A.; Ashraf, I.; Khan, I. Placement of Electric Vehicle Fast Charging Stations using Grey Wolf Optimization in Electrical Distribution Network. In Proceedings of the PESGRE 2022—IEEE International Conference on “Power Electronics, Smart Grid, and Renewable Energy”, Trivandrum, India, 2 January 2022; pp. 1–6. [Google Scholar] [CrossRef]
  11. Ray, S.; Kasturi, K.; Patnaik, S.; Nayak, M.R. Review of electric vehicles integration impacts in distribution networks: Placement, charging/discharging strategies, objectives and optimisation models. J. Energy Storage 2023, 72, 108672. [Google Scholar] [CrossRef]
  12. Lin, W.; Wei, H.; Yang, L.; Zhao, X. Technical review of electric vehicle charging distribution models with considering driver behaviors impacts. J. Traffic Transp. Eng. 2024, 11, 643–666. [Google Scholar] [CrossRef]
  13. Kumar, M.; Kumar, A.; Soomro, A.M.; Baloch, M.; Chaudhary, S.T.; Shaikh, M.A. A Comprehensive Review of Optimizing Multi-Energy Multi-Objective Distribution Systems with Electric Vehicle Charging Stations. World Electr. Veh. J. 2024, 15, 523. [Google Scholar] [CrossRef]
  14. Deb, S.; Tammi, K.; Kalita, K.; Mahanta, P. Impact of electric vehicle charging station load on distribution network. Energies 2018, 11, 178. [Google Scholar] [CrossRef]
  15. Kunj, T.; Pal, K. Optimal location planning of EV charging station in existing distribution network with stability condition. In Proceedings of the 2020 7th International Conference on Signal Processing and Integrated Networks, SPIN 2020, Noida, India, 27 February 2020; pp. 1060–1065. [Google Scholar] [CrossRef]
  16. Sonmez, Y.; Kizilkale, C.; Kurzhanskiy, A.; Arcak, M. Optimal Electric Vehicle Charging Station Placement as a Congestion Game Problem. In Proceedings of the 2024 European Control Conference, ECC 2024, Stockholm, Sweden, 25 June 2024; pp. 693–698. [Google Scholar] [CrossRef]
  17. Zhang, K.; Gao, B.; Han, Y.; Dong, Z. Optimization Scheduling of Electric Vehicle Charging Load Based on Improved PSO. In Proceedings of the 2022 IEEE 2nd International Conference on Mobile Networks and Wireless Communications, ICMNWC 2022, Tumkur, Karnataka, India, 2 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
  18. Albana, A.S.; Muzakki, A.R.; Fauzi, M.D. The Optimal Location of EV Charging Stations at Surabaya Using the Location Set Covering Problem. In Proceedings of the ICT-PEP 2022—International Conference on Technology and Policy in Energy and Electric Power: Advanced Technology for Transitioning to Sustainable Energy and Modern Power Systems, Proceedings, Jakarta, Indonesia, 18 October 2022; pp. 95–99. [Google Scholar] [CrossRef]
  19. Sayed, K.; Abo-Khalil, A.G.; Alghamdi, A.S. Optimum resilient operation and control DC microgrid based electric vehicles charging station powered by renewable energy sources. Energies 2019, 12, 4240. [Google Scholar] [CrossRef]
  20. Mohammed, A.; Saif, O.; Abo-Adma, M.; Fahmy, A.; Elazab, R. Strategies and sustainability in fast charging station deployment for electric vehicles. Sci. Rep. 2024, 14, 283. [Google Scholar] [CrossRef] [PubMed]
  21. Güven, A.F.; Yücel, E. Sustainable energy integration and optimization in microgrids: Enhancing efficiency with electric vehicle charging solutions. Electr. Eng. 2024, 107, 1541–1573. [Google Scholar] [CrossRef]
  22. Alsalemi, A.; Al-Zubiri, A.; Sadeghi, Y.; Massoud, A. Design of ultra-fast electric vehicle battery charger. In Proceedings of the ISCAIE 2021—IEEE 11th Symposium on Computer Applications and Industrial Electronics, Penang, Malaysia, 3 April 2021; pp. 191–196. [Google Scholar] [CrossRef]
  23. Tang, D. Congestion Assessment in Electric Vehicle Fast Charging Stations for Coupled Traffic-Power Systems in Smart Cities. In Proceedings of the 5th IEEE Conference on Energy Internet and Energy System Integration: Energy Internet for Carbon Neutrality, EI2 2021, Taiyuan, China, 22 October 2021; pp. 1760–1764. [Google Scholar] [CrossRef]
  24. Vasilev, K.; Kolev, V.; Draganova-Zlateva, I. Concept for building and managing a national infrastructure of charging stations for electric cars near substations, part of the electricity transmission network of Bulgaria. In Proceedings of the 2022 14th Electrical Engineering Faculty Conference, BulEF 2022, Varna, Bulgaria, 14 September 2022; pp. 1–5. [Google Scholar] [CrossRef]
  25. Hareshma, S.; Sivraj, P. Design and Development of Smart Charging Infrastructure for Electric Vehicles. In Proceedings of the 2023 3rd International Conference on Emerging Frontiers in Electrical and Electronic Technologies, ICEFEET 2023, Patna, India, 21 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
  26. Da Silva, E.C.; Melgar-Dominguez, O.D.; Romero, R. Simultaneous distributed generation and electric vehicles hosting capacity assessment in electric distribution systems. IEEE Access 2021, 9, 110927–110939. [Google Scholar] [CrossRef]
  27. Falchetta, G.; Noussan, M. Electric vehicle charging network in Europe: An accessibility and deployment trends analysis. Transp. Res. Part D Transp. Environ. 2021, 94, 102813. [Google Scholar] [CrossRef]
  28. Ucer, E.; Koyuncu, I.; Kisacikoglu, M.C.; Yavuz, M.; Meintz, A.; Rames, C. Modeling and analysis of a fast charging station and evaluation of service quality for electric vehicles. IEEE Trans. Transp. Electrif. 2019, 5, 215–225. [Google Scholar] [CrossRef]
  29. He, S.Y.; Kuo, Y.H.; Sun, K.K. The spatial planning of public electric vehicle charging infrastructure in a high-density city using a contextualised location-allocation model. Transp. Res. Part A Policy Pract. 2022, 160, 21–44. [Google Scholar] [CrossRef]
  30. Alshareef, S.M. Analyzing and Mitigating the Impacts of Integrating Fast-Charging Stations on the Power Quality in Electric Power Distribution Systems. Sustainability 2022, 14, 5595. [Google Scholar] [CrossRef]
  31. Pisano, G.; Ruggeri, S.; Soma, G.G.; Falabretti, D.; Grillo, S.; Gulotta, F.; Pilo, F. Impact of Electrical Vehicle Private Charging Stations on the Quality of the Low Voltage Network Supply. IEEE Open Access J. Power Energy 2023, 10, 351–362. [Google Scholar] [CrossRef]
  32. Riza; Margowadi, Y.; Aji, P.; Priyasta, D.; Rijanto, E.; Priandana, E.R.; Yusivar, F.; Nurdiana, E. A Design of Smart Charging Architecture for Battery Electric Vehicles. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe, Grenoble, France, 23 October 2023; pp. 1–5. [Google Scholar] [CrossRef]
  33. Dumont, P.; Petit, M.; Sainflou, D.P. Reducing Marginal Emissions of an Electric Vehicle Fleet through Smart Charging and Vehicle-to-grid. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe, Grenoble, France, 23 October 2023; pp. 1–5. [Google Scholar] [CrossRef]
  34. Hussien, D.A.; Omran, W.A.; Sharkawy, R.M. Smart Charging of Electric Vehicles in Charging Stations. In Proceedings of the 2023 5th International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE) 2023, Moscow, Russia, 16 March 2023; Volume 5, pp. 1–5. [Google Scholar] [CrossRef]
  35. Zenhom, Z.M.; Boghdady, T.A.; Youssef, H.K. A Proposed Economical Based Approach for Optimal Sizing and Placement of Distributed Generation. In Proceedings of the 2019 21st International Middle East Power Systems Conference, MEPCON 2019—Proceedings, Cairo, Egypt, 17 December 2019; pp. 342–347. [Google Scholar] [CrossRef]
  36. Ahmad, F.; Iqbal, A.; Ashraf, I.; Marzband, M.; Khan, I. Optimal Siting and Sizing Approach of Plug-in Electric Vehicle Fast Charging Station using a Novel Meta-heuristic Algorithm. In Proceedings of the 2022 2nd International Conference on Emerging Frontiers in Electrical and Electronic Technologies, ICEFEET 2022, Patna, India, 24 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
  37. Ahmad, F.; Ashraf, I.; Iqbal, A.; Khan, I.; Marzband, M. Optimal Location and Energy Management Strategy for EV Fast Charging Station with Integration of Renewable Energy Sources. In Proceedings of the 2022 IEEE Silchar Subsection Conference, SILCON 2022, Silchar, India, 4 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
  38. Adetunji, K.E.; Hofsajer, I.W.; Abu-Mahfouz, A.M.; Cheng, L. An optimization planning framework for allocating multiple distributed energy resources and electric vehicle charging stations in distribution networks. Appl. Energy 2022, 322, 119513. [Google Scholar] [CrossRef]
  39. Zhou, G.; Zhu, Z.; Luo, S. Location optimization of electric vehicle charging stations: Based on cost model and genetic algorithm. Energy 2022, 247, 123437. [Google Scholar] [CrossRef]
  40. Chen, H.; Wang, X.; Su, Y. Location planning of charging stations considering the total cost of charging stations and users. In Proceedings of the 2020 35th Youth Academic Annual Conference of Chinese Association of Automation, YAC 2020, Zhanjiang, China, 16 October 2020; pp. 717–721. [Google Scholar] [CrossRef]
  41. Liu, D.; Zhang, H.; Nie, H.; Zhao, Y. Location Analysis of Electric Vehicle Charging Station Based on Improved PSO. In Proceedings of the 2018 Chinese Automation Congress, CAC 2018, Xi’an, China, 30 November 2018; pp. 2184–2188. [Google Scholar] [CrossRef]
  42. Ouertani, M.W.; Manita, G.; Korbaa, O. Improved Antlion Algorithm for Electric Vehicle Charging Station Placement. In Proceedings of the 2022 IEEE 9th International Conference on Sciences of Electronics, Technologies of Information and Telecommunications, SETIT 2022, Hammamet, Tunisia, 28 May 2022; pp. 265–271. [Google Scholar] [CrossRef]
  43. Agash, P.; Kannan, G.; Sudhaharan, M.S.; Balamurugan, R. Optimized Electric Vehicle Charging Station for Remote Location. In Proceedings of the Proceedings—2024 5th International Conference on Mobile Computing and Sustainable Informatics, ICMCSI 2024, Lalitpur, Nepal, 18 January 2024; pp. 822–825. [Google Scholar] [CrossRef]
  44. Sharma, P.; Mishra, A.K.; Mishra, P.; Dutt Mathur, H. Optimal Capacity Estimation and Allocation of Distributed Generation Units with Suitable Placement of Electric Vehicle Charging Stations. In Proceedings of the TENSYMP 2021—2021 IEEE Region 10 Symposium, Jeju, Republic of Korea, 23 August 2021. [Google Scholar] [CrossRef]
  45. Chakraborty, R.; Das, D.; Das, P. Optimal Allocation of Electric Vehicle Charging Station using Symbiotic Organisms Search Algorithm and Reliability Index Approach. In Proceedings of the 2022 International Conference on Breakthrough in Heuristics and Reciprocation of Advanced Technologies, BHARAT 2022, Visakhapatnam, India, 7 April 2022; pp. 184–189. [Google Scholar] [CrossRef]
  46. Ahmad, F.; Ashraf, I.; Iqbal, A.; Bilal, M. Electric Vehicle Fast Charging Station Location and Capacity Planning Model Using Butterfly Optimization Algorithm. In Proceedings of the 2023 International Conference on Recent Advances in Electrical, Electronics and Digital Healthcare Technologies, REEDCON 2023, New Delhi, India, 1 May 2023; pp. 145–150. [Google Scholar] [CrossRef]
  47. Altundogan, T.G.; Yildiz, A.; Karakose, E. Genetic Algorithm Approach based on Graph Theory for Location Optimization of Electric Vehicle Charging Stations. In Proceedings of the 2021 Innovations in Intelligent Systems and Applications Conference, ASYU 2021, Elazig, Turkey, 6 October 2021. [Google Scholar] [CrossRef]
  48. Hosseini, A.; Amani, A.M.; Keshavarzain, K.; Jalili, M. Optimizing the Location of On-Route Fast-Charging Stations in a Battery Electric Bus System. In Proceedings of the 2023 10th International Conference on Power and Energy Systems Engineering, CPESE 2023, Nagoya, Japan, 8 September 2023; pp. 301–306. [Google Scholar] [CrossRef]
  49. Yousuf, A.K.M.; Wang, Z. An In-Depth Exploration of Electric Vehicle Charging Station Infrastructure: A Comprehensive Review of Challenges, Mitigation Approaches, and Optimization Strategies. IEEE Access 2024, 12, 51570–51589. [Google Scholar] [CrossRef]
  50. Christmann, L.S.; Offel, C.; Rahn, L.; Singh, N.; Géhin, L.; Hang, G.; Safaya, A.; Draz, M.; Albayrak, S. A Framework for Integrating Intelligent Mobile Energy Storage into Energy Distribution Systems. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe, ISGT-Europe 2019, Bucharest, Romania, 29 September 2019. [Google Scholar] [CrossRef]
  51. Marasciuolo, F.; Dicorato, M.; Forte, G.; Montegiglio, P. The influence of electric vehicle position on technical operation of a distribution grid. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe, EEEIC/I and CPS Europe 2022, Prague, Czech Republic, 28 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
  52. Safak Bayram, I.; Bayhan, S. Location Analysis of Electric Vehicle Charging Stations for Maximum Capacity and Coverage. In Proceedings of the 2020 IEEE 14th International Conference on Compatibility, Power Electronics and Power Engineering, CPE-POWERENG 2020, Setubal, Portugal, 10 July 2020; pp. 409–414. [Google Scholar] [CrossRef]
  53. Bao, Z.; Xie, C. Optimal station locations for en-route charging of electric vehicles in congested intercity networks: A new problem formulation and exact and approximate partitioning algorithms. Transp. Res. Part C Emerg. Technol. 2021, 133, 103447. [Google Scholar] [CrossRef]
  54. Akil, M.; Dokur, E.; Bayindir, R. Optimal Scheduling of on-Street EV Charging Stations. In Proceedings of the 2022 IEEE 20th International Power Electronics and Motion Control Conference, PEMC 2022, Brasov, Romania, 25 September 2022; pp. 679–684. [Google Scholar] [CrossRef]
  55. Lin, X.; Wang, Z.; Zeng, S.; Huang, W.; Li, X. Real-time optimization strategy by using sequence quadratic programming with multivariate nonlinear regression for a fuel cell electric vehicle. Int. J. Hydrogen Energy 2021, 46, 13240–13251. [Google Scholar] [CrossRef]
  56. Chen, S.; Li, J.; Li, L. Research on The Method for Optimal Location of Charging Stations Based on The Spatial and Temporal Characteristics of Electric Vehicle Charging Demand. In Proceedings of the 2022 IEEE Sustainable Power and Energy Conference, iSPEC 2022, Perth, Australia, 4 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
  57. Yazdi, L.; Ahadi, R.; Rezaee, B. Optimal Electric Vehicle Charging Station Placing with Integration of Renewable Energy. In Proceedings of the 2019 15th Iran International Industrial Engineering Conference, IIIEC 2019, Yazd, Iran, 24 January 2019; pp. 47–51. [Google Scholar] [CrossRef]
  58. Hassane, E.; Ahmed, E.A. The optimal location of the electric vehicle infrastructure utilizing wireless charging in a multipath network, round-trip. In Proceedings of the 2020 5th International Conference on Logistics Operations Management, GOL 2020, Rabat, Morocco, 30 October 2020. [Google Scholar] [CrossRef]
  59. Zafar, U.; Bayram, I.S.; Bayhan, S. A GIS-based Optimal Facility Location Framework for Fast Electric Vehicle Charging Stations. In Proceedings of the IEEE International Symposium on Industrial Electronics, Kyoto, Japan, 20 June 2021; pp. 1–5. [Google Scholar] [CrossRef]
  60. Pal, A.; Bhattacharya, A.; Chakraborty, A.K. Planning of EV Charging Station With Distribution Network Expansion Considering Traffic Congestion and Uncertainties. IEEE Trans. Ind. Appl. 2023, 59, 3810–3825. [Google Scholar] [CrossRef]
  61. Fredriksson, H.; Dahl, M.; Holmgren, J. Optimal placement of charging stations for electric vehicles in large-scale transportation networks. Procedia Comput. Sci. 2019, 160, 77–84. [Google Scholar] [CrossRef]
  62. Yılmaz, H.; Yagmahan, B. Range coverage location model: An optimization model for the charging station location problem in a transportation network to cover intercity travels. Int. J. Energy Res. 2022, 46, 1538–1552. [Google Scholar] [CrossRef]
  63. Ferro, G.; Minciardi, R.; Parodi, L.; Robba, M. Optimal Location and Line Assignment for Electric Bus Charging Stations. IEEE Syst. J. 2023, 17, 1950–1961. [Google Scholar] [CrossRef]
  64. Mondal, S.; Acharjee, P.; Bhattacharya, A. Determination of Voltage Security Constrained Maximum Loadability Limit for EV Charging Station with and Without DG. In Proceedings of the 2023 IEEE 3rd International Conference on Sustainable Energy and Future Electric Transportation, SeFet 2023, Bhubaneswar, India, 9 August 2023; pp. 1–6. [Google Scholar] [CrossRef]
  65. Mousavikhademi, M.; Kazemi, E.; Jahromi, M.Z. Optimal Probability Placement of the Charge Station of Electric Vehicles in a Distributed Power Network Containing the DG Using the Queuing Theory. In Proceedings of the 2023 31st International Conference on Electrical Engineering, ICEE 2023, Tehran, Iran, 9 May 2023; pp. 133–143. [Google Scholar] [CrossRef]
  66. Asna, M.; Shareef, H.; Achikkulath, P.; Mokhlis, H.; Errouissi, R.; Wahyudie, A. Analysis of an Optimal Planning Model for Electric Vehicle Fast-Charging Stations in Al Ain City, United Arab Emirates. IEEE Access 2021, 9, 73678–73694. [Google Scholar] [CrossRef]
  67. Hunter, L.; Sims, R.; Galloway, S. Open Data to Accelerate the Electric Mobility Revolution: Deploying Journey Electric Vehicle Chargers in Rural Scotland. IEEE Power Energy Mag. 2023, 21, 56–67. [Google Scholar] [CrossRef]
  68. Boonraksa, T.; Marungsri, B. Optimal Fast Charging Station Location for Public Electric Transportation in Smart Power Distribution Network. In Proceedings of the iEECON 2018—6th International Electrical Engineering Congress, Krabi, Thailand, 7 March 2018; pp. 1–4. [Google Scholar] [CrossRef]
  69. Du, Y.; Li, X.; Mao, S.; Cai, B.; He, J.; Nie, W. Optimal Placement of EV Charging Stations Based on Genetic Algorithm. In Proceedings of the 36th Chinese Control and Decision Conference, CCDC 2024, Xi’an, China, 25 May 2024; pp. 5721–5726. [Google Scholar] [CrossRef]
  70. Choi, M.; Van Fan, Y.; Lee, D.; Kim, S.; Lee, S. Location and capacity optimization of EV charging stations using genetic algorithms and fuzzy analytic hierarchy process. Clean Technol. Environ. Policy 2024, 27, 1785–1798. [Google Scholar] [CrossRef]
  71. Dharavat, N.; Sudabattula, S.K.; Velamuri, S.; Mishra, S.; Sharma, N.K.; Bajaj, M.; Elgamli, E.; Shouran, M.; Kamel, S. Optimal Allocation of Renewable Distributed Generators and Electric Vehicles in a Distribution System Using the Political Optimization Algorithm. Energies 2022, 15, 6698. [Google Scholar] [CrossRef]
  72. Ahmad, S.; Shafiullah, M.; Ahmed, C.B.; Alowaifeer, M. A Review of Microgrid Energy Management and Control Strategies. IEEE Access 2023, 11, 21729–21757. [Google Scholar] [CrossRef]
  73. Khan, M.O.; Kirmani, S.; Rihan, M.; Pandey, A.K. Optimal Integration of Electric Vehicle Charging Stations and Distributed Generation in Distribution Network. In Proceedings of the 2022 IEEE Students Conference on Engineering and Systems, SCES 2022, Prayagraj, India, 1 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
  74. Sriabisha, R.; Yuvaraj, T. Optimum placement of Electric Vehicle Charging Station using Particle Swarm Optimization Algorithm. In Proceedings of the 9th International Conference on Electrical Energy Systems, ICEES 2023, Chennai, India, 23 March 2023; pp. 283–288. [Google Scholar] [CrossRef]
  75. Maghami, M.R.; Thang, K.F.; Mutambara, A.G.; Firoozi, A.A.; Yaghoubi, E.; Jahromi, M.Z.; Yaghoubi, E. Optimized planning of electric vehicle charging infrastructure for grid performance improvement. Discov. Sustain. 2025, 6, 706. [Google Scholar] [CrossRef]
  76. Arabi, M.S.; Awasthi, A. A PSO-Based Approach for the Optimal Allocation of Electric Vehicle Parking Lots to the Electricity Distribution Network. Algorithms 2025, 18, 175. [Google Scholar] [CrossRef]
  77. Singh, K.; Mistry, K.D.; Patel, H.G. Optimal Placement of Electric Vehicle Charging Station and DG in a Distribution System for Loss Minimization. In Proceedings of the 2023 IEEE 3rd International Conference on Sustainable Energy and Future Electric Transportation, SeFet 2023, Bhubaneswar, India, 9 August 2023; pp. 1–6. [Google Scholar] [CrossRef]
  78. Ahmad, F.; Iqbal, A.; Ashraf, I.; Marzband, M.; Khan, I. Optimal location of Electric Vehicle Rapid Charging Stations in Power Distribution Network and Transportation Network with V2G Strategies. In Proceedings of the 2021 IEEE Transportation Electrification Conference, ITEC-India 2021, New Delhi, India, 16 December 2021; pp. 1–5. [Google Scholar] [CrossRef]
  79. Mohanty, A.K.; Babu, P.S. Multi Objective Optimal Planning of Fast Charging station and Distributed Generators in a Distribution System. In Proceedings of the 2021 IEEE 2nd International Conference on Electrical Power and Energy Systems, ICEPES 2021, Bhopal, India, 10 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
  80. Chakraborty, R.; Das, P.; Das, D. Optimal Planning of Electric Vehicle Charging Station in Radial Distribution Network considering System Average Interruption Frequency Index. In Proceedings of the 2022 6th International Conference on Condition Assessment Techniques in Electrical Systems, CATCON 2022, Durgapur, India, 17 December 2022; pp. 177–181. [Google Scholar] [CrossRef]
  81. Dey, D.; Chakraborty, R.; Bhowmik, A.R.; Das, D.; Jamatia, A. Optimal Placement of Electric Vehicle Charging Station in Distribution Network with SOS Algorithm. In Proceedings of the 2023 5th International Conference on Electrical, Computer and Communication Technologies, ICECCT 2023, Erode, India, 22 February 2023; pp. 1–5. [Google Scholar] [CrossRef]
  82. Bilal, M.; Rizwan, M.; Alsaidan, I.; Almasoudi, F.M. AI-Based Approach for Optimal Placement of EVCS and DG with Reliability Analysis. IEEE Access 2021, 9, 154204–154224. [Google Scholar] [CrossRef]
  83. Soliman, I.A.; Tulsky, V.; Abd el Ghany, H.A.; ElGebaly, A.E. Optimal allocation of electric vehicle charging stations and distributed generation in radial distribution networks. Eng. Sci. Technol. Int. J. 2024, 60, 101907. [Google Scholar] [CrossRef]
  84. Liu, L.; Zhang, Y.; Da, C.; Huang, Z.; Wang, M. Optimal allocation of distributed generation and electric vehicle charging stations based on intelligent algorithm and bi-level programming. Int. Trans. Electr. Energy Syst. 2020, 30, 1–21. [Google Scholar] [CrossRef]
  85. Wang, R.; Mu, J.; Sun, Z.; Wang, J.; Hu, A. NSGA-II multi-objective optimization regional electricity price model for electric vehicle charging based on travel law. Energy Rep. 2021, 7, 1495–1503. [Google Scholar] [CrossRef]
  86. Gao, B.; Gao, L.; Kang, K.; Ma, H. Optimization Study of Electric Vehicle Switching Station Scheduling Considering the Enhancement of Wind-solar Resources Consumption Based on Improved NSGA-II. In Proceedings of the 2022 IEEE 2nd International Conference on Mobile Networks and Wireless Communications, ICMNWC 2022, Tumkur, Karnataka, India, 2 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
  87. Wei, H.; Liang, J.; Li, C.; Zhang, Y. Real-time Locally Optimal Schedule for Electric Vehicle Load via Diversity-maximization NSGA-II. J. Mod. Power Syst. Clean Energy 2021, 9, 940–950. [Google Scholar] [CrossRef]
  88. Wang, Y.; Han, L.; Cai, C. An Improved NSGA-II for Coordinated Charging of Community Electric Vehicle Charging Station. In Proceedings of the 2021 3rd International Conference on Smart Power and Internet Energy Systems, SPIES 2021, Shanghai, China, 25 September 2021; pp. 386–391. [Google Scholar] [CrossRef]
  89. Abdelaziz, M.A.; Ali, A.A.; Swief, R.A.; Elazab, R. A reliable optimal electric Vehicle charging stations allocation. Ain Shams Eng. J. 2024, 15, 102763. [Google Scholar] [CrossRef]
  90. Estrada Poggio, A.; Rotondo, G.; Prina, M.G.; Zubaryeva, A.; Sparber, W. High-Resolution Monitored Data Analysis of EV Public Charging Stations for Modelled Grid Impact Validation. Appl. Sci. 2024, 14, 8133. [Google Scholar] [CrossRef]
  91. Dvorácek, L.; Horák, M.; Valentová, M.; Knápek, J. Optimization of electric vehicle charging points based on efficient use of chargers and providing private charging spaces. Energies 2020, 13, 6750. [Google Scholar] [CrossRef]
  92. Liu, J.; Yang, H.; Wei, D.; Song, X. Time distribution simulation of household power load based on travel chains and monte carlo—A study of Beijing in summer. Sustainability 2021, 13, 6651. [Google Scholar] [CrossRef]
  93. Veisi, M. Stochastic economic placement and sizing of electric vehicles charging station with renewable units and battery bank in smart distribution network. Sci. Rep. 2025, 15, 24235. [Google Scholar] [CrossRef]
  94. Sun, C.; Che, Y. Monte Carlo-based Prediction of Electric Vehicle Charging Load and Coupling Mechanisms of Multiple Information Sources. Int. J. Renew. Energy Res. 2025, 15, 42–55. [Google Scholar] [CrossRef]
  95. Liu, H.; Pang, A.; Yin, J.; Yi, H.; Mu, H. Collaborative Optimization Scheduling Strategy for Electric Vehicle Charging Stations Considering Spatiotemporal Distribution of Different Power Charging Demands. World Electr. Veh. J. 2025, 16, 176. [Google Scholar] [CrossRef]
  96. Chakraborty, R.; Das, D.; Das, P. Optimal Placement of Electric Vehicle Charging Station with V2G Provision using Symbiotic Organisms Search Algorithm. In Proceedings of the 2022 IEEE International Students’ Conference on Electrical, Electronics and Computer Science, SCEECS 2022, Bhopal, India, 30 March 2022. [Google Scholar] [CrossRef]
  97. Zhou, H.; Zhang, K.; Chen, Y.; Li, H. Research on electric vehicle load Optimal Access Point based on Grid operation risk assessment. In Proceedings of the IEEE Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Beijing, China, 3 October 2022; pp. 498–502. [Google Scholar] [CrossRef]
Energies 18 05616 g001
Figure 1. The selection process of articles and standards for the literature review is shown.
Figure 1. The selection process of articles and standards for the literature review is shown.
Energies 18 05616 g001
Energies 18 05616 g002
Figure 2. Classification of Optimization Techniques for Electric Vehicle Charging Stations.
Figure 2. Classification of Optimization Techniques for Electric Vehicle Charging Stations.
Energies 18 05616 g002
Energies 18 05616 g003
Figure 3. Distribution of publications based on the optimization method used for the location of electric vehicle charging stations.
Figure 3. Distribution of publications based on the optimization method used for the location of electric vehicle charging stations.
Energies 18 05616 g003
Energies 18 05616 g004
Figure 4. Distribution of publications on different metaheuristic methods.
Figure 4. Distribution of publications on different metaheuristic methods.
Energies 18 05616 g004
Table 1. Evolution of methods for EV charging station planning and optimization (2018–2025).
Table 1. Evolution of methods for EV charging station planning and optimization (2018–2025).
PeriodMain Trend and Methodological DescriptionRefs.
2018–2019Predominance of exact methods and heuristics. Exact formulations were often MILP; heuristics focused on demand estimation, facility location, and early impact studies on distribution networks.[7,14,28,61]
2020–2021Increasing use of heuristics and metaheuristics alongside some exact approaches. Metaheuristics commonly used: GA, PSO; attention to multi-objective formulations and reliability indices.[1,5,6,9,15]
2022–2023Clear predominance of metaheuristics and hybrids (GWO, NSGA-II, others), with stronger focus on reliability, power-quality impacts, and integration with DGs and renewables.[3,10,11,17,36]
2025Consolidated trend towards hybrid metaheuristics and ML integration, advanced multi-objective models addressing resilience, uncertainty, and large-scale deployment.[2,8,12,13,49]
Table 2. Classification of optimization methods by problem characteristics and application.
Table 2. Classification of optimization methods by problem characteristics and application.
Type of MethodProblem CharacteristicsApplicationReferences
Exact (MILP, MINLP, SQP, Partitioning)Small-scale problems, few stations, linear objective functionsOptimal location of 1–3 EV charging stations in small networks (variables to optimize: 1–3)[1,53,55,62]
Heuristic (Greedy, Clustering, GIS, Antlion, Location-Allocation)Simplified criteria, fast searchPre-selection of locations according to demand; rapid congestion analysis (variables to optimize: 2–6)[7,18,29,42,59]
Metaheuristic (GA, PSO, GWO, SOS, Butterfly, NSGA-II)Multiple objectives, nonlinear constraints, demand uncertainty, DG and V2G integrationJoint optimization of losses, costs, and reliability; location and sizing of fast-charging stations; integration of renewables and V2G (variables to optimize: 3–10)[10,36,45,46,69,74,85,86,87]
Combined (Exact + Metaheuristic/Hybrid)Large-scale problems with multiple objectives and complex constraintsCombination of exact and metaheuristic algorithms for multi-objective optimization in networks with DG and multiple EV stations (variables to optimize: 3–8)[38,71,79,83,84]
Table 3. Variables considered for the system optimization.
Table 3. Variables considered for the system optimization.
ArticleVariables That Aim to Optimize
[1,2,3,4,5,7,16,17,18,19,20,46,77,78]Energy losses
[36,37,38,39,40,96,97]Voltage deviation
[39,40,41,44,69,77]Costs
[10,37,42,43,45,73,79,81]Energy losses and costs
[71,74,80,81,82,83]Energy losses, voltage profile and costs
Table 4. Main constraints considered in the reviewed studies.
Table 4. Main constraints considered in the reviewed studies.
ArticleMain Constraints Addressed
[1,2,3,17,19,46,78]Voltage limits and transformer capacity constraints.
[10,79,81,83]Power losses and line loading limits.
[74,82]Voltage deviation and system stability constraints.
[41,44,69]Investment cost and maximum number of charging stations.
[36,37,73]Reliability and service quality indices (SAIFI, SAIDI, THD).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Lara Leon, D.; Gallego Landera, Y.; Garcia Santander, L.; León Viltre, L.T.; Cuaresma Zevallos, O.; Muñoz Jarpa, F.A. Optimal Location of Charging Stations for Electric Vehicles in Distribution Networks: A Literature Review. Energies 2025, 18, 5616. https://doi.org/10.3390/en18215616

AMA Style

Lara Leon D, Gallego Landera Y, Garcia Santander L, León Viltre LT, Cuaresma Zevallos O, Muñoz Jarpa FA. Optimal Location of Charging Stations for Electric Vehicles in Distribution Networks: A Literature Review. Energies. 2025; 18(21):5616. https://doi.org/10.3390/en18215616

Chicago/Turabian Style

Lara Leon, David, Yandi Gallego Landera, Luis Garcia Santander, Lesyani Teresa León Viltre, Oscar Cuaresma Zevallos, and Fredy Antonio Muñoz Jarpa. 2025. "Optimal Location of Charging Stations for Electric Vehicles in Distribution Networks: A Literature Review" Energies 18, no. 21: 5616. https://doi.org/10.3390/en18215616

APA Style

Lara Leon, D., Gallego Landera, Y., Garcia Santander, L., León Viltre, L. T., Cuaresma Zevallos, O., & Muñoz Jarpa, F. A. (2025). Optimal Location of Charging Stations for Electric Vehicles in Distribution Networks: A Literature Review. Energies, 18(21), 5616. https://doi.org/10.3390/en18215616

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop