A Virtual Power Plant Load Forecasting Approach Using COM Encoding and BiLSTM-Att-KAN
Abstract
1. Introduction
- (1)
- This paper proposes a cyclic order mapping (COM) encoding method, which explicitly preserves the gradual periodic variation patterns of electrical load by mapping weekly and intraday time sequences to continuous ordered vectors on the unit circle. Moreover, owing to its constant dimensionality, COM encoding substantially reduces feature space complexity and mitigates overfitting problems caused by high-dimensional sparsity.
- (2)
- This paper constructs a BiLSTM-Att-KAN ensemble model that integrates BiLSTM, an efficient self-attention mechanism, and KAN. Specifically, the primary BiLSTM captures short-term dependencies and local features from raw load data, while the self-attention mechanism extracts long-term dependencies and global structures. A secondary BiLSTM then fuses these multi-scale temporal features to further enhance dynamic representation. Finally, KAN maps the refined features into accurate forecasting results. The synergistic interaction of these components effectively resolves the difficulty of jointly modeling short- and long-term dependencies and significantly improves predictive performance.
- (3)
- This paper replaces conventional fully connected layers with KAN, which enhances the model’s nonlinear fitting capability and improves the reliability of forecasting results. By transforming complex temporal features into accurate forecasting results, KAN effectively overcomes the limitations of conventional architectures and ensures high-quality load forecasting.
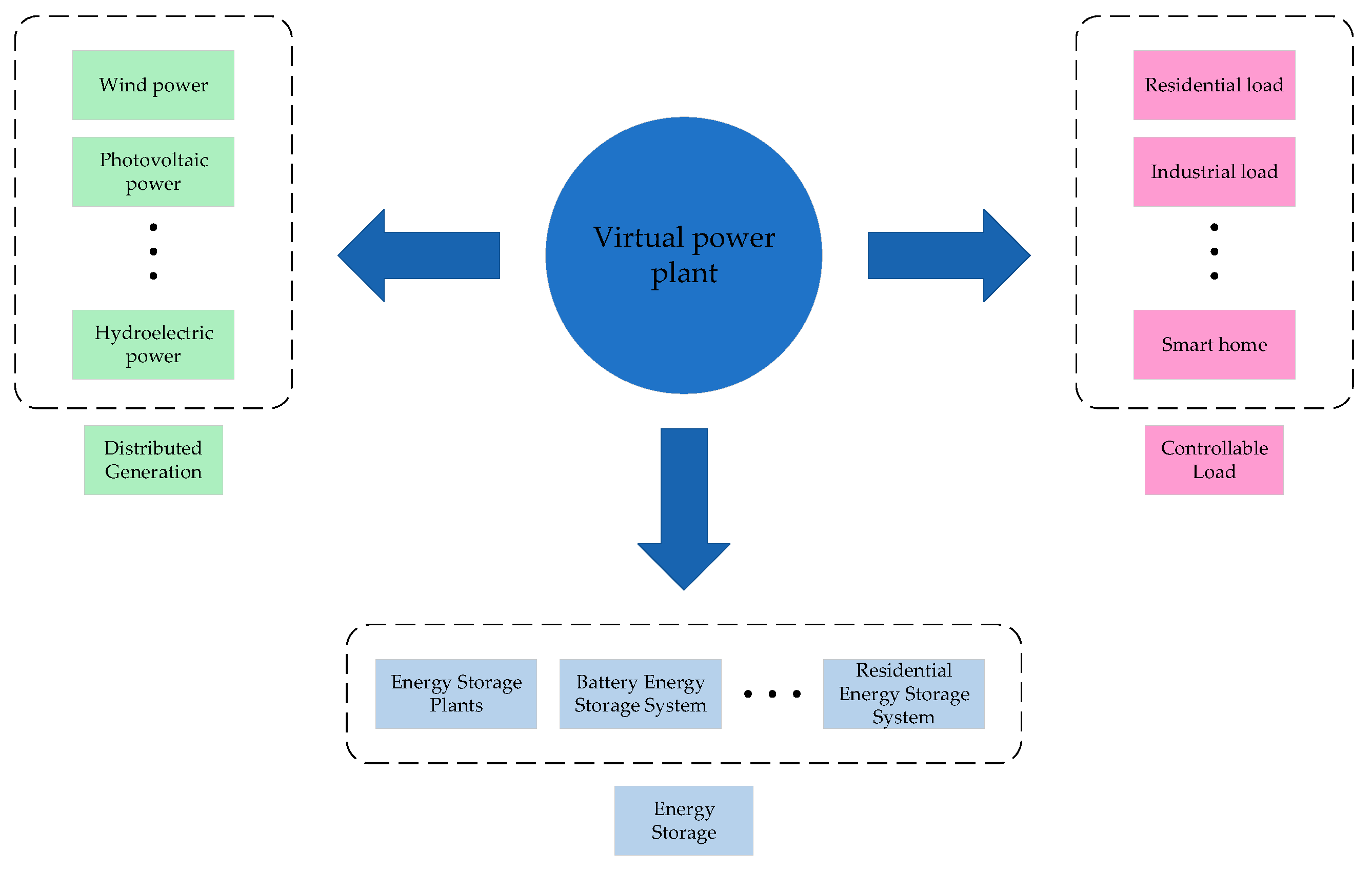
2. Virtual Power Plant
3. Methodology
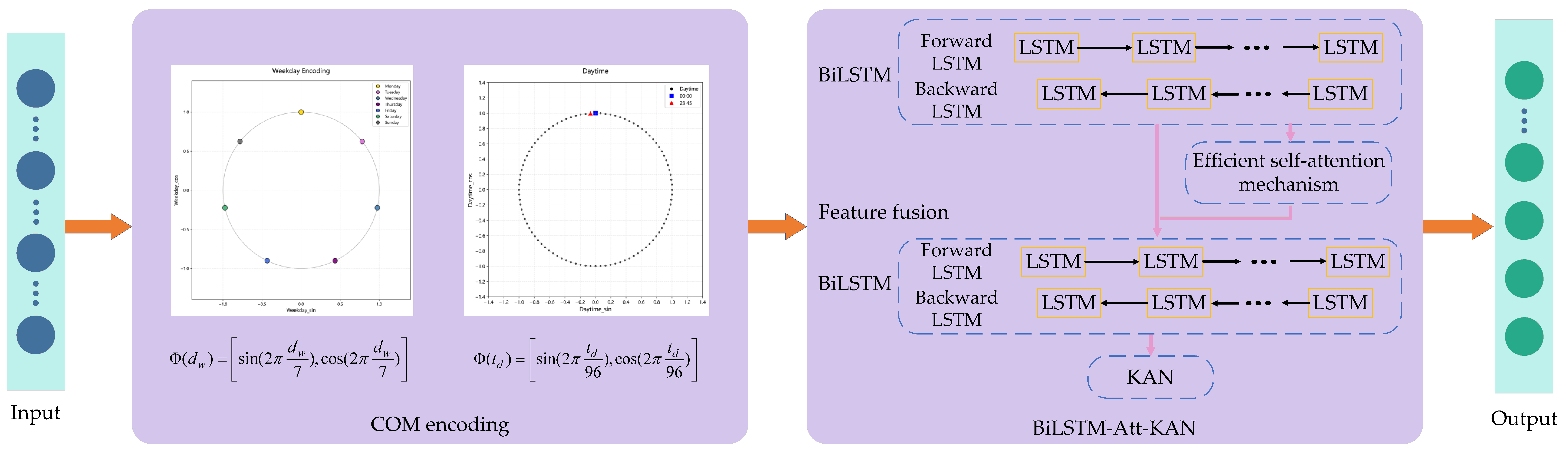
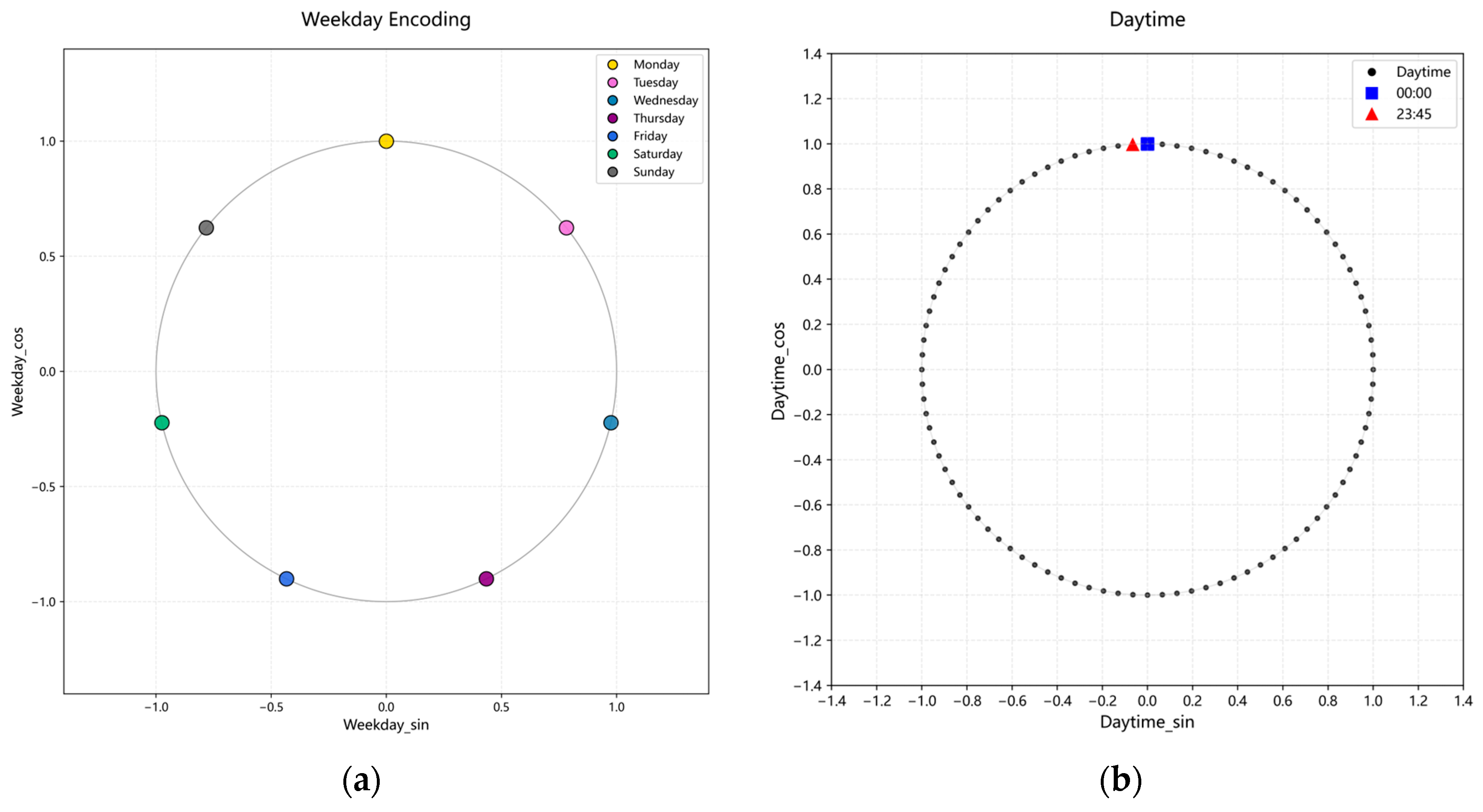
3.1. COM Encoding
3.2. Electrical Load Forecasting Model
3.2.1. BiLSTM-Att-KAN
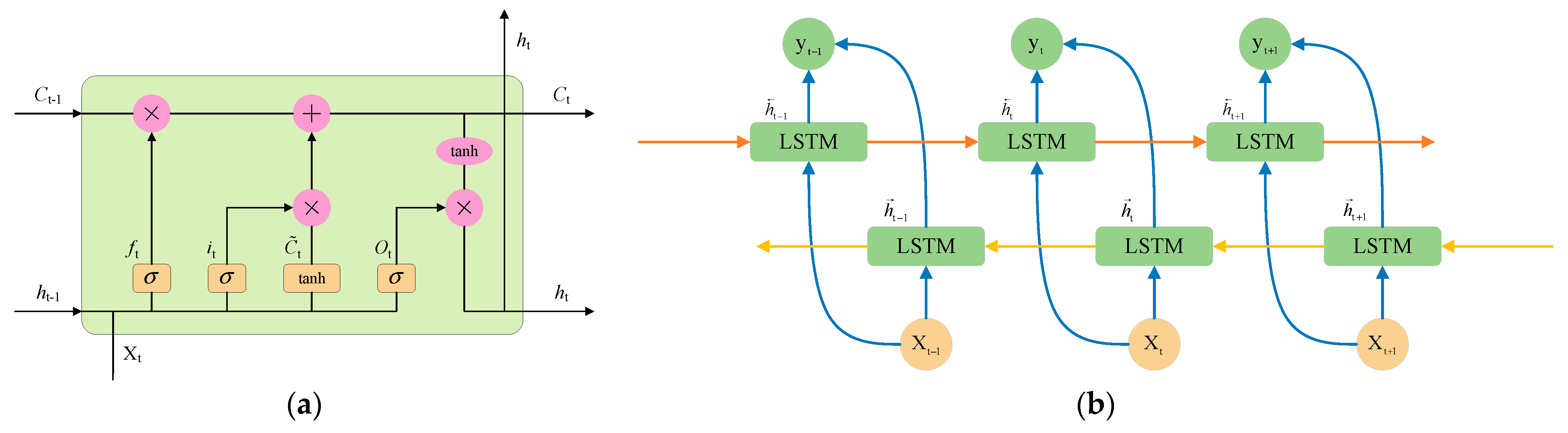
3.2.2. Bidirectional Long Short-Term Memory Network
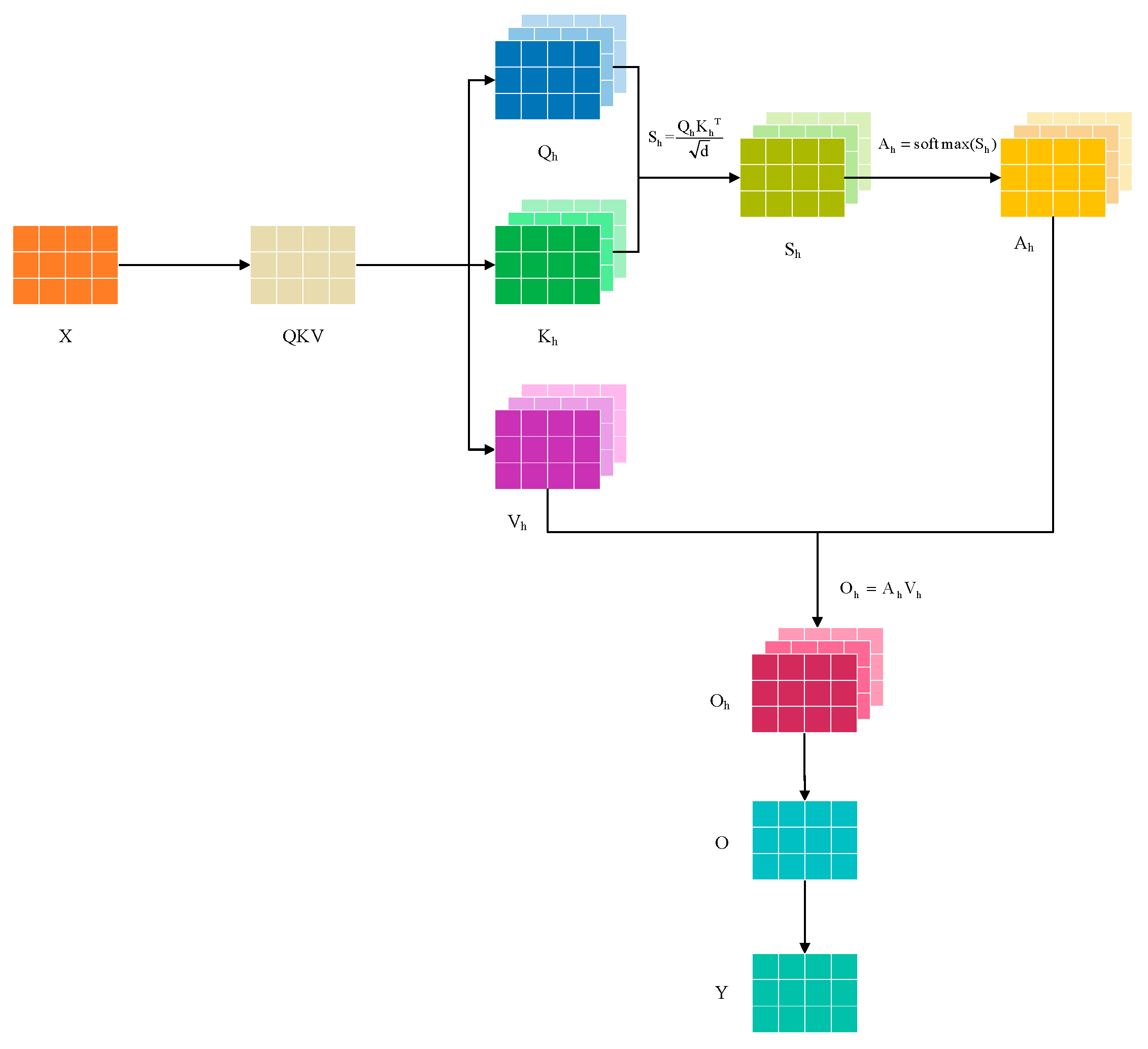
3.2.3. Efficient Self-Attention Mechanism
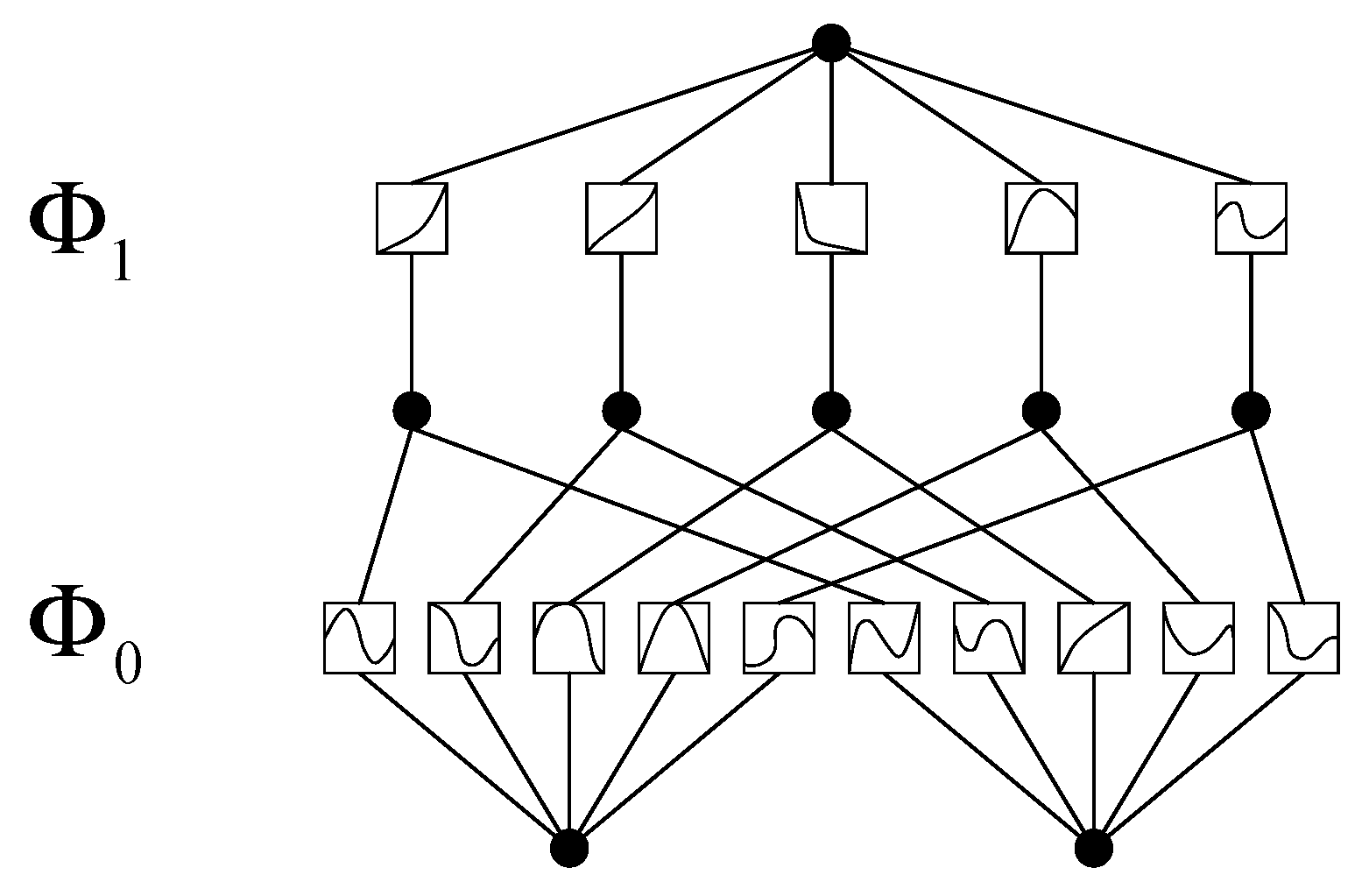
3.2.4. KAN
4. Experimental Procedures, Results and Analysis
4.1. Experimental Procedures
- (1)
- Data Collection and Feature Extraction. Historical load data were collected from the power load data acquisition platform. The periodic characteristics extracted from the electrical load data are encoded using the COM encoding to preserve intrinsic temporal patterns and facilitate subsequent modeling.
- (2)
- Dataset Partitioning. To rigorously evaluate model performance, the processed dataset is partitioned into a training set and a test set, with 80% of the data allocated for training and the remaining 20% reserved for testing.
- (3)
- Model Construction and Training. A BiLSTM-Att-KAN integrated forecasting model is constructed and trained using the training dataset. The integration of BiLSTM, an efficient self-attention mechanism, and KAN enables effective multi-scale temporal feature learning for electrical load forecasting.
- (4)
- Model Evaluation. BiLSTM-Att-KAN integrated model is evaluated using the test set to comprehensively assess its forecasting performance and validate its effectiveness in electrical load forecasting.
4.2. Feature Extraction and Encoding
4.3. Dataset Partitioning and Evaluation Indicators
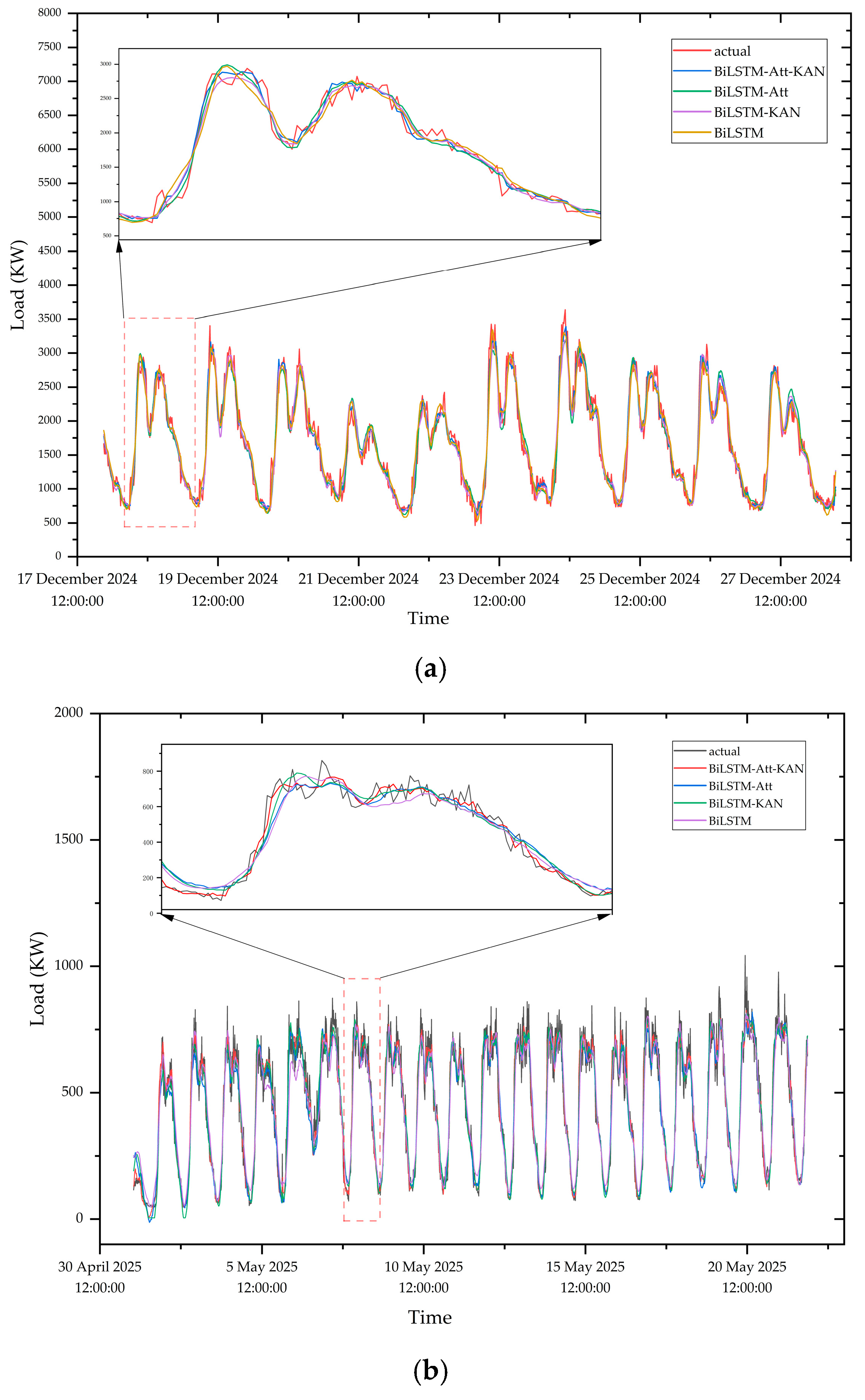
4.4. Comparative Analysis of Forecasting Models
4.5. Model Interpretability Analysis
4.5.1. Ablation Experiments
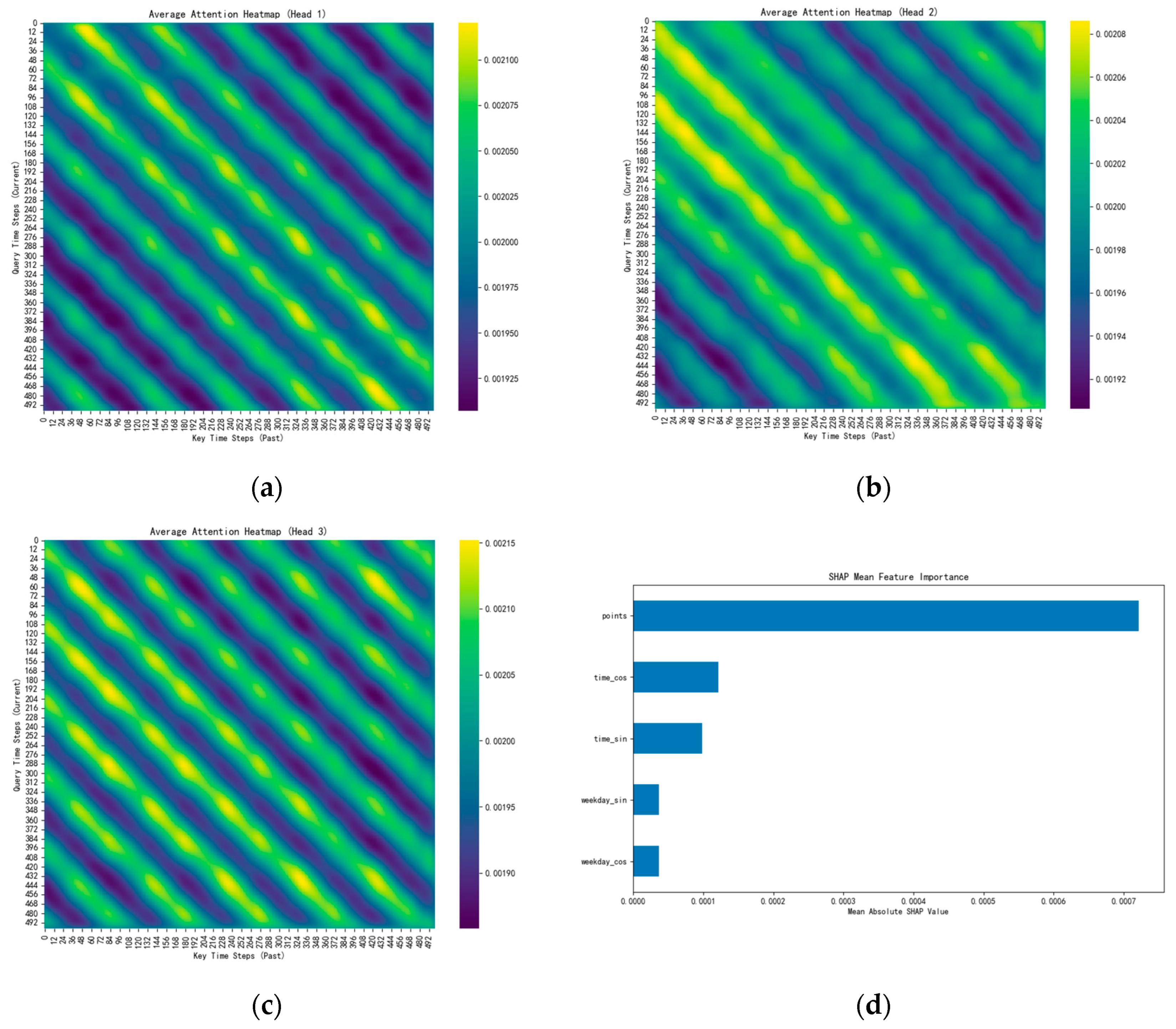
4.5.2. Visualizing Attention and Key Feature Contributions
4.6. Feature Comparison Experiments
4.7. Comprehensive Performance Analysis
4.8. Rolling-Origin Cross-Validation
4.9. Model Deployability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| COM | Cyclic Order Mapping |
| DERs | Distributed Energy Resources |
| Att | Efficient self-attention mechanism |
| VPP | Virtual Power Plant |
| MLP | Multi-Layer Perceptron |
| BiGRU | Bidirectional Gated Recurrent Unit |
| BiLSTM | Bidirectional Long Short-Term Memory |
| KAN | Kolmogorov-Arnold Network |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| R2 | Coefficient of Determination |
| List of Symbols | |
| dw | The week ordinal |
| td | The intraday time ordinal |
| ft | The output of the forget gate |
| it | The output of the input gate |
| Ct | Cell state |
| ot | The output of the output gate |
| ht | Hidden state |
| σ | The sigmoid activation function |
| tanh | The activation function |
| Q | The query vector |
| K | The key vector |
| V | The value vector |
References
- Venegas-Zarama, J.F.; Muñoz-Hernandez, J.I.; Baringo, L.; Diaz-Cachinero, P.; De Domingo-Mondejar, I. A Review of the Evolution and Main Roles of Virtual Power Plants as Key Stakeholders in Power Systems. IEEE Access 2022, 10, 47937–47964. [Google Scholar] [CrossRef]
- Alahyari, A.; Ehsan, M.; Mousavizadeh, M.S. A Hybrid Storage-Wind Virtual Power Plant (VPP) Participation in the Electricity Markets: A Self-Scheduling Optimization Considering Price, Renewable Generation, and Electric Vehicles Uncertainties. J. Energy Storage 2019, 25, 100812. [Google Scholar] [CrossRef]
- Liu, X.; Gao, C. Review and Prospects of Artificial Intelligence Technology in Virtual Power Plants. Energies 2025, 18, 3325. [Google Scholar] [CrossRef]
- Jin, W.; Wang, P.; Yuan, J. Key Role and Optimization Dispatch Research of Technical Virtual Power Plants in the New Energy Era. Energies 2024, 17, 5796. [Google Scholar] [CrossRef]
- Nti, I.K.; Teimeh, M.; Nyarko-Boateng, O.; Adekoya, A.F. Electricity Load Forecasting: A Systematic Review. J. Electr. Syst. Inf. Technol. 2020, 7, 13. [Google Scholar] [CrossRef]
- Lindberg, K.B.; Seljom, P.; Madsen, H.; Fischer, D.; Korpås, M. Long-Term Electricity Load Forecasting: Current and Future Trends. Util. Policy 2019, 58, 102–119. [Google Scholar] [CrossRef]
- Düzgün, B.; Bayındır, R.; Köksal, M.A. Estimation of Large Household Appliances Stock in the Residential Sector and Forecasting of Stock Electricity Consumption: Ex-Post and Ex-Ante Analyses. Gazi Univ. J. Sci. Part C Des. Technol. 2021, 9, 182–199. [Google Scholar] [CrossRef]
- Jahan, I.S.; Snasel, V.; Misak, S. Intelligent Systems for Power Load Forecasting: A Study Review. Energies 2020, 13, 6105. [Google Scholar] [CrossRef]
- Yazici, I.; Beyca, O.F.; Delen, D. Deep-Learning-Based Short-Term Electricity Load Forecasting: A Real Case Application. Eng. Appl. Artif. Intell. 2022, 109, 104645. [Google Scholar] [CrossRef]
- Aguilar Madrid, E.; Antonio, N. Short-Term Electricity Load Forecasting with Machine Learning. Information 2021, 12, 50. [Google Scholar] [CrossRef]
- Hafeez, G.; Alimgeer, K.S.; Khan, I. Electric Load Forecasting Based on Deep Learning and Optimized by Heuristic Algorithm in Smart Grid. Appl. Energy 2020, 269, 114915. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, J.; He, Y.; Fu, X.; Fan, L.; Yao, G.; Wen, Y. Short-Term Load Forecasting Based on the CEEMDAN-Sample Entropy-BPNN-Transformer. Energies 2022, 15, 3659. [Google Scholar] [CrossRef]
- Yang, Y.; Che, J.; Deng, C.; Li, L. Sequential Grid Approach Based Support Vector Regression for Short-Term Electric Load Forecasting. Appl. Energy 2019, 238, 1010–1021. [Google Scholar] [CrossRef]
- Baesmat, K.H.; Shokoohi, F.; Farrokhi, Z. SP-RF-ARIMA: A sparse random forest and ARIMA hybrid model for electric load forecasting. Glob. Energy Interconnect. 2025, 8, 486–496. [Google Scholar] [CrossRef]
- Baur, L.; Ditschuneit, K.; Schambach, M.; Kaymakci, C.; Wollmann, T.; Sauer, A. Explainability and Interpretability in Electric Load Forecasting Using Machine Learning Techniques—A Review. Energy AI 2024, 16, 100358. [Google Scholar] [CrossRef]
- Islam, B.; Ahmed, S.F. Short-term electrical load demand forecasting based on LSTM and RNN deep neural networks. Math. Probl. Eng. 2022, 2022, 2316474. [Google Scholar] [CrossRef]
- Kwon, B.S.; Park, R.J.; Song, K.B. Short-Term Load Forecasting Based on Deep Neural Networks Using LSTM Layer. J. Electr. Eng. Technol. 2020, 15, 1501–1509. [Google Scholar] [CrossRef]
- Sajjad, M.; Khan, Z.A.; Ullah, A.; Hussain, T.; Ullah, W.; Lee, M.Y.; Baik, S.W. A novel CNN-GRU-based hybrid approach for short-term residential load forecasting. IEEE Access 2020, 8, 143759–143768. [Google Scholar] [CrossRef]
- Ke, K.; Hongbin, S.; Chengkang, Z.; Brown, C. Short-term electrical load forecasting method based on stacked auto-encoding and GRU neural network. Evol. Intell. 2019, 12, 385–394. [Google Scholar] [CrossRef]
- Wu, K.; Peng, X.; Chen, Z.; Su, H.; Quan, H.; Liu, H. A Novel Short-Term Household Load Forecasting Method Combined BiLSTM with Trend Feature Extraction. Energy Rep. 2023, 9, 1013–1022. [Google Scholar] [CrossRef]
- Xu, Y.; Jiang, X. Short-term power load forecasting based on BiGRU-Attention-SENet model. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 973–985. [Google Scholar] [CrossRef]
- Zhang, G.; Wei, C.; Jing, C.; Wang, Y. Short-term electrical load forecasting based on time augmented transformer. Int. J. Comput. Intell. Syst. 2022, 15, 67. [Google Scholar] [CrossRef]
- Chan, J.W.; Yeo, C.K. A Transformer-Based Approach to Electricity Load Forecasting. Electr. J. 2024, 37, 107370. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhang, J.; Wei, Y.M.; Li, D.; Tan, Z.; Zhou, J. Short-Term Electricity Load Forecasting Using a Hybrid Model. Energy 2018, 158, 774–781. [Google Scholar] [CrossRef]
- Bashir, T.; Haoyong, C.; Tahir, M.F.; Liqiang, Z. Short-Term Electricity Load Forecasting Using Hybrid Prophet-LSTM Model Optimized by BPNN. Energy Rep. 2022, 8, 1678–1686. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, Y.; Wang, Q.; Geng, H. A Novel Interpretable Short-Term Load Forecasting Method Based on Kolmogorov–Arnold Networks. IEEE Trans. Power Syst. 2024, 40, 1180–1183. [Google Scholar] [CrossRef]
- Yi, Z.; Xu, Y.; Wang, H.; Sang, L. Coordinated Operation Strategy for a Virtual Power Plant with Multiple DER Aggregators. IEEE Trans. Sustain. Energy 2021, 12, 2445–2458. [Google Scholar] [CrossRef]
- Li, K.; Huang, W.; Hu, G.; Li, J. Ultra-Short-Term Power Load Forecasting Based on CEEMDAN-SE and LSTM Neural Network. Energy Build. 2023, 279, 112666. [Google Scholar] [CrossRef]
- Mounir, N.; Ouadi, H.; Jrhilifa, I. Short-Term Electric Load Forecasting Using an EMD-BiLSTM Approach for Smart Grid Energy Management System. Energy Build. 2023, 288, 113022. [Google Scholar] [CrossRef]
- Liu, F.; Liang, C. Short-Term Power Load Forecasting Based on AC-BiLSTM Model. Energy Rep. 2024, 11, 1570–1579. [Google Scholar] [CrossRef]
- Liu, C.L.; Chang, T.Y.; Yang, J.S.; Huang, K.-B. A Deep Learning Sequence Model Based on Self-Attention and Convolution for Wind Power Prediction. Renew. Energy 2023, 219, 119399. [Google Scholar]
- Somvanshi, S.; Javed, S.A.; Islam, M.M.; Pandit, D.; Das, S. A Survey on Kolmogorov–Arnold Network. ACM Comput. Surv. 2024, 58, 55. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov–Arnold Networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]








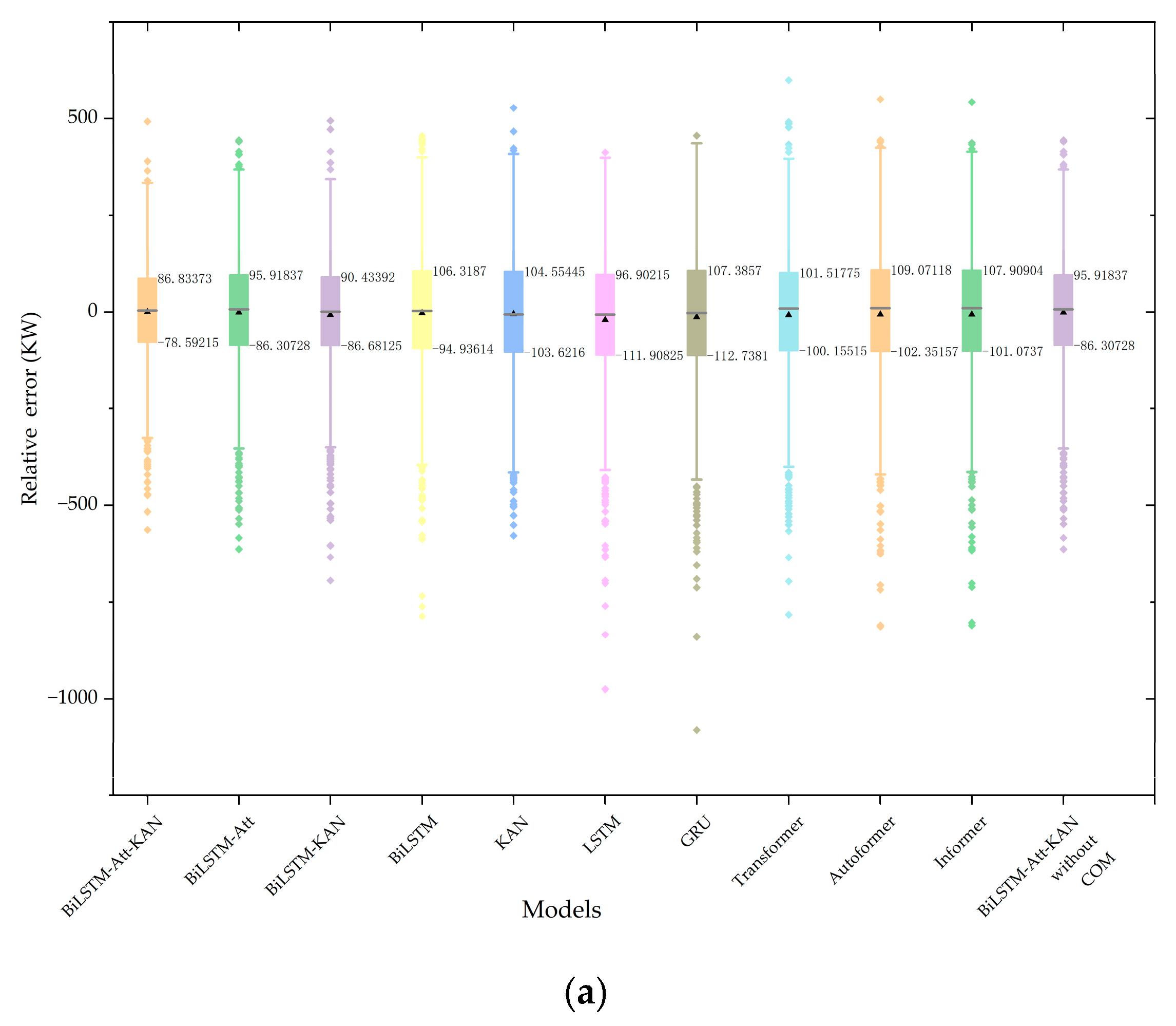
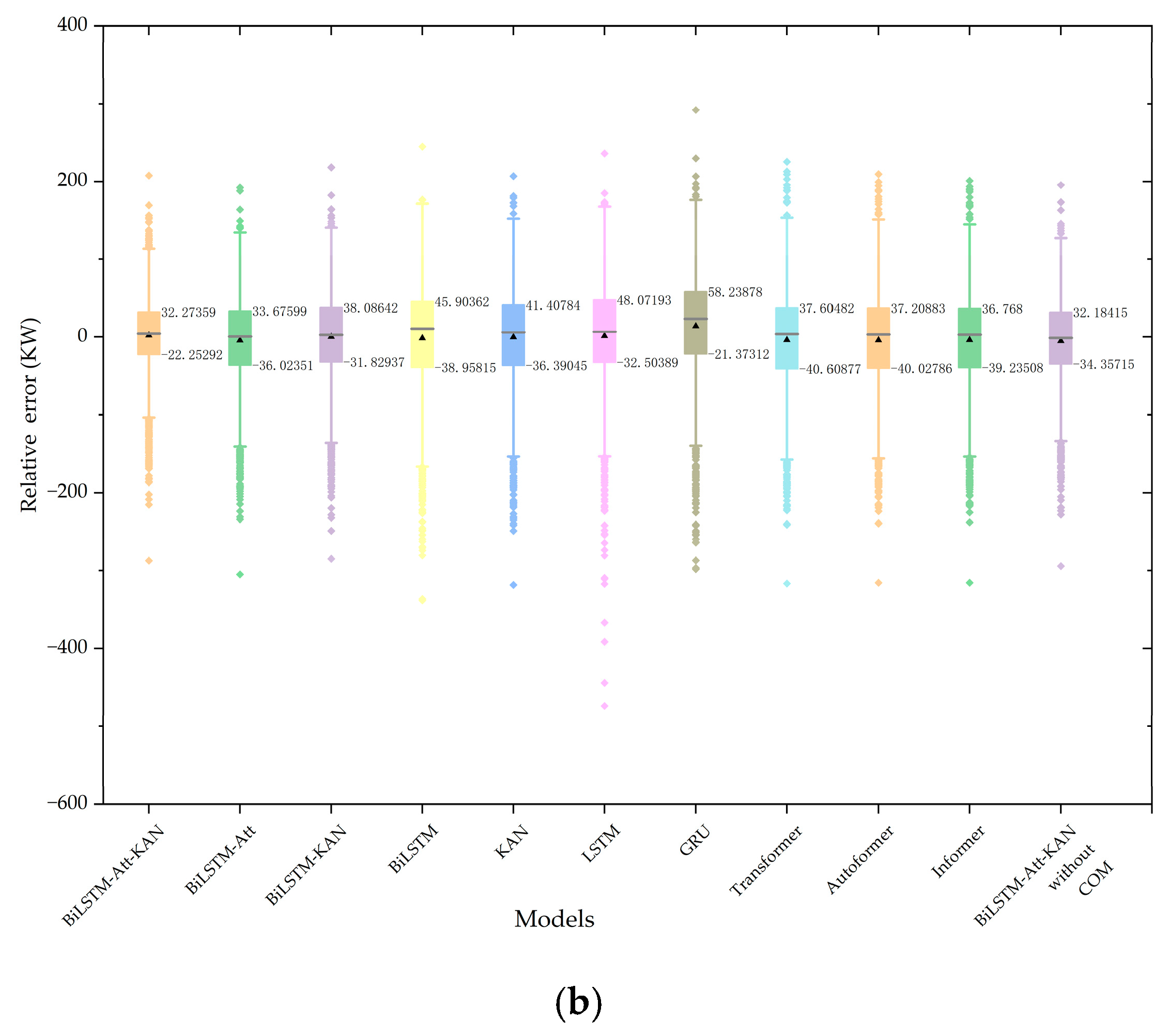
| Case | Models | RMSE | MAE | MAPE (%) | R2 |
|---|---|---|---|---|---|
| Case 1 | BiLSTM-Att-KAN | 141.403 | 106.687 | 6.958 | 0.962 |
| BiLSTM | 172.957 | 130.656 | 8.526 | 0.944 | |
| KAN | 166.437 | 129.631 | 8.455 | 0.948 | |
| LSTM | 181.989 | 136.529 | 8.814 | 0.938 | |
| GRU | 186.851 | 139.494 | 8.899 | 0.934 | |
| Transformer | 174.614 | 132.177 | 8.429 | 0.943 | |
| Informer | 183.387 | 139.976 | 8.959 | 0.937 | |
| Autoformer | 185.136 | 141.282 | 9.044 | 0.935 | |
| Case 2 | BiLSTM-Att-KAN | 53.489 | 39.145 | 10.329 | 0.950 |
| BiLSTM | 71.391 | 54.758 | 17.030 | 0.910 | |
| KAN | 65.560 | 50.111 | 16.489 | 0.924 | |
| LSTM | 73.304 | 54.304 | 15.585 | 0.906 | |
| GRU | 75.397 | 58.498 | 18.821 | 0.900 | |
| Transformer | 66.025 | 49.783 | 15.831 | 0.923 | |
| Informer | 64.594 | 48.683 | 15.177 | 0.927 | |
| Autoformer | 65.183 | 49.153 | 15.426 | 0.925 |
| Case | Models | RMSE | MAE | MAPE (%) | R2 |
|---|---|---|---|---|---|
| Case 1 | BiLSTM-Att-KAN | 141.403 | 106.687 | 6.958 | 0.962 |
| BiLSTM-Att | 159.029 | 119.926 | 7.635 | 0.952 | |
| BiLSTM-KAN | 161.354 | 121.226 | 7.761 | 0.951 | |
| BiLSTM | 172.957 | 130.656 | 8.526 | 0.944 | |
| Case 2 | BiLSTM-Att-KAN | 53.489 | 39.145 | 10.329 | 0.950 |
| BiLSTM-Att | 60.766 | 45.526 | 13.297 | 0.935 | |
| BiLSTM-KAN | 60.062 | 45.223 | 13.616 | 0.937 | |
| BiLSTM | 71.391 | 54.758 | 17.030 | 0.910 |
| Case | Models | RMSE | MAE | MAPE (%) | R2 |
|---|---|---|---|---|---|
| Case 1 | With COM encoding | 141.403 | 106.687 | 6.958 | 0.962 |
| Without COM encoding | 155.009 | 117.076 | 7.535 | 0.955 | |
| Case 2 | With COM encoding | 53.489 | 39.145 | 10.329 | 0.950 |
| Without COM encoding | 58.706 | 43.807 | 12.270 | 0.939 |
| Case | Baseline Models | p-Value |
|---|---|---|
| Case 1 | BiLSTM-Att | <0.001 |
| BiLSTM-KAN | <0.001 | |
| BiLSTM | <0.001 | |
| KAN | <0.001 | |
| LSTM | <0.001 | |
| GRU | <0.001 | |
| Transformer | <0.001 | |
| Informer | <0.001 | |
| Autoformer | <0.001 | |
| BiLSTM-Att-KAN without COM | <0.001 | |
| Case 2 | BiLSTM-Att | <0.001 |
| BiLSTM-KAN | <0.001 | |
| BiLSTM | <0.001 | |
| KAN | <0.001 | |
| LSTM | <0.001 | |
| GRU | <0.001 | |
| Transformer | <0.001 | |
| Informer | <0.001 | |
| Autoformer | <0.001 | |
| BiLSTM-Att-KAN without COM | <0.001 |
| Case | Training Set Ratio | RMSE | MAE | MAPE (%) | R2 |
|---|---|---|---|---|---|
| Case 1 | 10% | 381.674 | 297.382 | 21.397 | 0.698 |
| 30% | 241.521 | 188.411 | 13.144 | 0.880 | |
| 50% | 216.928 | 165.490 | 10.233 | 0.905 | |
| 80% | 141.403 | 106.687 | 6.958 | 0.962 | |
| 90% | 156.116 | 120.019 | 7.824 | 0.960 | |
| Case 2 | 10% | 123.191 | 96.673 | 76.216 | 0.698 |
| 30% | 71.820 | 53.734 | 29.088 | 0.909 | |
| 50% | 65.616 | 48.736 | 36.035 | 0.925 | |
| 80% | 53.489 | 39.145 | 10.329 | 0.950 | |
| 90% | 56.266 | 41.210 | 9.464 | 0.946 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Pu, L.; Yang, D.; Kang, T.; Liang, C.; Peng, M.; Zhai, C. A Virtual Power Plant Load Forecasting Approach Using COM Encoding and BiLSTM-Att-KAN. Energies 2025, 18, 5598. https://doi.org/10.3390/en18215598
Zhu Y, Pu L, Yang D, Kang T, Liang C, Peng M, Zhai C. A Virtual Power Plant Load Forecasting Approach Using COM Encoding and BiLSTM-Att-KAN. Energies. 2025; 18(21):5598. https://doi.org/10.3390/en18215598
Chicago/Turabian StyleZhu, Yong, Liangyi Pu, Di Yang, Tun Kang, Chao Liang, Mingzhi Peng, and Chao Zhai. 2025. "A Virtual Power Plant Load Forecasting Approach Using COM Encoding and BiLSTM-Att-KAN" Energies 18, no. 21: 5598. https://doi.org/10.3390/en18215598
APA StyleZhu, Y., Pu, L., Yang, D., Kang, T., Liang, C., Peng, M., & Zhai, C. (2025). A Virtual Power Plant Load Forecasting Approach Using COM Encoding and BiLSTM-Att-KAN. Energies, 18(21), 5598. https://doi.org/10.3390/en18215598






