Hybrid Drive Simulation Architecture for Power Distribution Based on the Federated Evolutionary Monte Carlo Algorithm
Abstract
1. Introduction
- 1.
- A decomposition method based on spectral clustering is proposed to achieve the multi-subsystem partitioning of distribution networks, providing a structural foundation for distributed reconstruction and collaborative optimization.
- 2.
- A data-driven module based on Long Short-Term Memory (LSTM) networks has been constructed, which achieves the high-precision prediction of distribution system parameters through feature extraction and dynamic mapping mechanisms and provides temporal decision support for reconstruction strategies.
- 3.
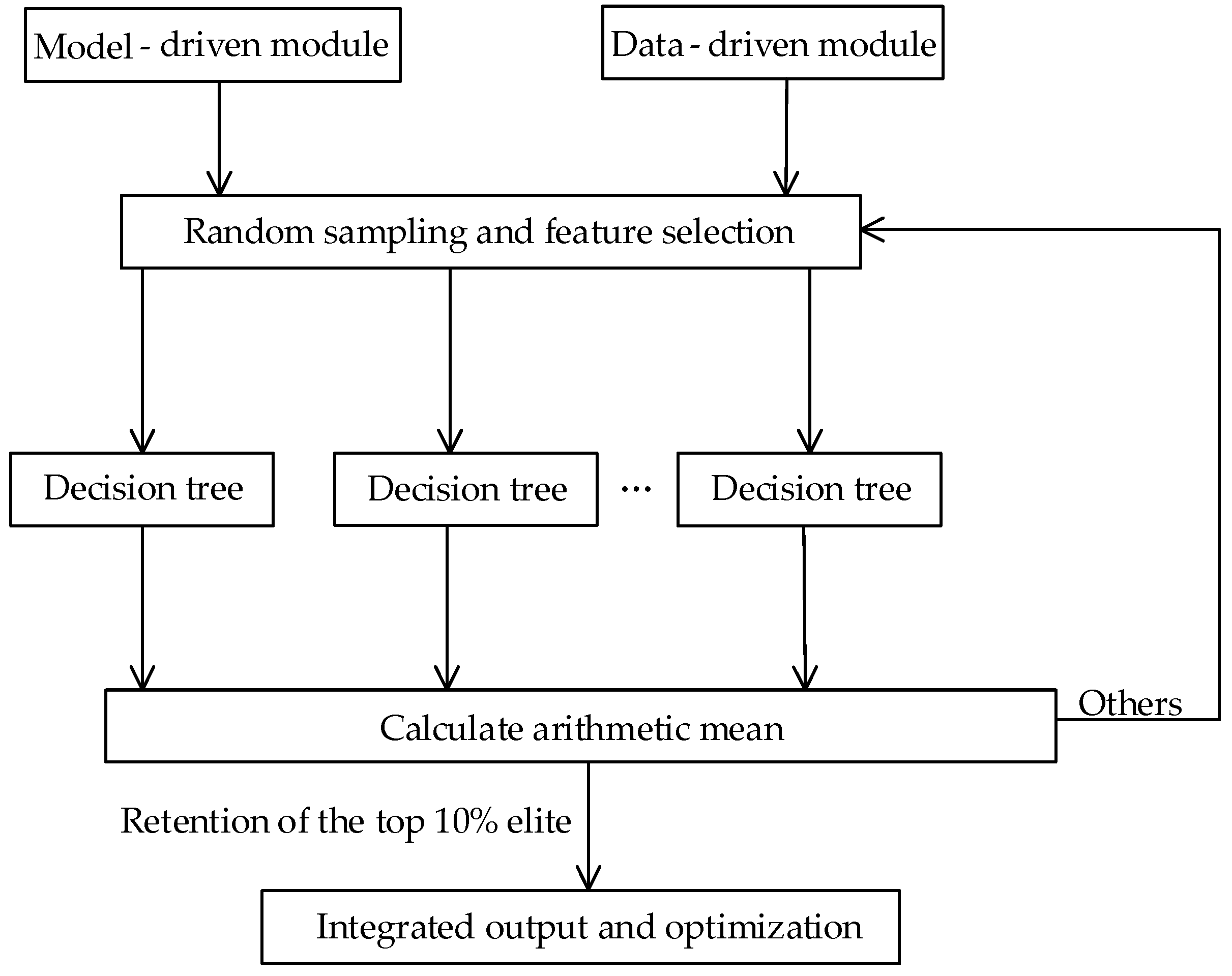
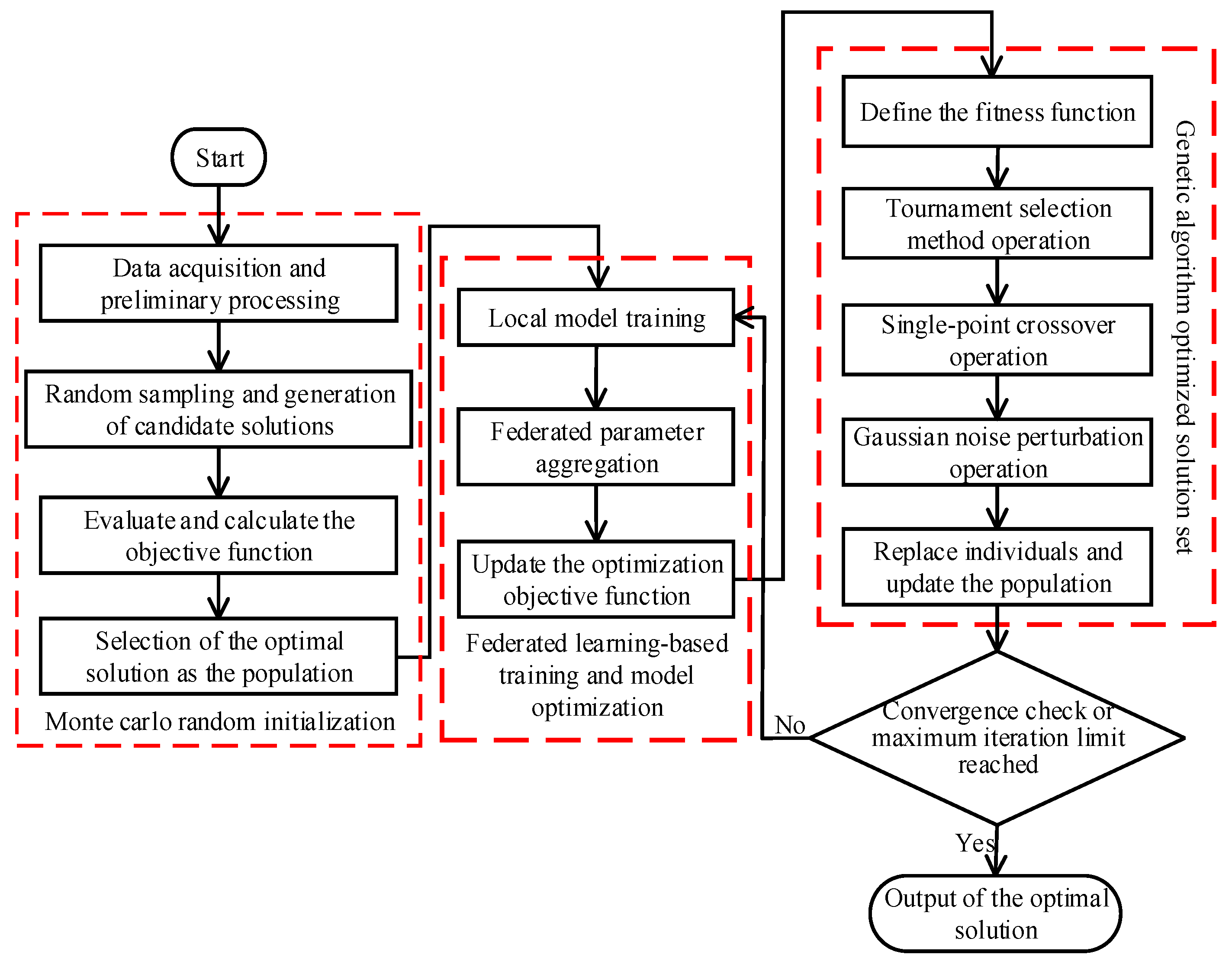
- By integrating the model-driven and data-driven modules through the Random Forest Algorithm and combining them with the FEMCO for optimization, the initial high-quality solution set of the hybrid model is constructed from a global perspective by integrating the global sampling of Monte Carlo, the distributed training of Federated Learning, and the evolutionary optimization mechanism of a Genetic Algorithm. This partially solves the dependence of traditional Genetic Algorithms on initial population selection.
2. Distribution System Model-Driven Module Analysis
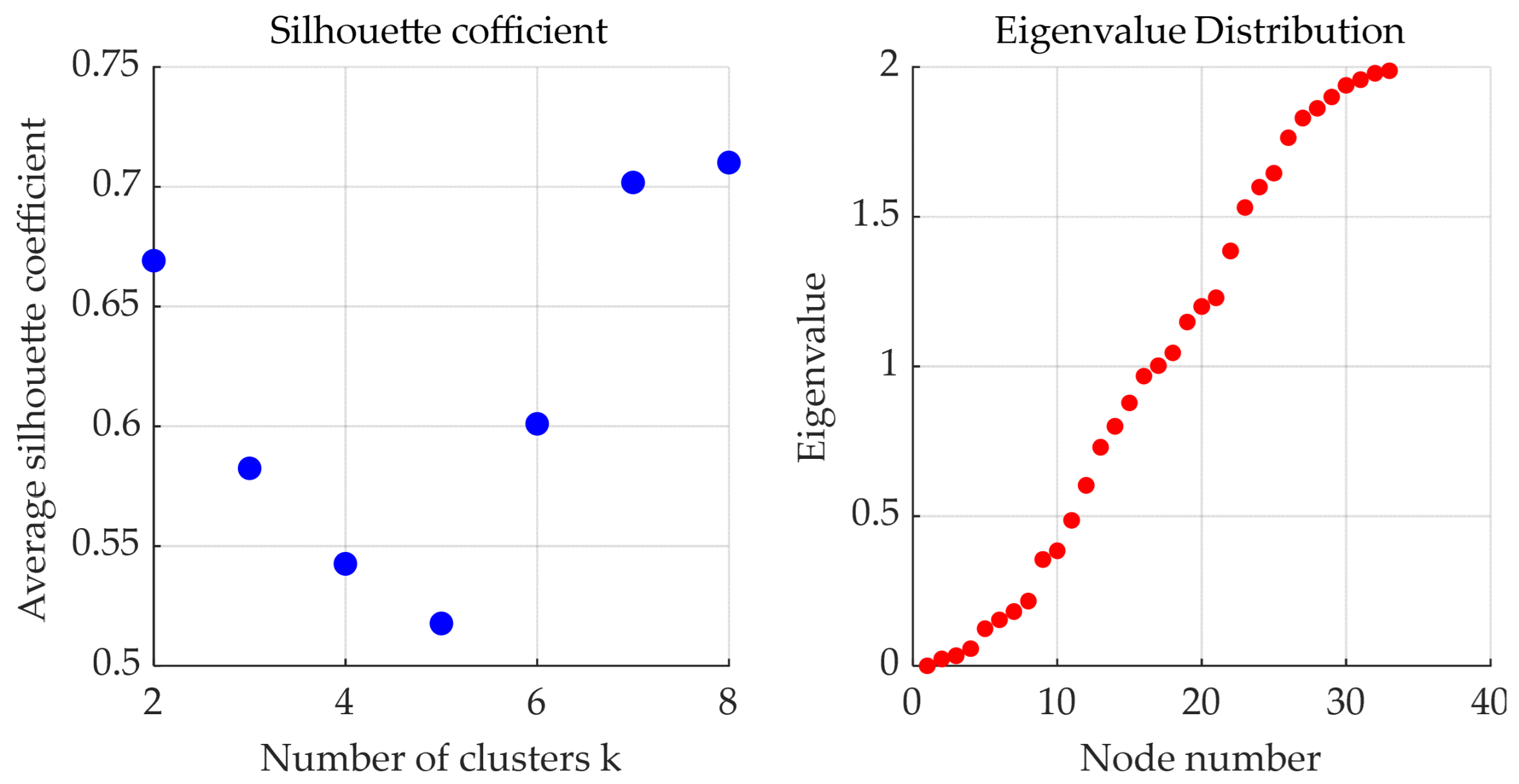
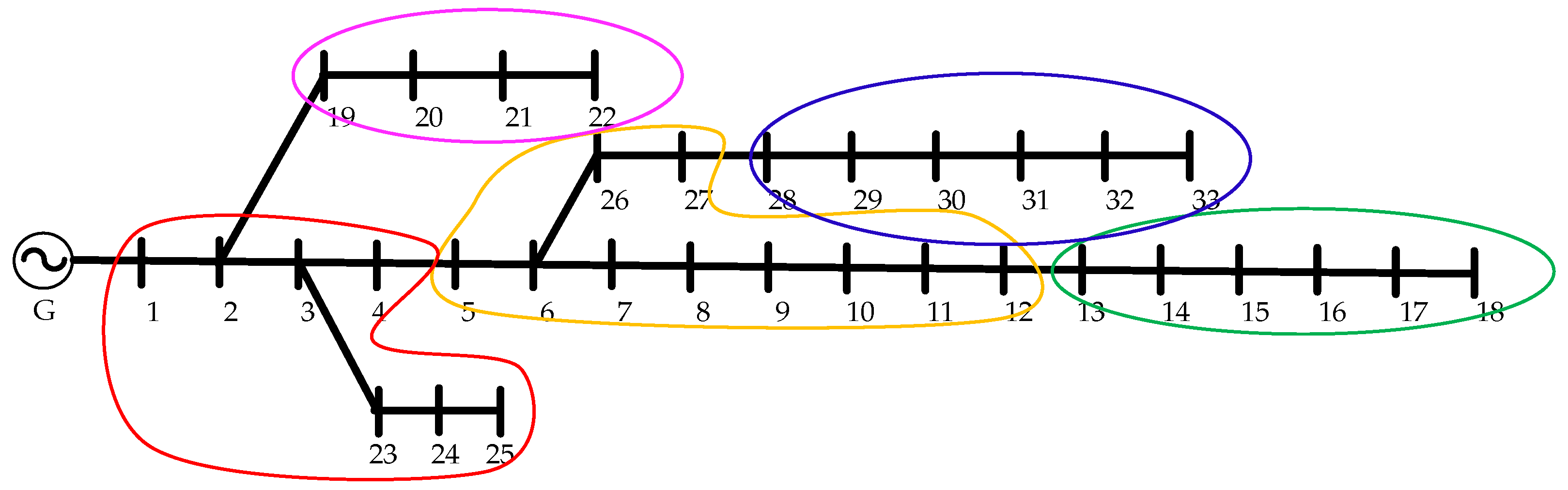
2.1. Spectral Clustering Decomposition Method for Distribution Systems
2.2. Distributed Reconstruction of Subsystems and Gradient Descent Algorithms
3. The Data-Driven Module Analysis of Distribution Systems
4. The Analysis of the Data-Model Hybrid-Driven Framework for the Distribution System
4.1. Integration Method Based on the Random Forest Algorithm
4.2. Operation Optimization Method Based on the FEMCO Algorithm
4.3. Binding Conditions
- (1)
- Nodal power flow equation constraints:
- (2)
- Branch current constraint:
- (3)
- Node voltage constraint:
5. Case Study Analysis
6. Conclusions
- 1.
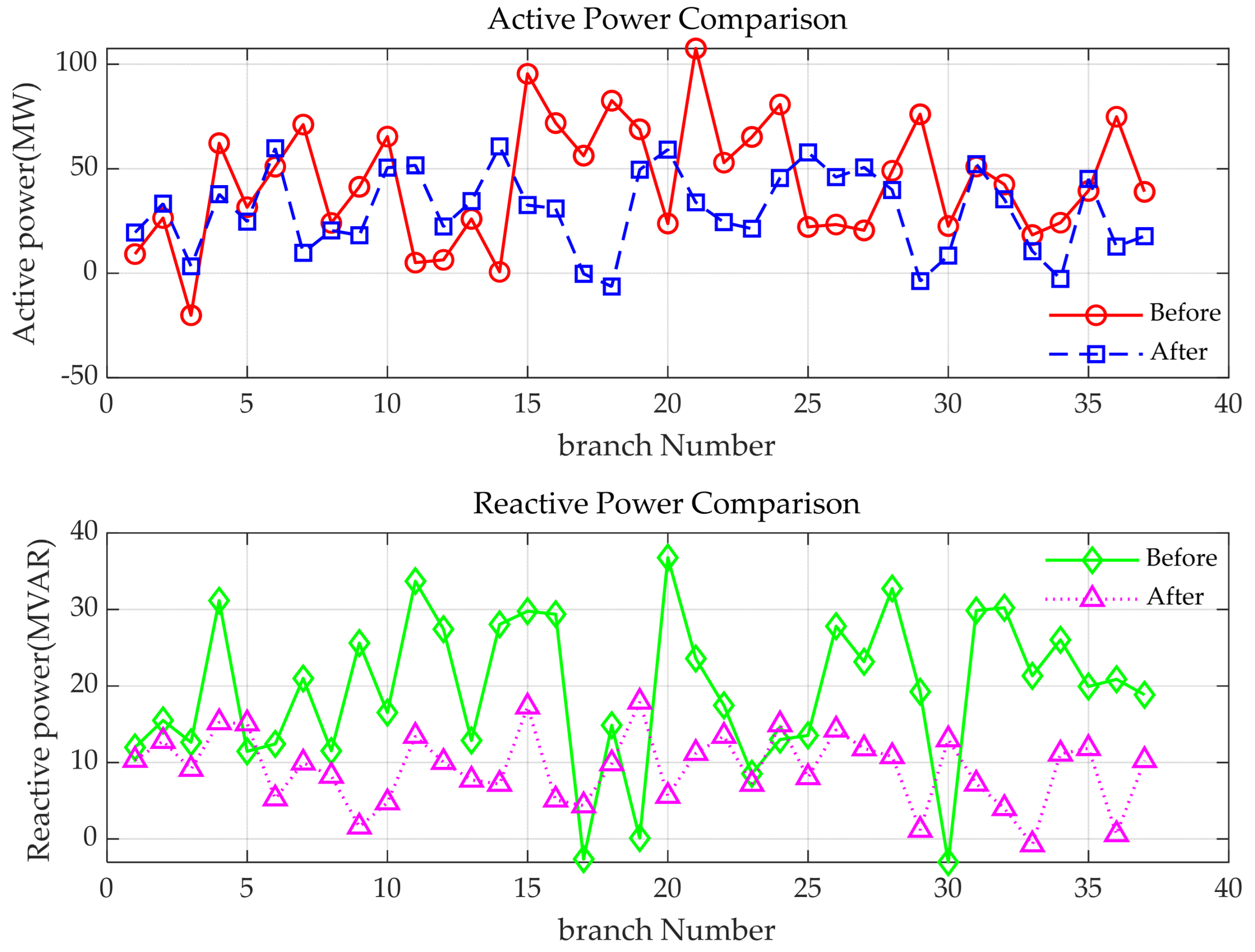
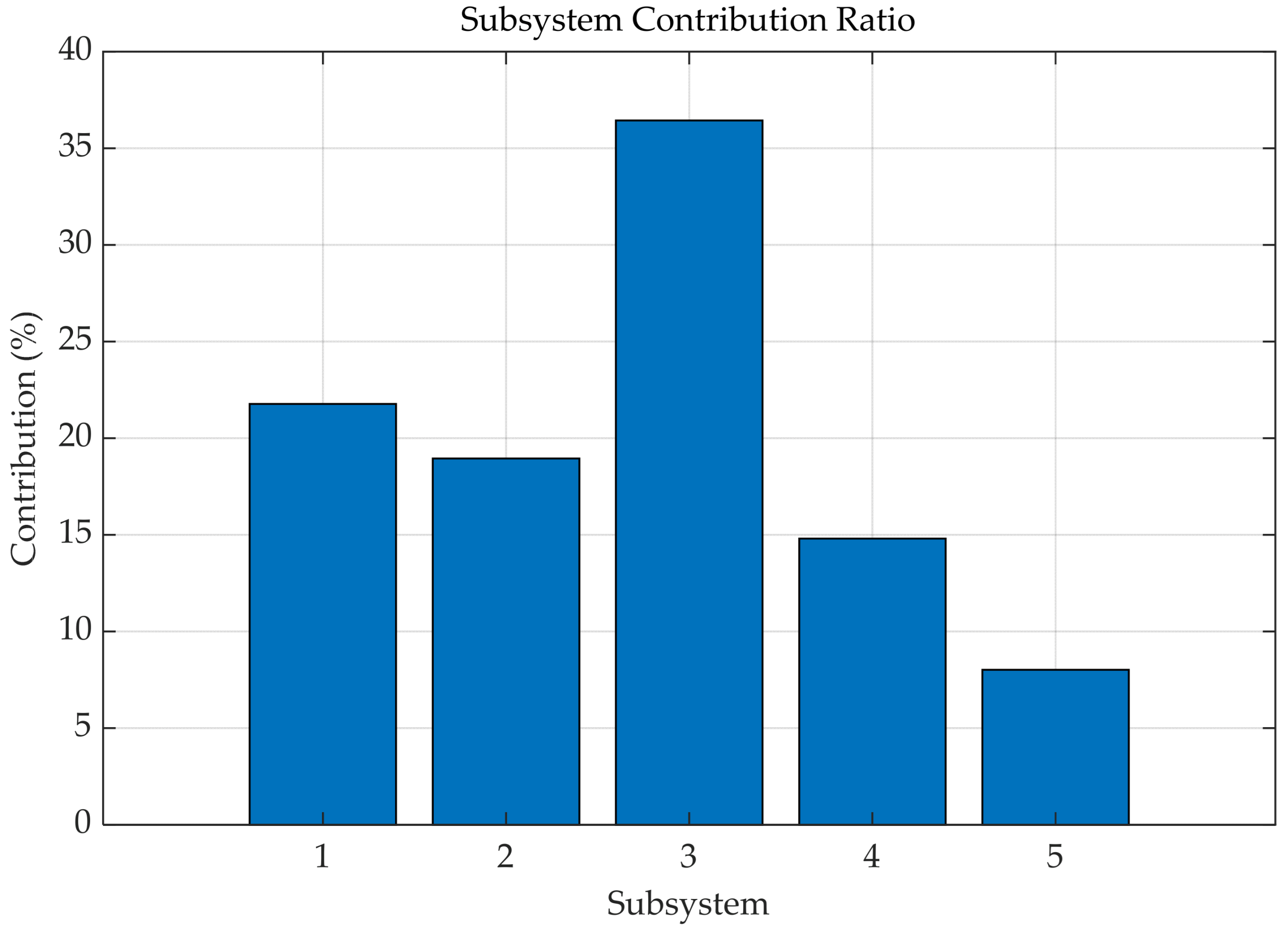
- The proposed model-driven module based on the spectral clustering decomposition method can effectively divide the distribution network into multiple independent subsystems and improve it through a distributed gradient descent algorithm. The experiment in the IEEE 33 bus distribution system shows that this method reduces the fluctuation of active/reactive power in the transmission branch.
- 2.
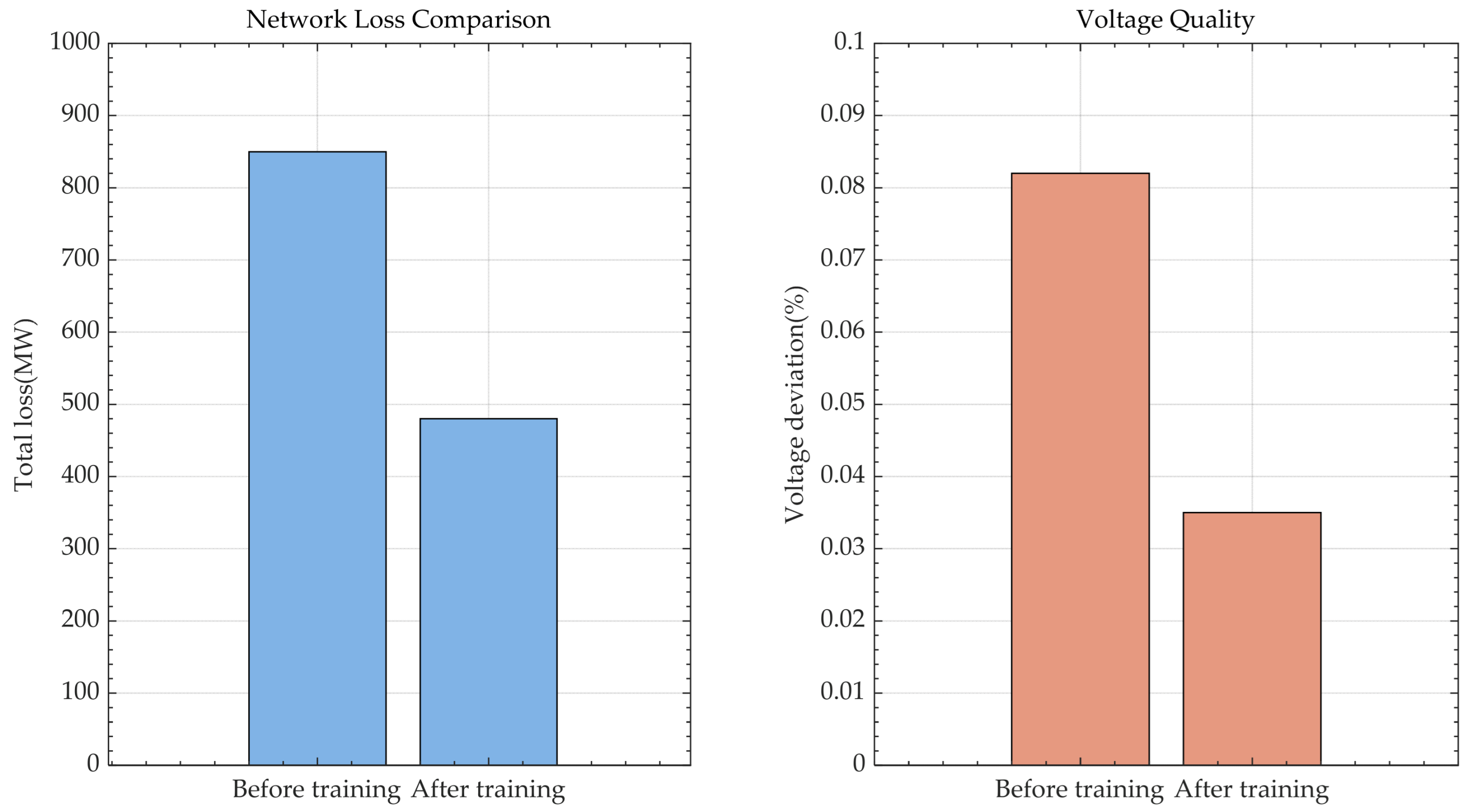
- The data-driven module based on a Long Short-Term Memory (LSTM) network has been constructed, which relies on a gate control mechanism and temporal modeling capability to predict relevant parameters of the distribution network. The case results show that after training, the model can reduce network loss by about 50% and voltage deviation by about 55%. RMSE can be reduced to 0.11, MAE can be reduced to 0.007, and R2 is 0.88, providing effective data support for the reconstruction strategy.
- 3.
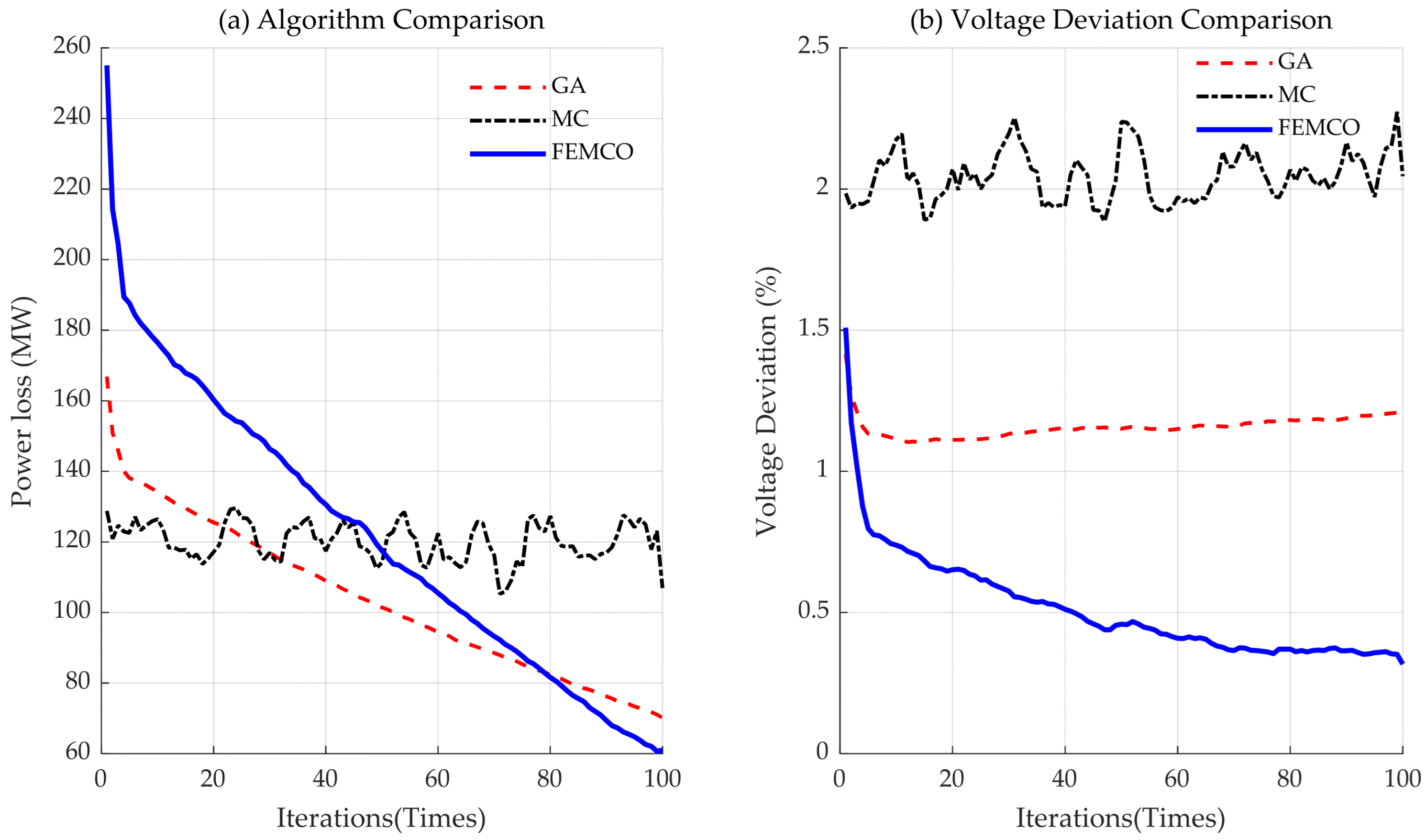
- By using the Random Forest algorithm to integrate model-driven and data-driven modules, combined with the FEMCO algorithm for optimization, the case shows that the algorithm exhibits excellent convergence stability on the IEEE 33 bus distribution system. Compared with the traditional Genetic Algorithm (GA) and Monte Carlo method (MC), FEMCO reduces power loss by about 25% and 45% and voltage deviation by 75% and 85%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Flueck., J.A.; Nguyen., P.C. Agent-Based Distributed Volt/Var Control With Distributed Power Flow Solver in Smart Grid. IEEE Trans. Smart Grid 2016, 7, 600–607. [Google Scholar] [CrossRef]
- Borghetti, A.; Bottura, R.; Barbiroli, M.; Nucci, C.A. Synchrophasors-Based Distributed Secondary Voltage/VAR Control via Cellular Network. IEEE Trans. Smart Grid 2017, 8, 262–274. [Google Scholar] [CrossRef]
- Ding, F.; Loparo, K.A. Hierarchical Decentralized Network Reconfiguration for Smart Distribution Systems-Part I: Problem Formulation and Algorithm Development. IEEE Trans. Power Syst. Publ. Power Eng. Soc. 2015, 30, 734–743. [Google Scholar] [CrossRef]
- Bahramipanah, M.; Cherkaoui, R.; Paolone, M. Decentralized voltage control of clustered active distribution network by means of energy storage systems. Electr. Power Syst. Res. 2016, 36, 370–382. [Google Scholar] [CrossRef]
- Jabr, R.A.; Singh, R.; Pal, B.C. Minimum Loss Network Reconfiguration Using Mixed-Integer Convex Programming. IEEE Trans. Power Syst. Publ. Power Eng. Soc. 2012, 27, 1106–1115. [Google Scholar] [CrossRef]
- Lee, C.; Liu, C.; Mehrotra, S.; Bie, Z. Robust Distribution Network Reconfiguration. IEEE Trans. Smart Grid 2015, 6, 836–842. [Google Scholar] [CrossRef]
- Dorostkar-Ghamsari, M.R.; Fotuhi-Firuzabad, M.; Lehtonen, M.; Safdarian, A. Value of Distribution Network Reconfiguration in Presence of Renewable Energy Resources. IEEE Trans. Power Syst. Publ. Power Eng. Soc. 2016, 31, 1879–1888. [Google Scholar] [CrossRef]
- Abdelaziz, M. Distribution network reconfiguration using a genetic algorithm with varying population size. Electr. Power Syst. Res. 2017, 142, 9–11. [Google Scholar] [CrossRef]
- Asrari, A.; Lotfifard, S.; Ansari, M. Reconfiguration of Smart Distribution Systems with Time Varying Loads Using Parallel Computing. IEEE Trans. Smart Grid 2016, 7, 2713–2723. [Google Scholar] [CrossRef]
- Zhou, Y.; Arghandeh, R.; Spanos, C.J. Partial Knowledge Data-Driven Event Detection for Power Distribution Networks. IEEE Trans. Smart Grid 2018, 9, 5152–5162. [Google Scholar] [CrossRef]
- Mishra, D.P.; Samantaray, S.R.; Joos, G. A Combined Wavelet and Data-Mining Based Intelligent Protection Scheme for Microgrid. IEEE Trans. Smart Grid 2016, 7, 2295–2304. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, B.; Sun, H.; Wang, B.; Yang, Y.; Liu, H.; Lin, C.; Wang, S. Energy Management and Distributed Resource Cluster Control in Active Distribution Networks. Autom. Electr. Power Syst. 2020, 44, 111–118. [Google Scholar] [CrossRef]
- Li, P.; Zhang, C.; Wu, Z.; Xu, Y.; Hu, M.; Dong, Z. Distributed Adaptive Robust Voltage/VAR Control with Network Partition in Active Distribution Networks. IEEE Trans. Smart Grid 2020, 11, 2245–2256. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, D.; Li, X.; Zhang, R.; Li, G. Distributed Optimization Control of Voltage in Active Distribution Networks with Distributed Photovoltaics. Electr. Power Autom. Equip. 2021, 41, 102–109. [Google Scholar] [CrossRef]
- Kou, L.; Wu, M.; Li, Y.; Qu, X.; Xie, H.; Gao, B.; Chen, F.; Hu, C. Distributed optimization and control method for active and reactive power in active distribution networks. Chin. J. Electr. Eng. 2020, 40, 1856–1865. [Google Scholar] [CrossRef]
- Li, X.; Huang, Y.; Yin, X. A Genetic Algorithm for Distribution Network Reconfiguration Based on an Improved Strategy. Chin. J. Electr. Eng. 2004, 02, 50–55. [Google Scholar] [CrossRef]
- Li, M.; Wang, L.; Liu, X.; Yang, D.; Li, P. Multi-objective proactive reconfiguration of distribution networks based on a well-matched genetic algorithm. Electr. Power Syst. Prot. Control. 2019, 47, 30–38. [Google Scholar]
- Wang, C.; Gao, Y. Determination of Power Distribution Network Configuration Using Non-Revisiting Genetic Algorithm. IEEE Trans. Power Syst. Publ. Power Eng. Soc. 2013, 28, 3638–3648. [Google Scholar] [CrossRef]
- Ma, C.; Li, C.; Zhang, X.; Li, G.; Han, Y. Reconfiguration of Distribution Networks with Distributed Generation Using a Dual Hybrid Particle Swarm Optimization Algorithm. Math. Probl. Eng. 2017, 2017, 1517435. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhong, J.; Li, Q.; Qin, M.; Tian, J.; Tian, B.; Long, Y. Application of a Hybrid Particle Swarm Optimization Algorithm in the Reconfiguration of Distribution Networks with Distributed Generation. Electr. Autom. 2019, 41, 55–57. [Google Scholar]
- Ding, T.; Yang, Q.; Yang, Y.; Li, C.; Bie, Z.; Blaabjerg, F. A Data-Driven Stochastic Reactive Power Optimization Considering Uncertainties in Active Distribution Networks and Decomposition Method. IEEE Trans. Smart Grid 2018, 9, 4994–5004. [Google Scholar] [CrossRef]
- Wang, D.; Sun, Z. Power Consumer-Side Big Data Analysis and Parallel Load Forecasting. Chin. J. Electr. Eng. 2015, 35, 527–537. [Google Scholar] [CrossRef]
- Yang, G.; Qian, A. Demand-side Response Strategy of Multi-microgrids Based on an Improved Co-evolution Algorithm. CSEE J. Power Energy Syst. 2021, 7, 903–910. [Google Scholar] [CrossRef]
- Kamel, M.; Dai, R.; Wang, Y.; Li, F.; Liu, G. Data-driven and Model-based Hybrid Reinforcement Learning to Reduce Stress on Power Systems Branches. CSEE J. Power Energy Syst. 2021, 7, 433–442. [Google Scholar] [CrossRef]
- Yu, Y.; Li, M.; Ji, T.; Wu, Q.H. Fault Location in Distribution System Using Convolutional Neural Network Based on Domain Transformation. CSEE J. Power Energy Syst. 2021, 7, 472–484. [Google Scholar] [CrossRef]
- Wei, L.; Liu, G.; Yan, S.; Dai, R.; Tang, Y. Graph Computing Based Security Constrained Unit Commitment in Hydro-thermal Power Systems Incorporating Pumped Hydro Storage. CSEE J. Power Energy Syst. 2021, 7, 485–496. [Google Scholar] [CrossRef]
- Finegan, D.P.; Zhu, J.; Feng, X.; Keyser, M.; Ulmefors, M.; Li, W.; Bazant, M.Z.; Cooper, S.J. The Application of Data-Driven Methods and Physics-Based Learning for Improving Battery Safety. Joule 2020, 5, 316–329. [Google Scholar] [CrossRef]
- Matignon, M.; Mcharek, M.; Azib, T.; Chaibet, A. Enhancing Fuel Cell Hybrid Electric Vehicle Energy Management with Real-Time LSTM Speed Prediction. Energies 2025, 18, 4340. [Google Scholar] [CrossRef]
- Miceli, A.V.; Cardona, F.; Lo Brano, V.; Micari, F. Assessing the Technical and Economic Viability of Onshore and Offshore Wind Energy in Pakistan Through a Data-Driven Machine Learning and Deep Learning Approach. Energies 2025, 18, 5080. [Google Scholar] [CrossRef]
- Sankhwar, P. Evaluation of transition to 100% electric vehicles (EVs) by 2052 in the United States. Sustain. Energy Res. 2024, 11, 35. [Google Scholar] [CrossRef]


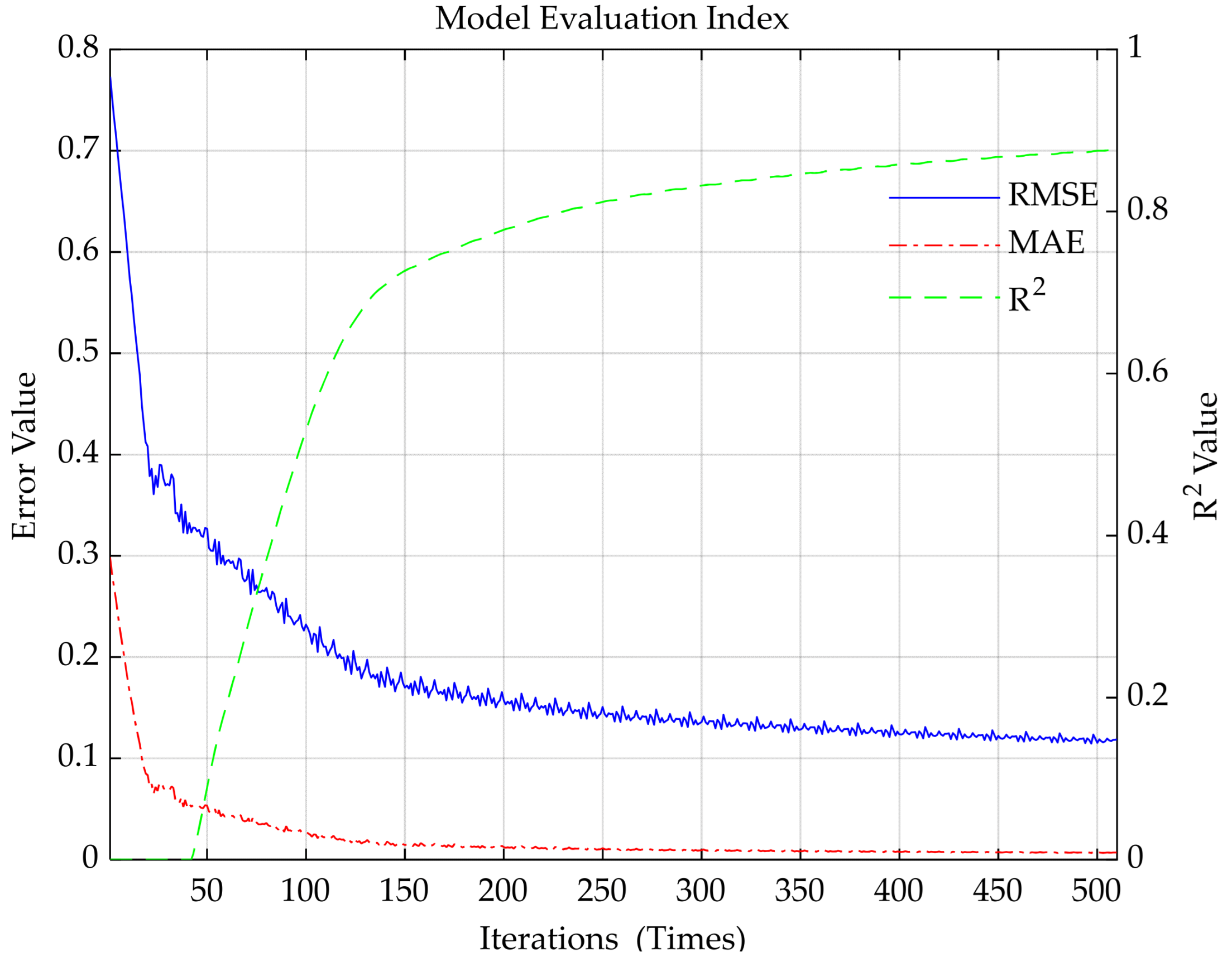


| Iterations | RMSE | MAE | R2 |
|---|---|---|---|
| 1 | 0.7731 | 0.2988 | 0 |
| 50 | 0.3267 | 0.0534 | 0.0885 |
| 100 | 0.2321 | 0.0269 | 0.5299 |
| 150 | 0.1698 | 0.0144 | 0.7269 |
| 200 | 0.1570 | 0.0123 | 0.7774 |
| 250 | 0.1507 | 0.0114 | 0.8119 |
| 300 | 0.1358 | 0.0100 | 0.8319 |
| 350 | 0.1258 | 0.0083 | 0.8464 |
| 400 | 0.1238 | 0.0077 | 0.8580 |
| 450 | 0.1224 | 0.0075 | 0.8674 |
| 500 | 0.1154 | 0.0067 | 0.8750 |
| 510 | 0.1188 | 0.0071 | 0.8756 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, D.; Yang, X.; Sheng, W.; Liu, K.; Jin, T.; Li, X.; Dong, W. Hybrid Drive Simulation Architecture for Power Distribution Based on the Federated Evolutionary Monte Carlo Algorithm. Energies 2025, 18, 5595. https://doi.org/10.3390/en18215595
Jia D, Yang X, Sheng W, Liu K, Jin T, Li X, Dong W. Hybrid Drive Simulation Architecture for Power Distribution Based on the Federated Evolutionary Monte Carlo Algorithm. Energies. 2025; 18(21):5595. https://doi.org/10.3390/en18215595
Chicago/Turabian StyleJia, Dongli, Xiaoyu Yang, Wanxing Sheng, Keyan Liu, Tingyan Jin, Xiaoming Li, and Weijie Dong. 2025. "Hybrid Drive Simulation Architecture for Power Distribution Based on the Federated Evolutionary Monte Carlo Algorithm" Energies 18, no. 21: 5595. https://doi.org/10.3390/en18215595
APA StyleJia, D., Yang, X., Sheng, W., Liu, K., Jin, T., Li, X., & Dong, W. (2025). Hybrid Drive Simulation Architecture for Power Distribution Based on the Federated Evolutionary Monte Carlo Algorithm. Energies, 18(21), 5595. https://doi.org/10.3390/en18215595








