Investigation of Roadway Anti-Icing Without Auxiliary Heat Using Hydronic Heated Pavements Coupled with Borehole Thermal Energy Storage
Abstract
1. Introduction
2. Development of Numerical Model
2.1. Overview of Modeling Approach
2.2. Modeling of HHPS-G
2.3. Modeling of BTES
3. Analysis of Pavement-Based Heat-Storage Performance According to BTES Installation Depth and Number
3.1. Overview of Parametric Analysis
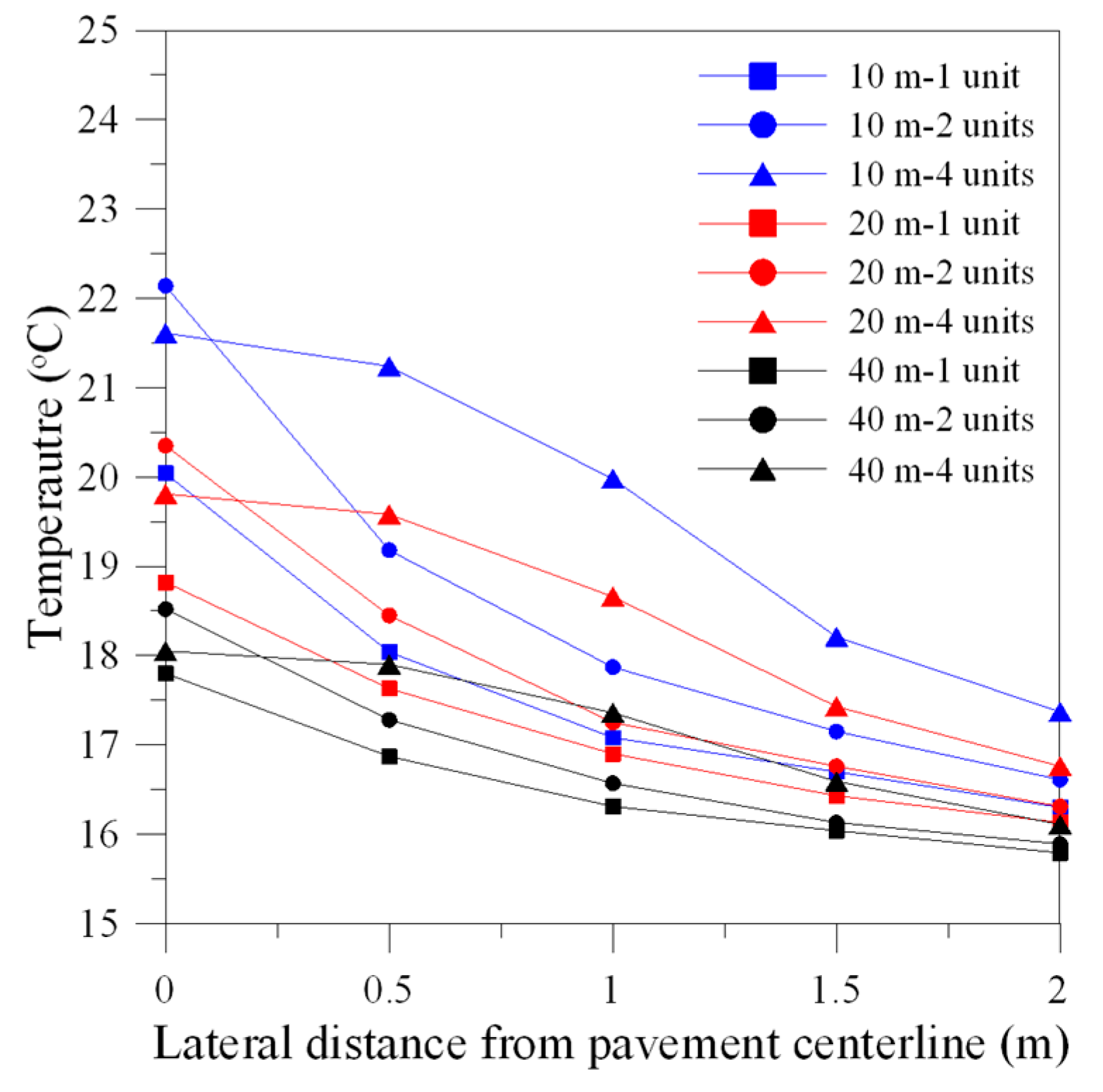
3.2. Parametric Analysis Results
4. Analysis of Anti-Icing Performance Using Heat Stored in BTES
5. Discussion
6. Conclusions
- (1)
- Model credibility was established through comparisons with prior experiments. The HHPS-G slab-heating replication and the BTES borehole-heating replication showed small errors, supporting the credibility of the component models used in the coupled analysis.
- (2)
- Using the validated methodology, a coupled HHPS-G–BTES model was developed. Increasing the depth of BTES consistently outperformed simply adding pipe units. Summer pavement cooling improved, and long-term drift diminished, while subsurface overheating was suppressed and total stored heat increased. Adding units at shallow depth yielded diminishing returns due to inter-borehole interference.
- (3)
- Under an anti-icing criterion (surface temperature at or above 0 °C), 40 m 4 units maintained a clear margin throughout winter, whereas 10 m–1 unit approached the threshold late in the period. Thus, a depth-first design is the most rational primary choice for robust auxiliary-free anti-icing.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, D.; Jung, S.; Yoon, S. Risk prediction for winter road accidents on expressways. Appl. Sci. 2021, 11, 9534. [Google Scholar] [CrossRef]
- Kristufek, L. The Effect of De-icing Salts on the Chemistry of the Pore Solution in Cement Pastes and Their Influence on Rebar Corrosion. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2020. [Google Scholar]
- Fournier, I.B.; Lovejoy, C.; Vincent, W.F. Road salt versus urban snow effects on lake microbial communities. Microorganisms 2022, 10, 803. [Google Scholar] [CrossRef]
- Hintz, W.D.; Fay, L.; Relyea, R.A. Road salts, human safety, and the rising salinity of our fresh waters. Front. Ecol. Environ. 2022, 20, 22–30. [Google Scholar] [CrossRef]
- Guelpa, E.; Verda, V. Thermal energy storage in district heating and cooling systems: A review. Appl. Energy 2019, 252, 113474. [Google Scholar] [CrossRef]
- Tian, Z.; Zhang, S.; Deng, J.; Fan, J.; Huang, J.; Kong, W.; Perers, B.; Furbo, S. Large-scale solar district heating plants in Danish smart thermal grid: Developments and recent trends. Energy Convers. Manag. 2019, 189, 67–80. [Google Scholar] [CrossRef]
- Yang, T.; Liu, W.; Kramer, G.J.; Sun, Q. Seasonal thermal energy storage: A techno-economic literature review. Renew. Sustain. Energy Rev. 2021, 139, 1–22. [Google Scholar] [CrossRef]
- Bott, C.; Dressel, I.; Bayer, P. State-of-technology review of water-based closed seasonal thermal energy storage systems. Renew. Sustain. Energy Rev. 2019, 113, 109241. [Google Scholar] [CrossRef]
- Mahon, H.; O’Connor, D.; Friedrich, D.; Hughes, B. A review of thermal energy storage technologies for seasonal loops. Energy 2022, 239, 122207. [Google Scholar] [CrossRef]
- Villasmil, W.; Fischer, L.J.; Worlitschek, J. A review and evaluation of thermal insulation materials and methods for thermal energy storage systems. Renew. Sustain. Energy Rev. 2019, 103, 71–84. [Google Scholar] [CrossRef]
- Chaib, M.; Benatiallah, A.; Dahbi, A.; Hachemi, N.; Baira, F.; Boublia, A.; Ernst, B.; Alam, M.; Benguerba, Y. Long-term performance analysis of a large-scale photoVoltaic plant in extreme desert conditions. Renew. Energy 2024, 236, 121426. [Google Scholar] [CrossRef]
- Schmidt, T.; Pauschinger, T.; Sørensen, P.A.; Snijders, A.; Djebbar, R.; Boulter, R.; Thornton, J. Design aspects for large-scale pit and aquifer thermal energy storage for district heating and cooling. Energy Procedia 2018, 149, 585–594. [Google Scholar] [CrossRef]
- Dahash, A.; Ochs, F.; Janetti, M.B.; Streicher, W. Advances in seasonal thermal energy storage for solar district heating applications: A critical review on large-scale hot- water tank and pit thermal energy storage systems. Appl. Energy 2019, 239, 296–315. [Google Scholar] [CrossRef]
- Fleuchaus, P.; Godschalk, B.; Stober, I.; Blum, P. Worldwide application of aquifer thermal energy storage—A review. Renew. Sustain. Energy Rev. 2018, 94, 861–876. [Google Scholar] [CrossRef]
- Fleuchaus, P.; Schüppler, S.; Godschalk, B.; Bakema, G.; Blum, P. Performance analysis of aquifer thermal energy storage (ATES). Renew. Energy 2020, 146, 1536–1548. [Google Scholar] [CrossRef]
- Shi, G.; Xi, S.; Wei, Z.; Li, C. Heat transfer performance of silicon carbide high thermal conductivity concrete energy piles. Int. J. Green Energy 2025, 22, 1185–1196. [Google Scholar] [CrossRef]
- Park, S.; Lee, S.; Sung, C.; Choi, H. Applicability evaluation of cast-in-place energy piles based on two-year heating and cooling operation. Renew. Sustain. Energy Rev. 2021, 143, 110906. [Google Scholar] [CrossRef]
- Park, S.; Lee, D.; Lee, S.; Ahn, D.; Choi, H. Effect of thermal interference on energy pile considering various configurations of heat exchangers. Energy Build. 2019, 199, 381–401. [Google Scholar] [CrossRef]
- Park, S.; Lee, S.; Oh, K.; Kim, D.; Choi, H. Engineering chart for thermal performance of cast-in-place energy pile considering thermal resistance. Appl. Therm. Eng. 2018, 130, 899–921. [Google Scholar] [CrossRef]
- Park, S.; Lee, S.; Park, S.; Choi, H. Empirical formulas for borehole thermal resistance of parallel U-type cast-in-place energy pile. Renew. Energy 2022, 197, 211–227. [Google Scholar] [CrossRef]
- Sibbitt, B.; McClenahan, D.; Djebbar, R.; Thornton, J.; Wong, B.; Carriere, J.; Kokko, J. The performance of a high solar fraction seasonal storage district heating system–five years of operation. Energy Procedia 2012, 30, 856–865. [Google Scholar] [CrossRef]
- Gao, W.; Qadrdan, M.; Chaudry, M.; Wu, J. Seasonal Storage of Heat in Boreholes; Technical note; UK Energy Research Centre: London, UK, 2023. [Google Scholar]
- Liu, X.; Rees, S.J.; Spitler, J.D. Modeling snow melting on heated pavement surfaces. Part I: Model development. Appl. Therm. Eng. 2007, 27, 1115–1124. [Google Scholar]
- Zhao, W.; Chen, X.; Zhang, Y.; Su, W.; Xu, F.; Li, B. Deicing performances of a road unit driven by a hydronic heating system in severely cold regions of China. Comput. Math. Appl. 2021, 81, 838–850. [Google Scholar] [CrossRef]
- Wu, X.; Ma, M.; Lu, J.; Su, L.; Yuan, X.; Chen, H.; Ishnazarov, O. A Passive Geothermal-Based Approach to Snow Melting Using Natural Circulation. Heat Transf. Eng. 2025, 46, 1–15. [Google Scholar] [CrossRef]
- Tan, Y.Q.; Zhang, C.; Xu, H.; Tian, D. Snow melting and deicing characteristics and pavement performance of active deicing and snow melting pavement. China J. Highw. Transp. 2019, 32, 1–17. [Google Scholar]
- Ziegler, W.; Nixon, C. Geothermal System for Airport Pavement Snowmelt and Terminal Cooling (No. DOT/FAA/TC-23/38); Department of Transportation, Federal Aviation Administration, William J. Hughes Technical Center: Washington, DC, USA, 2023. [Google Scholar]
- Shen, W.; Ceylan, H.; Gopalakrishnan, K.; Kim, S.; Taylor, P.C.; Rehmann, C.R. Life cycle assessment of heated apron pavement system operations. Transp. Res. Part D Transp. Environ. 2016, 48, 316–331. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Y.; Li, L.; Su, W.; Li, B.; Fu, Z. Snow melting on the road surface driven by a geothermal system in the severely cold region of China. Sustain. Energy Technol. Assess. 2020, 40, 100781. [Google Scholar] [CrossRef]
- Jaiswal, P.; Anupam, B.R.; Chandrappa, A.K.; Sahoo, U.C. Harvesting heat energy using geothermal and hydronic pavements for sustainable cities: A comprehensive review of an emerging idea. Sustain. Cities Soc. 2023, 93, 104539. [Google Scholar] [CrossRef]
- Guldentops, G.; Nejad, A.M.; Vuye, C.; Rahbar, N. Performance of a pavement solar energy collector: Model development and validation. Appl. Energy 2016, 163, 180–189. [Google Scholar] [CrossRef]
- Baumgaertel, S.; Schweighofer, J.A.; Rohn, J.; Luo, J. The performance of geothermal passive heating and cooling for asphalt and concrete pavement. Dev. Built Environ. 2021, 7, 100051. [Google Scholar] [CrossRef]
- Ghalandari, T.; Baetens, R.; Verhaert, I.; Nasir, D.S.; Vuye, C. Thermal performance of a controllable pavement solar collector prototype with configuration flexibility. Appl. Energy 2022, 313, 118908. [Google Scholar] [CrossRef]
- Lim, H.; Lee, S.; Lee, J. Effective snow removal devices for road pavement using geothermal heat pipe. Appl. Therm. Eng. 2025, 265, 125624. [Google Scholar] [CrossRef]
- Zhao, W.; Su, W.; Li, L.; Zhang, Y.; Li, B. Optimization design of the road unit in a hydronic snow melting system with porous snow. J. Therm. Anal. Calorim. 2020, 141, 1509–1517. [Google Scholar] [CrossRef]
- Johnsson, J. Winter Road Maintenance Using Renewable Thermal. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2017. [Google Scholar]
- Mirzanamadi, R.; Hagentoft, C.E.; Johansson, P. Numerical investigation of harvesting solar energy and anti-icing road surfaces using a hydronic heating pavement and borehole thermal energy storage. Energies 2018, 11, 3443. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. COMSOL Multiphysics Heat Transfer Module User’s Guide 5.5; COMSOL Inc.: Burlington, MA, USA, 2019. [Google Scholar]
- Lee, S.; Park, S.; Han, T.H.; Won, J.; Choi, H. Applicability evaluation of energy slabs installed in an underground parking lot. Sustainability 2023, 15, 2973. [Google Scholar] [CrossRef]
- Park, S.; Lee, D.; Lee, S.; Chauchois, A.; Choi, H. Experimental and numerical analysis on thermal performance of large-diameter cast-in-place energy pile constructed in soft ground. Energy 2017, 118, 297–311. [Google Scholar] [CrossRef]
- Côté, J.; Konrad, J.M. Thermal conductivity of base-course materials. Can. Geotech. J. 2005, 42, 61–78. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, D.H.; Moon, K.H.; Falchetto, A.C.; Kim, J.C.; Jeong, J.H. Development of representative section selection method for large-scale concrete pavement remodeling project based on trial and error correction approach. Int. J. Pavement Res. Technol. 2019, 12, 17–25. [Google Scholar] [CrossRef]
- Choi, H.J.; Kim, S.; Kim, Y.; Won, J. Predicting frost depth of soils in south Korea using machine learning techniques. Sustainability 2022, 14, 9767. [Google Scholar] [CrossRef]
- Adl-Zarrabi, B.; Gehlin, S.; Cetin, A.; Staudacher, L. Ground source de-icing and snow melting systems for infrastructure. Transp. Res. Procedia 2023, 72, 1621–1628. [Google Scholar] [CrossRef]
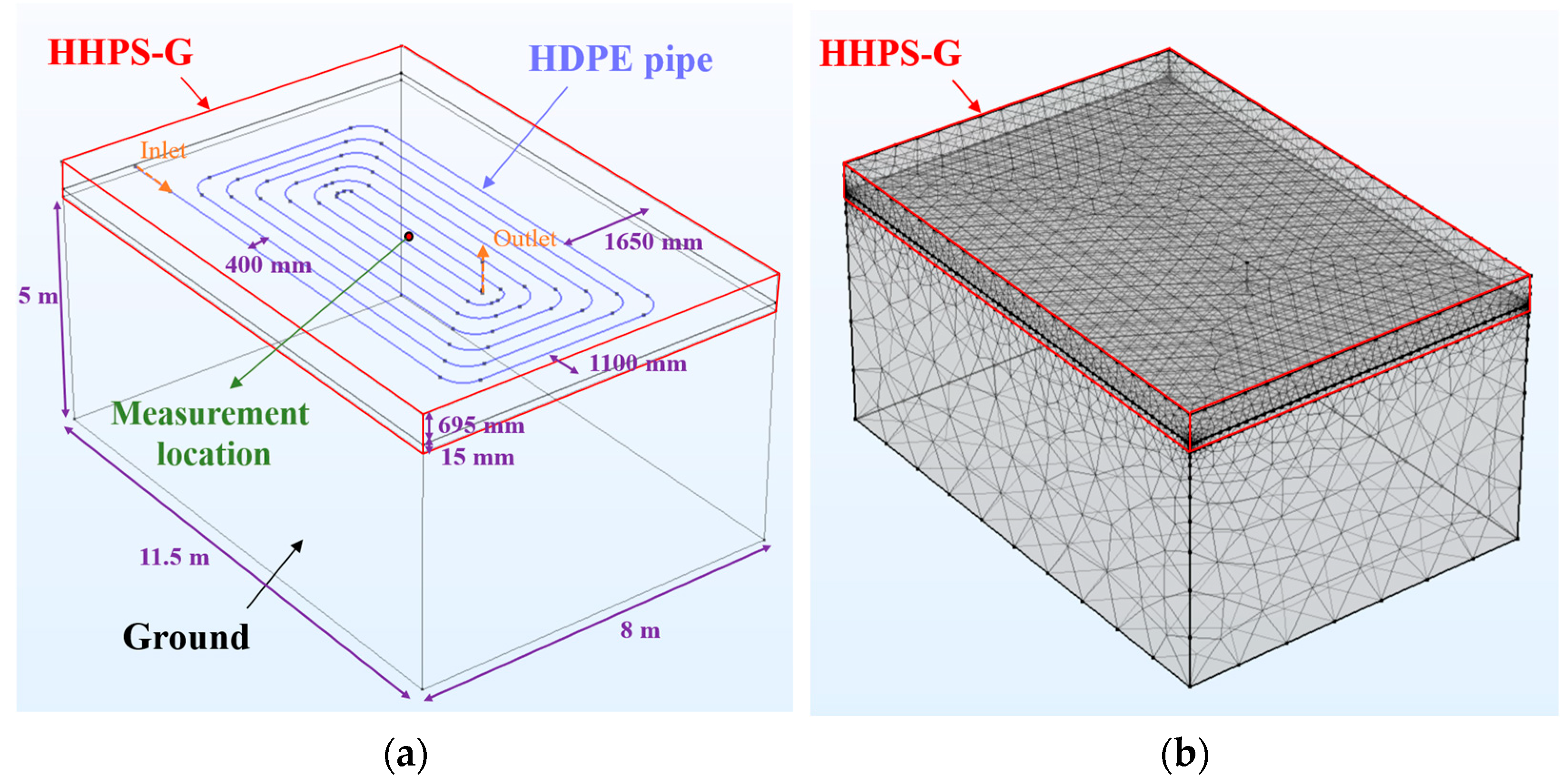














| Concrete Slab | Heat Exchange Pipe | ||||
|---|---|---|---|---|---|
| Area | Thickness | Installation depth | Length | Inner diameter | Outer diameter |
| 49.5 m2 | 710 mm | 695 mm | 123 m | 24.6 mm | 31.8 mm |
| Materials | Density (kg/m3) | Specific Heat Capacity (J/kg·K) | Thermal Conductivity (W/m·K) |
|---|---|---|---|
| Concrete | 2300 | 880 | 2.0 |
| Ground | 2400 | 2300 | 1.3 |
| Water | 998 | 4182 | 0.6 |
| HDPE pipe | 955 | 525 | 0.4 |
| Borehole (m) | Heat Exchange Pipe | ||||
|---|---|---|---|---|---|
| Diameter | Length | Installation depth | Length | Inner diameter | Outer diameter |
| 1.5 m | 60 m | Until 30 m | 103 m | 27.0 mm | 35.0 mm |
| Materials | Density (kg/m3) | Specific Heat Capacity (J/kg·K) | Thermal Conductivity (W/m·K) |
|---|---|---|---|
| Concrete | 2162 | 800 | 2.1 |
| Ground | 1700 | 2500 | 1.7 |
| Ref. | System | Pipe Geometry | Flow Rate (L/min) | Inlet Temp. (°C) | Operation | Mean Error (%) | RMSE (°C) |
|---|---|---|---|---|---|---|---|
| Lee et al. [39] | HHPS-G | 123 m HDPE pipe in a concrete slab | 7.6 | 25 | 8 h on/16 h off | 2.15 | 0.50 |
| Park et al. [40] | BTES | 103 m HDPE pipe in a 30 m-long borehole | 2.56 | 30 | 8 h on/16 h off | 0.75 | 0.13 |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Borehole depth (m) | 10 | 20 | 40 | ||||||
| Number of units | 1 | 2 | 4 | 1 | 2 | 4 | 1 | 2 | 4 |
| Total pipe length (m) | 26.85 | 46.51 | 85.82 | 46.85 | 86.51 | 165.82 | 86.85 | 166.51 | 325.82 |
| Materials | Density (kg/m3) | Specific Heat Capacity (J/kg·K) | Thermal Conductivity (W/m·K) |
|---|---|---|---|
| Concrete | 2162 | 800 | 2.1 |
| Thermal insulation layer | 1000 | 750 | 0.018 |
| Basecourse | 2000 | 900 | 1.5 |
| Subbase | 1800 | 850 | 1.2 |
| Ground | 1800 | 850 | 1.2 |
| Simulation Case | at 2 m Offset (°C) | (MJ) | |
|---|---|---|---|
| 10 m-deep BTES | 1 unit | 1.30 | 79.56 |
| 2 units | 1.61 | 98.53 | |
| 4 units | 2.37 | 145.04 | |
| 20 m-deep BTES | 1 unit | 1.13 | 138.31 |
| 2 units | 1.31 | 160.34 | |
| 4 units | 1.76 | 215.42 | |
| 40 m-deep BTES | 1 unit | 0.79 | 193.39 |
| 2 units | 0.89 | 217.87 | |
| 4 units | 1.11 | 271.73 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Abbasi, A.F.; Ullah, H.; Ha, W.; Lee, S. Investigation of Roadway Anti-Icing Without Auxiliary Heat Using Hydronic Heated Pavements Coupled with Borehole Thermal Energy Storage. Energies 2025, 18, 5546. https://doi.org/10.3390/en18205546
Park S, Abbasi AF, Ullah H, Ha W, Lee S. Investigation of Roadway Anti-Icing Without Auxiliary Heat Using Hydronic Heated Pavements Coupled with Borehole Thermal Energy Storage. Energies. 2025; 18(20):5546. https://doi.org/10.3390/en18205546
Chicago/Turabian StylePark, Sangwoo, Annas Fiaz Abbasi, Hizb Ullah, Wonjae Ha, and Seokjae Lee. 2025. "Investigation of Roadway Anti-Icing Without Auxiliary Heat Using Hydronic Heated Pavements Coupled with Borehole Thermal Energy Storage" Energies 18, no. 20: 5546. https://doi.org/10.3390/en18205546
APA StylePark, S., Abbasi, A. F., Ullah, H., Ha, W., & Lee, S. (2025). Investigation of Roadway Anti-Icing Without Auxiliary Heat Using Hydronic Heated Pavements Coupled with Borehole Thermal Energy Storage. Energies, 18(20), 5546. https://doi.org/10.3390/en18205546






