Beyond R2: The Role of Polynomial Degree in Modeling External Temperature and Its Impact on Heat-Pump Energy Demand
Abstract
1. Introduction
2. Materials and Methods
- Statistical accuracy relative to the reference series (RMSE, R2);
- Deviations in seasonal heat demand Qseason, electricity demand Eel, and the seasonal coefficient of performance SCOP;
- Changes in peak power (peak space–heating heat rate) and (seasonal peak electrical input power);
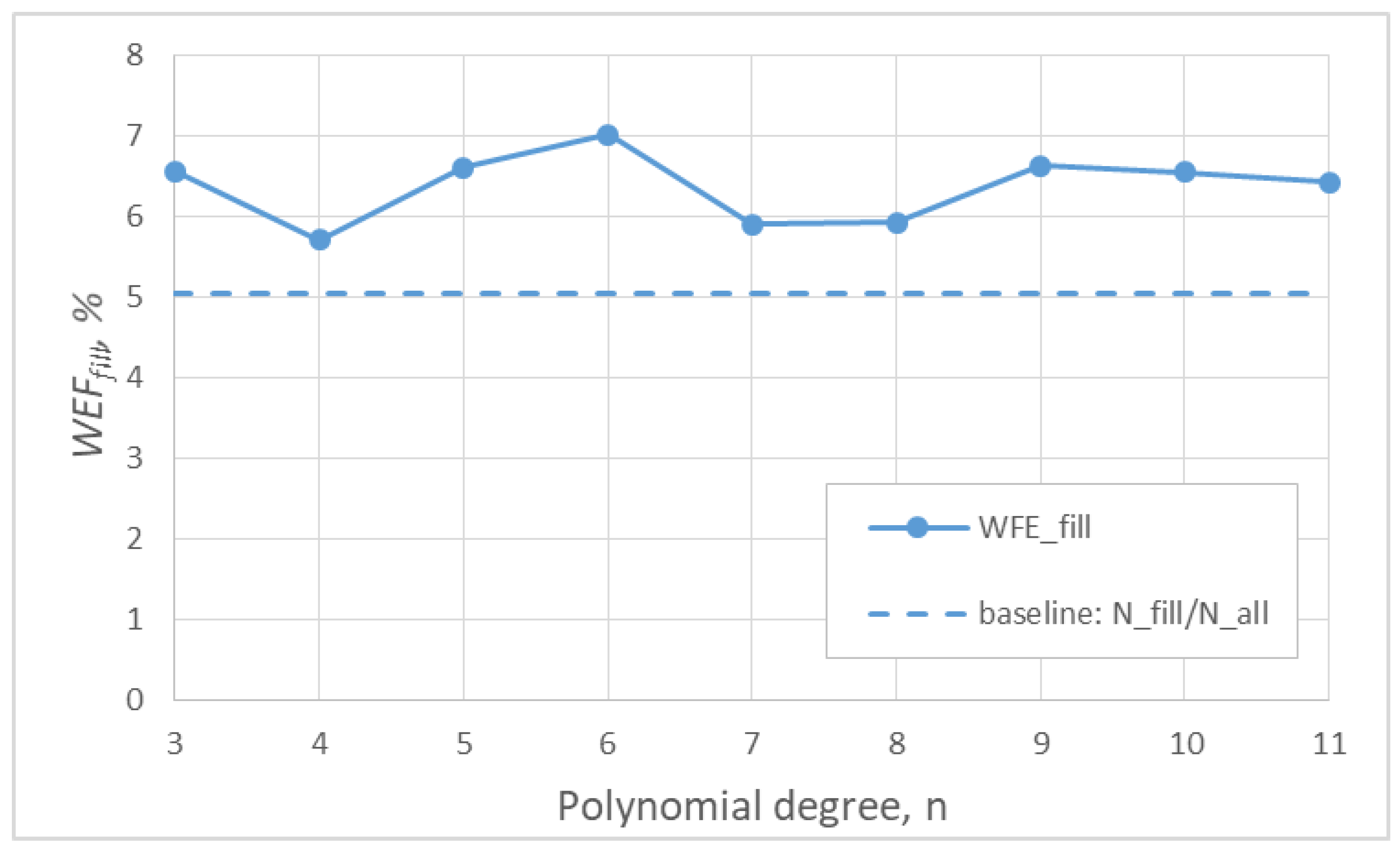
- Share of error originating solely from gaps (WFEfill);
- Computational complexity and susceptibility to overfitting.
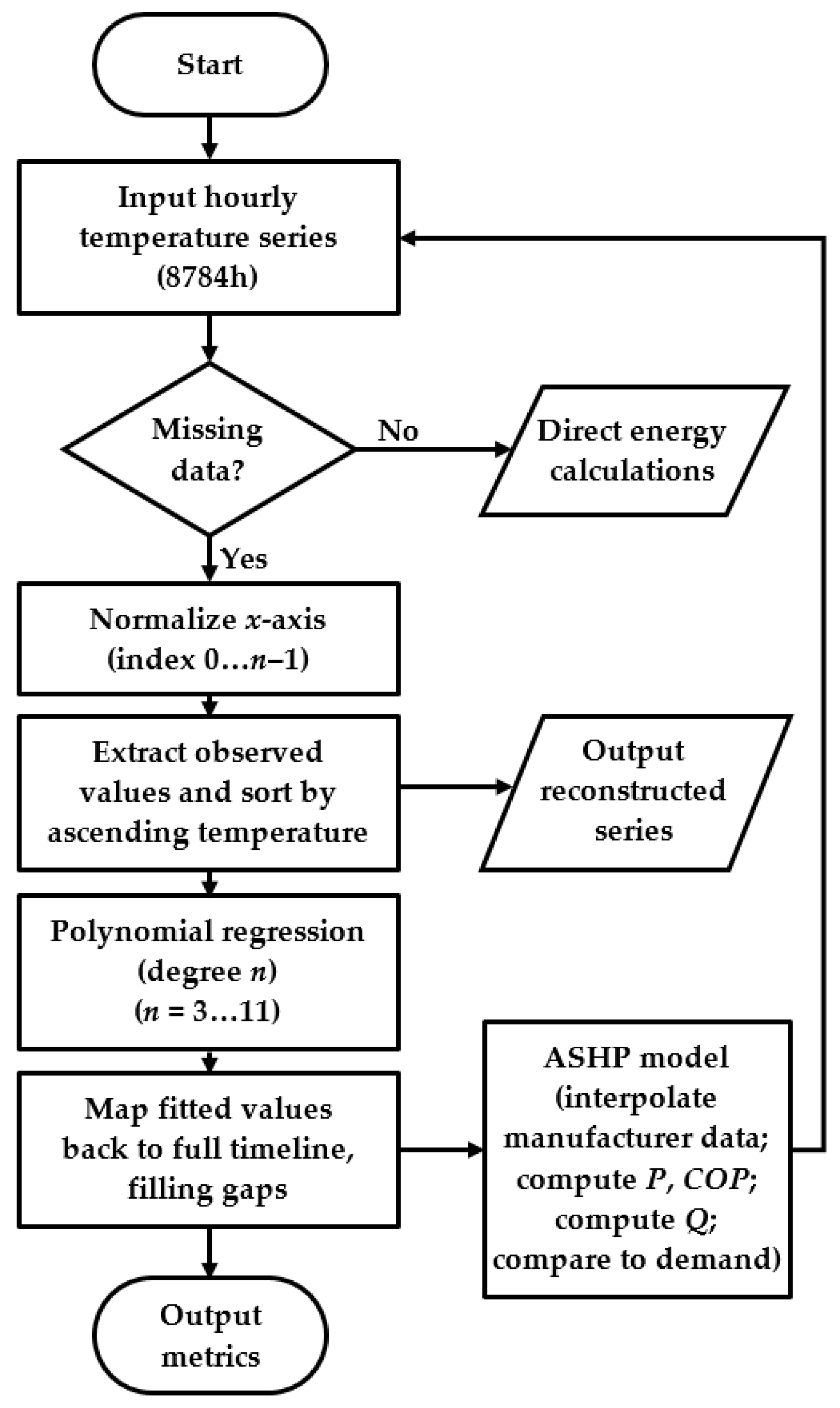
2.1. Method Overview
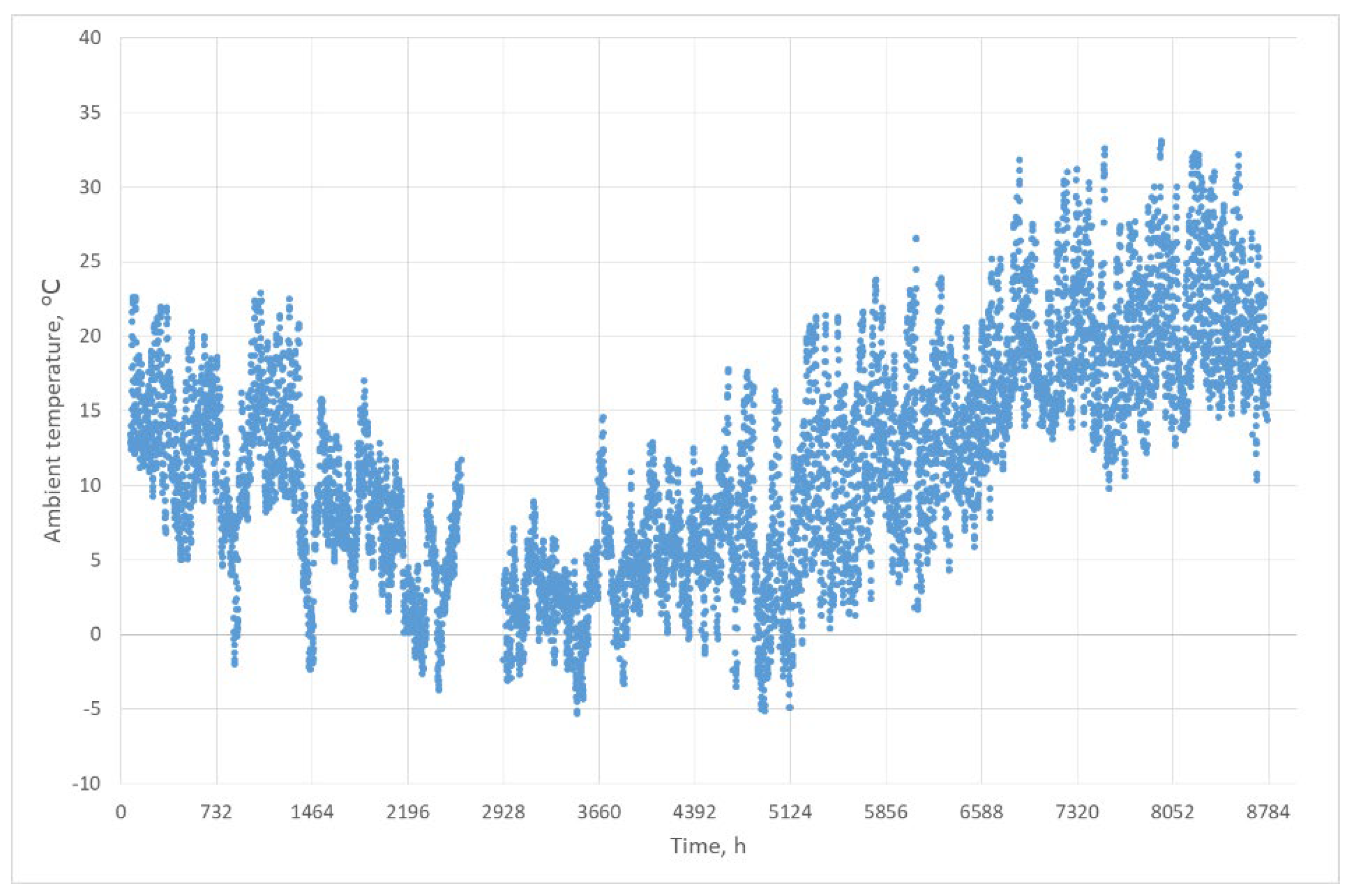
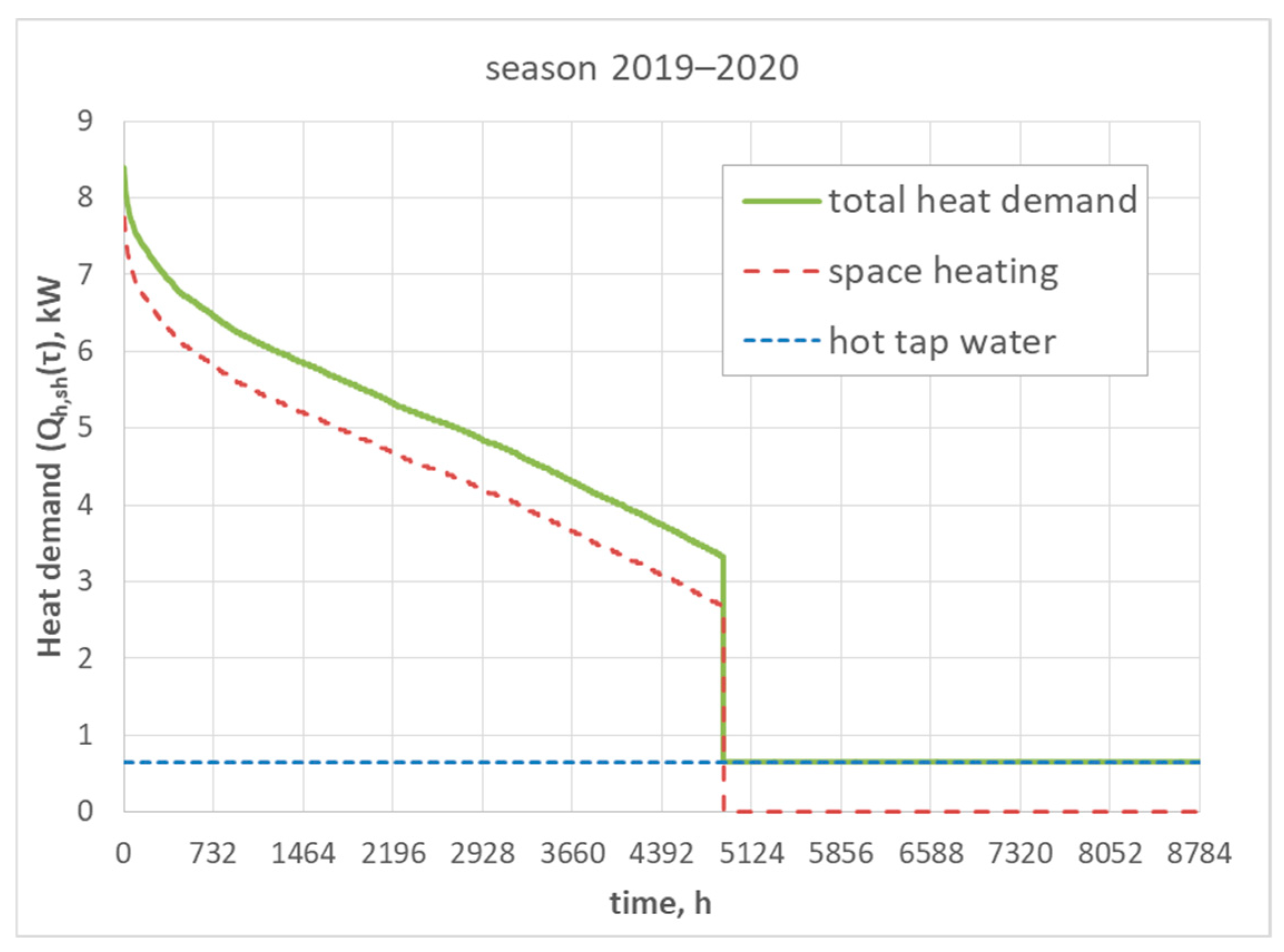
2.2. Data Source and Preliminary Data Processing
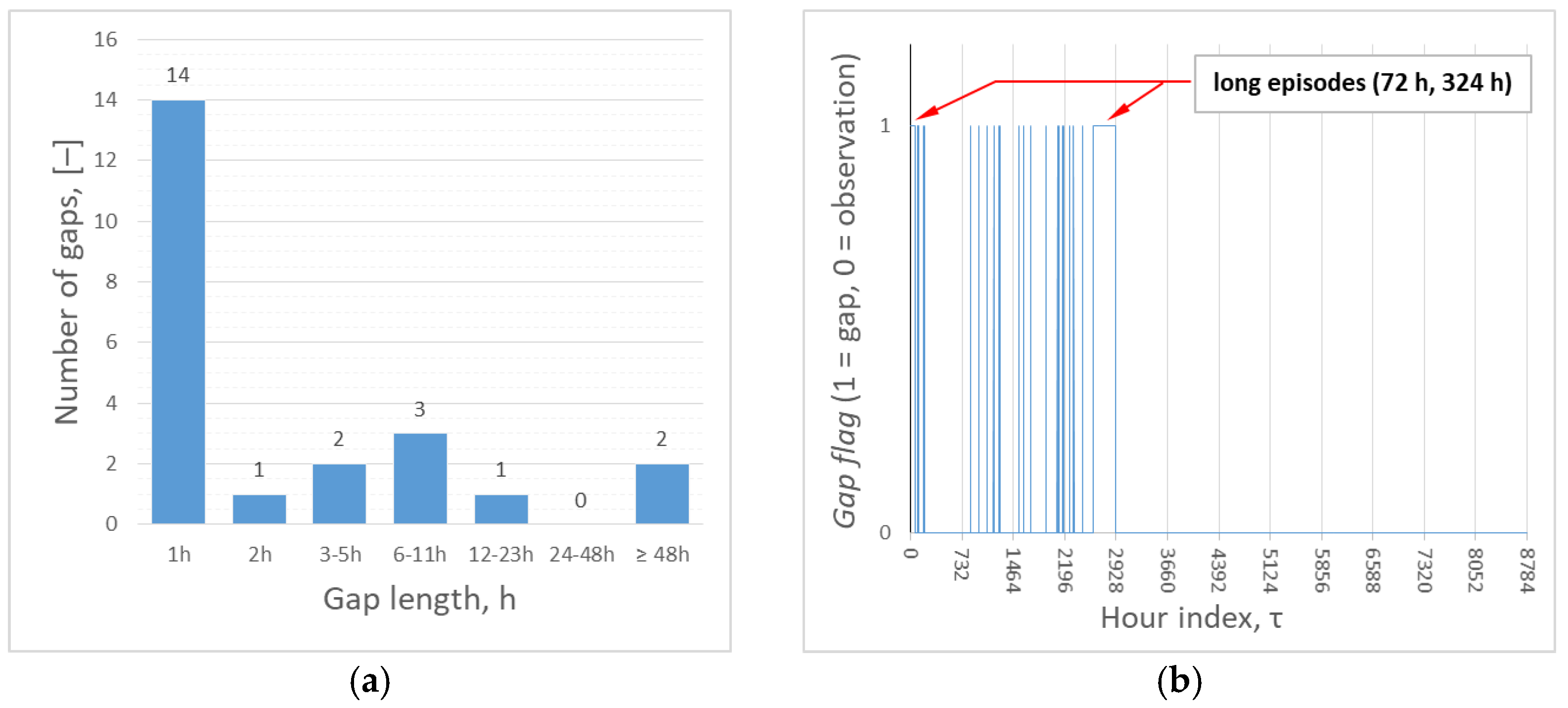
2.3. Characteristics of Temperature Data Gaps
2.4. Reconstruction of Temperature Data Using Polynomial Regression
- The time axis was normalized (index 0…Nobs − 1), according to Equation (2):for = 1, …, Nobs; where Nobs = 8734 h (number of hours with seasonal observations).
- Adding quality control flags (QC), extracting measurement points (tag obs = 0), and sorting in ascending order according to temperature ta,obs.
- Fitting a polynomial of degree n in the range n = 3, 4, …, 11, according to Equation (3):
- Mapping matched values to the whole timeline and filling gaps (gap = 1).
- Inserting the complete series into the ASHP model, where the manufacturer’s characteristics and are interpolated exponentially.
- Calculation of seasonal results: heat demand , electricity consumption (for LWT = 35 °C and 45 °C), and the seasonal coefficient of performance SCOP. Accuracy was assessed by determining MAE, RMSE, R2, ΔQseason, ΔEel, ΔSCOP, and separately, RMSEobs and RMSEfill.
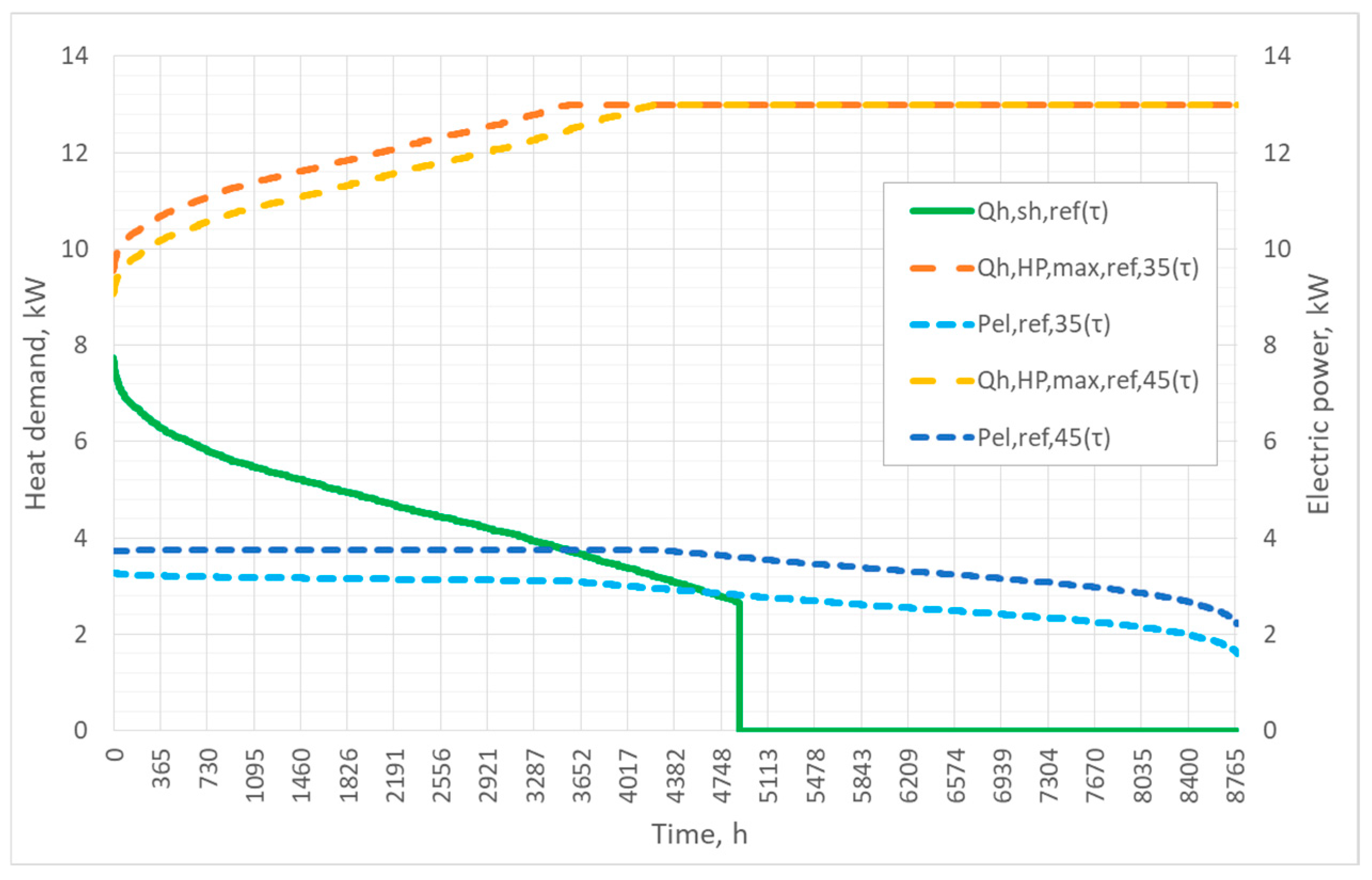
2.5. Building an ASHP Energy Model
2.6. Data Reconstruction Effect Assessment Metrics
- Statistical accuracy: RMSE, MAE, R2—calculated separately for subsets obs, fill, and the totals all;
- Contribution of error originating from gaps WFEfill (Equation (13));
- Relative peak power error (Equation (14));
- Seasonal errors: ΔQseason, ΔEel, and ΔSCOP obtained by integration at hourly intervals;
- Edge sensitivity: MAEcold and MAEhot—calculated for the 500 coldest and warmest hours.
3. Results
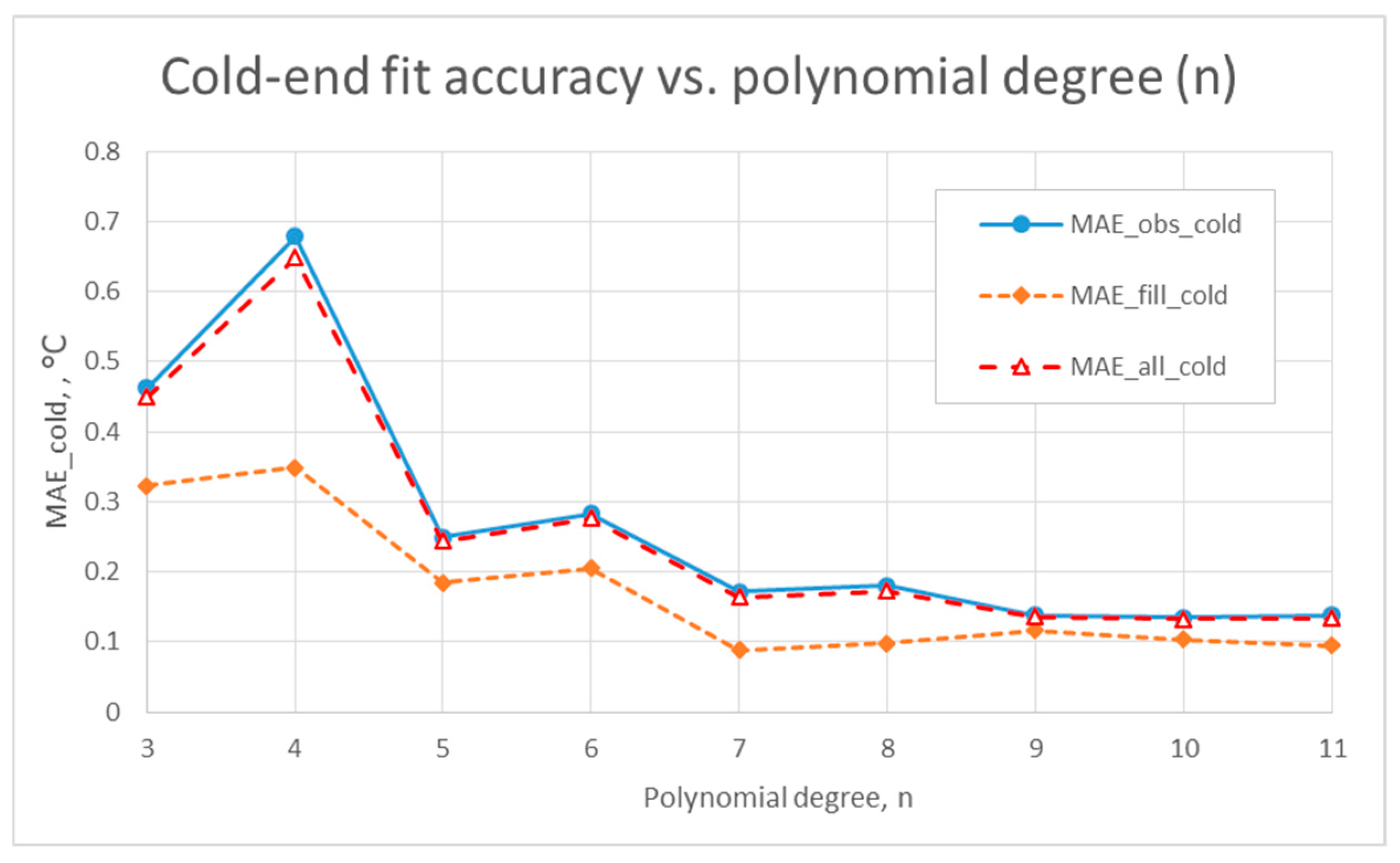
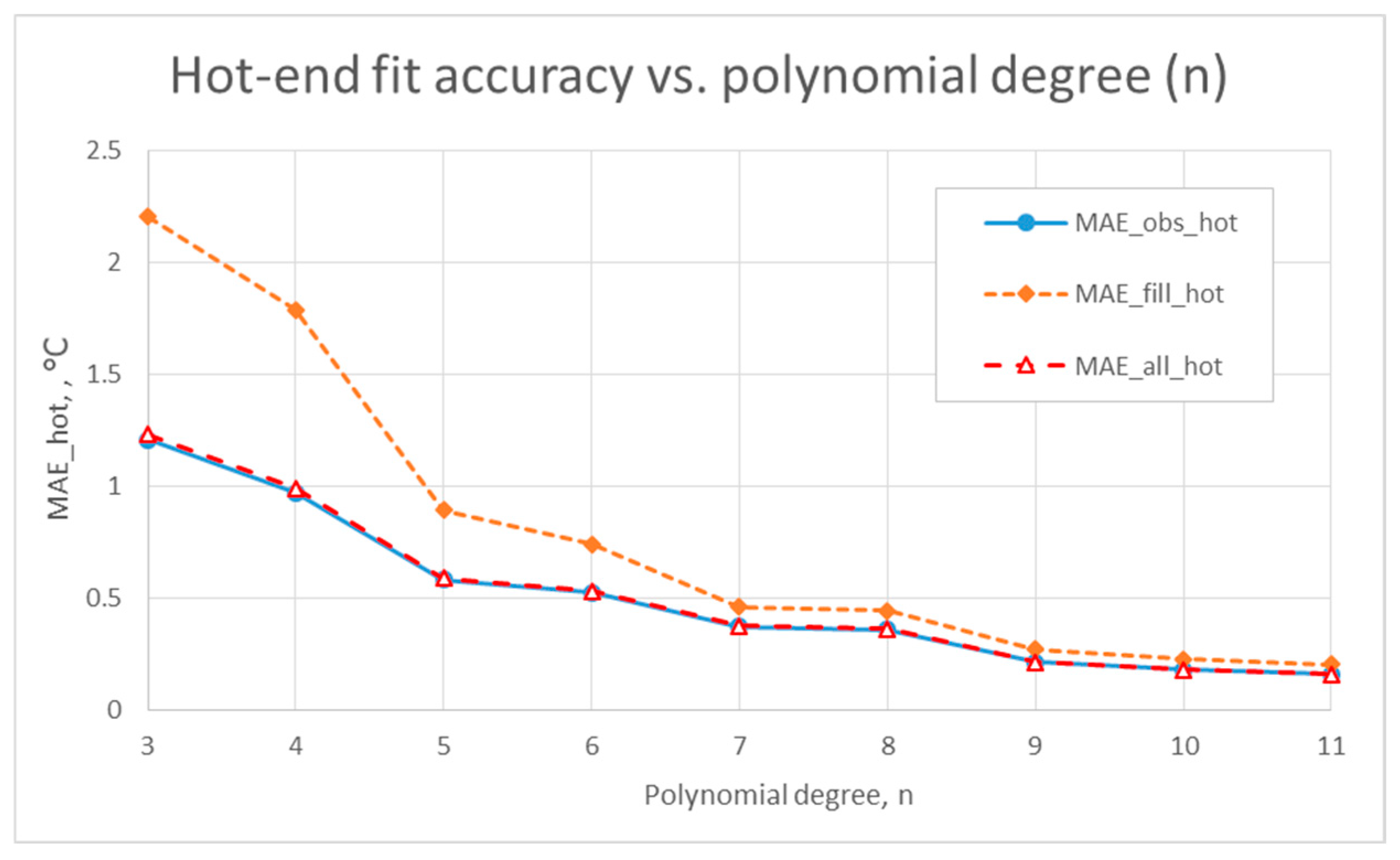
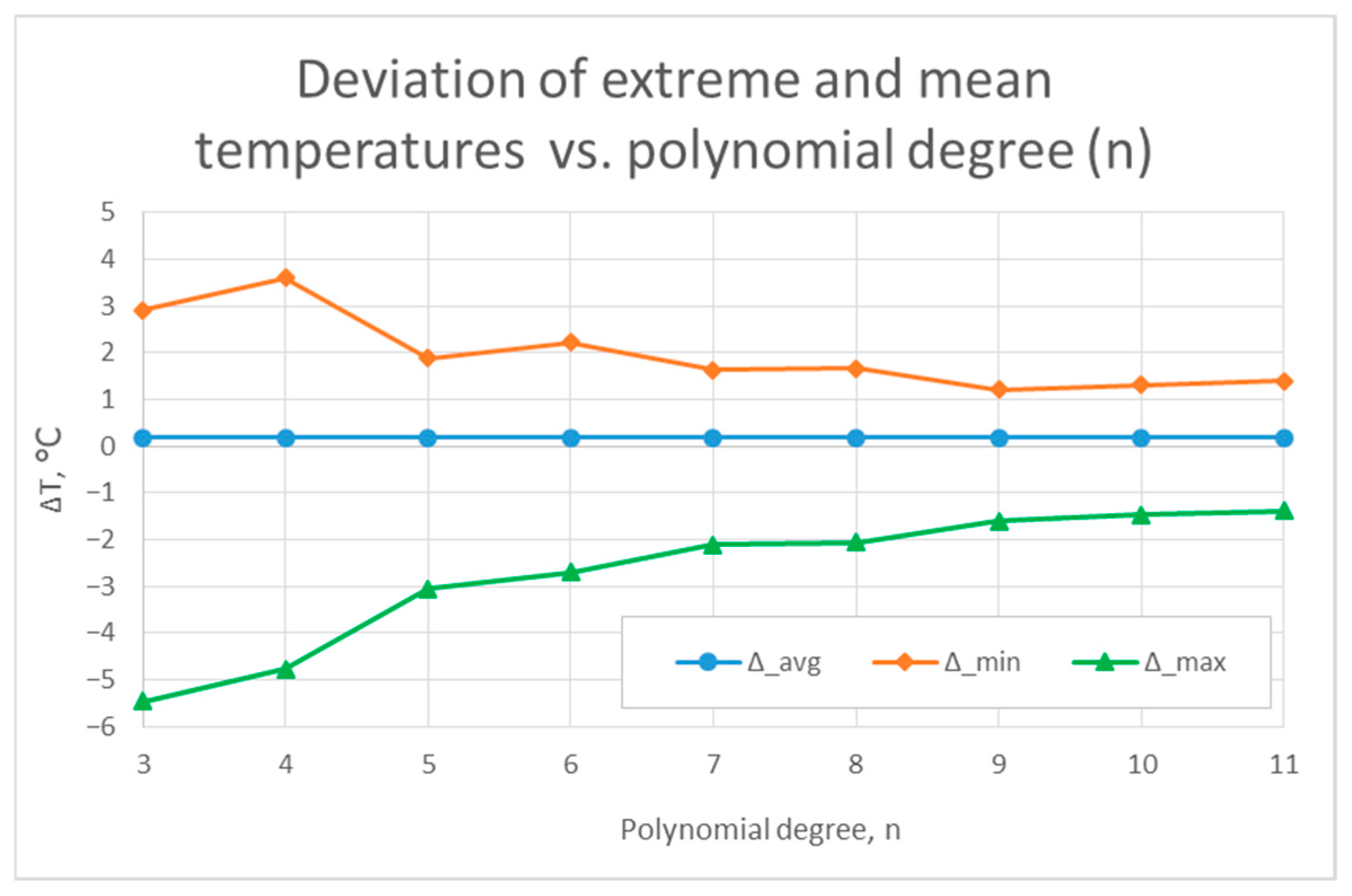
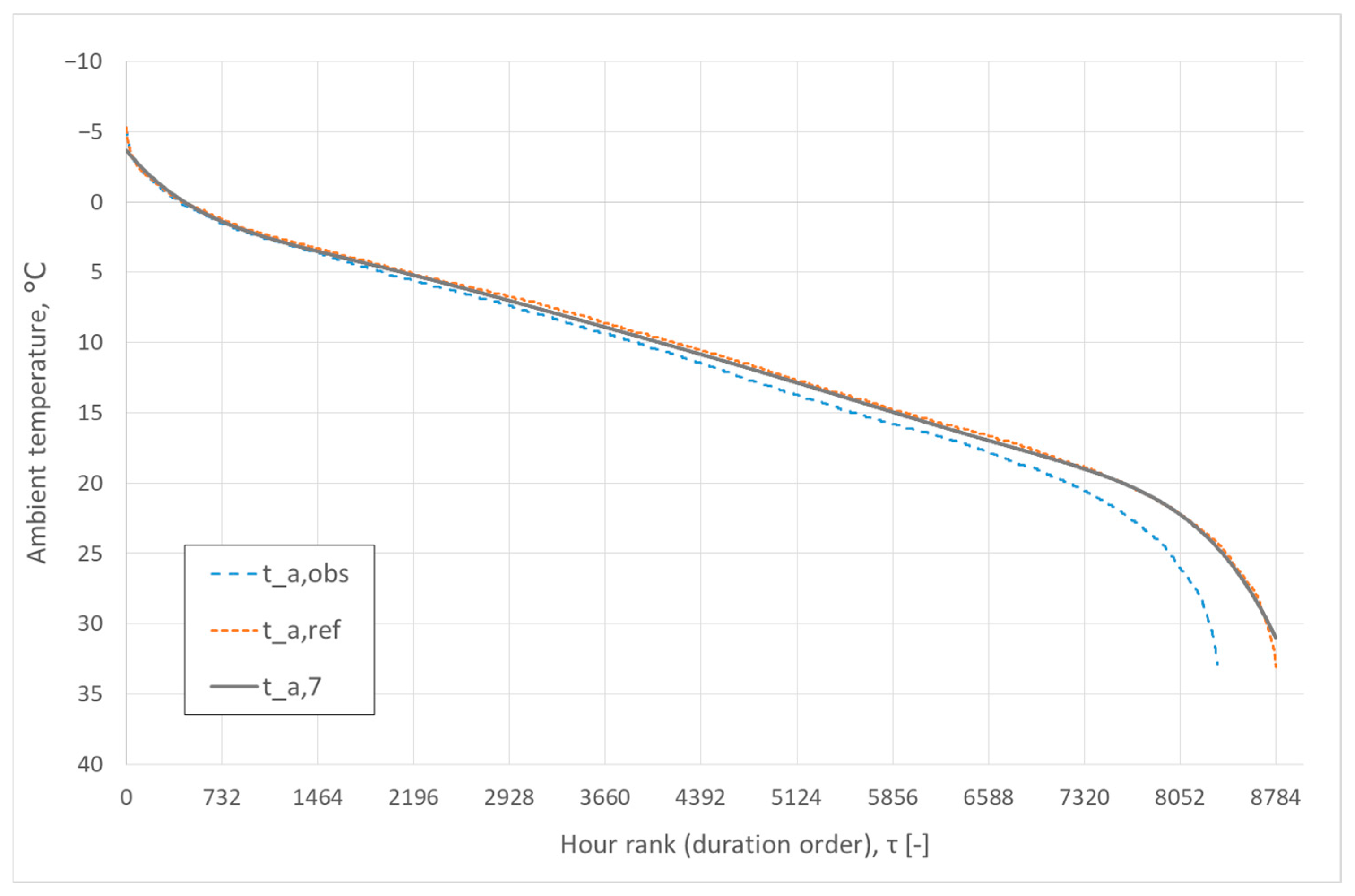
3.1. Accuracy of Temperature Profile Reconstruction ta
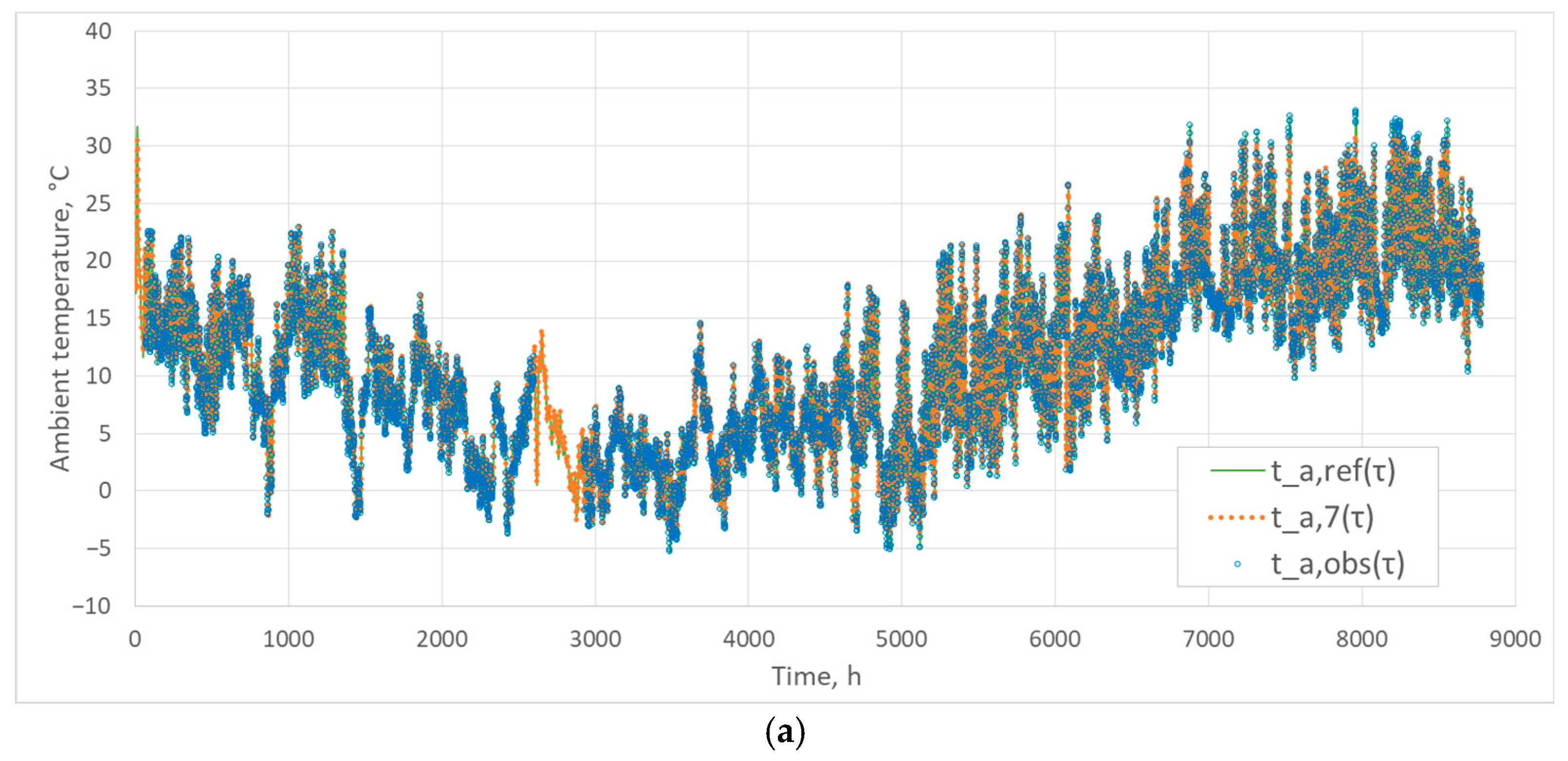
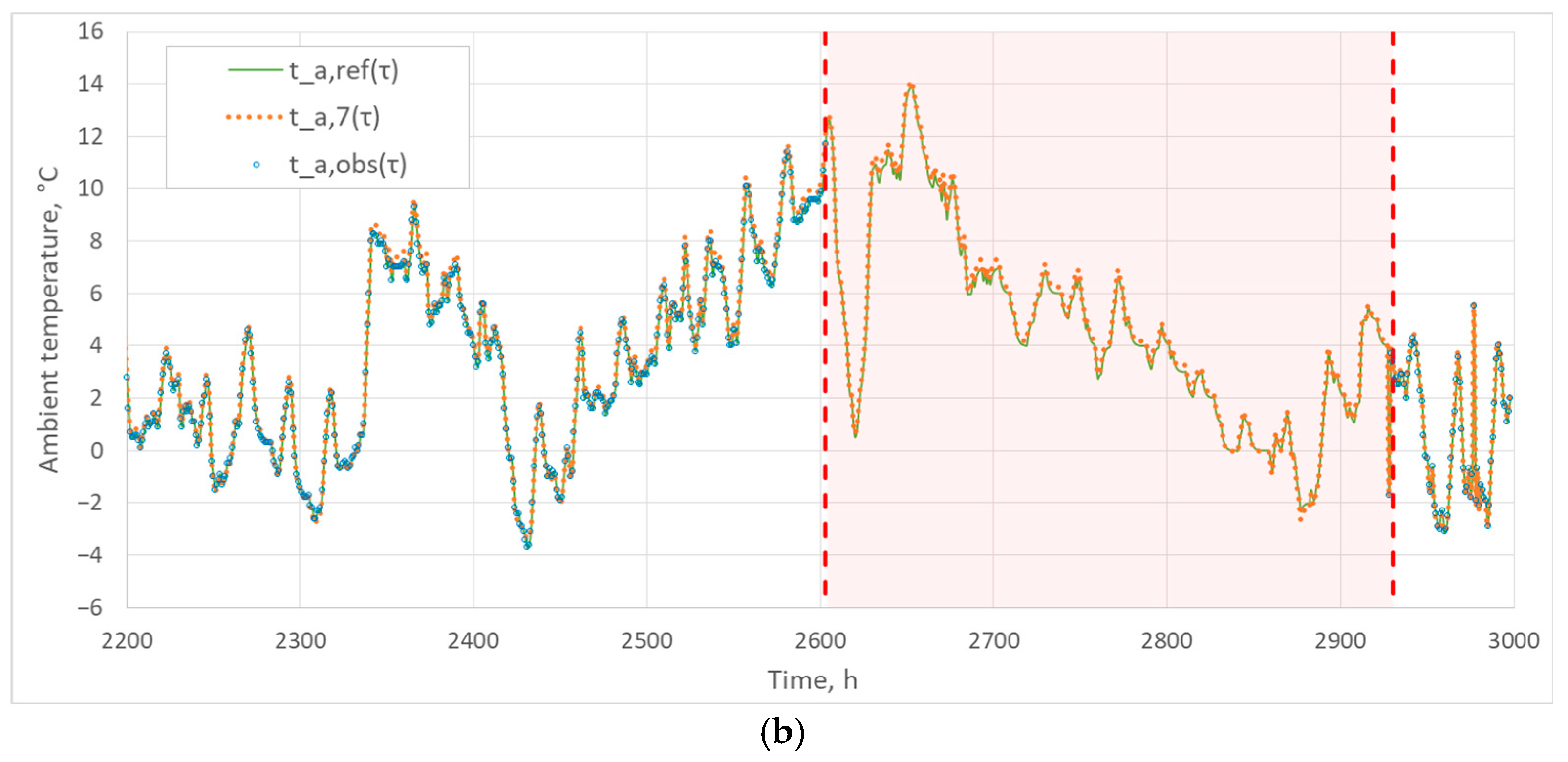
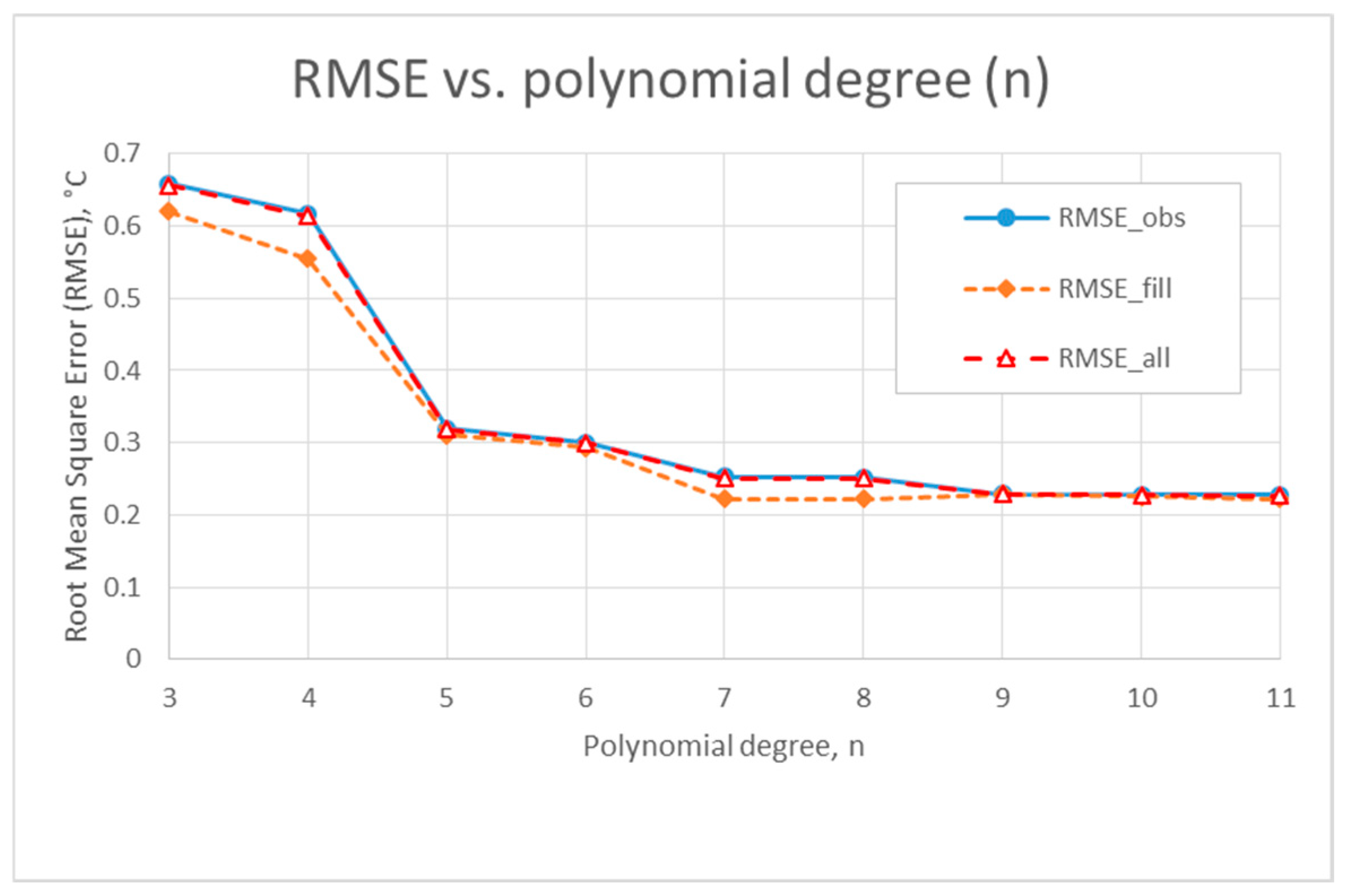
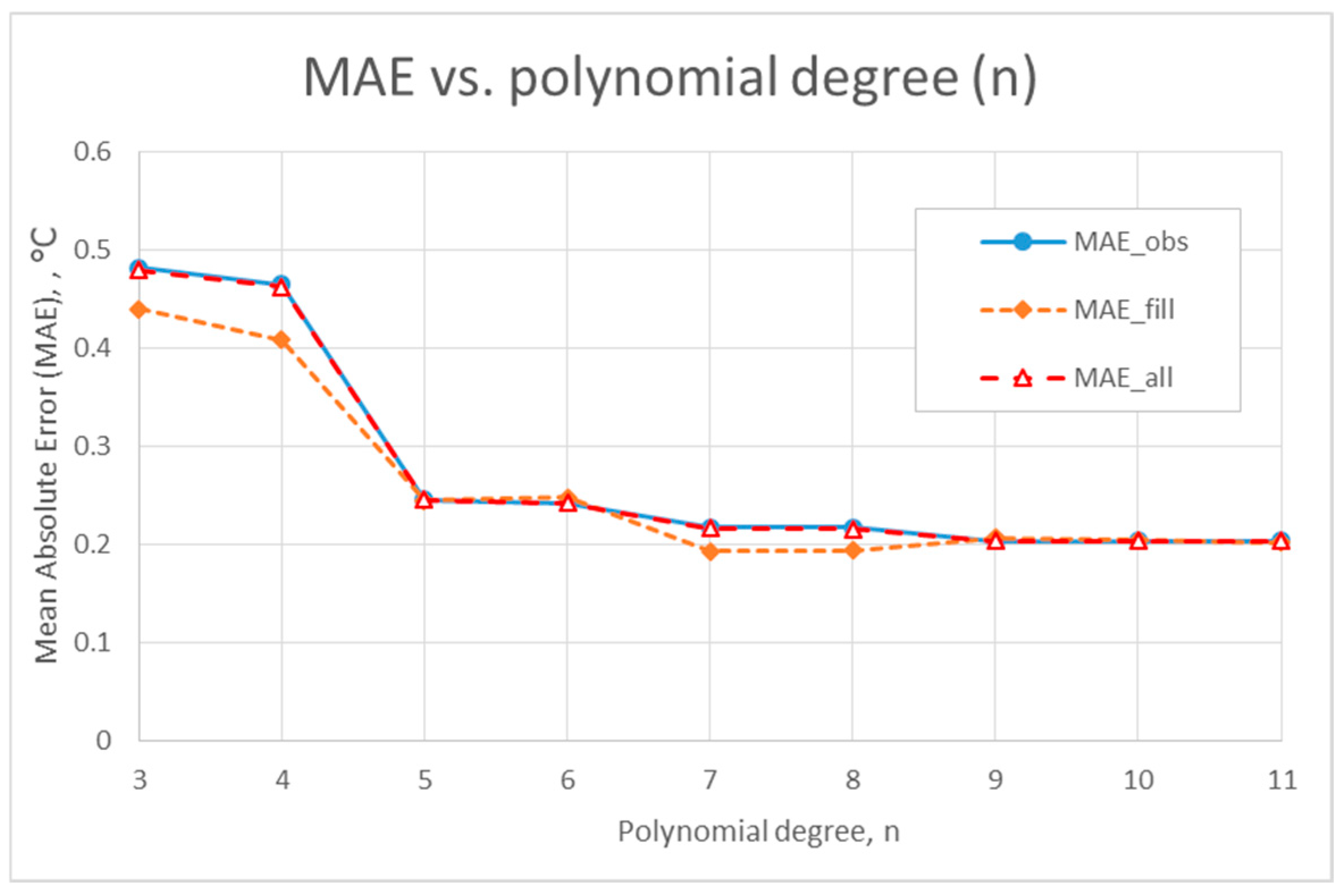

3.2. The Impact of n on the Thermal Load of a Building
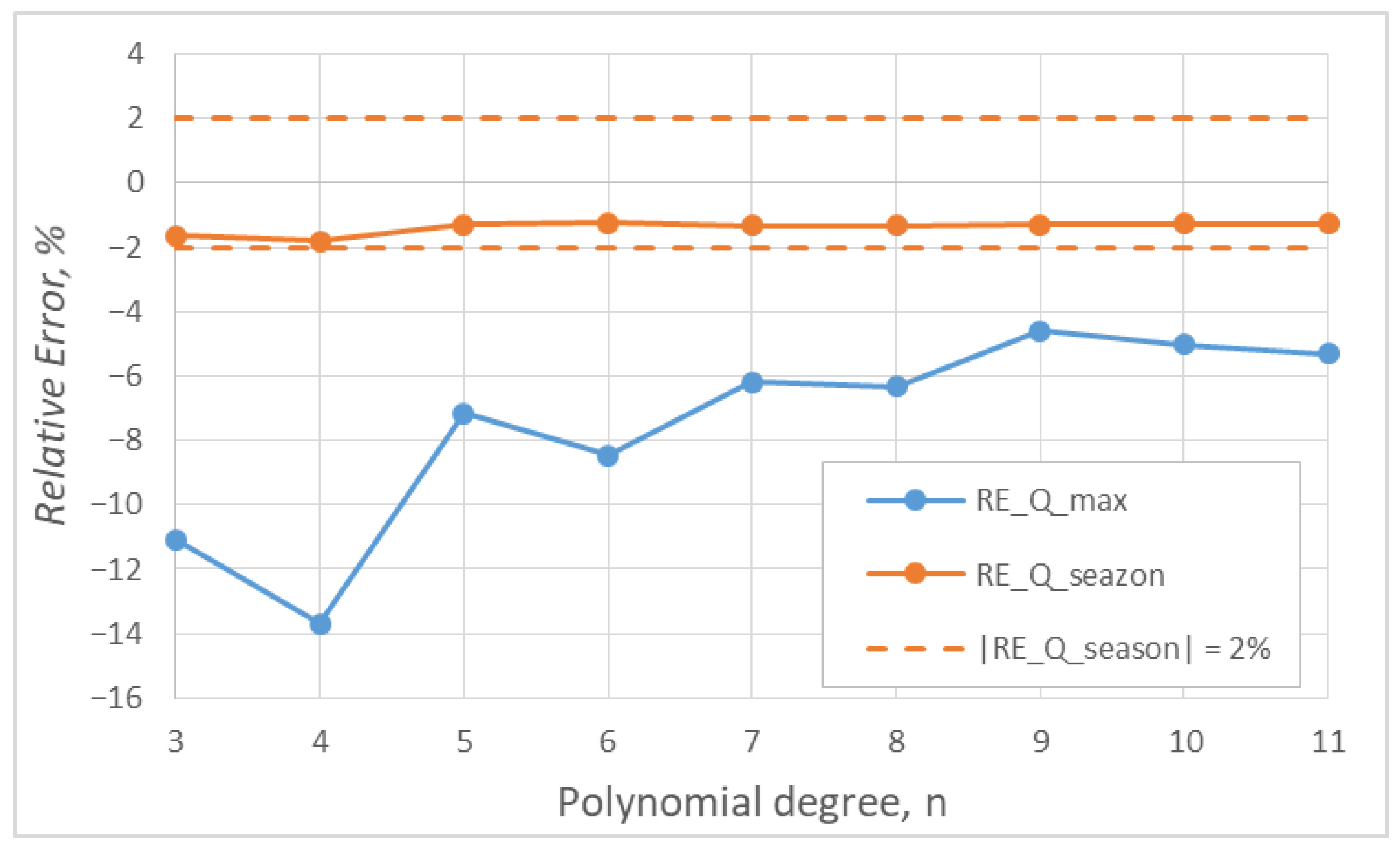
3.3. Impact of n on ASHP Energy Indicators
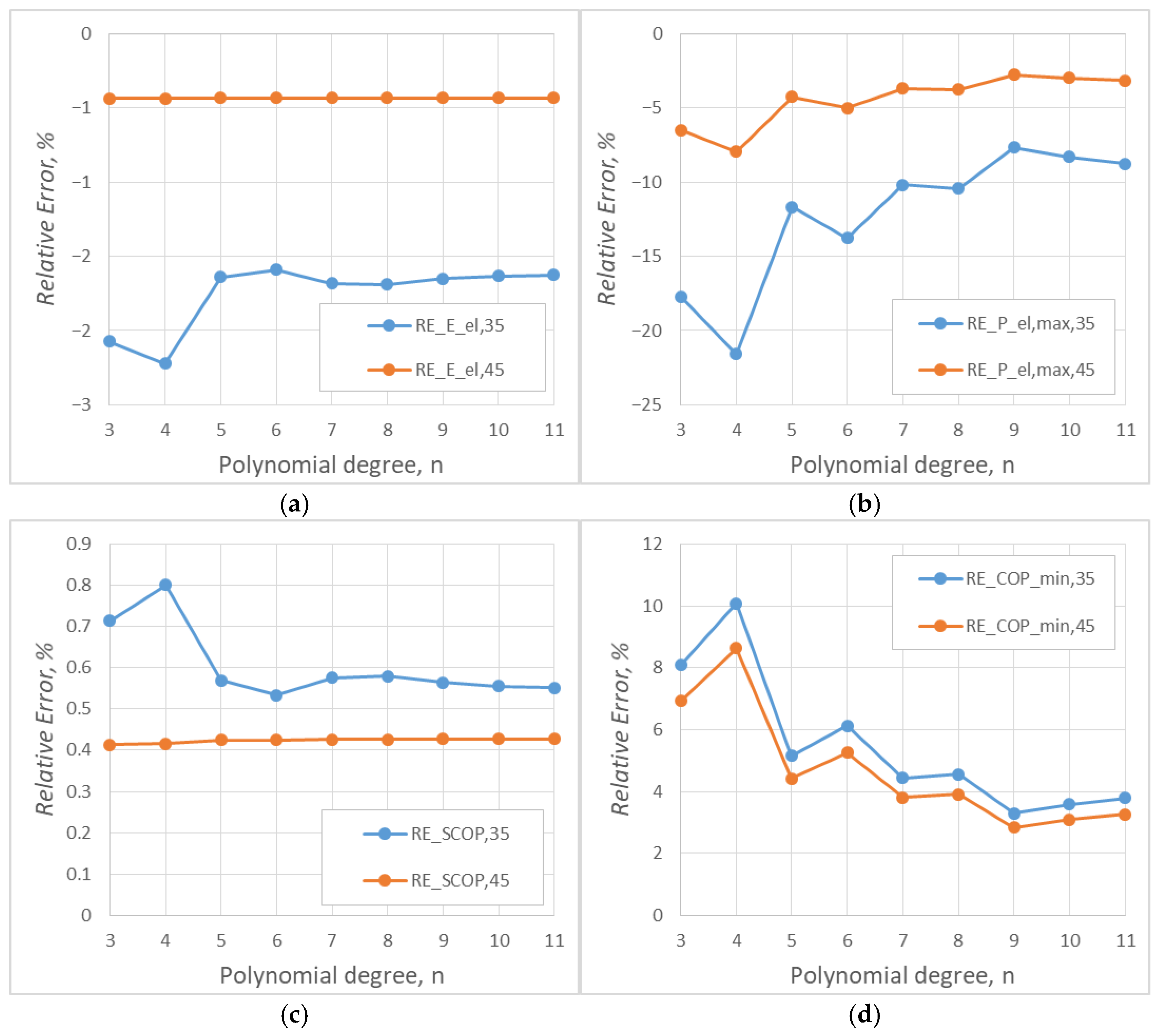
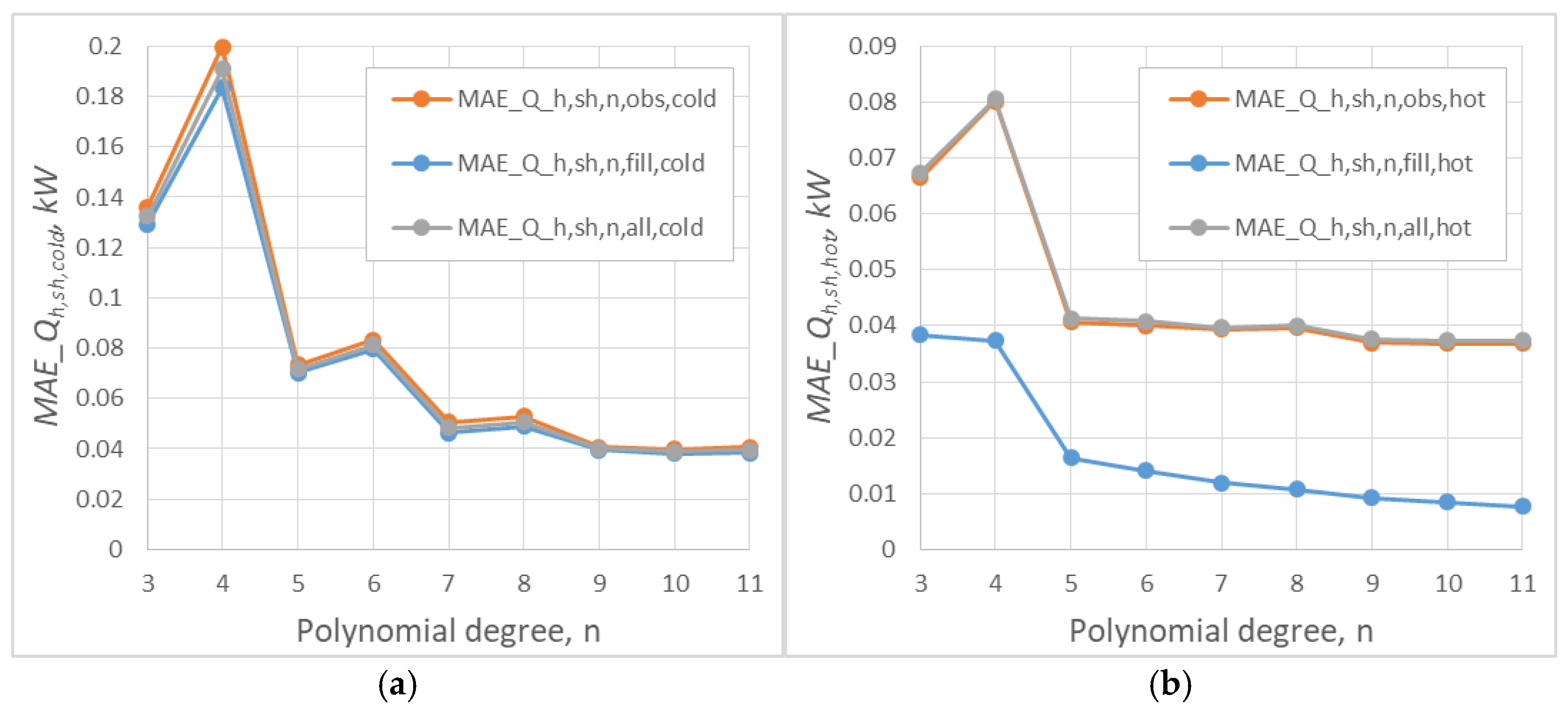
3.4. Sensitivity of the Method to Cold/Hot “Tails”
3.5. Choosing the Lowest Sufficient Degree n
- I—error acceptance threshold . Those that meet this criterion are identified.
- II—threshold for stabilizing energy indicators. For each and both regimes, LWT = 35 °C, 45 °C, the incremental change is compared → , , , for both LWT and is marked as follows (pp—percentage points):
- (✓)—if the criteria are met simultaneously;
- (△)—if only one of the thresholds is exceeded by 50%;
- (—)—all other cases.
- III—stabilization of for tails in Sall and is marked as follows:
- (✓)—if AND relatively ≤ 5%;
- (△)—if OR relatively ≤ 10%;
- (—)—all other cases.
- IV—contribution of missing data WFEfill. For b = (Nfill/Nall)⋅100% it is marked as follows:
- (✓)—if ;
- (△)—if ;
- (—)—all other cases.
4. Discussion
4.1. Quality of Temperature Reconstruction and Energy Effect
4.2. LWT Regimes and KPI Sensitivity
4.3. Edge Sensitivity and the Contribution of Complementary Hours Error
4.4. Justification for Selecting the Minimum Sufficient Degree n
4.5. Limitations and External Baselines (Method Positioning)
5. Conclusions
- Degree n = 7 is the lowest sufficient according to the criteria I–IV;
- Since in a building with underfloor heating, most of the ASHP’s work is carried out in a regime of 35 °C, the selection of n = 7 is conservative and practical: it stabilizes KPIs in a time-dominant regime, limiting the risk of seasonal deviations in energy and peak power;
- KPIs for 35 °C were more sensitive to n than for 45 °C; for 45 °C, values of remained at around −0.43%;
- Edge sensitivity stabilized from n ≥ 7; the share of error from complementary hours WFEfill approached the share of gaps at n = 4, 7, 8;
- Further increases in n above seven did not yield significant energy gains;
- The proposed criteria (I–IV) create a practical procedure for selecting the minimum degree of reconstruction, repeatable in both regimes. LWT.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms: | |
| ASHP | Air-source heat pump |
| COPmin | Minimum seasonal coefficient of performance |
| COP(ta) | Coefficient of performance vs. outdoor-air temperature (−) |
| DHW | Domestic hot water |
| KPI | Key performance indicator |
| Leaving water temperature (°C) | |
| MAE | Mean absolute error |
| QC | Quality control flags |
| RMSE | Root-mean-square error |
| SCOP | Seasonal COP |
| WFEfill | Weighted fill error—share of hours reconstructed/adjusted during gap-filling (%) |
| Symbols and units: | |
| ΔX | Absolute difference, defined in Equation (15) (units of X) |
| Seasonal electricity use (kWh) | |
| Number of hours in the full set (observed ∪ filled) (−) | |
| Number of filled (reconstructed) hours (−) | |
| Number of observed hours (−) | |
| Cardinality of set S (number of hours) (−) | |
| Electrical input power as a function of outdoor-air temperature (W) | |
| Seasonal peak electrical input power (W) | |
| Thermal energy (kWh) | |
| Thermal power (W) | |
| Seasonal space-heating demand (kWh) | |
| R2 | Coefficient of determination, defined in Equation (10) (−) |
| REX | Relative change reported in percent, defined in Equation (16) (%); for maxima, REX,max |
| Set of observed hours (−) | |
| Set of filled (reconstructed) hours (−) | |
| Complete set of hours (observed ∪ filled) (−) | |
| Cold-tail subset (lowest percentiles of ta) (−) | |
| Hot-tail subset (highest percentiles of ta) (−) | |
| Outdoor-air temperature (°C) | |
| Outdoor-air temperature at time τ (°C) | |
| Design outdoor temperature for winter per national standard (°C) | |
| Reconstructed outdoor-air temperature (degree n) (°C) | |
| Reconstructed outdoor-air temperature at time τ (degree n) (°C) | |
| Observed outdoor-air temperature at time index τ (after QC; gaps masked, original timestamps) (°C) | |
| Reference-completed series (°C) | |
| Reference-completed outdoor-air temperature at time index τ (validation baseline; same timestamps as ta,obs; not used for fitting) (°C) | |
| Indoor set temperature (per standard) (°C) | |
| X | Generic scalar KPI (e.g., Qseason, Eel, Pel,max, COPmin) (units of X) |
References
- Masiukiewicz, M.; Tańczuk, M.; Anweiler, S.; Streckienė, G.; Boldyryev, S. Long-Term Climate-Based Sizing and Economic Assessment of Air-Water Heat Pumps for Residential Heating. Appl. Therm. Eng. 2025, 258, 124627. [Google Scholar] [CrossRef]
- Masiukiewicz, M.; Tańczuk, M.; Anweiler, S.; Streckienė, G.; Boldyryev, S.; Chacartegui, R.; Olszewski, E. Performance Variability of Air-Water Heat Pumps in Cold and Warm Years Across European Climate Zones. Energy 2025, 324, 136001. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Anweiler, S.; Masiukiewicz, M. Experimental Based Determination of SCOP Coefficient for Ground-Water Heat Pump. E3S Web Conf. 2018, 44, 3. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)? -Arguments against Avoiding RMSE in the Literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Cerlini, P.B.; Silvestri, L.; Saraceni, M. Quality Control and Gap-Filling Methods Applied to Hourly Temperature Observations over Central Italy. Meteorol. Appl. 2020, 27, e1913. [Google Scholar] [CrossRef]
- Tanczuk, M.; Masiukiewicz, M.; Anweiler, S.; Junga, R. Technical Aspects and Energy Effects of Waste Heat Recovery from District Heating Boiler Slag. Energies 2018, 11, 796. [Google Scholar] [CrossRef]
- Lompar, M.; Lalić, B.; Dekić, L.; Petrić, M. Filling Gaps in Hourly Air Temperature Data Using Debiased ERA5 Data. Atmosphere 2019, 10, 13. [Google Scholar] [CrossRef]
- ClimateFiller 0.0.1 Documentation. Available online: https://climatefiller.readthedocs.io/en/latest/?utm_source=chatgpt.com (accessed on 20 August 2025).
- Masiukiewicz, M. Small Photovoltaic Setup for the Air Conditioning System. E3S Web Conf. 2017, 19, 01020. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-Mean-Square Error (RMSE) or Mean Absolute Error (MAE): When to Use Them or Not. Geosci. Model. Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Jacobs, A.; Top, S.; Vergauwen, T.; Suomi, J.; Käyhkö, J.; Caluwaerts, S. Filling Gaps in Urban Temperature Observations by Debiasing ERA5 Reanalysis Data. Urban Clim. 2024, 58, 102226. [Google Scholar] [CrossRef]
- Lalic, B.; Stapleton, A.; Vergauwen, T.; Caluwaerts, S.; Eichelmann, E.; Roantree, M. A Comparative Analysis of Machine Learning Approaches to Gap Filling Meteorological Datasets. Environ. Earth Sci. 2024, 83, 679. [Google Scholar] [CrossRef]
- Bessenbacher, V.; Seneviratne, S.I.; Gudmundsson, L. CLIMFILL v0.9: A Framework for Intelligently Gap Filling Earth Observations. Geosci. Model. Dev. 2022, 15, 4569–4596. [Google Scholar] [CrossRef]
- Baltazar, J.C.; Claridge, D.E. Study of Cubic Splines and Fourier Series as Interpolation Techniques for Filling in Short Periods of Missing Building Energy Use and Weather Data. J. Sol. Energy Eng. 2006, 128, 226–230. [Google Scholar] [CrossRef]
- Henn, B.; Raleigh, M.S.; Fisher, A.; Lundquist, J.D. A Comparison of Methods for Filling Gaps in Hourly Near-Surface Air Temperature Data. J. Hydrometeorol. 2013, 14, 929–945. [Google Scholar] [CrossRef]
- Dyukarev, E. Comparison of Artificial Neural Network and Regression Models for Filling Temporal Gaps of Meteorological Variables Time Series. Appl. Sci. 2023, 13, 2646. [Google Scholar] [CrossRef]
- Beguería, S.; Tomas-Burguera, M.; Serrano-Notivoli, R.; Peña-Angulo, D.; Vicente-Serrano, S.M.; González-Hidalgo, J.C. Gap Filling of Monthly Temperature Data and Its Effect on Climatic Variability and Trends. J. Clim. 2019, 32, 7797–7821. [Google Scholar] [CrossRef]
- EN 14825:2022; Air Conditioners, Liquid Chilling Packages and Heat Pumps, with Electrically Driven. Slovenian Institute for Standardization: Ljubljana, Slovenia, 2022. Available online: https://standards.iteh.ai/catalog/standards/cen/9fcc3835-2b65-478e-920e-3f3bacb6d2c5/en-14825-2022?utm_source=chatgpt.com (accessed on 20 August 2025).
- Institute of Meteorology and Water Management National Research Institute. Available online: https://danepubliczne.imgw.pl/en (accessed on 20 August 2025).
- Index of/Data/Dane_Pomiarowo_Obserwacyjne/Dane_Meteorologiczne/Terminowe/Klimat. Available online: https://danepubliczne.imgw.pl/data/dane_pomiarowo_obserwacyjne/dane_meteorologiczne/terminowe/klimat/ (accessed on 20 August 2025).
- Ghous, H.; Malik, A.; Ahmad, Z.; Jabeen, U.; Khawar, M. Climate Change Forecasting Using Time Series Techniques: A Comprehensive Review. South. J. Comput. Sci. 2025, 1, 37–61. [Google Scholar]
- Hudon, A.; Phraxayavong, K.; Potvin, S.; Dumais, A. Comparing the Performance of Machine Learning Algorithms in the Automatic Classification of Psychotherapeutic Interactions in Avatar Therapy. Mach. Learn. Knowl. Extr. 2023, 5, 1119–1131. [Google Scholar] [CrossRef]
- Gautschi, W. Optimally Conditioned Vandermonde Matrices. Numer. Math. 1975, 24, 1–12. [Google Scholar] [CrossRef]
- De Marchi, S. Mapped Polynomials and Discontinuous Kernels for Runge and Gibbs Phenomena. SEMA SIMAI Springer Ser. 2022, 29, 3–43. [Google Scholar] [CrossRef]
- Sieres, J.; Ortega, I.; Cerdeira, F.; Álvarez, E.; Santos, J.M. Seasonal Efficiency of a Brine-to-Water Heat Pump with Different Control Options According to Ecodesign Standards. Clean Technol. 2022, 4, 542–554. [Google Scholar] [CrossRef]
- Palkowski, C.; Zottl, A.; Malenkovic, I.; Simo, A. Fixing Efficiency Values by Unfixing Compressor Speed: Dynamic Test Method for Heat Pumps. Energies 2019, 12, 1045. [Google Scholar] [CrossRef]
- Szczotka, K.; Zimny, J.; Struś, M.; Michalak, P.; Szymiczek, J. Badania Parametrów Termodynamicznych Sprężarkowej Powietrznej Pompy Ciepła w Celu Poprawy Efektywności Energetycznej. Rynek Energii 2021, 153, 54–64. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
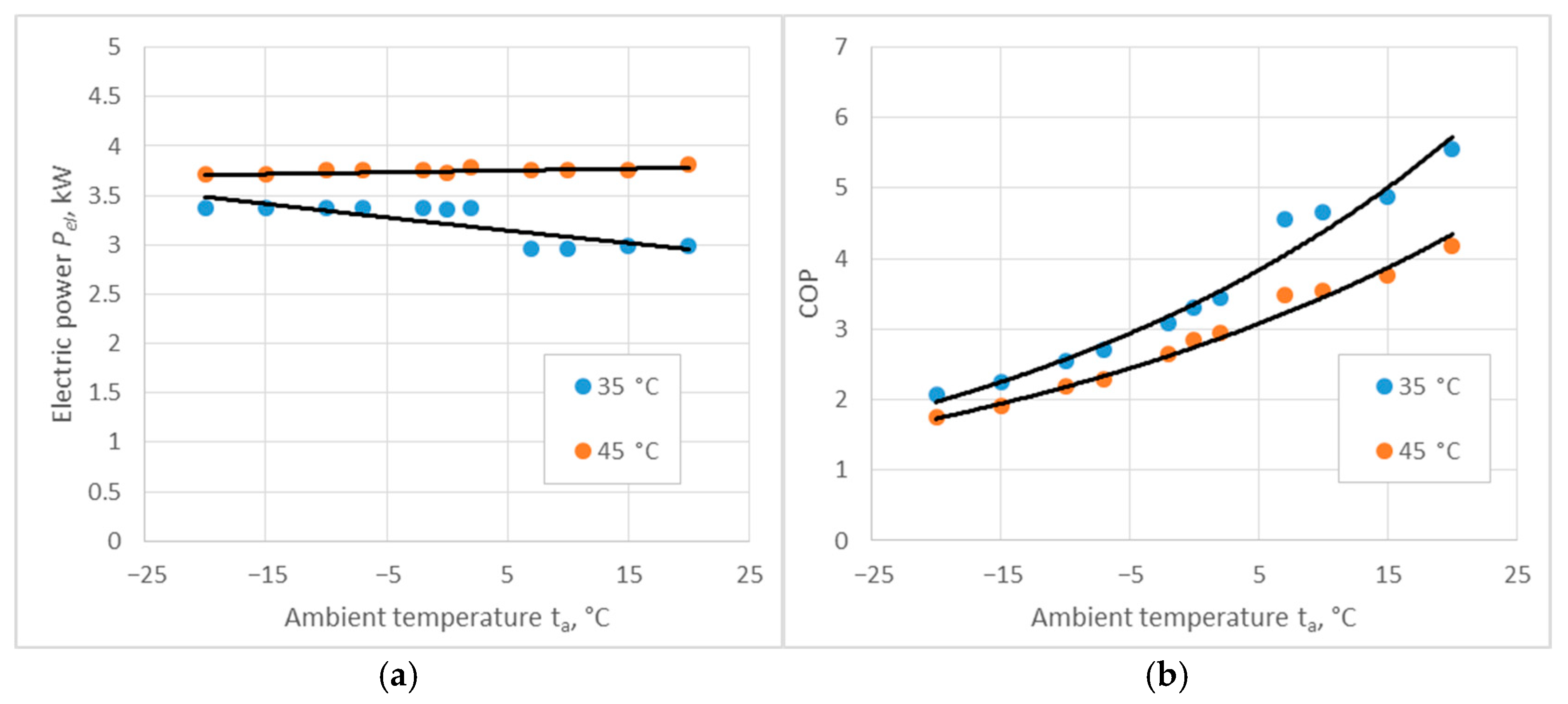
| Return Water Temperature LWT | Pel | COP | ||
|---|---|---|---|---|
| Constants of Function | ||||
| °C | a | b | a | b |
| 35 | 3.2097324 | −0.0041214 | 3.3559848 | 0.0266827 |
| 45 | 3.7426251 | 0.0004945 | 2.7413944 | 0.0230053 |
| Building Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Peak heat demand of the building | 12.72 | kW | |
| Temperature-controlled usable area | Af | 250 | m2 |
| Normal operating (service) temperature | ti | 21 | °C |
| Number of people residing in the facility | Li | 6 | j.o. |
| Individual daily hot water consumption | Vcw | 50 | dm3/person/day |
| Hot water mode (average hourly power) | 0.65 | kW | |
| Design outdoor temperature, climate zone III | ta,min | −20 | °C |
| Seasonal outdoor temperature limit | ta,bs | 12 | °C |
| n | ||||||
|---|---|---|---|---|---|---|
| kW | kW | kW | % | kWh | % | |
| 3 | 7.742 | 6.885 | −0.858 | −11.08 | −367.3 | −1.64 |
| 4 | 7.742 | 6.683 | −1.059 | −13.68 | −403.8 | −1.81 |
| 5 | 7.742 | 7.189 | −0.553 | −7.15 | −291.2 | −1.30 |
| 6 | 7.742 | 7.086 | −0.656 | −8.47 | −276.5 | −1.24 |
| 7 | 7.742 | 7.264 | −0.479 | −6.18 | −296.4 | −1.33 |
| 8 | 7.742 | 7.251 | −0.491 | −6.35 | −297.9 | −1.33 |
| 9 | 7.742 | 7.386 | −0.357 | −4.61 | −290.4 | −1.30 |
| 10 | 7.742 | 7.354 | −0.388 | −5.02 | −286.8 | −1.28 |
| 11 | 7.742 | 7.332 | −0.410 | −5.30 | −284.9 | −1.27 |
| LWT | n | ΔEel | ΔPel,max | ΔSCOP | ΔCOPmin | ||||
|---|---|---|---|---|---|---|---|---|---|
| °C | kWh | % | kW | % | [-] | % | [-] | % | |
| 35 | 3 | −123.0 | −2.07 | −0.471 | −17.73 | 0.0279 | 0.71 | 0.2355 | 8.08 |
| 4 | −131.7 | −2.22 | −0.574 | −21.59 | 0.0313 | 0.80 | 0.2936 | 10.08 | |
| 5 | −97.3 | −1.64 | −0.311 | −11.69 | 0.0222 | 0.57 | 0.1499 | 5.14 | |
| 6 | −94.4 | −1.59 | −0.366 | −13.76 | 0.0208 | 0.53 | 0.1785 | 6.13 | |
| 7 | −99.8 | −1.68 | −0.270 | −10.17 | 0.0225 | 0.58 | 0.1292 | 4.44 | |
| 8 | −100.2 | −1.69 | −0.277 | −10.42 | 0.0226 | 0.58 | 0.1327 | 4.55 | |
| 9 | −97.8 | −1.65 | −0.203 | −7.65 | 0.0220 | 0.56 | 0.0958 | 3.29 | |
| 10 | −96.9 | −1.63 | −0.221 | −8.30 | 0.0217 | 0.56 | 0.1044 | 3.58 | |
| 11 | −96.5 | −1.63 | −0.233 | −8.76 | 0.0215 | 0.55 | 0.1104 | 3.79 | |
| 45 | 3 | −7.2 | −0.44 | −0.017 | −6.48 | 0.0148 | 0.41 | 0.1682 | 6.93 |
| 4 | −7.2 | −0.44 | −0.021 | −7.95 | 0.0150 | 0.42 | 0.2095 | 8.63 | |
| 5 | −7.1 | −0.43 | −0.011 | −4.23 | 0.0153 | 0.42 | 0.1073 | 4.42 | |
| 6 | −7.1 | −0.43 | −0.013 | −5.00 | 0.0153 | 0.43 | 0.1276 | 5.26 | |
| 7 | −7.1 | −0.43 | −0.010 | −3.67 | 0.0153 | 0.43 | 0.0925 | 3.81 | |
| 8 | −7.1 | −0.43 | −0.010 | −3.77 | 0.0153 | 0.43 | 0.0950 | 3.91 | |
| 9 | −7.1 | −0.43 | −0.007 | −2.75 | 0.0154 | 0.43 | 0.0686 | 2.83 | |
| 10 | −7.1 | −0.43 | −0.008 | −2.99 | 0.0154 | 0.43 | 0.0748 | 3.08 | |
| 11 | −7.1 | −0.43 | −0.008 | −3.16 | 0.0154 | 0.43 | 0.0791 | 3.26 |
| n | Criteria | |||
|---|---|---|---|---|
| I | II | III | IV | |
| 3 | ✓ | — | — | △ |
| 4 | ✓ | — | — | ✓ |
| 5 | ✓ | △ | — | △ |
| 6 | ✓ | △ | △ | — |
| 7 | ✓ | ✓ | ✓ | ✓ |
| 8 | ✓ | ✓ | ✓ | ✓ |
| 9 | ✓ | ✓ | ✓ | △ |
| 10 | ✓ | ✓ | ✓ | △ |
| 11 | ✓ | ✓ | ✓ | △ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masiukiewicz, M.; Streckienė, G.; Gużda, A. Beyond R2: The Role of Polynomial Degree in Modeling External Temperature and Its Impact on Heat-Pump Energy Demand. Energies 2025, 18, 5547. https://doi.org/10.3390/en18205547
Masiukiewicz M, Streckienė G, Gużda A. Beyond R2: The Role of Polynomial Degree in Modeling External Temperature and Its Impact on Heat-Pump Energy Demand. Energies. 2025; 18(20):5547. https://doi.org/10.3390/en18205547
Chicago/Turabian StyleMasiukiewicz, Maciej, Giedrė Streckienė, and Arkadiusz Gużda. 2025. "Beyond R2: The Role of Polynomial Degree in Modeling External Temperature and Its Impact on Heat-Pump Energy Demand" Energies 18, no. 20: 5547. https://doi.org/10.3390/en18205547
APA StyleMasiukiewicz, M., Streckienė, G., & Gużda, A. (2025). Beyond R2: The Role of Polynomial Degree in Modeling External Temperature and Its Impact on Heat-Pump Energy Demand. Energies, 18(20), 5547. https://doi.org/10.3390/en18205547







