Toward Reliable FOWT Modeling: A New Calibration Approach for Extreme Environmental Loads
Abstract
1. Introduction
2. Numerical Framework
2.1. Simulation Tools Employing Potential Flow Principles
2.2. Computational Fluid Dynamic
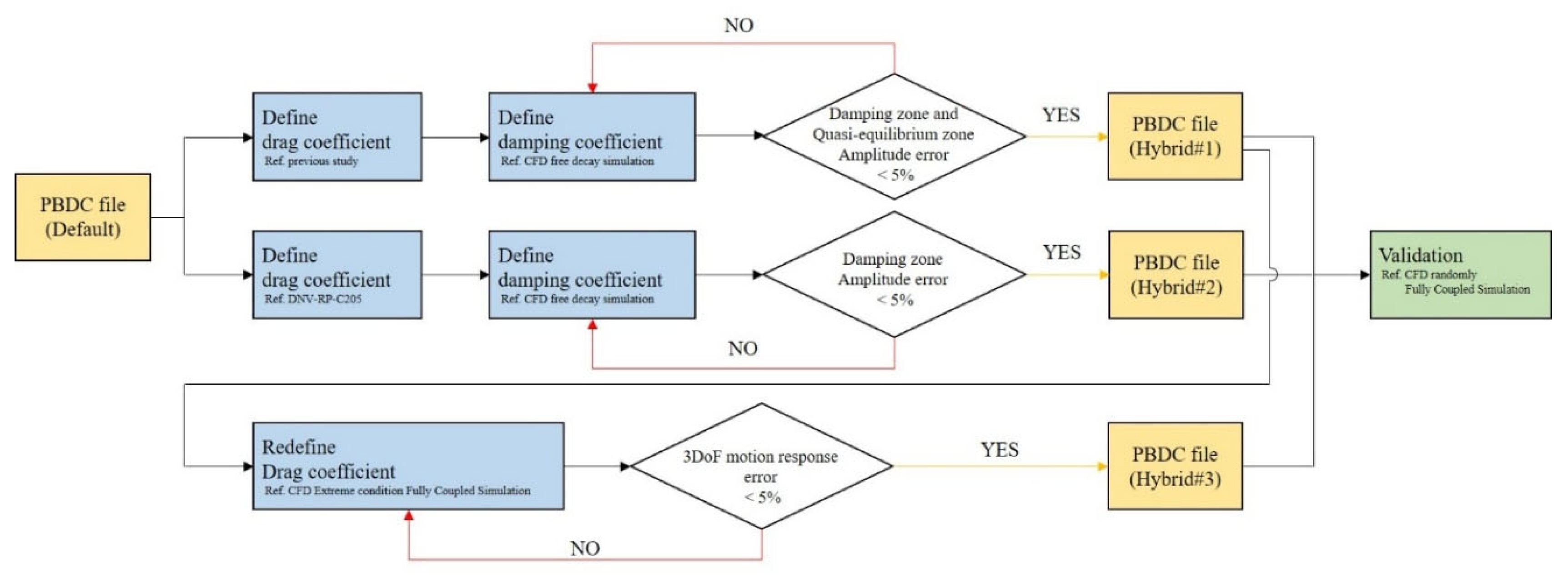
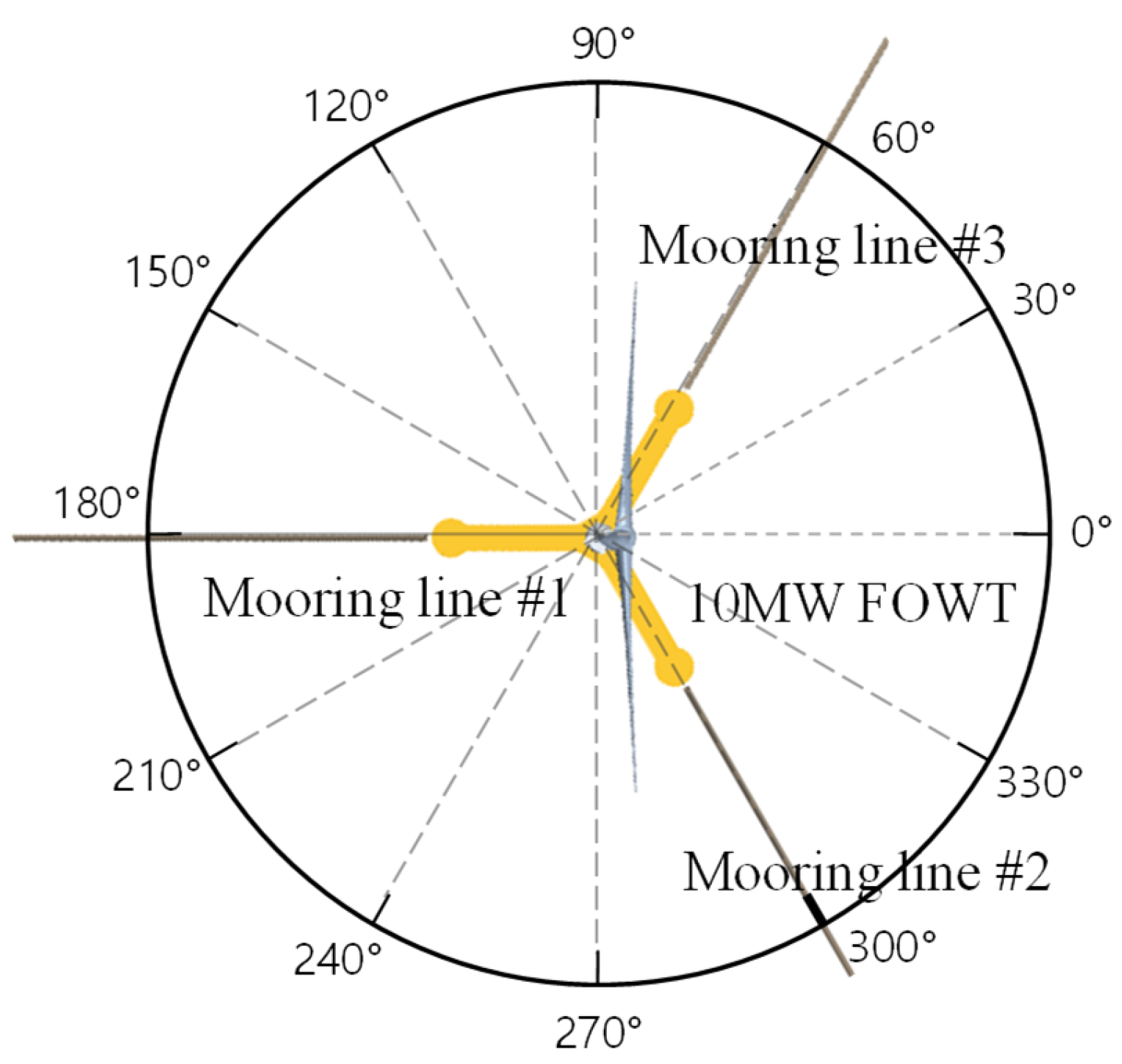
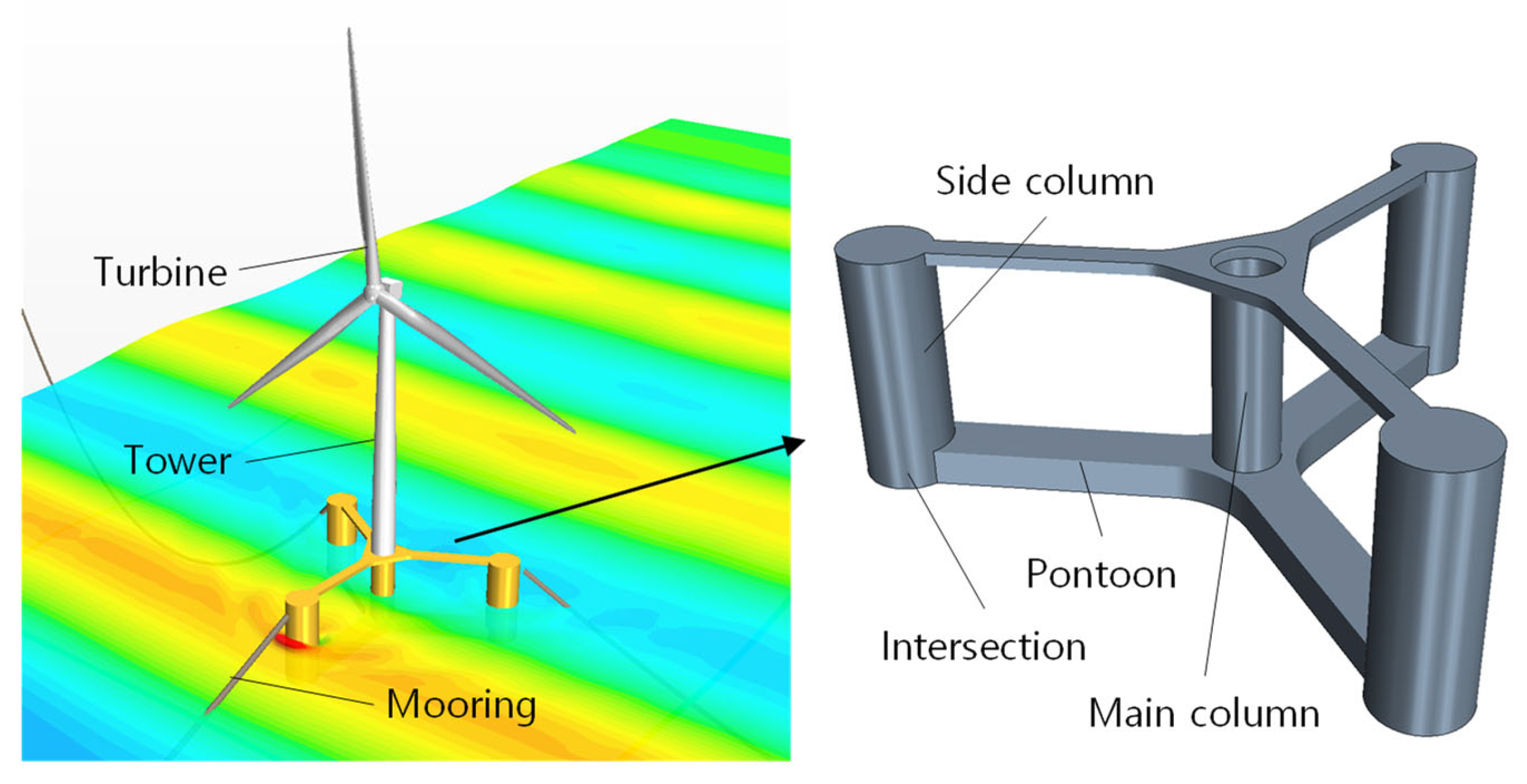
3. Methodology and Model Description
4. Numerical Simulation Statement
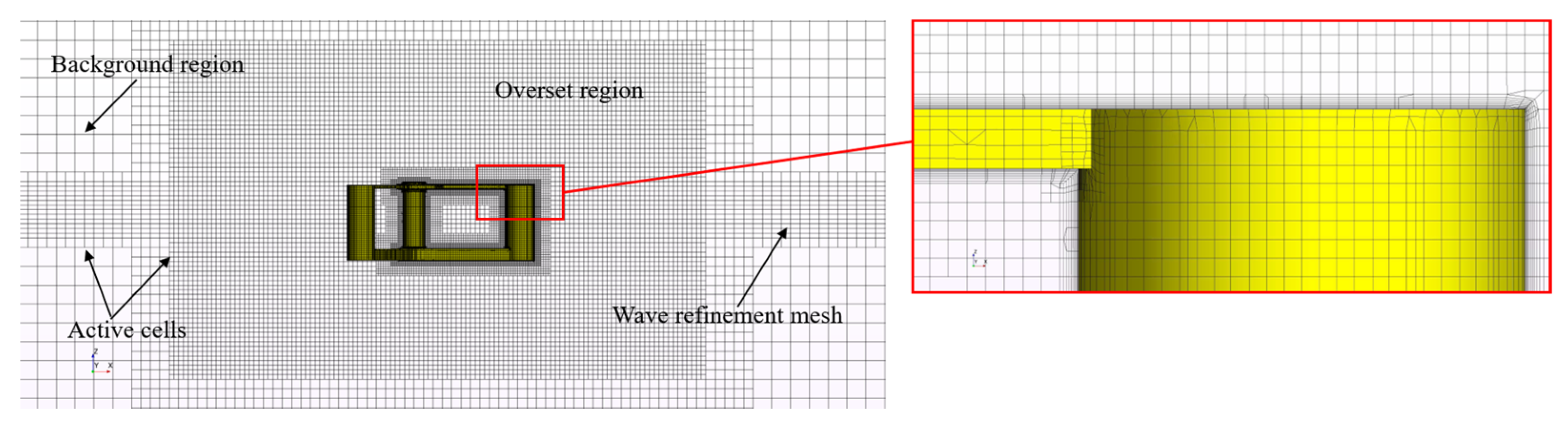
4.1. Flow Doamin and Applied Boundary Conditions

4.2. Overset Mesh Topology
4.3. Model Validation
5. Results and Discussions
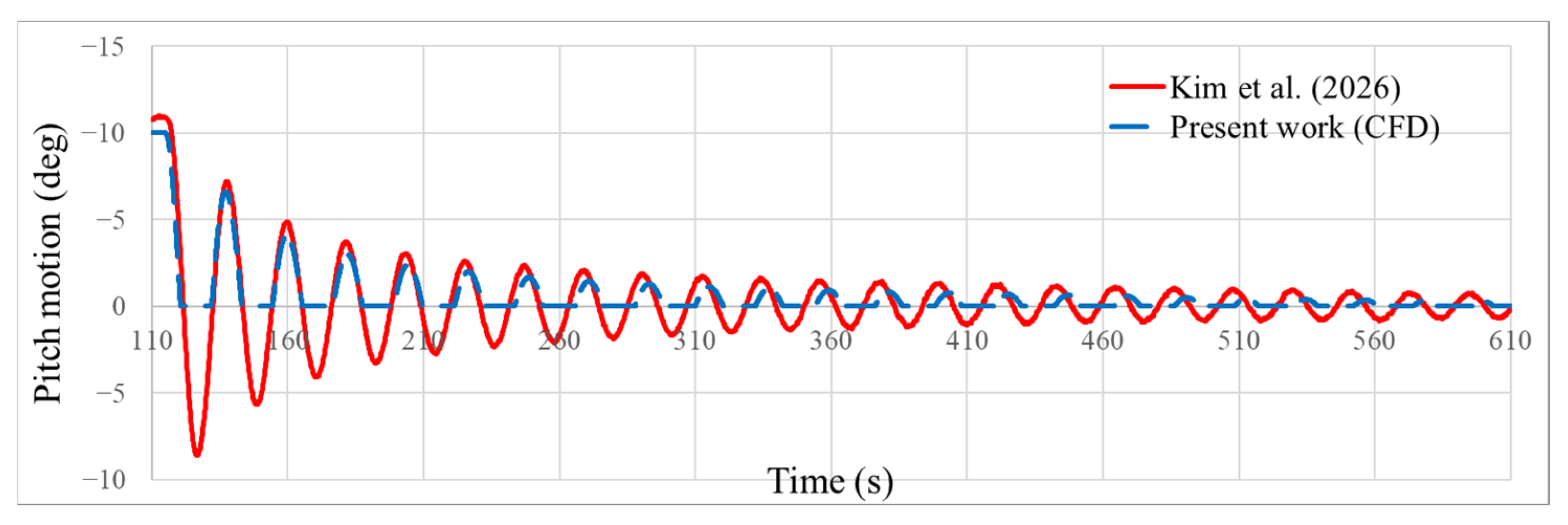
5.1. Free Decay Test
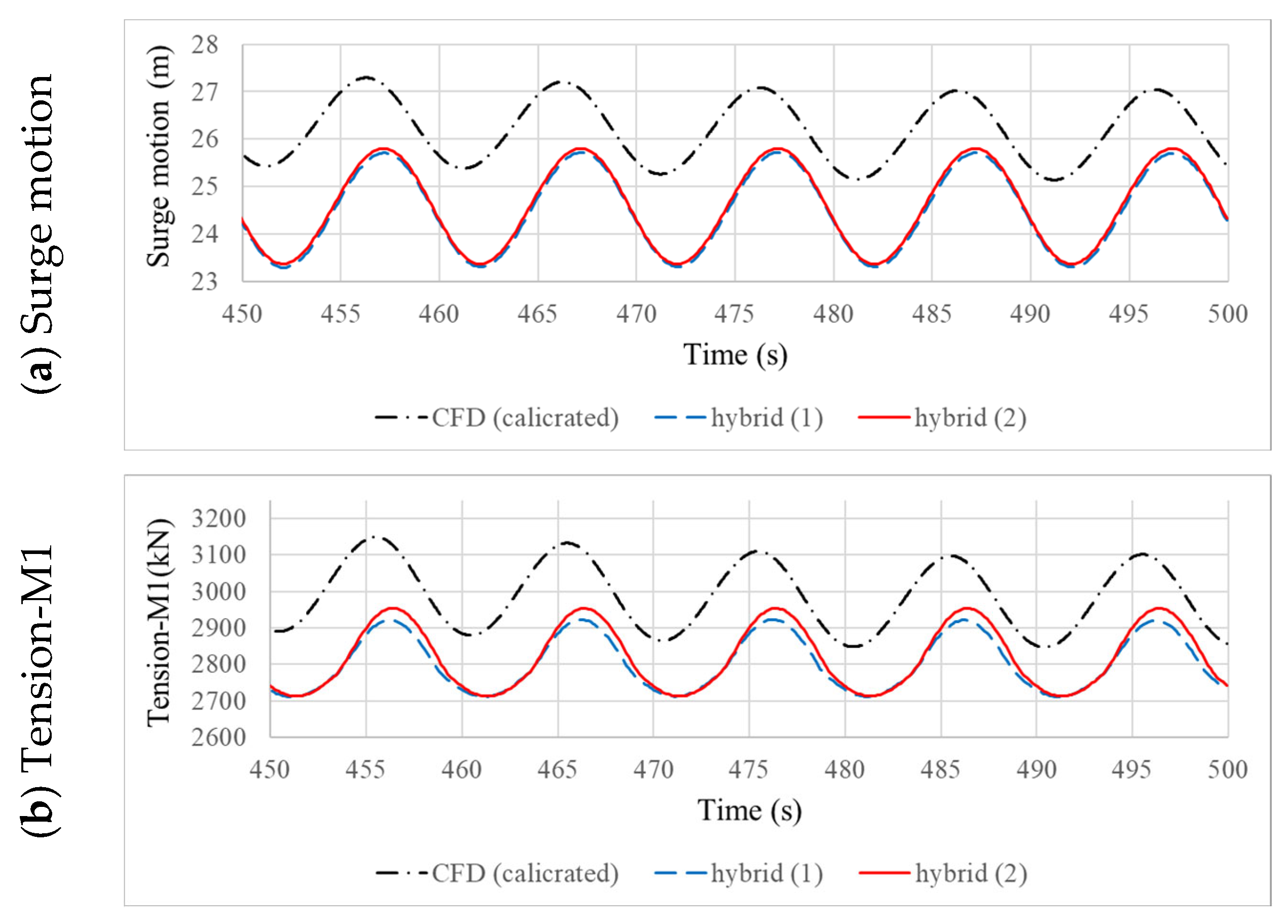
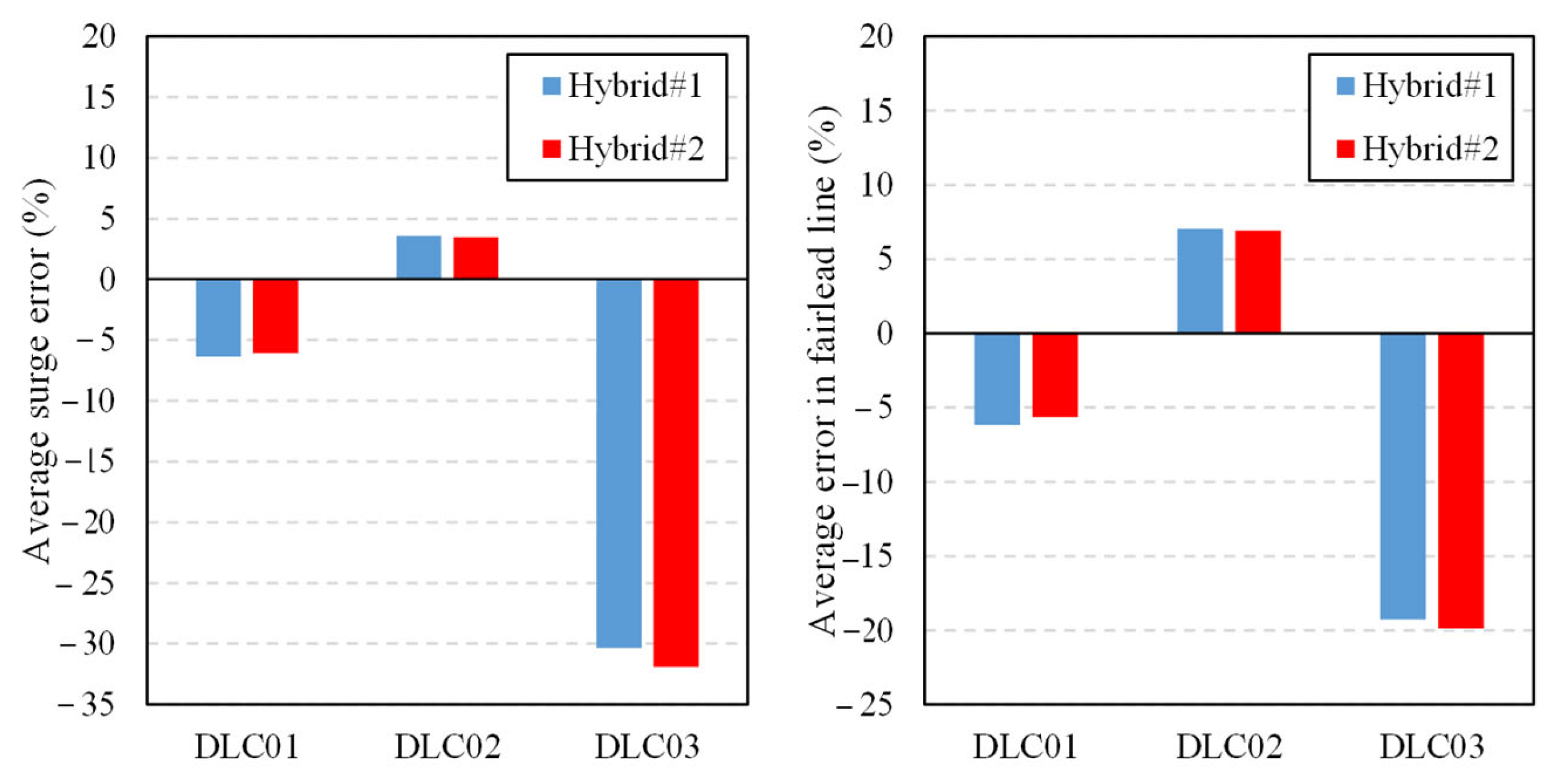
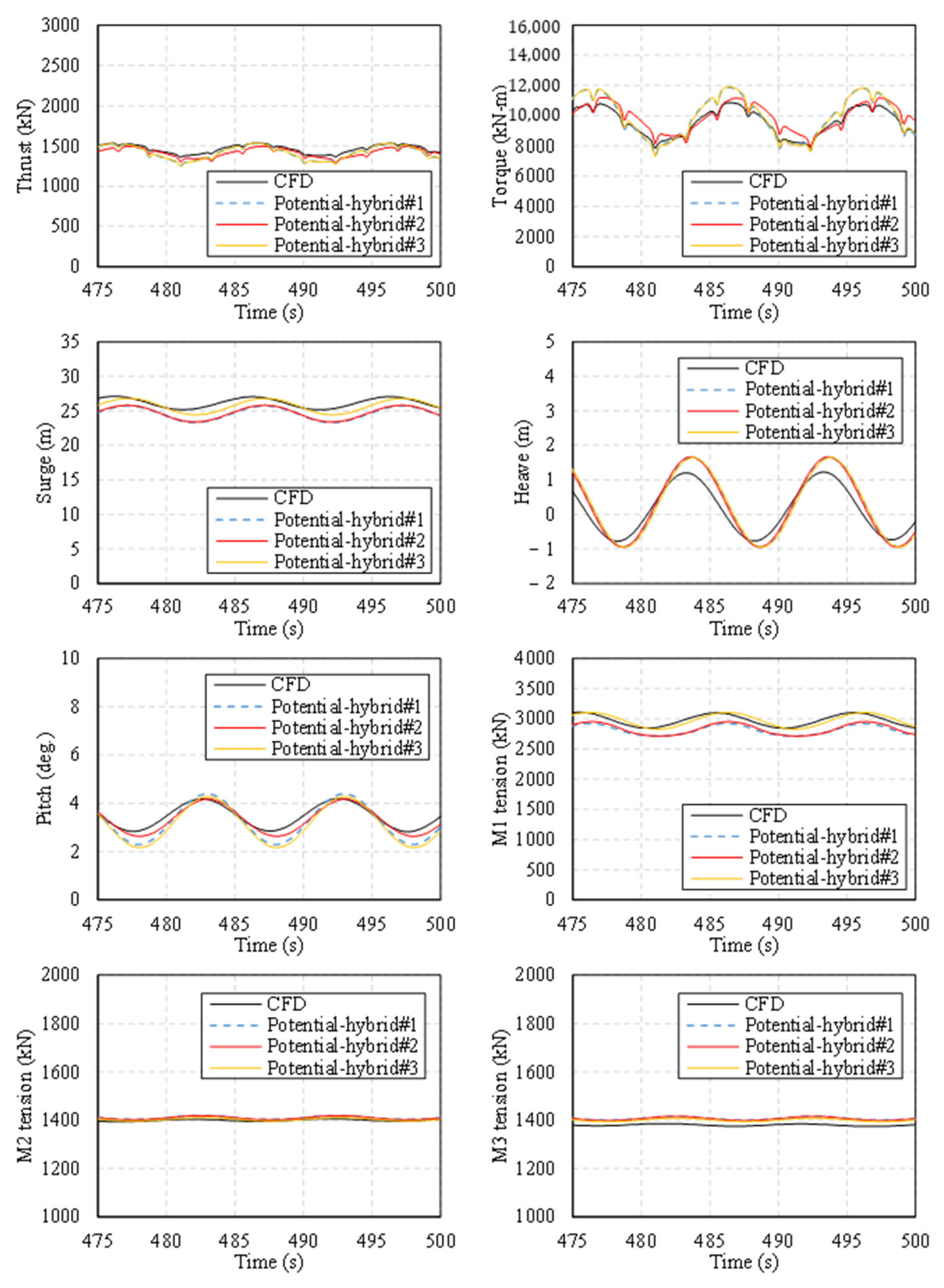
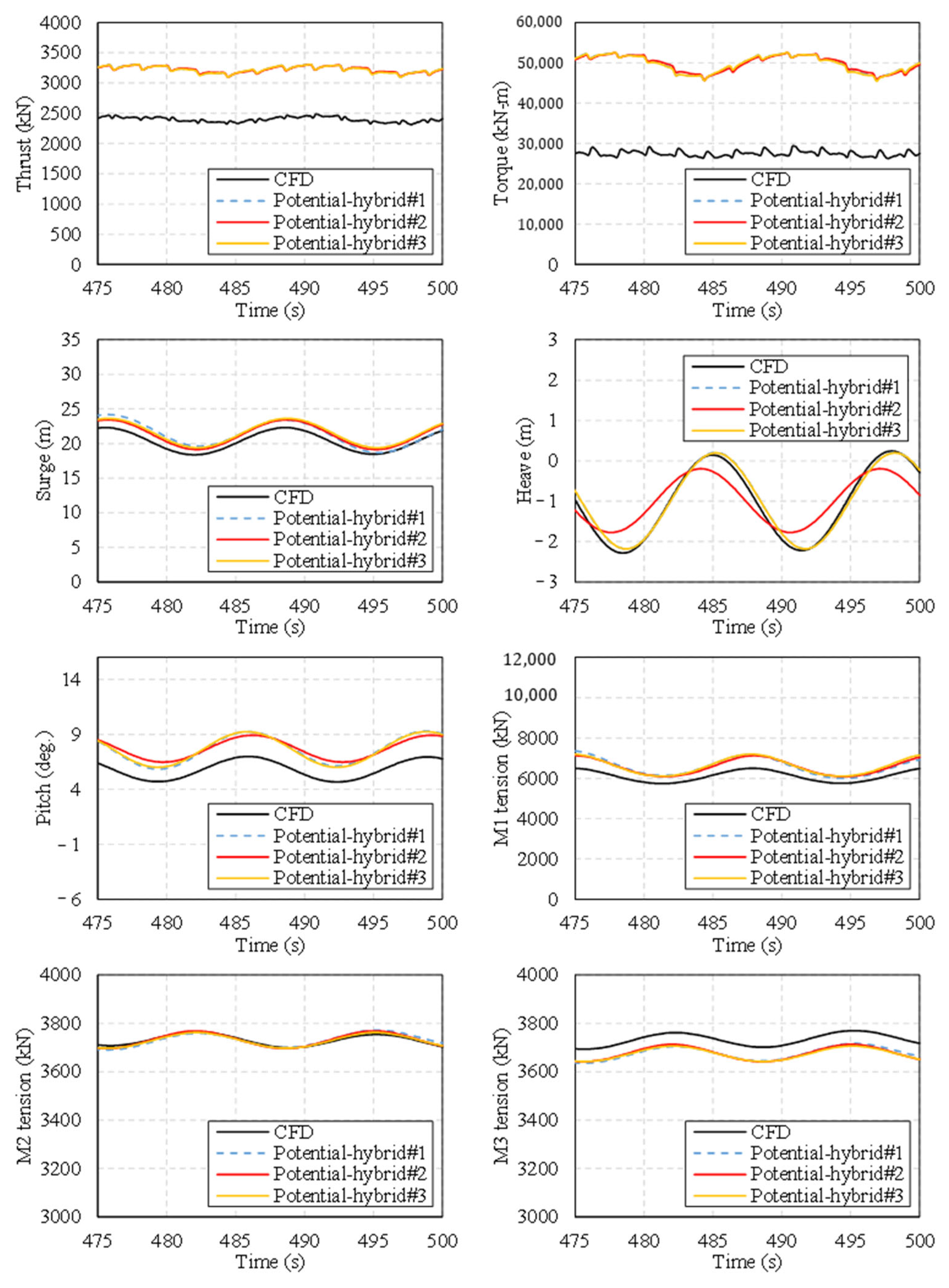
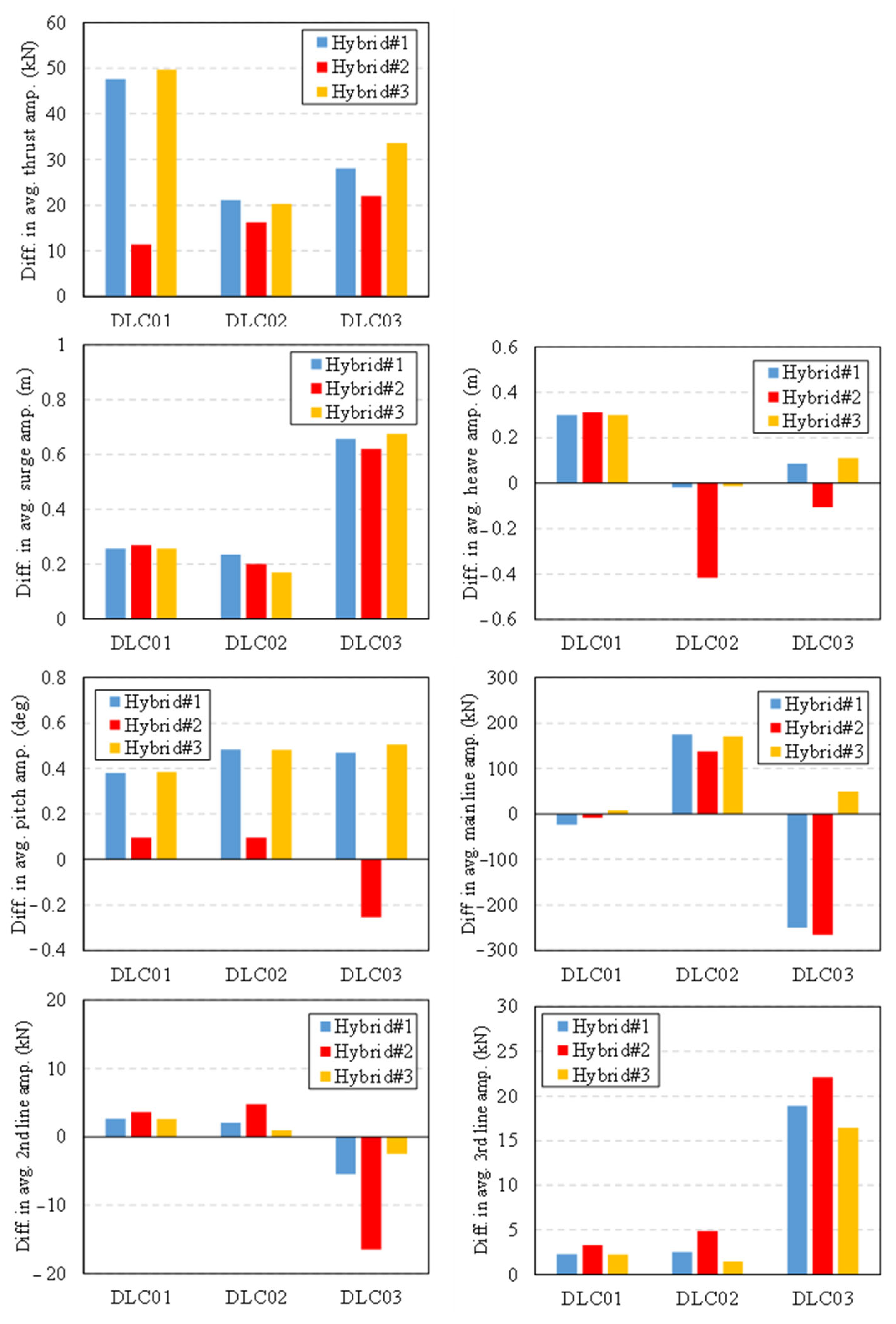
5.2. Hybrid Correction Framework Adapted for Advanced Potential Engineering Tool Applications
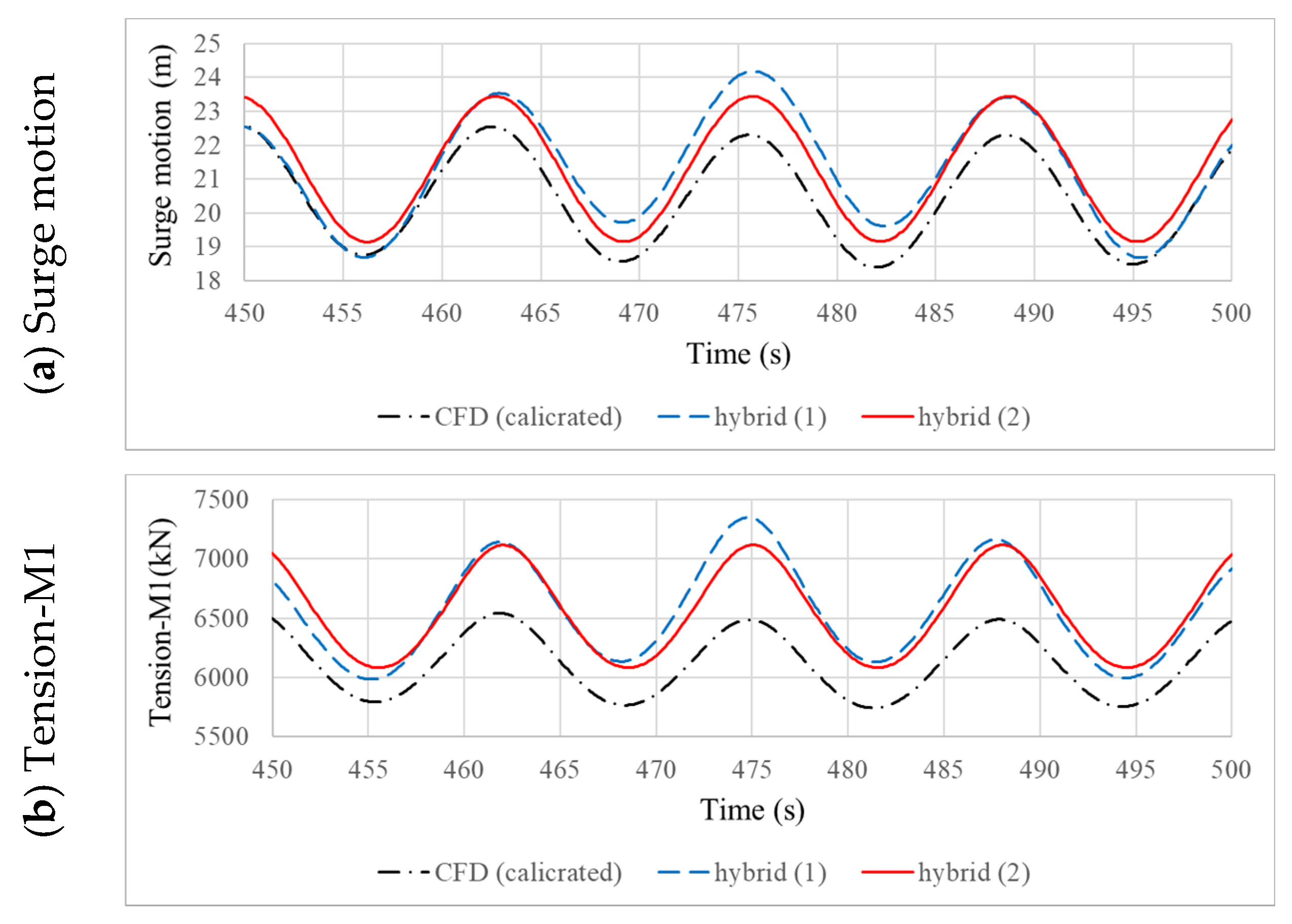
5.3. Improved Hybrid Correction Strategy for Potential Engineering Tool Applications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Blade element momentum | |
| Computational Fluid Dynamic | |
| Design load case | |
| Floating Offshore Wind Turbine | |
| RNA | Rotor-Nacelle Assembly |
References
- Zhou, L.; Li, Y.; Liu, F.; Jiang, Z.; Yu, Q.; Liu, L. Investigation of dynamic characteristics of a monopile wind turbine based on sea test. Ocean Eng. 2019, 189, 106308. [Google Scholar] [CrossRef]
- Jung, S.; Kim, S.-R.; Patil, A.; Hung, L.C. Effect of monopile foundation modeling on the structural response of a 5-MW offshore wind turbine tower. Ocean Eng. 2015, 109, 479–488. [Google Scholar] [CrossRef]
- Frick, D.; Achmus, M. An experimental study on the parameters affecting the cyclic lateral response of monopiles for offshore wind turbines in sand. Soils Found. 2020, 60, 1570–1587. [Google Scholar] [CrossRef]
- Häfele, J.; Gebhardt, C.G.; Rolfes, R. A comparison study on jacket substructures for offshore wind turbines based on optimization. Wind Energy Sci. 2019, 4, 23–40. [Google Scholar] [CrossRef]
- Häfele, J.; Hübler, C.; Gebhardt, C.G.; Rolfes, R. A comprehensive fatigue load set reduction study for offshore wind turbines with jacket substructures. Renew. Energy 2018, 118, 99–112. [Google Scholar] [CrossRef]
- Shi, W.; Han, J.; Kim, C.; Lee, D.; Shin, H.; Park, H. Feasibility study of offshore wind turbine substructures for southwest offshore wind farm project in Korea. Renew. Energy 2015, 74, 406–413. [Google Scholar] [CrossRef]
- Rodriguez, S.N.; Jaworski, J.W. Strongly-coupled aeroelastic free-vortex wake framework for floating offshore wind turbine rotors. Part 2: Application. Renew. Energy 2020, 149, 1018–1031. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, Y.; He, Y.; Shao, Y.; Mao, W.; Han, Z.; Huang, C.; Gu, X.; Jiang, Z. Transient response of a TLP-type floating offshore wind turbine under tendon failure conditions. Ocean Eng. 2021, 220, 108486. [Google Scholar] [CrossRef]
- Bagherian, V.; Salehi, M.; Mahzoon, M. Rigid multibody dynamic modeling for a semi-submersible wind turbine. Energy Convers. Manag. 2021, 244, 114399. [Google Scholar] [CrossRef]
- Yang, Y.; Bashir, M.; Michailides, C.; Li, C.; Wang, J. Development and application of an aero-hydro-servo-elastic coupling framework for analysis of floating offshore wind turbines. Renew. Energy 2020, 161, 606–625. [Google Scholar] [CrossRef]
- Kvittem, M.I.; Bachynski, E.E.; Moan, T. Effects of Hydrodynamic Modelling in Fully Coupled Simulations of a Semi-submersible Wind Turbine. Energy Procedia 2012, 24, 351–362. [Google Scholar] [CrossRef]
- Yang, H.-S.; Tongphong, W.; Ali, A.; Lee, Y.-H. Comparison of different fidelity hydrodynamic-aerodynamic coupled simulation code on the 10 MW semi-submersible type floating offshore wind turbine. Ocean Eng. 2023, 281, 114736. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.-H. Fully coupled aero-hydrodynamic analysis of a semi-submersible FOWT using a dynamic fluid body interaction approach. Renew. Energy 2016, 92, 244–261. [Google Scholar] [CrossRef]
- Yang, H.-S.; Alkhabbaz, A.; Tongphong, W.; Lee, Y.-H. Cross-comparison analysis of environmental load components in extreme conditions for pontoon-connected semi-submersible FOWT using CFD and potential-based tools. Ocean Eng. 2024, 304, 117248. [Google Scholar] [CrossRef]
- Deng, S.; Liu, Y.; Ning, D. Fully coupled aero-hydrodynamic modelling of floating offshore wind turbines in nonlinear waves using a direct time-domain approach. Renew. Energy 2023, 216, 119016. [Google Scholar] [CrossRef]
- Wang, W.; Hu, J.; Zhao, C.; Xie, Y.; Gong, X.; Jiang, D. Multi-Column Semi-Submersible Floating Body Hydrodynamic Performance Analysis. Energies 2025, 18, 1884. [Google Scholar] [CrossRef]
- Alkhabbaz, A.; Hamza, H.; Daabo, A.M.; Yang, H.-S.; Yoon, M.; Koprulu, A.; Lee, Y.-H. The aero-hydrodynamic interference impact on the NREL 5-MW floating wind turbine experiencing surge motion. Ocean Eng. 2024, 295, 116970. [Google Scholar] [CrossRef]
- Burmester, S.; Vaz, G.; el Moctar, O. Towards credible CFD simulations for floating offshore wind turbines. Ocean Eng. 2020, 209, 107237. [Google Scholar] [CrossRef]
- Li, H.; Bachynski-Polić, E.E. Validation and application of nonlinear hydrodynamics from CFD in an engineering model of a semi-submersible floating wind turbine. Mar. Struct. 2021, 79, 103054. [Google Scholar] [CrossRef]
- Wang, L.; Robertson, A.; Jonkman, J.; Yu, Y.-H. OC6 phase I: Improvements to the OpenFAST predictions of nonlinear, low-frequency responses of a floating offshore wind turbine platform. Renew. Energy 2022, 187, 282–301. [Google Scholar] [CrossRef]
- Wang, L.; Robertson, A.; Kim, J.; Jang, H.; Shen, Z.-R.; Koop, A.; Bunnik, T.; Yu, K. Validation of CFD simulations of the moored DeepCwind offshore wind semisubmersible in irregular waves. Ocean Eng. 2022, 260, 112028. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.-H. A CFD study into the influence of unsteady aerodynamic interference on wind turbine surge motion. Renew. Energy 2016, 90, 204–228. [Google Scholar] [CrossRef]
- Yang, H.-S.; Alkhabbaz, A.; Edirisinghe, D.S.; Tongphong, W.; Lee, Y.-H. FOWT Stability Study According to Number of Columns Considering Amount of Materials Used. Energies 2022, 15, 1653. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.-H. The coupled dynamic response computation for a semi-submersible platform of floating offshore wind turbine. J. Wind Eng. Ind. Aerodyn. 2015, 147, 104–119. [Google Scholar] [CrossRef]
- Dose, B.; Rahimi, H.; Herráez, I.; Stoevesandt, B.; Peinke, J. Fluid-structure coupled computations of the NREL 5 MW wind turbine by means of CFD. Renew. Energy 2018, 129, 591–605. [Google Scholar] [CrossRef]
- Hansen, M.O.L.; Sørensen, J.N.; Voutsinas, S.; Sørensen, N.; Madsen, H.A. State of the art in wind turbine aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2006, 42, 285–330. [Google Scholar] [CrossRef]
- Hansen, M. Aerodynamics of Wind Turbines; Routledge: Abingdon, UK, 2015. [Google Scholar] [CrossRef]
- Sebastian, T.; Lackner, M.A. Characterization of the unsteady aerodynamics of offshore floating wind turbines. Wind Energy 2013, 16, 339–352. [Google Scholar] [CrossRef]
- Alkhabbaz, A.; Yang, H.-S.; Weerakoon, A.H.S.; Lee, Y.-H. A novel linearization approach of chord and twist angle distribution for 10 kW horizontal axis wind turbine. Renew. Energy 2021, 178, 1398–1420. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics of offshore floating wind turbines model development and verification. Wind Energy 2009, 12, 459–492. [Google Scholar] [CrossRef]
- Masciola, M.; Robertson, A.; Jonkman, J.; Goupee, A.; Coulling, A. Assessment of the Importance of Mooring Dynamics on the Global Response of the DeepCwind Floating Semisubmersible Offshore Wind Turbine. In Proceedings of the Twenty-Third (2013) International Offshore and Polar Engineering Conference, Anchorage, Alaska, 30 June–5 July 2013; pp. 359–368. [Google Scholar]
- Rongé, É.; Peyrard, C.; Venugopal, V.; Xiao, Q.; Johanning, L.; Benoit, M. Evaluation of second and third-order numerical wave-loading models for floating offshore wind TLPs. Ocean Eng. 2023, 288, 116064. [Google Scholar] [CrossRef]
- Orcina, Ltd. OrcaFlex Manual; Version 9.6a; Orcina, Ltd.: Ulverston, UK, 2012; pp. 1–376. [Google Scholar]
- Shan, T.; Yang, J.; Li, X.; Xiao, L. Experimental Investigation on Wave Run-up Characteristics Along Columns and Air Gap Response of Semi-Submersible Platform. J. Hydrodyn. 2011, 23, 625–636. [Google Scholar] [CrossRef]
- Li, H.; Bachynski, E.E. Experimental and numerical investigation of nonlinear diffraction wave loads on a semi-submersible wind turbine. Renew. Energy 2021, 171, 709–727. [Google Scholar] [CrossRef]
- Butterfield, S.; Musial, W.; Jonkman, J.; Sclavounos, P. Engineering Challenges for Floating Offshore Wind Turbines; NREL/CP-500-38776; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2007.
- Carlson, D.W.; Modarres-Sadeghi, Y. Vortex-induced vibration of spar platforms for floating offshore wind turbines. Wind Energy 2018, 21, 1169–1176. [Google Scholar] [CrossRef]
- Kim, I.C.; Alkhabbaz, A.; Jeong, H.; Lee, Y.H. Optimization Methodology Of Small Scale Horizontal Axis Shrouded Tidal Current Turbine. In Proceedings of the 2019 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Melbourne, VIC, Australia, 9–11 December 2019. [Google Scholar] [CrossRef]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW Reference Wind Turbine; DTU Wind Energy, Technical University of Denmark: Kongens Lyngby, Denmark, 2013. [Google Scholar]
- Muggiasca, S.; Taruffi, F.; Fontanella, A.; di Carlo, S.; Giberti, H.; Facchinetti, A.; Belloli, M. Design of an aeroelastic physical model of the DTU 10MW wind turbine for a floating offshore multipurpose platform prototype. Ocean Eng. 2021, 239, 109837. [Google Scholar] [CrossRef]
- Siemens PLM Software, Version 13.06.012; Siemens Industry Software Inc.: Plano, TX, USA, 2018.
- Yang, H.-S.; Alkhabbaz, A.; Lee, Y.-H. Integrated CFD and hydrodynamic correction approach for load response analysis of floating offshore wind turbine. Ocean Eng. 2025, 328, 121007. [Google Scholar] [CrossRef]
- Srinivas, A.; Robertson, B.; Gadasi, J.B.; Simpson, B.G.; Lomónaco, P.; Ilzarbe, J.M.B. Impact of Limited Degree of Freedom Drag Coefficients on a Floating Offshore Wind Turbine Simulation. J. Mar. Sci. Eng. 2023, 11, 139. [Google Scholar] [CrossRef]
- Venugopal, V.; Varyani, K.S.; Westlake, P.C. Drag and inertia coefficients for horizontally submerged rectangular cylinders in waves and currents. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2009, 223, 121–136. [Google Scholar] [CrossRef]
- Det Norske Veritas. Environmental Conditions and Environmental Loads; DNV-RP-C2025; Det Norske Veritas: Bærum, Norway, 2010. [Google Scholar]
- Kim, B.W.; Sim, K.; Lee, K.; Hong, S.Y. Experimental and Numerical Evaluation of Hydrodynamic Behavior of 10 MW Floating Offshore Wind Turbine. In Advanced and Emerging Marine Engineering Technologies; Springer: Singapore, 2025; pp. 802–813. [Google Scholar] [CrossRef]
- Alkhabbaz, A.; Hamzah, H.; Hamdoon, O.M.; Yang, H.-S.; Easa, H.; Lee, Y.-H. A unique design of a hybrid wave energy converter. Renew. Energy 2025, 245, 122814. [Google Scholar] [CrossRef]
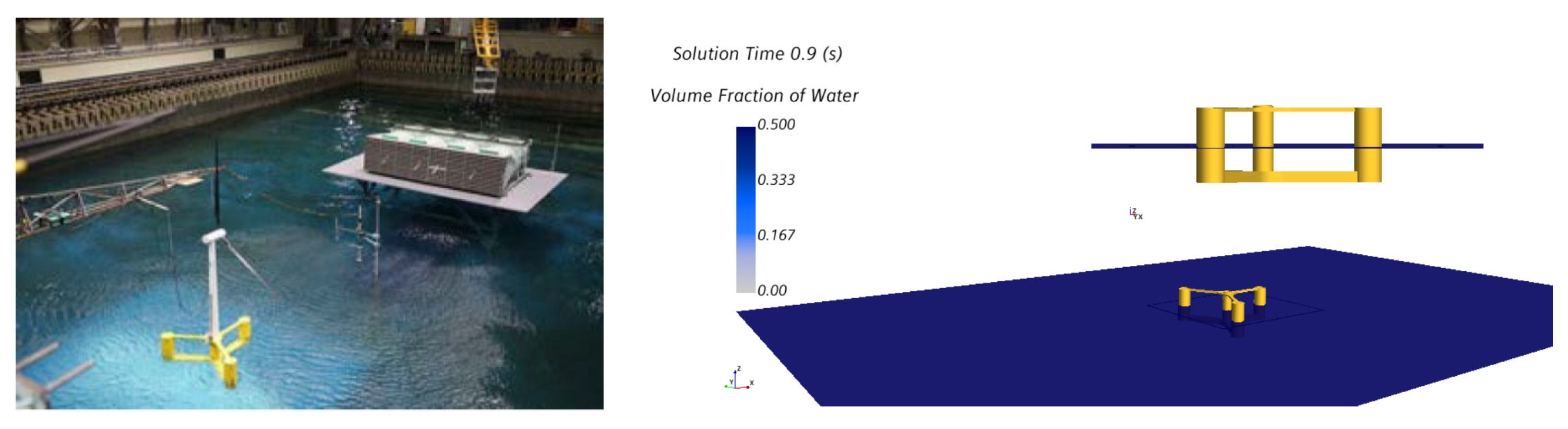





| Load Case No. | Wave | Current | Wind | Turbine Direction | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Condition | Dir. | Height | Period | Dir. | Speed | Condition | Dir. | Speed | ||
| 01 | Regular | 180° | 6.0 m | 10.0 s | - | - | Constant | 180° | 11.0 m/s | 180° |
| 02 | Regular | 180° | 6.0 m | 13.0 s | - | - | Constant | 180° | 24.0 m/s | 180° |
| 03 | Regular | 270° | 8.34 m | 13.1 s | 270° | 0.77 m/s | Constant | 270° | 40.28 m/s | 240° |
| Properties | Values | ||
|---|---|---|---|
| Overall (w/o mooring) | |||
| Mass | 1.025 107 kg | ||
| Displacement volume | 10,728 m3 | ||
| Center of mass (from SWL) | X | y | z |
| −0.04 m | 0 m | 4.185 m | |
| Draft | 15.5 m | ||
| Moment of inertia | Ixx | Iyy | Izz |
| 1.967 107 kg2-m | 1.961 107 kg2-m | 1.298 107 kg2-m | |
| Mooring | |||
| Unstretched length | 850 m | ||
| DLC01 | DLC02 | DLC03 | |
| Stiffness | 1.845 106 kN | 1.845 106 kN | 1.568 109 kN |
| Mooring mass | 162.51 kg/m | 432 kg/m | 373.87 kg/m |
| Fairlead and Anchor position | x (m) | y (m) | z (m) |
| Anchor | 0.00 | −852.69 | −150.0 |
| 738.45 | 426.35 | −150.0 | |
| −738.45 | 426.35 | −150.0 | |
| Fairlead | 0.00 | 52.69 | 13.08 |
| 45.631 | 26.345 | 13.08 | |
| −45.631 | 26.345 | 13.08 | |
| Hydride (1) | Hybrid (2) | |
|---|---|---|
| Drag coefficient | ||
| CDside col_trans. | 0.8 | 1 |
| CDside col_verti. | 0.8 | 0 |
| CDinter_trans. | 0.61 | 1 |
| CDinter_verti. | 2.4 | 0 |
| CDmain col_trans. | 0.8 | 1 |
| CDmain col_verti. | 2.4 | 0 |
| CDpootoon_trans. | 2.0 | 1.72 |
| CDpootoon_verti. | 3.0 | 0 |
| Damping coefficient | ||
| Linear surge (kN/(m/s)) | 130 | 0 |
| Linear heave (kN/(m/s)) | 0 | 1960 |
| Linear pitch (kN/(rad/s)) | 0 | 629 103 |
| Quadra surge (kN/(m/s)2) | −400 | 0 |
| Quadra heave (kN/(m/s)2) | 1500 | 0 |
| Quadra pitch (kN/(rad/s)2) | −20 106 | 0 |
| Experiment | CFD | CFD Error (%) | |
|---|---|---|---|
| Period (avg.) | 21.757 s | 22.039 s | 1.29 |
| Logarithmic decrement (1th~5th avg.) | 0.241 | 0.231 | −3.88 |
| Logarithmic decrement (6th~15th avg.) | 0.089 | 0.094 | 6.79 |
| Drag Coefficient | Hybrid (3) |
|---|---|
| CDside col_trans. | 3.5 |
| CDside col_verti. | 0.8 |
| CDinter_trans. | 0.61 |
| CDinter_verti. | 2.4 |
| CDmain col_trans. | 3.5 |
| CDmain col_verti. | 2.4 |
| CDpootoon_trans. | 2.0 |
| CDpootoon_verti. | 3.0 |
| Damping coefficient | |
| Linear surge (kN/(m/s)) | 130 |
| Linear heave (kN/(m/s)) | 0 |
| Linear pitch (kN/(rad/s)) | 0 |
| Quadra surge (kN/(m/s)2) | −400 |
| Quadra heave (kN/(m/s)2) | 1500 |
| Quadra pitch (kN/(rad/s)2) | −20 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.-S.; Alkhabbaz, A.; Lee, Y.-H. Toward Reliable FOWT Modeling: A New Calibration Approach for Extreme Environmental Loads. Energies 2025, 18, 5545. https://doi.org/10.3390/en18205545
Yang H-S, Alkhabbaz A, Lee Y-H. Toward Reliable FOWT Modeling: A New Calibration Approach for Extreme Environmental Loads. Energies. 2025; 18(20):5545. https://doi.org/10.3390/en18205545
Chicago/Turabian StyleYang, Ho-Seong, Ali Alkhabbaz, and Young-Ho Lee. 2025. "Toward Reliable FOWT Modeling: A New Calibration Approach for Extreme Environmental Loads" Energies 18, no. 20: 5545. https://doi.org/10.3390/en18205545
APA StyleYang, H.-S., Alkhabbaz, A., & Lee, Y.-H. (2025). Toward Reliable FOWT Modeling: A New Calibration Approach for Extreme Environmental Loads. Energies, 18(20), 5545. https://doi.org/10.3390/en18205545






