Day-Ahead Coordinated Reactive Power Optimization Dispatching Based on Semidefinite Programming
Abstract
1. Introduction
2. Optimization Model
2.1. Reactive Equipment Model
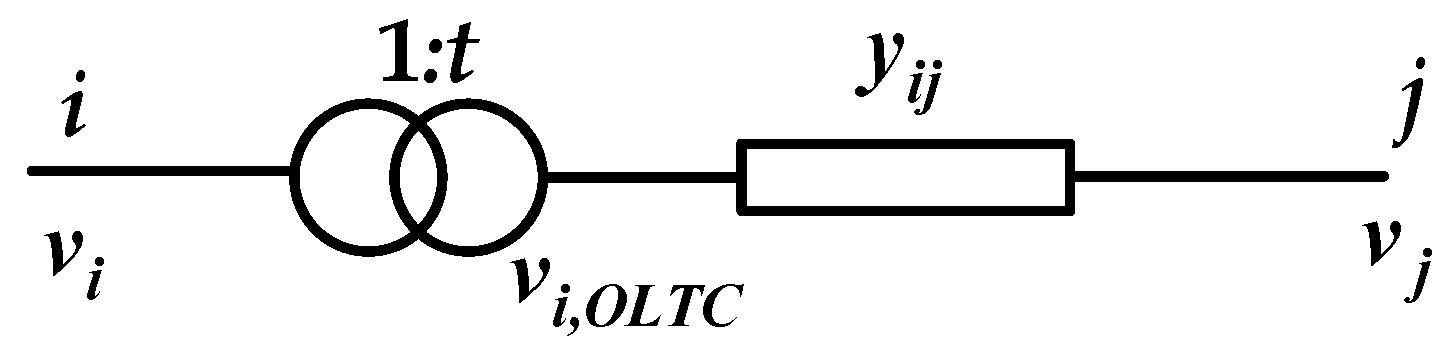
2.1.1. Model of the OLTC
- Transformer voltage
- Transformer power equation
2.1.2. Model of the CBs
2.1.3. Model of the DGs
2.1.4. Model of the SVG
2.2. Reactive Power Optimization Model
2.2.1. Objective Function
- Active power losses cost
- Switching cost of OLTC
- Switching cost of CBs
2.2.2. Constraints for Reactive Power Optimization
3. Optimization Model Conversion
3.1. Define Vectors
3.2. Define the Auxiliary Matrix
3.3. Convert to SDP
3.3.1. Objective Function
3.3.2. Constraints for Reactive Power Optimization
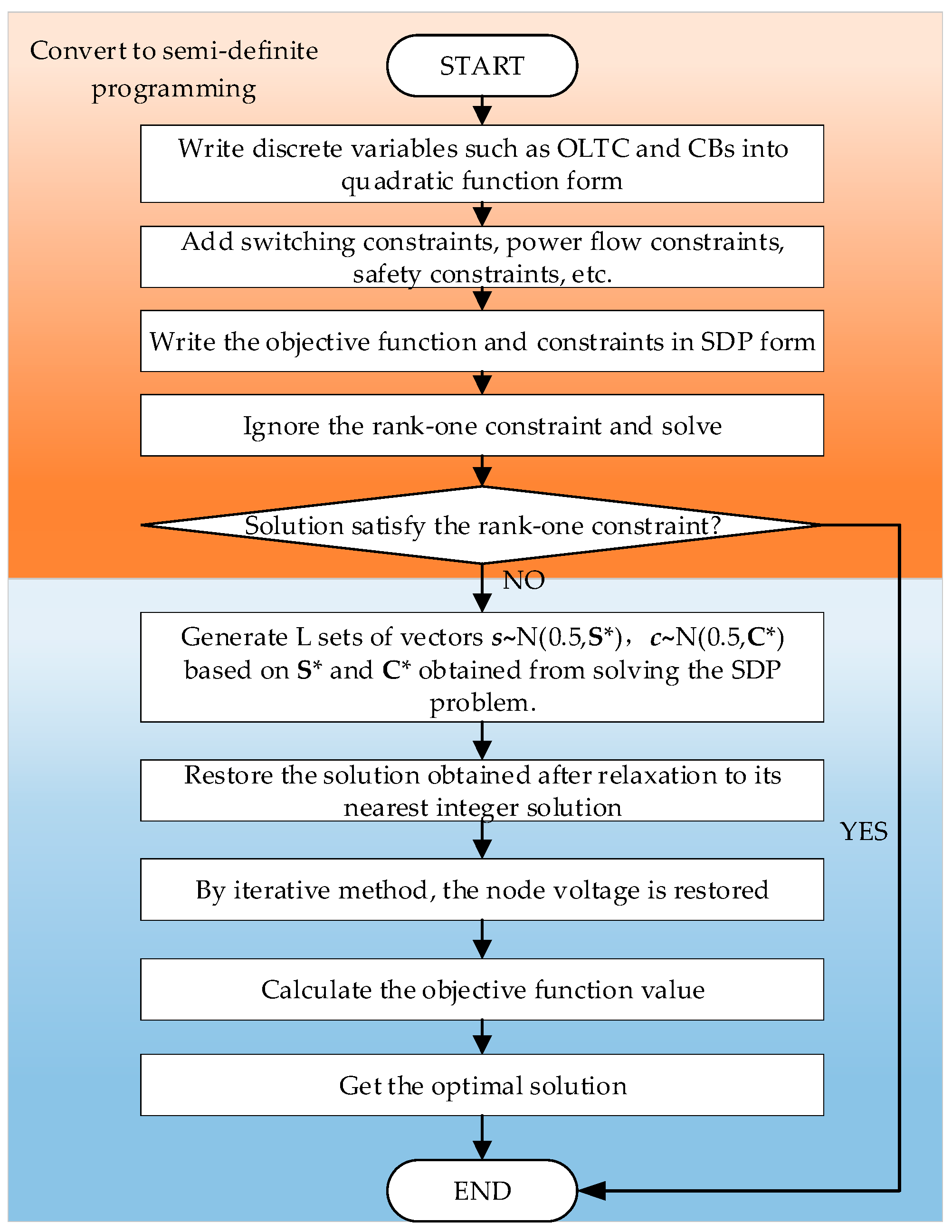
4. Solving the Semidefinite Programming Problems
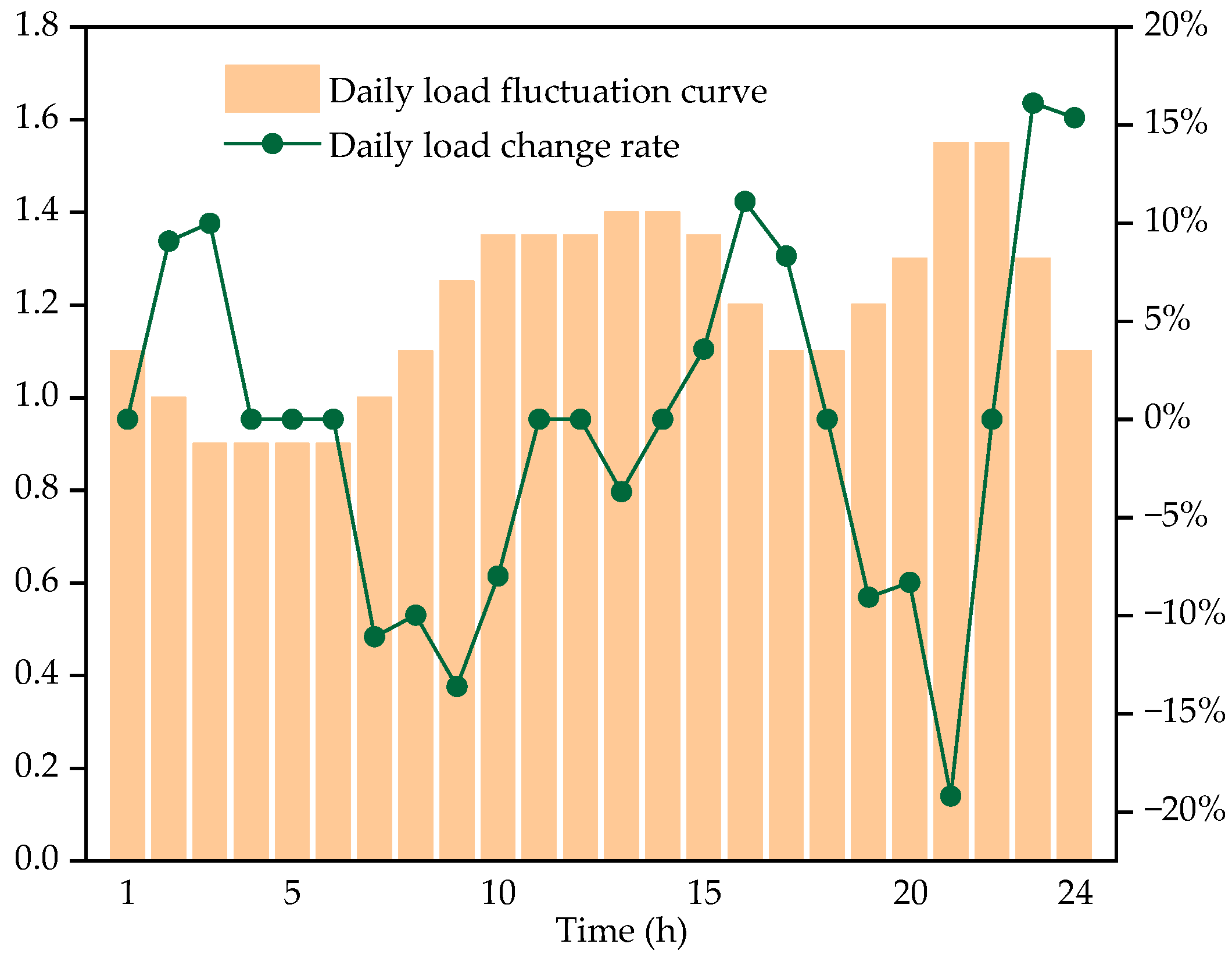
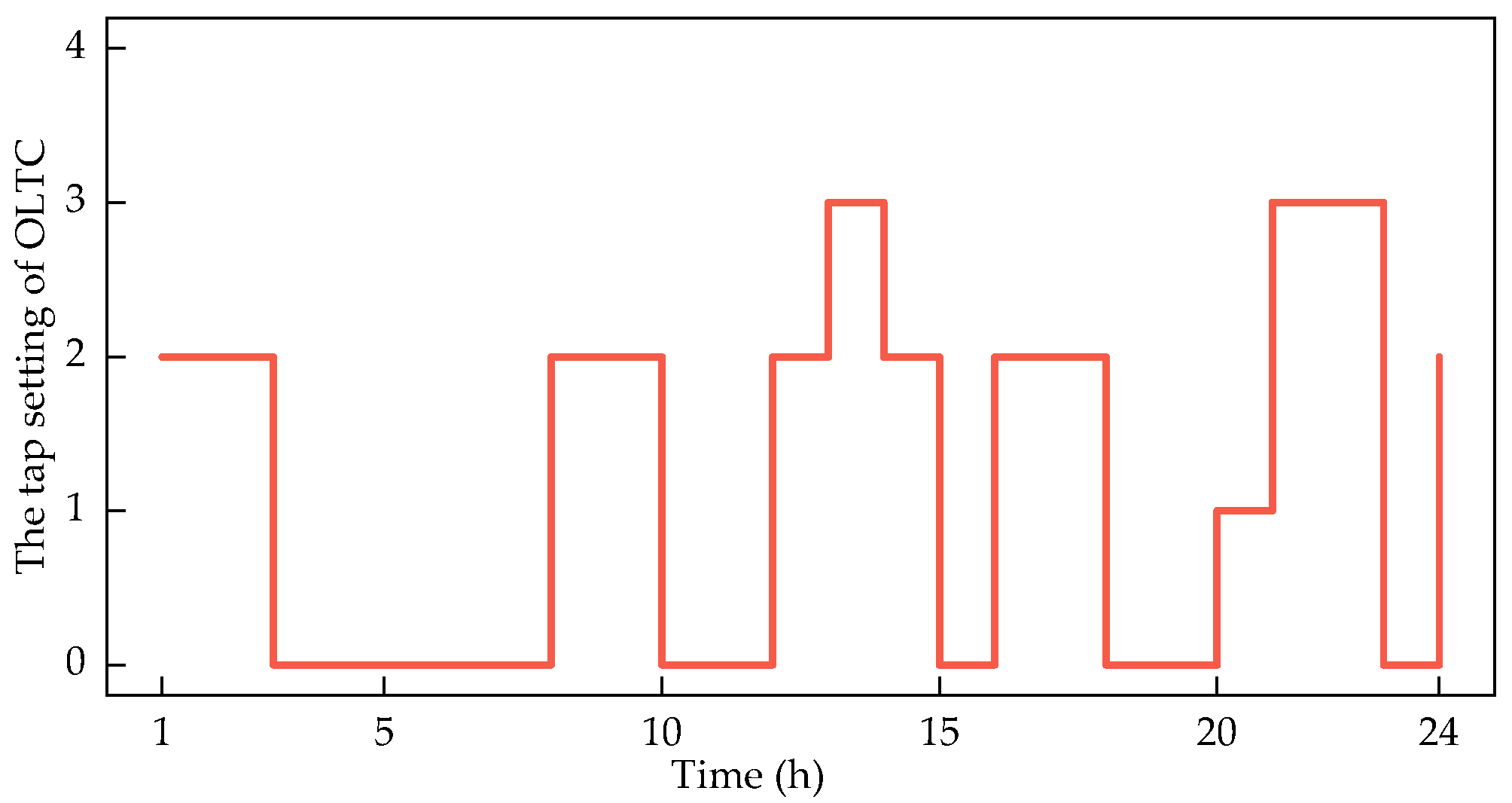
5. Case Study and Discussion
5.1. Case 9 Network
5.2. Other Network
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| The voltage of OLTC at node i at time t | |
| The tap setting of OLTC at time t | |
| OLTC output active power at time t | |
| OLTC output reactive power at time t | |
| Reactive power generated by CBs at node i at time t | |
| Number of CBs put into operation at node i at time t | |
| Active power generated by DG at node i at time t | |
| Reactive power generated by DG at node i at time t | |
| Reactive power generated by SVG at node i at time t | |
| Line loss cost of the system | |
| OLTC switching cost | |
| Switching cost of CBs | |
| Real part of the voltage at node i at time t | |
| Imaginary part of the voltage at node i at time t | |
| Real part of the admittance between node i and node j | |
| Imaginary part of the admittance between node i and node j | |
| Line current from node l to node m | |
| Voltage matrix | |
| OLTC matrix variables | |
| CBs matrix variables | |
| OLTC voltage base value | |
| OLTC voltage regulation for each tap | |
| OLTC output active power maximum | |
| OLTC output active power minimum | |
| OLTC output reactive power maximum | |
| OLTC output reactive power minimum | |
| Reactive power that can be generated by each group of capacitors | |
| DG can generate active power upper limit | |
| DG can generate active power lower limit | |
| DG can generate reactive power upper limit | |
| DG can generate reactive power lower limit | |
| SVG can generate reactive power upper limit | |
| SVG can generate reactive power lower limit | |
| Time period | |
| Unit network loss cost | |
| Unit switching cost of OLTC | |
| Unit switching cost of CBs | |
| Maximum value of voltage at node i | |
| Minimum value of voltage at node i | |
| Maximum transmission capacity of lm branch | |
| Line resistance from node l to node m | |
| Self-admittance at node i | |
| Re( ) | Real part calculation |
| Im( ) | Imaginary part calculation |
| Tr( ) | Matrix trace calculation |
| rank( ) | Calculate the rank of a matrix |
| Calculate the maximum eigenvalue of a matrix |
Appendix A
References
- Luo, S.; Hu, W.; Liu, W.; Xu, X.; Huang, Q.; Chen, Z.; Lund, H. Transition pathways towards a deep decarbonization energy system—A case study in Sichuan, China. Appl. Energy 2021, 302, 117507. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, G.; Hu, W.; Huang, Q.; Chen, Z.; Blaabjerg, F. Meta-Learning Based Voltage Control for Renewable Energy Integrated Active Distribution Network Against Topology Change. IEEE Tran. Power Syst. 2023, 38, 5937–5940. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, W.; Zhao, J.; Cao, D.; Chen, Z.; Blaabjerg, F. A novel deep reinforcement learning enabled multi-band PSS for multi-mode oscillation control. IEEE Trans. Power Syst. 2021, 36, 3794–3797. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, H.; Li, C.; Liu, Y.; Li, W.; Terzija, V. Optimization of the event-driven emergency load-shedding considering transient security and stability constraints. IEEE Trans. Power Syst. 2017, 32, 2581–2592. [Google Scholar] [CrossRef]
- Cao, D.; Hu, W.; Zhao, J.; Huang, Q.; Chen, Z.; Blaabjerg, F. Amulti-agent deep reinforcement learning based voltage regulation using coordinated PV inverters. IEEE Trans. Power Syst. 2020, 35, 4120–4123. [Google Scholar] [CrossRef]
- Win, T.S.; Hisada, Y.; Tanaka, T.; Hiraki, E.; Okamoto, M.; Lee, S.R. Novel Simple Reactive Power Control Strategy with DC Capacitor Voltage Control for Active Load Balancer in Three-Phase Four-Wire Distribution Systems. IEEE Trans. Ind. Appl. 2015, 51, 4091–4099. [Google Scholar] [CrossRef]
- Akagi, H.; Kanazawa, Y.; Nabae, A. Instantaneous reactive power compensators comprising switching devices without energy storage components. IEEE Trans. Ind. Appl. 1984, IA-20, 625–630. [Google Scholar] [CrossRef]
- Peng, F.Z.; Ott, G.; Adams, D. Adams. Harmonic and reactive power compensation based on the generalized instantaneous reactive power theory for the three-phase four-wire systems. IEEE Trans. Power Electron. 1998, 13, 1174–1181. [Google Scholar] [CrossRef]
- Santoso, S. On Determining the Relative Location of Switched Capacitor Banks. IEEE Trans. Power Del. 2007, 22, 1108–1116. [Google Scholar] [CrossRef]
- Lehmann, K.; Grastien, A.; Van Hentenryck, P. AC-feasibility on tree networks is NP-hard. IEEE Trans. Power Syst. 2016, 31, 798–801. [Google Scholar] [CrossRef]
- Rabiee, A.; Parniani, M. Voltage security constrained multi-period optimal reactive power flow using benders and optimality condition de compositions. IEEE Trans. Power Syst. 2013, 28, 696–708. [Google Scholar] [CrossRef]
- Sharif, S.; Taylor, J. MINLP formulation of optimal reactive power flow. In Proceedings of the 1997 American Control Conference, Albuquerque, NM, USA, 4–6 June 1997; Volume 3, pp. 1974–1978. [Google Scholar]
- Iba, K. Reactive power optimization by genetic algorithm. IEEE Trans. Power Syst. 1994, 9, 685–692. [Google Scholar] [CrossRef]
- da Silva, A.A.; Abrão, P.J. Application of evolutionary computation in electric power systems. In Proceedings of the International Congress on Evolutionary Computation, Honolulu, HI, USA, 2–17 May 2002; pp. 1057–1062. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Zhao, B.; Guo, C.X.; Cao, Y.J. A multiagent-based particle swarm optimization approach for optimal reactive power dispatch. IEEE Trans. Power Syst. 2005, 20, 1070–1078. [Google Scholar] [CrossRef]
- Yoshida, H.; Kawata, K.; Fukuyama, Y.; Takayama, S.; Nakanishi, Y. A particle swarm optimization for reactive power and voltage control considering voltage security assessment. IEEE Trans. Power Syst. 2000, 15, 1232–1239. [Google Scholar] [CrossRef]
- Bakare, G.A.; Krost, G.; Venayagamoorthy, G.K.; Aliyu, U.O. Differential Evolution Approach for Reactive Power Optimization of Nigerian Grid System. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar]
- Zhang, W.; Liu, Y.; Clerc, M. An adaptive PSO algorithm for reactive power optimization. In Proceedings of the 2003 Sixth International Conference on Advances in Power System Control, Operation and Management ASDCOM 2003 (Conf. Publ. No. 497), Hong Kong, China, 11–14 November 2003; pp. 302–307. [Google Scholar]
- Park, S.; Chen, W.; Mak, T.W.; Van Hentenryck, P. Compact Optimization Learning for AC Optimal Power Flow. IEEE Tran. Power Syst. 2023, 39, 4350–4359. [Google Scholar] [CrossRef]
- Han, L.; Liu, B. Optimal Power Flow Calculation Method Based on Adaptive Artificial Frog Jumping Foraging Algorithm. Chang. Inf. Commun. 2024, 37, 34–36. [Google Scholar]
- Wu, X.; Guo, S.; Dai, W. Feature Dimension Reduction and Partitioning Based Deep Learning Method for Probabilistic Optimal Power Flow of Transmission Network. Electr. Power Autom. Equip. 2023, 43, 174–180. [Google Scholar]
- Jabr, R.A. Radial distribution load flow using conic programming. IEEE Trans. Power Syst. 2006, 21, 1458–1459. [Google Scholar] [CrossRef]
- Lavaei, J.; Low, S.H. Zero Duality Gap in Optimal Power Flow Problem. IEEE Trans. Power Syst. 2012, 27, 92–107. [Google Scholar] [CrossRef]
- Lv, C.X.; Liang, R.; Zhang, G.; Zhang, X.T.; Jin, W. Energy accommodation-oriented interaction of active distribution network and central energy station considering soft open points. Energy 2023, 268, 126574. [Google Scholar] [CrossRef]
- Low, S.H. Convex relaxation of optimal power flow part II: Exactness. IEEE Trans. Control Netw. Syst. 2014, 1, 177–189. [Google Scholar] [CrossRef]
- Jha, R.R.; Dubey, A. Exact distribution optimal power flow (D-OPF) model using convex iteration technique. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting, Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- Low, S.H. Convex Relaxation of Optimal Power Flow—Part I: Formulations and Equivalence. IEEE Trans. Control Netw. Syst. 2014, 1, 15–27. [Google Scholar] [CrossRef]
- Chen, K.; Wu, W.; Zhang, B.; Djokic, S.; Harrison, G.P. A Method to Evaluate Total Supply Capability of Distribution Systems Considering Network Reconfiguration and Daily Load Curves. IEEE Trans. Power Syst. 2016, 31, 2096–2104. [Google Scholar] [CrossRef]
- Novara, C.; Formentin, S. Data-Driven Inversion-Based Control of Nonlinear Systems with Guaranteed Closed-Loop Stability. IEEE Trans. Auto. Cont. 2018, 63, 1147–1154. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, X.; Rao, R. Asymptotic Capacity of Infrastructure Wireless Mesh Networks. IEEE Trans. Mob. Comput. 2008, 7, 1011–1024. [Google Scholar] [CrossRef]
- Bruno, R.; Conti, M.; Gregori, E. Mesh Networks: Commodity Multihop ad hoc Networks. IEEE Comm. Mag. 2005, 43, 123–131. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Wang, X.; Wang, W. Wireless Mesh Networks: A Survey. Comput. Netw. J. 2005, 47, 445–487. [Google Scholar] [CrossRef]
- Josz, C.; Maeght, J.; Panciatici, P.; Gilbert, J.C. Application of the Moment-SOS Approach to Global Optimization of the OPF Problem. IEEE Trans. Power Syst. 2015, 30, 463–470. [Google Scholar] [CrossRef]
- Yu, X.; Shen, J.-C.; Zhang, J.; Letaief, K.B. Alternating Minimization Algorithms for Hybrid Precoding in Millimeter Wave MIMO Systems. IEEE J. Sel. Top. Signal Process 2016, 10, 485–500. [Google Scholar] [CrossRef]
- Shi, Y.; Tuan, H.D.; Tuy, H.; Su, S. Global optimization for optimal power flow over transmission networks. J. Glob. Optim. 2017, 69, 745–760. [Google Scholar] [CrossRef]
- Xu, T.; Ding, T.; Li, L.; Wang, K.; Chi, F.; Gao, H. Second-order cone relaxation model adapting to reactive power optimization for three-phase unbalanced active distribution network. Autom. Electr. Power Syst. 2021, 45, 81–88. [Google Scholar]
- Luo, Z.Q.; Ma, W.K.; So, A.M.C.; Ye, Y.; Zhang, S. Semidefinite Relaxation of Quadratic Optimization Problems. IEEE Signal Process. Mag. 2010, 27, 20–34. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MAT POWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
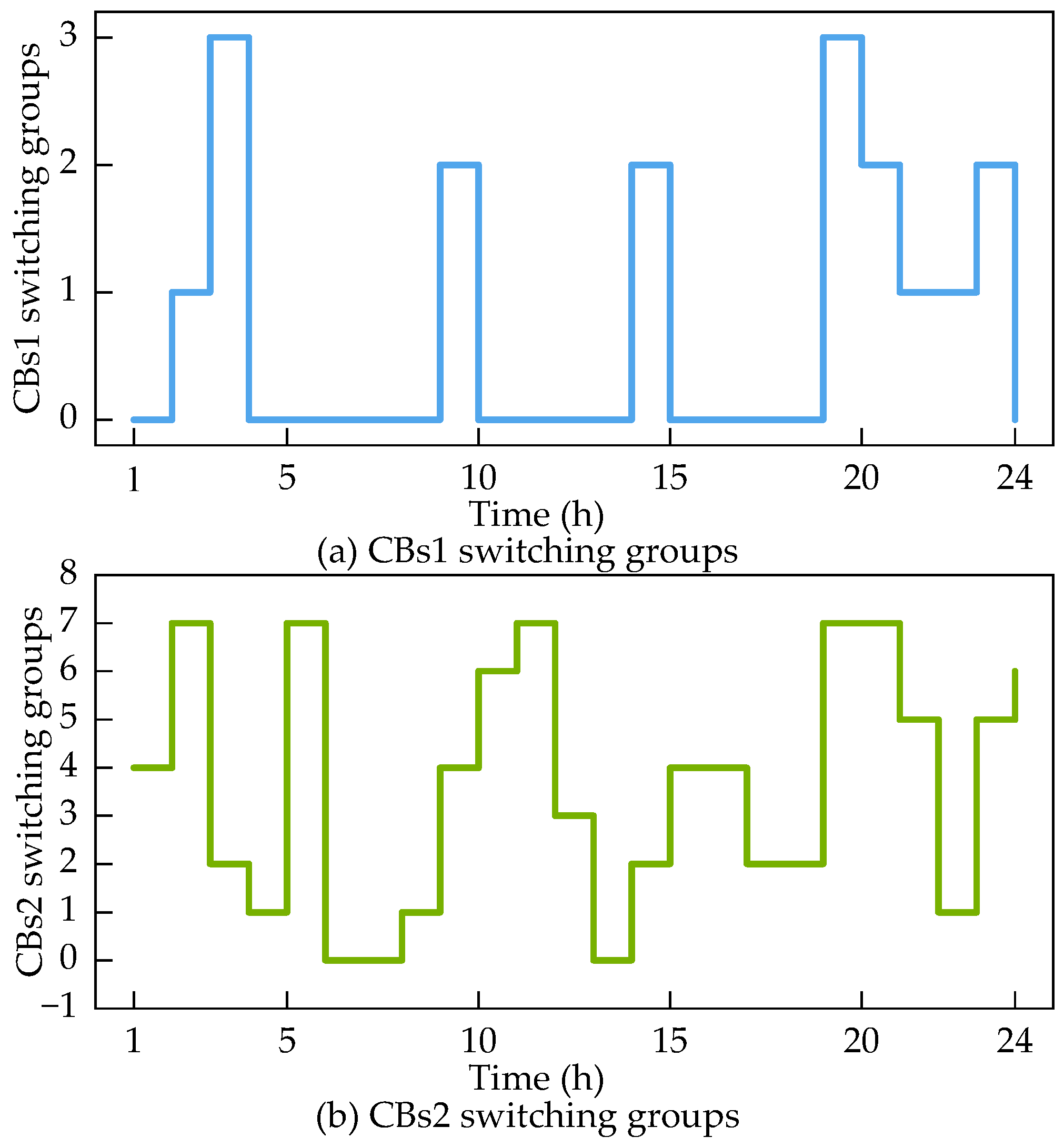
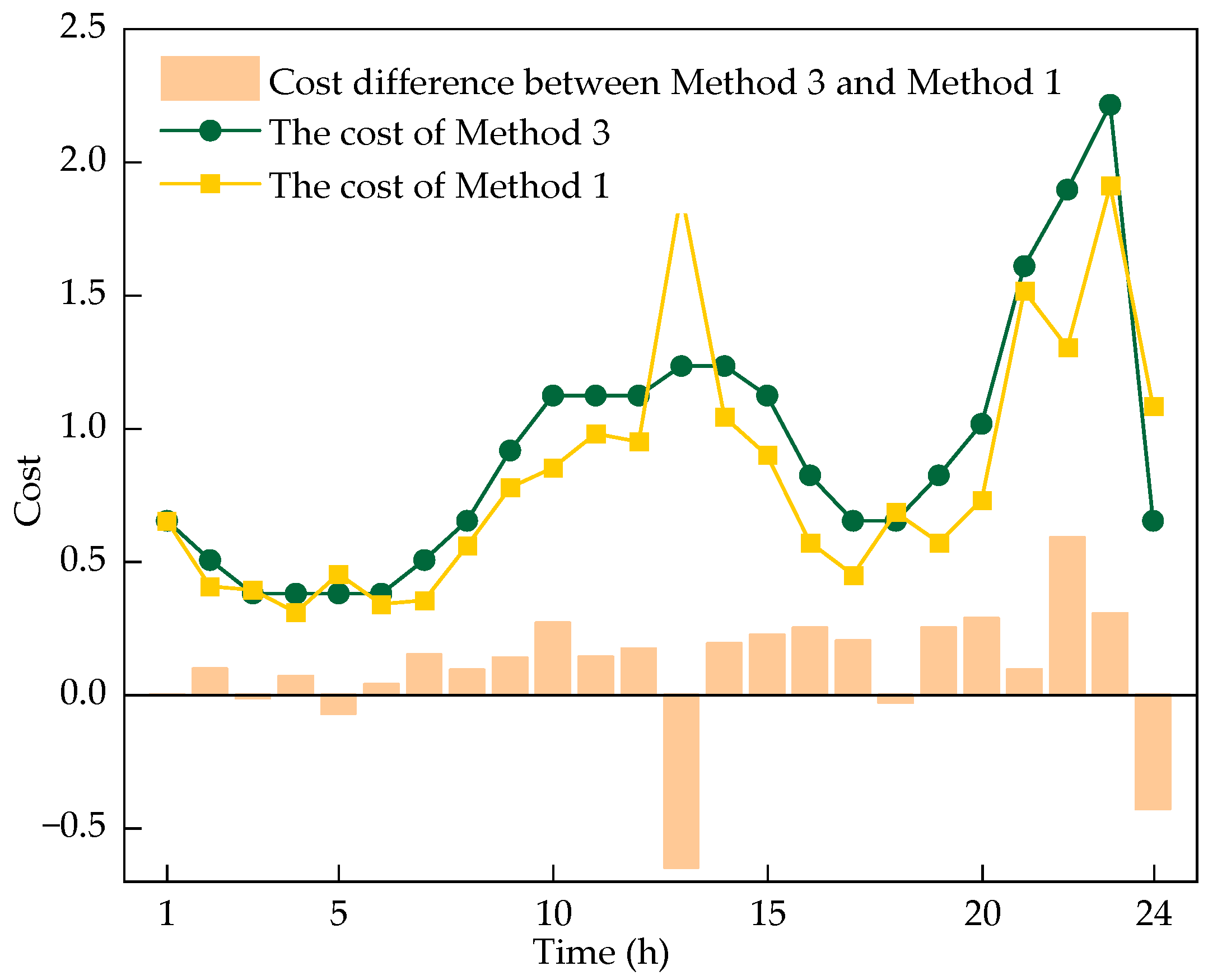
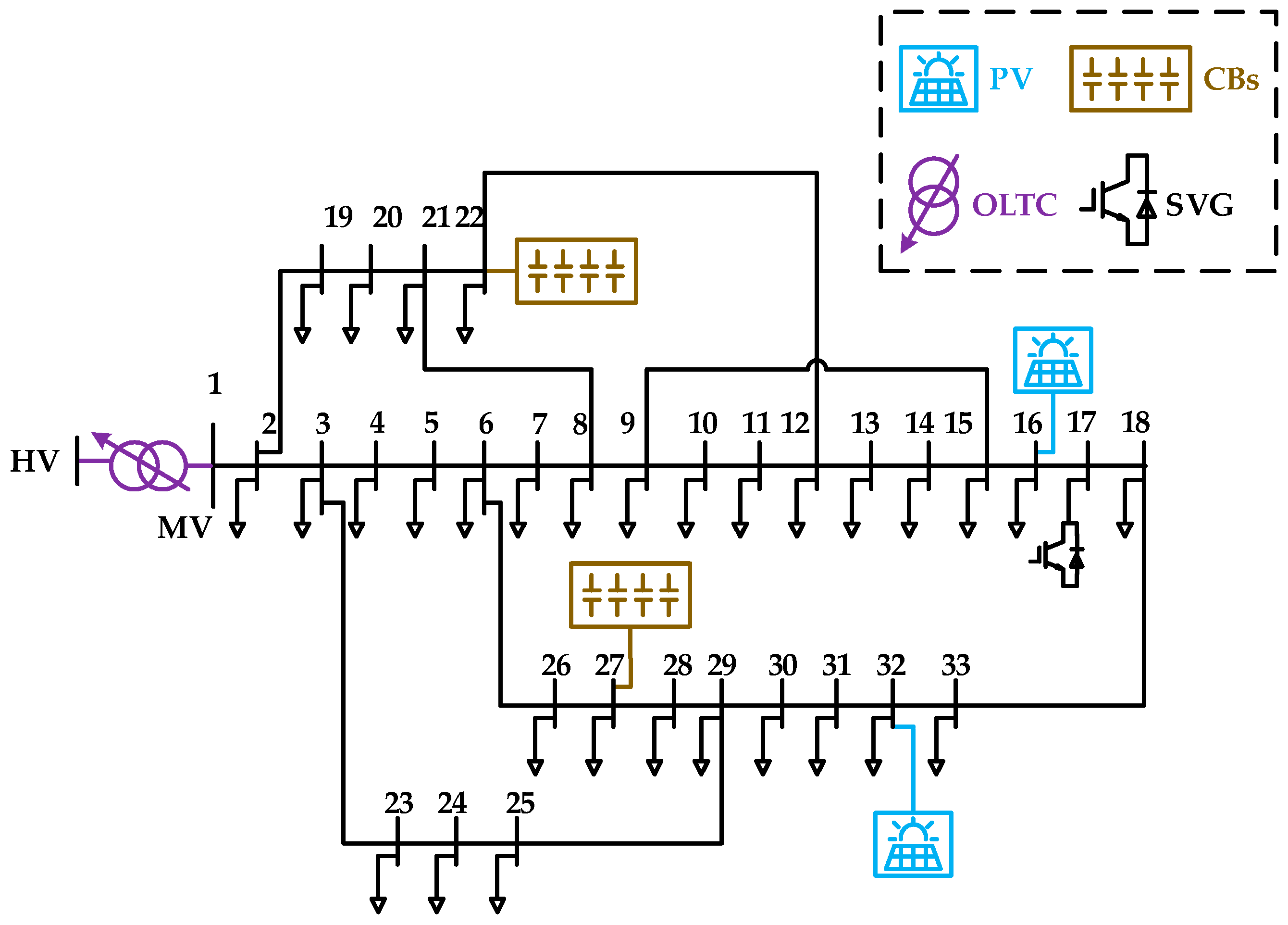
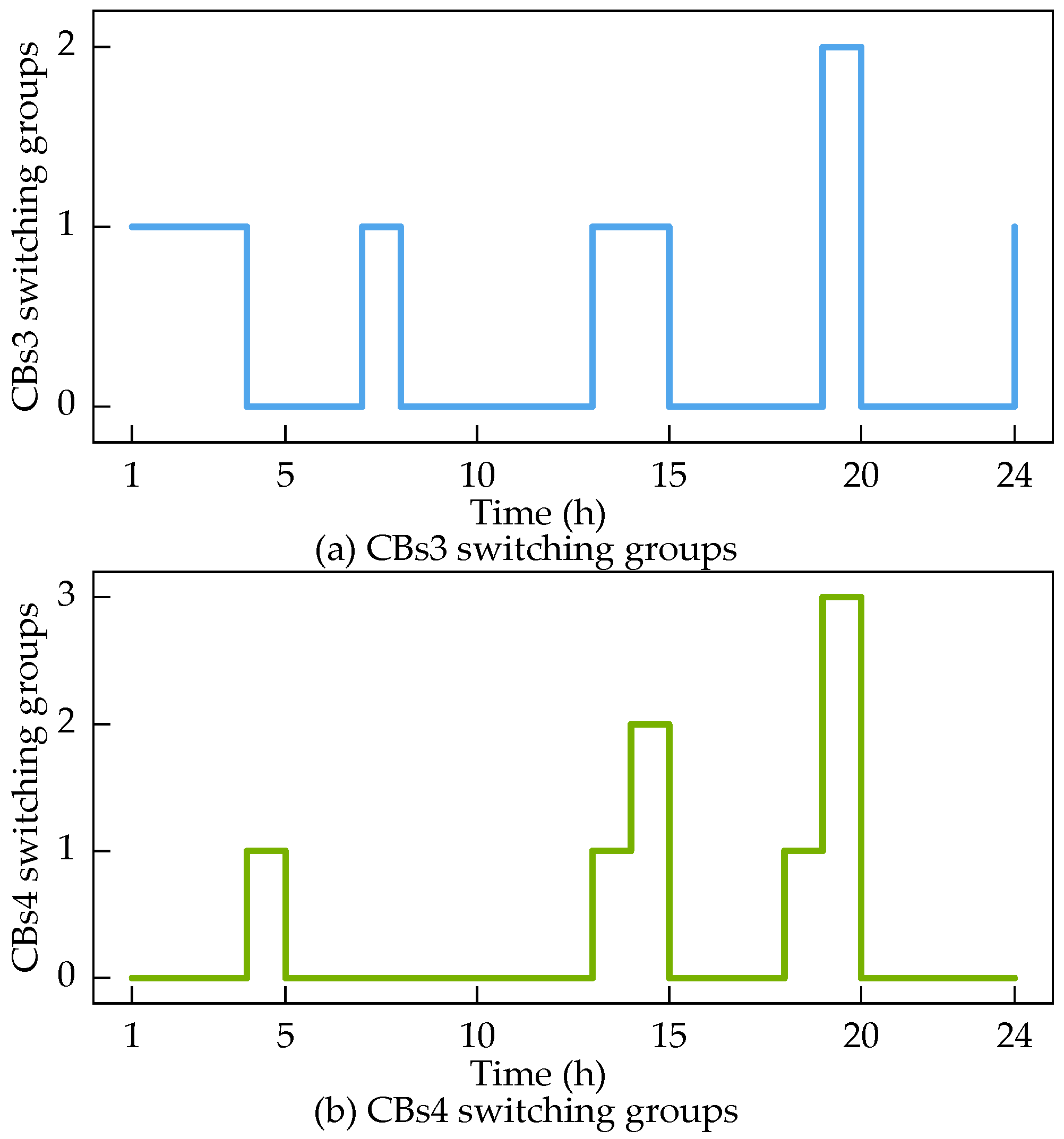
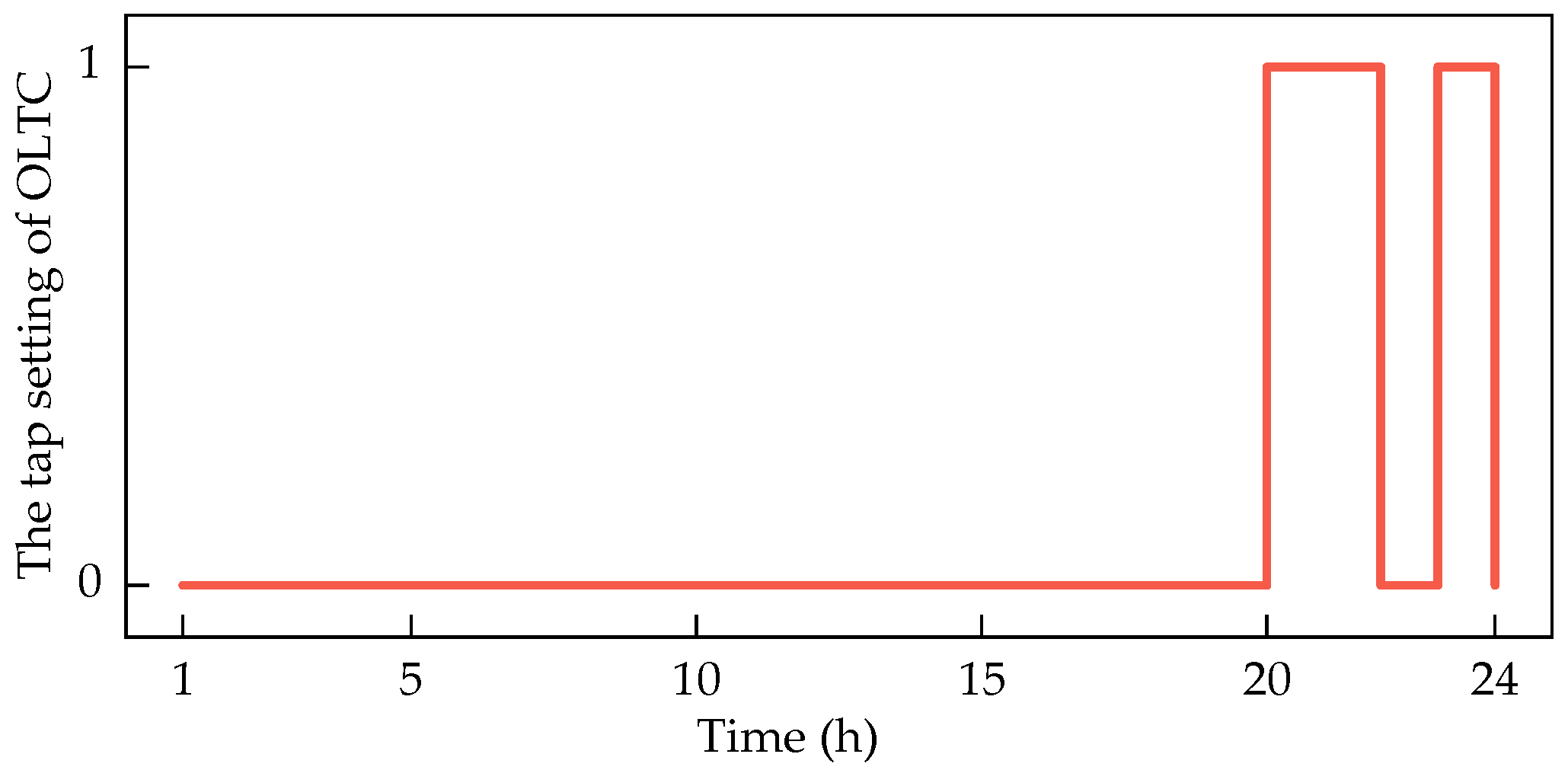
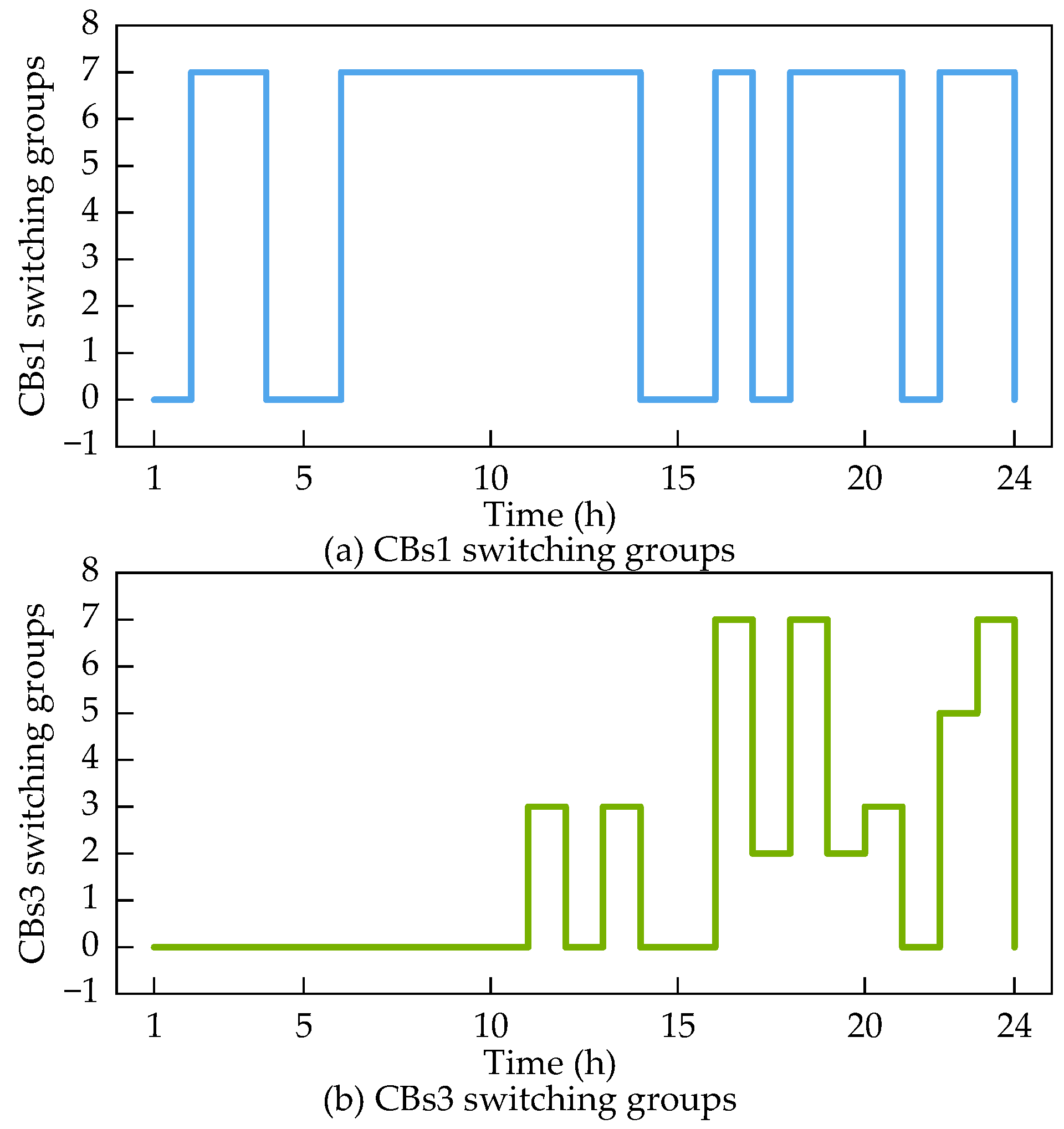
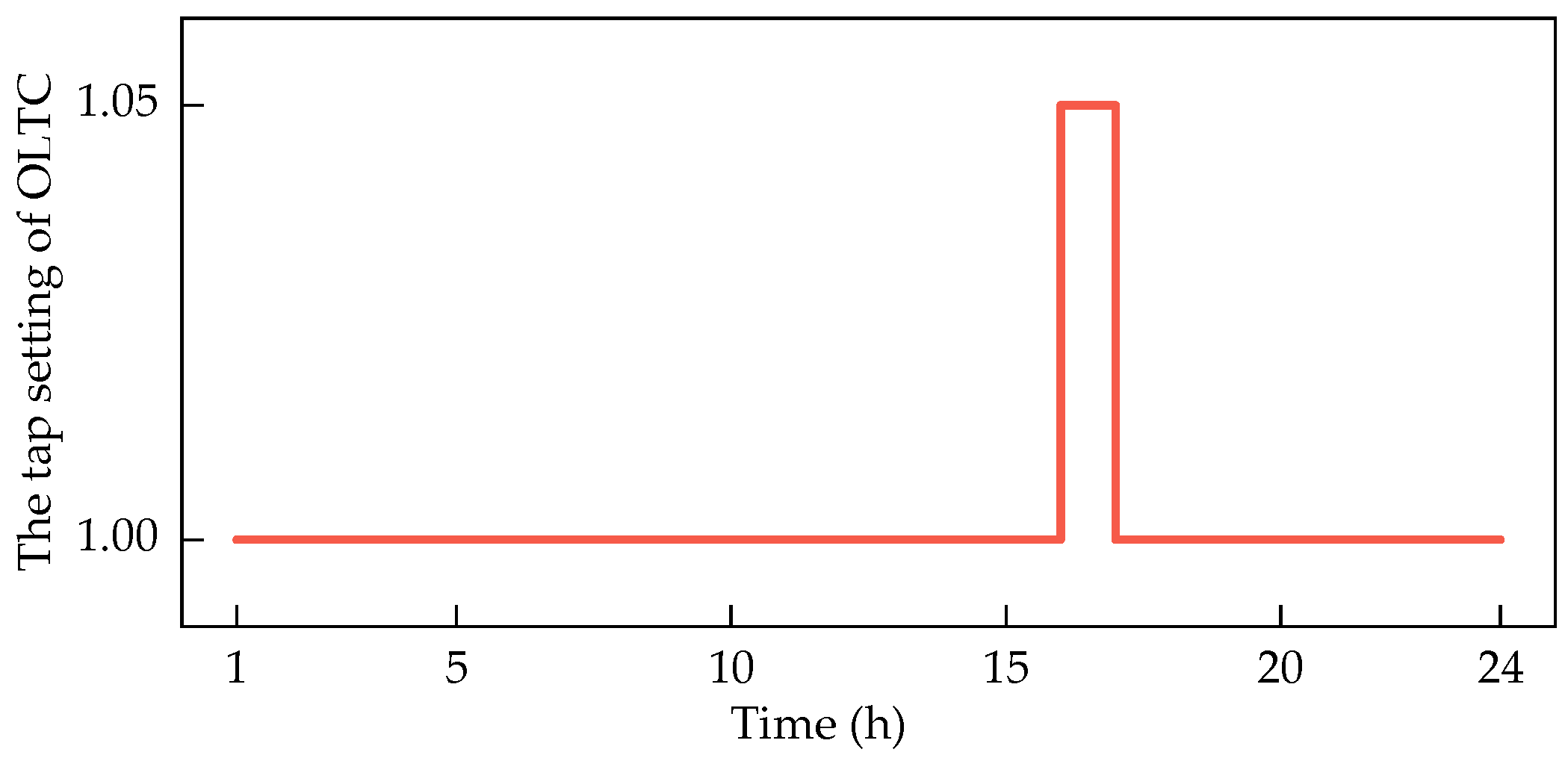
| Equipment | Location |
|---|---|
| SVG | 3, 4 |
| DGs | 2, 3 |
| CBs | 7, 9 |
| OLTC | 1 |
| Equipment | Location |
|---|---|
| SVG | 3, 14, 22 |
| DGs | 2, 3, 5, 8, 13, 17, 20, 24, 29, 31 |
| CBs | 7, 9, 15, 19, 27 |
| OLTC | 1 |
| Equipment | Location |
|---|---|
| SVG | 3, 14, 22 |
| DGs | 30, 31, 32, 33, 34, 35, 36, 37, 38, 39 |
| CBs | 7, 9, 15 |
| OLTC | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Liu, M.; Zhong, Y.; Cong, P.; Zhu, B.; Liu, T.; Li, Y.; Du, Z. Day-Ahead Coordinated Reactive Power Optimization Dispatching Based on Semidefinite Programming. Energies 2025, 18, 5469. https://doi.org/10.3390/en18205469
Xu B, Liu M, Zhong Y, Cong P, Zhu B, Liu T, Li Y, Du Z. Day-Ahead Coordinated Reactive Power Optimization Dispatching Based on Semidefinite Programming. Energies. 2025; 18(20):5469. https://doi.org/10.3390/en18205469
Chicago/Turabian StyleXu, Binbin, Mengqi Liu, Yilin Zhong, Peijie Cong, Bo Zhu, Tao Liu, Yujun Li, and Zhengchun Du. 2025. "Day-Ahead Coordinated Reactive Power Optimization Dispatching Based on Semidefinite Programming" Energies 18, no. 20: 5469. https://doi.org/10.3390/en18205469
APA StyleXu, B., Liu, M., Zhong, Y., Cong, P., Zhu, B., Liu, T., Li, Y., & Du, Z. (2025). Day-Ahead Coordinated Reactive Power Optimization Dispatching Based on Semidefinite Programming. Energies, 18(20), 5469. https://doi.org/10.3390/en18205469




