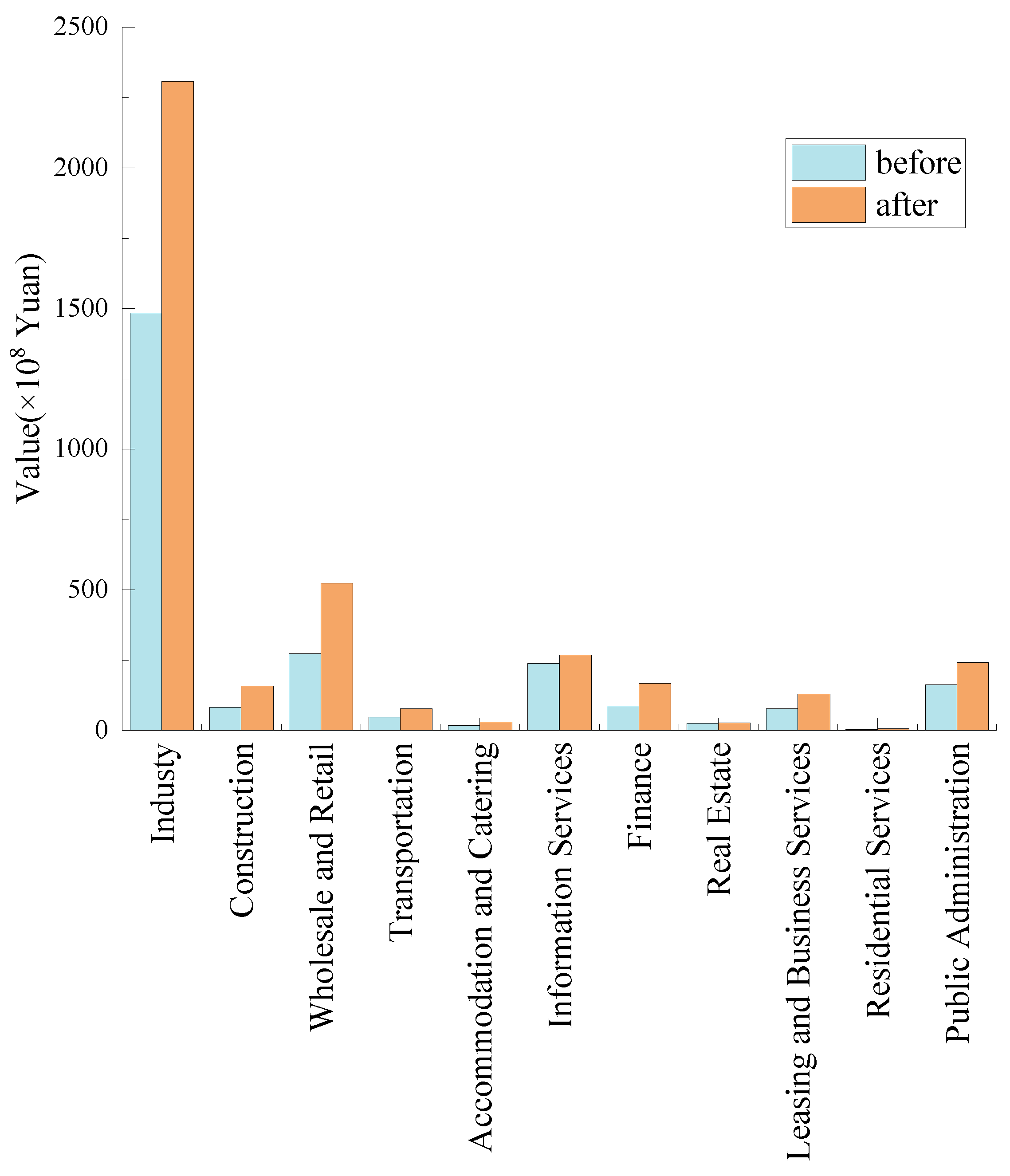Multi-Objective Optimization of Industrial Productivity and Renewable Energy Allocation Based on NSGA-II for Carbon Reduction and Cost Efficiency: Case Study of China

Abstract

This study develops a novel framework for optimizing regional power generation structures in support of China’s “dual carbon” goals. The framework introduces three main innovations. First, it formulates a comprehensive optimization paradigm that simultaneously balances industrial output, carbon emissions, and electricity costs, thereby directly addressing the trade-offs in regional energy planning. Second, it enhances data reliability and representativeness through systematic augmentation strategies, improving the robustness of optimization under data scarcity. Third, it incorporates an intelligent multi-objective search mechanism that yields a practical, three-dimensional decision space for policymakers. Beyond its methodological contributions, this research provides significant scientific value by offering a replicable framework for accelerating low-carbon energy transitions in rapidly industrializing economies. The proposed approach directly supports global sustainability targets and aligns with the United Nations Sustainable Development Goals (SDG 7, SDG 9, and SDG 13) by promoting clean energy adoption, fostering industrial innovation, and contributing to climate action. Together, these contributions provide a scalable and actionable pathway for adjusting regional power structures, aligning with national policies and accelerating the achievement of the carbon peak target by 2030.

1. Introduction

As global attention on sustainable development intensifies, achieving a balance between economic growth and environmental protection has become a critical challenge. China, as the world’s largest carbon emitter with a rapidly expanding economy, faces significant pressure to reconcile its economic growth with carbon emissions reduction. According to the International Energy Agency, China’s share of global carbon emissions is projected to reach 33% by 2035, largely driven by urbanization and industrial expansion. Experts argue that without substantial reductions in China’s emissions, it will be difficult to meet global climate goals [1].

In response to this challenge, China officially announced its dual carbon goals (DCGs) on 22 September 2020, aiming to peak carbon emissions by 2030 and achieve carbon neutrality by 2060 [2]. Additionally, the “14th Five-Year Plan” emphasizes the strategic goal of “promoting emission reductions through industrial upgrading,” aiming to achieve a green transformation of the economy and decouple economic growth from carbon emissions [3].

Given that industrial electricity consumption accounts for a significant portion of carbon emissions, optimizing the power structure—particularly the distribution of green electricity, non-green electricity, and photovoltaic power generation—has become a critical strategy for achieving emission reduction targets. Regional industries face the challenge of balancing output value growth, carbon emissions reduction, and electricity cost management. How to achieve this balance through power structure adjustments has become a crucial question in the context of China’s energy transition.

At the same time, it is important to recognize that the energy transition is often constrained by a range of economic, policy, social, and technical barriers, particularly in developing countries. Financial constraints, regulatory uncertainty, infrastructure limitations, and public acceptance issues can all slow the deployment of renewable energy technologies and hinder decarbonization progress [4,5,6,7,8,9]. Addressing these barriers is essential to achieving national and global climate objectives, and analytical models that incorporate such constraints into planning decisions—as proposed in this study—can provide valuable support for policymaking and energy system design.

To address these challenges, this study develops a data-driven, tri-objective optimization framework that simultaneously incorporates regional economic performance, carbon emissions, and energy expenditures. The proposed approach integrates advanced deep learning and evolutionary computation techniques, providing policymakers with actionable pathways for supporting China’s carbon peak targets.

Guided by these objectives, this study seeks to answer the following research questions:

• RQ1: How can regional power structures be optimized to simultaneously maximize industrial output, minimize carbon emissions, and reduce electricity costs?
• RQ2: How can dynamic, consumption-driven carbon emission modeling improve the precision and policy relevance of optimization outcomes compared to traditional static emission factor approaches?
• RQ3: How can data augmentation techniques such as CGAN enhance model robustness and reliability under conditions of limited energy data?
• RQ4: What policy-relevant insights can be derived from the optimization results to guide China’s regional energy transition in alignment with the “dual carbon” targets?

By addressing these questions, this study aims to advance current research on multi-objective energy optimization and provide actionable strategies to support China’s carbon peaking and neutrality goals.

Accordingly, this study tests the central hypothesis that regional power structure optimization can be significantly improved by integrating economic performance, dynamic carbon forecasting, and data-augmented optimization into a unified multi-objective framework. The research activities involve developing a CGAN-CNN model for data augmentation and emission prediction and embedding it within an NSGA-II algorithm to solve the tri-objective optimization problem, as detailed in Section 3.

The remainder of this study is organized as follows. Section 2 provides a literature review of the topic of energy structure optimization, analyzing relevant research findings from other authors. Section 3 outlines the research methodology, including the principles of CGAN data augmentation, the construction of the CNN model, and the application of the NSGA-II multi-objective optimization approach. Section 4 presents the experimental design, including the associated constraints, followed by a detailed analysis of the experimental results. Section 5 presents and discusses the experimental results, compares and analyzes them with relevant papers, and introduces the limitations of practical implementation. Section 6 concludes this study, offering recommendations for optimizing the power energy structure and providing insights for industry development strategies.

2. Background of Analysis

In recent years, research on power system planning has increasingly focused on multi-objective optimization approaches that incorporate regional characteristics and evolving energy demands. To further validate the effectiveness of the proposed CGAN–CNN–NSGA-II framework, the results are compared with recent studies in the domains of carbon emission forecasting and multi-objective optimization for energy and industrial systems.

A range of studies have explored optimization models to support power structure transformation. For example, Xie et al. [10] constructed a power structure optimization model for Shandong Province that considered coal consumption limits and pollutant emission constraints, demonstrating how regional policies shape generation planning. Luz et al. [11] proposed a model tailored to Brazil’s high renewable energy share, balancing generation mix and economic efficiency. Similarly, Ioannou et al. [12] applied a multi-stage stochastic optimization approach to determine optimal regional generation configurations under uncertainty. While these studies provide valuable frameworks, they largely overlook the direct linkage between power structure decisions and industrial economic output.

Many existing studies focus on two-objective formulations, such as minimizing operating costs and reducing carbon emissions. For example, Duan et al. [13] formulated a bi-objective optimization model targeting operating cost and carbon emissions for integrated energy systems and employed an improved genetic algorithm to obtain Pareto-optimal solutions. While effective in achieving balanced trade-offs between economic and environmental objectives, such models do not explicitly consider industrial output value, which is a critical economic indicator for regional development planning. Other research has focused on improving optimization efficiency, such as the work by Deveci et al. [14] to maximize renewable generation while minimizing electricity costs and that by Ullah et al. [15,16], who applied multi-objective evolutionary algorithms (MOGAs) to balance cost, emissions, and load reduction. These works, however, still focus primarily on cost and emissions, often omitting broader economic considerations.

Advances in optimization techniques have further diversified the field, with approaches such as ant colony optimization (ACO) [17,18], multi-objective wind-driven optimization (MOWDO) [19], and particle swarm optimization (PSO-STSMC) [20] being applied. From the algorithmic perspective, Cheraghi et al. [21] demonstrated that NSGA-II outperforms MOPSO in generating diverse and converged Pareto fronts for hybrid renewable energy system planning, while Ranjbar et al. [22] confirmed NSGA-II’s robustness in greenhouse gas reduction optimization within remote microgrid scenarios. Despite the maturity of these techniques, they often remain focused on operational performance and lack a holistic integration of industrial output and structural planning goals.

Although extensive research has explored multi-objective optimization for regional power planning, three critical gaps remain. First, most existing studies optimize generation mix, emissions, or cost ratios but neglect industrial output value, a key indicator linking power structure adjustments to regional economic growth. This results in a lack of a unified approach to simultaneously optimize economic output, carbon reduction, and electricity costs. Second, carbon emissions are often modeled using static emission factors or empirical formulas, limiting the ability to capture dynamic, consumption-driven variations and reducing predictive accuracy. Regarding carbon emission prediction models, prior works have applied various deep learning architectures to address this. For example, Zhang et al. [23] employed a hybrid CNN–LSTM model for short-term carbon emission prediction, while Han et al. [24] proposed a spatial-weighted LSTM–CNN architecture to incorporate regional correlations. Furthermore, demonstrating the power of data augmentation, He et al. [25] applied a CGAN-based framework for renewable energy scenario generation, improving forecast realism and diversity. Third, most existing frameworks focus on dual-objective optimization (e.g., cost and emissions), lacking a unified approach to simultaneously optimize economic output, carbon reduction, and electricity costs.

In summary, the comparison indicates that the proposed CGAN–CNN–NSGA-II framework offers a broader objective scope than typical bi-objective approaches by incorporating industrial output alongside carbon emissions and electricity costs. To address these deficiencies, this study proposes a data-driven, tri-objective optimization framework that integrates advanced predictive modeling and evolutionary optimization to support regional energy transition decisions. The core innovations and contributions of this research are summarized as follows:

• Integration of Industrial Output as a Core Objective: Unlike previous models that primarily target cost and emissions, this study explicitly incorporates regional industrial output value into the optimization framework, directly linking power structure decisions to economic development objectives. This tri-objective approach provides a more comprehensive tool for policymakers than traditional dual-objective models, which often overlook the direct economic impacts of energy transitions.
• Dynamic Carbon Emission Forecasting: The framework replaces traditional static emission factor methods with a CNN-based, consumption-driven forecasting model that captures temporal dynamics in electricity consumption and carbon emissions, substantially improving prediction accuracy and decision relevance. This moves beyond the limitations of static calculations, which fail to capture consumption-driven variations.
• Data Augmentation for Enhanced Robustness: To overcome limitations caused by scarce time-series data, a conditional generative adversarial network (CGAN) is employed to generate high-fidelity synthetic datasets, thereby improving the reliability and generalizability of the optimization results. This provides a robust solution to the pervasive problem of data scarcity that often hinders advanced modeling in energy research.

Building on these contributions, this study tests the following hypothesis: regional power structure optimization can be significantly improved by integrating economic performance, dynamic carbon forecasting, and data-augmented optimization into a unified, multi-objective framework. Guided by this hypothesis, this study addresses four key research questions (RQ1–RQ4) concerning optimization strategies, carbon modeling, data augmentation, and policy implications, as presented at the end of the Introduction. Together, these innovations advance the current state of research by bridging the gap between power system optimization and sustainable industrial development.

3. Methodology

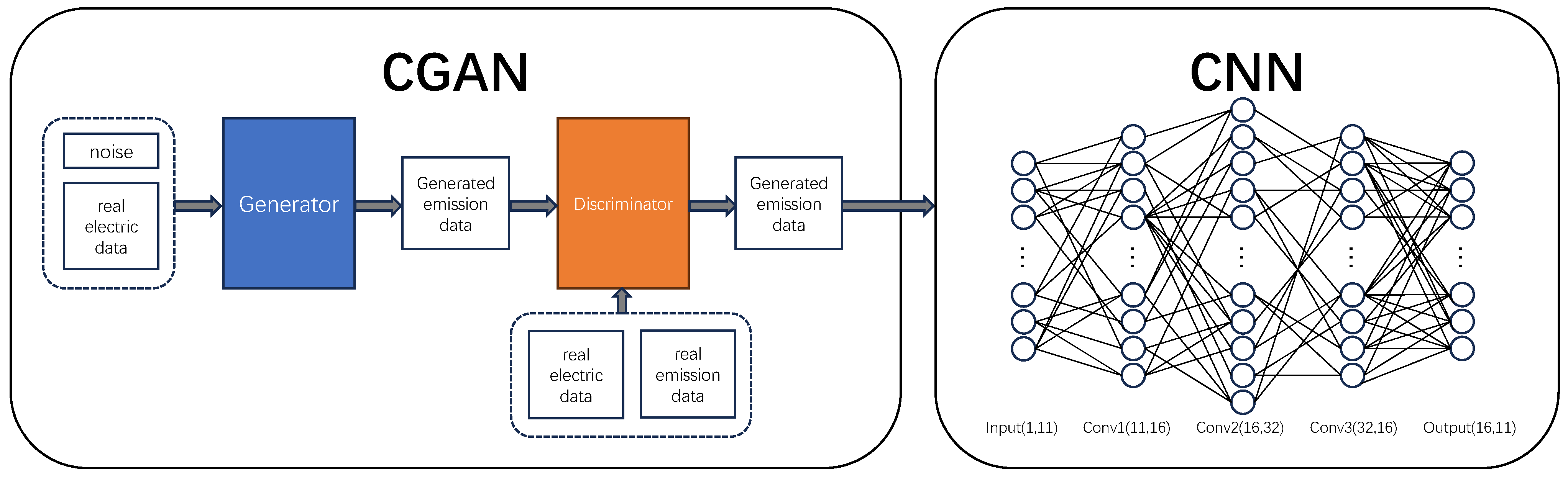
This section outlines the research methodology. As illustrated in Figure 1, the proposed multi-objective optimization framework integrates CGAN for data augmentation, applies a CNN model to predict carbon emissions, and employs the NSGA-II algorithm to perform multi-objective optimization. The approach aims to simultaneously maximize industrial output, minimize carbon emissions, and reduce electricity costs. The following subsections detail the core principles of each module, along with the decision variables, objective functions, and constraints used in this study.

Figure 1 illustrates the overall framework combining NSGA-II with CGAN-CNN for multi-objective optimization, subject to industry output bounds and energy allocation constraints. The model takes industrial output values and power allocation ratios as input and optimizes three objectives, namely, industrial output, carbon emissions, and cost. The model produces outputs including the output of each industry, power allocation ratio, total industrial output value, total carbon emissions, and total cost.

$F_1$ is the maximization of industrial output value; $F_2$ is the minimization of total carbon emissions; $F_3$ is the minimization of annualized cost; $p_i$ is the output value of industry i (11 industries are considered in this study); $f_{non}$ is the ratio of non-green electricity; $f_{green}$ is the ratio of green electricity; $f_{PV}$ is the ratio of photovoltaic generation. Green power, non-green power, and photovoltaic generation together constitute the electricity supply structure of the Beijing Yizhuang region.

3.1. Generative Adversarial Network (GAN)

Generative adversarial networks (GANs), introduced by Goodfellow et al. in 2014 [26], provide a generative framework based on a dual-network adversarial training mechanism involving a generator and a discriminator. GANs are designed to model the data distribution through a dynamic game process.

3.1.1. Model Architecture

Generator G: Receives a random noise vector z, which follows a prior distribution $p_z\left(z\right)$ (typically Gaussian), and generates synthetic data $G\left(z\right)$ through non-linear mapping. The output data distribution is denoted as $p_g$.

Discriminator D: Receives real data $x\sim p_{\mathrm{data}}\left(x\right)$ or generated data $G\left(z\right)$ and outputs a scalar probability value $D(·)\in [0,1]$ to evaluate the likelihood that the input data comes from the real distribution.

3.1.2. Adversarial Training Objective

The generator and discriminator are jointly optimized via a minimax game, and the overall objective function is [27]

$$\begin{array}{cc}\hfill \underset{G}{min}\underset{D}{max}V(D,G)& ={\mathbb{E}}_{X\sim P_{\mathrm{data}}}\left[logD\left(X\right)\right]\hfill \\ \hfill & +{\mathbb{E}}_{Z\sim P_Z}\left[log\left(1-D\left(G\right(Z\left)\right)\right)\right]\hfill \end{array}$$

(1)

In the formula, ${\mathbb{E}}_{X\sim P_{\mathrm{data}}}[logD\left(X\right)]$ represents the discriminator’s assessment of real data; ${\mathbb{E}}_{Z\sim P_Z}log(1-D\left(G\left(Z\right)\right))$ signifies the discriminator’s evaluation of generated data.

The objective of the generator G is to approximate the real data distribution $p_{\mathrm{data}}$ with the generated data distribution $p_g$, thereby deceiving the discriminator into assigning high confidence scores to the generated data. The objective function is defined as [27]

$$\underset{G}{min}{E}_{Z\sim P_Z\left(z\right)}[log(1-D\left(G\left(z\right)\right))]$$

(2)

The generator is designed to minimize the discriminator’s ability to distinguish generated data, thereby driving $D\left(G\right(z\left)\right)\to 1$.

The discriminator D aims to accurately distinguish between real and generated data, establishing a dynamically balanced adversarial training process. Its objective function is defined as [27]

$$\begin{array}{cc}\hfill \underset{D}{max}[& {\mathbb{E}}_{X\sim P_{\mathrm{data}}\left(X\right)}\left[logD\left(X\right)\right]\hfill \\ \hfill & +{\mathbb{E}}_{Z\sim P_Z\left(z\right)}\left[log\left(1-D\left(G\right(z\left)\right)\right)\right]]\hfill \end{array}$$

(3)

A higher sum of the two results indicates superior discriminator performance.

At the Nash equilibrium, the generator’s output distribution converges to the data distribution. Consequently, the discriminator’s probability output for all inputs degrades to $D\left(x\right)=0.5$, indicating that the generated data is indistinguishable from the real data.

3.2. Conditional Generative Adversarial Network (CGAN)

The traditional GAN algorithm’s data generation process is characterized by randomness and unpredictability, resulting in unclear objectives and limited controllability. Consequently, traditional GAN framework models exhibit significant limitations when handling large datasets with multi-class features [28,29]. Therefore, this study opted for the use of CGAN. The construction of CGAN involves incorporating additional conditional variables into the input layers of both the discriminator and generator. The generation process of the generator and the recognition process of the discriminator are then guided by the conditional label, with the aim of enhancing the performance of the predictive model [25].

The core concept of CGAN revolves around the joint optimization of a conditional generator and a discriminator. The generator takes a joint input of noise z and a conditional variable y. Through non-linear mapping, it generates synthetic data that adheres to the conditional constraints. The discriminator, in turn, performs a joint probability assessment based on the data and the condition, thereby outputting a confidence score that reflects the authenticity of the data given the condition. Consequently, the objective function is defined as a conditional minimax game [27].

$$\begin{array}{cc}\hfill \underset{G}{min}\underset{D}{max}V(D,G)& ={\mathbb{E}}_{X\sim P_{\mathrm{data}}\left(X\right)}\left[logD(X\mid y)\right]\hfill \\ \hfill & +{\mathbb{E}}_{Z\sim P_Z\left(z\right)}\left[log\left(1-D\left(G\right(z\mid y\left)\right)\right)\right]\hfill \end{array}$$

(4)

In this formula, $G\left(z\right|y)$ denotes the generator’s output, which is the data produced upon receiving noise z and conditional variable y. $D\left(X\right|y)$ represents the discriminator’s output, which is the conditional probability that X is real given y, after receiving data X and its corresponding condition y. This is used to assess the authenticity of X under the condition y.

The discriminator’s objective is to maximize the conditional probability estimate for real data while minimizing misclassification of generated data. Conversely, the generator, through adversarial training, strives to approximate the real data distribution. In this process, conditional information is integrated into the network input via feature concatenation or embedding layers, thereby ensuring that both the generation and discrimination processes are strictly constrained by semantic conditions.

3.3. Convolutional Neural Network (CNN)

A CNN represents a class of feedforward neural networks characterized by a convolutional architecture [30]. It efficiently extracts spatial features from data through local connections and weight-sharing mechanisms, making them widely applicable in processing structured data such as images and time series. In this study, a CNN was employed to construct predictive models for industrial electricity consumption and carbon emissions. The primary advantage of this approach lies in its capacity to automatically learn nonlinear mappings within complex datasets, thereby circumventing the limitations inherent in manual feature engineering, which is typical of traditional methods.

CNNs offer a key advantage in their ability to automatically learn complex feature representations from input data, reducing the reliance on manual feature engineering. The CNN model used in this study comprises an input layer, multiple convolutional and pooling layers, followed by fully connected and output layers.

(1)

Input layer: The input layer receives CGAN-enhanced industrial electricity consumption data with dimensions N × T × F, where N is the number of samples, T is the time steps, and F is the feature dimensions.

(2)

Convolutional layer: The convolution operation is mathematically defined as [31]

$$X_j^l=f\left(\sum _{i\in M_j}{X}_i^{l-1}\ast K_{ij}^l+b_j^l\right)$$

(5)

Here, $X_j^l$ denotes the j-th feature map in the l-th layer, while $X_i^{l-1}$ represents the i-th feature map in the (l − 1)-th layer. $K_{ij}^l$ signifies the convolutional kernel connecting the i-th input feature map and the j-th output feature map in the l-th layer and $b_j^l$ is the bias term. The symbol * indicates the convolution operation and f represents the activation function. Finally, $M_j$ is the set of input feature maps.

(3)

Pooling layer: The pooling layer employs max-pooling operations to reduce data dimensionality through downsampling. The formula is as follows [31]

$$Y_j^l=\underset{i\in S_j}{max}{X}_i^l$$

(6)

Here, $Y_j^l$ denotes the j-th feature map at the l-th pooling layer and $S_j$ represents the set of pixels within the pooling window.

(4)

Fully connected layer: The feature maps are transformed into a one-dimensional vector and passed through matrix multiplication to produce the final output.

(5)

The output layer: The final output layer uses a linear activation function to generate predicted values for carbon emissions.

3.4. Multi-Objective Optimization

In this study, the problem at hand involves optimizing multiple objectives, necessitating a comprehensive optimal solution across several objective functions. Consequently, a multi-objective optimization approach is employed. Unlike single-objective optimization, the objective functions in multi-objective optimization problems typically conflict, making simultaneous optimization challenging. This characteristic complicates the search within the solution space. Furthermore, the disparate dimensions of the objective functions preclude direct comparison; therefore, the effective solutions for multi-objective optimization problems usually constitute a set of Pareto optimal solutions [32].

Traditional multi-objective optimization methods often utilize the weighted sum method, transforming the original problem into a single-objective optimization problem for resolution. However, this method presents significant limitations. Firstly, the rational setting of weight parameters lacks a unified standard, often relying on subjective experience. Secondly, this method can only yield a solution under a specific set of weights each time, failing to comprehensively explore the diversity of the Pareto optimal solution set, thereby inadequately addressing practical decision-making needs.

Currently, genetic algorithms (GAs) exhibit significant advantages in the domain of multi-objective optimization [33]. They possess the characteristic of multi-point, multi-directional search, enabling the derivation of multiple Pareto optimal solutions within a single search iteration. Consequently, GAs are particularly well-suited for addressing multi-objective optimization problems. A key advantage of this algorithm lies in its ability to yield solutions with a single program execution [21]. Furthermore, in contrast to conventional methods, this algorithm can effectively tackle complex, non-linear problems even with limited information [34]. This study employed NSGA-II for multi-objective optimization, which seeks to maximize the total industry output value $F_1$, minimize carbon emissions $F_2$, and minimize electricity costs $F_3$.

3.5. Non-Dominated Sorting Genetic Algorithm (NSGA-II)

NSGA-II was introduced by Kalyanmoy Deb in 2002 [35]. It is a specific variant of the genetic algorithm (GA), designed to address multi-objective optimization problems. While traditional GAs are primarily used for single-objective optimization, NSGA-II is tailored for problems that involve multiple, often conflicting objectives, aiming to find a set of Pareto-optimal solutions. It incorporates dominance ranking and crowding distance mechanisms to efficiently sort and select individuals in a population. NSGA-II provides a balance between Pareto front search efficiency and solution distribution, making it particularly useful for optimizing energy systems [36,37,38,39,40]. For a detailed explanation of the specific optimization steps of the NSGA-II algorithm, please refer to the comprehensive discussions in references [41,42,43,44].

3.6. Decision Variables

The decision variables in the optimization model were as follows:

• Industry outputs ($p_1$, $p_2$, …, $p_{11}$)
• Proportion of green electricity consumption ($f_{\mathrm{green}}$)
• Proportion of non-green electricity consumption ($f_{\mathrm{non}}$)
• Proportion of photovoltaic electricity consumption ($f_{\mathrm{PV}}$)

3.7. Objective Functions

The objective function, central to multi-objective optimization problems, serves to quantify the desirability of decision variables, thereby acting as a critical metric for evaluating solution quality. Unlike single-objective optimization, multi-objective optimization problems involve multiple objective functions, necessitating the simultaneous consideration of several objectives. In this study, the objective functions were defined as the maximization of total industry output value, the minimization of carbon emissions, and the minimization of electricity costs, as represented below.

$$y=[max{F}_1,min{F}_2,min{F}_3]$$

(7)

Here, $F_1$ denotes total industry output, $F_2$ denotes carbon emissions, and $F_3$ denotes total electricity costs.

3.8. Constraints

Constraints are rules that restrict the range of values for decision variables within an optimization problem, thereby ensuring the feasibility and rationality of the solution. They reflect limitations inherent in real-world problems, such as resource constraints or regulatory policies. Defining constraints in an optimization problem allows for more accurate and efficient solutions. The constraints in this context are represented as follows:

$$p_i^{min}\le p_i\le p_i^{max},i=1,2,\dots ,11$$

(8)

$$f_{green}+f_{non}+f_{PV}=1$$

(9)

$$E_{PV}\le E_{PV}^{max}:E_{PV}^{max}=1.35\times {10}^{10}\mathrm{kWh}$$

(10)

$$f_{green}\le 0.15$$

(11)

Here, $p_i$ denotes the annual output value of the ith industry; $p_i^{min}$ denotes the lower limit of the output value of the ith industry; $p_i^{max}$ denotes the upper limit of the output value of the ith industry; $E_{PV}$ denotes the PV power generation capacity; $E_{PV}^{max}$ denotes the upper limit of the PV power generation capacity.

3.9. Complexity and Algorithm Suitability

The formulated optimization problem in this study was characterized by multiple conflicting objectives, high-dimensional continuous decision variables, and nonlinear, non-convex black-box objective functions. Specifically, the carbon emission objective was predicted by a convolutional neural network (CNN), which introduced a nonlinear and implicit mapping from industrial electricity consumption to emissions. Such neural network-based functions are not analytically differentiable or convex, thereby precluding the use of gradient-based or linear programming approaches.

Furthermore, the joint optimization of 14 decision variables—11 industry outputs and 3 electricity structure proportions—under multiple constraints resulted in a large and complex search space. This problem shares structural similarities with well-established NP-hard problems, such as multi-objective production scheduling or portfolio optimization with nonlinear constraints. The presence of conflicting objectives and black-box evaluation functions makes the problem computationally intractable for exact algorithms, especially when aiming to obtain a well-distributed Pareto front.

Exact methods such as mixed-integer linear programming (MILP), branch-and-bound, or dynamic programming are infeasible in this context due to the following reasons:

• The black-box nature of the CNN-based emission function prevents analytical formulation.
• There is a combinatorial explosion of the feasible space with multiple industries and energy types.
• There is a need to identify not just one optimal solution, but a diverse set of Pareto-optimal trade-offs.

As a result, metaheuristic algorithms such as NSGA-II are well-suited for this problem. NSGA-II offers several advantages: (1) It does not require gradient information. (2) It efficiently handles non-convex and nonlinear multi-objective problems. (3) It is capable of identifying a well-distributed set of Pareto-optimal solutions in a single run. In this study, grid search was used to automatically tune its core parameters, further improving convergence and solution diversity.

4. Experimenal Results and Analysis

4.1. Datasets

The primary goal of this study was to explore the synergistic optimization of three key objectives: maximizing industry output, minimizing carbon emissions, and reducing electricity costs through strategic adjustments to the power infrastructure. To this end, a comprehensive dataset was compiled from Beijing’s Yizhuang area, covering industry output, electricity consumption, and photovoltaic (PV) installed capacity. The dataset included 72 entries on electricity consumption across various industries, as well as 6 annual entries representing industry output. Output data for 11 industries were sourced from the Statistical Yearbook published by the Beijing Municipal Bureau of Statistics. The carbon emission factors for non-green electricity were obtained from the carbon emission factor announcements issued by the National Bureau of Statistics. This data served as the foundation for the optimization models and analysis conducted in the subsequent sections.

4.2. Experimental Setup

This study established a tri-objective optimization model. The decision variables encompassed the output values of eleven industries, alongside the proportions of green electricity, non-green electricity, and photovoltaic power generation. Each objective function is detailed below, accompanied by its mathematical expression.

4.2.1. The Objective of Maximizing the Gross Output Value

The gross output was derived by summing the annual output values of eleven sectors, as demonstrated in Equation (12).

$$max{F}_1=\sum _{i=1}^{16}{p}_i$$

(12)

Here, $p_i$ denotes the annual output value of the i-th industry, expressed in units of CNY 100 million. The output values of each industry were subject to upper and lower bound constraints, as detailed in

Table 1. Upper and lower limits of industry output.

Industry Name	Lower Limit (CNY 100 Million)	Upper Limit (CNY 100 Million)
Industry	1484.4	2968.8
Construction	82.7	165.4
Wholesale and retail trade	274.4	548.8
Transportation, warehousing, and postal services	47.8	95.6
Accommodation and food services	18.0	36.0
Information transmission, software, and information technology services	238.3	476.6
Finance	87.9	175.8
Real estate	24.9	49.8
Leasing and business services	76.5	153.0
Residential services, repairs, and other services	4.1	8.2
Public service and management organizations	326.2	707.4

. The data utilized in this study was sourced from the Beijing Statistical Yearbook published by the Beijing Municipal Bureau of Statistics. To ensure practical and realistic optimization results, the output value for each industry was constrained to not fall below its recorded level in 2023 and not exceed twice the 2023 value. This upper bound was informed by historical trends, which indicate that industry output values can approximately double over a seven-year period.

4.2.2. The Objective of Minimizing Carbon Emissions

The carbon emissions generated by industrial production were computed using a CNN. Initially, the total electricity consumption of an industry was calculated based on its output value and the electricity consumption. This total electricity consumption was used as input to the CNN, which estimated the industry’s total carbon emissions. Detailed values for electricity consumption per unit of output are provided in

Table 2. Electricity consumption intensity by industry.

Industry Name	Electricity Consumption (kWh/100 Million CNY)
Industry	3,410,194.98
Construction	1,151,508.923
Wholesale and retail trade	471,677.7319
Transportation, warehousing, and postal services	2,438,320.632
Accommodation and food services	1,946,626.351
Information transmission, software, and information technology services	9,746,860.234
Finance	97,958.04664
Real estate	11,738,661.29
Leasing and business services	2,738,530.153
Residential services, repairs, and other services	2,040,604.155
Public service and management organizations	3,793,394.982

.

Based on the computational framework illustrated in Figure 2, the carbon emission prediction process began by addressing data scarcity through conditional generative adversarial network (CGAN) augmentation. Due to the limited availability of real-world industrial electricity consumption and corresponding carbon emission datasets, the CGAN synthesized 1000 realistic training samples using existing data distributions and conditional constraints. These augmented samples, alongside original data, trained a convolutional neural network (CNN) that took hourly electricity consumption patterns from eleven industrial sectors as input features. The CNN architecture processed this multi-dimensional input to predict sector-specific carbon emissions, which were aggregated into total industrial carbon output. The trained CNN was rigorously validated against held-out real-world measurements to ensure prediction accuracy. Finally, this validated carbon emission model was embedded as an objective function within the NSGA-II multi-objective optimization framework, enabling simultaneous optimization of industrial output value, electricity costs, and carbon reduction targets during power structure adjustments. This integrated pipeline ensured data-driven, high-fidelity carbon accounting while overcoming data limitations.

4.2.3. The Objective of Minimizing the Total Electricity Cost

The total cost encompassed the procurement expenses for both green and non-green electricity, alongside the construction and maintenance costs associated with photovoltaic (PV) power generation facilities. In this study, both electricity prices and PV costs were modeled in detail to ensure that all cost items were expressed on the same annual time scale. For grid-purchased electricity, historical data from 2006 to 2025 were collected, and the data indicated that both green and non-green electricity prices remained essentially fixed during this period. Green electricity was consistently priced slightly lower than non-green electricity due to policy subsidies in Beijing. For photovoltaic systems, the construction cost in the base year 2025 was CNY 3.4 per watt, and, based on historical trends, this value decreased by CNY 0.1 per watt every three years. The optimization model determined the required PV capacity addition according to the optimized PV supply proportion, taking into account the existing capacity and upper-limit constraints. The total construction cost for the additional capacity was evenly allocated over the 20-year service life specified by the International Electrotechnical Commission standards, resulting in an annualized construction cost. The maintenance cost was CNY 0.045 per watt in 2025, and, based on historical trends, decreased by CNY 0.001 per watt each subsequent year. The maintenance cost was calculated based on the total installed PV capacity after optimization. The annualized PV cost was then obtained by adding the annualized construction cost to the annual maintenance cost. Finally, this value was combined with the fixed procurement expenses of green and non-green electricity, reflecting their policy-driven price differences, to form the total cost objective of the NSGA-II optimization model. The formula for calculating the total cost is presented in Equation (13).

$$\begin{array}{cc}\hfill min{F}_3& =\sum _{i=1}^{16}{p}_i{u}_i\left(f_{\mathrm{green}}{c}_{\mathrm{green}}+f_{\mathrm{non}}{c}_{\mathrm{non}}\right)\hfill \\ \hfill & +C_{\mathrm{PV}}^{\mathrm{build}}·\mathsf{\Delta }PV+C_{\mathrm{PV}}^{\mathrm{maintain}}·P{V}_{\mathrm{total}}\hfill \end{array}$$

(13)

Here, $f_{\mathrm{green}}$ is the percentage of green electricity ($f_{\mathrm{green}}\le 15\%$). $c_{\mathrm{green}}$ and $c_{\mathrm{non}}$ represent the unit prices of green electricity and non-green electricity, respectively. $C_{\mathrm{PV}}^{\mathrm{build}}$ is the unit construction cost of PV equipment, and the calculation takes into account the cost decline. The calculation formula is shown in Equation (14):

$$C_{\mathrm{PV}}^{\mathrm{build}}\left(t\right)=max\left(3.4-0.1⌊{\displaystyle \frac{t}{3}}⌋,0\right)$$

(14)

$C_{\mathrm{PV}}^{\mathrm{maintain}}$ is the unit maintenance cost of PV equipment, with the calculation accounting for cost reductions over time. The formula is shown in Equation (15):

$$C_{\mathrm{PV}}^{\mathrm{maintain}}\left(t\right)=max(0.045-0.001t,0)$$

(15)

where $\mathsf{\Delta }PV$ is the PV capacity to be newly constructed. $P{V}_{\mathrm{total}}$ is the total PV capacity.

4.3. Model Construction

As illustrated in Figure 2, this study employed NSGA-II to optimize objectives including industrial output value, carbon emissions, and electricity cost. Decision variables encompassed the industrial output value of 11 sectors, the proportion of green electricity, the proportion of non-green electricity, and the proportion of photovoltaic power generation, resulting in solutions of 14 dimensions. The following constraints were established in the construction of the multi-objective optimization model:

(1)

Industry output value constraint: The optimized output value for each industry must not be lower than the 2023 industry output value and should not exceed twice the 2023 industry output value (based on historical data, the output value can double approximately every seven years).

(2)

Power distribution ratio constraint: The sum of the proportions of green electricity, non-green electricity, and photovoltaic generation should not exceed 1.

(3)

Photovoltaic generation capacity upper-limit constraint: The upper limit of PV generation is determined by the maximum technical potential of PV installation in the Beijing Yizhuang District. The district has a total area of 225 km², of which approximately 15% is suitable for rooftop PV installation. According to technical specifications and regional solar energy statistics, the module power density is 200 W/m², the average conversion efficiency of PV modules is 80%, and the annual average sunshine duration in Beijing is approximately 2500 h. Based on these data, the maximum potential annual PV generation for the Yizhuang District was calculated to be $1.35\times {10}^{10}$ kWh. This value was used as the upper bound for PV generation in the optimization model.

(4)

Green electricity proportion upper-limit constraint: When the proportion of green electricity in the grid exceeds the 15% threshold, it will face limitations in long-distance transmission and large grid absorption. The power transmission system must undergo digital transformation, apply intelligent technologies, and construct supporting energy storage facilities, leading to an increase in overall system costs.

Multi-objective optimization was solved using NSGA-II, combined with grid search for automatic tuning of core parameters. The parameters being searched included population size, crossover probability, crossover distribution index, mutation probability, and mutation distribution index. The configuration of the optimization algorithm parameters is detailed in

Table 3. Range of grid search parameters.

Parameter Type	Search Range
Population size	$[50,100,200]$
Probability of crossover	$[0.8,0.85,0.9]$
Index of crossover distribution	$[15,20,25]$
Probability of variation	$[0.01,0.05,0.1]$
Index of distribution of variation	$[20,30,40]$

.

Due to the lack of data required for direct calculation of carbon emissions, this study employed a CNN to predict total carbon emissions. The experiment initially trained the model on historical industry electricity consumption and total carbon emission data. However, due to the limited dataset, the preliminary model performed inadequately. To address this, this study introduced a CGAN to augment the existing data: real industry electricity consumption data served as a condition to which noise was added in the generator, producing carbon emission data corresponding to the electricity consumption data. Subsequently, the generated electricity and carbon emission data were combined with the real data and input into the discriminator for training. Ultimately, the CGAN generated 1000 data points that closely resembled the characteristics of the original real data, which were then utilized for the subsequent training of the convolutional neural network.

During the training process of the CNN model, synthetic data was utilized to augment the sample size for training, while real data was employed for validation. The models that passed validation were ultimately applied to the carbon emission calculations within NSGA-II. The specific architecture of the convolutional neural network is detailed in

Table 4. CNN model architecture.

No.	Model	Channels	Kernel Size	Stride	Activation	Dropout	Batch Norm
1	Conv1d	(1, 16)	3	1	ReLU	0.2	✓ *
2	Conv1d	(16, 32)	3	1	ReLU	0.2	✓
3	Conv1d	(32, 16)	5	2	ReLU	-	-
4	Flatten	(16, 16 × 11)	-	-	-	-	-
5	Linear	(16 × 11, 11)	-	-	ReLU	-	-

* The checkmark indicates that batch normalization is applied in the corresponding layer.

.

4.4. Evaluation Metrics

4.4.1. Hypervolume (HV)

The hypervolume metric was used to measure the volume of the region dominated by the solution set in the target space and a combined metric was used for assessing the convergence and distribution of the solution set. Its mathematical definition was

$$\mathrm{HV}=\mathrm{Volume}\left(\bigcup _{\mathrm{x}\in \mathcal{P}}[\mathrm{x},\mathrm{r}]\right)$$

(16)

Here, $\mathcal{P}$ is the Pareto solution set and r is the reference point, which is usually taken as the worst point in the objective space. The reference point was taken as $[1.1,1.1,1.1]$ after normalizing the data of the solution set of the three objective functions in this experiment. $[x,r]$ denotes the hypercube between the solution x and the reference point r.

The larger the value of HV, the better the convergence and distribution of the solution set in the target space. In this experiment, the reference point r was set to $[1.1,1.1,1.1]$, so if the value of HV was closer to $1.1^3=1.331$, this indicated the better convergence and distribution of the solution set.

4.4.2. Violations of Constraints

Constraint violation is a measure of whether a solution satisfies the constraints of the optimization problem. In this study, the optimization problem contained four constraints, i.e., industry output constraint, power ratio conservation constraint, PV power cap constraint, and green electricity ratio constraint. For each solution, if the constraints were not satisfied, the solution was considered infeasible. Ideally, all solutions needed to satisfy these constraints when the number of constraint violations was zero.

4.4.3. Pareto Frontier

A Pareto frontier is the set of all non-dominated solutions in a multi-objective optimization problem, i.e., there is no other solution that simultaneously outperforms the current set of solutions in all objectives. In this study, there was an obvious trade-off relationship between industrial output value, carbon emissions, and total cost. Based on the actual production requirements, the most appropriate solution could be subsequently selected in the Pareto frontier.

4.4.4. Evaluation Metrics for the CNN Model

Mean squared error (MSE) is used to measure the average of the squares of the errors between predicted values and actual values, reflecting the overall magnitude of a prediction error. A smaller value indicates higher predictive accuracy of a model, and its calculation formula is as follows:

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2$$

(17)

The mean absolute error (MAE) reflects the average absolute error between predicted values and actual values, providing an intuitive description of the average deviation of prediction errors. The calculation formula is as follows:

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n|y_i-{\widehat{y}}_i|$$

(18)

$R^2$ measures the extent to which a model explains the variability of data, with values ranging from 0 to 1. A value closer to 1 indicates a better fit of the model. The calculation formula is as follows:

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}$$

(19)

where $\overline{y}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{y}_i$.

The mean absolute percentage error (MAPE) represents the average percentage of the absolute error between predicted values and actual values, providing an intuitive display of the relative magnitude of forecasting errors. The calculation formula is as follows:

$$\mathrm{MAPE}={\displaystyle \frac{100\%}{n}}\sum _{i=1}^n\left|{\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}\right|$$

(20)

where $y_i$ denotes the true value of the i-th sample, ${\widehat{y}}_i$ represents the predicted value of the i-th sample, and n signifies the total number of samples.

4.5. Dataset Inputs

To support the integrated optimization framework involving CGAN, CNN, and NSGA-II, this study utilized multiple types of input data tailored to the distinct functions of each model component. The dataset inputs and their roles are summarized as follows:

(1)

Inputs for the NSGA-II Optimization Model

(a)

Industry output constraints: The model incorporated the upper and lower bounds of annual output values for 11 major industries based on historical data trends.

(b)

Electricity intensity: Each industry’s electricity consumption per unit of output (kWh per 100 million CNY) was used to estimate total electricity demand.

(c)

Electricity cost parameters:

(1)

Unit purchase costs of green and non-green electricity.

(2)

Construction and maintenance costs of photovoltaic (PV) systems, annualized over a 20-year expected lifecycle to ensure comparability. These parameters were embedded in the optimization process to evaluate the three objective functions: total output, carbon emissions, and electricity costs.

(2)

Inputs for CGAN Training

(a)

Input features: Real electricity consumption data for 11 industries, obtained from the Yizhuang region of Beijing.

(b)

Output labels: Corresponding industry-level carbon emissions derived from government-published emission factors.

These paired samples formed the basis for CGAN training, where electricity consumption served as the conditional input and carbon emissions as the output. The CGAN generated 1000 synthetic samples to augment the dataset.

(3)

Inputs for CNN Model

(a)

Pre-training phase: The 1000 synthetic electricity–emission pairs generated by the CGAN were used to pre-train the CNN model; 80% of this synthetic data was used for training and the remaining 20% was used for validation.

(b)

Fine-tuning phase: Real electricity–emission data was used to fine-tune the pre-trained model. In this stage, 80% of the real data was used for training and 20% was held out for testing.

(4)

Integrated Optimization Execution

During NSGA-II optimization, the algorithm evolved candidate solutions represented by a 14-dimensional vector: 11 industry outputs and three electricity consumption proportions (green, non-green, PV). For each candidate, the following applied:

Economic output was directly calculated from the 11 industry outputs.

Electricity demand was computed as the product of industry output and its electricity intensity, forming the input to the trained CNN to predict total carbon emissions.

Electricity cost was calculated by distributing total electricity across the three energy sources based on the proportions in the candidate solution and applying the respective cost parameters.

This dataset design ensured that each model component received the necessary structured input to fulfill its predictive or optimization function within the overall framework.

4.6. Analysis of Results

In the test, the NSGA-II algorithm performed 1000 iterations for each set of parameters to select the optimal parameters, which are presented in

Table 5. Optimal parameters for grid search.

Parameter Type	Optimal Value
Population size	100
Probability of crossover	0.85
Index of crossover distribution	15
Probability of variation	0.1
Index of distribution of variation	20

. Next, an analysis of the various metrics of the CGAN-CNN model was carried out, focusing on the distribution of the Pareto front, the distribution of the solution set across the three objectives, the hypervolume indicator, and the assessment of constraint violations to evaluate the optimization results of NSGA-II.

4.6.1. Analysis of CGAN-CNN Results

Table 6. Comparison of carbon emission forecasting models.

Model	MSE	MAE	${\mathit{R}}^2$	MAPE
MLP	1.9032	0.4098	0.7809	9.31%
Random Forest	1.2974	0.4449	0.6498	12.06%
XGBOOST	1.1761	0.4574	0.6960	10.00%
CNN	1.0396	0.3869	0.7787	8.98%
LSTM	3.9503	0.7574	0.7029	9.78%
BiGRU	2.9244	0.7468	0.5611	12.95%
CGAN-CNN	0.0765	0.1064	0.9887	1.96%

presents the performance of various models in calculating carbon emissions. In the process of estimating carbon emissions, models such as Multi-Layer Perceptron (MLP), Random Forest, XGBoost, CNN, Long Short-Term Memory (LSTM), and Bidirectional Gated Recurrent Unit (BiGRU) were tested. However, due to the limited dataset, the predictive performance of these baseline models was suboptimal. Among them, the CNN achieved the best overall performance. By contrast, the sequential models LSTM and BiGRU did not perform as well since the industry output–carbon emission dataset did not contain temporal features and thus did not benefit from sequential dependency modeling. After employing the CGAN for data augmentation, 1000 synthetic data points were generated and used to pre-train the CNN model, which had previously shown promising results in the baseline comparison. Subsequently, 80% of the real data was utilized as the training set for fine-tuning, while 20% was reserved for testing. The final test results are displayed in Table 6. Compared to other models that did not utilize data augmentation, the proposed CGAN–CNN achieved favorable outcomes across all evaluation metrics, with an MSE of 0.0765, an MAE of 0.1064, an $R^2$ value of 98.87%, and a MAPE of 1.96%, demonstrating strong performance in the regression task of predicting carbon emissions from industry electricity consumption.

4.6.2. Pareto Frontier Analysis

Figure 3 illustrates the Pareto front derived from the final optimization, showcasing 100 solutions plotted against the axes of carbon emissions, gross domestic product, and production costs. This visualization highlights the distribution of various solutions within the solution space concerning the three objectives. Additionally, projections of the three-dimensional Pareto front onto each axis were presented to facilitate the subsequent analysis of the trade-offs among the multiple objectives.

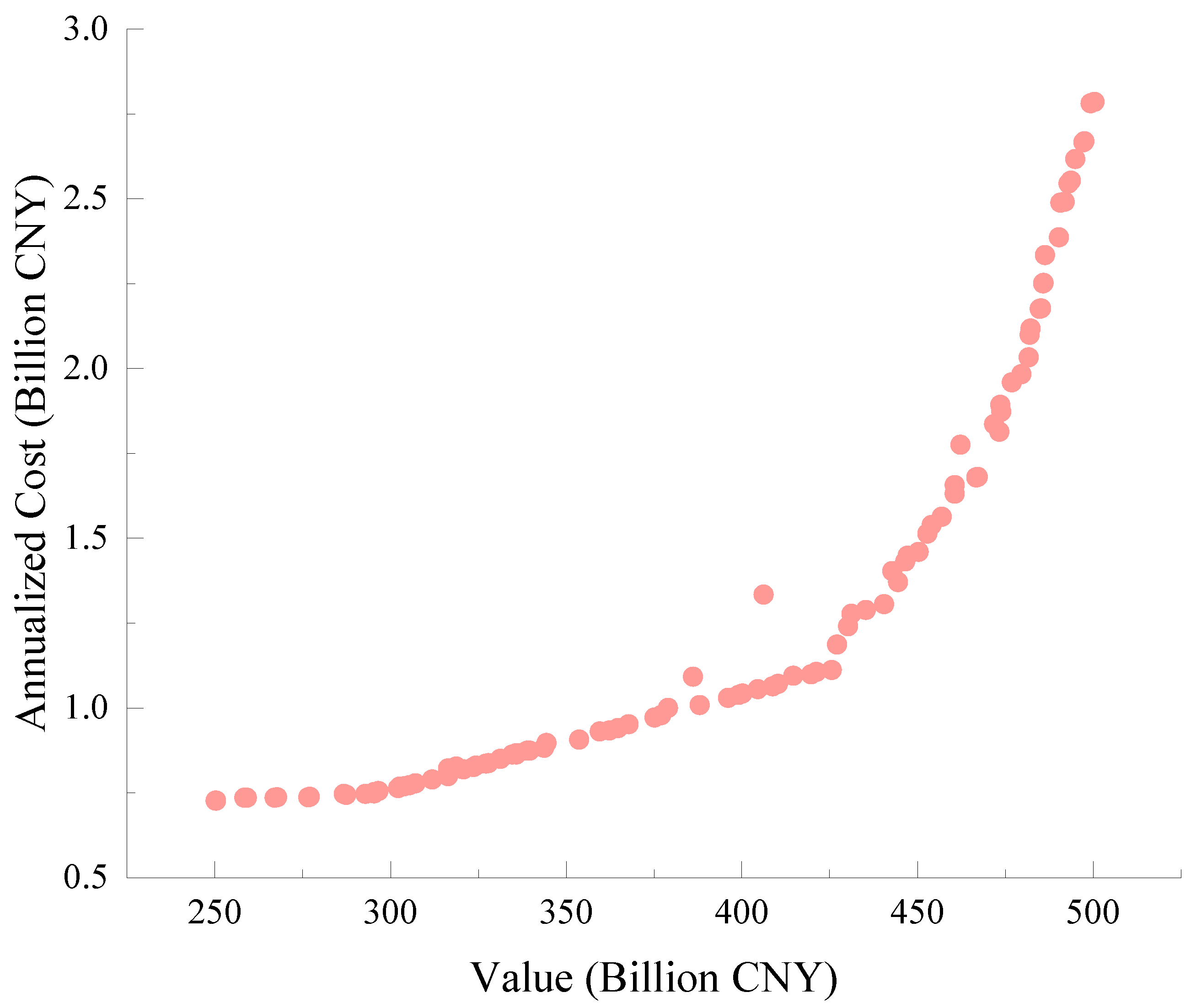
Figure 4 reveals a generally positive correlation between output value and annualized cost. As the output value increased, the annualized cost also rose. Notably, the distribution of solutions exhibited a nonlinear pattern: in the lower-output region, costs increased at a relatively slow rate, whereas, in the higher-output region, the rate of cost increase accelerated significantly. This indicated the presence of compromise solutions that balanced lower costs with moderate output values, offering flexibility for practical decision-making.

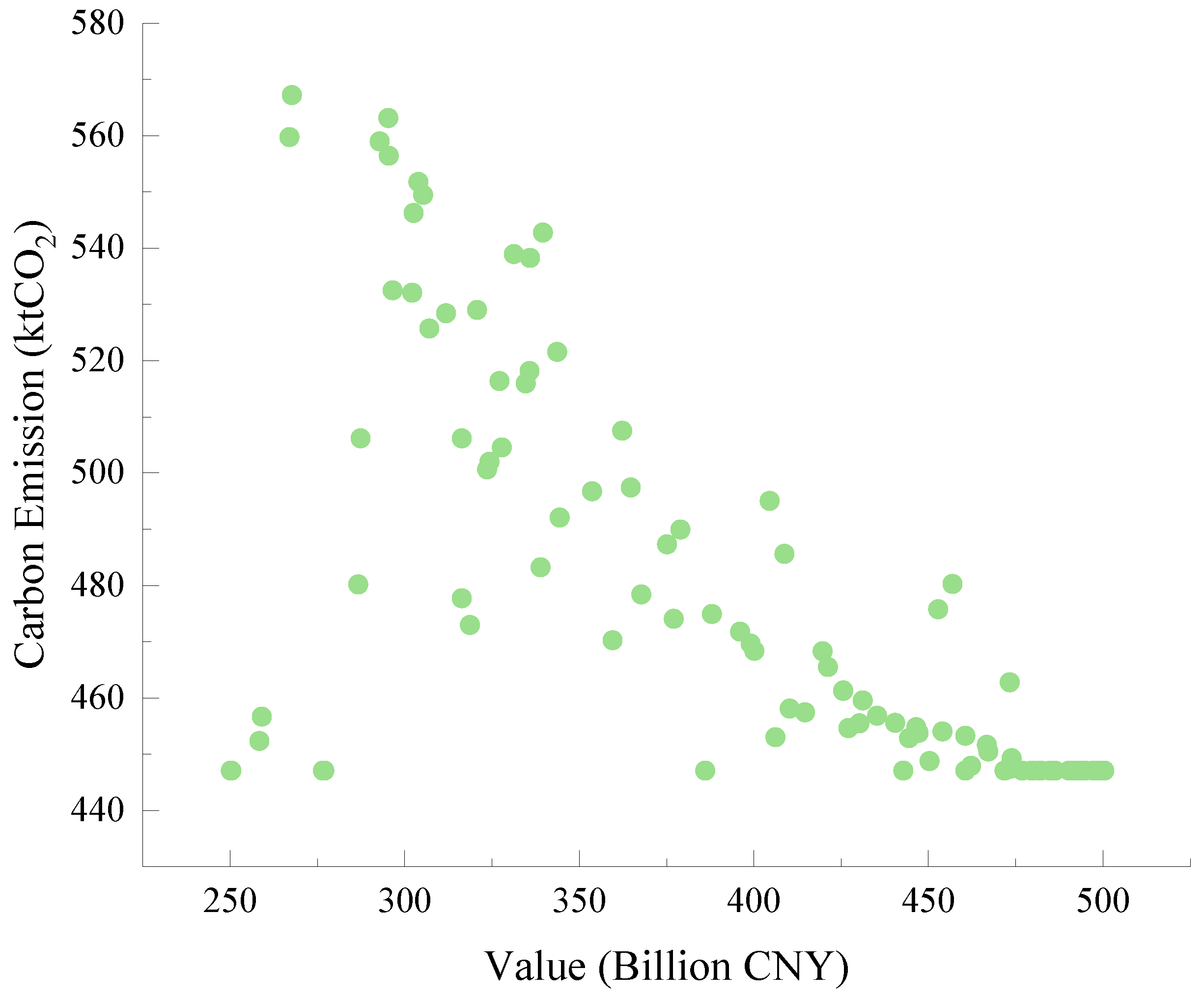
In Figure 5, a negative correlation is observed in this projection. As the output value increased, carbon emissions generally decreased, suggesting that certain high-output solutions achieved higher productivity while maintaining lower emissions. This was largely attributed to the greater proportion of green electricity and photovoltaic energy incorporated during optimization, achieving economic growth and carbon emissions reduction simultaneously.

Figure 6 shows a negative correlation, where lower carbon emissions were associated with higher annualized costs. The trend indicates that achieving significant emission reductions often requires greater investment in cleaner energy sources, such as green electricity and photovoltaic systems.

4.6.3. Analysis of Solution Distribution and Quantity

To systematically evaluate the solution set structure of multi-objective optimization models across different objective dimensions, this paper presents distribution histograms of three objective functions—output value, carbon emissions, and annualized electricity costs—illustrated in Figure 7, Figure 8, and Figure 9, respectively. By analyzing the distribution patterns of each objective function within the solution space, we can gain deeper insights into the trade-off relationships among the objectives during the optimization process, as well as the preference characteristics of the model.

(1)

Value of output

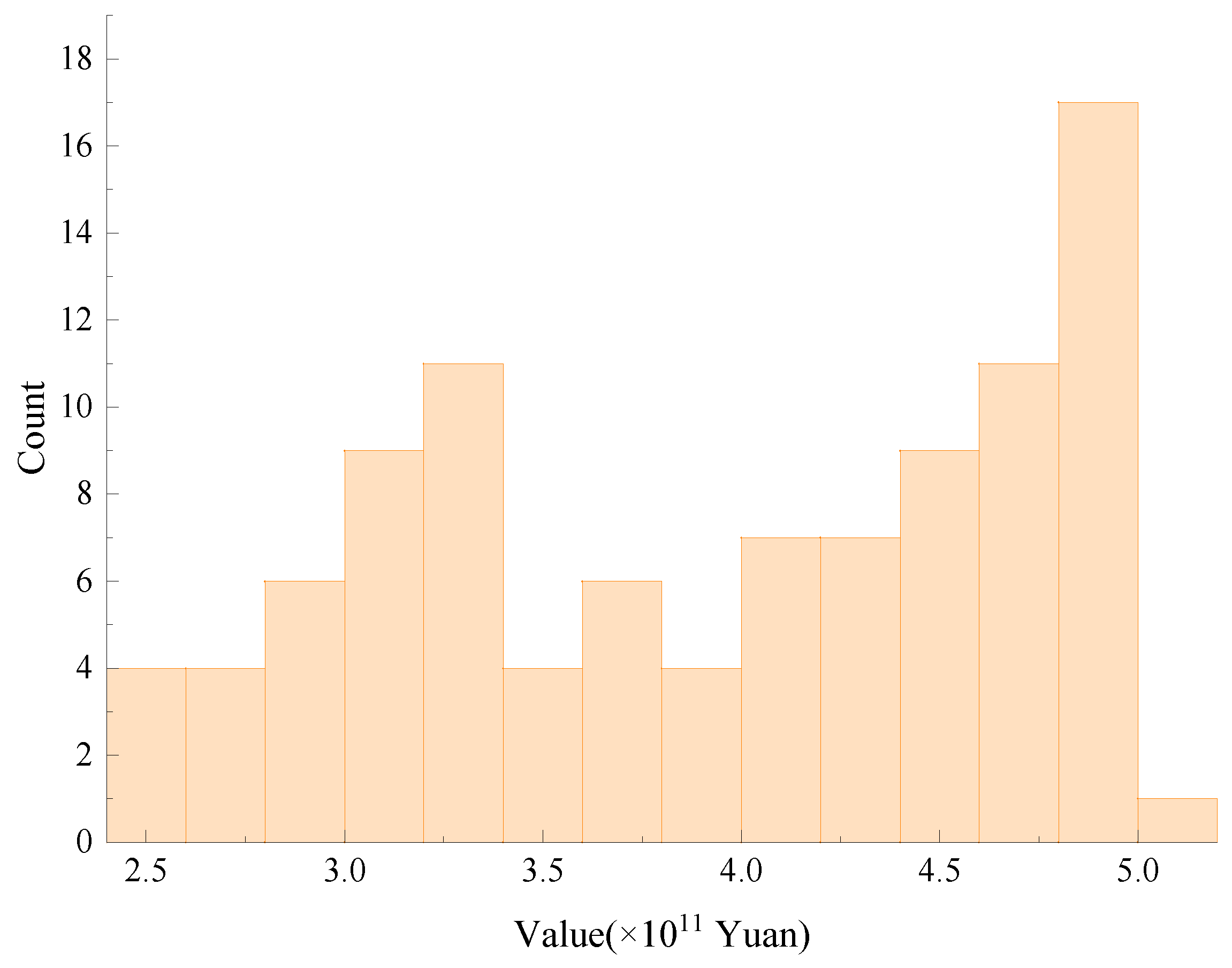
Figure 7 illustrates the distribution of solutions within the optimized solution set concerning the output value objective. The horizontal axis represents the output value range (CNY 100 million), while the vertical axis indicates the number of solutions within each output value range. The distribution of solutions was concentrated primarily in the CNY 450–500 billion range, indicating that the optimization algorithm strongly favored high-output strategies under the current parameters. A secondary concentration occurred around CNY 300–350 billion, reflecting a trade-off region where the model balanced output and cost objectives. The overall right-skewed distribution suggests that most Pareto-optimal solutions achieved medium-to-high output levels, highlighting the framework’s capacity to support robust economic growth.

(2)

Carbon emission

Figure 8 illustrates the distribution of solutions for carbon emission targets within the Pareto front, with the x-axis representing the range of carbon emissions (measured in ten thousand tons of CO₂) and the y-axis indicating the number of solutions within that range. The solution set exhibited a clear left-skewed distribution, with most solutions concentrated in the low-emission range. This indicates the model’s effectiveness in identifying strategies that significantly reduce carbon emissions while still considering output and cost performance. As emission levels increased, the number of solutions decreased steadily, confirming that low-carbon pathways dominated the Pareto front and demonstrating the environmental orientation of the optimization results.

(3)

Annualized cost

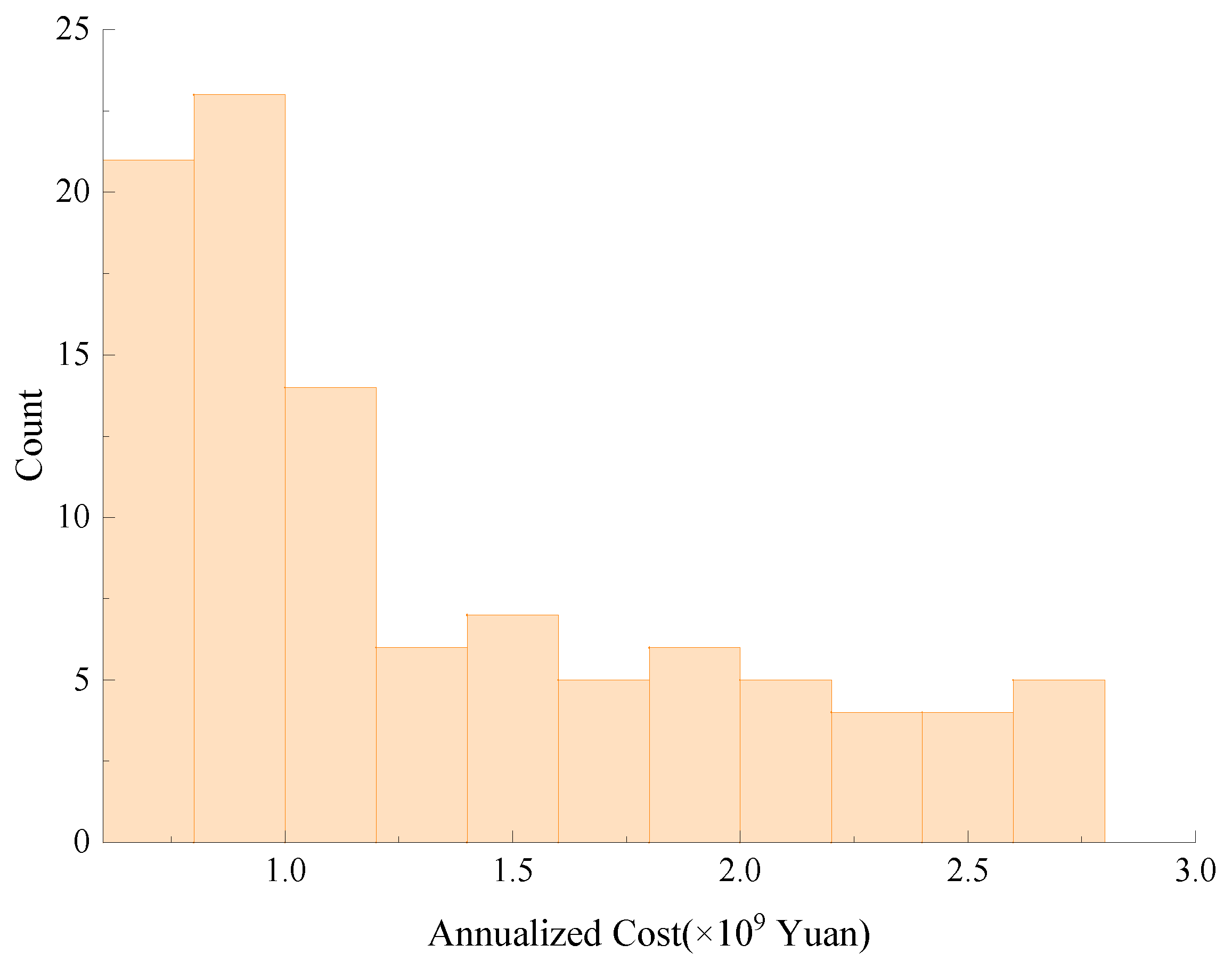
Figure 9 illustrates the distribution of solutions within the optimal solution set across different ranges of annualized costs, with the x-axis representing various intervals of annualized costs (in CNY) and the y-axis indicating the number of solutions within each interval. Most solutions fell within an annualized cost of below CNY 1 billion, suggesting that the optimization model is capable of delivering cost-efficient solutions while meeting output and emissions targets. The number of solutions gradually decreased as costs rose, indicating a strong optimization preference for low-cost, high-output, and low-emission solutions while retaining flexibility in trade-off scenarios.

Overall, the distribution patterns reveal that the majority of Pareto-optimal solutions clustered in regions characterized by high output, low emissions, and low cost. This confirms the framework’s ability to identify feasible strategies that simultaneously support economic development, environmental goals, and financial efficiency.

4.6.4. Hypervolume Targets and Constraint Violations

To quantitatively assess the results of the multi-objective optimization algorithm, this study employed the hypervolume indicator to evaluate the set of optimal solutions. To facilitate the setting of the reference point for the hypervolume indicator, the data was normalized prior to evaluation, with the reference point established at $[1.1,1.1,1.1]$, representing the worst normalized solutions across the three dimensions. The evaluation results indicate that the hypervolume of the current optimal solution set at this reference point was 1.1402, demonstrating that the optimal solution set exhibited strong coverage and diversity within the objective space.

Additionally, a statistical analysis of constraint violations across all solutions revealed no violations under the three constraint conditions, resulting in a feasibility ratio of 100%. This indicates that the optimization algorithm successfully maintained feasibility while optimizing the three objectives, thereby validating the stability and effectiveness of the multi-objective optimization model constructed in this study.

4.6.5. Computational Efficiency and Resource Requirements

To evaluate the computational burden of the proposed CGAN-CNN-NSGA-II optimization framework, all experiments were conducted on a computer equipped with an AMD Ryzen 7 5800H with Radeon Graphics CPU, 16 GB RAM, and an NVIDIA GeForce RTX 3060 Laptop GPU (6 GB). The computer model is LEGION R9000X 2021R, manufactured in Beijing, China.

Table 7. The computational resource usage and runtime of each component.

Model	Runtime	GPU Utilization	CPU Utilization	Device	Memory Usage
CGAN training	1 min 18 s	100%	25%	GPU	14 GB
CNN pre-training	5 min 35 s	100%	30%	GPU	14.2 GB
CNN fine-tuning (with early stopping)	46 s	100%	30%	GPU	14.2 GB
NSGA-II + CNN (optimization process)	52 min 20 s	22%	12%	NSGA-II:CPU CNN:GPU	14.8 GB

summarizes the computational resource usage and runtime of each component.

The CGAN model was relatively lightweight, completing training in under 90 s with full GPU usage. CNN training, including both pre-training and fine-tuning, was completed in under 7 min with GPU acceleration and early stopping. The main computational effort lay in the multi-objective optimization phase, where NSGA-II evolved a population over multiple generations. This process took approximately 52 min in total, during which the CPU handled population operations, and the trained CNN (running on GPU) was used to evaluate carbon emissions efficiently in each iteration.

5. Discussion

5.1. Interpretation of Results

This study presents a comprehensive multi-objective optimization framework that explores the coupling between regional industrial output and carbon emissions by jointly optimizing industry output levels and the allocation of green, non-green, and photovoltaic (PV) electricity. The model simultaneously maximizes industrial output, minimizes carbon emissions, and reduces electricity costs, forming an integrated decision-support tool for regional energy and industrial planning.

The optimization framework combines NSGA-II with a CGAN-CNN predictive module. The CGAN enhances data diversity, while the CNN captures complex relationships between electricity consumption and carbon emissions, significantly improving forecasting accuracy. Standard performance metrics (MSE, MAE, MAPE, and R2) confirmed the model’s strong predictive capability. The resulting Pareto front was well distributed, and all solutions satisfied constraint conditions, achieving a 100% feasibility rate, which validates the robustness of the optimization approach.

From the optimization outcomes, the proposed model demonstrates the ability to balance economic development with environmental responsibility. The total industrial output increased significantly—from CNY 250.24 billion to CNY 393.71 billion—representing growth of 57.3%. In scenarios where output was prioritized, the total value could reach up to CNY 500.41 billion, marking a 99.97% increase. At the same time, total carbon emissions dropped from 797,642.2 tons to 478,000 tons, and could be further reduced to 447,037.8 tons with additional cost investment, reaching just 56% of the original level. These results affirm the model’s potential to guide sustainable development strategies.

Figure 10 compares industrial output across sectors before and after optimization. The industrial and wholesale and retail sectors showed the largest increases, reinforcing their role as pillars of the regional economy. Sustained development of the construction, financial, and leasing services sectors is also recommended. In contrast, the real estate sector showed limited growth potential and higher emissions intensity, suggesting that resource allocation should be redirected toward industries with greater potential for high output, lower emissions, and lower costs.

In terms of energy allocation, the model recommends a significant increase in investment in PV infrastructure. Across the 100 Pareto-optimal solutions generated by the optimization model, the share of PV electricity ranged from 75% to 99%, with an average of 94% of total consumption. During periods of low solar radiation, such as nighttime, grid-purchased electricity was used as a complementary source. In this case, green electricity was prioritized but subject to a 15% allocation limit, which was imposed to ensure grid stability, and any remaining demand was met by non-green electricity. Each solution comprehensively satisfied the imposed constraints, and feasibility checks confirmed that none of the solutions violated the initial restrictions. These optimization results therefore represent theoretically attainable solutions, from which policymakers can select the scenarios that best align with practical, technical, and operational considerations.

5.2. Comparison with Related Works

To further validate the effectiveness of the proposed CGAN–CNN–NSGA-II framework, the results were compared with recent studies in the domains of carbon emission forecasting and multi-objective optimization for energy and industrial systems.

In terms of optimization objectives, many existing studies focus on two-objective formulations, such as minimizing operating costs and reducing carbon emissions. For example, in Multi-Objective Optimization for the Low-Carbon Operation of Integrated Energy Systems Based on an Improved Genetic Algorithm [13], the authors formulated a bi-objective optimization model targeting operating cost and carbon emissions for integrated energy systems and employed an improved genetic algorithm to obtain Pareto-optimal solutions. While effective in achieving balanced trade-offs between economic and environmental objectives, such models do not explicitly consider industrial output value, which is a critical economic indicator for regional development planning. In contrast, the present work incorporated industrial output value as a third objective alongside carbon emissions and electricity costs, thereby providing a more comprehensive framework that simultaneously supported environmental sustainability and industrial productivity growth.

The optimization results suggest that PV electricity could account for a high share of total consumption, with an average of 94% across the 100 Pareto-optimal solutions obtained. It is important to note that this value is not a fixed prediction but rather an aggregated outcome: the PV share in individual solutions ranged between 75% and 99%. Since the three optimization objectives, maximizing industrial output, minimizing carbon emissions, and minimizing cost, were mutually constraining, the resulting solutions formed a Pareto frontier, in which all solutions are non-dominated. Decision-makers are therefore expected to choose among these solutions based on practical needs, such as balancing economic benefits with operational feasibility.

In addition, the optimization was performed under the explicit consideration of the technical upper limit of PV generation in the Beijing Yizhuang District. This limit was calculated using the district’s total area (225 km²), the estimated rooftop availability (15%), the PV module power density (200 W/m²), the average conversion efficiency (80%), and the annual average sunshine duration in Beijing (2500 h). The resulting maximum annual PV generation potential of $1.35\times {10}^{10}$ kWh was incorporated as the upper-bound constraint in the optimization model. Thus, the high PV shares reported here reflect the maximum feasible utilization of local PV potential under the given constraints.

Furthermore, while this study is specific to the Yizhuang District, the methodology can be applied to other regions by adjusting the parameters used to calculate the PV generation potential, such as rooftop availability, module efficiency, and solar irradiation duration. This ensures that spatial variability in solar resources is captured in a region-specific manner.

From an algorithmic perspective, Cheraghi et al. [21] demonstrated that NSGA-II outperforms MOPSO in generating diverse and converged Pareto fronts for hybrid renewable energy system planning, while Ranjbar et al. [22] confirmed NSGA-II’s robustness in greenhouse gas reduction optimization within remote microgrid scenarios. In our study, NSGA-II achieved a hypervolume (HV) value of 1.1402 with 100% constraint satisfaction, indicating a well-distributed Pareto front and high solution feasibility despite the high-dimensional decision space (14 variables). This performance is competitive with and, in some cases, superior to the reported HV values in the related literature with similarly complex problem settings.

Regarding carbon emission prediction models, prior works have applied various deep learning architectures. He et al. [25] applied a CGAN-based framework for renewable energy scenario generation, demonstrating improved forecast realism and diversity through data augmentation. Zhang et al. [23] employed a hybrid CNN–LSTM model for short-term carbon emission prediction, achieving an R2 of approximately 0.93, while Han et al. [24] proposed a spatial-weighted LSTM–CNN architecture to incorporate regional correlations, reaching similar accuracy levels. In contrast, our CGAN–CNN model achieved an R2 of 0.9887 and a MAPE of 1.96%, demonstrating a substantial improvement in predictive accuracy. This gain can be attributed to the CGAN-based data augmentation strategy, which expands sample diversity and mitigates overfitting, thereby enhancing generalization to unseen data.

In summary, the comparison indicates that the proposed CGAN–CNN–NSGA-II framework offers a broader objective scope than typical bi-objective approaches by incorporating industrial output alongside carbon emissions and electricity costs. The optimization results demonstrate competitive Pareto front quality in a high-dimensional setting, while the CGAN-enhanced CNN achieves strong predictive accuracy through effective data augmentation. These features suggest the framework’s potential applicability to practical low-carbon industrial and energy planning scenarios.

5.3. Practical Implementation Considerations

While the proposed CGAN–CNN–NSGA-II framework demonstrates strong technical performance in optimizing industrial output, carbon emissions, and electricity costs, its successful real-world deployment depends on addressing economic and organizational factors that influence feasibility and scalability.

(1)

Economic Factors: The adoption of the optimized low-carbon electricity mix requires significant capital investment, particularly for photovoltaic (PV) construction. Although this study annualized construction costs over a 20-year lifecycle to ease the financial burden, practical implementation depends on financing availability, capital recovery periods, and interest rates. Market price volatility—such as changes in green electricity subsidies or increases in non-green electricity tariffs—can also impact the cost-effectiveness of the optimized solutions. Incorporating these uncertainties into planning is essential to ensure the long-term economic viability of the proposed framework.

(2)

Organizational Factors: Implementing the optimization results demands coordinated action among multiple industries and energy providers. Industrial sectors may face challenges in adjusting production schedules to align with the optimized energy allocation, while energy suppliers must coordinate to achieve the targeted electricity mix. Regulatory requirements, such as renewable energy integration policies and carbon trading mechanisms, also affect implementation feasibility. Furthermore, data-sharing agreements are critical to enable ongoing model updates, especially when electricity consumption and carbon emission data are subject to confidentiality constraints.

(3)

Storage Considerations: Large-scale energy storage is expected to play a key role in enabling high levels of renewable energy penetration. While this study relied on grid-purchased electricity to compensate for photovoltaic intermittency, practical deployment will increasingly require storage systems to ensure reliability during nighttime and periods of low solar radiation. To enhance the realism of the optimization framework, both the capacity sizing of storage systems and their associated capital and operational costs should be incorporated into future modeling efforts. Including these parameters will allow the framework to generate more robust and actionable results for long-term energy planning.

By integrating these economic, organizational, and storage-related perspectives, the proposed framework moves closer to practical applicability, ensuring that optimization results are not only theoretically sound but also aligned with the realities of industrial and energy system planning.

6. Conclusions

The scientific aim of this work was to develop a data-driven, tri-objective optimization framework that aligns regional economic performance, carbon emissions, and electricity expenditures within a single power-structure model. This research focused on three core components: obtaining high-precision, consumption-driven emission forecasts via a CNN-based predictor; enriching scarce time-series data through a conditional generative adversarial network (CGAN); and integrating these predictive components into an NSGA-II optimization engine capable of simultaneously maximizing industrial output value, minimizing total carbon emissions, and reducing electricity costs. This study advances the current state of research in regional power planning by explicitly incorporating industrial output as a core optimization objective, replacing static emission factors with dynamic, data-driven forecasts and uniting economic, environmental, and cost considerations in a unified, policy-aligned framework tailored to China’s dual carbon goals.

The findings of this study provide clear answers to the research questions posed in the Introduction:

• RQ1: The proposed tri-objective optimization framework successfully balances industrial output, carbon emissions, and electricity costs, demonstrating that these competing goals can be jointly optimized to support sustainable regional development.
• RQ2: The integration of a CNN-based carbon forecasting model significantly improved estimation precision by capturing dynamic, consumption-driven variations, overcoming the limitations of traditional static emission-factor approaches.
• RQ3: The application of CGAN-based data augmentation enhanced the robustness and representativeness of the dataset under data-scarce conditions, strengthening the reliability of the optimization outcomes.
• RQ4: The optimization results offer actionable policy insights, including prioritizing photovoltaic generation (up to 94% of total electricity supply) and implementing differentiated sectoral strategies—such as promoting growth in industrial, construction, wholesale, and service sectors while restricting real estate activity—thereby supporting China’s dual carbon targets.

The experimental results based on real-world data from Beijing’s Yizhuang region confirm the effectiveness and practical relevance of the proposed method. The model not only optimized the distribution of electricity across green, non-green, and photovoltaic sources but also achieved measurable gains in industrial output and substantial reductions in carbon emissions. These outcomes underscore the framework’s utility as a decision-support tool for guiding low-carbon energy transitions and industrial policy in urban settings.

The findings of this study provide meaningful implications for policymakers and regional planners, offering a scalable and adaptable solution for promoting low-carbon transformation without compromising economic growth. Looking ahead, future research will seek to enhance the model’s realism by incorporating additional factors such as real-time electricity pricing, grid capacity constraints, and temporal energy fluctuations. Expanding its application to other regions will further test its generalizability and adaptability across diverse energy and policy environments.