Transformer-Based Transfer Learning for Battery State-of-Health Estimation

Abstract

The accurate prediction of batteries’ state of health has been an important research topic in recent years, given the surge in electric vehicle production. Dynamically assessing the current state of health of a battery can help predict how long the battery will last during the next discharge cycle, which is directly related to an electric vehicle’s autonomy calculations. Data-driven approaches have been successful in accurately estimating the state of health through machine learning-based models. Within this research topic, limited studies have been carried out to explore the transfer learning capabilities of these models to improve performance and reduce computational costs related to training. This paper aims to compare the performance of different machine learning models to adapt to diverse battery working conditions, as well as their transfer learning capabilities to batteries with different electrochemical compositions. A new transformer-based model is proposed for the SOH estimation problem. The results show that the proposed transformer model can improve its prediction performance through transfer learning when compared to the same model trained exclusively on the target dataset. When pre-trained on the NASA dataset and fine-tuned on the Oxford dataset, the transformer achieved an average RMSE of 0.01461, outperforming the best-performing model (an ANN with an RMSE of 0.01747) trained exclusively on the target data by 17%. On top of improving its performance, the model is also able to outperform a competing transformer model from the literature, which reported an RMSE of 0.90170 on a similar cross-composition transfer task.

1. Introduction

The recent push toward the electrification of the automotive industry by governments and society has sparked new interest in the safety and performance of battery technology, which has become a prevalent topic in recent years. State-of-health (SOH) estimation has been central in ensuring reliable and cost-effective operations of modern lithium-ion batteries. SOH is an indicator of the battery life stage and is particularly difficult to predict due to inconsistencies in manufacturing processes and its nonlinear nature [1]. Due to limited hardware, only a limited set of features can be used to estimate SOH in a non-laboratory setting. For example, some direct estimation methods, which can only be performed in controlled environments, such as impedance spectroscopy [2], are not practical [1]. In lithium-ion batteries, the main issue is cell degradation, which reduces the battery’s maximum capacity and power output over time by increasing internal resistance [3]. Due to the performance drop, estimating the remaining useful life (RUL) of a battery is particularly important for battery management systems (BMSs) and ensuring reliable and safe operations [4]. BMSs supervise charge control, cell balancing, and temperature in electric vehicles to guarantee nominal operations and avoid accidents [5].

Various methods have been used to estimate the SOH of lithium-ion batteries accurately and robustly. These methods can be categorized as model-based methods and data-driven methods. Model-based methods attempt to represent the estimation problem based on equivalent electrochemical [3,6,7,8], or equivalent circuit electrical models [7,9,10,11,12], taking into account material properties, degradation mechanisms, and load conditions [13]. Data-driven approaches, such as machine learning, use the battery’s historical data to map future states from current features. However, these models do not consider the batteries’ physical properties; instead, they consider the SOH estimation a black box problem.

Recent progress in machine learning and artificial intelligence has provided new tools for estimating the SOH and RUL compared to older model-based and filter-based methods [14]. Many popular machine learning architectures have been successfully applied to the SOH estimation problem, such as support vector machines (SVMs) [15,16], convolutional neural networks (CNNs) [17,18], and recurrent neural networks (RNNs) [19,20], to name a few [21]. However, the literature still lags in applying the most recent machine learning models and tools, such as attention-based architectures and transfer learning.

Given the recent success of attention-based architectures, it is no surprise that many novel hybrid frameworks have also been explored for the SOH estimation problem [22,23,24,25,26]. In machine learning, attention is used to improve models’ performance and overcome overfitting. Attention first gained traction in natural language processing (NLP), where attention weights influence learning by highlighting and correlating relevant keywords present in a sentence [27,28]. In recent times, attention has also been widely adopted in machine vision to focus the model on salient regions of an image or specific channel correlations, improving performance [29] and, in time series problems, to weigh temporal dependencies and spatial correlation within the model’s latent spaces [30]. Intelligent fault diagnosis of machinery is an example of a time series problem. Attention mechanisms have been mainly applied to fault classification and life prediction of bearings, gearboxes, and rotary machinery, but hardly to battery management [31].

Qu et al. were the first to introduce a long short-term memory (LSTM) and attention mechanism combined solution for estimating the RUL of lithium-ion batteries [32]. Their proposed online method for estimating the SOH and RUL leverages Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) to filter the data and particle swarm optimization to optimize the weights of the constructed LSTM neural network. Attention is used to weigh the effects of each feature on the final prediction and is iteratively calculated for each time window [32]. Similarly, Zhang et al. implemented an LSTM-based framework followed by an attention layer without CEEMDAN denoising but normalizing the input data [33]. Cui et al. proposed a temporal attention (TPA)-based LSTM network for the SOH estimation problem [34]. He et al. take a similar approach, using a TPA-based LSTM but introducing the quantum genetic algorithm to optimize the network parameters and testing various window sizes to find the evolutionary target [35]. Cavus and Bell introduced V2G-HealthNet, a hybrid LSTM–transformer framework for battery health prediction in EV fleets that enables SOH-informed adaptive load scheduling and predictive maintenance [26]. Other LSTM-based approaches include hybrid architectures that add other machine learning algorithms alongside LSTM and gated recurrent unit (GRU) networks for increased performance. These include CNN hybrid architectures [18,36,37] and support vector regression [38], as well as variations in classical LSTM models such as bi-directional LSTMs [39] and deep LSTMs [40].

Data-driven approaches have produced satisfactory results in predicting the RUL and SOH of batteries, with some assumptions. However, these studies were, for the most part, performed on one battery type with a specific cell composition [41]. At the same time, various lithium-ion battery types with different capacities, cell compositions, and cell chemistry are present in the market [42]. Given the high variability in battery cell composition and capacity, many machine-learning models fail to adapt across battery datasets, having to be retrained from scratch every time [13]. Especially in new operating environments, the variability of data distribution and possible scarcity of data points present further complications. Transfer learning (TL) has been utilized to enhance the flexibility of models and create more cost-effective solutions that can be applied to various datasets with different distributions with minimal fine-tuning. The application of TL to battery SOH estimation problems has been shown to reduce the cost of collecting data, shorten the retrain time, and improve accuracy [43].

In the literature, TL has been mainly explored for NLP. Using novel transformer architecture and self-learning, it was possible to make models perform tasks that they were not explicitly trained on. Transformers are encoder–decoder-style machine learning architectures that leverage a mechanism denoted as self-attention to capture long-term dependencies and generate rich latent spaces. Due to their nature, transformers have been proven to be highly adaptable and excellent for TL, reusing trained weights for different tasks and datasets [44].

Training conventional data-driven and machine learning models usually requires a large amount of labeled data, which is a limitation for implementing such strategies [13]. In practice, constructing large battery datasets under various working conditions is a timely and expensive process. Given the variety of lithium-ion compositions, the various domains in which they are used, and the dynamic working conditions in which they operate, the creation of a one-for-all dataset is impossible. In most cases, state-of-the-art models need to be retrained for new operating conditions and battery types every time. Furthermore, these variations cause discrepancies in data distribution, creating an imbalance, which is known to affect the machine learning algorithm’s performance [45]. Due to the differences in electrochemical reactions at different stages of the battery degradation process, the historical data distribution of a given battery may differ from the current window data distribution of the same battery [43]. Often, data distribution is assumed to be the same for training and testing data samples, severely limiting the adaptation of the model to other datasets and its performance in general [46]. Therefore, to successfully create a model flexible enough to adapt to different battery types and working conditions, data distribution variations must be considered.

This paper aims to explore the utilization of a transformer architecture for TL applied to the battery’s SOH estimation. The intuition is that through multi-head attention, transformers will be able to adapt across battery datasets more easily. Different from the vision transformer proposed in [17,47,48,49], as well as similar approaches in recent studies like those by [17] and Zhao et al. [50], we propose a time series transformer composed of multiple blocks containing a normalization layer, a multi-head attention layer, and a dropout layer with an overarching residual connection. The result from the repeated blocks is then fed to a multilayer perceptron (MLP) layer that outputs the final estimation. Inspired by approaches such as those of Li et al. [51], Nakano et al. [52], and Lu et al. [53], this paper represents one of the first attempts to apply time series transformer-based models to the SOH estimation problem across different batteries’ electrochemical compositions.

Previous studies have explored the use of attention mechanisms within hybrid network structures, most notably by integrating LSTM networks with attention layers or combining CNNs with transformer components to improve local feature extraction, as summarized in Table 1. In contrast, the present work employs a complete encoder–decoder transformer architecture applied directly to the time series formulation of the SOH estimation problem, without the inclusion of convolutional embedding stages or positional encoding. Rather than encoding temporal order through positional embeddings, the proposed framework incorporates the cycle number as an explicit input feature, allowing the attention mechanism to infer temporal dependencies directly from the data. Through the use of multi-head self-attention, the model captures global degradation relationships across successive discharge cycles and represents the SOH evolution as a continuous temporal regression process. This approach differs from previously reported vision transformer and CNN transformer hybrid configurations, which have often relied on image-style patch embeddings or convolutional preprocessing to extract intermediate features. Moreover, the present study extends the application of transformer-based models beyond single-dataset experiments by examining their adaptability across distinct battery chemistries and working conditions. Specifically, by pre-training the network on the NASA dataset and fine-tuning it using the Oxford dataset, this study evaluates the model’s capacity to transfer knowledge between lithium-ion cells of different electrochemical compositions. This design enables an explicit assessment of how attention-based architectures generalize across datasets with non-identical feature distributions, a capability that remains largely unaddressed in earlier transformer-based SOH estimation research. The observed results confirm that the proposed transformer model can retain information learned from one battery domain and successfully adapt to another, highlighting its suitability for scenarios where direct re-training on new data is limited or costly. The main contributions can be summarized as follows:

• A new transformer-based model is proposed for the SOH estimation problem.
• A comprehensive comparison of the TL capabilities of artificial neural networks (ANNs), LSTM, and transformer models in adapting to new environmental operating conditions is conducted.
• The proposed model and other conventional machine learning architectures are applied to TL across batteries with varying electrochemical compositions.
• The results demonstrate that pre-training on different datasets can significantly improve estimation performance.

Table 1. Comparison of methodologies explored in the literature and our proposed methodology.

Method Category	Key Studies	Core Approach	Key Limitations and Scope
Model-Based	[3,6,7,8,9,10,11,12]	Electrochemical or Equivalent Circuit Models	Expert knowledge of degradation mechanisms; complex to parameterize.
Data-Driven (Single Domain)	[15,16,17,18,19,20,21]	SVM, CNN, RNN (LSTM/GRU)	Treat SOH as a black box; typically trained and tested on a single battery type/chemistry.
Hybrid Attention Frameworks	[26,32,33,34,35]	LSTM + Attention Mechanism	Focus on feature/temporal weighting within a single domain.
Transfer Learning (Parameter Transfer)	[41,54]	LSTM/DNN Pre-training and Fine-tuning	Standard architectures with limited temporal feature extraction; transfer between similar batteries/conditions.
Transfer Learning (Vision-Based)	[17,47,48,49]	Vision Transformer (ViT)	Requires conversion of time series to 2D images; not a native time series processor.
Proposed Method (This Work)	-	Native Time Series Transformer	Native time series processing with multi-head attention; cross-composition transfer learning.

Table 1. Comparison of methodologies explored in the literature and our proposed methodology.

Method Category	Key Studies	Core Approach	Key Limitations and Scope
Model-Based	[3,6,7,8,9,10,11,12]	Electrochemical or Equivalent Circuit Models	Expert knowledge of degradation mechanisms; complex to parameterize.
Data-Driven (Single Domain)	[15,16,17,18,19,20,21]	SVM, CNN, RNN (LSTM/GRU)	Treat SOH as a black box; typically trained and tested on a single battery type/chemistry.
Hybrid Attention Frameworks	[26,32,33,34,35]	LSTM + Attention Mechanism	Focus on feature/temporal weighting within a single domain.
Transfer Learning (Parameter Transfer)	[41,54]	LSTM/DNN Pre-training and Fine-tuning	Standard architectures with limited temporal feature extraction; transfer between similar batteries/conditions.
Transfer Learning (Vision-Based)	[17,47,48,49]	Vision Transformer (ViT)	Requires conversion of time series to 2D images; not a native time series processor.
Proposed Method (This Work)	-	Native Time Series Transformer	Native time series processing with multi-head attention; cross-composition transfer learning.

The remainder of this paper is structured as follows. Section 2 frames the SOH estimation problem and defines how battery capacity is calculated based on charge and discharge cycles. Section 3 describes the methodology used, including data preprocessing, denoising, windowing, and the model’s architecture. Section 4 presents and compares the results under multiple regression metrics. Section 5 presents the major conclusions drawn from the study and future directions.

2. State-of-Health Estimation

Battery SOH estimation is a measure of battery degradation over time. It is affected by various factors, such as operating conditions, usage time, manufacturing process, charging and discharging rates, and cycles. In addition, the mechanisms for the cathode and anode differ in nature and contribute to the nonlinearity of battery degradation [8,14,55]. Key factors that characterize such degradation are capacity fade and internal impedance increase, affecting performance and safety. Generally, a lithium-ion battery pack is not safe to use for an electric vehicle after its total capacity falls below 80% of the initial capacitance [16,55,56], as the increase in internal resistance can cause the battery to heat up and possibly catch fire [57]. Furthermore, given the capacity drop, the range of the vehicle on a single charge is severely limited. A battery’s SOH is usually expressed as a percentage that reflects either the change in rated capacity or the increase in internal resistance. This can be mathematically expressed as follows:

$$SOH={\displaystyle \frac{C_{max}}{C_{rated}}} \times 100\%$$

(1)

$$SOH={\displaystyle \frac{∆R_{current}}{{∆R}_{nominal}}}\times 100\%$$

(2)

where in the former, $C_{max}$ is the nominal battery capacity, and $C_{rated}$ is the estimated current battery capacity [58], while in the latter, $∆R_{current}$ is the difference between end-of-life resistance and current resistance, and $∆R_{nominal}$ is the difference between the end-of-life resistance and nominal resistance [36].

Resistance-based SOH estimation is usually carried out through electrochemical impedance spectroscopy (EIS). EIS involves the use of a frequency response analyzer (FRA) in combination with an electrochemical interface to calculate the battery’s internal resistance [59]. Although accurate, the need for additional hardware for the estimation of a battery’s SOH presents some limitations in real-world applications. Electrical model-based methods attempt to represent the SOH of the battery using either an equivalent electrochemical [3,6,7,8] or an equivalent circuit electrical model [7,9,10,11,12]. Circuital models used to represent the system include Sheperd, RC, and Thevenin, among others. The interested reader is referred to [60] for more information on these types of models. The problem with these models is that they are specific to the battery and lack generalization, as the model is manually tuned based on battery characteristics and does not allow for flexibility. Due to its simplicity and rapid deployment, capacity-based estimation is the most popular and explored in the literature. The most common method to estimate the current capacitance of a battery is through Coulomb counting algorithms, which depend exclusively on current and time measurements. Coulomb counting algorithms rely on the integration of the current drawn and supplied to a battery over time, as follows:

$$C= C_n- {\int }_0^t\eta Id\tau$$

(3)

where $C_n$ is the nominal capacity of the battery, $\eta$ is the battery charge and discharge efficiency, and I is the current load [61].

Machine learning techniques are generally more efficient than model-based approaches and, depending on the selected architecture size, less complex. The most researched machine learning architectures for RUL estimation are RNNs, widely recognized for their performance in time series prediction. Many researchers have applied long short-term memory (LSTM) networks [62,63] and gated recurrent unit (GRU) networks [36], both particular types of RNNs, to the SOH estimation problem, with promising results. These RNNs compensate for long series and avoid the vanishing gradient problem. Furthermore, researchers have combined RNNs with other classes of neural networks, such as autoencoders, CNNs, and more [64,65,66], to increase performance. As a result, in the past two years, a surge of mixed architectures has come to light for the SOH estimation problem, providing state-of-the-art performance.

Li et al. were the first to propose that TL could be applied to the SOH estimation problem to mitigate the high economic and timely costs of obtaining battery aging data to train data-driven machine learning models [13]. The authors proposed a new model based on semi-supervised transfer component analysis (SSTCA), leveraging maximum mean discrepancy (MMD) to minimize the differences in distributions between four different battery datasets. After tuning features into model inputs by passing the data through the SSTCA algorithm, the authors used a kernel ridge regression to predict the battery’s SOH [13]. Vilsen et al. highlight data-driven model performance discrepancy when tested in laboratory and field conditions [67]. Using the same metric for data distribution discrepancy (MMD) and kernel mean matching (KMM), they show that it is possible to transfer the learning of simpler model builds. Multiple linear regression (MLR) and bootstrapped variants of random vector functional link (BRVFL) neural networks were used to estimate the SOH of multiple battery cells without measurements in the target domain [67]. Ye et al. went one step further and utilized a mixture metric to align the deep representations of different domains [46]. Pairing MMD and correlation alignment for deep domain adaptation (CORAL), they formulated a custom loss function for a GRU-based feature generator with dense connections using adversarial learning [46]. Ma et al. also adopted the MMD metric to construct a CNN-based SOH estimation model [68].

Other studies on TL for the SOH estimation problem diverge from the data distribution difference approach. Instead, they focus solely on the machine learning side by transferring the learned parameters to reduce the computational burden of re-training. The TL process, in this case, is composed of a pre-training phase and an adaptation phase. In the former, the models are trained on a general source dataset, usually of considerable size, to then be fine-tuned in the latter to the target dataset. Unfortunately, the existing literature contains only a few of these cases, including various architecture types used for TL, which include a classical deep neural network [54], LSTM networks [41,69,70], CNNs [66,71], and an adapted vision transformer model [17,47,48,49].

3. Methodology

This section describes all of the necessary methodologies used in the study and analysis of the results.

3.1. Composition of Datasets

To assess the performance of the proposed model, two publicly available datasets of lithium-ion battery cycling were selected as the source and target datasets. The NASA [72] and Oxford [73] battery degradation datasets were chosen due to the difference in the electrochemical composition of the batteries used, rated capacity, geometry, and discharge current utilized for the cycles. A comparative table of the characteristics of each dataset can be seen in Table 2.

Table 2. Comparison of source and target datasets.

Datasets	Source	Target
Data Source	NASA PCoE [72]	Oxford [73]
Geometry	Cylindrical	Pouch
Number of Cells	34	8
Cell Chemistry	LiCoO2	LiNiCoMnO2
Rated Capacity	2 Ah	740 mAh
Charging Current	0.75 C	1 C

Table 2. Comparison of source and target datasets.

Datasets	Source	Target
Data Source	NASA PCoE [72]	Oxford [73]
Geometry	Cylindrical	Pouch
Number of Cells	34	8
Cell Chemistry	LiCoO2	LiNiCoMnO2
Rated Capacity	2 Ah	740 mAh
Charging Current	0.75 C	1 C

The NASA degradation dataset contains cycling data of 34 Li-ion 18650 cylindrical batteries cycled to 30% capacity fade at lower, average, and increased room temperatures ranging from 4 to 43 °C. The discharge cutoff voltage also varies for different batteries, from 2 to 2.7 V for each cycle. The dataset contains current and voltage readings of both the charger and the load, as well as temperature, capacity, and relative time for cyclic charge and discharge cycles. Due to the variety of conditions under which the different battery cells were cycled, the dataset represents a good picture of the degradation patterns of this type of battery over its lifetime, having great potential to create rich latent spaces in the model in the training phase. The dataset also contains impedance spectroscopy measures between each charge–discharge cycle, but this was omitted from the study as it was considered out of this paper’s scope.

The Oxford degradation dataset contains cycling data of 8 Kokam (SLPB533459H4) Li-ion pouch cells operated in a binder thermal chamber at an elevated temperature of 40 °C. In contrast with the NASA degradation dataset, it contains more consistent charge and discharge cycle measurement data.

3.2. Data Preprocessing

Before feeding the data to the model for pre-training and fine-tuning, some data preprocessing steps were performed. To make the model fit both the source and target datasets, the voltage and current measured at the charger for the NASA dataset were dropped and not included in the window used for training, as were the impedance class of measurements. The input used for training and testing was constructed to be of the form $X \in R^{m,l}$, where m is the number of features, and l is the window length. The features used to estimate the SOH of the battery were battery voltage, current, temperature, relative time, cycle number, and the maximum capacity of the previous cycle, approximated using the Coulomb counting method. This resulted in an input matrix, X_i, with 6 features and a window length, l, of 300. Given X_i, the model predicts the battery capacity of the next window, Y_i+1, of the form $Y_{i+1} \in R^{1,l}$. Matrix representations of inputs and outputs can be seen in Equations (4) and (5).

$$X_i=\left[\begin{array}{ccc}{x}_{1,j}& \dots & x_{1,l-1}\\ ⋮& \ddots & ⋮\\ x_{6,j}& \dots & x_{6,l-1}\end{array}\right]$$

(4)

$$Y_{i+1}=(y_j,y_{j+1},\dots , y_{l-1})$$

(5)

After the extraction and aggregation of the data in the required matrix format, the matrices were run through an outlier rejection function. Any data point that fell outside two standard deviations from the feature mean was dropped to increase prediction performance. Furthermore, before training, each feature, aside from the cycle number, was normalized between 0 and 1 using the following formula:

$$x_{scaled}= {\displaystyle \frac{x-x_{min}}{x_{max}-x_{min}}}$$

(6)

This step is crucial to avoid overfitting the model to the features with the largest size; normalization ensures that the model weights all the features on the same scale and is not influenced by their magnitude.

Ultimately, the labels used to calculate the loss function in the model represent the actual battery capacity after a given cycle and are filtered using a Savitzky–Golay digital filter with a window size of 111 and fourth-degree polynomial interpolation to be used in the training. The output predictions are also run through the filter to achieve a smoother degradation curve. Optimal window size and polynomial order were selected to fit the average length of a discharge cycle. The smoothing of the capacity degradation curve proved to increase model performance by a factor of 10. The Savitzky–Golay filter algorithm uses a least-squares polynomial approximation of the given window to generate an envelope curve [74,75]. A visual representation of the filter functioning can be seen in Figure 1, adopted from [76].

3.3. Model Architecture

The function of the transformer architecture is to predict the SOH of the battery for the next discharge cycle. The model can map the feature expression to the SOH value of the battery. During the TL process, the model is first trained on the source dataset and then fine-tuned on a single epoch of the target dataset to align it to the different battery parameters while maintaining the knowledge accumulated from the training performed on the source dataset. During validation, the model weights are frozen, performing a forward pass of the validation cells.

Transformers are characterized by the self-attention mechanism they employ to extract global features by calculating the attention weights of all inputs. The recent success of transformer-based NLP architectures has proven their ability to efficiently leverage the attention scores to focus the computation on the most relevant parameters at the current time step. However, this comes at a computational cost when compared to simpler architectures such as general ANNs and LSTMs. Traditionally, transformers embed the relative position of the input data before feature encoding. In the transformer architecture employed, this is replaced by adding the cycle number as a feature in the input matrix, as well as the relative time of the discharge cycles. This allows the attention layer to make use of this information and weigh its relevance based on the current state of the system, which has been shown to increase model performance in time series modeling.

Fu et al. were the first to implement a transformer-based model for battery SOH estimation; the model makes use of positional and patch embeddings that are fed to a transformer encoder block with self-attention [47]. The resulting predictions are processed through a fully connected layer for regression, complemented by batch normalization to reduce vanishing gradient effects on the architecture. In contrast with the model employed by Fu et al., the proposed model does not use positional embeddings; instead, the cycle number is used as a feature for the estimation problem, as already mentioned [47].

Gu et al. were the first to implement a combination of CNNs and transformer-based architecture for the SOH estimation problem [17]. The study suggests a CNN–transformer-based framework, where the CNN layer is used to embed the raw input data, aiming to enrich the local detail and feature extraction from the data and the transformer component to reinforce the global perception capabilities of the model through self-attention [17]. The authors also opt to use the Pearson correlation coefficient to select highly related features and principal component analysis (PCA) to reduce dimensionality and decrease the computational burden. However, this article, along with many others, such as [63,77,78,79,80,81], does not discuss the application of the proposed framework across diverse battery datasets nor mention the TL capabilities of the proposed model.

Different from the model employed by Gu et al. [17], the proposed model is a full encoder–decoder transformer that does not rely on CNN for feature extraction; instead, convolutions are used after the multi-head attention block, and it does not rely on PCA for dimensionality reduction, further reducing computational cost [17]. Another dissimilarity is that their model was trained and validated on singular batteries, where a battery’s lifetime cycles were split into testing and training, while the model proposed in this paper was trained on a different set of batteries of the same composition and working conditions to then be tested on the full lifecycle of another battery.

The paper by Wang et al. [82] is the only available comparison paper that evaluates battery state-of-health (SOH) estimation using a transformer model with convolutional layers. The authors also examine the TL capabilities of their model. However, the model proposed in this paper differs from Wang et al.’s model, as it does not include convolutional layers. Additionally, the proposed model outperforms Wang et al.’s model in TL across batteries with distinct electrochemical compositions, as demonstrated in latter sections. The architecture of the proposed model is as follows.

The first layer of the model is the input layer, which embeds windows of the input data based on batch size, encoding the information and passing it to the rest of the network. The output shape of this layer is of the form (L,6,1), where l represents the variable window length that the model will use to process the data. The window length used in the experiments carried out in this paper was chosen to be 300-unit steps, as this is the average size of a full discharge cycle. The windowed data is fed directly into the transformer encoder and, subsequently, to the transformer decoder. The encoder–decoder layers are then stacked as blocks and repeated n times. The input to the first block will be the input layer, while for the subsequent blocks, the input will be the output of the previous block. A schematic representation of this process can be seen in Figure 2.

Each encoder–decoder block is identical and formed by 7 layers. The first layer is the batch normalization layer, which in the first block normalizes the windowed data to be better processed by the rest of the network. In the subsequent blocks, this layer normalizes the weighted output of the previous blocks to be used in the next layers.

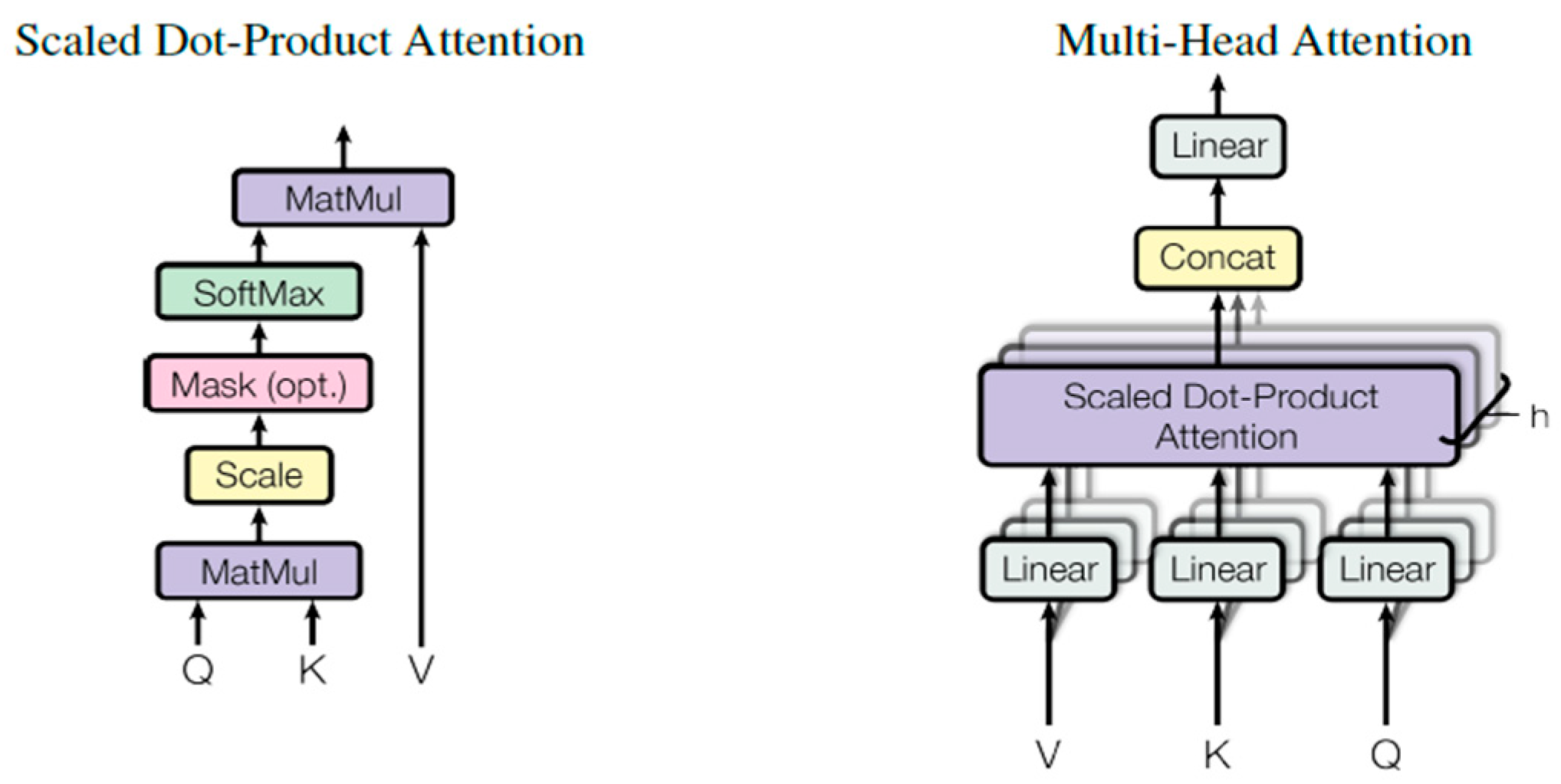
The second layer is the multi-head attention layer, which compares all sequence members with each other by mapping a query {Query} with a set of key–value pairs {Key, Value}. The key–value pairs and the query are computed as follows:

$$Q_i= {w^Q}_i x_i$$

(7)

$$K_i={w^K}_i x_i$$

(8)

$$V_i={w^V}_i x_i$$

(9)

where ${w^Q }_i\in R^{L \times d_{model}}$, ${w^K}_i R^{L \times d_{model}}$, and ${w^V}_i R^{L \times d_{model}}$. The scaled dot-product attention is then calculated by computing the dot product of the query and the key, dividing the result by the square root of the key dimension, and applying the softmax function to obtain the weights on the key values to be multiplied by the value matrix. This calculation is formalized in Equation (7) and visualized in Figure 3 (left).

$$Attention\left(Q,K,V\right)=softmax\left({\displaystyle \frac{Q{K}^T}{\surd d_k}}\right)V$$

(10)

This process is parallelized and computed h number of times, where h is the parameter representing the heads of the multi-head attention layer. Instead of performing a single attention function, the queries, keys, and values are linearly projected h times to a different set of learnable parameters, yielding $d_v$ dimensional values, ${W^Q}_h\in R^{d_{model}\times d_k}$, ${W^K}_h\in R^{d_{model}\times d_k}$, and ${W^V}_h\in R^{d_{model}\times d_v}$. The results are then concatenated and once again projected by parameter matrix $W^O\in R^{h{d}_v\times d_{model}}$ to be the layer’s output, visualized in Figure 3 (right).

$${head}_h\left(Q,K,V\right)=Attention(Q_i{W}_h^Q, K_i{W}_h^K, V_i{W}_h^V)W^O$$

(11)

$$MultiHead\left(Q,K,V\right)=Concat({head}_1, \dots , {head}_h)W^O$$

(12)

The multi-head attention layer is followed by a dropout layer, which randomly sets input units to 0 with a frequency rate, r, to prevent model overfitting. The dropout layer results are then added to the encoder block’s original input in the form of a residual connection, effectively applying the calculated attention scores to the inputs. Layers one to three compose the transformer encoder part of the blocks and are followed by the decoder layers. The fourth block layer is another normalization layer that bounds the encoder outputs to be of a Gaussian distribution with a mean of 1 and a standard deviation of 1. The fifth layer is a one-dimensional convolution layer that slides a one-dimensional kernel across the sequence, expanding the input dimensions. The sixth layer is another dropout layer, followed by a reverse one-dimensional convolution that brings the sequence back to its original form. A residual connection is also employed across the decoder layers to preserve some of the original encoder outputs. The encoder–decoder block is repeated 4 times and feeds into the final MLP layer block. The MLP layer block is composed of a one-dimensional global average pooling, followed by two fully connected layers of the shape (L,300,1), with a dropout layer separating them. The final MLP layer outputs the SOH prediction for the next window.

The model results were compared with the performance of a general ANN and a modified LSTM. The ANN architecture is composed of 3 fully connected linear layers of the shape (L,258), followed by a dropout layer of the same size and an output layer. Conversely, the LSTM model comprises 4 alternating LSTM and dropout layers, followed by an output layer. The hyperparameters of each layer and losses used for each model can be seen in

Table 3. Model hyperparameter comparisons.

Model	Transformer	ANN	LSTM
Optimizer	Adam	Adam	Adam
Loss	MSE	MSE	MSE
Activation	Relu	Relu	Relu
Dropout Rate	0.25/0.4	0.25	0.25
Number of Heads	8	-	-
Head Size	512	-	-
Layer Unit Size	300	256	70
Total Parameters	117,161	133,633	138,671

. The ANN model architecture was selected to be the baseline general deep neural network, while the LSTM model was chosen based on its state-of-the-art performance in the problem at hand, shown in the literature [83].

Before evaluating the results, the prediction from each of the models was run through a Savitzky–Golay filtering function to smooth the resulting regression curve. The polynomial used by the filter to interpolate was of the third order and was tested with three different window sizes: 999, 3001, and 5001.

Figure 3. (Left) Scaled dot-product attention steps. (Right) Multi-head attention composition with the concatenation of multiple attention heads [84].

Figure 3. (Left) Scaled dot-product attention steps. (Right) Multi-head attention composition with the concatenation of multiple attention heads [84].

3.4. Evaluation Metrics

To assess the performance of the proposed method in comparison with the baseline models, 4 different metrics were chosen: mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE), and the coefficient of determination (R²). The metrics represent the accuracy of the regression, providing different insights into its performance.

$$MSE=\sum _{i=1}^n{\displaystyle \frac{{(y_i-{\widehat{y}}_i)}^2}{n}}$$

(13)

$$RMSE=\sqrt{\sum _{i=1}^n{\displaystyle \frac{{(y_i-{\widehat{y}}_i)}^2}{n}}}$$

(14)

$$MAE=\sum _{i=1}^n{\displaystyle \frac{\left|{{\widehat{y}}_i-y}_i\right|}{n}}$$

(15)

$$R^2=1-{\displaystyle \frac{\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}{\sum _{i=1}^n{(y_i-\overline{y})}^2}}$$

(16)

4. Results and Discussion

This section describes the results of the study and discusses the findings and their implications for the literature.

4.1. Model Performance on the Source and Target Datasets

The ability of the proposed model to estimate the SOH of batteries was first benchmarked on the source and target datasets without pre-training. For the NASA battery degradation dataset, the models were trained on batteries B0005, B0006, and B0007 to then be tested on battery B0018; this group of batteries shares the same operating conditions in terms of temperature and discharge current, with the difference that the cutoff discharge voltages were, respectively 2.7 V, 2.5 V, 2.2 V, and 2.7 V. All models were trained for 5, 20, and 50 epochs to ensure the global minimum of the loss function was reached. The best results were obtained after only five epochs, showing that the higher number of epochs was detrimental to the learning due to overfitting. Furthermore, the variation in the Savitzky–Golay window size did not have a significant impact on the results. When comparing different models’ performance, the LSTM architecture performed best, as seen in

Table 4. Model performance on the NASA degradation dataset. Bold entries represent the best methods on each dataset.

Model	MAE ↓	MSE ↓	RMSE ↓	R2 ↑
ANN	0.017560	0.000373	0.01932	0.938
LSTM	0.009836	0.000135	0.01161	0.978
Transformer	0.023232	0.000633	0.02517	0.895

.

To assess the SOH estimation performance of the models on the Oxford degradation dataset, the same procedure employed on the NASA degradation dataset was used. The models were trained on Cells 1 to 7 and subsequently tested on Cell 8. All batteries shared the same operating conditions and discharge cutoff, set at 2.7 V. The training was performed for 5, 20, and 50 epochs to ensure maximum model performance. Contrary to the NASA degradation dataset, the best result was achieved by the general ANN after 50 epochs, while the transformer model achieved the best result with the lowest epoch size. The variable window size of the Savitzky–Golay filter did not have a significant impact on the results. A performance comparison can be seen in

Table 5. Model performance on the Oxford degradation dataset. Bold entries represent the best methods on each dataset.

Model	MAE ↓	MSE ↓	RMSE ↓	R2 ↑
ANN	0.01383	0.000305	0.01747	0.933
LSTM	0.01609	0.000382	0.01953	0.916
Transformer	0.01565	0.000368	0.01918	0.919

.

4.2. Transfer Learning

To study the TL capabilities of the proposed model, two sets of experiments were performed. First, the ability to adapt the estimation of batteries operating in different environmental conditions was tested, and then, the ability to transfer the learning to batteries with different electrochemical compositions was assessed. The aim is, therefore, to leverage pre-training to reduce the re-training computational burden and increase overall efficiency. Fine-tuning allows the model to adapt to new battery parameters, such as initial maximum capacitance and electrochemical composition, faster and make accurate predictions without the need for the full dataset of the target battery. To this end, parameter sharing was used as the chosen TL method. This consists of transferring the learning weights from one model to another. The two models may have different structures depending on the task, but in this case, the source and target models were identical, and therefore, no modifications were made to the pre-trained model. Given that the source and target tasks shared input features, the same model structure was used for the prediction of the SOH degradation curve. The features were selected for commonality between the source and target datasets, as well as for their role in the estimation of the battery’s health. The main features to estimate the degradation of a battery with respect to time are voltage, current, and relative time, and through them, we can estimate the capacitance of the previous cycle using the Coulomb counting algorithm. Temperature and cycle number were selected to account for variations in battery environmental conditions and charge and discharge cycle number. Other features included in the NASA battery degradation dataset, such as impedance spectroscopy measures between each charge–discharge cycle, were purposely omitted, as they are hard to collect and rarely included in datasets. Using features that can be easily collected allows the model to be used in real-life scenarios and reduces the overall complexity. Furthermore, characterizing an increase in the resistance of the battery due to aging mechanisms is sufficient to observe the discharge current relative to time. It is common that old batteries last less than new ones due to the degradation of the solid electrolyte layer, among other factors, which makes ion transfer less efficient. The other features complement the current and relative time correlation by providing context, which results in a more precise characterization of the black box problem, as seen by the algorithm.

Given the different operating modes of the batteries contained in the NASA degradation dataset, the performance of the proposed model on the same battery type operating at different temperatures was tested. The models were trained on a set of discharge cycles of batteries operating at room temperature, batteries B0005, B0006, B0007, and B0018, to then be tested on a battery operating at an elevated room temperature of 43 C (B0029) without fine-tuning. The models were trained for 5, 20, and 50 epochs on the training set and tested on the target battery. The best results were achieved by the models trained for the least number of epochs due to the direct effect of overfitting on TL capabilities. The window size chosen for the filter had a large impact on the accuracy of the estimation due to the higher noise present in the predicted SOH curve. As shown in Table 6, the accuracy of the prediction was improved by 16% on average when comparing the results of the transformer prediction with and without filtering. A visual comparison of the effects of the Savitzky–Golay filter can be seen in Figure 4.

The TL ability of the model was then tested to validate model performance across battery operating conditions and electrochemical composition. The experiment was divided into three phases: pre-training, fine-tuning, and testing.

• The pre-training was performed on batteries B0005, B0006, B0007, and B0018 from the NASA dataset. Models were trained on the source battery set for five epochs to avoid overfitting, as higher epochs resulted in worse or marginally better results.
• The fine-tuning was performed on one battery cell from the target Oxford battery degradation dataset. The cell was selected in an arbitrary manner to be Cell 6. The fine-tuning procedure was carried out for a single epoch over the entire cell degradation lifetime until end-of-life criteria were met.
• Finally, the performance was tested by predicting the SOH over the lifetime of the remaining batteries contained in the target Oxford degradation dataset, Cell 1, Cell 2, Cell 3, Cell 4, Cell 5, Cell 6, and Cell 8. The comparison metrics of the resulting battery degradation curve of each cell were averaged out to represent the SOH estimation performance more comprehensively and over the whole dataset.

The experimental results of TL across batteries with different electrochemical compositions can be seen in Table 7, showcasing that the proposed model performs best in predicting the target dataset SOH degradation curve. As noted in the TL experiment on the NASA battery degradation dataset, for cells operated at different temperatures, the prediction results contain a degree of noise, as seen in Figure 5. The Savitzky–Golay filter improved the results by a relative 18% margin by eliminating some of the noise present in the predictions. The observed performance dichotomy, where the transformer is outperformed by LSTM in single-dataset training but excels in cross-dataset adaptation, may be attributed to their fundamental architectural biases. LSTM’s recurrent gating mechanism is highly effective at modeling local, short-term temporal dependencies within a homogeneous dataset, leading to superior single-domain performance. The transformer’s self-attention mechanism is architected to model global, long-range dependencies across an entire sequence. This characteristic, while potentially less optimal for fitting a specific, constrained dataset, enables the model to learn more generalized and reusable representations of underlying degradation physics. As such, when pre-trained on a heterogeneous source dataset, the transformer develops a transferable latent feature space, allowing for efficient adaptation via fine-tuning to new target domains with different electrochemical characteristics. It is important to note that some noisy behavior was likely due to capacity regeneration, but the use of the filter does not impact the overall prediction of the degradation curve. The best window size result, once again, was 5001, with third-degree polynomial interpolation. Higher epochs for the training phase were tested, but this resulted in either marginal improvement or worse performance. When compared to the performance of the models trained exclusively on the Oxford degradation dataset, the transformer model pre-trained on the NASA battery degradation dataset and fine-tuned to the Oxford battery degradation dataset performs 17% better than the best result in terms of RMSE. The fitness of the curve is slightly worse due to the cross-dataset adaptation, but all other metrics show improvements.

Table 6. Model performance on transfer learning to battery B0029 compared with other models found in the literature. Bold entries represent the best methods on each dataset.

Model	MAE ↓	MSE ↓	RMSE ↓	R2 ↑
ANN	0.011120	0.0001590	0.01261	0.8510
LSTM	0.008240	0.0001335	0.01156	0.8750
Transformer	0.005950	0.0000628	0.00792	0.9410
Transformer without SV	0.006445	0.0000911	0.00974	0.9110
DANN [46]	0.069000	0.0091968	0.09590	-
DAN [46]	0.074100	0.0086863	0.09320	-
CORAL [46]	0.088400	0.0137124	0.11710	-
TL-DNN [46]	0.021980	0.0007500	0.02738	0.9594

Table 6. Model performance on transfer learning to battery B0029 compared with other models found in the literature. Bold entries represent the best methods on each dataset.

Model	MAE ↓	MSE ↓	RMSE ↓	R2 ↑
ANN	0.011120	0.0001590	0.01261	0.8510
LSTM	0.008240	0.0001335	0.01156	0.8750
Transformer	0.005950	0.0000628	0.00792	0.9410
Transformer without SV	0.006445	0.0000911	0.00974	0.9110
DANN [46]	0.069000	0.0091968	0.09590	-
DAN [46]	0.074100	0.0086863	0.09320	-
CORAL [46]	0.088400	0.0137124	0.11710	-
TL-DNN [46]	0.021980	0.0007500	0.02738	0.9594

Table 7. Model average performance in transfer learning to the Oxford battery degradation dataset compared with other models found in the literature. Bold entries represent the best methods on each dataset.

Model	MAE ↓	MSE ↓	RMSE ↓	R2 ↑
ANN	0.011269	0.000256	0.01481	0.929
LSTM	0.024223	0.000956	0.02931	0.781
Transformer	0.010850	0.000249	0.01461	0.932
Transformer without SV	0.014560	0.000312	0.01781	0.919
Transformer [82]	0.658100	0.008300	0.90170	-

Table 7. Model average performance in transfer learning to the Oxford battery degradation dataset compared with other models found in the literature. Bold entries represent the best methods on each dataset.

Model	MAE ↓	MSE ↓	RMSE ↓	R2 ↑
ANN	0.011269	0.000256	0.01481	0.929
LSTM	0.024223	0.000956	0.02931	0.781
Transformer	0.010850	0.000249	0.01461	0.932
Transformer without SV	0.014560	0.000312	0.01781	0.919
Transformer [82]	0.658100	0.008300	0.90170	-

Compared to domain adaptation TL techniques based on the distribution alignment method, such as the one proposed by Ye et al. in [46], the proposed model performs better under all metrics, as shown in Table 6. The mixture of MMD and CORAL used for domain alignment allows for a good fit in the prediction curve, but it performs worse overall by a considerable amount. Compared to a general DNN approach trained in a similar fashion, such as the one from Maleki et al. in [54], the proposed model outperforms the deep neural network with an autoregressive integrated moving average (ARIMA) under all metrics except the R² score. This is likely due to the adjustments to the forecast by the ARIMA tuners, which control the moving average, effects of time lags, and trace alignment. Overall, the proposed transformer architecture demonstrates its principal advantage in scenarios requiring cross-domain generalization across different battery electrochemical compositions, attributed to the self-attention mechanism’s ability to model all elements in a sequence simultaneously, thereby capturing global, long-range dependencies for a generalizable latent representation of the underlying degradation physics. This is empirically validated by the results in Table 7, where the pre-trained and fine-tuned transformer significantly outperformed both the LSTM and ANN on the Oxford dataset after being pre-trained on the NASA dataset. The adaptability comes with the practical limitations that make simpler models preferable in many real-world settings, contingent on substantial computational resources for the initial pre-training phase, and it carries a persistent overhead due to its quadratic memory complexity with sequence length. This makes it poorly suited for direct, real-time deployment on resource-constrained hardware like an embedded BMS. In such latency-sensitive and memory-limited environments, the more streamlined architecture of an LSTM or even an ANN is a more pragmatic and power-efficient choice. Furthermore, in stable, single-domain applications where the battery type and operating conditions are consistent, the transformer’s sophisticated architecture offers no distinct advantage. As shown in Table 4, LSTM achieved the best performance on the native NASA dataset, suggesting that for a fixed, well-understood system, its inherent temporal inductive bias is sufficient and more computationally efficient.

5. Future Directions

The results of this study indicate that TL may enhance model prediction performance by leveraging information captured from a source dataset and adapting it through fine-tuning to a target dataset. This cross-adaptation of previously learned knowledge is crucial for creating flexible and cost-efficient models, improving performance while reducing the need for complete re-training when new environments are introduced. The proposed model achieved state-of-the-art performance in estimating the SOH of lithium-ion batteries when compared with models such as LSTM and ANN. Although this improvement comes with a higher computational cost, it highlights the importance of TL in reducing the overall training burden. Experimental findings showed that longer pre-training or additional epochs did not necessarily improve performance and could lead to overfitting. Thus, effective SOH estimation benefits from moderate pre-training, allowing the model to remain adaptable to new conditions. Future work should examine the optimal ratio between pre-training and fine-tuning to balance knowledge retention and adaptability. An ablation study of the attention weights in the encoder could also reveal how the model correlates input features, potentially providing insights into the degradation mechanisms of lithium-ion batteries. Extending this approach to predict the RUL using the same framework would further test the TL capabilities of the proposed model. Building on the proof of concept established here, several research directions can strengthen the robustness and practical deployment of transformer-based frameworks for battery health estimation. In terms of the validation of the proposed model on real-world data, validation using real-world electric vehicle (EV) fleet data would be the next step, which introduces variations in driving cycles, ambient conditions, and sensor noise absent in laboratory data. Evaluating the model’s resilience under these conditions is essential for translating it into field applications. To meet the constraints of BMS, future work will explore optimized, lightweight transformer variants through model pruning, quantization, and efficient attention mechanisms, enabling deployment on resource-limited edge devices without significant accuracy loss. The TL results also motivate a systematic study of few-shot learning to quantify the relationship between fine-tuning data volume and prediction accuracy, determining the minimal data needed for effective adaptation in data-scarce settings. The framework’s generalization should further be tested under imbalanced or incomplete data conditions, including missing points or truncated cycle life, and extended across different batteries. To link data-driven outputs with electrochemical understanding, future efforts will focus on improving model interpretability through a detailed examination of self-attention mechanisms, uncovering how learned correlations relate to physical degradation modes.

6. Limitations of the Study

While this study demonstrates the promising capabilities of transformer-based models for TL in battery SOH estimation, it is important to acknowledge its limitations to provide a balanced perspective and guide future research. This study’s validation is confined to controlled laboratory datasets. While the NASA and Oxford datasets provide invaluable, well-characterized cycling data, they operate under predefined, often fixed, stress conditions (e.g., constant ambient temperature in a thermal chamber). This does not fully replicate the complex, dynamic, and highly variable loading profiles seen in real-world electric vehicle (EV) operation, which include aggressive acceleration/regeneration, varying climate control loads, and diverse driving terrains. Furthermore, laboratory data are typically clean, whereas real-world BMS data are plagued by issues like sensor drift, communication packet loss, and asynchronous sampling rates, which our current preprocessing pipeline has not been tested against. The computational and architectural complexity of the proposed transformer model presents a significant barrier to edge deployment. With 117,161 parameters, the model demands substantial memory and processing power for inference. While TL reduces the need for re-training, the initial pre-training is computationally intensive. More critically, the self-attention mechanism has a quadratic complexity with respect to the sequence length, which becomes a major bottleneck for long time series data. For a real-time BMS that must process continuous, high-frequency data streams, this computational overhead may be prohibitive, making simpler models like LSTM or even ANNs more pragmatic choices for on-board deployment, despite their potentially lower peak accuracy in cross-domain tasks. Another limitation lies in the sensitivity and specificity of the TL framework. Our results indicate that performance is sensitive to the pre-training and fine-tuning regimen, where we found that just five epochs of pre-training were optimal. This suggests that the model is susceptible to negative transfer if pre-trained for too long on the source domain, causing it to become overly specialized and lose its flexibility, which is a balancing act. Moreover, the success of transfer is likely contingent on a fundamental, albeit unproven, similarity in the underlying degradation dynamics between the source and target batteries, even with different chemistries. The framework might fail if the target battery exhibits a novel or radically different failure mode (e.g., lithium plating dominant vs. SEI growth-dominant degradation) not represented in the source data. Additionally, the issue of electrochemical generalization, while partially addressed, requires further nuance. Our study successfully transferred knowledge between NCA (LiNiCoAlO₂, in the NASA cells) and NMC (LiNiMnCoO₂, in the Oxford cells) chemistries. However, it remains an open question whether the model can effectively generalize to chemistries with vastly different voltage profiles and degradation behaviors. Finally, the “black box” nature of the model presents a fundamental limitation for both scientific insight and practical trust. Although the multi-head attention mechanism can highlight temporal correlations within the input sequence, interpreting these attention weights in a physically meaningful way is challenging. The model does not provide explicit, quantifiable insights into the root causes of degradation, such as the loss of active lithium inventory or increased charge transfer resistance. For engineers and scientists, a model that predicts SOH accurately is useful, but a model that can also explain why the SOH is degrading would be far more valuable for guiding battery design and failure analysis. Bridging this gap between data-driven prediction and electrochemical interpretability remains a critical challenge for the field.

7. Conclusions

This paper presents a new adapted transformer architecture for time series processing and TL. The transformer achieves excellent performance in the estimation of the SOH of the battery throughout its lifetime. As outlined in this paper, other models, such as LSTM-based networks, can perform better when training and testing on the same battery and environmental conditions, although the proposed model achieves better performance overall through TL. The role of the multi-head attention mechanism, characteristic of transformer models, proved fundamental in retaining key information learned during pre-training and adapting it to batteries with different electrochemistry and different environmental conditions. Furthermore, to attenuate the prediction noise caused by adapting the model to a new dataset, a digital filter such as the Savitzky–Golay filter can be used, as it was shown to further improve performance.