Modeling of Electric Vehicle Energy Demand: A Big Data Approach to Energy Planning
Abstract
1. Introduction
1.1. Context and Motivation
1.2. State of the Art
1.2.1. Evolution of Agent-Based Modelling
1.2.2. Big Data Architectures for Energy Simulation
1.2.3. Synchronization Effects and Time-of-Use Tariffs
1.2.4. Specific Conditions of High-Altitude Cities
1.3. Problem Statement and Research Gap
- Current approaches to modelling electric vehicle (EV) demand exhibit three critical limitations when applied to high-penetration scenarios in complex urban environments:
- Traditional database systems become computationally prohibitive when processing the billions of time-series records generated by large-scale EV simulations, thereby limiting the depth of scenario analysis and uncertainty quantification [34].
1.4. Research Contributions
- The development of a scalable agent-based model that incorporates experimentally calibrated behavioral parameters, heterogeneity in price elasticity, and thermal effects, validated against real-world charging data from 764 charging points.
- The implementation of a TimescaleDB-based pipeline capable of ingesting, processing, and querying billions of quarter-hourly records, with query response times of <2 ms and a 91% data compression rate.
- An analysis of the “charging cliff” phenomenon demonstrates that a non-optimized implementation of TOU tariffs can increase system peaks by up to 67% in high-elasticity scenarios.
- A Monte Carlo analysis with over 1000 iterations provides probabilistic bounds (P10/P50/P90) for peak demand, energy consumption, and infrastructure requirements through 2040.
- It is important to note that the scope of this paper is strictly limited to the Grid-to-Vehicle (G2V) paradigm, focusing on the challenges of modeling and planning for EV charging demand. The potential of Vehicle-to-Grid (V2G) services for ancillary support or grid restoration, while important, represents a distinct area of research and is considered beyond the scope of this study.
1.5. Research Questions and Hypotheses
- RQ1: What are the probabilistic bounds for peak electric vehicle (EV) charging demand under different adoption and tariff scenarios?
- RQ2: How do temperature variations and thermal effects influence charging profiles in high-altitude environments?
- RQ3: What demand response mechanisms can mitigate the synchronization risks posed by simple TOU tariffs?
1.6. Methodological Approach
- Data Collection and Preprocessing. Experimental data from 764 charging points were collected over six months, resulting in more than 2.1 million charging sessions that underwent comprehensive preprocessing and quality assurance protocols.
- Model Development. An Agent-Based Model (ABM) framework was developed, featuring heterogeneous agents, calibrated behavioral functions, and Monte Carlo-based uncertainty propagation, utilizing validated statistical distributions.
- Infrastructure Implementation. TimescaleDB hypertable architecture was implemented, featuring continuous aggregates, compression policies, and query optimization for datasets comprising billions of records.
- Scenario Analysis. An evaluation of three scenarios (conservative, baseline, and optimistic cases) was conducted with comprehensive uncertainty quantification.
1.7. Document Structure
2. Materials and Methods
2.1. Theoretical Foundations of Agent-Based Modelling
2.1.1. Complex Adaptive Systems Theory
- Internal State: State of Charge (SoC), location, and energy requirement.
- Decision Rules: When to initiate charging; duration of charging.
- Interactions: Competition for charging points; response to price signals.
2.1.2. Game Theory and Nash Equilibrium
- is the perceived cost for user i to initiate charging at time t.
- is the cost of electricity per kWh at time t.
- is the total energy required by user i’s vehicle.
- α is the user’s price sensitivity coefficient.
- is a function representing the non-monetary cost of delaying the charge.
- β is the inconvenience aversion coefficient.
- represents an imperative need to charge.
- γ is the weight of the specified urgency.
2.2. Data Sources and Collection Protocol
2.2.1. Primary Data Sources
2.2.2. Electric Vehicle Catalogue
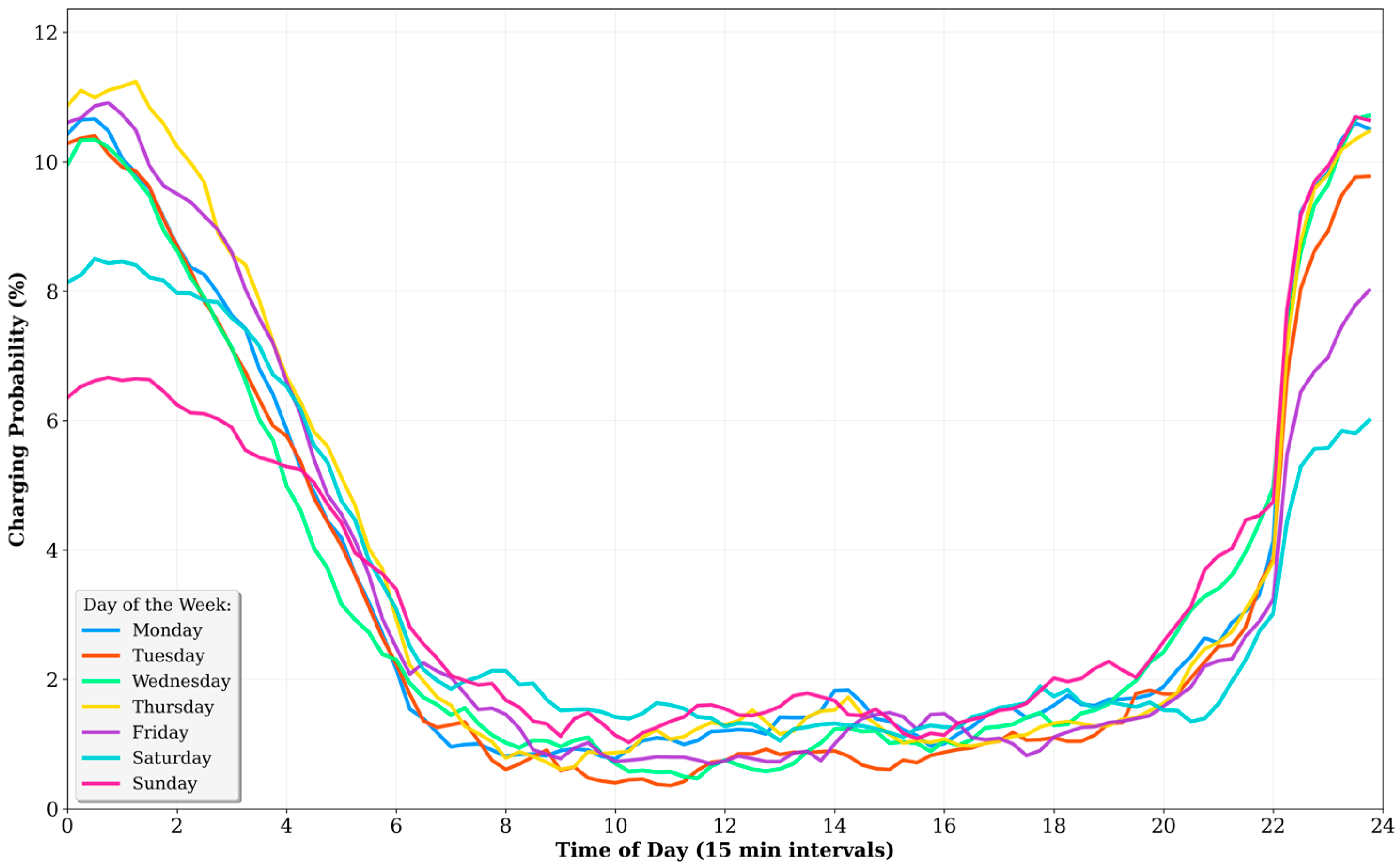
2.2.3. Daily Charging Probability Profiles
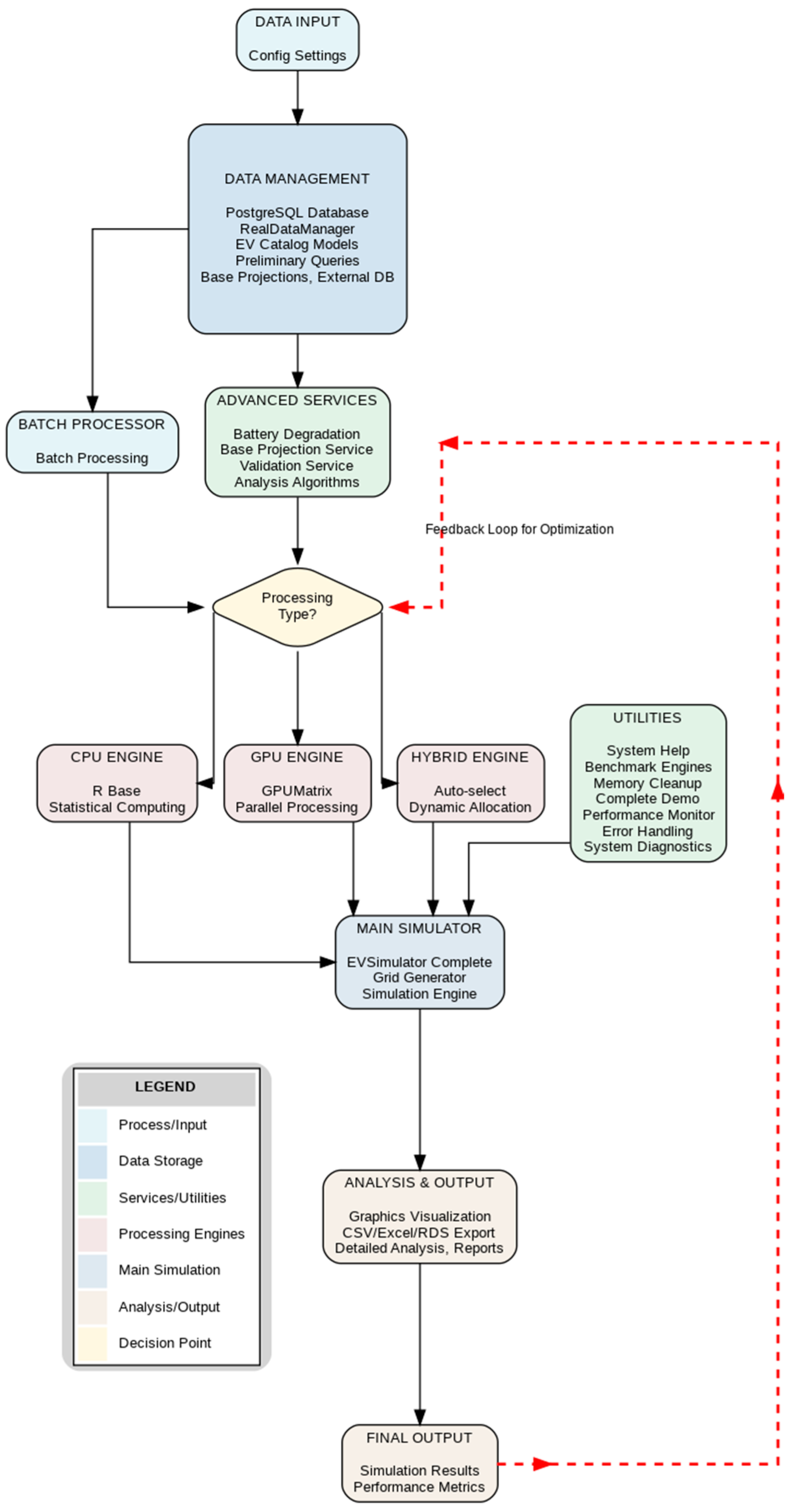
2.3. Computational Architecture for Big Data
Database Selection and Configuration
- Partitioned Hypertables. Temporal partitioning by day with 24-h chunks.
- Continuous Aggregates. Pre-calculation of demand metrics per time interval.
- Adaptive Compression. Compression algorithms that achieve 91% compression ratios.
- Optimized Indexing. BRIN indexes are used for temporal queries, while B-tree indexes are utilized for metadata.
2.4. Dynamic Coincidence Factor
2.5. Software Implementation and Computational Framework
- -
- R6 (v2.5.1) for object-orientated architecture.
- -
- data. table (v1.14.8) for high-performance data processing.
- -
- future/furrr (v1.33.0) for parallel processing.
- -
- RPostgreSQL (v0.7-5) for TimescaleDB connectivity.
- -
- GPUmatrix (v1.0.0) for GPU acceleration (optional).
3. Results
3.1. Computational Performance and System Validation
- Compression: 91% reduction in storage.
- Queries: <2 ms response time for typical aggregate queries.
- Robustness: Successful processing of 5844 daily batches without failure.
3.2. Model Validation
- MAPE: 4.2 ± 0.8%
- RMSE: 12.3 MW
- R2: 0.967
- nRMSE: 0.34
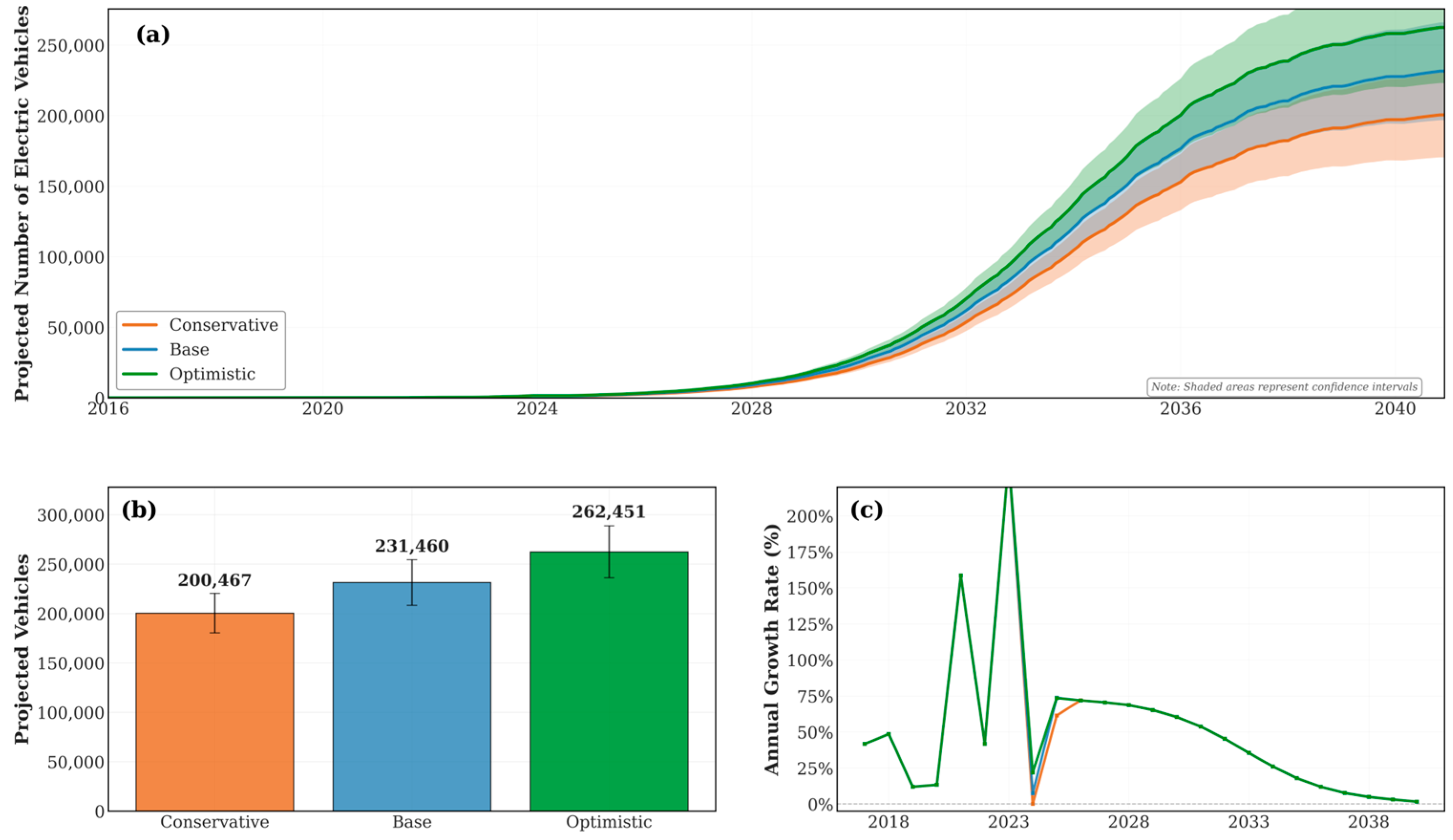
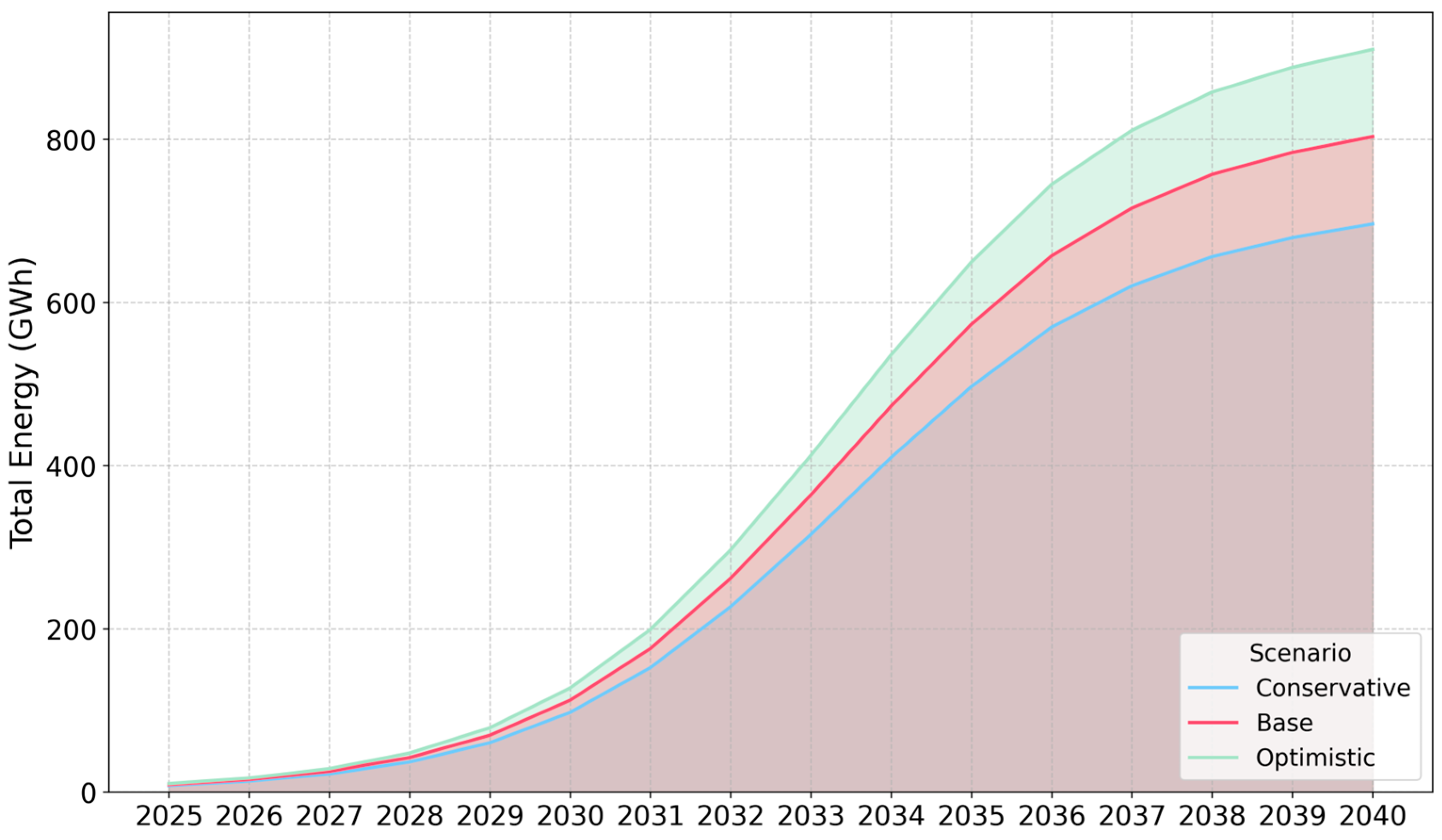
3.3. Energy Demand Projections
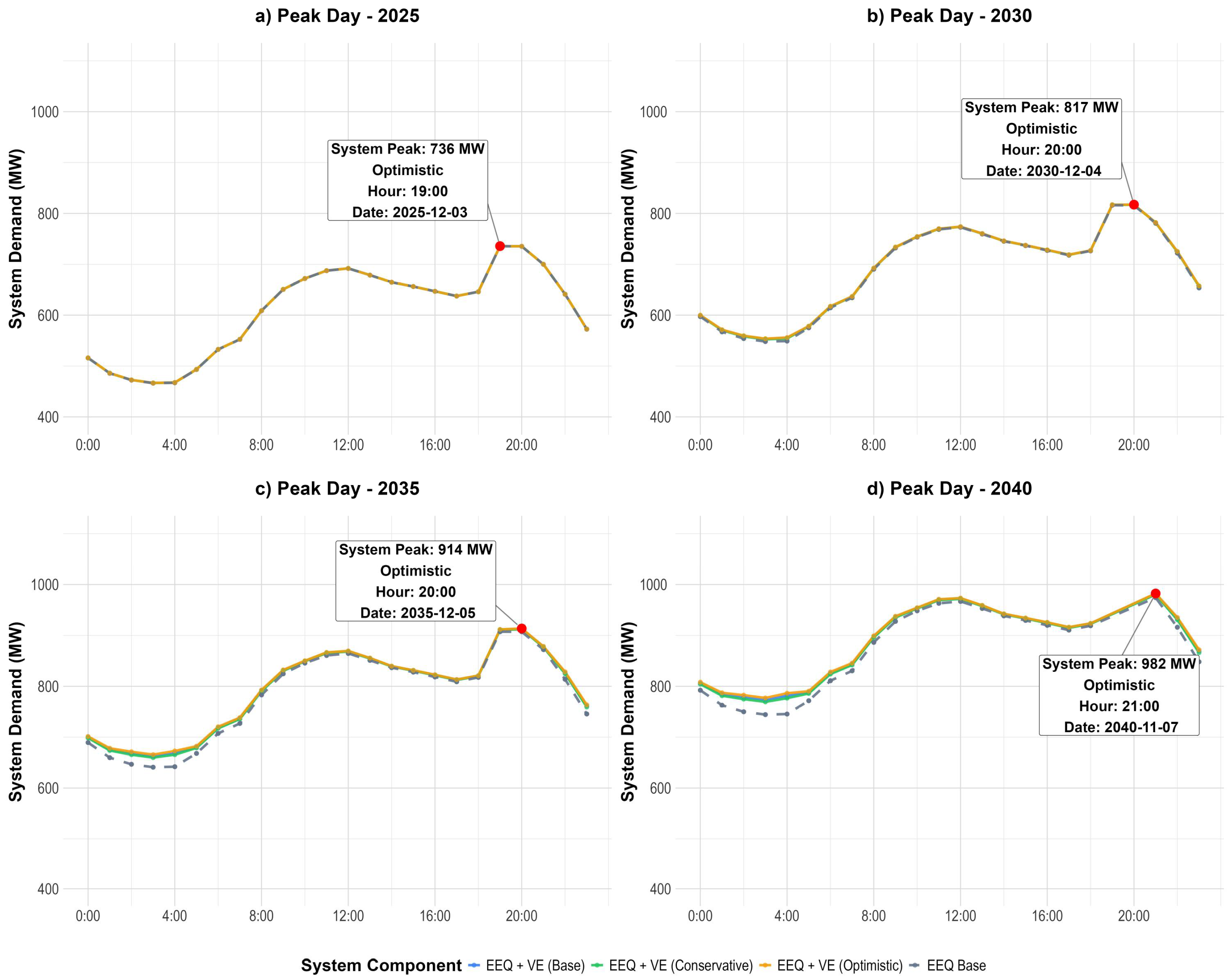
3.4. Impact on the Existing Electrical System
- 2025. The impact of EV charging on the system’s demand profile is negligible. The combined demand curve (EEQ + EV) is indistinguishable from the baseline curve.
- 2030. An incipient yet discernible impact is observed. The EV load manifests as a slight increase in demand during the overnight valley period (00:00 to 06:00), without altering the time or magnitude of the system’s peak.
- 2035. The impact has become significant. The addition of the EV demand generates a pronounced secondary peak in the early morning (04:00), constituting an apparent “valley-filling” effect.
- 2040. The valley-filling effect intensifies. The early morning EV demand is fully realized, creating an overnight peak that drastically reduces the difference between the system’s valley and peak. Nevertheless, the absolute system peak remains in the evening (21:00), reaching 981 MW in the Baseline scenario.
3.5. Temporal and Spatial Distribution
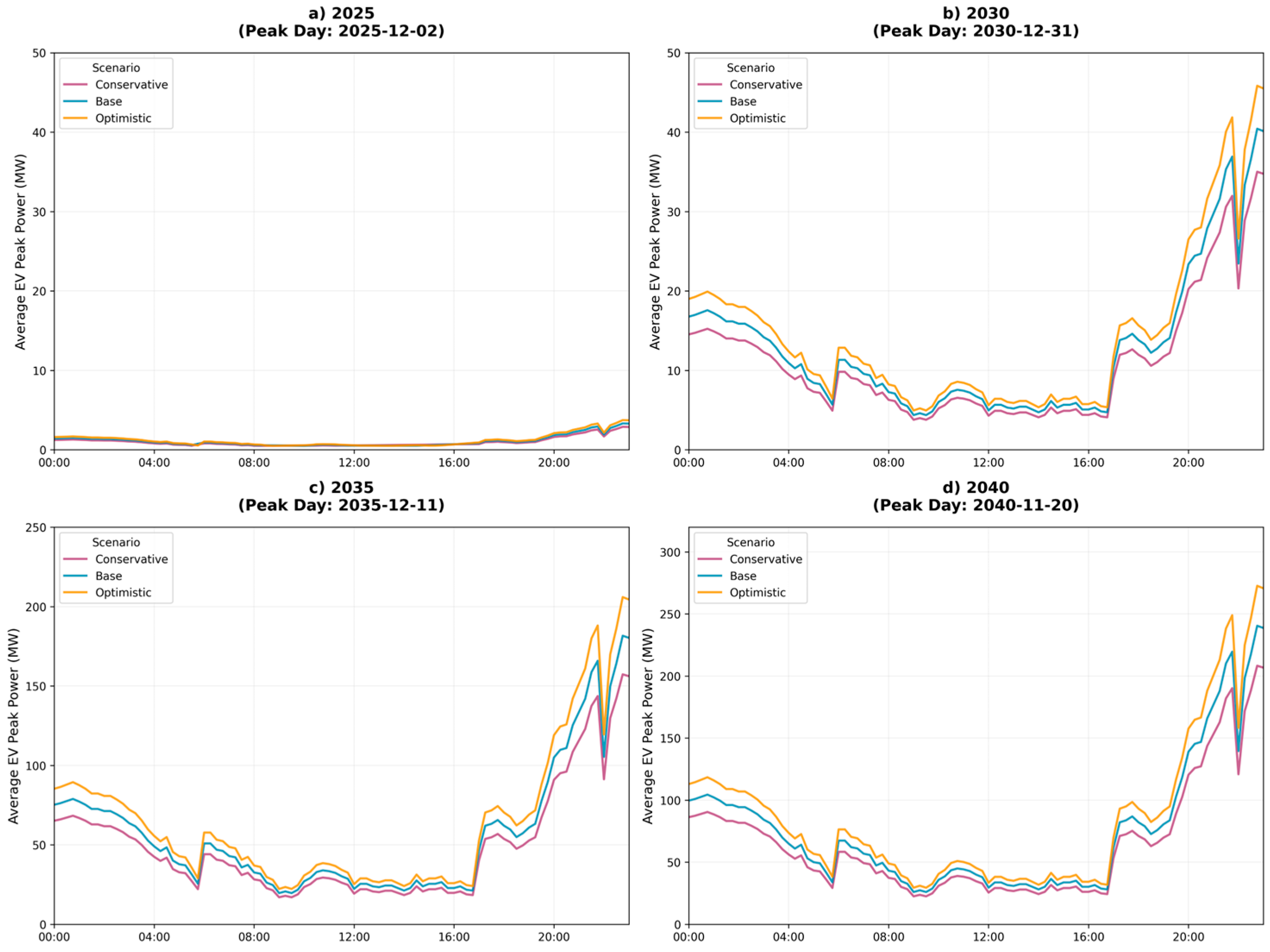
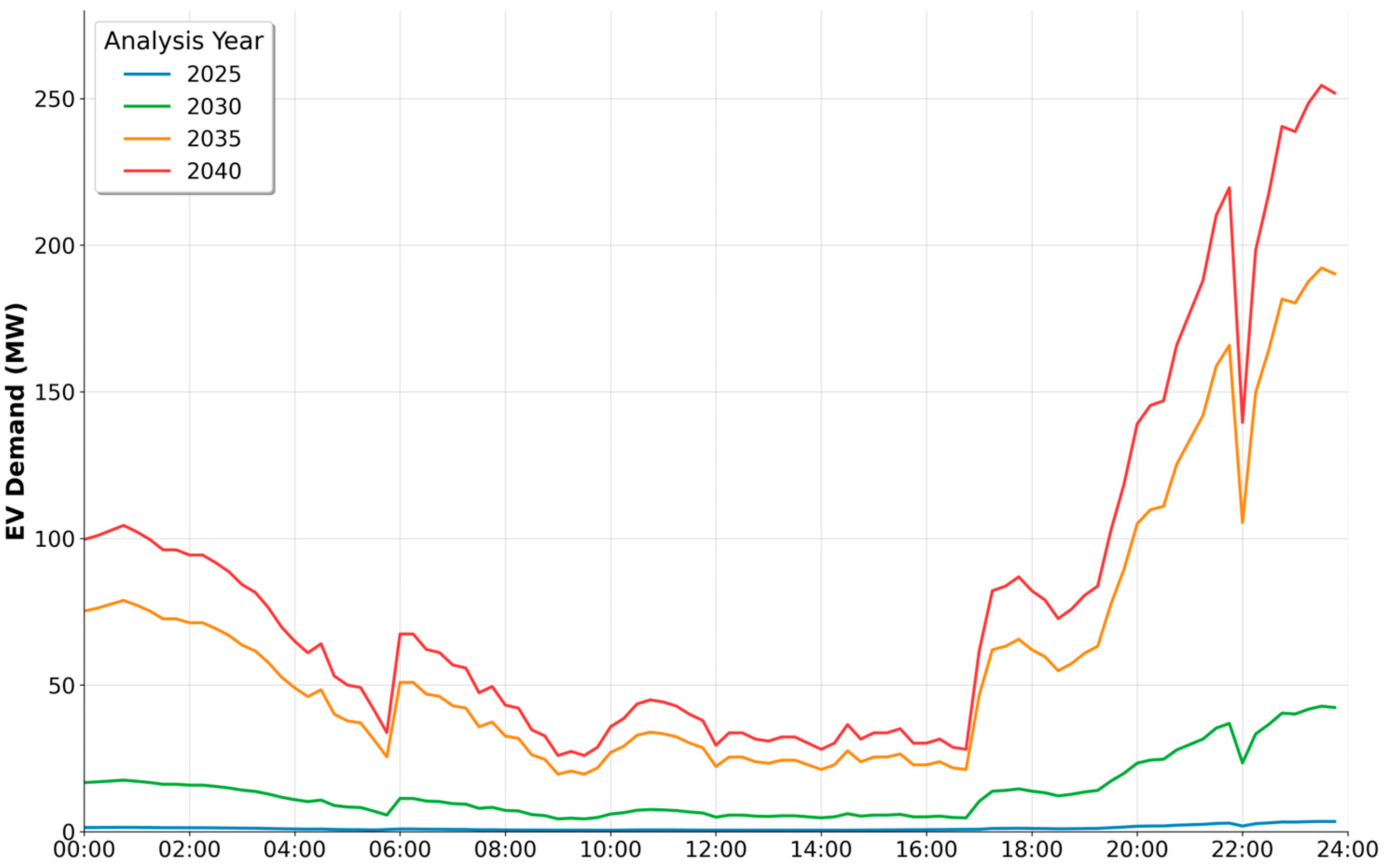
3.6. Temporal Evolution on Annual Peak Days
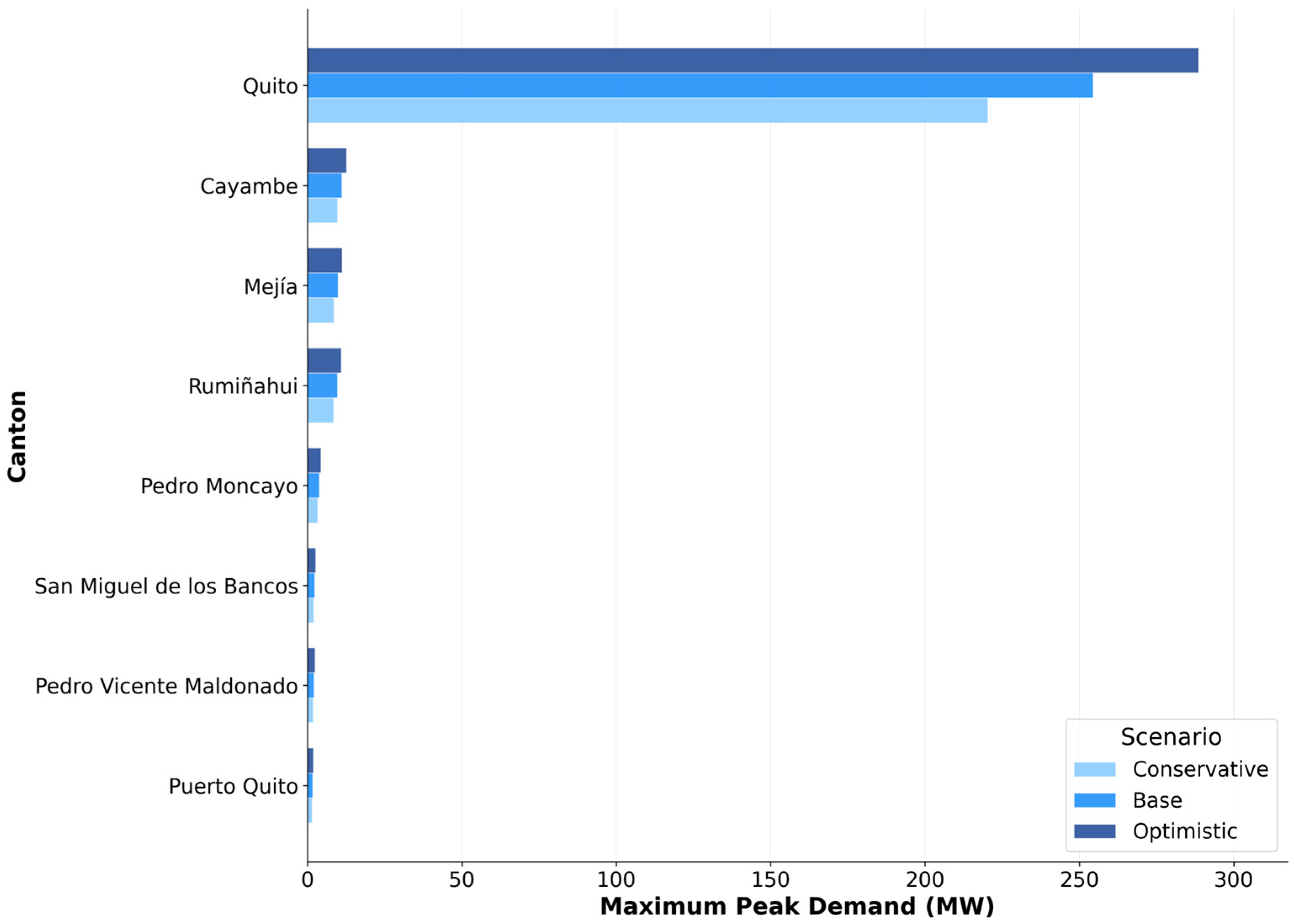
3.7. Spatial Distribution of Demand
- Quito Canton: Accounts for 85% of the total demand (255 MW in the baseline scenario).
- Other Cantons: Each account for less than 20 MW, even in the optimistic scenario.
3.8. Characterization of the ‘Cliff Effect’
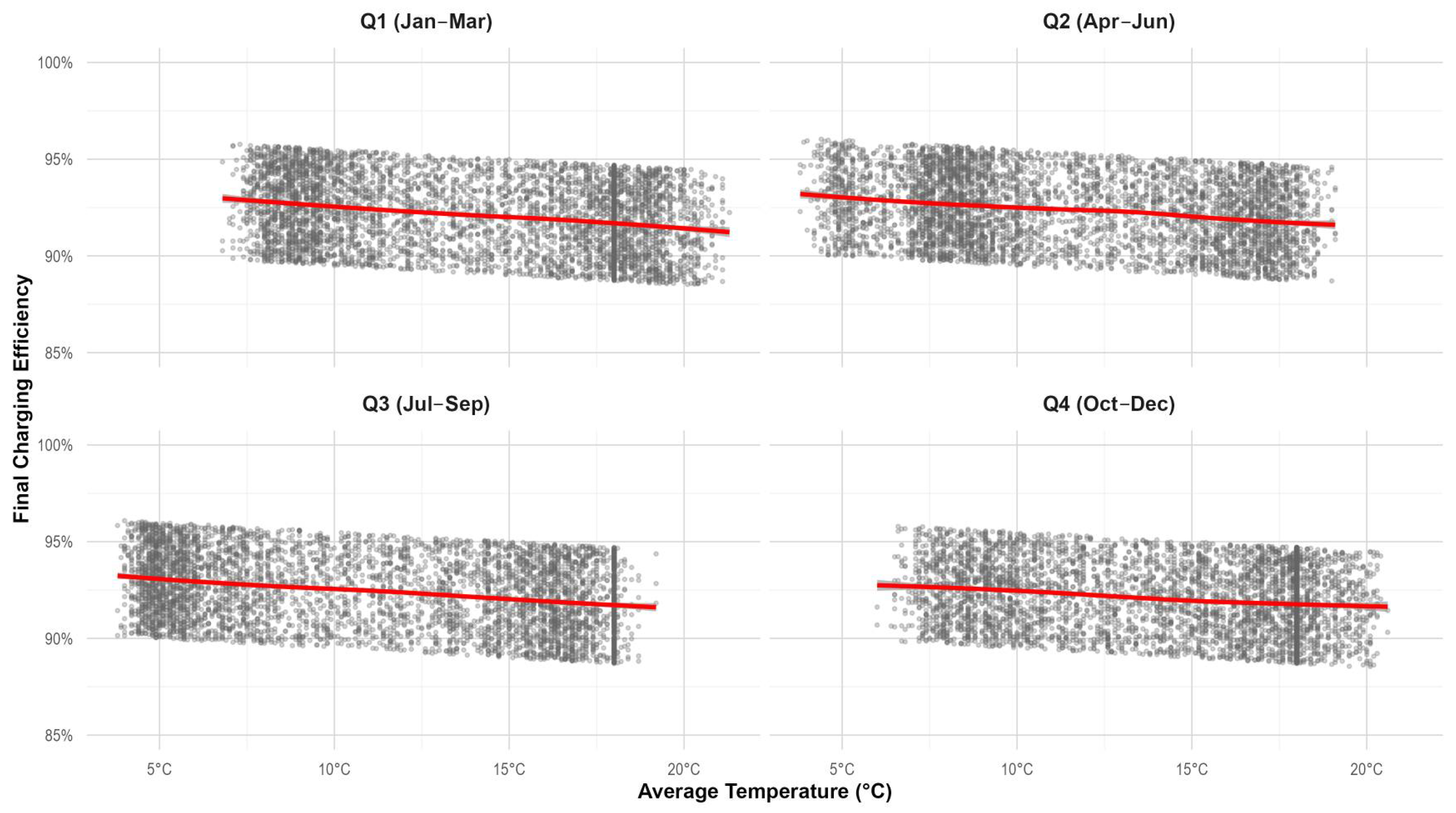
3.9. Thermal and Altitudinal Effects
4. Discussion
4.1. Comparison with Alternative Methodological Approaches
4.2. Implications for Infrastructure Planning
4.3. Specific Contributions for High-Altitude Cities
4.4. Validation of Coincidence Factors
4.5. Physical Layer Constraints and Their Relevance for Long-Term Demand Modeling
5. Conclusions
5.1. Answering the Research Questions and Hypothesis
- Answer: The developed methodological framework provides actionable insights by accurately quantifying future demand (a peak of 255 MW and 800 GWh annually by 2040), identifying and measuring previously underestimated systemic risks (the “cliff effect” which amplifies peak demand by 32%), and validating the effectiveness of specific mitigation strategies (smart charging reduces it by 18%). Big Data architecture is the enabling component that makes this metropolitan-scale simulation computationally feasible, processing data at 2398.7 records per second.
- Answer: For the year 2040, the model projects a peak demand in the baseline scenario of 255 MW, with a 95% confidence interval establishing the probabilistic bounds between 240 MW and 270 MW. The conservative and optimistic scenarios set the outer bounds of the planning range at 220.44 MW and 288.60 MW, respectively.
- Answer: A consistent negative correlation between ambient temperature and charging efficiency has been quantified. The influence is estimated as an efficiency reduction of −0.1% per degree Celsius increase in temperature, providing a specific and validated correction parameter for planning in Andean cities.
- Answer: The most effective demand response mechanism to mitigate synchronization risk is smart charging management that incorporates stochastic (randomized) charging initiation. This strategy effectively desynchronizes aggregate demand and has been shown to reduce peak demand by 18 ± 2.5% compared to the baseline.
- Answer: The central hypothesis is strongly confirmed. The simulation demonstrates that advanced DSM strategies, through randomized charging initiation, reduce peak demand by 18 ± 2.5%, exceeding the established 15% threshold and thereby validating the core premise of the research.
5.2. Key Findings
- Proven Methodological Scalability: The ABM-TimescaleDB architecture successfully processes over 13.5 million records with a throughput of 2398.7 records per second, demonstrating its viability for metropolitan-scale applications.
- Precise Risk Quantification: The documented “cliff effect” (a 32% increase in peak demand) provides quantitative evidence for implementing smart management policies over simple TOU tariffs.
- Validated Predictive Accuracy: A MAPE of 4.2 ± 0.8% surpasses established benchmarks for aggregate models and approaches the standards for individual applications, providing quantitative validation that previous studies had not established.
- Specific High-Altitude Parameters: Thermal correction factors (−0.1%/°C) and a dynamic coincidence factor provide refined technical tools for planning in Andean cities, complementing and improving upon previous frameworks.
5.3. Implementation Recommendations
- Utilize the optimistic scenario projections (289 MW) to avoid infrastructure undersizing, which represents an additional investment of $200–400 million but prevents future disruptions.
- Implement randomized charging systems instead of simple time-of-use (TOU) tariffs to prevent mass synchronization effects. Their effectiveness depends on managed implementation to avoid the “cliff effect,” as demonstrated in this study.
- Establish telemetry systems for the continuous validation and calibration of coincidence factors as EV penetration evolves.
- Integrate thermal effects (−0.1%/°C) into capacity planning, particularly for seasonal demand peaks.
5.4. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABM | Agent-Based Modelling (Agent-Based Modelling) |
| API | Application Programming Interface |
| AEADE | Asociación de Empresas Automotrices del Ecuador |
| BMS | Battery Management System |
| CF | Coincidence Factor |
| DR | Demand Response |
| DSM | Demand Side Management |
| EEQ | Empresa Eléctrica Quito |
| ENEM | Estrategia Nacional de Electromovilidad |
| FC | Coincidence Factor |
| GPU | Graphics Processing Unit |
| IC | Confidence Interval |
| INAMHI | Instituto Nacional de Meteorología e Hidrología del Ecuador |
| LFP | Lithium Iron Phosphate |
| LLM | Large Language Model |
| MAPE | Mean Absolute Percentage Error |
| NCM | Nickel Cobalt Manganese |
| NREL | National Renewable Energy Laboratory |
| RDBMS | Relational Database Management System |
| RMSE | Root Mean Square Error |
| SoC | State of Charge |
| SoH | State of Health |
| SQL | Structured Query Language |
| TOU | Time of Use |
| TSDB | Time Series Database |
| UNESCO | United Nations Educational, Scientific and Cultural Organisation |
| V2G | Vehicle-to-Grid |
| EV | Electric Vehicle |
Appendix A
Appendix A.1
- Off-Peak. From 00:00 to 06:00 and from 22:00 to 24:00, there is a reduced cost of $0.05/kWh.
- Standard. From 06:00 to 18:00, with an intermediate rate of $0.08/kWh.
- Peak. From 18:00 to 22:00, the highest rate of $0.10/kWh is applied to discourage charging during these peak demand hours.
- Off-Peak. An extended period from 00:00 to 18:00 and from 22:00 to 24:00, maintaining the minimum rate of $0.05/kWh.
- Peak. The same period, from 18:00 to 22:00, is maintained at the $0.10/kWh rate, coinciding with the residential demand peak.
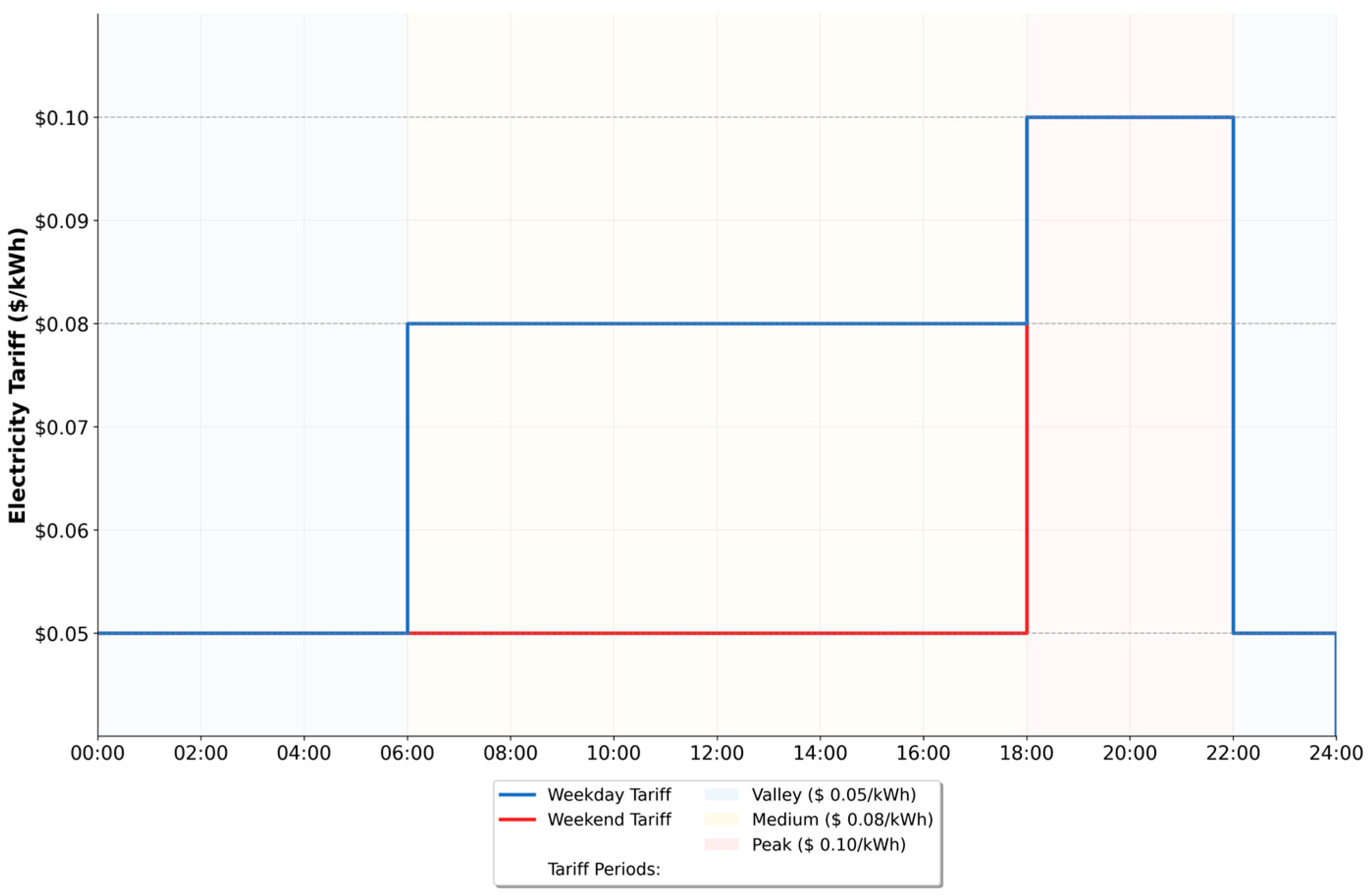
Appendix A.2

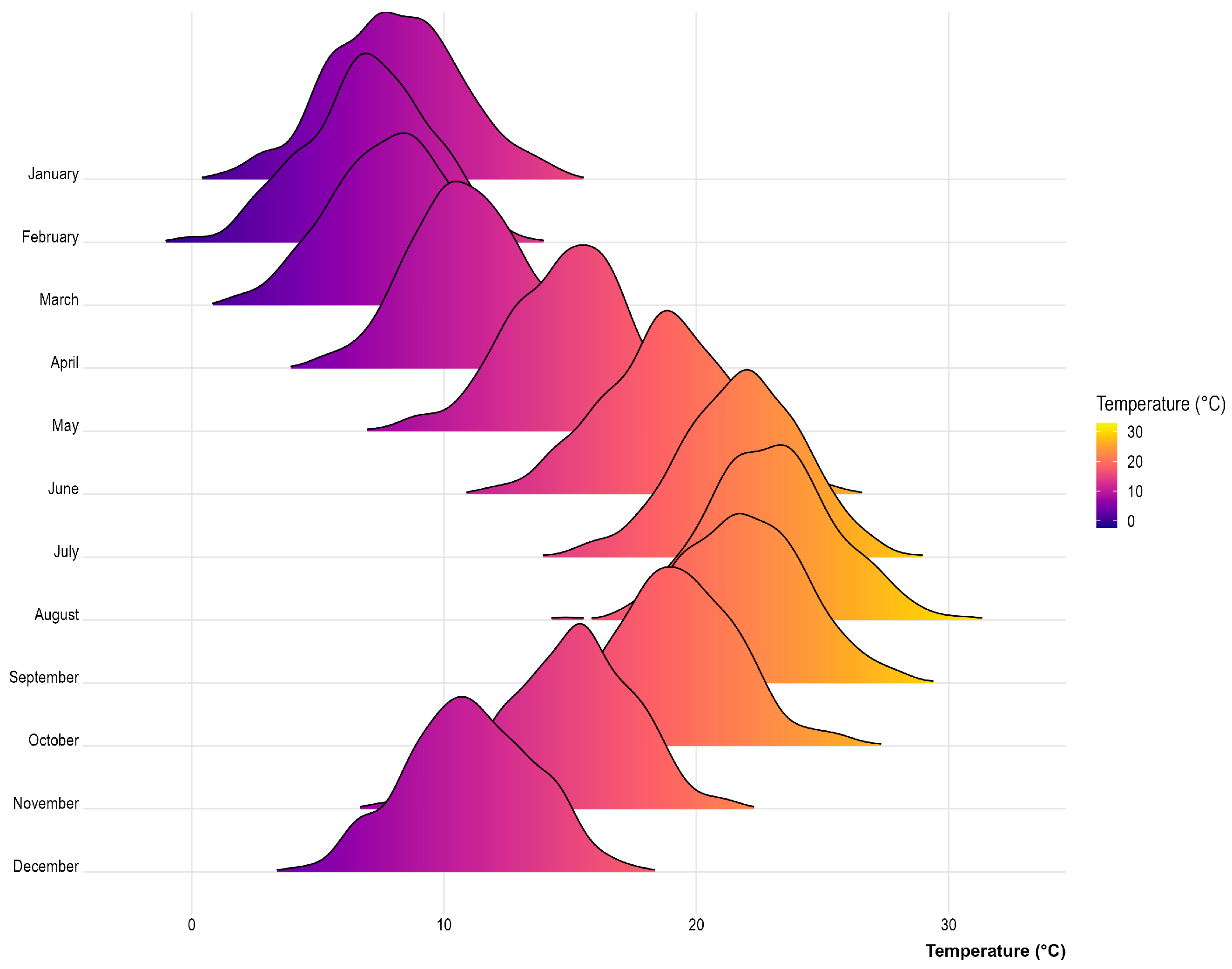
Appendix A.3
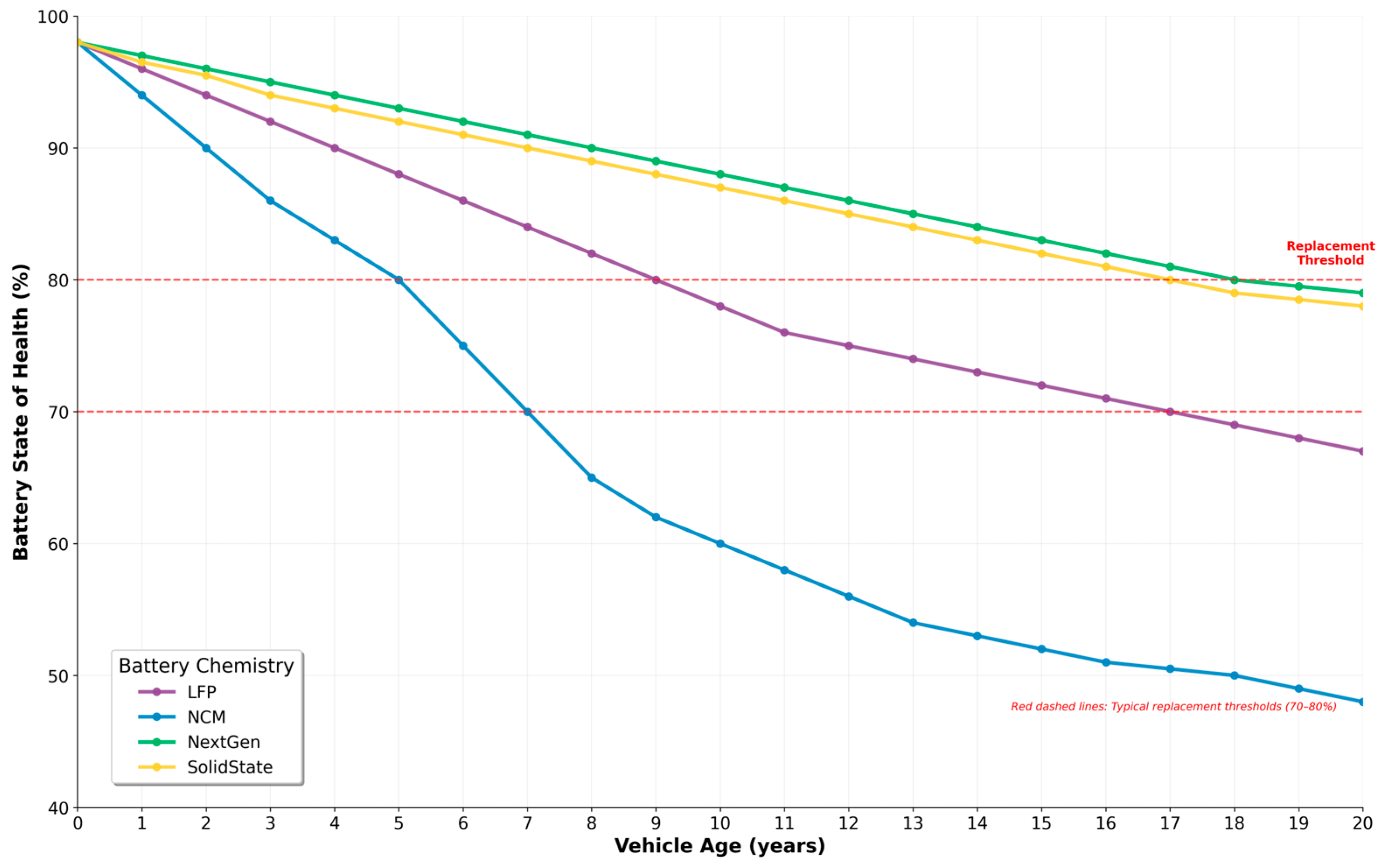
Appendix A.4
- NCM (Nickel-Manganese-Cobalt) Battery. It exhibits the most pronounced degradation rate, dropping below the 80% replacement threshold in approximately the fourth year of use and reaching less than 50% of its original capacity by the end of 20 years.
- LFP (Lithium Iron Phosphate) Battery. It offers considerably greater durability than NCM. Its SoH remains above 80% until approximately year 11 and crosses the 70% threshold around year 18.
- NextGen and Solid-State Batteries. Both emerging technologies exhibit minimal degradation and superior performance. Their profiles are nearly identical, maintaining a SoH near 80% even after 20 years, indicating an extended lifespan that far exceeds current standards.
References
- González, L.G.; Cordero-Moreno, D.; Espinoza, J.L. Public transportation with electric traction: Experiences and challenges in an Andean city. Renew. Sustain. Energy Rev. 2021, 141, 110768. [Google Scholar] [CrossRef]
- Dávila-Sacoto, M.; Toledo, M.A.; Hernández-Callejo, L.; González, L.G.; Alvarez Bel, C.; Zorita-Lamadrid, Á.L. Location of Electric Vehicle Charging Stations in Inter-Andean Corridors Considering Road Altitude and Nearby Infrastructure. Sustainability 2023, 15, 16582. [Google Scholar] [CrossRef]
- Sánchez Loor, L.I. Modelo Para la Proyección de Vehículos Eléctricos Particulares en el Ecuador y Sus Requerimientos de Demanda, Utilizando Patrones de Crecimiento Logístico y Simulación de Montecarlo. Master’s Thesis, Escuela Politecnica Nacional, Quito, Ecuador, 2022. Available online: https://bibdigital.epn.edu.ec/handle/15000/23435 (accessed on 12 August 2025).
- Cal y Mayor y Asociados. Plan Maestro de Movilidad Sostenible del Distrito Metropolitano de Quito–PMMS DMQ (2023–2042); Cal y Mayor y Asociados: Quito, Ecuador, 2024. [Google Scholar]
- HINICIO. Estrategia Nacional de Electromovilidad para Ecuador; BID: Washington, DC, USA, 2021. [Google Scholar]
- Ministerio de Energia y Minas. Plan Maestro de Electricidad 2023–2032; BID: Washington, DC, USA, 2024. [Google Scholar]
- Liu, J.; Zhuge, C.; Tang, J.H.C.G.; Meng, M.; Zhang, J. A spatial agent-based joint model of electric vehicle and vehicle-to-grid adoption: A case of Beijing. Appl. Energy 2022, 310, 118581. [Google Scholar] [CrossRef]
- Asociación de Empresas Automotrices del Ecuador. Anuario 2024; AEADE: Quito, Ecuador, 2024; Available online: https://www.aeade.net/wp-content/uploads/2025/03/AEADE-ANUARIO-2024_digital.pdf (accessed on 17 July 2025).
- Yu, Q.; Wang, Z.; Song, Y.; Shen, X.; Zhang, H. Potential and flexibility analysis of electric taxi fleets V2G system based on trajectory data and agent-based modeling. Appl. Energy 2024, 355, 122323. [Google Scholar] [CrossRef]
- Brady, J.; O’Mahony, M. Travel to work in Dublin. The potential impacts of electric vehicles on climate change and urban air quality. Transp. Res. Part Transp. Environ. 2011, 16, 188–193. [Google Scholar] [CrossRef]
- Flath, C.M.; Ilg, J.P.; Gottwalt, S.; Schmeck, H.; Weinhardt, C. Improving Electric Vehicle Charging Coordination Through Area Pricing. Transp. Sci. 2014, 48, 619–634. [Google Scholar] [CrossRef]
- Foley, A.; Tyther, B.; Calnan, P.; Ó Gallachóir, B. Impacts of Electric Vehicle charging under electricity market operations. Appl. Energy 2013, 101, 93–102. [Google Scholar] [CrossRef]
- Grunewald, P.; Diakonova, M. Flexibility, dynamism and diversity in energy supply and demand: A critical review. Energy Res. Soc. Sci. 2018, 38, 58–66. [Google Scholar] [CrossRef]
- Helmus, J.R.; Lees, M.H.; Van Den Hoed, R. A data driven typology of electric vehicle user types and charging sessions. Transp. Res. Part C Emerg. Technol. 2020, 115, 102637. [Google Scholar] [CrossRef]
- Xing, Y.; Li, F.; Sun, K.; Wang, D.; Chen, T.; Zhang, Z. Multi-type electric vehicle load prediction based on Monte Carlo simulation. Energy Rep. 2022, 8, 966–972. [Google Scholar] [CrossRef]
- Hashemi, S.; Østergaard, J. Methods and strategies for overvoltage prevention in low voltage distribution systems with PV. IET Renew. Power Gener. 2017, 11, 205–214. [Google Scholar] [CrossRef]
- Lojowska, A.; Kurowicka, D.; Papaefthymiou, G.; Van Der Sluis, L. Stochastic Modeling of Power Demand Due to EVs Using Copula. IEEE Trans. Power Syst. 2012, 27, 1960–1968. [Google Scholar] [CrossRef]
- Maigha; Crow, M.L. Cost-Constrained Dynamic Optimal Electric Vehicle Charging. IEEE Trans. Sustain. Energy 2017, 8, 716–724. [Google Scholar] [CrossRef]
- Prehofer, C.; Mehmood, S. Big Data Architectures for Vehicle Data Analysis. In Proceedings of the 2020 IEEE International Conference on Big Data (Big Data), Atlanta, GA, USA, 10–13 December 2020; pp. 3404–3412. [Google Scholar] [CrossRef]
- Wehrmeister, K.; Pastor, A.; Carreras Rodriguez, L.; Monti, A. Big Data Reference Architecture for the Energy Sector. Sustainability 2025, 17, 6488. [Google Scholar] [CrossRef]
- Liu, R.; Yuan, J.; Huang, X. Benchmarking Time Series Databases with IoTDB-Benchmark for IoT Scenarios. arXiv 2019. [Google Scholar] [CrossRef]
- Li, Y.; Jenn, A. Impact of electric vehicle charging demand on power distribution grid congestion. Proc. Natl. Acad. Sci. USA 2024, 121, e2317599121. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, D.; Dehghanian, P.; Tian, Y.; Hong, T. Aggregated Electric Vehicle Load Modeling in Large-Scale Electric Power Systems. IEEE Trans. Ind. Appl. 2020, 56, 5796–5810. [Google Scholar] [CrossRef]
- Birk Jones, C.; Vining, W.; Lave, M.; Haines, T.; Neuman, C.; Bennett, J.; Scoffield, D.R. Impact of Electric Vehicle customer response to Time-of-Use rates on distribution power grids. Energy Rep. 2022, 8, 8225–8235. [Google Scholar] [CrossRef]
- Deori, L.; Margellos, K.; Prandini, M. On the connection between Nash equilibria and social optima in electric vehicle charging control games. IFAC-Pap. 2017, 50, 14320–14325. [Google Scholar] [CrossRef]
- Torres-Moscoso, D.F.; Cordero-Moreno, D.G.; Tonon-Ordóñez, L.B.; Fernández-Palomeque, E.E. Análisis Financiero para la Implementación de un Bus Eléctrico Urbano en la Ciudad de Cuenca. Econ. Negocios 2022, 13, 133–149. [Google Scholar] [CrossRef]
- Maita Jaramillo, L.; Díaz-Sinche, D. Advancing Electric Mobility in Andean Countries: A Systematic Review and Case Study of Ecuador. Sustainability 2025, 17, 8075. [Google Scholar] [CrossRef]
- Amara-Ouali, Y.; Goude, Y.; Massart, P.; Poggi, J.-M.; Yan, H. A Review of Electric Vehicle Load Open Data and Models. Energies 2021, 14, 2233. [Google Scholar] [CrossRef]
- Buzna, L.; De Falco, P.; Ferruzzi, G.; Khormali, S.; Proto, D.; Refa, N.; Straka, M.; Van Der Poel, G. An ensemble methodology for hierarchical probabilistic electric vehicle load forecasting at regular charging stations. Appl. Energy 2021, 283, 116337. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, L.; Ouyang, M.; Wang, H.; Lu, L.; Li, J.; Li, Z. Optimal decentralized valley-filling charging strategy for electric vehicles. Energy Convers. Manag. 2014, 78, 537–550. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, M.; Hao, H.; Johnson, L.; Wang, H.; Hao, H. Plug-in electric vehicle market penetration and incentives: A global review. Mitig. Adapt. Strateg. Glob. Chang. 2015, 20, 777–795. [Google Scholar] [CrossRef]
- Yuan, J.; Zeng, X.; Zhou, J.; Li, J.; Lv, J.; Chen, R.; Chen, K.; Yang, W.; Zhang, Y. Data-driven real-time home energy management system based on adaptive dynamic programming. Electr. Power Syst. Res. 2025, 238, 111055. [Google Scholar] [CrossRef]
- Ruan, J.; Liu, G.; Qiu, J.; Liang, G.; Zhao, J.; He, B.; Wen, F. Time-varying price elasticity of demand estimation for demand-side smart dynamic pricing. Appl. Energy 2022, 322, 119520. [Google Scholar] [CrossRef]
- Zhu, X.; Nie, X.; Liu, J. Time Series Database Optimization Based on InfluxDB. In Proceedings of the 2023 International Conference on Power, Electrical Engineering, Electronics and Control (PEEEC), Athens, Greece, 25–27 September 2023; pp. 879–885. [Google Scholar] [CrossRef]
- Hayajneh, H.S.; Bani Salim, M.N.; Bashetty, S.; Zhang, X. Optimal Planning of Battery-Powered Electric Vehicle Charging Station Networks. In Proceedings of the 2019 IEEE Green Technologies Conference(GreenTech), Lafayette, LA, USA, 3–6 April 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Chen, H.; Liu, G.F.; Zhang, D.; Qin, T.; Sun, X.K. A study of performance comparison of databases for HALF data archiving system. J. Instrum. 2023, 18, P12015. [Google Scholar] [CrossRef]
- Rudakov, V.; Timur, M.; Yedilkhan, A. Comparison of Time Series Databases. In Proceedings of the 2023 17th International Conference on Electronics Computer and Computation (ICECCO), Kaskelen, Kazakhstan, 1–2 June 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Bollerslev, J.; Andersen, P.B.; Jensen, T.V.; Marinelli, M.; Thingvad, A.; Calearo, L.; Weckesser, T. Coincidence Factors for Domestic EV Charging From Driving and Plug-In Behavior. IEEE Trans. Transp. Electrif. 2022, 8, 808–819. [Google Scholar] [CrossRef]
- Opstad, A.; Bekken, B.H.; Nygård, H.S.; Doorman, G.; Sevdari, K. Flexibility from Electric Vehicles-Residential Charging Coincidence Factors in Norway; CIGRE: Paris, France, 2024. [Google Scholar]
- Sanchez-Loor, I. Ev-Demand-Modeling-Abm-Timescaledb. Available online: https://github.com/ivelec1981/ev-demand-modeling-abm-timescaledb.git (accessed on 12 August 2025).
- Aldossary, M.; Alharbi, H.A.; Ayub, N. Optimizing Electric Vehicle (EV) Charging with Integrated Renewable Energy Sources: A Cloud-Based Forecasting Approach for Eco-Sustainability. Mathematics 2024, 12, 2627. [Google Scholar] [CrossRef]
- Chaudhari, K.; Kandasamy, N.K.; Krishnan, A.; Ukil, A.; Gooi, H.B. Agent-Based Aggregated Behavior Modeling for Electric Vehicle Charging Load. IEEE Trans. Ind. Inform. 2019, 15, 856–868. [Google Scholar] [CrossRef]
- Islam, E.; Vijayagopal, R.; Rousseau, A. A Comprehensive Simulation Study to Evaluate Future Vehicle Energy and Cost Reduction Potential; Argonne National Laboratory (ANL): Argonne, IL, USA, 2022; p. ANL/ESD--22/6, 2204856, 179337. [CrossRef]
- Lee, D.; Reinicke, N.; Wood, E.; Burrell, E. Electric Vehicle Infrastructure Projection Tool (Evi-Pro); National Renewable Energy Lab. (NREL): Golden, CO, USA, 2021. Available online: https://www.osti.gov/biblio/1764904 (accessed on 17 July 2025).
- Niu, S.; Yu, H.; Niu, S.; Jian, L. Power loss analysis and thermal assessment on wireless electric vehicle charging technology: The over-temperature risk of ground assembly needs attention. Appl. Energy 2020, 275, 115344. [Google Scholar] [CrossRef]


| Manufacturer | Model | Year | Class | Battery Capacity (kWh) | Battery Chemistry | AC Charging Power (kW) | WLTP Range (km) | Consumption (kWh/100 km) |
|---|---|---|---|---|---|---|---|---|
| BYD | Dolphin | 2024 | Compact | 44.9 | LFP | 7.0 | 340 | 13.1 |
| BYD | Seagull | 2024 | Compact | 38.9 | LFP | 6.6 | 305 | 12.1 |
| BYD | Yuan Plus v2 | 2024 | SUV | 60.5 | LFP | 7.0 | 430 | 14.1 |
| Nissan | Leaf v2 | 2024 | Compact | 39.0 | NCM | 6.6 | 270 | 14.1 |
| Kia | EV6 | 2024 | SUV | 74.0 | NCM | 11.0 | 491 | 15.0 |
| Leapmotor | T03 | 2024 | City | 37.0 | NCM | 6.6 | 300 | 12.3 |
| Chevrolet | Bolt EUV | 2024 | Compact | 65.0 | NCM | 11.0 | 416 | 15.1 |
| Dongfeng | Seres 3 | 2024 | SUV | 51.0 | NCM | 6.6 | 350 | 14.1 |
| JAC | E-JS4 | 2024 | SUV | 65.7 | NCM | 11.0 | 445 | 14.1 |
| Neta | V | 2024 | City | 38.5 | NCM | 6.6 | 318 | 12.1 |
| Leapmotor | C11 | 2024 | SUV | 90.0 | NCM | 11.0 | 550 | 16.1 |
| Skywell | BE11 | 2024 | SUV | 86.0 | NCM | 11.0 | 330 | 16.1 |
| Gen2-Premium | SUV | 2028 | SUV | 95.0 | NCM | 22.0 | 550 | 17.1 |
| Gen2-Mass | Sedan | 2028 | Sedan | 75.0 | LFP | 11.0 | 450 | 16.1 |
| Gen2-Urban | City | 2028 | City | 50.0 | Na-ion | 7.0 | 300 | 16.1 |
| Gen3-Premium | SUV | 2032 | SUV | 120.0 | SSB | 22.0 | 700 | 17.1 |
| Gen3-Mass | Sedan | 2032 | Sedan | 110.0 | NCM | 22.0 | 650 | 16.1 |
| Gen3-Urban | City | 2032 | City | 85.0 | LFP | 11.0 | 500 | 17.0 |
| Gen4-Premium | SUV | 2036 | SUV | 150.0 | SSB | 900 | 16.1 | |
| Gen4-Mass | Sedan | 2036 | Sedan | 90.0 | NCM | 550 | 16.1 | |
| Gen4-Urban | City | 2036 | City | 200.0 | Li-S |
| Key Metric (2040) | Conservative Case | Base Case | Optimistic Case |
|---|---|---|---|
| Total Annual Energy (GWh) | 700 | 800 | 870 |
| System Peak Demand (MW) | 220.44 | 254.52 | 288.60 |
| System Load Factor (%) | 36.2% | 35.8% | 34.4% |
| Avg. Coincidence Factor | 0.236 | 0.235 | 0.234 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Loor, I.; Ayala-Chauvin, M. Modeling of Electric Vehicle Energy Demand: A Big Data Approach to Energy Planning. Energies 2025, 18, 5429. https://doi.org/10.3390/en18205429
Sánchez-Loor I, Ayala-Chauvin M. Modeling of Electric Vehicle Energy Demand: A Big Data Approach to Energy Planning. Energies. 2025; 18(20):5429. https://doi.org/10.3390/en18205429
Chicago/Turabian StyleSánchez-Loor, Iván, and Manuel Ayala-Chauvin. 2025. "Modeling of Electric Vehicle Energy Demand: A Big Data Approach to Energy Planning" Energies 18, no. 20: 5429. https://doi.org/10.3390/en18205429
APA StyleSánchez-Loor, I., & Ayala-Chauvin, M. (2025). Modeling of Electric Vehicle Energy Demand: A Big Data Approach to Energy Planning. Energies, 18(20), 5429. https://doi.org/10.3390/en18205429







