Numerical Study of a Solar Dryer Prototype with Microencapsulated Phase Change Materials for Rice Drying †
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model
2.1.1. Air Flow Inside the Dryer
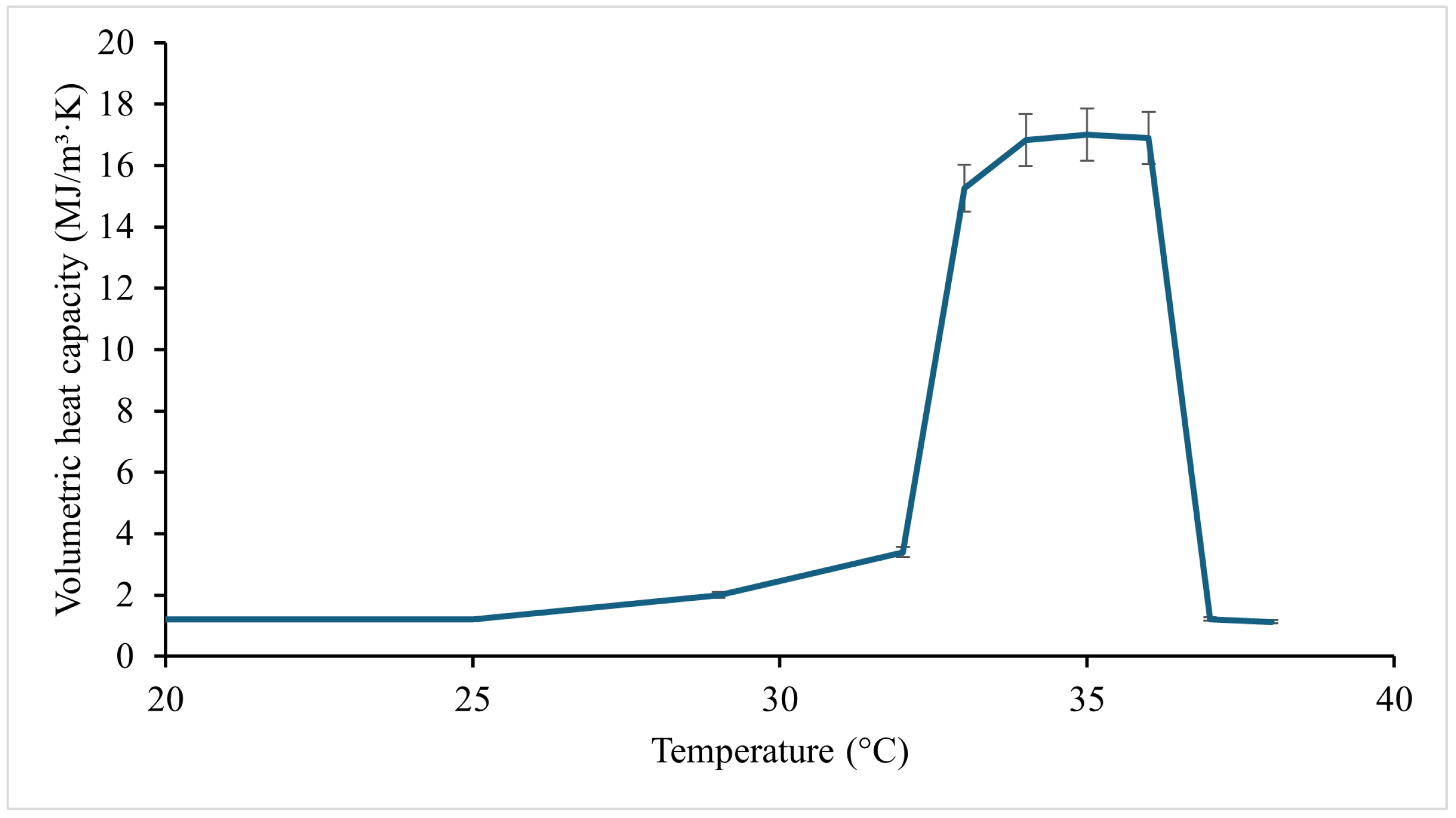
2.1.2. Microencapsulated Phase Change Material
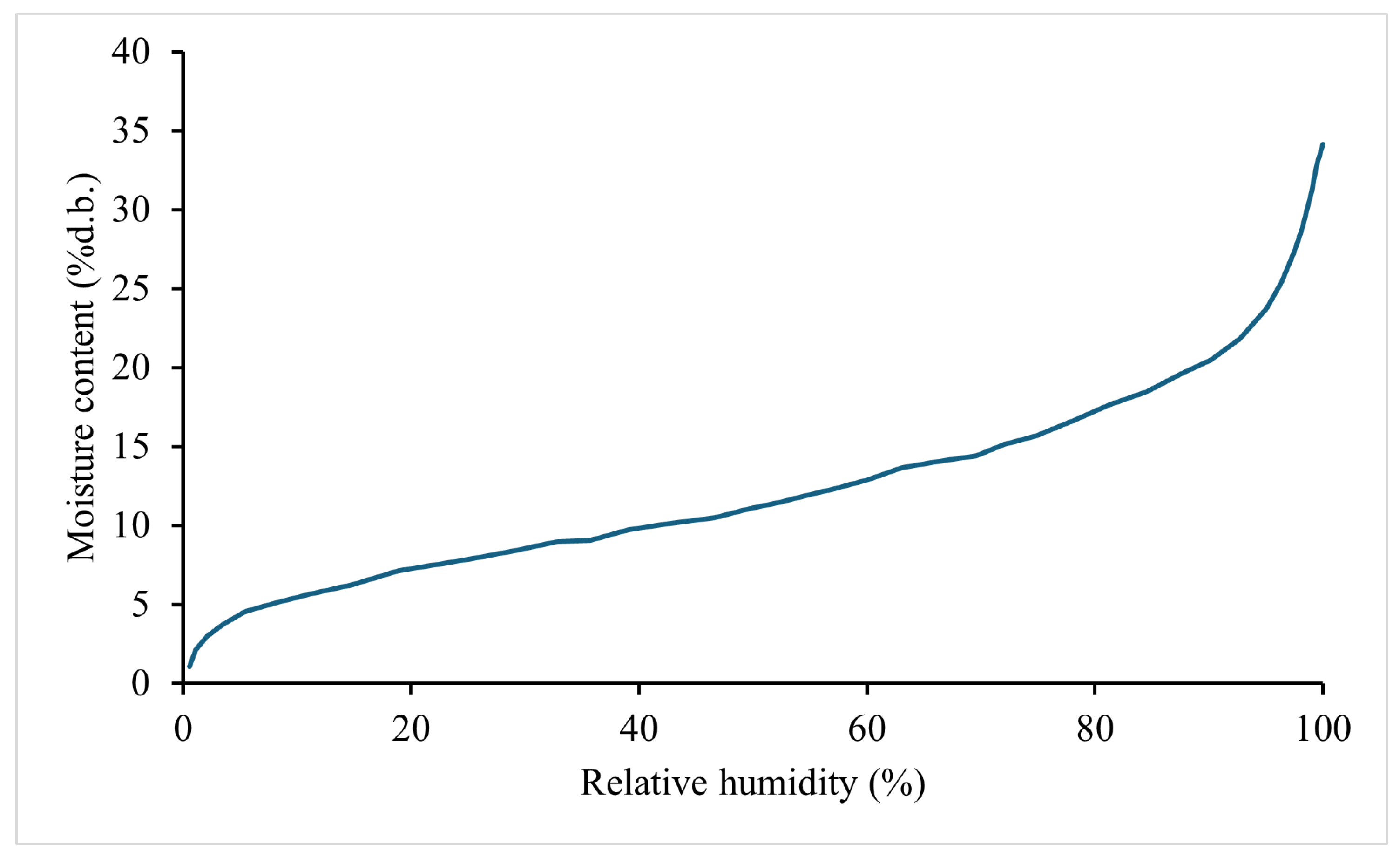
2.1.3. Rice Layer
2.1.4. Boundary and Initial Conditions
2.1.5. Numerical Methodology and Error Analysis
3. Results and Discussion
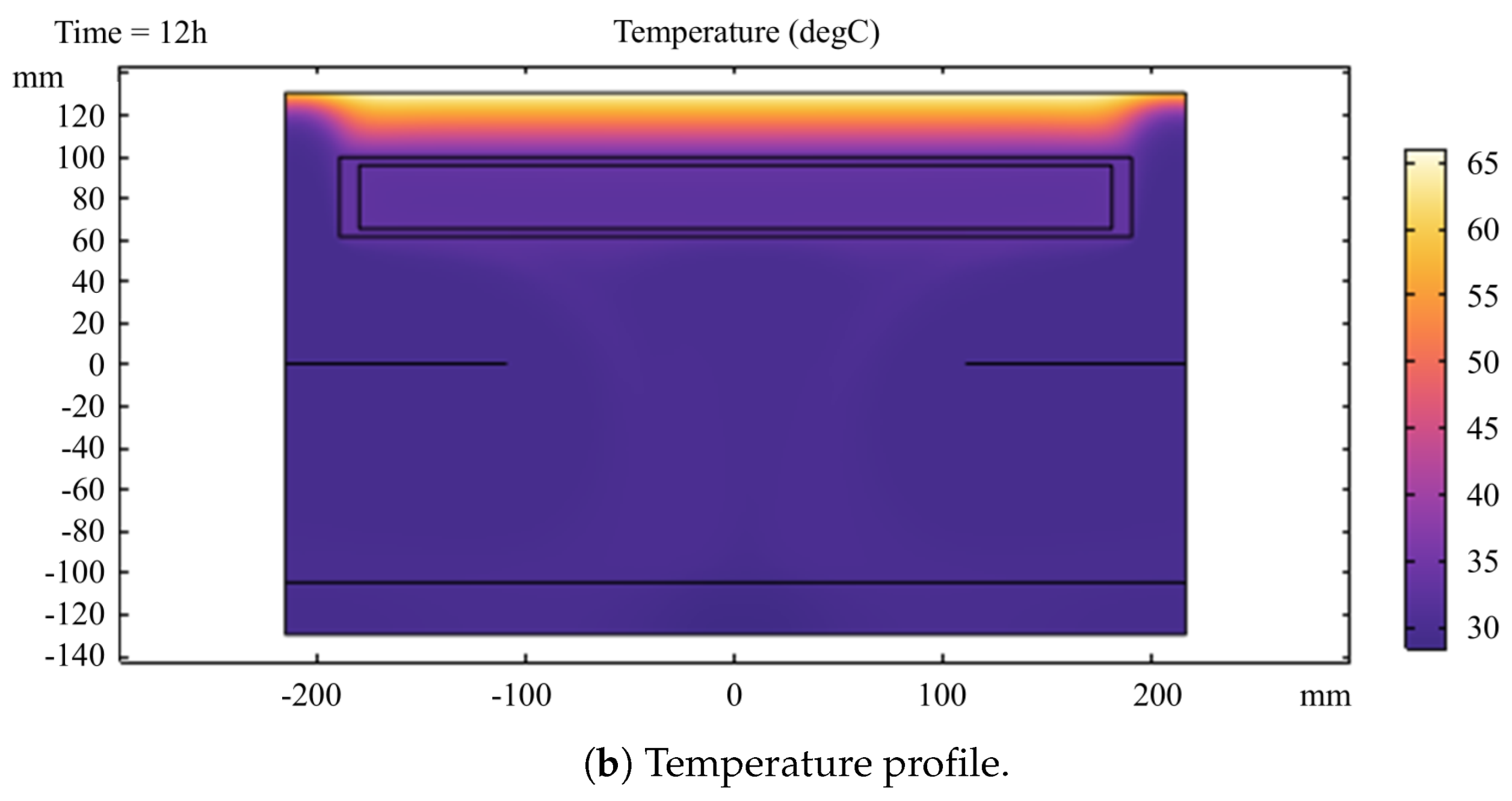
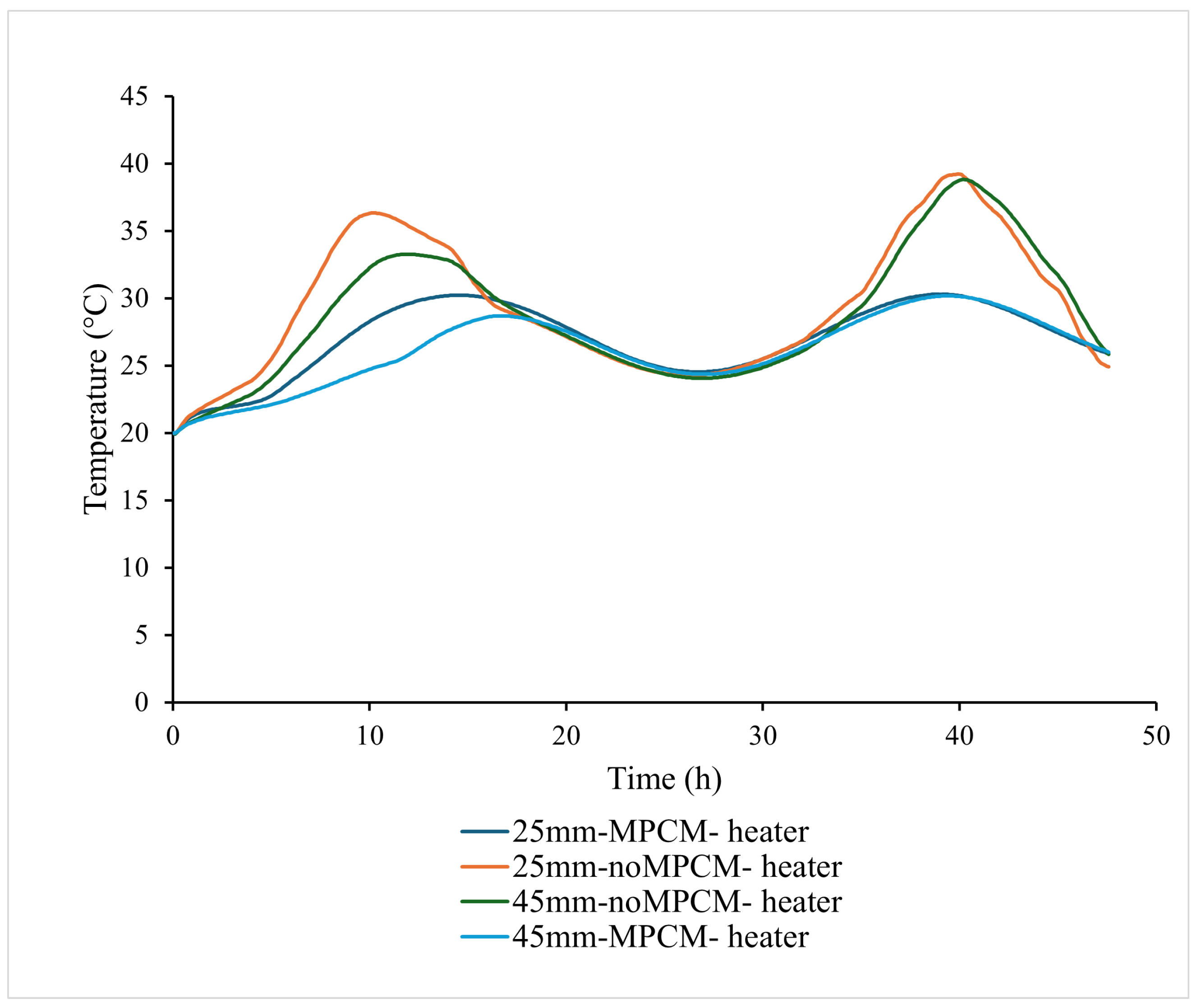
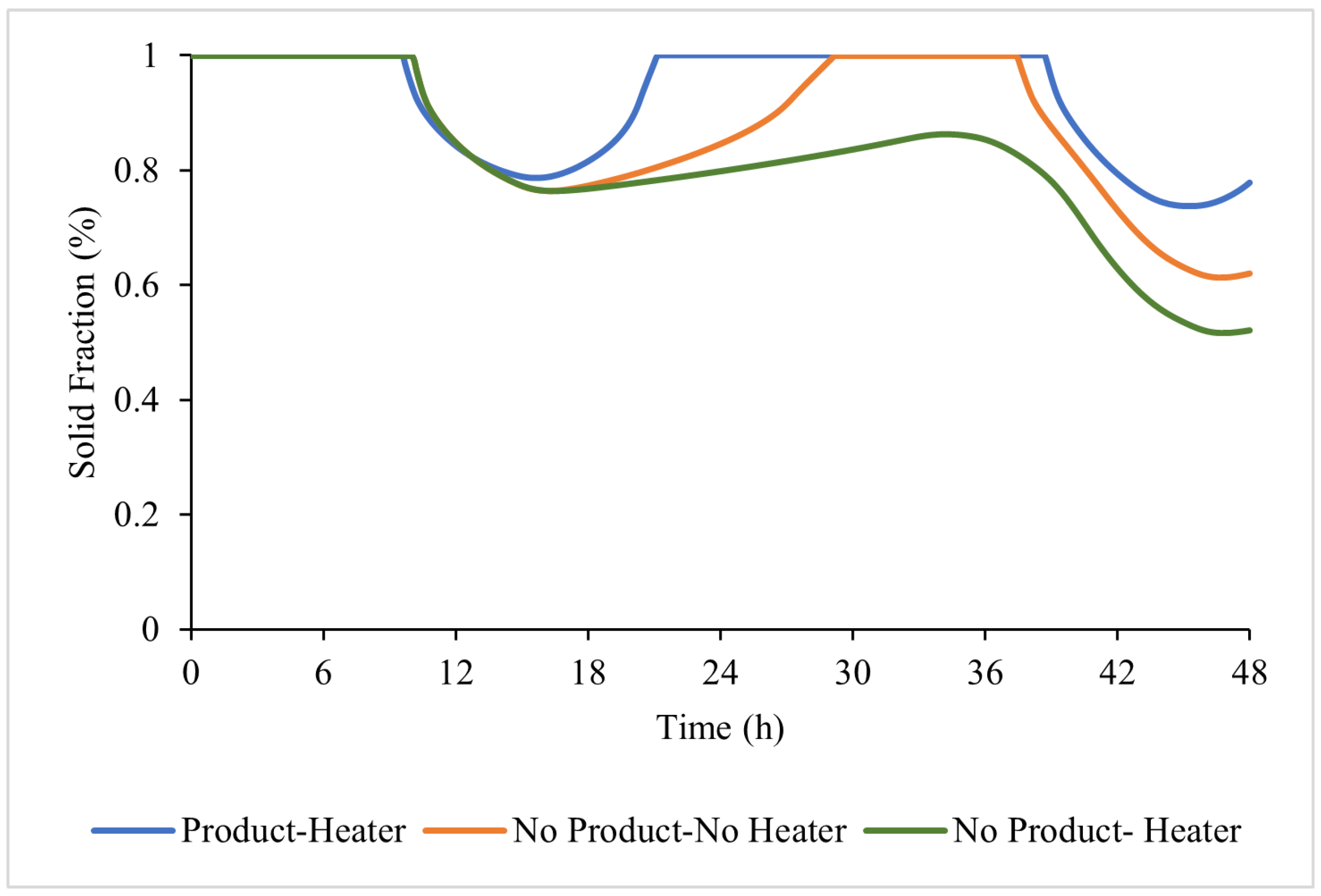
3.1. Thermal Performance of the Solar Dryer with Microencapsulated Phase Change Material Without Product
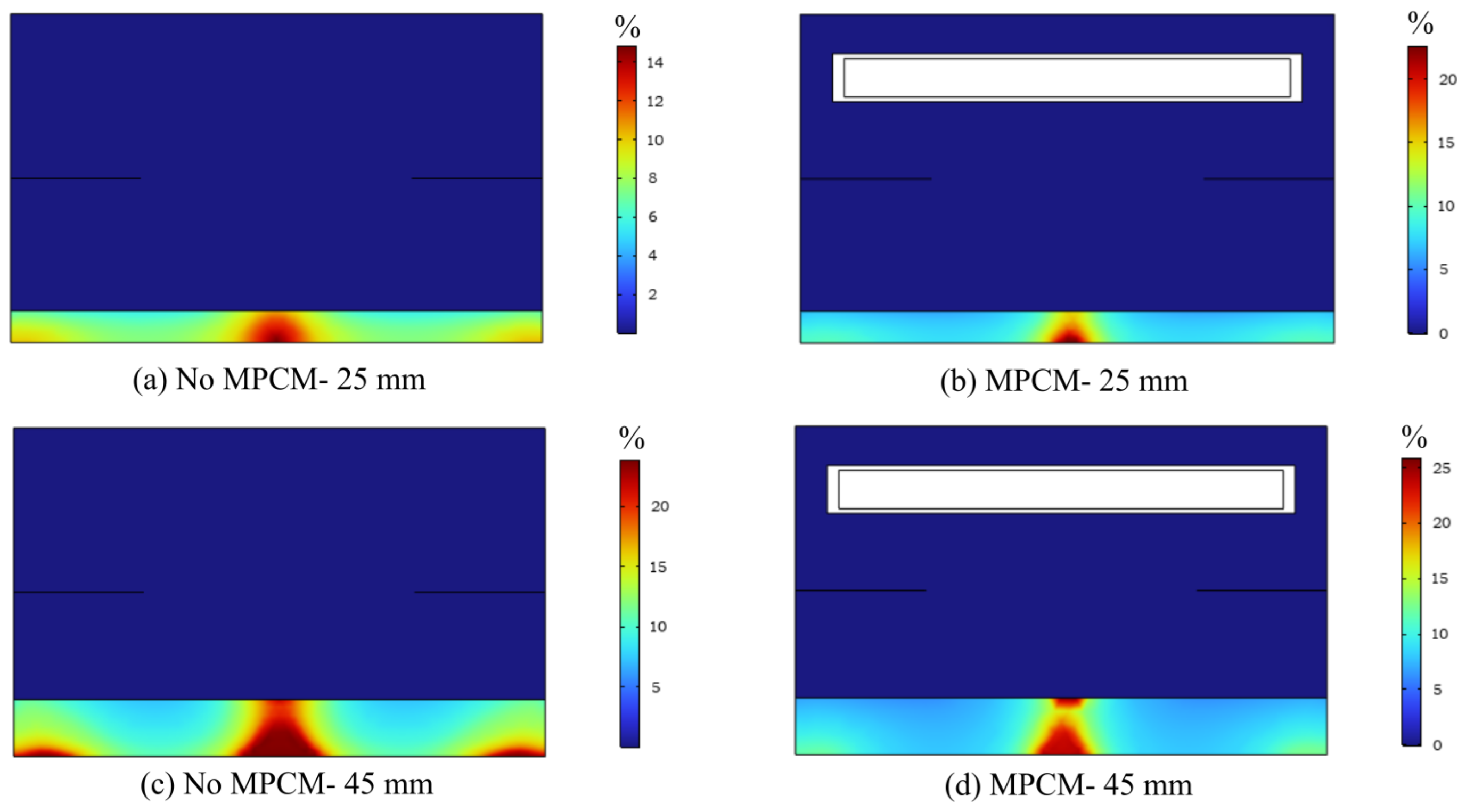
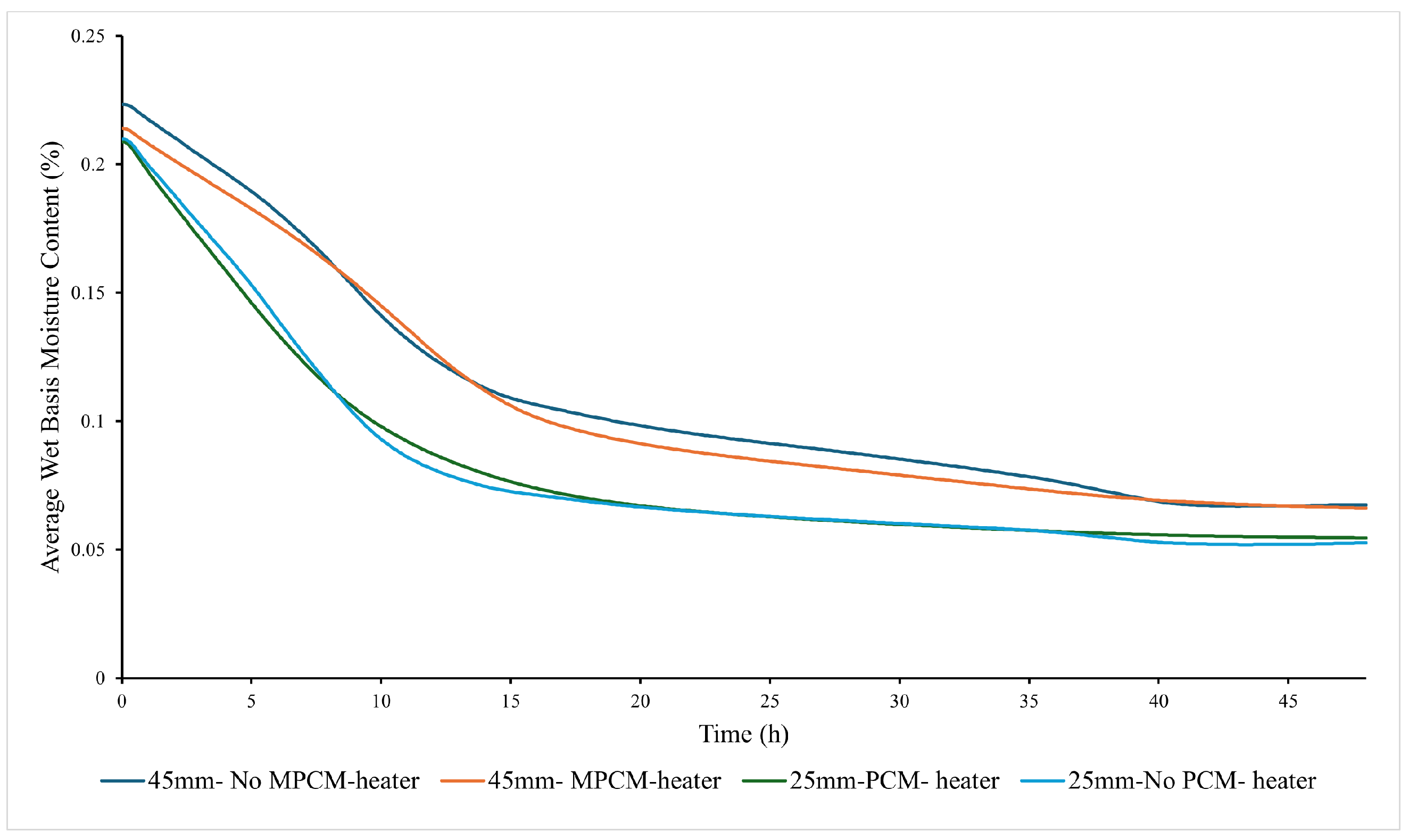
3.2. Drying of Rice with the Prototype of a Solar Dryer with MPCM
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MPCM | Microencapsulated Phase Change Material |
| PCM | Phase Change Material |
| WBMC | Wet-Basis Moisture Content |
| CFD | Computational Fluid Dynamics |
| RH | Relative Humidity |
| PDE | Partial Differential Equation |
| TPS | Transient Plane Source |
| COMSOL | COMSOL Multiphysics (Simulation Software) |
| Nomenclature | |
| Main Symbols | |
| Specific heat capacity (J/kg·K) | |
| C | Constant |
| D | Diffusivity (m2/s) |
| Activation energy for diffusion (J/mol) | |
| F | Body force (N) |
| Evaporation rate (s) | |
| H | Enthalpy (J/kg) |
| Convective mass transfer coefficient (m/s) | |
| Convective heat transfer coefficient (K) | |
| I | Solar irradiance (W/m2) |
| Rate of evaporation (s) | |
| k | Thermal conductivity (W/m·K) |
| Latent heat of vaporization (J/kg) | |
| P | Pressure (Pa) |
| q | Heat flux (W/m2) |
| Volumetric heat source term (W/m3) | |
| Internal heat source term (W/m3) | |
| R | Universal gas constant (J/mol·K) |
| Relative humidity (%) | |
| S | Saturation |
| t | Time (s) |
| T | Temperature (K or °C) |
| Volumetric liquid water content | |
| u | Air velocity (m/s) |
| w | Mass fraction |
| X | Moisture content (kg/kg dry basis) |
| Subscripts | |
| 0 | Initial condition |
| Effective | |
| Equilibrium condition | |
| g | Gas phase |
| Heater | |
| Inlet condition | |
| l | Liquid phase |
| Microencapsulated phase change material | |
| Maximum value | |
| Mean condition | |
| Minimum value | |
| Outlet condition | |
| s | Solid phase |
| Solar | |
| v | Vapor phase |
| ∞ | Ambient condition |
| Greek Letters | |
| Solid-phase fraction of the MPCM | |
| Liquid-phase fraction of the MPCM | |
| Permeability (m2) | |
| Density (kg/m3) | |
| Transmittance | |
| Volumetric liquid water content | |
| Porosity | |
| Dynamic viscosity |
References
- Asnaz, M.S.K.; Dolcek, A.O. Comparative performance study of different types of solar dryers towards sustainable agriculture. Energy Rep. 2021, 7, 6107–6118. [Google Scholar] [CrossRef]
- Venkatesh, R.; Sharma, P.; Subbarao, C.C.; Mohanavel, V.; Veerababu, K.; Jadhav, A.; Ravichandran, M.; Soudagar, M.E.M.; Alotaibi, M.A.; Sivanraju, R. Enhancement solar dryer performance and collector efficiency of paraffin PCM/copper fin featured solar dryer. Sci. Rep. 2025, 15, 31746. [Google Scholar] [CrossRef]
- Jain, A.; Kumar, A.; Shukla, A.; Sharma, A. Development of Phase Change Materials (PCMs) for Solar Drying Systems. In Solar Drying Technology; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Kumar, K.S.; Vasanthi, R.; Jaafar, M.S.; Munimathan, A.; Shanmugam, M.K.; Alwetaishi, M.; Afzal, A.; Rajendran, P.; Lee, I.E. Experimental and exergy evaluation of a PCM integrated active indirect solar dryer for Turkey berries with economic and environmental assessment. Sci. Rep. 2025, 15, 21661. [Google Scholar] [CrossRef] [PubMed]
- Drissi, S.; Ling, T.C.; Mo, K.H.; Eddhahak, A. A review of microencapsulated and composite phase change materials: Alteration of strength and thermal properties of cement-based materials. Renew. Sustain. Energy Rev. 2019, 110, 467–484. [Google Scholar] [CrossRef]
- Harris, I.; James Rivas, A.; Ortega Del Rosario, M.D.L.A.; Saghir, M.Z. Recent developments in phase change material-based solar water heating systems: Insights on research trends and opportunities. Int. J. Thermofluids 2023, 20, 100359. [Google Scholar] [CrossRef]
- Gupta, A.; Shukla, S.; Srivastava, A. Analysis of solar drying unit with phase change material storage systems. Int. J. Agil. Syst. Manag. 2013, 6, 164. [Google Scholar] [CrossRef]
- Thanompongchart, P.; Pintana, P.; Tippayawong, N. Improving solar dryer performance with automatic control of auxiliary heated air. Energy Rep. 2023, 9, 109–113. [Google Scholar] [CrossRef]
- El-Sebaii, A.A.; Shalaby, S.M. Experimental Investigation of Drying Thymus Cut Leaves in Indirect Solar Dryer With Phase Change Material. J. Sol. Energy Eng. 2017, 139, 061011. [Google Scholar] [CrossRef]
- Kant, K.; Shukla, A.; Sharma, A.; Kumar, A.; Jain, A. Thermal energy storage based solar drying systems: A review. Innov. Food Sci. Emerg. Technol. 2016, 34, 86–99. [Google Scholar] [CrossRef]
- Iranmanesh, M.; Samimi Akhijahani, H.; Barghi Jahromi, M.S. CFD modeling and evaluation the performance of a solar cabinet dryer equipped with evacuated tube solar collector and thermal storage system. Renew. Energy 2020, 145, 1192–1213. [Google Scholar] [CrossRef]
- Aumporn, O.; Zeghmati, B.; Chesneau, X.; Janjai, S. Numerical study of a solar greenhouse dryer with a phase-change material as an energy storage medium. Heat Transf. Res. 2018, 49, 509–528. [Google Scholar] [CrossRef]
- Venkateswarlu, K.; Reddy, S.V.K. Recent trends on energy-efficient solar dryers for food and agricultural products drying: A review. Waste Dispos. Sustain. Energy 2024, 6, 335–353. [Google Scholar] [CrossRef]
- Sadaka, S. Determination of short-grain rough rice drying kinetics under isothermal conditions using an integrated model. BioResources 2022, 17, 4001–4017. [Google Scholar] [CrossRef]
- Iguaz, A.; San Martin, M.B.; Arroqui, C.; Fernandez, T.; Mate, J.I.; Virseda, P. Thermophysical properties of medium grain rough rice (LIDO cultivar) at medium and low temperatures. Eur. Food Res. Technol. 2003, 217, 224–229. [Google Scholar] [CrossRef]
- Li, J.; Chang, K.; Yin, J.; Jin, Y.; Yi, X.; Zhang, Z.; He, Y.; Yang, Q.; Tang, Z.; Liu, X.; et al. Study on Optimization of Rice-Drying Process Parameters and Directional Regulation of Nutrient Quality. Appl. Sci. 2024, 14, 10825. [Google Scholar] [CrossRef]
- Li, B.; Feng, S.; He, Q.; Zhu, Y.; Hu, Z.; Jiang, Y.; Su, L. Numerical simulation of rice drying process in a deep bed under an angular air duct. J. Food Process. Eng. 2023, 46, e14438. [Google Scholar] [CrossRef]
- Naghavi, Z.; Moheb, A.; Ziaei-rad, S. Numerical simulation of rough rice drying in a deep-bed dryer using non-equilibrium model. Energy Convers. Manag. 2010, 51, 258–264. [Google Scholar] [CrossRef]
- Sadaka, S. Impact of grain layer thickness on rough rice drying kinetics parameters. Case Stud. Therm. Eng. 2022, 35, 102026. [Google Scholar] [CrossRef]
- Müller, A.; Nunes, M.T.; Maldaner, V.; Coradi, P.C.; Moraes, R.S.D.; Martens, S.; Leal, A.F.; Pereira, V.F.; Marin, C.K. Rice Drying, Storage and Processing: Effects of Post-Harvest Operations on Grain Quality. Rice Sci. 2022, 29, 16–30. [Google Scholar] [CrossRef]
- Zhang, N.; Yin, S.Y.; Yang, H.H. Transient performance of coupled heat and mass transfer in cross-flow hollow fiber membrane module for air dehumidification. Int. J. Refrig. 2019, 108, 190–199. [Google Scholar] [CrossRef]
- Nguyen, Q.B.; Nai, M.L.S.; Zhu, Z.; Sun, C.N.; Wei, J.; Zhou, W. Characteristics of Inconel Powders for Powder-Bed Additive Manufacturing. Engineering 2017, 3, 695–700. [Google Scholar] [CrossRef]
- ASTM B527-24; Test Method for Tap Density of Metal Powders and Compounds. ASTM International: Conshohocken, PA, USA, 2023. Available online: http://www.astm.org/cgi-bin/resolver.cgi?B527-24 (accessed on 10 October 2025). [CrossRef]
- Basunia, M.; Abe, T. Moisture adsorption isotherms of rough rice. J. Food Eng. 1999, 42, 235–242. [Google Scholar] [CrossRef]
- Steffe, J.F.; Singh, R.P. Note on Volumetric Reduction of Short Grain Rice During Drying. Cereal Chem. 1979, 2, 148–150. [Google Scholar]
- Prakash, B.; Pan, Z. Effect of Geometry of Rice Kernels on Drying Modeling Results. Dry. Technol. 2012, 30, 801–807. [Google Scholar] [CrossRef]
- Lakhdar, B.; Salaheddine, A.; Brahim, M.; Mohamed, D. Exergetic analysis and optimization of a flat plate solar collector. J. Biodivers. Environ. Sci. 2019, 14, 1–12. [Google Scholar]
- Nierode, D.E. The Cyclical Sine Model Explanation for Climate Change. Int. J. Plant Anim. Environ. Sci. 2022, 12, 175–191. [Google Scholar] [CrossRef]
- Du, J.; Lin, Y.; Gao, Y.; Tian, Y.; Zhang, J.; Fang, G. Nutritional changes and early warning of moldy rice under different relative humidity and storage temperature. Foods 2022, 11, 185. [Google Scholar] [CrossRef] [PubMed]
- Salvatierra-Rojas, A.; Ramaj, I.; Romuli, S.; Müller, J. CFD-Simulink Modeling of the Inflatable Solar Dryer for Drying Paddy Rice. Appl. Sci. 2021, 11, 3118. [Google Scholar] [CrossRef]
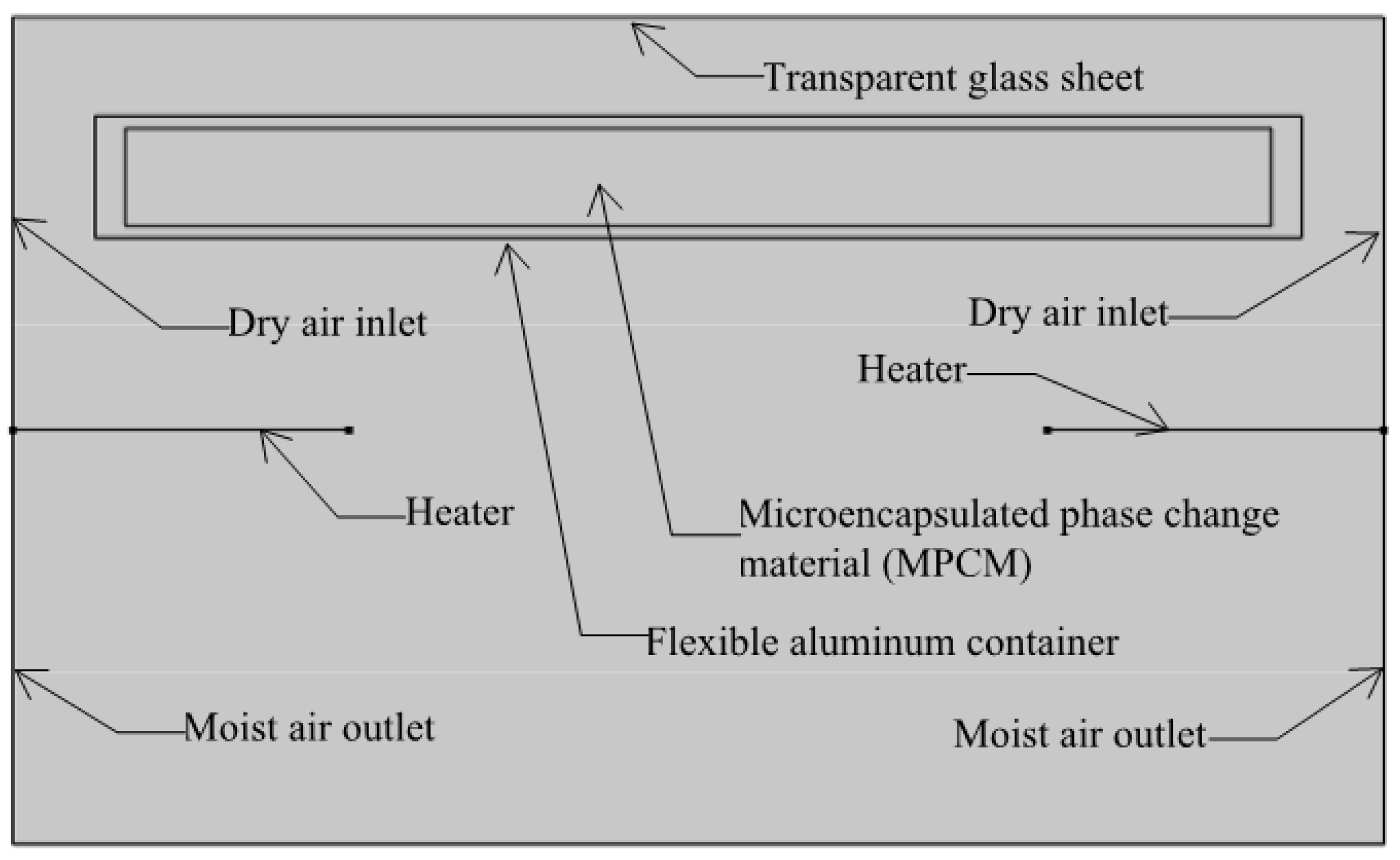
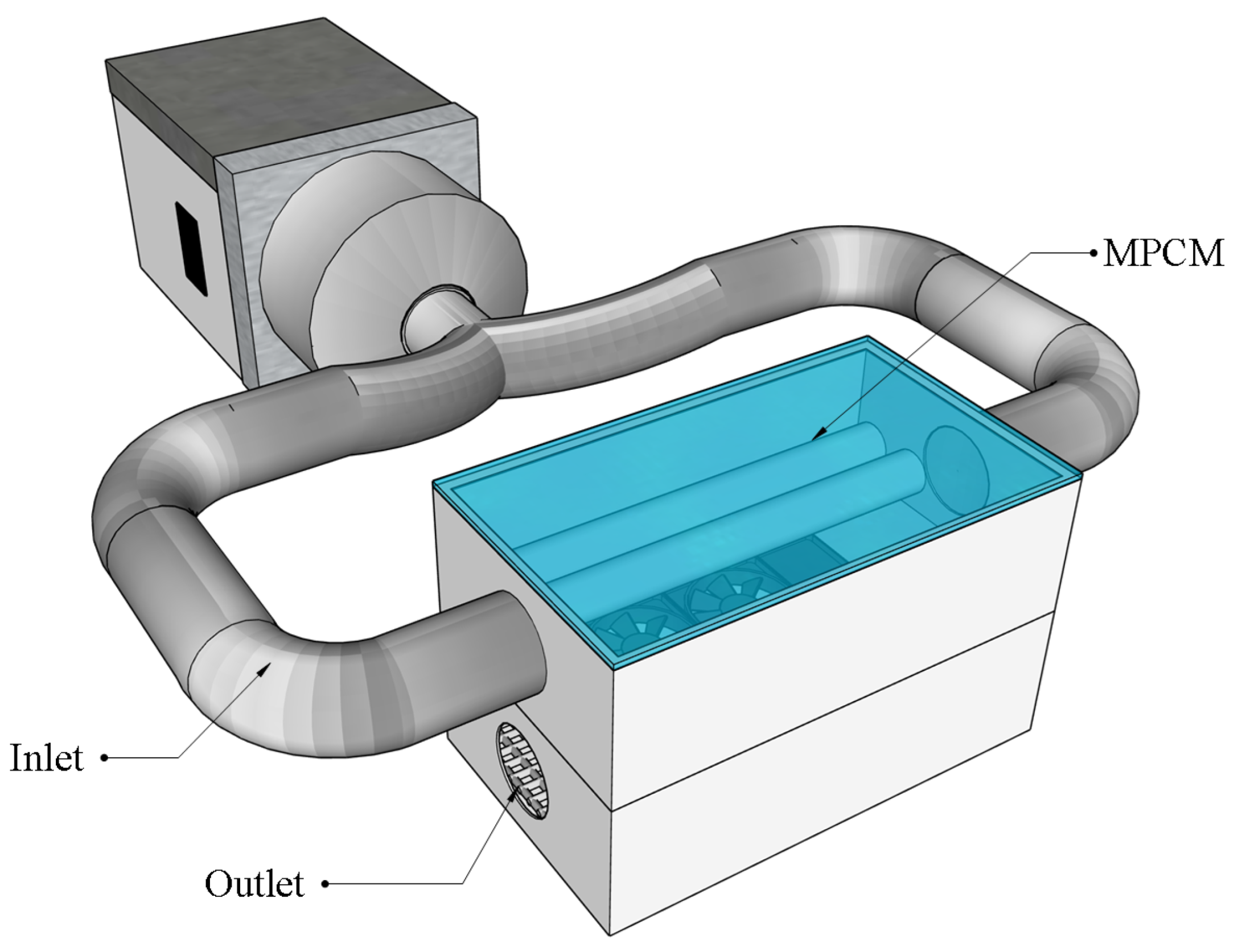
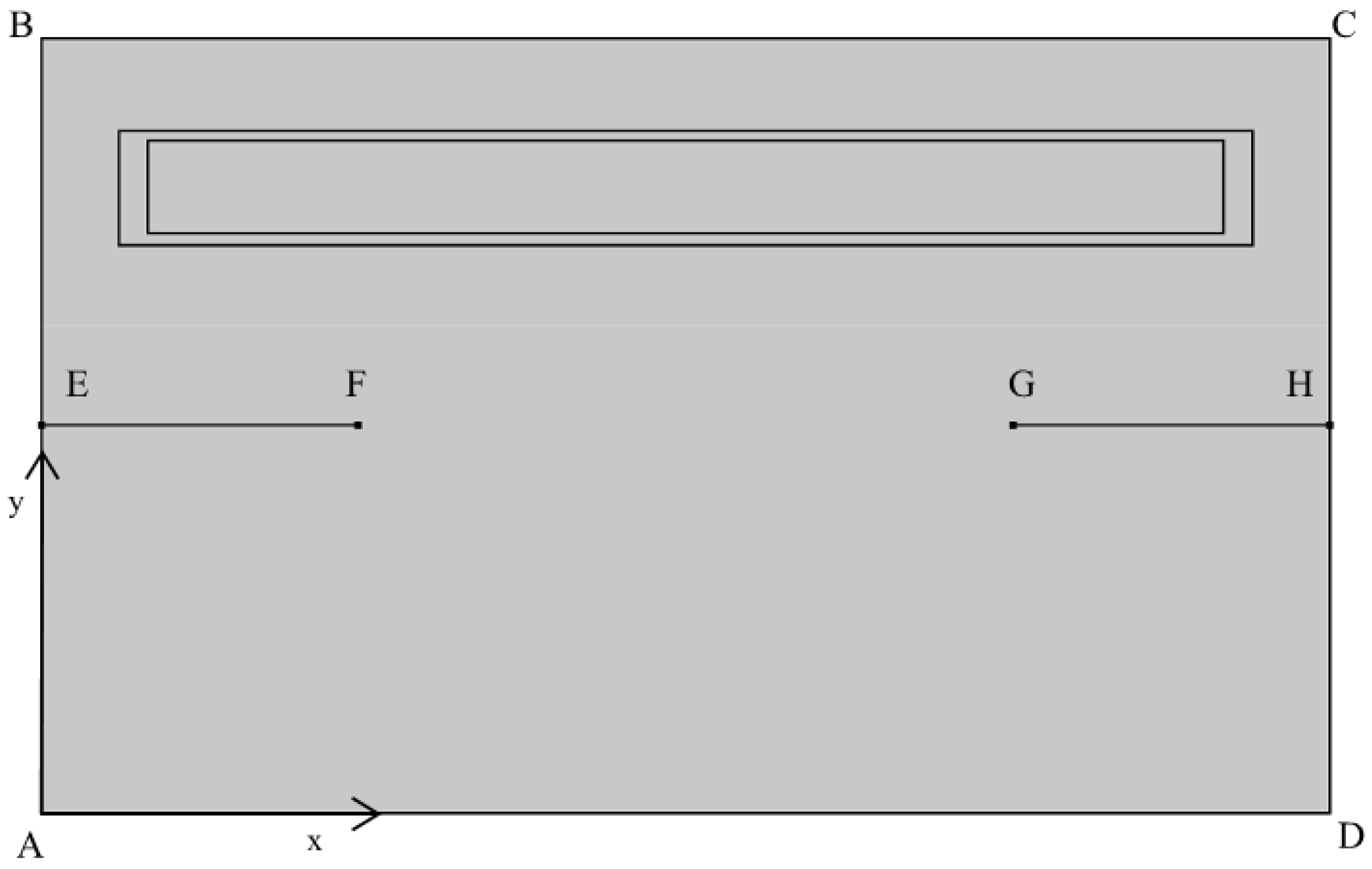
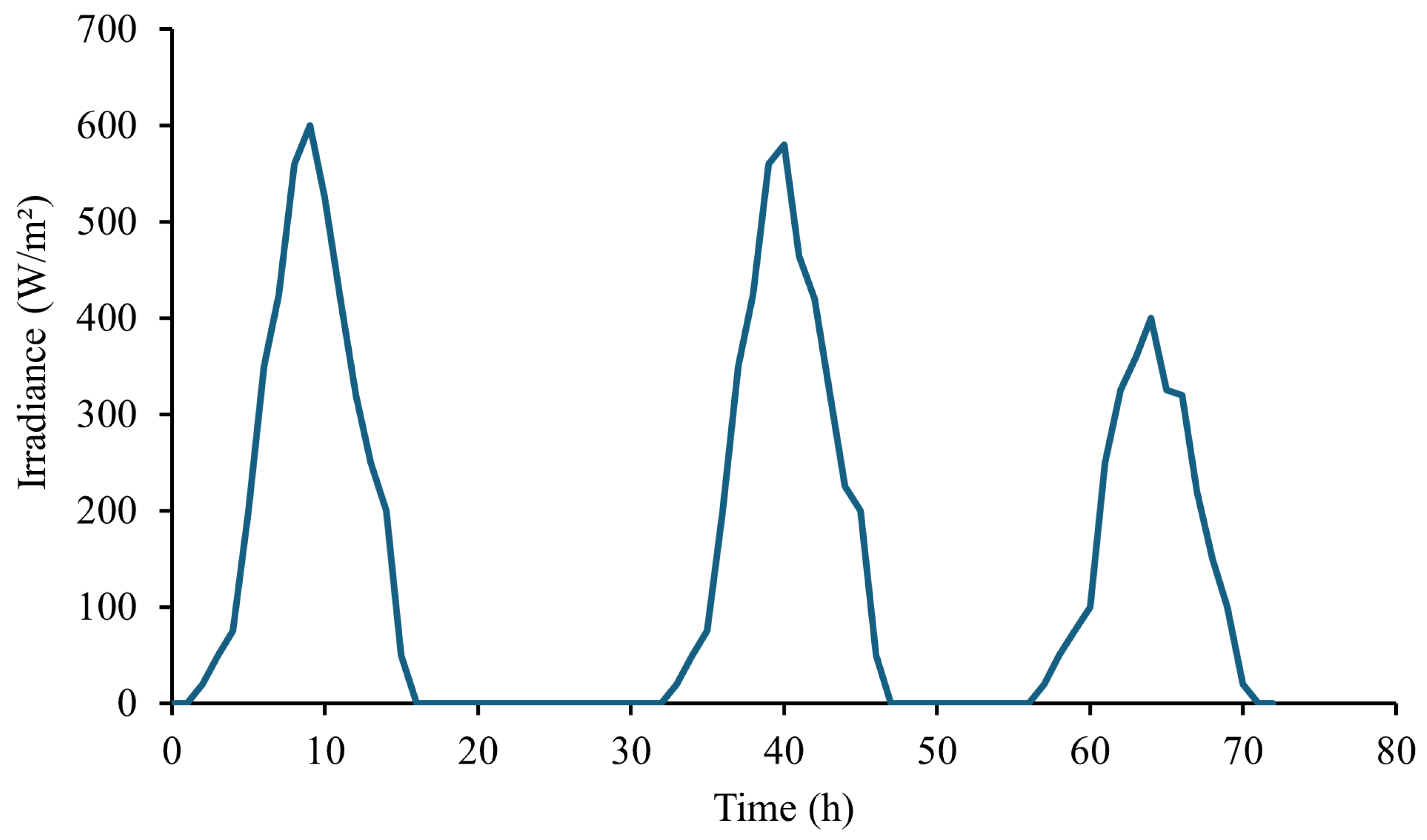


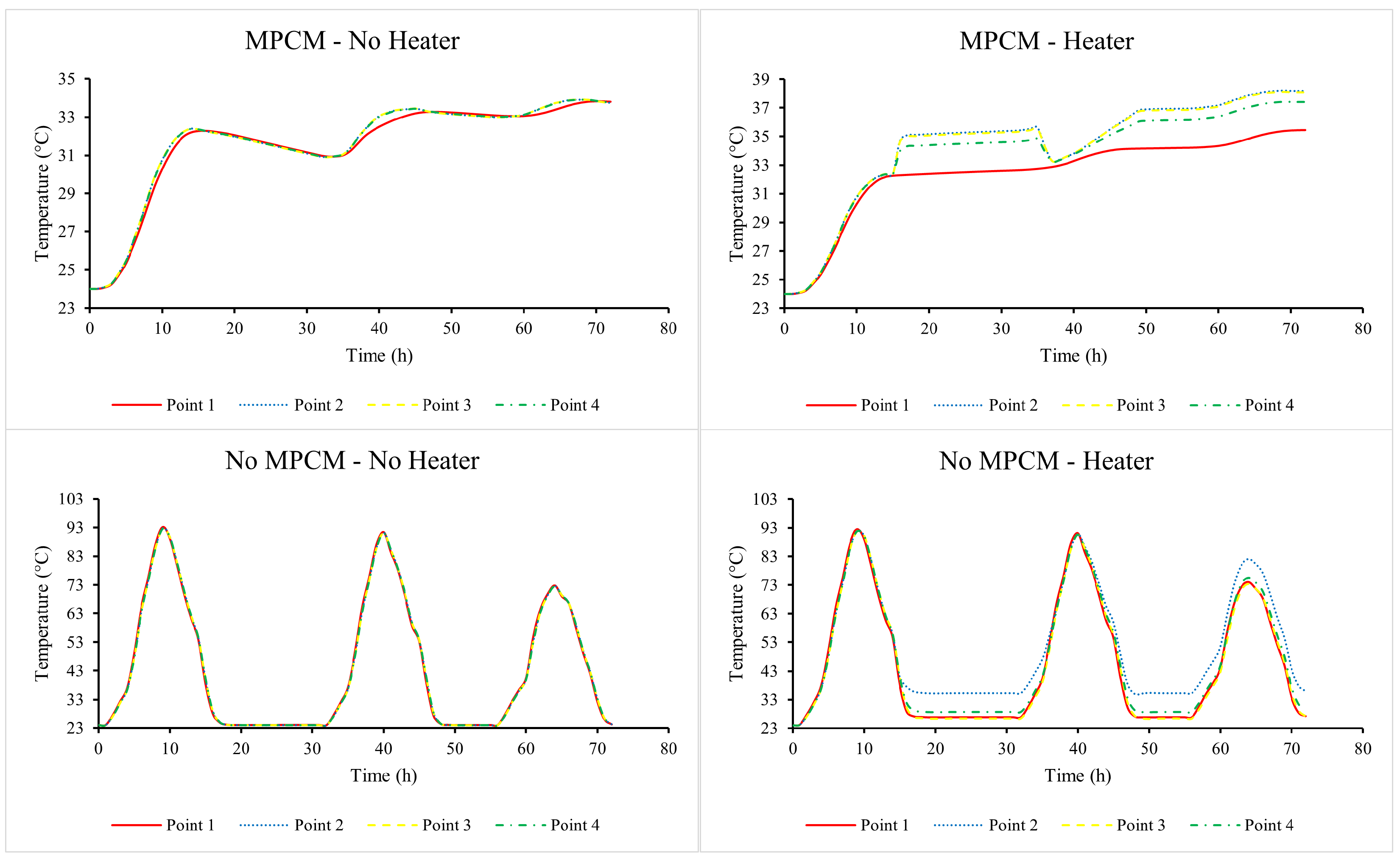
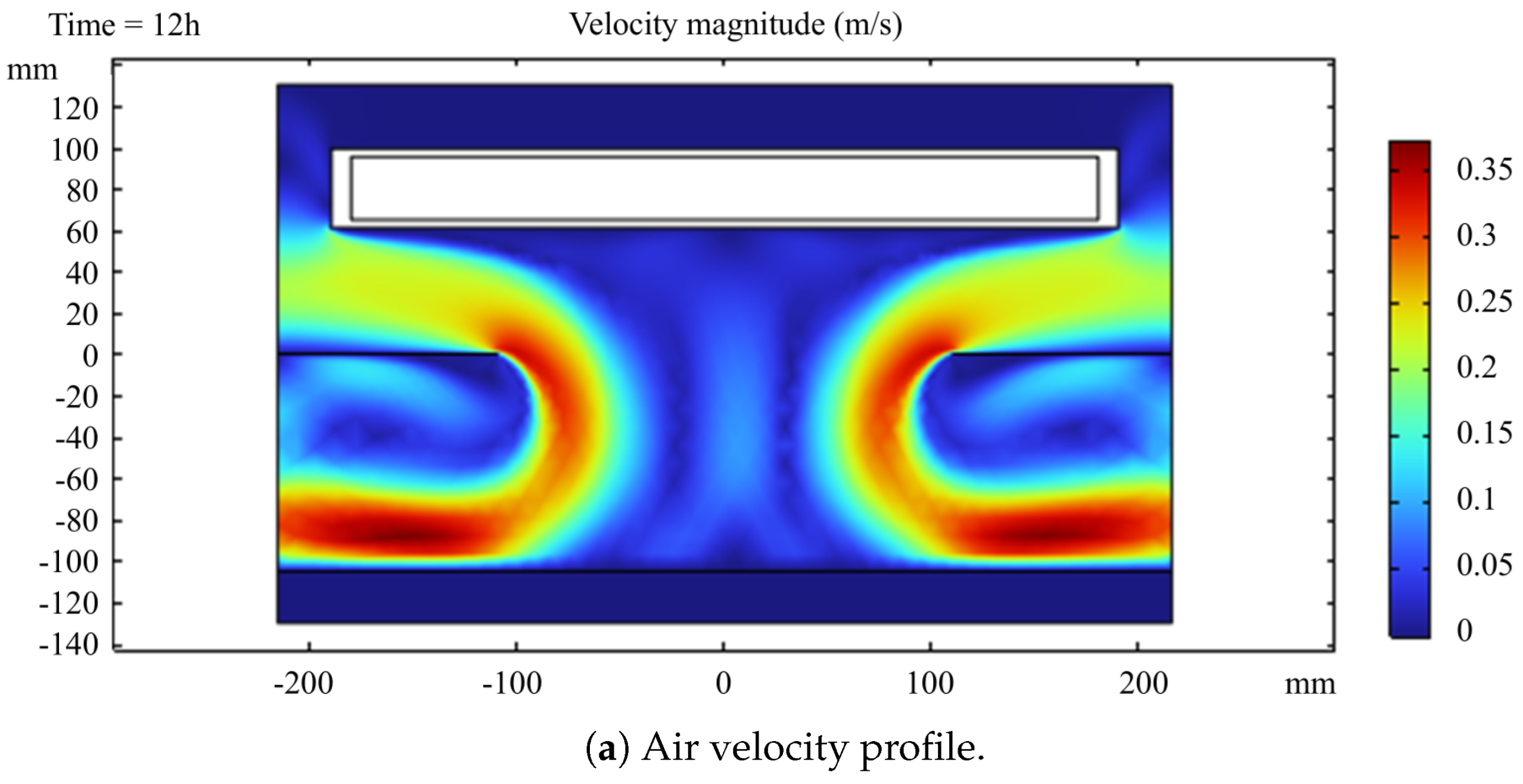
| Name | Value | Description |
|---|---|---|
| (m) | Dryer length | |
| (m) | Dryer height | |
| (m) | Diameter of MPCM tube | |
| (m) | Dryer width |
| Surface | Description | Thermal B.C. |
|---|---|---|
| (BC) | Glass cover | |
| (AD) | Insulated base | |
| (BE, CH) | Inlets | |
| (AE, DH) | Outlets | |
| Initial dryer temperature | ; 20 °C | |
| Initial air velocity |
| Case | (°C) | (°C) | (°C) | (%) |
|---|---|---|---|---|
| 25 mm—Heater only | 20.00 | 39.21 | 19.21 | 75.0 |
| 25 mm—Heater + MPCM | 20.00 | 30.30 | 10.31 | 73.9 |
| 45 mm—Heater only | 20.00 | 38.82 | 18.82 | 69.8 |
| 45 mm—Heater + MPCM | 20.00 | 30.18 | 10.18 | 69.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riande, H.; Harris, I.; Collado, E.; Garcia, A.; Saez, Y. Numerical Study of a Solar Dryer Prototype with Microencapsulated Phase Change Materials for Rice Drying. Energies 2025, 18, 5427. https://doi.org/10.3390/en18205427
Riande H, Harris I, Collado E, Garcia A, Saez Y. Numerical Study of a Solar Dryer Prototype with Microencapsulated Phase Change Materials for Rice Drying. Energies. 2025; 18(20):5427. https://doi.org/10.3390/en18205427
Chicago/Turabian StyleRiande, Hector, Itamar Harris, Edwin Collado, Antony Garcia, and Yessica Saez. 2025. "Numerical Study of a Solar Dryer Prototype with Microencapsulated Phase Change Materials for Rice Drying" Energies 18, no. 20: 5427. https://doi.org/10.3390/en18205427
APA StyleRiande, H., Harris, I., Collado, E., Garcia, A., & Saez, Y. (2025). Numerical Study of a Solar Dryer Prototype with Microencapsulated Phase Change Materials for Rice Drying. Energies, 18(20), 5427. https://doi.org/10.3390/en18205427






