Sustainable Component-Level Prioritization of PV Panels, Batteries, and Converters for Solar Technologies in Hybrid Renewable Energy Systems Using Objective-Weighted MCDM Models
Abstract
1. Introduction
| Focus and Context | Criteria/Methods | Core Findings | Limitations/Gaps | How This Paper Advances Knowledge | Ref. |
|---|---|---|---|---|---|
| PCM selection for sustainable solar drying | Six MCDM methods (TOPSIS, EDAS, MOORA, MARCOS, CoCoSo, VIKOR) + Borda aggregation + Spearman rank correlation + sensitivity | validated stability of ranking | Limited to thermal energy applications | Demonstrates multi-model and robustness analysis strategy adopted here for PV–Battery–Converter selection | [24] |
| Hybrid energy systems for EV charging by demographic groups | HOMER optimization + MCDM ranking of on/off-grid scenarios by economic, technical, environmental criteria | PV/Wind/Battery/Converter system best for daytime users; PV/Wind/Grid best for night users | Sector-specific; no component-level prioritization | Reinforces the need for context-sensitive criteria weighting in MCDM frameworks | [26] |
| Off-grid HRESs for wetland areas (WIL-CoCoSo) | HOMER simulation + LBWA for weights + Wins-in-League (CoCoSo) ranking + sensitivity | PV/WT/DG/HKT + Li-ion battery optimal; flood-resilient; CO2 ↓96% vs. DG-only | Region-specific; no component-type analysis | Adds resilience and environmental criteria to decision matrix for HRES design | [25] |
| PV cleaning techniques and SDG alignment | 18 criteria linked to SDGs (6–13); TOPSIS ranking | Manual cleaning is best for energy and water SDGs | Operation-phase only; not tech-family selection | Illustrates integration of sustainability indices into MCDM framework | [22] |
| PV panel cleaning in UAE (sustainability) | TOPSIS + entropy + stochastic dominance + sensitivity analysis | Robot water-based cleaning method top-ranked (0.65–0.75) | Survey-based; local bias | Validates objective–subjective weight fusion approach similar to ours (Bonferroni fusion) | [23] |
| Site selection of on-grid HRESs | GIS spatial filters + MCDM (technical, economic, environmental, climatic criteria) + TEA | Identified Izadkhast as optimal site with 60% RE fraction | Location-focused; no component ranking | Demonstrates structured criteria taxonomy, later adapted for PV/Battery/Converter evaluation | [27] |
| PV/Wind/Storage for RO desalination | FAHP (weighting) + Fuzzy-VIKOR (ranking) | Fully renewable design (100% RES); NPC 0.091 $/kWh | Water-sector application | Extends fuzzy-AHP/VIKOR combination to energy technology selection | [33] |
| Solar-strategy prioritization at neighborhood scale | Expert survey + adoption-score MCDM tool | Framework for passive/active solar integration in urban design | Planning domain; not component-level | Validates stakeholder-driven criteria weighting adopted for our fused objective weights | [34] |
| Industrial HRES sustainability optimization (4E) | Multi-objective Pareto front + MCDM post-ranking of configurations by 4E indices | Solar + Wind most sustainable (SI = 0.89) | Macro-level system view | Translates economic, environmental and technical indices into component criteria | [35] |
| HRESs with hydrogen & battery (PMS optimization) | Entropy weight method (EWM) + CODAS ranking (9 criteria) | PV/WT/Battery/H2 configurations evaluated; LPSP highest weight | System-level focus only | Adds PMS/aging/reliability dimensions to converter and storage criteria | [30] |
| Island microgrid planning (China) | HOMER + reference-point MCDM + uncertainty analysis | PV-WT-DG-Battery mix best under resilience criteria | Case-study only | Embeds resilience and uncertainty handling in criteria design | [36] |
| Off-grid HRESs with green hydrogen production | TOPSIS ranking of six configurations using techno-economic and environmental metrics | PV-WT-BG-Battery-H2 system top rank (RC = 0.817) | No intra-technology comparison | Establishes multi-criteria trade-off structure for PV/Battery/Converter families | [37] |
| MCDM evaluation of renewable systems with hysteresis control | Hybrid Entropy + CODAS approach; 9 technical/economic/env. indicators | Quantified weights for PV, WT, Battery, H2 systems; LPSP dominant | Energy-system scale; no component family distinction | Demonstrates objective entropy weighting replicated in our Bonferroni-fusion framework | [30] |
| DSS for PV module and battery selection | AHP + TOPSIS vs. Entropy + TOPSIS comparative decision support | Li-ion + CIGS pair optimal across methods; rank consistency verified | Limited criteria breadth | Confirms robustness of objective-weight fusion and sensitivity testing applied in this study | [38] |
Research Gaps, Questions, Objectives, and Significance
- Research Question
- Research Objectives
- To critically evaluate photovoltaic, battery, and converter technologies relevant to solar-based HRESs while considering technical, economic, environmental, and reliability criteria.
- To apply an advanced MCDM framework (MARCOS with fused weighting) for systematic prioritization of component technologies.
- Conduct correlation and sensitivity analyses to assess the consistency and robustness of ranking outcomes across diverse decision scenarios.
- Significance of the Study
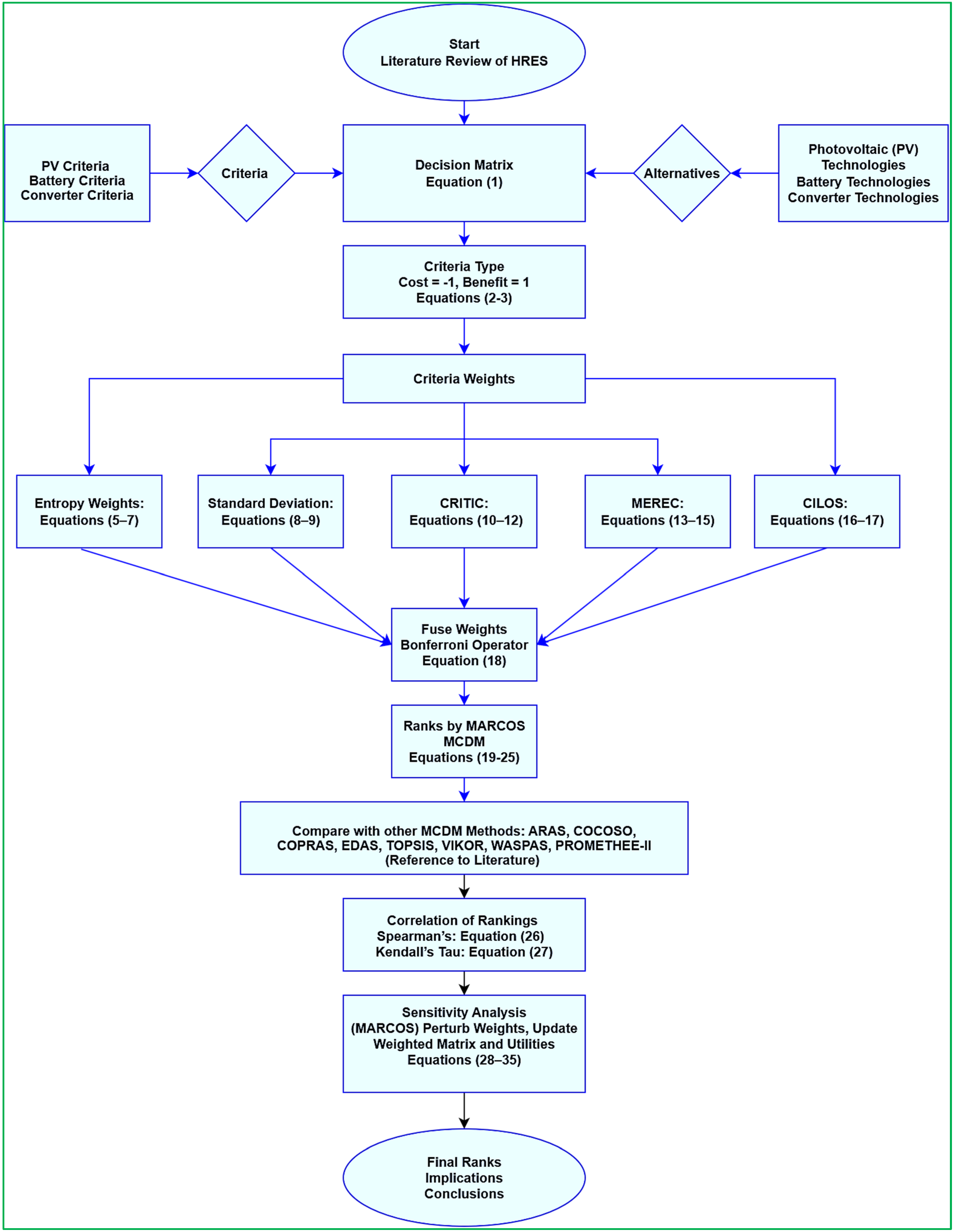
2. Materials and Methods
2.1. MCDM Methodology: Prioritizing PV, Battery, and Converter Technologies
- Step 1: Construct the initial decision matrix; PV, battery, and converter technologies
- Step 2: Determine the criteria types of PV, battery, and converter technologies
- Step 3: MARCOS method
- Step 4: Add anti-ideal and ideal alternatives as let as per Equation (4).
- Step 5: Subjective weights computation: Application of weighting methods (Entropy, standard deviation, CRITIC, MEREC, and CILOS). Each method calculates weights for each criterion:
- (a). Entropy Weight: Normalize the decision matrix by Equation (5), calculate the entropy of each criterion by Equation (6), and determine weights by Equation (7) [29].
- (b). Standard Deviation Weight: Find the standard deviation of criterion j by Equation (8), and the weight of criterion j using Equation (9) [48].
- (c). CRITIC Weight: Compute correlation coefficients between criteria using Equation (10), compute information content of criterion j by Equation (11), and normalize to obtain weights utilizing Equation (12) [49].
- (d). MEREC Weight: Compute the overall score of each alternative by Equation (13), then remove criterion j, recalculate scores by finding the absolute error, measure the error caused by removing criterion j by Equation (14), and normalize to get the final weights, Equation (15) [50].
- (e). CILOS Weight: Compute reciprocal impact for each criterion j using Equation (16) and normalize to determine weights by Equation (17) [51].
- (f). Bonferroni Operator Fused Weights
- Step 6: Construct weighted normalized matrix (weights by fused with Bonferroni Operator), use Equation (19), calculate overall utility score for each alternative by Equation (20), determine ideal (AI) and anti-ideal scores (AAI) using Equations (21) and Equation (22), respectively, relative utility of each alternative, relative to ideal by Equation (23) and relative to anti-ideal by Equation (24), and then compute utility functions by Equation (25). Rank the alternatives in descending order based on .
- Step 7: Other MCDM Methods (Applied for Comparison)
- Step 8: Ranks by different MCDM methods: Correlation module
- Step 9: Sensitivity Analysis in MCDM (with MARCOS)
- Baseline Weight Vector
- Perturbation of Weight(s)
- Recalculate Weighted Matrix
- Update Scores
- Re-rank Alternatives: Sort in descending order to obtain the new ranking:
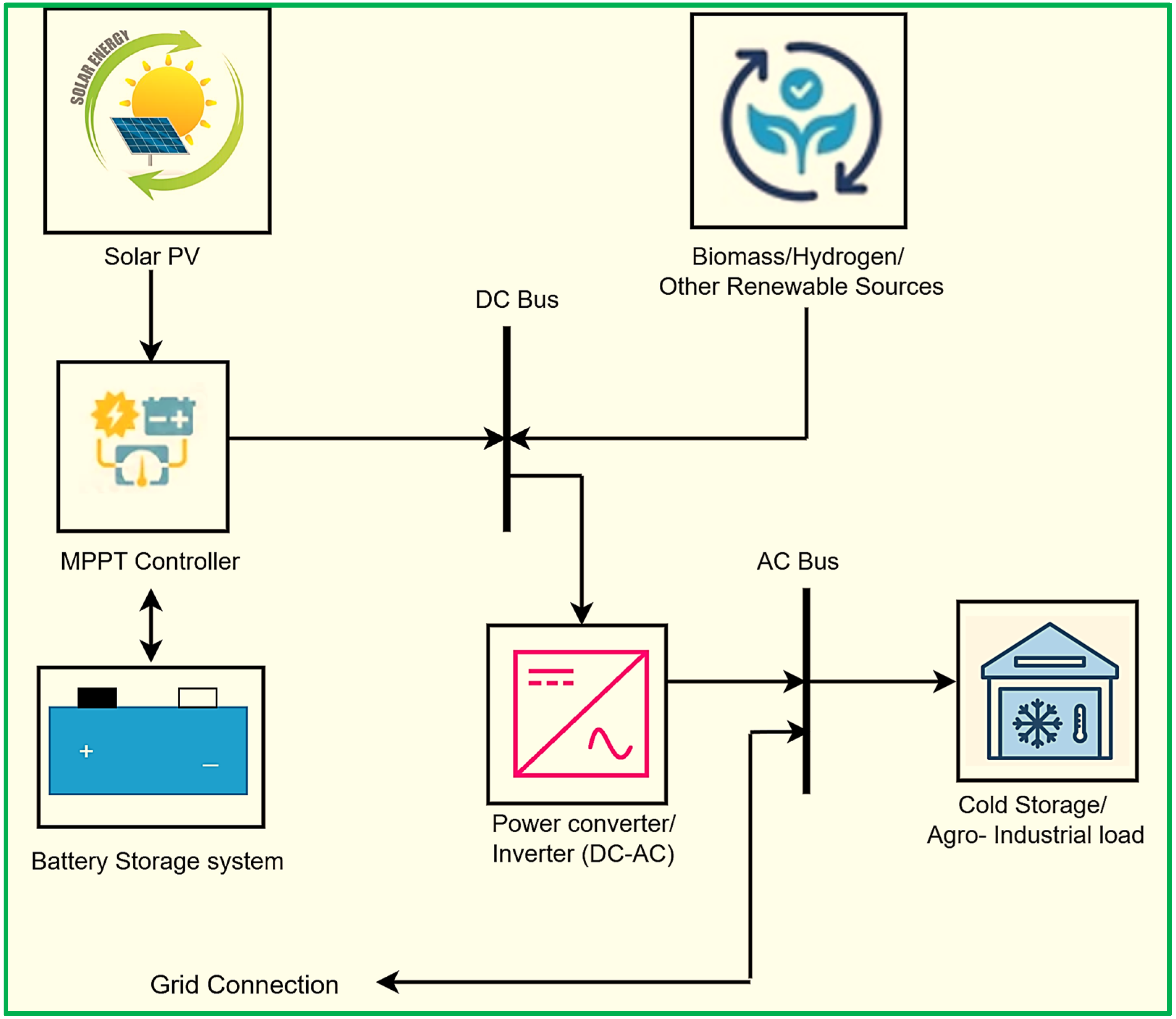
2.2. Multi-Domain Decision Matrix Framework for Component Prioritization in Solar-Based HRESs
2.2.1. Decision Matrix: PV Technologies for Solar-Based HRESs
| PV Technology | CO2 (kg) | EPBT (yr) | ($) (Cst/W) | (%/yr) Drt | (yr) (War) | (yr) (Lfs) | (%) (Eff) | (%/°C) (Tcof) | Weight (kg/m2) | (LIP) | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PV-Mcs | 600 | 1.1 | 1.25 | 0.5 | 27.5 | 27.5 | 21 | 0.35 | 13 | 3 | [70,71,72,73,74,75,76] |
| PV-Pcs | 600 | 1.1 | 0.85 | 0.7 | 27.5 | 27.5 | 16 | 0.45 | 13 | 2 | [70,71,72,73,74,75,76] |
| PV-Prc | 600 | 1.1 | 0.485 | 0.4 | 25 | 27.5 | 21 | 0.35 | 13 | 3 | [70,71,72,73,74,75,76,77] |
| PV-Thf | 300 | 0.6 | 0.6 | 0.2 | 22.5 | 22.5 | 12.5 | 0.28 | 14 | 4 | [71,72,73,74,75,76,78] |
| PV-Hjt | 600 | 0.94 | 1.2 | 0.3 | 30 | 27.5 | 24 | 0.25 | 17 | 5 | [70,72,73,74,75,76,79] |
| PV-Tpc | 600 | 1.1 | 0.33 | 0.4 | 25 | 25 | 23 | 0.3 | 15 | 5 | [70,71,72,73,74,75,76] |
| PV-Bfmc | 650 | 1.1 | 1.35 | 0.5 | 30 | 25 | 21 | 0.35 | 20 | 5 | [71,72,73,74,76] |
| −1 | −1 | −1 | −1 | 1 | 1 | 1 | −1 | −1 | 1 |
2.2.2. Decision Matrix: Battery Technologies for Solar-Based HRESs
| Battery Type | CL (No. of Cycles) | DoD (%) | RTE (%) | SE (Wh/kg) | VED (Wh/L) | C-Rate | CpkWh ($/kWh) | Maint (0–5 Scale) | Tox (0–5 Scale) | CF (kg CO2/kWh) | Recycle (0–5 Scale) | Safety (0–5 Scale) | BMS (0–5 Scale) | SoC_RT (%) | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LFP | 6000 | 100 | 95 | 160 | 333 | 1.5 | 110 | 5 | 5 | 60 | 3 | 4 | 5 | 98 | [89,90,91,92] |
| LA | 500 | 50 | 80 | 40 | 75 | 0.2 | 100 | 2 | 1 | 150 | 5 | 4 | 2 | 80 | [89,90,92] |
| NMC | 2000 | 80 | 90 | 220 | 580 | 1 | 140 | 5 | 3 | 100 | 4 | 3 | 5 | 96 | [89,90] |
| Na-Ion | 1500 | 100 | 90 | 150 | 275 | 3 | 90 | 5 | 5 | 80 | 3 | 4 | 4 | 95 | [89,90,93] |
| 2ndEV | 1200 | 80 | 85 | 120 | 400 | 1 | 70 | 5 | 3 | 40 | 4 | 3 | 3 | 90 | [89,90,92,93] |
| VRFB | 15,000 | 100 | 75 | 25 | 30 | 0.25 | 350 | 4 | 2 | 180 | 5 | 5 | 3 | 100 | [89,90,93] |
| Zn-Br | 5000 | 100 | 75 | 85 | 65 | 0.25 | 400 | 3 | 1 | 180 | 5 | 5 | 2 | 100 | [89,90,92,93] |
| NiFe | 2500 | 100 | 65 | 25 | 125 | 0.5 | 500 | 1 | 3 | 160 | 4 | 4 | 1 | 90 | [89,90,93] |
| NiZn | 800 | 80 | 85 | 100 | 280 | 2 | 450 | 5 | 4 | 16 | 5 | 5 | 3 | 92 | [89] |
| Zn-Air | 1000 | 100 | 60 | 300 | 1000 | 0.25 | 250 | 3 | 5 | 60 | 5 | 5 | 2 | 100 | [89,90,92,93] |
| Al-Ion | 2000 | 100 | 90 | 400 | 450 | 5 | 200 | 5 | 5 | 60 | 5 | 5 | 4 | 98 | [89,90,93] |
| LTO | 10,000 | 100 | 90 | 100 | 177 | 10 | 600 | 5 | 3 | 150 | 3 | 5 | 5 | 98 | [89,90,92] |
| HSC | 100,000 | 100 | 95 | 30 | 20 | 100 | 1000 | 5 | 5 | 70 | 3 | 5 | 5 | 100 | [89,90,93,94] |
| SSB | 5000 | 100 | 90 | 350 | 500 | 4 | 200 | 5 | 3 | 100 | 4 | 5 | 5 | 98 | [89,90,92] |
| 1 | 1 | 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 |
2.2.3. Decision Matrix: Converter Technologies for Solar-Based HRESs
| ConvEff (%) | PF | THD (%) | MTBF (h) | CpkW ($/kW) | Maint (0–5 Scale) | Tox (0–5 Scale) | CF (kg CO2/kW) | Recycle (0–5 Scale) | Safety (0–5 Scale) | GridComp (0–5 Scale) | Redund (0–5 Scale) | Ref. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SC | 97 | 0.99 | 3 | 80,000 | 120 | 3 | 4 | 35 | 3 | 4 | 5 | 3 | [74,91,101,102,103] |
| MC | 96 | 0.98 | 2 | 90,000 | 160 | 2 | 4 | 30 | 4 | 5 | 5 | 5 | [74,101,102,103] |
| PC | 98 | 0.99 | 2.5 | 85,000 | 150 | 2 | 4 | 32 | 3 | 5 | 5 | 4 | [74,101,102,103] |
| MMC | 98.5 | 0.99 | 2 | 95,000 | 200 | 3 | 5 | 40 | 4 | 5 | 5 | 5 | [74,101,102,103] |
| BDC | 97.5 | 0.98 | 2.5 | 92,000 | 180 | 3 | 4 | 38 | 4 | 5 | 5 | 4 | [74,101,102,103] |
| NPC | 98 | 0.99 | 2.2 | 94,000 | 210 | 4 | 5 | 42 | 4 | 5 | 5 | 5 | [74,101,102,103,104] |
| FC | 95 | 0.97 | 3.5 | 75,000 | 90 | 2 | 3 | 28 | 3 | 4 | 3 | 2 | [74,101,102,103] |
| 1 | 1 | −1 | 1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 |
2.3. Data Collection and Validation
2.4. Operational Context and System Specifications for Component Evaluation
3. Results and Discussion
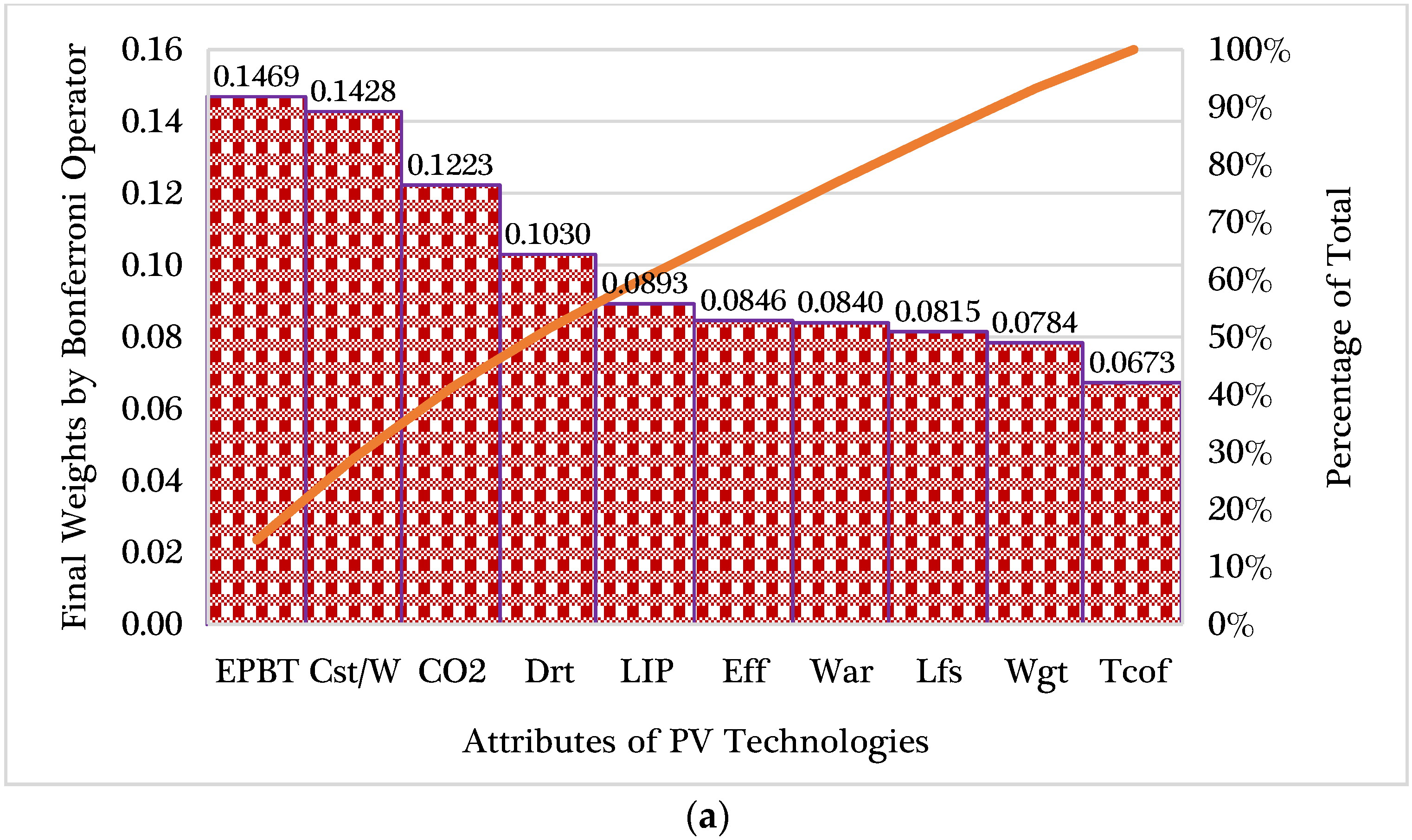
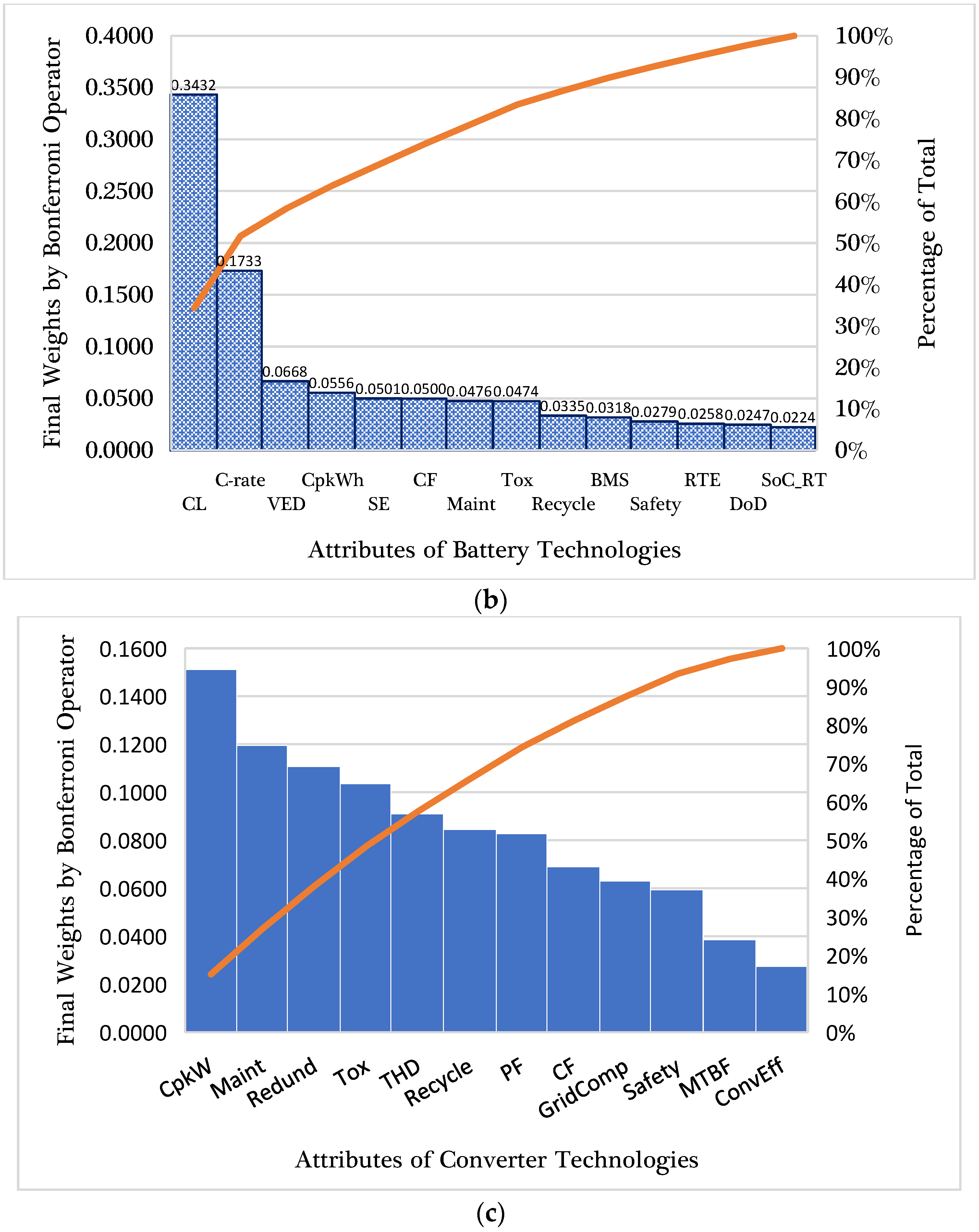
3.1. Objective Weights Computation
- CILOS: Focuses on inverse values, primarily low-performing metrics, emphasizing performance from the perspective of loss.
- Entropy: Captures the degree of disorder within the criterion values, with greater variability indicating higher importance.
- MEREC: Evaluates the direct contribution of each criterion to the overall performance.
- CRITIC: Incorporates both the standard deviation of each criterion and the degree of correlation among criteria.
- STD_DEV: A dispersion-based method that assigns greater weight to more variable criteria.
3.2. Prioritizing Benchmark by MARCOS: PV, Battery, and Converter Technologies for HRESs
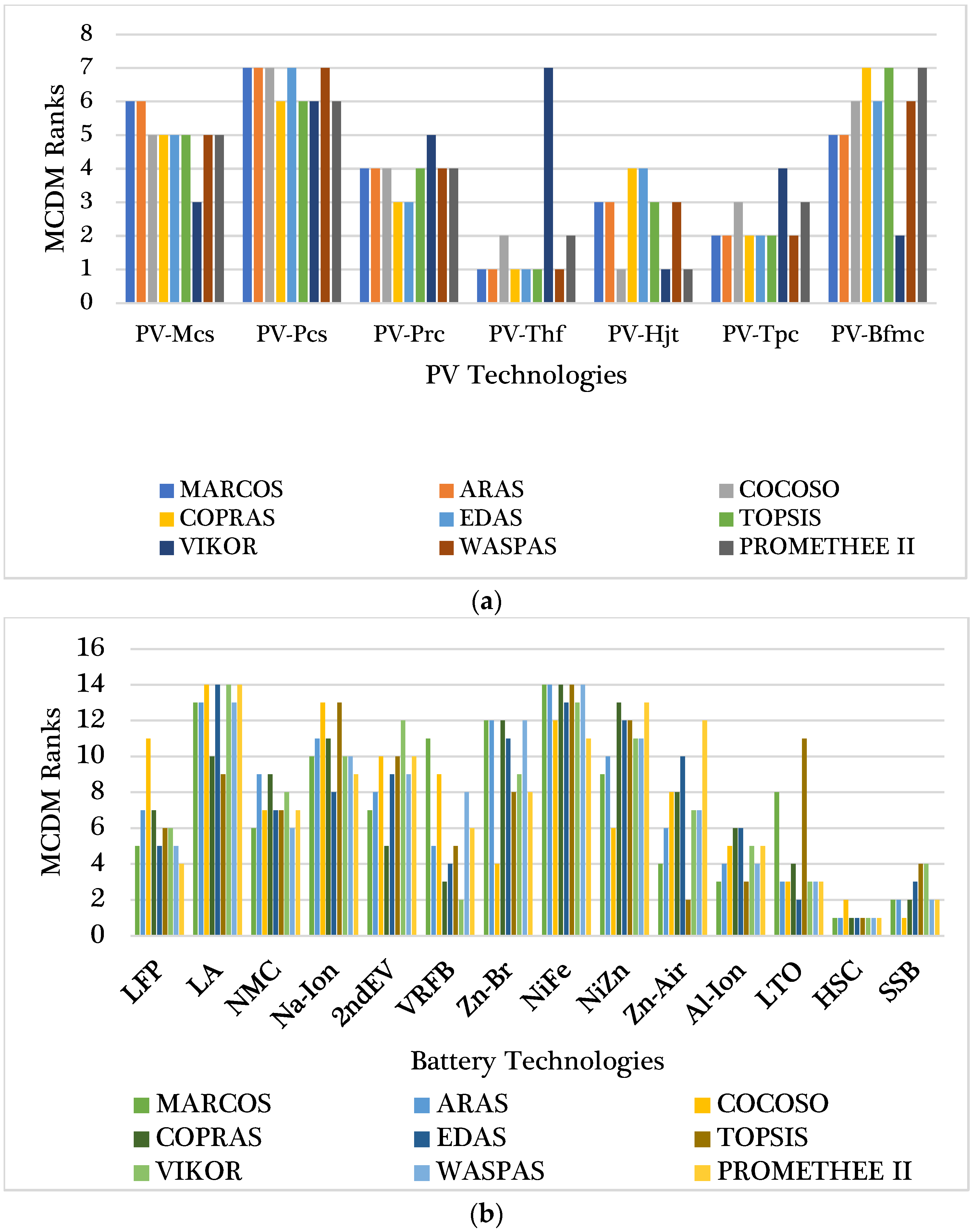
3.3. Comparative Rankings and Correlation Analysis of Technologies
4. Sensitivity Analysis
5. Discussion of Top-Ranked Technologies and Implications of the Study
5.1. Discussion of Top-Ranked Technologies
5.2. Implications of the Study
- Theoretical Implications
- Practical Implications
- Policy and Sustainability Implications
6. Conclusions
Limitations and Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Full Form/Description |
| –1/+1 | Cost/Benefit criterion orientation |
| 2ndEV | Second-Life EV Battery |
| AAI | Anti-Ideal Alternative |
| AI | Ideal Alternative |
| Al-Ion | Aluminium-Ion Battery |
| ARAS | Additive Ratio Assessment Method |
| BDC | Bidirectional DC–DC Converter |
| BMS | Battery Management System |
| Bonferroni | Bonferroni Operator for Fusion of Weights |
| CF | Carbon Footprint (kg CO2/kWh or kW) |
| CILOS | Criteria Importance through Level of Significance |
| CL | Cycle Life (number of cycles) |
| CO2 | Carbon Dioxide Emission (kg CO2 eq.) |
| COCOSO | Combined Compromise Solution |
| ConvEff | Conversion Efficiency (%) |
| COPRAS | Complex Proportional Assessment |
| CpkW | Cost per kW |
| CpkWh | Cost per kWh |
| C-rate | Charge/Discharge Rate (1/h) |
| CRITIC | Criteria Importance through Intercriteria Correlation |
| Cst/W | Cost per Watt (USD/W) |
| Dc/Drt | Degradation Constant/Rate |
| DoD | Depth of Discharge (%) |
| Drt/Dc | Degradation Rate or Constant (% per year) |
| EDAS | Evaluation based on Distance from Average Solution |
| Eff | Efficiency (%) |
| Entropy | Entropy Objective Weighting Method |
| EPBT | Energy Payback Time (years) |
| FC | Flyback Converter |
| GridComp | Grid Compatibility |
| HJT | Heterojunction Photovoltaic |
| HRES | Hybrid Renewable Energy System |
| HSC | Hybrid Supercapacitor |
| Kendall τ | Kendall’s Rank Correlation Coefficient |
| LA | Lead–Acid Battery |
| LFP | Lithium-Iron-Phosphate Battery |
| LFS | Lifespan |
| Lfs | Lifespan (years) |
| LIP | Low-Irradiance Performance |
| LTO | Lithium-Titanate Battery |
| m | Number of Alternatives |
| Maint | Maintenance Requirement (scale 0–5) |
| MARCOS | Measurement of Alternatives and Ranking according to Compromise Solution |
| MC | Modular Converter |
| MCDM | Multi-Criteria Decision-Making |
| MEREC | Method based on Removal Effects of Criteria |
| MMC | Modular Multilevel Converter |
| MTBF | Mean Time Between Failures (hours) |
| n | Number of Criteria |
| Na-Ion | Sodium-Ion Battery |
| NiFe | Nickel–Iron Battery |
| NiZn | Nickel–Zinc Battery |
| NMC | Nickel–Manganese-Cobalt Battery |
| NPC | Neutral-Point-Clamped Converter |
| PC | Power Optimizer–Central Converter Hybrid |
| PF | Power Factor |
| PROMETHEE-II | Preference Ranking Organization Method for Enrichment Evaluations-II |
| PV | Photovoltaic |
| PV-Bfmc | Bifacial Monocrystalline PV |
| PV-Hjt | Heterojunction PV |
| PV-Mcs | Monocrystalline Silicon PV |
| PV-Pcs | Polycrystalline Silicon PV |
| PV-Prc | Passivated-Emitter Rear Cell (PERC) PV |
| PV-Thf | Thin-Film Photovoltaic |
| PV-Tpc | Tunnel-Oxide Passivated Contact PV |
| Recycle | Recyclability or Second-life Potential (scale 0–5) |
| Redund | Redundancy (scale 0–5) |
| RTE | Round-Trip Efficiency (%) |
| Safety | Safety and Risk Index (scale 0–5) |
| SC | String Converter |
| SDGs | Sustainable Development Goals |
| SE | Specific Energy (Wh kg−1) |
| SoC | State of Charge |
| SoC_RT | State-of-Charge Retention (%) |
| Spearman ρ | Spearman’s Rank Correlation Coefficient |
| SSB | Solid-State Battery |
| STD_DEV | Standard Deviation Weighting Method |
| Tcof | Temperature Coefficient (%/°C) |
| THD | Total Harmonic Distortion (%) |
| TOPSIS | Technique for Order Preference by Similarity to Ideal Solution |
| Tox | Toxicity or Environmental Hazard (scale 0–5) |
| VED | Volumetric Energy Density (Wh L−1) |
| VIKOR | VlseKriterijumska Optimizacija I Kompromisno Resenje (Multicriteria Optimization and Compromise Solution) |
| VRFB | Vanadium Redox Flow Battery |
| War | Warranty (years) |
| WASPAS | Weighted Aggregated Sum Product Assessment |
| Wgt | Weight (kg m−2) |
| Zn-Air | Zinc–Air Battery |
| Zn-Br | Zinc–Bromine Flow Battery |
| δ | Perturbation factor for Sensitivity Analysis |
| ρ, τ | Correlation Coefficients used for validation |
References
- Xu, C.; Isabella, O.; Vogt, M.R. Future material demand for global silicon-based PV modules under net-zero emissions target until 2050. Resour. Conserv. Recycl. 2024, 210, 107824. [Google Scholar] [CrossRef]
- Imandoust, M.; Alghorayshi, S.T.K.; Abbasi, S.; Seifollahi, M.; Zahedi, R. Simultaneous Energy, Fresh Water, and Biogas Production Process Utilizing Solar Thermal and Sewage Sludge. Energy Sci. Eng. 2025, 13, 530–550. [Google Scholar] [CrossRef]
- Badran, G.; Dhimish, M. Comprehensive study on the efficiency of vertical bifacial photovoltaic systems: A UK case study. Sci. Rep. 2024, 14, 18380. [Google Scholar] [CrossRef]
- Iturralde Carrera, L.A.I.; Molina-Santana, E.; Álvarez-Alvarado, J.M.; García-Martínez, J.R.; Rodríguez-Reséndiz, J. Energy Efficiency Analysis of East-West Oriented Photovoltaic Systems for Buildings: A Technical-Economic-Environmental Approach. IEEE Access 2023, 11, 137660–137679. [Google Scholar] [CrossRef]
- Buerhop, C.; Stroyuk, O.; Mashkov, O.; Barabash, A.; Hauch, J.A.; Marius Peters, I.M. Polymer encapsulation impact on potential-induced degradation in PV modules revealed by a multi-modal field study. Sol. Energy Mater. Sol. Cells 2024, 277, 113111. [Google Scholar] [CrossRef]
- Wu, X.; Wang, X.; Yang, W.; Nie, J.; Yuan, J.; Khan, M.U.; Ciesla, A.; Sen, C.; Qiao, Z.; Hoex, B. Enhancing the reliability of TOPCon technology by laser-enhanced contact firing. Sol. Energy Mater. Sol. Cells 2024, 271, 112846. [Google Scholar] [CrossRef]
- Castriotta, L.A.; Stefanelli, M.; Vesce, L.; Magliano, E.; Leonardi, E.; Di Giacomo, F.; Nikbakht, H.; Serenelli, L.; Martini, L.; Menchini, F. Semitransparent Perovskite Solar Submodule for 4T Tandem Devices: Industrial Engineering Route Toward Stable Devices. IEEE J. Photovolt. 2024, 14, 433–441. [Google Scholar] [CrossRef]
- Akram Cheema, H.; Ilyas, S.; Kang, H.; Kim, H. Comprehensive review of the global trends and future perspectives for recycling of decommissioned photovoltaic panels. Waste Manag. 2024, 174, 187–202. [Google Scholar] [CrossRef]
- Konstantinavičiūtė, I.; Bobinaitė, V.; Lekavičius, V.; Venckunaite, U. Assessing the sustainability of solar photovoltaics: The case of glass–glass and standard panels manufactured in Lithuania. Clean Technol. Environ. Policy 2025, 27, 1877–1898. [Google Scholar] [CrossRef]
- Munawer Al-Otum, H. Classification of anomalies in electroluminescence images of solar PV modules using CNN-based deep learning. Sol. Energy 2024, 278, 112803. [Google Scholar] [CrossRef]
- Li, Y.; Gao, J.; Li, Y.; Chen, C.; Li, S.; Shahidehpour, M.; Chen, Z. Physical Informed-Inspired Deep Reinforcement Learning Based Bi-Level Programming for Microgrid Scheduling. IEEE Trans. Ind. Appl. 2025, 61, 1488–1500. [Google Scholar] [CrossRef]
- Esmaeel Nezhad, A.; Nardelli, P.H.J. Multiple-Criteria Decision-Making (MCDM) Applications in Optimizing Multi-objective Energy System Performance. In Handbook of Smart Energy Systems; Fathi, M., Zio, E., Pardalos, P.M., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 1477–1508. [Google Scholar]
- Almulaisi, T.A.; Wahab, N.I.A.; Zaynal, H.I.; Hassan, M.K.; Majdi, H.S.; Radhi, A.D.; Solke, N.; Sekhar, R. Optimization of Harmonic Elimination in PV-Fed Asymmetric Multilevel Inverters Using Evolutionary Algorithms. Int. J. Robot. Control Syst. 2025, 5, 902–916. [Google Scholar] [CrossRef]
- Rashid, Z.; Amjad, M.; Anjum, W. Indirect grid power factor tuning with PV-STATCOM using shift mode phase locking strategy. Electr. Eng. 2023, 105, 1317–1329. [Google Scholar] [CrossRef]
- Srikanth, S.; Nayak, B. Reliability Improvement of Grid Connected PV Inverter Considering Monofacial and Bifacial Panels Using Hybrid IGBT. Int. J. Electr. Electron. Res. 2024, 12, 443–452. [Google Scholar] [CrossRef]
- Li, S.; Zhou, J.; Zhou, F.; Niu, F.; Deng, W. A Reduced Current Ripple Overmodulation Strategy for Indirect Matrix Converter. IEEE Trans. Ind. Electron. 2025, 72, 3768–3777. [Google Scholar] [CrossRef]
- Li, N.; Cao, Y.; Liu, X.; Zhang, Y.; Wang, R.; Jiang, L.; Zhang, X. An Improved Modulation Strategy for Single-Phase Three-Level Neutral-Point-Clamped Converter in Critical Conduction Mode. J. Mod. Power Syst. Clean Energy 2024, 12, 981–990. [Google Scholar] [CrossRef]
- Li, N.; Zhang, C.; Liu, Y.; Zhuo, C.; Liu, M.; Yang, J.; Zhang, Y. Single-Degree-of-Freedom Hybrid Modulation Strategy and Light-Load Efficiency Optimization for Dual-Active-Bridge Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 3936–3947. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhu, C.; Goetz, S.M. Fault-Tolerant Multiparallel Three-Phase Two-Level Converters with Adaptive Hardware Reconfiguration. IEEE Trans. Power Electron. 2024, 39, 3925–3930. [Google Scholar] [CrossRef]
- Gao, S.; Chen, Y.; Song, Y.; Yu, Z.; Wang, Y. An Efficient Half-Bridge MMC Model for EMTP-Type Simulation Based on Hybrid Numerical Integration. IEEE Trans. Power Syst. 2024, 39, 1162–1177. [Google Scholar] [CrossRef]
- Jing, Y.; Zhang, J.; Su, L.; Shi, G.; Zang, J.; Zhou, J.; Cai, X. A Novel Modular DC Chopper Based on Combination of Fully and Semi-Controlled Devices for Offshore Wind VSC-HVDC Transmission System. IEEE Trans. Power Electron. 2025, 1–14. [Google Scholar] [CrossRef]
- Aljaghoub, H.; Abumadi, F.; AlMallahi, M.N.; Obaideen, K.; Al-Alami, A.H. Solar PV cleaning techniques contribute to Sustainable Development Goals (SDGs) using Multi-criteria decision-making (MCDM): Assessment and review. Int. J. Thermofluids 2022, 16, 100233. [Google Scholar] [CrossRef]
- AlMallahi, M.N.; El Haj Assad, M.; Al-Shihabi, S.; Alayi, R. Multi-criteria decision-making approach for the selection of cleaning method of solar PV panels in United Arab Emirates based on sustainability perspective. Int. J. Low-Carbon Technol. 2022, 17, 380–393. [Google Scholar] [CrossRef]
- Ajithkumar, A.; Poongavanam, P. A systematic framework for the optimum selection of organic PCM in sustainable solar drying process: A multi-criteria decision-making methodology. J. Energy Storage 2025, 116, 116080. [Google Scholar] [CrossRef]
- Ali, T.; Sunny, M.; Aghaloo, K.; Wang, K. Planning off-grid hybrid energy system using techno-economic optimization and wins in league theory-based multi-criteria decision-making method in the wetland areas of developing countries. Energy Convers. Manag. 2024, 313, 118587. [Google Scholar] [CrossRef]
- Alanazi, A.; Jan, S.T.; Alanazi, M.; Khan, Z. Analysis of hybrid energy systems for electric vehicle charging of different demographics. Clean Technol. Environ. Policy 2025, 27, 1067–1092. [Google Scholar] [CrossRef]
- Dehghan, H.; Pourfayaz, F.; Shahsavari, A. Multicriteria decision and Geographic Information System-based locational analysis and techno-economic assessment of a hybrid energy system. Renew. Energy 2022, 198, 189–199. [Google Scholar] [CrossRef]
- Tajik, M.; Makui, A.; Tosarkani, B.M. Sustainable cathode material selection in lithium-ion batteries using a novel hybrid multi-criteria decision-making. J. Energy Storage 2023, 66, 107089. [Google Scholar] [CrossRef]
- Sadeghitabar, E.; Ghasempour, R.; Vaziri Rad, M.A.; Toopshekan, A. Optimization and Shannon entropy multi-criteria decision-making method for implementing modern renewable energies in stand-alone greenhouses. Energy Convers. Manag. X 2025, 27, 101139. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.; Xie, J.; Cheng, Y.; Shi, L. Hybrid multi-criteria decision-making evaluation of multiple renewable energy systems considering the hysteresis band principle. Int. J. Hydrog. Energy 2024, 49, 450–462. [Google Scholar] [CrossRef]
- Makai, L.; Popoola, O. Assessment and selection of a micro-hybrid renewable energy system for sustainable energy generation in rural areas of Zambia. Renew. Energy 2024, 232, 121036. [Google Scholar] [CrossRef]
- Setiawan, E.A.; Radevito, A.; Dewi, K. A Combined Ranking and Sensitivity Analysis of Power Generation Using Multi-Criteria Decision-Making and Monte-Carlo Simulation. Int. J. Energy Econ. Policy 2024, 14, 358–367. [Google Scholar] [CrossRef]
- Elsayed, I.; Kanaan, H.; Mehanna, M. Feasibility and optimal sizing analysis of hybrid PV/Wind powered seawater desalination system: A case study of four ports, Egypt. Heliyon 2024, 10, e40313. [Google Scholar] [CrossRef]
- Grewal, K.S.; Hachem, C.; Yadav, S. Decision-making method to prioritize and implement solar strategies on neighborhood level. Energy Rep. 2024, 12, 2062–2076. [Google Scholar] [CrossRef]
- Habibzadeh, S.; Razi Astaraei, F.R.; Jahangir, M.H. Sustainability assessment of a petrochemical plant electricity supply based on 4E optimization of various hybrid renewable energy systems scenarios. Energy Convers. Manag. 2025, 325, 119357. [Google Scholar] [CrossRef]
- Miao, H.; Yu, Y.; Kharrazi, A.; Ma, T. Multi-criteria decision analysis for the planning of island microgrid system: A case study of Yongxing island, China. Energy 2023, 284, 129264. [Google Scholar] [CrossRef]
- Roy, D.; Bhowmik, M.; Roskilly, A.P. Technoeconomic, environmental and multi criteria decision making investigations for optimisation of off-grid hybrid renewable energy system with green hydrogen production. J. Clean. Prod. 2024, 443, 141033. [Google Scholar] [CrossRef]
- Serrano-Gomez, L.; Gil-Garcia, I.C.; Garcia-Cascales, M.S.; Fernández–Guillamón, A. Improving the Selection of PV Modules and Batteries for Off-Grid PV Installations Using a Decision Support System. Information 2024, 15, 380. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Methods for Multiple Attribute Decision Making. In Multiple Attribute Decision Making: Methods and Applications A State-of-the-Art Survey; Hwang, C.-L., Yoon, K., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Duckstein, L. Multiobjective optimization in river basin development. Water Resour. Res. 1980, 16, 14–20. [Google Scholar] [CrossRef]
- Hussain, S.; Mandal, U. Entropy Based MCDM Approach for Selection of Material. In Proceedings of the National Level Conference on Engineering Problems and Application of Mathematics, Barjala, Jirania, 4 June 2016; NIT Agartala: Barjala, Jirania, 2016. [Google Scholar]
- Shekhovtsov, A.; Sałabun, W. The New Algorithm for Effective Reducing the Number of Pairwise Comparisons in the Decision Support Methods. In European Conference on Artificial Intelligence; Springer: Cham, Switzerland, 2023; pp. 243–254. [Google Scholar]
- Tuş, A.; Aytaç Adalı, E. The new combination with CRITIC and WASPAS methods for the time and attendance software selection problem. Opsearch 2019, 56, 528–538. [Google Scholar] [CrossRef]
- Ulutaş, A.; Karabasevic, D.; Popovic, G.; Stanujkic, D.; Nguyen, P.T.; Karaköy, Ç. Development of a Novel Integrated CCSD-ITARA-MARCOS Decision-Making Approach for Stackers Selection in a Logistics System. Mathematics 2020, 8, 1672. [Google Scholar] [CrossRef]
- Zavadskas, E.; Turskis, Z. A new additive ratio assessment (ARAS) method in multicriteria decision-making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Podvezko, V. Integrated Determination of Objective Criteria Weights in MCDM. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 267–283. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to COmpromise solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Sidhu, A.S.; Singh, S.; Kumar, R.; Pimenov, D.Y.; Giasin, K. Prioritizing energy-intensive machining operations and gauging the influence of electric parameters: An industrial case study. Energies 2021, 14, 4761. [Google Scholar] [CrossRef]
- Xu, C.; Ke, Y.; Li, Y.; Chu, H.; Wu, Y. Data-driven configuration optimization of an off-grid wind/PV/hydrogen system based on modified NSGA-II and CRITIC-TOPSIS. Energy Convers. Manag. 2020, 215, 112892. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, P.; Zavadskas, E.K.; Stevic, Ž.; Vujovic, V. A New Joint Strategy for Multi-Criteria Decision-Making: A Case Study for Prioritizing Solid-State Drive. Int. J. Comput. Commun. Control 2022, 17, 1–17. [Google Scholar] [CrossRef]
- Lotfi, F.H.; Fallahnejad, R. Imprecise Shannon’s Entropy and Multi Attribute Decision Making. Entropy 2010, 12, 53–62. [Google Scholar] [CrossRef]
- Kurama, O.; Luukka, P.; Collan, M. A Similarity Classifier with Bonferroni Mean Operators. Adv. Fuzzy Syst. 2016, 2016, 7173054. [Google Scholar] [CrossRef]
- Bilandi, N.; Verma, H.K.; Dhir, R. AHP-neutrosophic decision model for selection of relay node in wireless body area network. CAAI Trans. Intell. Technol. 2020, 5, 222–229. [Google Scholar] [CrossRef]
- Brauers, W. Optimization Methods for a Stakeholder Society. A Revolution in Economic Thinking by Multi-Objective Optimization; Springer New York: New York, NY, USA, 2004. [Google Scholar]
- Vakilifard, N.; Bahri, P.A.; Anda, M.; Ho, G. An interactive planning model for sustainable urban water and energy supply. Appl. Energy 2019, 235, 332–345. [Google Scholar] [CrossRef]
- Kumar, R.; Saha, R.; Simic, V.; Dev, N.; Kumar, R.; Kumar Banga, H.; Bacanin, N.; Singh, S. Rooftop solar potential in micro, small, and medium size enterprises: An insight into renewable energy tapping by decision-making approach. Sol. Energy 2024, 276, 112692. [Google Scholar] [CrossRef]
- Prabatha, T.; Hager, J.; Carneiro, B.; Hewage, K.; Sadiq, R. Analyzing energy options for small-scale off-grid communities: A Canadian case study. J. Clean. Prod. 2020, 249, 119320. [Google Scholar] [CrossRef]
- Kaneesamkandi, Z.; Rehman, A.U. Optimum and sustainable cooling technology selection for different climatic conditions. Energies 2021, 14, 6136. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Shekhovtsov, A.; Więckowski, J.; Wątróbski, J.; Sałabun, W. The Compromise-COMET Method for Identifying an Adaptive Multi-Criteria Decision Model. IEEE Access 2024, 12, 157083–157106. [Google Scholar] [CrossRef]
- Haddad, B.; Díaz-Cuevas, P.; Ferreira, P.; Djebli, A.; Pérez, J.P. Mapping concentrated solar power site suitability in Algeria. Renew. Energy 2021, 168, 838–853. [Google Scholar] [CrossRef]
- Ignacz, G.; Beke, A.K.; Toth, V.; Szekely, G. A hybrid modelling approach to compare chemical separation technologies in terms of energy consumption and carbon dioxide emissions. Nat. Energy 2025, 10, 308–317. [Google Scholar] [CrossRef]
- Gnanasekaran, G.; Sivakumar, R.; Ilangkumaran, M.; Ikua, B.W. Selection of optimum fish oil fuel blend to reduce the greenhouse gas emissions in an IC engine—A hybrid multiple criteria decision aid approach. Int. J. Green Energy 2016, 13, 1517–1533. [Google Scholar] [CrossRef]
- Lokhande, S.; Kalbar, P.P. Economic and environmental benefits of natural treatment systems for sewage treatment: A life cycle perspective. Water Res. 2024, 257, 121710. [Google Scholar] [CrossRef]
- Yang, S.; Luo, Y. Short-term photovoltaic power prediction based on RF-SGMD-GWO-BiLSTM hybrid models. Energy 2025, 316, 134545. [Google Scholar] [CrossRef]
- Abdallah, A.A.; Kivambe, M.; Abdelrahim, M.; Elgaili, M.; Ahmed, A.; Mroue, K.; Stroyuk, O.; Mashkov, O.; Peters, I.M.; Buerhop-Lutz, C. Early degradation of silicon heterojunction PV modules installed on horizontal single-axis trackers in desert climate. Sol. Energy Mater. Sol. Cells 2026, 294, 113899. [Google Scholar] [CrossRef]
- Duan, X.; Mi, W.; Guo, S.; Shen, C.; Kalogirou, S.A. Experimental Investigation on a Novel PV-Trombe Wall for Air Heating and Purification in the Severe Cold Region. Renew. Energy 2025, 248, 123126. [Google Scholar] [CrossRef]
- Wei, T.; Zhang, Y.; Zhang, Y.; Miao, R.; Kang, J.; Qi, H. City-Scale Roof-Top Photovoltaic Deployment Planning. Appl. Energy 2024, 368, 123461. [Google Scholar] [CrossRef]
- Yang, M.; Jiang, Y.; Guo, Y.; Su, X.; Li, Y.; Huang, T. Ultra-Short-Term Prediction of Photovoltaic Cluster Power Based on Spatiotemporal Convergence Effect and Spatiotemporal Dynamic Graph Attention Network. Renew. Energy 2025, 255, 123843. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Zheng, B.; Cui, H.; Qi, H. Statistical Analysis for Estimating the Optimized Battery Capacity for Roof-Top PV Energy System. Renew. Energy 2025, 242, 122491. [Google Scholar] [CrossRef]
- Bhandari, K.P.; Collier, J.M.; Ellingson, R.J.; Apul, D.S. Energy payback time (EPBT) and energy return on energy invested (EROI) of solar photovoltaic systems: A systematic review and meta-analysis. Renew. Sustain. Energy Rev. 2015, 47, 133–141. [Google Scholar] [CrossRef]
- Ashby, L.; Haghdadi, N.; Passey, R.; Bruce, A.; Egan, R.J. National Survey Report of PV Power Applications in AUSTRALIA 2023; IEA Photovoltaic Power Systems Programme (IEA PVPS), Task 1: Australia; IEA: Paris, France, 2024. [Google Scholar]
- Fraunhofer Institute for Solar Energy Systems ISE. Photovoltaics Report; Fraunhofer ISE: Freiburg, Germany, 2023. [Google Scholar]
- Jordan, D.C.; Kurtz, S.R. Photovoltaic Degradation Rates—An Analytical Review; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2012.
- SMA SMART CONNECTED. SUNNY TRIPOWER 15000TL/20000TL/25000TL Data Sheet; SMA Solar Technology AG: Niestetal, Germany, 2021. [Google Scholar]
- REC Solar Panels. REC Alpha Pure-RX Datasheet; REC Group: Singapore, 2025. [Google Scholar]
- Stein, J.S.; Maugeri, G.; Riedel-Lyngskær, N.; Ovaitt, S.; Müller, T.; Wang, S.; Huerta, H.; Leloux, J.; Vedde, J.; Berwind, M.; et al. Best Practices for the Optimization of Bifacial Photovoltaic Tracking Systems (IEA-PVPS T13-26:2024); IEA Photovoltaic Power Systems Programme (IEA-PVPS), Task 13; IEA: Paris, France, 2024; ISBN 978-3-907281-62-8. [Google Scholar]
- Global Module Prices Trend Upward in Q2. Pv-Magazine International. 2025. Available online: https://www.pv-magazine.com/2025/03/14/global-module-prices-trend-upward-in-q2/ (accessed on 9 October 2025).
- International Energy Agency. Energy Technology Perspectives 2024; International Energy Agency: Paris, France, 2024. [Google Scholar]
- Rajput, S.; Averbukh, M.; Rodriguez, N. Energy Harvesting and Energy Storage Systems; MDPI AG: Basel, Switzerland, 2024; Volume II. [Google Scholar]
- Torul Yürek, Y.; Bulut, M.; Özyörük, B.; Özcan, E. Evaluation of the hybrid renewable energy sources using sustainability index under uncertainty. Sustain. Energy Grids Netw. 2021, 28, 100527. [Google Scholar] [CrossRef]
- Nagaraju, D.; Chiranjeevi, C.; Raja Sekhar, Y.; Senthil Kumaran, S.K.; Chadha, U.; Nagalakshmi, R.; Paramasivam, V. Semantic Approach for Evaluation of Energy Storage Technologies under Fuzzy Environment. Adv. Fuzzy Syst. 2022, 2022, 1149503. [Google Scholar] [CrossRef]
- Lv, S.; Wang, J.; Zhai, Y.; Chen, Y.; Yang, J.; Zhu, Z.; Peng, R.; Fu, X.; Yang, W.; Wang, Y. Lithium-Ion Dynamic Interface Engineering of Nano-Charged Composite Polymer Electrolytes for Solid-State Lithium-Metal Batteries. Nano-Micro Lett. 2025, 18, 46. [Google Scholar] [CrossRef]
- Lai, T.; Wang, L.; Liu, Z.; Bhayo, A.M.; Wang, Y.; He, X. Tackling Challenges and Exploring Opportunities in Cathode Binder Innovation. Nano-Micro Lett. 2025, 18, 9. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Liu, H.; Xiang, W.; Chen, L.; Li, X.; Xue, B.; Ma, J.; Wu, Y.; Wang, C.; Bao, Y.; et al. Highly compressible garnet thin films for high-energy-density Li metal batteries. J. Mater. Sci. Technol. 2026, 251, 30–38. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, Y.; Xing, B.; Guan, X.; Zeng, H.; Zhao, S.; Qu, X.; Xing, Y. Magnesiothermic reduction synthesis of C@Si composite from fly ash cenospheres as high-performance anode materials for lithium-ion batteries. Fuel 2026, 406, 136787. [Google Scholar] [CrossRef]
- Li, F.; Xie, J.; Fan, Y.; Qiu, J. Potential of Different Forms of Gravity Energy Storage. Sustain. Energy Technol. Assess. 2024, 64, 103728. [Google Scholar] [CrossRef]
- Niu, X.; Ma, N.; Bu, Z.; Hong, W.; Li, H. Thermodynamic Analysis of Supercritical Brayton Cycles Using CO2-Based Binary Mixtures for Solar Power Tower System Application. Energy 2022, 254, 124286. [Google Scholar] [CrossRef]
- Meng, Q.; He, Y.; Hussain, S.; Lu, J.; Guerrero, J.M. Design and Optimization of Solar Photovoltaic Microgrids with Adaptive Storage Control for Residential Standalone Systems. Energy Rep. 2025, 14, 989–997. [Google Scholar] [CrossRef]
- U.S. Department of Energy; Sandia National Laboratories. DOE Global Energy Storage Database; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2024.
- National Renewable Energy Laboratory. 2023 Electricity Annual Technology Baseline (ATB); National Renewable Energy Laboratory: Golden, CO, USA, 2023.
- Feldman, D.; Zuboy, J.; Dummit, K.; Heine, M.; Grossman, S.; Narayanaswami, M. Spring 2025 Solar Industry Update; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2025.
- Frith, J.T.; Lacey, M.J.; Ulissi, U. A non-academic perspective on the future of lithium-based batteries. Nat. Commun. 2023, 14, 420. [Google Scholar] [CrossRef]
- Contemporary Amperex Technology Co., Ltd. Breaking Through the Bottleneck of Sodium-Ion Battery Technology. CATL News. 2021. Available online: https://www.catl.com/en/news/665.html (accessed on 9 October 2025).
- Allah, S.M.; Aslam, M.K.; Hussain, I.; Hassan, F.M.; Al-Marzouqi, A.; Xu, M. Ultra-high-performance zinc-ion supercapacitor based on single-copper molybdate urchins. J. Energy Storage 2025, 131, 117610. [Google Scholar] [CrossRef]
- Manirathinam, T.; Narayanamoorthy, S.; Geetha, S.; Othman, M.F.I.; Alotaibi, B.S.; Ahmadian, A.; Kang, D. Sustainable renewable energy system selection for self-sufficient households using integrated fermatean neutrosophic fuzzy stratified AHP-MARCOS approach. Renew. Energy 2023, 218, 119292. [Google Scholar] [CrossRef]
- Barcellona, S.; Barresi, M.; Codecasa, L.; Grillo, S. Multilevel converter based on cascaded three-phase six-leg modules. Electr. Power Syst. Res. 2025, 249, 112090. [Google Scholar] [CrossRef]
- Radecic, I.; Filipovic-Grcic, B.; Akiki, P.; Xémard, A.; Jurisic, B. Investigation of resonance between HVDC-MMC link and AC network. Electr. Power Syst. Res. 2026, 251, 112231. [Google Scholar] [CrossRef]
- Hsu, C.Y.; Pallathadka, H.; Patel, P.; Kottala, K.S.; Bokov, D.O.; Rao, S.B.; Kumar, A.V.; Verma, A.; Mamory, T.R.A.; Faaq, A.S. A novel approach for optimizing a photovoltaic thermal system combined with solar thermal collector: Integrating RSM, multi-objective bat algorithm and VIKOR decision maker. J. Taiwan Inst. Chem. Eng. 2025, 168, 105927. [Google Scholar] [CrossRef]
- Ranjbaran, P.; Yousefi, H.; Javadinia, M.; Izanloo, N.; Astaraei, F.R.; Abdoos, M. Integrated modeling of energy generation and water resource management utilizing floating photovoltaic (FPV) technology in semi-arid regions. Sol. Energy 2025, 301, 113983. [Google Scholar] [CrossRef]
- Zhou, B.; He, J.; Li, B.; Li, Y.; Li, Y.; Cao, R. A novel fault analysis method considering control states for MMC grid-forming system with renewable energy generation. Int. J. Electr. Power Energy Syst. 2025, 171, 111031. [Google Scholar] [CrossRef]
- Enphase Energy, I. IQ8 Series Microinverters Data Sheet (North America, Rev 2.0); Enphase Energy, Inc.: Fremont, CA, USA, 2024. [Google Scholar]
- SolarEdge Technologies, Ltd. SolarEdge Single-Phase Inverter with HD-Wave Technology Data Sheet; SolarEdge Technologies, Ltd.: Herzliya, Israel, 2021. [Google Scholar]
- Wang, Y.; Aksoz, A.; Geury, T.; Ozturk, S.B.; Kivanc, O.C.; Hegazy, O. A Review of Modular Multilevel Converters for Stationary Applications. Appl. Sci. 2020, 10, 7719. [Google Scholar] [CrossRef]
- Husev, O.; Roncero-Clemente, C.; Romero-Cadaval, E.; Vinnikov, D.; Jalakas, T. Three-level three-phase quasi-Z-source neutral-point-clamped inverter with novel modulation technique for photovoltaic application. Electr. Power Syst. Res. 2016, 130, 10–21. [Google Scholar] [CrossRef]
- Xiahou, K.; Du, W.; Xu, X.; Lin, Z.; Liu, Y.; Liu, Z.; Wu, Q. Resilience Assessment for Hybrid AC/DC Cyber-Physical Power Systems Under Cascading Failures. IEEE Trans. Reliab. 2025, 74, 3442–3453. [Google Scholar] [CrossRef]
- Sivasankar, S.M.; Amorim, C.D.O.; Cunha, A.F.D. Progress in Thin-Film Photovoltaics: A Review of Key Strategies to Enhance the Efficiency of CIGS, CdTe, and CZTSSe Solar Cells. J. Compos. Sci. 2025, 9, 143. [Google Scholar] [CrossRef]
- Tian, X.; Chi, Y.; Li, L.; Liu, H. Review of the Configuration and Transient Stability of Large-Scale Renewable Energy Generation Through Hybrid DC Transmission. CES Trans. Electr. Mach. Syst. 2024, 8, 115–126. [Google Scholar] [CrossRef]
- Jamil, U.; Pearce, J.M. Experimental impacts of transparency on strawberry agrivoltaics using thin film photovoltaic modules under low light conditions. Sol. Energy 2025, 290, 113375. [Google Scholar] [CrossRef]
- Sarwar, S.; Javed, M.Y.; Jaffery, M.H.; Ashraf, M.S.; Naveed, M.T.; Hafeez, M.A. Modular Level Power Electronics (MLPE) Based Distributed PV System for Partial Shaded Conditions. Energies 2022, 15, 4797. [Google Scholar] [CrossRef]


| PV Technologies for Solar-Based HRESs | ||||||
|---|---|---|---|---|---|---|
| CILOS | ENTROPY | MEREC | CRITIC | STD_DEV | Bonferroni | |
| CO2 | 0.1614 | 0.1548 | 0.1064 | 0.0889 | 0.0921 | 0.1223 |
| EPBT | 0.1399 | 0.3614 | 0.0678 | 0.0943 | 0.1030 | 0.1469 |
| Cst/W | 0.1911 | 0.0979 | 0.1983 | 0.1106 | 0.1091 | 0.1428 |
| Drt | 0.1725 | 0.0544 | 0.1327 | 0.0684 | 0.0876 | 0.1030 |
| War | 0.0398 | 0.0627 | 0.0904 | 0.1236 | 0.1013 | 0.0840 |
| Lfs | 0.0193 | 0.0514 | 0.1039 | 0.1296 | 0.1074 | 0.0815 |
| Eff | 0.0653 | 0.0532 | 0.1017 | 0.0996 | 0.0969 | 0.0846 |
| Tcof | 0.0837 | 0.0506 | 0.0410 | 0.0683 | 0.0887 | 0.0673 |
| Wgt | 0.0420 | 0.0492 | 0.0797 | 0.1163 | 0.1032 | 0.0784 |
| LIP | 0.0850 | 0.0644 | 0.0782 | 0.1004 | 0.1106 | 0.0893 |
| Battery Technologies for Solar-based HRESs | ||||||
| CL | 0.2943 | 0.9712 | 0.0568 | 0.3461 | 0.0714 | 0.3432 |
| DoD | 0.0031 | 0.0006 | 0.0607 | 0.0001 | 0.0714 | 0.0247 |
| RTE | 0.0019 | 0.0004 | 0.0680 | 0.0006 | 0.0714 | 0.0258 |
| SE | 0.0709 | 0.0046 | 0.0637 | 0.0228 | 0.0714 | 0.0501 |
| VED | 0.0807 | 0.0101 | 0.0575 | 0.0853 | 0.0714 | 0.0668 |
| C-rate | 0.3883 | 0.0010 | 0.0570 | 0.3551 | 0.0714 | 0.1733 |
| CpkWh | 0.0636 | 0.0097 | 0.0687 | 0.0412 | 0.0714 | 0.0556 |
| Maint | 0.0141 | 0.0001 | 0.0918 | 0.0512 | 0.0714 | 0.0476 |
| Tox | 0.0219 | 0.0001 | 0.0980 | 0.0372 | 0.0714 | 0.0474 |
| CF | 0.0335 | 0.0020 | 0.0706 | 0.0547 | 0.0714 | 0.0500 |
| Recycle | 0.0049 | 0.0000 | 0.1032 | 0.0037 | 0.0714 | 0.0335 |
| Safety | 0.0033 | 0.0000 | 0.0781 | 0.0006 | 0.0714 | 0.0279 |
| BMS | 0.0190 | 0.0001 | 0.0714 | 0.0011 | 0.0714 | 0.0318 |
| SoC_RT | 0.0004 | 0.0002 | 0.0544 | 0.0003 | 0.0714 | 0.0224 |
| Converter Technologies for Solar-based HRESs | ||||||
| ConvEff | 0.0033 | 0.0004 | 0.0068 | 0.0692 | 0.0753 | 0.0275 |
| PF | 0.3269 | 0.0001 | 0.0028 | 0.0792 | 0.0830 | 0.0827 |
| THD | 0.1321 | 0.0942 | 0.0702 | 0.0602 | 0.0778 | 0.0910 |
| MTBF | 0.0000 | 0.0178 | 0.0328 | 0.0666 | 0.0798 | 0.0386 |
| CpkW | 0.0022 | 0.2343 | 0.3567 | 0.1110 | 0.0756 | 0.1511 |
| Maint | 0.1264 | 0.1669 | 0.1031 | 0.0938 | 0.0798 | 0.1195 |
| Tox | 0.0797 | 0.0728 | 0.1684 | 0.1035 | 0.0728 | 0.1035 |
| CF | 0.0094 | 0.0541 | 0.0901 | 0.1026 | 0.0793 | 0.0688 |
| Recycle | 0.0919 | 0.0531 | 0.0441 | 0.1027 | 0.1128 | 0.0844 |
| Safety | 0.0689 | 0.0258 | 0.0138 | 0.0811 | 0.1030 | 0.0593 |
| GridComp | 0.0705 | 0.0674 | 0.0187 | 0.0660 | 0.0798 | 0.0630 |
| Redund | 0.0889 | 0.2131 | 0.0923 | 0.0642 | 0.0812 | 0.1107 |
| PV Technologies for Solar-based HRESs | |||||
|---|---|---|---|---|---|
| PV Technology | Sum of Weighted Values | Utility vs. Ideal | Utility vs. Anti-Ideal | Final Utility Score | Rank |
| PV-Mcs | 0.6327 | 0.6327 | 1.2687 | 0.5426 | 6 |
| PV-Pcs | 0.5925 | 0.5925 | 1.1881 | 0.5082 | 7 |
| PV-Prc | 0.6954 | 0.6954 | 1.3946 | 0.5965 | 4 |
| PV-Thf | 0.8287 | 0.8287 | 1.6619 | 0.7108 | 1 |
| PV-Hjt | 0.7294 | 0.7294 | 1.4628 | 0.6256 | 3 |
| PV-Tpc | 0.7740 | 0.7740 | 1.5521 | 0.6638 | 2 |
| PV-Bfmc | 0.6331 | 0.6331 | 1.2695 | 0.5430 | 5 |
| Battery Technologies for Solar-based HRESs | |||||
| HSC | 0.7085 | 0.7085 | 5.7318 | 0.6990 | 1 |
| SSB | 0.3116 | 0.3116 | 2.5208 | 0.3074 | 2 |
| Al-Ion | 0.3053 | 0.3053 | 2.4699 | 0.3012 | 3 |
| Zn-Air | 0.2999 | 0.2999 | 2.4263 | 0.2959 | 4 |
| LFP | 0.2798 | 0.2798 | 2.2636 | 0.2761 | 5 |
| NMC | 0.2770 | 0.2770 | 2.2407 | 0.2733 | 6 |
| 2ndEV | 0.2741 | 0.2741 | 2.2176 | 0.2705 | 7 |
| LTO | 0.2640 | 0.2640 | 2.1354 | 0.2604 | 8 |
| NiZn | 0.2614 | 0.2614 | 2.1143 | 0.2579 | 9 |
| Na-Ion | 0.2580 | 0.2580 | 2.0871 | 0.2545 | 10 |
| VRFB | 0.2561 | 0.2561 | 2.0720 | 0.2527 | 11 |
| Zn-Br | 0.2516 | 0.2516 | 2.0353 | 0.2482 | 12 |
| LA | 0.2481 | 0.2481 | 2.0067 | 0.2447 | 13 |
| NiFe | 0.2151 | 0.2151 | 1.7398 | 0.2122 | 14 |
| Converter Technologies for Solar-based HRESs | |||||
| SC | 0.7687 | 0.7687 | 1.2494 | 1.009 | 7 |
| MC | 0.8999 | 0.8999 | 1.4626 | 1.1812 | 1 |
| PC | 0.8395 | 0.8395 | 1.3644 | 1.1019 | 2 |
| MMC | 0.815 | 0.815 | 1.3247 | 1.0698 | 4 |
| BDC | 0.798 | 0.798 | 1.297 | 1.0475 | 5 |
| NPC | 0.7807 | 0.7807 | 1.269 | 1.0249 | 6 |
| FC | 0.8257 | 0.8257 | 1.3421 | 1.0839 | 3 |
| PV Technologies: Spearman Correlation Matrix | |||||||||
| Method | MARCOS | ARAS | COCOSO | COPRAS | EDAS | TOPSIS | VIKOR | WASPAS | PROMETHEE II |
| MARCOS | 1 | 1.0000 | 0.8571 | 0.8571 | 0.9286 | 0.8929 | −0.1429 | 0.9643 | 0.7857 |
| ARAS | 1 | 0.8571 | 0.8571 | 0.9286 | 0.8929 | −0.1429 | 0.9643 | 0.7857 | |
| COCOSO | 1 | 0.7500 | 0.7857 | 0.8571 | 0.1429 | 0.8929 | 0.9643 | ||
| COPRAS | 1 | 0.9643 | 0.9643 | −0.4643 | 0.9286 | 0.7857 | |||
| EDAS | 1 | 0.9286 | −0.3214 | 0.9643 | 0.7500 | ||||
| TOPSIS | 1 | −0.3214 | 0.9643 | 0.8929 | |||||
| VIKOR | 1 | −0.1786 | 0.0000 | ||||||
| WASPAS | 1 | 0.8571 | |||||||
| PROMETHEE II | 1 | ||||||||
| PV Technologies: Kendall Rank Correlation Matrix | |||||||||
| Method | MARCOS | ARAS | COCOSO | COPRAS | EDAS | TOPSIS | VIKOR | WASPAS | PROMETHEE II |
| MARCOS | 1 | ||||||||
| ARAS | 1.0000 | 1 | |||||||
| COCOSO | 0.7143 | 0.7143 | 1 | ||||||
| COPRAS | 0.7143 | 0.7143 | 0.6190 | 1 | |||||
| EDAS | 0.8095 | 0.8095 | 0.7143 | 0.9048 | 1 | ||||
| TOPSIS | 0.8095 | 0.8095 | 0.7143 | 0.9048 | 0.8095 | 1 | |||
| VIKOR | −0.0476 | −0.0476 | 0.0476 | −0.3333 | −0.2381 | −0.2381 | 1 | ||
| WASPAS | 0.9048 | 0.9048 | 0.8095 | 0.8095 | 0.9048 | 0.9048 | −0.1429 | 1 | |
| PROMETHEE II | 0.6190 | 0.6190 | 0.9048 | 0.7143 | 0.6190 | 0.8095 | −0.0476 | 0.7143 | 1 |
| Battery Technologies: Spearman Correlation Matrix | |||||||||
| Method | MARCOS | ARAS | COCOSO | COPRAS | EDAS | TOPSIS | VIKOR | WASPAS | PROMETHEE II |
| MARCOS | 1 | 0.8198 | 0.5956 | 0.6747 | 0.6659 | 0.7495 | 0.6308 | 0.8857 | 0.6220 |
| ARAS | 1 | 0.7011 | 0.9121 | 0.8945 | 0.7055 | 0.8989 | 0.9429 | 0.7934 | |
| COCOSO | 1 | 0.5121 | 0.5956 | 0.4813 | 0.6703 | 0.6791 | 0.6527 | ||
| COPRAS | 1 | 0.8637 | 0.6615 | 0.8022 | 0.8374 | 0.7582 | |||
| EDAS | 1 | 0.5209 | 0.9209 | 0.9121 | 0.9385 | ||||
| TOPSIS | 1 | 0.6835 | 0.6747 | 0.4989 | |||||
| VIKOR | 1 | 0.8549 | 0.8593 | ||||||
| WASPAS | 1 | 0.8593 | |||||||
| PROMETHEE II | 1 | ||||||||
| Battery Technologies: Kendall Rank Correlation Matrix | |||||||||
| Method | MARCOS | ARAS | COCOSO | COPRAS | EDAS | TOPSIS | VIKOR | WASPAS | PROMETHEE II |
| MARCOS | 1 | ||||||||
| ARAS | 0.7363 | 1 | |||||||
| COCOSO | 0.4286 | 0.5165 | 1 | ||||||
| COPRAS | 0.4945 | 0.7582 | 0.3626 | 1 | |||||
| EDAS | 0.5165 | 0.7363 | 0.4286 | 0.7143 | 1 | ||||
| TOPSIS | 0.6264 | 0.5824 | 0.3187 | 0.5165 | 0.4066 | 1 | |||
| VIKOR | 0.4945 | 0.7143 | 0.4945 | 0.6923 | 0.8022 | 0.5165 | 1 | ||
| WASPAS | 0.7582 | 0.8462 | 0.5385 | 0.6923 | 0.7582 | 0.5165 | 0.6923 | 1 | |
| PROMETHEE II | 0.4725 | 0.6484 | 0.4725 | 0.5824 | 0.8242 | 0.4066 | 0.7143 | 0.7143 | 1 |
| Converter Technologies: Spearman Correlation Matrix | |||||||||
| Method | MARCOS | ARAS | COCOSO | COPRAS | EDAS | TOPSIS | VIKOR | WASPAS | PROMETHEE II |
| MARCOS | 1 | 0.9640 | 0.9640 | −0.7500 | 0.9640 | 0.8930 | −0.2860 | 0.9640 | 0.8930 |
| ARAS | 1 | 0.9290 | −0.6430 | 0.9290 | 0.8570 | −0.2140 | 0.9290 | 0.8570 | |
| COCOSO | 1 | −0.8210 | 1.0000 | 0.8930 | −0.3570 | 1.0000 | 0.8210 | ||
| COPRAS | 1 | −0.8210 | −0.7860 | 0.7140 | −0.8210 | −0.5710 | |||
| EDAS | 1 | 0.8930 | −0.3570 | 1.0000 | 0.8210 | ||||
| TOPSIS | 1 | −0.5000 | 0.8930 | 0.7500 | |||||
| VIKOR | 1 | −0.3570 | −0.0710 | ||||||
| WASPAS | 1 | 0.8210 | |||||||
| PROM-II | 1 | ||||||||
| Converter Technologies: Kendall Rank Correlation Matrix | |||||||||
| Method | MARCOS | ARAS | COCOSO | COPRAS | EDAS | TOPSIS | VIKOR | WASPAS | PROMETHEE II |
| MARCOS | 1 | ||||||||
| ARAS | 0.8570 | 1 | |||||||
| COCOSO | 0.9050 | 0.8100 | 1 | ||||||
| COPRAS | −0.6670 | −0.5240 | −0.7620 | 1 | |||||
| EDAS | 0.9050 | 0.8100 | 1.0000 | −0.7620 | 1 | ||||
| TOPSIS | 0.8100 | 0.7140 | 0.8100 | −0.7140 | 0.8100 | 1 | |||
| VIKOR | −0.1430 | −0.0950 | −0.1900 | 0.7140 | −0.1900 | −0.2860 | 1 | ||
| WASPAS | 0.9050 | 0.8100 | 1.0000 | −0.7620 | 1.0000 | 0.8100 | −0.1900 | 1 | |
| PROM-II | 0.7620 | 0.6670 | 0.6670 | −0.4290 | 0.6670 | 0.5710 | 0.0480 | 0.6670 | 1 |
| PV Technologies | ||||||||||||||||
| Scenario | Target | Delta | CO2 | EPBT | Cst/W | Drt | War | Lfs | Eff | Tcof | Wgt | LIP | ||||
| Sc01 | S-4 (Drt) | −0.15 | 0.1244 | 0.1494 | 0.1452 | 0.0875 | 0.0854 | 0.0829 | 0.0860 | 0.0685 | 0.0797 | 0.0908 | ||||
| Sc02 | S-4 (Drt) | −0.1 | 0.1237 | 0.1486 | 0.1444 | 0.0927 | 0.0850 | 0.0824 | 0.0856 | 0.0681 | 0.0793 | 0.0903 | ||||
| Sc03 | S-4 (Drt) | −0.05 | 0.1230 | 0.1477 | 0.1436 | 0.0978 | 0.0845 | 0.0820 | 0.0851 | 0.0677 | 0.0788 | 0.0898 | ||||
| Sc04 | S-4 (Drt) | 0.05 | 0.1216 | 0.1460 | 0.1420 | 0.1081 | 0.0835 | 0.0810 | 0.0841 | 0.0669 | 0.0779 | 0.0888 | ||||
| Sc05 | S-4 (Drt) | 0.1 | 0.1209 | 0.1452 | 0.1411 | 0.1133 | 0.0830 | 0.0806 | 0.0836 | 0.0665 | 0.0775 | 0.0883 | ||||
| Sc06 | S-4 (Drt) | 0.15 | 0.1202 | 0.1444 | 0.1403 | 0.1184 | 0.0825 | 0.0801 | 0.0831 | 0.0661 | 0.0770 | 0.0878 | ||||
| Sc07 | S-1 (CO2) | −0.15 | 0.1039 | 0.1500 | 0.1458 | 0.1051 | 0.0857 | 0.0832 | 0.0864 | 0.0687 | 0.0800 | 0.0912 | ||||
| Sc08 | S-1 (CO2) | −0.1 | 0.1101 | 0.1489 | 0.1448 | 0.1044 | 0.0852 | 0.0826 | 0.0858 | 0.0682 | 0.0795 | 0.0905 | ||||
| Sc09 | S-1 (CO2) | −0.05 | 0.1162 | 0.1479 | 0.1438 | 0.1037 | 0.0846 | 0.0821 | 0.0852 | 0.0678 | 0.0789 | 0.0899 | ||||
| Sc10 | S-1 (CO2) | 0.05 | 0.1284 | 0.1459 | 0.1418 | 0.1023 | 0.0834 | 0.0809 | 0.0840 | 0.0668 | 0.0778 | 0.0887 | ||||
| Sc11 | S-1 (CO2) | 0.1 | 0.1345 | 0.1448 | 0.1408 | 0.1016 | 0.0828 | 0.0804 | 0.0834 | 0.0664 | 0.0773 | 0.0880 | ||||
| Sc12 | S-1 (CO2) | 0.15 | 0.1406 | 0.1438 | 0.1398 | 0.1008 | 0.0822 | 0.0798 | 0.0828 | 0.0659 | 0.0768 | 0.0874 | ||||
| Sc13 | S-7 (Eff) | −0.15 | 0.1240 | 0.1489 | 0.1448 | 0.1044 | 0.0852 | 0.0826 | 0.0719 | 0.0682 | 0.0795 | 0.0905 | ||||
| Sc14 | S-7 (Eff) | −0.1 | 0.1234 | 0.1482 | 0.1441 | 0.1039 | 0.0848 | 0.0822 | 0.0761 | 0.0679 | 0.0791 | 0.0901 | ||||
| Sc15 | S-7 (Eff) | −0.05 | 0.1229 | 0.1476 | 0.1434 | 0.1035 | 0.0844 | 0.0819 | 0.0804 | 0.0676 | 0.0788 | 0.0897 | ||||
| Sc16 | S-7 (Eff) | 0.05 | 0.1217 | 0.1462 | 0.1421 | 0.1025 | 0.0836 | 0.0811 | 0.0888 | 0.0670 | 0.0780 | 0.0889 | ||||
| Sc17 | S-7 (Eff) | 0.1 | 0.1212 | 0.1455 | 0.1415 | 0.1020 | 0.0832 | 0.0807 | 0.0931 | 0.0667 | 0.0777 | 0.0885 | ||||
| Sc18 | S-7 (Eff) | 0.15 | 0.1206 | 0.1448 | 0.1408 | 0.1016 | 0.0828 | 0.0804 | 0.0973 | 0.0664 | 0.0773 | 0.0881 | ||||
| Battery Technologies | ||||||||||||||||
| Scen | Target | Δ | CL | DoD | RTE | SE | VED | C-rate | CpkWh | Maint | Tox | CF | Recycle | Safety | BMS | SoC_RT |
| Sc01 | S-4 (SE) | −0.15 | 0.3459 | 0.0249 | 0.0260 | 0.0425 | 0.0673 | 0.1747 | 0.0561 | 0.0479 | 0.0478 | 0.0504 | 0.0337 | 0.0281 | 0.0320 | 0.0226 |
| Sc02 | S-4 (SE) | −0.1 | 0.3450 | 0.0248 | 0.0259 | 0.0450 | 0.0671 | 0.1742 | 0.0559 | 0.0478 | 0.0477 | 0.0503 | 0.0336 | 0.0280 | 0.0319 | 0.0226 |
| Sc03 | S-4 (SE) | −0.05 | 0.3441 | 0.0248 | 0.0258 | 0.0476 | 0.0669 | 0.1738 | 0.0558 | 0.0477 | 0.0476 | 0.0502 | 0.0336 | 0.0280 | 0.0318 | 0.0225 |
| Sc04 | S-4 (SE) | 0.05 | 0.3423 | 0.0246 | 0.0257 | 0.0526 | 0.0666 | 0.1728 | 0.0555 | 0.0474 | 0.0473 | 0.0499 | 0.0334 | 0.0278 | 0.0317 | 0.0224 |
| Sc05 | S-4 (SE) | 0.1 | 0.3414 | 0.0246 | 0.0256 | 0.0551 | 0.0664 | 0.1724 | 0.0554 | 0.0473 | 0.0472 | 0.0498 | 0.0333 | 0.0277 | 0.0316 | 0.0223 |
| Sc06 | S-4 (SE) | 0.15 | 0.3405 | 0.0245 | 0.0256 | 0.0576 | 0.0662 | 0.1719 | 0.0552 | 0.0472 | 0.0471 | 0.0496 | 0.0332 | 0.0277 | 0.0315 | 0.0223 |
| Sc07 | S-1 (CL) | −0.15 | 0.2917 | 0.0267 | 0.0278 | 0.0540 | 0.0720 | 0.1869 | 0.0600 | 0.0513 | 0.0511 | 0.0540 | 0.0361 | 0.0301 | 0.0342 | 0.0242 |
| Sc08 | S-1 (CL) | −0.1 | 0.3089 | 0.0260 | 0.0271 | 0.0527 | 0.0703 | 0.1824 | 0.0586 | 0.0500 | 0.0499 | 0.0526 | 0.0352 | 0.0294 | 0.0334 | 0.0236 |
| Sc09 | S-1 (CL) | −0.05 | 0.3260 | 0.0254 | 0.0264 | 0.0514 | 0.0685 | 0.1778 | 0.0571 | 0.0488 | 0.0487 | 0.0513 | 0.0343 | 0.0286 | 0.0326 | 0.0230 |
| Sc10 | S-1 (CL) | 0.05 | 0.3603 | 0.0241 | 0.0251 | 0.0487 | 0.0650 | 0.1688 | 0.0542 | 0.0463 | 0.0462 | 0.0487 | 0.0326 | 0.0272 | 0.0309 | 0.0219 |
| Sc11 | S-1 (CL) | 0.1 | 0.3775 | 0.0234 | 0.0244 | 0.0474 | 0.0633 | 0.1642 | 0.0527 | 0.0451 | 0.0449 | 0.0474 | 0.0317 | 0.0264 | 0.0301 | 0.0213 |
| Sc12 | S-1 (CL) | 0.15 | 0.3947 | 0.0228 | 0.0237 | 0.0461 | 0.0615 | 0.1597 | 0.0513 | 0.0438 | 0.0437 | 0.0461 | 0.0308 | 0.0257 | 0.0293 | 0.0207 |
| Sc13 | S-7 (CpkWh) | −0.15 | 0.3462 | 0.0249 | 0.0260 | 0.0505 | 0.0674 | 0.1748 | 0.0473 | 0.0480 | 0.0478 | 0.0505 | 0.0338 | 0.0281 | 0.0320 | 0.0226 |
| Sc14 | S-7 (CpkWh) | −0.1 | 0.3452 | 0.0249 | 0.0259 | 0.0504 | 0.0672 | 0.1743 | 0.0501 | 0.0478 | 0.0477 | 0.0503 | 0.0337 | 0.0281 | 0.0319 | 0.0226 |
| Sc15 | S-7 (CpkWh) | −0.05 | 0.3442 | 0.0248 | 0.0258 | 0.0502 | 0.0670 | 0.1738 | 0.0529 | 0.0477 | 0.0476 | 0.0502 | 0.0336 | 0.0280 | 0.0318 | 0.0225 |
| Sc16 | S-7 (CpkWh) | 0.05 | 0.3422 | 0.0246 | 0.0257 | 0.0499 | 0.0666 | 0.1728 | 0.0584 | 0.0474 | 0.0473 | 0.0499 | 0.0334 | 0.0278 | 0.0317 | 0.0224 |
| Sc17 | S-7 (CpkWh) | 0.1 | 0.3412 | 0.0246 | 0.0256 | 0.0498 | 0.0664 | 0.1723 | 0.0612 | 0.0473 | 0.0471 | 0.0497 | 0.0333 | 0.0277 | 0.0316 | 0.0223 |
| Sc18 | S-7 (CpkWh) | 0.15 | 0.3402 | 0.0245 | 0.0255 | 0.0496 | 0.0662 | 0.1718 | 0.0640 | 0.0471 | 0.0470 | 0.0496 | 0.0332 | 0.0276 | 0.0315 | 0.0222 |
| Converter Technologies | ||||||||||||||||
| Criterion | ConvEff | PF | THD | MTBF | CpkW | Maint | Tox | CF | Recycle | Safety | GridComp | Redund | ||||
| Sc01 | CpkW −15% | 0.0282 | 0.0849 | 0.0934 | 0.0396 | 0.1285 | 0.1227 | 0.1062 | 0.0706 | 0.0866 | 0.0609 | 0.0647 | 0.1136 | |||
| Sc02 | CpkW −10% | 0.0280 | 0.0841 | 0.0926 | 0.0393 | 0.1360 | 0.1217 | 0.1053 | 0.0700 | 0.0859 | 0.0604 | 0.0641 | 0.1126 | |||
| Sc03 | CpkW −5% | 0.0277 | 0.0834 | 0.0918 | 0.0390 | 0.1436 | 0.1206 | 0.1044 | 0.0694 | 0.0851 | 0.0598 | 0.0635 | 0.1116 | |||
| Sc04 | CpkW +5% | 0.0273 | 0.0819 | 0.0902 | 0.0383 | 0.1587 | 0.1185 | 0.1025 | 0.0682 | 0.0836 | 0.0588 | 0.0624 | 0.1097 | |||
| Sc05 | CpkW +10% | 0.0270 | 0.0812 | 0.0894 | 0.0379 | 0.1662 | 0.1174 | 0.1016 | 0.0676 | 0.0829 | 0.0583 | 0.0618 | 0.1087 | |||
| Sc06 | CpkW +15% | 0.0268 | 0.0804 | 0.0885 | 0.0376 | 0.1738 | 0.1163 | 0.1007 | 0.0670 | 0.0821 | 0.0577 | 0.0613 | 0.1077 | |||
| Sc07 | Maint −15% | 0.0281 | 0.0843 | 0.0928 | 0.0394 | 0.1542 | 0.1016 | 0.1056 | 0.0702 | 0.0861 | 0.0605 | 0.0643 | 0.1129 | |||
| Sc08 | Maint −10% | 0.0279 | 0.0838 | 0.0922 | 0.0391 | 0.1532 | 0.1076 | 0.1049 | 0.0697 | 0.0855 | 0.0601 | 0.0638 | 0.1122 | |||
| Sc09 | Maint −5% | 0.0277 | 0.0832 | 0.0916 | 0.0389 | 0.1522 | 0.1136 | 0.1042 | 0.0693 | 0.0850 | 0.0597 | 0.0634 | 0.1114 | |||
| Sc10 | Maint +5% | 0.0273 | 0.0821 | 0.0904 | 0.0383 | 0.1501 | 0.1255 | 0.1028 | 0.0683 | 0.0838 | 0.0589 | 0.0625 | 0.1099 | |||
| Sc11 | Maint +10% | 0.0271 | 0.0815 | 0.0897 | 0.0381 | 0.1491 | 0.1315 | 0.1021 | 0.0679 | 0.0832 | 0.0585 | 0.0621 | 0.1092 | |||
| Sc12 | Maint +15% | 0.0269 | 0.0810 | 0.0891 | 0.0378 | 0.1481 | 0.1375 | 0.1014 | 0.0674 | 0.0827 | 0.0581 | 0.0617 | 0.1084 | |||
| Sc13 | Redund −15% | 0.0280 | 0.0842 | 0.0927 | 0.0393 | 0.1539 | 0.1218 | 0.1054 | 0.0701 | 0.0860 | 0.0604 | 0.0641 | 0.0941 | |||
| Sc14 | Redund −10% | 0.0278 | 0.0837 | 0.0921 | 0.0391 | 0.1530 | 0.1210 | 0.1048 | 0.0697 | 0.0854 | 0.0601 | 0.0638 | 0.0996 | |||
| Sc15 | Redund −5% | 0.0277 | 0.0832 | 0.0915 | 0.0388 | 0.1521 | 0.1203 | 0.1041 | 0.0692 | 0.0849 | 0.0597 | 0.0634 | 0.1051 | |||
| Sc16 | Redund +5% | 0.0273 | 0.0821 | 0.0904 | 0.0384 | 0.1502 | 0.1188 | 0.1028 | 0.0684 | 0.0839 | 0.0589 | 0.0626 | 0.1162 | |||
| Sc17 | Redund +10% | 0.0272 | 0.0816 | 0.0898 | 0.0381 | 0.1492 | 0.1180 | 0.1022 | 0.0680 | 0.0833 | 0.0586 | 0.0622 | 0.1217 | |||
| Sc18 | Redund +15% | 0.0270 | 0.0811 | 0.0893 | 0.0379 | 0.1483 | 0.1173 | 0.1015 | 0.0675 | 0.0828 | 0.0582 | 0.0618 | 0.1273 | |||
| Technology | Key Benefits (Ranking Justification) | Limitations/Real-World Constraints | Practical Relevance and Outlook |
|---|---|---|---|
| PV-Thf (Thin-Film PV) | Short EPBT, low CO2 footprint, lightweight, good performance under high-temp and diffuse light | Lower efficiency vs. crystalline, shorter lifespan, reliability issues in harsh climates | Strong option for sustainability-focused and rooftop/large-scale projects; long-term reliability needs improvement |
| HSC (Hybrid Supercapacitors) | >100,000 cycles, high power density, fast charge–discharge, high safety | Limited production scale, high costs, uncertain raw material supply | Future-oriented option; complements Li-ion for high cycling applications; promising for next-gen HRESs |
| MC (Modular Converter) | Scalability, redundancy, high efficiency, low THD, grid compatibility | Higher capital cost, complex design, compliance challenges | Commercially feasible for multi-source HRESs; lifecycle reliability offsets upfront cost |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaur, S.; Kumar, R.; Singh, K. Sustainable Component-Level Prioritization of PV Panels, Batteries, and Converters for Solar Technologies in Hybrid Renewable Energy Systems Using Objective-Weighted MCDM Models. Energies 2025, 18, 5410. https://doi.org/10.3390/en18205410
Kaur S, Kumar R, Singh K. Sustainable Component-Level Prioritization of PV Panels, Batteries, and Converters for Solar Technologies in Hybrid Renewable Energy Systems Using Objective-Weighted MCDM Models. Energies. 2025; 18(20):5410. https://doi.org/10.3390/en18205410
Chicago/Turabian StyleKaur, Swapandeep, Raman Kumar, and Kanwardeep Singh. 2025. "Sustainable Component-Level Prioritization of PV Panels, Batteries, and Converters for Solar Technologies in Hybrid Renewable Energy Systems Using Objective-Weighted MCDM Models" Energies 18, no. 20: 5410. https://doi.org/10.3390/en18205410
APA StyleKaur, S., Kumar, R., & Singh, K. (2025). Sustainable Component-Level Prioritization of PV Panels, Batteries, and Converters for Solar Technologies in Hybrid Renewable Energy Systems Using Objective-Weighted MCDM Models. Energies, 18(20), 5410. https://doi.org/10.3390/en18205410






