Prediction Modeling of External Heat Exchangers in a 660 MW Ultra-Supercritical Circulating Fluidized Bed Boiler Based on Model Reduction

Abstract

To ensure the safe operation of the external heat exchanger (EHE) in a circulating fluidized bed (CFB) boiler, it is essential to obtain real-time information on the flow conditions within the bed. This paper establishes a predictive model for the external heat exchanger of the high-temperature reheater in an ultra-supercritical CFB boiler by combining computational fluid dynamics (CFD) with model order reduction and artificial neural networks. The model enables rapid prediction of the solid volume fraction, solid temperature, and gas temperature within the external heat exchanger. The results show that the three predictive models can accurately forecast flow field information under unknown operating conditions. For inlet velocities of 0.225 m/s and 0.325 m/s, the calculation errors are 2.89%, 1.04%, 1.03% and 2.99%, 1.08%, 1.09%, respectively. The predictive models significantly save computational resources, reducing the computation time from 6000 min for the full-order model to approximately 1 s. This lays the foundation for real-time monitoring of the external heat exchanger.

1. Introduction

With the continuous scaling up of circulating fluidized bed boilers, the steam temperatures of superheaters and reheaters have shown a gradual upward trend. In China’s under-construction 660 MW ultra-supercritical CFB boiler, the external heat exchanger altered the arrangement of the tube panels and secured the tube clamps to the hanger tubes through welding, thereby reducing the probability of tube wall rupture caused by ash particle erosion and collisions within the bed [1]. However, the external heat exchanger of a high-temperature reheater in ultra-supercritical CFB boilers experiences the dual influence of high-temperature ash particles and high-temperature steam, increasing the likelihood of overheating and tube burst incidents as the operating time increases, which inevitably affects the operational stability of the external heat exchanger. During actual operation [2,3], it was observed that, owing to the significant thermal deviation characteristics of the external heat exchanger, the temperature distribution of the tube panels assumed a saddle shape. The wall temperature of the central tube panel often deviates considerably from the outlet gas temperature, further exacerbating the risk of overheating the external heat exchanger tube walls [4]. The current insufficiency of monitoring points for high-temperature flue gas and steam in power plants hinders accurate characterization of the flow and heat transfer conditions within the EHE. Consequently, developing an EHE thermal model and a predictive framework on the existing infrastructure to acquire real-time, accurate EXE data holds significant theoretical and practical importance for the safe operation of the generating unit.

The external heat exchanger, a key component of large-scale circulating fluidized bed boilers, primarily exists in the following forms: the Lurgi-type external heat exchanger [5], the Foster Wheeler INTREX (Integrated Heat Exchanger) [6], the compact split-loop ash return heat exchanger [7], the non-mechanical valve-controlled external heat exchanger [8], and the integrated external heat exchanger [9]. The subject of this study is the Lurgi-type external heat exchanger.

To acquire detailed characteristics of the EHE, numerous researchers have employed advanced numerical simulation methods, thereby accurately obtaining the distributions of key parameters such as the temperature, velocity, and concentration fields. However, the drawbacks of numerical simulation methods are evident. Kim [10] investigated the influence of gas-phase velocity on the heat transfer coefficient; Li [11], based on a numerical model, studied the effects of airflow velocity and pipe arrangement on flow patterns; Yurong [12] employed the Euler-Euler two-phase flow model to explore the processes of bubble formation, aggregation, and eruption within the pipes; and Córcoles [13] utilized a two-dimensional model to obtain accurate heat transfer coefficients at the pipe walls. According to Zhang et al., CFD simulations and experimental studies demonstrated that the flow non-uniformity (deviation) in the external heat exchanger could be resolved by improving the particle concentration distribution in the boundary layer. Proposed solutions included implementing zonal air distribution, a dedicated air distribution plate, and sidewall purge air systems [14]. A novel heat exchanger was proposed by Wang, drawing upon the CFB fluidization principle, and flow and heat transfer behaviors were evaluated utilizing the DPM model [15].

Traditional numerical simulation approaches can provide comprehensive flow information for the external heat exchanger region, but these methods consume significant computational resources and are time-consuming, making them unable to meet the demand for timely feedback on bed information in the intelligent operation and maintenance of power units. Therefore, there is a need for a computational method that enables the real-time acquisition of detailed internal system information. Model Order Reduction serves as an effective technique for significantly accelerating computational speed.

Model-order reduction is a crucial technical approach for simplifying models, enhancing computational speed, and achieving real-time system performance. In the fields of science and engineering, numerous researchers have proposed various model-order reduction methods aimed at reducing the system degrees of freedom and improving computational efficiency. Various methods have been developed for model order reduction, such as the Galerkin method [16], nonlinear Galerkin method [17], balanced truncation method [18], center manifold method [19], Proper Orthogonal Decomposition (POD) method [20,21], and Dynamic Mode Decomposition method [22,23]. One of the most commonly used reduction methods is Proper Orthogonal Decomposition. As a powerful model reduction tool, POD lowers computational costs by sacrificing a certain degree of model accuracy and serves as a primary tool for dimensionality reduction based on the dominant features of the datasets. Dynamic Mode Decomposition (DMD) is primarily used for linear time-invariant dynamical systems, where it approximates the system operator via data pairs to analyze its eigenmodes. However, power plant systems are inherently non-linear and time-varying. In contrast, Proper Orthogonal Decomposition (POD) seeks a set of optimal, orthogonal basis functions that minimize the mean square error after truncation, thereby capturing the dominant characteristics of the original data. It is upon this data, which preserves the essential original properties, that predictive models can more accurately describe future system behavior. POD is particularly well-suited as a model reduction technique for power plant data, given its inherent characteristics.

The primary motivation for characterizing EHE behavior is to prevent tube rupture incidents; however, the mapping relationships derived from model order reduction cannot yet accurately predict its variations. Given that both artificial neural networks and reduced-order models fall under the category of data-driven models, many scholars have begun actively exploring methods for integrating them to tackle the limitations in the model’s predictive capability. Li [24] utilized the POD method to extract the modes and mode coefficients under a wide range of operating conditions for a four-corner tangential pulverized coal boiler. This study compared the performances of different neural networks in constructing fast prediction reduced-order models for the velocity field of a boiler. Lu combined compressive sensing with POD-Kriging to solve the stochastic problems of CFD and achieve efficient uncertainty quantification [25]. Fang [26] combined Principal Component Analysis (PCA) and Bidirectional Long Short-Term Memory (BiLSTM) networks with the POD method to construct a reduced-order model for a fluidized bed, effectively extracting dynamic evolution information and achieving reduced-order modeling of unsteady flow fields. Most of the aforementioned reduced-order prediction studies focus on the furnace section of fluidized bed boilers, with a notable lack of research targeting the external heat exchanger. A noticeable research gap exists, as the aforementioned studies have not thoroughly investigated the EHE in the context of high-temperature operation.

This study focuses on the construction of an ultra-supercritical circulating fluidized bed high-temperature reheater external heat exchanger as the research subject. Using CFD numerical simulation results from multiple operating conditions validated against design and experimental data as sample data, a reduced-order model was constructed with a small number of POD modes through linear superposition to describe the dynamic characteristics within the external heat exchanger. A POD-SVM prediction model combining Proper Orthogonal Decomposition and Support Vector Machine (SVM) is developed. This model ensures computational accuracy while significantly reducing computational costs and provides detailed dynamic characteristics of the bed interior. This research establishes a basis for real-time EHE monitoring and prediction in power plants, thereby developing a modeling framework applicable to the inspection and forecasting of heat exchangers in analogous industrial settings.

2. Numerical Simulation Model

Due to limitations in sensor technology and the physical constraints of EHE arrangement, power plants are unable to obtain detailed internal temperature and flow field data from the EHE. In such high-temperature environments, most researchers resort to CFD to acquire detailed temperature and flow field information. The EHE investigated in this paper involves complex gas–solid two-phase flow. To accurately characterize its thermal-hydraulic behavior, a Euler-Euler two-phase flow model was established, and key sub-models including those for drag force and heat exchange were optimized based on existing literature.

2.1. Model Introduction

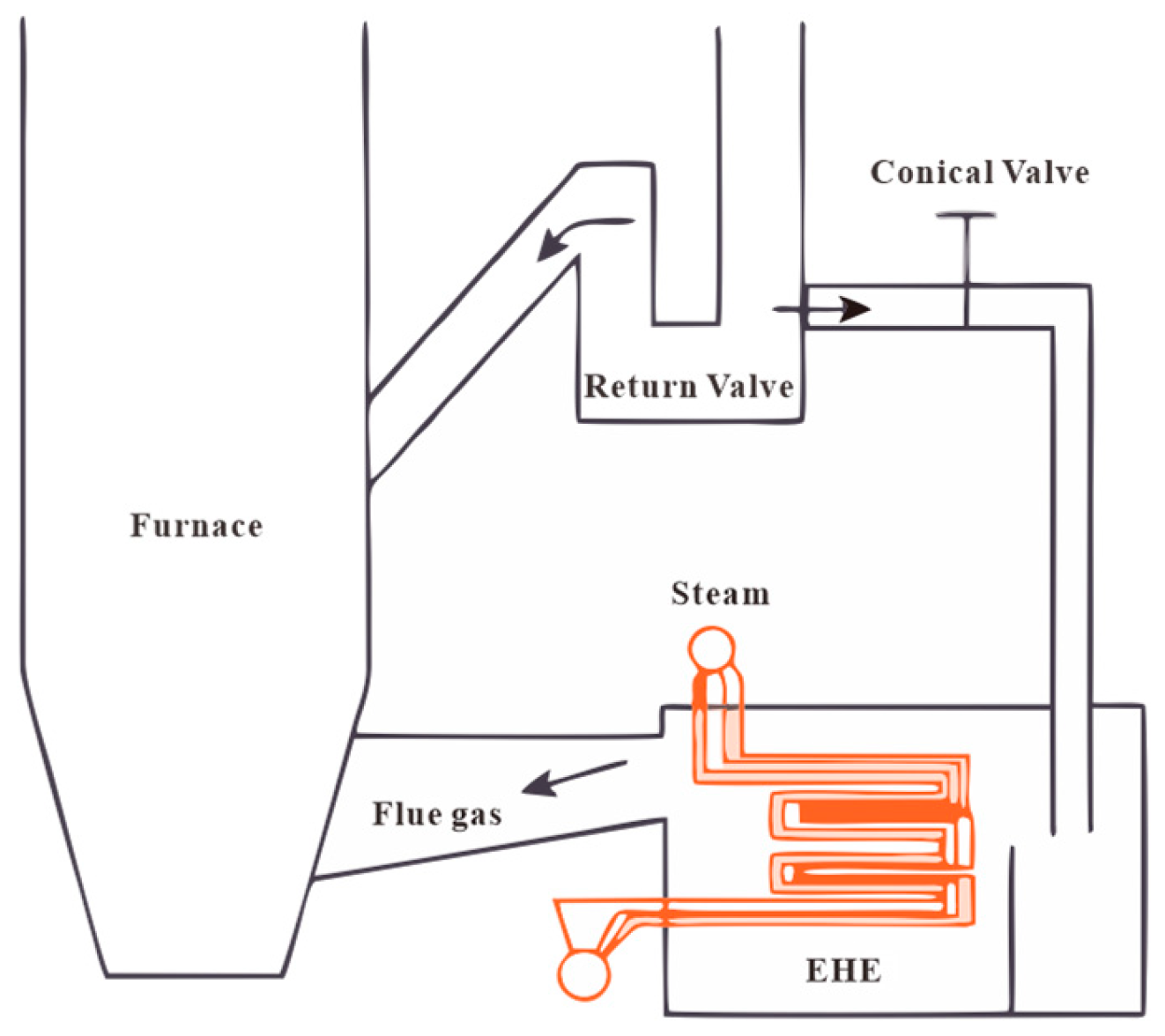
The external heat exchanger, also known as the external heat exchanger, was designed and manufactured by the Dongfang Boiler Group for the world’s largest capacity 660 MW ultra-supercritical circulating fluidized bed boiler, which is a fluidized bed heat exchanger located in the ash circulation loop outside the CFB boiler furnace. It consists of one or more compartments forming a non-combustible fine-particle bubbling fluidized bed. The system included six symmetrically distributed external heat exchangers, comprising two high-temperature reheaters and four medium-temperature superheaters. Among these, the high-temperature reheater external heat exchanger operated under the most severe conditions with the highest steam parameters.

The structure of the external heat exchanger investigated in this study is shown in Figure 1.

The high-temperature reheater external heat exchanger of the 660 MW CFB boiler has an overall height, depth, and width of 5 m, 7.25 m, and 5.01 m, respectively, with the heat exchange chamber depth being 5.7 m. This study primarily focused on the numerical simulation of the flow and heat transfer within the tube bundle of a heat exchange chamber. Based on actual operating conditions, this study emphasizes the calculation of the upper seven rows of the tube bundle in an external heat exchanger. In light of the actual on-site tube failure incidents, bursting primarily occurs in the upper rows of the tube panel [28]. Given that the numerical computation involves a two-phase flow and heat transfer within the bed, employing a three-dimensional simulation would result in a significant disparity between the tube bundle dimensions and those of the external heat exchanger of the high-temperature reheater, leading to a surge in the number of grids. Additionally, the complex two-phase flow and heat transfer in a large-scale high-temperature reheater external heat exchanger would render the computational cost of a three-dimensional numerical simulation unacceptably high. Therefore, this study adopts a two-dimensional model for the numerical simulation. Furthermore, because the upper part of the high-temperature reheater external heat exchanger is filled with air, which has minimal heat exchange with the tube walls, the transverse center cross section of the uppermost tube bundle is selected as the outlet cross section of the high-temperature reheater external heat exchanger.

Given the numerous tube bundles in the calculated cross-section of the high-temperature reheater external heat exchanger, determining an appropriate computational domain is crucial for this study. According to the study by Hou et al. [29], on the relationship between the angle and distance among tube bundle arrays within a fluidized bed, the interaction between adjacent tubes becomes insignificant when the distance between the tube bundles exceeds 2.5D (where D is the tube diameter). Therefore, in this study, the tube bundle with the highest temperature in the calculated cross-section and two adjacent tube bundles had the greatest impact as the computational domain. To avoid the influence of the walls on the tube bundles, a sufficiently wide computational domain was chosen; even in a relatively dense particle flow, the side walls could only affect the flow within a range of 10 dp (where dp is the particle diameter) [30]. The accuracy of the simplified computational domain selected in this study was validated through global simulation results of the high-temperature reheater external heat exchanger. The grid of the numerical model is shown in Figure 2.

The computational domain mesh model is constructed using ICEM. The mesh area is divided into two parts: the tube bundle region and the non-tube bundle region. In the tube bundle region, an O-grid is employed for construction, and the mesh near the heat exchange tube walls is refined. The tube wall boundary is divided into 60 nodes, with the smallest mesh size being 2 × 10⁻⁵ m. The mesh size increases with distance from the tubes. In the non-tube bundle region, a structured mesh is used, with the maximum mesh size being 0.005 m.

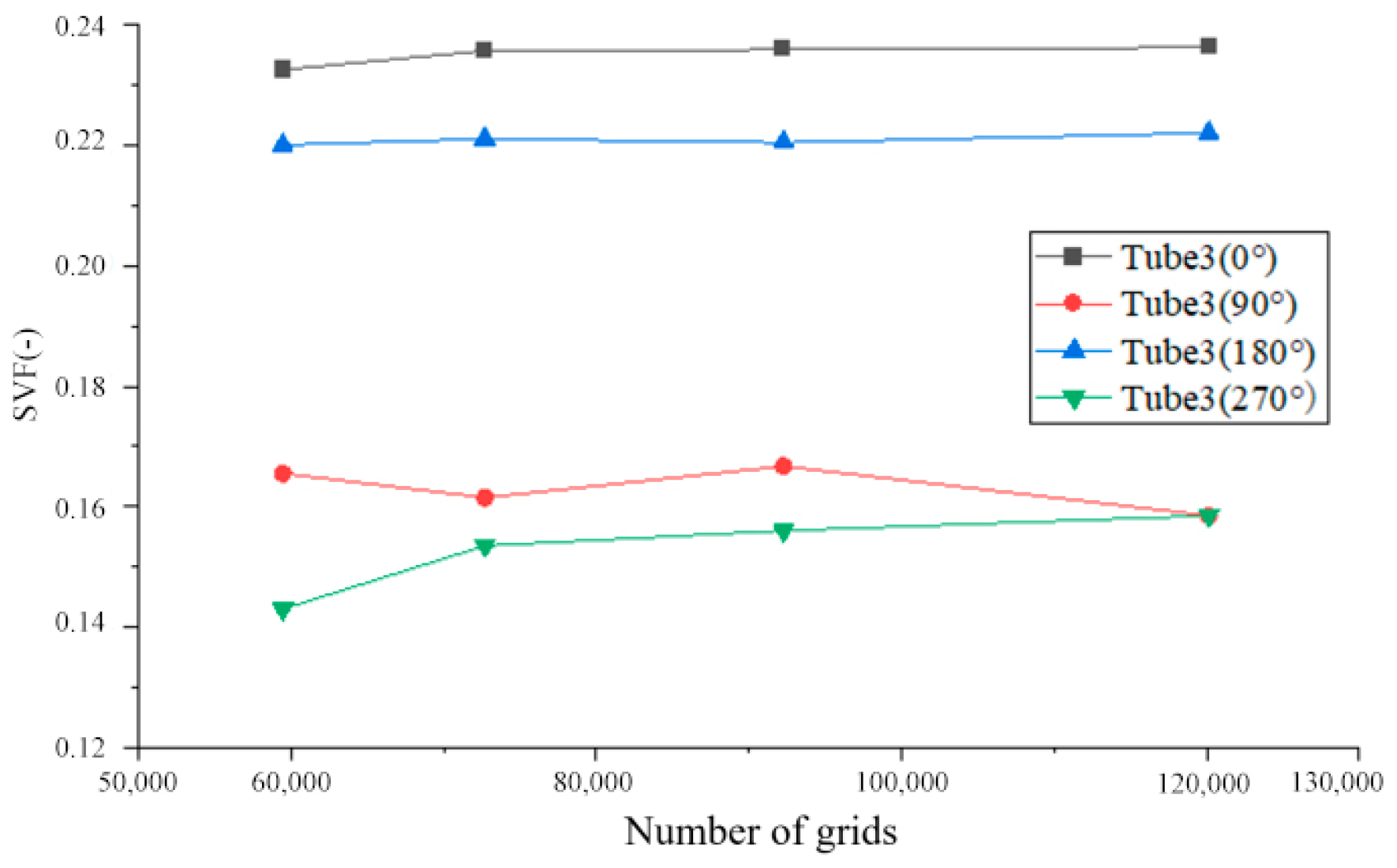
This study primarily focuses on refining the mesh in the tube bundle region, employing grids with 59,452, 72,702, 92,267, and 120,136 elements for independence verification. Given that the CFD calculations are intended to provide flow field data samples for the reduced-order model, the comparison mainly involves the solid volume fraction contours and the solid volume fraction at typical points on the tube walls across the three mesh configurations. As illustrated in Figure 3, near the third tube, the points at 0° and 90° exhibit minimal variation across different mesh densities. However, the points at 180° and 270° show significant differences in solid volume fraction when using the 59,452-element mesh compared to the other mesh densities. The overall distribution of solid volume fraction with the 72,702-element mesh is similar to that of the 92,267- and 120,136-element meshes, with only minor discrepancies at the 90° point. Therefore, balancing computational accuracy and speed, subsequent CFD calculations in this study utilize a mesh with 72,702 elements.

This study calculated the flow and heat transfer of a full-domain model with an inlet air fluidization velocity of 0.2 m/s. The validation was performed by selecting the heat exchange tubes in the tube panel of the high-temperature reheater external heat exchanger full-domain model that corresponded to the local model. The time-averaged solid phase volume fractions at eight points along the tube wall at angles of 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315° were compared for the first, third, fifth, and seventh tubes in the top row. Figure 4 presents the validation comparison results for the eight points on each tube.

As shown in Figure 4, the variation trends of the solid-phase volume fraction along the tube wall in the full-domain and local models were generally consistent. The calculation results of the solid-phase volume fraction in the full-domain and local models showed high agreement at the 90°, 135°, 180°, 225°, and 270° positions in each tube. However, the computational differences increased slightly in the upper region of the tube bundle (0°, 45°, and 315°). The largest absolute error occurred at the 45° position of the seventh tube (0.026), and all calculation errors were within an acceptable range. To save computational resources and validate the rationality of the reduced-order prediction model more quickly, this study employed a local grid for the computational analysis.

2.2. Model Calculation Setup

This study investigates the high-temperature reheater external heat exchanger with a steam inlet temperature of 559 °C, an outlet temperature of 623 °C, an inlet pressure of 6.11 MPa, and an outlet pressure of 6.07 MPa. The ash particle inlet temperature is 886 °C, and the outlet temperature is 692 °C. The particle density is 2540 kg/m³, the average particle diameter is 0.11 mm, and the specific heat capacity of the particles is 840 J/(kg·K). The inlet air density is 1.225 kg/m³, the inlet air temperature is 60 °C, and the inlet air velocity ranges from 0.2 to 0.4 m/s. A total of 21 operating conditions were calculated to serve as the initial sample data for the reduced-order model, encompassing most of the operating conditions of commercial external heat exchangers. The inlet gas temperature is 333.15 K. The numerical model employed the Euler-Euler two-fluid model, and the P1 model was used for radiation.

Under the Euler-Euler two-phase framework, the governing energy conservation equation for the p-th phase is:

$${\displaystyle \frac{\partial }{\partial t}}({\alpha }_q{\rho }_q)+\nabla \cdot ({\alpha }_q{\rho }_q\overrightarrow{v_q})={\displaystyle \sum _{p=1}^n({\stackrel{\cdot }{m}}_{pq}-{\stackrel{\cdot }{m}}_{qp})+S_q}$$

(1)

where ${\stackrel{·}{m}}_{pq}$ is the mass transfer from phase p to phase q, and ${\stackrel{·}{m}}_{qp}$ is the mass transfer from phase q to phase p.

$$\begin{array}{ll}{\displaystyle \frac{\partial }{\partial t}}({\alpha }_q{\rho }_q\overrightarrow{v_q})+\nabla \cdot ({\alpha }_q{\rho }_q\overrightarrow{v_q}\overrightarrow{v_q})=& -{\alpha }_q\nabla p+\nabla {\tau }_q+{\alpha }_q{\rho }_q\overrightarrow{g}\\ & +{\displaystyle \sum _{p=1}^n(R_{pq}+{\stackrel{\cdot }{m}}_{pq}\overrightarrow{v_{pq}}-{\stackrel{\cdot }{m}}_{qp}\overrightarrow{v_{qp}})}\\ & +({\overrightarrow{F}}_q+{\overrightarrow{F}}_{lift,q}+{\overrightarrow{F}}_{wl,q}+{\overrightarrow{F}}_{vm,q}+{\overrightarrow{F}}_{td,q})\end{array}$$

(2)

In this equation, the first three terms on the right-hand side correspond to the force components due to pressure, shear stress, and gravity, respectively. The fourth term is the change in momentum caused by interphase mass transfer. ${\overrightarrow{R}}_{pq}$ is the interaction force between phases. ${\overrightarrow{v}}_{pq}$ denotes the interphase velocity. When mass is transferred from one phase to another, this velocity is assigned the value of the donating phase’s velocity. The fifth item is the interactional forces. ${\overrightarrow{F}}_q$ denotes the external volumetric force, ${\overrightarrow{F}}_{lift,q}$ denotes the lift force, ${\overrightarrow{F}}_{wl,q}$ denotes the wall surface lubrication force ${\overrightarrow{F}}_{vm,q}$ denotes the virtual mass force and ${\overrightarrow{F}}_{td,q}$ denotes the turbulent dissipation force.

$$\begin{array}{ll}{\displaystyle \frac{\partial }{\partial t}}({\alpha }_q{\rho }_q{h}_q)+\nabla \cdot ({\alpha }_q{\rho }_q{\overrightarrow{v}}_q{h}_q)& ={\alpha }_q{\displaystyle \frac{d{p}_q}{dt}}+{\stackrel{=}{\tau }}_q:\nabla {\overrightarrow{u}}_q-\nabla \cdot {\overrightarrow{q}}_q+S_q\\ & +{\displaystyle \sum _{p=1}^n}(Q_{pq}+{\dot{m}}_{pq}{h}_{pq}-{\dot{m}}_{qp}{h}_{qp})\\ & -\nabla \cdot \sum _j{h}_{j,q}{\overrightarrow{J}}_{j,q}\end{array}$$

(3)

In this equation, ${\overrightarrow{q}}_q$ is the heat flux. ${\overrightarrow{S}}_q$ is the source item including the chemical reactions or radiation heat transfer, $Q_{pq}$ denotes the heat exchange intensity, and the last term denotes the energy transfer through component diffusion.

The primary model settings and equations are listed in

Table 1. The main model setting of CFD calculation of external heat exchanger.

Euler-Euler Two-Fluid Model
Gas–solid drag coefficient model	Gidaspow [31]	$\beta =\left\{\begin{array}{c}150{\displaystyle \frac{{\alpha }_{\mathrm{s}}^2{\mu }_{\mathrm{g}}}{{\alpha }_{\mathrm{g}}{d}_{\mathrm{s}}}}+1.75{\displaystyle \frac{{\rho }_{\mathrm{g}}{\alpha }_{\mathrm{s}}|v_{\mathrm{g}}-v_{\mathrm{s}}|}{d_{\mathrm{s}}}}, {\alpha }_{\mathrm{g}}\le 0.8\\ {\displaystyle \frac{3}{4}}{C}_D{\displaystyle \frac{{\alpha }_{\mathrm{g}}{\alpha }_{\mathrm{s}}{\alpha }_{\mathrm{s}}|v_{\mathrm{g}}-v_{\mathrm{s}}|}{d_{\mathrm{s}}}}{\alpha }_{\mathrm{g}}^{-2.65}, {\alpha }_{\mathrm{g}}\ge 0.8\end{array}\right.$
Solid–Solid Drag Coefficient Model	Syamlal [32]	$\begin{array}{c}{\mu }_{s,kin}={\displaystyle \frac{{\alpha }_s{\rho }_s{d}_s\sqrt{{\Theta }_s\pi }}{6(3-e_{ss})}}[1+{\displaystyle \frac{2}{5}}(1+e_{ss})\\ (3e_{ss}-1){\alpha }_s{g}_{0,ss}]\end{array}$
Gas–Solid Interphase Heat Transfer Model	Gunn [33]	$\begin{array}{c}N{u}_s=\left(7-10{\alpha }_g+5{\alpha }_g^2\right)\left(1+0.7 {\mathit{Re}}_s^{0.2} {\mathit{Pr}}^{13}\right)\\ +\left(1.33-2.4{\alpha }_g+1.2{\alpha }_g^2\right) {\mathit{Re}}_s^{0.7} {\mathit{Pr}}^{1/3}\end{array}$
Effective Thermal Conductivity Coefficient	Legawiec-Ziolkowski [34]	$h={\displaystyle \frac{{\alpha }_g{k}_g^{eff}\left|\frac{\partial T_g}{\partial n}\right|+{\alpha }_s{k}_s^{eff}\left|\frac{\partial T_s}{\partial n}\right|}{T_b-T_w}}$
Solid Pressure Model	Lun [35]	$P_s={\alpha }_s{\rho }_s{\Theta }_s+2{\rho }_s(1+e_{ss}){\alpha }_s^2{g}_{0,ss}{\Theta }_s$
Solid Viscosity Model	Lun	${\gamma }_{{\Theta }_s}={\displaystyle \frac{12(1-e_{ss}^2)g_{0,ss}}{d_s\sqrt{\pi }}}{\rho }_s{\alpha }_s^2{\Theta }_s^{3/2}$

.

The gas-phase wall boundary condition was set as a no-slip boundary, whereas the solid-phase wall boundary condition had a specularity coefficient of 0.1. The solid-phase restitution coefficient was 0.9. Using the above model, numerical simulations of a high-temperature reheater external heat exchanger were conducted under different fluidization velocities, and the simulation results were used as sample data to establish a reduced-order model. The upper outlet was simplified as the outlet of the external heat exchanger of the high-temperature reheater, and the outlet boundary condition was set as the pressure outlet.

In this study, a transient approach was adopted to simulate the flow and heat transfer in a high-temperature reheater external heat exchanger. The simulation time is 15 s, with a fixed time step of 10⁻⁴ s. As shown in Figure 5, the system was not fully fluidized during the first 5 s of the simulation. After 5 s, the overall solid-phase volume fraction became relatively uniform compared to the pre-fluidization state. During this period, the bubbles within the bed continuously grew and ruptured, and new bubbles formed and merged, causing solid particles to rise to the upper part of the bed, break apart, and descend. Therefore, the bed state after 5 s of fluidization was time-averaged over a sampling period of 10 s for further analysis.

3. POD Reduced-Order Model Method

The heat transfer process within the boiler’s external bed is nonlinear, making it difficult to derive accurate dynamic governing equations, which poses challenges for establishing embedded reduced-order models. However, the extensive operational data stored by the plant’s Distributed Control System is conducive to the development of such non-embedded ROMs. The core concept of a non-embedded ROM lies in its ability to learn a black-box mapping from input parameters to output responses directly from high-fidelity data, without relying on the original governing equations. Subsequently, a Support Vector Machine model can be applied to optimize this mapping relationship based on the non-embedded ROM, thereby enabling accurate data prediction. Therefore, this paper adopts the POD method, which is a non-embedded reduced-order method.

3.1. Fundamental Principles of POD Reduced-Order Method

The snapshot POD algorithm proposed by Sirovich primarily addresses the issue in which the number of discrete spatial points far exceeds that of discrete temporal points in practical processes. Typically, flow field sample data obtained from traditional CFD calculations are in the form of discrete points. The constructed sample snapshots store the data at each time point or under each operating condition as column vectors, thereby forming a sample data matrix. This matrix serves as the basis for extracting the POD modes and coefficients.

1.

Snapshots of sample data were constructed. Snapshots were generated from the preliminary CFD calculation results. The flow field data at N time points $t_j$ (where $j=1,2,\cdots ,N$) were selected to generate snapshots. Each snapshot stores data from M grid nodes $x_i$ (where $x=1,2,\cdots ,M$) in the form of column vectors to create a Sirovich sample data matrix [36]:

$$\begin{array}{c}U\left(x_i,t_j\right)=\end{array}\left(\begin{array}{cccc}u(x_1,t_1)& u(x_1,t_2)& \dots & u(x_1,t_N)\\ u(x_2,t_1)& u(x_2,t_2)& \dots & u(x_2,t_N)\\ ⋮& ⋮& \ddots & ⋮\\ u(x_M,t_1)& u(x_M,t_2)& \dots & u(x_M,t_N)\end{array}\right)$$

(4)

2.

Extraction of the modes and mode coefficients. Any moment in the flow field system of the established reduced-order model can be constructed using Equation (4):

$$U^{\prime }(x,t)\approx {\displaystyle \sum }_{k=1}^K{a}_k(t)\cdot {\phi }_k(x)$$

(5)

In this equation, ${\alpha }_k(t)$ is a function of time $t$, ${\phi }_k(x)$ represents the mode coefficients of the reduced-order model, and $K$ denotes the number of selected POD bases, which is typically considerably smaller than the spatial dimensions of $M$.

For the reduced-order modeling of high-dimensional problems, Sirovich introduced the snapshot POD algorithm, defining the autocorrelation matrix $C$:

$$C=U^{T}U$$

(6)

By solving the eigenvalues and eigenvectors of matrix $C$, the first $K$ eigenvalues are obtained. Let ${\overrightarrow{v}}_k$ be the eigenvector corresponding to the eigenvalue ${\lambda }_k$. Then, the POD basis can be derived using the following equation:

$${\phi }_k(x)={\displaystyle \sum }_{k=1}^K{v}_k(i)\cdot U\left(x,t_i\right)(i=1,2,\cdots ,N;k=1,2,\cdots ,K)$$

(7)

3.

POD Mode Selection and Flow Field Reconstruction. For the velocity field, the relationship between kinetic energy and eigenvalues is as follows:

$$E=\left(U^{\prime },U^{\prime }\right)=={\displaystyle \sum }_{i=1}^N{\lambda }_i$$

(8)

For nonvelocity fields, $E$ does not have a clear physical meaning and is referred to as the “generalized energy”. Based on this, Sirovich proposed the “generalized energy” method using eigenvalues ${\lambda }_i$ to retain the dominant modes of the flow field.

Sort the eigenvalue ${\lambda }_i$ in descending order from largest to smallest, and define the energy percentage as

$$I(k)={\displaystyle \frac{{\lambda }_k}{{{\displaystyle \sum }}_{i=1}^N{\lambda }_i}}$$

(9)

The number of POD modes $K$ to be selected is calculated using the following formula:

$$K=\mathit{arg}\mathit{min}(I(k)/I(k)\ge \epsilon )$$

(10)

In this equation, $\epsilon$ represents the percentage of energy contained in the selected reduced-order subspace relative to the total energy. $\epsilon$ is usually set to 0.99; however, its value may need to be adjusted depending on the specific research problem. The final POD mode ${\phi }_k(x)(x=1,2,\cdots ,k)$ was obtained, which corresponded to the first $K$ eigenvalues selected.

The numerical simulation results in this study consisted of 21 operating conditions, each containing 76,344 grid nodes. This number significantly exceeded the dimensionality that could be handled using the direct POD method. Therefore, in this study, the snapshot POD method was selected as the computational approach for constructing the reduced-order model.

3.2. Reduced-Order Model Construction

Sample snapshots were constructed based on the 21 operating conditions calculated for the 660 MW external heat exchanger, and the snapshot POD method was employed to build the reduced-order model. Each operating condition comprises 76,344 grid data points. Based on this research focus, reduced-order models were established for solid volume fraction, solid temperature, and gas temperature. The computed data were exported and organized into a data matrix of size 3 × 21 × 76,344 to form the original sample data for the reduced-order model.

Typically, the selection of the number of modes needs to consider the energy proportion of each mode and the cumulative energy contribution rate of all selected modes, which is calculated using the following formula [37]:

$$e(i)={\displaystyle \frac{{\lambda }_i}{{{\displaystyle \sum }}_{i=1}^N{\lambda }_i}}$$

(11)

$$\eta (k)={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^K{\lambda }_i}{{{\displaystyle \sum }}_{i=1}^N{\lambda }_i}}$$

(12)

Based on the varying energy proportions of the flow field, the modes were selected and sorted according to their energy levels to extract the primary information of the flow field. Figure 6 illustrates the cumulative energy contribution rate and energy proportion of each mode for the reduced-order model of the solid volume fraction, showing how these metrics change with the number of modes.

As the number of modes increased, the energy contribution of each mode gradually decreased. For the solid volume-fraction flow field, when the number of modes reached 13, the cumulative energy contribution exceeded 95%. Considering that the energy contributions of the subsequent modes were relatively weak, selecting modes to achieve an energy proportion of over 99% would require an excessive number of modes. Therefore, this study selects 13 modes as the number of modes for the reduced-order model of the solid volume fraction flow field.

The reduced-order model of the solid volume fraction flow field constructed using these 13 POD modes effectively reconstructed the full-order model with an overall error of 2.69%. Similar to the full-order model, the reduced-order model can reconstruct the main features of the solid volume fraction flow field at different wind speeds, including a detached solid particle cap above the tube wall and air bubbles below the tube wall. In addition, it can accurately reconstruct the distribution characteristics of solid particles throughout the flow field.

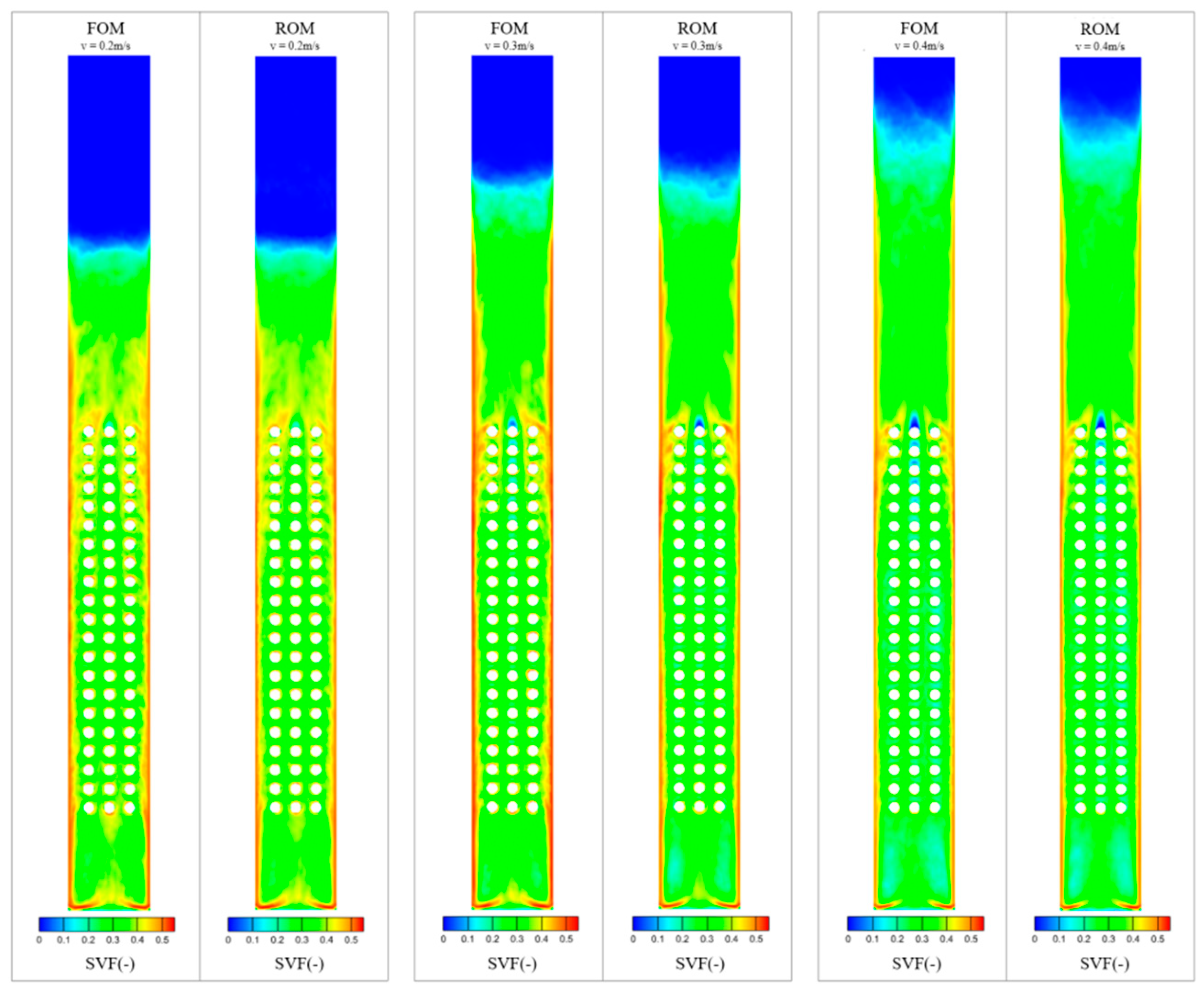
A reduced-order model for the solid volume fraction is constructed based on the selected number of POD modes. Three operating conditions with inlet velocities of 0.2 m/s, 0.3 m/s, and 0.4 m/s are chosen for the analysis of the reduced-order model results. Figure 7 shows the contour plots of the solid volume fraction for both the full- and reduced-order models under these three conditions.

Figure 7 shows that the errors in the reduced-order model of the solid volume fraction were mainly located in areas with significant changes in the gas and solid volume fractions, such as near the bed height and above the tube bundle. This is because the reduced-order model is constructed through the linear superposition of the mode coefficients and modes, which inherently include flow field information from other operating conditions. Consequently, some regions of the flow field may exhibit the characteristics of other operating conditions. However, for the overall flow field, such errors had a minimal impact on the overall computational accuracy because of their small proportion in the entire flow field.

In addition to the reduced-order model for the solid volume fraction described above, we constructed reduced-order models for the solid and gas temperature fields using the same approach, providing a modal basis for the subsequent prediction model.

Figure 8 shows the overall computational errors of the three reduced-order models at different fluidization air velocities. Since the reduced-order model is data-driven, the error is the average error over all the data. The error distribution of the solid-phase volume fraction reduced-order model is relatively uniform across various air velocities, with computational errors within 3.5%. For the reduced-order models of both the solid- and gas-phase volume fractions, the computational errors were within 0.2% at low air velocities and within 0.4% at high air velocities.

4. POD-SVM Prediction Model

For the reduced-order model, after obtaining the mode coefficients through the aforementioned calculations, it is necessary to establish a corresponding mapping relationship between the mode coefficients and modes for other operating conditions. Typically, embedded reduced-order models use methods such as the Galerkin projection for mapping, whereas non-embedded reduced-order models rely on interpolation, neural networks, or other surrogate modeling techniques to compute the mode coefficients. The reduced-order model constructed in this study is nonembedded; therefore, a surrogate model is used to predict the mode coefficients, allowing the prediction of operating condition data by superimposing the POD modes for any condition within the domain.

4.1. SVM Mode Coefficient Prediction Model

Given the high output dimensionality of the mode coefficient prediction model and limited training set, support vector machines (SVMs) are suitable choices. The SVM is a model used for binary classification, with its core objective being to find an optimal hyperplane that ensures the correct classification of all samples. This classification is based on maximizing the geometric margin between the sample dataset and hyperplane. The SVM model in this study primarily employs the Gaussian kernel function, also known as the Radial Basis Function (RBF) kernel, which offers advantages, such as fast learning and computation speeds, high generalization capability, and the ability to overcome local minima. The constructed neural network exhibited excellent performance.

This study introduced the Root Mean Square Error (RMSE) and coefficient of determination $R^2$ (Squared Correlation Coefficient) to evaluate the accuracy and fitting performance of an (SVM) model. The RMSE was used to measure the difference between the model’s predicted and actual values, quantify the variation in the training and testing sets, and effectively reflect the accuracy of the model. The coefficient of determination $R^2$ represents the proportion of the variance in the dependent variable explained by the model, reflecting the model’s ability to fit the actual data. Both metrics were calculated using the following formulae:

$$\mathit{RMSE}=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^n}{\left(X_o-X_p\right)}^2}{n}}}$$

(13)

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n}{\left(X_o-X_p\right)}^2}{{\displaystyle \sum _{i=1}^n}{\left(X_o-\overline{X}\right)}^2}}$$

(14)

where $X_0$ represents the actual value, $X_p$ is the predicted value, and $\overline{X}$ is the average value. The smaller the Root Mean Square Error (RMSE), the more accurate the model; the closer the coefficient of determination $R^2$ is to 1, the better the fitting performance of the model. The regularization parameter $C^{\prime }$ and kernel function parameter $\delta$ for the Support Vector Machine (SVM) selected in this study, along with the RMSE and $R^2$, are listed in

Table 2. Support Vector Machine Model Parameters and Performance Metrics.

Support Vector Machine Model	${\mathit{C}}^{\prime }$	$\mathit{\delta }$	RMSE	${\mathit{R}}^2$
Solid Volume Fraction	−0.4567	−0.4779	0.0356	0.989
Solid Temperature	−4.4152	−0.2903	0.0509	0.973
Gas Temperature	−4.4130	−0.2894	0.0509	0.973

.

4.2. Prediction Result Analysis

The 13 reduced-order model mode bases selected above were used as the bases for the POD-SVM prediction model. By training the Support Vector Machine (SVM) model to predict the mode coefficients based on input-output data, the model can predict the mode coefficients for full-range fluidization velocity conditions in real time. These predicted mode coefficients were then linearly combined with the bases to establish a POD-SVM prediction model. The workflow for constructing the POD-SVM prediction model for the high-temperature reheater external heat exchanger is as follows. The unknown operating condition parameters are input into the SVM mode coefficient fitting model constructed earlier to obtain the corresponding mode coefficient values. These mode coefficients were then linearly combined with the modes to build a prediction model that reconstructed and calculated the flow field and temperature field predictions for the high-temperature reheater external heat exchanger under the corresponding operating conditions.

In this study, the inlet air velocity is calculated for a range of 0.2–0.4 m/s, with a total of 21 operating conditions computed as the initial sample data for the reduced-order model. Operating conditions with inlet fluidization velocities of 0.225 and 0.325 m/s were selected to demonstrate and validate the accuracy of the constructed POD-SVM prediction model. The relative error of the prediction model was calculated using the following formula:

$$\mathit{Error}={\displaystyle \frac{‖X_{\mathit{Predict}}-X_{\mathit{Fom}}‖}{‖X_{\mathit{Fom}}‖}}$$

(15)

where $X_{Predict}$ represents the calculated value of the prediction model and $X_{Fom}$ represents the actual calculated value of the full-order model.

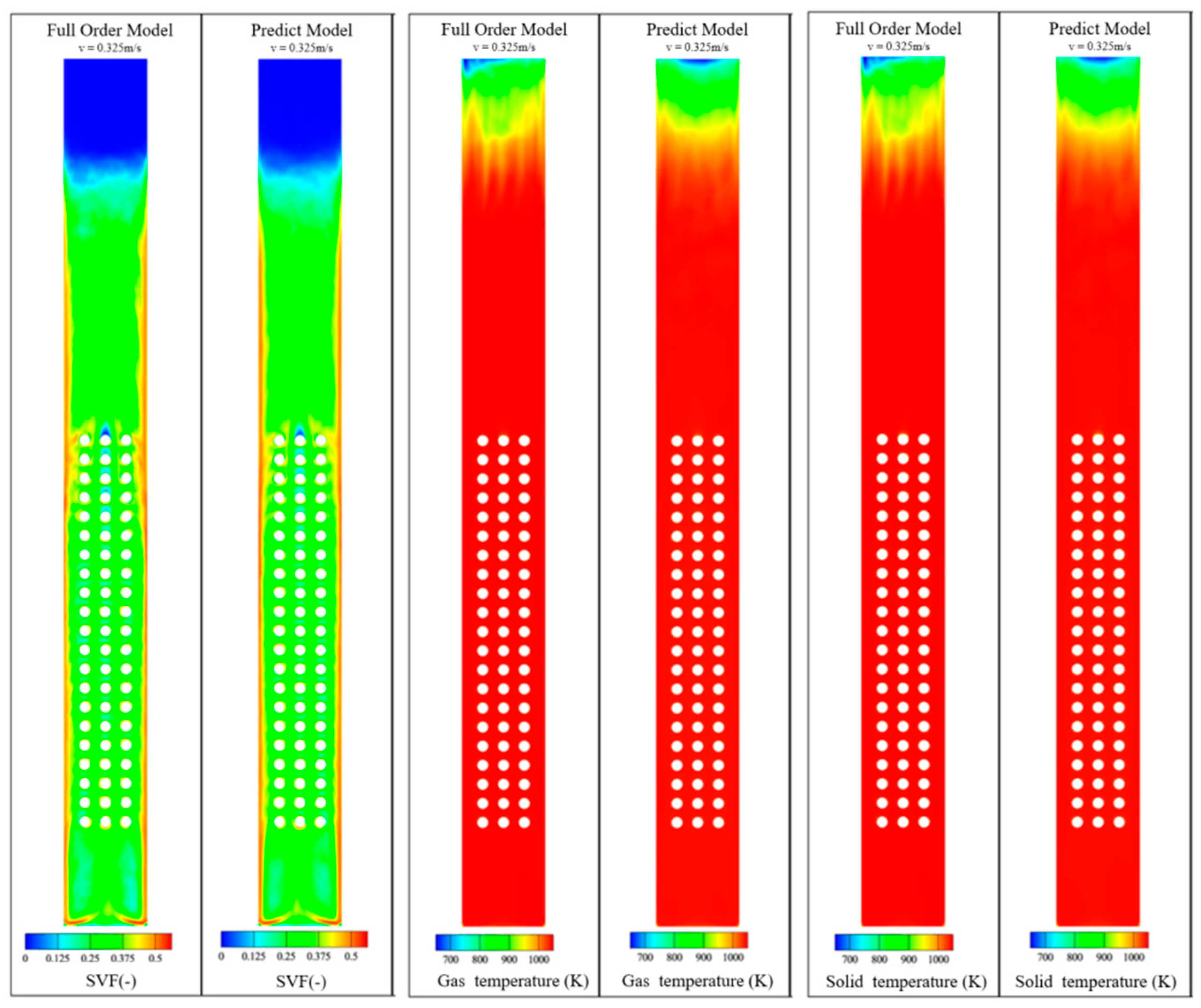
From Figure 9 and Figure 10, it can be observed that the errors of the POD-SVM prediction model are mainly concentrated in the upper half of the bed. This was because the prediction model was constructed based on the modes of the reduced-order model, which included modes from different operating conditions. In the upper part of the temperature field, where the gas phase dominated, the temperature differences between the modes of the reduced-order model were significant, leading to a reduction in the computational accuracy of the reduced-order model. The prediction model could predict the main flow characteristics of the corresponding operating conditions; however, its accuracy was limited to regions with rapid parameter changes. For operating conditions with an inlet fluidization velocity of 0.225 m/s, the overall computational accuracies of the solid volume fraction, solid temperature field, and gas temperature field prediction models were 2.89%, 1.04%, and 1.03%, respectively. For operating conditions with an inlet velocity of 0.325 m/s, the overall computational accuracies were 2.99%, 1.08%, and 1.09%.

Table 3. Calculation error of solid phase volume fraction prediction model.

Prediction Model Inlet Fluidization Velocity	Average Relative Error	Maximum Absolute Error	Proportion of Absolute Errors > 0.003	Proportion of Absolute Errors > 0.005
0.225 m/s	2.89%	0.0563	4.11%	0.043%
0.325 m/s	2.99%	0.0497	2.92%	-

,

Table 4. Calculation error of solid phase temperature field prediction model.

Prediction Model Inlet Fluidization Velocity	Average Relative Error	Maximum Relative Error	Proportion of Relative Errors > 5%
0.225 m/s	1.04%	7.29%	0.64%
0.325 m/s	1.08%	6.41%	0.49%

and

Table 5. Calculation error of gas phase temperature field prediction model.

Prediction Model Inlet Fluidization Velocity	Average Relative Error	Maximum Relative Error	Proportion of Relative Errors > 5%
0.225 m/s	1.03%	7.48%	1.78%
0.325 m/s	1.09%	6.43%	0.49%

present the computational errors of the three prediction models, indicating that the models generally have a high prediction accuracy. For the solid volume fraction prediction model, the maximum absolute errors at inlet velocities of 0.225 and 0.325 m/s were 0.0563 and 0.0497, respectively, with the distribution of absolute errors remaining at a relatively low level. For the gas and solid temperature field prediction models, the maximum absolute errors under the two velocity conditions were 7.29%, 7.48%, 6.41%, and 6.43%. The proportion of points with relative errors greater than 5% was small in the flow field, and points with larger errors were mainly concentrated in the upper half of the bed, which had a minimal impact on the fluidization and heat transfer calculations in the tube bundle region.

4.3. Computational Cost and Real-Time Analysis

Table 6. Comparison of calculation time between full-order model and prediction model.

Inlet Fluidization Velocity	Full-Order Model Computation Time	Prediction Model Computation Time
0.225 m/s	Approximately 60,000 min	1.05 s
0.325 m/s	Approximately 60,000 min	1.29 s

presents the computation times for the full-order and prediction models. In the CFD simulations using the full-order model in this study, the computation time for a single operating condition was approximately 60,000 min (approximately one week). By contrast, the prediction model required only 1 s to predict a single operating condition. While ensuring computational accuracy, the prediction model significantly reduces computational costs and enables real-time calculation of the flow field and temperature field distribution in a high-temperature reheater external heat exchanger.

5. Conclusions

This study focuses on an ultra-supercritical circulating fluidized bed high-temperature reheater external heat exchanger and establishes a computational fluid dynamics model. Using the simulation results at different flow velocities as sample data, a reduced-order model was constructed with 13 modes through linear superposition to describe the dynamic characteristics of the external heat exchanger. In the reduced-order model, the cumulative energy contribution rate of the solid volume fraction reduced-order model exceeded 95% with an overall computational error of 2.69%. The error between the reduced- and full-order models was within 3%. Building on this, supervised learning was applied to classify the data, and a POD-SVM prediction model is developed. The three prediction models could effectively predict the flow field data for unknown operating conditions, with average errors of 2.89%, 1.04%, and 1.03% at 0.225 m/s and 2.99%, 1.08%, and 1.09% at 0.325 m/s. This model significantly reduces computational costs while maintaining accuracy, with the full-order model requiring 6000 min and the prediction model requiring only 1 s.

The POD-SVM prediction model can quickly and accurately obtain detailed dynamic characteristics within the bed, providing a theoretical basis for the design and verification of ultra-supercritical CFB high-temperature reheater external heat exchangers. It also lays the foundation for subsequent operational fault prediction and online monitoring. The rapid prediction method based on model-order reduction offers a responsive simulation validation solution for the design of different ultrasupercritical CFB high-temperature reheater external heat exchangers, thereby saving time and resources. With the advancement of sensor technology, predictive models can source data directly from field installations in the future, thereby enhancing their reliability. Concurrently, progress in artificial intelligence is expected to further improve the speed and accuracy of these models, potentially enabling faster-than-real-time fault prediction and intelligent operation of power plants.