Forecasting the Power Generation of a Solar Power Plant Taking into Account the Statistical Characteristics of Meteorological Conditions

Abstract

The integration of solar generation into national energy balances is associated with a wide range of technical, economic, and organizational challenges, the solution of which requires the adoption of innovative strategies for energy system management. The inherent variability of electricity production, driven by fluctuating climatic conditions, complicates system balancing processes and necessitates the reservation of capacities from conventional energy sources to ensure reliability. Under modern market conditions, the pricing of generated electricity is commonly based on day-ahead forecasts of day energy yield, which significantly affects the economic performance of solar power plants. Consequently, achieving high accuracy in day-ahead electricity production forecasting is a critical and highly relevant task. To address this challenge, a physico-statistical model has been developed, in which the analytical approximation of daily electricity generation is represented as a function of a random variable—cloud cover—modeled by a β-distribution. Analytical expressions were derived for calculating the mathematical expectation and variance of daily electricity generation as functions of the β-distribution parameters of cloudiness. The analytical approximation of daily generation deviates from the exact value, obtained through hourly integration, by an average of 3.9%. The relative forecasting error of electricity production, when using the mathematical expectation of cloudiness compared to the analytical approximation of daily generation, reaches 15.2%. The proposed forecasting method, based on a β-parametric cloudiness model, enhances the accuracy of day-ahead production forecasts, improves the economic efficiency of solar power plants, and contributes to strengthening the stability and reliability of power systems with a substantial share of solar generation.

1. Introduction

The increasing share of solar energy in the structure of the energy balance of developed countries generates a number of specific challenges that require a comprehensive approach to their mitigation. One of the key factors is the instability of electricity generation, caused by the dependence of solar installations on climatic conditions and diurnal variations in solar radiation intensity. This necessitates capacity reservation based on conventional energy sources or the wide application of energy storage systems. Another important issue is the uneven distribution of generation over time, which complicates power system balancing processes and requires improvements in dispatch control mechanisms. At the same time, the growing share of solar generation calls for the modernization of grid infrastructure, primarily through the deployment of smart grids capable of flexibly responding to fluctuations in both demand and production. A significant challenge also arises from the reduced efficiency of conventional power plants, which are forced to operate in load-following modes, leading to shortened service life and increased electricity costs. The economic dimension is likewise of major importance, since the intensive financing of renewable energy requires state support and imposes an additional burden on public budgets. In the long term, the excessive concentration of solar power plants may result in local grid overloads and the deterioration of power quality indicators.

Under current market conditions, a pricing practice has been established for the generated electricity, based on day energy yield forecasting, which has a significant impact on the economic efficiency of solar power plants. This further highlights the importance of developing methods that ensure accurate and timely forecasting of day energy yield.

The authors have analyzed modern publications dedicated to the problems of short- and medium-term forecasting of solar energy production. The latest approaches based on artificial neural networks, deep learning, and other machine learning methods, such as Conv-GRU, NARX-GA, ARIMA, Grey Wolf Optimizer, Takagi–Sugeno–Kang neural networks, and Kohonen self-organizing maps, were considered. The use of statistical methods and deep learning models for processing satellite and meteorological data is also discussed, including models such as CNN, LSTM, GRU, CNN-LSTM, Extreme Learning Machine, and various hybrid approaches.

In the paper, the authors proposed an approach based on the use of β-distribution to describe the random nature of cloudiness. It is shown that β-distribution is a universal and convenient tool for modeling cloudiness since it allows effective consideration of regional climatic features. Based on this distribution, a mathematical model was developed that allows for analytical calculation of the main statistical characteristics of day energy yield, such as expected value and variance, taking into account the random nature of cloudiness changes during the day.

The paper provides analytical expressions for calculating day energy yield, taking into account the geographic location of the power plant, solar incidence angle, as well as atmospheric transmittance coefficients depending on cloudiness, humidity, and height above the sea level. A comparative analysis of the exact and approximate methods for calculating daily electric power generation was carried out, showing satisfactory accuracy of the proposed analytical approach.

The authors considered two main generation forecasting strategies: the first strategy is based on the use of the expected value of cloudiness provided by third-party meteorological services, while the second one takes into account cloudiness as a random variable with β-distribution. The analysis showed that taking into account the statistical nature of cloudiness significantly increases forecasting accuracy, while the relative error of calculations using the traditional method can exceed 15%.

Thus, the proposed approach allows significantly improve the accuracy of forecasting the day energy yield of solar power plants, taking into account regional features of cloudiness and other meteorological conditions. The results obtained can be used in the operational activities of solar power plants and contribute to increasing the efficiency of integrating solar generation into energy systems.

2. A Review of Modern Literature

In contemporary electricity markets, the reliable forecasting of photovoltaic (PV) power generation has become a decisive factor for the efficient operation and financial performance of solar plants, as day-ahead production declarations must be aligned with grid requirements and influence market revenues. The inherent variability of solar irradiance, compounded by the limited accuracy of short- and medium-term meteorological forecasts, continues to pose significant challenges to operators and system planners. In recent years, considerable progress has been made in addressing these challenges through the development of advanced forecasting methodologies that exploit statistical analysis, artificial intelligence, and hybrid learning frameworks. To ensure a systematic and balanced representation of this progress, the present review focuses on peer-reviewed studies published between 2021 and 2025 in high-impact journals that reflect the main directions of methodological innovation. Rather than presenting the literature chronologically, the analysis is organized by classes of models to highlight both methodological distinctions and the incremental improvements introduced by each approach. Statistical baselines, including ARIMA and gray prediction models, continue to serve as important reference methods and are still competitive when enriched with high-quality exogenous variables. Neural and deep learning architectures such as convolutional, recurrent, temporal convolutional, and transformer-based networks have demonstrated the ability to capture nonlinear and spatio-temporal dependencies, significantly reducing forecasting error across multiple horizons. Hybrid approaches that combine fuzzy logic, clustering, ensemble learning, wavelet decomposition, or bias correction modules with machine learning have emerged as particularly effective in leveraging complementary strengths and enhancing robustness under highly variable conditions. At the same time, probabilistic and physics-informed formulations, including generative and diffusion models, have gained increasing attention for their capacity to quantify forecast uncertainty and provide interpretable indicators of daily energy yield, thereby addressing the requirements of system operators and energy markets. Comparative and survey studies underscore that despite these advances, critical gaps remain in terms of interpretability and probabilistic performance, particularly for day-ahead horizons. This structured synthesis of the literature establishes the basis for the subsequent class-by-class discussion of models and situates the present contribution within ongoing efforts to improve both the accuracy and transparency of solar power forecasting.

Statistical models—such as autoregressive formulations, gray prediction methods, and related time-series techniques—constitute the traditional foundation of solar forecasting and remain a necessary reference point for assessing methodological progress. Their analytical tractability, interpretability, and modest data requirements make them particularly valuable in contexts of limited data availability or when transparency is a priority. Despite the rapid proliferation of advanced machine learning and deep learning architectures, statistical approaches continue to demonstrate competitiveness when supplied with high-quality exogenous meteorological inputs and careful preprocessing. The studies reviewed here illustrate how these methods have been adapted and extended to meet contemporary challenges, including data scarcity, variability of meteorological drivers, and the demand for reliable day-ahead predictions.

As a baseline statistical approach, Das [1] applied an ARIMA model for forecasting solar irradiance and the output of an 89.6 kWp PV plant, showing that even traditional time-series formulations can achieve competitive accuracy when sufficient historical data are available and exogenous variables are properly incorporated. Extending beyond classical autoregressive methods, He et al. [2] introduced a structurally adaptive gray prediction framework optimized with the Grey Wolf Algorithm, enabling the model to assign greater weight to new information and thereby improving adaptability in dynamic renewable energy contexts. This transition from conventional ARIMA to adaptive gray modeling illustrates how statistical paradigms have been modernized through algorithmic optimization. Further advancing this trajectory, Despotovic et al. [3] addressed the persistent challenge of limited historical data–particularly relevant for new PV installations—by combining autoregressive structures with extreme learning methods and implementing transfer learning across meteorological stations. The addition of clustering further enhanced model generalization, demonstrating how statistical approaches can be enriched with concepts from machine learning to mitigate data scarcity. A complementary perspective was offered by Gyeltshen et al. [4], who conducted a statistical evaluation of diversified irradiance repositories in Bhutan. Although their framework incorporated recurrent neural elements, the key contribution lay in underscoring the importance of high-quality and diverse statistical datasets as a foundation for robust forecasting performance. Completing this group of contributions, Benitez et al. [5] carried out a comparative study of SARIMAX, LSTM, and XGBoost for day-ahead photovoltaic output forecasting in the Philippines. Strikingly, their results revealed that SARIMAX, a classical statistical model, outperformed more advanced deep learning and gradient boosting methods when satellite-adjusted irradiance and other exogenous meteorological variables were carefully integrated. Taken together, these studies show that while statistical formulations remain essential benchmarks—and in specific contexts may even surpass more sophisticated methods –their inherent limitations in capturing nonlinear dynamics have ultimately motivated the transition toward neural and deep learning architectures.

Consequently, the next line of research has focused on neural and deep learning approaches. These architectures—including recurrent, convolutional, and more recently transformer-based networks—are specifically designed to capture complex spatio-temporal dependencies and to integrate heterogeneous input features such as irradiance, temperature, cloud cover, and satellite imagery. With the rapid expansion of computational resources and the increasing availability of large-scale datasets, deep learning has become one of the dominant directions of research in solar forecasting, demonstrating substantial improvements in predictive accuracy across a variety of temporal horizons. Against this background, a growing body of literature has explored deep learning techniques for solar forecasting, introducing diverse architectures and methodological refinements aimed at reducing forecast error and enhancing operational reliability.

A number of recent contributions exemplify the growing role of deep learning in photovoltaic forecasting, each highlighting a different methodological strand and collectively illustrating the evolution from early convolutional–recurrent hybrids to more specialized architectures and comparative evaluations against statistical baselines.

Abdel-Basset et al. [6] propose PV-Net, a Conv-GRU architecture that integrates convolutional layers to capture local spatial features with gated recurrent units capable of learning temporal dependencies in photovoltaic generation data. The architecture is enhanced through bidirectional recurrence and residual connections, which improve information flow and reduce training instabilities such as vanishing gradients. The model was validated on Australian PV datasets and consistently outperformed classical statistical baselines and shallow machine learning models in short-term forecasting tasks, especially under conditions of high irradiance variability. The significance of this work lies not only in demonstrating the superiority of convolutional–recurrent hybrids over traditional time-series methods but also in setting a structural template that has been adopted in subsequent spatio-temporal forecasting research.

Hassan et al. [7] extend the recurrent modeling paradigm by developing a genetically optimized nonlinear autoregressive recurrent neural network (NARX-GA). In this framework, the genetic algorithm is applied to optimize hyperparameters and network weights, thereby addressing the sensitivity of recurrent networks to parameter initialization and tuning. The study focused on ultra-short-term forecasting, where rapid irradiance fluctuations can cause significant challenges for standard recurrent models. Results demonstrated that the GA-enhanced NARX network achieved more stable and accurate predictions across diverse meteorological conditions, outperforming both unoptimized RNNs and statistical benchmarks. This contribution is important as it illustrates how evolutionary optimization techniques can complement deep learning, enhancing robustness and making recurrent models more reliable in real-world PV operation scenarios.

Arias Velásquez [8] investigates NeuralProphet, a neural extension of the classical Prophet time-series model, applied to short-term PV power forecasting. NeuralProphet combines seasonality and trend decomposition with neural network components, enabling the model to handle both deterministic structures and nonlinear fluctuations in solar generation. The case study demonstrated that the approach can achieve competitive accuracy while offering greater interpretability than purely black-box deep learning models, an aspect highly valued in operational contexts where forecast transparency is required for grid integration. This work underscores the potential of hybrid frameworks that combine the interpretability of statistical models with the adaptability of deep learning, thereby bridging two methodological paradigms in solar forecasting.

Khan et al. [9] present a dual-stream network augmented with an attention mechanism, explicitly designed for photovoltaic forecasting tasks. The architecture processes spatial and temporal information in parallel streams, while the attention layer adaptively assigns weights to the most informative features. This design allows the model to emphasize patterns most relevant to energy generation and to suppress noise or redundant inputs. Experimental validation showed that the dual-stream attention network outperformed standard CNN and RNN baselines, achieving lower forecast errors across several case studies. This contribution is significant in that it reflects the broader trend of incorporating attention mechanisms into PV forecasting, paralleling their transformative impact in natural language processing and computer vision.

Azizi et al. [10] shift the focus from short-term horizons to long-term forecasting of global irradiance and temperature for a 20 MW PV plant in Iran. Their study employed a range of deep learning architectures–including MLP, LSTM, GRU, CNN, and CNN-LSTM–to develop a multivariate, multi-step forecasting framework. By integrating multiple climatic variables and extending the forecasting horizon, the authors demonstrated that deep learning models can maintain predictive accuracy even in long-term settings where variability and uncertainty are higher. This work is important because it broadens the application of deep learning beyond the traditional short-term domain, showing its viability for long-range planning and operational decision-making in utility-scale PV systems.

Finally, Kim et al. [11] provide a comprehensive comparative study of statistical and deep learning methods using South Korean solar datasets from 2017 to 2021. The analysis included Holt–Winters, ARIMA, SARIMA, and LSTM models. Results indicated that LSTM consistently delivered the lowest forecast errors, particularly under conditions of rapidly fluctuating irradiance, outperforming traditional statistical approaches across multiple test scenarios. The study offers empirical justification for adopting LSTM in operational contexts where sufficient historical data are available, thereby reinforcing the practical advantage of deep learning models over conventional baselines.

Viewed as a whole, these contributions demonstrate the maturation of deep learning in PV forecasting—beginning with convolutional–recurrent hybrids such as PV-Net, progressing through evolutionary-optimized recurrent designs like NARX-GA, and advancing to interpretable frameworks such as NeuralProphet and attention-based dual-stream networks. More recent work extends the scope to multivariate long-term formulations and comparative evaluations that confirm the practical advantage of LSTM architectures over statistical baselines. Collectively, this progression highlights how deep learning has evolved toward solutions that are not only more accurate but also increasingly robust, interpretable, and operationally relevant across different forecasting horizons.

Building on the advances of convolutional–recurrent hybrids, evolutionary optimization, and attention-based mechanisms, more recent research has expanded the scope of deep learning applications in solar forecasting. A distinctive feature of these contributions is the explicit integration of spatial–temporal correlations, the incorporation of satellite imagery and climate variables, and the development of hybrid and physics-informed models that address the limitations of purely data-driven learning. This stream of studies not only extends deep learning to different forecasting horizons, from intra-hour to day-ahead and long-term, but also demonstrates how combining neural architectures with clustering, ensemble methods, or domain knowledge can enhance robustness and interpretability. Within this context, the following works published between 2024 and 2025 [12,13,14,15,16,17,18] illustrate the methodological diversification of deep learning and its increasing alignment with practical forecasting challenges in distributed and large-scale PV systems.

Cui et al. [12] exemplify the integration of novel input sources by employing geostationary satellite imagery in deep learning architectures such as DGMR-SO and UNet. Their framework moves beyond traditional ground-based observations by capturing cloud dynamics in near real time, substantially reducing errors in solar radiation nowcasting. The study illustrates how the inclusion of spatial image data complements temporal modeling, setting a precedent for multimodal approaches in ultra-short-term forecasting.

Building on the idea of capturing spatial structure, Lai et al. [13] extend deep learning forecasting to distributed PV networks by introducing a sub-region division method that explicitly accounts for spatio-temporal correlations among installations. Their results show that localized forecasting models outperform centralized approaches, especially in fragmented PV systems with heterogeneous characteristics. This contribution emphasizes the growing importance of geographically adaptive strategies in managing distributed renewable energy resources.

While Lai et al. focus on distributed systems, Xu et al. [14] address the long-term horizon by proposing a complementary fusion of GRU and XGBoost. This hybrid ensemble leverages the sequential modeling strengths of recurrent networks while harnessing the noise resilience and interpretability of gradient boosting. By demonstrating improved stability and accuracy over extended horizons, their work highlights the potential of combining deep learning with machine learning ensembles to overcome the degradation typically observed in long-term forecasts.

A different innovation is introduced by Li et al. [15], who target ultra-short-term irradiance forecasting using a K-means-ELM model. Their approach applies clustering to identify characteristic weather patterns before using an Extreme Learning Machine for prediction. This preprocessing step improves adaptability to rapid fluctuations and ensures computational efficiency, making the method well suited for operational contexts that require near real-time forecasts. In this way, the study illustrates how the integration of unsupervised learning with fast neural algorithms can yield practical forecasting tools for grid operators.

Further advancing the integration of meteorological information, Ma et al. [16] develop the D-Informer architecture, which combines attention mechanisms and differential transformations to explicitly embed climate variables such as temperature, humidity, and pressure into the forecasting process. By leveraging these atmospheric drivers, the model achieves superior accuracy under weather-sensitive conditions, underscoring the importance of climate-aware neural forecasting frameworks in operational planning.

The shift from short-term and weather-driven designs to regional and market-relevant horizons is represented by Perera et al. [17], who propose hierarchical temporal convolutional networks (HTCNN) for day-ahead regional forecasting. Their approach jointly processes aggregated and site-level data, thereby capturing multi-scale dependencies that flat models fail to represent. Experimental validation demonstrates that hierarchical learning enhances accuracy in large-scale forecasting tasks, reinforcing the operational value of day-ahead predictions for energy markets and system scheduling.

Finally, Han et al. [18] contribute a hybrid approach for intra-hour forecasting that combines topological data analysis with physics-informed deep learning. This framework extracts structural features of irradiance variability while incorporating physical constraints of solar generation, producing forecasts that are not only accurate but also interpretable under highly stochastic conditions. Such physics-aware designs represent a promising direction for bridging the gap between purely data-driven models and the operational transparency required by grid operators.

As the evidence accumulates, a pattern emerges in deep learning–based solar forecasting: the transition moves from the incorporation of new data modalities (satellite imagery, distributed PV correlations) to hybridizations with clustering and boosting methods, and finally toward climate-aware and physics-informed architectures. This trajectory not only delivers consistent improvements in accuracy across different horizons but also enhances robustness, scalability, and interpretability–qualities that are increasingly critical for integrating PV generation into modern electricity markets.

In parallel with earlier advances in spatial–temporal modeling and climate-aware neural designs, the latest body of research increasingly emphasizes multimodal, hybrid, and probabilistic frameworks. These approaches aim to exploit heterogeneous data inputs–such as ground-based cloud imagery, meteorological time series, and contextual climate variables–while simultaneously addressing two critical challenges: ensuring scalability across diverse PV systems and providing explicit quantification of forecast uncertainty. The most recent works published in 2025 [19,20,21,22,23] exemplify this orientation, introducing deep clustering strategies, advanced hybrid learning schemes, multimodal fusion architectures, transformer-based feature enhancements, and probabilistic forecasting formulations that together represent the current research frontier in photovoltaic power prediction.

Within this line of work, Dou et al. [19] foreground multimodality for day-ahead irradiance forecasting by coupling ground-based cloud imagery with meteorological time-series through a deep clustering framework. The approach first structures heterogeneous inputs via representation learning and cluster assignment, then fuses image- and sequence-derived features for prediction. This design addresses two persistent issues–noisy visual inputs and regime heterogeneity–by letting the model discover weather regimes that mediate how visual and temporal cues should be combined. The study is retained because it establishes a principled route for regime-aware multimodal fusion at a day-ahead horizon, a setting where image information is often underexploited.

Extending the emphasis on complementarity, Song et al. [20] present an advanced hybrid deep-learning pipeline aimed at improving point accuracy for PV power prediction. Rather than relying on a single architecture, the method stages feature extraction, temporal modeling, and fusion/ensembling to capture interactions among meteorological drivers and historical power signals. The value of this contribution lies in demonstrating how carefully engineered hybrid stacks can translate into consistent error reductions across datasets, thereby offering a practical blueprint for utilities seeking accuracy gains without committing to a single “all-purpose” network.

Abad-Alcaraz et al. [21] reinforce the case for multimodal learning in solar radiation forecasting by formalizing feature-level and/or decision-level fusion within a unified deep model. By treating radiation-relevant covariates (e.g., irradiance proxies, meteorology, image or contextual signals) as complementary views, the architecture learns cross-modal dependencies that single-stream models tend to miss. This paper is included because it provides a clear, generalizable template for multimodal fusion, helping explain when and why heterogeneous inputs yield measurable accuracy gains.

On the architectural frontier, Liu et al. [22] refine transformer-based forecasting with targeted feature enhancement for short-term PV power prediction. The model augments attention with learnable feature refinement (e.g., gating/selection or cross-feature interactions), improving the network’s ability to prioritize informative signals under rapidly changing conditions. This work is representative of a broader movement to adapt transformers to energy time-series by controlling feature noise and improving data efficiency–an essential step toward robust deployment beyond image or text domains.

Finally, Song et al. [23] move from pure point prediction to probabilistic ultra-short-term forecasting by combining attention-enhanced neural representations with natural-gradient boosting. The hybrid yields calibrated predictive distributions–rather than single values–thus addressing the operational need to quantify uncertainty for reserve scheduling and risk-aware bidding. We retain this study because it exemplifies how modern DL can be integrated with probabilistic learners to deliver both accuracy and well-behaved uncertainty, closing a gap identified in earlier literature.

Overall, the reviewed contributions trace a coherent methodological arc in deep learning–based solar forecasting—beginning with multimodal fusion strategies that integrate diverse data sources such as cloud imagery and meteorological time series, advancing through hybrid pipelines and generalized multimodal architectures that strengthen cross-modal representation and accuracy, and culminating in transformer-based refinements and probabilistic formulations that deliver calibrated uncertainty estimates.While these advances have significantly improved predictive accuracy, scalability, and robustness, purely deep learning–based approaches continue to face persistent challenges, particularly in terms of interpretability, adaptability across heterogeneous PV systems, and reliance on large-scale training datasets. To address these gaps, a complementary research stream has emerged around hybrid models that integrate neural architectures with fuzzy logic, statistical formulations, ensemble methods, predictive control, or physics-based corrections. By combining the nonlinear representation capacity of machine and deep learning with the robustness, transparency, and domain-awareness of traditional approaches, hybrid frameworks aim to deliver forecasts that are not only accurate but also interpretable, adaptive, and operationally reliable across diverse climatic and market contexts.

The trajectory of this research begins with efforts to explicitly model uncertainty and interpretability. Li and Liu [24] introduce interval type-2 Takagi–Sugeno–Kang fuzzy systems for short-term PV power prediction, where fuzzy logic captures uncertainty while neural components approximate nonlinear patterns. This design provides interval forecasts rather than point estimates, offering decision-makers confidence bounds better suited for grid operations under variable irradiance. Building on the goal of interpretability, Sehrawat et al. [25] combine digital twin technology with machine learning to forecast solar irradiance. By creating virtual replicas of PV systems that are continuously updated with real data, the framework ensures forecasts remain system-specific and adaptive, representing a shift toward hybrid digital environments where physical system knowledge is directly embedded in predictive workflows.

Moving from interpretability to ensemble stabilization, Abumohsen et al. [26] propose a CNN–LSTM–RF model, in which convolutional and recurrent networks extract spatio-temporal patterns, while a Random Forest ensemble improves generalization and reduces overfitting. Their study demonstrates how blending deep and tree-based learners can achieve more robust predictions than either family of methods alone. A different hybrid pathway is illustrated by Mbungu et al. [27], who frame solar forecasting within a predictive control paradigm. Here, forecasts are continuously refined in response to deviations between expected and actual outputs, highlighting the operational role of hybrid forecasting not only in accuracy improvement but also in real-time responsiveness–a critical attribute for grid management.

The importance of weather regime adaptation is emphasized by Dai et al. [28]. Their method combines credibility prediction for weather types with a dynamic ensemble of forecasting models, assigning higher weights to those models best suited for current meteorological conditions. This approach reflects an evolution toward adaptive hybridization, where models are not fixed but context-sensitive to the prevailing weather regime. Extending to signal decomposition and enriched feature design, Bai et al. [29] introduce a hybrid model that incorporates wavelet packet decomposition and an improved similar-day method before feeding data into an LSTM predictor. By disentangling multi-scale frequency components and enhancing input selection, their model achieves superior day-ahead forecasts, particularly under fluctuating irradiance conditions.

At a larger scale, Dou et al. [30] demonstrate how numerical weather prediction (NWP) data can be effectively hybridized with machine learning. Their framework disentangles seasonal and trend components of NWP outputs and corrects them with a mixture-of-experts (MoE) model, bridging the gap between meteorological physics and data-driven refinement. Finally, Pereira et al. [31] present one of the most comprehensive physics-informed hybrid frameworks, combining deterministic solar radiation models with data-driven predictors. By embedding physical laws into the learning process, their approach prevents unrealistic outputs, reduces error propagation, and strengthens interpretability–an attribute increasingly demanded by system operators.

These contributions outline a clear evolutionary path in hybrid solar forecasting research. The trajectory begins with fuzzy and digital twin frameworks designed to enhance interpretability, progresses through ensemble- and control-based hybrids that improve robustness and adaptability, and culminates in physics-informed and NWP-enhanced architectures that integrate domain knowledge with machine intelligence. This progression highlights the pivotal role of hybrid models as a bridge between purely data-driven deep learning and operationally transparent forecasting systems, providing solutions that are not only accurate but also robust, interpretable, and practical for deployment in modern electricity markets.

Alongside the advances in hybrid and deep learning frameworks, a further strand of research has increasingly focused on physico-statistical and probabilistic models, reflecting the growing importance of uncertainty quantification and interpretability in PV forecasting. Unlike purely deterministic approaches, these models explicitly characterize the stochastic nature of solar irradiance and power generation, often combining statistical formulations with physical insights or probabilistic inference. Their value lies not only in providing point forecasts but also in generating confidence intervals, probability distributions, or scenario sets that can be directly incorporated into grid operation, reserve scheduling, and market bidding strategies.

This research stream has gained momentum in recent years, particularly as system operators and market regulators place greater emphasis on risk-aware decision-making and the reliable integration of high shares of variable renewable energy. The selected contributions [32,33,34,35,36,37] illustrate the breadth of methodological innovation in this area, spanning diffusion-based generative models, weather-informed probabilistic forecasting, hidden Markov formulations, copula-based temporal decomposition, and ensemble-based Gaussian mixture networks. Together, these studies exemplify how probabilistic and physico-statistical approaches complement machine and deep learning by enhancing transparency, capturing uncertainty, and aligning forecasting outcomes with the operational requirements of modern electricity markets.

Huang et al. [32] advance the state of probabilistic forecasting by introducing an enhanced conditional diffusion model tailored for net load prediction in grids with high renewable penetration. Diffusion-based generative modeling, widely adopted in computer vision, is here adapted to the energy domain, enabling the model to capture complex probability distributions of load and PV generation under uncertainty. Unlike deterministic predictors, the diffusion framework produces diverse, calibrated scenarios that can inform reserve planning and reliability assessment. This contribution is significant as it marks one of the first attempts to apply conditional diffusion techniques to renewable-heavy power systems, showing how generative models can be leveraged to improve both accuracy and probabilistic calibration.

Zhang et al. [33] complement this direction with a weather-informed probabilistic framework that integrates scenario generation into day-ahead system operation. By coupling meteorological forecasts with probabilistic learning, their approach not only predicts PV output but also generates scenario sets consistent with weather uncertainty, directly usable in stochastic optimization for unit commitment and market bidding. This work is notable because it bridges the gap between forecasting and operational decision-making, highlighting how scenario-based probabilistic outputs can enhance system flexibility and resilience in high-VRE environments.

Ahmad et al. [34] propose a hybrid strategy that combines deterministic forecasts with the NB-DST probabilistic enhancement method. Their framework integrates Neural Bayesian (NB) inference with a Deterministic–Stochastic Transformation (DST), yielding both accurate point forecasts and well-calibrated probability distributions. The results demonstrate that augmenting deterministic predictors with probabilistic layers substantially improves reliability, especially under volatile irradiance. This study illustrates how deterministic deep learning models can be extended into the probabilistic domain without compromising accuracy, offering a pragmatic pathway for operators accustomed to conventional forecasting tools.

Zhang and Shang [35] take a different route, focusing on interpretability through a multi-observation non-homogeneous Hidden Markov Model (HMM). By modeling solar power generation as a sequence of hidden states influenced by exogenous meteorological variables, their approach delivers fast and interpretable probabilistic forecasts. Unlike black-box neural models, the HMM structure allows operators to directly associate hidden states with physical regimes (e.g., clear sky, partial cloud, overcast), thereby enhancing transparency while maintaining competitive predictive performance. This contribution is particularly relevant in regulatory and operational contexts where explainability is as critical as accuracy.

Wang et al. [36] present a copula-based approach, combining temporal decomposition with vine copula functions to model dependency structures in solar power time series. By first decomposing the PV output into trend and fluctuation components, and then capturing nonlinear dependencies via vine copulas, the method generates probabilistic forecasts that respect temporal correlations across different horizons. Their results show improved calibration and sharpness compared to traditional Gaussian-based approaches, underscoring the importance of advanced statistical tools for capturing joint variability in renewable energy time series.

Doelle et al. [37] extend the probabilistic forecasting paradigm by leveraging ensembles of deep Gaussian mixture density networks (GMDNs) for intraday PV prediction. Unlike classical probabilistic regressors, GMDNs directly estimate conditional probability densities, allowing the generation of full predictive distributions rather than single-point estimates. The ensemble design further improves robustness by reducing variance and mitigating overfitting, while the mixture density formulation captures multimodal uncertainty inherent in rapidly changing irradiance conditions. Their findings demonstrate that deep probabilistic ensembles can achieve high calibration quality and sharpness, making them particularly suitable for intraday horizons where uncertainty quantification is most critical for grid balancing and reserve allocation.

The evidence from [32,33,34,35,36,37] underscores the distinctive role of probabilistic and physics–statistical approaches in advancing photovoltaic forecasting. Diffusion-based generative models enable calibrated scenario generation, weather-informed and Bayesian–deterministic hybrids enhance operational usability, hidden Markov structures provide transparent links between statistical states and physical regimes, copula-based formulations capture nonlinear temporal dependencies, and deep Gaussian mixture ensembles demonstrate how probabilistic learning can be embedded into neural architectures. What unites these methods is their explicit capacity to quantify uncertainty and produce scenario-based outputs that are both interpretable and operationally relevant. In this way, probabilistic and physics–statistical frameworks complement neural and hybrid deep learning models by addressing the challenges of calibration, robustness, and transparency, thereby offering tools that are increasingly indispensable for reliable system operation in renewable-dominated power grids.

A distinct stream of research is represented by survey and comparative studies, which provide meta-analyses of methodological progress and consolidate lessons from the diverse body of work reviewed above. Rather than focusing on single architectures, these contributions synthesize statistical, machine learning, hybrid, and probabilistic approaches, while also mapping their operational implications for modern energy systems.

Di Leo et al. [38] present a comprehensive review of advancements and challenges in PV forecasting, offering a structured analysis of statistical, machine learning, deep learning, and hybrid methodologies. Their findings emphasize that forecasting performance depends not only on algorithmic sophistication but also on the quality of meteorological inputs, preprocessing strategies, and horizon-specific model adaptation. Importantly, the authors argue that future improvements will require integrated frameworks that couple forecasting accuracy with practical constraints of grid operation, market bidding, and reserve scheduling.

Yu et al. [39] focus specifically on deep learning models, providing one of the most detailed reviews of convolutional, recurrent, attention-based, and hybrid neural networks for PV power forecasting. Their analysis demonstrates that deep learning has rapidly become the dominant paradigm due to its superior capacity for capturing spatio-temporal dependencies and handling heterogeneous data. However, they also stress unresolved challenges, including limited interpretability, difficulties in generalizing across heterogeneous PV systems, and the high computational cost of training advanced architectures.

Blazakis et al. [40] extend the discussion by conducting an empirical evaluation of one-day-ahead solar irradiation and wind speed forecasting using state-of-the-art deep learning techniques. Their results confirm the competitive advantage of advanced neural models over traditional statistical methods but also reveal vulnerability to performance degradation under extreme weather variability. This underscores the importance of integrating deep learning with hybrid and probabilistic refinements to achieve consistent reliability across diverse operating conditions.

Delgado et al. [41] examine the integration of Hidden Markov Models (HMM) with Long Short-Term Memory (LSTM) networks under both single-input and multiple-input configurations. Their study illustrates how combining interpretable statistical state-space representations with recurrent neural architectures can improve both robustness and transparency. This line of work points to the potential of hybrid architectures that preserve interpretability while retaining the nonlinear representation capacity of deep learning.

Beyond PV-specific applications, Lim et al. [42] provide a broader review of deep learning in power system decision-making. Their study situates PV forecasting within the larger ecosystem of energy management, unit commitment, and reliability assessment, stressing that forecasting models must ultimately be evaluated by their capacity to inform operational and market-level decisions. The authors highlight the growing need for explainable artificial intelligence (XAI) and risk-aware frameworks, which can bridge the gap between black-box predictors and decision-making requirements in regulated energy markets.

Kousounadis-Knousen et al. [43] complement this perspective by focusing on scenario generation methods for solar forecasting, with particular attention to weather classifications, temporal horizons, and the application of deep generative models. Their review highlights how scenario-based forecasting enables stochastic optimization and robust decision-making under uncertainty, offering practical pathways for integrating probabilistic forecasts into energy market operations and grid reliability assessments.

Viewed collectively, the survey and comparative contributions [38,39,40,41,42,43] show that while methodological innovations—ranging from statistical baselines to advanced neural and hybrid models–have substantially improved forecasting accuracy, persistent gaps remain at the interface between algorithms and operational practice. These reviews converge on several key points: the necessity of high-quality and diverse input data; the value of hybridization to balance accuracy, interpretability, and robustness; and the importance of probabilistic and scenario-based outputs for risk-aware system management. In this way, meta-analyses provide not only a synthesis of methodological evolution but also a roadmap for future research directions, linking algorithmic advances to the practical demands of modern electricity markets.

As highlighted by the reviewed literature, reliable forecasting of solar power generation remains especially critical for short-term resource planning, power dispatching, and ensuring the operational safety of energy systems. While most research efforts concentrate on improving short-term prediction methods–primarily through weather-informed deep learning architectures–existing approaches still fall short in effectively addressing the problem of forecasting the average daily energy yield of PV plants. This gap is of particular importance for operational interaction with the power grid and for maximizing plant revenues under market conditions.

To address this challenge, the present research aims to develop methods for estimating statistical indicators of daily energy yield based on the probabilistic characterization of meteorological conditions. Specifically, the objectives include: developing a mathematical model of hourly PV generation that accounts for geographical location and key meteorological drivers; constructing a model of daily energy yield derived from hourly generation; justifying the appropriate probability density law for meteorological inputs as random variables; and deriving analytical expressions for the main statistical indicators of daily yield as functions of the probability density parameters.

3. Research Materials

3.1. Calculation of the Day Energy Yield of a Solar Panel

The expression for calculating the daily solar panel generation, considering the geographical location and meteorological conditions of the atmosphere, is described by the well-known expression [44]:

$$E=S·{\int }_{t_{sunrise}}^{t_{sunset}}{I}_0\left(t\right)·f_{atm}\left(H,h,c\right)·\cos \left(\theta \left(t,LAT,LON\right)\right)dt,$$

(1)

where

$E$ is a day energy yield (W·h);

$S$ is a solar panel area (m²);

$t_{sunrise}, t_{sunrise}$ are moments of sunrise and sunset (hours);

$I_0\left(t\right)$ is the solar constant (~1361 W/m²), adjusted for the time of day and day of the year;

$f_{atm}\left(H,h,c\right)$ is an atmospheric transmittance coefficient, depending on the altitude $H$, humidity $h$ and cloudiness $c$;

$\theta \left(t,LAT,LON\right)$ is the angle of incidence of sun rays on the horizontal surface, which depends on the time of the day, latitude, and longitude of the location.

Let us give formulas for calculating the components of Equation (1).

3.1.1. Atmospheric Transmittance Coefficient

Atmospheric conditions including humidity, cloudiness and solar panel altitude above sea level are approximately taken into account as follows [44,45]:

$$f_{atm}\left(H,h,c\right)= \left(1-0.75·{\mathrm{c}}^{3.4}\right)·\left(1-0.1·h\right)·\left(1+0.0001·H\right)$$

(2)

At low altitude of solar panel installation above sea level H (up to 500 m) the last factor in Equation (2) can be neglected. We also neglect the effect of humidity h.

$$f_{atm}\left(h,c\right)=\left(1-0.75·{\mathrm{c}}^{3.4}\right)·\left(1-0.1·h\right)\approx \left(1-0.75·{\mathrm{c}}^{3.4}\right)$$

(3)

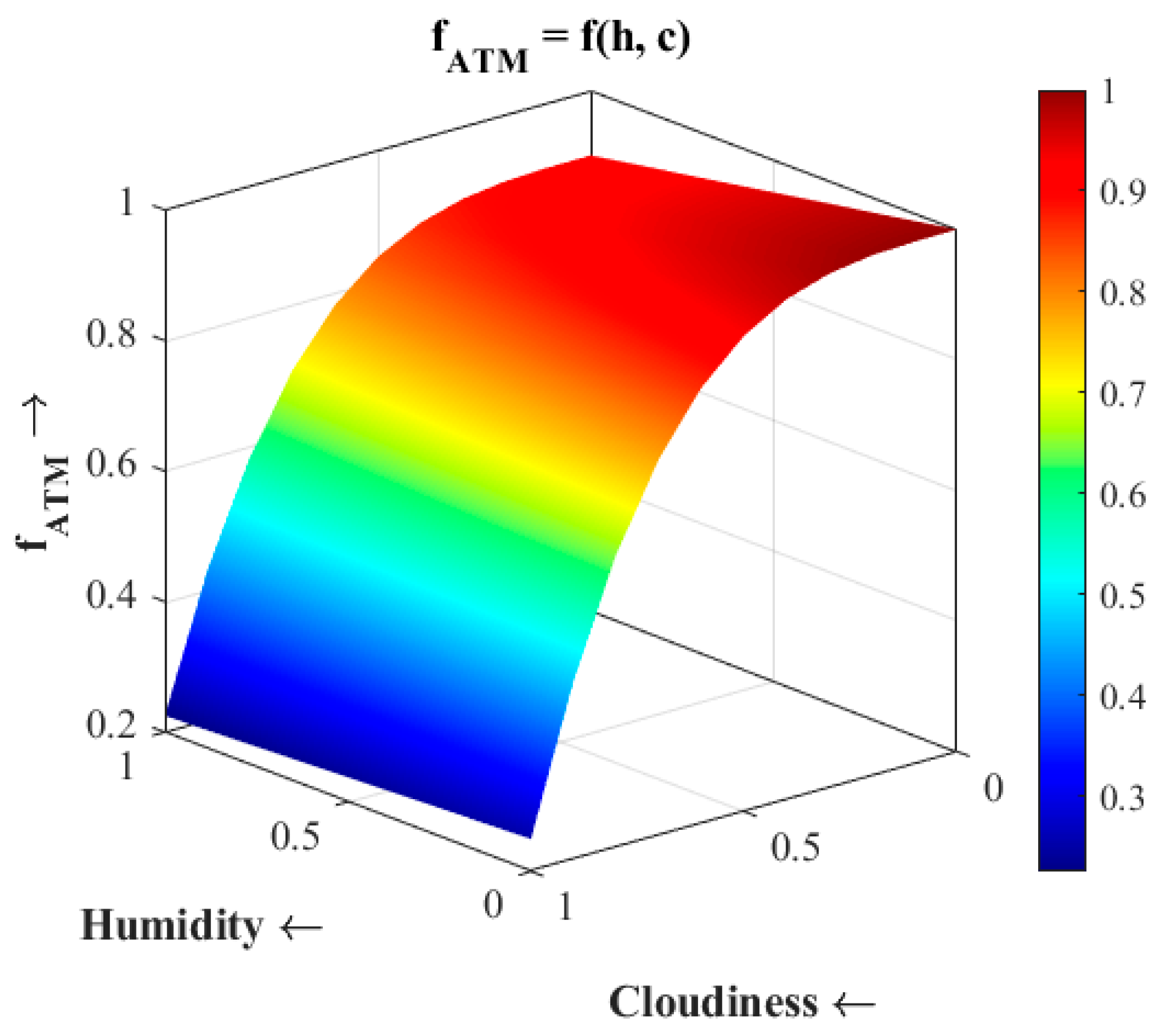
As can be seen from Figure 1, the value of the atmospheric transmittance coefficient is decisively influenced by the “Cloudiness” parameter. Later, Humidity’s influence can be neglected.

3.1.2. Angle of Incidence of Solar Rays ($\theta$)

$$\cos \left(\theta \right)=\sin \left(\delta \right)·\sin \left(\phi \right)+\cos \left(\delta \right)·\cos \left(\phi \right)·\cos \left(\omega \right),$$

(4)

where

$\delta$ is declination of the Sun (calculated depending on the date);

$\phi$ is latitude of the location (LAT);

$\omega$ is an hour angle (depends on the time of day and longitude LON).

3.1.3. Solar Constant $I_0$

The value of the solar constant I_sc ≈ 1361 W/m² is used with a correction for the Earth-Sun distance, depending on the day of the year:

$$I_0=I_{SC}\left(1+0.034·\cos \left(\left({\displaystyle \frac{2\pi }{365}}·N\right)\right)\right)$$

(5)

where $N$ is the day number of the year.

This expression takes into account the main factors that influence the daily generation of solar panels, allowing for accurate calculations taking into account climatic and geographical features.

3.1.4. Sunrise and Sunset Times ($t_{sunrise},t_{sunset})$

The hourly sunrise/sunset angle (ω_s) is determined by the formula:

$$\cos \left({\omega }_s\right)=-\tan \left(\phi \right)·\tan \left(\delta \right)$$

(6)

Then

• $t_{sunrise}$ =$12-{\omega }_s/15$, hourly time of sunrise;
• $t_{sunset}$=$12+{\omega }_s/15$, hourly time of sunset.

Here $\phi$ is the latitude, $\delta$ is the declination of the Sun.

The declination of the Sun ($\delta$) is calculated as follows:

$$\delta =23.45°\sin \left({\displaystyle \frac{360}{365}}·\left(284+N\right)\right)$$

(7)

Let us present the results of calculations of hourly power generation by a solar panel throughout the day, under the following conditions: area of the panel—1 m²; humidity $h=0.1$; cloudiness $c=0.1$; panel tilt angle 30°; panel efficiency 18%. The results of the performed calculations are illustrated in Figure 2, which shows the hourly distribution of solar panel electricity production for two representative days of the year.

These results were obtained under constant cloud cover and atmospheric humidity.

Below are the results of experimental studies of solar radiation carried out using the meteorological station instruments at the solar power plant in Saran, Kazakhstan [46]. The solar power plant occupies an area of 160 ha in the northeastern part of the city of Saran, at geographic coordinates (49.8138, 72.8256). The site elevation is 491 m above sea level, and the official time zone is UTC+5. The panel tilt angle is 30°. Measurements were performed with a Kipp & Zonen SMP10-V spectrally flat Class A pyranometer (Figure 3), configured for GHI (Global Horizontal Irradiance). The data logging interval is 1 hour.

Main technical characteristics of Kipp & Zonen SMP10-V pyranometer: analog outputs—0–1 V; directional desponse—˂15 W/m²; irradiance saturation—4000 W/m²; operating temperature range—−40 to +80 °C; spectral accuracy—285 to 2800 nm.

As the initial data, the company’s management provided access only to information on solar radiation registration.

For the approximate pipeline GHI → DNI/DHI → POA → DC → AC, based on the hourly GHI profile, we make the following assumptions: the Sun’s position is calculated according to standard astronomy (e.g., NREL SPA) [47]; for the decomposition GHI → DNI/DHI, the Erbs model is used, [48]; for transposition onto the module plane (POA), the isotropic sky model [49] is chosen; albedo is used (0.15 for soil/vegetation); the DC module model is assumed to be linear with respect to irradiance and temperature; cable/connector losses are considered as constant DC losses; and the inverter efficiency and DC/AC ratio are assumed constant.

The complete MATLAB 2025b program for calculating the actual daily energy of a solar panel, implementing the specified calculations, is given in Appendix A.

Figure 4 shows the results of the experimental study of hourly solar radiation during the day, as well as the results of calculating the actual daily energy of a solar panel.

Attention is drawn to the asymmetry of the GHI solar radiation histograms, Figure 4. In addition, the analytical results of the hourly solar panel output calculation, Figure 2, do not coincide with the results of the experimental study, Figure 4. This can be explained by changes in cloudiness during the day.

The following discussion is devoted to the development of methods for accounting for cloudiness as a probabilistic process in the calculations of solar panel power generation.

3.2. Analytical Determination of Daily Energy Yield

Analytical integration of the given expression (1) is possible if we accept some simplifications:

• The solar constant $I_0$ by (5) is considered constant throughout the day (for a specific day $N$).
• To consider the symmetry of the sun’s position relative to solar noon.
• The atmospheric transmittance coefficient $f_{atm}\left(c\right)$ can be considered constant throughout the day.

Last assumption can be reasonably substantiated as follows. In the present study, our primary concern is the value of the definite integral over a prescribed time interval. The parameters of the β-distribution may likewise be interpreted as integral descriptors of cloudiness. Accordingly, it is permissible to approximate the atmospheric transmittance coefficient not as a time-dependent function, but rather as a constant defined by the β-distribution parameters corresponding to the specified calculation date.

Let us transform the Formula (1) under the assumption of a constant atmospheric transmittance coefficient and taking into account (3):

$$E=S·I_0\left(t\right)·f_{atm}\left( c\right)·{\int }_{t_{sunrise}}^{t_{sunset}}\cos \left(\theta \left(t, LAT, LON\right)\right)dt$$

(8)

Since the function $\cos \left(\theta \right)$ changes sinusoidally during the day, the integral can be simplified to the following analytical expression.

The final formula after integration of (8):

$$E=\alpha ·S·I_0\left(t\right)·f_{atm}\left( c\right)·{\displaystyle \frac{24}{\pi }}\left[\mathit{sin}\left(\delta \right)·\mathit{sin}\left(\phi \right)·{\omega }_s+\mathit{cos}\left(\delta \right)·\mathit{cos}\left(\phi \right)·\mathit{sin}\left({\omega }_s\right)\right]$$

(9)

where

$S$ is the area of the panel, m²;

$I_0$ is an extraterrestrial solar constant for day $N$;

$f_{atm}\left( h, c\right)$ is an average daily atmospheric transmittance;

$\phi$ is the latitude of the location;

$\delta$ is the declination of the Sun;

${\omega }_s$ is an angle of sunrise (sunset) in radians.

$\alpha$ is the coefficient accounting for panel soiling and degradation.

Thus, with the indicated simplifications, it is possible to make analytical integration and obtain the final formula that can be used for an approximate calculation of the daily generation of a solar panel.

Let us compare the results of the exact (1) and approximate (9) formulas for calculating daily solar generation.

From the analysis of the graphs in Figure 5, we can conclude that the approximate model for calculating solar generation has satisfactory accuracy. The mean relational error value in the calculation using the approximate model (9) was 3.9%.

The main reason for the calculated data deviation according to Equation (9) is that the calculations according to (1) consider the daily movement of the Sun and the change in the solar panel’s illumination level more accurately.

3.3. Physical and Statistical Nature of the Variable “Cloudiness”

Cloudiness (c) is a continuous random variable taking values in the interval [0, 1], where

c = 0—absolutely clear;

c = 1—fully cloudy.

This makes it a typical candidate for modeling using random variable distributions on the interval [0, 1], where the β-distribution is the most universal [50].

$\beta$-distribution of a random variable X is given by the probability density $f_X$, which has the following form:

$$f_X\left(x\right)={\displaystyle \frac{1}{B\left(\alpha ,\beta \right)}}{x}^{\alpha -1}{\left(1-x\right)}^{\beta -1},$$

(10)

where $\alpha$ and $\beta$ are distribution parameters.

$B\left(\alpha ,\beta \right)={\int }_0^1{x}^{\alpha -1}{\left(1-x\right)}^{\beta -1}dx$—beta-function.

In this case, the random variable X has a $\beta$-distribution. Formally, this fact is written by the expression $\mathrm{X}~B\left(\alpha ,\beta \right)$.

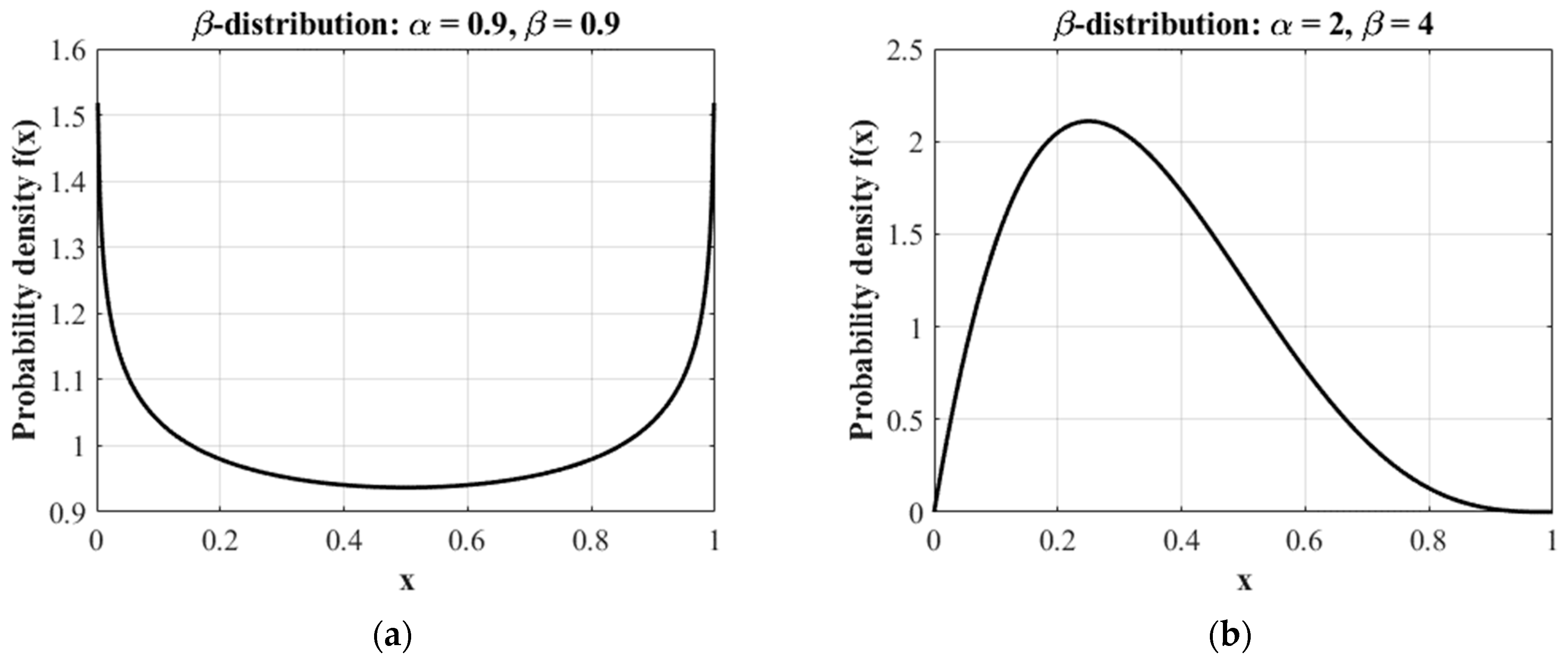
The beta-distribution depends on the values of the distribution parameters α and β, and can take various forms:

• Unimodal (bell-shaped),
• U-shaped (often clear or often cloudy), Figure 6a,
• Uniform (when $\alpha$ = $\beta$ = 1),
• Shifted to the left/right (if the weather is often clear or cloudy), Figure 6b.

This makes it easy to adjust the distribution to the climatic features of the region.

As an alternative to the $\beta$-distribution, the probability density function of the Kumaraswamy distribution can be applied to model a random variable taking values in the interval [0, 1]. It is an analog of the $\beta$-distribution but is simpler for analytical work due to the closed-form expression of its distribution function.

If a random variable X follows the Kumaraswamy distribution with parameters $a>0, b>0$, its probability density function (PDF) is given by:

$$f\left(x;a,b\right)=ab{x}^{a-1}{\left(1-x^a\right)}^{b-1}, 0<x<1$$

where

a—shape parameter;

b—shape parameter.

Similarly to the β-distribution, it flexibly describes various density shapes on [0, 1] (U-shaped, increasing, decreasing, bell-shaped).

The main advantage is the simple closed form of the cumulative distribution function (CDF), which is convenient for generating random numbers using the inverse transform method.

In the case of bimodal weather with sharply variable cloudiness during the day, the β-distribution may be insufficient to describe multi-peaked probability density functions. In such cases, a Beta Mixture Distribution (BMD) can be used. The main areas of application of BMD include:

• Bayesian statistics (approximation of complex posterior distributions on [0, 1]);
• models for fractions, probabilities, and proportions (for example, the share of renewable energy in the energy balance, distribution of humidity, etc.).

In the further discussion, we will use the β-distribution, since integration with the β-function is relatively straightforward. The importance of this property will become evident when deriving the formulas for the statistical characteristics of the daily energy yield.

3.4. The Statistical Nature of Solar Panel Generation

The statistical nature of the variable “Cloudiness” which is a part of the expressions for the atmospheric transmittance coefficient, Equations (2) and (3), leads to the fact that the value of the atmospheric transmittance coefficient will also be a random variable. Since the variable “Cloudiness” is a part of expressions (2) and (3) in the form of a power dependence, the statistical characteristics of the atmospheric transmittance coefficient as a random variable will differ significantly from the characteristics of the β-distribution of the variable “Cloudiness”. The same applies to the daily power generation of the solar panel, calculated according to (9).

Determining the statistical characteristics of daily generation, which is formally a function of the random argument “Cloudiness”, is a non-trivial mathematical problem, the solution to which we will try to obtain below.

Let us consider the process of electric power $E\left(t\right)$ generation as a random function, that is, a function of its argument whose value for any value of the argument t is a random variable. If the argument of the random function $t$ takes any values in a given interval, then the random function will also be a random process.

For conducting a statistical analysis of the daily energy yield of a solar power plant, it is necessary to address two interrelated research tasks. The first task is associated with determining the actual probability distribution law of the random variable “Cloudiness,” which has a decisive influence on the transmission of solar radiation through the atmosphere and, consequently, on the operation of photovoltaic modules. To achieve this goal, it is essential to establish the form of the probability density function describing cloudiness, identify the distribution parameters, and calculate its statistical characteristics, including the mean, variance, skewness, and kurtosis.

The second task concerns the investigation of the statistical distribution of the daily energy yield, considered as a random function of the parameter “Cloudiness.” Since cloudiness varies within the interval [0, 1] and is described by a specific probability distribution, the resulting value of the daily energy yield also acquires a stochastic nature. In this regard, it becomes necessary to determine the probability distribution function and statistical characteristics of this random variable, including the mean value, variance, and the possible range of fluctuations.

Solving these tasks makes it possible to form a substantiated understanding of the statistical nature of electricity generation by solar power plants. This approach provides an opportunity for a more accurate description of uncertainties associated with the variability of meteorological conditions and establishes a basis for developing reliable probabilistic models for forecasting the daily energy yield of photovoltaic systems.

To address this problem, methods of mathematical statistics can be applied to determine the numerical characteristics of functions of random variables [50]. In the present case, the random variable $E\left(c\right)$ is a function of a single random variable. Therefore, the task reduces to estimating the statistical characteristics of this random variable, provided that the distribution law of the random argument is known.

The general method for solving the problem is to find the distribution law of the function of a random argument when the distribution law of the argument is known.

The problem of finding the distribution law of the function $E\left(c\right)$ often turns out to be quite complex. However, for practical purposes it is quite sufficient to know only the numerical characteristics of this distribution, which significantly simplifies the solution of the problem.

Let us consider the problem of determining the numerical characteristics of a function of one random argument with a known law of its distribution.

There is a random variable $\gamma$ with a known distribution law $\phi \left(\gamma \right)$; another random variable, $e$, is related to $\gamma$ by a functional dependence $e=\phi \left(\gamma \right)$. Then, according to [50], the expected value of a function of one random argument can be determined by the formula:

$$M\left[e\right]=\underset{-\infty }{\overset{+\infty }{\int }}\phi \left(\gamma \right)·f(\gamma )d\gamma ,$$

(11)

The variance of a function of one random argument can be determined by the formula:

$$D\left[e\right]=\underset{-\infty }{\overset{+\infty }{\int }}{\left(\phi \right(\gamma )-M\left[e\right])}^{2}f(\gamma )d\gamma ,$$

(12)

3.5. Statistical Characteristics of Daily Energy Yield by a Solar Panel

In the considered case, the random argument is the “Cloudiness” parameter, denoted by the symbol c.

As it was justified above, the random variable c has a β-distribution with a probability density $f\left(c\right)$ of the form:

$$f\left(c\right)={\displaystyle \frac{1}{B\left(\alpha ,\beta \right)}}{c}^{\alpha -1}{\left(1-c\right)}^{\beta -1}.$$

(13)

Let us write down the functional dependence of the daily power generation by a solar panel on the “Cloudiness” parameter in expanded form.

Substituting the simplified expression for the atmospheric transmittance coefficient (3) into the expression for calculating the daily power generation by a solar panel (9), we obtain:

$$E=A·f_{atm}\left(c\right),$$

(14)

where $A=\alpha ·S·I_0\left(t\right)·{\displaystyle \frac{24}{\pi }}\left[\sin \left(\delta \right)·\sin \left(\phi \right)·{\omega }_s+\cos \left(\delta \right)·\cos \left(\phi \right)·\sin \left({\omega }_s\right)\right]$ is a constant depending on the day number of the year for the date of forecasting the daily generation.

Substituting Equation (3) into (14), we obtain

$$E=A·\left(1-0.75·c^{3.4}\right).$$

(15)

Then, according to Equations (3) and (11), the expected value of daily generation can be determined by the formula:

$$M=A·{\displaystyle \frac{1}{B\left(\alpha ,\beta \right)}}·\underset{0}{\overset{1}{\int }}\left(1-0.75·c^{3.4}\right)·c^{\alpha -1}{\left(1-c\right)}^{\beta -1}dc.$$

(16)

When deriving Formula (16), it was taken into account that the “Cloudiness” parameter varies within the range from 0 to 1.

Let us calculate the definite integral (16). We expand the integrand as follows:

$$\begin{gathered} \left(1-0.75·c^{3.4}\right)\times \\ {c}^{\alpha -1}{\left(1-c\right)}^{\beta -1}=c^{\alpha -1}{\left(1-c\right)}^{\beta -1}-0.75·c^{3.4}·c^{\alpha -1}{\left(1-c\right)}^{\beta -1}. \end{gathered}$$

(17)

Let us integrate each term of (17):

$$\begin{array}{l}\underset{0}{\overset{1}{\int }}{c}^{\alpha -1}{\left(1-c\right)}^{\beta -1}dc=B\left(\alpha ,\beta \right),\\ \underset{0}{\overset{1}{\int }}0.75·c^{3.4}·c^{\alpha -1}{\left(1-c\right)}^{\beta -1}=0.75·B\left(\alpha +3.4,\beta \right).\end{array}$$

(18)

Combining the results, we obtain

$$M=A·{\displaystyle \frac{1}{B\left(\alpha ,\beta \right)}}·\left(B\left(\alpha ,\beta \right)-0.75·B\left(\alpha +3.4,\beta \right) \right).$$

(19)

or in an alternative form

$$M=A·\left(1-0.75·{\displaystyle \frac{B\left(\alpha +3.4,\beta \right) }{B\left(\alpha ,\beta \right)}}\right).$$

(20)

According to Equations (3) and (12), the variance of daily generation can be determined by the formula:

$$D={\displaystyle \frac{1}{B\left(\alpha ,\beta \right)}}·{\int }_0^1{\left(A·\left(1-0.75·c^{3.4}\right)-M\right)}^2·c^{\alpha -1}{\left(1-c\right)}^{\beta -1}dc.$$

(21)

By expanding the square in the integrand, we get

$${\left(A·\left(1-0.75·c^{3.4}\right)-M\right)}^2=A^2{\left(1-0.75·c^{3.4}\right)}^2-2·A·M\left(1-0.75·c^{3.4}\right)+M^2.$$

(22)

and

$${\left(1-0.75·c^{3.4}\right)}^2=1-1.5·c^{3.4}+0.5625·c^{6.8}.$$

(23)

Let us represent the integral (21) as the sum of three integrals:

$$\begin{array}{c}I=\underset{0}{\overset{1}{\int }}{\left(A·\left(1-0.75·c^{3.4}\right)-M\right)}^2·c^{\alpha -1}{\left(1-c\right)}^{\beta -1}dc\\ =A^2\underset{0}{\overset{1}{\int }}\left(1-1.5·c^{3.4}+0.5625·c^{6.8}\right)·c^{\alpha -1}{\left(1-c\right)}^{\beta -1}dc\\ \begin{array}{l}-2AM\underset{0}{\overset{1}{\int }}\left(1-0.75·c^{3.4}\right)·c^{\alpha -1}{\left(1-c\right)}^{\beta -1}dc+\\ +M^2\underset{0}{\overset{1}{\int }}{c}^{\alpha -1}{\left(1-c\right)}^{\beta -1}dc\end{array}\end{array}$$

(24)

We use the following equality. For any $k\ge 0$

$$\underset{0}{\overset{1}{\int }}{c}^{\alpha +k-1}{\left(1-c\right)}^{\beta -1}dc=B\left(\alpha +k,\beta \right)$$

(25)

Then from (24) we obtain the following:

$$\begin{array}{c}\underset{0}{\overset{1}{\int }}{c}^{\alpha -1}{\left(1-c\right)}^{\beta -1}dc=B\left(\alpha ,\beta \right)\\ \underset{0}{\overset{1}{\int }}{c}^{\alpha +3.4-1}{\left(1-c\right)}^{\beta -1}dc=B\left(\alpha +3.4, \beta \right)\\ \underset{0}{\overset{1}{\int }}{c}^{\alpha +6.8-1}{\left(1-c\right)}^{\beta -1}dc=B\left(\alpha +6.8,\beta \right)\end{array}$$

(26)

By combining (21), (24) and (26) we finally obtain the following:

$$\begin{gathered} D={\displaystyle \frac{1}{B\left(\alpha ,\beta \right)}}· \\ \left({\left(A-M\right)}^{2}B\left(\alpha ,\beta \right)-1.5·A·\left(A-M\right)B\left(\alpha +3.4, \beta \right)+0.5625A^{2}B\left(\alpha +6.8,\beta \right)\right) \end{gathered}$$

(27)

or in an alternative form

$$D={\left(A-M\right)}^2-1.5·A·\left(A-M\right){\displaystyle \frac{B\left(\alpha +3.4, \beta \right)}{B\left(\alpha ,\beta \right)}}+0.5625A^2{\displaystyle \frac{B\left(\alpha +6.8,\beta \right)}{B\left(\alpha ,\beta \right)}}$$

(28)

Expressions (20) and (28) allow us to calculate the main statistical characteristics of the daily power generation by a solar panel based on the given parameters of the β-distribution of cloudiness. The proposed approach considers the statistical nature of cloudiness and allows us to more accurately predict power generation by a solar panel.

Currently, in order to forecast the power generation by a solar panel, the personnel of a solar power plant is forced to rely on forecast values of meteorological conditions provided by third-party meteorological services. Thus, the expected value of the cloudiness parameter is used to forecast generation, and the statistical nature of the change in cloudiness throughout the day is not taken into account.

Let us consider two main strategies for forecasting solar panel power generation:

• Strategy “Baseline A”. The influence of the “Cloudiness” parameter is taken into account in the form of a constant, which is equal to the mathematical expectation of the β-distribution of cloudiness. This value is provided by third-party meteorological services. The forecast of power generation is calculated according to expression (9) for the specified constant value of the cloudiness parameter;
• Strategy “Probabilistic B”. The influence of the “Cloudiness” parameter is taken into account as a random variable with β-distribution. The forecast of power generation is calculated using expression (20) for the given values of the parameters of the β-distribution of cloudiness.

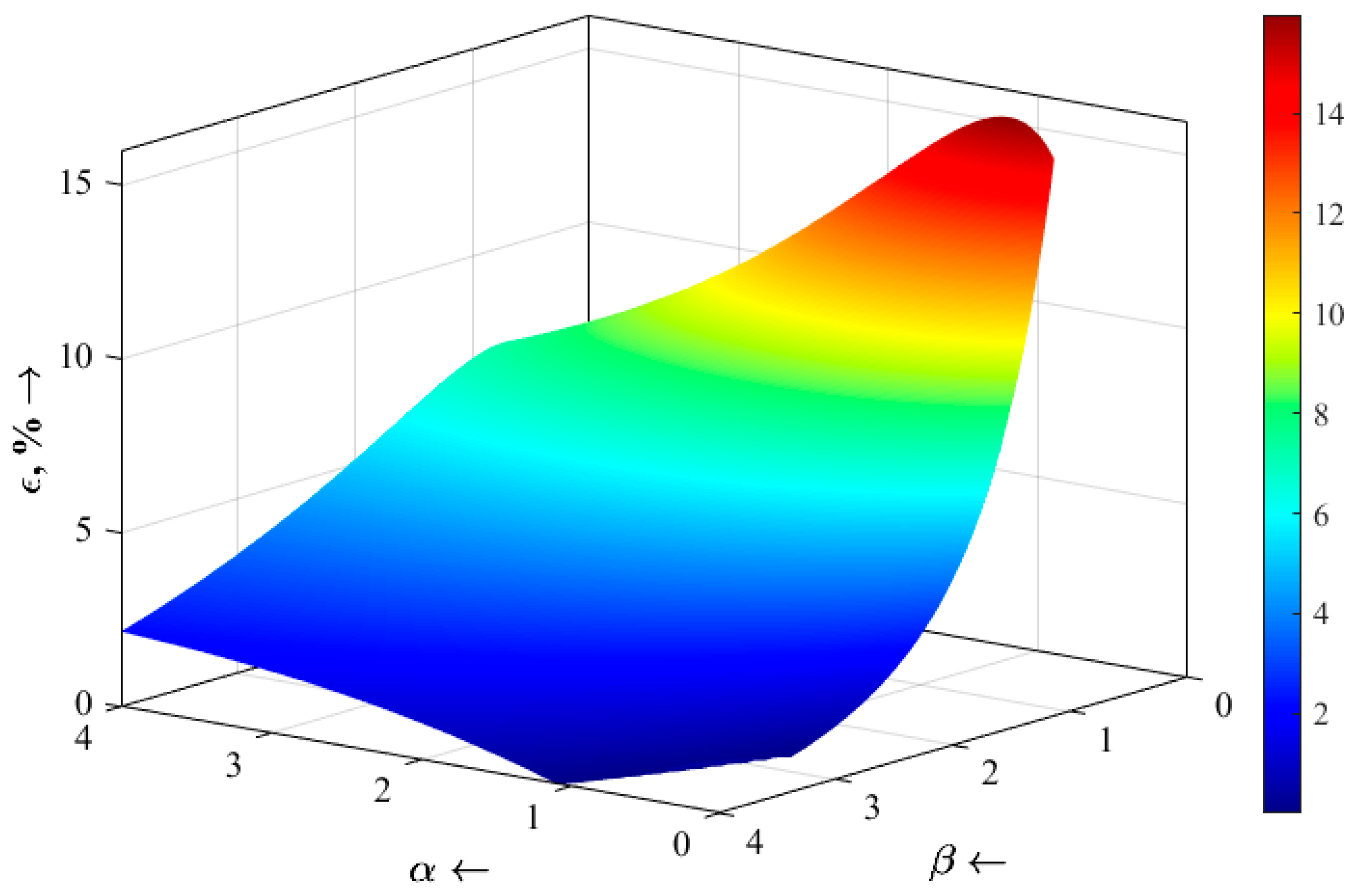
Below, in Figure 7, the dependence of the relative error of power generation forecasts is given from the parameters of the β-distribution of cloudiness, calculated using the forecasting strategies “Baseline A” and “Probabilistic B”.

Below, Figure 7 shows the dependence of the relative error between the values of daily forecast of power generation calculated by Baseline A and Probabilistic B forecasting strategies on the parameters of β-distribution of cloudiness.

As the analysis of the obtained results shows, in a fairly wide area of determining the parameters of the β-distribution of cloudiness, the relative error in calculating the forecast of solar generation exceeds 5%, and the maximum value of this error reaches 15.2%. The forecast of solar generation calculated taking into account the statistical nature of cloudiness according to strategy “Probabilistic B” turns out to be less than the forecast calculated based on the average value of cloudiness according to strategy “Baseline A”.

4. Discussion

The study shows that the β-distribution can be applied for the description of cloudiness and for the estimation of its impact on the daily energy yield of photovoltaic (PV) systems. The analytical model gave an average error of less than 4%, which confirms the possibility of using this approach in practice. This result also shows that simple probabilistic models can be more effective than methods based only on average meteorological parameters.

The comparison of analytical and experimental data indicates that the model is able to reproduce the main shape of the GHI histograms and also their asymmetry, which is connected with the random nature of cloudiness. Similar conclusions are given in previous studies, where probabilistic models of cloud cover were used to improve the accuracy of PV energy yield forecasts. This confirms that probabilistic methods are more suitable than deterministic ones when day-ahead forecasts are needed under variable weather conditions.

Some restrictions of the model must also be mentioned. The influence of humidity is not taken into account, which may limit the scope of application of the results to areas with arid or specific climatic conditions. The paper also considers only β-distribution does not allow describing multimodal or extreme cases of cloudiness. This can reduce the accuracy in regions with strong seasonal changes or with unstable weather. Future research should also include additional meteorological factors, such as humidity, to improve the applicability of the model. Another direction for future research is to utilize Beta Mixture Model as a more flexible and powerful cloudiness distribution law.

The use of hybrid models can be one more way to increase accuracy. The combination of the proposed probabilistic framework with machine learning can give both interpretability and predictive performance. Such development can make the method more universal for different climate zones and improve the reliability of PV energy yield forecasting for practical tasks in power systems.

From a practical perspective, prediction of instantaneous values of solar power generation using machine learning and ANN-based methods can be important for ensuring the stability of the power grid. However, in practice, data on instantaneous values of power generation are often redundant. Much more valuable is information about the predicted value of daily solar generation. Based on these data, the economic relationship between the solar power plant and the state power system is formed. For example, in the Republic of Kazakhstan, insufficient power generation is the basis for penalties, and excessive power generation is paid for at reduced tariffs, which also reduces the technical and economic performance of the solar power plant. Therefore, accurate probabilistic forecasting of daily PV yield is of particular importance not only for technical stability but also for the economic sustainability of solar energy projects.

A quantitative comparison of the proposed β-distribution model with methods based on the application of machine learning and ANN is not performed within the framework of this study due to the limited scope of the publication. It should be noted that the application of machine learning methods is actually an alternative method to account for the nonstationarity of meteorological conditions. Estimation of the statistical characteristics of the β-distribution of cloudiness on the basis of analytical methods for calculating meteorological conditions is, in our opinion, a more accurate approach.

5. Conclusions

This research solves the current scientific and practical problem of forecasting daily power generation by solar power plants based on statistical characteristics of meteorological conditions, in particular, random variation in cloudiness. The importance of the topic considered is due to the need to ensure the high accuracy of generation forecasts for coordinating production plans of power plants with dispatch control of energy systems, as well as optimizing the financial performance of power plants.

The analysis conducted of the modern scientific literature has shown that the problem of forecasting power generation by solar installations is actively studied using various methods of artificial intelligence, deep learning, genetic algorithms and statistical models. The authors of the research have proposed a methodological approach based on the use of β-distribution to describe the statistical characteristics of cloudiness as a random variable. This favorable approach differs in terms of universality and the ability to adapt to regional climatic conditions, which allows to significantly increase the accuracy of power generation forecasts.

An analytical model has been developed during research. This model considers main factors affecting daily generation, such as the power plant’s geographic location, the angle of incidence of solar rays, and atmospheric characteristics. The resulting analytical expressions for calculating daily power generation made it possible to estimate statistical indicators, including the expected value and variance of power generation, taking into account random changes in cloudiness throughout the day.

As a result of comparing the exact and approximate analytical calculation of daily power generation, it was found that the proposed approach provides satisfactory forecasting accuracy, with the average calculation error not exceeding 4%. It was also demonstrated that taking into account the statistical characteristics of cloudiness, expressed through the β-distribution, allows reducing the maximum relative forecasting error to a level of less than 5%, which is significantly better than the traditional forecasting method based on the average cloudiness value.

Despite the high level of elaboration of the proposed approach, the research revealed certain drawbacks that limit the application of the obtained results in practice.

The first drawback is the simplified consideration of the influence of humidity on the atmospheric transmittance coefficient. During the research, it was assumed that at low altitudes of solar panels placement, the influence of humidity can be ignored. However, in real conditions, humidity can significantly affect the transmission of solar radiation, especially in regions with high variability of atmospheric humidity during the year. The underestimation of this factor can lead to inaccuracies in the calculation of energy production.

The second drawback is related to the limitation of the research to one type of distribution (β-distribution) for cloudiness modeling. Although the β-distribution is quite universal, it cannot always accurately reflect the statistical features of cloudiness in different climatic zones, especially in the presence of extreme meteorological conditions and rapid changes in weather conditions throughout the day.

The authors see the following potential areas for further research:

-

Comprehensive research of the influence of humidity and other meteorological parameters on solar power generation: It is advisable to develop and test an extended mathematical model that takes into account the variability of humidity and its statistical distribution along with cloudiness, which will improve the accuracy of power generation forecasting.

-

Development and research of hybrid forecasting models that combine different types of distributions (for example, combinations of β-distribution with other statistical models) to more accurately account for regional and seasonal features of cloudiness changes: It is also possible to use machine learning and deep learning methods for adaptive adjustment of models based on operational weather data, which will further improve the quality of short-term forecasts of solar power generation.

Thus, the implementation of the proposed directions will significantly improve the accuracy and efficiency of solar power plants power generation forecasting, which is an important task for the further development and integration of renewable energy sources into energy systems.