Development of a Hybrid Expert Diagnostic System for Power Transformers Based on the Integration of Computational and Measurement Complexes
Abstract
1. Introduction
1.1. Relevance of the Problem
- -
- Supplement the possibilities of integral assessment of the PT state as a whole and to forecast the change in the state of its subsystems with determination of their residual resource;
- -
- Ensure the formation of more adequate diagnostic models for forecasting and predictive analysis of the technical condition of PT on the basis of both deterministic approach and machine learning methods;
- -
- Develop a system of optimal decision-making when selecting effective operational impacts on the object (creation of a “digital twin” of the PT).
1.2. Experience of the Team of Authors
1.3. Overview of Diagnostic Methods for Selected Subsystems of the PT
- (1)
- (2)
- The concept of EMP as possible combinations of coefficients at operating parameters (currents and voltages of windings) of power transformers has been clarified and expanded [41];
- (3)
- Methods and algorithms for diagnosing EMP of power transformers in conditions of insufficient information have been developed;
- (4)
- Methods and algorithms have been developed to solve the diagnostic tasks set in conditions of PT nonlinearity and non-sinusoidal operating parameters [45];
- (5)
- The feasibility of the approach has been confirmed in relation to a four-pole circuit (the case of a single-phase two-winding transformer);
- (6)
- Electrical method. Principle: measurement of electrical signals from partial discharges, followed by interpretation of these signals in terms of apparent charge units [72]. Advantages of the method: high sensitivity, accuracy, and reliability of apparent charge characteristics assessment. The disadvantages are the need to tune out interference, the complexity of the calibration procedure, and the conversion to apparent charge units under operating conditions [73].
- Registration of electromagnetic radiation from corona discharges. The advantage of the method is its noise immunity, but the complexity of interpreting the results severely limits the possible implementation of the method [74]. The method has found its main application in the control of overhead and cable lines.
- Acoustic method based on the recording of mechanical vibrations arising from the pressure of the expanding discharge channel. The advantages of acoustic monitoring include the ability to diagnose equipment without disrupting its normal operating mode. The disadvantages of the acoustic method of PD detection include the difficulty of locating the PD source in complex equipment structures, low sensitivity to PD compared to the electrical method, the inability to calibrate measurements in units of apparent PD charge according to the IEC 60270 standard, and, as a result, difficulties in comparing results obtained with different equipment, etc. [78,79].
2. Concept of the Hardware–Software Complex
- Liquid and solid insulation (dissolved gas analysis and moisture content), external and internal temperature monitoring—Module 1;
- Electromagnetic diagnostics (operating currents and voltages of windings)—Module 2;
- Voltage regulation devices (phase currents and voltages, drive motor current, vibration levels during tap changes, ambient and cabinet temperatures, number of operations)—Module 3;
- High-voltage bushings (internal partial discharges, surface discharges, bushing leakage currents)—Module 4.
- Parameters of seasonal loads and operating modes;
- Parameters and models of PT subsystems and adjacent equipment, derived from both offline and online data sources;
- Indicators of reliability and power quality at the power center (PC);
- Diagnostic reports, testing protocols, and maintenance diagnostics (identified defects, control parameters).
- Normative characteristics of subsystems;
- “Reference models” of subsystem parameters and characteristics recorded at the start of operation;
- Normative and reference information (NRI) concerning substation equipment in operation;
- Tables of permissible parameter thresholds and decision-making matrices;
- Condition-based maintenance and repair schedules.
- Predictive analytics, aimed at recognizing the current state of a subsystem at any given time by comparing it with a reference model and forecasting the evolution of its technical condition;
- Residual life estimation, based on the analysis of key characteristics and parameters of PT components (e.g., voltage and load levels, PT electromagnetic field properties including no-load and short-circuit losses, gas concentrations, etc.).
- Management and scalability: The architecture employs modern orchestration and containerization methods, enabling efficient management and scalability of the system.
- Availability and reliability: Load balancing and container-based deployment ensure high availability and fault tolerance, as local installations tend to be less reliable and more prone to failures.
- Client interaction: Communication with clients is facilitated via an API, streamlining integration and enabling seamless network-based interaction.
- Artifacts—These are data elements generated and stored during the training and operation of AI models. Artifacts include neural network weight coefficients, training parameters, training results, and configuration files. They are essential for model reproducibility and proper deployment, allowing retraining or fine-tuning processes to be accelerated without restarting from scratch.
- Metadata—Special data that describes the characteristics of models and their components. Metadata may include training parameters, artifact locations, and other important attributes. This information facilitates the tracking of model performance and supports full lifecycle management.
- Datalayer—A key component that governs the interaction between AI models, data, and system logic. Its responsibilities include:
- ○
- Database queries—A module responsible for retrieving data needed for AI model operation, such as training datasets or input data for inference;
- ○
- Artifact storage and retrieval—This component ensures the storage of artifacts (e.g., model weights) and their retrieval when needed, expediting model deployment and reuse;
- ○
- Metadata management—This ensures effective control over model lifecycle and performance tracking.
- Artifact storage—An infrastructure designed for the centralized storage of large volumes of data associated with AI models. It provides secure and efficient management of critical model data, which can be stored locally or via MongoDB-based solutions (e.g., GridFS), depending on system requirements. This storage is essential for preserving all artifacts used by the models and streamlining scalable data management.
- Metadata storage—This component serves as a repository for critical information associated with AI models, such as training parameters, data locations, and the components and artifacts used during training. The metadata storage plays a key role in optimizing model selection, performance monitoring, and retraining processes. It also supports compliance with security and auditing requirements.
- API layer—An interface facilitating interaction between AI models and the database. The API supports tools such as pymongo for MongoDB and ibis for SQL-based data. This interface enables efficient database querying, vector search operations, and the execution of more complex queries. By providing a unified access layer, the API integrates AI model functionality with database systems, thereby accelerating training, testing, and optimization workflows.
- Significantly faster operation than MLPs;
- Potentially higher classification accuracy;
- High robustness to noisy data;
- Precise probabilistic estimation of target values;
- Approximate implementation of Bayes-optimal classification.
- Slower classification of new inputs compared to perceptrons;
- Increased memory requirements to store the trained model.
- 1.
- Nominal transformer parameters are entered:
- 1.1.
- Nominal voltages and currents: U1nom, I1nom, U2nom, I2nom.
- 1.2.
- No-load parameters (current and losses): i0, P0.
- 1.3.
- Short-circuit parameters (impedance and losses): Zk, Pk.
- 2.
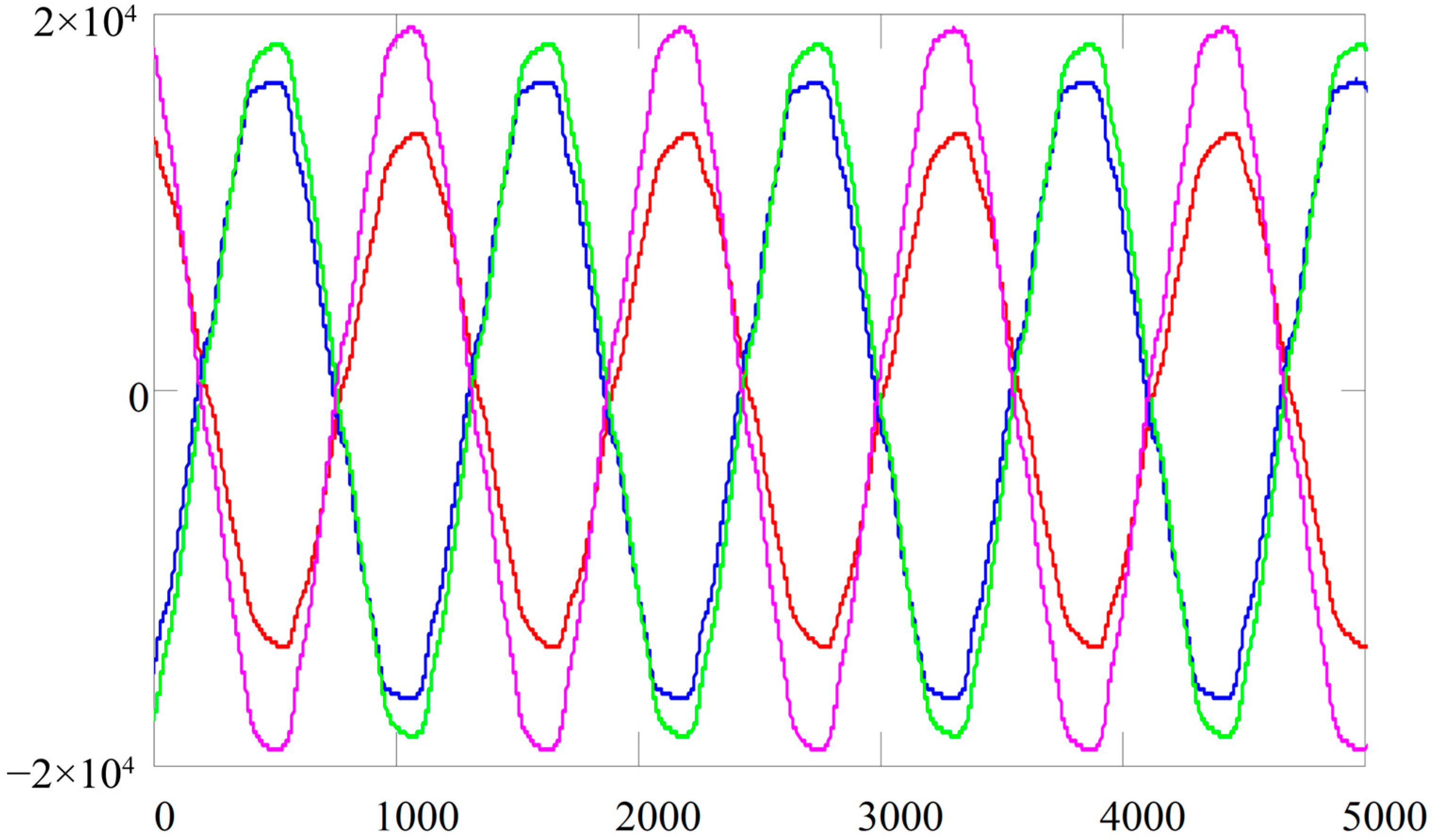
- Measurement and accumulation of instantaneous values of operating currents and voltages of the windings are performed:(u1)1, (u1)2 … (u1)m;(i1)1, (i1)2 … (i1)m;(u2)1, (u2)2 … (u2)m;where —period,(i2)1, (i2)2 … (i2)m,
- 3.
- Vectors of instantaneous values are formed:us = [(us)1, (us)2 … (us)m]twhere s = 1, 2.is = [(is)1, (is)2 … (is)m]t,
- 4.
- The root-mean-square (RMS) values and phase shifts in the operating currents and voltages are calculated:Us = m−1/2[(us)t, (us)]1/2Is = m−1/2[(is)t, (is)]1/2,where As = U2, I1, I2; as = u2, i1, i2; [(u1)′, (as)], [(u1)′, (u1)]0.5, and [(as)′, (as)]0.5—denote scalar products of the corresponding vectors.
- 5.
- The electromagnetic parameters are calculated based on simplified modeling:wherewhere
- 6.
- Based on the calculated values (Y11)0, (Y22)0, (Z11)0, (Z22)0, all possible diagnostic parameters are determined (Table 4).
- 7.
- Steps 2–5 are repeated for the next measurement cycle, and the data from different cycles are assigned an additional superscript corresponding to the cycle number: (U1)2 … (Z22)02
- 8.
- Matrices of variables are formed:
- 9.
- The matrices of Z, Y, and A parameters are calculated:
- 9.1.
- ZI = UI−1 YI = (ZI)−1
- 9.2.
- YU = IU−1 ZU = (YU)−1
- 9.3.
- H1V1 = V2(V1)−1
- 9.4.
- H2V2 = V1(V2)−1
- 10.
- 11.
- Graphs showing the temporal dependence of the diagnostic parameters being determined are constructed, as well as other options for presenting (processing) diagnostic information.
- 1.
- Accounting for nonsinusoidality. Nonlinearity, external influences, and the nature of the load cause distortions of the sinusoidal shape of voltages and currents, which complicates the use of the phasor method for the mathematical description of electromagnetic processes and requires adjustments to the developed transformer models. To overcome these difficulties, the method of equivalent sinusoids is usually applied; however, this method has certain peculiarities, neglecting which leads to calculation errors.
- 2.
- Accounting for nonlinearity. The transformer’s nonlinearity leads to difficulties in comparing data from different operating modes. In particular, the no-load and short-circuit parameters of a real transformer correspond to different linear models and therefore are not mutually consistent. This also results in a mismatch between the transformer impedance measured under load conditions and in a short-circuit test. Therefore, an essential task is to develop a methodology for reconciling the different modes (modes with different levels of core magnetization). A practical implementation of this approach is presented below.
3. Results and Discussion
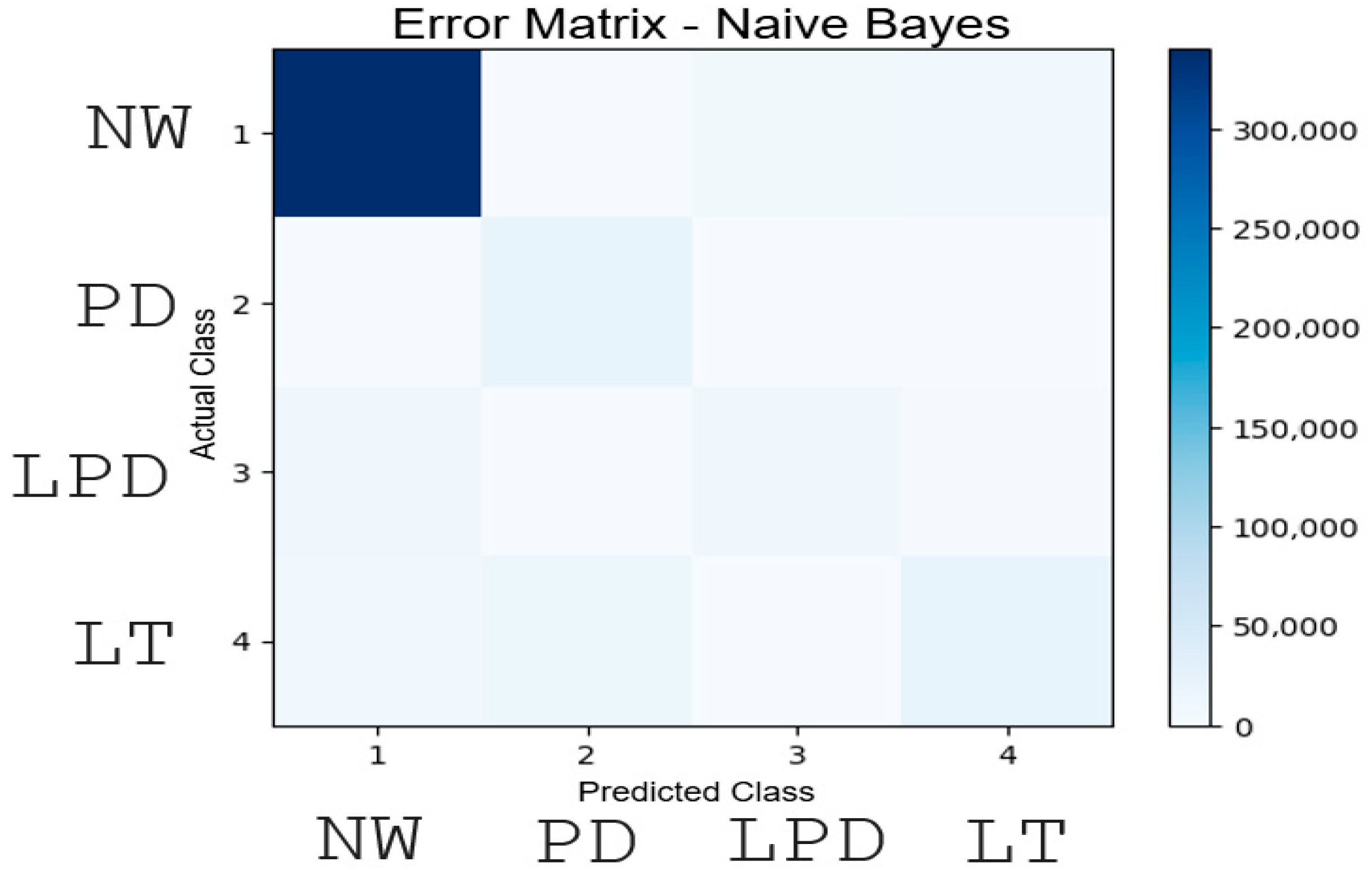
- Normal Operation (NW): The system operates without any anomalies or signs of malfunction. This state is characterized by stable and correct functioning of the equipment.
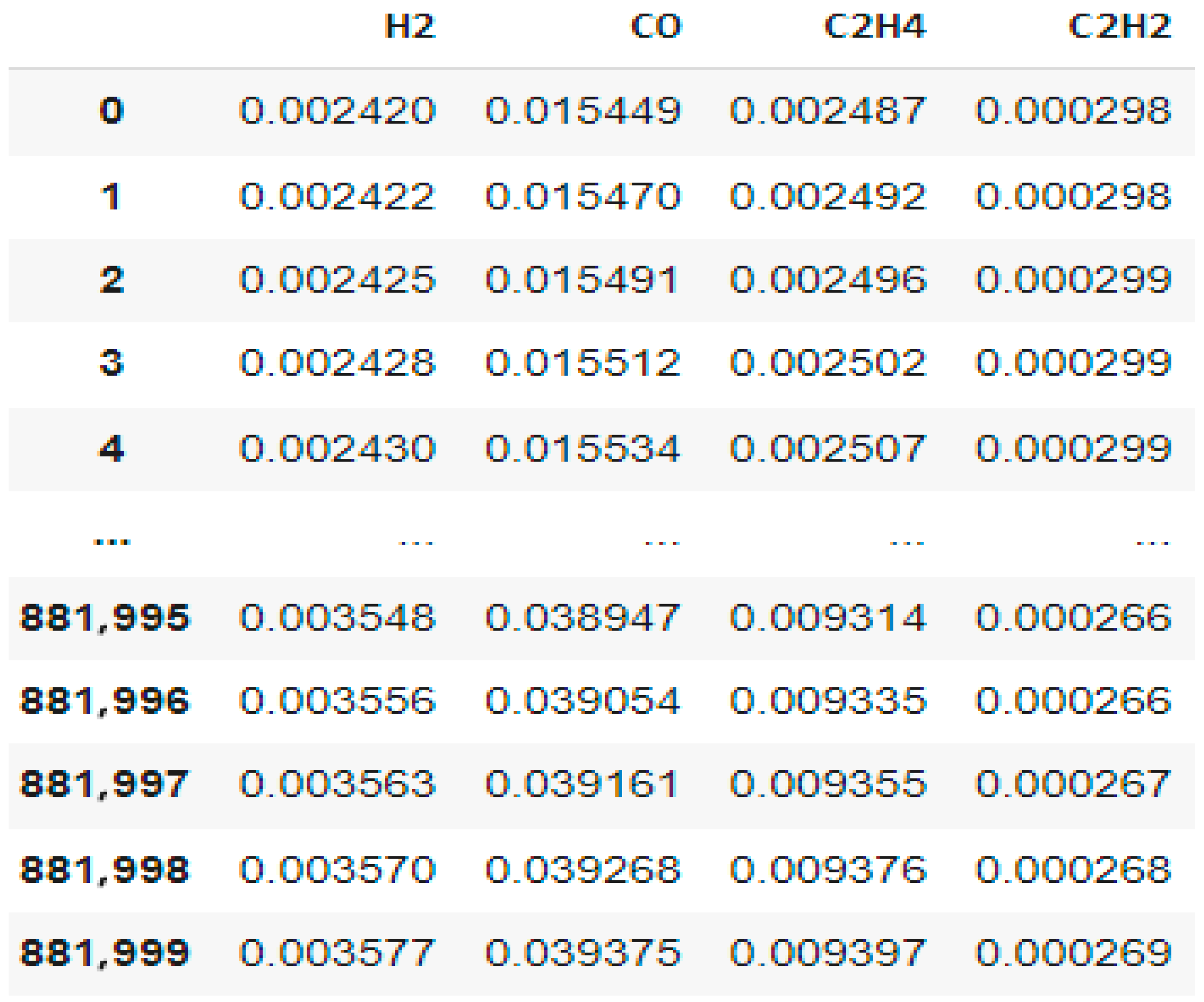
- Partial Discharge (PD): This condition indicates the presence of a partial electrical discharge within the system, which may serve as an early indicator of wear or impending failure. Timely detection of such conditions is crucial for preventing serious faults, as outlined in [90] (see Table 2, Item 1—“Typical Defects in Power Transformers and Reactors”).
- Combined Partial Discharge and Low-Temperature Overheating (LPD): This state reflects the simultaneous occurrence of partial discharge and low-temperature overheating. It is a complex condition that may indicate more severe underlying issues within the system—representing a combination of Items 4 and 1 in Table 2 [90].
- (1)
- The DGA data prediction model based on the current time series (LSTM network);
- (2)
- The defect classification model (Probabilistic Neural Network—PNN).
- NW (Normal Operation);
- PD (Partial Discharge);
- LPD (Combination of Partial Discharge and Low-Temperature Overheating);
- LT (Low-Temperature Overheating).
- The model successfully recognizes normal operating conditions, which is critical for monitoring;
- Nearly all cases of partial discharges are accurately detected, ensuring a high level of safety;
- The overall accuracy of 0.88 shows that the model handles the multi-level classification task well, even with complex classes.
- 2.
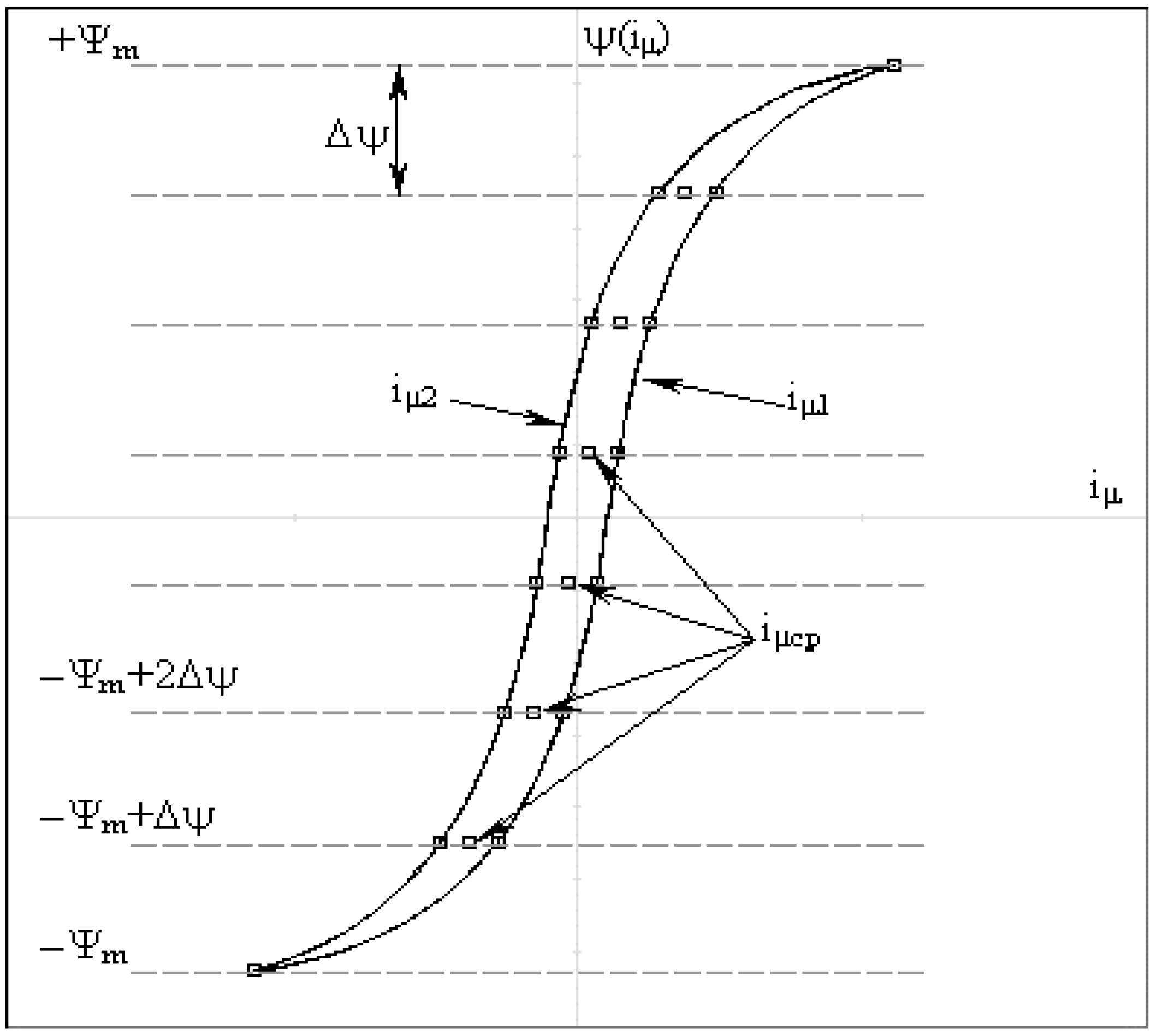
- The single-valued (non-looped) volt-ampere characteristic for instantaneous values is determined computationally (see Figure 14).
- 3.
- The volt-ampere characteristic (VAC) for root-mean-square values is computed.
- 4.
- From two points on the VAC for root-mean-square values, the amplitude and phase of the complex nonlinearity coefficient χ are calculated.
- (1)
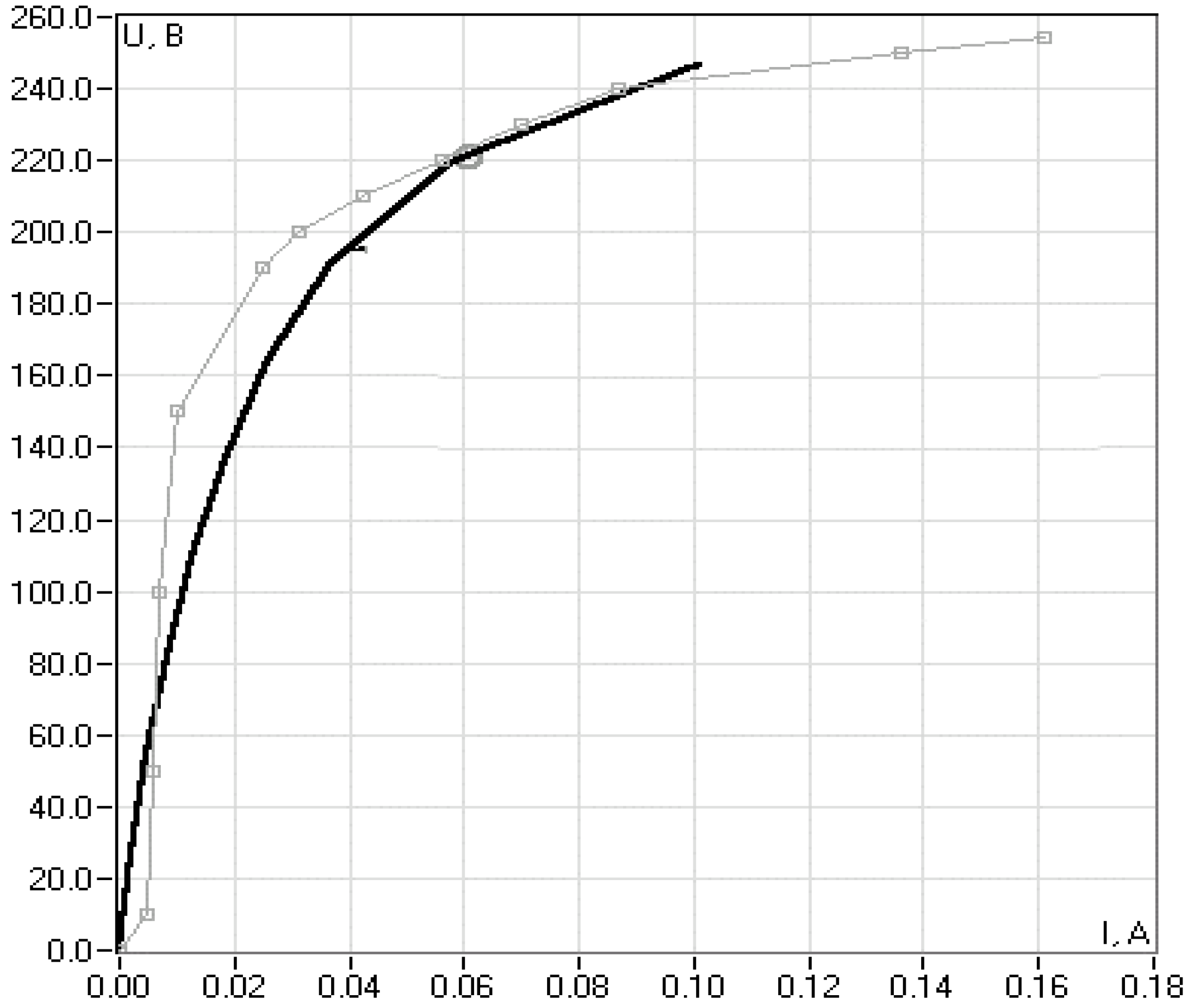
- The experimental setup was far from perfect—the measurement of circuit parameters was carried out with significant errors (up to 10%), especially with regard to winding voltages (the “imperfection” of the voltage divider).
- (2)
- It was not possible to accurately reproduce various modes, which also prevented the achievement of the necessary efficiency in solving the task at hand.
- (a)
- The fundamental feasibility of the method;
- (b)
- The influence of the accuracy of circuit parameter measurements (currents and voltages) on the solution of the EMP diagnostic task (including the influence of the sampling frequency of the measured signals);
- (c)
- The influence of load fluctuation levels on the conditionality of the diagnostic model;
- (d)
- The influence of transformer nonlinearity on the accuracy of diagnostics.
- The method is workable, as evidenced by the comparison of the obtained matrices with the results of test diagnostics (no-load tests and, partially, short-circuit tests).
- The difference in winding currents in different modes is important, as it affects the conditionality of the current and voltage matrices (used in the solution). Preliminary conclusion: the specified deviation must be at least 10% (as an illustration, compare the data for modes 1, 2, 3, and 5, 6 in Table 9).
- The signal sampling frequency (SSF) has a significant impact on the accuracy of the solution. Thus, an SSF of 50 kHz compared to an SSF of 8 kHz increases the accuracy of the solution by approximately (5–7)%.
- The calculation of short-circuit conductivity based on operational diagnostics data (e.g., based on mode 1) differs significantly from the data obtained from direct test measurements (mode 4): by a factor of 3.33 in terms of modulus. This shows that the modulus of the complex nonlinearity coefficient, which can be used to make the necessary correction, is quite large. At the same time, we emphasize that this difference is not an error of the diagnostic method, but the essence of the manifestation of transformer nonlinearity in operating mode (which is not mentioned in textbooks and monographs on transformers).
4. Conclusions
- A concept of a hybrid expert diagnostic system based on the functionality of measurement and analytical complexes has been proposed. The system is built on a minimalist approach to the number of monitored parameters and types of measuring equipment for four subsystems of power transformers.
- A methodology and algorithm for diagnosing the electromagnetic parameters of a transformer have been developed, taking into account the nonlinearity and nonsinusoidality of the winding currents and voltages. The method allows for determining not only the Zk parameter and its variations but also other electromagnetic parameters necessary for a comprehensive assessment of transformer condition. The feasibility of the method has been demonstrated through an experiment on a physical transformer model under conditions of measurement errors in primary voltages and currents. The signal sampling frequency has been shown to have a significant impact on the accuracy of the solution.
- In the field of information technologies, an optimal client–service architecture for training hybrid system models based on data storage and management processes has been implemented. This includes effective management of data and hyperparameters and improved system scalability through the use of data lakes and message brokers. The adoption of these technologies enables more efficient real-time big data processing, improves the overall system performance, and reduces latency, which is particularly important for high-load computing platforms.
- The optimal search path for smoothing coefficients of synaptic trajectories in the probabilistic neural network training algorithm has been improved. Spiral trajectories were replaced with linear ones, which enhanced the algorithm’s ability to find optimal solutions and avoid getting stuck in local minima. Additionally, the introduction of a chaotic operator significantly improved global search and increased the likelihood of finding global optima. These changes provided a balance between the required diagnostic accuracy and the efficient use of computational resources.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davidenko, I.V.; Dyakov, A.V.; Lopatin, V.V.; Vladimirova, M.N. Analysis of changes in the technical condition of the electrical equipment fleet using artificial intelligence. Electr. Transm. Distrib. 2020, 5, 122–133. [Google Scholar]
- C57.143-2024; IEEE Guide for Application of Monitoring Equipment to Liquid-Immersed Transformers and Components. Revision of IEEE Std C57.143-2012; IEEE: New York, NY, USA, 2025; pp. 1–177. [CrossRef]
- Yahya, A.A. Improving Models of Predictive Diagnostics and Assessment of the State of Transformer Equipment of Power Facilities. Ph.D. Thesis, Novosibirsk State University, Novosibirsk, Russia, 2022. [Google Scholar]
- Makletsov, A.M.; Galiev, I.F.; Galiev, R.I. Remote monitoring of 0.4 kV power transmission line mode parameters. In Proceedings of the Dispatching and Control in Electric Power Industry: XIV All-Russian Open Youth Scientific and Practical Conference, Kazan, Russia, 6–8 November 2019; Kazan State Power Engineering University: Kazan, Russia, 2019; pp. 250–254. [Google Scholar]
- Makletsov, A.M.; Galiev, I.F.; Galiev, R.I. Monitoring system for transformer voltage regulators under load. In Instrument Making and Automated Electric Drive in the Fuel and Energy Complex and Housing and Communal Services, Proceedings of the VI National Scientific and Practical Conference, Kazan, Russia, 10–11 December 2020; Kazan State Power Engineering University: Kazan, Russia, 2020; Volume 1, pp. 378–380. [Google Scholar]
- Makletsov, A.M.; Khamitov, I.G.; Galiev, I.F.; Galiev, R.I. Monitoring of 6–10 kV circuit breakers. In New Technologies, Materials, and Equipment in the Energy Sector; Kazan State Power Engineering University: Kazan, Russia, 2018; Volume 3, pp. 95–111. [Google Scholar]
- Butyrin, P.A.; Alpatov, M.E.; Alekseychik, L.V. Method for Diagnosing Power Transformers: No. 94034034/07. Patent No. 94034034 A1; Russian Federation, IPC H02H 7/04, G01R 35/02, 19 September 1994. [Google Scholar]
- Kuok Kyong, L.; Makletsov, A.M.; Alzakkar, A.; Maksimov, V.V.; Galiev, I.F. Development of an algorithm for balancing loads in 0.4 kV networks with distributed load along the line. News of Higher Educational Institutions. Probl. Power Eng. 2022, 24, 87–97. [Google Scholar] [CrossRef]
- Yakhin, S.R.; Pigalin, A.A.; Galiev, I.F.; Makletsov, A.M. Analysis of load modes and voltage regulation capacity of the distribution network during optimization of sectioning on its sections. Electric Power. Transm. Distrib. 2024, 1, 34–42. [Google Scholar]
- Garifullin, M.S.; Slobodina, Y.N.; Bikzinurov, A.R.; Giniatullin, R.A.; Chernyshov, V.A. Investigation of the content of unsaturated hydrocarbons in transformer oils using IR spectroscopy. Power Eng. Res. Equip. Technol. 2023, 25, 3–19. [Google Scholar] [CrossRef]
- Rakhmankulov, S.F.; Garifullin, M.S.; Galiev, I.F. Optimization of Power Transformer Defect Recognition Algorithm with DGA Based on Probabilistic Neural Network. In Proceedings of the 2024 International Russian Smart Industry Conference (SmartIndustryCon), Sochi, Russia, 25–29 March 2024; pp. 121–126. [Google Scholar] [CrossRef]
- JSC “FGC UES”. Standard Program for Comprehensive Diagnostic Examination of Power Transformers (Autotransformers) and Shunt Reactors 110–750 kV; JSC “FGC UES”: Moscow, Russia, 2005. [Google Scholar]
- Butyrin, P.A.; Vaskovskaya, T.A.; Alpatov, M.E. Investigation of simplified diagnostic models of transformers. Electro. Electr. Eng. Electr. Power Eng. Electr. Eng. Ind. 2007, 10–12. Available online: https://transform.ru/issledovanie-uproshhennyh-diagnosticheskih-modelej-transformatorov/ (accessed on 28 September 2025).
- Butyrin, P.A.; Alpatov, M.E. Digitalization and analytics in electrical engineering. Digital doubles transformers. Electricity 2021, 10, 4–10. [Google Scholar]
- CIGRE Working Group A2.26 report. Mechanical condition assessment of transformer windings using Frequency Response Analysis (FRA). Electra, no. 228. October 2006. Available online: https://www.e-cigre.org/publications/detail/342-mechanical-condition-assessment-of-transformer-windings-using-frequency-response-analysis-fra.html (accessed on 28 September 2025).
- Picher, P.; Riendeau, S.; Gauvin, M.; Leonard, F.; Dupont, L.; Goulet, J.; Rajotte, C. New technologies for monitoring transformer tap-changers and bushings and their integration into a modern IT infrastructure. In Proceedings of the CIGRE Session, Paris, France, 26–30 August 2012. [Google Scholar]
- Lukenda, N. Not all mineral oils are equal. Transform. Mag. 2019, 6, 112–117. [Google Scholar]
- CMM-10 Mobile oil Plant. Available online: https://globecore.com/products/degassing-thermal-vacuum-drying-oil/uvm-1015-mobile-oil-plant/ (accessed on 1 September 2025).
- Khalyasmaa, A.I.; Ovchinnikov, V.K. Methods for interpreting the results of chromatographic analysis of transformer equipment oil. Bull. Kazan State Power Eng. Univ. 2021, 13, 177–190. [Google Scholar]
- Nanfak, A.; Samuel, E.; Fofana, I.; Meghnefi, F.; Ngaleu, M.; Kom, C. Traditional fault diagnosis methods for mineral oil—Immersed power transformer based on dissolved gas analysis: Past, present and future. IET Nanodielectrics 2024, 7, 97–130. [Google Scholar] [CrossRef]
- Fofana, I.; Imani, M.; Farahani, M.; Gockenbach, E.; Borsi, H. Influence of Transformer Oil Aging By-products on the Dissolved Gas Analysis. In Proceedings of the International Symposium on High Voltage Engineering (ISH 2013), Seoul, Republic of Korea, 25–30 August 2013. [Google Scholar]
- Ibrahim, I.; Saleh, S.M.; Sherif Ghoneim, S.M.; Ibrahim Taha, B.M. DGALab: An Extensible Software Implementation for DGA. IET Gener. Transm. Distrib. 2018, 12, 4117–4124. [Google Scholar] [CrossRef]
- Ibrahim Taha, B.M.; Hoballah, A.; Ghoneim, S.S.M. Optimal ratio limits of rogers’ four-ratios and IEC 60599 code methods using particle swarm optimization fuzzy-logic approach. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 222–230. [Google Scholar] [CrossRef]
- Shintemirov, A.; Tang, W.; Wu, Q.H. Power Transformer Fault Classification Based on Dissolved Gas Analysis by Implementing Bootstrap and Genetic Programming. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2009, 39, 69–79. [Google Scholar] [CrossRef]
- Shintemirov, A.; Tang, W.H.; Wu, Q.H.; Fitch, J. Genetic programming feature extraction with bootstrap for dis-solved gas analysis of power transformers. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Taha, I.B.M.; Mansour, D.-E.A.; Ghoneim, S.S.M.; Elkalashy, N.I. Conditional probability-based interpretation of dissolved gas analysis for transformer incipient faults. IET Gen. Transm. Distrib. 2017, 11, 943–951. [Google Scholar] [CrossRef]
- Nanfak, A.; Eke, S.; Meghnefi, F.; Fofana, I.; Ngaleu, G.M.; Kom, C.H. Hybrid DGA Method for Power Transformer Faults Diagnosis Based on Evolutionary k-Means Clustering and Dissolved Gas Subsets Analysis. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 2421–2428. [Google Scholar] [CrossRef]
- Benmahamed, Y.; Kherif, O.; Teguar, M.; Boubakeur, A.; Ghoneim, S.S.M. Accuracy Improvement of Transformer Faults Diagnostic Based on DGA Data Using SVM-BA Classifier. Energies 2021, 14, 2970. [Google Scholar] [CrossRef]
- Poonnoy, N.; Suwanasri, C.; Suwanasri, T. Fuzzy Logic Approach to Dissolved Gas Analysis for Power Transformer Failure Index and Fault Identification. Energies 2021, 14, 36. [Google Scholar] [CrossRef]
- Lu, W.; Shi, C.; Fu, H.; Xu, Y. Fault Diagnosis Method for Power Transformers Based on Improved Golden Jackal Optimization Algorithm and Random Configuration Network. IEEE Access 2023, 11, 35336–35351. [Google Scholar] [CrossRef]
- Ibrahim, S.; Taha, I.B.M.; Ghoneim, S.S.M. DGA Tool GitHub Repository. 2018. Available online: https://github.com/Saleh860/DGA (accessed on 1 September 2025).
- Taha, I.B.M.; Ibrahim, S.; Mansour, D. -E.A. Power Transformer Fault Diagnosis Based on DGA Using a Convolu-tional Neural Network With Noise in Measurements. IEEE Access 2021, 9, 111162–111170. [Google Scholar] [CrossRef]
- Ghalkhani, M.; Fofana, I.; Bouaïcha, A.; Hemmatjou, H. Influence of aging by products on the gassing tendency of transformer oils. In Proceedings of the 2012 Annual Conference Electrical Insulation and Dielectric Phenomena, Montreal, QC, Canada, 14–17 October 2012; pp. 870–873. [Google Scholar] [CrossRef]
- Senoussaoui, M.E.A.; Fofana, I.; Brahami, M. Influence of Oil Quality on the Interpretation of Dissolved Gas Analysis Data. In Proceedings of the 2021 IEEE 5th International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Kozhikode, India, 3–5 December 2021; pp. 170–175. [Google Scholar] [CrossRef]
- Jiang, T.; Yang, J.; Yang, X.; Li, Y.; Bi, M.; Zhou, X. Diffusion Mechanisms of Dissolved Gases in Transformer Oil Influenced with Moisture Based on Molecular Dynamics Simulation. ACS Omega 2022, 7, 39812–39821. [Google Scholar] [CrossRef]
- Elele, U.; Nekahi, A.; Arshad, A.; Fofana, I. Towards Online Aging Detection in Transformer Oil: A Review. Sensors 2022, 22, 7923. [Google Scholar] [CrossRef]
- Tippannavar, S.S.; Mishra, V.; Yashwanth, S.D.; Gowda, R.R.; Sathvik, H.R.; Ajay, M. Smart Transformer—An Analysis of Recent Technologies for Monitoring Transformer. In Proceedings of the 2023 International Conference on Recent Trends in Electronics and Communication (ICRTEC), Mysore, India, 10–11 February 2023; pp. 1–11. [Google Scholar] [CrossRef]
- Shinkarenko, G.V. Measurement of short-circuit resistance of block transformers under operating voltage. Power Eng. Electrif. 1996, 19–24. [Google Scholar]
- Konov, Y.S.; Tsurpal, S.V. Method for Monitoring Internal Windings of Power Transformers. USSR A.s. No. 1221620; cl. G01R31/02, B.I. No. 12, 1986,
- Butyrin, P.A.; Alpatov, M.E. Diagnostics of power transformers under load. Proc. Russ. Acad. Sci. Power Eng. 1996, 74–81. [Google Scholar]
- Butyrin, P.A.; Alpatov, M.E. Continuous diagnostics of transformers. Electricity 1998, 45–55, ISSN 0013-5380. [Google Scholar]
- Butirin, P.A.; Alpatov, M.Y. The Continuous Diagnostics of Transformers. Electr. Technol. Russ. 1998, 23–42. [Google Scholar]
- Butyrin, P.A.; Alekseychik, L.V.; Alpatov, M.E. Method for Diagnosing Power Transformers: No. 93033648/28. Patent No. 2069371 C1; Russian Federation, IPC G01R 35/02, 29 June 1993. [Google Scholar]
- Report “Development of Algorithms for Diagnostics of Electromagnetic Parameters of Transformers” (Contract No. 2431000); MPEI: Moscow, Russia, 2001.
- Demirchyan, K.S. Reactive power in the case of non-sinusoidal functions. Orthopower Izv. RAS Power Eng. 1992, 15–38. [Google Scholar]
- Alpatov, M. On-line detection of winding deformation. In Proceedings of the Conference Record of the 2004 IEEE International Symposium on Electrical Insulation, Indianapolis, IN, USA, 19–22 September 2004; pp. 113–116. [Google Scholar] [CrossRef]
- Alpatov, M.E.; Butyrin, P.A. Analytical Theory of Transformers; MPEI Publishing House: Moscow, Russia, 2019; 112p. [Google Scholar]
- Goldstein, E.I. Method of Operational Monitoring of Short-Circuit Resistance of a Single-Phase Two-Winding Transformer in Operating Mode. RU2390034C1, 20 May 2010. [Google Scholar]
- Berezhnoy, A.V. Method for Monitoring Deformation of Windings of a Step-Down Three-Phase Two-Winding Three-Rod Power Transformer Under Operating Currents and Voltages. RU2478977C1, 10 April 2013. [Google Scholar]
- Sapunkov, M.L. Method for Detecting Turn-to-Turn Short Circuits in Windings of Three-Phase Transformers. RU2645811C1, 28 February 2018. [Google Scholar]
- Avtaev, P.N. Method for Detecting a Defect in a Power Transformer. RU2539821C2, 27 January 2015. [Google Scholar]
- Murataev, I.A. Method for Diagnosing the Magnetic System of a Transformer. RU2354982C1, 10 May 2009. [Google Scholar]
- Alyunov, A.N. Method for Diagnosing Power Transformers. RU2237254C1, 27 September 2004. [Google Scholar]
- Kozlov, V.K. Method of Forming a Diagnostic Parameter During Testing of Electromagnetic Energy Converters. RU2374656C1, 27 November 2009. [Google Scholar]
- Feizifar, B.; Müller, Z.; Fandi, G.; Usta, O. A Collective Condition Monitoring Algorithm for On-Load Tap-Changers. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Abeywickrama, N.; Kouzmine, O.; Kornhuber, S.; Cheim, L.; Lorin, P.; Gauvin, M.; Leonard, F.; Picher, P. Application of novel algorithms for continuous bushing and OLTC monitoring for increasing network reliability. In Proceedings of the CIGRE Session, Paris, France, 24 August 2014; Paper A2-113. [Google Scholar]
- Kang, P.; Birtwhistle, D. Condition Assessment of Power Transformer on-Load Tap-Changers Using Wavelet Analysis and Self-Organizing Map: Field Evaluation. IEEE Power Eng. Rev. 2002, 22, 69. [Google Scholar] [CrossRef]
- Kang, P.; Birtwhistle, D.; Daly, J.; McCulloch, D. Non-invasive-line condition monitoring of on load tap changers. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No. 00CH37077), Singapore, 23–27 January 2000; Volume 3, pp. 2223–2228. [Google Scholar] [CrossRef]
- Foata, M.; Girard, B.; Landry, C.; Mow, A.; Rajotte, C. Field experience with the implementation of a new on-line vibro-acoustic diagnostic for on-load tap changers. In Proceedings of the Doble Users Conference, Boston, MA, USA, 28 February–4 March 2005. [Google Scholar]
- Kang, P.; Birtwhistle, D. Condition Assessment of Power Transformer on-Load Tap-Changers Using Wavelet Analysis. IEEE Power Eng. Rev. 2001, 21, 64. [Google Scholar] [CrossRef]
- Rivas, E.; Burgos, J.; García-Prada, J.C. Vibration Analysis Using Envelope Wavelet for Detecting Faults in the OLTC Tap Selector. IEEE Trans. Power Deliv. 2010, 25, 1629–1636. [Google Scholar] [CrossRef]
- Rivas, E.; Burgos, J.; Garcia-Prada, J.C. Methodology for Vibration Signal Processing of an On-load Tap Changer. Adv. Vib. Anal. Res. 2011, 17, 329–342. [Google Scholar] [CrossRef]
- Seo, J.; Ma, H.; Saha, T. A Joint Vibration and Arcing Measurement System for Online Condition Monitoring of On-Load Tap Changer of Power Transformer. IEEE Trans. Power Deliv. 2017, 32, 1031–1038. [Google Scholar] [CrossRef]
- Seo, J.; Ma, H.; Saha, T. On Savitzky-Golay Filtering for Online Condition Monitoring of Transformer On-Load Tap Changer. IEEE Trans. Power Deliv. 2018, 33, 1689–1698. [Google Scholar] [CrossRef]
- Dabaghi-Zarandi, F.; Behjat, V.; Gauvin, M.; Picher, P.; Ezzaidi, H.; Fofana, I. Power Transformers OLTC Condition Monitoring Based on Feature Extraction from Vibro-Acoustic Signals: Main Peaks and Euclidean Distance. Sensors 2023, 23, 7020. [Google Scholar] [CrossRef]
- Dabaghi-Zarandi, F.; Picher, P.; Gauvin, M.; Ezzaidi, H.; Fofana, I.; Rao, U.M.; Behjat, V.; Souza, J. Evaluating OLTC condition based on feature extraction from vibro-acoustic signals. In Proceedings of the 23rd International Symposium on High Voltage Engineering (ISH 2023), Glasgow, UK, 28 August–1 September 2023; pp. 133–137. [Google Scholar] [CrossRef]
- Dabaghi-Zarandi, F.; Behjat, V.; Gauvin, M.; Picher, P.; Ezzaidi, H.; Fofana, I. Using Deep Learning to Detect Anomalies in On-Load Tap Changer Based on Vibro-Acoustic Signal Features. Energies 2024, 17, 1665. [Google Scholar] [CrossRef]
- Beheshti Asl, M.; Fofana, I.; Meghnefi, F. Review of Various Sensor Technologies in Monitoring the Condition of Power Transformers. Energies 2024, 17, 3533. [Google Scholar] [CrossRef]
- Transformer Reliability Survey: CIGRE WG A2.37. Technical Brochure C1GRE; 642; CIGRE: Paris, France, 2015; 120p.
- STO 34.01-23.1-001-2017; Scope and Standards for Testing Electrical Equipment. PJSC Rosseti: Moscow, Russia, 2017.
- Korobeynikov, S.M.; Ovsyannikov, A.G. Physical Mechanisms of Partial Discharges; Publishing House of NSTU: Novosibirsk, Russia, 2021; 266p. [Google Scholar]
- Guidelines for the Operation of High-Voltage Bushings with RIP Insulation Manufactured by Massa LLC—Izolyator Plant at the Facilities of PJSC FGC UES Moscow, 2016 [Electronic Resource]. Available online: https://mosizolyator.ru/files/nodus_items/0002/1410/attaches/Metod.-ukaz.-po-ekspluatatsii-vvodov-s-RIP.pdf (accessed on 1 September 2025).
- GOST R 55191-2012 (IEC 60270:2000); High-Voltage Test Methods: Partial Discharge Measurements. Gosstandart: Moscow, Russia, 2012.
- On the Mass Operational Testing of the High-Frequency Flaw Detection Method for High-Voltage Insulation; Information Message No. E-7/61; Soyuzglavenergo, ORGRES: Moscow, Russia, 1961; 38p.
- Halyasmaa, A.I.; Dmitriev, S.A.; Cokin, S.E.; Glushkov, D.A. Diagnostics of Electrical Equipment of Power Plants and Substations: A Tutorial; Izdvo Ural University: Ekaterinburg, Russia, 2015; 64p. (In Russian) [Google Scholar]
- GOST 18353-79; Non-Destructive Testing: Classification of Types and Methods. Interstate Standard: Moscow, Russia, 1979.
- RD 153-34.0-20.363-99; Basic Provisions of the Methodology for Infrared Diagnostics of Electrical Equipment and Overhead Lines. Ministry of Energy of the Russian Federation: Moscow, Russia, 1999.
- Lundgaard, L.E. Partial discharge. XIII. Acoustic partial discharge detection-fundamental considerations. IEEE Electr. Insul. Mag. 1992, 8, 25–31. [Google Scholar] [CrossRef]
- Lundgaard, L.E. Partial discharge. XIV. Acoustic partial discharge detection-practical application. IEEE Electr. Insul. Mag. 1992, 8, 34–43. [Google Scholar] [CrossRef]
- Galiev, I.F.; Garifullin, M.S.; Alekseev, I.P.; Gizatullin, A.R.; Makletsov, A.M. Development of an Integrated Expert System for Distribution Network Diagnostics Based on Artificial Intelligence Technology. In Proceedings of the 2023 International Russian Smart Industry Conference (SmartIndustryCon), Sochi, Russia, 27–31 March 2023; pp. 6–14. [Google Scholar]
- Weruaga, L. Frequency-Selective Noise-Compensated Autoregressive Estimation. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 2469–2476. [Google Scholar] [CrossRef]
- Hendel, M.; Bousmaha, I.; Meghnefi, F.; Fofana, I.; Brahami, M.M. An Intelligent Power Transformers Diagnostic System Based on Hierarchical Radial Basis Functions Improved by Linde Buzo Gray and Single-Layer Perceptron Algorithms. Energies 2024, 17, 3171. [Google Scholar] [CrossRef]
- Safdari-Vaighani, A.; Heryudono, A.; Larsson, E. A Radial Basis Function Partition of Unity Collocation Method for Convection–Diffusion Equations Arising in Financial Applications. J. Sci. Comput. 2015, 64, 341–367. [Google Scholar] [CrossRef]
- Traveling Salesman Problem. Available online: https://en.wikipedia.org/wiki/Travelling_salesman_problem (accessed on 1 September 2025).
- The Traveling Salesman Problem. Available online: http://www.math.uwaterloo.ca/tsp/index.html (accessed on 1 September 2025).
- Rosenkrantz, D.J.; Stearns, R.E.; Lewis, P.M. Approximate algorithms for the traveling salesperson problem. In Proceedings of the 15th Annual Symposium on Switching and Automata Theory (Swat 1974), New Orleans, LA, USA, 14–16 October 1974; pp. 33–42. [Google Scholar] [CrossRef]
- Baughman, D.R.; Liu, Y.A. Classification: Fault Diagnosis and Feature Categorization. In Neural Networks in Bioprocessing and Chemical Engineering; Academic Press: Cambridge, MA, USA, 1995; pp. 110–171. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H.; Fatahi, A.; Mirjalili, S. MFO-SFR: An Enhanced Moth-Flame Optimization Algorithm Using an Effective Stagnation Finding and Replacing Strategy. Mathematics 2023, 11, 862. [Google Scholar] [CrossRef]
- Rakhmankulov, S.F.; Garifullin, M.S.; Galiev, I.F. The “Butterfly Flame” Algorithm for Optimizing the Topography of a Neural Network for Diagnostics of Power Transformers Using Chromatographic Analysis. In Energy and Resource Saving—XXI Century, Proceedings of the XXI International Scientific and Practical Conference, Orel, Bucharest, Romania, 15–16 November 2023; Atlantic Press: New York City, NY, USA; pp. 57–61.
- STO 34.01-23-003-2019; Guidelines for Technical Diagnostics of Developing Defects in Oil-Filled High-Voltage Electrical Equipment Based on the Results of Analysis of Gases Dissolved in Mineral Transformer Oil. PJSC “ROSSETI”: Moscow, Russia, 2019; 63p.



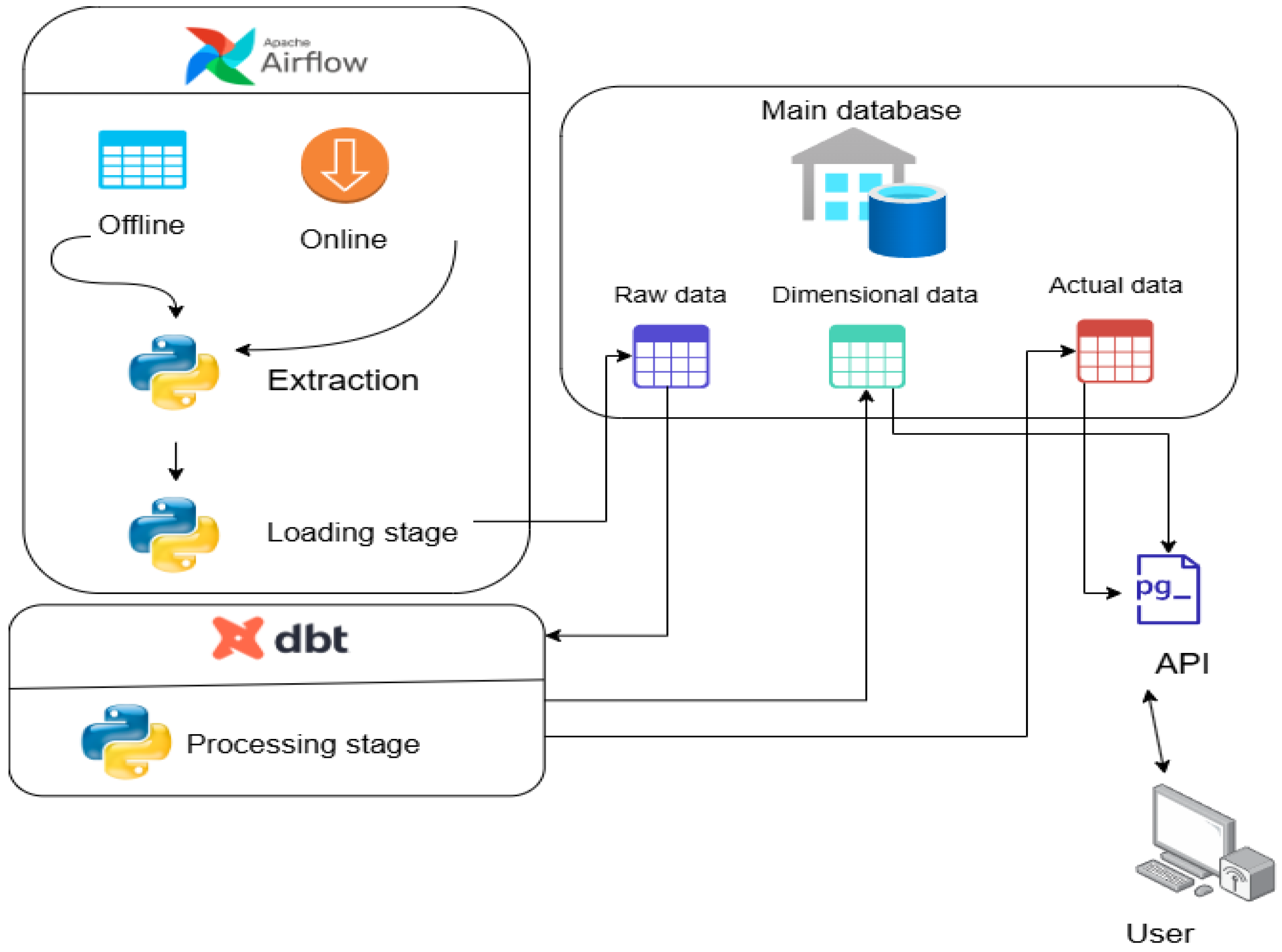
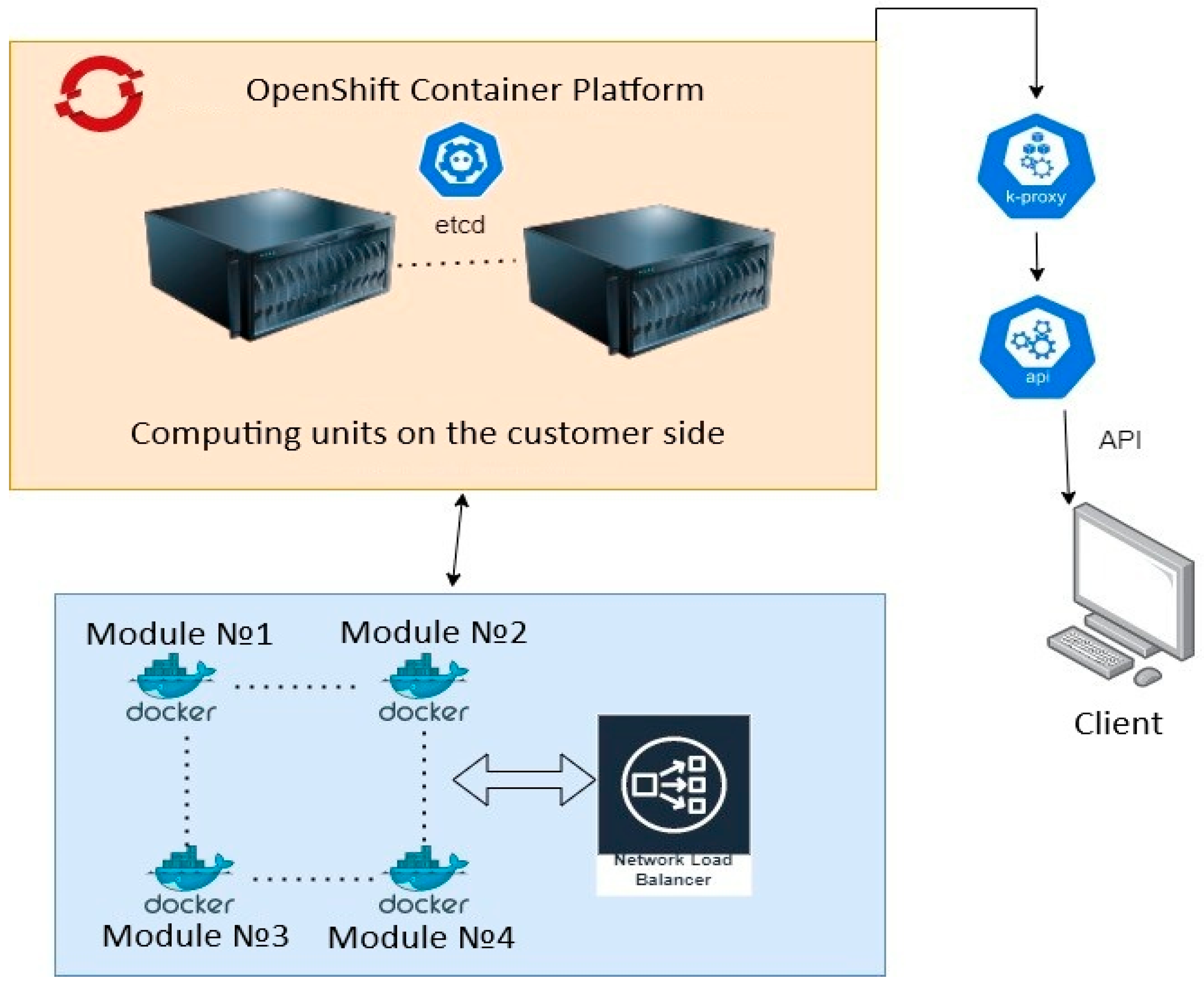
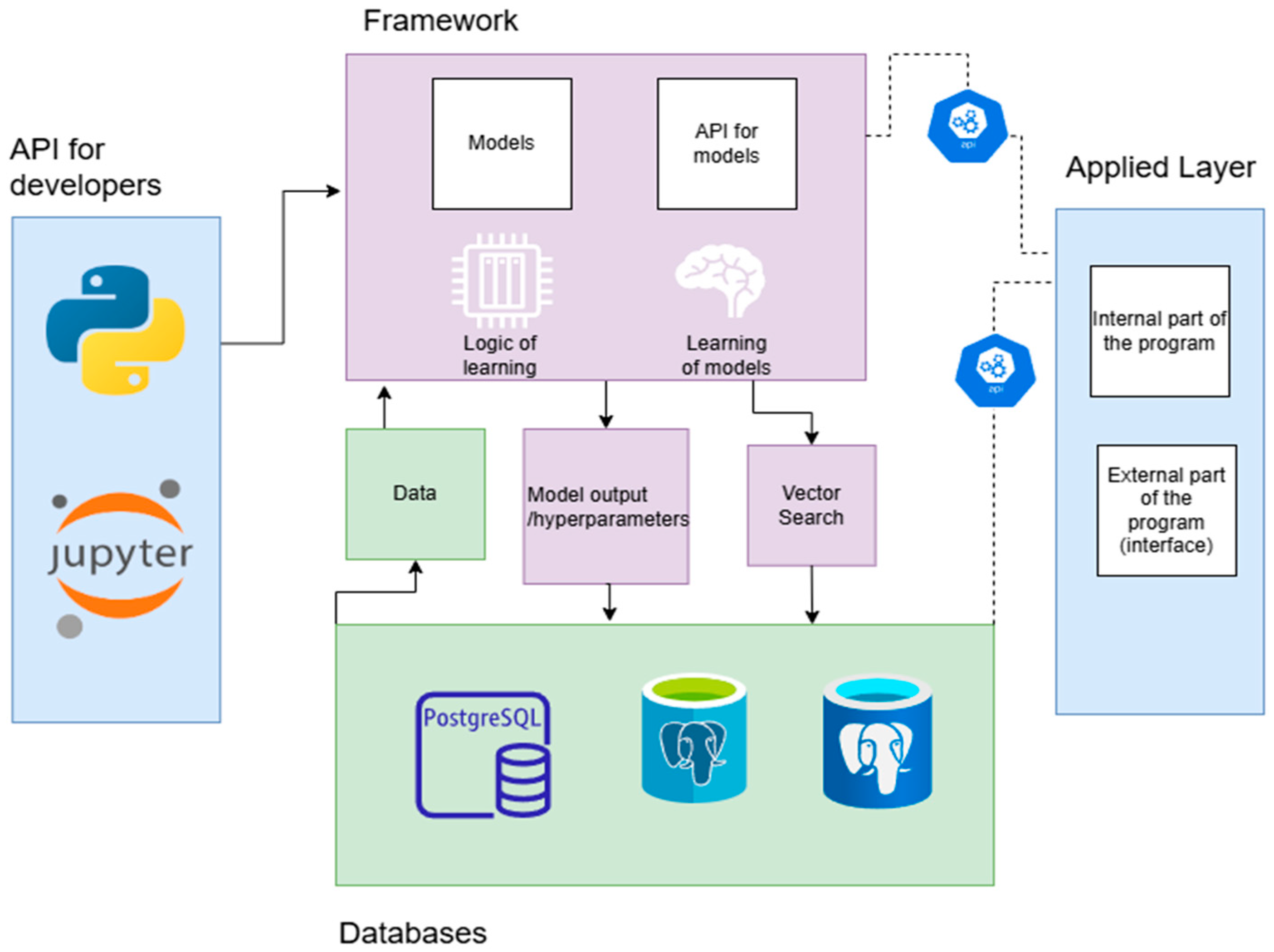



| Development Stage and Property | Standard Approach | Author’s Approach |
|---|---|---|
| Data extraction via API | Standard invocation using arbitrary programmatic means | Invocation within a local microservice |
| Noise removal in data | Missing values are approximated; anomalies and noise are addressed using robust statistical estimators | Missing values are approximated. Noise and anomalies are detected using an autoregressive model tailored to data characteristics and tuned to specific time discretization or frequency [81], offering greater effectiveness than Z-score or other direct methods |
| Transformation of raw data into fact and dimension tables | Typically not performed; rarely implemented as an optimization technique | Algorithm splits a raw data table into two structured tables representing facts and dimensions respectively |
| Re-training countdown mechanism | Rarely used in practice; neural networks are often not retrained or fine-tuned | The countdown to the next stage of pre-training is underway |
| Vector search, transformation, and storage | No separation of numeric values, vectors, and other data types | An additional layer significantly accelerates vector search in PostgreSQL compared to built-in VectorSearch, while saving disk space |
| Prediction and defect classification result generation | Model weights are loaded; input is passed through the pre-trained model to produce an output | Due to a custom NN architecture, results are obtained significantly faster since most parameters reside in RAM, optimizing computational resource usage |
| Storage of prediction results | Simply added to the database | Identical approach |
| System integrity | Monolithic solution, difficult to scale and extend | Flexible microservice-based architecture that can be easily scaled up or down based on hardware constraints and requirements |
| Availability | Standalone enterprise application for desktop systems | Web application accessible from any device (phone, tablet, PC); supports service delivery models such as Software as a Service (SaaS) |
| Time Series Forecasting | ||
|---|---|---|
| Process Stage | Standard Approach | Proposed (Author’s) Approach |
| Data preprocessing, outlier and noise removal | Selection of autoregression level based on predefined periodicity (e.g., lags 1, 2, 3) | Selection of autoregressive order. To move beyond the constraints of a Markovian process, a specific case of the coefficient is derived. Its suitability is verified using the Ordinary Least Squares (OLS) criterion. The nearest integer value is then determined. A deliberate and data-informed choice of the autoregressive coefficient is regarded as a step toward increased predictive accuracy. |
| Classification Model Training | ||
| Process Stage | Standard Approach | Proposed (Author’s) Approach |
| Architecture selection | Typically receives little attention in terms of resource allocation and hardware communication efficiency | Architecture selection accounts not only for model accuracy, but also for efficient utilization of computational and switching resources |
| Batch preparation | Standard partitioning into:
| Same procedure applied |
| Neural network algorithm implementation | Often lacks fine-tuning or algorithmic precision; architectures are frequently selected arbitrarily or approximated. | The algorithm is designed to ensure that each retraining phase includes iterative subsampling, allowing the model to continuously refine itself using segmented training batches |
| Predictive Model Training | Recurrent neural networks (RNN), convolutional neural networks (CNN), and LSTM are commonly used | LSTM networks are employed exclusively due to their capacity to retain relevant information across long temporal dependencies, making them especially well-suited for sequential diagnostics and forecasting |
| Compared Aspects | Standard Solution | Proposed Solution |
|---|---|---|
| Efficiency relative to computational units | Not evaluated in terms of computational efficiency, which complicates scaling and/or deployment on real-world systems | The architectures of both neural networks were selected with regard to relative accuracy and efficiency of computational resources |
| Preparedness for retraining | It is generally assumed that neural network solutions function without retraining or require manual supervision, which limits the autonomy and scalability of the developed models | The framework described in the hardware section allows for efficient storage, retraining, or fine-tuning of models, while the Moth–Flame Optimization algorithm used in the classification model enables accurate parameter estimation at each iteration |
| № | Diagnostic Parameter | Parameter Designation | Expression |
|---|---|---|---|
| 1 | No-load current from the j-th winding | i0j,% | |
| 2 | No-load losses from the j-th winding | P0j | |
| 3 | Short-circuit impedance from the j-th winding | Zкj | |
| 4 | Short-circuit losses from the j-th winding | Pкj | |
| 5 | Transformation ratio (voltage transfer ratio) | kZ | |
| 6 | Current transfer ratio | kY | |
| 7 | Mutual active resistance between windings | Rm | |
| 8 | Mutual inductive reactance between windings (mutual inductance) | Xm (M) | |
| 9 | Active component of short-circuit impedance | Rкj | |
| 10 | Inductive component of short-circuit impedance (short-circuit inductance) | Xкj (Lкj) | |
| 11 | Active resistance of the j-th winding | Rj | |
| 12 | Leakage inductive reactance of the j-th winding (leakage inductance of the j-th winding) | Lσj |
| Condition Index | State Mapping | Interpretation |
|---|---|---|
| 1 | NW | Normal Working |
| 2 | NW on the verge | Normal Working (borderline) |
| 3 | LT | Low-Temperature Overheating |
| 4 | PD | Partial Discharge |
| 5 | LPD | Combined overheating and partial discharge |
| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| NW | 0.94 | 0.95 | 0.95 | 357,801 |
| PD | 0.59 | 0.99 | 0.74 | 18,745 |
| LPD | 0.57 | 0.46 | 0.51 | 23,644 |
| LT | 0.61 | 0.43 | 0.50 | 40,810 |
| Accuracy | 0.88 | |||
| Macro avg | 0.68 | 0.71 | 0.67 | 441,000 |
| Weighted avg | 0.87 | 0.88 | 0.87 | 441,000 |
| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| NW | 0.84 | 0.80 | 0.82 | 357,801 |
| PD | 0.29 | 0.26 | 0.23 | 18,745 |
| LPD | 0.00 | 0.00 | 0.00 | 23,644 |
| LT | 0.16 | 0.05 | 0.09 | 40,810 |
| Accuracy | 0.67 | |||
| Macro avg | 0.32 | 0.28 | 0.28 | 441,000 |
| Weighted avg | 0.70 | 0.67 | 0.68 | 441,000 |
| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| NW | 0.93 | 0.13 | 0.23 | 357,801 |
| PD | 0.18 | 0.17 | 0.17 | 18,745 |
| LPD | 0.01 | 0.93 | 0.01 | 23,644 |
| LT | 0.07 | 0.00 | 0.01 | 40,810 |
| Accuracy | 0.16 | |||
| Macro avg | 0.30 | 0.31 | 0.10 | 441,000 |
| Weighted avg | 0.84 | 0.16 | 0.19 | 441,000 |
| Mode № | Mode Parameters | Measured Voltages, V | Measured Currents, A | Z-Parameter Matrix, Ohm | |||
|---|---|---|---|---|---|---|---|
| 1 | Sampling frequency: 8 kHz | ||||||
| 1—load 100% | 208.95 | 223.26 | −26.96–104.78i | −12.21–97.45i | 46.44 + 232.75i | 38.50 + 185.20i | |
| 2—load 61.5% | 228.52 + 19.63i | 231.24 + 24.45i | 33.00 + 130.65i | 14.58 + 121.23i | 39.09 + 185.47i | 32.61 + 147.17i | |
| 2 | 8 kHz | ||||||
| 1—100% | 208.946 | 211.483 | 5.529–1.20i | 5.99–1.19i | −87.22 + 66.56i | −78.52 + 52.49i | |
| 2—97.3% | 228.52 + 19.63i | 237.40 + 19.79i | −8.162 + 0.56i | −8.725 + 0.575i | −59.10 + 27.34i | −65.41 + 20.29i | |
| 3 | 8 kHz | ||||||
| 1—100% | 208.946 | 220 | 5.53–1.20i | 0.18–0.91i | 47.09 + 232.76i | 29.96 + 152.82i | |
| 2—no-load | 228.52 + 19.63i | 275.45 + 2.96i | −8.16 + 0.56i | 0 | 55.83 + 292.06i | 39.63 + 189.97i | |
| 4 | 8 kHz | ||||||
| 1—no-load | 220 | 32.89 | 0.18–0.91i | 4.29–2.48i | 47.09 + 232.77i | 30.98 + 156.11i | |
| 2—short-circuit | 275.45 + 2.96i | 15.55 + 8.66i | 0 | −6.35 + 3.525i | 55.83 + 292.07i | 40.33 + 196.6i | |
| 5 | Sampling frequency: 50 kHz | ||||||
| 1—100% | 211.94 | 212.5 | −3.59 + 0.04i | −3.68 + 0.06i | 72.94 + 210.76i | 48.46 + 163.94i | |
| 2—97.5% | 235.00 + 20.21i | 236.68 + 20.56i | 5.03–1.45i | 5.14–1.49i | 59.72 + 177.42i | 48.99 + 144.41i | |
| 6 | 50 kHz | ||||||
| 1—100% | 211.936 | 216.497 | 5.894–1.162i | 0.249–0.944i | 56.56 + 214.42i | 33.23 + 144.84i | |
| 2—no-load | 235.00 + 20.21i | 265.97 + 2.04i | −8.416 + 0.628 | 0 | 67.46 + 263.95i | 42.61 + 176.32i | |
| 7 | 50 kHz | ||||||
| 1—no-load | 216.497 | 35.253 | 0.25–0.94i | 4.47–2.25i | 56.56 + 214.42i | 33.49 + 135.87i | |
| 2—short-circuit | 265.97 + 2.04i | 16.89 + 8.27i | 0 | −6.96 + 3.43i | 67.46 + 263.95i | 43.37 + 167.82i | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beloev, I.; Alpatov, M.E.; Garifullin, M.S.; Galiev, I.F.; Rakhmankulov, S.F.; Iliev, I.; Valeeva, Y.S. Development of a Hybrid Expert Diagnostic System for Power Transformers Based on the Integration of Computational and Measurement Complexes. Energies 2025, 18, 5360. https://doi.org/10.3390/en18205360
Beloev I, Alpatov ME, Garifullin MS, Galiev IF, Rakhmankulov SF, Iliev I, Valeeva YS. Development of a Hybrid Expert Diagnostic System for Power Transformers Based on the Integration of Computational and Measurement Complexes. Energies. 2025; 18(20):5360. https://doi.org/10.3390/en18205360
Chicago/Turabian StyleBeloev, Ivan, Mikhail Evgenievich Alpatov, Marsel Sharifyanovich Garifullin, Ilgiz Fanzilevich Galiev, Shamil Faridovich Rakhmankulov, Iliya Iliev, and Ylia Sergeevna Valeeva. 2025. "Development of a Hybrid Expert Diagnostic System for Power Transformers Based on the Integration of Computational and Measurement Complexes" Energies 18, no. 20: 5360. https://doi.org/10.3390/en18205360
APA StyleBeloev, I., Alpatov, M. E., Garifullin, M. S., Galiev, I. F., Rakhmankulov, S. F., Iliev, I., & Valeeva, Y. S. (2025). Development of a Hybrid Expert Diagnostic System for Power Transformers Based on the Integration of Computational and Measurement Complexes. Energies, 18(20), 5360. https://doi.org/10.3390/en18205360








