Hierarchical Multi-Communities Energy Sharing Management with Electric Vehicle Integration

Abstract

The widespread adoption of Electric Vehicles (EVs) in the smart grid is transforming the traditional grid into a more complex system. EVs have the ability to both charge and discharge, acting as loads that draw high power and sources that inject energy back into the grid. Consequently, energy sharing and management within smart grid communities integrated with EVs have become interesting aspects to study in order to efficiently utilize this energy. However, most existing research focuses solely on energy sharing within single communities, utilizing homogeneous energy profiles and neglecting the potential of heterogeneous energy across multiple communities. EVs also possess the capability to travel to different places and communities, where they can engage in energy sharing with areas that have varying load profiles and prices. In this work, a novel three-level energy sharing management approach is proposed for a multiple community system integrating movable energy storage such as EVs. This model involves three main entities: the Utility Company (UC), Community Energy Aggregator (CEA), and EVs. The energy sharing problem is formulated as a Stackelberg game, with all entities striving to maximize their utility through optimal strategies, including pricing, energy demand, or supply. The proposed model is validated through comparison with typical human charging behavior, as well as single- and multiple-community two-level game models. The findings reveal that the proposed model successfully optimizes pricing and energy strategies, significantly lowering the peak-to-average ratio and smoothing the overall energy profile.

1. Introduction

The traditional energy landscape has long been characterized by centralized power generation, with large-scale power plants supplying electricity to passive consumers [1]. However, recent advancements in renewable energy (RE) technologies, along with the decrease in installation costs, have led to their widespread adoption [2]. This shift is transforming the energy sector into a new era, moving away from centralized power generation and empowering consumers to become prosumers who can both generate and consume electricity [3]. However, despite the advantages prosumers gain from generating and using their own electricity from RE, the intermittent nature of RE, driven by fluctuating weather conditions, presents challenges to its reliability as an energy source [4]. Moreover, irregular human behavior and the widespread adoption of high-demand loads lead to significant fluctuations in energy demand and generation. This leads to immediate peak periods requiring electricity to be supplied by conventional peaking power plants, which are both economically and technically inefficient. Additionally, these plants emit harmful pollutants, posing significant health risks [5].

To address these challenges and promote a more resilient and sustainable energy infrastructure, the integration of energy storage systems (ESSs) emerges as a crucial solution. Notably, the innovative use of movable energy storage, such as electric vehicles (EVs), within smart grids offers significant potential to adjust the total energy profile. EVs possess the distinct ability to both charge and discharge energy from their battery storage to the community grid. The integration of electric vehicles (EVs) into the smart grid, particularly through grid-to-vehicle (G2V) and vehicle-to-grid (V2G) systems, has become a central area of research. G2V involves efficiently managing EV battery charging using energy sourced from the utility grid and renewables. Conversely, V2G explores the use of EVs to deliver ancillary services to the grid by discharging stored energy, helping to mitigate challenges such as renewable energy intermittency and contributing to essential grid operations, including peak demand reduction, frequency and voltage regulation, and spinning reserve support [6]. Specifically, EVs can be efficiently managed to store energy during periods of low demand and release it during periods of high demand. By strategically deploying EVs in conjunction with energy sharing and demand-side management, smart grid communities can leverage the benefits of energy storage to balance supply and demand, mitigate fluctuations in energy demand and generation, and reduce reliance on costly and environmentally harmful peak power plants.

Typically, the electricity market is a hierarchical structure with multiple layers [7]. The first and lowest layer consists of end-users and prosumers, such as smart homes equipped with various appliances, and other prosumers, like electric vehicle owners utilizing public charging facilities. Since small prosumers have limited demand and supply capacity, they need to belong to aggregators in order to provide energy sharing to the system. The higher layer, or middle layer, comprises community aggregators that consolidate all demand and supply within the community or region and facilitate exchanges with other communities in different regions and utility companies for energy and information. In some cases, they may be so-called ancillary service providers or demand response service providers. Additionally, this layer could include significant prosumers who do not need to go through the aggregators, such as commercial and industrial buildings, as well as public places with high demand, like schools. The highest layer is occupied by the market operator or the utility company, which centrally manages electricity production to meet the demands of a multi-communities power system. In each layer, there are challenges that should be investigated.

The key contributions of this paper can be outlined as follows:

• A novel energy sharing management model for hierarchical multi-communities energy sharing is proposed. This model incorporates EVs as movable energy storage units capable of charging and discharging in different locations, with two distinct pricing structures: community sharing price and multi-communities sharing price.
• A three-level Stackelberg game is proposed to model the interactions among three key participants: the Utility Company (UC), Community Energy Aggregators (CEAs), and Electric Vehicles (EVs). The framework identifies optimal pricing and energy strategies while ensuring and proving the existence and uniqueness of the Stackelberg equilibrium.
• The three-level optimal energy–price equilibrium (3OEP) algorithm is developed to attain the game equilibrium. It guarantees that no participant can improve their payoff by independently deviating from the equilibrium strategy.

This paper is organized as follows. Section 2 reviews the existing literature relevant to the topic. Section 3 describes the system model for the proposed three-level energy sharing management, covering the models for the utility company, community energy aggregators, and electric vehicles. Section 4 focuses on the hierarchical Stackelberg game, detailing its formulation, the validation of existence and uniqueness, and the algorithm developed to achieve equilibrium. Section 5 provides a detailed presentation and analysis of the simulation results. Section 6 summarizes the paper and proposes directions for future research.

2. Related Works

For energy sharing management, the literature explores two main categories: energy sharing within a single community with and without EV integration, and energy sharing across multiple communities.

Several studies have made efforts toward energy sharing within single communities without considering EVs [3,8,9,10,11,12]. In [8], a novel energy sharing model is proposed by utilizing the supply-to-demand ratio (SDR) to determine internal buying and selling prices, facilitating energy sharing among PV prosumers within a single community. The simulation reveals the model’s effectiveness in reducing prosumers’ costs and improving the sharing economy. A game-theoretic approach for energy sharing management is proposed in [9], where it is used to find the optimal energy price and consumption of prosumers. A novel profit model of the microgrid operator, utility model of prosumers, and billing mechanism are introduced. The results show increased benefits for all players. A. Paudel et al. [10] introduced a novel peer-to-peer energy trading model among prosumers in a single community. The Stackelberg game is formulated for the interaction between sellers and buyers, where the sellers are the leaders and the buyers are the followers of the game. The results confirm the effectiveness of the model in improving both technical and financial benefits for the community. In [11], a community-based energy trading model is proposed, where a coordinator helps facilitate the trading process between market participants. Demand-side management is also implemented using a non-cooperative game. The findings show that the model can increase prosumers’ profits and greatly reduce peak energy demand. Ref. [3] introduced direct energy sharing between small-scale prosumers who possess both loads and renewable energy resources in a low-voltage microgrid. A non-cooperative game is employed within the energy-sharing platform. The findings indicate that the proposed model strengthens the local energy balance of a microgrid by decreasing energy exchanges with the utility grid. Additionally, they demonstrate that the diversity in generation and demand profiles can further amplify benefits for participants and improve the overall system balance. In [12], the authors proposed a peer-to-peer energy sharing scheme to reduce the peak energy consumption of prosumers in a community using a game-theoretic approach, where the price is determined to incentivize prosumers to adjust their energy usage. Numerical results confirm the benefits of the proposed scheme for all participating entities in the system.

On the other hand, some work has focused on a single community energy sharing integrating EV [13,14,15,16,17,18,19]. In [13], a peer-to-peer energy trading model among plug-in hybrid electric vehicles (PHEVs) is proposed. The model provides incentives for PHEVs to discharge energy to balance the energy profile of the system. Agreed-upon energy and electricity prices are determined using a double auction. Simulation results reveal that the model can achieve maximum social welfare. J. Kim et al. [14] presented an energy trading and demand response system for electric vehicles in a single isolated microgrid system. In the model, sellers and buyers submit transaction prices, and buyers determine optimal results. Revenue and energy are allocated according to payments and sales. Results show that participants can maximize their profit while stabilizing energy supply and demand. A framework for peer-to-peer energy trading among electric vehicles, charging stations, and office buildings is introduced in [15]. Electricity price depends on the price of stored energy in the battery. Analysis shows that the model can help reduce prosumers’ costs by 23%, improve PV self-consumption by 10%, and guarantee willingness to participate. In [16], an energy dispatching model for a microgrid and prosumers possessing EVs is introduced, where the microgrid aims to balance supply and demand while increasing profit, and EVs aim to lower energy costs. The results show an increase in microgrid profit and a reduction in prosumers’ costs. A distributed charging model is introduced in [17] to determine the optimal price for a charging station operator. The model consists of a profit model for a PV charging station operator and the cost for EV users. The model is verified through a practical case, demonstrating an increase in operational profit and a reduction in charging costs. Ref. [18] proposed an optimal dispatch model for a single microgrid containing EVs, where the microgrid aims to minimize operating costs while EVs seek to maximize individual benefits by adjusting their charging and discharging energy. The simulation reveals a reduction in the peak-to-valley difference of the microgrid’s energy profile. In [19], a novel power scheduling scheme for electric vehicle (EV) charging facilities is proposed, utilizing a two-level Stackelberg game between charging facilities and EVs within a single community. The results demonstrate improved financial profits for both EV users and charging facilities.

There is limited research on energy sharing in multi-communities smart grid [20,21,22,23,24,25,26]. With the increasing installation of distributed energy resources, F. Moret et al. [20] presented the concept of a community-based energy market structure called ’energy collectives’, where prosumers can share energy at a community level. Additionally, the community manager can further facilitate energy sharing with other communities under the market or system operator. A peer-to-peer energy-sharing system with multiple regions is studied in [21], where the large scale of PV prosumers is considered. The distributed network can be divided into multiple energy-sharing regions where the electricity price varies. Prosumers can choose the region they want to join and can provide demand response to the system, with profit maximization formulated, taking into account electricity prices and fees. The results show an increase in prosumer profit compared to scenarios without divided regions. A new charging scheme for EVs within smart communities incorporating RE is presented in [22]. The model involves three key entities: the grid, aggregators (AGGs), and EVs. A trust model is implemented to facilitate EVs in selecting an AGG for charging, as information sharing is required among all participating entities. The analysis demonstrates that the proposed scheme outperforms traditional approaches in effectiveness. In [23], the authors proposed a strategic framework for planning and managing EV charging and discharging operations across multiple charging stations in various locations. The framework aims to improve the microgrid’s flexibility and efficiency by modeling the problem as a non-cooperative game involving the distribution company, charging stations, and EVs. The results demonstrate that the framework increases microgrid flexibility by 0.3% and efficiency by 67.4% compared to a reference case study. Ref. [24] presented an energy sharing mechanism between multiple microgrids and consumers to improve the utilization of renewable energy resources where consumers adjust their load schedules. The results confirm that the approach can significantly improve the utilization of renewable energy resources. Yu et al. [25] proposed a method to maximize profit and reduce costs by coordinating microgrids that include EV prosumers. The optimal price is determined within the model. The results illustrate the effectiveness of the proposed model. In [26], an optimal vehicle-to-grid pricing strategy is introduced, employing a two-level Stackelberg game between multiple aggregators and EVs. However, the work considers only V2G operations and excludes G2V interactions. The results show an improvement in EV users’ benefits while taking into account user satisfaction and inconvenience.

To the best of our knowledge, no existing research has introduced a three-level hierarchical energy-sharing management framework for multiple communities that integrates mobile energy storage systems, such as electric vehicles, while accounting for the interests of all stakeholders involved in such systems.

Unlike previous works that utilize two-level models, this work presents a three-level Stackelberg game framework that addresses the hierarchical nature of electricity markets. It incorporates decision making at three critical levels: individual prosumers (e.g., EVs), community aggregators, and the utility company or market operator. This multi-level approach allows for a more accurate and realistic representation of interactions within and between communities. Such modeling is crucial for ensuring that the benefits for each entity are adequately considered, which is a necessary condition for the successful real-world deployment of these systems.

Furthermore, this framework extends beyond the single-community systems that dominate the literature by considering multiple communities with varying energy profiles. This is a more realistic scenario, as communities differ significantly in terms of consumer types and energy demands. The model facilitates energy and information exchange across communities and ensures reasonable electricity pricing, addressing gaps left by earlier single-community or limited multi-communities models.

Another key novelty is the integration of mobile EVs that can dynamically move between communities, enabling optimal energy redistribution and demand–supply balancing. Unlike prior works that restricted EVs to a single community or specific functionalities like G2V or V2G, this framework considers the dynamic nature of EVs across multiple communities. This integration enhances grid flexibility and reduces peak demand, addressing critical challenges in modern smart grid systems.

In conclusion, this work employs a three-level game-theoretic approach for a novel hierarchical multi-communities energy sharing management framework. By integrating mobile EVs and addressing the dynamics of multiple entities, it aims to provide a more realistic and effective solution for energy sharing in smart grids.

Table 1. Comparison of related works.

Reference	Proposed Solution	Method	Communities	RE/Loads/EVs	Results
[8]	An energy-sharing model with price-based demand response	Supply-to-demand ratio	Single community	PV, residential loads	Save costs for PV prosumers while improving the sharing of PV energy
[9]	A new game-theoretic model for facilitating peer-to-peer energy trading among prosumers within a community.	2-level Stackelberg game: seller prosumers, buyer prosumers	Single community	PV, residential loads, battery storage	Provide significant financial benefits where the cost are greatly reduced
[11]	A community-based energy trading model using blockchain	Non-cooperative game: suppliers, prosumers	Single community	PV, residential loads	Increase prosumers’ profits and significantly reduce peak energy demand
[16]	An energy dispatching model for a microgrid and prosumers possessing EVs	2-level Stackelberg game: microgrid, prosumers	Single community	PV, prosumer loads, EVs	Increase in microgrid profits and reduction in prosumers’ costs
[19]	A novel power scheduling scheme for EV charging facility	2-level Stackelberg game: charging facility, EVs	Single community	EVs	Improve the financial profit of EV users and the charging facility
[21]	An energy sharing framework for distributed network with a multi-energy-sharing region	2-level Stackelberg game: energy sharing provider, prosumers	Multiple regions	PV, prosumer loads (No ESSs/EVs)	Increase the profit of players compared to the case without regional
[22]	A charging scheme for EVs in a smart communities integrated with RES	Non-cooperative game: microgids, EVs	Multiple microgrids	PV, buildings, EVs (only G2V)	Enhance the profit of EVs
[26]	An optimal V2G pricing strategy	2-level Stackelberg game: aggregators, EVs	Multiple aggregators	EVs (only V2G)	Enhance the benefits for EV users while considering their satisfaction and inconvenience
This work	A hierarchical multi-communities energy sharing management framework in smart grid	Three-level Stackelberg game involving prosumers (EVs), a set of single communities, and multi-communities levels	Multiple communities (EVs are movable to different communities)	PV, buildings, EVs (both G2V and V2G)	Win-Win situation for every entity, reduce cost, lower peak energy, fill valleys, and decrease PAR

concludes and compares the main related works in the energy sharing field.

3. System Model

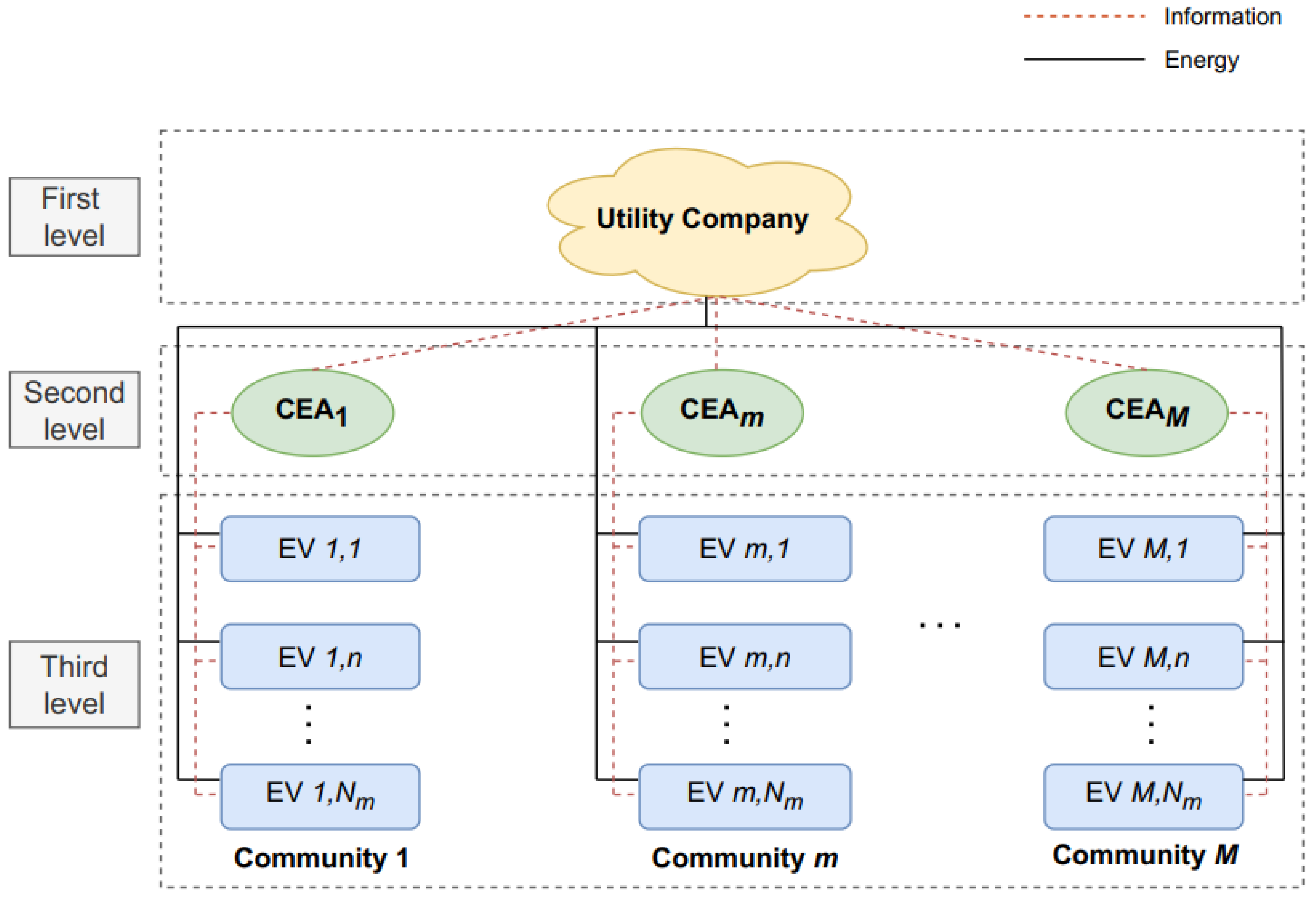
3.1. Overview Structure

Figure 1 illustrates the system model for energy sharing among multiple communities, which includes a single utility company (UC), multiple community energy aggregators (CEA), and multiple EVs within multiple communities. We will briefly explain each entity as follows:

• Electric Vehicle (EV): Each electric vehicle is capable of charging and discharging energy through CEA. We assume that all EVs are equipped with a smart energy management system (SEMS), through which they can communicate with CEA via charging facilities. The SEMS sends consumption data and receives shared price information. It is able to perform necessary computational tasks and control charging and discharging.
• Community Energy Aggregator (CEA): Each CEA facilitates energy sharing within the community by engaging in two-way communication with EVs within its community. It also communicates with UC for the purpose of energy sharing between communities and determines the energy sharing prices within the community. The CEA ensures payment and energy balance for the community in which it sells or buys energy to or from EVs within the community and the utility company. If there is a net surplus of energy within the community, the CEA is responsible for selling the excess energy to the utility company. Similarly, if the generated energy within the community is insufficient, the CEA is responsible for purchasing the energy from the utility company.
• Utility Company (UC): The UC sells or buys energy to or from CEAs at real-time pricing according to the net aggregated energy from the multiple communities.

The proposed energy sharing management model consists of three hierarchical levels: UC level, CEA level, and electric vehicle level. Firstly, at the upper level, the UC supplies/buys electricity to/from the multi-communities system. The price between the UC and multiple CEAs is called the “multi-communities sharing price”. The UC tries to maximize profit by setting the optimal multi-communities sharing price ($p_{uc}^t$), which is related to the amount of net energy in the multi-communities system at a given time slot. Secondly, at the middle level, CEAs act as intermediaries who buy/sell energy from/to the UC and also buy/sell energy from/to EVs within their community. The CEAs try to maximize their profit by setting the optimal sharing price within their own community ($p_{CEA,m}^t$), considering the amount of net energy of the community and the multi-communities sharing price from the upper level. Finally, at the bottom level, each EV within the community determines its optimal charging/discharging energy in response to the energy sharing prices from its CEA to maximize its own utility.

Let $\mathcal{M}=1,2,\dots ,M$ represent the set of communities and their corresponding CEAs, where each community $m\in \mathcal{M}$ is associated with a single CEA. Additionally, let ${\mathcal{N}}_m^t=1,2,\dots ,N$ denote the set of EVs within a specific community, with $n\in {\mathcal{N}}_m^t$. The set of all EVs in the system is represented by $\mathcal{K}$. The time operation in one day is divided into T time slots, where $t\in \mathcal{T}=1,2,\dots ,T$. For simplicity, we consider each t to represent 1 h, and thus, $T=24$.

3.2. Electric Vehicle (EV) Model

Let $x_{m,n}^t$ denote the charging/discharging energy of the $m,n$-th EV. When $x_{m,n}^t\ge 0$, the $m,n$-th EV is charging. However, the EV will discharge when $x_{m,n}^t<0$. Let $p_{CEA,m}^t$ be the energy sharing price inside community m, which is sent from CEA $m\in \mathcal{M}$. In this model, the utility function of an EV consists of increase of satisfaction function and cost/revenue from energy sharing. The goal of each $m,n$-th EV is to maximize its own utility as follows:

$$\underset{x_{m,n}^t}{max}{U}_{m,n}^t=\psi (E_{m,n}^t+x_{m,n}^t)-\psi \left(E_{m,n}^t\right)-p_{CEA,m}^t{x}_{m,n}^t$$

(1)

$$s.t.x_{m,n}^{min,t}\le x_{m,n}^t\le x_{m,n}^{max,t}$$

(2)

where $E_{m,n}^t$ denotes the remaining energy in the EV available for use at time t before a decision is made to charge or discharge. It is defined as $E_{m,n}^t=E{S}_{m,n}^t-E{S}_{min}$, where $E_{m,n}^t$ represents the energy stored in the battery in kilowatt-hours (kWh) and $E{S}_{min}$ indicates the minimum required energy stored in the battery, also measured in kWh. The first term, $\psi \left(E_{m,n}^t\right)$, represents the satisfaction value of having $E_{m,n}^t+x_{m,n}^t$ stored energy after charging for $x_{m,n}^t$. The second term also represents a satisfaction value, but it is the original satisfaction before deciding on the amount of energy. The satisfaction cost should be an increasing function with decreasing marginal profit. In this study, we employ a quadratic satisfaction function, which is extensively utilized in previous studies [10,27,28]:

$$\psi \left(E_{m,n}^t\right)={\lambda }_{m,n}{E}_{m,n}^t-{\displaystyle \frac{{\theta }_{m,n}}{2}}{\left(E_{m,n}^t\right)}^2$$

(3)

where ${\lambda }_{m,n}>0$ is the preference parameter of the $m,n$-th EV, which distinguishes the EV from other EVs, and ${\theta }_{m,n}>0$ is a predetermined constant. The EV with a higher value of ${\lambda }_{m,n}$ will obtain more satisfaction compared to the EV with a lower value of ${\lambda }_{m,n}$ for the same amount of $E_{m,n}^t$.

The third term, $-p_{CEA,m}^t{x}_{m,n}^t$, represents the energy sharing term, which denotes the cost/revenue from buying/selling energy from/to CEA m. If the EV is charging, this term will be negative, indicating the cost of charging. If the EV is discharging, this term will be positive, indicating the revenue from discharging. From Equation (1), if $x_{m,n}^t$ is positive and increases, the satisfaction function will increase. However, the cost of charging will also increase. Hence, there is a trade-off between the satisfaction function and the cost/revenue from energy sharing, and thus, the EV needs to adjust the charging/discharging energy to maximize utility. When CEA m sends the sharing price $p_{CEA,m}^t$ to EVs, the EVs will adjust their charging/discharging energy $x_{m,n}^t$ in response to $p_{CEA,m}^t$ from CEA m to maximize utility, which results in a change in the net energy of the system. If $p_{CEA,m}^t$ is high, the discharging EVs tend to increase their discharged energy to maximize their utility by selling more energy. In contrast, if $p_{CEA,m}^t$ decreases, the discharging EVs will discharge less or instead charge some energy to increase utility instead of selling the energy at a low price.

Constraint (2) provides the lower and upper limits of the $m,n$-th EV’s charging/discharging at time slot t.

3.3. Community Energy Aggregator (CEA) Model

The CEAs at the middle level of the multi-communities system facilitate energy sharing by connecting with both EVs at the lower level for inside-community energy sharing and the UC at the upper level for multi-communities energy sharing. If there is a net surplus of energy inside community m, CEA m is responsible for selling the surplus energy to the UC. Likewise, if the generated energy inside community m is not sufficient, CEA m is responsible for buying the deficit energy from the UC. CEA $m\in \mathcal{M}$ aims to maximize its utility by selecting the optimal energy sharing price $p_{CEA,m}^t$ inside community m, considering the multi-communities sharing price $p_{uc}^t$ from the UC and the aggregated net energy inside community $D_{CEA,m}^t$, which can be written as follows:

$$\underset{p_{CEA,m}^t}{max}{U}_{CEA,m}^t=(p_{CEA,m}^t-p_{uc}^t)D_{CEA,m}^t$$

(4)

$$s.t.p_{CEA,m}^{min}\le p_{CEA,m}^t\le p_{CEA,m}^{max}$$

(5)

Constraint (5) provides the lower and upper limits of the sharing price within community m at time slot t. The aggregated net energy within a community can be computed as:

$$\begin{array}{c}\hfill D_{CEA,m}^t=E_{CEA,m}^t+L_m^t\end{array}$$

(6)

where $L_m^t$ is the fixed demand of community m at time t, and $E_{CEA,m}^t$ is the net energy from EV charging and discharging in community m at time t, given by:

$$E_{CEA,m}^t=\sum _{n\in {\mathcal{N}}_m^t}{x}_{m,n}^t$$

(7)

Note that, in the model, both charging and discharging EVs receive the same unit price $p_{CEA,m}^t$ for selling and buying energy, as the CEAs and UC focus on maximizing their own benefits when issuing the sharing prices. This might contrast with other studies, particularly those proposing a two-level game, where a fixed time-of-use (ToU) price is often assumed for the UC to purchase additional energy from suppliers, generators, or markets. In such cases, the buying and selling prices differ, with the buying price being higher due to the need to acquire additional energy externally, and the UC might also not be considered as an active player in the game, unlike this work.

3.4. Utility Company (UC) Model

The UC, located at the upper level, buys and sells energy with multiple CEAs in the middle level. The objective of the UC is to maximize the profit of selling energy to the multi-communities system by setting the optimal multi-communities sharing price $p_{uc}^t$. The objective function is composed of two parts: the revenue from selling the net aggregated energy $D_{uc}^t$ and the cost of generating that amount of energy ($C_{gen}^t\left(D_{uc}^t\right)$):

$$\underset{p_{uc}^t}{max}{U}_{uc}^t=p_{uc}^t{D}_{uc}^t-C_{gen}^t\left(D_{uc}^t\right)$$

(8)

$$s.t.p_{uc}^{min}\le p_{uc}^t\le p_{uc}^{max}$$

(9)

The generation cost $C_{gen}^t\left(D_{uc}^t\right)$ is generally assumed to be a monotonically increasing function of the amount of generated energy $D_{uc}^t$ and is strictly convex [27,29,30]. The quadratic cost function is widely utilized in the literature [27,28,29,31]. Therefore, we also use it in this work, where it can be formulated as follows:

$$C_{gen}^t\left(D_{uc}^t\right)=a{\left(D_{uc}^t\right)}^2+b{D}_{uc}^t+c$$

(10)

where a, b, and c denote the generation cost function’s coefficients.

Constraint (9) provides the lower and upper limits of the multi-communities sharing price $p_{uc}^t$ at time slot t; the aggregated net energy of the multi-communities system is the summation of the aggregated net energy of each community $m\in \mathcal{M}$:

$$D_{uc}^t=\sum _{m\in \mathcal{M}}{D}_{CEA,m}^t=\sum _{m\in \mathcal{M}}(E_{CEA,m}^t+L_m^t)$$

(11)

4. Hieracrchical Stackelberg Game Among Players

The non-cooperative Stackelberg game simulates situations in which players are arranged in a hierarchical structure. It was originally proposed by Heinrich von Stackelberg [32]. In this game, players are rational, self-interested, and seek to maximize their own utility. Typically, this type of game is applied in a two-level framework with one leader and multiple followers. The leader makes the first move, after which the followers choose their strategies based on the leader’s action. Followers employ the best response strategy to maximize their own payoff. Anticipating the followers’ responses, the leader seeks to choose a strategy that optimizes their utility. The outcome of this game is referred to as the Stackelberg equilibrium. The hierarchical structure of the Stackelberg game is analogous to the structure of electrical systems, particularly the distribution networks we are focusing on. This similarity makes the game particularly suitable for modeling interactions related to energy sharing and trading.

4.1. Game Formulation

This paper adopts a two-loop Stackelberg game to model the three-level multi-communities energy sharing management. This model includes three types of players: UC, CEAs, and EVs. The first loop represents the game between UC and CEAs, while the second loop represents the game between each CEA and its associated EVs within that community. The graphical game-theoretic framework is illustrated in Figure 2.

The operation of each loop is explained below:

(1)

First loop between the top level and middle level

In the first loop, the UC takes the role of the leader, seeking to maximize its utility (8) by determining the optimal multi-communities sharing price for the entire system and announcing it to the CEAs. This involves a trade-off between the revenue from selling the generated energy and the cost of producing the energy in the UC’s utility model. The followers in this loop are the CEAs of communities $m\in \mathcal{M}$, where each CEA responds to the multi-communities sharing price set by the UC by participating in the second loop game with the EVs. The CEA issues its community energy-sharing price to the EVs within its community, and once the EVs respond with their energy usage, the CEAs calculate the net aggregated community energy for each community and send it back to the UC level. Consequently, the multi-communities sharing price set by UC will influence the total aggregated energy in the system that UC needs to accommodate.

(2)

Second loop between the middle level and bottom level

The second loop is the game between the CEA and its EVs within the community. In this loop, after each CEA receives the multi-communities sharing price from the UC, each CEA m takes on the leader role and determines the optimal community sharing price for its community m to maximize its utility (4). In the CEA’s utility model, there is a trade-off between the revenue/cost from selling/buying energy with EVs inside the community and the payment/revenue from buying/selling the net aggregated community energy with the UC. The EVs $m,n$ within community m, who are the followers, respond to the community sharing price sent by CEA m by adjusting their energy strategy, specifically the amount of charging or discharging energy, to maximize their utility (1). Again, this involves a trade-off between the satisfaction function and the revenue/cost of selling/buying energy with CEA m.

Note that CEAs play two roles in the three-level Stackelberg game, acting as followers in the upper loop and leaders in the lower loop.

For this hierarchical Stackelberg game, the solution for the game that is the Stackelberg equilibrium is defined as follows.

Definition 1.

In the proposed three-level Stackelberg game, a strategy set (${\mathit{x}}^{\mathit{t}*},{\mathit{p}}_{\mathit{CEA}}^{\mathit{t}*},p_{uc}^{t*}$) achieves Stackelberg equilibrium if and only if the following conditions are met:

$$U_{m,n}^t({\mathit{x}}_{\mathit{m}}^{\mathit{t}*},p_{CEA,m}^{t*})\ge U_{m,n}^t(x_{m,n}^t,{\mathit{x}}_{-\mathit{m},\mathbf{n}}^{\mathit{t}*},p_{CEA,m}^{t*})$$

(12)

$$U_{CEA,m}^t({\mathit{x}}_{\mathit{m}}^{\mathit{t}*},p_{CEA,m}^{t*},p_{uc}^{t*})\ge U_{CEA,m}^t({\mathit{x}}_{\mathit{m}}^{\mathit{t}*},p_{CEA,m}^t,p_{uc}^{t*})$$

(13)

$$U_{uc}^t({\mathit{x}}^{\mathit{t}*},{\mathit{p}}_{\mathit{CEA}}^{\mathit{t}*},p_{uc}^{t*})\ge U_{uc}^t({\mathit{x}}^{\mathit{t}*},{\mathit{p}}_{\mathit{CEA}}^{\mathit{t}*},p_{uc}^t)$$

(14)

where ${\mathit{x}}_{-\mathit{m},\mathbf{n}}^{\mathit{t}*}=\{x_{m,1}^{t*},x_{m,2}^{t*},\dots ,x_{m,n-1}^{t*},x_{m,n+1}^{t*},\dots ,x_{m,N}^{t*}\}$ represents the optimal strategies of all EVs in community m during time slot t, excluding EV $m,n$. Consequently, the optimal strategies for all EVs in community m during time slot t can be expressed as ${\mathit{x}}_{\mathit{m}}^{\mathit{t}*}=\{x_{m,n}^{t*},{\mathit{x}}_{-\mathit{m},\mathbf{n}}^{\mathit{t}*}\}$. ${\mathit{x}}^{\mathit{t}*}=\{{\mathit{x}}_{\mathbf{1}}^{\mathit{t}*},{\mathit{x}}_{\mathbf{2}}^{\mathit{t}*},\dots ,{\mathit{x}}_{\mathit{m}}^{\mathit{t}*}\}$ denotes the set of the optimal strategies of all EVs in the multi-communities system. Lastly, ${\mathit{p}}_{\mathit{CEA}}^{\mathit{t}*}=\{p_{CEA,1}^{t*},p_{CEA,2}^{t*},\dots ,p_{CEA,M}^{t*}\}$ is the set of optimal strategies of all CEAs.

Equations (12)–(14) imply that at the Stackelberg equilibrium, no EV can improve its utility by altering its strategy from $x_{m,n}^{t*}$, no CEA can enhance their utility by adopting a strategy other than $p_{CEA,m}^{t*}$, and the UC cannot improve their utility by choosing a strategy other than $p_{uc}^{t*}$.

4.2. Existence and Uniqueness of the Equilibrium

In a Stackelberg game, the existence of an equilibrium in pure strategies is not always assured. Therefore, it is necessary to verify whether a Stackelberg equilibrium exists in the proposed game. To address this, a theorem and its corresponding proof are presented in this section for clarification.

Theorem 1.

A unique Stackelberg equilibrium exists in the proposed three-level Stackelberg game among UC, CEAs, and EVs, which satisfies (12)–(14).

Proof 

Considering that the proposed game model has a hierarchical structure, backward induction is an effective approach to derive the equilibrium of the game. This method is ideal for hierarchical game-theoretic models, especially three-level games, as it aligns naturally with their sequential and layered decision-making structure. By solving the game starting from the lowest level, it ensures that each decision maker optimizes their strategy based on the anticipated actions of others, cascading rational strategies upwards. Backward induction simplifies the complexity of multi-level interactions by breaking the problem into manageable subgames, enabling the determination of optimal responses at each level. Moreover, it guarantees the existence and stability of equilibrium outcomes, making it particularly well-suited for applications such as energy management and demand response mechanisms, where decisions at each level significantly impact the overall system.

In this work, the proof begins at the first level by determining the optimal energy consumption ($x_{m,n}^{t*}$) for each EV, which serves as the best response to the CEA’s strategy ($p_{CEA,m}^t$) at the second level. Based on the best response of each EV, the process then traces back to identify the optimal sharing price ($p_{CEA,m}^{t*}$) within community m, representing the best strategy for each CEA. Lastly, at the final step, given the information from all CEAs, the best strategy of UC that is the multi-communities sharing price ($p_{uc}^{t*}$) will be found. The mathematical proof is provided below.

(1) First level: optimal energy consumption of EVs

With the community sharing price $p_{CEA,m}^t$ provided by CEA m at the second level, the optimal response strategy for each EV $m,n$ at the first level can be determined by deriving the first-order derivative of $U_{m,n}^t$, as defined in (1), with respect to $x_{m,n}^t$:

$${\displaystyle \frac{\partial U_{m,n}^t}{\partial x_{m,n}^t}}={\lambda }_{m,n}-{\theta }_{m,n}(E_{m,n}^t+x_{m,n}^t)-p_{CEA,m}^t$$

(15)

By setting (15) equal to zero, the optimal energy consumption for EV $m,n$, which maximizes its utility function, can be determined as follows:

$$x_{m,n}^t={\displaystyle \frac{{\lambda }_{m,n}-p_{CEA,m}^t}{{\theta }_{m,n}}}-E_{m,n}^t$$

(16)

From (16), we can see that the optimal energy consumption of $m,n$-th EV depends on the strategy of CEA m that is the community sharing price $p_{CEA,m}^t$. The second-order derivative of $U_{m,n}^t$ can be expressed as:

$${\displaystyle \frac{{\partial }^2{U}_{m,n}^t}{\partial {x_{m,n}^t}^2}}=-{\theta }_{m,n}<0$$

(17)

As the second-order derivative of $U_{m,n}^t$ is always negative, as indicated in (17) due to ${\theta }_{m,n}>0$, this confirms that $U_{m,n}^t$ is strictly concave with respect to $x_{m,n}^t$. As a result, the best response strategy for EV $m,n$, as defined in (16), is assured to be unique and optimal.

(2) Second level: optimal community sharing price of CEA

Using the best-response strategy of EVs derived from the first level in (16), the utility function of CEA m can be reformulated by substituting the optimal energy consumption from (16) into (4). Therefore, $U_{CEA,m}^t$ can be reformulated as:

$$\begin{array}{cc}\hfill U_{CEA,m}^t& =(p_{CEA,m}^t-p_{uc}^t)(\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{{\lambda }_{m,n}-p_{CEA,m}^t}{{\theta }_{m,n}}}-\sum _{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t+L_m^t)\hfill \\ & =-{\left(p_{CEA,m}^t\right)}^2\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{1}{{\theta }_{m,n}}}+p_{CEA,m}^t(\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}-\sum _{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t+p_{uc}^t\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{1}{{\theta }_{m,n}}}\hfill \\ & +L_m^t)+p_{uc}^t(\sum _{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t-\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}-L_m^t)\hfill \end{array}$$

(18)

The optimal response strategy for each CEA m at the second level is determined by deriving the first-order derivative of $U_{CEA,m}^t$ in (18) with respect to $p_{CEA,m}^t$:

$${\displaystyle \frac{\partial U_{CEA,m}^t}{\partial p_{CEA,m}^t}}=-2p_{CEA,m}^t\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{1}{{\theta }_{m,n}}}+\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}-\sum _{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t+p_{uc}^t\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{1}{{\theta }_{m,n}}}+L_m^t$$

(19)

Setting (19) to zero allows for calculating the optimal community sharing price for CEA m, which maximizes its utility function, as shown below:

$$p_{CEA,m}^{t*}={\displaystyle \frac{1}{2}}{p}_{uc}^t+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\sum }_{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{L_m^t}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}}$$

(20)

From (20), we can make some observations that the optimal community price ($p_{CEA,m}^{t*}$) consists of four terms. The first term tells that the community sharing price depends on the multi-communities sharing price from UC ($p_{uc}^t$). The second term says that the parameter of each EV also affects the community sharing price. Furthermore, the third term reveal that, if the community has high stored energy in EVs, the community sharing price will be low. Furthermore, finally, the fourth term indicates that if the fixed load demand is high, the $p_{CEA,m}^{t*}$ will also be high, aligning with reality. Hence, this shows that each CEA m acts as a representative of community m for participating in the multi-communities energy sharing.

The second-order derivative of $U_{CEA,m}^t$ with respect to $p_{CEA,m}^{t*}$ is derived as:

$${\displaystyle \frac{{\partial }^2{U}_{CEA,m}^t}{\partial {p_{CEA,m}^t}^2}}=-2\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{1}{{\theta }_{m,n}}}<0$$

(21)

Given that ${\theta }_{m,n}>0$, the second-order derivative of $U_{m,n}^t$ is always negative, as shown in (21). This implies that $U_{CEA,m}^t$ is strictly concave with respect to $p_{CEA,m}^t$. Consequently, the best response strategy of CEA m, as expressed in (20), is guaranteed to be both unique and optimal.

(3) Third level: optimal multi-communities sharing price of UC

Now, we have obtained the best response function of EVs and CEAs in (16) and (20) which can be used to find the best response strategy of UC. First, from the best-response strategy of CEA m that we derived in the second level, we can substitute (20) into the EV’s best-response function (16) in order to find optimal energy consumption $x_{m,n}^{t*}$ of each $m,n$-th EV given the optimal sharing price of CEA m as:

$$\begin{array}{cc}\hfill x_{m,n}^{t*}& ={\displaystyle \frac{{\lambda }_{m,n}-\frac{1}{2}{p}_{uc}^t-\frac{1}{2}\frac{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}+\frac{1}{2}\frac{{\sum }_{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}+\frac{1}{2}\frac{L_m^t}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}}{{\theta }_{m,n}}}-E_{m,n}^t\hfill \\ & =-{\displaystyle \frac{1}{2}}{\displaystyle \frac{p_{uc}^t}{{\theta }_{m,n}}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}}{\displaystyle \frac{1}{{\theta }_{m,n}}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\sum }_{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}}{\displaystyle \frac{1}{{\theta }_{m,n}}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{L_m^t}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}}{\displaystyle \frac{1}{{\theta }_{m,n}}}\hfill \\ & +{\displaystyle \frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}+E_{m,n}^t\hfill \end{array}$$

(22)

Then, the aggregated net energy of EVs in community m can be obtained by substituting (22) into (7) as:

$$\begin{array}{cc}\hfill E_{CEA,m}^{t*}& =\sum _{n\in {\mathcal{N}}_m^t}{x}_{m,n}^{t*}\hfill \\ & =-{\displaystyle \frac{1}{2}}{p}_{uc}^t\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{1}{{\theta }_{m,n}}}-{\displaystyle \frac{1}{2}}[\sum _{n\in {\mathcal{N}}_m^t}(\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}{\displaystyle \frac{1}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}}{\displaystyle \frac{1}{{\theta }_{m,n}}})]\hfill \\ & +{\displaystyle \frac{1}{2}}[\sum _{n\in {\mathcal{N}}_m^t}(\sum _{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t{\displaystyle \frac{1}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}}{\displaystyle \frac{1}{{\theta }_{m,n}}})]-{\displaystyle \frac{1}{2}}[\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{L_m^t}{{\sum }_{n\in {\mathcal{N}}_m^t}\frac{1}{{\theta }_{m,n}}}}{\displaystyle \frac{1}{{\theta }_{m,n}}}]\hfill \\ & +\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}-\sum _{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t\hfill \\ & =-{\displaystyle \frac{1}{2}}{p}_{uc}^t\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{1}{{\theta }_{m,n}}}+{\displaystyle \frac{1}{2}}\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}-{\displaystyle \frac{1}{2}}\sum _{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t-{\displaystyle \frac{1}{2}}{L}_m^t\hfill \end{array}$$

(23)

After that, the total aggregated net energy of the entire multi-communities system can be calculated by summarizing all net energy of community $m\in \mathcal{M}$ as:

$$\begin{array}{cc}\hfill D_{uc}^t& =\sum _{m\in \mathcal{M}}{D}_{CEA,m}^{t*}\hfill \\ & =\sum _{m\in \mathcal{M}}(E_{CEA,m}^{t*}+L_m^t)\hfill \\ & =-{\displaystyle \frac{1}{2}}{p}_{uc}^t\sum _{m\in \mathcal{M}}\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{1}{{\theta }_{m,n}}}+{\displaystyle \frac{1}{2}}\sum _{m\in \mathcal{M}}\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}-{\displaystyle \frac{1}{2}}\sum _{m\in \mathcal{M}}\sum _{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t+{\displaystyle \frac{1}{2}}\sum _{m\in \mathcal{M}}{L}_m^t\hfill \end{array}$$

(24)

where we define new parameters at time slot t for the summation parts in (24) as $\alpha$, ${\beta }^t$, and ${\gamma }^t$:

$${\alpha }^t=\sum _{m\in \mathcal{M}}\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{1}{{\theta }_{m,n}}}$$

(25)

$${\beta }^t=\sum _{m\in \mathcal{M}}\sum _{n\in {\mathcal{N}}_m^t}{\displaystyle \frac{{\lambda }_{m,n}}{{\theta }_{m,n}}}$$

(26)

$${\gamma }^t=\sum _{m\in \mathcal{M}}\sum _{n\in {\mathcal{N}}_m^t}{E}_{m,n}^t$$

(27)

$${\delta }^t=\sum _{m\in \mathcal{M}}{L}_m^t$$

(28)

Hence, (24) can be rewritten as:

$$D_{uc}^t=-{\displaystyle \frac{1}{2}}{p}_{uc}^t{\alpha }^t+{\displaystyle \frac{1}{2}}{\beta }^t-{\displaystyle \frac{1}{2}}{\gamma }^t+{\displaystyle \frac{1}{2}}{\delta }^t$$

(29)

By substituting (29) and (10) into (8), the original utility function of UC can be reformulated as:

$$\begin{array}{cc}\hfill U_{uc}^t& =p_{uc}^t(-{\displaystyle \frac{p_{uc}^t}{2}}\alpha +{\displaystyle \frac{1}{2}}{\beta }^t-{\displaystyle \frac{1}{2}}{\gamma }^t+{\displaystyle \frac{1}{2}}{\delta }^t)-a{(-{\displaystyle \frac{p_{uc}^t}{2}}\alpha +{\displaystyle \frac{1}{2}}{\beta }^t-{\displaystyle \frac{1}{2}}{\gamma }^t+{\displaystyle \frac{1}{2}}{\delta }^t)}^2\hfill \\ & -b(-{\displaystyle \frac{p_{uc}^t}{2}}\alpha +{\displaystyle \frac{1}{2}}{\beta }^t-{\displaystyle \frac{1}{2}}{\gamma }^t+{\displaystyle \frac{1}{2}}{\delta }^t)-c\hfill \\ & =-a{(-{\displaystyle \frac{p_{uc}^t}{2}}\alpha +{\displaystyle \frac{1}{2}}{\beta }^t-{\displaystyle \frac{1}{2}}{\gamma }^t+{\displaystyle \frac{1}{2}}{\delta }^t)}^2-b(-{\displaystyle \frac{p_{uc}^t}{2}}\alpha +{\displaystyle \frac{1}{2}}{\beta }^t-{\displaystyle \frac{1}{2}}{\gamma }^t+{\displaystyle \frac{1}{2}}{\delta }^t)\hfill \\ & -{\displaystyle \frac{{\left(p_{uc}^t\right)}^2}{2}}\alpha +{\displaystyle \frac{p_{uc}^t}{2}}{\beta }^t-{\displaystyle \frac{p_{uc}^t}{2}}{\gamma }^t+{\displaystyle \frac{p_{uc}^t}{2}}{\delta }^t-c\hfill \end{array}$$

(30)

The optimal response strategy for the UC at the third level is determined by deriving the first-order derivative of $U_{uc}^t$, as expressed in (30), with respect to $p_{uc}^t$ as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial U_{uc}^t}{\partial p_{uc}^t}}& =-2a(-{\displaystyle \frac{\alpha p_{uc}^t}{2}}+{\displaystyle \frac{{\beta }^t}{2}}-{\displaystyle \frac{{\gamma }^t}{2}}+{\displaystyle \frac{1}{2}}{\delta }^t)(-{\displaystyle \frac{\alpha }{2}})+{\displaystyle \frac{b\alpha }{2}}-\alpha p_{uc}^t+{\displaystyle \frac{{\beta }^t}{2}}-{\displaystyle \frac{{\gamma }^t}{2}}+{\displaystyle \frac{1}{2}}{\delta }^t\hfill \\ & =a\alpha ({\displaystyle \frac{{\beta }^t}{2}}-{\displaystyle \frac{{\gamma }^t}{2}}+{\displaystyle \frac{1}{2}}{\delta }^t)-{\displaystyle \frac{a{\alpha }^2}{2}}{p}_{uc}^t-\alpha p_{uc}^t+{\displaystyle \frac{b\alpha }{2}}+{\displaystyle \frac{{\beta }^t}{2}}-{\displaystyle \frac{{\gamma }^t}{2}}+{\displaystyle \frac{1}{2}}{\delta }^t\hfill \\ & =p_{uc}^t(-{\displaystyle \frac{a{\alpha }^2}{2}}-\alpha )+a\alpha ({\displaystyle \frac{{\beta }^t}{2}}-{\displaystyle \frac{{\gamma }^t}{2}}+{\displaystyle \frac{1}{2}}{\delta }^t)+{\displaystyle \frac{b\alpha }{2}}+{\displaystyle \frac{{\beta }^t}{2}}-{\displaystyle \frac{{\gamma }^t}{2}}+{\displaystyle \frac{1}{2}}{\delta }^t\hfill \end{array}$$

(31)

By setting (31) to zero, the optimal multi-communities sharing price for the UC, which maximizes its utility function, can be determined as follows:

$$p_{uc}^{t*}={\displaystyle \frac{a\alpha ({\beta }^t-{\gamma }^t+{\delta }^t)+b\alpha +{\beta }^t-{\gamma }^t+{\delta }^t}{\alpha (a\alpha +2)}}$$

(32)

The second-order derivative of $U_{uc}^t$ with respect to $p_{uc}^{t*}$ is derived as:

$${\displaystyle \frac{{\partial }^2{U}_{uc}^t}{\partial {p_{uc}^t}^2}}=-{\displaystyle \frac{a{\alpha }^2}{2}}-\alpha <0$$

(33)

Given that the values of a and $\alpha$ are positive, the second-order derivative of $U_{uc}^t$ is always negative, as shown in (33). This indicates that $U_{uc}^t$ is strictly concave with respect to $p_{uc}^t$. Therefore, the best-response strategy of the UC, as expressed in (32), is guaranteed to be both unique and optimal.

Based on the above proof, it is clear that once the unique and optimal strategy of the UC ($p_{uc}^{t*}$) is determined, the unique and optimal strategies for all CEAs $m\in \mathcal{M}$ can also be established. Subsequently, the unique and optimal strategy for each EV $m,n$ can be calculated and adjusted accordingly. As a result, the proposed three-level Stackelberg energy sharing management game ensures the existence of a unique Stackelberg equilibrium represented by (${\mathit{x}}^{\mathit{t}*},{\mathit{p}}_{\mathit{CEA}}^{\mathit{t}*},p_{uc}^{t*}$).    □

4.3. Three-Level Optimal Energy–Price (3OEP) Equilibrium Algorithm

In the previous subsection, the analytical solution is obtained in a centralized way in order to prove that the proposed three-level Stackelberg game always has a unique and optimal solution, in which we assume that the UC has the private parameters of all the EVs. However, such an approach is not desirable in which all EVs have to reveal their private preferences to UC. Therefore, we design an algorithm in a distributed manner to obtain the approximate solution.

As established in the previous subsection, the objective function of the UC is strictly convex with respect to $p_{uc}^t$. Consequently, in the context of a leader–follower game, finding the Stackelberg equilibrium requires determining the leader’s optimal strategy. This can be achieved by enumerating the leader’s strategy, $p_{uc}^t$, over the range from $p_{uc,min}^t$ to $p_{uc,max}^t$. The optimal solution is the one that maximizes the UC’s utility. Once the optimal multi-communities sharing price $p_{uc}^{t*}$ is determined, the corresponding optimal sharing prices $p_{CEA,m}^{t*}$ for all $m\in \mathcal{M}$, as well as the optimal energy consumption for the $m,n$-th EV, $x_{m,n}^{t*}$, are also identified. Thus, the Stackelberg equilibrium strategy profile (${\mathit{x}}^{\mathit{t}*},{\mathit{p}}_{\mathit{CEA}}^{\mathit{t}*},p_{uc}^{t*}$) is found.

In Algorithm 1, we try to find the Stackelberg equilibrium at each time slot t. First, the algorithm is iteratively update $p_{uc}^t$ from $p_{uc,min}^t$ to $p_{uc,max}^t$. At each $p_{uc}^t$, after CEA m recieved broadcasted $p_{uc}^t$ from UC, the CEA m will calculate the optimal sharing price ($p_{CEA,m}^t$), responding to $p_{uc}^t$ by (20) and then announce it to EVs inside its community m. Each EV $m,n$ further calculates the optimal energy consumption ($x_{m,n}^t$) that maximizes their utility given the $p_{CEA,m}^t$ by (16) and send this information back to CEA m. Then, CEA will gather the optimal energy consumption from EVs inside its community m and fix load demand $L_m^t$ of its community m and calculate the aggregated net energy in the community ($D_{CEA,m}^t$) using (6), then further send it back to the UC. The UC summarizes all aggregated net energy from all communities $m\in \mathcal{M}$ using (11) and use it to calculate the value of the UC’s utility function using (8). Finally, the UC compares the value of newly calculated utility with the recorded utility, and if the new one is higher, the UC updates the recorded utility value $U_{uc}^{t*}$ and $p_{uc}^{t*}$ of that utility value. If the newly calculated price and utility value are not higher, the UC disregards them. The algorithm continues to iterate until the conditions specified in (12)–(14) are fulfilled, indicating that the Stackelberg equilibrium has been reached.

Algorithm 1: Three-Level Optimal Energy–Price (3OEP) Equilibrium Algorithm

1: UC initialize ${\mathit{U}}_{\mathit{uc}}^{*}=0,{\mathit{p}}_{\mathit{uc}}^{*}=0$ 2: for$t=1$ to $\mathcal{T}$ do 3:     for $p_{uc}^t$ from $p_{uc}^{min,t}$ to $p_{uc}^{max,t}$ do 4:           Broadcast $p_{uc}^t$ to all CEAs in multi-communities system 5:           for each CEA $m\in \mathcal{M}$ do 6:                 Calculates the optimal community sharing price ($p_{CEA,m}^t$) using (20) 7:                 Announce $p_{CEA,m}^t$ to EVs in community m 8:                 for each EV $n\in {\mathcal{N}}_m^t$ in community m do 9:                     Calculate optimal energy consumption ($x_{m,n}^t$) using (16) 10:                      Send $x_{m,n}^t$ back to CEA m 11:                 end for 12:                 Calculates aggregated net energy in community m ($D_{CEA,m}^t$) using (6) 13:                 Then return $D_{CEA,m}^t$ to UC 14:           end for 15:           UC calculates the total aggregated net energy across all communities using (11) 16:           UC computes the utility function value based on (8) 17:           if $U_{uc}^t\ge U_{uc}^{t*}$ then 18:                 UC record new multi-communities sharing price and utility value 19:                 $p_{uc}^{t*}=p_{uc}^t$, $U_{uc}^{t*}=U_{uc}^t$ 20:           end if 21:     end for 22:     The equilibrium $({\mathit{D}}^{\mathit{t}*},{\mathit{p}}_{\mathit{CEA},\mathit{m}}^{\mathit{t}*},p_{uc}^{t*})$ is achieved when the UC’s utility is maximized 23: end for

5. Evaluation Studies

5.1. Simulation Setup

This section examines the performance of the proposed model, where all players aim to maximize their utility functions. The energy profile is shown Figure 3, illustrating the net energy of each community, already calculated as the difference between demand and PV generation. The data are obtained from the IEEE open data [33], which include three communities. Community 1 is a residential area consisting of 1000 households, Community 2 comprises two shopping malls, and Community 3 is an office area with three office buildings. Given that the average number of cars per household in the U.S. is approximately two [34], a total of 2000 EVs are assumed to move around these three communities. For simulation purposes, we employ two EVs for different sizes of EV battery capacities: the Nissan Leaf, with a 40 kWh battery capacity and an energy consumption rate of 0.16 kWh/km, and the Tesla Model S 70D, with a 75 kWh battery capacity and an energy consumption rate of 0.21 kWh/km. [35]. The EV trip data are sourced from [36,37], which generates synthesized data using information from the actual US National Household Travel Survey [38]. The preference parameter is randomly assigned from the range between 50 and 70, and $\theta$ is set to 2. The State of Charge (SoC) at the beginning of the day is 50%. The minimum and maximum SoC are set to 20% and 90% [39,40], respectively, to prolong battery life. The maximum charging and discharging rate is 7 kW, as this is the typical wall charging rate widely used in residential areas and office buildings. The simulation is implemented in MATLAB R2024a.

Table 2. Example dataset of trips for 10 EVs.

Period	EV1	EV2	EV3	EV4	EV5	EV6	EV7	EV8	EV9	EV10
1
2
3
4
5
6
7	30 C1,3	40 C1,3	50 C1,3
8				30 C1,3	40 C1,3	20 C1,3	30 C1,2	60 C1,2
9									40 C1,2	50 C1,2
10
11
12		10 C3,2,3	10 C3,2,3			5 C3,2
13				10 C3,2,3	10 C3,2,3	5 C2,3
14
15
16	30 C3,1
17		40 C3,1
18			50 C3,1	30 C3,1	40 C3,1	5 C3,2
19							30 C2,1	60 C2,1
20						20 C2,1			40 C2,1	50 C2,1
21
22
23
24

shows an example dataset of trips for 10 EVs, where individuals typically depart from their households between 7 and 9 a.m. and reach their workplace to start working between 8–10 a.m. Those working in shopping malls depart later than those working in offices. About half of the office workers will have lunch near their office and will not use their cars during lunchtime. However, the other half of the office workers choose to go to the shopping mall to have lunch with their colleagues during lunchtime. People working in the office area usually leave work between 4 and 6 p.m. On the other hand, people working in the mall will return home between 7 and 8 p.m. If the cell is blank, it means the EV stays in the same community. However, if there is information in the cell, it means the EV moves from one community to another. For example, “30 C1,3” in slot 7 for EV1 means that EV1 moves from community 1 to community 3 by driving for 30 km during 7 a.m.–8 a.m. So, during that time, EVs will not be able to charge or discharge energy.

Figure 3 show the original energy profile, which includes the net energy profiles of communities 1, 2, and 3, as well as the total energy profile of the entire system.

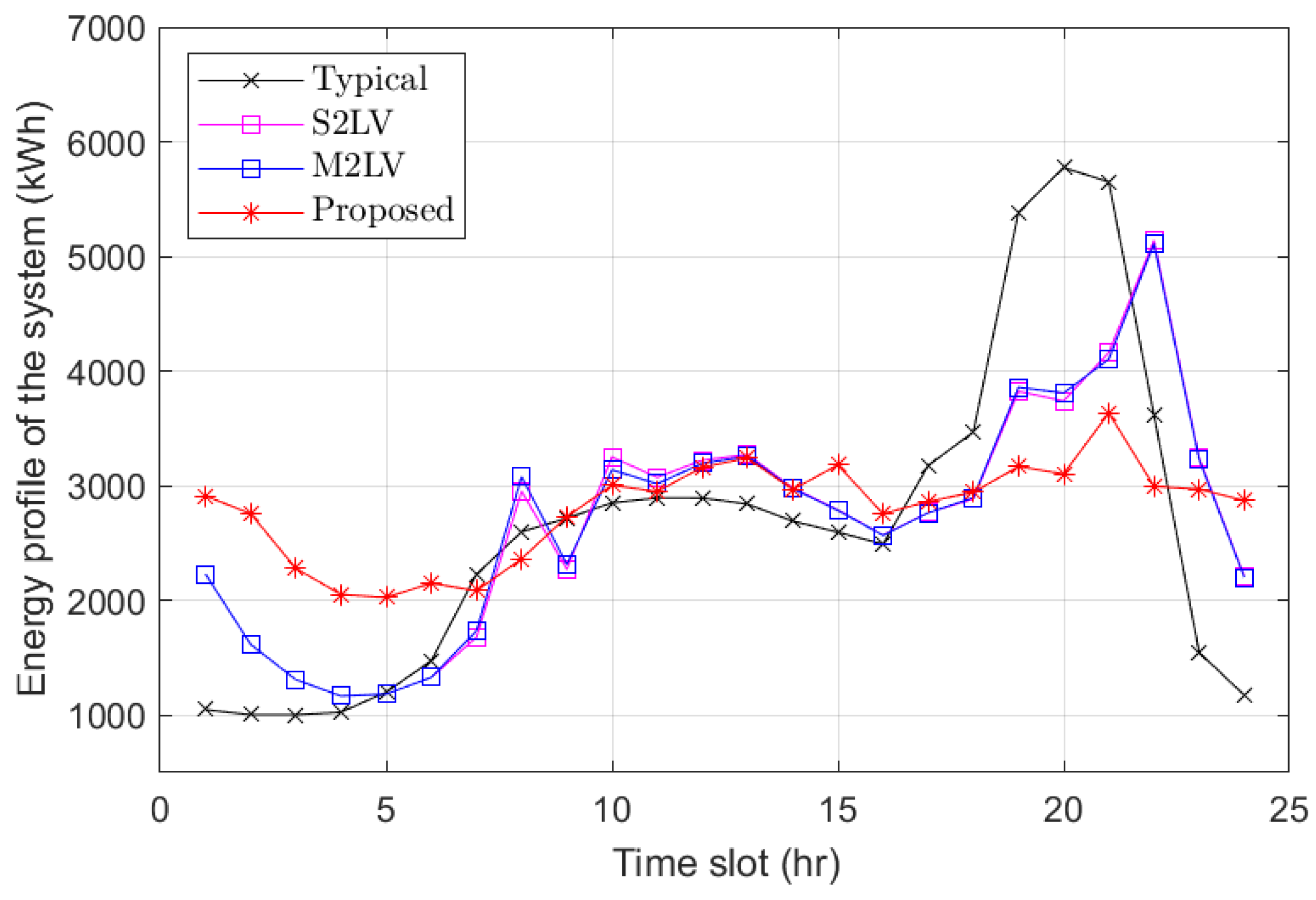
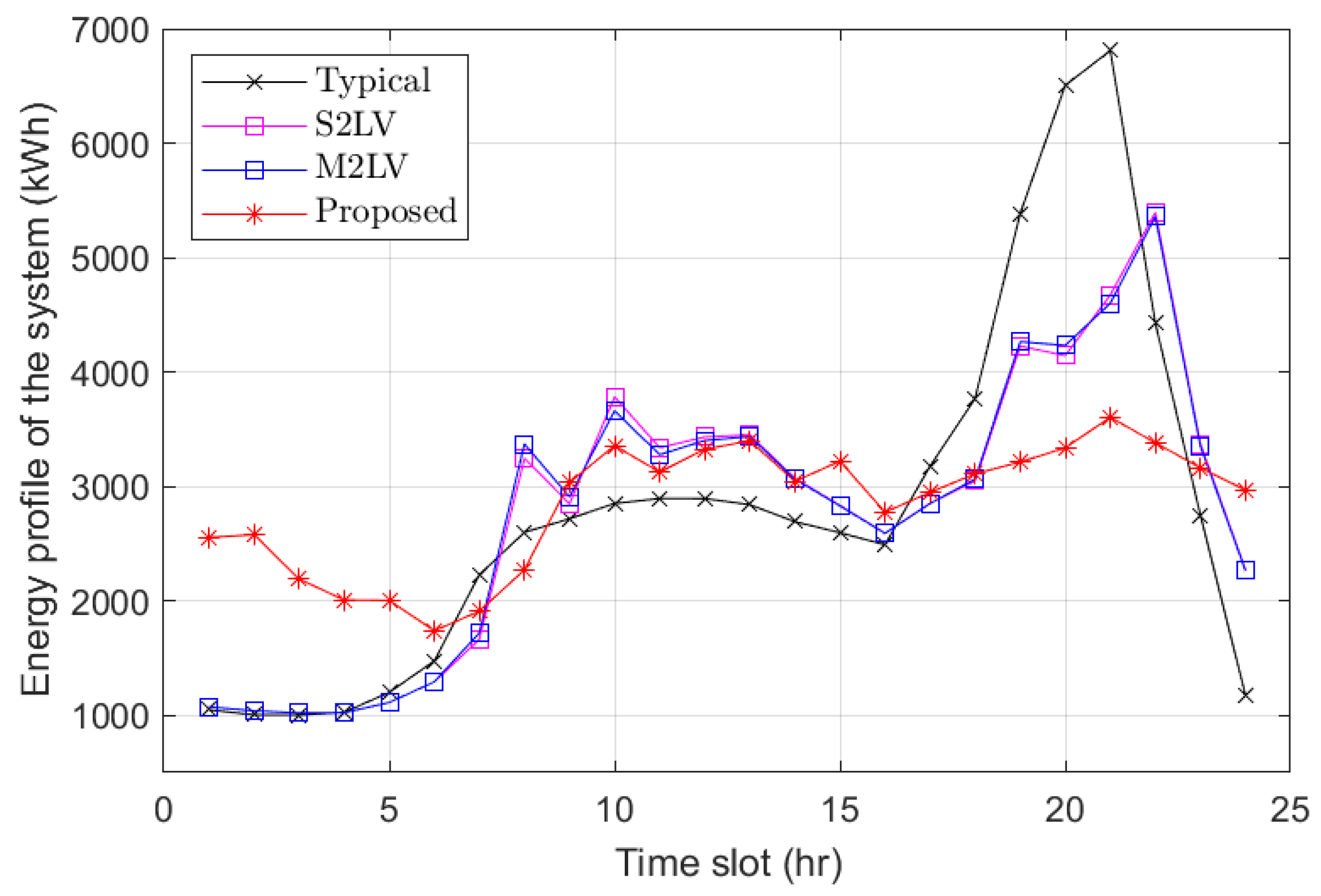
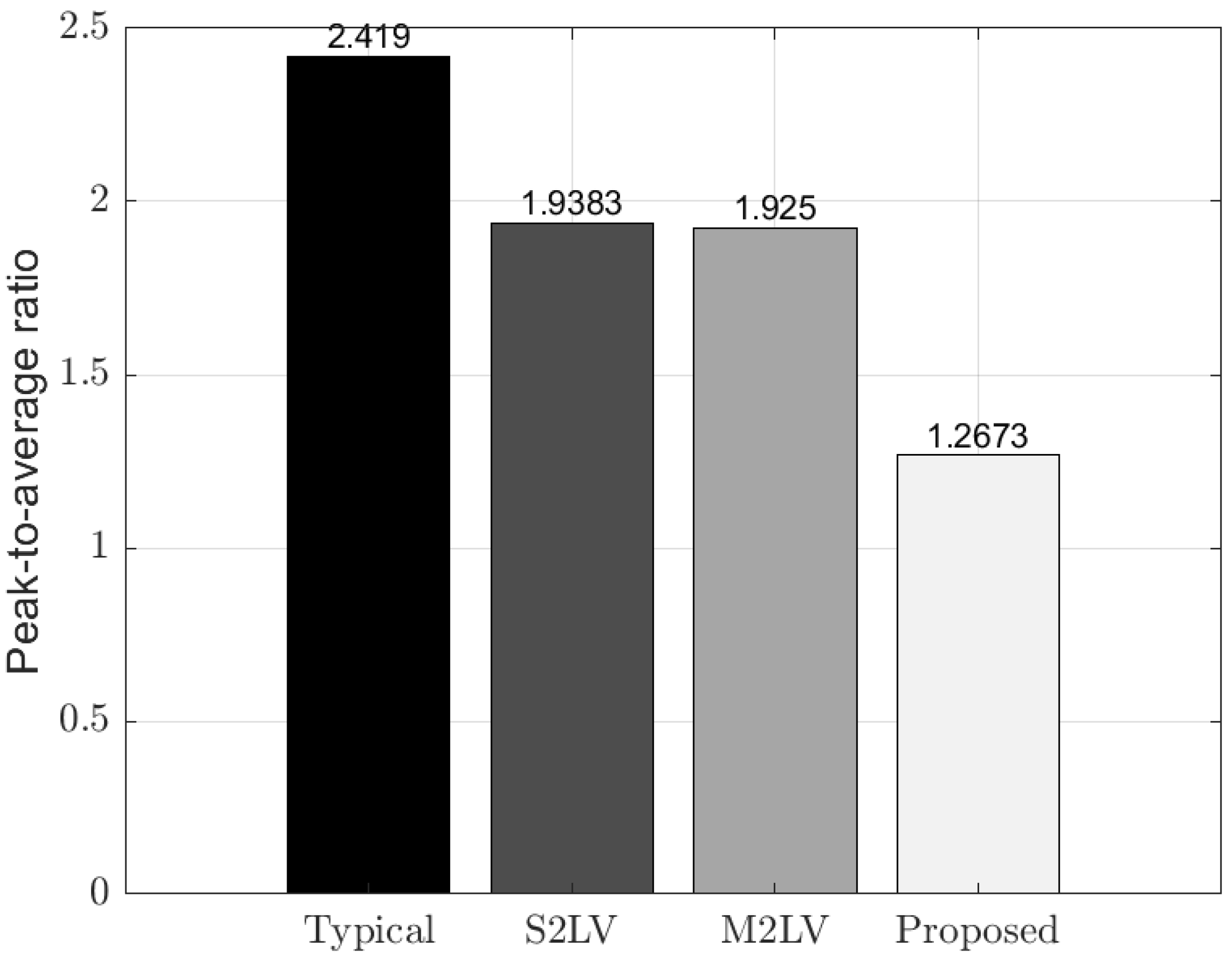
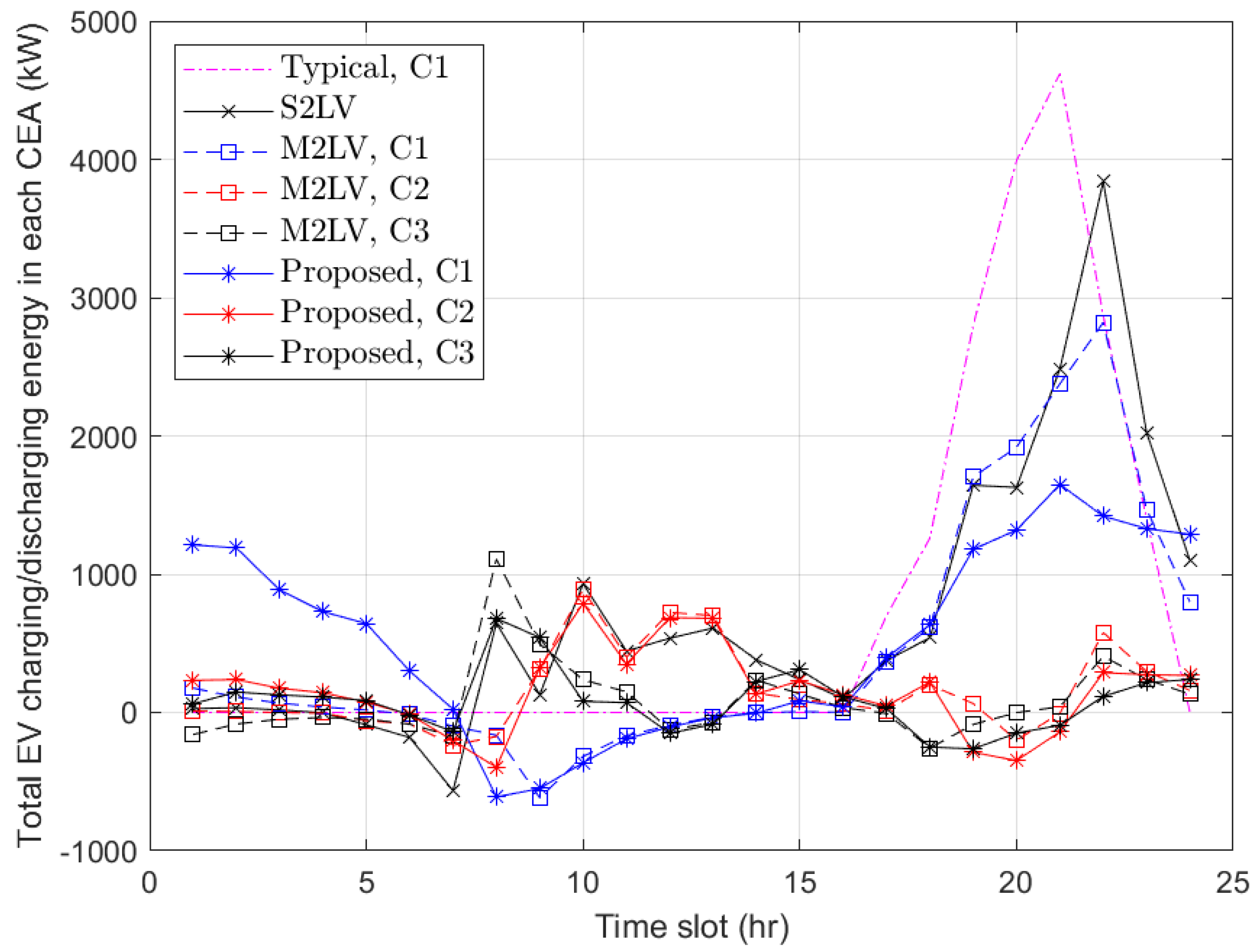
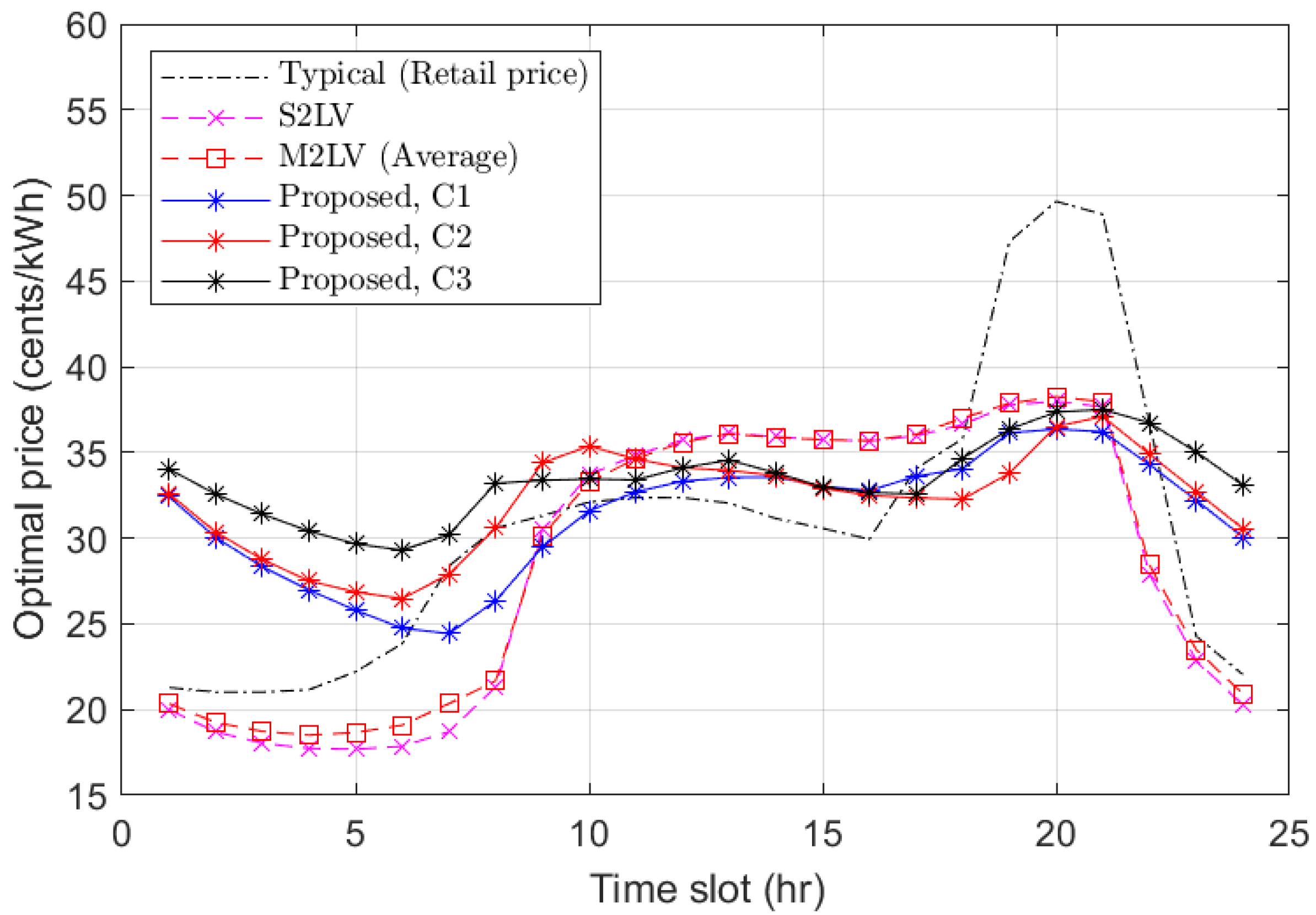
5.2. Results and Discussion

This subsection compares and discusses four scenarios: typical charging, two types of two-level games (S2LV and M2LV), and the proposed three-level optimal energy–price (3OEP) model.

• Typical charging [41]: Individuals charge their EVs upon returning home in the evening, following typical human behavior.
• The single-community two-level Stackelberg game (S2LV) [19]: The two-level Stackelberg game is widely utilized in the literature, where it typically considers the interaction between an aggregator or a coordinator and end-users such as prosumers and EVs. However, the literature often overlooks the benefit model of the UC and frequently assumes pricing based on time-of-use (ToU), where the on-peak period is from 9 a.m. to 10 p.m., and the rest of the time is considered off-peak. This approach is commonly found in the literature, where the system is treated as a single community, and a uniform energy-sharing price is applied across all users.
• The multi-communities two-level Stackelberg game (M2LV) [26]: This scheme employs the commonly used two-level model, but extends it to consider multiple communities. In this approach, the energy profile and pricing differ across communities, reflecting a more realistic representation of real-world scenarios. Typically, different types of consumers with varying load profiles are charged different prices, aligning with the unique characteristics and demands of each community.
• Proposed multi-communities three-level optimal energy–price (3OEP) model: The proposed 3OEP model introduces a three-level framework designed to optimize energy allocation and pricing across multiple communities. Unlike traditional two-level models, this approach incorporates an additional layer to address interactions among the utility company (UC), aggregators (AGGs), and end-users, such as electric vehicles (EVs), within distinct communities. The energy profiles and pricing structures vary across communities, reflecting the unique characteristics and demands of their respective load profiles. EVs capable of moving between different communities engage in charging and discharging at various locations, such as residential areas, offices, and shopping malls. The electricity price varies across these locations, and the amount of charging and discharging is determined by the proposed algorithm.

Figure 4 and Figure 5 depict the total energy profiles for the systems integrated with the 40 kWh Nissan Leaf and 75 kWh Tesla Model S EVs, respectively. The graphs compare energy profiles under different scenarios: typical charging, S2LV, M2LV, and 3OEP model. In the typical charging scenario, a sharp energy peak is observed during the evening when EV owners charge their vehicles after returning home. This uncoordinated behavior creates significant stress on the grid, leading to higher operational inefficiencies. The S2LV and M2LV approaches improve upon this by redistributing charging loads across time slots, reducing peaks. However, they still show noticeable demand variations due to uniform or semi-coordinated pricing mechanisms. The 3OEP model, on the other hand, achieves a much flatter energy profile, efficiently balancing charging during off-peak and peak hours. This is achieved by dynamically coordinating the interactions between EVs, CEAs, and UC, while accounting for differentiated community profiles.

The results further exhibit notable differences due to variations in battery capacity and energy consumption rates of the two vehicle types. The Nissan Leaf, with a smaller battery capacity (40 kWh) and lower energy consumption rate (0.16 kWh/km), shows less energy usage during charging and discharging events compared to the Tesla Model S, which has a larger battery (75 kWh) and a higher consumption rate (0.21 kWh/km). Consequently, the Tesla fleet imposes a higher overall energy demand on the grid, as seen in the relatively higher peaks in the energy profile. However, in both cases, the proposed 3OEP model achieves a flatter energy profile than other methods, with the Tesla EVs system benefiting even more from coordinated management due to its higher energy capacity and greater flexibility in balancing charging and discharging.

Figure 6 and Figure 7 compare the Peak-to-Average Ratio (PAR) across the same scenarios for systems using Nissan Leaf and Tesla Model S EVs. The PAR is a key metric indicating the disparity between peak and average demand. It is calculated by dividing the peak value over a 24-h period by the mean value of that period. A higher PAR indicates that the peak is significantly higher than the mean value, while a lower PAR is more desirable, as it reflects a more balanced load profile. The ideal PAR is 1, which would indicate a perfectly flat load profile over 24 h. However, this is typically unachievable in practice. Therefore, most management strategies aim to minimize the PAR as much as possible.

The typical charging scenario has the highest PAR due to the notable evening peaks. S2LV and M2LV offer moderate improvements, reducing PAR by incorporating uniform and differentiated pricing schemes, respectively. However, the proposed 3OEP model significantly outperforms both, reducing the PAR by 40.7% compared to typical charging and by 31.5% compared to the two-level approaches for the Nissan car. For the Tesla car, the 3OEP model further reduces the PAR by 47.6% compared to typical charging and by 34.4% compared to the two-level approaches. This improvement highlights the model’s effectiveness in flattening the energy profile, leading to reduced peak loads and more efficient grid operation. By dynamically coordinating energy sharing and pricing among communities and leveraging the mobility of EVs, the 3OEP model minimizes fluctuations and ensures optimal load management, making it the most grid-friendly approach among the compared methods.

Furthermore, Figure 6 and Figure 7 show that the Tesla Model S system contributes higher PAR values in all scenarios compared to the Nissan Leaf. This is attributed to Tesla’s larger battery capacity, which amplifies the peak loads during uncoordinated charging periods, especially in the typical charging scenario. However, under the 3OEP model, the PAR reduction is slightly more pronounced for the Tesla fleet, indicating that the model effectively manages higher-capacity EVs. This result highlights the adaptability of the 3OEP framework across diverse EV fleets by leveraging dynamic pricing and multi-level coordination to mitigate peak loads while accommodating the larger energy demands of Tesla vehicles.

Figure 8 and Figure 9 provide insights into the charging and discharging power trends under different energy management methods for Nissan Leaf and Tesla Model S EVs, respectively. In the typical charging scenario, the charging power is concentrated almost exclusively in the evening, reflecting uncoordinated EV behavior where users charge their vehicles upon returning home. This results in sharp peaks in charging power during evening hours, while discharging operations are minimal or absent. Such a pattern increases stress on the grid and fails to utilize the potential of V2G systems to support grid stability. The S2LV and M2LV models show improvements over the typical charging scenario by distributing the charging load more evenly across different hours, particularly during off-peak periods. However, due to the uniform pricing in S2LV and limited inter-community coordination in M2LV, these methods still exhibit localized peaks in charging or discharging power, particularly during periods of high energy demand. The proposed 3OEP model, on the other hand, demonstrates a significant improvement by efficiently balancing charging and discharging across all time slots. The model ensures that EVs charge primarily during off-peak hours and discharge during peak demand, leveraging dynamic pricing and multi-level coordination to maintain a flatter charging and discharging profile throughout the day.

When comparing Figure 8 and Figure 9, Tesla Model S EVs show a more noticeable charging and discharging pattern, with higher peaks in both charging and discharging power compared to Nissan Leaf EVs. This is consistent with Tesla’s larger battery size, which enables it to absorb and release more energy. Despite this difference, the 3OEP model optimally coordinates both EV types.

Figure 10 and Figure 11 present the energy-sharing prices associated with charging and discharging operations for different methods, reflecting the efficiency of pricing strategies in influencing EV behavior. In the typical charging scenario, energy-sharing prices exhibit a significant spike during evening hours, aligning with the uncoordinated charging behavior of EV users. The lack of price differentiation throughout the day results in underutilization of low-demand periods, leading to inefficient energy distribution. This pricing strategy does not provide sufficient incentives for EV owners to adjust their charging and discharging times to align with grid needs. The S2LV and M2LV models show some improvements by incorporating energy-sharing pricing mechanisms. The primary similarity between S2LV and M2LV lies in their pricing mechanism: they neither effectively adjust energy-sharing prices dynamically across communities nor fully account for the interdependence between communities. For instance, both methods experience localized pricing inefficiencies during peak periods, as they cannot redistribute energy or leverage inter-community collaboration. The 3OEP model surpasses S2LV and M2LV by introducing a hierarchical third layer that incorporates the utility company (UC) as a key player in determining energy-sharing prices. Unlike S2LV and M2LV, which treat pricing within individual communities as isolated events, the 3OEP model optimizes prices across the entire system by considering aggregated demand and supply at the community and inter-community levels.

The charging and discharging power pricing trends for Nissan Leaf and Tesla Model S, as shown in Figure 10 and Figure 11, are largely similar. Both vehicle models exhibit price reductions during off-peak hours, such as late at night and early in the morning. Conversely, energy-sharing prices rise slightly during peak hours when discharging operations are utilized to support grid stability. The observed pricing patterns indicate that the hierarchical energy management strategy applies to both EV models, effectively distributing charging and discharging operations to balance the grid. Despite the differences in battery capacity and energy consumption rates between the two EV types, the pricing structures remain comparable across all periods. This is because both Nissan Leaf and Tesla Model S EVs follow the same strategic coordination principles, responding to the pricing signals set by the energy-sharing model. The slight variations in pricing magnitude are primarily influenced by the higher energy consumption of Tesla vehicles, but the overall pricing trends and distribution patterns are consistent for both models.

Figure 12 and Figure 13 illustrate the total costs incurred by Nissan Leaf and Tesla Model S EV users under different methods: typical charging, S2LV, M2LV, and the proposed 3OEP model. In the typical charging scenario, EV owners experience the highest costs because charging predominantly occurs during peak-demand hours when energy prices are elevated. This uncoordinated charging behavior results in significant expenses, as no mechanism exists to incentivize cost-effective charging or discharging patterns. The S2LV and M2LV models offer cost reductions compared to typical charging by coordinating energy-sharing prices at the community level. However, the lack of dynamic inter-community coordination limits their potential for cost optimization. Both methods distribute costs more evenly throughout the day, leading to moderate savings compared to the typical charging scenario. The 3OEP model, however, achieves the lowest overall costs for EV users across both Nissan and Tesla vehicles, showing a reduction of 8.5% compared to typical charging and 6.2% compared to the two-level approaches for the Nissan car. For the Tesla car, the 3OEP model further reduces costs by 30.7% compared to typical charging and by 24% compared to the two-level approaches. By introducing hierarchical coordination and real-time pricing mechanisms, the 3OEP model incentivizes charging during off-peak periods and strategically utilizes discharging during high-price periods to offset costs, providing the most efficient cost management among all methods.

Figure 12 and Figure 13 show the differences in charging costs between the Nissan Leaf (40 kWh) and Tesla Model S (75 kWh), primarily influenced by their energy consumption rates during travel. The Tesla Model S consumes more energy during trips compared to the Nissan Leaf, particularly in the S2LV and M2LV methods. These methods do not fully optimize energy usage across time or communities, resulting in Tesla vehicles consuming more energy at higher prices. However, in the 3OEP model, both vehicles benefit significantly from hierarchical optimization, with Tesla vehicles able to charge during low-cost, low-demand periods and utilize their larger capacity for strategic discharging during high-demand periods. This highlights that while Tesla’s higher energy consumption leads to higher costs in less optimized systems, it also enables greater cost-saving potential in advanced models like 3OEP.

6. Conclusions

This paper presents a novel multi-communities energy sharing management scheme integrated with electric vehicles capable of traversing multiple areas across diverse communities characterized by different energy profiles and prices. The model is formulated as a three-level Stackelberg game to capture the interaction among three entities at three levels: the UC, CEAs, and EVs. The UC and CEAs aim to find optimal energy sharing prices to maximize their respective benefits, while EVs seek to determine optimal charging/discharging strategies to maximize their utility. The scheme presents the optimal three-level energy–price (3OEP) equilibrium algorithm to obtain an equilibrium that is proven to be unique and always existent. The results demonstrate that the proposed scheme outperforms typical human charging behavior and the two-level game approaches, significantly lowering the peak-to-average ratio and smoothing the overall energy profile.