Bi-Level Game Strategy for Virtual Power Plants Based on an Improved Reinforcement Learning Algorithm
Abstract
1. Introduction
- (1)
- Two-level structure to build the optimization methods for economic dispatch: the lower level focuses on the operational costs and environmental pollution costs of VPPs; the upper level establishes a game market framework between the VPO and the VPPs.
- (2)
- An improved reinforcement learning algorithm validates the feasibility of the proposed strategy.
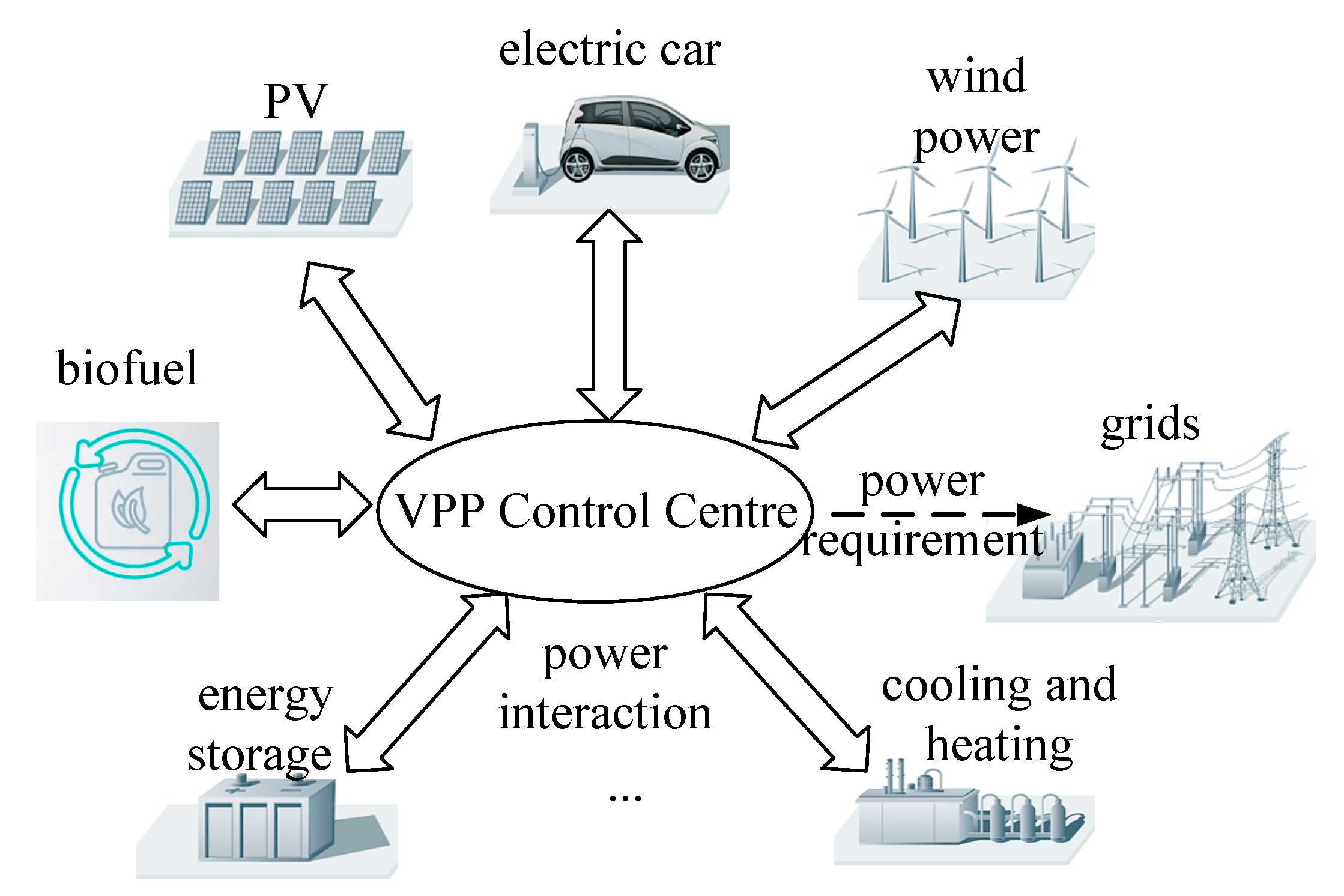
2. Virtual Power Plant and Its Objective Function
2.1. Constraints of VPP
2.1.1. Load Constraints
2.1.2. Energy Storage Constraints
2.1.3. Power Exchange Constraints with VPO
2.2. Objective Functions of VPP
2.2.1. VPP Operational Cost Model
2.2.2. Environmental Pollution Cost Model
3. Bi-Level Game Model and Its Design
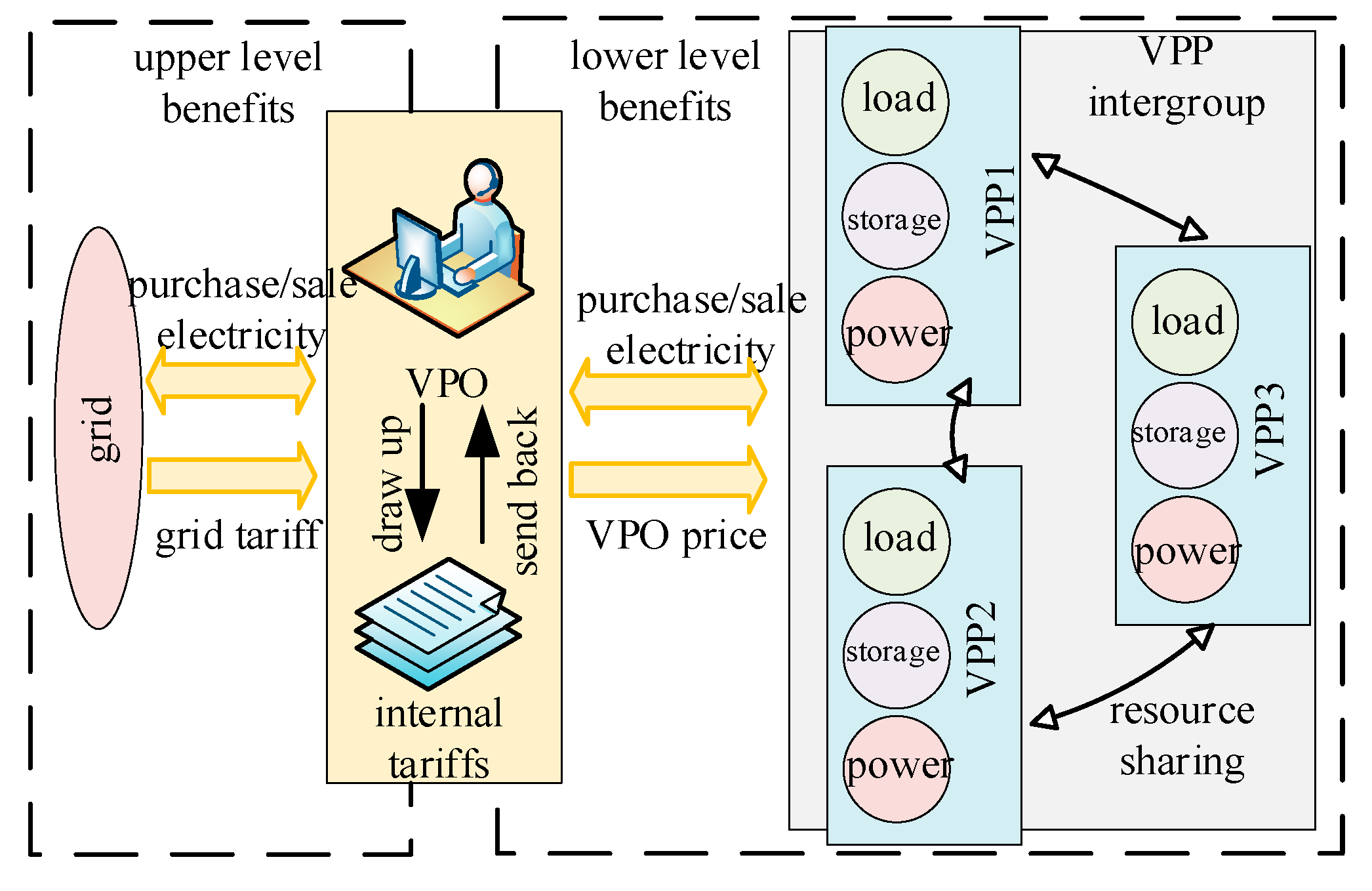
3.1. Energy Trading Framework of the Bi-Level Game Model
3.2. Lower-Level Cost Model
3.3. Upper-Level Benefit Model
3.4. Bilevel Game Model and Objective Functions
3.4.1. Bilevel Game Model
3.4.2. Nash Equilibrium Model
3.5. Algorithm and Solution Process
3.5.1. Adjustment Factor
3.5.2. Particle Search
3.5.3. Particle Transfer
3.5.4. Population Feedback
4. Case Study
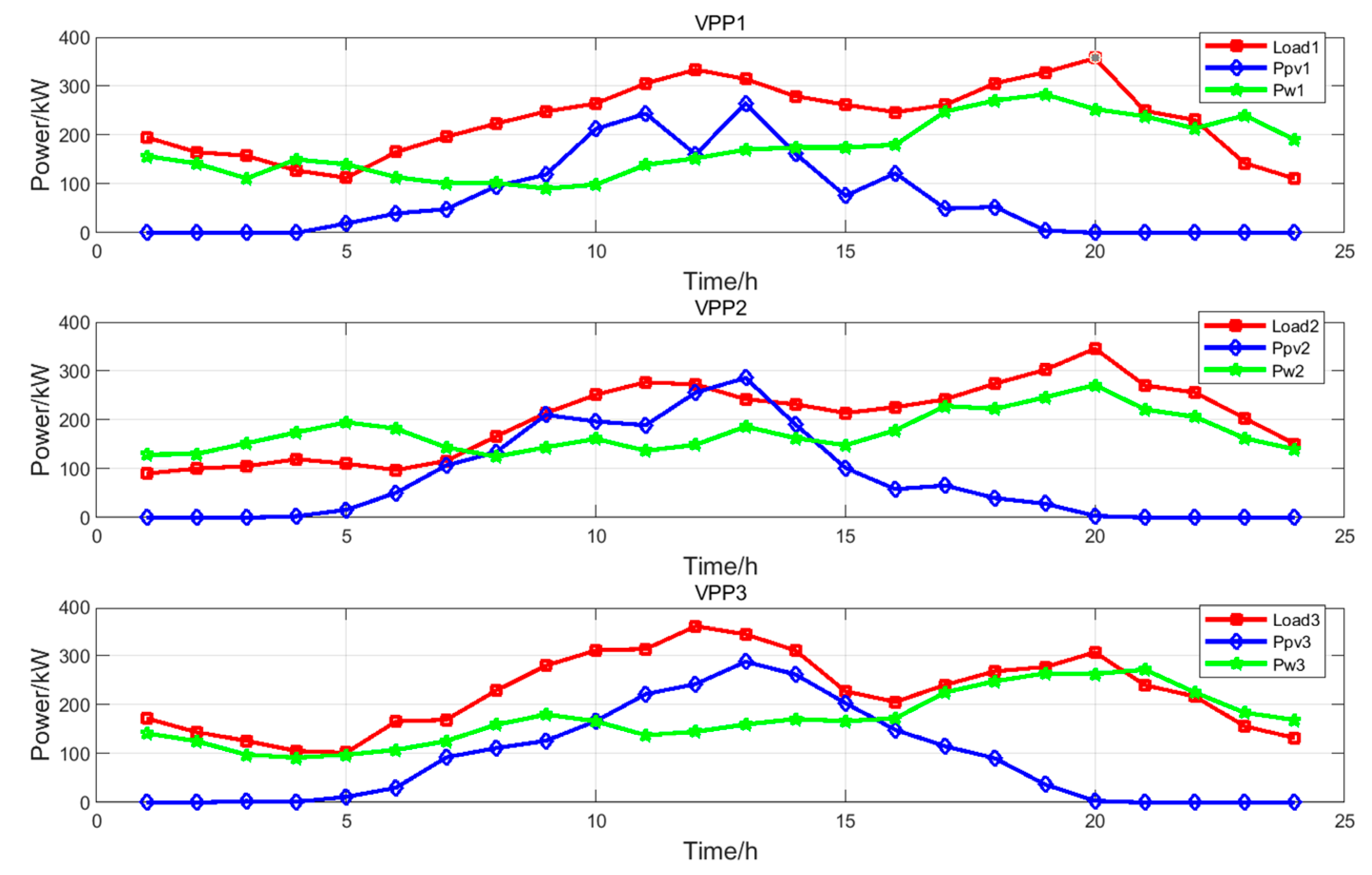
4.1. Basic Data
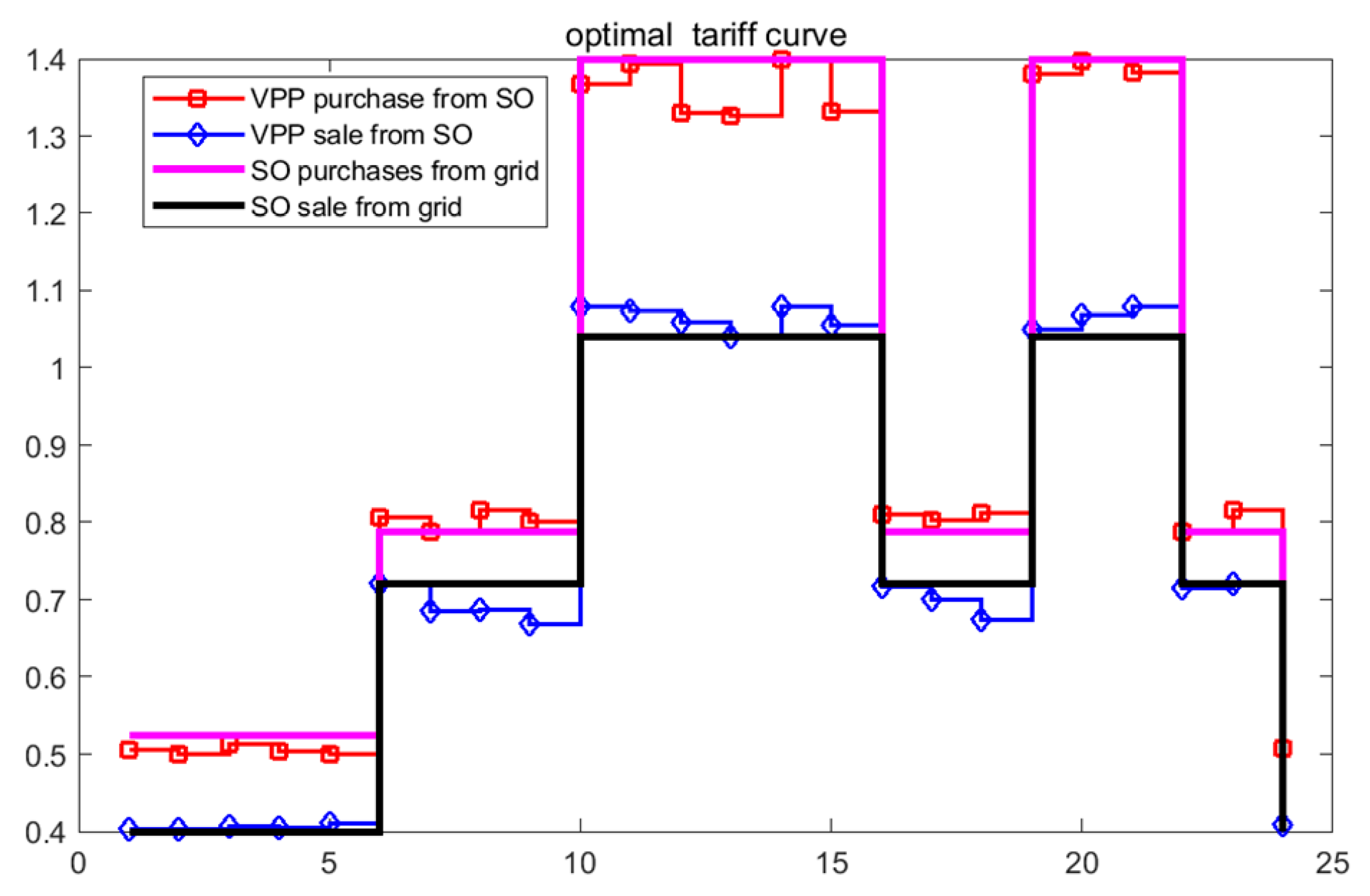
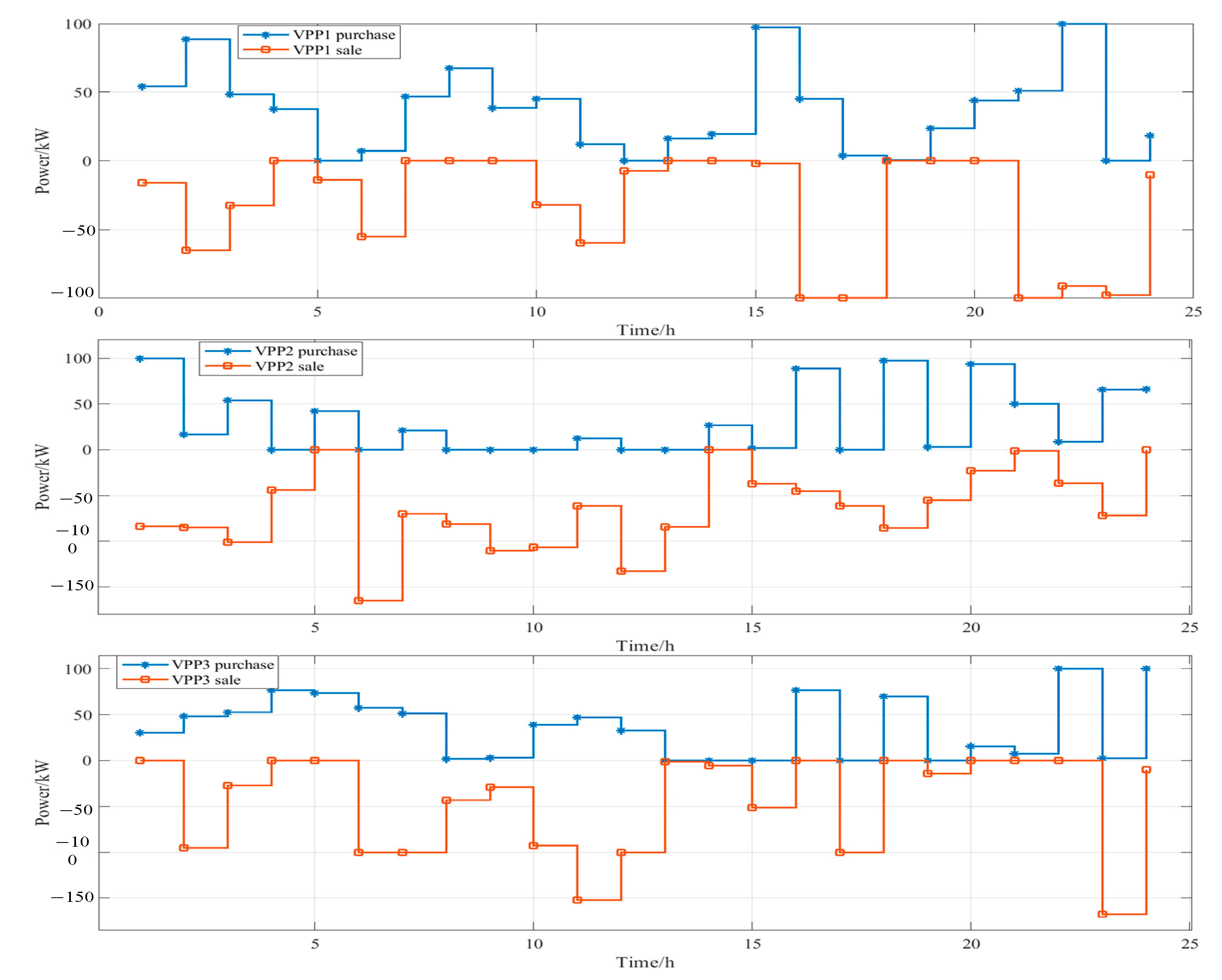
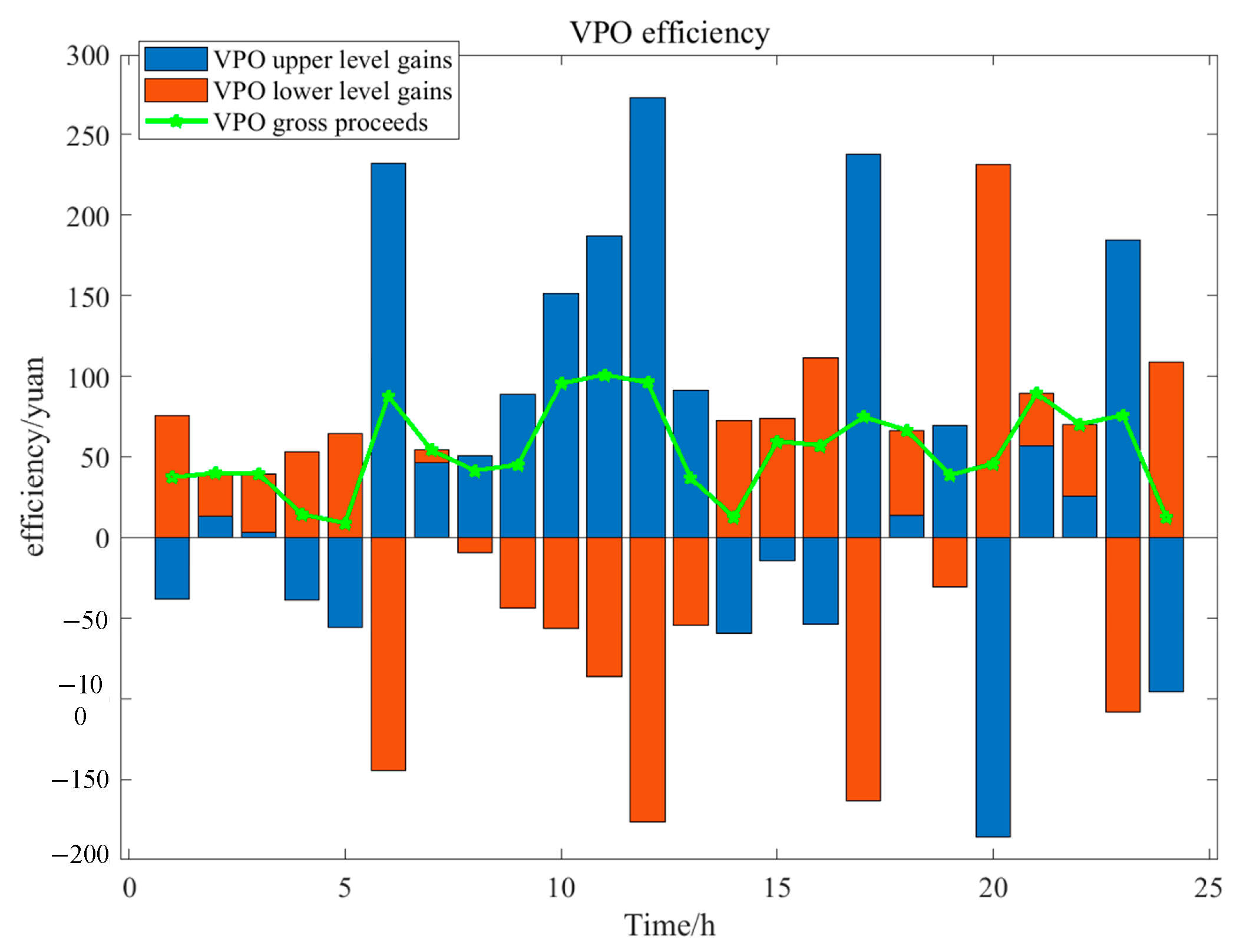
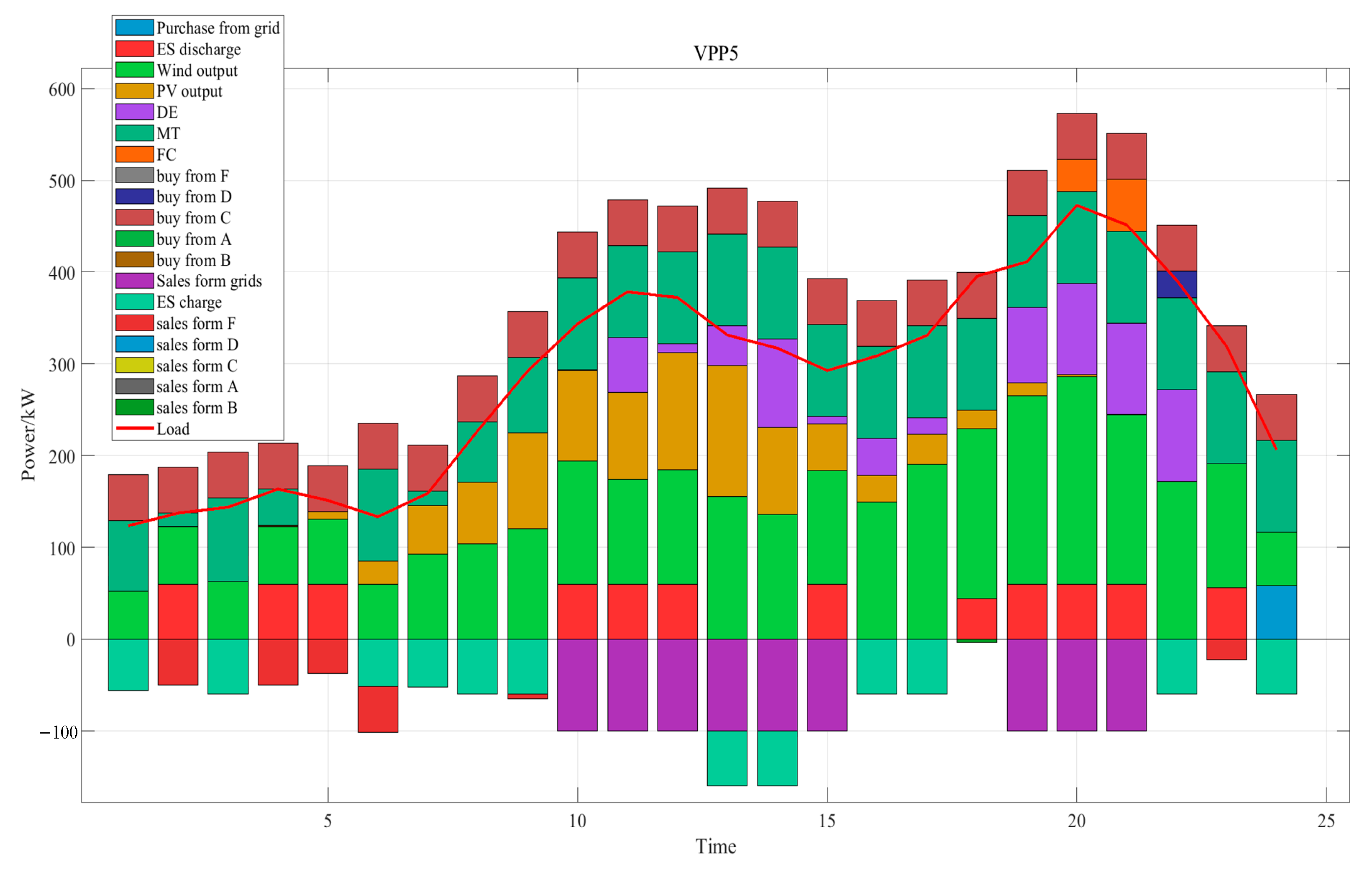
4.2. Results Analysis of the Bi-Level Game Optimization Strategy
Analysis of Electricity Trading Results
4.3. Comparative Analysis
- Model 1: This model dispenses with day-ahead forecasting, wherein the VPO does not establish dynamic lower-level pricing. Instead, it directly adopts the electricity prices from the distribution network as presented in Table 3 to formulate the internal prices for the VPP cluster.
- Model 2: This model employs the bi-level game optimization model introduced in this research, which yields the optimized dynamic electricity prices depicted in Figure 5.
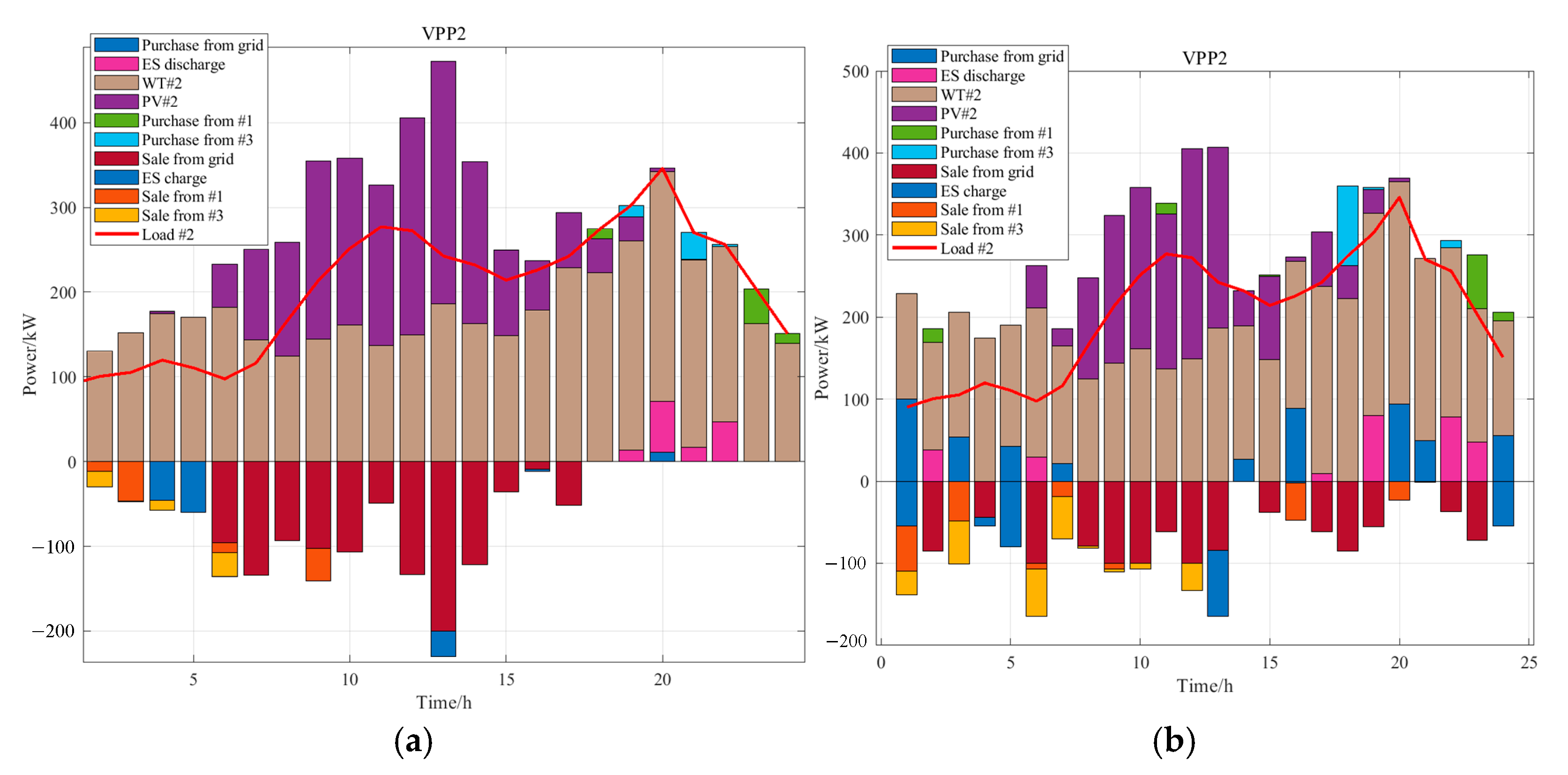
4.3.1. Wind and Solar Power Results Analysis
4.3.2. VPP Internal Power Generation Analysis
4.3.3. Total Cost Analysis
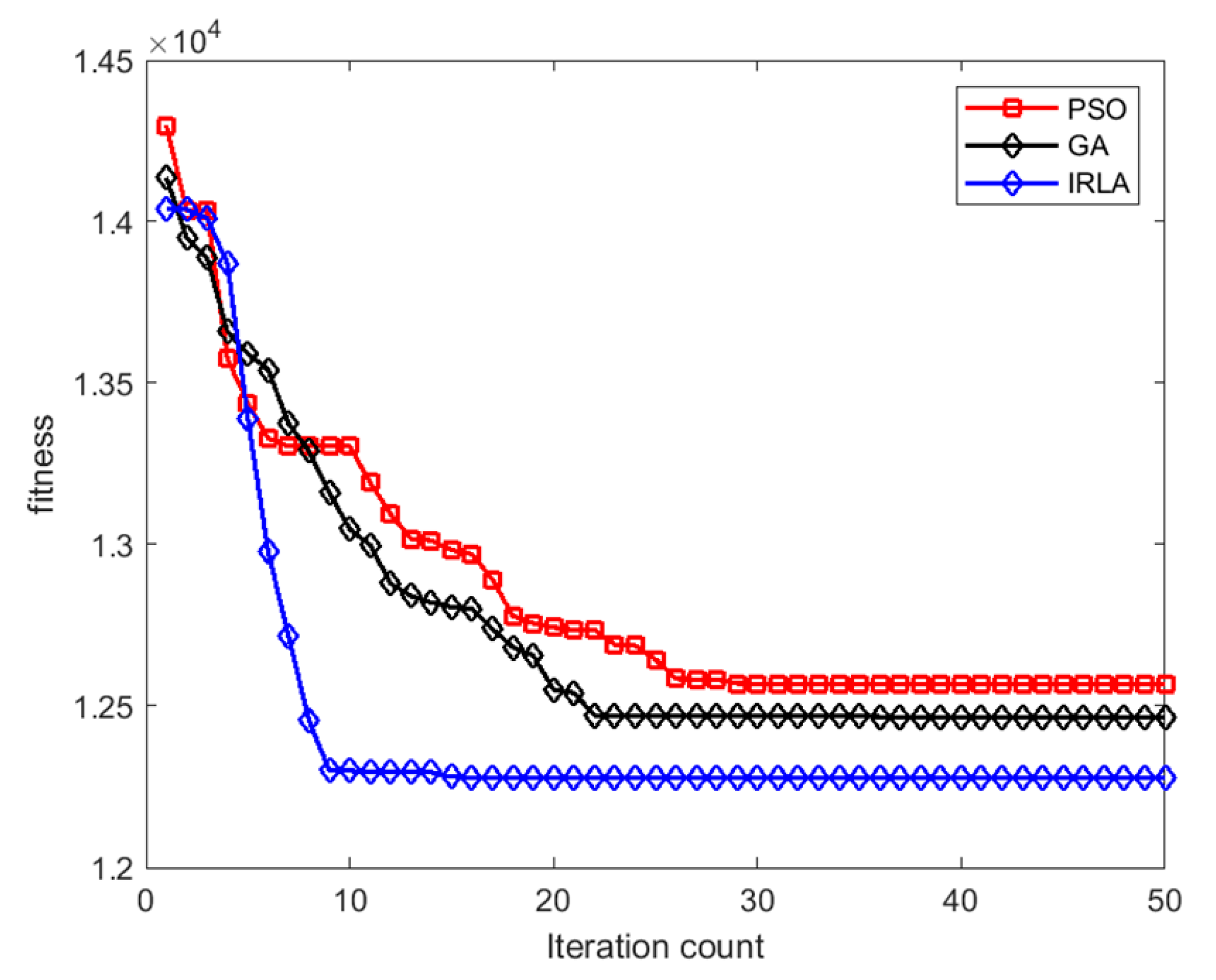
4.3.4. Fitness Analysis
4.3.5. Multi-Objective Model Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, K.X.; Zhou, X.N.; Chen, X.M.; Liu, Y.; Yan, P.F.; Liu, M. Daily electricity forecast of regional power grid considering large scale access of distributed generation. Renew. Energy Resour. 2022, 40, 1407–1414. [Google Scholar]
- Hu, J.; Zhou, H.; Li, Y.; Hou, P.; Yang, G. Multi-time scale energy management strategy of aggregator characterized by photovoltaic generation and electric vehicles. J. Mod. Power Syst. Clean Energy 2020, 8, 727–736. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, W.; Wang, B.; Li, M.; Zhu, T. Optimal decomposition of stochastic dispatch schedule for renewable energy cluster. J. Mod. Power Syst. Clean Energy 2021, 9, 711–719. [Google Scholar] [CrossRef]
- Yu, Y.; Quan, L.; Mi, Z.; Lu, J.; Chang, S.; Yuan, Y. Improved model predictive control with prescribed performance for aggregated thermostatically controlled loads. J. Mod. Power Syst. Clean Energy 2022, 10, 430–439. [Google Scholar] [CrossRef]
- Wang, S.; Wu, W. Aggregate flexibility of virtual power plants with temporal coupling constraints. IEEE Trans. Smart Grid 2021, 12, 5043–5051. [Google Scholar] [CrossRef]
- Ge, X.X.; Fu, Z.Y.; Xu, F.; Wang, F.; Wang, J.L.; Wang, T. Business Model and Key Technologies of Virtual Power Plant for New Power System. Autom. Electr. Power Syst. 2022, 46, 129–146. [Google Scholar]
- Wang, H.; Wang, J.; Wang, C.; Zhang, G.; Fan, M. Risk-constrained Energy Management Modeling of Virtual Power Plant. Proc. CSEE 2021, 41, 8334–8349. [Google Scholar]
- Lin, L.; Guan, X.; Peng, Y.; Wang, N.; Maharjan, S.; Ohtsuki, T. Deep Reinforcement Learning for Economic Dispatch of Virtual Power Plant in Internet of Energy. IEEE Internet Things J. 2020, 7, 6288–6301. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Wu, W. Allocating Ex-post Deviation Cost of Virtual Power Plants in Distribution Networks. J. Mod. Power Syst. Clean Energy 2023, 11, 1014–1019. [Google Scholar] [CrossRef]
- Alahyari, A.; Ehsan, M.; Mousavizadeh, M.S. A hybrid storage-wind virtual power plant (VPP) participation in the electricity markets: A self-scheduling optimization considering price, renewable generation, and electric vehicles uncertainties. J. Energy Storage 2019, 25, 100812. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, W.; Qi, F.; Wang, L.; Zou, B.; Wen, F.; Xue, Y. Economic Dispatch of a Virtual Power Plant Considering Demand Response in Electricity Market Environment. Electr. Power 2017, 50, 107–113. [Google Scholar]
- Li, Y.; Tang, H.; Lv, K.; Wang, K.; Wang, G. Optimization of Dynamic Dispatch for Multiarea Integrated Energy System Based on Hierarchical Learning Method. IEEE Access 2020, 8, 72485–72497. [Google Scholar] [CrossRef]
- Hou, H.Y.; Ge, X.L.; Cao, X.D. Coalition game optimization method for multiple virtual power plants considering carbon trading. Proc. CSU-EPSA 2023, 35, 77–85. [Google Scholar]
- Liu, Z.; Zheng, W.; Qi, F.; Wang, L.; Zou, B.; Wen, F.; Xue, Y. Pricing strategy of energy service provider based on non-cooperative game and revenue sharing contract. Electr. Power Autom. Equip. 2022, 42, 1–8. [Google Scholar]
- Xu, Z.; Guo, Y.; Sun, H. Competitive Pricing Game of Virtual Power Plants: Models, Strategies, and Equilibria. IEEE Trans. Smart Grid 2022, 13, 4583–4595. [Google Scholar] [CrossRef]
- Chen, W.; Qiu, J.; Zhao, J.; Chai, Q.; Dong, Z.Y. Customized Rebate Pricing Mechanism for Virtual Power Plants Using a Hierarchical Game and Reinforcement Learning Approach. IEEE Trans. Smart Grid 2023, 14, 424–439. [Google Scholar] [CrossRef]
- Chen, Z.H.; Chen, S.H.; Chen, H. Large-scale FJSP based on improved multi-group NSGA-II algorithm. Transducer Microsyst. Technol. 2021, 40, 51–54. [Google Scholar]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.D.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Gu, W.; Wu, Z.; Wang, R. Muti-objective optimization of combined heat and power microgrid considering pollutant emission. Autom. Electr. Power Syst. 2012, 36, 183–191. [Google Scholar]
- Chen, J.D.; Hou, Z.F.; Zhao, R.F.; Li, B.; Wang, C.; Lin, G.H. Autonomous optimal economic dispatch of active distribution system based on multi-microgrid access. Electr. Meas. Instrum. 2024, 61, 150–156. [Google Scholar]
- Zhang, Y. Neural Network Algorithm with Reinforcement Learning for Parameters Extraction of Photovoltaic Models. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 2806–2816. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.D.; Zhang, Y.N.; Guo, L.M.; Jiang, J.L.; Zhao, Y.Z. Moth-flame optimization algorithm based on crossover operator and non-uniform mutation operato. Comput. Digit. 2020, 48, 2622–2627. [Google Scholar]

| 1 Input | - Load, PV, and wind power data from VPP |
| - Input the initial particle position x0 and velocity v0, and perform initialization. - The position x0 includes VPO’s internal electricity purchase and sale prices, the electricity purchase and sale quantities for the three VPPs, and the VPO’s storage capacity | |
| 2 Bi-Level Game | |
| - The IRLA calculates the VPO benefits using Equation (9) | |
| - The Cplex solver computes the internal cost of the VPP using Equation (6) | |
| 3 IRLA interation | |
| - Modification factor βd check using Equation (14) | |
| - If satisfied, use the particle transfer equation (Equation (18)). - If not satisfied, use the particle search equation (Equation (16)). | |
| - Update the particle position xd+1. | |
| - Compute feedback using the particle feedback equation (Equation (20)). | |
| - Calculate the fitness value pbest | |
| - Update the global optimum gbest | |
| Repeat | |
| Until the stop conditions thatd > dmax or |pbestd − pbestd−1| ≤ ξ | |
| 4 Output | - the gbestd as the final result |
| Type | Total Capacity/kW | Initial State of Charge (SOC) | SOC Range | Maximum Charging/Discharging Power/kW |
|---|---|---|---|---|
| VPP1 | 250 | 0.4 | 0.2~0.95 | ±60 |
| VPP2 | 320 | 0.4 | 0.2~0.9 | ±80 |
| VPP3 | 300 | 0.5 | 0.3~0.95 | ±70 |
| Staggered | Time/h | Sale Price/Yuan | Purchase Price/Yuan |
|---|---|---|---|
| peaks | 11:00–15:00, 19:00–21:00 | 1.04 | 1.40 |
| leveling | 8:00–10:00, 16:00–18:00, 22:00–24:00 | 0.72 | 0.79 |
| trough | 0:00–7:00 | 0.40 | 0.53 |
| Model 1/CNY | Model 2/CNY | |
|---|---|---|
| VPP1 | 4681.06 | 4892.83 |
| VPP2 | 4035.85 | 4251.40 |
| VPP3 | 4571.28 | 4435.56 |
| total cost | 13,288.20 | 13,579.79 |
| VPO benefits | / | 1300.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Guo, G.; Gong, D.; Xuan, L.; He, F.; Wan, X.; Zhou, D. Bi-Level Game Strategy for Virtual Power Plants Based on an Improved Reinforcement Learning Algorithm. Energies 2025, 18, 374. https://doi.org/10.3390/en18020374
Liu Z, Guo G, Gong D, Xuan L, He F, Wan X, Zhou D. Bi-Level Game Strategy for Virtual Power Plants Based on an Improved Reinforcement Learning Algorithm. Energies. 2025; 18(2):374. https://doi.org/10.3390/en18020374
Chicago/Turabian StyleLiu, Zhu, Guowei Guo, Dehuang Gong, Lingfeng Xuan, Feiwu He, Xinglin Wan, and Dongguo Zhou. 2025. "Bi-Level Game Strategy for Virtual Power Plants Based on an Improved Reinforcement Learning Algorithm" Energies 18, no. 2: 374. https://doi.org/10.3390/en18020374
APA StyleLiu, Z., Guo, G., Gong, D., Xuan, L., He, F., Wan, X., & Zhou, D. (2025). Bi-Level Game Strategy for Virtual Power Plants Based on an Improved Reinforcement Learning Algorithm. Energies, 18(2), 374. https://doi.org/10.3390/en18020374





