Versatile LCL Inverter Model for Controlled Inverter Operation in Transient Grid Calculation Using the Extended Node Method
Abstract
1. Introduction
2. Materials and Methods
2.1. The Extended Node Method
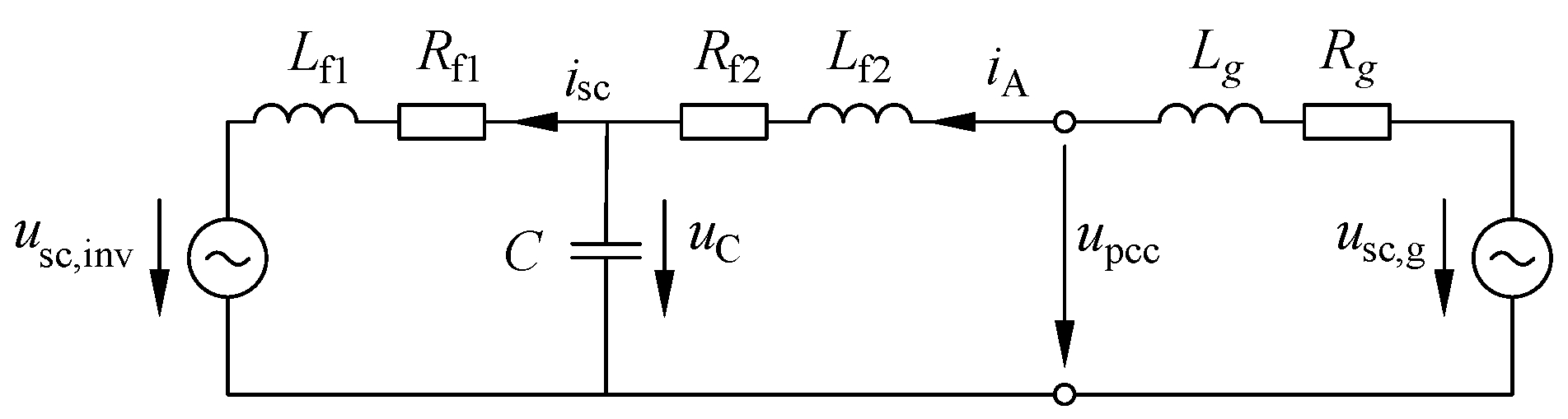
2.2. Two-Level Three-Phase LCL Inverter
2.2.1. LCL Filter Design
2.2.2. Resonance Damping
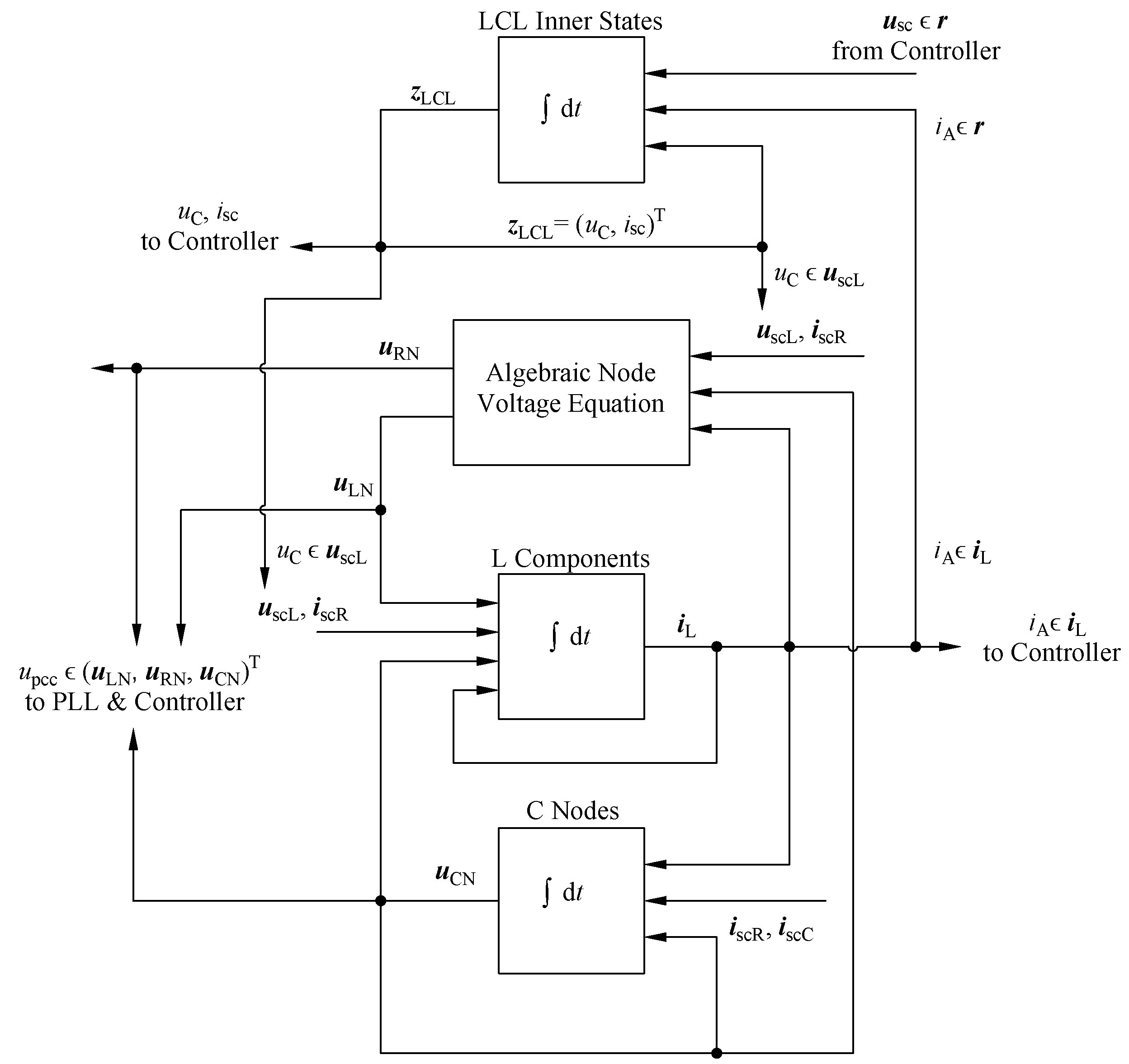
2.3. LCL Inverter Model in the Extended Node Method
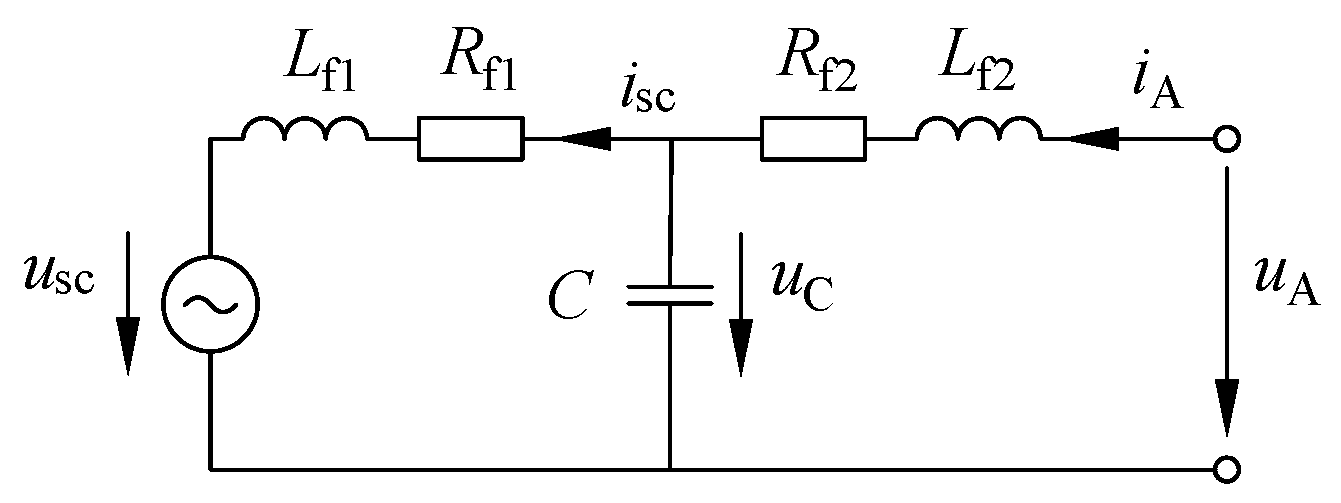
2.3.1. Basic LCL Inverter
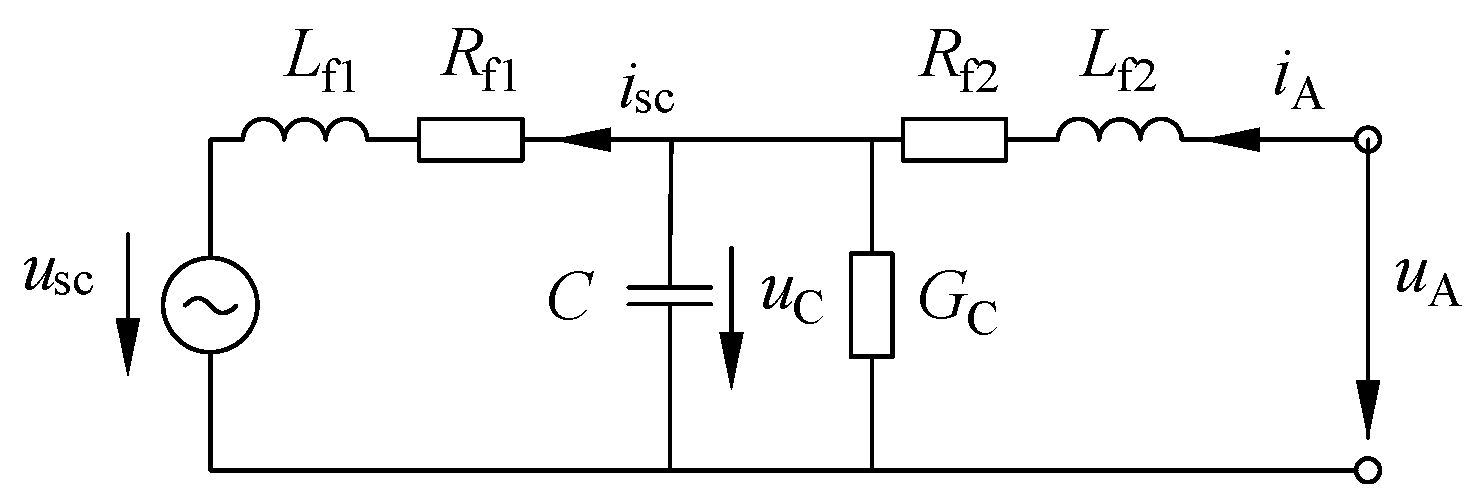
2.3.2. LCL Inverter with Parallel Damping Resistor
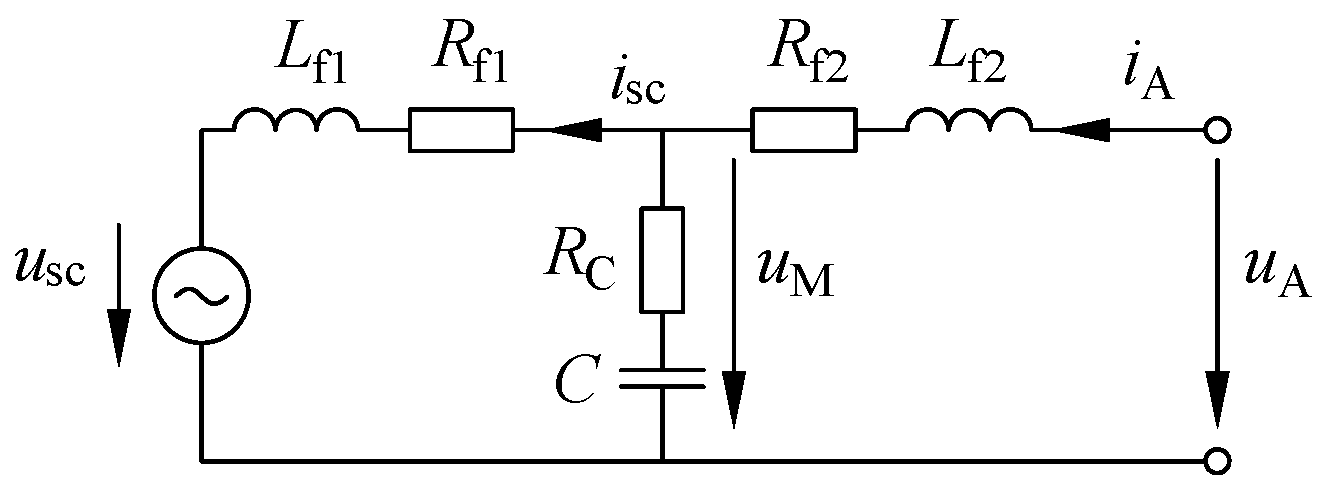
2.3.3. LCL Inverter with Series Damping Resistor
2.3.4. Sensitivity of Filter Parameters
2.3.5. On Solving Inner Differential Equation Systems vs. Stating Additional Grid Nodes
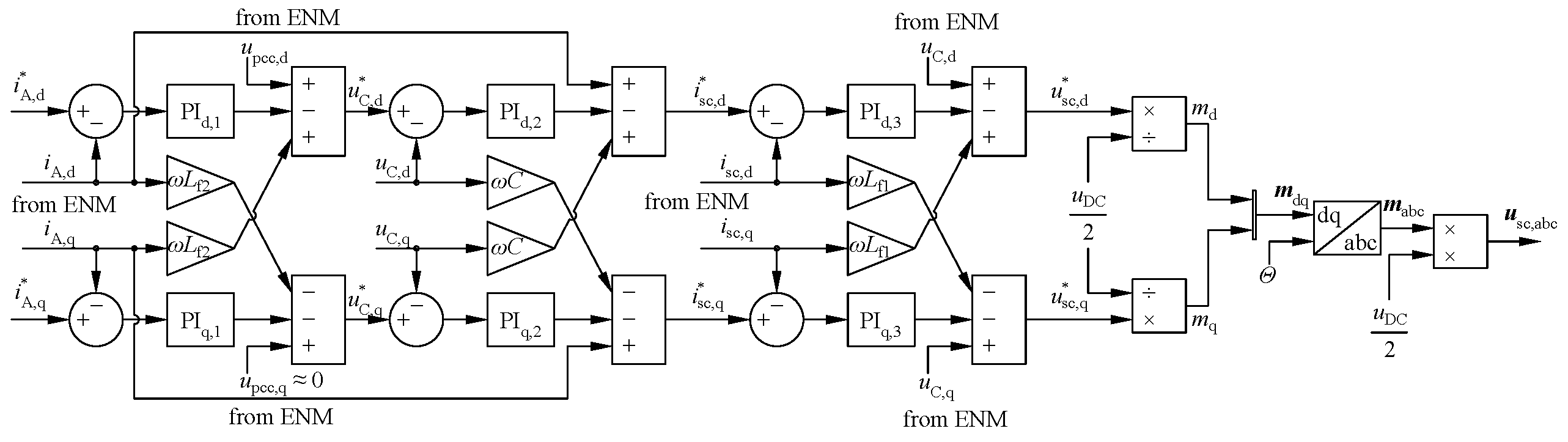
2.4. Inverter Control
2.4.1. Control in dq Frame
2.4.2. Current Control
2.4.3. Phase-Locked Loop
2.5. Software Tool for Transient Grid Calculation with ENM
Combined Control and Grid Calculation Algorithm
3. Results
3.1. Filter Design and Control Parameters
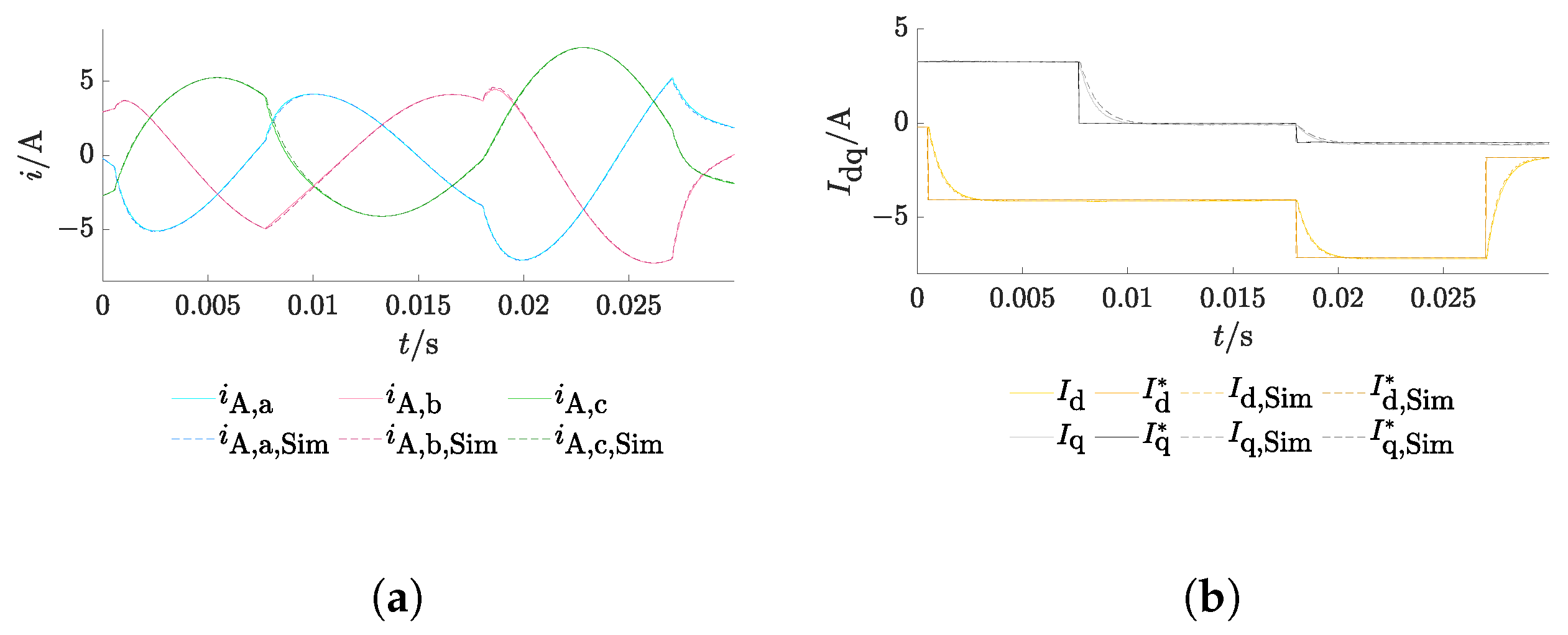
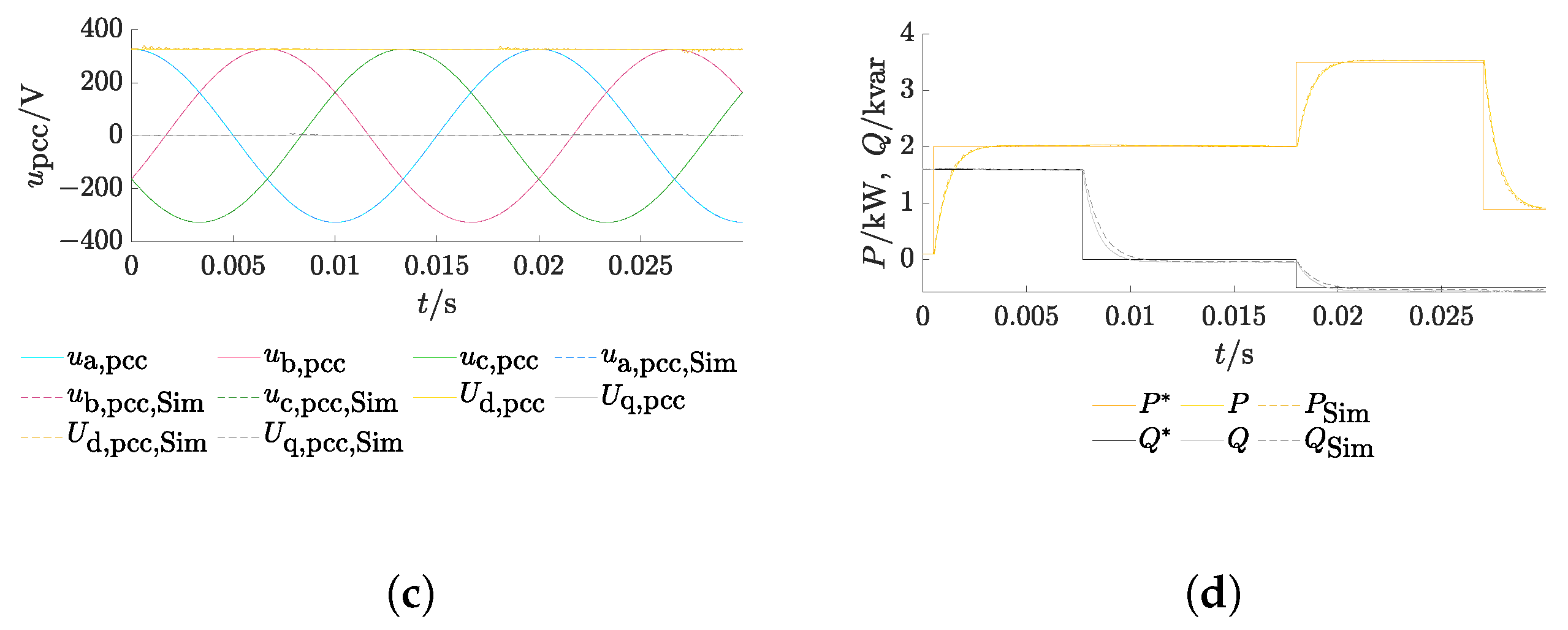
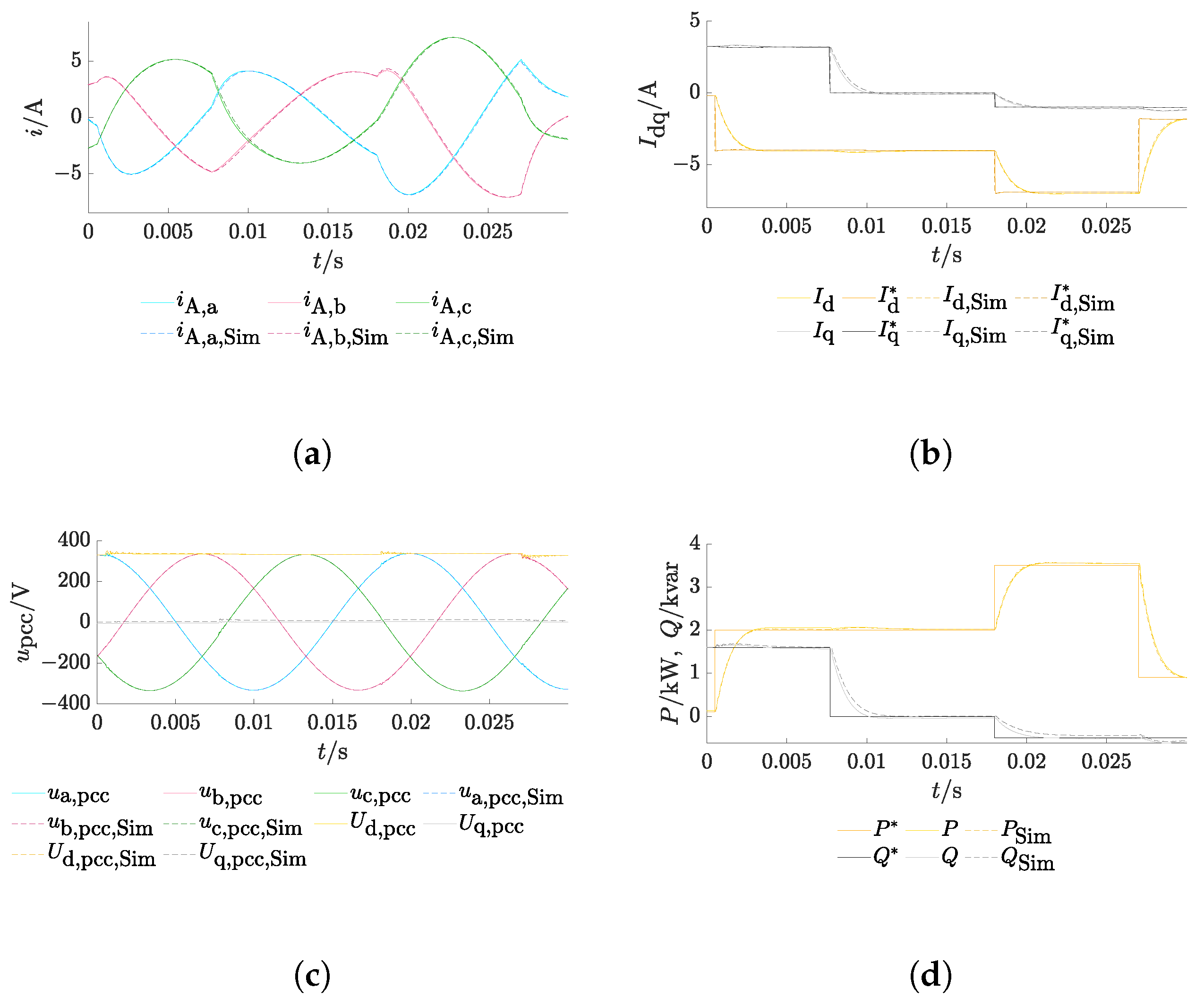
3.2. Single Inverter at Low-Voltage Grid
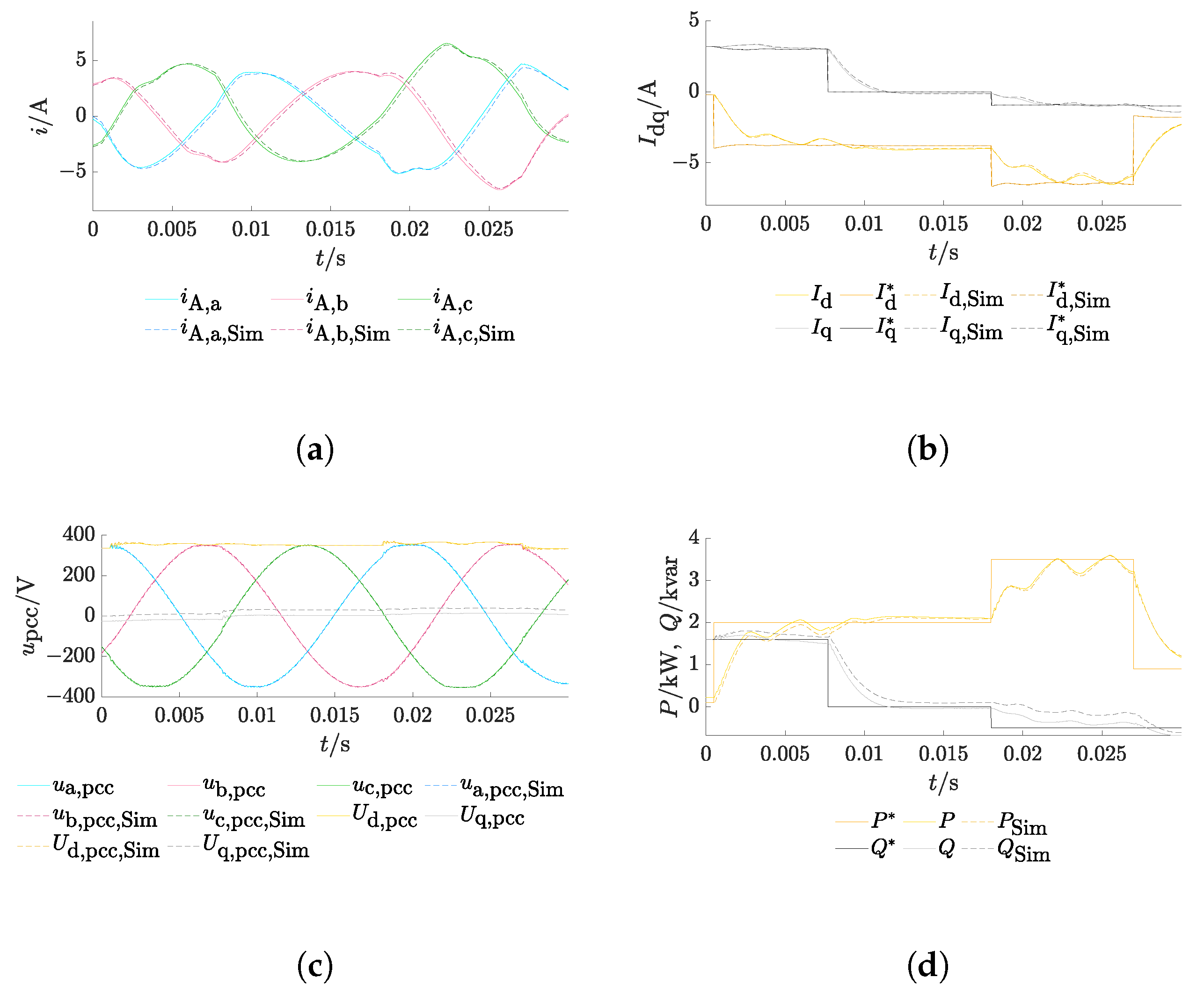
Impact of Filter Parameter Deviations
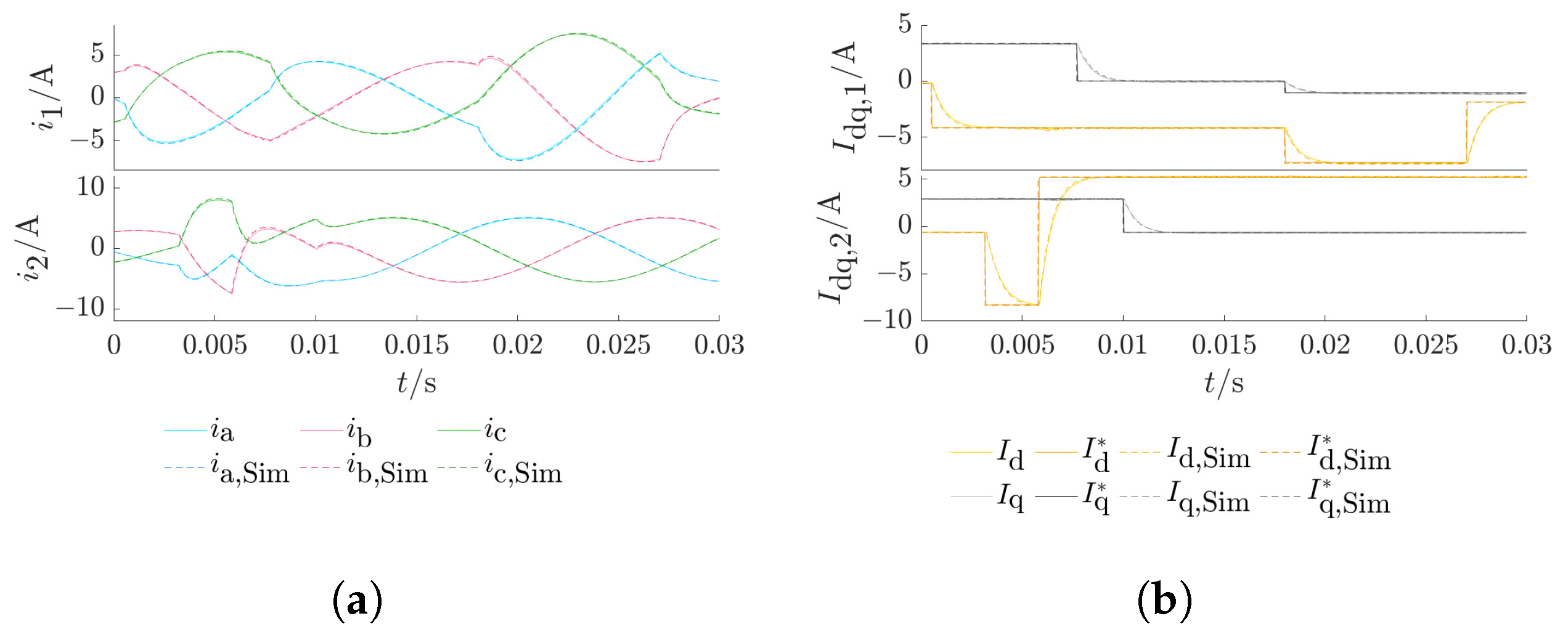
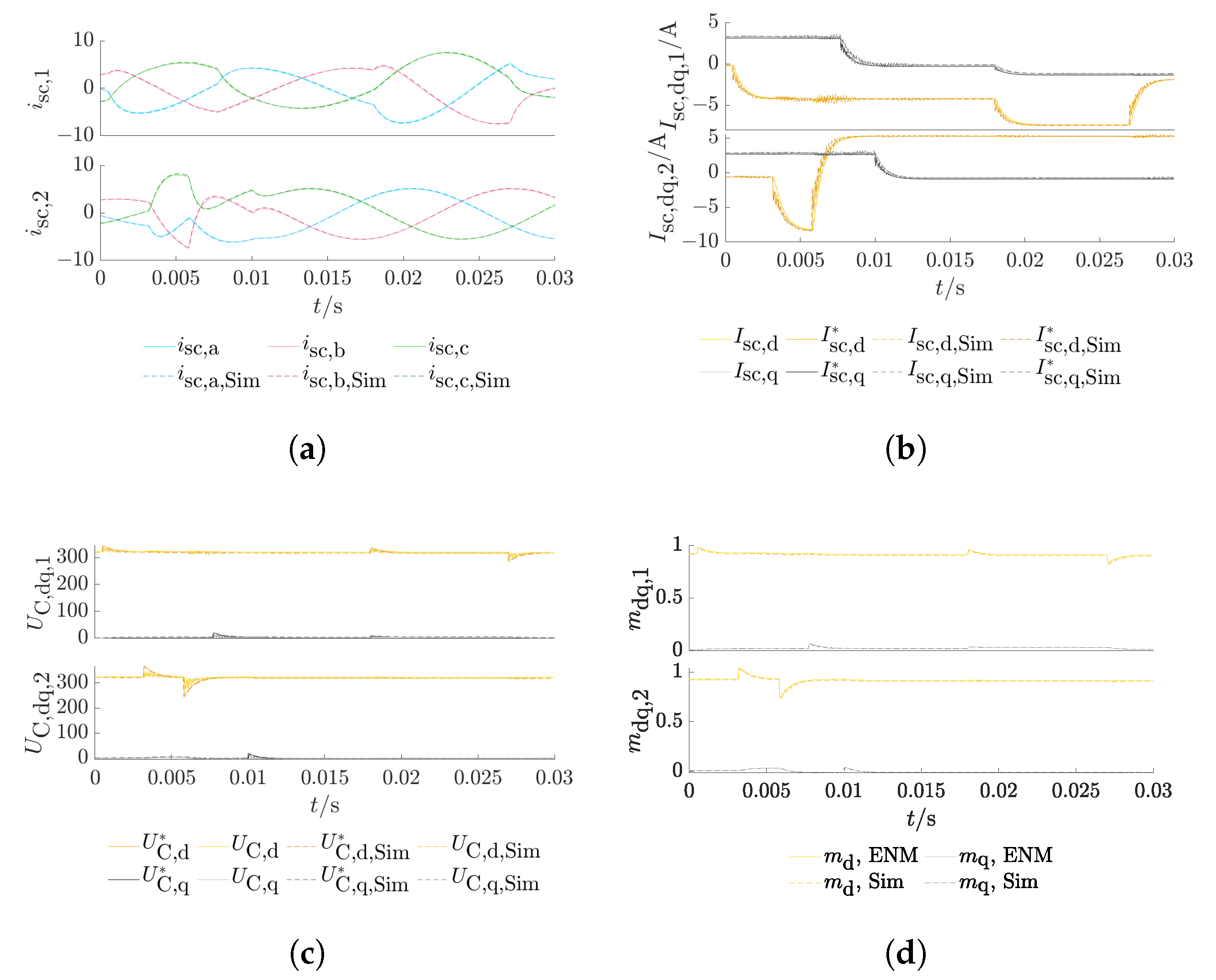
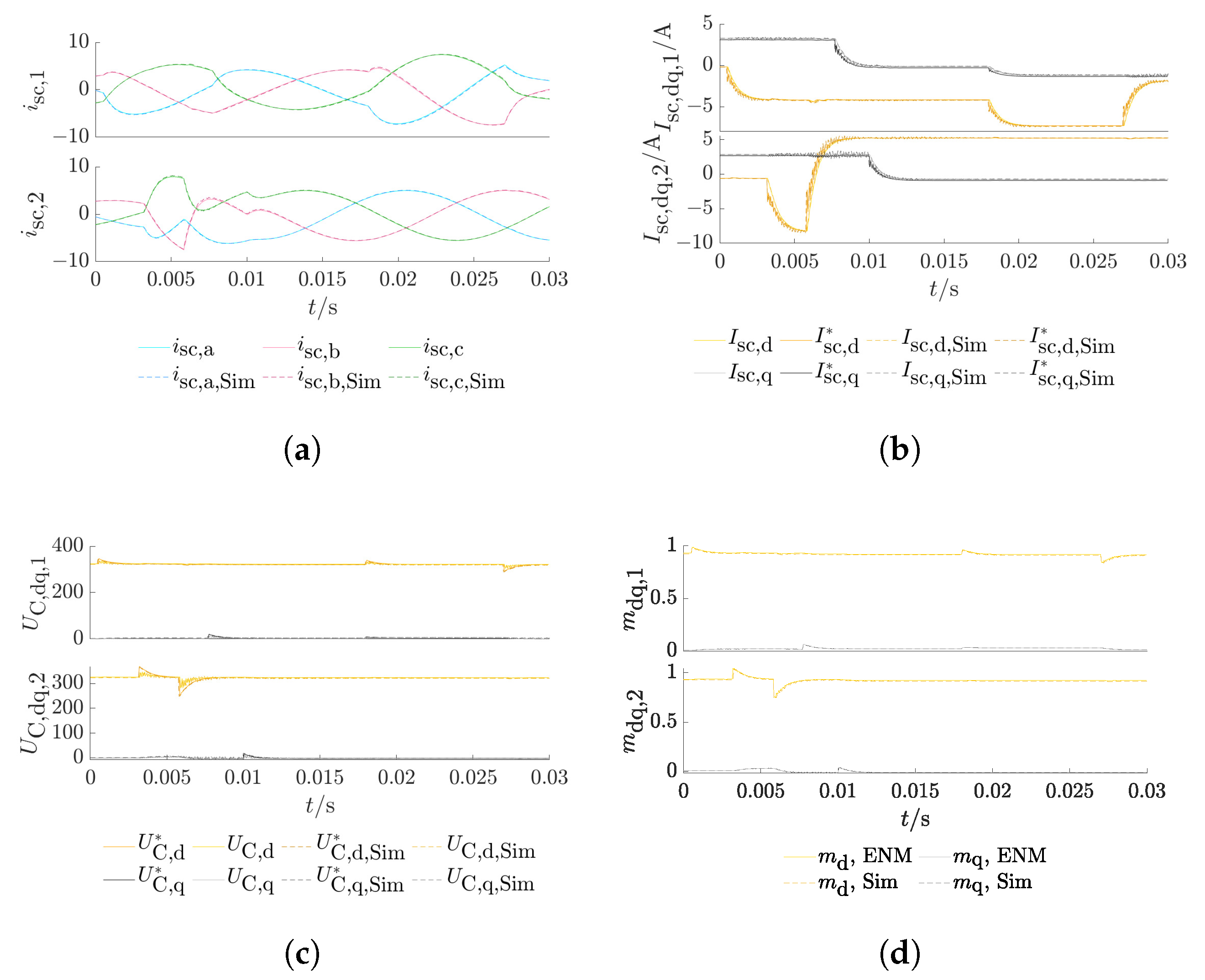
3.3. Inverters at Simbench Testgrid
- Study case 1: All loads (1–13) are resistive–inductive.
- Study case 2: Loads 1, 6, and 11 behave capacitively; all other loads are resistive–inductive.
3.4. Discussion
4. Conclusions
- The inverter with the LCL filter is classified as an L component for the ENM. Its terminal current is part of the current vector and thus results directly from the DES in Equation (4). The parameters for the component matrices and are the grid-sided resistor and inductor .
- The LCL inverter has internal state variables to be considered in the IDES in Equation (5). These are the capacitor voltage and the source current , which are solved by the IDES in Equation (5). In order to avoid these internal variables, the model can also be broken down into its individual components, whereby the actual size of the DAE increases.
- A cascaded control loop was developed for a grid-following inverter in the dq frame for decoupled active and reactive power control. An interface between the ENM network calculation results and the controller has been derived and displayed in detail. This framework is universally applicable for diverse inverter control approaches.
- Different study cases were used to evaluate the ENM with grid-tied inverters, also with varying filter parameters, different load parameters, and node types of the pcc. The results show generally high accordance in comparison with the network calculation in Simulink. The differences between both tools were greatest for particularly weak networks. This approach is thus considered as validated to be further used for transient grid calculations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AES | Algebraic Equation System |
| AI | Artificial Intelligence |
| ENM | Extended Node Method |
| DAE | Differential-Algebraic-Equation-System |
| DES | Differential Equation System |
| IDES | Inner Differential Equation System |
| PLL | Phase-Locked Loop |
References
- Mahr, F.; Henninger, S.; Biller, M.; Jäger, J. Electrical Power Systems; Knowledge Networking of Converters, Grid Operation and Grid Protection; (Orig. German: Elektrische Energiesysteme; Wissensvernetzung von Stromrichter, Netzbetrieb und Netzschutz); Springer: Wiesbaden, Germany, 2021. [Google Scholar]
- Said-Romdhane, M.B.; Naouar, M.W.; Belkhodja, I.S.; Monmasson, E. An Improved LCL Filter Design in Order to Ensure Stability without Damping and Despite Large Grid Impedance Variations. Energies 2017, 10, 336. [Google Scholar] [CrossRef]
- Han, Y.; Yang, M.; Li, H.; Yang, P.; Xu, L.; Coelho, E.A.A. Modeling and Stability Analysis of LCL-Type Grid-Connected Inverters: A Comprehensive Overview. IEEE Access 2019, 7, 114975–115001. [Google Scholar] [CrossRef]
- Dursun, M.; Döşoğlu, M.K. LCL Filter Design for Grid Connected Three-Phase Inverter. In Proceedings of the 2018 2nd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 19–21 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Adamas-Pérez, H.; Ponce-Silva, M.; Mina-Antonio, J.D.; Claudio-Sánchez, A.; Rodríguez-Benítez, O.; Rodríguez-Benítez, O.M. A New LCL Filter Design Method for Single-Phase Photovoltaic Systems Connected to the Grid via Micro-Inverters. Technologies 2024, 12, 89. [Google Scholar] [CrossRef]
- Bolsi, P.C.; Prado, E.O.; Sartori, H.C.; Lenz, J.M.; Pinheiro, J.R. LCL Filter Parameter and Hardware Design Methodology for Minimum Volume Considering Capacitor Lifetimes. Energies 2022, 15, 4420. [Google Scholar] [CrossRef]
- Huang, L.; Wu, C.; Zhou, D.; Blaabjerg, F. Grid Impedance Impact on the Maximum Power Transfer Capability of Grid-Connected Inverter. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 1487–1490. [Google Scholar] [CrossRef]
- Huang, L.; Wu, C.; Zhou, D.; Blaabjerg, F. Impact of Grid Strength and Impedance Characteristics on the Maximum Power Transfer Capability of Grid-Connected Inverters. Appl. Sci. 2021, 11, 4288. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems; Modeling, Control and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Fan, B.; Wang, X. Equivalent Circuit Model of Grid-Forming Converters with Circular Current Limiter for Transient Stability Analysis. IEEE Trans. Power Syst. 2022, 37, 3141–3144. [Google Scholar] [CrossRef]
- Gu, Y.; Bottrell, N.; Green, T.C. Reduced-order models for representing converters in power system studies. IEEE Trans. Power Electron. 2018, 33, 3644–3654. [Google Scholar] [CrossRef]
- Shah, C.; Vasquez-Plaza, J.D.; Campo-Ossa, D.D.; Patarroyo-Montenegro, J.F.; Guruwacharya, N.; Bhujel, N. Review of Dynamic and Transient Modeling of Power Electronic Converters for Converter Dominated Power Systems. IEEE Access 2021, 9, 82094–82117. [Google Scholar] [CrossRef]
- Paolone, M.; Gaunt, T.; Guillaud, X.; Liserre, M.; Meliopoulos, S.; Monti, A.; Van Cutsem, T.; Vittal, V.; Vournas, C. Fundamentals of power systems modelling in the presence of converter-interfaced generation. Electr. Power Syst. Res. 2020, 189, 106811. [Google Scholar] [CrossRef]
- Ajala, O.; Roberts, T.; Domínguez-García, A.D. Power-Flow Formulation for Inverter-Based Grids. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Bao, C.; Ruan, X.; Wang, X.; Li, W.; Pan, D.; Weng, K. Step-by-Step Controller Design for LCL-Type Grid-Connected Inverter with Capacitor–Current-Feedback Active-Damping. IEEE Trans. Power Electron. 2014, 29, 1239–1253. [Google Scholar] [CrossRef]
- Dmitruk, K. A Simplified Guide to Control Algorithms for Grid Converters in Renewable Energy Systems. Energies 2024, 17, 4690. [Google Scholar] [CrossRef]
- Yoon, S.-J.; Lai, N.B.; Kim, K.-H. A Systematic Controller Design for a Grid-Connected Inverter with LCL Filter Using a Discrete-Time Integral State Feedback Control and State Observer. Energies 2018, 11, 437. [Google Scholar] [CrossRef]
- Judewicz, M.G.; González, S.A.; Fischer, J.R.; Martínez, J.F.; Carrica, D.O. Inverter-Side Current Control of Grid-Connected Voltage Source Inverters with LCL Filter Based on Generalized Predictive Control. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1732–1743. [Google Scholar] [CrossRef]
- Wang, X.; Wang, D.; Zhou, S. A Control Strategy of LCL-Type Grid-Connected Inverters for Improving the Stability and Harmonic Suppression Capability. Machines 2022, 10, 1027. [Google Scholar] [CrossRef]
- Park, K.S.; Seo, B.J.; Jo, K.R.; Heo, J.Y.; Kim, H.; Nho, E.C. Current Controller Design of a Grid Connected Inverter Using LCL Filter. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Republic of Korea, 27–30 May 2019; pp. 2356–2361. [Google Scholar] [CrossRef]
- Kumari, K.; Jain, A.K. Cascaded control for LCL filter based grid-tied system with reduced sensors. IET Power Electron. 2022, 15, 1526–1539. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, Z.; Wu, W.; Yao, Z. An Improved Three-Level Cascaded Control for LCL-Filtered Grid-Connected Inverter in Complex Grid Impedance Condition. IEEE Access 2022, 10, 65485–65495. [Google Scholar] [CrossRef]
- Xie, L.; Zeng, S.; Liu, J.; Zhang, Z.; Yao, J. Control and Stability Analysis of the LCL-Type Grid-Connected Converter without Phase-Locked Loop under Weak Grid Conditions. Electronics 2022, 11, 3322. [Google Scholar] [CrossRef]
- Lai, N.B.; Kim, K.H. Robust Control Scheme for Three-Phase Grid-Connected Inverters with LCL-Filter Under Unbalanced and Distorted Grid Conditions. IEEE Trans. Energy Convers. 2018, 33, 506–515. [Google Scholar] [CrossRef]
- Su, M.; Cheng, B.; Sun, Y.; Tang, Z.; Guo, B.; Yang, Y. Single-Sensor Control of LCL-Filtered Grid-Connected Inverters. IEEE Access 2019, 7, 38481–38494. [Google Scholar] [CrossRef]
- Gomes, C.C.; Cupertino, A.F.; Pereira, H.A. Damping techniques for grid-connected voltage source converters based on LCL filter: An overview. Renew. Sustain. Energy Rev. 2018, 81 Pt 1, 116–135. [Google Scholar] [CrossRef]
- Khan, D.; Zhu, K.; Hu, P.; Waseem, M.; Ahmed, E.M.; Lin, Z. Active damping of LCL-Filtered Grid-Connected inverter based on parallel feedforward compensation strategy. Ain Shams Eng. J. 2023, 14, 101902. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, S.; Dragicevic, T.; Wheeler, P.; Zanchetta, P. Artificial Intelligence Techniques for Enhancing the Performance of Controllers in Power Converter-Based Systems—An Overview. IEEE Open J. Ind. Appl. 2023, 4, 366–375. [Google Scholar] [CrossRef]
- Fu, X.; Li, S. Control of Single-Phase Grid-Connected Converters with LCL Filters Using Recurrent Neural Network and Conventional Control Methods. IEEE Trans. Power Electron. 2016, 31, 5354–5364. [Google Scholar] [CrossRef]
- Uddin, M.N.; Tabrizi, Y.H. Artificial Intelligence Based Control Strategy of a Three-Phase Neutral-Point Clamped Back-to-Back Power Converter with Ensured Power Quality for WECS. In Proceedings of the 2022 IEEE Industry Applications Society Annual Meeting (IAS), Detroit, MI, USA, 9–14 October 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Noura, H.N.; Allal, Z.; Salman, O.; Chahine, K. Explainable artificial intelligence of tree-based algorithms for fault detection and diagnosis in grid-connected photovoltaic systems. Eng. Appl. Artif. Intell. 2025, 139 Pt A, 109503. [Google Scholar] [CrossRef]
- Ramasubramanian, D.; Yu, Z.; Ayyanar, R.; Vittal, V.; Undrill, J. Converter model for representing converter interfaced generation in large scale grid simulations. IEEE Trans. Power Syst. 2017, 32, 765–773. [Google Scholar] [CrossRef]
- PLECS, The Simulation Platform for Power Electronic Systems. Available online: https://www.plexim.com/products/plecs (accessed on 7 January 2025).
- DIgSILENT | Power System Solutions, Powerfactory Applications. Available online: https://www.digsilent.de/en/powerfactory.html (accessed on 7 January 2025).
- Simulink, Simulink is for Model-Based Design. Available online: https://www.mathworks.com/products/simulink.html (accessed on 7 January 2025).
- Oswald, B.R. Three-Phase Grid Calculation; Calculation of Stationary and Transient Processes with Symmetrical Components and Space Phasors, 5th ed.; (orig. German: Berechnung von Drehstromnetzen; Berechnung stationärer und nichtstationärer Vorgänge mit Symmetrischen Komponenten und Raumzeigern); Springer: Wiesbaden, Germany, 2023. [Google Scholar]
- Hofmann, L. Efficient Calculation of Transients in Expanded Electrical Systems; (orig. German: Effiziente Berechnung von Ausgleichsvorgängen in ausgedehnten Elektroenergiesystemen); Shaker Verlag: Aachen, Germany, 2003. [Google Scholar]
- Oswald, B.R. Calculation of Transients in Electric Power Systems, Grid Calculation; (orig. German: Berechnung transienter Vorgänge in Elektroenergieversorgungsnetzen, Netzberechnung); VDE-Verlag: Berlin, Germany, 1996; Volume 2. [Google Scholar]
- Oswald, B.R. Computation of power systems transients by using sets of algebraic and of state space equations. In Proceedings of the International Conference on Power Systems Transients, Seattle, WA, USA, 22–26 June 1997; pp. 35–40. [Google Scholar]
- Oswald, B.R. Node-Oriented Methods of Grid Calculation, 2nd ed.; (orig. German: Knotenorientierte Verfahren der Netzberechnung); Leipziger University-Verlag: Leipzig, Germany, 2000. [Google Scholar]
- Oswald, B.R. Computation of Power Systems Eigenvalues Using the Modified Nodal Approach. Eur. Trans. Electr. Power 2000, 10, 7–12. [Google Scholar] [CrossRef]
- Hofmann, L. Extended Node Method: Separation of Slow and Dynamic Parts; (orig. German: Erweitertes Knotenpunktverfahren (EKPV): Entkopplung des langsamen vom dynamischen Teilsystem); Bericht IEE 629, Institut für Elektrische Energieversorgung, Universität Hannover: Hannover, Germany,, 2000. [Google Scholar]
- Hofmann, L.; Oswald, B. Efficient simulation of the dynamical behavior of large-scale power systems. Electr. Eng. 2001, 83, 307–311. [Google Scholar]
- Weidner, J. Contribution to Stationary and Transient Stability Analysis in Distribution Grids, (Orig. German: Beitrag zur statischen und transienten Stabilitätsanalyse in Verteilungsnetzen). Ph.D. Dissertation, Leibniz Universität Hannover, Hannover, Germany, 2021. [Google Scholar]
- Huisinga, H.; Hofmann, L. Analytical Properties of Differential-Algebraic Equations Arising in Circuit Simulation Using the Extended Nodal Approach, (orig. German: Strukturanalyse des mit dem Erweiterten Knotenpunktverfahren formulierten Differential-algebraischen Gleichungssystems). Automatisierungstechnik 2021, 69, 353–363. [Google Scholar] [CrossRef]
- Vorwerk, D.; Schumann, M.; Schulz, D. A Multi-Energy Fuel Cell Model in the Extended Node Method. In Proceedings of the NEIS 2023; Conference on Sustainable Energy Supply and Energy Storage Systems, Hamburg, Germany, 4–5 September 2023; pp. 245–254. [Google Scholar]
- Vorwerk, D.; Schumann, M.; Schulz, D. PEM-electrolyzer modelling and control strategies in the extended node method for hybrid power system modelling. In Proceedings of the 8th International Hybrid Power Plants & Systems Workshop (HYB 2024), Hybrid Conference, Azores, Portugal, 14–15 May 2024; pp. 385–392. [Google Scholar] [CrossRef]
- Vorwerk, D.; Schulz, D. Extended Node Method for Steady-State Heating Network Calculation based on Electric Analogies. In Proceedings of the 2023 11th International Conference on Smart Grid (icSmartGrid), Paris, France, 4–7 June 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Maialen, B.; Thomas, J.-L. A review on synchronization methods for grid-connected three-phase VSC under unbalanced and distorted conditions. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–10. [Google Scholar]
- MathWorks, Specialized Power Systems. Available online: https://de.mathworks.com/help/sps/specialized-power-systems.html (accessed on 24 October 2024).
- Simbench, Datasets. Available online: https://simbench.de/de/datensaetze/ (accessed on 24 October 2024).




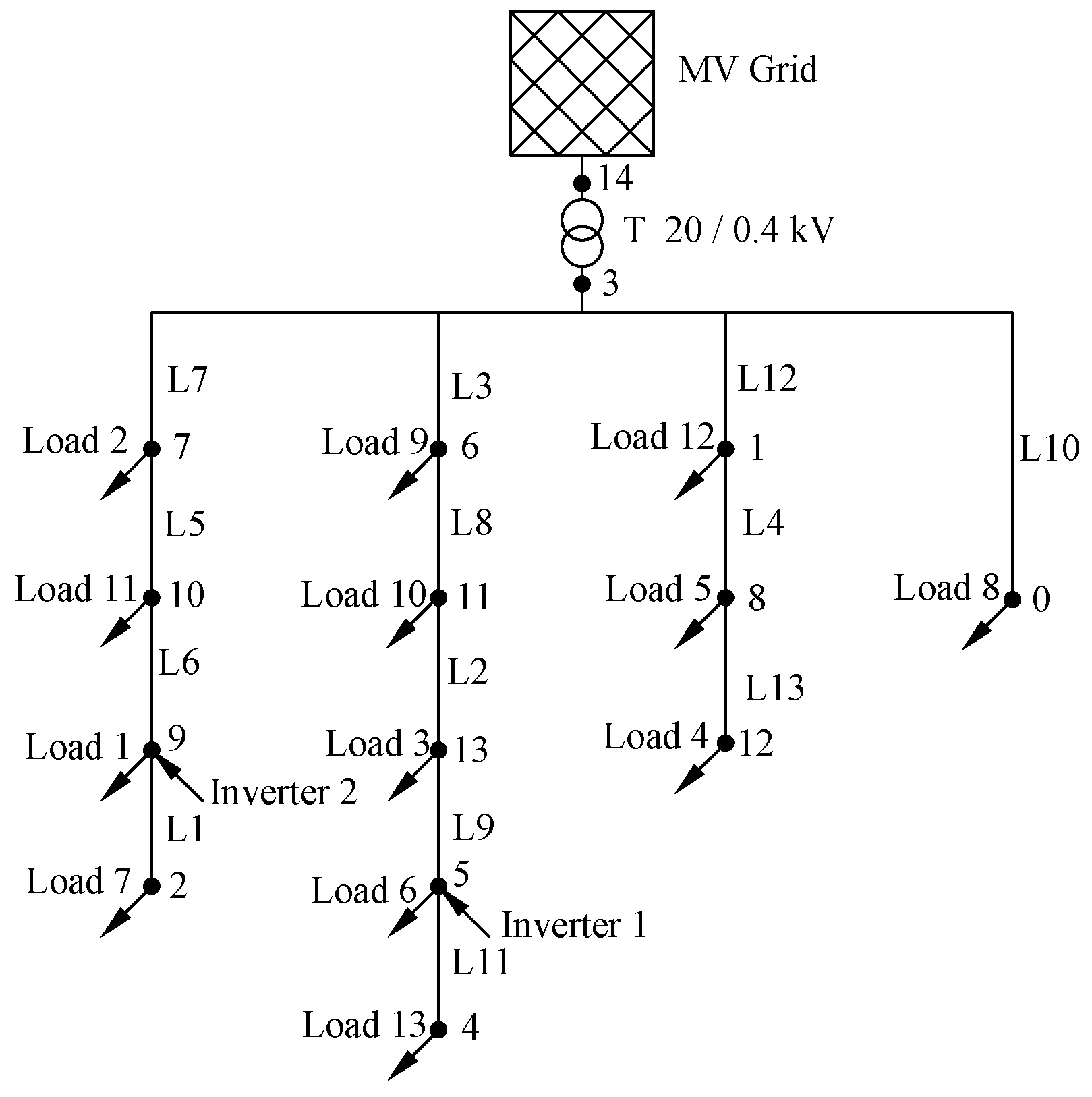


| Component Type | State Equation |
|---|---|
| L component | |
| R component | |
| C component |
| Component | Parameter |
|---|---|
| Inverter with LCL Filter | mH, , mH, , µF, V, kHz |
| PLL | , , kHz |
| Cascaded Controller | , , , , , , kHz |
| Feed-Forward Compensation | , s |
| Component | Parameter |
|---|---|
| MV Grid | kV, mH, , rad/s |
| Transformer | kV, V, , Type: Yy0, mH, |
| Load | Load Active and Reactive Power Demand, Study Case 1 | Impedance Parameters, Study Case 1 | Load Active and Reactive Power Demand, Study Case 2 | Impedance Parameters, Study Case 2 |
|---|---|---|---|---|
| Load 1 | kW, kvar | mH, | kW, kvar | µF, S |
| Load 2 | kW, kvar | mH, | kW, kvar | mH, |
| Load 3 | kW, kvar | mH, | kW, kvar | mH, |
| Load 4 | kW, kvar | mH, | kW, kvar | mH, |
| Load 5 | kW, kvar | mH, | kW, kvar | mH, |
| Load 6 | kW, kvar | mH, | kW, kvar | µF, S |
| Load 7 | kW, kvar | mH, | kW, kvar | mH, |
| Load 8 | kW, kvar | mH, | kW, kvar | mH, |
| Load 9 | kW, kvar | mH, | kW, kvar | mH, |
| Load 10 | kW, kvar | mH, | kW, kvar | mH, |
| Load 11 | kW, kvar | mH, | kW, kvar | µF, |
| Load 12 | kW, kvar | mH, | kW, kvar | mH, |
| Load 13 | kW, kvar | mH, | kW, kvar | mH, |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vorwerk, D.; Schulz, D. Versatile LCL Inverter Model for Controlled Inverter Operation in Transient Grid Calculation Using the Extended Node Method. Energies 2025, 18, 344. https://doi.org/10.3390/en18020344
Vorwerk D, Schulz D. Versatile LCL Inverter Model for Controlled Inverter Operation in Transient Grid Calculation Using the Extended Node Method. Energies. 2025; 18(2):344. https://doi.org/10.3390/en18020344
Chicago/Turabian StyleVorwerk, Daniela, and Detlef Schulz. 2025. "Versatile LCL Inverter Model for Controlled Inverter Operation in Transient Grid Calculation Using the Extended Node Method" Energies 18, no. 2: 344. https://doi.org/10.3390/en18020344
APA StyleVorwerk, D., & Schulz, D. (2025). Versatile LCL Inverter Model for Controlled Inverter Operation in Transient Grid Calculation Using the Extended Node Method. Energies, 18(2), 344. https://doi.org/10.3390/en18020344







