Experimental Characterization of Reversible Oil-Flooded Twin-Screw Compressor/Dry Expander for a Micro-Scale Compressed Air Energy Storage System
Abstract
:1. Introduction
1.1. State of the Art
1.1.1. CAES
1.1.2. Twin-Screw Volumetric Machines
1.2. Scope of the Paper
- -
- Highlight the limitation of the tested technology when run as a dry expander with air, rather than as an oil-flooded machine;
- -
- Develop black-box models of the compressor and the expander, which allows ascertaining the performance of hypothetical systems, such as (but not limited to) a small-scale CAES system based on the reversible operation of the tested screw machines.
2. Experiments: Materials and Methods
2.1. Description of the Geometry of the Compressor
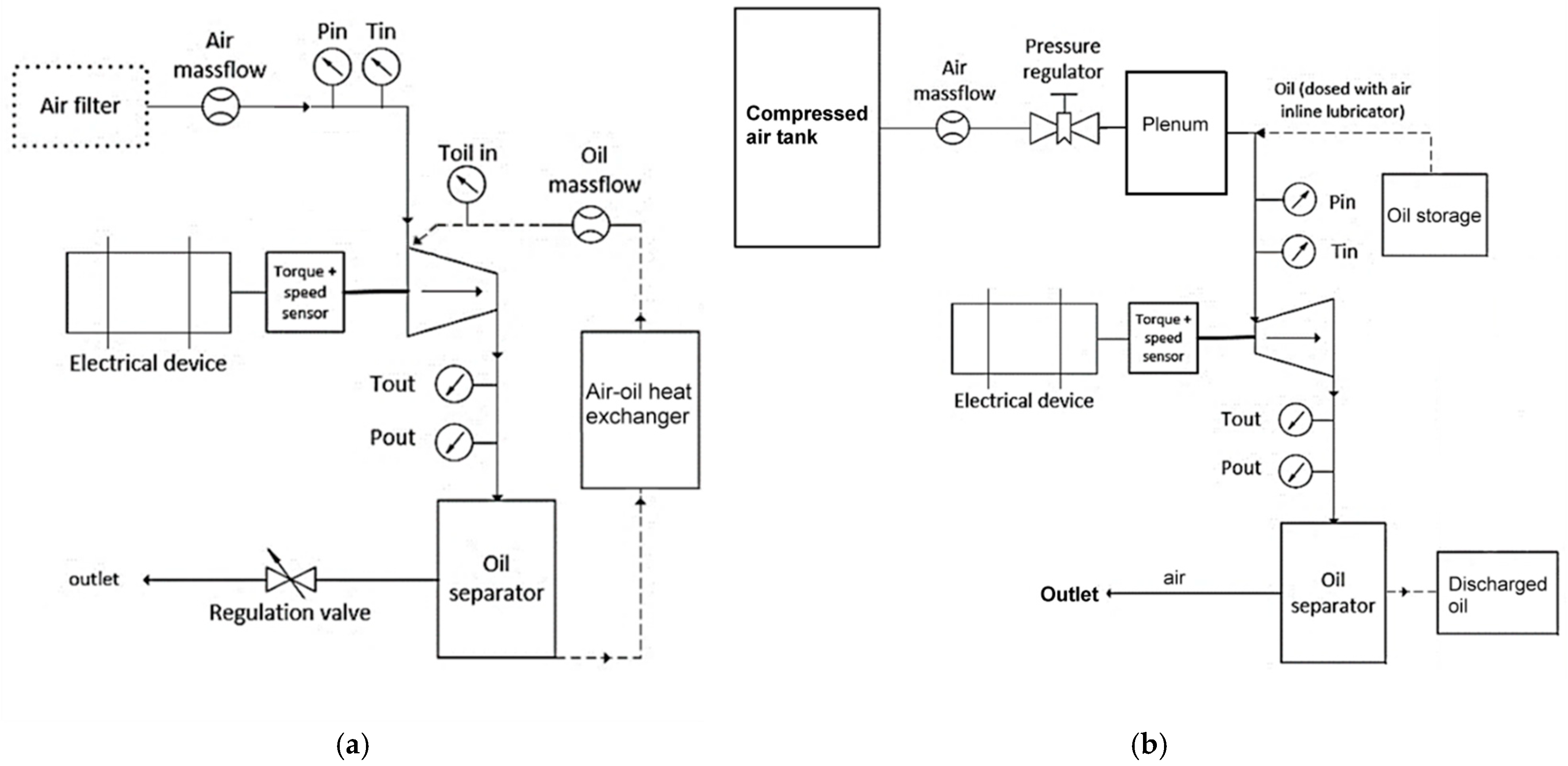
2.2. Test Bench Layout
- -
- An electrical DC machine that worked both as a motor and a generator.
- -
- Pipelines equipped with valves.
- -
- Pressure regulation system (in the compressor mode. The adjustment of the discharge pressure relies on a valve downstream of the device, while in the expander mode, the pressure of the air is regulated by a pressure regulator upstream of the inlet port of the device).
- -
- A 1 m3-volume plenum between the pressure regulator and the expander to damp the unavoidable pressure fluctuations.
- -
- Air filter, necessary to clean the environment air before compression.
- -
- Compressed air storage tank.
- -
- A separate oil circuit to ensure the proper operation of the compressor as an oil-flooded machine: it consists of a pipeline, an air–oil separator, and a heat exchanger to inject, collect, and cool the oil. The use of a circulation pump is not mandatory because the discharge pressure provided by the compressor ensured the oil circulation through the whole circuit.
- -
- The lack of a significant oil injection implied that the expander operated under unfavorable conditions, such as higher friction and leaks, thus demonstrating the potentiality to recover wasted energy without modifying the geometry of an existing compressor and reducing the investment and operating costs.
- -
- Poor lubrication entailed fewer difficulties during the operation of the expander because of a simplified design of the oil circuit and the lowest contamination of the working fluid [3].
- -
- The operation of the same device as an almost-dry expander and as a wet compressor provided the maximum variations in the performances between these two operating modes that otherwise would not be shown by using the expander as a wet machine.
2.3. Measurement Equipment and Direct Acquisitions
- -
- Thermocouples upstream and downstream of the machine (Type T, accuracy of 0.5 °C, and operating range from −40 °C to +350 °C);
- -
- Pressure sensors upstream and downstream of the machine (Aventics Series PE6, piezoresistive sensors, FSS ± 3%, and operating range of 0–10 bar, manufactured by EMERSON, website https://www.emerson.com/en-us);
- -
- A flowmeter to measure the air mass flow rate processed (VPflowScope thermal mass flow rate sensors, ±0.5% FSS (0 … 60 °C), and operating range of 0.23 … 80 m3/h produced by VPinstruments, Marlotlaan 1G 2614 GV The Netherlands, website https://www.vpinstruments.com);
- -
- A torque sensor between the twin-screw compressor and the electrical machine, whose rotating speed control depends on a dedicated driver (Kistler type 4503A, rated torque of 0.2 … 5000 Nm, speed ranges up to 50,000 rpm, and accuracy class in standard measuring, developed by Kistler, website https://www.kistler.com).
2.4. Indirect Measurements
2.4.1. Compressor Characterization
2.4.2. Expander Characterization
2.5. Design of Experiments
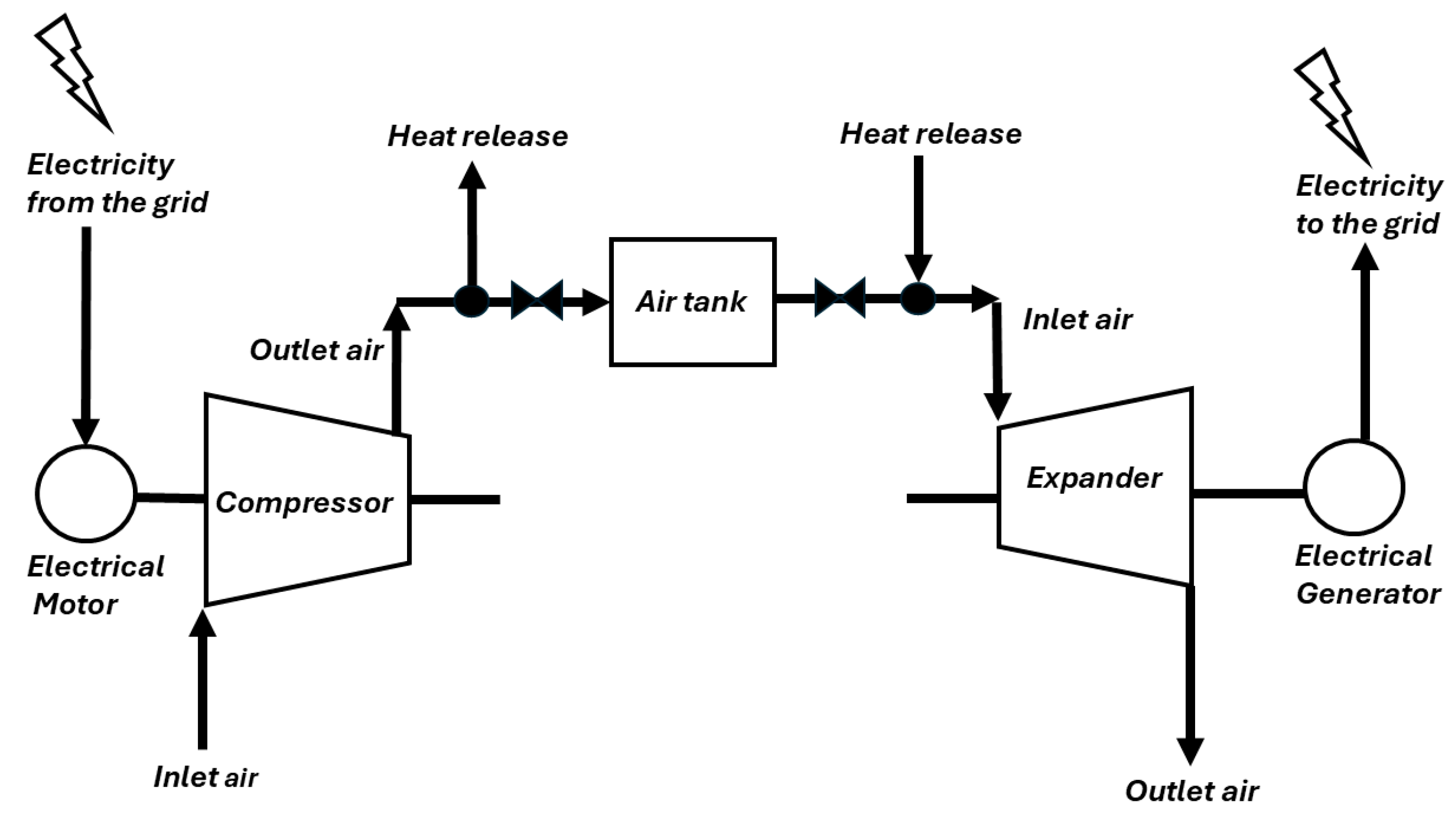
2.6. Micro-CAES Model
- -
- When an energy surplus is available, the device works as an oil-flooded twin-screw compressor to suck ambient air and compress it up to a given pressure, thus charging the reservoir (charge process);
- -
- The compressed air is then cooled to become isothermal with the surrounding environment. As a result, the compressed air is stored in the reservoir at the ambient temperature and a given pressure;
- -
- When energy production is required, the compressed air in the tank is first heated up to a specified temperature at the same pressure and then expanded in the device that works as a dry-running expander (discharge process).
- -
- CAES unitary roundtrip efficiency which exclusively assesses the behavior of the tested twin-screw machine in this hypothetical CAES system without considering the filling and emptying process of the reservoir. is expressed by Equation (12), in which the compression work per unit is calculated by considering that the compressor processes both air and oil.
- -
- Power ratio (PR, Equation (13)), expressing the percentage of the delivered power during the real discharge process with respect to the requested power in the charge process.
3. Results
3.1. Experimental Results of the Working Mode as a Compressor
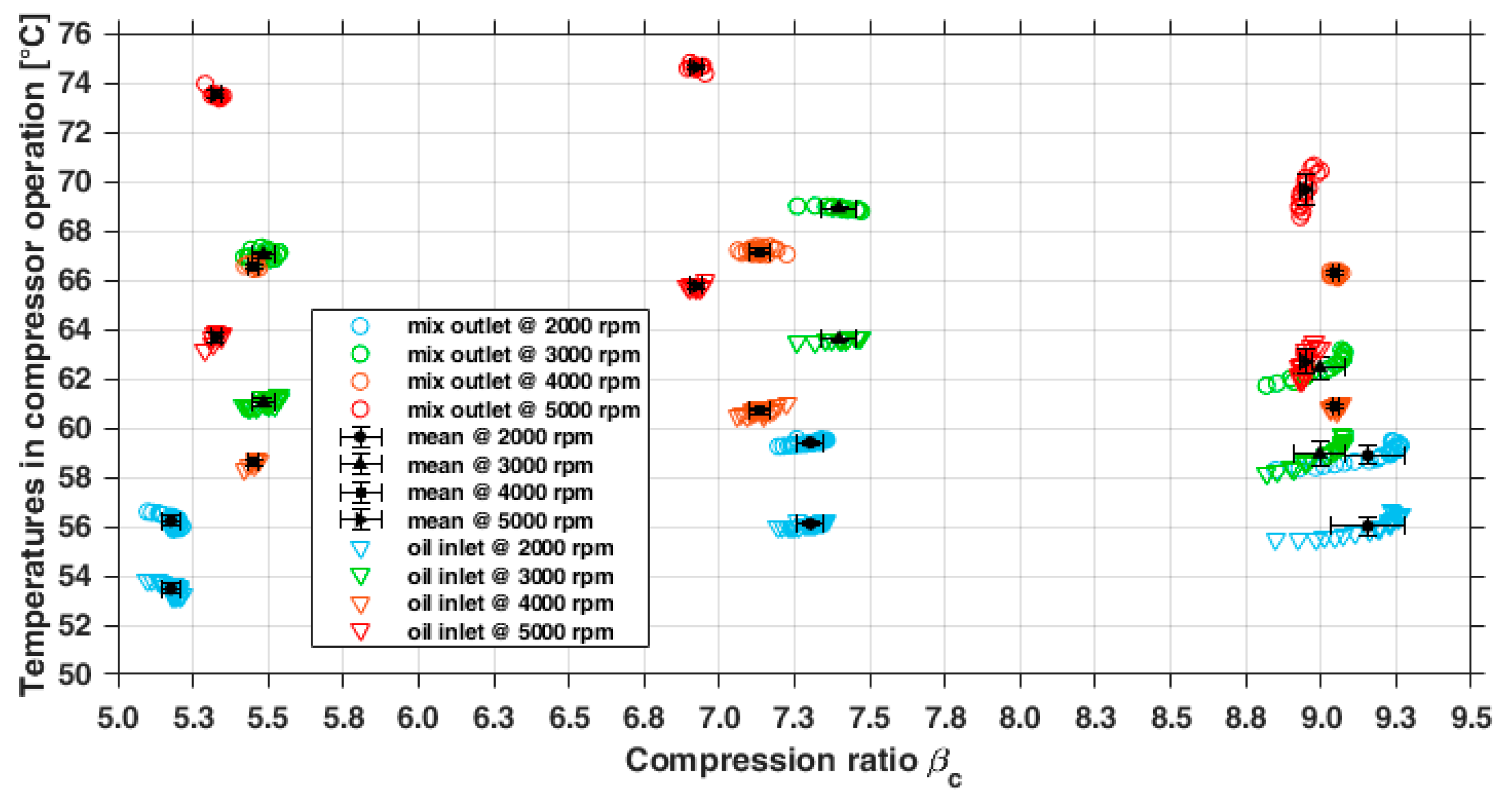
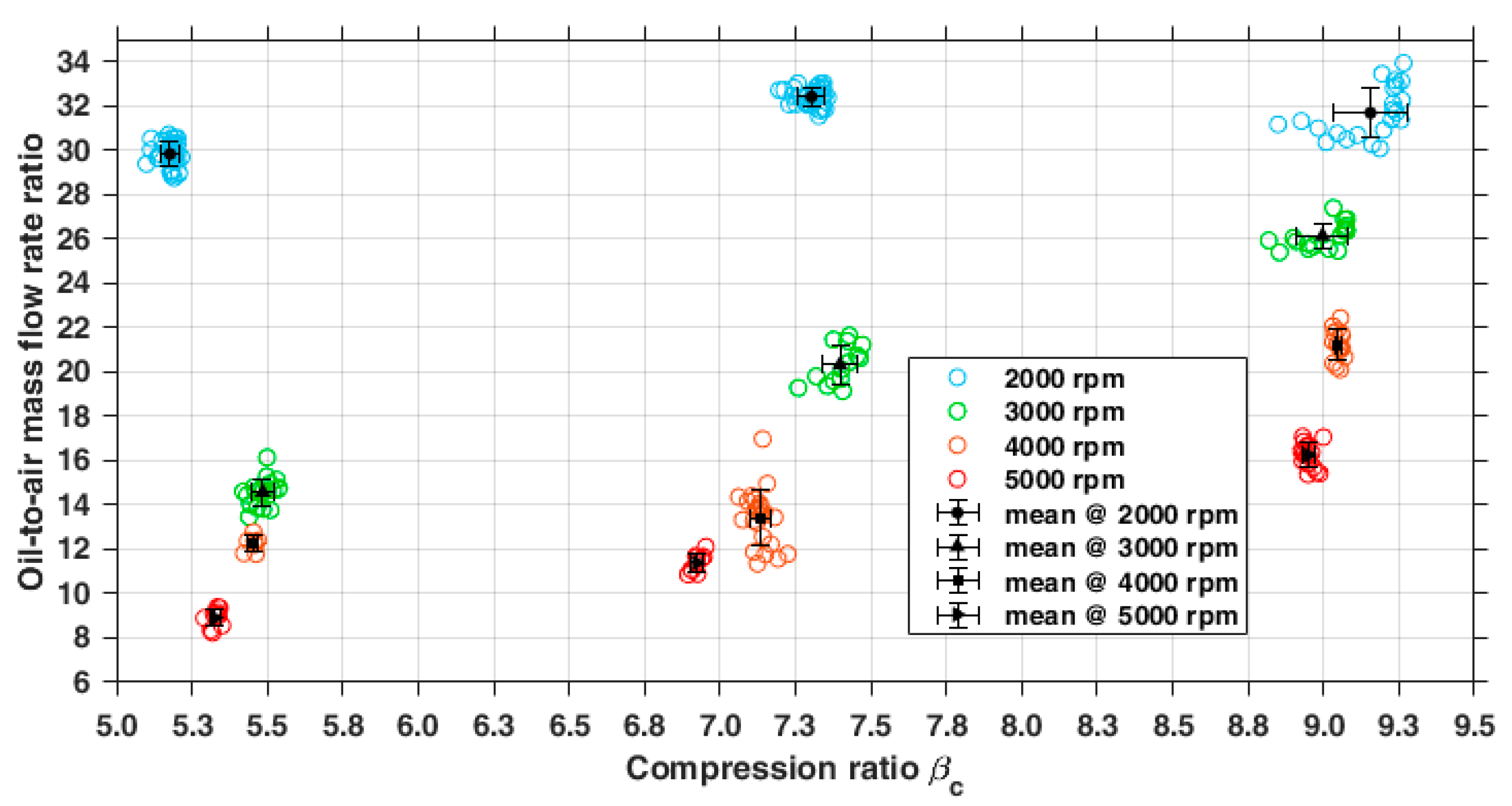
3.1.1. Direct Measurement: Characteristic Curves of the Compressor
- -
- Higher density of the fluid in the working chamber due to leak reductions, as a consequence of the increased rotating speed;
- -
- Greater air mass flow rate and, at the same time, decrease in the oil-to-air mass flow rate ratio, thus suggesting that the injected oil may not be sufficient to cool adequately the increased air mass within the device.
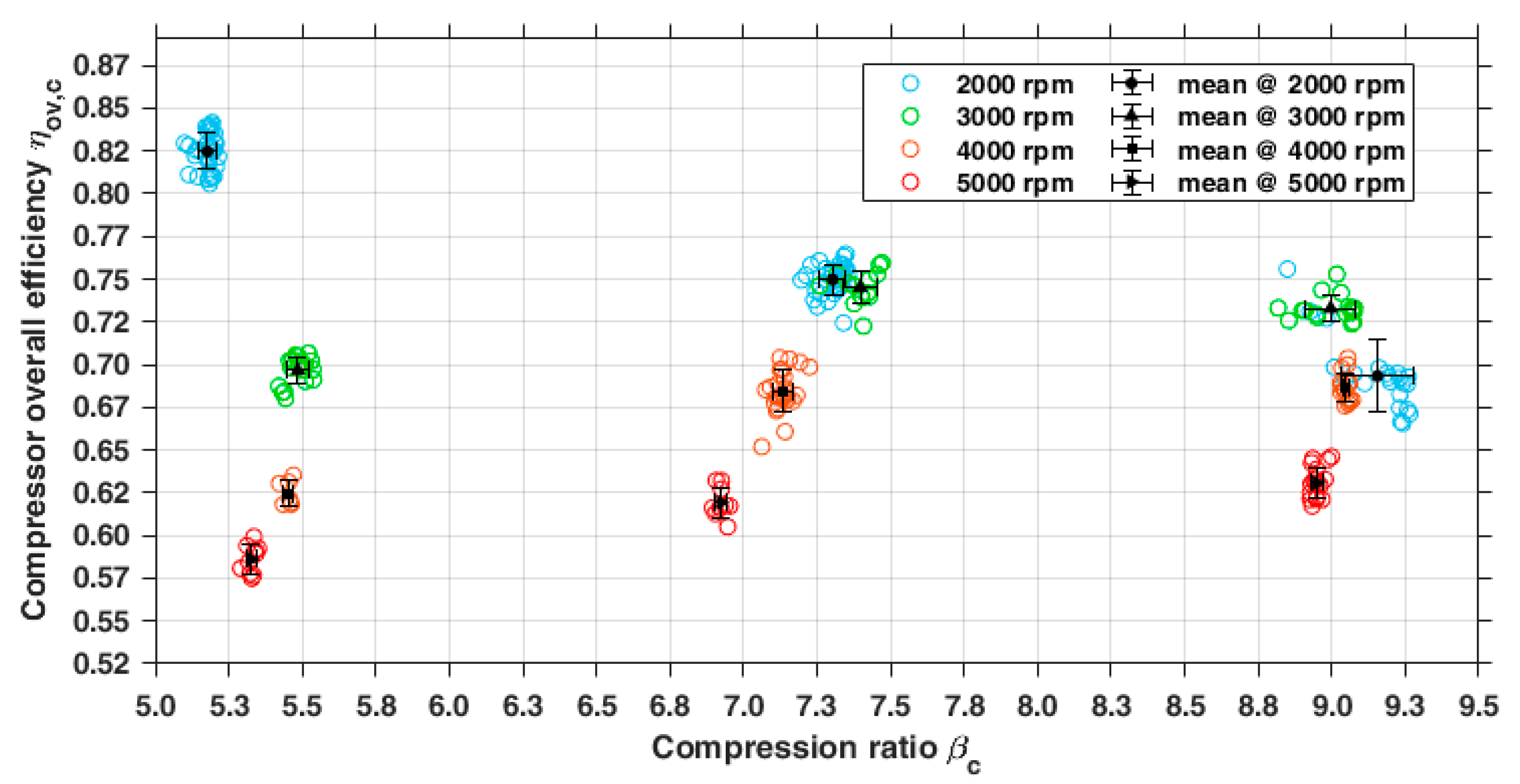
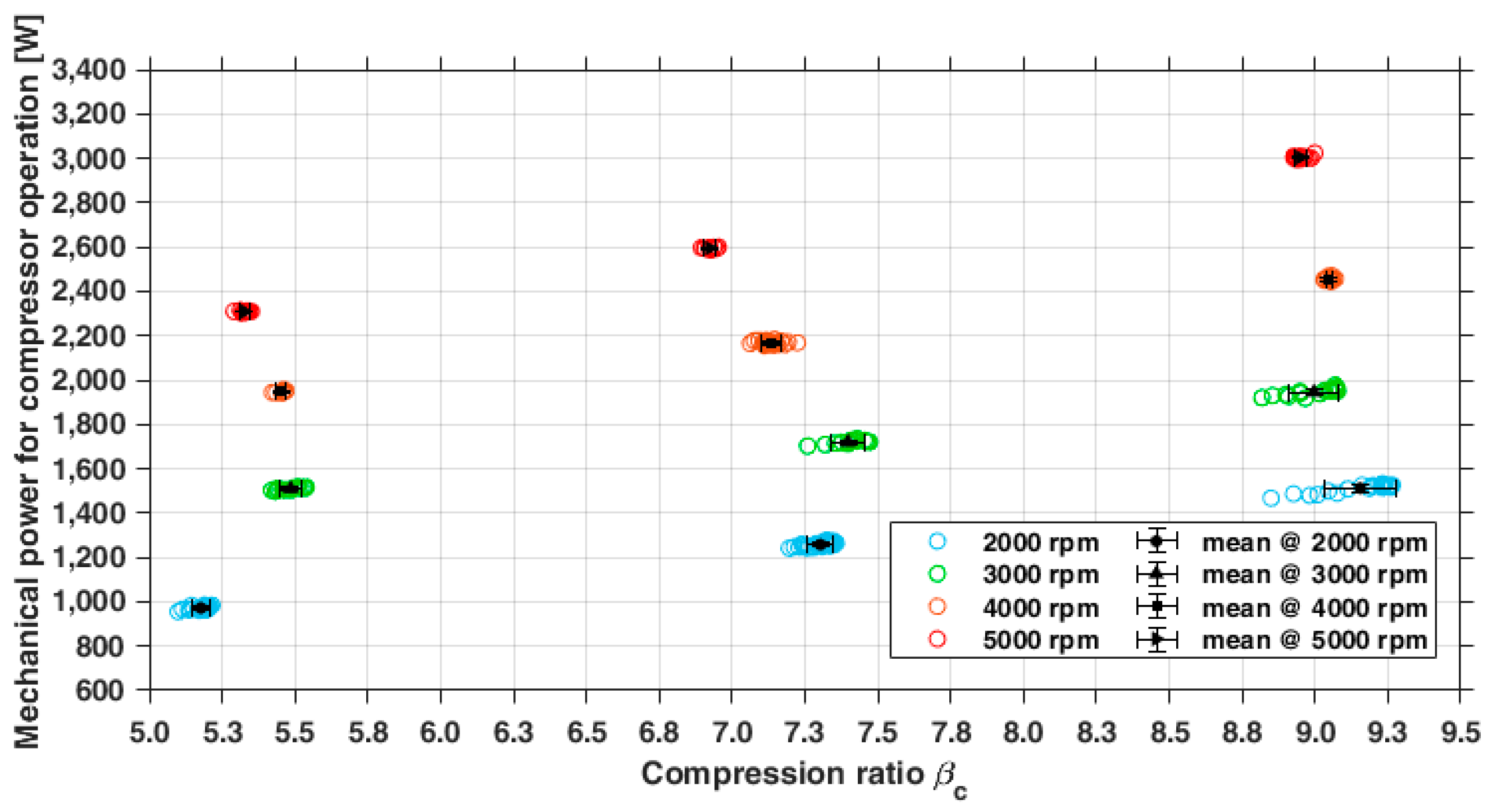
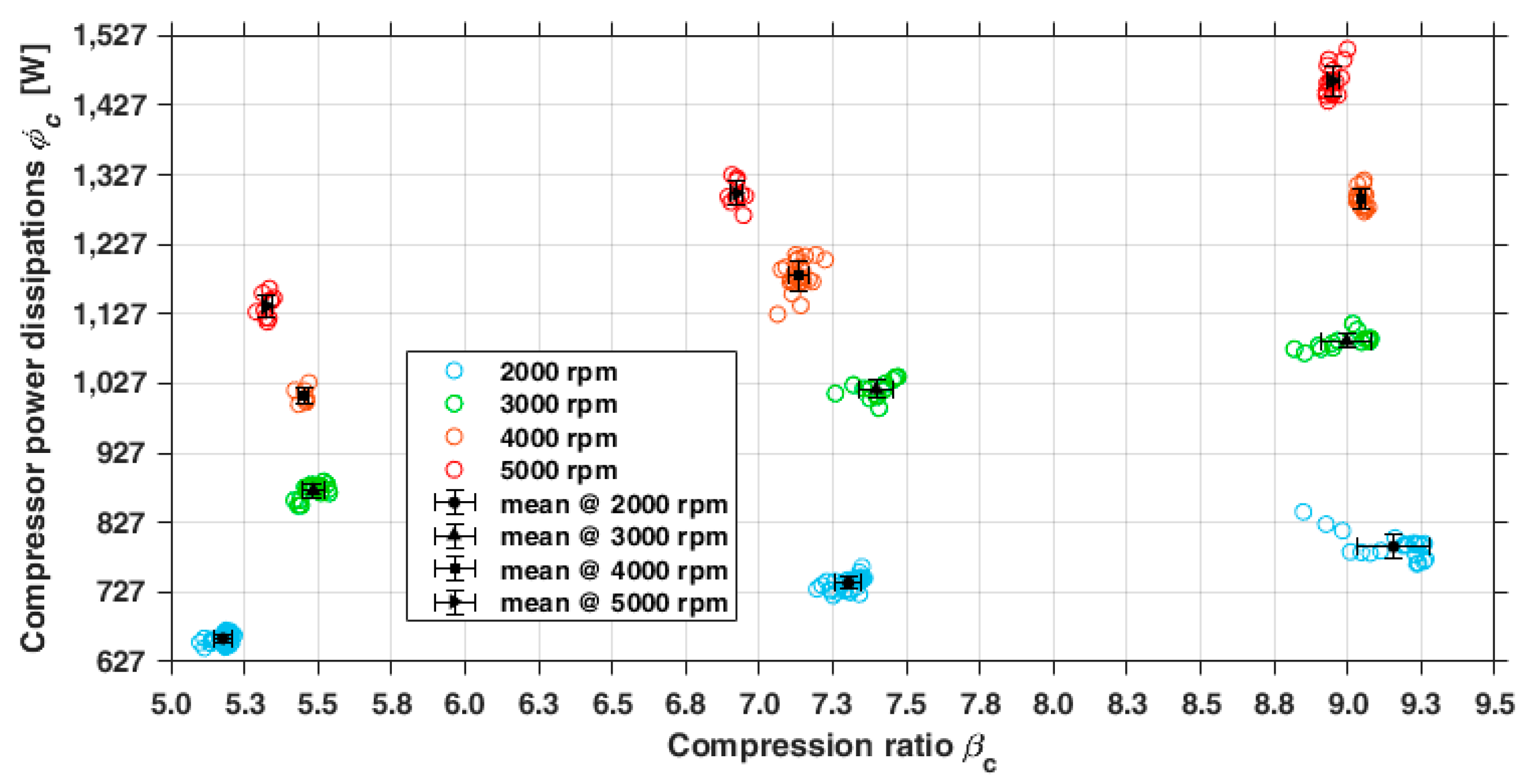
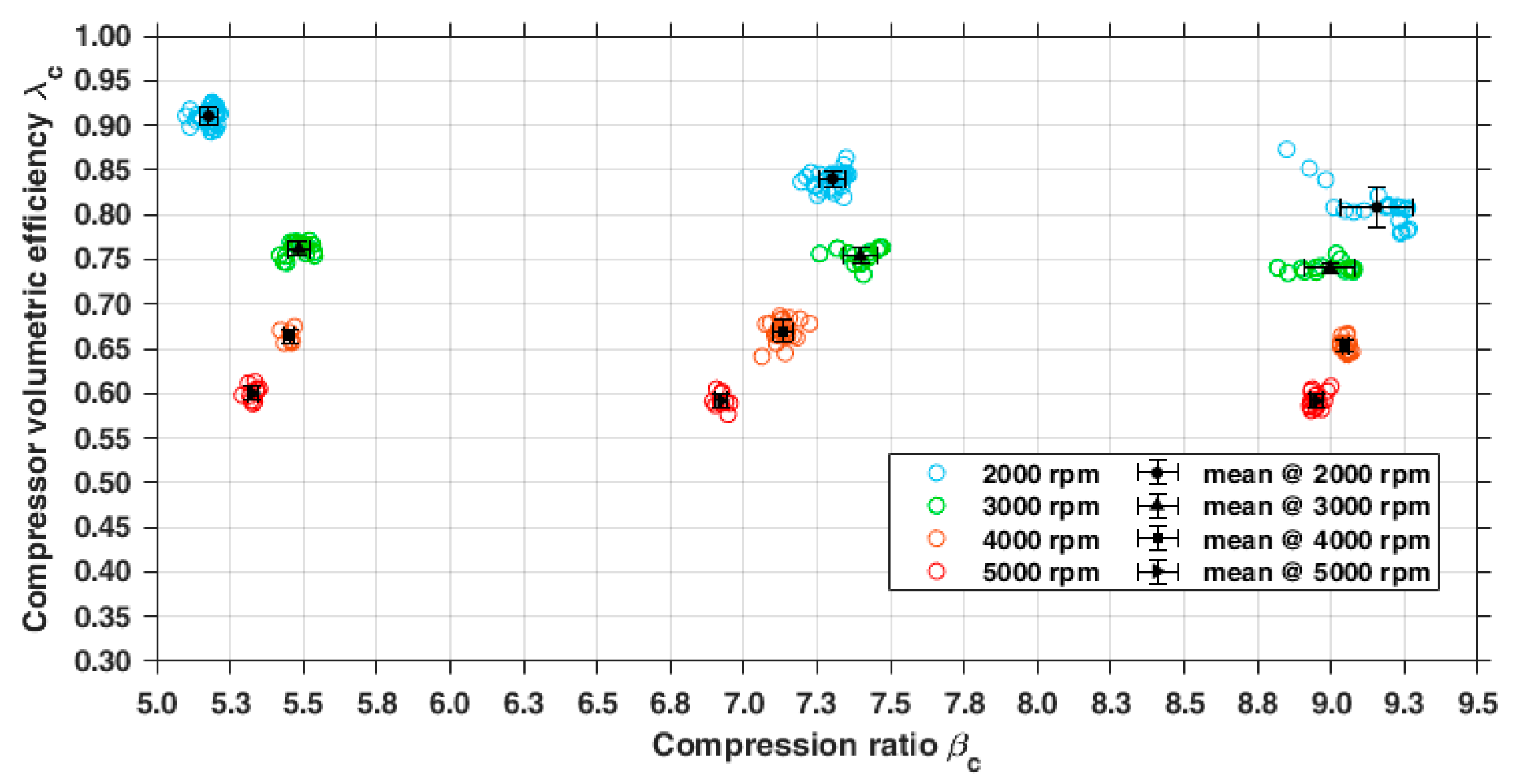
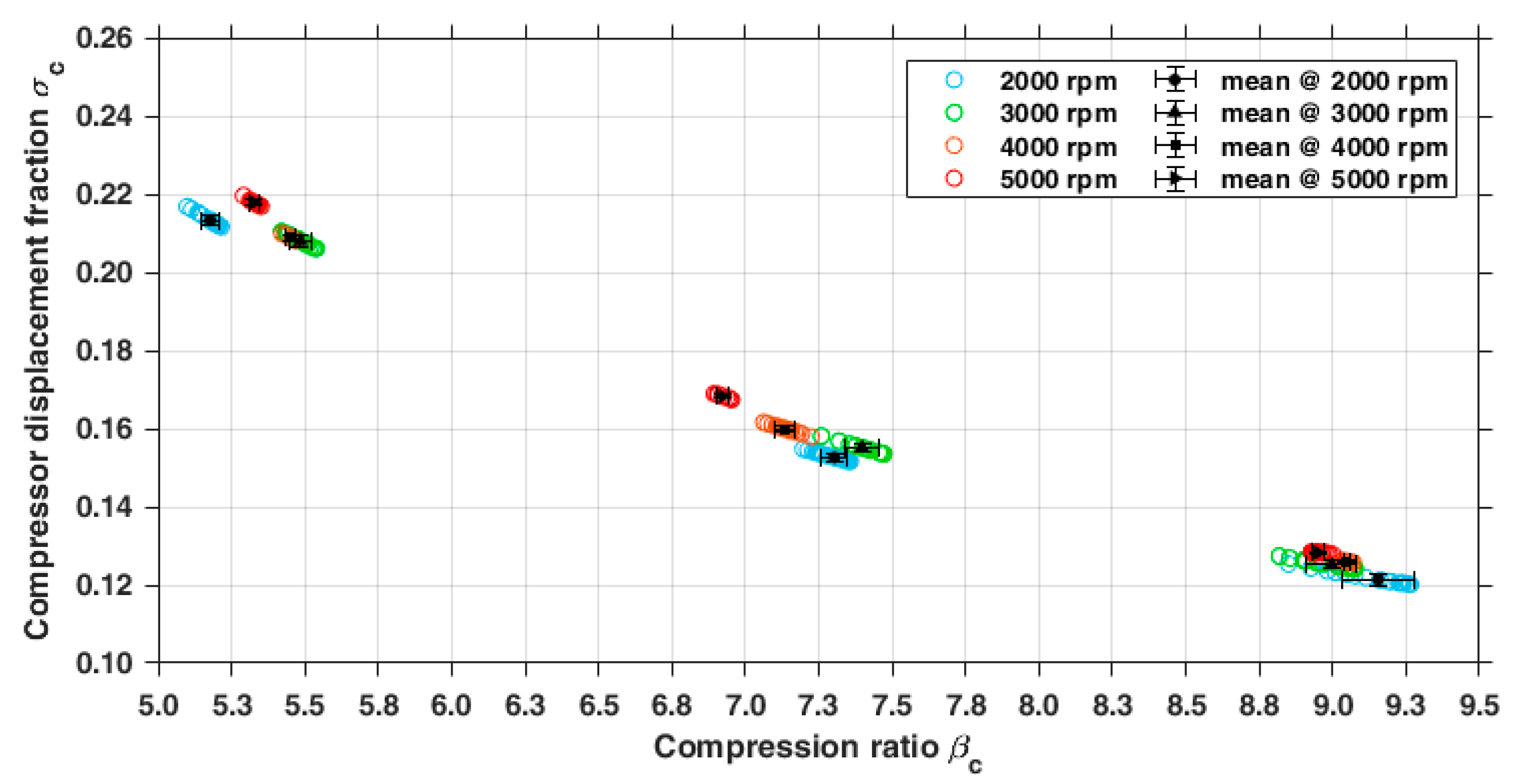
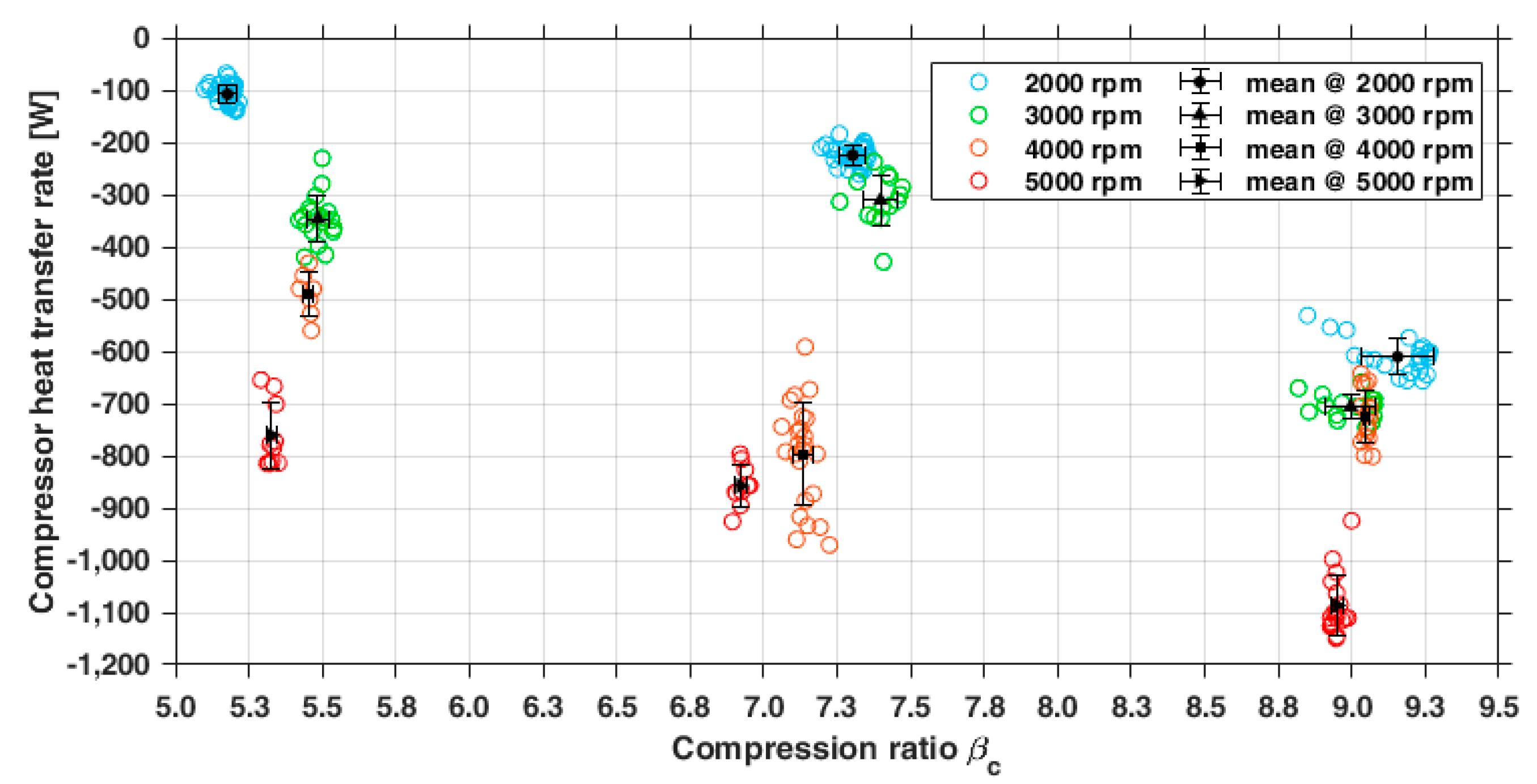
3.1.2. Indirect Measurements: Performance Parameters of the Compressor
- The lowest : the efficiency monotonically decreases from 0.8 to 0.6.
- Intermediate and the highest the overall compression efficiency is almost constant in the range of 2000–3000 rpm and then decreases to 0.6 while the rotating speed grows.
3.2. Experimental Results of the Working Mode as an Expander
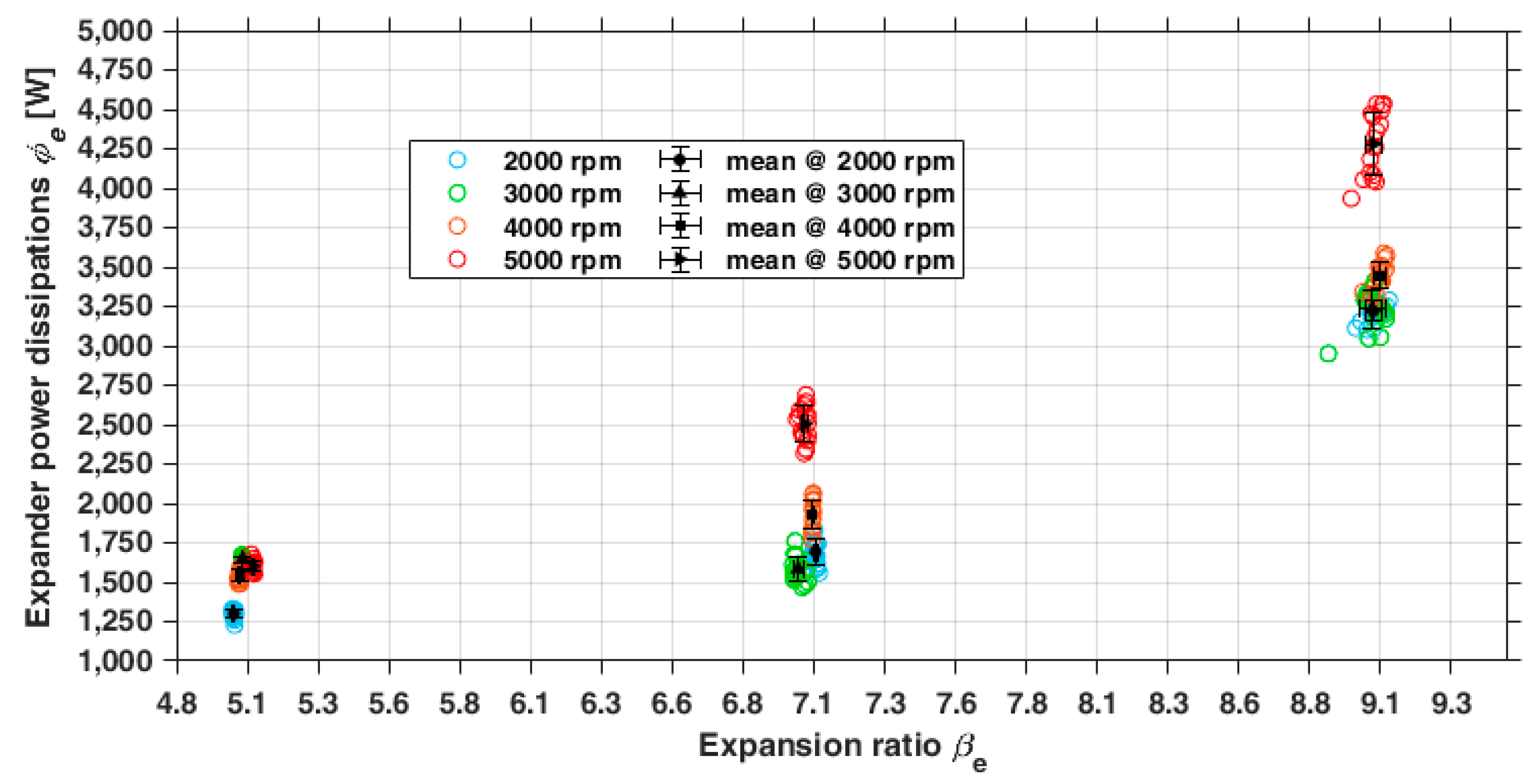
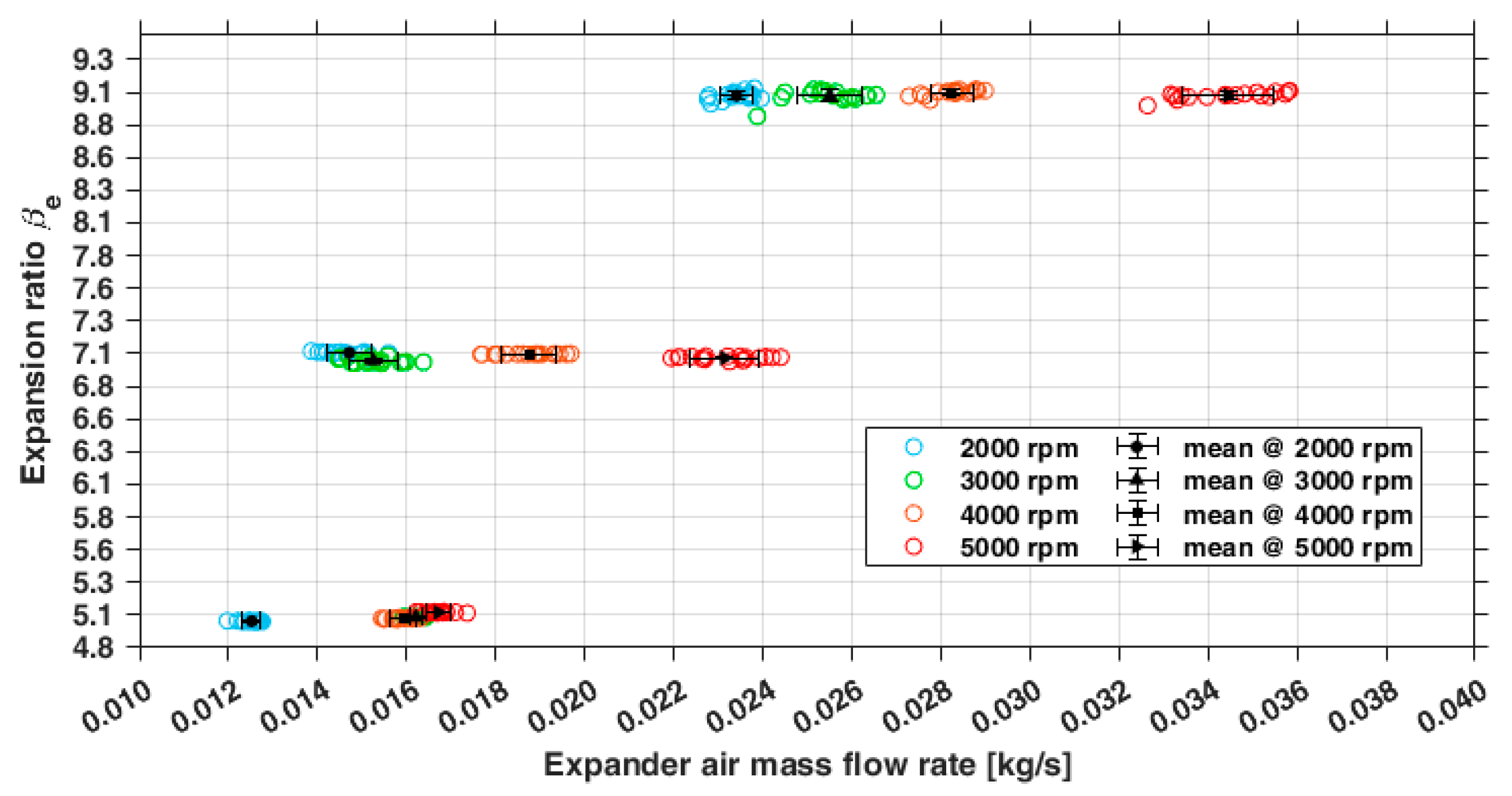
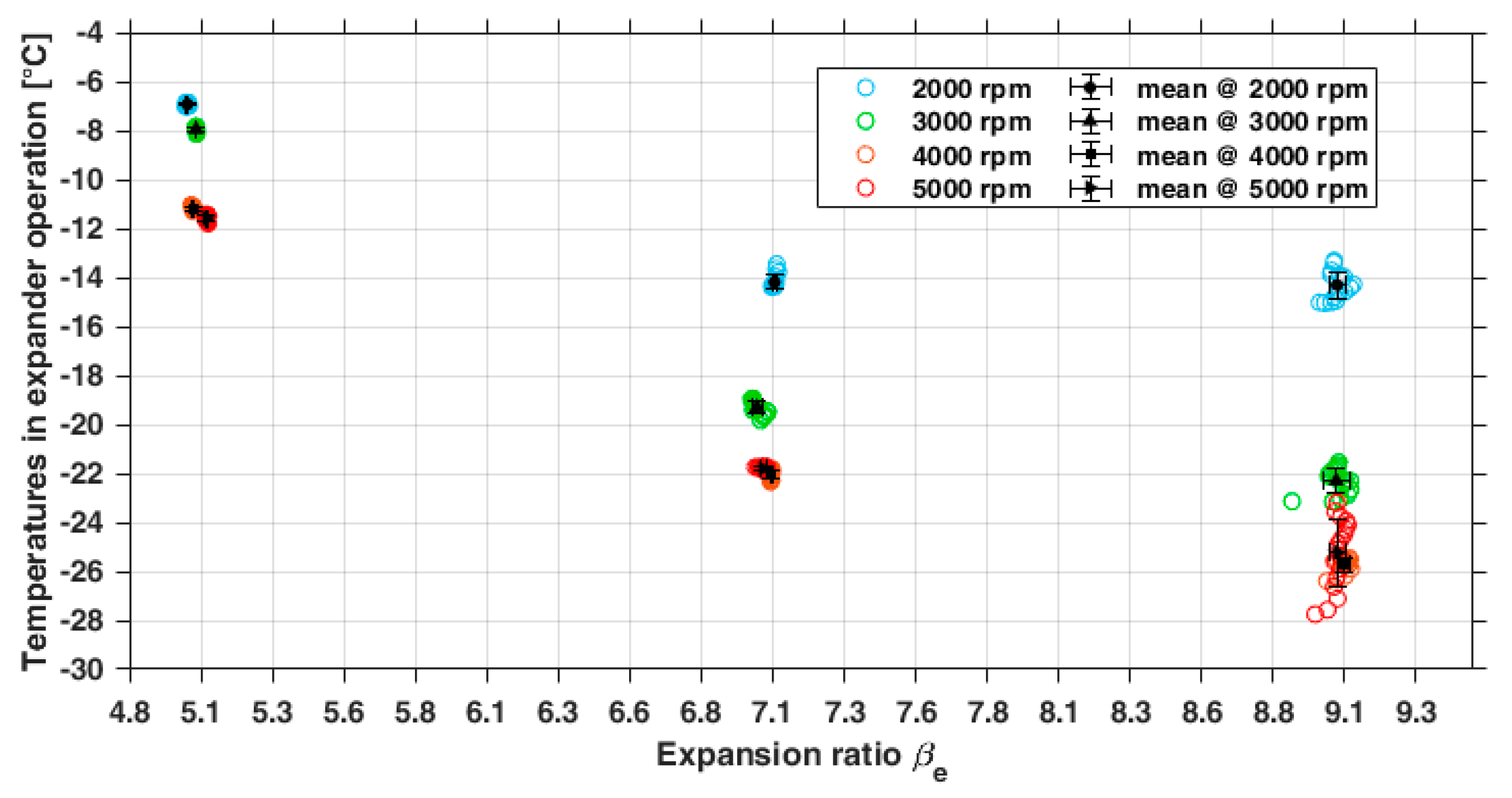
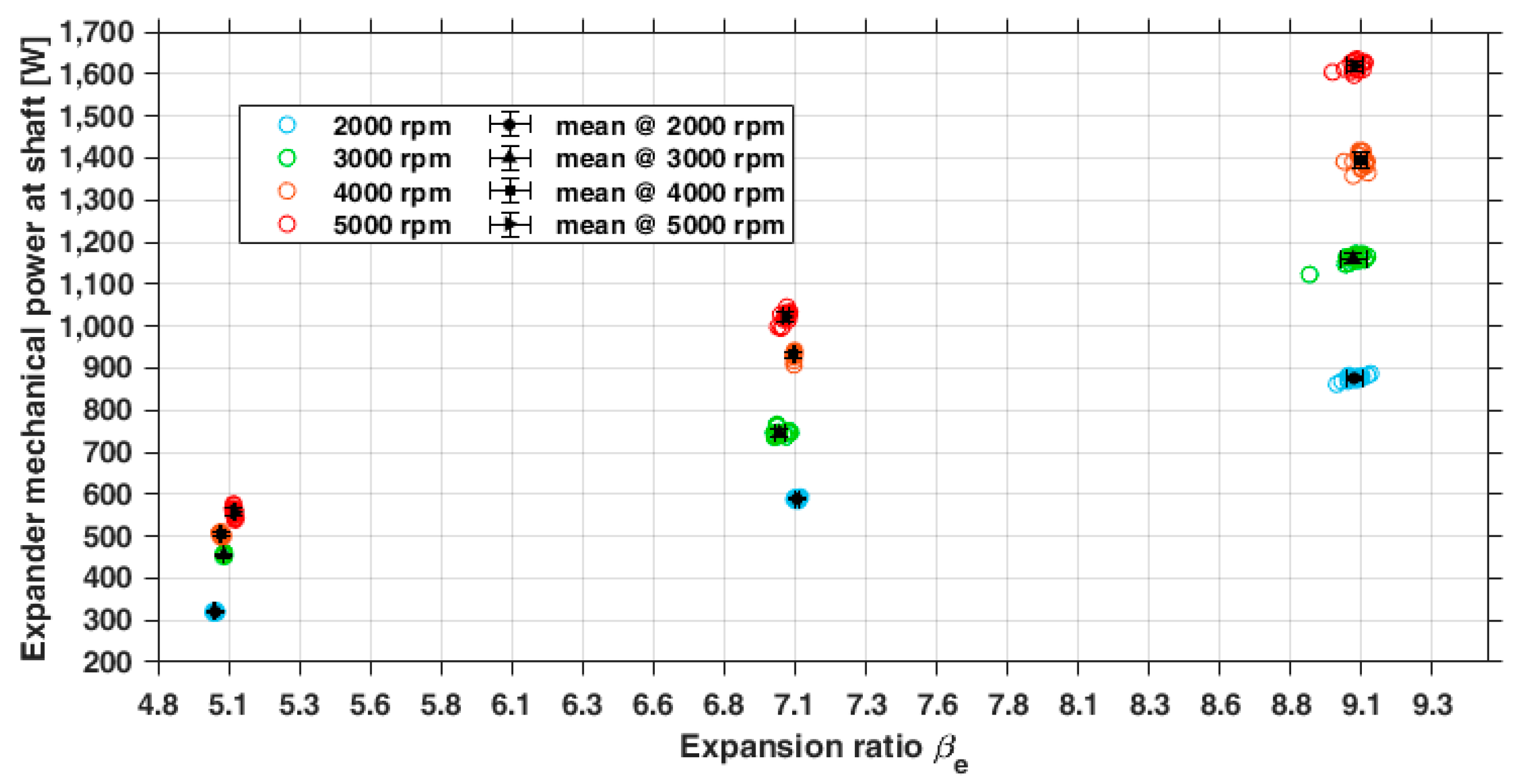
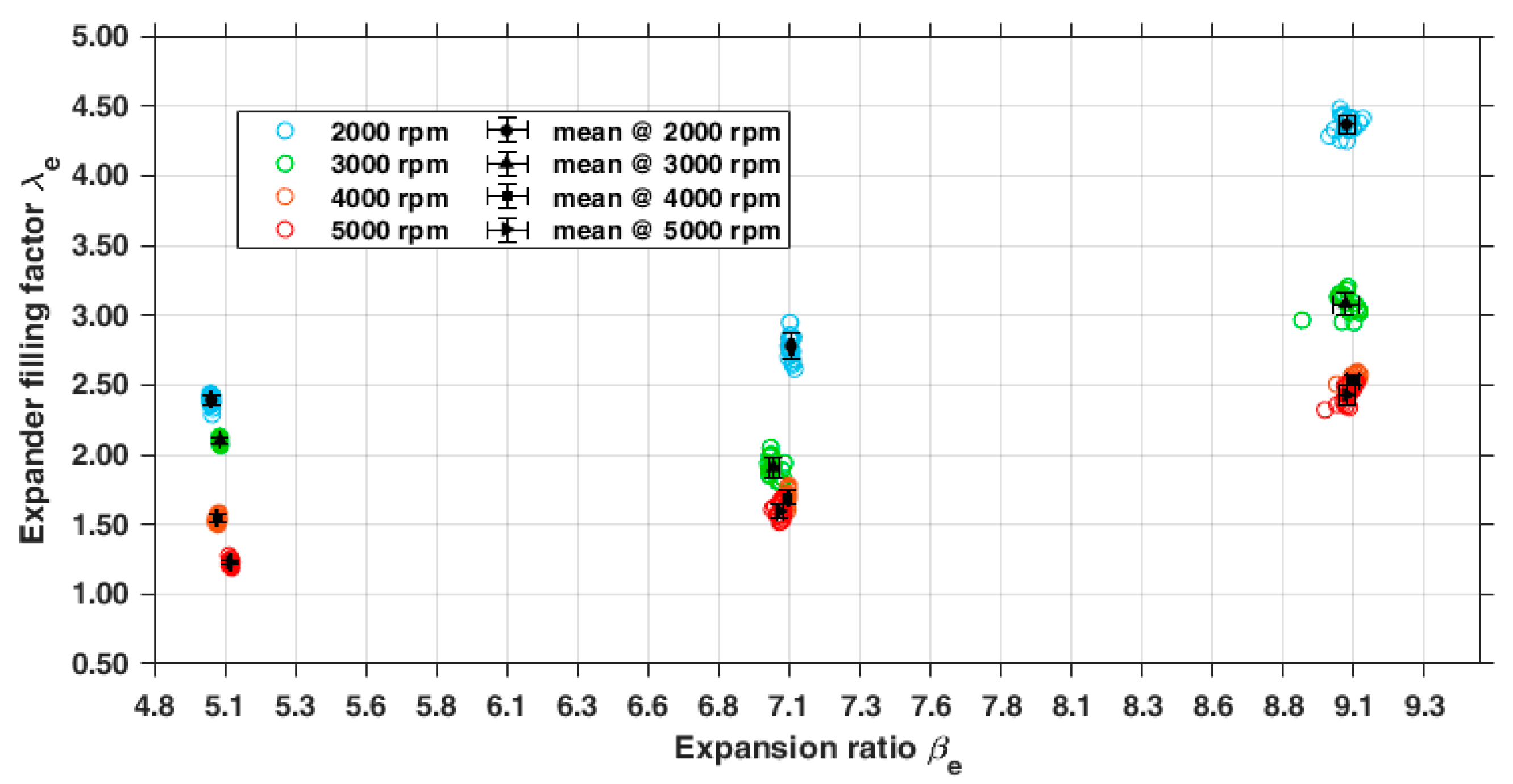
3.2.1. Direct Measurement: Characteristic Curves of the Expander
- -
- Among adjacent working chambers;
- -
- Along the casing between the inlet and exhaust ports because of the complete bypass of the working chambers.
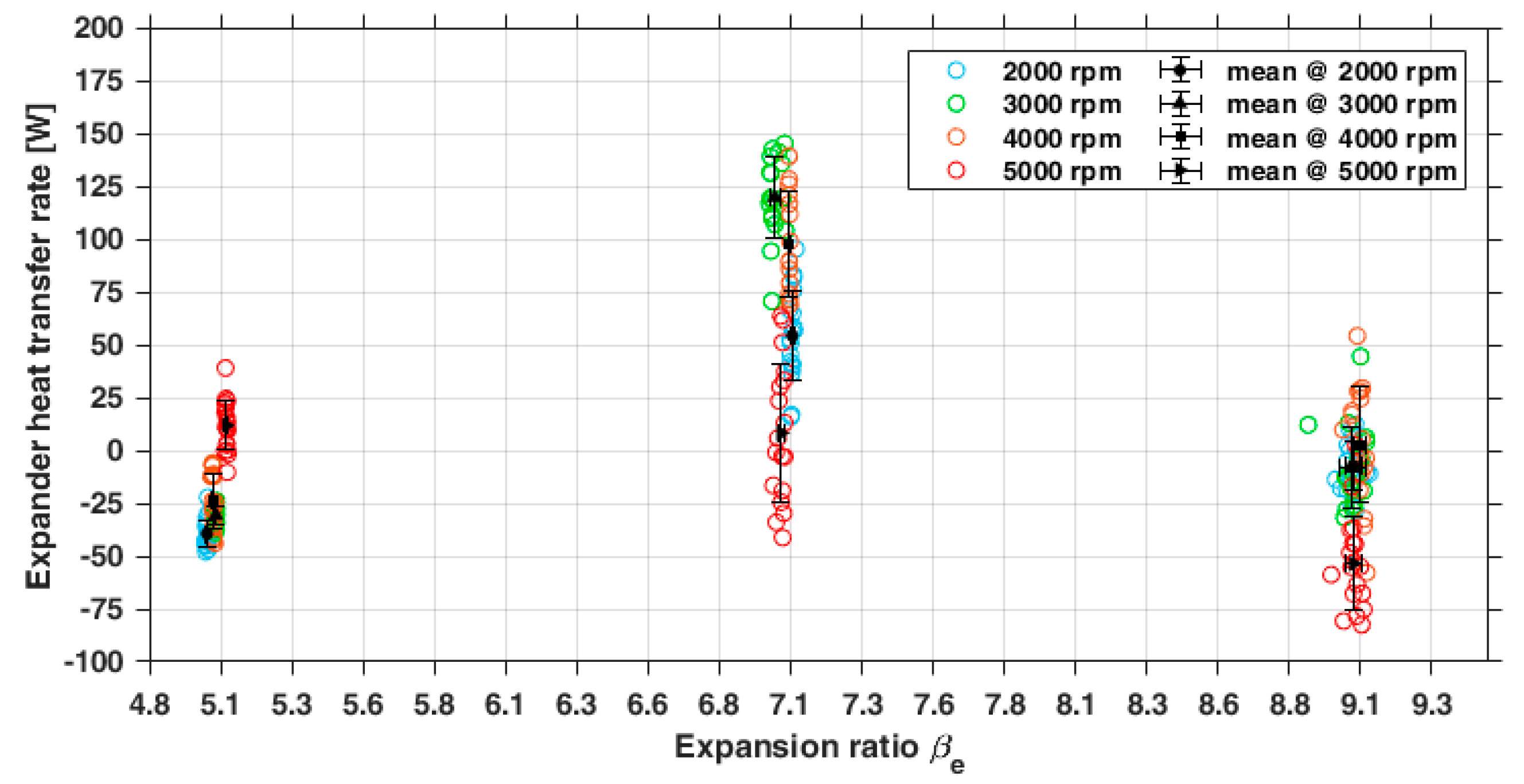
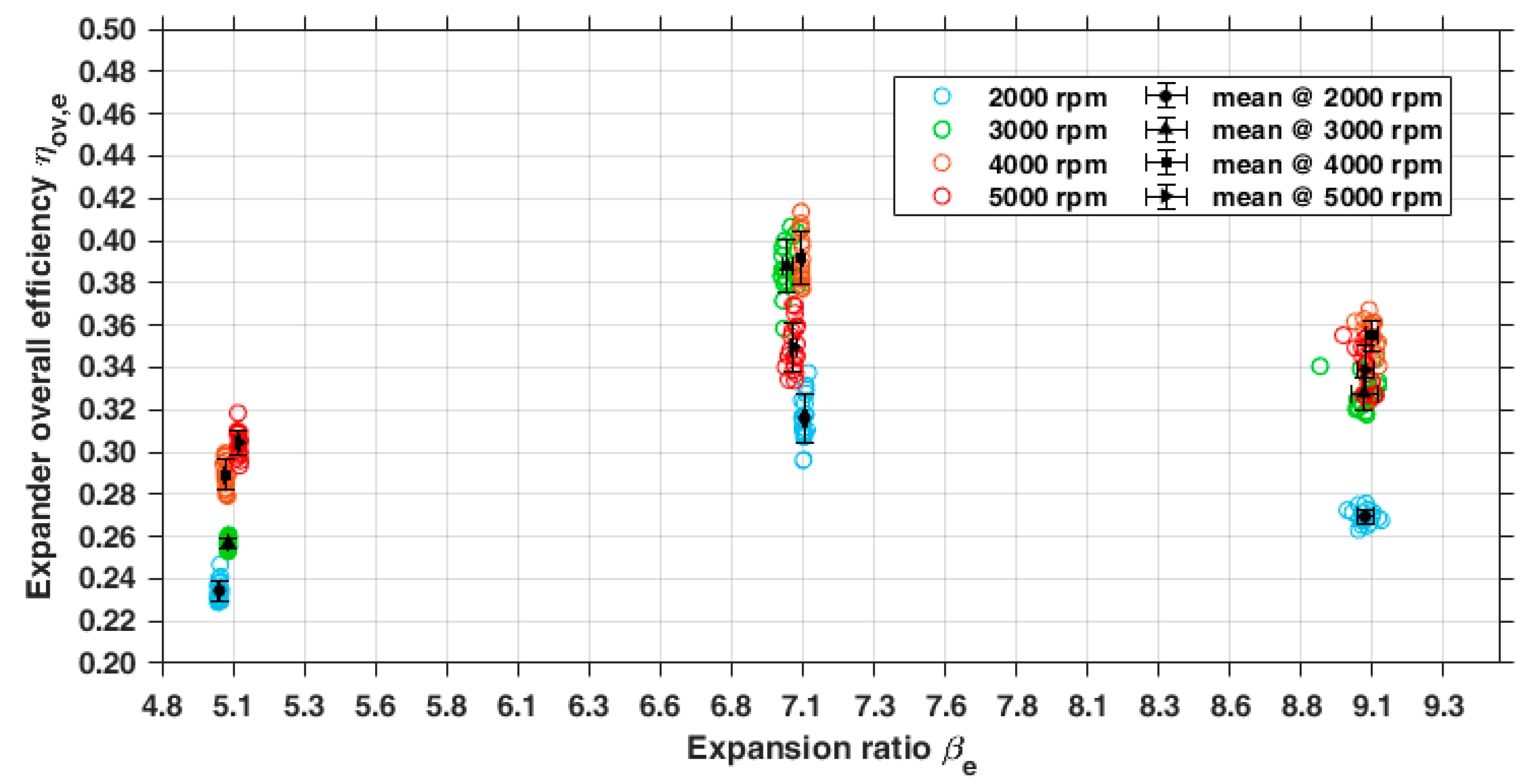
3.2.2. Indirect Measurements: Performance Parameters of the Expander
- -
- Rotor profiles designed for compressor operation and not suitable for the expansion process;
- -
- A mismatching between built-in volume ratio and fluid-specific volume ratio that caused under or over-expansion losses;
- -
- An improper value of the resulting cut-off grade that affected the expansion process;
- -
- Heat transfer due to the lack of thermal insulation.
4. Discussion
- -
- The geometries of the rotors and the corresponding meshing properties (e.g., sealing line and blow hole area) were designed for a compression process with oil and not for an expansion in dry conditions.
- -
- The limited oil flow rate required for the operation of the device as an almost-dry expander resulted in higher leaks and significant friction losses, although it was sufficient to prevent damages to the bearings.
- -
- The throttling pressure losses across the intake and exhaust ports were higher in the expander than in the compressor because the reverse flow direction resulted in lower flow coefficients of the ports.
- -
- Inject a significant oil quantity upstream of the device to obtain an air–oil mixture subsequently conveyed to its suction port;
- -
- Inject the oil within the device by the oil inlet port accommodated the casing, thus creating the air–oil mixture inside each working chamber.
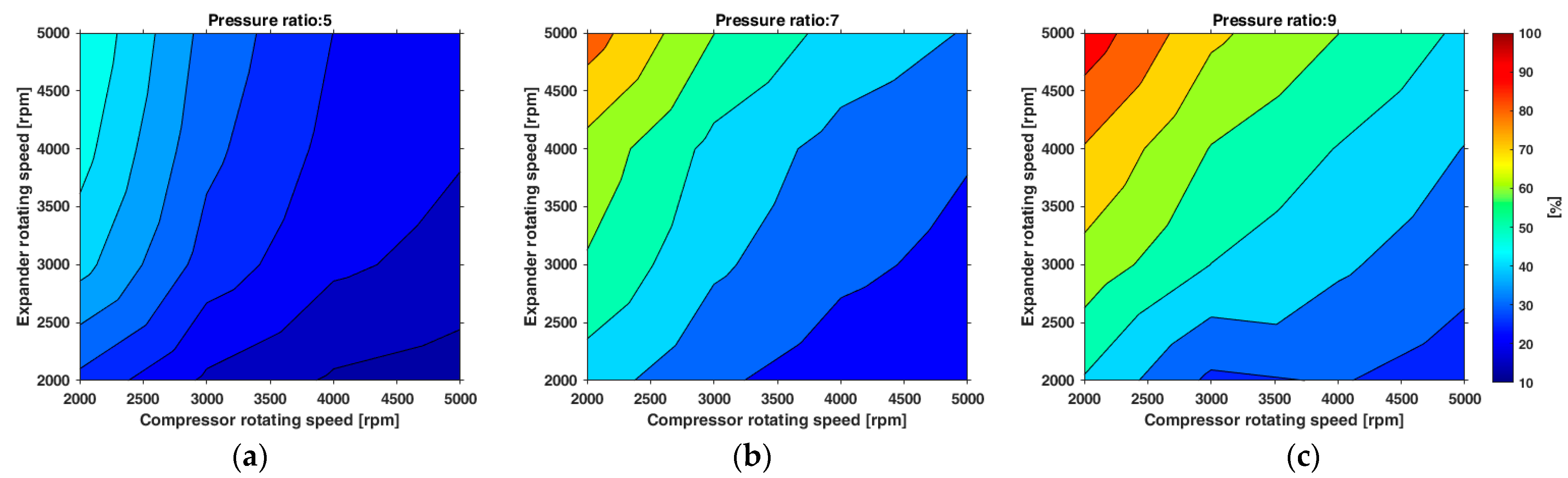
Analysis of the Operation of the Screw Device in a CAES System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Analysis of the Compressor Operating Mode
Appendix A.2. Analysis of the Expander Operating Mode
Appendix B
Micro-CAES Key Perfomance Indicators’ Calculations
References
- Leszczyński, J.S.; Gryboś, D.; Markowski, J. Analysis of optimal expansion dynamics in a reciprocating drive for a micro-CAES production system. Appl. Energy 2023, 350, 121742. [Google Scholar] [CrossRef]
- Sun, J.; Peng, B.; Zhu, B.; Li, Y. Research on the performance characteristics of an oil-free scroll expander that is applied to a micro-scale compressed air energy storage system. J. Energy Storage 2023, 63, 106896. [Google Scholar] [CrossRef]
- Quoilin, S.; Van Den Broek, M.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic survey of organic rankine cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar] [CrossRef]
- Olabi, G.; Wilberforce, T.; Ramadan, M.; Ali, M.; Hai, A. Compressed air energy storage systems: Components and operating parameters—A review. J. Energy Storage 2021, 34, 102000. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Xie, D.; Wu, H. Unsteady characteristic and flow mechanism of a scroll compressor in small-scale compressed air energy storage system. J. Energy Storage 2022, 51, 104368. [Google Scholar] [CrossRef]
- Chen, S.; Arabkoohsar, A.; Zhu, T.; Pagh, M. Development of a micro-compressed air energy storage system model based on experiments. Energy 2020, 197, 117152. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Li, M.; Chen, T.; Wang, Z. An optimal matching strategy for screw compressor for heat pump applications. Appl. Therm. Eng. 2018, 132, 333–340. [Google Scholar] [CrossRef]
- Imran, M.; Usman, M.; Park, B.S.; Lee, D.H. Volumetric expanders for low grade heat and waste heat recovery applications. Renew. Sustain. Energy Rev. 2016, 57, 1090–1109. [Google Scholar] [CrossRef]
- Kovacevic, N.S.K.S. Screw Compressors Mathematical Modelling and Performance Calculation; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Singh, P.; Bowman, J. Heat Transfer in Oil-Flooded Screw Compressors. In Proceedings of the International Compressor Engineering Conference; 1986; pp. 135–153. Available online: https://docs.lib.purdue.edu/icec/521 (accessed on 8 January 2025).
- Basha, N.; Kovacevic, A.; Stosic, N.; Smith, I. Effect of oil-injection on twin screw compressor performance. IOP Conf. Ser. Mater. Sci. Eng. 2018, 425, 012009. [Google Scholar] [CrossRef]
- Wu, X.; Xing, Z.; He, Z.; Wang, X.; Chen, W. Effects of lubricating oil on the performance of a semi-hermetic twin screw refrigeration compressor. Appl. Therm. Eng. 2017, 112, 340–351. [Google Scholar] [CrossRef]
- Li, J.; Wu, H.; Wang, B.; Xing, Z.; Shu, P. Research on the performance of water-injection twin screw compressor. Appl. Therm. Eng. 2009, 29, 3401–3408. [Google Scholar] [CrossRef]
- Wang, C.; Xing, Z.; Chen, W.; Sun, S.; He, Z. Analysis of the leakage in a water-lubricated twin-screw air compressor. Appl. Therm. Eng. 2019, 155, 217–225. [Google Scholar] [CrossRef]
- Shen, J.; Xing, Z.; Zhang, K.; He, Z.; Wang, X. Development of a water-injected twin-screw compressor for mechanical vapor compression desalination systems. Appl. Therm. Eng. 2016, 95, 125–135. [Google Scholar] [CrossRef]
- Shen, J.; Xing, Z.; Wang, X.; He, Z. Analysis of a single-effect mechanical vapor compression desalination system using water injected twin screw compressors. Desalination 2014, 333, 146–153. [Google Scholar] [CrossRef]
- Wu, H.; Lin, K.; Huang, H.; Xiong, B.; Zhang, B.; Xing, Z. Research on Effects of Vapor Injection on Twin-screw Compressor Performance. Int. J. Refrig. 2020, 118, 483–490. [Google Scholar] [CrossRef]
- Guerrato, D.; Nouri, J.M.; Stosic, N.; Arcoumanis, C.; Smith, I.K. Flow measurements in the discharge port of a screw compressor. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2008, 222, 201–210. [Google Scholar] [CrossRef]
- Guerrato, D.; Nouri, J.M.; Stosic, N.; Arcoumanis, C. Flow and pressure characteristics within a screw compressor. J. Phys. Conf. Ser. 2007, 85, 012012. [Google Scholar] [CrossRef]
- Read, M.; Smith, I.; Stosic, N. Port Flow Losses in Internally Geared Positive Displacement Machines. In Proceedings of the 24th International Compressor Engineering Conference at Purdue, West Lafayette, IN, USA, 9–12 July 2018; pp. 1–9. [Google Scholar]
- Tian, Y.; Lu, J.; Shen, J.; Wu, H.; Xing, Z. Optimization on shaft seals for a twin-screw steam compressor based on a novel uniform property region (UPR) model on discharge end-face. Int. J. Refrig. 2018, 91, 167–176. [Google Scholar] [CrossRef]
- Leibowitz, H.; Smith, I.K.; Stosic, N. Cost effective small scale ORC systems for power recovery from low grade heat sources. In Proceedings of the ASME 2006 International Mechanic Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006. [Google Scholar]
- Qiu, G.; Liu, H.; Riffat, S. Expanders for micro-CHP systems with organic Rankine cycle. Appl. Therm. Eng. 2011, 31, 3301–3307. [Google Scholar] [CrossRef]
- Antonelli, M.; Baccioli, A.; Francesconi, M.; Martorano, L. Numerical and experimental analysis of the intake and exhaust valves of a rotary expansion device for micro generation. Energy Procedia 2015, 81, 461–471. [Google Scholar] [CrossRef]
- Rahbar, K.; Mahmoud, S.; Al-Dadah, R.K.; Moazami, N.; Mirhadizadeh, S.A. Review of organic Rankine cycle for small-scale applications. Energy Convers. Manag. 2017, 134, 135–155. [Google Scholar] [CrossRef]
- Tang, H.; Wu, H.; Wang, X.; Xing, Z. Performance study of a twin-screw expander used in a geothermal organic Rankine cycle power generator. Energy 2015, 90, 631–642. [Google Scholar] [CrossRef]
- Wang, C.; Xing, Z.; Sun, S.; Chen, W.; He, Z. Experimental study on the performance of oil-free twin-screw expanders for recovering energy in fuel cell systems. Appl. Therm. Eng. 2020, 165, 114613. [Google Scholar] [CrossRef]
- Wang, C.; Xing, Z.; Sun, S.; He, Z. Loss analysis of oil-free twin-screw expanders for recovering energy in fuel cell systems by means of p-θ diagrams. Energy 2020, 201, 117581. [Google Scholar] [CrossRef]
- Tian, Y.; Xing, Z.; He, Z.; Wu, H. Modeling and performance analysis of twin-screw steam expander under fluctuating operating conditions in steam pipeline pressure energy recovery applications. Energy 2017, 141, 692–701. [Google Scholar] [CrossRef]
- Yao, S.; Zhang, Y.; Deng, N.; Yu, X.; Dong, S. Performance research on a power generation system using twin-screw expanders for energy recovery at natural gas pressure reduction stations under off-design conditions. Appl. Energy 2019, 236, 1218–1230. [Google Scholar] [CrossRef]
- Bianchi, G.; Kennedy, S.; Zaher, O.; Tassou, S.A.; Miller, J.; Jouhara, H. Numerical modeling of a two-phase twin-screw expander for Trilateral Flash Cycle applications. Int. J. Refrig. 2018, 88, 248–259. [Google Scholar] [CrossRef]
- Nikolov, A.; Brümmer, A. Two-phase mass flow rate through restrictions in liquid-flooded twin-screw compressors or expanders. Int. J. Refrig. 2023, 148, 152–167. [Google Scholar] [CrossRef]
- Wang, C.; Liu, M.; Li, Z.; Xing, Z.; Shu, Y. Performance improvement of twin-screw air expander used in PEMFC systems by two-phase expansion. Energy 2023, 273, 127249. [Google Scholar] [CrossRef]
- Francesconi, M.; Briola, S.; Antonelli, M. A Review on Two-Phase Volumetric Expanders and Their Applications. Appl. Sci. 2022, 12, 10328. [Google Scholar] [CrossRef]
- Daniarta, P.; Kolasìnski, S.; Imre, A.R. A Preliminary Design and Modeling Analysis of Two-Phase Volumetric Expanders for a Novel Reversible Organic Rankine-Based Cycle for Carnot Battery Technology. Appl. Sci. 2022, 12, 3557. [Google Scholar] [CrossRef]
- Steger, D.; Feist, M.; Schlücker, E. Using a screw-type machine as reversible compressor–expander in a Carnot Battery: An analytical study towards efficiency. Appl. Energy 2022, 316, 118950. [Google Scholar] [CrossRef]
- Eppinger, B.; Steger, D.; Regensburger, C.; Karl, J.; Schlücker, E.; Will, S. Carnot battery: Simulation and design of a reversible heat pump-organic Rankine cycle pilot plant. Appl. Energy 2021, 288, 116650. [Google Scholar] [CrossRef]
- He, Y.; Xing, L.; Zhang, Y.; Zhang, J.; Cao, F.; Xing, Z. Development and experimental investigation of an oil-free twin-screw air compressor for fuel cell systems. Appl. Therm. Eng. 2018, 145, 755–762. [Google Scholar] [CrossRef]
- Abdan, S.; Stosic, N.; Kovacevic, A.; Smith, I.; Asati, N. Oil drag loss in oil-flooded, twin-screw compressors. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023, 237, 1137–1144. [Google Scholar] [CrossRef]
- Wang, C.; Xing, Z.; Chen, W.; Yang, Q.; He, Z. Development of an oil free water-lubricated twin-screw air compressor. Appl. Therm. Eng. 2018, 143, 396–402. [Google Scholar] [CrossRef]
- Utri, M.; Brümmer, A. Improvement of the Efficiency of Twin-Screw Refrigeration Compressors by means of Dual Lead Rotors. In Proceedings of the 23rd International Compressor Engineering Conference at Purdue, West Lafayette, IN, USA, 11–14 July 2016; pp. 1–10. [Google Scholar]
- Basha, N.; Kovacevic, A.; Rane, S. Analysis of oil-injected twin-screw compressor with multiphase flow models. Designs 2019, 3, 54. [Google Scholar] [CrossRef]
- He, Z.; Wang, T.; Wang, X.; Peng, X.; Xing, Z. Experimental investigation into the effect of oil injection on the performance of a variable speed twin-screw compressor. Energies 2018, 11, 1342. [Google Scholar] [CrossRef]
- Dhayanandh, K.K.; Rameshkumar, K.; Sumesh, A.; Lakshmanan, N. Influence of oil injection parameters on the performance of diesel powered screw air compressor for water well application. Meas. J. Int. Meas. Confed. 2020, 152, 107323. [Google Scholar] [CrossRef]
- Abdan, S.; Stosic, N.; Kovacevic, A.; Smith, I.; Deore, P. Identification and analysis of screw compressor mechanical losses. IOP Conf. Ser. Mater. Sci. Eng. 2018, 425, 012015. [Google Scholar] [CrossRef]
- Francesconi, M.; Antonelli, M. A numerical model for the prediction of the fluid dynamic and mechanical losses of a Wankel-type expansion device. Appl. Energy 2017, 205, 225–235. [Google Scholar] [CrossRef]
- Francesconi, M.; Caposciutti, G.; Antonelli, M. An experimental and numerical analysis of the performances of a Wankel steam expander. Energy 2018, 164, 615–626. [Google Scholar] [CrossRef]
- Wang, B.; Wu, X.; Wang, C.; Zhang, Z.; Li, Y.; Xing, Z. Performance improvement of twin screw refrigeration compressors for chillers by modifying the suction arrangement. Int. J. Refrig. 2024, 158, 100–110. [Google Scholar] [CrossRef]
- Fujiwara, M.; Osada, Y. Performance analysis of an oil-injected screw compressor and its application. Int. J. Refrig. 1995, 18, 220–227. [Google Scholar] [CrossRef]
- Ma, Y.; Zhou, Y.; Zhu, Z. The Investigation of Two-Phase Expansion Performance with Indicator Diagram in a Twin-Screw Expander. Processes 2023, 11, 1862. [Google Scholar] [CrossRef]
- Lin, S. A CFD-based study of twin-screw expander performance and inlet structure optimization. J. Phys. Conf. Ser. 2023, 2441, 012069. [Google Scholar] [CrossRef]
- Yao, S.; Zhang, Y.; Yang, H. Performance Research on a Twin Screw Expander Applied to a Power Generation System for Recovering Waste Pressure Energy of Natural Gas. J. Phys. Conf. Ser. 2018, 1072, 012016. [Google Scholar] [CrossRef]
- Eyerer, S.; Dawo, F.; Rieger, F.; Schuster, A.; Aumann, R.; Wieland, C.; Spliethoff, H. Experimental and numerical investigation of direct liquid injection into an ORC twin-screw expander. Energy 2019, 178, 867–878. [Google Scholar] [CrossRef]
- Hu, F.; Zhang, Z.; Chen, W.; He, Z.; Wang, X.; Xing, Z. Experimental Investigation on the Performance of a Twin-screw Expander Used in an ORC System. Energy Procedia 2017, 110, 210–215. [Google Scholar] [CrossRef]
- Nikolov, A.; Brümmer, A. Investigating a small oil-flooded twin-screw expander for waste-heat utilisation in organic rankine cycle systems. Energies 2017, 10, 869. [Google Scholar] [CrossRef]
- Papes, I.; Degroote, J.; Vierendeels, J. New insights in twin screw expander performance for small scale ORC systems from 3D CFD analysis. Appl. Therm. Eng. 2015, 91, 535–546. [Google Scholar] [CrossRef]
- Dumont, O.; Dickes, R.; Lemort, V. Experimental investigation of four volumetric expanders Experimental investigation of four volumetric expanders. Energy Procedia 2017, 129, 859–866. [Google Scholar] [CrossRef]
- Fatigati, F.; Di Bartolomeo, M.; Di Battista, D.; Cipollone, R. A dual-intake-port technology as a design option for a Sliding Vane Rotary Expander of small-scale ORC-based power units. Energy Convers. Manag. 2020, 209, 112646. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, C.; Wu, Y.; Lei, B.; Yan, D.; Zhi, R.; Shen, L. Numerical optimization of intake and exhaust structure and experimental verification on single-screw expander for small-scale ORC applications. Energy 2020, 199, 117478. [Google Scholar] [CrossRef]



| Male Rotor | Female Rotor | |
|---|---|---|
| Number of lobes | 5 | 6 |
| External diameter | 54 mm | 45 mm |
| Inner diameter | 34 mm | 25 mm |
| Wrap angle | 300° | 250° |
| Rotor center distance | 39.7 mm | |
| Rotor length | 83 mm | |
| Direct Measurement | Abbreviation |
|---|---|
| Air temperature upstream the twin-screw machine | ; |
| Air temperature downstream the twin-screw machine | ; |
| Oil temperature upstream of the compressor | ; |
| Oil temperature downstream of the compressor | ; |
| Pressure upstream the twin-screw machine | ; |
| Pressure downstream the twin-screw machine | ; |
| Air mass flow rate | ; |
| Oil mass flow rate | ; |
| Mechanical torque at shaft (required/delivered) | ; |
| Rotating speed of the male shaft | . |
| Parameter | Pressure Ratio | Rotating Speed rpm | Suction Pressure | Average Environment Temperature | |||
|---|---|---|---|---|---|---|---|
| Compressor | 5 | 2000 | 3000 | 4000 | 5000 | 1 barA | 24.5 °C |
| 7 | 2000 | 3000 | 4000 | 5000 | 1 barA | 24.5 °C | |
| 9 | 2000 | 3000 | 4000 | 5000 | 1 barA | 24.5 °C | |
| Expander | 5 | 2000 | 3000 | 4000 | 5000 | 5 barA | 24.5 °C |
| 7 | 2000 | 3000 | 4000 | 5000 | 7 barA | 24.5 °C | |
| 9 | 2000 | 3000 | 4000 | 5000 | 9 barA | 24.5 °C | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Francesconi, M.; Baldinelli, A.; Sani, L.; Antonelli, M. Experimental Characterization of Reversible Oil-Flooded Twin-Screw Compressor/Dry Expander for a Micro-Scale Compressed Air Energy Storage System. Energies 2025, 18, 320. https://doi.org/10.3390/en18020320
Francesconi M, Baldinelli A, Sani L, Antonelli M. Experimental Characterization of Reversible Oil-Flooded Twin-Screw Compressor/Dry Expander for a Micro-Scale Compressed Air Energy Storage System. Energies. 2025; 18(2):320. https://doi.org/10.3390/en18020320
Chicago/Turabian StyleFrancesconi, Marco, Arianna Baldinelli, Luca Sani, and Marco Antonelli. 2025. "Experimental Characterization of Reversible Oil-Flooded Twin-Screw Compressor/Dry Expander for a Micro-Scale Compressed Air Energy Storage System" Energies 18, no. 2: 320. https://doi.org/10.3390/en18020320
APA StyleFrancesconi, M., Baldinelli, A., Sani, L., & Antonelli, M. (2025). Experimental Characterization of Reversible Oil-Flooded Twin-Screw Compressor/Dry Expander for a Micro-Scale Compressed Air Energy Storage System. Energies, 18(2), 320. https://doi.org/10.3390/en18020320









